Mesoscale phase-field modeling of silver dissolution in Cast Stone with AgM granules

A mesoscale model is developed to study silver (Ag) dissolution in Cast Stone (CS) matrix containing silver mordenite (AgM) particles. The model captures microstructure-dependent thermodynamic and kinetic properties, including multispecies diffusion, redox reactions, and Ag precipitation. Simulations show that Ag-rich precipitate formation at the AgM/CS interface slows dissolution by reducing chemical potential gradients and diffusivity, while oxidation reactions enhance Ag release by increasing retention around unreacted reagents (e.g., slag, cement). Smaller AgM particles dissolve more rapidly due to shorter diffusion paths. This model offers a mechanistic framework to assess how microstructure and redox chemistry influence Ag retention and can be integrated with geochemical speciation models for multiscale performance evaluation of nuclear waste forms.

1 Introduction

The long-term disposal of radioactive waste at the U.S. Department of Energy’s Hanford Site involves the management of over 50 million gallons of chemically complex and radioactive wastes (Asmussen et al., 2020). The Hanford Waste Treatment and Immobilization Plant is designed to treat and immobilize these wastes through vitrification. However, significant volumes of solid secondary waste (SSW) will be generated from waste processing, vitrification, off-gas management, and supporting activities. One such SSW stream is a silver mordenite (AgM) sorbent used for radioiodine capture in the high-level waste vitrification facility. These I-laden AgM sorbent particulates are planned to be stabilized (microencapsulated) in cementitious waste forms for disposal in the Integrated Disposal Facility (IDF) at Hanford. In addition, AgM has been shown to be effective at the capture of iodine from liquid waste streams, although such an application is not yet planned for use. If used for liquid capture, the I-laden AgM would also require stabilization for disposal. One candidate waste form formulation that has been studied for this application is Cast Stone (CS), a ternary blend of 47 wt% ground granulated blast furnace slag (BFS), 45 wt% of fly ash (FA) and 8 wt% ordinary Portland cement (OPC, although replacement with Portland lime cement is likely in future studies). In cementitious systems such as Cast Stone (comprising BFS, FA, and OPC), the pore water (PW) typically exhibits high alkalinity (pH ∼12–13) and reducing conditions (low Eh). Under such conditions, ${Ag}^{+}$ is likely to precipitate as metallic $Ag$, ${Ag}_{2}S$ and/or ${Ag}_{2}O$, depending on redox state and sulfur availability in BFS and OPC (Westsik et al., 2013). This process can be deleterious to the waste form as reduction of the Ag would remove its ability to retain the target radionuclide, iodine.

Accurately representing the long-term performance of these cementitious matrices for the isolation of radionuclides is required in performance assessment, such as the IDF performance assessment (LEE and Site, 2018). Previous studies (Emmanuel and Berkowitz, 2007; Emmanuel et al., 2010; Liu and Jacques, 2017) have identified pore size-dependent solubility as a key factor influencing precipitation and porosity evolution during mineral dissolution in porous media, with pores smaller than 0.1 μm exhibiting markedly altered solubility behavior. Cast Stone, like other cementitious materials, exhibits a wide pore size distribution, ranging from approximately 10 μm down to sub-nanometer scales (as small as 0.5 nm) (Jennings et al., 2002). Much of this porosity is associated with the calcium silicate hydrate (C-S-H) gel phase, often referred to as gel porosity (Taylor, 1997).

Experimental studies have demonstrated that both the formation of silver-rich layers at the AgM/pore water interface and the grout composition play critical roles in governing redox behavior and iodine retention (Inagaki et al., 2008; Li et al., 2019). Microstructural characterization of CS with embedded AgM particles further revealed highly inhomogeneous distributions of silver and iodine: silver tends to segregate at particle interfaces, whereas iodine is largely absent in these regions. These findings underscore the complex interplay among dissolution, redox reaction, and transport processes in multiphase systems (Yamagata et al., 2022).

Despite the importance of these mechanisms, prior assessments of long-term performance have often relied on simplifying assumptions and limited material-specific data (Asmussen et al., 2020). Current efforts therefore focus on developing mechanistically informed models that more accurately represent SSW behavior in cementitious matrices under disposal conditions.

Dissolution modeling of waste forms, particularly glass and crystalline ceramics, has long employed kinetic models based on transition state theory, incorporating the effects of solution saturation, temperature, and Eh/pH. Geochemical modeling tools such as the Grambow-Müller model, GRAAL (Frugier et al., 2008; Fournier et al., 2018), and the immobilized low-activity waste glass corrosion model have been widely applied to simulate the long-term dissolution behavior of nuclear waste glass. Similarly, geochemical speciation models (Chen et al., 2021; Chen et al., 2023a; Chen et al., 2023b; Arnold et al., 2017) have been developed to quantify the influence of oxidation and carbonation on radionuclide release rates from cementitious waste forms. However, most existing models are point-source representations, constrained by limited data and computational capacity, and unable to capture microstructural heterogeneity or localized thermodynamic or kinetic variability—features particularly critical in systems containing embedded reactive phases such as AgM. Advances in experimental characterization and computational capabilities now enable the development of predictive, spatially resolved models.

Mesoscale approaches provide a promising pathway for capturing the effect of heterogenous microstructures and spatially varying material properties on waste form performance. Building on work at the Center for Hierarchical Waste Form Materials Energy Frontier Research Center (EFRC), mesoscale simulations can resolve coupled multi-physics phenomena—including diffusion, leaching, interfacial reactions, microstructural evolution, and electrochemical potential gradients—within representative volumes of porous materials (Li et al., 2022a; Li et al., 2022b). These models provide critical insights into the spatiotemporal evolution of species concentrations, electrochemical environments, and effective material properties, while also generating virtual datasets that support upscaling, inform higher length scale mechanistic models, and enable uncertainty quantification for performance assessments.

In this study, we present a mesoscale phase-field (PF) model of Ag dissolution from AgM granules embedded in the CS formulation [9]. By incorporating microstructure-dependent thermodynamic and kinetic properties, the model enables detailed analysis of dissolution, diffusion, redox reaction, and precipitation kinetics. This approach provides a mechanistic basis for understanding microstructural and property evolution in systems where mean-field assumptions fail, ultimately enhancing the predictive capability of macroscale models for long-term cementitious waste form performance.

2 Methods

2.1 Description of the mesoscale phase-field model

Figure 1 illustrates the complex microstructure and elemental distribution within CS samples containing embedded silver mordenite (AgM) granules. The samples presented were prepared using the CS blend (47 wt% BFS, 45 wt% FA, 8 wt% OPC) mixed with water and I-laden Ag-mordenite (silver exchanged zeolite, Sigma Aldrich) at 20 vol%. The samples were cured for 28 days at > 90% relative humidity. The fabrication and characterization of AgM granules embedded in the CS formulation follow the procedures described in Ref. Chen et al., 2023a, where the experimental details are provided. As shown in Figures 1A–D, each millimeter-scale AgM granule is composed of micrometer-scale AgM grains separated by pores. The surrounding CS—including FA, BFS, and pores—exhibits structural features with a wide range of sizes. Figure 1E presents the spatial distribution of dissolved silver, highlighting the formation of a distinct Ag-rich layer approximately 100 μm thick at the AgM/CS interface. Silver concentrations also vary markedly among FA particles, BFS inclusions, and the surrounding porous matrix. The sample displayed in Figure 1E contained iodine as well, however due to the prominent overlap between Ca (major component of the grout matrix and zeolite) and I (present at ppm amount) in the X-ray energy spectrum, I is not a reliable measurement via EDS. Yamagata et al. (2022) showed that for similar samples, I is present at the interface behind the Ag migration using time-of-flight secondary ion mass spectroscopy (TOF-SIMS), which can resolve the Ca/I signal challenge. This spatial heterogeneity suggests significant local variations in electrochemical potential and in the rates of silver dissolution and subsequent reactions across the multiphase system.

Figure 1

Figure 1. (A–D) Optical and scanning electron microscopy/backscattered electron images of microstructures in CS containing AgM granules. (A) AgM particles embedded in CS; (B) The yellow arrow points the AgM/CS interface; (C) Zoomed-in view of a AgM granule showing mesoscale pores and AgM polycrystalline grains; (D) Zoomed-in view of porous CS showing macroscale pores and FA and BFS particles; the red arrow points to a spherical FA particle while the dashed yellow arrow points to a BFS particle; and (E) elemental energy dispersive X-ray spectroscopy dot map near the interface between an AgM granule and CS shown in (D).

To capture the heterogeneous properties of the material, the mesoscale model of silver dissolution incorporates key microstructural features, including the average sizes and volume fractions of AgM, FA, and BFS particles, as well as the porosity of both CS and AgM granules. The model simplifies the microstructure and assumes the coexistence of five distinct phases: AgM, FA, BFS, the porous CS matrix, and Ag precipitates.

Within the mesoscale PF framework, two sets of field variables are used to describe the spatial and temporal evolution of chemical species and microstructure. The first set comprises concentration fields, $c_i\left(\mathit{r},t\right)$, for the diffusive species: silver ions (${Ag}^{+}$), metallic silver ($Ag$), and pore water ($PW$). The second set consists of order parameter fields, ${\eta }_p\left(\mathit{r},t\right)$, which characterize the morphological distribution of each phase $p\in \left\{AgM,FA,BFS,porousCSmatrix,Agprecipitate\right\}$. Here, $\mathit{r}=\left(x,y,z\right)$ denotes the spatial coordinate, and t represents time.

The Ag lattice is taken as the reference frame for the system. Initially, the normalized total silver concentration within Ag is defined as $c_{\text{Ag}}\left(\mathit{r},0\right)=1.0$, which corresponds to an absolute concentration of $c_0=9.71\times {10}^{4}mol/m^3$. The value C₀ corresponds to the atomic concentration of Ag in pure fcc Ag, calculated based on its lattice constant of 4.09 Å. Equilibrium concentrations for each species $i\in \left\{{Ag}^{+},Ag,PW\right\}$ within each phase $p\in \left\{AgM,FA,BFS,porousCSmatrix,Agprecipitate\right\}$ are denoted as $c_{p,i}^{eq}$. These concentrations represent the thermodynamic partitioning of each species among the phases under local equilibrium conditions. For instance, in metallic Ag particles, the equilibrium concentrations are $c_{Ag,{Ag}^{+}}^{eq}=0.0$, $c_{Ag,Ag}^{eq}=1.0,$ and $c_{Ag,PW}^{eq}=0.0$. In AgM grains inside AgM granules, the equilibrium concentrations—$c_{AgM,{Ag}^{+}}^{eq},c_{AgM,Ag}^{eq},$ and $c_{AgM,PW}^{eq}$—reflect the chemical affinity of the AgM phase for Ag⁺, Ag, and PW, respectively.

These equilibrium values are governed by the intrinsic thermodynamic properties of each phase and are sensitive to environmental conditions such as temperature, pH, Eh, and local aqueous chemistry. Pore structure, including pore size, may also influence local equilibria. Experimentally determined sorption and desorption coefficients ($k_d$) from batch studies can be used to estimate or constrain these equilibrium concentrations.

The order parameter field, ${\eta }_p\left(\mathit{r},t\right)$, takes a value of one inside the phase $p$ and 0 outside of it, and transitions smoothly between 0 and one across the interface, enabling accurate representation of interfacial regions.

In the mesoscale PF framework, microstructure evolution is governed by the minimization of the system’s total free energy. The dynamics of the non-conserved order parameters, ${\eta }_p\left(\mathit{r},t\right)$, which represent the spatial distribution of distinct phases $p$, are described by the Allen–Cahn equations:

$\frac{\partial {\eta }_p}{\partial t}=-L_p\frac{\delta F}{\delta {\eta }_p}=-L_p\left({\kappa }_p{\nabla }^2{\eta }_p+m_0\left[{\eta }_p^3-{\eta }_p+{\eta }_p{\displaystyle \sum _{q\ne p}}{\lambda }_{qp}{\eta }_q^2\right]+{\displaystyle \sum _q}\frac{\partial h_q\left(\mathit{\eta }\right)}{\partial {\eta }_p}{f}_q\left(\mathit{c}\right)\right)$

$p=AgM,FA,BFS,\text{porous\hspace{0.17em}CS\hspace{0.17em}matrix},Ag\text{\hspace{0.17em}precipitate}(1)$

where $L_p$ is the interface mobility of phase $p$ (units: $m^3/Js$), ${\kappa }_p$ is the gradient energy coefficient (units: $J/m$), $m_0$ is the energy gradient coefficients (units: $J/m^3$), ${\lambda }_{pq}$ is a dimensionless model parameter describing the interaction between phases $p$ and $q$, $f_p\left(\mathit{c}\right)$ is the chemical free energy density of phase $p$, which depends on the local concentration $\mathit{c}$ and has units of J/ ${\mathrm{m}}^3$, and $h_q\left(\mathit{\eta }\right)$ is a shape function representing the volume fraction of phase $p$ at point $\mathit{r}$.

In contrast, the evolution of conserved concentration fields, $c_i\left(\mathit{r},t\right)$, corresponding to species $i$, is governed by the Cahn–Hilliard equations (Cahn, 1961; Allen and Cahn, 1979):

$\frac{\partial c_i}{\partial t}=-\nabla ·{\mathit{J}}_i=\nabla ·\left(M_i\nabla \frac{\delta F}{\delta c_i}\right)=\nabla ·\left[M_i\nabla \left({\mu }_i\right)\right]+{\dot{R}}_{i,react}+{\dot{R}}_{i,diss}$

$i={Ag}^{+},Ag,PW(2)$

Here, $F$ denotes the total free energy of the system, and ${\mu }_i$ represents the chemical potential of species $i$, with units of J/ ${\mathrm{m}}^3$. The term ${\dot{R}}_{i,react}$ corresponds to the rate of the reduction reaction ${Ag}^{+}+PW\to Ag$, while ${\dot{R}}_{i,diss}$ denotes the rate for the oxidative dissolution reaction $Ag\to {Ag}^{+}+e^{-}$. $M_i$ denotes the diffusional mobility of species $i$.

The total free energy $F$ of the system is expressed as a functional of the order parameter field $\mathit{\eta }=\left\{{\eta }_p\left(\mathit{r},t\right)\right\}$ and concentration field $\mathit{c}=\left\{c_{\mathrm{i}}\left(\mathit{r},t\right)\right\}$, and is given by:

$F\left(\mathit{\eta },\mathit{c}\right)={\int }_V\left[f_{intf}\left(\mathit{\eta }\right)+f_{bulk}\left(\mathit{\eta },\mathit{c}\right)\right]dV(3)$

Here, $V$ denotes the volume of the simulation domain. The total free energy density consists of two contributions: the bulk chemical free energy density, $f_{bulk}\left(\mathit{\eta },\mathit{c}\right)$, and the interfacial free energy density, $f_{intf}\left(\mathit{\eta }\right)$. These components are expressed in terms of the PF variables as follows (Moelans et al., 2008; Moelans, 2011):

$f_{bulk}\left(\mathit{\eta },\mathit{c}\right)={\displaystyle \sum _p}{h}_p\left(\mathit{\eta }\right)f_p\left({\mathit{c}}_{\mathit{p}}\right)(4)$

$h_p\left(\mathit{\eta }\right)=\frac{{\eta }_p^2}{{\displaystyle {\sum }_q}{\eta }_q^2}(5)$

$f_p\left({\mathit{c}}_{\mathit{p}}\right)={\displaystyle \sum _i}\frac{1}{2}{A_{p,i}\left(c_{p,i}-c_{p,i}^{eq}\right)}^2(6)$

$f_{intf}\left(\mathit{\eta }\right)=m_0{f}_0\left(\mathit{\eta }\right)+{\displaystyle \sum _p}\frac{{\kappa }_p}{2}{\left(\nabla {\eta }_p\right)}^2(7)$

$f_0\left(\mathit{\eta }\right)={\displaystyle \sum _p}\left(\frac{{\eta }_p^4}{4}-\frac{{\eta }_p^2}{2}+\frac{1}{2}{\displaystyle \sum _{q\ne p}}{\lambda }_{pq}{\eta }_p^2{\eta }_q^2\right)+\frac{1}{4}(8)$

The function $f_0\left(\mathit{\eta }\right)$ is a multi-well potential that defines the energetic preference for distinct phase, The concentration field within phase $p$ is denoted by ${\mathit{c}}_{\mathit{p}}=\left\{c_{\mathrm{p},\mathrm{i}}\left(\mathit{r},t\right)\right\}$. In principle, any chemically consistent free energy functional, $f_p\left({\mathit{c}}_{\mathit{p}}\right)$, such as those derived from CALPHAD (van de Walle and Ceder, 2002) or other thermodynamic databases, may be used. However, for simplicity, a parabolic form of the chemical free energy as a function of species concentration ${\mathit{c}}_{\mathit{p}}$ was adopted in the present model.

The total concentration of each species at position $\mathit{r}$ is given by the sum of its contributions from all phases:

$\mathit{c}={\displaystyle \sum _p}{h}_p\left(\mathit{\eta }\right){\mathit{c}}_{\mathit{p}}(9)$

It is assumed that the chemical free energy, $f_p\left({\mathit{c}}_{\mathit{p}}\right)$, satisfies the condition of chemical equilibrium, such that the chemical potential of species $i$ is equal across any coexisting phases $p$ and $q$. That is (Kim et al., 1999):

$\frac{\partial f_p\left({\mathit{c}}_{\mathit{p}}\right)}{\partial c_{p,i}}=\frac{\partial f_q\left({\mathit{c}}_{\mathit{q}}\right)}{\partial c_{q,i}}={\mu }_i,p\ne q(10)$

All model parameters—such as the gradient energy coefficient ${\kappa }_p$, energy density coefficient $m_0$, interaction parameter ${\lambda }_{pq}$, free energy curvature $A_{p,i}$, and equilibrium concentration $c_{p,i}^{eq}$—can be determined based on thermodynamic properties. These include the common tangent construction, equilibrium compositions, interfacial energy, interface thickness between distinct phases, phase transition energy barriers, and the thermodynamic driving forces for phase nucleation.

2.2 Phase-dependent thermodynamic and kinetic properties

The thermodynamic and kinetic properties of species $i$ in CS are inherently inhomogeneous due to the complex and heterogeneous microstructure. For example, the mobility of PW within the porous CS matrix and within mesopores inside AgM granules can be significantly higher than in dense phases such as FA, BSF, and AgM grains. In general, the mobility of each species can vary substantially between different phases. Additionally, the chemical potential of a species at phase interfaces may differ from that in the bulk due to interface-associated defects, which can alter local formation energies. Redox reaction and dissolution rates may also exhibit spatial dependence linked to phase distribution and microstructural features.

To capture these inhomogeneities, two shape functions are introduced based on the order parameters $\mathit{\eta }$:

• $h_p\left(\mathit{\eta }\right)$, defined in Equation 5, characterizes the local volume fraction of phase $p$, and

• $g_{pq}\left(\mathit{\eta }\right)=2\left(1-{\eta }_p^2-{\eta }_q^2\right)$, which identifies the interface region between phases $p$ and $q$. This function is zero within the bulk of phases $p$ and $q$, and transitions smoothly across their interface.

Using these shape functions and the mixture rule (Kim, 2007), the spatially varying thermodynamic and kinetic properties in the multiphase system can be effectively described.

$M_{\mathrm{i}}={\displaystyle \sum _p}{M}_{p,i}{h}_p\left(\mathit{\eta }\right)+{\displaystyle \sum _{p\ne q}}\Delta M_{pq,i}{g}_{pg}\left(\mathit{\eta }\right)(11)$

$D_{\mathrm{i}}={\displaystyle \sum _p}{D}_{p,i}{h}_p\left(\mathit{\eta }\right)+{\displaystyle \sum _{p\ne q}}\Delta D_{pq,i}{g}_{pg}\left(\mathit{\eta }\right)+\Delta D_{p,i}{h}_p\left(\mathit{\eta }\right)(12)$

${\mu }_i={\displaystyle \sum _p}{\mu }_{p,i}{h}_p\left(\mathit{\eta }\right)+{\displaystyle \sum _{p\ne q}}\Delta {\mu }_{pq,i}{g}_{pq}\left(\mathit{\eta }\right)+{\displaystyle \sum _p}{\Delta \mu }_{p,i}h\left(\mathit{\eta }\right)(13)$

${\dot{R}}_{i,react}={\displaystyle \sum _p}{r}_{p,{Ag}^{+}}\left(c_{{Ag}^{+}}-c_{{Ag}^{+}}^{crit}\right)\left(c_{PW}-c_{PW}^{crit}\right)h_p\left(\mathit{\eta }\right)$

$+{\displaystyle \sum _{p\ne q}}{\Delta r}_{pq,{Ag}^{+}}\left(c_{{Ag}^{+}}-c_{{Ag}^{+}}^{crit}\right)\left(c_{PW}-c_{PW}^{crit}\right)g_{pq}\left(\mathit{\eta }\right)(14)$

${\dot{R}}_{i,diss}={\displaystyle \sum _p}{r}_{p,Ag}\left(c_{Ag}-c_{Ag}^{crit}\right)h_p\left(\mathit{\eta }\right)+{\displaystyle \sum _{p\ne q}}\Delta r_{pq,Ag}\left(c_{Ag}-c_{Ag}^{crit}\right)g_{pq}\left(\mathit{\eta }\right)(15)$

Here, ${\psi }_{p,i}$ represents the intrinsic property of species $i$ within phase $p$, $\Delta {\psi }_{pq,i}$ represents the interfacial contribution between phases $p$ and $q$, and $\Delta {\psi }_{p,i}$ accounts for the modification within phase $p$ due to the retention of species $i$ at absorption sites. The symbol $\psi$ refers generally to the property defined in Equations 11–15. $c_i^{crit}$ represents the critical concentration of species $i$ for initiating reduction or oxidation reactions.

In conventional geochemical modeling (Fang et al., 2003; Chen et al., 2021), chemical reactions are often assumed to reach equilibrium instantaneously–implying an effectively infinite reaction rate. However, in the present model, finite reaction kinetics are explicitly considered. In Equations 14, 15, $r_{p,{Ag}^{+}}$ is the reaction rate coefficient for the reduction reaction ${Ag}^{+}+PW\to Ag$ within phase $p$, while $r_{p,Ag}$ is the coefficient for the oxidative dissolution reaction $Ag\to {Ag}^{+}+e^{-}$ in the same phase. The terms ${\Delta r}_{pq,{Ag}^{+}}$ and $\Delta r_{pq,Ag}$ represent the interfacial enhancements or modifications of these reaction rates at the boundary between phases $p$ and $q$, capturing inhomogeneous kinetics due to interfacial effects.

These reaction rates depend not only on the local concentration fields and microstructure but can also be modified by additional local environmental conditions, such as pH and Eh, to better reflect reactive transport behavior in heterogeneous systems. It is important to note that the reaction rate coefficients appear with opposite signs in the evolution Equation 2 of $Ag$ and ${Ag}^{+}$, ensuring mass conservation. For instance, the reduction reaction ${Ag}^{+}+PW\to Ag$ increases the concentration of Ag while decreasing that of ${Ag}^{+}$.

2.3 Nucleation scheme

Ag precipitates are represented in the PF model using an order parameter, ${\eta }_{Ag}\left(\mathit{r},t\right),$ and a concentration field, $c_{Ag,i}\left(\mathit{r},t\right)$. Initially, the system is assumed to contain no Ag precipitates, and the order parameter is set to zero throughout the domain, i.e., ${\eta }_{Ag}\left(\mathit{r},0\right)=0$. Precipitation may occur via homogeneous or heterogeneous nucleation mechanisms. In the case of homogeneous nucleation, thermal fluctuations lead to the spontaneous formation of Ag clusters of varying sizes. When a cluster exceeds a critical size, it becomes thermodynamically stable and begins to grow. To mimic this process, random fluctuations are introduced in both the order parameter, ${\eta }_{Ag}\left(\mathit{r},t\right)$, and the local concentration field, $c_{Ag,i}\left(\mathit{r},t\right)$, thereby enabling the stochastic formation of nuclei. For heterogeneous nucleation, spatial variations in chemical potential drive the segregation of Ag species to microstructural features such as interfaces or defects, where nucleation is energetically favored. Experimental observations showing Ag precipitates predominantly located at the AgM/CS interface support the assumption of heterogeneous nucleation in this system.

In the simulations, a simplified heterogeneous nucleation scheme is implemented using two model parameters: the critical concentration $c_{Ag}^{*}$, and the nucleation search frequency $N_{Nuclt}^{*}$. The procedure consists of the following steps:

1. At every $N_{Nuclt}^{*}$ time step, identify candidate nucleation sites where the local Ag concentration satisfies ${c_{Ag}>c}_{Ag}^{*}$ and ${\eta }_{Ag}\left(\mathit{r},t\right)=0$;

2. At these sites, initialize nuclei by setting ${\eta }_{Ag}\left(\mathit{r},t\right)=1$;

3. Repeat steps (1) and (2) periodically.

This scheme allows for the continuous introduction of Ag precipitate nuclei during the simulation. The fate of each nucleus—whether it grows or dissolves—is governed by the local thermodynamic driving forces for phase transformation.

2.4 Simulation input parameters

In solving the evolution equations (Equations 1, 2), all the thermodynamic and kinetic properties are normalized using characteristic quantities: the characteristic energy density, $e_0$, characteristic length, $l_0$, and characteristic time, $t_0$. The normalization procedure is as follows:

$t^{*}=\frac{t}{t_0},M_i^{*}=\frac{M_i}{M_c},{\nabla }^{*}=l_0\nabla =l_0\left(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right),{\kappa }_p^{*}=\frac{{\kappa }_p}{e_0{l}_0^2},L_p^{*}=\frac{L_p}{L_0},A_{p,i}^{*}=\frac{A_{p,i}}{e_0},{\Delta \mu }_{pq,i}^{*}=\frac{{\Delta \mu }_{pq,i}}{e_0},{\Delta \mu }_{p,i}^{*}=\frac{{\Delta \mu }_{p,i}}{e_0},t_0=\frac{l_0^2}{M_c{e}_0},M_c=\frac{V_{mol}{D}_0}{R{T}_0},L_0=M_c\backslash \backslash /l_0^2=\frac{1}{e_0{t}_0}(16)$

Here, $V_{mol}$ represents the molar volume and $D_0$ is the maximum diffusivity of diffusive species ($Ag,{Ag}^{+}$) in CS and CS containing AgM granules; the characteristic energy density, $e_0$, is usually set to be $R{T}_0$, where $R$ is the gas constant and $T_0$ is the reference state temperature. In general, the mobility of a species depends on both temperature and material structure, and thus the following expression is assumed for its dependence:

$M_{p,i}=\frac{D_{p,i}{V}_{p,i}}{RT},D_{p,i}=D_{p,i}^0\mathit{exp}\left(-\frac{\Delta Q_{p,i}}{RT}\right)(17)$

Here, $D_{p,i}^0$ is the diffusion coefficient, $V_{p,i}$ is the molar volume of species $i$ in phase $p$; and ${\Delta Q}_{p,i}$ represents the activation energy of the species in phase $p$, respectively. $T$ is the temperature. Similarly, the interface mobility $L_p$ is temperature-dependent and expressed as:

$L_p=L_p^0\mathit{exp}\left(-\frac{\Delta Q_p}{RT}\right)(18)$

The free energy coefficients ${\kappa }_p$, $m_0$ and ${\lambda }_{pq}$ can be estimated from the interface energy σ and interface thickness $l_{thickness}$, using the following relationships:

$\sigma =\frac{\sqrt{2}}{3}\sqrt{m_0{\kappa }_p},l_{thickness}=\sqrt{\frac{8{\kappa }_p}{m_0}}(19)$

Assuming the dimensionless model parameter ${\lambda }_{pq}$ = 1.5 (Moelans et al., 2008). The normalized coefficients are then given by:

${\kappa }_p^{*}=\frac{3\sigma l_{thickness}}{4e_0{l}_0^2},m_0^{*}=\frac{6\sigma }{l_{thickness}{e}_0}(20)$

The chemical free energy coefficient $A_{p,i}$ and equilibrium concentration $c_{p,i}^{eq}$ can be derived from experimental measurements of absorption $k_{d\left(adsorb\right)}$ and desorption $k_{d\left(desorb\right)}$ coefficients in batch tests using pure phases (AgM, FA, BFS, CS) in contact with PW. Under fixed conditions (temperature, pH, Eh, chemistry of PW), these coefficients are related through:

$k_{d\left(adsorb\right)}=c_{p,i}^{eq}/c_{PW,i}^{eq},\text{and}/\text{or\hspace{0.17em}}{k}_{d\left(desorb\right)}=c_{p,i}^{eq}/c_{PW,i}^{eq}(21)$

These data can be used to construct the chemical free energy functional $f_p\left({\mathit{c}}_{\mathit{p}}\right)$. The coefficient $A_{p,i}$ is associated with the second derivative of $f_p\left({\mathit{c}}_{\mathit{p}}\right)$ with respect to concentration, evaluated at equilibrium:

$A_{p,i}={\left.\frac{{\partial }^2{f}_p}{{\partial }^2{c}_{p,i}}\right|}_{c_{p,i}^{eq}}(22)$

The chemical potential increment ${\mu }_{pq,i}$ of species $i$ at the interface between phases $p$ and $q$ is linked to the formation energy difference between the interface and the bulk reference phase.

The diffusivity $D_{p,i}$ of species $i$ in phase $p$ can be computed using density functional theory (DFT) and molecular dynamics (MD) simulations. Alternatively, leaching experiments can provide effective diffusivity measurements. For example, the measured diffusivity of iodine in CS and CS containing AgM granules ranges from $5.8\times {10}^{-13}\sim 5.0\times {10}^{-17}{m}^2/s$ (Flach et al., 2016; Cantrell et al., 2016).

The reaction rate coefficient $r_{p,i}$ can be determined from the activation energy barrier of the reaction. Overall, model parameters can be assessed by the thermodynamic and kinetics properties of the system components.

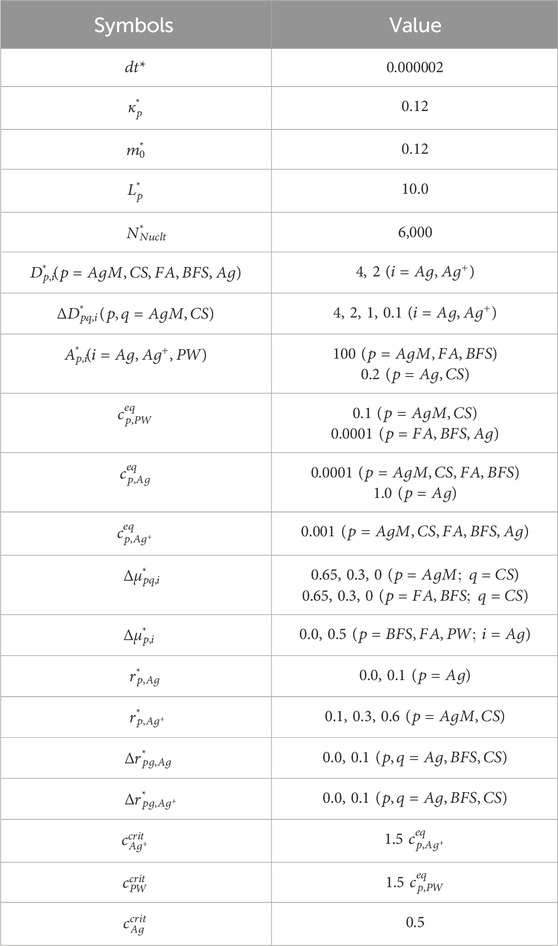
In this work, model parameters were estimated using available data and reasonable assumptions. The fundamental thermodynamic and kinetic parameters used in Equation 16 are listed in Table 1 while Table 2 summarizes the normalized model parameters for parametric studies.

Table 1

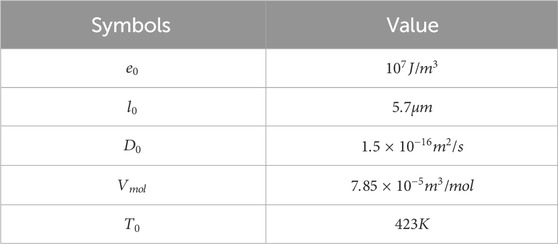
Table 1. Fundamental thermodynamic and kinetic parameters used in Equation 16.

Table 2

Table 2. Normalized model parameters for parametric studies.

2.5 Simulation setup and boundary conditions

The developed mesoscale model for Ag dissolution is formulated in three dimensions; however, to reduce computational cost, simulations are conducted in a quasi-three-dimensional domain. Specifically, the simulation cell is thin along the y-direction and extended in the x- and z-directions. The physical dimensions of the simulation domain are $256l_0\times 4l_0\times 256l_0$, where $l_0$ is the characteristic length scale used for normalization in the model. Periodic boundary conditions are applied in all three spatial directions (x, y, and z).

To generate the initial microstructure, a multiphase phase-field grain growth model is employed, based on specified microstructural features such as the volume fractions of different phases and average particle sizes (Moelans, 2011). In the multiphase phase-field grain growth model, order parameters that vary smoothly from 0 to one represent different phases (AgM grains, FA, BFS, and CS). The volume fraction of each phase is calculated by integrating the regions where the corresponding order parameter values exceeds 0.5. For AgM particles, the mesopore volume fraction is included by accounting for regions where the AgM order parameter is below 0.8, representing the space between AgM grains. Figure 2 shows a representative simulation domain that includes a large AgM particle at the center, along with smaller FA and BFS particles embedded in a porous CS matrix. The volume fractions of AgM, FA, BFS and porous CS matrix are approximately 30%, 12.6%, 23.8%, and 33.6%, respectively. The mesopore volume within AgM accounts for 16% of the total volume of the AgM particle.

Figure 2

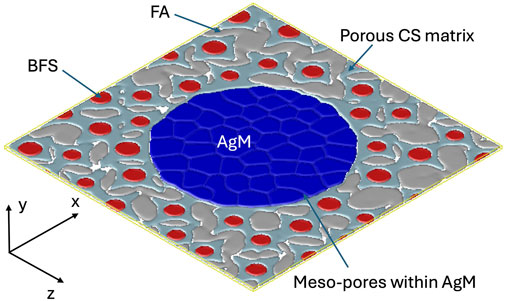
Figure 2. Schematic of the simulation cell, illustrating a AgM particle, FA inclusions, BFS particles, a porous CS matrix and meso-pores within the AgM particle. The AgM particle is represented as a cluster of smaller AgM grains. The volume fractions of AgM, FA, and BFS in the CS matrix are approximately 30%, 12.6%, and 23.8%, respectively. The mesopore volume within AgM is about 16% of the total volume of the AgM particle.

Ag dissolution simulations are conducted under batch experiment conditions. It is assumed that the PW within the porous CS matrix rapidly reaches a saturated concentration, denoted as $c_{CS,PW}^0$. This assumption is valid if the CS matrix exhibits a high pore volume fraction and well-connected porosity. However, if the material contains closed pores, the model must be extended to treat these closed pores as a distinct phase with unique pore properties. The mesopores within the AgM particle are represented as a phase in which diffusive species exhibit high diffusivity and distinct chemical potentials.

The large AgM particle is modeled as a polycrystalline structure composed of numerous smaller AgM grains [1], with meso-pores—submicron-sized voids—existing between them. During Ag dissolution, PW is assumed to infiltrate these meso-pores and microchannels within the AgM grains, where it reacts with AgM to release dissolved Ag. The dissolved Ag then diffuses, segregates, and forms Ag precipitates. Additionally, Ag may undergo oxidation depending on the local chemical environment. The detailed dissolution mechanisms have been discussed in prior literature [7]. Accordingly, a constant concentration $c_{CS,PW}^0$ is imposed at the periodic boundaries to simulate PW diffusion into the AgM granule.

Table 3 summarizes the initial and equilibrium concentrations used in the simulations, which are employed to validate the model’s predictive capabilities. Nonetheless, more accurate experimental data are needed to enable quantitatively predictive simulations of leaching behavior, especially for defining initial and boundary conditions.

Table 3

Table 3. Initial concentrations.

2.6 Numerical method

In the simulations, the normalized equations (Equations 1, 2) are solved using the Fastest Fourier Transform in the West (FFTW) library, combined with a semi-explicit numerical scheme (Chen and Shen, 1998). To model Ag precipitation, a nucleation algorithm is employed in which nuclei are introduced once the local Ag concentration exceeds a critical threshold. By solving these equations, the temporal and spatial evolution of the concentration fields, $c_i\left(\mathit{r},t\right)$, and order parameter fields, ${\eta }_j\left(\mathit{r},t\right)$, are captured, enabling the simulation of Ag segregation and precipitation processes.

3 Results

Using the model, we conducted a comprehensive parametric study to validate its predictive capabilities. To characterize the kinetics of Ag dissolution, we defined two key quantities: $w_{Ag,ppt}\left(t\right)$ and $w_{Ag,CS}\left(t\right)$. The term $w_{Ag,ppt}\left(t\right)$ represents the percentage of Ag contained in the Ag-rich precipitates at time t, while $w_{Ag,CS}\left(t\right)$ denotes the percentage of $Agand{Ag}^{+}$ remaining in the CS matrix. These metrics are defined as follows:

$w_{Ag,ppt}\left(t\right)={\int }_{V_{Ag}}{c}_{Ag,Ag}\left(t\right)dV/{\displaystyle \sum _p}{\int }_{V_p}\left[c_{p,Ag}\left(0\right)+c_{p,{Ag}^{+}}\left(0\right)\right]dV(23)$

$w_{Ag,CS}\left(t\right)=\{{\displaystyle \sum _p}\left.{\int }_{V_{CS}}\left[c_{p,Ag}\left(t\right)+c_{p,{Ag}^{+}}\left(t\right)\right]dV\right\}/{\displaystyle \sum _p}{\int }_{V_p}\left[c_{p,Ag}\left(0\right)+c_{p,{Ag}^{+}}\left(0\right)\right]dV(24)$

In equations (Equations 23, 24), the denominator is the total amount of $Ag$ and ${Ag}^{+}$ present in the simulation domain at initial time $t=0$. The numerators correspond to the amount of $Ag$ in the precipitates and in the CS at time $t$, respectively. In the following sections, we present selected simulation results and key conclusions.

3.1 Influence of Ag chemical potential at interfaces on dissolution behavior

The chemical potential of $Ag$ at the interfaces among AgM, FA, BFS, and the porous CS matrix may differ from its chemical potential within each individual phase. Initially, Ag is confined to the AgM particles. Overtime, $Ag$ diffuses and either dissolves into the surrounding CS matrix or precipitates as discrete particles. Figure 3a shows the evolution of the percentage of Ag that precipitates, denoted as $w_{Ag,ppt}\left(t\right)$. Figure 3b illustrates the evolution of the percentage of Ag that dissolves into the CS matrix, denoted as $w_{Ag,CS}\left(t\right)$. In the Figure, $\Delta {\mu }_{pq,Ag}^{*}$ represents the chemical potential increment of $Ag$ at the interface between phase $p=AgM$ and $q=CS$. Similarly, $\Delta {\mu }_{p_1{q}_1,Ag}^{*}$ denotes the chemical potential increment of $Ag$ at the interface between phase $p_1=CS$ and $q_1=FA$ or $BFS$.

Figure 3

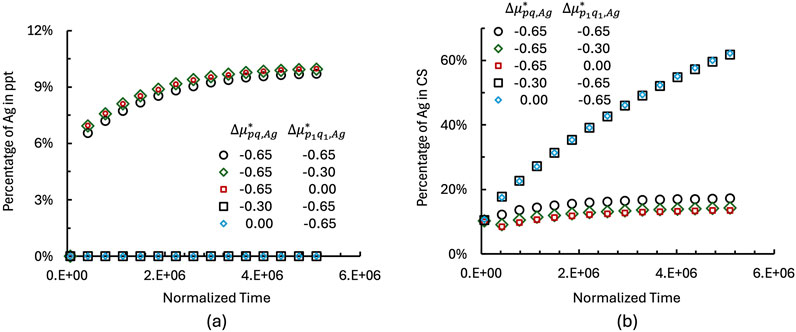
Figure 3. Temporal evolution of $Ag$ distribution in the system. (a) Percentage of Ag contained in precipitates, $w_{Ag,ppt}\left(t\right)$. (b) Percentage of Ag dissolved in the CS matrix, $w_{Ag,CS}\left(t\right)$. The simulation was performed using the following model parameters: $r_{p,{Ag}^{+}}^{*}=0.2$, $\Delta r_{AgCS,Ag}^{*}=-0.1$, $\Delta D_{p_1{q}_1,i}^{*}=10$, $d_{Ag,i}^0=0.0$, $D_{{Ag}^{+}}^{*}=2.0$, and $D_{Ag}^{*}=4.0$.

As shown in Figure 3a, no Ag precipitates form at the AgM/CS interface when $\Delta {\mu }_{pq,Ag}^{*}\ge -0.3$. Figure 3b confirms that under these conditions, all Ag dissolves into the CS matrix. However, the sharp increase in the percentage of precipitated Ag when $\Delta {\mu }_{pq,Ag}^{*}=0.65$ (with varying $\Delta {\mu }_{p_1{q}_1,Ag}^{*}$), as seen in Figure 3a, indicates the onset of Ag precipitate nucleation. In this case, significantly less Ag dissolves into the matrix compared to when $\Delta {\mu }_{pq,Ag}^{*}\ge -0.3$.

In the simulations, it is assumed that the diffusivity of Ag and Ag⁺ in the Ag-rich layer or in the Ag precipitates decreases with increasing Ag concentration, as described by:

$\Delta D_{Ag,i}^{*}={-d_{Ag,i}^{0}D}_{Ag,i}^{*}\frac{1}{\left.\exp \left(-10.0\left(c_{Ag}-0.3\right)\right)+1\right)}(25)$

Here, $d_{Ag,i}^0$ is a positive coefficient. This relation ensures that $\Delta D_{Ag,i}^{*}=0$ when $c_{Ag}=0.0$, and $\Delta D_{Ag,i}^{*}={-d_{Ag,i}^{0}D}_{Ag,i}^{*}$, when $c_{Ag}=1.0$.

The sum of Ag in Ag precipitates and in CS represents the total dissolved Ag. For example, at a normalized time of 5,820,000, the amount of dissolved Ag reaches approximately 63% for the case where $\Delta {\mu }_{AgM/CS,Ag}^{*}\ge -0.3$, compared to only about 25% when $\Delta {\mu }_{AgM/CS,Ag}^{*}=-0.65$. This indicates that the dissolution kinetics are significantly slower for $\Delta {\mu }_{AgM/CS,Ag}^{*}=-0.65$ than for less negative chemical potential differences. The reduced kinetics are attributed to Ag precipitate formation at the AgM/CS interface, which reduces the chemical potential gradient within the AgM particle, hindering Ag diffusion.

Figures 4a,c present the distribution of the Ag concentration at a normalized time of 5,820,000 under different interfacial chemical potential conditions. In Figure 4a, a high Ag concentration is observed at the interface between AgM and CS when the interfacial chemical potential difference is set as $\Delta {\mu }_{pq,Ag}^{*}=-0.65$ and $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=0.0$. Conversely, Figure 4c shows that Ag preferentially segregates at the interface among FA, BFS and CS—rather than at AgM/CS interface—when $\Delta {\mu }_{pq,Ag}^{*}=0.0$ and $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=-0.65$. These results indicate that a lower chemical potential at the AgM/CS interface ($\Delta {\mu }_{pq,Ag}^{*}=-0.65$) promotes Ag precipitation at that interface. In contrast, a lower chemical potential at the FA/BFS/CS matrix interface ($\Delta {\mu }_{p_1{q}_1,Ag}^{*}=-0.65$) leads to Ag segregation at that location.

Figure 4

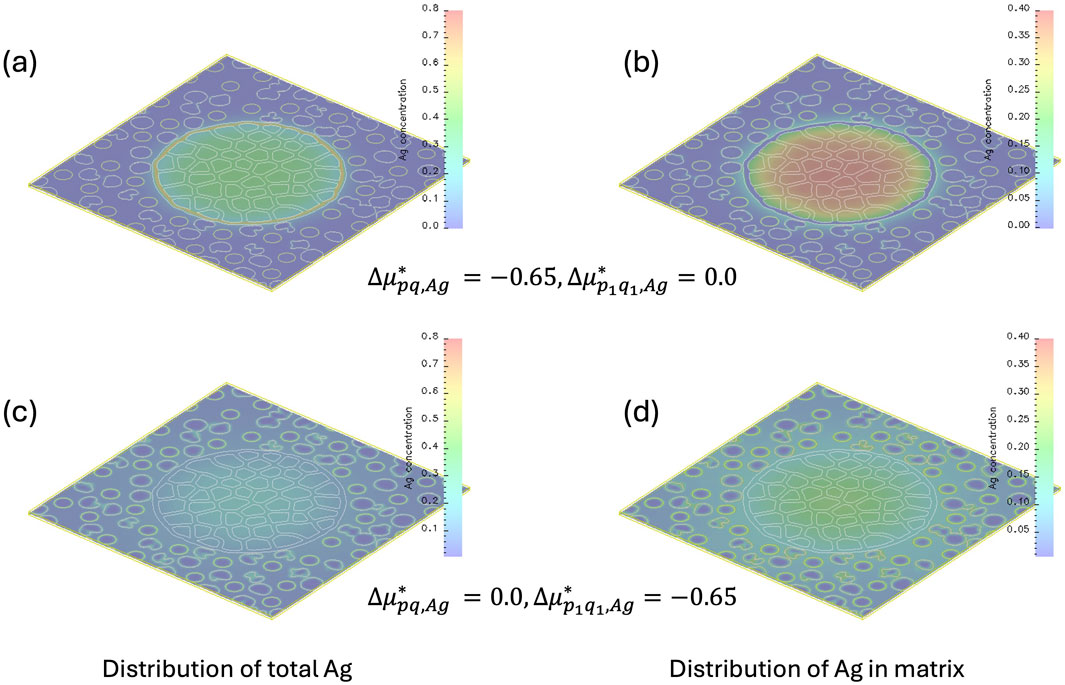
Figure 4. Distribution of Ag concentration within the Ag precipitate and CS matrix. Panels (a,b) correspond to the case where $\Delta {\mu }_{pq,Ag}^{*}=-0.65$ and $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=0.0$, while panels (c,d) correspond to $\Delta {\mu }_{pq,Ag}^{*}=0.0$ and $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=-0.65$. Panels (a,c) show the total Ag concentration, whereas panels (b,d) exclude Ag precipitates by assigning zero concentration inside the precipitates to highlight the diffusion profile in the CS matrix.

To better visualize the distribution of Ag in the CS matrix, excluding the Ag precipitates, Figures 4b,d show the Ag concentration with values set to zero inside the Ag-rich precipitates. In Figure 4b, a diffusion field is visible within the CS matrix, but no Ag segregation is present at the FA/BFS/CS matrix interface due to $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=0.0$. By contrast, Figure 4d reveals more extensive Ag diffusion in the matrix, resulting from the increased Ag availability under $\Delta {\mu }_{pq,Ag}^{*}=0.0$, along with clear segregation at the FA/BFS/CS matrix interface caused by $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=-0.65$.

These results demonstrate that Ag distribution is highly sensitive to interfacial chemical potential conditions, as has been seen in experimental testing of AgM-CS sample compared with non-reducing formulation (Yamagata et al., 2022). The inhomogeneous chemical potential of Ag at the interfaces among AgM, BFS, FA, and CS leads to heterogeneous segregation and precipitation of Ag. This highlights the model’s ability to effectively capture the influence of interfacial chemical potential gradients on both the thermodynamic driving forces and kinetic processes governing Ag dissolution, segregation, and precipitation.

3.2 Influence of redox reaction rates on Ag dissolution

The redox reactions ${Ag}^{+}+PW\to Ag$ and $Ag\to {Ag}^{+}+e^{-}$ are influenced by the local concentrations of ${Ag}^{+}$ and PW, their associated energy barriers, as well as environmental conditions such as pH Eh. Figure 5 illustrates the temporal evolution of the fraction of total Ag forming precipitates (Ag ppt) and the fraction that dissolves into the CS matrix under different reducing reaction rates, $r_{p,{Ag}^{+}}^{*}$, with the oxidation reaction rate fixed at $r_{p,Ag}^{*}=0.0$.

Figure 5

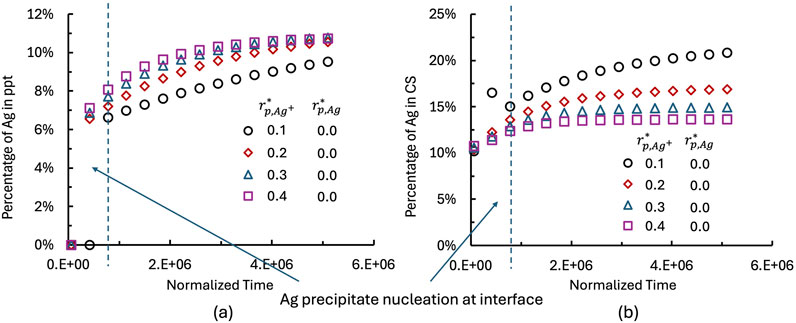
Figure 5. Effect of reaction rates on the temporal evolution of $Ag$ content in (a) Ag precipitate (ppt) and (b) the CS matrix. The curves represent different values of the forward and reverse reaction rates $r_{p,{Ag}^{+}}^{*}$ and $r_{p,Ag}^{*}$, illustrating how reaction kinetics influence Ag partitioning between precipitates and the surrounding matrix over time. Dashed lines indicate the onset of Ag ppt nucleation. Model parameters are $\Delta D_{p_1{q}_1,i}^{*}=10$, $d_{Ag,i}^0=0.0$, $D_{{Ag}^{+}}^{*}=2.0$, $D_{Ag}^{*}=4.0$, $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=-0.65$, and $\Delta {\mu }_{pq,Ag}^{*}=-0.65$.

When the reduction reaction rate is set to $r_{p,{Ag}^{+}}^{*}=0.1$ and oxidation is suppressed ($r_{p,Ag}^{*}=0.0$), a greater amount of ${Ag}^{+}$ dissolves into the CS matrix, delaying the nucleation of Ag precipitates at the AgM/CS interface. The dashed lines in Figures 5a,b indicate the onset of Ag precipitate nucleation. The high Ag content in the CS matrix indicates a supersaturated state prior to nucleation. The subsequent nucleation of Ag precipitates depletes Ag in the CS matrix, resulting in a sharp decrease in its Ag content. Increasing the reduction reaction rate, $r_{p,{Ag}^{+}}^{*}$, from 0.1 to 0.4 accelerates the nucleation and growth of Ag ppt, while simultaneously decreasing the amount of Ag dissolving into the CS matrix, as shown in Figure 5b.

In a purely diffusion-controlled process, Ag dissolution driven by a concentration gradient would lead to a dissolved Ag fraction that scales linearly with $\sqrt{t^{*}}$ (Thomas, 1987; Crank, 1979). This relationship can be used to estimate the effective diffusivity of Ag. However, in complex waste form systems, heterogeneous chemical potentials lead to Ag segregation and precipitation, causing deviations from this ideal linear behavior. As a result, the effective diffusivity and dissolution kinetics of Ag are governed by evolving microstructural features associated with segregation and precipitation.

Figure 6 presents the temporal evolution of $Ag$ and ${Ag}^{+}$ concentrations for two cases: (a) $r_{p,{Ag}^{+}}^{*}=0.4$, $r_{p,Ag}^{*}=0.2$, and (b) $r_{p,{Ag}^{+}}^{*}=0.05$, $r_{p,Ag}^{*}=0.2$. Consistent color bars are used to represent total $Ag$ and ${Ag}^{+}$ concentrations. For a given set of thermodynamic and kinetic properties, PW boundary conditions, and AgM microstructure, the Ag⁺ concentration is primarily governed by the reduction rate $r_{p,{Ag}^{+}}^{*}$. A larger reduction rate accelerates the conversion of Ag⁺ to Ag, increasing Ag accumulation within the AgM particle. This accumulation enhances the chemical potential gradient, thereby promoting Ag diffusion and dissolution kinetics.

Figure 6

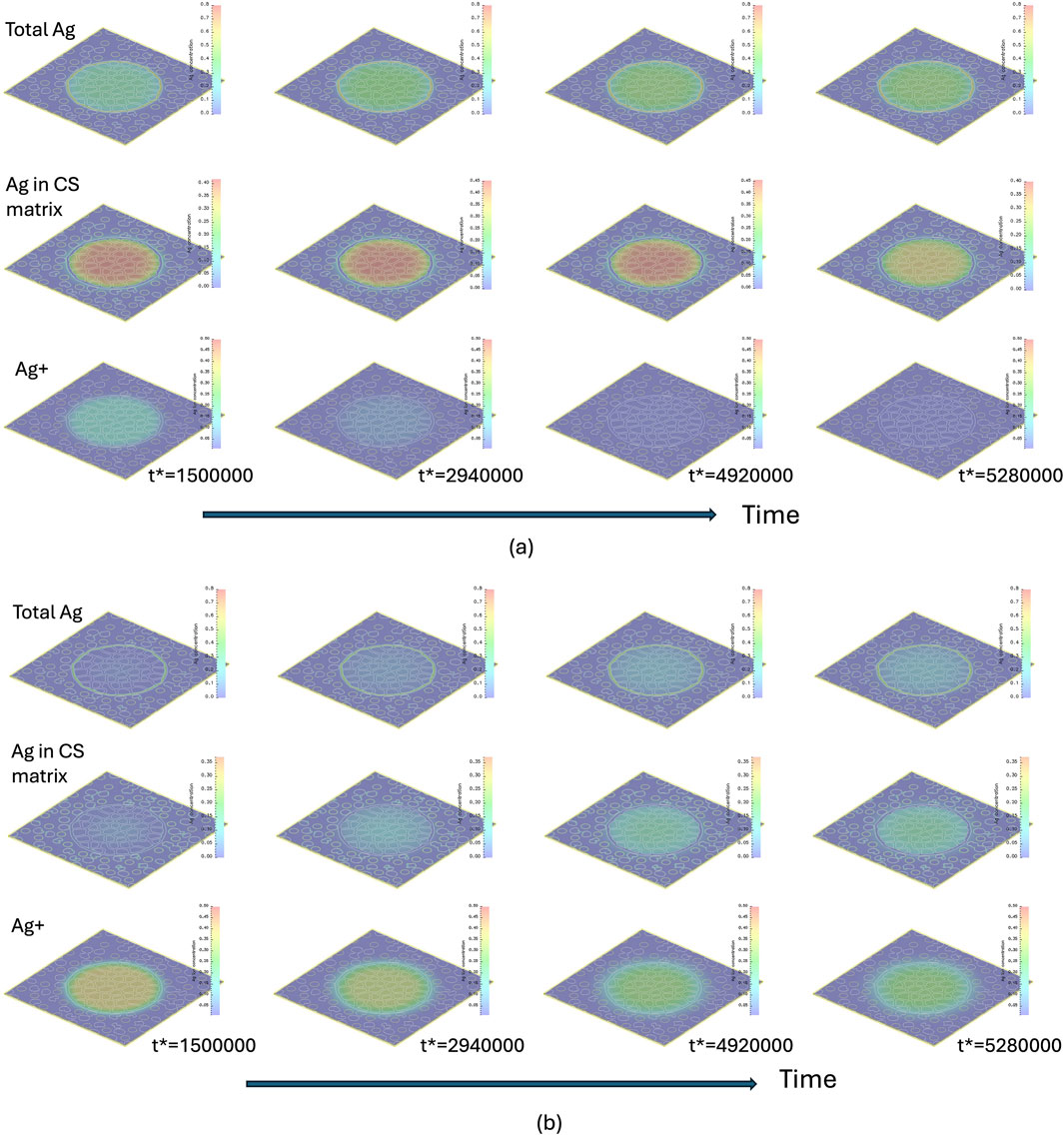
Figure 6. Temporal evolution of $Ag$ and ${Ag}^{+}$ concentrations under different interfacial reaction rate conditions. (a) $r_{p,{Ag}^{+}}^{*}=0.4$ and $r_{p,Ag}^{*}=0.2$; (b) $r_{p,{Ag}^{+}}^{*}=0.05$ and $r_{p,Ag}^{*}=0.2$. The plots illustrate how variations in reaction rates affect the distribution and transformation dynamics of Ag species over time. Identical color bars are used for $Ag$ and ${Ag}^{+}$ to enable direct visual comparison.

The concentration profiles in Figure 6, along with the increased precipitation rate of Ag at early times in Figure 5a for $r_{p,{Ag}^{+}}^{*}=0.4$ demonstrate the model’s ability to capture the interplay between coupled multi-physics processes. At later stages, the decline in Ag precipitation kinetics is attributed to the rising chemical potential barrier caused by the growth of an Ag-rich layer at the AgM/CS interface.

3.3 Effect of AgM particle size on Ag dissolution

The size of the AgM particle influences the diffusion length and kinetics of Ag dissolution. Figure 7 illustrates the effect of AgM particle size on Ag dissolution behavior. The particle radius $R_0$ is normalized by the characteristic length as ${R^{*}=R}_0/\left(l_0\right)$. The simulation results reveal two key trends: (1) smaller AgM particles delay the nucleation of Ag precipitates, and (2) decreasing the particle size leads to greater segregation of Ag both within the precipitate and in the CS matrix. These findings suggest that reducing the AgM particle size enhances the overall dissolution kinetics of Ag by shortening diffusion pathways and increasing the effective interface area for mass transport.

Figure 7

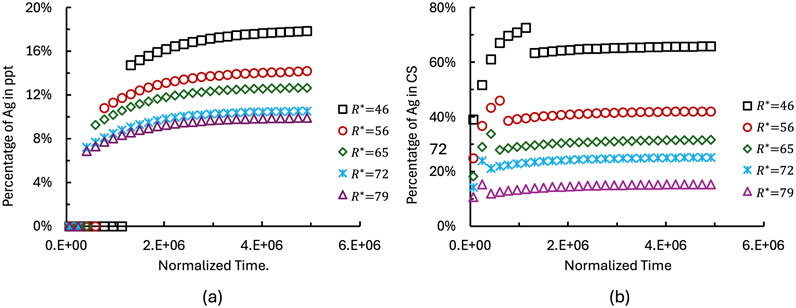
Figure 7. Effect of AgM particle size on the temporal evolution of $Ag$ content (a) in Ag precipitate (ppt) and (b) the CS matrix. Model parameters are $r_{p,{Ag}^{+}}^{*}=0.3$, $\Delta r_{AgCS,Ag}^{*}=-0.1$, $\Delta D_{p_1{q}_1,i}^{*}=10$, $d_{Ag,i}^0=0.0$, $D_{{Ag}^{+}}^{*}=2.0$, $D_{Ag}^{*}=4.0$, $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=-0.65$, and $\Delta {\mu }_{pq,Ag}^{*}=-0.65$.

3.4 Effect of heterogeneous diffusivity on Ag dissolution behavior

The diffusivity of $Ag$, ${Ag}^{+}$ and PW within pores and Ag-rich layers can differ significantly from those in phase $p$ ($AgM,FA,\text{and\hspace{0.17em}}BFS$). Figure 8 illustrates the influence of the normalized diffusivity $d_{Ag,i}^0$ in Ag-rich layer (where $i=Ag,{Ag}^{+},PW$), and the increment of diffusivity $\Delta D_{p_1{q}_1,i}^{*}$ at meso- and macro-pores (where $i={Ag}^{+}\text{and\hspace{0.17em}}PW,p_1\ne q_1=AgM,FA,BFS$) on Ag dissolution behavior.

Figure 8

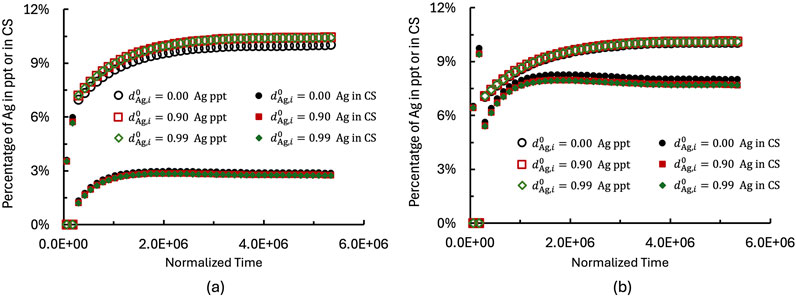
Figure 8. Effect of species diffusivity ($d_{Ag,i}^0$) in the Ag-rich layer and ($\Delta D_{p_1{q}_1,i}^{*}$) in meso- and macro-pores on the temporal evolution of $Ag$ content in the Ag-rich layer and CS matrix. (a) the diffusivity in meso- and macro-pores is equal to that in the bulk phases ($\Delta D_{p_1{q}_1,i}^{*}=0$) and (b) the diffusivity in meso- and macro-pores is ten times higher than that in the bulk phases ($\Delta D_{p_1{q}_1,i}^{*}=10$). Model parameters are $r_{p,{Ag}^{+}}^{*}=0.3$, $\Delta r_{AgCS,Ag}^{*}=-0.1$, $D_{{Ag}^{+}}^{*}=2.0$, $D_{Ag}^{*}=4.0$, $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=0.0$, and $\Delta {\mu }_{pq,Ag}^{*}=-0.65$.

Compared to Figure 8a, the higher $w_{Ag,CS}\left(t\right)$ value observed prior to the formation of the Ag-rich layer in Figure 8b indicates that a higher diffusivity ($\Delta D_{p_1{q}_1,i}^{*}=10$) accelerates Ag dissolution into CS matrix. This occurs because increased diffusivity of ${Ag}^{+}\text{and\hspace{0.17em}}PW$ in the meso- and macro-pores enhances PW flux into the AgM particle and ${Ag}^{+}$ flux out of it, thereby accelerating Ag dissolution kinetics.

Once the Ag-rich layer forms at the AgM/CS interface, however, it reduces Ag diffusivity as described in Equation 25, leading to Ag accumulation within the layer and a suppressed Ag flux across it. As shown in Figure 8a, Ag accumulation within the layer becomes more sensitive to Ag dissolution into the CS matrix as $d_{Ag,i}^0$ increases (i.e., as Ag diffusivity in the Ag-rich layer decreases). When the diffusivity of Ag⁺ and PW in meso- and macro-pores is increased (e.g., $\Delta D_{p_1{q}_1,i}^{*}=10$.), Ag dissolution into the CS matrix becomes increasingly sensitive to Ag accumulation within the layer as $d_{Ag,i}^0$ increases.

Analysis of Ag and Ag⁺ content evolution in the CS matrix reveals that Ag⁺ dissolution dominates the overall kinetics. Overtime, the dissolution kinetics slows down and gradually approaches equilibrium, with the dissolution rate tending toward zero. This behavior is attributed to the formation and growth of an Ag-rich layer, which block the PW diffusion, reduces the chemical gradient and lowers both reaction rates and overall driving force for species transport.

Comparing Figure 8a with Figure 8b demonstrates that 1) increased diffusivity in meso- and macro-pores enhances Ag dissolution into the CS matrix prior to Ag rich layer formation; 2) the diffusivity of species in Ag rich layer has only a minor effect on the dissolution kinetics, even when reduced by nearly two orders of magnitude (from $d_{Ag,i}^0=0$ to 0.99); and 3) after the Ag rich layer formation, the dissolution kinetics is primarily governed by the oxidation rate, $\Delta r_{AgCS,Ag}^{*}$.

These findings underscore the importance of species-specific diffusivities and redox reaction rates in governing dissolution behavior, which depends critically on the dominant flux pathways of each species.

3.5 Effect of Ag retention within BFS on Ag dissolution

In cementitious systems such as CS (comprising BFS, FA, and OPC), the PW typically exhibits high alkalinity (pH ∼12–13) and reducing conditions (low Eh). Under such conditions, ${Ag}^{+}$ is likely to precipitate as metallic $Ag$, ${Ag}_{2}S$ and/or ${Ag}_{2}O$, depending on redox state and sulfur availability in BFS and OPC (Westsik et al., 2013). This process can be deleterious to the waste form as reduction of the Ag would remove its ability to retain the target radionuclide, iodine.

In the model, the reduction of ${Ag}^{+}$ and its subsequent precipitation are described using a phase-dependent reaction rate, $r_{p,{Ag}^{+}}^{*}$, and a chemical potential, $\Delta {\mu }_{p,Ag}^{*}$, as defined in Equations 11, 12. Figure 9a shows the evolution of Ag concentration for the following parameters $\Delta {\mu }_{BFS,Ag}^{*}=-0.5$ and $r_{BFS,{Ag}^{+}}^{*}=0.1$ in BFS, $\Delta {\mu }_{CS,Ag}^{*}=-0.005$ and $r_{CS,{Ag}^{+}}^{*}=0.001$ in OPC, and $\Delta {\mu }_{FA,Ag}^{*}=0$ and $r_{FA,{Ag}^{+}}^{*}=0$ in FA. The closed white contours represent irregular BFS particles, while the yellow circular outlines denote FA particles. In the model porous CS matrix is assumed to consist of macropores and OPC. Because Ag has a lower chemical potential of $\Delta {\mu }_{BFS,Ag}^{*}=-0.5$ in BFS than that in FA and OPC to mimic Ag retention by Ag₂S formation, most of the dissolved Ag preferentially segregates into the BFS particles, as expected. In contrast, the $Ag$ concentration remains low in FA and OPC due to its negligible solubility in these phases and the low reduction kinetics. The highest Ag concentrations occur at the AgM/CS interface and within BFS particles near this interface, where ${Ag}^{+}$ availability is greatest during dissolution.

Figure 9

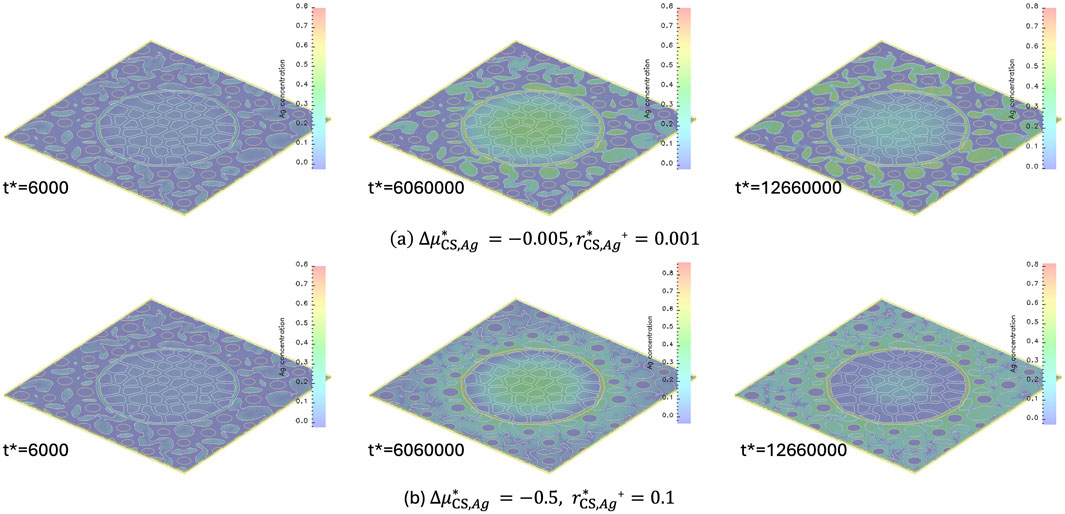
Figure 9. Temporal and spatial evolution of Ag concentration. (a) ${\mu }_{CS,Ag}^{*}=-0.005,$ $\Delta r_{CS,{Ag}^{+}}^{*}=0.001$, and (b) $\Delta {\mu }_{CS,Ag}^{*}=-0.5,$ $\Delta r_{CS,{Ag}^{+}}^{*}=0.1$. Model parameters are $r_{p,{Ag}^{+}}^{*}=0.3$, $\Delta r_{AgCS,Ag}^{*}=-0.1$, $\Delta D_{p_1{q}_1,i}^{*}=10$, $d_{Ag,i}^0=0.0$, $D_{{Ag}^{+}}^{*}=2.0$, $D_{Ag}^{*}=4.0$, $D_{Ag}^{*}=4.0$, $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=0$, $\Delta {\mu }_{pq,Ag}^{*}=-0.65$, and $R^{*}=97$.

Increasing $r_{CS,{Ag}^{+}}^{*}$ and reducing $\Delta {\mu }_{CS,Ag}^{*}$ while remaining the rest model parameters the evolution of the Ag concentration is shown in Figure 9b. $Ag$ concentrations in BFS and CS become comparable due to their identical chemical potentials and reaction rates. However, the Ag concentration remains low in FA, as $\Delta {\mu }_{FA,Ag}^{*}=0$ and $r_{FA,{Ag}^{+}}^{*}=0$.

The Ag concentration profiles in Figure 9 highlight the role of phase-specific chemical potential and reduction kinetics in determining Ag segregation and retention. Variations of these properties among FA, BFS, and OPC significantly influence the spatial distribution and immobilization of Ag within the CS matrix.

Figure 10 shows the temporal evolution of $Ag$ content within both Ag-rich precipitate (ppt) and the CS matrix for the two modeled cases. The overall dissolution process can be divided into three distinct stages: 1) segregation of $Ag$ along the AgM/CS interface; 2) nucleation and growth of Ag-rich precipitates; and 3) dissolution of Ag from the precipitates. Two dashed vertical lines in the figure indicate the onset of nucleation and subsequent dissolution of Ag precipitates.

Figure 10

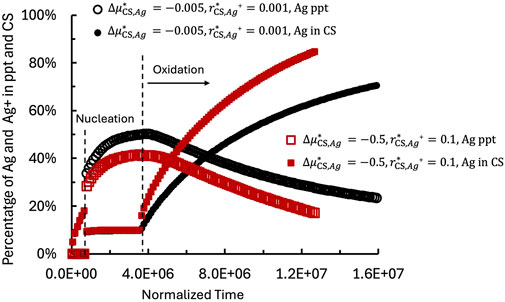
Figure 10. Temporal evolution of $Ag$ content in Ag precipitate (ppt) and the CS matrix. Black symbols represent the case where $\Delta {\mu }_{CS,Ag}^{*}=-0.005,$ and $\Delta r_{CS,{Ag}^{+}}^{*}=0.001$ while red symbols correspond to $\Delta {\mu }_{CS,Ag}^{*}=-0.5,$ and $\Delta r_{CS,{Ag}^{+}}^{*}=0.1$. Model parameters used are $r_{p,{Ag}^{+}}^{*}=0.3$, $\Delta r_{AgCS,Ag}^{*}=-0.1$, $\Delta D_{p_1{q}_1,i}^{*}=10$, $d_{Ag,i}^0=0.0$, $D_{{Ag}^{+}}^{*}=2.0$, $D_{Ag}^{*}=4.0$, $D_{Ag}^{*}=4.0$, $\Delta {\mu }_{p_1{q}_1,Ag}^{*}=0$, $\Delta {\mu }_{pq,Ag}^{*}=-0.65$, and $R^{*}=97$.

According to Equation 15, the dissolution of Ag precipitates occurs when the local Ag concentration at the Ag precipitate/CS interface (${i.e.,g}_{pq}\left(\mathit{\eta }\right)>0$) exceeds a threshold, $c_{Ag}>c_{Ag}^{crit}$. In the figure, empty symbols represent the Ag content in Ag-rich precipitates, while filled symbols indicate the Ag content retained in the CS matrix.

During the growth of Ag precipitates, the Ag concentration at the precipitate/CS interface continues to increase. Once it exceeds the critical concentration $c_{Ag}^{crit}$, an oxidation reaction is triggered, leading to a decrease in Ag content within the precipitate. The dissolved Ag then redistributes and segregates primarily into BFS and OPC particles which results in an increase in Ag content in the CS matrix.

Comparison of the two modeled cases reveals that the system with $\Delta {\mu }_{CS,Ag}^{*}=-0.005,$ $\Delta r_{CS,{Ag}^{+}}^{*}=0.001$ exhibits slower overall dissolution kinetics compared to the case with ${\mu }_{CS,Ag}^{*}=-0.5,$ $\Delta r_{CS,{Ag}^{+}}^{*}=0.1$. This is consistent with expectation: a lower chemical potential combined with a higher reduction rate suppresses the Ag⁺ concentration in the CS matrix, thereby enhancing the diffusion driving force for Ag⁺ from AgM particles.

These results demonstrate that the oxidation reaction facilitates Ag dissolution by increasing the retention capacity of BFS and the CS matrix and accelerating the transport of Ag species from the source.

4 Conclusion

In this work, a mesoscale model was developed to describe Ag dissolution in a CS cementitious waste form containing AgM particles. The model accounts for phase-dependent thermodynamic and kinetic properties and includes the following key capabilities:

1. For given microstructure features—such as the volume fractions and average particle sizes (and/or morphology) of BFS, FA, and OPC phases—the model can generate a three-dimensional microstructure to realistically represent the CS waste form.

2. It incorporates multiphysics processes, including: a) multispecies diffusion (${Ag}^{+}$, $Ag$ and $PW$) driven by chemical potential gradients; b) two non-equilibrium redox reactions: ${Ag}^{+}+PW\to Ag$ and $Ag\to {Ag}^{+}+e^{-}$; and c) segregation and nucleation/growth of Ag-rich precipitates.

3. The model captures spatially heterogeneous thermodynamic behavior by incorporating microstructure-dependent chemical potentials and reaction energy barriers.

4. It also accounts for inhomogeneous kinetic properties, including microstructure-dependent diffusivities and reaction rates for different species and phases.

This mesoscale model was applied in a parametric study to explore the impact of microstructural and physicochemical properties on Ag dissolution. The key findings are as follows: 1) Formation of Ag-rich precipitates at the AgM/CS interface reduces both the chemical potential gradient within AgM particles and the diffusivity of species in Ag-rich precipitates. This effect slows down the overall dissolution kinetics of Ag; 2) The oxidation reaction accelerates Ag dissolution by enhancing Ag retention in BFS and OPC phases and increasing the transport flux of Ag species from the AgM source; and 3) Particle size significantly affects dissolution rates: smaller AgM particles exhibit faster dissolution kinetics under equivalent thermodynamic and kinetic conditions, due to shorter diffusion paths and higher surface area.

These parametric studies demonstrate the mesoscale model enables quantitative assessment of how microstructure, thermodynamics, and kinetics influence Ag dissolution behavior. However, for predictive modeling of real systems, it is essential to link model parameters to experimentally determined thermodynamic and kinetic properties.

Geochemical speciation models have been widely used to study the performance of nuclear waste forms in macroscale. The thermodynamic and kinetic data from such models can inform parameter selection in the mesoscale framework. Moreover, local outputs from geochemical modeling—such as pH, Eh, and species concentrations—can serve as boundary conditions for mesoscale simulations.

Future work will focus on coupling mesoscale and macroscale approaches to address critical questions: When do mean-field models fail in heterogeneous materials? When are microstructure-dependent corrections essential for accurate macroscale predictions? How do mean-field models predict the migration of other contaminants and radionuclides? Answering these questions will enable improved multiscale modeling of nuclear waste forms, enhancing confidence in long-term performance assessments.

Data availability statement

Data will be made available upon request to the authors.

Author contributions

SH: Conceptualization, Methodology, Formal Analysis, Writing – review and editing, Writing – original draft. YL: Writing – review and editing, Validation, Data curation, Investigation, Software. RA: Project administration, Funding acquisition, Resources, Writing – review and editing, Conceptualization.

Funding

The authors declare that financial support was received for the research and/or publication of this article. This work was supported by the U.S. Department of Energy, the Network of National Laboratories for Environmental Management and Stewardship (NNLEMS) funding program. Pacific Northwest National Laboratory is a multiprogram national laboratory operated by Battelle Memorial Institute for the U.S. Department of Energy under DE-AC05-76RL01830. Computations were performed on the Deception cluster at Pacific Northwest National Laboratory.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, S. M., and Cahn, J. W. (1979). A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27, 1085–1095. doi:10.1016/0001-6160(79)90196-2

CrossRef Full Text | Google Scholar

Arnold, J., Duddu, R., Brown, K., and Kosson, D. S. (2017). Influence of multi-species solute transport on modeling of hydrated Portland cement leaching in strong nitrate solutions. Cem. Concr. Res. 100, 227–244. doi:10.1016/j.cemconres.2017.06.002

CrossRef Full Text | Google Scholar

Asmussen, R., Rod, K., Saslow, S., Lonergan, C., Neeway, J., Johnson, B., et al. (2020). Development and characterization of cementitious waste forms for immobilization of granular activated carbon, silver mordenite, and HEPA filter media solid secondary waste. PNNL-28545.

Google Scholar

Cahn, J. W. (1961). On spinodal decomposition. Acta Metall. 9, 795–801. doi:10.1016/0001-6160(61)90182-1

CrossRef Full Text | Google Scholar

Cantrell, K., Jh Westsik, J., Serne, R., Um, W., and Cozzi, A. (2016). Secondary waste cementitious waste form data package for the integrated disposal facility performance assessment.

Google Scholar

Chen, L. Q., and Shen, J. (1998). Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 108, 147–158. doi:10.1016/s0010-4655(97)00115-x

CrossRef Full Text | Google Scholar

Chen, Z., Zhang, P., Brown, K. G., Branch, J. L., VAN DER Sloot, H. A., Meeussen, J. C. L., et al. (2021). Development of a geochemical speciation model for use in evaluating leaching from a cementitious radioactive waste form. Environ. Sci. and Technol. 55, 8642–8653. doi:10.1021/acs.est.0c06227

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Zhang, P., Brown, K. G., VAN DER Sloot, H. A., Meeussen, J. C. L., Garrabrants, A. C., et al. (2023a). Evaluating the impact of drying on leaching from a solidified/stabilized waste using a monolithic diffusion model. Waste Manag. 165, 27–39. doi:10.1016/j.wasman.2023.04.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Zhang, P., Brown, K. G., VAN DER Sloot, H. A., Meeussen, J. C. L., Garrabrants, A. C., et al. (2023b). Impact of oxidation and carbonation on the release rates of iodine, selenium, technetium, and nitrogen from a cementitious waste form. J. Hazard. Mater. 449, 131004. doi:10.1016/j.jhazmat.2023.131004

PubMed Abstract | CrossRef Full Text | Google Scholar

Crank, J. (1979). The mathematics of diffusion. London United Kingdom: Oxford University Press.

Google Scholar

Emmanuel, S., and Berkowitz, B. (2007). Effects of pore-size controlled solubility on reactive transport in heterogeneous rock. Geophys. Res. Lett. 34. doi:10.1029/2006gl028962

CrossRef Full Text | Google Scholar

Emmanuel, S., Ague, J. J., and Walderhaug, O. (2010). Interfacial energy effects and the evolution of pore size distributions during quartz precipitation in sandstone. Geochimica Cosmochimica Acta 74, 3539–3552. doi:10.1016/j.gca.2010.03.019

CrossRef Full Text | Google Scholar

Fang, Y., Yeh, G.-T., and Burgos, W. D. (2003). A general paradigm to model reaction-based biogeochemical processes in batch systems. Water Resour. Res. 39. doi:10.1029/2002wr001694

CrossRef Full Text | Google Scholar

Flach, G. P., Kaplan, D. I., Nichols, R. L., Seitz, R. R., and Serne, R. J. (2016). Solid secondary waste data package supporting hanford integrated disposal facility performance assessment. United States.

Google Scholar

Fournier, M., Frugier, P., and Gin, S. (2018). Application of GRAAL model to the resumption of international simple glass alteration. npj Mater. Degrad. 2, 21. doi:10.1038/s41529-018-0043-4

CrossRef Full Text | Google Scholar

Frugier, P., Gin, S., Minet, Y., Chave, T., Bonin, B., Godon, N., et al. (2008). SON68 nuclear glass dissolution kinetics: current state of knowledge and basis of the new GRAAL model. J. Nucl. Mater. 380, 8–21. doi:10.1016/j.jnucmat.2008.06.044

CrossRef Full Text | Google Scholar

Inagaki, Y., Imamura, T., Idemitsu, K., Arima, T., Kato, O., Nishimura, T., et al. (2008). Aqueous dissolution of silver iodide and associated iodine release under reducing conditions with FeCl2 solution. J. Nucl. Sci. Technol. 45, 859–866. doi:10.3327/jnst.45.859

CrossRef Full Text | Google Scholar

Jennings, H. M., Thomas, J. J., Rothstein, D., and Chen, J. J. (2002). “Cements as porous materials,” in Handbook of porous solids.

Google Scholar

Kim, S. G. (2007). A phase-field model with antitrapping current for multicomponent alloys with arbitrary thermodynamic properties. Acta Mater 55, 4391–4399. doi:10.1016/j.actamat.2007.04.004

CrossRef Full Text | Google Scholar

Kim, S. G., Kim, W. T., and Suzuki, T. (1999). Phase-field model for binary alloys. Phys. Rev. E 60, 7186–7197. doi:10.1103/physreve.60.7186

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K. P., and Site, H. (2018). Performance assessment for the integrated disposal facility. Washington: Washington River Protection Solutions, INTERA Inc.

Google Scholar

Li, D., Kaplan, D. I., Price, K. A., Seaman, J. C., Roberts, K., Xu, C., et al. (2019). Iodine immobilization by silver-impregnated granular activated carbon in cementitious systems. J. Environ. Radioact. 208-209, 106017. doi:10.1016/j.jenvrad.2019.106017

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Hu, S., Hilty, F. W., Montgomery, R., Park, K. C., Martin, C. R., et al. (2022a). Leaching model of radionuclides in metal-organic framework particles. Comput. Mater. Sci. 201, 110886. doi:10.1016/j.commatsci.2021.110886

CrossRef Full Text | Google Scholar

Li, Y., Hu, S., Montgomery, R., Grandjean, A., Besmann, T., and Loye, H.-C. Z. (2022b). Effect of charge and anisotropic diffusivity on ion exchange kinetics in nuclear waste form materials. J. Nucl. Mater. 572, 154077. doi:10.1016/j.jnucmat.2022.154077

CrossRef Full Text | Google Scholar

Liu, S., and Jacques, D. (2017). Coupled reactive transport model study of pore size effects on solubility during cement-bicarbonate water interaction. Chem. Geol. 466, 588–599. doi:10.1016/j.chemgeo.2017.07.008

CrossRef Full Text | Google Scholar

Moelans, N. (2011). A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater. 59, 1077–1086. doi:10.1016/j.actamat.2010.10.038

CrossRef Full Text | Google Scholar

Moelans, N., Blanpain, B., and Wollants, P. (2008). Quantitative analysis of grain boundary properties in a generalized phase field model for grain growth in anisotropic systems. Phys. Rev. B 78, 024113. doi:10.1103/physrevb.78.024113

CrossRef Full Text | Google Scholar

Taylor, H. F. (1997). Cement chemistry. Thomas Telford London.

Google Scholar

Thomas, G. F. (1987). Diffusional release of a single component material from a finite cylindrical waste form. Ann. Nucl. Energy 14, 283–294. doi:10.1016/0306-4549(87)90131-9

CrossRef Full Text | Google Scholar

VAN De Walle, A., and Ceder, G. (2002). Automating first-principles phase diagram calculations. J. Phase Equilibria 23, 348–359. doi:10.1361/105497102770331596

CrossRef Full Text | Google Scholar

Westsik, J. J. H., Serne, R. J., Pierce, E. M., Cozzi, A. D., Chung, C., and Swanberg, D. J. (2013). Supplemental immobilization cast stone technology development and waste form qualification testing plan PNNL.

Google Scholar

Yamagata, A. F., Saslow, S. A., Neeway, J. J., Varga, T., Reno, L. R., Zhu, Z., et al. (2022). The behavior of iodine in stabilized granular activated carbon and silver mordenite in cementitious waste forms. J. Environ. Radioact. 244, 106824.

PubMed Abstract | Google Scholar