- 1Department of Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States
- 2Department of Pharmaceutical Sciences, University of Michigan, Ann Arbor, MI, United States
- 3Department of Mechanical Engineering, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
- 4Department of Pediatrics, Division of Pediatric Cardiology, University of Michigan, Ann Arbor, MI, United States
- 5Department of Pediatrics, Nationwide Children’s Hospital, Columbus, OH, United States
- 6Department of Surgery, University of Michigan, Ann Arbor, MI, United States
- 7School of Biomedical Engineering and Imaging Sciences, King’s College London, London, United Kingdom
- 8Department of Mechanical Engineering, Michigan State University, East Lansing, MI, United States
Pulmonary arterial hypertension (PAH) is a complex disease involving increased resistance in the pulmonary arteries and subsequent right ventricular (RV) remodeling. Ventricular-arterial interactions are fundamental to PAH pathophysiology but are rarely captured in computational models. It is important to identify metrics that capture and quantify these interactions to inform our understanding of this disease as well as potentially facilitate patient stratification. Towards this end, we developed and calibrated two multi-scale high-resolution closed-loop computational models using open-source software: a high-resolution arterial model implemented using CRIMSON, and a high-resolution ventricular model implemented using FEniCS. Models were constructed with clinical data including non-invasive imaging and invasive hemodynamic measurements from a cohort of pediatric PAH patients. A contribution of this work is the discussion of inconsistencies in anatomical and hemodynamic data routinely acquired in PAH patients. We proposed and implemented strategies to mitigate these inconsistencies, and subsequently use this data to inform and calibrate computational models of the ventricles and large arteries. Computational models based on adjusted clinical data were calibrated until the simulated results for the high-resolution arterial models matched within 10% of adjusted data consisting of pressure and flow, whereas the high-resolution ventricular models were calibrated until simulation results matched adjusted data of volume and pressure waveforms within 10%. A statistical analysis was performed to correlate numerous data-derived and model-derived metrics with clinically assessed disease severity. Several model-derived metrics were strongly correlated with clinically assessed disease severity, suggesting that computational models may aid in assessing PAH severity.
1 Introduction
Pulmonary arterial hypertension (PAH), defined by a mean pulmonary arterial pressure greater than 20 mmHg (Simonneau et al., 2019), is a complex disease that causes functional and structural changes in the pulmonary circulation and right ventricle (RV). Ventricular-arterial interactions play an important role in the progression of PAH, where increases in resistance and decreases in compliance of the pulmonary circulation lead to structural remodeling and increased contractility of the RV, in an attempt to maintain normal cardiac outputs (Vonk Noordegraaf et al., 2019). RV contractility can increase four- to five-fold until the ventricle cannot compensate for further increases in pulmonary pressures, leading to “uncoupling” between the RV and pulmonary arteries. Consequently, RV stroke volume and ejection fraction decrease, ultimately leading to decompensated RV failure (Vonk Noordegraaf et al., 2017). Given that ventricular-arterial interactions are a key determinant of the clinical course of PAH (Shimoda and Laurie 2013), there is a pressing need to identify metrics that consider these interactions to accurately describe PAH pathology.
Pediatric PAH is especially difficult to manage as diagnostic metrics are often derived from adult data due to the lack of clinical trials in the pediatric population (Ivy et al., 2010). Using adult population data to guide pediatric PAH treatment can be problematic as younger subjects present significant differences in cardiovascular structure and function (Strait and Lakatta 2012) and show worse survival rates (Douwes et al., 2013). Furthermore, there are population-based differences in children with PAH compared to adults, such as impaired lung development and higher incidence of congenital heart disease (Berger and Bonnet 2010). Clinical trials designed to focus on pediatric PAH patients could help elucidate novel diagnostic metrics for this population.
Computational models based on patient-specific clinical data have widely been used to study mechanics and hemodynamics of cardiovascular diseases (Humphrey and Taylor 2008; Taylor and Figueroa 2009; Nordsletten et al., 2011; Bikia et al., 2020; Miller et al., 2021) including hemodynamics in the cardiopulmonary circulation (Kheyfets et al., 2013). Previous PAH modeling efforts have focused on either the pulmonary arteries (Tang et al., 2012; Kheyfets et al., 2015; Zambrano et al., 2018; Yang et al., 2019) or the RV (Rausch et al., 2011; Avazmohammadi et al., 2019; Shavik et al., 2019). The absence of high-resolution (3D) bi-directional (ventricular-arterial) hemodynamic interactions in these models restricts their ability to capture phenomena such as ventricular-arterial uncoupling. In this work, we aim to overcome this limitation by developing high-resolution (3D) models of both RV and pulmonary artery mechanics, a first step towards a fully 3D bi-directional model of the cardiopulmonary system.
The overall goals of this work are to (Figure 1): (1 develop and calibrate multi-scale closed-loop models of the cardiopulmonary circulation in PAH patients, and (2 use clinical and computational metrics to stratify patients according to disease severity. Two different models will be developed: a “High-Resolution Arterial Model,” whereby image-based 3D fluid-structure interaction (FSI) models of the large vessels are coupled to 0D models of ventricles and distal circulation; and a “High-Resolution Ventricular Model”, whereby image-based 3D models of passive and active ventricular mechanics are coupled to 0D models of arterial and pulmonary circulation. These computational models rely on the quality and consistency of clinical data. Data were acquired using diagnostic tools with varying tolerances, temporal and spatial resolutions, and physiological states (i.e., level of sedation), which led to inconsistencies. In this work, we also propose and implement strategies to mitigate data inconsistencies to inform and calibrate these computational models.
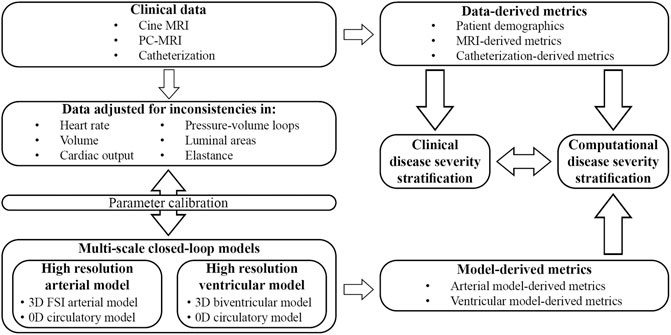
FIGURE 1. Clinical data was prospectively acquired in pediatric PAH patients and adjusted to mitigate inconsistencies. Parameters of two different closed-loop multiscale models were calibrated and used to study computational metrics of disease severity. Clinically assessed disease severity, data-derived metrics, and model-derived metrics were correlated to stratify patients according to disease severity.
2 Materials and methods
Clinical data were acquired prospectively from a cohort of 8 pediatric PAH patients treated at the University of Michigan (UM) C.S. Mott Children’s Hospital (ClinicalTrials.gov ID No. NCT03564522). This study was approved by the UM Institutional Review Board (HUM00117706), and informed consent was obtained from subjects or their parents/guardians. World Health Organization functional class (WHO-FC) was determined for each patient.
2.1 Clinical data
Clinical data on anatomy, flow, and pressure, were acquired using MRI and catheterization. Both MRI and catheterization data were acquired with the patient at rest in the supine position. The mean time between MRI acquisition and catheterization was 4.4 days (range 0–29 days).
2.1.1 Magnetic resonance imaging
MRI was performed using a 1.5 Tesla scanner (Achieva or Ingenia; Philips, Best, the Netherlands). Three-dimensional diastolic vascular anatomy was obtained with a 3D steady state free precession (SSFP) sequence (TE: 2.2 ms, TR: 4.3–4.4 ms, flip angle: 90°, field of view: 260–350 mm, slice thickness = 1.4–1.6 mm, image resolution = 0.63–0.78 mm) with cardiac and respiratory gating (Figure 2A). Gated phase-contrast MRI (PC-MRI) (TE: 2.7–3.3 ms, TR: 4.1–5.1 ms, flip angle: 12°, field of view: 250–350 mm, slice thickness = 6 mm, image resolution = 1.4–1.6 mm) was performed to obtain dynamic data at 40 phases of luminal area and blood flow at five anatomical locations: ascending aorta (AAo), descending thoracic aorta (DTA), main pulmonary artery (MPA), left pulmonary artery (LPA), and right pulmonary artery (RPA). Multi-slice (10–13 slices, slice thickness: 6–8 mm), multi-phase (30 phases) cine MR images (TE: 1.2–1.6 ms, TR: 2.5–3.1 ms, flip angle: 60°, field of view: 250–350 mm, image resolution = 1.6–1.8 mm) were acquired by positioning the scans in the short-axis planes perpendicular to the long-axis of the left ventricle (LV), capturing both the LV and RV from the cardiac base to the apex (Figure 2B).
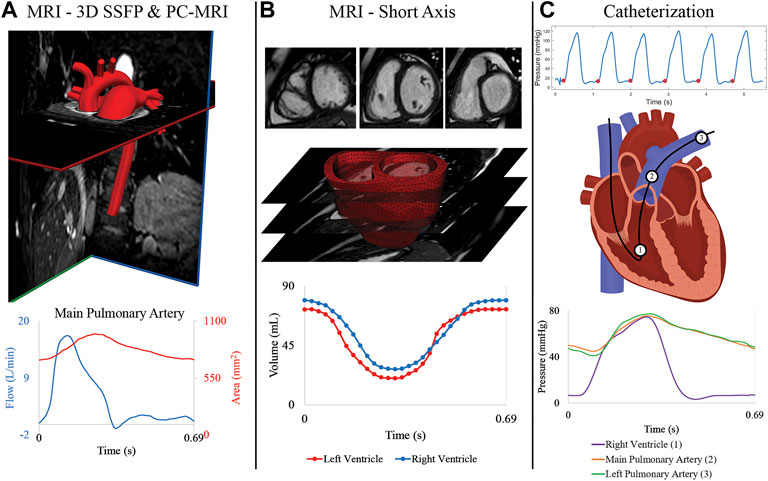
FIGURE 2. (A) MRI 3D SSFP data is used to construct the anatomical arterial models. Flow and area waveforms were reconstructed from PC-MRI data containing 40 phases. (B) 30 temporal phases of endocardial and epicardial surfaces were segmented from the short-axis stack of cine MRI data to generate the ventricular volume waveforms. High-resolution (3D) ventricular models were created from these segmented surfaces. (C) Pressures at the (1) right ventricle, (2) main pulmonary artery, and (3) right pulmonary artery were acquired with catheterization for all patients.
2.1.2 Catheterization
Right heart catheterization was performed in all subjects (Figure 2C) to measure invasive hemodynamics and assess PAH progression. Intracardiac pressures were measured in the right atrium, RV, and pulmonary arteries (MPA, and either LPA or RPA) using a balloon wedge catheter (Arrow, Reading, PA) or thermodilution catheter (Edwards Lifesciences, Irvine, CA). Pulmonary capillary wedge pressure was measured, and femoral arterial access was acquired for blood pressure monitoring and blood gas analysis. In select patients with suspected left heart disease, retrograde left heart catheterization was performed using a pigtail catheter (Merit Medical, South Jordan, UT) and direct pressures were measured in the LV, AAo, and DTA. Pulmonary vascular resistance index (PVRi) was calculated by dividing the pressure gradient (mean pulmonary arterial pressure—mean pulmonary capillary wedge pressure) over cardiac index, which was calculated by the Fick principle or thermodilution.
2.2 Patient demographics and clinical metrics
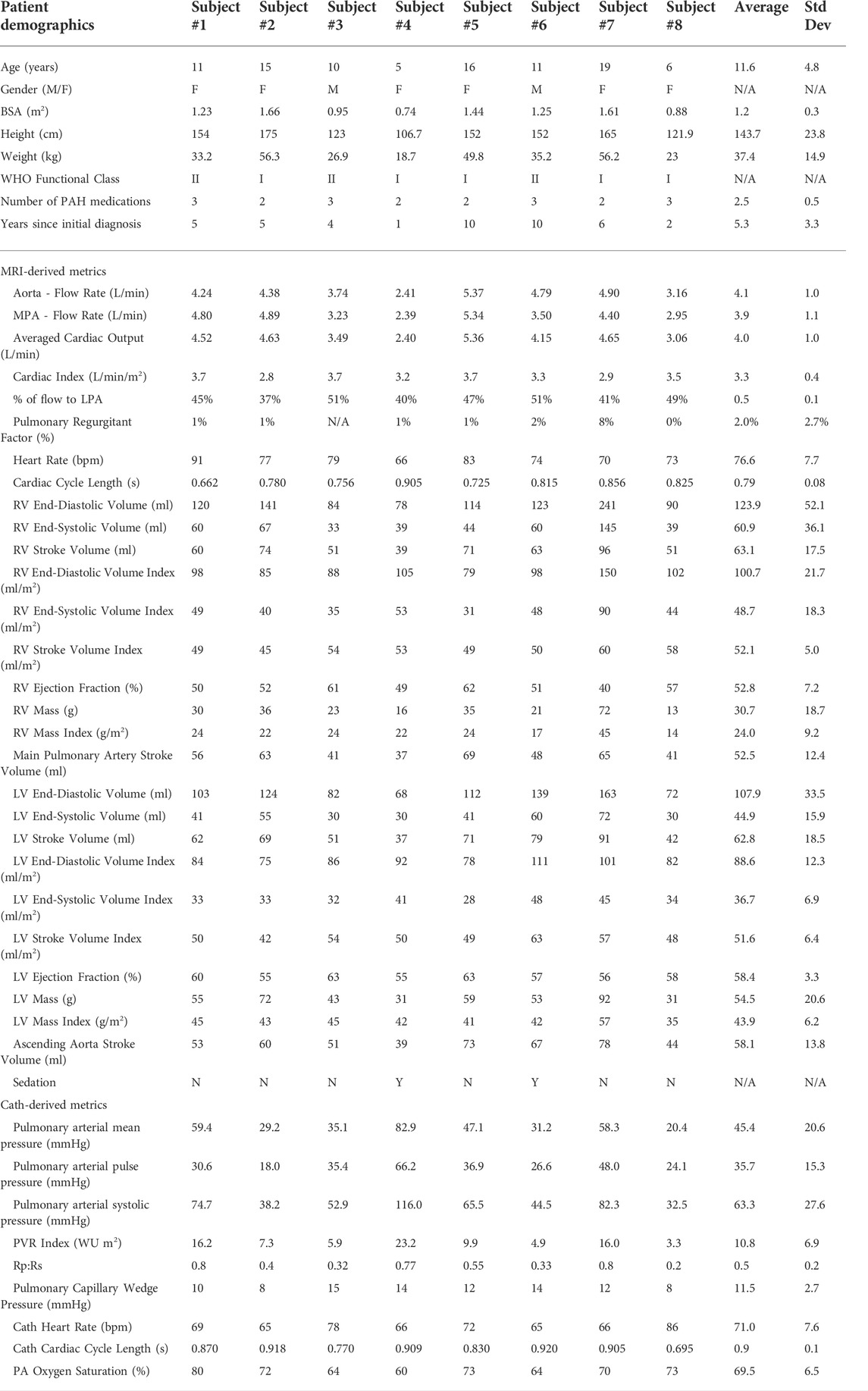
Eight PAH patients (age: 11.8 ± 4.4 years; range 6–19 years) underwent catheterization and MRI examinations. Table 1 summarizes mean and standard deviations of basic patient demographics and several key clinical metrics, derived from MRI and catheterization. Five patients were classified as WHO-FC I and three as WHO-FC II. Four patients were on dual PAH therapy, and four on triple PAH therapy.
2.3 Strategies for mitigation of inconsistencies in clinical data
Despite best efforts made to acquire MRI and catheterization data in close temporal proximity, the studies were on average 4.4 days apart. Furthermore, catheterization and MRI were performed under varying levels of sedation. This, together with the different tolerances and temporal resolutions of MRI and catheterization, leads to inconsistencies in the data that must be addressed in order to use the data for simulations, where conservation laws of mass and momentum balance must be satisfied. Data inconsistencies include: 1) LV and RV volume waveforms segmented from cine MRI short-axis data do not match values obtained with PC-MRI, and 2) misaligned ventricular pressure-volume (PV) data. Additional examples of data inconsistencies are detailed in the Supplementary Material.
2.3.1 Ventricular volume waveforms
2.3.1.1 Ventricular volumes derived from short-axis cine MRI data
LV and RV volume waveforms were first obtained by manually segmenting each of the 30 phases of the cine MRI data using the software package CVI42 (Circle Cardiovascular Imaging, Calgary, Canada). Ventricular segmentation is a time-consuming task susceptible to inter- and intra-observer variability (Miller et al., 2013). It required delineation of LV and RV endocardial surfaces from the apex to the mitral and tricuspid valve, respectively, for each of the 30 phases of the MRI data. In the short-axis cine MRI data, slice thickness (6–8 mm) is much larger than the in-plane image resolution (0.80–0.91 mm). Higher variability in RV segmentation is expected since its shape varies significantly throughout the slices (Petitjean and Dacher 2011; Caudron et al., 2012). Furthermore, delineation of the basal regions of the ventricles can be challenging due to the 10%–20% end-systolic shortening (Rogers et al., 1991; Klein et al., 1998) and the motion of the valves along the long-axis. Average RV and LV stroke volumes of 62.8 ± 18.5 ml and 63.1 ± 17.5 ml, respectively, were obtained.
2.3.1.2 Truncated ventricular volumes
A fixed plane below the tricuspid valve was used to define truncated volume data used in the high-resolution ventricular computational models. This truncation yielded average LV and RV stroke volumes of 43.0 ± 14.7 ml and 40.4 ± 14.9 ml, respectively (see Supplementary Table S1 for values for each patient). These volumes are 31% and 36% smaller than those corresponding to the full ventricle. Then, the end-systolic phase was segmented using MeVisLab (www.mevislab.de) to define STL models of LV and RV. These end-systolic segmentations were adjusted to match the CVI42 ventricular volume data.
The discrepancy between full ventricular and truncated volumes used in the high-resolution computational arterial models is accounted for by different model parameters of the lumped parameter heart model (Section 2.4.2). Conversely, the high-resolution computational ventricular models use the truncated definition of the ventricular volumes. The implications of this inconsistency will be discussed in the limitations section.
2.3.1.3 Ventricular volumes derived from PC-MRI data
Integration of PC-MRI flow waveforms at AAo and MPA provide alternative definitions for LV and RV ventricular volume waveforms, respectively. Average PC-MRI-derived RV and LV stroke volumes of 53.8 ± 11.3 ml and 51.1 ± 10.8 ml, respectively, were obtained. This represents a difference of 19% and 23% relative to the values obtained via segmentation of the short-axis cine-MRI data. This difference could be due to patients holding their breath only for the short-axis cine-MRI sequence, which can increase stroke volume (Guz et al., 1987). In Section 2.4.3, we describe how to combine the PC-MRI and short-axis cine MRI definitions of volume waveforms to improve the comparison between simulated and measured AAo and MPA flow waveforms.
2.3.2 Automated alignment of ventricular pressure and volume data
Ventricular pressure and volume waveforms were combined to form a PV loop. Given the difference in temporal resolution, pressure waveforms were down sampled to 30 phases to match the resolution of the volume data. Then, pressure and volume waveforms were aligned using the R-peaks of the ECG and a PV loop was plotted. However, in most cases, the shape of the resulting PV loop lacked defined isovolumetric contraction and relaxation phases (Figure 3A), which can even occur when PV loop data is acquired simultaneously with an interventional cardiac MRI. Gusseva et al. (2021; 2022) developed a biophysical heart model to align PV data. In this work, we developed an algorithm to systematically shift the pressure waveforms to determine optimally aligned PV loops.
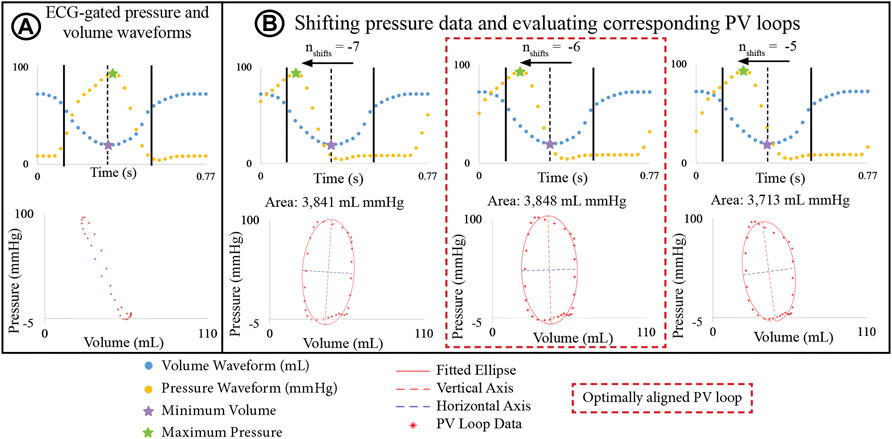
FIGURE 3. (A) PV loop built by ECG-aligning pressure and volume waveforms shows physiologically unrealistic shape. (B) Optimization algorithm incrementally shifts pressure waveforms to define a new PV loop and an ellipse is fitted to the PV. The optimally aligned PV loop, showing clearly defined isovolumetric relaxation and contraction phases, is that with the largest area.
The basis of this algorithm is as follows: Pressure data was shifted by time increments Δt = T/30 s, where T is the cardiac cycle length, and 30 is the number of phases. Since maximum pressure and minimum volume must remain in close temporal proximity, the number of Δt increments (
The aligned PV loops were used to estimate ventricular stroke work, construct the elastance waveforms of the lumped parameter (0D) heart model used in combination with the high-resolution arterial models (Section 2.4.2), and to calibrate the parameters of the high-resolution ventricular models (Section 2.5).
2.4 High-resolution arterial model
These models consist of a 3D FSI component representing the large systemic and pulmonary arteries, and 0D lumped-parameter models representing the heart (H) (see Figure 4) and the distal systemic and pulmonary circulations via 3-element Windkessel models (W) (Vignon-Clementel et al., 2006).
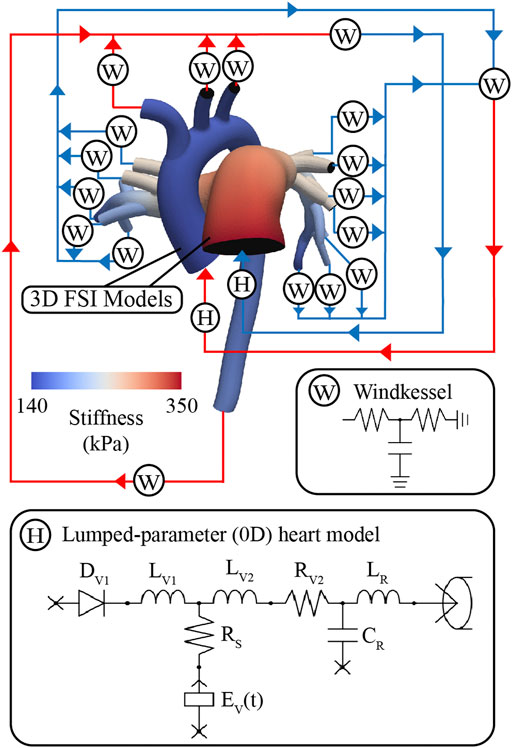
FIGURE 4. Multi-scale closed-loop model consisting of high-resolution (3D) arterial models of aorta and large pulmonary arteries, coupled to (0D) lumped parameter models of heart (H) and distal circulations (W).
2.4.1 3D FSI arterial models
Anatomical models of the large systemic and pulmonary arteries were constructed from the diastolic phase of the 3D steady-state free precession MRI data, adjusted to match diastolic areas measured with PC-MRI (Alastruey et al., 2016), see Supplementary Material. Models were built using the open-source cardiovascular simulation software CRIMSON (Arthurs et al., 2021), rendering smooth analytical (NURBS) surfaces enclosing the volume of the vessels of interest. Models were then discretized into linear tetrahedral elements, and field-based adaptivity was used to refine the mesh in regions of high velocity gradients (Sahni et al., 2006). A mesh sensitivity analysis was performed to ensure mesh independence in flow and pressure waveforms, and determine the mesh sizes. The combined finite element mesh size for the aortic and pulmonary models ranged from 1,214,922 to 1,780,093 elements.
The arterial wall was modeled as a linear elastic membrane with spatially varying isotropic stiffness and wall thickness (Figueroa et al., 2006). Luminal area and pressure data were used to derive linearized stiffness, defined as (Hirai et al., 1989; Silva Vieira et al., 2018):
where
Once the parameters of 3D and 0D compartments of model are defined, multi-scale FSI simulations were performed using the CRIMSON flow solver to solve for the Navier-Stokes equations for an incompressible Newtonian fluid (Figueroa et al., 2006; Xiao et al., 2013; Lau and Figueroa, 2015). All simulations were performed using a time step size of 0.1 ms. Blood was modeled as an incompressible Newtonian fluid with density of ρ = 0.00106 g/mm3 and viscosity of μ = 0.004 g/mm∙s. Simulations were run until flow and pressure fields achieved cycle-to-cycle periodicity.
2.4.2 Lumped-parameter (0D) heart model
A lumped-parameter (0D) heart model (H) was defined using CRIMSON’S Netlist Editor Boundary Condition Toolbox (Arthurs et al., 2017) (Figure 4). The lumped-parameter heart model used in this work, developed by Kim et al. (2009), captures how changes in either cardiac or arterial properties influence each other. This model was chosen as it was developed by our group, it is implemented in the CRIMSON flow solver, and it has been widely adopted by the 3D hemodynamic modeling field (Sankaran et al., 2012; Marsden 2013; Arthurs et al., 2016; van Bakel et al., 2019). Resistors (
LV and RV contractility was represented via a time-varying pressure volume chamber representing ventricular elastance
where
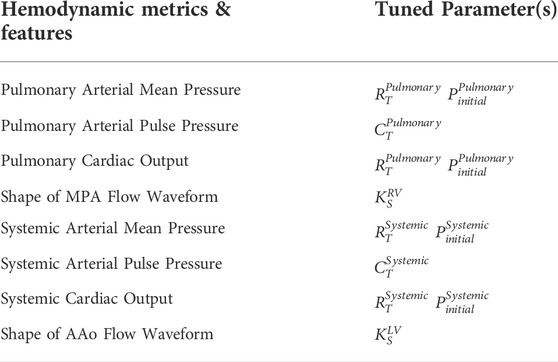
2.4.3 Boundary condition design and calibration
Boundary condition design and calibration are achieved via a process which includes three stages of lumped parameter model circuit design, iterative tuning of parameters, and adjustment of truncated ventricular volume and elastance waveforms (Figure 5A). The boundary condition design consists of the following three stages (Arthurs et al., 2017):
Stage 1 open-loop arterial model with imposed aortic and MPA flows (Figure 5B).
Stage 2 open-loop arterial model with a 0D heart model (Figure 5C).
Stage 3 closed-loop arterial model with a 0D heart model (Figure 5D).
Within each stage, parameters were iteratively tuned until simulated results matched clinical data on flow and pressure (Xiao et al., 2014). Calibrated parameters were transferred to the corresponding lumped parameter circuits of the subsequent stage.
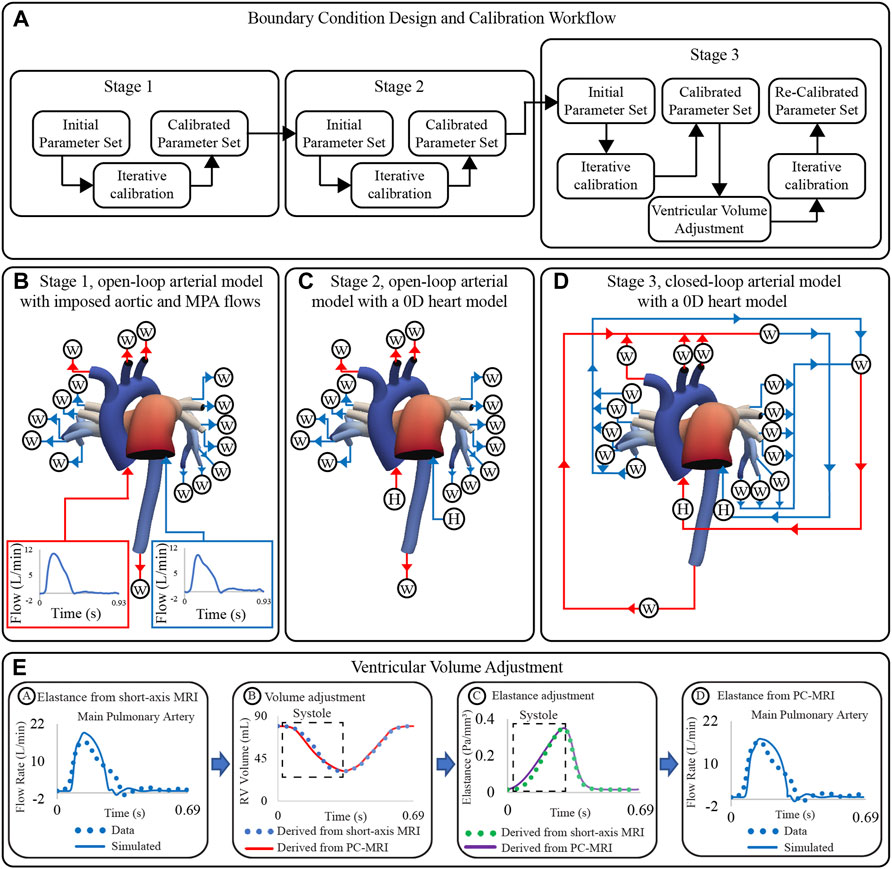
FIGURE 5. (A) Workflow for boundary condition design and calibration of high-resolution arterial models. (B) Stage 1: open-loop arterial model with imposed inflow waveforms. (C) Stage 2: open-loop arterial model with 0D heart models. (D) Stage 3: closed-loop arterial model with a 0D heart models. (E) Strategy for ventricular volume adjustment.
Following the three-stage parameter calibration, simulated inflow waveforms did not match the shape of the measured clinical flow waveforms (even though the mean values did). Specifically, simulated inflow waveforms underestimated the length of systole, which led to an overestimated peak systolic flow (Figure 5E, stage A). To fix this discrepancy, PC-MRI data were used to re-define the ventricular volume during systole (Figure 5E, stage B). The adjusted volume waveforms were used to define a new ventricular elastance (Figure 5E, stage C), and simulations with the Stage 3 circuit design were re-run. The new computed inflow waveforms reproduced better the shape of the clinical waveforms (Figure 5E, stage D). A detailed description of the calibration process is given next.
2.4.3.1 Iterative tuning of lumped parameters
Lumped parameter values (Table 2) were estimated using a fixed-point iteration algorithm (Xiao et al., 2014; Alastruey et al., 2016). The iterative algorithm laid out by Xiao et al., (2014) leverages their 1D models to efficiently calibrate outflow boundary condition parameters in 3D patient-specific arterial models. This work was used to define the iterative formulas presented below that aim to match simulated results with clinical hemodynamic data.
Stage 1, open-loop arterial model with imposed aortic and MPA flows. 3-element Windkessel models were used to represent the resistance and compliance of the distal vascular bed. Windkessel resistances
where the total arterial resistance RT and total arterial compliance CT were iteratively estimated as:
where
Stage 2, open-loop arterial model with a 0D heart model. Initial nodal pressures of the lumped-parameter heart models and Windkessel models for each branch were iteratively tuned:
Simulated (
Stage 3, closed-loop arterial model with a 0D heart model. Systemic and pulmonary venous systems, represented via 3-element Windkessel models, were added to connect the arterial outlets to the atria of the lumped-parameter heart models, creating a closed-loop circulation (Figure 5D). Windkessel resistances (Formulas (4) and (5)), Windkessel compliances (Formulas (4) and (6)), and initial nodal pressures of the lumped-parameter models (Formula (7)) were iteratively tuned.
For each patient-specific model, 30–70 lumped parameter values were calibrated until all relative errors between measured and simulated hemodynamics were below 10%. Relative errors were calculated as
2.4.3.2 Adjustment of volume and elastance waveforms
The systolic phase of the PC-MRI flow waveform was integrated over time to derive ejected volume. PC-MRI-derived stroke volume was scaled to match short-axis MRI stroke volume. End-diastolic volume was assigned directly from short-axis MRI data, and the scaled PC-MRI-derived volume guided the systolic phase of the ventricular volume waveform. The filling phase of the volume waveform remained unchanged (Figure 5E, stage B). Adjusted ventricular volume waveforms were used to re-derive elastance waveforms (Figure 5E, stage C). Adjusted ‘Two-Hill’ elastance parameter values are found in Supplementary Table S3.
The discrepancies between clinical and simulated MPA and AAo flow waveforms were evaluated using a L2-norm metric
2.5 High-resolution ventricular model
In this model, truncated 3D biventricular geometries (see Section 2.3.1) were coupled to a 0D closed-loop circulatory model representing the distal systemic and pulmonary circulations, atria, and heart valves (Figure 6).
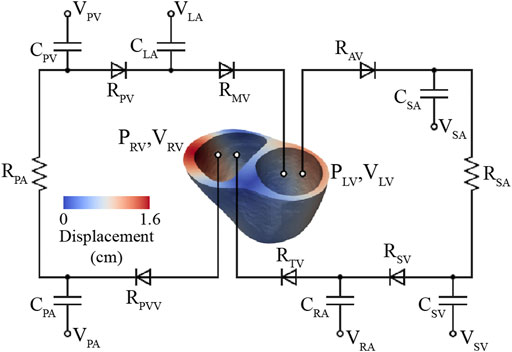
FIGURE 6. High-resolution (3D) ventricular model coupled to a 0D closed-loop circulatory model, which includes the systemic and pulmonary arteries, venous systems, atria, and valves.
2.5.1 3D biventricular models
Governing equations of the 3D biventricular models based on a quasi-static formulation and assuming that the cardiac tissue behaves as an incompressible material were solved using the open-source software FEniCS (Alnæs et al., 2015), as detailed in Shavik et al. (2019), Shavik et al. (2020), Shavik et al. (2021). An active stress formulation was used to describe the mechanical behavior of myocardial tissue whereby the first Piola Kirchhoff stress tensor
STL models of the truncated ventricles (Section 2.3.1) generated at the end-systolic phase define the unloaded configuration (Hadjicharalambous et al., 2021). This truncation was performed to avoid modeling the basal regions of the heart, including the valves and atria, which are often poorly resolved in the short-axis MRI sequence and are represented with lumped-parameter circuits. The 3D biventricular model was divided into three material regions: LV free wall, septum, and RV free wall. Helix angles of the myocardial fibers were linearly varied along the transmural direction from 60° at the endocardium to −60° at the epicardium (Streeter et al., 1969) using a Laplace-Dirichlet rule-based algorithm (Bayer et al., 2012).
These models were discretized using GMSH (Geuzaine and Remacle 2009) to define tetrahedral grids of 9,159 to 11,726 elements and 2,884 to 3,548 nodes. Mesh refinement studies were performed to ensure that hemodynamic results were independent of mesh size.
2.5.1.1 Active contraction model
The active stress
where
where
where
The choice of active contraction constitutive models in ventricular biomechanics depends on the needs of the study (Wong 1971; Guccione et al., 1993; Niederer et al., 2006; Rice et al., 2008; Chabiniok et al., 2016). In this work, we used an active contraction model based on that from Guccione et al., (1993) which led to the slope of RV ESPVR having a value of 1.32 ± 0.78 mmHg/ml, which is well aligned with values reported in literature (Dell’Italia and Walsh 1988; Brown and Ditchey 1988). Complex active contraction models that consider tropomyosin kinetics (Hunter et al., 1998) or crossbridge cycling (Rice et al., 2008) could have more accurately captured ventricular active mechanics at the expense of more model parameters. However, the modified Guccione et al., (1993) active contraction model is computationally efficient, captures a wide range of myocardial responses, and successfully reproduced clinical data that satisfied the needs of our study.
2.5.1.2 Passive constitutive model
Cardiac tissue is known to be an orthotropic, viscoelastic material (Pinto and Fung 1973; Sommer et al., 2015). Numerous passive constitutive models have assumed a hyper-elastic orthotropic behavior (Holzapfel et al., 2000; Costa et al., 2001; Schmid et al., 2007), and some have included viscoelasticity (Gültekin et al., 2016; Nordsletten et al., 2021; Zhang et al., 2021). Orthotropic viscoelastic models can better represent ventricular biomechanics, at the expense of a larger number of model parameters. For the sake of simpler model parameterization, in this work we have opted for a phenomenological transversely isotropic hyper-elastic model (Guccione et al., 1991; Shavik et al., 2021). In this model, the strain energy function was given by
Components of Green-Lagrange strain tensor
2.5.2 Lumped-parameter (0D) vascular models
The lumped-parameter models of systemic and pulmonary circulation are divided into arterial and venous segments with compliances (
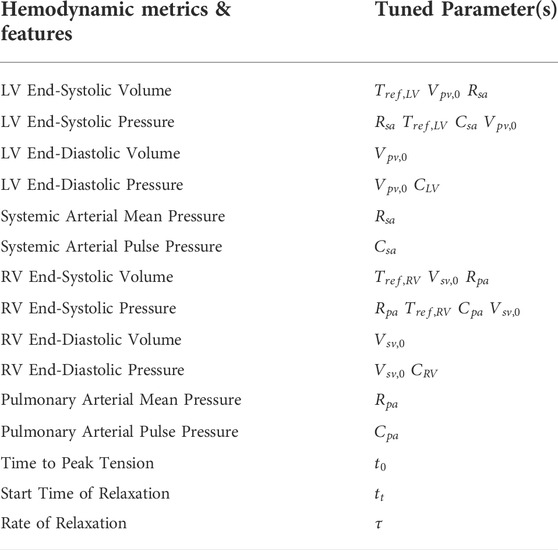
2.5.3 Model calibration
2.5.3.1 Parameters of the lumped-parameter vascular models
Parameters were iteratively calibrated until the following simulated and clinical metrics matched within 10%: LV and RV end-diastolic and end-systolic volumes, LV and RV end-systolic pressures, and systemic and pulmonary arterial mean and pulse pressures (Finsberg et al., 2018; Shavik et al., 2019; Shavik et al., 2020), see Table 3. Resting volumes of pulmonary and systemic veins (
2.5.3.2 Parameters of the 3D biventricular models
LV free wall and septum were assigned to have the same passive stiffness
For each patient-specific model, 16 parameters related to the lumped-parameter vascular models, active contraction models, and passive constitutive models were calibrated and are detailed in Supplementary Table S4.
2.6 Metrics for disease severity stratification
Patients were stratified from lowest to highest disease severity, by a team composed of 3 pediatric cardiologists with extensive experience in treating PAH, based on the available clinical metrics (see Table 4). We explored the correlation between the disease severity stratification and clinical metrics and model-derived metrics (from both high-resolution arterial and ventricular models). For each metric, the correlation was assessed using Spearman’s rank correlation coefficient

TABLE 4. Stratification of patients from lowest (value of 1) to highest (value of 8) disease severity.
2.6.1 Clinical metrics
A total of 36 data-derived metrics were evaluated in the disease severity stratification study, including patient demographics (age, height, weight, etc.), indexed MRI-derived metrics (ventricular volume indices, ventricular mass indices, cardiac index etc.), and catheterization-derived metrics (pulmonary arterial pressures, pulmonary vascular resistance, etc.), see Table 1.
2.6.2 Model-derived metrics
A total of 21 model-derived metrics and parameters were included in the disease severity stratification study. The inclusion of the parameters and metrics was determined by the following criteria:
(1) Lumped-parameter model and 3D parameters with a direct counterpart in the clinical data (i.e., total arterial compliance and resistance, linearized arterial stiffness).
(2) All 3D ventricular model parameters (i.e., ventricular contractility and passive stiffness).
(3) Model metrics with well-established clinical meaning such as arterial pulse wave velocity and ventricular-vascular coupling (i.e., RV ESPVR, RV Ea, RV ESPVR/Ea).
Individual lumped parameters for which there were no direct measurements (i.e., proximal and distal resistances, venous circuit parameters, etc.) were excluded.
2.6.2.1 High-resolution arterial models
Stiffness derived at five anatomical locations (AAo, DTA, MPA, LPA, and RPA), peak LV and RV elastance (Section 2.4.2), MPA-LPA, MPA-RPA, and AAo-DTA pulse wave velocities, and distribution of central and peripheral pulmonary vasculature resistance and compliance (Cuomo et al., 2019) were evaluated.
2.6.2.2 High-resolution ventricular models
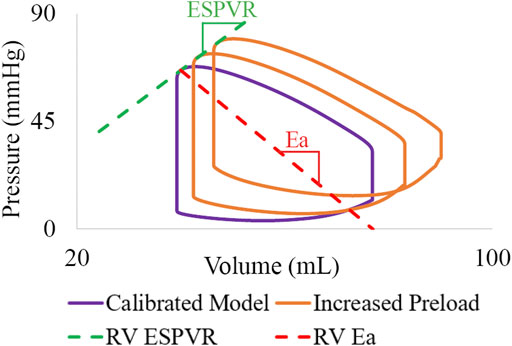
RV end-systolic pressure volume relationship (ESPVR), arterial elastance (Ea), and (ESPVR/Ea) ratio were evaluated. For each calibrated subject, RV ESPVR was estimated by varying preload (
All clinical and model-derived metrics included in the disease severity stratification study are detailed in Supplementary Table S5.
3 Results
3.1 High-resolution arterial models
Following model parameter calibration (see Table 2), simulation results successfully reproduced patient-specific clinical hemodynamic data within 10% (Figure 8). Pressures were compared between our patient cohort and a cohort of healthy pediatric subjects (Douwes et al., 2013). Pulmonary arterial mean pressures (45.4 ± 19.3 mmHg), and pulmonary arterial pulse pressures (35.7 ± 14.3 mmHg) were higher than values measured in healthy pediatric subjects. Mean systemic arterial pressures (69.9 ± 11.6 mmHg) were similar to those measured in healthy pediatric subjects.
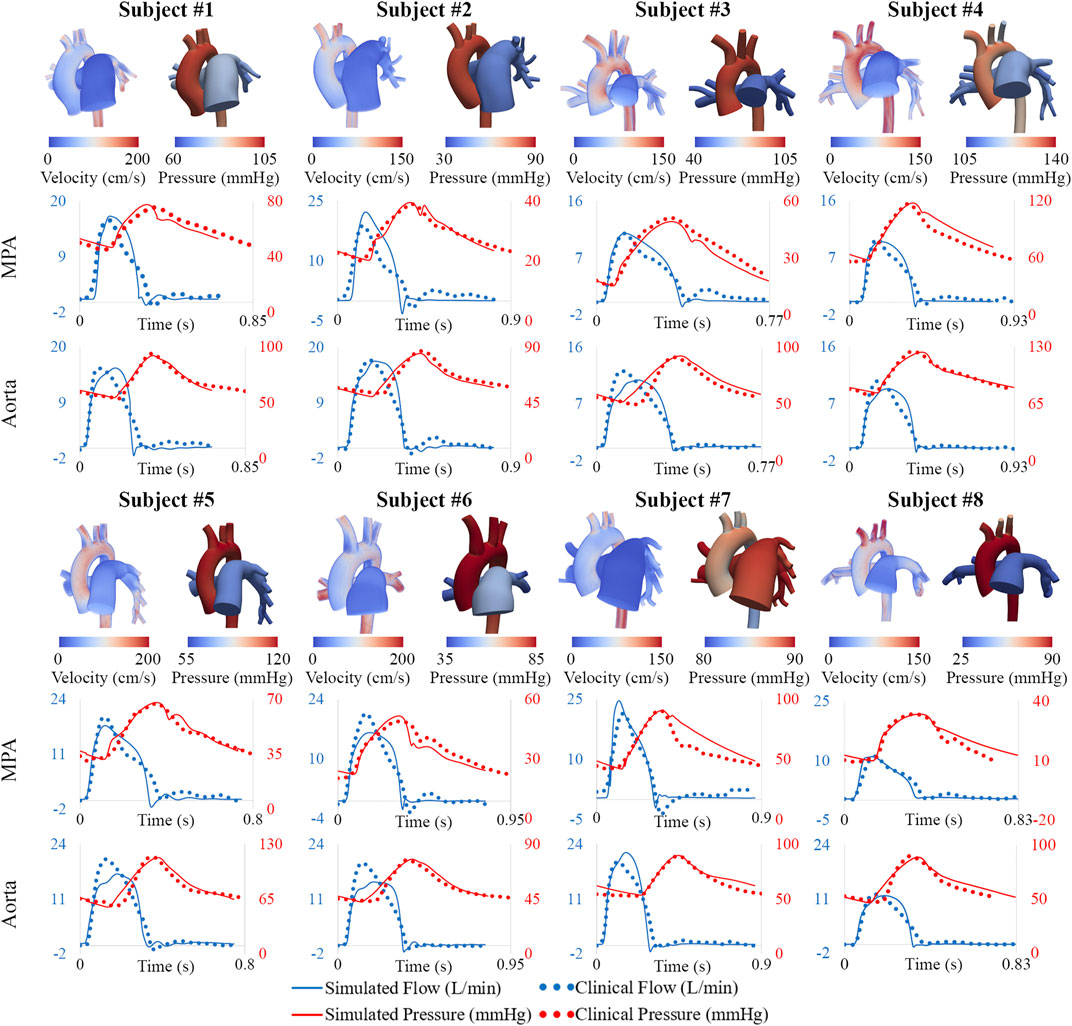
FIGURE 8. Velocity and pressure maps of the high-resolution arterial models at peak systole. Hemodynamic comparison shows agreement between simulated and clinical data.
The distribution of central and peripheral pulmonary vasculature resistance and compliance was obtained. Central (e.g., 3D) pulmonary arteries contributed to 8% ± 8% and 56% ± 19% of the total pulmonary resistance and compliance, respectively (Figure 9).
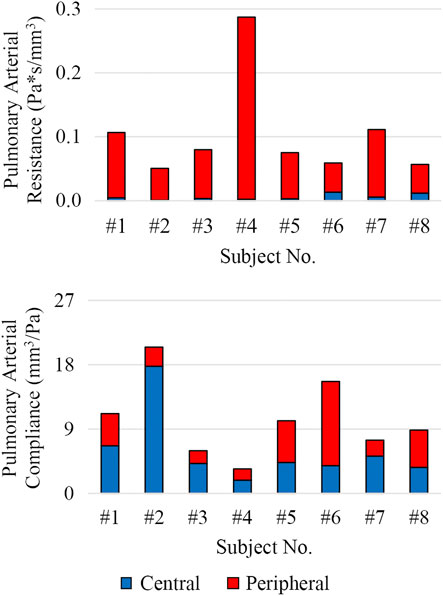
FIGURE 9. Distribution of total pulmonary arterial resistance and compliance between central (3D model, shown in blue) and peripheral (lumped-parameter models, shown in red) pulmonary vessels.
MPA stiffness (206.6 ± 159.7 kPa) was found to be higher and have a greater variability than AAo stiffness (146.7 ± 19.2 kPa), in line with the severity and disease heterogeneity of these patients. LPA, RPA, and DTA stiffness were estimated to be 163.0 ± 192.3 kPa, 130.4 ± 105.6 kPa, and 227.3 ± 66.4 kPa, respectively.
Pulmonary and systemic arterial pulse wave velocity were estimated to be 3.5 ± 1.5 m/s from the MPA to the LPA, 3.0 ± 0.9 m/s from the MPA to the RPA, and 3.9 ± 1.0 m/s from the AAo to the DTA. Pulmonary arterial stiffness and pulse wave velocity in our patient cohort were higher than in healthy pediatric subjects (Friesen et al., 2019), confirming that our results capture arterial remodeling reflective of PAH.
Subject #4 had the highest pulmonary resistance, lowest pulmonary arterial compliance, highest pulmonary artery stiffness, highest MPA-LPA pulse wave velocity, and near systemic level of pulmonary arterial pressure, indicating that this subject has the most severe form of pulmonary arterial dysfunction. Furthermore, Subject #4 was the only subject with a pulmonary arterial compliance index below the critical threshold value of 0.9 ml/mmHg/m2, which has been correlated with a significant reduction in life expectancy (Mahapatra et al., 2006).
3.2 High-resolution ventricular models
Following model calibration (see Table 3), simulated PV loops and arterial pressures were closely matched to clinical data (Figure 10). On average, RV end-diastolic (99.0 ± 44.6 ml) and end-systolic (58.5 ± 23.4 ml) volumes were larger than their LV counterparts (83.5 ± 23.4 ml and 43.0 ± 14.7 ml, respectively). RV stroke work (0.30 ± 0.17 J) was calculated to be 69% of LV stroke work (0.42 ± 0.14 J). RV ejection fraction (42% ± 5%) was lower than LV ejection fraction (51% ± 5%). Of note, RV ejection fraction in our patients was found to be significantly lower than in healthy pediatric subjects (58% ± 5%) (Friesen et al., 2019), indicating ventricular remodeling.
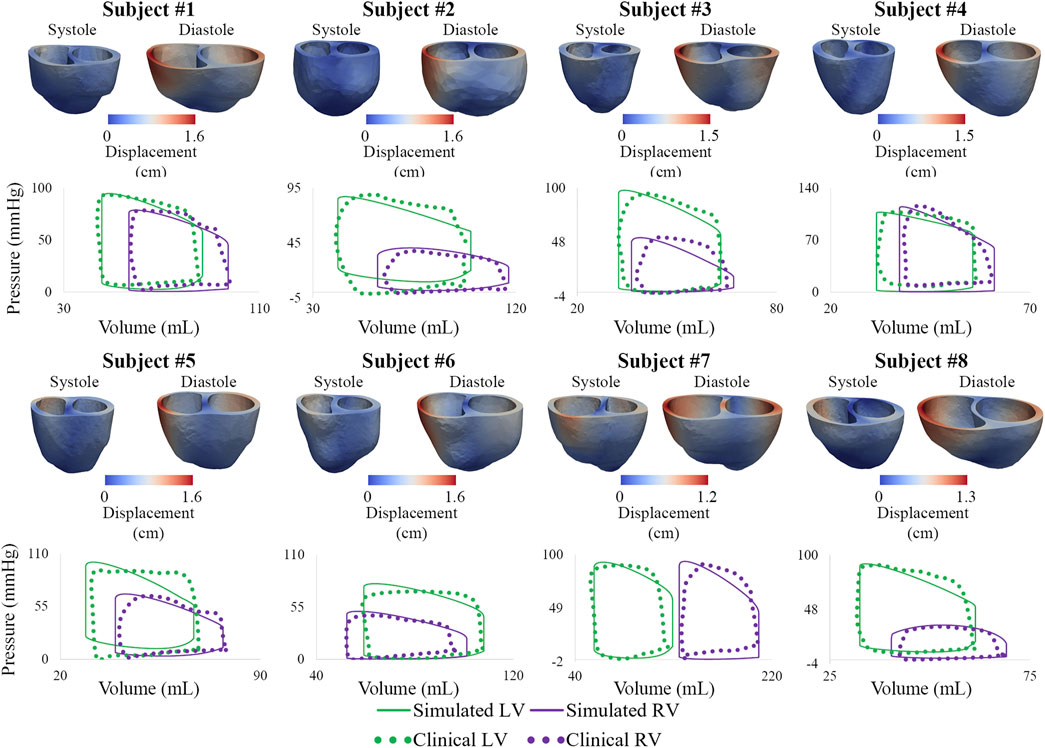
FIGURE 10. Displacement maps of ventricular models at end-systole and end-diastole. Comparison of LV and RV PV loops shows agreement between simulated and clinical data.
Calibrated ventricular models were used to derive arterial and RV elastance metrics: ESPVR = 1.32 ± 0.78 mmHg/ml; Ea = 1.84 ± 0.78 mmHg/ml; ESPVR/Ea = 0.75 ± 0.21. RV ESPVR in our cohort was found to be higher than in pediatric patients with repaired tetralogy of Fallot (0.32 ± 0.15 mmHg/ml) (Apitz et al., 2009).
Subject #7 had the largest RV end-diastolic volume, largest RV end-systolic volume (Z-score = 5.4), lowest RV ejection fraction (Z-score = −4.0), and largest RV stroke work (0.71 J), suggesting that this patient had the most severe form of RV dysfunction (Alfakih et al., 2003; Sarikouch et al., 2010). Subject #4, who has the most severe form of pulmonary arterial dysfunction (Section 3.1), has relatively normal RV volumes (Friesen et al., 2019), suggesting that this patient has not undergone significant RV remodeling. These results highlight the importance of simultaneously describing arterial and ventricular hemodynamics and biomechanics.
3.3 Metrics for disease severity stratification
The correlation between clinically assessed disease severity (Table 4) and each data- and model-derived metric were ranked using the absolute value of the Spearman’s rank correlation coefficient

TABLE 5. Spearman’s rank correlation coefficients (ρ), p-values, and Benjamini-Hochberg critical value (iQ/m) of each data-derived and model-derived metric resulting from a comparison to clinical disease severity rankings are shown in two columns. A metric is statistically significant if its p-value is lower than its Benjamini-Hochberg critical value (iQ/m).
Mean, systolic, and diastolic pulmonary arterial pressures were significantly correlated with clinically assessed disease severity. Pulmonary capillary wedge pressure, which is a measure of the post-capillary pulmonary circulation (i.e., pulmonary venous pressure and LV end-diastolic pressure), was weakly correlated to disease severity (ρ = −0.071). Systemic mean, systolic, and diastolic pressures were not significantly correlated to disease severity. There were 5 model-derived metrics (Table 5; green) strongly correlated with disease severity. RV contractility (
4 Discussion
Pediatric PAH is a complex disease with a heterogeneous population and multiple compounding factors that contribute to disease progression. It is thus important to identify metrics to stratify patients and to predict disease progression. Computational models enable the study of hemodynamics and biomechanics in the cardiopulmonary and systemic circulations and can be used to describe PAH pathophysiology. In this work, computational models were used to complement clinical data by providing high-resolution description of hemodynamics and biomechanics, including those that are not easy to assess in a clinical setting. To our knowledge, this is one of the first efforts to construct and calibrate two separate high-resolution closed-loop models of pulmonary and systemic arteries and ventricles using data from a pediatric PAH cohort.
Model calibration entailed tuning of numerous model parameters, identifying inconsistencies in clinical data, and developing strategies to mitigate these inconsistencies. Calibrated models could reproduce the following patient-specific data: cardiac output in the MPA and AAo, pressure waveforms at the MPA and DTA, mean flows at the DTA, LPA, and RPA, and LV and RV PV loops. Following calibration, our models were used to derive metrics such as RV ESPVR, arterial elastance (Ea), ESPVR/Ea, ventricular contractility, central pulmonary arterial stiffness and pulse wave velocity, and distribution of pulmonary arterial resistance and compliance between central and peripheral vessels.
Numerous data-derived metrics were correlated with clinical stratification of disease severity. MRI-derived metrics were not significantly correlated with clinical disease severity stratification. The correlation in RV mass index (ρ = 0.738) can be attributed to the adaptive response of the RV (myocardial hypertrophy) to a sustained afterload increase, which can also be linked to the strong correlation seen in RV contractility (
RV contractility (
Our models captured PAH-induced biomechanical adaptations, both in the central (i.e., increase in stiffness and pulse wave velocity) and peripheral (i.e., increase in PVR index) vessels, as well as in the ventricles (i.e., changes in contractility). Increases in pulmonary pressures (i.e., arterial load) were accompanied by increases in RV contractility for the cohort. This suggests that ventricular-arterial coupling was maintained. The weak correlation between model-derived RV ESPVR/Ea and disease severity further supports this observation for the cohort (Vonk Noordegraaf et al., 2017). These findings confirm that computational models of ventricular-arterial interactions can provide additional insight on PAH pathophysiology.
4.1 Clinical Applications
The main clinical application areas of our work are two: 1) the potential for replacing or minimizing the number of invasive catheterization procedures in PAH patients, and 2) a more sensitive method for patient stratification.
4.1.1 Potential for minimization of catheter-based assessment in PAH
Computational models required catheterization data and extensive calibration efforts. However, once calibrated using a large cohort of patient data, these computational models could then be validated against new cohorts of patient data without directly inputting measures derived from invasive pressure. This would entail developing correlations between imaging markers such as MPA diameter and relative area change, RV volume, RV ejection fraction, shape of MPA flow waveforms, etc. (Alunni et al., 2010; Lungu et al., 2014; Lungu et al., 2016; Dawes et al., 2017). Furthermore, our calibrated computational models were used to virtually increase ventricular preload to estimate RV ESPVR which obviates the need for an invasive procedure. This model-derived estimation of RV ESPVR can then be used to provide a description of RV contractility and ventricular-arterial coupling (via ESPVR/Ea), which are both known to play key roles in PAH pathophysiology (Vonk Noordegraaf et al., 2019).
4.1.2 Patient stratification in PAH
Despite significant improvements in the understanding of PAH pathological hemodynamics (Kheyfets et al., 2013; Avazmohammadi et al., 2019; Finsberg et al., 2019; Yang et al., 2019), hurdles remain in PAH patient stratification. In this work, computational models were combined with clinical data to stratify PAH patients according to disease severity, confirming well-established data-derived markers (Sanz et al., 2009; Courand et al., 2015; Yang et al., 2018; Simpson et al., 2019) and elucidating model-derived markers that could aid in risk stratification.
PAH requires life-long medical care, and construction and calibration of each computational model typically requires nearly 1 month. This long calibration timeframe could be reduced with advances in data assimilation methods (Troianowski et al., 2011; Ismail et al., 2013; Arthurs et al., 2020). Therefore, patient-specific computational models could be used to provide insight on PAH pathophysiology and stratification and could ultimately help clinicians tailor a long-term management plan.
5 Limitations
A small number (n = 8) of pediatric PAH patients were included in this study, which affects the strength of the statistical analysis performed to correlate metrics with clinical disease severity stratification. Therefore, due to this small sample size, our analysis was used to broadly describe observed correlations rather than to identify optimal metrics to use in patient stratification. Furthermore, control subjects were not included in our study, which further hinders the ability to identify model parameters for patient stratification. Future extensions of this work will include a greater number of PAH patients as well as control subjects to provide a more robust patient stratification analysis.
A key data inconsistency not addressed in our work was the mismatch in cardiac output between high-resolution arterial and ventricular models. Arterial models were calibrated to match cardiac outputs from PC-MRI data, whereas ventricular models were calibrated to match stroke volumes from truncated ventricular segmentations which yielded lower cardiac outputs. This mismatch stems from truncating the ventricular geometries at the tricuspid valve. Even with this truncation of the ventricular geometries, our ventricular models produced lower RV ejection fraction than those seen in healthy pediatric subjects (Friesen et al., 2019), and outputted metrics that correlated strongly with clinically assessed disease severity.
The number of parameters in our models is much larger than the amount of data used to calibrate our models, which leads to issues of parameter uniqueness and identifiability. However, our choices for the different components of the lumped-parameter circuits are based on well accepted, physiology-motivated, previously developed designs for heart and segments of the circulation (Kim et al., 2009; Lau and Figueroa, 2015; Silva Vieira et al., 2018). The lack of data was offset by (arbitrary) modeling choices such as breakdown of flows proportional to surface areas, ratios of proximal to distal resistances in Windkessel models (Laskey et al., 1990), literature values for certain components of heart models (Mynard et al., 2012; Lau and Figueroa, 2015), etc.
A traditional parameter sensitivity analysis was performed, where the sensitivity of certain computed hemodynamic metrics to 10% changes in model parameters was obtained. The analysis was performed using both the arterial and ventricular models of Subject #6 (Supplementary Tables S6, S7, respectively). The analysis showed that the ventricular models had a larger sensitivity to model parameters than the arterial models. However, this simple analysis does deal address parameter identifiability, as it fails to consider correlation between parameters (Colebank et al., 2021). Therefore, a rigorous sensitivity analysis (outside the scope of this study) that overcomes these limitations is required to assess parameter uniqueness (Matzuka et al., 2015; Perdikaris and Karniadakis, 2016; Caiazzo et al., 2017; Tran et al., 2017; Arthurs et al., 2020; Colebank et al., 2021). This analysis would therefore provide confidence in model-derived metrics and estimated parameters, and also quantify variability in parameters due to uncertainty in clinical data.
Clinically assessed disease severity rankings (Table 4) were used as the gold standard in our disease severity stratification analysis. However, these rankings were based on a combination of hemodynamic metrics and the clinical team’s experience. Even though the clinical team is comprised of pediatric cardiologists with extensive experience in pediatric PAH management, conclusions drawn in our study could be affected by the subjective nature of the disease severity rankings.
High-resolution arterial and ventricular models were not coupled bidirectionally; therefore, parameter calibration in one model does not affect results in the other. The work presented here serves a first step towards the ultimate goal of studying ventricular-vascular coupling in PAH using high-resolution 3D ventricular and arterial models.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics statement
The studies involving human participants were reviewed and approved by the University of Michigan Institutional Review Board. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
CT-B and CF developed and implemented the strategies to mitigate inconsistencies in clinical data. CT-B and NL performed the computational analysis and drafted the manuscript. SS and LL developed and implemented the ventricular modeling framework. CF developed the arterial modeling framework, provided supervision, and drafted the manuscript. KA, BB, RGG, WW, SL, HL, JL, AD, MO, CP, and RJG led patient recruitment and clinical data acquisition. CF, LL, SB, and AD jointly conceived and coordinated the study. All authors read and approved the final manuscript.
Funding
This work was supported by the National Institutes of Health (U01 HL135842), Edward B. Diethrich Professorship, and the Frankel Cardiovascular Center. Computing resources were provided by the National Science Foundation (Grant 1531752): Acquisition of Conflux, A Novel Platform for Data-Driven Computational Physics (Tech. Monitor: Ed Walker). CT-B acknowledges financial support from the National Science Foundation Graduate Research Fellowship Program (DGE1256260) and the University of Michigan Rackham Merit Fellowship.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2022.958734/full#supplementary-material
References
Ahmed Y., Tossas-Betancourt C., van Bakel P. A. J., Primeaux J. M., Weadock W. J., Lu J. C., et al. (2021). Interventional planning for endovascular revision of a lateral tunnel fontan: A patient-specific computational analysis. Front. Physiol. 12, 718254. doi:10.3389/fphys.2021.718254
Alastruey J., Xiao N., Henry F., Tobias S., Figueroa C. A. (2016). On the impact of modelling assumptions in multi-scale , subject-specific models of aortic haemodynamics. J. R. Soc. Interface 13 (119), 20160073. doi:10.1098/rsif.2016.0073
Alfakih K., Plein S., Thiele H., Jones T., Ridgway J. P., Sivananthan M. U. (2003). Normal human left and right ventricular dimensions for MRI as assessed by turbo gradient echo and steady-state free precession imaging sequences. J. Magn. Reson. Imaging 17 (3), 323–329. doi:10.1002/jmri.10262
Alnæs M. S., Blechta J., Hake J., Johansson A., Kehlet B., Logg A., et al. (2015). The FEniCS Project Version 1.5. Arch. Numerical Softw. 3 (100), 9–23. doi:10.11588/ans.2015.100.20553
Alunni J. P., Bruno D., Arnaud C., Tétu L., Blot-Soulétie N., Didier A., et al. (2010). Cardiac MRI in pulmonary artery hypertension: Correlations between morphological and functional parameters and invasive measurements. Eur. Radiol. 20 (5), 1149–1159. doi:10.1007/s00330-009-1664-3
Apitz C., Ludger A. E., Sieverding A. E., Latus H., Anselm A. E., Uebing A. E., et al. (2009). Right ventricular dysfunction and B-type natriuretic peptide in asymptomatic patients after repair for tetralogy of Fallot. Pediatr. Cardiol. 30, 898–904. doi:10.1007/s00246-009-9453-y
Arthurs C. J., Xiao N., Moireau P., Tobias S., Figueroa C. A. (2020). A flexible framework for sequential estimation of model parameters in computational hemodynamics. Adv. Model. Simul. Eng. Sci. 7, 48. doi:10.1186/s40323-020-00186-x
Arthurs C J., Grifka R. G., Agarwal P., Adam L., Dorfman A. J., Figueroa C. A. (2017). Reproducing patient-specific hemodynamics in the blalock–taussig circulation using a flexible multi-domain simulation framework: Applications for optimal shunt design. Front. Pediatr. 5, 78–13. doi:10.3389/fped.2017.00078
Arthurs C. J., Khlebnikov R., Melville A., Marčan M., Gomez A., Dillon-Murphy D., et al. (2021). Crimson: An open-source software framework for cardiovascular integrated modelling and simulation. PLoS Comput. Biol. 17 (5), e1008881. doi:10.1371/journal.pcbi.1008881
Arthurs C. J., Lau K. D., Asrress K. N., Redwood S. R., Figueroa C. A. (2016). A mathematical model of coronary blood flow control: Simulation of patient-specific three-dimensional hemodynamics during exercise.fic three-dimensional hemodynamics during exercise. Am. J. Physiol. Heart Circ. Physiol. 310 (9), H1242–H1258. doi:10.1152/ajpheart.00517.2015
Avazmohammadi R., Mendiola E. A., Li D. S., Vanderslice P., Dixon R. A. F., Sacks M. S. (2019). Interactions between structural remodeling and hypertrophy in the right ventricle in response to pulmonary arterial hypertension. J. Biomech. Eng. 141 (9), 091016. doi:10.1115/1.4044174
Bayer J. D., Blake R. C., Plank G., Trayanova N. A. (2012). A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models. Ann. Biomed. Eng. 40 (10), 2243–2254. doi:10.1007/s10439-012-0593-5
Benjamini Y., Hochberg Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Methodol. 57 (1), 289–300. doi:10.1111/J.2517-6161.1995.TB02031.X
Berger R. M. F., Bonnet D. (2010). Treatment options for paediatric pulmonary arterial hypertension. Eur. Respir. Rev. 19 (118), 321–330. doi:10.1183/09059180.00008410
Bikia V., Pagoulatou S, Trachet B., Soulis D., Protogerou A. D., Papaioannou T. G., et al. (2020). Noninvasive cardiac output and central systolic pressure from cuff-pressure and pulse wave velocity. IEEE J. Biomed. Health Inf. 24 (7), 1968–1981. doi:10.1109/JBHI.2019.2956604
Brown K. A., Ditchey R. v. (1988). Human right ventricular end-systolic pressure-volume relation defined by maximal elastance. Circulation 78 (1), 81–91. doi:10.1161/01.CIR.78.1.81
Caiazzo A., Caforio F., Montecinos G., Muller L. O., Blanco P. J., Toro E. F. (2017). Assessment of reduced-order unscented kalman filter for parameter identification in 1-dimensional blood flow models using experimental data. Int. J. Numer. Method. Biomed. Eng. 33 (8), e2843. doi:10.1002/CNM.2843
Caudron J., Fares J., Lefebvre V., Vivier P. H., Petitjean C., Dacher J. N. (2012). Cardiac MRI assessment of right ventricular function in acquired heart disease. Factors of variability. Acad. Radiol. 19 (8), 991–1002. doi:10.1016/j.acra.2012.03.022
Chabiniok R., Wang V. Y., Hadjicharalambous M., Asner L., Lee J., Sermesant M., et al. (2016). Multiphysics and multiscale modelling, data–model fusion and integration of organ physiology in the clinic: Ventricular cardiac mechanics. Interface Focus 6 (2), 20150083. doi:10.1098/RSFS.2015.0083
Colebank M. J., Umar Qureshi M., Olufsen M. S. (2021). Sensitivity analysis and uncertainty quantification of 1-D models of pulmonary hemodynamics in mice under control and hypertensive conditions. Int. J. Numer. Method. Biomed. Eng. 37 (11), e3242. doi:10.1002/CNM.3242
Costa K. D., Holmes J. W., Mcculloch A. D. (2001). Modelling cardiac mechanical properties in three dimensions. Philosophical Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 359 (1783), 1233–1250. doi:10.1098/RSTA.2001.0828
Courand P. Y., Jomir G. P., Khouatra C., Scheiber C., Turquier S., Glérant J. C., et al. (2015). Prognostic value of right ventricular ejection fraction in pulmonary arterial hypertension. Eur. Respir. J. 45 (1), 139–149. doi:10.1183/09031936.00158014
Cuomo F., Ferruzzi J., Agarwal P., Chen L., Zhuang Z. W., Humphrey J. D., et al. (2019). Sex-dependent differences in central artery haemodynamics in normal and fibulin-5 deficient mice: Implications for ageing. Proc. Math. Phys. Eng. Sci. 475 (2221), 20180076. doi:10.1098/rspa.2018.0076
Dawes T. J. W., de Marvao A, Shi W., Fletcher T., Geoffrey M., Watson J., et al. (2017). Machine learning of threedimensional right ventricular motion enables outcome prediction in pulmonary hypertension: A cardiac MR imaging study. Radiology 283 (2), 381–390. doi:10.1148/RADIOL.2016161315/SUPPL_FILE/RY161315SUPPF3.JPG
Dell’Italia L. J., Walsh R. A. (1988). Application of a time varying elastance model to right ventricular performance in man. Cardiovasc. Res. 22 (12), 864–874. doi:10.1093/cvr/22.12.864
Douwes J. M., Roofthooft M. T. R., Bartelds B., Talsma M. D., Hillege H. L., Berger R. M. F. (2013). Pulsatile haemodynamic parameters are predictors of survival in paediatric pulmonary arterial hypertension. Int. J. Cardiol. 168 (2), 1370–1377. doi:10.1016/j.ijcard.2012.12.080
Figueroa C. A., Vignon-Clementel I. E., Jansen K. E., Hughes T. J. R., Taylor C. A. (2006). A coupled momentum method for modeling blood flow in three-dimensional deformable arteries. Comput. Methods Appl. Mech. Eng. 195 (41–43), 5685–5706. doi:10.1016/j.cma.2005.11.011
Finsberg H., Xi C., Tan J. L., Zhong L., Genet M., Sundnes J., et al. (2018). Efficient estimation of personalized biventricular mechanical function employing gradient-based optimization. Int. J. Numer. Method. Biomed. Eng. 34 (7), e2982. doi:10.1002/cnm.2982
Finsberg H., Xi C., Zhao X., Tan J., Genet M., Sundnes J., et al. (2019). Computational quantification of patient-specific changes in ventricular dynamics associated with pulmonary hypertension. Am. J. Physiol. Heart Circ. Physiol. 317 (6), H1363–H1375. doi:10.1152/AJPHEART.00094.2019
Friesen R. M., Michal Schäfer D., Dunbar I., Abman S. H., Stenmark K., Browne L. P., et al. (2019). Proximal pulmonary vascular stiffness as a prognostic factor in children with pulmonary arterial hypertension. Eur. Heart J. Cardiovasc. Imaging 20 (2), 209–217. doi:10.1093/ehjci/jey069
Gan C. T. J., Lankhaar J.-W., Marcus J. T., Westerhof N., Marques K. M., Bronzwaer J. G. F., et al. (2006). Impaired left ventricular filling due to right-to-left ventricular interaction in patients with pulmonary arterial hypertension. Am. J. Physiol. Heart Circ. Physiol. 290, 1528–1533. doi:10.1152/ajpheart.01031.2005
Geuzaine C., Remacle J. F. (2009). Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 79 (11), 1309–1331. doi:10.1002/nme.2579
Guccione J. M., Waldman L. K., McCulloch A. D. (1993). Mechanics of active contraction in cardiac muscle: Part II—cylindrical models of the systolic left ventricle. J. Biomech. Eng. 115 (1), 82–90. doi:10.1115/1.2895474
Guccione J. M., Mcculloch A. D., Waldman L. K. (1991). Passive material properties of intact ventricular myocardium determined from a cylindrical model. J. Biomech. Eng. 113 (1), 42–55. doi:10.1115/1.2894084
Gültekin O., Sommer G., Holzapfel G. A. (2016). An orthotropic viscoelastic model for the passive myocardium: Continuum basis and numerical treatment. Comput. Methods Biomech. Biomed. Engin. 19 (15), 1647–1664. doi:10.1080/10255842.2016.1176155
Gusseva M., Castellanos D. A., Greer J S., Hussein M. A., Hasbani K., Greil G., et al. (2022). Time-synchronization of interventional cardiovascular magnetic resonance data using a biomechanical model for pressure-volume loop analysis. J. Magn. Reson. Imaging. doi:10.1002/JMRI.28216
Gusseva M., Greer J. S., Castellanos D. A., Hussein M. A., Greil G., Surendranath R., et al. (2021). “Model-assisted time-synchronization of cardiac MR image and catheter pressure data,” in Lecture notes in computer science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformatics) (Cham: Springer), 12738 LNCS, 362–372. doi:10.1007/978-3-030-78710-3_35
Guz A., Innes J. A., Murphy K. (1987). Respiratory modulation of left ventricular stroke volume in man measured using pulsed Doppler ultrasound. J. Physiol. 393 (1), 499–512. doi:10.1113/JPHYSIOL.1987.SP016836
Hadjicharalambous M., Stoeck C. T., Weisskopf M., Cesarovic N., Ioannou E., Vavourakis V., et al. (2021). Investigating the reference domain influence in personalised models of cardiac mechanics: Effect of unloaded geometry on cardiac biomechanics. Biomech. Model. Mechanobiol. 20, 1579–1597. doi:10.1007/s10237-021-01464-2
Hardziyenka M., Campian M. E., Reesink H. J., Surie S., Bouma B. J., Groenink M., et al. (2011). Right ventricular failure following chronic pressure overload is associated with reduction in left ventricular mass: Evidence for atrophic remodeling. J. Am. Coll. Cardiol. 57 (8), 921–928. doi:10.1016/j.jacc.2010.08.648
Hirai T., Sasayama S., Kawasaki T., Yagi S. I. (1989). Stiffness of systemic arteries in patients with myocardial infarction. A noninvasive method to predict severity of coronary atherosclerosis. Circulation 80 (1), 78–86. doi:10.1161/01.CIR.80.1.78
Holzapfel G. A., Gasser T. C., Ogden R. W. (2000). A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 61 (1), 1–48. doi:10.1023/A:1010835316564
Humphrey J. D., Taylor C. A. (2008). Intracranial and abdominal aortic aneurysms: Similarities, differences, and need for a new class of computational models. Annu. Rev. Biomed. Eng. 10 (1), 221–246. doi:10.1146/annurev.bioeng.10.061807.160439
Hunter P. J., McCulloch A. D., ter Keurs H. E. D. J. (1998). Modelling the mechanical properties of cardiac muscle. Prog. Biophys. Mol. Biol. 69 (2–3), 289–331. doi:10.1016/S0079-6107(98)00013-3
Ismail M., Wall W. A., Gee M. W. (2013). Adjoint-based inverse analysis of Windkessel parameters for patient-specific vascular models. J. Comput. Phys. 244, 113–130. doi:10.1016/J.JCP.2012.10.028
Ivy D. D., Rosenzweig E. B., Lemarié J. -C., Brand M., Rosenberg D., Barst R. J. (2010). Long-term outcomes in children with pulmonary arterial hypertension treated with bosentan in real-world clinical settings. Am. J. Cardiol. 106 (9), 1332–1338. doi:10.1016/j.amjcard.2010.06.064
Kass D. A., Yamazaki T., Burkhoff D., Maughan W. L., Sagawa K. (1986). Determination of left ventricular end-systolic pressure-volume relationships by the conductance (volume) catheter technique. Circulation 73 (3), 586–595. doi:10.1161/01.CIR.73.3.586
Kheyfets V. O., Rios L., Smith T., Schroeder T., Mueller J., Murali S., et al. (2015). Patient-specific computational modeling of blood flow in the pulmonary arterial circulation. Comput. Methods Programs Biomed. 120 (2), 88–101. doi:10.1016/j.cmpb.2015.04.005
Kheyfets V. O., O’Dell W., Smith T., Reilly J. J., Finol E. A. (2013). Considerations for numerical modeling of the pulmonary circulation - a Review with a focus on pulmonary hypertension. J. Biomechanical Eng. 135 (6), 61011–61015. American Society of Mechanical Engineers Digital Collection. doi:10.1115/1.4024141
Kim H. J., Vignon-Clementel I. E., Figueroa C. A., Ladisa J. F., Jansen K. E., Feinstein J. A., et al. (2009). On coupling a lumped parameter heart model and a three-dimensional finite element aorta model. Ann. Biomed. Eng. 37 (11), 2153–2169. doi:10.1007/s10439-009-9760-8
Kjellström B., Anthony L., Ostenfeld E. (2020). Cardiac magnetic resonance imaging in pulmonary arterial hypertension: Ready for clinical practice and guidelines? Curr. Heart Fail. Rep. 17 (5), 181–191. doi:10.1007/s11897-020-00479-7
Klein S. S., Graham T. P., Lorenz C. H. (1998). Noninvasive delineation of normal right ventricular contractile motion with magnetic resonance imaging myocardial tagging. Ann. Biomed. Eng. 26 (5), 756–763. doi:10.1114/1.75
Laskey W. K., Parker H. G., Ferrari V. A., Kussmaul W. G., Noordergraaf A. (1990). Estimation of total systemic arterial compliance in humans. J. Appl. Physiol., 69, 112–119. doi:10.1152/JAPPL.1990.69.1.112
Lau K. D., Figueroa C. A. (2015). Simulation of short-term pressure regulation during the tilt test in a coupled 3D–0D closed-loop model of the circulation. Biomech. Model. Mechanobiol. 14 (4), 915–929. doi:10.1007/s10237-014-0645-x
Lazar J. M., Flores A. R., Grandis D. J., Orie J. E., Schulman D. S. (1993). Effects of chronic right ventricular pressure overload on left ventricular diastolic function. Am. J. Cardiol. 72 (15), 1179–1182. doi:10.1016/0002-9149(93)90990-T
Li N., Zhang S., Hou J., Jang I. K., Yu B. (2012). Assessment of pulmonary artery morphology by optical coherence tomography. Heart Lung Circ. 21 (12), 778–781. doi:10.1016/j.hlc.2012.07.014
Lungu A., Swift A. J., Capener D., Kiely D., Hose R., Wild J. M. (2016). Diagnosis of pulmonary hypertension from magnetic resonance imaging-based computational models and decision tree analysis. Pulm. Circ. 6 (2), 181–190. doi:10.1086/686020
Lungu A., Wild J. M., Capener D., Kiely D. G., Swift A. J., Hose D. R. (2014). MRI model-based non-invasive differential diagnosis in pulmonary hypertension. J. Biomech. 47 (12), 2941–2947. doi:10.1016/J.JBIOMECH.2014.07.024
Manders E., Jan Bogaard H., Handoko M. L., van de Veerdonk M. C., Keogh A., Westerhof N., et al. (2014). Contractile dysfunction of left ventricular cardiomyocytes in patients with pulmonary arterial hypertension. J. Am. Coll. Cardiol. 64 (1), 28–37. doi:10.1016/J.JACC.2014.04.031
Marsden A. L. (2013). Simulation based planning of surgical interventions in pediatric cardiology. Phys. Fluids 25 (10), 101303. doi:10.1063/1.4825031
Matzuka B., Mehlsen J., Tran H., Olufsen M. S. (2015). Using kalman filtering to predict time-varying parameters in a model predicting baroreflex regulation during head-up tilt. IEEE Trans. Biomed. Eng. 62 (8), 1992–2000. doi:10.1109/TBME.2015.2409211
Miller C. A., Jordan P., Borg A., Argyle R., Clark D., Pearce K., et al. (2013). Quantification of left ventricular indices from SSFP cine imaging: Impact of real-world variability in analysis methodology and utility of geometric modeling. J. Magn. Reson. Imaging 37 (5), 1213–1222. doi:10.1002/jmri.23892
Miller R., Kerfoot E., Mauger C., Ismail T. F., Young A. A., Nordsletten D. A. (2021). An implementation of patient-specific biventricular mechanics simulations with a deep learning and computational pipeline. Front. Physiol. 12, 1398. doi:10.3389/fphys.2021.716597
Mynard J. P., Davidson M. R., Penny D. J., Smolich J. J. (2012). A simple, versatile valve model for use in lumped parameter and one-dimensional cardiovascular models. Int. J. Numer. Method. Biomed. Eng. 28 (6–7), 626–641. doi:10.1002/cnm.1466
Niederer S. A., Hunter P. J., Smith N. P. (2006). A quantitative analysis of cardiac myocyte relaxation: A simulation study. Biophys. J. 90, 1697–1722. doi:10.1529/biophysj.105.069534
Nordsletten D. A., Niederer S. A., Nash M. P., Hunter P. J., Smith N. P. (2011). Coupling multi-physics models to cardiac mechanics. Prog. Biophys. Mol. Biol. 104 (1–3), 77–88. doi:10.1016/J.PBIOMOLBIO.2009.11.001
Nordsletten D., Capilnasiu A., Zhang W., Anna W., Hadjicharalambous M., Sommer G., et al. (2021). A viscoelastic model for human myocardium. Acta Biomater. 135, 441–457. doi:10.1016/J.ACTBIO.2021.08.036
Perdikaris P., Karniadakis G. E. (2016). Model inversion via multi-fidelity bayesian optimization: A new paradigm for parameter estimation in haemodynamics, and beyond. J. R. Soc. Interface 13 (118), 20151107. doi:10.1098/RSIF.2015.1107
Petitjean C., Dacher J. N. (2011). A Review of segmentation methods in short Axis cardiac MR images. Med. Image Anal. 15 (2), 169–184. Elsevier. doi:10.1016/j.media.2010.12.004
Pinto J. G., Fung Y. C. (1973). Mechanical properties of the heart muscle in the passive state. J. Biomech. 6 (6), 597–616. doi:10.1016/0021-9290(73)90017-1
Rausch M. K., Dam A., Göktepe S., Abilez O. J., Kuhl E. (2011). Computational modeling of growth: Systemic and pulmonary hypertension in the heart. Biomech. Model. Mechanobiol. 10 (6), 799–811. doi:10.1007/s10237-010-0275-x
Rice J. J., Wang F., Bers D. M., de Tombe P. P. (2008). Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys. J. 95 (5), 2368–2390. doi:10.1529/BIOPHYSJ.107.119487
Roccabianca S., Figueroa C. A., Tellides G., Humphrey J. D. (2014). Quantification of regional differences in aortic stiffness in the aging human. J. Mech. Behav. Biomed. Mat. 29, 618–634. doi:10.1016/j.jmbbm.2013.01.026
Rogers W. J., Shapiro E. P., Weiss J. L., Buchalter M. B., Rademakers F. E., Weisfeldt M. L., et al. (1991). Quantification of and correction for left ventricular systolic long-Axis shortening by magnetic resonance tissue tagging and slice isolation. Circulation 84 (2), 721–731. doi:10.1161/01.CIR.84.2.721
Sahni O., Müller J., Jansen K. E., Shephard M. S., Taylor C. A. (2006). Efficient anisotropic adaptive discretization of the cardiovascular system. Comput. Methods Appl. Mech. Eng. 195 (41–43), 5634–5655. doi:10.1016/j.cma.2005.10.018
Sankaran S., Esmaily Moghadam M., Kahn A. M., Tseng E. E., Guccione J. M., Marsden A. L. (2012). Patient-specific multiscale modeling of blood flow for coronary artery bypass graft surgery. Ann. Biomed. Eng. 40 (10), 2228–2242. doi:10.1007/s10439-012-0579-3
Sanz J., Kariisa M., Dellegrottaglie S., Prat-González S., Garcia M. J., Fuster V., et al. (2009). Evaluation of pulmonary artery stiffness in pulmonary hypertension with cardiac magnetic resonance. JACC. Cardiovasc. Imaging 2 (3), 286–295. doi:10.1016/j.jcmg.2008.08.007
Sarikouch S., Peters B., Gutberlet M., Leismann B., Kelter-Kloepping A., Koerperich H., et al. (2010). Sex-specific pediatric percentiles for ventricular size and mass as reference values for cardiac MRI assessment by steady-state free-precession and phase-contrast MRI flow. Circ. Cardiovasc. Imaging 3 (1), 65–76. doi:10.1161/CIRCIMAGING.109.859074
Schmid H., O’Callaghan P., Nash M. P., Lin W., LeGrice I. J., Smaill B. H., et al. (2007). Myocardial material parameter estimation: A non-homogeneous finite element study from simple shear tests. Biomech. Model. Mechanobiol. 7 (3), 161–173. doi:10.1007/S10237-007-0083-0
Shavik S. M., Tossas-Betancourt C., Figueroa C. A., Baek S., Lee L. C. (2020). Multiscale modeling framework of ventricular-arterial Bi-directional interactions in the cardiopulmonary circulation. Front. Physiol. 11, 2–13. doi:10.3389/fphys.2020.00002
Shavik S. M., Wall S., Sundnes J., Guccione J. M., Sengupta P., et al. (2021). Computational modeling studies of the roles of left ventricular geometry, afterload, and muscle contractility on myocardial strains in heart failure with preserved ejection fraction. J. Cardiovasc. Transl. Res. 14, 1131–1145. doi:10.1007/S12265-021-10130-Y
Shavik S. M., Zhong L., Zhao X., Lee L. C. (2019). In-silico assessment of the effects of right ventricular assist device on pulmonary arterial hypertension using an image based biventricular modeling framework. Mech. Res. Commun. 97, 101–111. doi:10.1016/j.mechrescom.2019.04.008
Shimoda L. A., Laurie S. S. (2013). Vascular remodeling in pulmonary hypertension. J. Mol. Med. 91 (3), 297–309. doi:10.1007/s00109-013-0998-0
Silva Vieira M., Arthurs C. J., Hussain T., Razavi R., Figueroa C. A. (2018). Patient-specific modeling of right coronary circulation vulnerability post-liver transplant in alagille’s syndrome. PLoS ONE 13 (11), e0205829–16. doi:10.1371/journal.pone.0205829
Simonneau G., Montani D., Celermajer D. S., Denton C. P., Gatzoulis M. A., Krowka M., et al. (2019). Haemodynamic definitions and updated clinical classification of pulmonary hypertension. Eur. Respir. J. 53 (1), 1801913. doi:10.1183/13993003.01913-2018
Simpson C. E., Damico R. L., Todd M., Kolb S. C. M., Khair R. M., Sato T., et al. (2019). Ventricular mass as a prognostic imaging biomarker in incident pulmonary arterial hypertension. Eur. Respir. J. 53 (4), 1802067. doi:10.1183/13993003.02067-2018
Sommer G., Schriefl A. J., Andrä M., Sacherer M., Viertler C., Wolinski H., et al. (2015). Biomechanical properties and microstructure of human ventricular myocardium. Acta Biomater. 24, 172–192. doi:10.1016/J.ACTBIO.2015.06.031
Strait J. B., Lakatta E. G. (2012). Aging-associated cardiovascular changes and their relationship to heart failure. Heart fail. Clin. 8, 143–164. doi:10.1016/j.hfc.2011.08.011
Streeter D. D., Spotnitz H. M., Patel D. P., Ross J., Sonnenblick E. H. (1969). Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 24 (3), 339–347. doi:10.1161/01.RES.24.3.339
Tang B. T., Pickard S. S., Chan F. P., Tsao P. S., Tsao P. S., Taylor C. A., et al. (2012). Wall shear stress is decreased in the pulmonary arteries of patients with pulmonary arterial hypertension: An image-based, computational fluid dynamics study. Pulm. Circ. 2 (4), 470–476. doi:10.4103/2045-8932.105035
Taylor C. A., Figueroa C. A. (2009). Patient-specific modeling of cardiovascular mechanics. Annu. Rev. Biomed. Eng. 11, 109–134. doi:10.1146/annurev.bioeng.10.061807.160521
Tran J. S., Schiavazzi D. E., Ramachandra A. B., Kahn A. M., Marsden A. L. (2017). Automated tuning for parameter identification and uncertainty quantification in multi-scale coronary simulations. Comput. Fluids 142, 128–138. doi:10.1016/J.COMPFLUID.2016.05.015
Troianowski G., Taylor C. A., Feinstein J. A., Vignon-Clementel I. E. (2011). Three-dimensional simulations in glenn patients: Clinically based boundary conditions, hemodynamic results and sensitivity to input data. J. Biomech. Eng. 133 (11), 111006. doi:10.1115/1.4005377
van Bakel T. M. J., Arthurs C. J., Nauta F. J. H., Eagle K. A., van Herwaarden J. A., Moll F. L., et al. (2019). Cardiac remodelling following thoracic endovascular aortic repair for descending aortic aneurysms. Eur. J. Cardiothorac. Surg. 55 (6), 1061–1070. doi:10.1093/ejcts/ezy399
Vignon-Clementel I. E., Figueroa C. A., Jansen K. E., Taylor C. A. (2006). Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput. Methods Appl. Mech. Eng. 195, 3776–3796. doi:10.1016/j.cma.2005.04.014
Vonk Noordegraaf A., Chin K. M., Haddad F., Hassoun P. M., Hemnes A. R., Hopkins S. R., et al. (2019). Pathophysiology of the right ventricle and of the pulmonary circulation in pulmonary hypertension: An update. Eur. Respir. J. 53, 1801900. doi:10.1183/13993003.01900-2018
Vonk Noordegraaf A., Westerhof B. E., Westerhof N. (2017). The relationship between the right ventricle and its load in pulmonary hypertension. J. Am. Coll. Cardiol. 69 (2), 236–243. doi:10.1016/j.jacc.2016.10.047
Wong A. Y. K. (1971). Mechanics of cardiac muscle, based on huxley’s model: Mathematical simulation of isometric contraction. J. Biomechanics 4 (6), 529–540. doi:10.1016/0021-9290(71)90042-X
Xiao N., Alastruey J., Figueroa C. A. (2014). A systematic comparison between 1-D and 3-D hemodynamics in compliant arterial models. Int. J. Numer. Method. Biomed. Eng. 30 (2), 204–231. doi:10.1002/CNM.2598
Xiao N., Humphrey J. D., Figueroa C. A. (2013). Multi-scale computational model of three-dimensional hemodynamics within a deformable full-body arterial network. J. Comput. Phys. 244, 22–40. doi:10.1016/j.jcp.2012.09.016
Yang W., Dong M., Rabinovitch M., Chan F. P., Marsden A. L., Feinstein J. A. (2019). Evolution of hemodynamic forces in the pulmonary tree with progressively worsening pulmonary arterial hypertension in pediatric patients. Biomech. Model. Mechanobiol. 18 (3), 779–796. doi:10.1007/s10237-018-01114-0
Yang W., Marsden A. L., Ogawa M. T., Sakarovitch C., Hall K. K., Rabinovitch M., et al. (2018). Right ventricular stroke work correlates with outcomes in pediatric pulmonary arterial hypertension. Pulm. Circ. 8 (3), 2045894018780534. doi:10.1177/2045894018780534
Zambrano B. A., McLean N. A., Zhao X., Tan J. L., Zhong L., Figueroa C. A., et al. (2018). Image-based computational assessment of vascular wall mechanics and hemodynamics in pulmonary arterial hypertension patients. J. Biomech. 68, 84–92. doi:10.1016/j.jbiomech.2017.12.022
Keywords: pulmonary arterial hypertension, computational modeling, ventricular-arterial coupling, biomechanics, patient stratification, ventricular mechanics, arterial hemodynamics
Citation: Tossas-Betancourt C, Li NY, Shavik SM, Afton K, Beckman B, Whiteside W, Olive MK, Lim HM, Lu JC, Phelps CM, Gajarski RJ, Lee S, Nordsletten DA, Grifka RG, Dorfman AL, Baek S, Lee LC and Figueroa CA (2022) Data-driven computational models of ventricular-arterial hemodynamics in pediatric pulmonary arterial hypertension. Front. Physiol. 13:958734. doi: 10.3389/fphys.2022.958734
Received: 31 May 2022; Accepted: 01 August 2022;
Published: 07 September 2022.
Edited by:
Fang-Bao Tian, University of New South Wales Canberra, AustraliaReviewed by:
Brody Foy, Harvard Medical School, United StatesVasiliki Bikia, Swiss Federal Institute of Technology Lausanne, Switzerland
Copyright © 2022 Tossas-Betancourt, Li, Shavik, Afton, Beckman, Whiteside, Olive, Lim, Lu, Phelps, Gajarski, Lee, Nordsletten, Grifka, Dorfman, Baek, Lee and Figueroa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: C. Alberto Figueroa, ZmlndWVyb2NAbWVkLnVtaWNoLmVkdQ==
 Christopher Tossas-Betancourt
Christopher Tossas-Betancourt Nathan Y. Li
Nathan Y. Li Sheikh M. Shavik
Sheikh M. Shavik Katherine Afton4
Katherine Afton4 Heang M. Lim
Heang M. Lim Jimmy C. Lu
Jimmy C. Lu Simon Lee
Simon Lee David A. Nordsletten
David A. Nordsletten Ronald G. Grifka
Ronald G. Grifka Adam L. Dorfman
Adam L. Dorfman Seungik Baek
Seungik Baek Lik Chuan Lee
Lik Chuan Lee C. Alberto Figueroa
C. Alberto Figueroa