- 1Institute of Data Science, Data Analysis and Intelligence, German Aerospace Center(DLR), Jena, Germany
- 2Data Science in Earth Observation(SiPEO), Technical University of Munich(TUM), Munich, Germany
- 3Remote Sensing Technology Institute, Earth Observation Center, German Aerospace Center(DLR), Oberpfaffenhofen, Jena, Germany
Deep Learning usually requires large amounts of labeled training data. In remote sensing, deep learning is often applied for land cover and land use classification as well as street network and building segmentation. In case of the latter, a common way of obtaining training labels is to leverage crowdsourced datasets which can provide numerous types of spatial information on a global scale. However, labels from crowdsourced datasets are often limited in the sense that they potentially contain high levels of noise. Understanding how such noisy labels impede the predictive performance of Deep Neural Networks (DNNs) is crucial for evaluating if crowdsourced data can be an answer to the need for large training sets by DNNs. One way towards this understanding is to identify the factors which affect the relationship between label noise and predictive performance of a model. The size of the training set could be one of these factors since it is well known for being able to greatly influence a model’s predictive performance. In this work we pick the size of the training set and study its influence on the robustness of a model against a common type of label noise known as omission noise. To this end, we utilize a dataset of aerial images for building segmentation and create several versions of the training labels by introducing different amounts of omission noise. We then train a state-of-the-art model on subsets of varying size of those versions. Our results show that the training set size does play a role in affecting the robustness of our model against label noise: A large training set improves the robustness of our model against omission noise.
1 Introduction
Deep Neural Networks (DNNs) are the state of the art for the classification and segmentation of imagery data. The training of such models usually requires large amounts of labeled samples, which are often difficult to obtain. In the remote sensing domain, one way of acquiring such a labeled dataset is the utilization of crowdsourcing for label generation. For example, the popular source OpenStreetMap project (OSM) combines data from volunteers and public institutions into a large-scale geographic dataset from which locations and shapes of streets and buildings can be extracted and be used as training labels. However, using such information can introduce registration noise and omission noise in the training data (Mnih and Hinton, 2012). Registration noise describes inaccuracies of the location of objects in the label map, while the term of omission noise is used when objects that appear in the imagery are completely missing in the label map. The latter poses a big challenge when crowdsourced datasets are used to generate the training labels, since the spatial distribution of user activity is often very inhomogeneous and thus the degree of omission noise can be extremely high, depending on the area of interest. Therefore, it is of major importance to understand how this type of noise affects the training of a DNN. As of now, this understanding is far from complete. While it has been shown that DNNs are able to memorize label noise completely (Zhang et al., 2017), it also has been observed frequently that DNNs tend to focus on clean labels first and only later in the training process overfit to noise (Arpit et al., 2017; Arazo et al., 2019). Different impacts of noisy labels on predictive performance have been reported, ranging from highly damaging (Rahaman et al., 2021) over negligible (Rolnick et al., 2018; Wang et al., 2018) up to even beneficial under certain circumstances (Henry et al., 2021). This raises the question of what makes a model robust against label noise. It has already been shown that the type of noise is an important factor to consider (Vorontsov and Kadoury, 2021). Other important factors might be the capacity of the model and the complexity of the dataset. To answer the above question, all potentially relevant properties of the model, the data and the noise should be examined and their impact on the model robustness evaluated. We see the size of the training set as one of these potentially relevant properties, since it is an important factor for the model’s predictive performance as well: In order to achieve good performance, a model must be trained on a sufficiently large dataset, otherwise it will likely overfit to the training data. Therefore, in this work we analyze whether the size of a training set has an impact on a model’s robustness against label noise. We view model robustness as the ability of a model to keep the difference between its performance when trained on a clean dataset and its performance when trained on a noisy dataset as low as possible. Our contributions are the following:
• creation of multiple datasets for building segmentation with different sizes and different levels of omission noise
• reporting of multiple performance metrics on a clean test set of DNNs trained on these datasets
• interpreting these results with regard to the role of training set size for model robustness
To this end, we use imagery and corresponding labels from the SpaceNet dataset (Shermeyer et al., 2020). We subsequently introduce noise in the labels and generate subsets of the original dataset with different sizes and different levels of noise. We then train a DNN on each of those subsets and report the performance metrics on a clean test set. Our results will show that changing the training set size does not have an observable impact on the model robustness in most cases, except for very small training set sizes which negatively affect the robustness of our model.
2 Materials and Methods
In this section, we describe the process of creating the dataset, introducing omission noise into the labels, and creating subsets of different sizes. Furthermore, the chosen model and the training procedure are explained.
2.1 Base Dataset
For our experiments, we are using imagery from the 6th SpaceNet competition (Shermeyer et al., 2020). The dataset contains 3,401 image tiles of the port area in the city of Rotterdam. Each tile has a resolution of 900, ×, 900 pixels. Corresponding labels for building footprints are also provided. The dataset was then split into a training set of 2,770 images and a test set of 631 images. In order to increase the number of samples, data augmentation was performed on the training set by rotating each tile and the corresponding labels by 90, 180 and 270 degrees. The augmented samples were added to the original ones so that after the augmentation, the final training set contained 11,080 images.
2.2 Introducing Label Noise
To determine the impact of label noise on model performance, we created several copies of the training set described above and introduced a different amount of label noise in each copy. In our analysis we focus on the noise type of omission noise which means that objects that are visible in the image are missing in the label mask. We introduce omission noise by removing whole buildings at random from the ground truth labels until a predetermined threshold regarding the fraction of missing building pixels is reached. The building data is available as vector data, which makes removing single instances straightforward. In the following, we refer to the noise level as the fraction of missing building pixels that was aimed for in this procedure. Since we avoid removing individual pixels for the sake of a more realistic noise scenario, those predetermined noise levels are not reached accurately in the datasets. We created 11 copies of the dataset with noise levels ranging between 0 and 1, with 0 meaning that we did not introduce any additional noise and 1 meaning that every single building in the training labels was removed. Examples from those copies are shown in Figure 1.

FIGURE 1. A sample of the imagery and labels used in our experiments. (A) SpaceNet imagery. (B) Ground truth label mask. (C) Label mask with noise level 0.5. (D) Label mask with noise level 0.9.
2.3 Generating Subsets of the Training Set of Different Size
In addition to different levels of label noise, we also need datasets of different size to determine the impact of training set size on model robustness. Therefore, we sample from the initial training set to gain access to training set sizes of 100, 500, 1,000, 5,000 and 10,000. In the experiments described below, the training sets are sampled newly in each training run to exclude the possibility of biased results due to characteristics of a single sample.
2.4 Model Training
For our experiments we use DeepLabV3+, a state of the art architecture for semantic segmentation based on an encoder-decoder structure (Chen et al., 2018). We train the model on each of the 66 types of training sets (6 different training set sizes and 11 noise levels) and report performance metrics always on the same test set of 631 images. Each model was trained for 30 epochs, using the Adam optimizer (Kingma and Ba, 2014), an initial learning rate of 10−4 and an exponential learning rate decay schedule with a decay rate of 0.9 and 10,000 decay steps. The number of epochs was chosen because after 30 epochs, the models trained on the biggest training set did not show considerable changes in the test accuracy anymore. Note that the labels of the test set are not affected by introducing omission noise as it was done for the training set. Furthermore, we repeat each training run 10 times to capture the variety in results due to random initialization.
3 Results
For assessing the impact of the training set size and the noise level on the performance of our models, we evaluate the models’ performances on a clean validation set. To capture as many aspects of the models’ behaviour as possible, we consider a variety of metrics:
• Pixelwise accuracy
• Intersection over Union (IoU) of the ‘building’ class, given by
• Intersection over Union (IoU) of the ‘background’ class, given by
• Precision of the ‘building’ class, given by
• Precision of the ‘background’ class, given by
• Recall of the ‘building’ class, given by
• Recall of the ‘background’ class, given by
where TP is the number of pixels correctly classified as buildings, TN is the number of pixels correctly classified as background, FP is the number of pixels wrongly classified as buildings and FN is the number of pixels wrongly classified as background. For each of those metrics and each of the examined training set sizes, we show how the metric changes when the training data is corrupted with varying levels of omission noise. Next to the absolute metric values, we also provide relative values by scaling all values of the same dataset size between 0 and 1. This makes it easier to compare the ‘sensitivity’ towards label noise between models trained on datasets of different sizes.
The development of pixelwise accuracies with label noise is shown in Figure 2. What can be clearly seen, is that the accuracies decrease with increasing noise levels and do not get worse than 0.928, which is exactly the fraction of pixels from the background class to the overall pixel count in the validation set. This behaviour is a necessary consequence of the experimental setup, since at the maximum noise level no buildings are present anymore in the training data and therefore all models learn to always predict the background class, regardless of the input. For the smaller dataset sizes of 100, 500 and 1,000 samples the corresponding models reach almost the same accuracy even without any label noise in the training data, indicating that they in general predict only the background class. Furthermore, we observe as expected that–with the exception of the training set size of 500–a larger training set size leads to better accuracies. This can also be observed by looking at the predictions of the respective models shown in Figure 3, where one can see how the prediction for one sample gradually gets better when more samples are used to train the model.
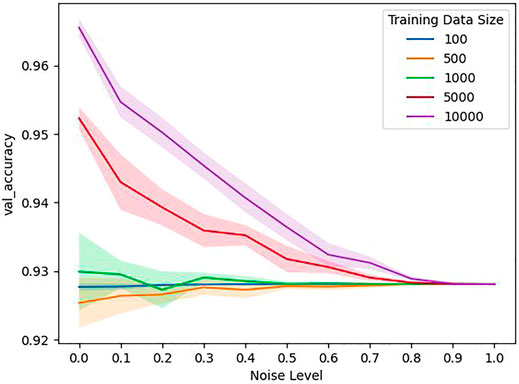
FIGURE 2. Accuracy on a clean validation set for different noise levels and sizes of the training set. Transparent area gives the standard deviation of 10 repetitions of the training procedure.
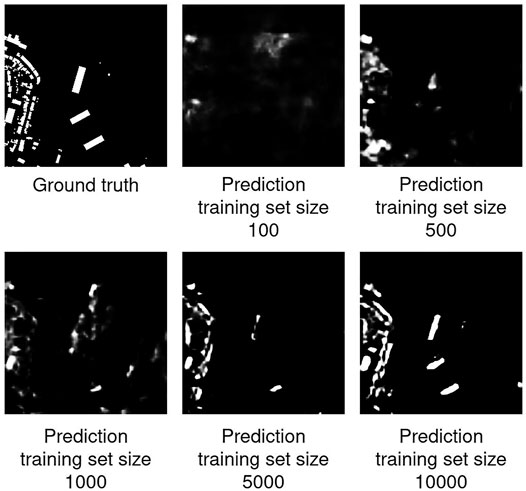
FIGURE 3. Predictions and ground truth for one image in the validation set. Predictions were made by models trained on clean training data.
A better choice for a segmentation metric than the pixelwise accuracy in the case of highly unbalanced classes is often the Intersection over Union (IoU). It captures the overlap between predictions and labels, with a value of 0 meaning that there is no overlap and a value of 1 meaning that predictions and labels are perfectly identical. Thus, a value approaching 1 is preferable. In Figure 4, we visualize the pixelwise IoU for the ‘building’ class and ‘background’ class, respectively.
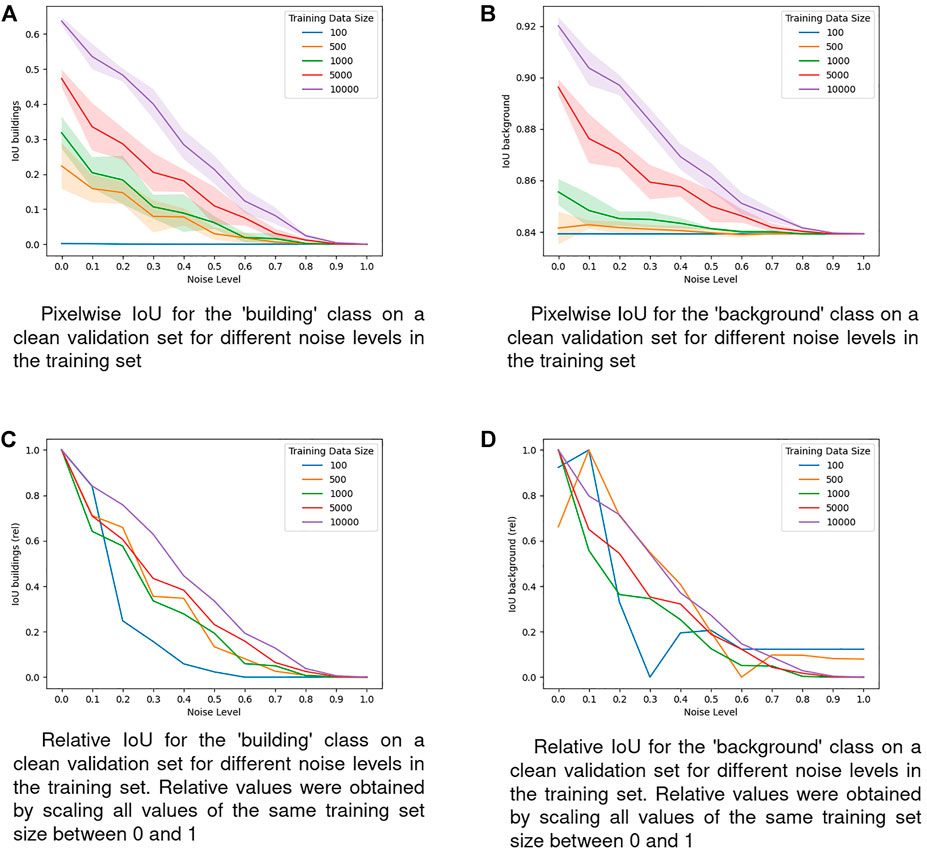
FIGURE 4. IoU on the validation dataset for the two classes. (A) Pixelwise loU for the ‘building’ class on a clean validation set for different noise levels in the training set. (B) Pixelwise loU for the ‘background’ class on a clean validation set for different noise levels in the training set. (C) Relative loU for the ‘building’ class on a clean validation set for different noise levels in the training set. Relatives values were obtained by scaling all values of the same training set size between 0 and 1. (D) Relative loU for the ‘background’ class on a clean validation set for different noise levels in the training set. Relatives values were obtained by scaling all values of the same training set size between 0 and 1.
For the ‘building’ class, we observe a performance decrease with higher noise levels and lower training set sizes, see Figure 4A. At the maximum noise level there are no buildings left in the training data, which necessarily results in a validation IoU of zero. The same seems to be true for models trained on the smallest training set of 100 samples, where the IoU is almost at zero even without any label noise in the training set. The overall pattern of the IoU for the ‘building’ class is remarkably similar to the pattern of the precision for the ‘background’ class and the recall of the ‘building’ class, what we see later in Figure 5C and Figure 6C, respectively. This is an expected behaviour in the case of training data that is biased towards one class and models that get gradually more biased towards this class. Looking at the relative values shown in Figure 4C, it becomes visible that the models trained on the biggest training set of 10,000 samples display a higher relative performance than the other models trained on smaller training sets across all noise levels. Also, models trained on the smallest training set of 100 samples exhibit the lowest relative performance across most of the noise levels. In other words, the models trained on the biggest training set are more robust against omission noise while the models trained on the smallest training set are the most vulnerable. In the ‘background’ class shown in Figure 4B, we observe a similar pattern as for the ‘buildings’ class. All models converge towards an IoU of
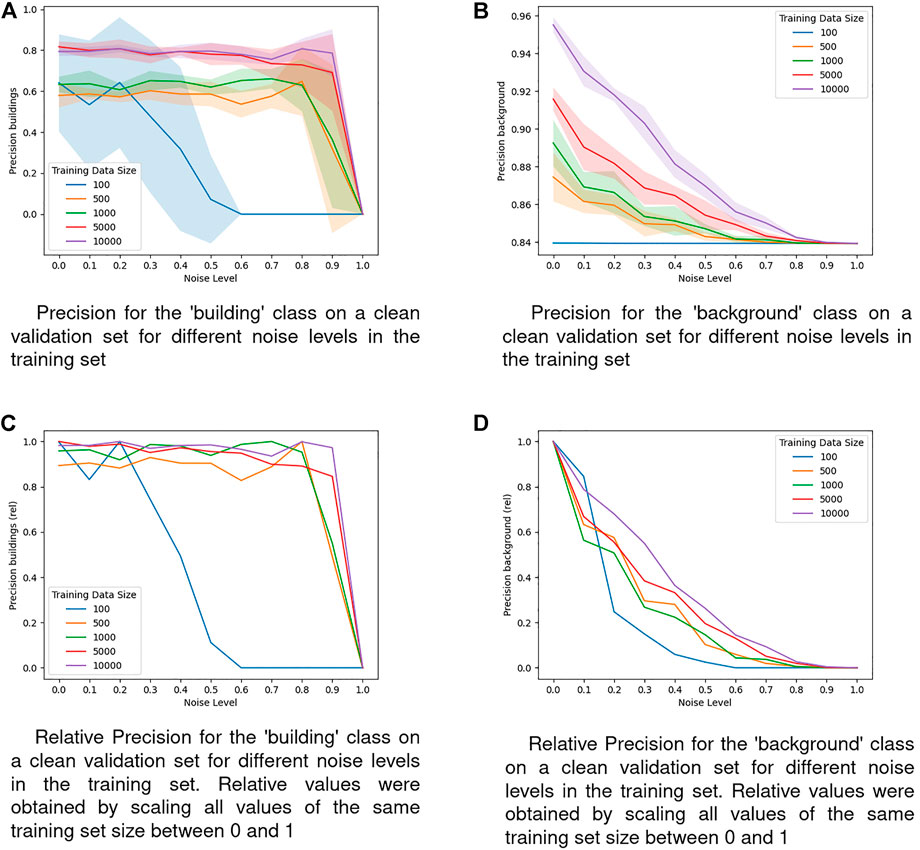
FIGURE 5. Precision on a clean validation set for different noise levels in the training set. (A) Precision for the ‘building’ class on a clean validation set for different noise levels in the training set. (B) Precision for the ‘background’ class on a clean validation set for different noise levels in the training set. (C) Relative Precision for the ‘building’ class on a clean validation set for different noise levels in the training set. Relative values were obtaining by scaling all values of the same training set size between 0 and 1. (D) Relative Precision for the ‘background’ class on a clean validation set for different noise levels in the training set. Relative values were obtaining by scaling all values of the same training set size between 0 and 1.
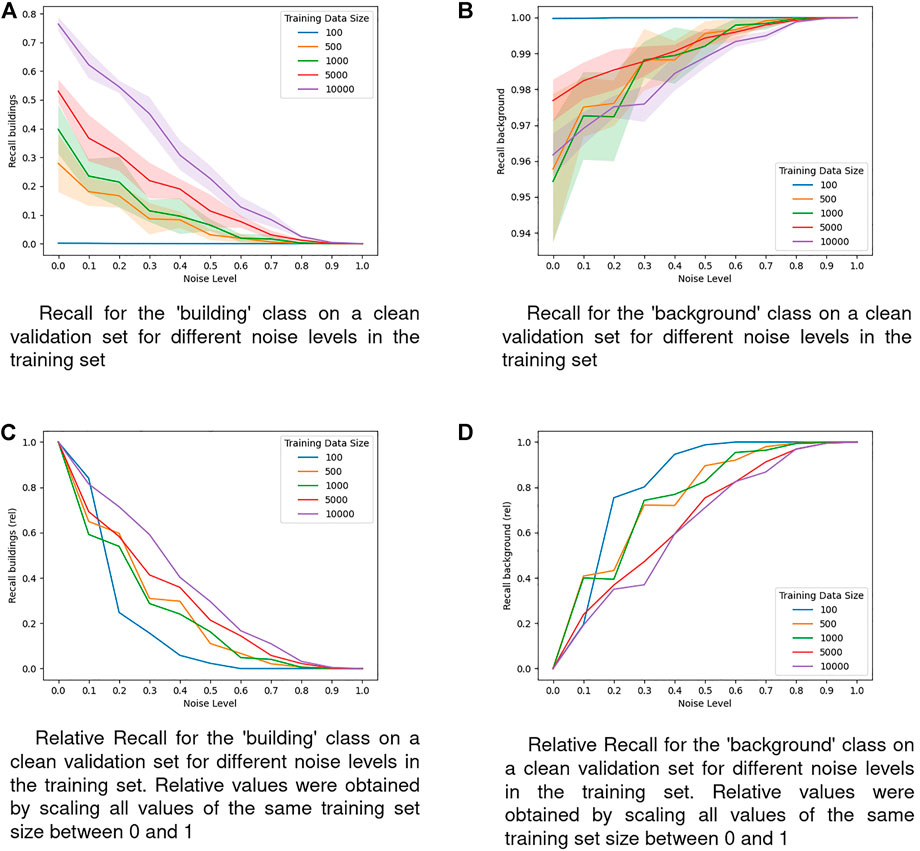
FIGURE 6. Recall on a clean validation set for different noise levels in the training set. (A) Recall for the ‘building’ class on a clean validation set for different noise levels in the training set. (B) Recall for the ‘background’ class on a clean validation set for different noise levels in the training set. (C) Relative Recall for the ‘building’ class on a clean validation set for different noise levels in the training set. Relatives values were obtained by scalling all values of the same training set size between 0 and 1. (D) Relative Recall for the ‘background’ class on a clean validation set for different noise levels in the training set. Relatives values were obtained by scalling all values of the same training set size between 0 and 1.
To analyze the behaviour of models trained on different dataset sizes further, we also study precision and recall performances. The former are shown in Figure 5. The precision of the ‘building’ class shown in Figures 5A,C is not affected very much by the noise level until the very end for almost all dataset sizes. It seems that the model is very robust against omission noise in this regard. This is an interesting property that–if true in the general case–it would mean that applications which place particular importance on the precision of the minority class could utilize noisy labels for training without suffering disadvantages for their primary goal. Only the models trained on the smallest dataset sizes exhibit a clear decrease of the precision also for low and medium noise levels. Additionally, those models also display a very high variability, making them not only less robust against label noise but also unstable in general performance.
Looking at the recall curves of the building class in Figures 6A,C, we see again the exact same pattern as in the ‘background’ precision in Figures 5B,C and the ‘building’ IoU in Figures 4A,C. The recall of the ‘background’ class shown in Figure 6B converges to 1 at the maximum noise level for all training set sizes, which makes sense since there can be no false negatives when always the ‘background’ class is predicted. For the smallest dataset size of 100, the recall even is almost at 1 without any noise in the training data, indicating a heavy focus on the ‘background’ class in those model’s predictions. A look at the relative recall values of the ‘background’ class (Figure 6D) shows that in comparison to the ‘building’ class, the pattern is roughly reversed: Models trained on the smallest training set size achieve the highest relative performance across most of the noise levels, followed by the models trained on medium-sized training sets. The models trained on the two biggest training set sizes show the least reaction to the noise level and consequently achieve the lowest relative recall across all noise levels.
4 Discussion
In this section, we discuss and evaluate the observed results in order to draw conclusions about the effects of noisy training data and different training set sizes to the model performances of a DeepLab V3+ architecture for the building segmentation task.
4.1 Minimum Required Training Set Size
One can see in Figure 2 that models trained on datasets of the sizes 100, 500, and 1,000 perform very poorly even when no omission noise is introduced in the training labels. For the sizes 100 and 500, the models trained on clean test sets perform even worse than models that always predict the background class. It is therefore safe to assume that those training sets sizes are not sufficient for the task at hand, and that a training set of more than 1,000 samples is required in our setting for a model to at least outperform a model that always predicts the majority class.
4.2 High Concentration of Background by Models Trained on Small Dataset Sizes
As one can see in Figure 2, Figures 4A,B, Figure 5B, Figures 6A,B, the performance of models trained on the smallest dataset size of 100 samples does almost not change at all when increasing the noise level, indicating that the models are heavily biased towards the ‘background’ class independently of the noise level. A look at the predictions of those models on unseen test data shown in Figure 3 confirms that, while not consisting purely of background, the fraction of building pixels seems to be considerably smaller than in the other model’s predictions.A possible reason for this behaviour could be overfitting combined with the class imbalance in the training data. It is very likely that models trained on small datasets will overfit on those datasets and merely memorize the data instead of recognizing actual patterns, as shown in Zhang et al. (2017). In our case, it could be that, due to overfitting, the models are unable to detect any buildings in the test images with high confidence. Furthermore, the models might have learned from the imbalance in the training data that most pixels belong to the background class and therefore assign this class to every input where they can’t detect a building with high confidence. Consequently, the ‘background’ class is assigned to almost every input that does not belong to the original training data.
4.3 Higher Sensitivity of Small Dataset Sizes Towards Label Noise
In all of the observed metrics that evaluate the ‘building’ class we see that for most of the noise levels, models trained on smaller training sets display worse relative performances, meaning that omission noise does affect these models disproportionately stronger (see Figure 4C for IoU, Figures 5C,D for Precision, and Figure 6C for Recall). Especially models trained on the smallest training set size of 100 samples are highly vulnerable to omission noise in the training data, although those models are unable to learn reasonable patterns anyway, so this vulnerability does not have any implications in practice. However, the observation that models trained on less samples are more vulnerable to omission noise still holds when comparing the two largest training sets of 5,000 and 10,000 samples.
4.4 Effect of Class Imbalance on the Experiments
The abovementioned trends do not hold for the IoU of the ‘background’ class shown in Figure 4D or the recall of the ‘background’ class shown in Figure 6D. While in Figure 4D there is no clear pattern visible, in Figure 6D we can see that the recall of models trained on smaller training sets benefits stronger from omission noise than the recall from models trained on bigger datasets. We know that at the maximum noise level, all models will always predict the ‘background’ class, therefore a natural interpretation of Figure 6D is that models trained on smaller training sets converge towards this state faster. Since this is not desirable, we view the pattern in Figure 6D as in line with the observations from the other metrics where models trained on smaller datasets are more negatively affected by omission noise than models trained on bigger datasets, even though the order of the training set sizes in Figure 6D is reversed.
5 Conclusion
In this study, we explored the effect of the training set size to the robustness of a deep learning model for building detection in satellite imagery against omission noise. For that, we artificially introduced omission noise to a dataset to simulate the issue of limited labels in crowdsourced datasets in a controlled environment. In our particular setup, we could observe a clear impact of the training set size on the robustness of the model. First, what is not surprising, too small training datasets should be avoided in terms of absolute performance measures, as they are so small that the model does not generalize well for unseen data. In terms of the robustness against label noise, the relative decreases in all metrics except precision for the ‘building’ class and recall for the ‘background’ class are rather similar with a slightly more robust behaviour with the largest training set. With respect to the precision in the ‘building’ class the models are robust against labels noise up to a noise level of 0.8. Based on this result we can confirm previous findings (Gütter et al., 2022) in support of the hypothesis that the training set size does affect model robustness of DNNs against omission noise positively. It is important to note that this is not an obvious property: Unlike the better performance of larger training sets in absolute terms, to our knowledge there is no prior reason for assuming that larger training sets are also more robust against label noise. Testing this hypothesis more extensively and deriving methods to increase the robustness will be a task for future work.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://zenodo.org/record/6651463#.YqsMKjnP2V4.
Author Contributions
JG came up with the initial idea of analysing training set size, which was put in concrete terms together with XZ and JN. XZ gave advice on which dataset to use. JG performed the data collection and data processing, conducted the experiments and created the plots. JN consulted in all of these steps. AK gave additional input on the argumentation and gave editorial assistance. The final paper was formulated by JG and JN.
Funding
This research was funded by the German Aerospace Center (DLR).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Chenying Liu and Nikolai Skuppin for pointing out possible explanations for model behaviour at small training set sizes.
References
Arazo, E., Ortego, D., Albert, P., O’Connor, N., and McGuinness, K. (2019). “Unsupervised Label Noise Modeling and Loss Correction,” in International Conference on Machine Learning (PMLR), 312–321.
Arpit, D., Jastrzkebski, S., Ballas, N., Krueger, D., Bengio, E., Kanwal, M. S., et al. (2017). A Closer Look at Memorization in Deep Networks. Int. Conf. Mach. Learn. 70, 233–242.
Chen, L.-C., Zhu, Y., Papandreou, G., Schroff, F., and Adam, H. (2018). “Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation,” in Proceedings of the European conference on computer vision (ECCV), 801–818. doi:10.1007/978-3-030-01234-2_49
Gütter, J., Niebling, J., and Zhu, X. X. (2022). “Analysing the Interactions between Training Dataset Size, Label Noise and Model Performance in Remote Sensing Data,” in 2022 IEEE International Geoscience and Remote Sensing Symposium IGARSS (IEEE). accepted for publication.
Henry, C., Fraundorfer, F., and Vig, E. (2021). “Aerial Road Segmentation in the Presence of Topological Label Noise,” in 2020 25th International Conference on Pattern Recognition (ICPR) (IEEE), 2336–2343. doi:10.1109/icpr48806.2021.9412054
Kingma, D. P., and Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv preprint arXiv:1412.6980
Mnih, V., and Hinton, G. E. (2012). “Learning to Label Aerial Images from Noisy Data,” in Proceedings of the 29th International conference on machine learning (ICML-12), 567–574.
Rahaman, M., Hillas, M. M., Tuba, J., Ruma, J. F., Ahmed, N., and Rahman, R. M. (2021). Effects of Label Noise on Performance of Remote Sensing and Deep Learning-Based Water Body Segmentation Models. Cybern. Syst. 53, 1–26. doi:10.1080/01969722.2021.1989171
Rolnick, D., Veit, A., Belongie, S., and Shavit, N. (2018). Deep Learning Is Robust to Massive Label Noise. arXiv preprint arXiv:1705.10694
Shermeyer, J., Hogan, D., Brown, J., Van Etten, A., Weir, N., Pacifici, F., et al. (2020). “Spacenet 6: Multi-Sensor All Weather Mapping Dataset,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 196–197. doi:10.1109/cvprw50498.2020.00106
Vorontsov, E., and Kadoury, S. (2021). “Label Noise in Segmentation Networks: Mitigation Must Deal with Bias,” in Deep Generative Models, and Data Augmentation, Labelling, and Imperfections (Springer), 251–258. doi:10.1007/978-3-030-88210-5_25
Wang, F., Chen, L., Li, C., Huang, S., Chen, Y., Qian, C., et al. (2018). “The Devil of Face Recognition Is in the Noise,” in Proceedings of the European Conference on Computer Vision (ECCV), 765–780. doi:10.1007/978-3-030-01240-3_47
Keywords: deep learning, remote sensing, label noise, robustness, segmentation, building segmentation
Citation: Gütter J, Kruspe A, Zhu XX and Niebling J (2022) Impact of Training Set Size on the Ability of Deep Neural Networks to Deal with Omission Noise. Front. Remote Sens. 3:932431. doi: 10.3389/frsen.2022.932431
Received: 29 April 2022; Accepted: 06 June 2022;
Published: 06 July 2022.
Edited by:
Biplab Banerjee, Indian Institute of Technology Bombay, IndiaReviewed by:
Taïs Grippa, Université libre de Bruxelles, BelgiumChunyuan Diao, University of Illinois at Urbana-Champaign, United States
Copyright © 2022 Gütter, Kruspe, Zhu and Niebling. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jonas Gütter, am9uYXMuZ3VldHRlckBkbHIuZGU=
 Jonas Gütter
Jonas Gütter Anna Kruspe
Anna Kruspe Xiao Xiang Zhu2,3
Xiao Xiang Zhu2,3