- Department of Civil and Environmental Engineering, BIT Mesra, Ranchi, India
Groundwater fluoride contamination poses serious health effects to humans, as excess amounts of fluoride can cause skeletal and dental fluorosis. The problem is critical in areas where the aquifers are surrounded by fluoride-bearing rocks. Apart from the geology, the meteorology of the place also plays an important role. The excess fluoride in water can also be associated with chemical ions found in water. Groundwater fluoride modeling using an artificial neural network (ANN) is a valuable approach. Inputs are selected through statistical analysis. The modeling process is carried out using the “nntool” in MATLAB software. This ANN model can be used to predict future fluoride levels based on primary data obtained from water sample analyses. The results of the correlation analysis help in deciding the inputs for the model. The network architecture can be determined through the trial-and-error method. The network should be trained, tested, and validated on separate datasets. The prediction accuracy of the network can be assessed using root mean square error (RMSE) analysis and the coefficient of determination (R2). Groundwater fluoride can also be modeled using logistic regression (LR), random forest (RF), Monte Carlo simulation (MCS), artificial neural network (ANN), support vector machine (SVM), gradient boosting (XGBoost), and Classification and Regression tree (CART) methods. However, ANN is best suited as it can address numerous inaccuracies within the data and extract information about the associations between input and output variables. The accurate prediction will help in decision-making and the proper management of groundwater fluoride contamination.
1 Introduction
Groundwater is considered the safest source of drinking water (Saha et al., 2024). It constitutes 0.6% of the total water resources available on Earth. It caters to 80% of the total drinking water requirement and 50% of the agricultural requirement in rural India (Adimalla et al., 2018; Maheshwari, 2006). Major sources of fluoride in groundwater are fluoride-bearing rocks such as fluorite (CaF2), cryolite (Na3AlF6), topaz [Al2SiO4(F,OH2)], apatite [Ca5(Cl,F,OH)(PO4)3], amphiboles [A0–1B2C5T8O22(OH,F,Cl)], micas [AB2–3(X,Si)4O10(O,F,OH)2] and sellaite (MgF2) (Hanse et al., 2019; Chicas et al., 2022; Agarwal et al., 1997). Fluorine is the major constituent found in large quantities in rock-forming minerals such as apatite, micas, amphiboles, and clay minerals (Chicas et al., 2022; Kumari and Pathak, 2019). In 1984, the WHO estimated that more than 260 million people worldwide consume water with a fluoride concentration above 1 mg/L (World Health Organization, 1984). The standard maximum fluoride concentration in drinking water is 1.5 mg/L, while the permissible limit is 1.0 mg/L (Saha et al., 2024; Su et al., 2013; World Health Organization, 2011). The desirable limit of fluoride is 0.6–1.0 mg/L as per BIS 10500. The upper limit may be extended to 1.5 mg/L in cases where no alternative source of drinking water is available (Bureau of Indian Standards, 2012; Standard DI, 2022).
Fluoride is mainly present in groundwater in the form of dissolved ions. Its concentration depends on many factors, such as the presence of fluoride minerals and their solubility in water, the velocity of flowing water, pH, temperature, and the concentration of Ca+2 and HCO3−2 ions in water (Adimalla, 2020). Anthropogenic sources of fluoride include glass factories, aluminum smelters, superphosphate fertilizers, clay used in brick industries, irrigation with fluoride-enriched water, and coal-based power stations (Ali et al., 2016). Fluorite (CaF2) is a fluorine mineral that naturally occurs in nature and is often found as an accessory in granitic gneiss (Saxena and Ahmed, 2003). The key geochemical processes that affect groundwater fluoride mobilization are the dissolution and precipitation of carbonate, hydrolysis, evapotranspiration, halite, gypsum, and silicate weathering, among others (Su et al., 2015).
High concentrations of F- in groundwater are found in many parts of the world, notably in Asia and Africa (Saha et al., 2024; Kumar et al., 2020). Fluorosis is the condition that is most severe and widespread in the two largest countries—India and China. According to the UNICEF, fluorosis is endemic in at least 25 countries, with approximately 200 million people at health risk due to high fluoride levels in groundwater (Yadav et al., 2023; Hanse et al., 2019; Ayoob and Gupta, 2006). The issue of high fluoride concentration in the groundwater is a global concern. Many countries, such as India, Sri Lanka, China, East African nations (including those in the Rift Valley), Türkiye, and parts of South Africa, are facing this problem on a large scale (Yadav et al., 2023; Adimalla, 2020). The Rift Valley passes through countries in the Middle East, such as Jordan, Lebanon, and Israel, as well as East African nations including Ethiopia, Tanzania, Kenya, Uganda, Eritrea, and Djibouti (Adimalla, 2020) (Figure 1). In India, groundwater supplies mostly have water quality issues (Central Groundwater Board of India, 2024). Fluoride contamination in groundwater is more pronounced in states such as Andhra Pradesh, Bihar, Gujarat, Madhya Pradesh, Punjab, Rajasthan, Tamil Nadu, and Uttar Pradesh (Kumar et al., 2024). Among these, the most affected states are Rajasthan, Gujarat, and Andhra Pradesh (Adimalla, 2020; Susheela et al., 1999; Choubisa, 2018). Major factors responsible for the higher concentration of fluoride in groundwater are the influence of local lithology and the semi-arid climate of the region. The fluoride concentration in groundwater is a natural phenomenon, mainly influenced by the geological setting at both local and regional levels, as well as hydrogeological conditions. The main sources of fluoride in natural water are fluoride-bearing minerals such as cryolite, fluorapatite, fluorite, and apophyllite, as well as the replacing of F- for OH- in ferromagnesium silicates such as micas and amphiboles, and in soil having clay minerals (Narsimha and Rajitha, 2018; Adimalla and Venkatayogi, 2017, 2018; Dey et al., 2012).
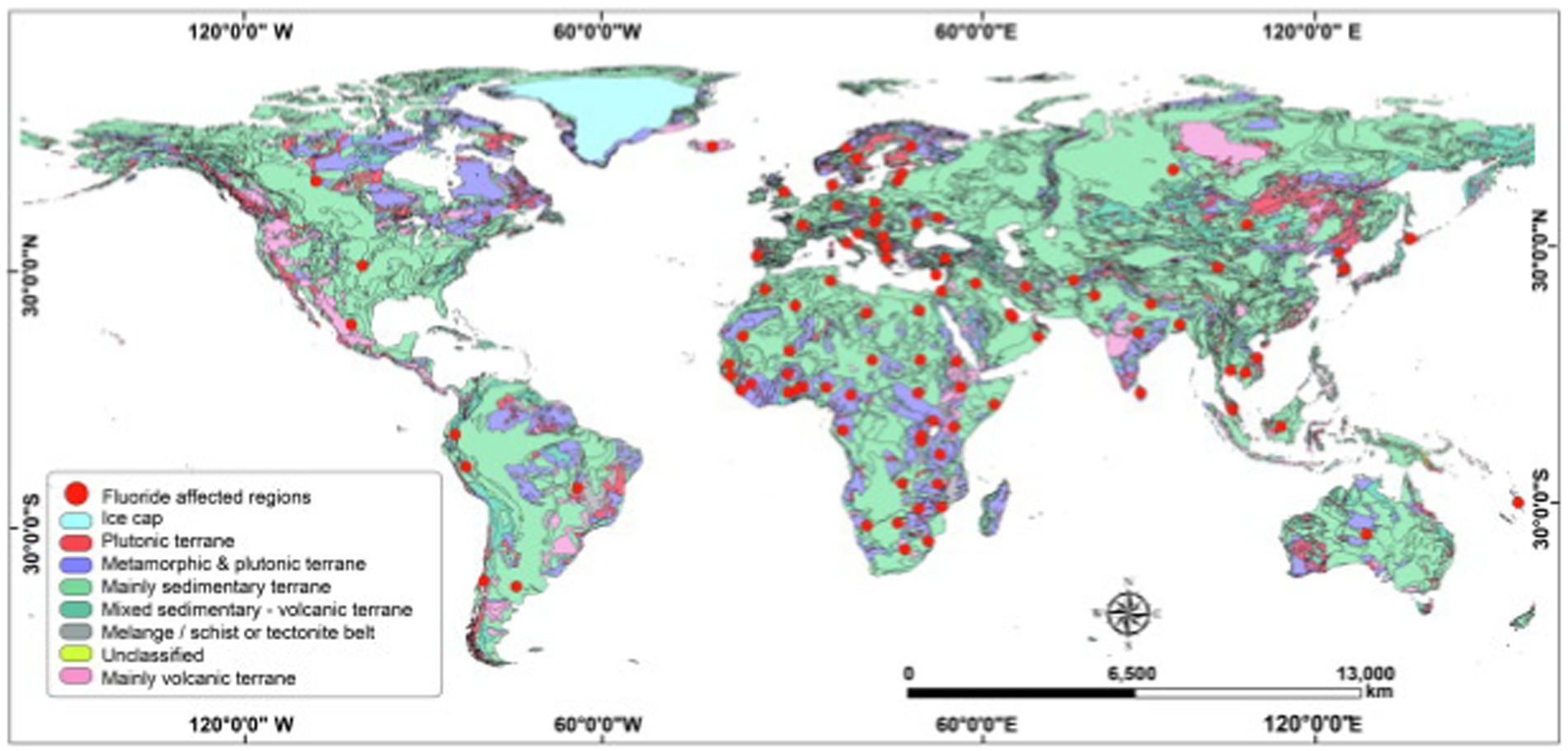
Figure 1. Worldwide groundwater fluoride-affected countries and their geological setting (source: https://mrdata.usgs.gov/geology/world/, Shaji et al., 2024).
The health impact associated with excess fluoride in groundwater is that it causes dental and skeletal fluorosis in humans. A fluoride concentration higher than 1.5 mg/L and less than 3 mg/L can cause dental fluorosis, while elevated levels of fluoride (>3 mg/L) can cause skeletal fluorosis (Sunitha et al., 2022; Kom et al., 2022). Dental fluorosis causes tooth discoloration, ranging from white spots to brown staining and pitting on the tooth enamel. Skeletal fluorosis is characterized by joint pain, stiffness, and bone deformities, which can eventually lead to immobility. Therefore, fluoride levels in groundwater must be managed through reverse osmosis treatment and artificial recharge systems (Kom et al., 2022). Proper waste disposal facilities should be installed to stop the leaching of contaminants. Fluoride concentration in groundwater is closely related to hydrogeochemical characteristics and ionic composition (Yarlanki et al., 2025). Total dissolved solids (TDS), chloride (Cl−), nitrate (NO3−), sodium (Na+), bicarbonate (HCO3−), sulfate (SO42−), potassium (K+), zinc (Zn + 2), calcium (Ca2+), and magnesium (Mg2+) are some of the chemical parameters that influence groundwater fluoride mobility (Yarlanki et al., 2025; Etikala et al., 2024). Thus, statistical analysis using descriptive statistics (DS), correlation and regression analysis, and cluster analysis (CA) can help in understanding the related ionic composition. Software such as “SPSS” and “R” can be used for statistical analysis. Based on the insights gained from statistical analysis, groundwater modeling can be performed to predict the fluoride levels in groundwater.
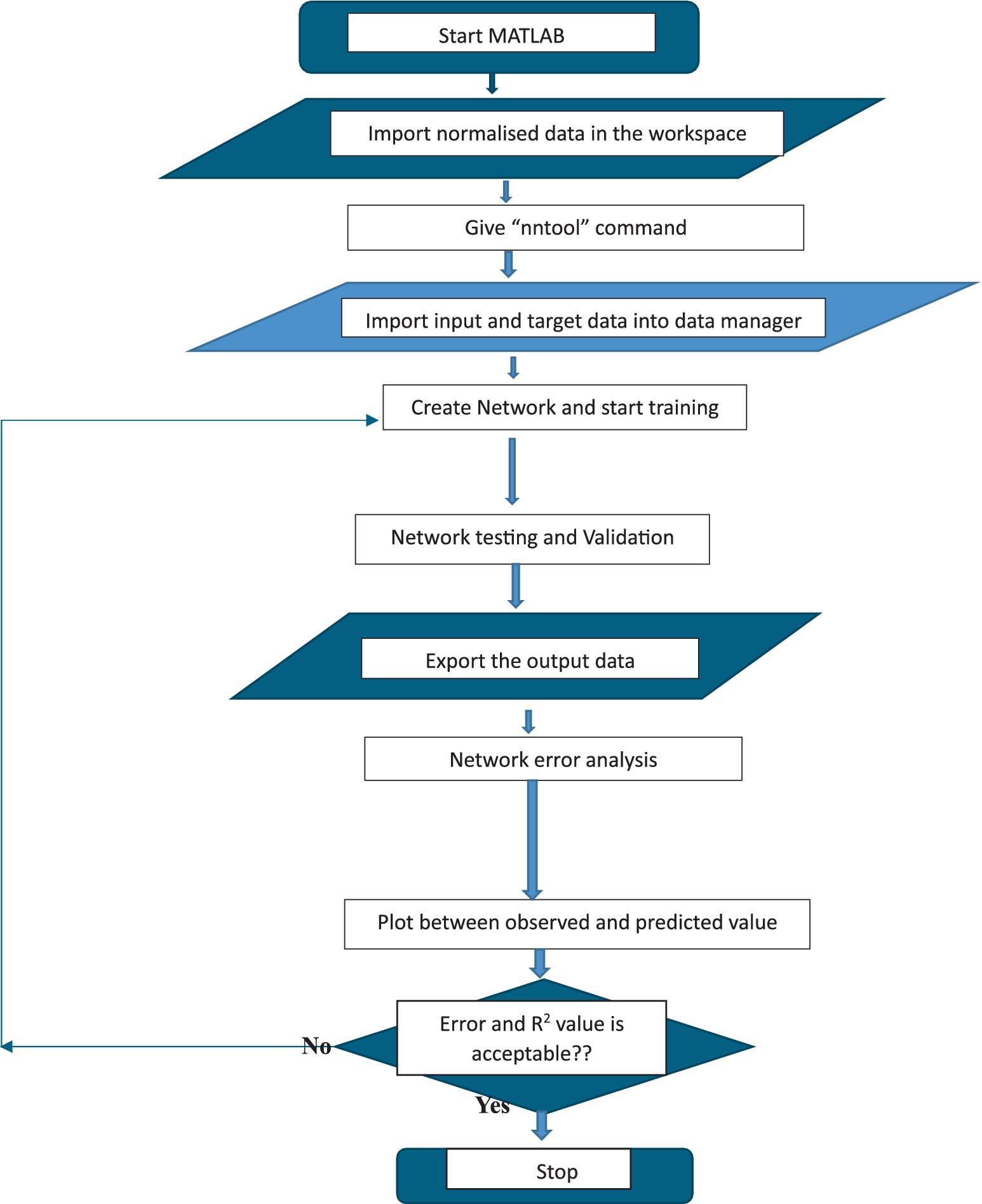
The groundwater fluoride is modeled using various methods such as logistic regression (LR), random forest (RF), Monte Carlo simulation (MCS), artificial neural network (ANN), support vector machine (SVM), extreme gradient boosting (XGBoost), multilayer perceptron (MLP), extreme learning machine (ELM), Gaussian process (GP), long- and short-term memory (LSTM), principal component analysis (PCA), firefly algorithm (FA), multi-criteria decision making (MCDM) models, Fuzzy-TOPSIS, and Classification and Regression Tree (CART). Among these models, ANN is considered an important non-parametric modeling technique, where the model output is non-linearly associated with the input (Mayilvaganan and Naidu, 2011). It is inspired by biological neuron processing and is widely applied to pattern recognition, time series forecasting, and process control. MATLAB is a mathematical software developed by MathWorks (USA) in 1982, known for its powerful capabilities in numerical computation and data visualization (Zhang, 1999). The “nntool” and graphical user interface (GUI) functions of MATLAB can be used to create a water quality forecast model. The flowchart for ANN model development using the “nntool” of MATLAB GUI function is shown in Figure 2. ANN is used in rainfall-runoff prediction, groundwater simulation, variations in groundwater quality, forecasting groundwater contamination, water demand forecasting, water table depth fluctuations, and the prediction of nitrate distribution in groundwater (Minns and Hall, 1996; El-Shafie et al., 2011; Jalalkamali and Jalalkamali, 2011; Gholami et al., 2024; Wang et al., 2011; Brédy et al., 2020).
2 Groundwater fluoride modeling using machine learning methods
Different machine learning techniques, which are also considered artificial intelligence methods, generally extract patterns from data based on which they make predictions. These techniques can also assess and interpret non-linear and intricate associations among input and output data. The large amounts of data collected over the years can be used for groundwater level and quality parameter predictions (Feng et al., 2024). Different machine learning methods are used to develop models for groundwater quality prediction. Some of them are listed below:
a. Logistic Regression (LR): LR is a supervised learning approach. It works by rapid training of the dataset using binary classification.
b. Support vector machine (SVM): SVM is one of the most popular supervised learning algorithms in machine learning, used for both regression and classification tasks. It is used to produce the best hyperplane that can divide n-D space into categories, allowing new data to be added to the correct category in future analysis. This optimal decision boundary is known as a hyperplane, which is created by choosing points or vectors; hence, its algorithm is known as SVM. The first stage of the model is developed by preparing a dataset, which is divided into training and testing. The testing data are used post-training for calibration and validation purposes. Function fitting using SVM aims to diminish the variation between the observed values and the output of the model.
c. Random forest (RF): Random forest (RF) is a supervised learning approach that grows multiple decision trees to form a ‘forest’ and provide outputs. Individual trees in the RF model are trained on a random subset of the data, hence it is called ‘random’. Thus, a substantial number of different trees can be grown through random resampling of the original data. Variables are also randomly selected for forecasting the dependable variable. The forecasting result is the concluding outcome of the entire tree population. The RF model can handle multi-scaled data, dichotomous data, and misplaced data (Singh and Mehta, 2024).
d. CART model: The Classification and Regression Trees (CART) model is a powerful and flexible machine learning tool that has gained prominence for prediction and decision-making tasks. It excels at identifying crucial features within datasets by analyzing their tree structure, helping with feature selection, dimensionality reduction, and anomaly detection. This model helps with the prediction of both categorical and continuous numerical values, while maintaining high interpretability, prioritizing transparency, and accountability. It can also capture intricate non-linear relationships in data, accommodating interactions between variables that linear models may struggle to capture, which is an advantage over linear regression models. This model can handle missing data gracefully, making decisions based on the available information for each observation.
e. Monte Carlo simulation (MCS): A Markov chain is a mathematical model for stochastic systems whose states, whether discrete or continuous, are governed by transition probabilities. The current state in a Markov chain only depends on the most recent previous states. Monte Carlo simulation (MCS) is a strong probabilistic tool that allows for the evaluation of health risks by modeling a large range of possible exposure scenarios using probability distributions of important variables (Islam et al., 2024). MCS has demonstrated effectiveness in generating more realistic risk estimations by accounting for variability in parameters such as fluoride content and individual intake rates. While MCS captures uncertainty, it may not always accurately represent the complex, non-linear connections between numerous exposure variables and health consequences (Ali et al., 2023).
f. Gradient boosting (GB): GB relies on weak learners that, when combined, create an effective learning model. Each learner improves by learning from previous misclassifications (Singh and Mehta, 2024).
g. Artificial neural network (ANN): ANN operates like a “black box” model, requiring no detailed information about the physical parameters of the system (Tabach et al., 2007). Training of the network on the recorded dataset results in learning the relationship between the input and output parameters. ANN can handle complex and large datasets with many interconnected parameters. It is made up of a large number of interconnected processing elements referred to as neurons. ANN is an error-tolerant, self-adaptable, self-organizing, and widely adopted technology for forecasting water quality (Niu et al., 2006). The advantage of using ANN in place of statistical and conventional models is that it stores information on the entire network and can work even with incomplete data. It has fault tolerance, meaning that if one layer becomes corrupted, the network can still generate output. ANN also features distributed memory and undergoes gradual corruption. The network does not get corrupted immediately, which allows time for correction. It first learns from events and then comments on similar events. Its numerical strength allows it to efficiently perform more than one task at the same time (Mijwel, 2021). The groundwater contamination depends upon the variables that change over time, thus a flexible algorithm is necessary. Thus, ANN provides the requisite flexibility.
The ANN model network consists of three layers, namely the input layer, output layer, and hidden layer. ANN models can be specified by the following major aspects: (1) processing units called “neurons,” (2) activation function, (3) an output function, (4) network topology, and (5) a propagation rule. The activation rule updates each unit’s activity using the activation value. The external input provides information to the network, allowing it to interact with the network. In an ANN, the accuracy is also influenced by the number of hidden layers. Increasing the number of hidden layers can increase accuracy, but this improvement is typically effective for up to three layers (Awan et al., 2018; Uzair and Jamil, 2020). The algorithmic structure decides the predictive capacity of the network. The performance of any algorithm depends on data quality, algorithm structure, and input parameter selection (Asim et al., 2018). The process of identifying the decisive variable responsible for groundwater contamination is very complicated. Therefore, a more flexible network is required to accommodate the complexity (De’ath and Fabricius, 2000). A learning rule modifies the connectivity pattern by using external environment information. Modeling methods other than ANN, such as logistic regression (LR), random forest (RF), Monte Carlo simulation (MCS), and support vector machine (SVM), can be used to increase the accuracy of the model. Table 1 shows the modeling methods used for groundwater fluoride management, including ANN and other suitable modeling techniques. Table 1 lists the modeling methods that, alongside ANN, can effectively predict groundwater fluoride. The flowchart for the ANN model development is shown in Figure 2.
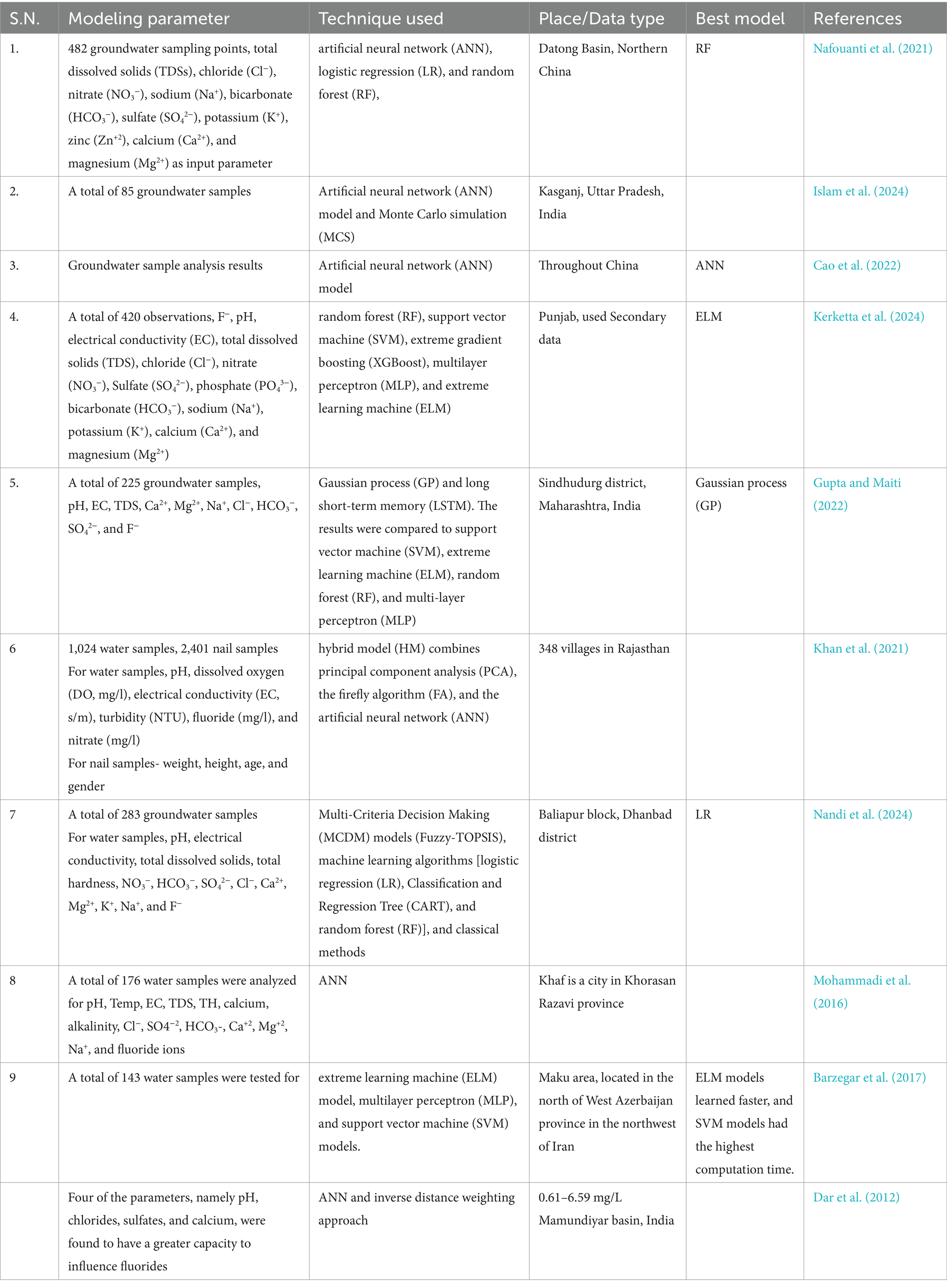
Table 1. Modeling methods used for groundwater fluoride management using ANN and other suitable modeling methods.
Among all the methods discussed, the ANN is best suited for groundwater quality prediction as it can address numerous inaccuracies within the data. It can extract information regarding the association between the input and output variables. The RF model is efficient at managing binary and continuous data, missing values, and high-dimensional data (Singh and Mehta, 2024).
3 Discussion
Groundwater is considered the safest source of drinking water worldwide. Most countries depend on groundwater sources for agricultural, household, and industrial purposes (Sutradhar and Mondal, 2021; Singh and Mehta, 2024). Groundwater fluoride concentration is affected by various natural and anthropogenic processes. The major geochemical processes affecting fluoride dissolution include precipitation, weathering of silicate, evapotranspiration, carbonate dissolution, and hydrolysis (Etikala et al., 2024). Fluoride is present in mainly three forms: Apatite, which is also called calcium phosphate (Ca3 F(PO4)3), fluorspar, also known as calcium fluoride (CaF2), and cryolite, which is represented as sodium hexafluoroaluminate (Na3 AlF6) (Sunitha et al., 2022; Sreedevi et al., 2017). In correlation analysis, the variables most closely related to fluoride are TDS, Cl−, NO3−, Na+, HCO3_, SO4−2, Ca+2, and Mg+2. The pH of the groundwater sample should lie within the range of 6.5 to 7.5 (Bureau of Indian Standards, 2012). The electrical conductivity (EC) increases with TDS. Higher EC and TDS values represent increased geochemical processes and anthropogenic activities. The increase in sodium ion concentration is related to the leaching of the deposits and the breakdown of certain minerals (Sunitha et al., 2022). High sodium levels are not recommended as they degrade the soil. Industrial and municipal waste, as well as runoff from various sources, contribute to sodium in the natural water. Higher chloride content indicates the leaching of rocks and soil and industrial pollution. The permissible limit and the desirable limit of groundwater fluoride are 1.5 mg/L and 1 mg/L, respectively (World Health Organization, 2006; World Health Organization, 2009). A fluoride level of 0.8–1 mg/L is beneficial for human health as it prevents dental caries and helps with enamel growth in children (Sunitha et al., 2022). A fluoride concentration beyond 1.5 mg/L and less than 3 mg/L causes dental fluorosis, which is characterized by the presence of white spots, brown staining, and pitting on the teeth’s enamel. An exceeded level of fluoride (>3 mg/L) causes skeletal fluorosis, which is characterized by stiff bones and joint pain, which eventually leads individuals to become unable to move (Singh and Mehta, 2024; Sunitha et al., 2022).
The association of fluoride with other water quality parameters can be assessed through statistical analysis such as DS, correlation and regression analysis, principal component analysis (PCA), CA, and analysis of variance (ANOVA), which helps in identifying the input parameter for the modeling (Singh and Mehta, 2024). This analysis determines the accuracy of fluoride forecasting through machine learning methods (Singh and Mehta, 2024). In a few decades, groundwater quality modeling will be considered the most effective method as it could save time and money.
Through groundwater modeling, it becomes easier to understand and predict the behavior of groundwater systems, solute flow, transport processes, and anthropogenic impact. Various machine learning algorithms, such as logistic regression (LR) and random forest (RF), Monte Carlo simulation (MCS), artificial neural network (ANN), and support vector machine (SVM), are used to model the groundwater systems (Singh and Mehta, 2024). ANN has an advantage over all other algorithms in that it can work with incomplete knowledge or datasets. It has fault tolerance, meaning that if any one layer gets corrupted, the network can still generate output. It has distributed memory and undergoes gradual corruption (Mijwel, 2021). The accuracy of these algorithms is assessed by calculating the root mean square error (RMSE), coefficient of determination (R2), and biases. The performance of the model is assessed before and after network runs. RMSE serves as a global measure of the goodness-of-fit between the target and simulated, predicted, or calculated values. A lower value of RMSE indicates more accuracy and vice versa. The proportion of total variance in the observed data and its value ranges between 0 and 1. The coefficient of determination (R2) represents the proportion of total variance in the observed data, with values ranging between 0 and 1 (Islam et al., 2024). The higher the value of the coefficient, the greater the agreement between the observed and simulated or predicted values.
ANN works efficiently with large amounts of data as well as with inadequate data. It provides the requisite flexibility as it is suitable for groundwater fluoride modeling. Among all the methods, ANN is best suited for groundwater quality prediction since it can address numerous inaccuracies within the data (Singh and Mehta, 2024; Islam et al., 2024). It can extract information about the association between the input and output variables. RF model is efficient in managing binary and continuous data, missing values, and high-dimensional data.
4 Limitations
ANN modeling requires processors with parallel processing power, making it equipment-dependent. The determination of network structure is not governed by a fixed rule but is based on a trial-and-error method; therefore, an optimal network can be achieved through experience. Thus, the performance of the network depends on the user’s ability. ANN can only understand problems in numerical terms; thus, problems must be translated in terms of numerical values. Overfitting during ANN training is a complex problem that decreases its efficiency. While ANN is evolving each day, ongoing research is aimed at overcoming its limitations. In the future, it is predicted to become highly important and indispensable (Mijwel, 2021).
5 Conclusion and recommendations
Groundwater fluoride concentration is affected by various natural and anthropogenic processes. Different machine learning techniques that are also considered artificial intelligence techniques generally extract patterns from the data based on which it makes predictions. It also assesses and interprets non-linear and intricate associations among input–output data. The large amounts of data collected over the years can be used for quality parameter prediction. Different machine learning methods are used to develop models for groundwater quality prediction. Various researchers have proved that ANN modeling has a very good predictive capability for fluoride levels. Groundwater contamination depends upon the variables that change over time; therefore, a flexible algorithm is required to enhance the reliability of the model. The ANN provides the requisite flexibility, making it suitable for groundwater fluoride modeling. Inputs are selected based on correlation analysis, and the hidden layers are taken. A maximum of two hidden layers can be taken, with the output representing fluoride concentration. The network undergoes sufficient training through the trial-and-error method. After the training, the model undergoes testing and validation, and the network’s predictive efficiency is measured based on root mean square error and the coefficient of determination. Overfitting during ANN training is a complex problem that decreases the efficiency of the ANN.
Author contributions
NK: Conceptualization, Supervision, Writing – original draft, Writing – review & editing. GK: Investigation, Writing – original draft. SH: Conceptualization, Formal analysis, Resources, Writing – original draft.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adimalla, N. (2020). Assessment and mechanism of fluoride enrichment in groundwater from the hard rock terrain: a multivariate statistical approach. Geochem. Int. 58, 456–471. doi: 10.1134/S0016702920040060
Adimalla, N., Vasa, S. K., and Li, P. (2018). Evaluation of groundwater quality, Peddavagu in central Telangana (PCT), South India: an insight of controlling factors of fluoride enrichment. Model. Earth Syst. Environ. 4, 841–852. doi: 10.1007/s40808-018-0443-z
Adimalla, N., and Venkatayogi, S. J. E. E. S. (2017). Mechanism of fluoride enrichment in groundwater of hard rock aquifers in Medak, Telangana state, South India. Environ. Earth Sci. 76, 1–10. doi: 10.1007/s12665-016-6362-2
Adimalla, N., and Venkatayogi, S. (2018). Geochemical characterization and evaluation of groundwater suitability for domestic and agricultural utility in semi-arid region of Basara, Telangana state, South India. Appl Water Sci 8, 1–14. doi: 10.1007/s13201-018-0682-1
Agarwal, V., Vaish, A. K., and Vaish, P. (1997). Groundwater quality: Focus on fluoride and fluorosis in Rajasthan on JSTOR. Curr. Sci. 73, 743–746.
Ali, S., Baboo Agarwal, M., Verma, S., Islam, R., Kumar Deolia, R., Singh, S., et al. (2023). Variability of groundwater fluoride and its proportionate risk quantification via Monte Carlo simulation in rural and urban areas of Agra district, India. Sci. Rep. 13:18971. doi: 10.1038/s41598-023-46197-7
Ali, S., Thakur, S. K., Sarkar, A., and Shekhar, S. (2016). Worldwide contamination of water by fluoride. Environ. Chem. Lett. 14, 291–315. doi: 10.1007/s10311-016-0563-5
Asim, Y., Shahid, A. R., Malik, A. K., and Raza, B. (2018). Significance of machine learning algorithms in professional blogger's classification. Comput. Elect. Engin. 65, 461–473. doi: 10.1016/j.compeleceng.2017.08.001
Awan, S. M., Riaz, M. U., and Khan, A. G. (2018). Prediction of heart disease using artificial neural network. VFAST Transact. Softw. Engin. 6, 51–61.
Ayoob, S., and Gupta, A. K. (2006). Fluoride in drinking water: a review on the status and stress effects. Crit. Rev. Environ. Sci. Technol. 36, 433–487. doi: 10.1080/10643380600678112
Barzegar, R., Asghari Moghaddam, A., Adamowski, J., and Fijani, E. (2017). Comparison of machine learning models for predicting fluoride contamination in groundwater. Stoch. Env. Res. Risk A. 31, 2705–2718. doi: 10.1007/s00477-016-1338-z
Brédy, J., Gallichand, J., Celicourt, P., and Gumiere, S. J. (2020). Water table depth forecasting in cranberry fields using two decision-tree-modeling approaches. Agric. Water Manag. 233:106090. doi: 10.1016/j.agwat.2020.106090
Bureau of Indian Standards (2012). Indian standards institution – Indian Standard specification for drinking water. New Delhi: Bureau of Indian Standards.
Cao, H., Xie, X., Wang, Y., and Liu, H. (2022). Predicting geogenic groundwater fluoride contamination throughout China. J. Environ. Sci. 115, 140–148. doi: 10.1016/j.jes.2021.07.005
Central Groundwater Board of India (2024). “Report on Dynamic groundwater resources of river basins of India ”. 287–411.
Chicas, S. D., Omine, K., Prabhakaran, M., Sunitha, T. G., and Sivasankar, V. (2022). High fluoride in groundwater and associated non-carcinogenic risks at Tiruvannamalai region in Tamil Nadu, India. Ecotoxicol. Environ. Safety 233:113335. doi: 10.1016/j.ecoenv.2022.113335
Choubisa, S. L. (2018). Fluoride distribution in drinking groundwater in Rajasthan, India. Curr. Sci. 114, 1851–1857. doi: 10.18520/cs/v114/i09/1851-1857
Dar, I. A., Sankar, K., Dar, M. A., and Majumder, M. (2012). Fluoride contamination-artificial neural network modeling and inverse distance weighting approach. Revue Sciences Eau 25, 165–182. doi: 10.7202/1011606ar
De’ath, G., and Fabricius, K. E. (2000). Classification and regression trees: a powerful yet simple technique for ecological data analysis. Ecology 81, 3178–3192. doi: 10.1890/0012-9658(2000)081[3178:CARTAP]2.0.CO;2
Dey, R. K., Swain, S. K., Mishra, S., Sharma, P., Patnaik, T., Singh, V. K., et al. (2012). Hydrogeochemical processes controlling the high fluoride concentration in groundwater: a case study at the Boden block area, Orissa, India. Environ. Monit. Assess. 184, 3279–3291. doi: 10.1007/s10661-011-2188-2
El-Shafie, A., Mukhlisin, M., Najah, A. A., and Taha, M. R. (2011). Performance of artificial neural network and regression techniques for rainfall-runoff prediction. Int. J. Physical. Sci. 6, 1997–2003.
Etikala, B., Vangala, S., and Madhav, S. (2024). Groundwater geochemistry using modified integrated water quality index (IWQI) and health indices with special emphasis on nitrates and heavy metals in southern parts of Tirupati, South India. Environ. Geochem. Health 46:465. doi: 10.1007/s10653-024-02229-3
Feng, F., Ghorbani, H., and Radwan, A. E. (2024). Predicting groundwater level using traditional and deep machine learning algorithms. Front. Environ. Sci. 12:1291327. doi: 10.3389/fenvs.2024.1291327
Gholami, V., Sahour, H., Khaleghi, M. R., Ghajari, Y. E., and Sahour, S. (2024). Combining artificial neural networks and genetic algorithms to model nitrate contamination in groundwater. Nat. Hazards 120, 4789–4809. doi: 10.1007/s11069-023-06387-y
Gupta, P. K., and Maiti, S. (2022). Enhancing data-driven modeling of fluoride concentration using new data mining algorithms. Environ. Earth Sci. 81:89. doi: 10.1007/s12665-022-10216-z
Hanse, A., Chabukdhara, M., Gohain Baruah, S., Boruah, H., and Gupta, S. K. (2019). Fluoride contamination in groundwater and associated health risks in Karbi Anglong District, Assam. Environ. Monitor. Assessment 191:782. doi: 10.1007/s10661-019-7970-6
Islam, R., Sinha, A., Hussain, A., Usama, M., Ali, S., Ahmed, S., et al. (2024). Application of Monte Carlo simulation and artificial neural network model to probabilistic health risk assessment in fluoride-endemic areas. Heliyon 10:e40887. doi: 10.1016/j.heliyon.2024.e40887
Jalalkamali, A., and Jalalkamali, N. (2011). Groundwater modeling using hybrid of artificial neural network with genetic algorithm. Afr. J. Agric. Res. 6, 5775–5784. doi: 10.5897/AJAR11.1892
Kerketta, A., Kapoor, H. S., and Sahoo, P. K. (2024). Groundwater fluoride prediction modeling using physicochemical parameters in Punjab, India: a machine-learning approach. Front. Soil Sci. 4:1407502. doi: 10.3389/fsoil.2024.1407502
Khan, F. M., Gupta, R., and Sekhri, S. (2021). A novel PCA-FA-ANN based hybrid model for prediction of fluoride. Stoch. Env. Res. Risk A. 35, 2125–2152. doi: 10.1007/s00477-021-02001-4
Kom, K. P., Gurugnanam, B., and Bairavi, S. (2022). Non-carcinogenic health risk assessment of nitrate and fluoride contamination in the groundwater of Noyyal basin, India. Geodesy Geodynam. 13, 619–631. doi: 10.1016/j.geog.2022.04.003
Kumar, M., Goswami, R., Patel, A. K., Srivastava, M., and Das, N. (2020). Scenario, perspectives and mechanism of arsenic and fluoride co-occurrence in the groundwater: a review. Chemosphere 249:126126. doi: 10.1016/j.chemosphere.2020.126126
Kumar, P., Kumar, M., Barnawi, A. B., Maurya, P., Singh, S., Shah, D., et al. (2024). A review on fluoride contamination in groundwater and human health implications and its remediation: a sustainable approach. Environ. Toxicol. Pharmacol. 106:104356. doi: 10.1016/j.etap.2023.104356
Kumari, N., and Pathak, G. (2019). “Study of chemical nature of groundwater in the Western parts of Jharkhand with a focus on fluoride” in Wastewater reuse and watershed management (Apple Academic Press), 273–286.
Maheshwari, R. C. (2006). Fluoride in drinking water and its removal. J. Hazard. Mater. 137, 456–463. doi: 10.1016/j.jhazmat.2006.02.024
Mayilvaganan, M. K., and Naidu, K. B. (2011). “Application of Artificial Neural Network for the Prediction of Groundwater Level in Hard Rock Region ”, Springer-Verlag: Berlin Heidelberg. 673–682.
Mijwel, M. M. (2021). Artificial neural networks advantages and disadvantages. Mesopotamian J. Big Data 2021, 29–31. doi: 10.58496/MJBD/2021/006
Minns, A. W., and Hall, M. J. (1996). Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 41, 399–417. doi: 10.1080/02626669609491511
Mohammadi, A. A., Ghaderpoori, M., Yousefi, M., Rahmatipoor, M., and Javan, S. (2016). Prediction and modeling of fluoride concentrations in groundwater resources using an artificial neural network: a case study in Khaf 4, 217–224.
Nafouanti, M. B., Li, J., Mustapha, N. A., Uwamungu, P., and Dalal, A. A. (2021). Prediction on the fluoride contamination in groundwater at the Datong Basin, northern China: comparison of random forest, logistic regression and artificial neural network. Appl. Geochem. 132:105054. doi: 10.1016/j.apgeochem.2021.105054
Nandi, R., Mondal, S., Mandal, J., and Bhattacharyya, P. (2024). From fuzzy-TOPSIS to machine learning: a holistic approach to understanding groundwater fluoride contamination. Sci. Total Environ. 912:169323. doi: 10.1016/j.scitotenv.2023.169323
Narsimha, A., and Rajitha, S. (2018). Spatial distribution and seasonal variation in fluoride enrichment in groundwater and its associated human health risk assessment in Telangana state, South India. Hum. Ecol. Risk Assess. Int. J. 24, 2119–2132. doi: 10.1080/10807039.2018.1438176
Niu, Q. W., Lin, S. S., Reyes, J. L., Chen, K. C., Wu, H. W., Yeh, S. D., et al. (2006). Expression of artificial microRNAs in transgenic Arabidopsis thaliana confers virus resistance. Nat Biotechnol. 24, 1420–8. doi: 10.1038/nbt1255
Saha, R., Wankhede, T., Majumdar, R., and Das, I. C. (2024). Pan India fluoride hazard assessment in groundwater. J. Hazard. Mater. 478:135543. doi: 10.1016/j.jhazmat.2024.135543
Saxena, V., and Ahmed, S. (2003). Inferring the chemical parameters for the dissolution of fluoride in groundwater. Environ. Geol. 43, 731–736. doi: 10.1007/s00254-002-0672-2
Shaji, E., Sarath, K. V., Santosh, M., Krishnaprasad, P. K., Arya, B. K., and Babu, M. S. (2024). Fluoride contamination in groundwater: a global review of the status, processes, challenges, and remedial measures. Geosci. Front. 15:101734. doi: 10.1016/j.gsf.2023.101734
Singh, G., and Mehta, S. (2024). Prediction of geogenic source of groundwater fluoride contamination in Indian states: a comparative study of different supervised machine learning algorithms. J. Water Health 22, 1387–1408. doi: 10.2166/wh.2024.063
Sreedevi, P. D., Ahmed, S., and Reddy, D. V. (2017). Mechanism of fluoride and nitrate enrichment in hard-rock aquifers in Gooty Mandal, South India. Environ. Process. 4, 625–644. doi: 10.1007/s40710-017-0254-7
Su, C., Wang, Y., Xie, X., and Li, J. (2013). Aqueous geochemistry of high-fluoride groundwater in Datong Basin, northern China. J. Geochem. Explor. 135, 79–92. doi: 10.1016/j.gexplo.2012.09.003
Su, C., Wang, Y., Xie, X., and Zhu, Y. (2015). An isotope hydrochemical approach to understand fluoride release into groundwaters of the Datong Basin, Northern China. Environ. Sci. Process. Impacts 17, 791–801. doi: 10.1039/C4EM00584H
Sunitha, V., Reddy, Y. S., Suvarna, B., and Reddy, B. M. (2022). Human health risk assessment (HHRA) of fluoride and nitrate using pollution index of groundwater (PIG) in and around hard rock terrain of Cuddapah, AP South India. Environ. Chem. Ecotoxicol. 4, 113–123. doi: 10.1016/j.enceco.2021.12.002
Susheela, A. K., Bhatnagar, M., Gnanasundram, N., and Saraswathy, T. R. (1999). Structural aberrations in fluorosed human teeth: biochemical and scanning electron microscopic studies. Curr. Sci. 77, 1677–1681.
Sutradhar, S., and Mondal, P. (2021). Groundwater suitability assessment based on water quality index and hydrochemical characterization of Suri Sadar sub-division, West Bengal. Ecol. Inform. 64:101335. doi: 10.1016/j.ecoinf.2021.101335
Tabach, Y., Brosh, R., Buganim, Y., Reiner, A., Zuk, O., Yitzhaky, A., et al. (2007). Wide-scale analysis of human functional transcription factor binding reveals a strong bias towards the transcription start site. PloS one, 2:e807.
Wang, S. W., Kuo, Y. M., Kao, Y. H., Jang, C. S., Maji, S. K., Chang, F. J., et al. (2011). Influence of hydrological and hydrogeochemical parameters on arsenic variation in shallow groundwater of southwestern Taiwan. J. Hydrol. 408, 286–295. doi: 10.1016/j.jhydrol.2011.08.017
World Health Organization (2009). Calcium and magnesium in drinking water: Public health significance. Geneva, Switzerland: World Health Organization.
World Health Organization (2011). Guidelines for Drinking Water Quality. 4th Edition Geneva, Switzerland: World Health Organization. Available at: http://apps.who.int/iris/bitstream/10665/44584/1/9789241548151_eng.pdf
Yadav, A., Kumari, N., Kumar, R., Kumar, M., and Yadav, S. (2023). Fluoride distribution, contamination, toxicological effects and remedial measures: a review. Sustainable Water Resour. Manag. 9:150. doi: 10.1007/s40899-023-00926-y
Yarlanki, V. K., Vadithya, G. N., Etikala, B., and Golla, V. (2025). Hydrogeochemical characterization and source evaluation of groundwater contamination in parts of the Uddanam CKDu area, southern India: integrating statistical, geochemical modeling, pollution, and health indices. Int. J. Environ. Res. 19, 1–24. doi: 10.1007/s41742-024-00730-2
Keywords: artificial neural network (ANN), fluoride, geogenic, groundwater, MATLAB, root mean square error analysis (RMSE)
Citation: Kumari N, Kumar G and Hembrom S (2025) Groundwater fluoride modeling using an artificial neural network: a review. Front. Water. 7:1580202. doi: 10.3389/frwa.2025.1580202
Edited by:
Shraddha Singh, Bhabha Atomic Research Centre (BARC), IndiaReviewed by:
Balaji Etikala, Yogi Vemana University, IndiaCopyright © 2025 Kumari, Kumar and Hembrom. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Neeta Kumari, bmVldGFrQGJpdG1lc3JhLmFjLmlu
 Neeta Kumari
Neeta Kumari Gaurav Kumar
Gaurav Kumar Saahil Hembrom
Saahil Hembrom