- 1Department of Mathematics, Centre for Predictive Modelling in Healthcare and Centre for Systems Dynamics and Control, University of Exeter, Exeter, UK
- 2Department of Mathematics, EPSRC Centre for Predictive Modelling in Healthcare, University of Exeter, Exeter, UK
- 3Institute of Mathematics, National Academy of Sciences of Ukraine, Kiev, Ukraine
For a system of coupled identical phase oscillators with full permutation symmetry, any broken symmetries in dynamical behavior must come from spontaneous symmetry breaking, i.e., from the nonlinear dynamics of the system. The dynamics of phase differences for such a system depends only on the coupling (phase interaction) function g(φ) and the number of oscillators N. This paper briefly reviews some results for such systems in the case of general coupling g before exploring two cases in detail: (a) general two harmonic form: g(φ) = qsin(φ − α) + rsin(2φ − β) and N small (b) the coupling g is odd or even. We extend previously published bifurcation analyses to the general two harmonic case, and show for even g that the dynamics of phase differences has a number of time-reversal symmetries. For the case of even g with one harmonic it is known the system has N − 2 constants of the motion. This is true for N = 4 and any g, while for N = 4 and more than two harmonics in g, we show the system must have fewer independent constants of the motion.
1. Introduction
The last 30 years has seen a lot of progress in understanding the collective behavior of coupled oscillating dynamical systems, especially since the pioneering work of Winfree [1] and the coupled phase oscillators of Kuramoto [2, 3] which has inspired many studies of criteria for synchronization and applications in a variety of areas, notably neuroscience [4]; see also Acebrón et al. [5] and Strogatz [6] for reviews. Most of the theoretical work has focussed on the continuum limit of large populations of various types of oscillator, and has been guided by large numerical simulations—see for example Ullner and Politi [7].
Nonetheless, relatively small networks may show a lot of nontrivial and remarkable behavior that will be present in larger networks. We consider a general system of N coupled identical phase oscillators as in Kuramoto [2] but with a general coupling/phase interaction function g(φ):
where represents the phase of the oscillators, ω the natural frequency of the oscillators and g(φ) is the 2π-periodic smooth coupling function (also called the phase interaction function). Such systems arise naturally as approximations of coupled limit cycle oscillators in a weak coupling limit; see for example Ashwin and Rodrigues [8].
1.1. Identical Coupled Oscillators and Symmetric Dynamics
This case of identical oscillators is clearly highly symmetric—indeed, it is equivariant under the group of permutation symmetries SN acting by permutation of coordinates as well as being equivariant under translation along the diagonal (1, …, 1)—giving a symmetry group Γ = SN × 𝕋. Some consequences of these symmetries have been studied in Ashwin and Swift [9] and subsequently in Brown et al. [10]—tools from symmetric dynamics [11] allow one to understand a lot of the behavior of the system by looking at the action of the symmetry group on phase space. In particular, for any point in θ ∈ 𝕋N we associate the isotropy subgroup which is the subgroup {g ∈ Γ | gθ = θ} ⊂ Γ. For each subgroup G ⊂ Γ we can define the fixed point subspace Fix(G) = {θ | gθ = θ ∀ g ∈ G}; it is a standard result from Golubitsky et al. [11] that for any G, Fix(G) is dynamically invariant for any Γ-equivariant dynamical system. There is a twist in the story in that here Γ acts on the manifold 𝕋N rather than ℝN, giving rise to more non-trivial structures than expected from Golubitsky et al. [11]. In this paper we also explore the presence of time-reversal symmetries [12, 13] for even g.
In order to understand how (Equation 1) may have complex spatio-temporal attractors of various symmetry types, we study this fully symmetric case for small N and specific g to gain an insight into the general case. For the case of Kuramoto–Sakaguchi coupling [14]
one can perform a detailed analysis of the general N case and one finds either synchrony or antisynchrony are attracting, with the cases α = π/2, 3π/2 giving special integrable structure [15] that corresponds to “vertical branches” at bifurcation. However, this sort of behavior is highly degenerate for a general dissipative system. On addition of higher harmonics to the coupling function we expect, and usually find, that the degeneracies typically unfold into generic situations. Indeed such higher harmonic terms are present in a generic system even near Hopf bifurcation [8, 16]. A range of solutions, their stabilities and bifurcations, and the invariant subspaces imposed on phase space for the case of general g is discussed in Ashwin and Swift [9]. This paper briefly reviews and then extends and applies some of these results in two contexts.
The first aim of the paper is to consider the detailed bifurcation behavior for the most generic two harmonic coupling function. This means we determine which degeneracies of Equation (2) are unfolded by addition of the second harmonic, for the cases of N ≤ 4. In doing so we extend the analysis in Ashwin et al. [17] to the most general two harmonic coupling. The paper [17] examines the cases N = 3 and 4 for Equation (1) and presents complete global bifurcation diagrams for the phase interaction function discussed in Hansel et al. [18]
However, for this parameterized family the only even coupling functions are already in Equation (2). To next order [8], the generic lowest order terms will be of the form
where q, r, α and β are arbitrary constants (specific cases of such coupling was considered by [19] in the context of N = 5). More generally one can consider as in Daido [20] L-harmonic coupling
where, without loss of generality, we can assume q1qL ≠ 0, and Equation (4) corresponds to L = 2.
The second aim of this paper is to consider the behavior of the system (Equation 1) for arbitrary, but even g(φ) = g(−φ). Following Bick [21], we note there will be special structure in the dynamics, and a range of non-trivial recurrent dynamics appears for g that are small perturbations of even functions. This has been illustrated by the observation of chaotic attractors [22] and extreme sensitivity to detuning [17] for fully symmetric systems of oscillators. Indeed, chimera states [23–25] for structured (but not necessarily fully symmetric) networks are usually found close to even coupling. We observe that there is zero divergence for Equation (1) and time-reversal symmetries for the system of phase difference (though typically not for the original system). It is known there are N − 2 independent smooth integrals of the motion for any N ≥ 3 for the special case g(φ) = cos(φ) [15]. This still holds for general even g and N = 3 but, surprisingly, we show here that it does not hold for N = 4 and general even g: the flow is not fully integrable.
The paper is structured as follows: after discussing some parameter and phase symmetries, we recall the reduction of the dynamics to a canonical invariant region. In Section 2 we summarize some stability properties and bifurcations of periodic orbits by symmetry type. Section 3 applies this to general two harmonic coupling and N = 3 or 4 oscillators, extending the bifurcation analysis in Ashwin et al. [17] to general second harmonic coupling. This includes a new characterization of bifurcation of two-cluster states as the discriminant of a certain polynomial equation. Section 4 examines some consequences of the coupling function g itself being odd, or even for small N. If g is odd, it is known that the system for phase differences (but not the original system) has a variational structure and can be written as a gradient flow. If g is even, there are additional time-reversal symmetries [13] for the system for phase differences, as well as a zero divergence condition. We characterize the points with nontrivial time-reversal symmetries for N = 3 and N = 4 in detail. Finally, Section 5 considers the relation between even coupling and integrability. For N = 3 and general even g, or for N ≥ 4 and g(φ) = cos(φ) it is known since [15] that there are N − 2 independent integrals of the motion. This constrains the dynamics for N ≥ 4 to be at most two-frequency quasiperiodic. We show this is not the case for N ≥ 4 and more general even g: for examples with N = 4 and g with L ≤ 4 harmonics, we find structures that respect the time-reversal symmetries, but that cannot appear in a fully integrable structure. We discuss this, and highlight some open questions.
1.2. Parameter Symmetries for Two Harmonic Coupling
If we consider general two harmonic coupling of the form (Equation 4), the case (Equation 3) considered in Ashwin et al. [17] corresponds to q = −1, β = 0. We wish to understand the behavior of Equations (1, 4) on varying the parameters
There are parameter symmetries (such that g(φ) ↦ g(φ) for all φ)
Using Equation (6) and rescaling time by a positive scaling, we assume from hereon that q = −1: using Equation (7) we can assume from hereon that r ≥ 0. We choose q = −1 to give easy comparability to Ashwin et al. [17]. There is a time-reversal parameter symmetry (such that g(φ) ↦ −g(φ) for all φ), assuming q = −1 this is
By classifying qualitative dynamics up to time-reversal, we will can reduce to parameters in the region
in the later bifurcation analyses; using Equation (8) we can classify for β ∈ [π, 2π). Finally, there is a phase-reversal parameter symmetry (i.e., such that g(φ) ↦ −g(−φ) for all φ), assuming q = −1 this is
This means in principle we can reduce to Equation (9) with β ∈ [0, π/2] and apply phase and time reversal as necessary.
1.3. Phase Symmetries: the Canonical Invariant Region
Because the dynamics of Equation (1) depends only on phase differences, one can usefully reduce the dynamics from a flow on 𝕋N to one on 𝕋N−1 which represents only the phase differences. This corresponds to looking at the quotient dynamics of the system on the 𝕋-orbits. More precisely, if we consider a projection Π : 𝕋N → 𝕋N−1 that maps the 𝕋-orbits onto points and consider , the original system (Equation 1) becomes a reduced system on 𝕋N−1 of the form
This clearly depends on g and N but not on ω.
There are several ways to choose Π, or, equivalently, a set of N − 1 phase differences θj − θk that span the set of all phase differences. However, permutation symmetry will never act orthogonally on such a set of phase differences if N ≥ 3, meaning that symmetries are not obvious from plots of phase differences. For N = 3 and N = 4 there is a useful representation introduced by Ashwin and Swift [9] that avoids this problem. If we examine an orthogonal projection of the dynamics onto a codimension one subspace orthogonal to the diagonal (1, …, 1), this will carry an orthogonal (and irreducible) representation of SN on ℝN−1, the covering space of 𝕋N−1. In addition, the complement of fixed point subspaces where two of the phases are identical (isotropy S2) forms a partition of ℝN−1 into connected components that are all images of the canonical invariant region (or CIR) [9]. This is the set
whose boundary consists of points with S2 isotropy. There is a residual symmetry ℤN = ℤ/Nℤ = 〈τ〉 on generated by
Note that Θsplay = (0, θ2, …, θN) ∈ with is the only fixed point of the action of τ in [9].
Figure 1 illustrates the for the cases N = 3 and N = 4–the boundaries of are invariant for dynamics governed by Equation (1) for any coupling function g, though they may not be invariant for arbitrarily small perturbations that make the g or the ω different for different oscillators–in this case we may have extreme sensitivity to detuning [17]. Nonetheless, even in this case the trajectory will remain most of the time in one image of the CIR, and the dynamics can usefully be understood as being a perturbation of the highly symmetric case.
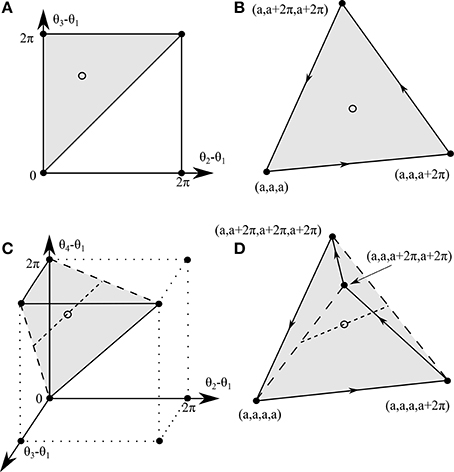
Figure 1. Structure of the canonical invariant region for N = 3 and N = 4. (A,C) show (shaded) in terms of the phase differences θj − θ1 and (B,D) as an orthogonal projection of the diagonal into ℝ2 and ℝ3, respectively. The edges of for (A,B) and the faces of for (C,D) are points with S2 isotropy. The filled circles represent different points on the lift that that correspond to fully synchrony on the torus. The open circle represents the splay phase solution in . In (C,D) the solid lines have isotropy S3 × S1 while the long dashes have isotropy S2 × S2. The short dashed lines have isotropy —typical points being (a, b, a + π, b + π). In each case there is a residual ℤN−1 symmetry indicated by the arrows in (B,D) and (N − 1)! symmetric copies of pack a generating region for the torus.
Within there are representatives of points with all possible symmetry types. Particularly important are ℓ-cluster states which correspond to states where for some partition of N = m1 + ⋯ + mℓ there are precisely mk oscillators at the same phase, for some ℓ ≥ 2 (the number of clusters) and mk ≥ 1 (the size of the kth cluster). These correspond to fixed point subspaces for isotropy groups Sm1 × ⋯ × Smℓ. These are located on the boundary of –there are also points with spatio-temporal symmetries with M > 1 and N = M(m1 + ⋯ + mℓ); see Ashwin and Swift [9]. NB: To simplify notation we omit copies of S1 when describing cluster states where this is clear from context: for example S2 for the case N = 4 corresponds to a three cluster state with isotropy group S2 × S1 × S1.
2. Stabilities and Bifurcations of Solutions Forced by Symmetries
We recall from Ashwin and Swift [9] a number of important synchronous solutions that are forced by symmetry, and their bifurcation properties.
2.1. Stability and Bifurcation of Synchronized Solutions
The fully synchronous solution (in-phase oscillation) of Equation (1) is a periodic orbit given by
where θ(t) = Ωsynct + θ0 and Ωsync = ω + g(0).
Lemma 1 ([9]). The fully synchronous solution Θsync(t) is linearly stable if and only if
For general two harmonic coupling (Equation 4) with q = −1, we have g(0) = 2r cos β − cos α and so there is bifurcation to loss of stability of this solution when
independent of N.
A splay phase solution (rotating wave) is, up to permutation, a periodic orbit of the form
where θ(t) = Ωsplayt + θ0. There are (N − 1)! different splay phase solutions from the possible permutations, but only one in the canonical invariant region . Let .
Lemma 2 ([9]). The splay phase solutions are linearly stable if the real parts of
are positive for p = 1, …N − 1, where .
Let and . If Θ = Θsplay then the matrix given by
for i = 1, …, N and
for i, j = 1, …, N, j ≠ i has eigenvalues
Note that implies λN(Θ) = 0 for any splay phases. The system has [N/2] complex conjugate pairs
in the even–dimensional case . Splay states Θ are stable when
The system for phase differences near the splay state has an Andronov–Hopf bifurcation (which can be degenerate or multiple) when Re(λp(Θ)) = 0 for some index p = 1, …N − 1, p ≠ N/2, and Im(λp(Θ)) ≠ 0.
For general two harmonic coupling (Equation 4) this can be expressed as conditions on the parameters q, r, α, β, though note that unlike the synchronous state, this will depend on N in a fairly complex way. The cases for N = 3 and N = 4 are discussed in Section 3.
2.2. Antiphase States: the Set with Zero Order Parameter.
We discuss briefly a set that is a union of invariant manifolds for some forms of coupling or for small enough N. We note that it is not invariant for generalized coupling N ≥ 5. Consider the Kuramoto order parameter for system (Equation 1) is
and define the set with zero order parameter R = 0 by
This set M(N) is union of (N − 2)-dimensional manifolds in 𝕋N [17]; it can be characterized by the set where two variables are given in terms of the other N − 2 variables by expressions
where
The manifolds can be written in phase differences (for example φi = θ1 − θi, i = 1, …N − 1) is (N − 3)–dimensional set in phase space 𝕋N−1.
Proposition 1 ([26, Lemma 1]). If the coupling function has only one harmonic, for any N the set M(N) is dynamically invariant; moreover it consists of solutions with fixed phase differences of Equation (1).
However, although some solutions (in particular, splay states Equation 17) belong to M(N) for arbitrary coupling function and arbitrary g, quite surprisingly it is not generally invariant for general coupling.
Proposition 2. The set M(N) is invariant for the system (Equation 1) for arbitrary coupling function g(φ) when N = 2, 3, 4 (ω = 0), but not in general for N ≥ 5.
Proof. For N = 2, the equation exp(iθ1) + exp(iθ2) = 0 has solution θ2 = θ1 + π, while for N = 3, the equation has solution , . Both cases correspond to the splay phase state which is a zero dimensional fixed point subspace for the phase differences—hence it is dynamically invariant. For N = 4, the equation has solution θ3 = θ1 + π, θ4 = θ2 + π. This corresponds to the fixed point subspace of which is also therefore invariant.
On the other hand, in the case N ≥ 5 the corresponding sets M(N) are not fixed point subspaces, and therefore not necessarily invariant. For example, the set M(5) includes points of the form
which is a two dimensional subspace on which
However, the smallest fixed point subspaces the contains all points of this form is the trivial subspace 𝕋5, meaning the symmetry does not force invariance of M(5). □
Note that for N = 4 coupled oscillators, the set
(one half-line in each invariant region) as a union of invariant manifolds that correspond to the states with isotropy ℤ2.
2.3. Stability and Bifurcation of Two Cluster States
Consider any two-cluster states with isotropy Sp × SN − p given by
such that θi = θa(t) for i = 2, …, p and θi = θb(t) for i = p + 1, …, N. If we denote φp = θa − θb then (see for example Orosz et al. [27] for the general case) Equation (1) gives
In this phase difference coordinate we can write
Any fixed point in the phase differences will therefore satisfy
For general two harmonic coupling (Equation 4) this means that
This has a trivial solution: the synchronous state with φp = 0. Removing the factor of sin(φp/2) this means the nontrivial two-cluster states will have a phase difference φp where
Note that two cluster-states for g(φ) = −sin(φ − α) (i.e., the special case r = 0) are considered in Burylko and Pikovsky [26][Equation 17]. By setting τ = tanφp/2, then Equation (23) can be expressed as a cubic equation. If we write p = NP so that 0 < P < 1, this implies the bifurcations occur precisely when the cubic equation for τ
has discriminant zero, namely when
where ak are polynomials in q, r, and cos and sin of α and β. The expressions for the ak are given in Appendix A (Supplementary Material).
There are also bifurcations with fixed points of two-cluster manifold that occur in transversal to this manifold direction: these create three-cluster states. For example, pitchfork bifurcations (bifurcation line ID in Ashwin et al. [17], Figure 1 for three oscillators can occur transverse to the lines φ1 = 0 (or φ2 = 0, φ1 = φ2). Such bifurcations cannot be found by examination just of the equation on invariant manifold (Equation 20) or (Equation 21) but need to consider the transverse eigenvalues of the solutions, expressions for which are given in Orosz et al. [27]. Later on we use numerical path following to locate these.
3. Bifurcation Scenarios for Low N and Two Harmonic Coupling
We review and extend the exploration of parameter space of Equation (1) with general two harmonic coupling Equation (4) from the special case β = 0 [17] for N = 3 and N = 4 to more general β ≠ 0.
3.1. Bifurcations for N = 3
Figure 2 illustrates the bifurcations that determine the structure of the phase space for N = 3 in the case q = −1, on varying α ∈ [0, π) and r ≥ 0, for four choices of β. Note that the case β = 0 in the dot-dashed region corresponds to the case considered in Ashwin et al. [17]. Some of the curves are calculated analytically while the remainder of the curves on Figure 2 are obtained by numerical path following of bifurcations in the reduced system (Equation 11) using XPPAUT [28].
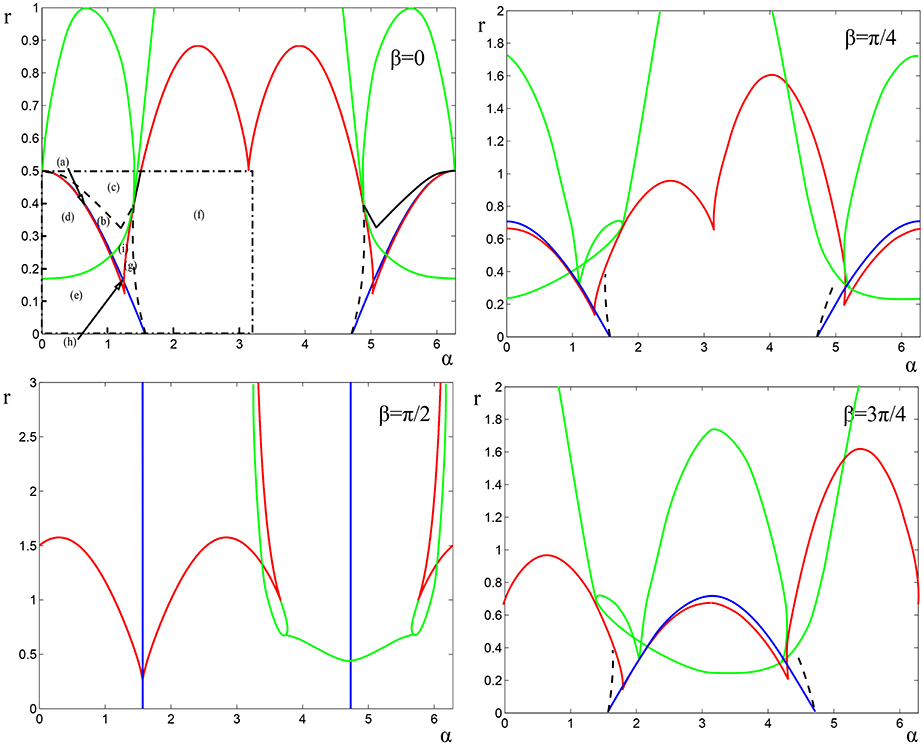
Figure 2. Summary of bifurcations for N = 3 on varying α and r for four choices of β. The blue lines (Equation 16) indicate (simultaneous) steady bifurcation of in-phase and Hopf bifurcation of splay phase solutions. The red lines (Equation 28) indicate saddle-node bifurcations of non-trivial S2 states. The green lines (found using XPPAUT) give the location of steady bifurcations involving equilibria where all phase differences are non-zero. The black dashed lines indicate homoclinic/heteroclinic bifurcations of periodic solutions. The letters (a–i) show the location of points corresponding to the phase planes shown in Figure 3. The dot-dashed regions for the case β = 0 corresponds to the diagram detailed in Ashwin et al. [17]. Note that in the case β = π/2 and α = π/2 or 3π/2 the system is integrable, while the case β = 3π/4 can be found from that for π/4 by the phase-and time-reversal symmetry (r, α, β) ↦ (r, π − α, π − β).
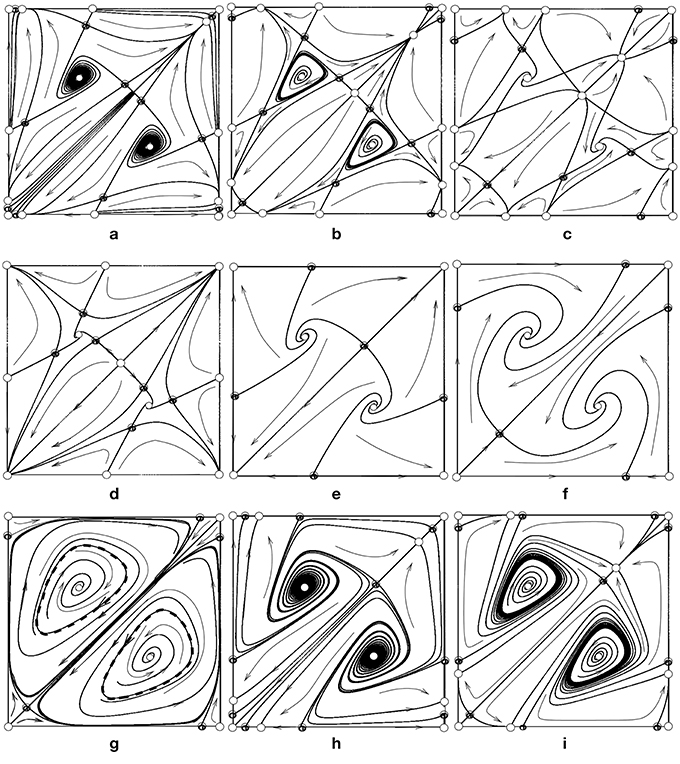
Figure 3. Phase portraits for N = 3 and β = 0, displayed as in Figure 1A on varying α and r, at the locations indicated by (a–i) in Figure 2. The transitions and codimension two points are described in detail in Ashwin et al. [17].
Note that from the previous section, we know that the in-phase solution undergoes bifurcation at (Equation 16). The splay phase solution with N = 3 the stability is governed by the eigenvalues
meaning there is a Hopf bifurcation of the splay phase also at
This is precisely the same location as (Equation 16)—a non-generic phenomenon! For N = 3 there is only one type of two-cluster state: this is for p = 1. Setting P = 1/3 and q = −1, (Equation 23) can be expressed as the cubic equation for τ = tan(φ/2):
which has bifurcations of solutions precisely when the discriminant is zero: this implies the bifurcations of two-cluster states occur when
We summarize the bifurcations for β ≠ 0 in Figure 2. One of the more surprising observations of the analysis above can be summarized as follows.
Corollary 1. In order for the Hopf bifurcation of splay phase and the bifurcation of in-phase to occur at different points in parameter space for Equation (1) with N = 3, it is necessary to have a coupling function g with at least three harmonics.
3.2. Bifurcations for N = 4
Figure 4 illustrates a selection of the local bifurcations that determine the structure of the phase space for N = 4 in the case q = −1 on varying α ∈ [0, π) and r ≥ 0 for four values of β. Note that the case β = 0 in the dot-dashed region corresponds to the case considered in Ashwin et al. [17] for N = 4. As before, the in-phase solution has a bifurcation at locations where (Equation 16) is satisfied. For the splay phase solution with N = 4 the stability transverse to the rotating block (0, π, θ, θ + π) is governed by the complex eigenvalues
meaning there is a Hopf bifurcation of the splay phase when cos α = 0, namely at α = π/2 independent of β. There can also be bifurcation from splay phase to rotating block where
meaning there is a bifurcation from the splay phase to rotating blocks (0, π, θ, θ + π) when cos β = 0.
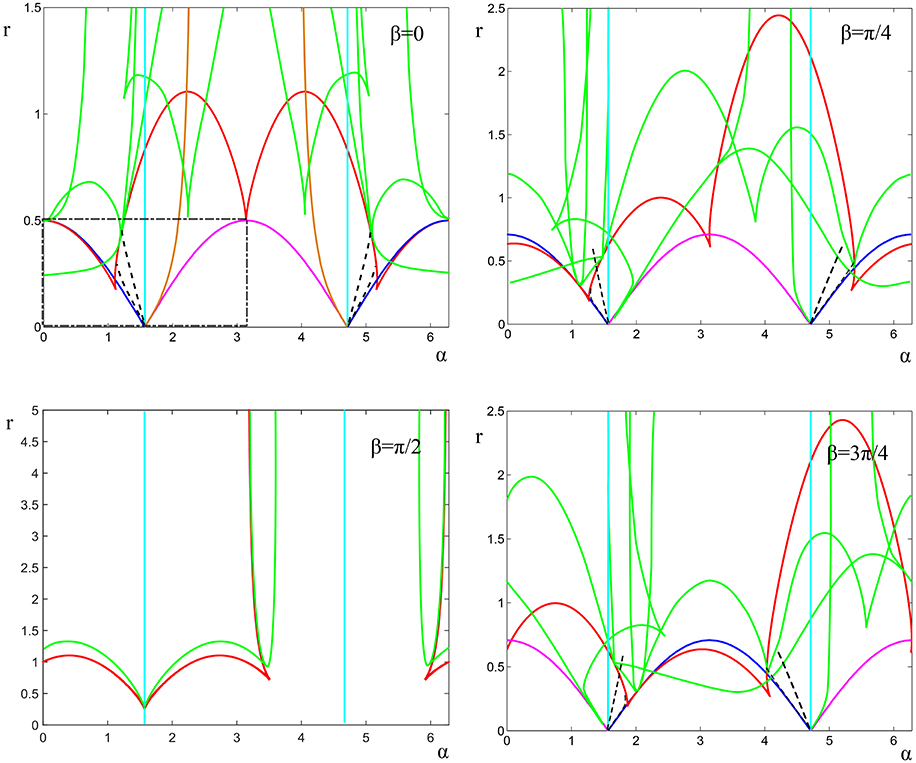
Figure 4. Summary of bifurcations for N = 4 on varying α and r for four choices of β. The blue lines indicate steady bifurcation of the in-phase (Equation 16) while the cyan lines indicate Hopf bifurcation of splay phase solutions (cosα = 0). The red lines indicate saddle-node bifurcations of two cluster states with isotropy S3. The green lines indicate the location of steady bifurcations involving three cluster states with isotropy S2. The dashed lines indicate (incomplete lines of) bifurcations of periodic orbits. The dot-dashed regions for the case β = 0 corresponds to the diagram in Ashwin et al. [17]—see there for more details of the dynamics in this case. Note that the case β = π/2 and α = π/2 (or 3π/2) correspond to an even coupling function.
The dynamics of the points with isotropy (S1 × S1) × sℤ2 (rotating blocks (0, π, θ, θ + π)) is determined by
meaning this is degenerate for β = π/2, independent of α! Note that the bifurcations for the rotating blocks only becomes non-degenerate on addition of the fourth harmonic—only then can we get nontrivial solutions with this symmetry. There are two possible two-cluster state: for N = 4 and p = 1 so that P = 1/4 and setting q = −1, (Equation 23) can be expressed as the cubic equation
There are bifurcations of two cluster states with isotropy S3 when the discriminant of Equation (31) (not shown here) is zero.
For isotropy S2 × S2 we can set N = 4, p = 2 and q = −1 in Equation (23) to find a quadratic expression
with discriminant
Hence the bifurcations of these states are at
The remainder of the curves on Figure 4 are obtained by numerical path following of local bifurcations on the two dimensional fixed point subspace of S2 in the reduced system (Equation 11) using XPPAUT [28]. We remark there may well be more local bifurcations that involve fully symmetry broken (four-cluster) states, as well as global bifurcations that are not shown on this diagram.
4. Dynamics for Odd and Even Coupling Functions
In the case that the coupling function g in Equation (1) is even or odd, the system has additional structure. Write g = g+ + g− where
are the even and odd parts respectively. For the coupling functions of the form (Equation 4) we have
The remaining results in this section are independent of N and apply to general even or odd g.
If g is odd (i.e., g+(φ) ≡ 0) then the system for phase differences is a gradient system [10, 29]. More precisely, if we write G′(φ) = g(φ) which is single-valued if g is odd and periodic, we can define a potential
then Equation (1) can be written in the form
This can be seen as a gradient system for the phase differences (Equation 11) on identifying 𝕋N − 1 as the set θ ∈ 𝕋N such that .
Hence, the only have attractors that are local minima of the potential V. In general, for ω ≠ 0 one can write a potential for the full system on ℝN but note that this is multivalued on 𝕋N.
The case where the coupling function g is even (g− ≡ 0) is dynamically more interesting: there are hints that it organizes the emergence of chaotic dynamics for nearby parameter values [22].
Lemma 3. If g is even then the flow of Equation (1) is divergence free. Moreover, the reduced system (Equation 11) is also divergence free.
Proof. To see this, consider
and so
Since g is even, this implies that g′ is odd. Thus, and we have
More than this, note that the Jacobian in the direction of the 𝕋 action is trivial, meaning that the dynamics of the phase differences (Equation 11) transverse to this direction is also divergence free. □
Recall that an involution : 𝕋N → 𝕋N is a time-reversal symmetry if
that is, maps any solution to another solution with the direction of the flow is inverted [13].
Lemma 4. If g is even then the system (Equation 1) has a time and parameter-reversal symmetry : 𝕋N → 𝕋N where
For the reduced system (Equation 11) this corresponds to a time-reversal symmetry where
Proof. Note that for ω = 0 we have
At the same time,
which implies that is a time-reversal symmetry of Equation (1) for the special case ω = 0. This immediately implies that there is a time-reversal symmetry of Equation (11) in general, but only a time and parameter reversal symmetry in general for Equation (1). □
Note that given any symmetry g ∈ Γ and a time-reversal symmetry , the composition of the two °g is also a time-reversal symmetry. In fact, the set of time-reversal symmetries on 𝕋N−1 is in one-to-one correspondence with the set of symmetries Γ [13] and can be generated in this way: given any time-reversal symmetry , the set of time-reversal symmetries is Γ. A consequence is that if θ ∈ 𝕋N has isotropy H ⊂ SN × 𝕋 then so does (θ).
If is a time reversal-symmetry, the fixed point subspace Fix() = {θ ∈ 𝕋N | θ = θ} is not necessarily dynamically invariant, but it is of interest as it yields a natural way to find families of periodic solutions and homoclinic and heteroclinic orbits [13]. In particular, the reversible Lyapunov Centre Theorem asserts that, subject to nonresonance conditions, near an equilibrium in Fix() with pairs of purely imaginary eigenvalues there is a two parameter family of reversible periodic orbits, even if there are additional zero eigenvalues [30, 31].
There is a particular time-reversal symmetry that maps the canonical invariant region to itself. More precisely, let us define
on the canonical invariant region and note that this is a reversing symmetry corresponding to reversing the order of the components and composing with . We characterize all points in that are mapped to themselves by a reversing symmetry. Thus, we define
These are the fixed points of time-reversal symmetries within . Let us define
and note that
On ∂ we have for . Moreover, the splay state (Equation 17) is contained in . We now turn to the time-reversal symmetries for N = 3 and N = 4 oscillators. In each case we rescale time by N for simplicity.
4.1. Dynamics for Even Coupling Functions: N = 3
A system for N = 3 oscillators has and additional degeneracy: there is a constant of motion
with G′ = g which generalizes a specific case of the Watanabe–Strogatz constant of motion [21, 32]. Hence, the dynamics of the system is effectively one-dimensional.
For the relative fixed point sets of the time-reversal symmetry, we have
which define three line segments that meet at the splay state. The configurations of the oscillators are depicted in Figure 5. Figure 6 shows = QN, 0 ∪ QN, 1 ∪ QN, 2 superimposed on the dynamically invariant curves determined by the level sets of Equation (41) for an even coupling function with four Fourier modes:
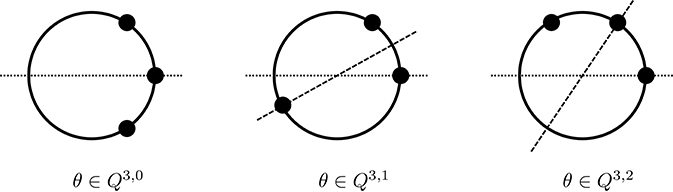
Figure 5. Configurations of phases of three oscillators that are invariant under reflections. Phases 0 = θ1 < θ2 < θ3 are aligned anticlockwise around the circle and the ℤ3 symmetry operates by rotating the operators anticlockwise by a common phase shift until θ3 = 0 (and then relabeling oscillators). For Q3, q, reflection along the dashed line corresponds to .
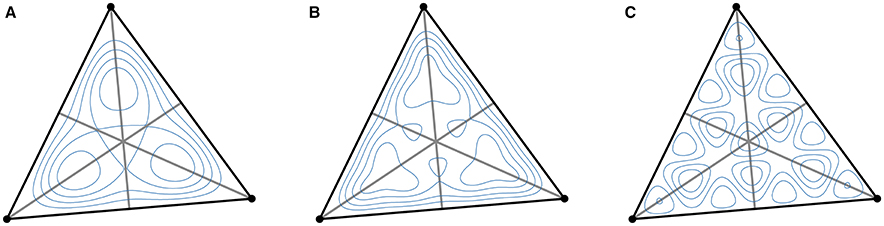
Figure 6. For N = 3 oscillators, the points of organize the dynamics in for even coupling functions. As in Figure 1B, the boundary of are points of S2 (black lines) which intersect in Θsync (black dot). The union of fixed point subspaces for time-reversal symmetries are depicted by gray lines which intersect in Θsplay. The level curves (blue lines) of the constant of motion (Equation 41) for different parameter values of the coupling function (Equation 43) are superimposed in each panel: the nontrivial Fourier coefficients are c1 = 1, c2 = 1 in (A), c1 = −2, c2 = −2, c3 = −1, and c4 = −0.88 in (B), and c1 = −2, c2 = −2, c3 = −1, and c4 = 10 in (C). Note that in the third panel we are close to an additional symmetry: a high order Fourier component dominates.
The points with time-reversal symmetry intersect the boundary of the canonical invariant region at (0, 0, 0), (0, 0, π), (0, π, π).
To find the equilibria in it suffices to evaluate the equilibria in Q3, 0 since Q3, 1, Q3, 2 are the images of Q3, 0 under the action of ℤ3. Write ψk = θk − θ1 and . On Q3, 0 we have the vector field
perpendicular to Q3, 0. A point is an equilibrium if and . The linearization of Fψ at ,
has eigenvalues
where indices are taken modulo N = 3. The eigenvalues thus always take either real or pure imaginary values.
Figure 6 shows examples where it appears that the only equilibria in lie in . Equilibria with a pair of imaginary eigenvalues give rise to “islands” of neutrally stable periodic orbits. These are organized by the stable and unstable manifolds of the saddle points on which form heteroclinic connections and yield the topological obstructions bounding the islands. The equilibria should relate directly to the constant of motion where the level sets are not smooth manifolds.
4.2. Dynamics for Even Coupling Functions: N = 4
For N = 4 we calculate
The configuration of phases are depicted in Figure 7. Note that τQ4, 0 = Q4, 2 and τQ4, 1 = Q4, 3. The sets Q4, 1, Q4, 3 are subsets of planes that intersect the edges of the canonical invariant in the cluster states with S2 × S2 isotropy and lines on the faces corresponding to cluster states with S2 isotropy. The planes intersect in the interior of the canonical invariant region in the set of points with ℤ2 isotropy1 and subdivide the CIR into four connected components. The sets Q4, 0, Q4, 2 are line segments that intersect ∂ in (0, π, π, π), (0, 0, π, 0), (0, 0, 0, π), and (0, π, 0, 0). We have . Figure 8 shows a projection of the canonical invariant region and for coupling function (Equation 43) with four nontrivial Fourier modes. Note that while is not necessarily invariant as fixed point subspaces of a time-reversal symmetry, it may contain invariant subsets, such as points of nontrivial isotropy.
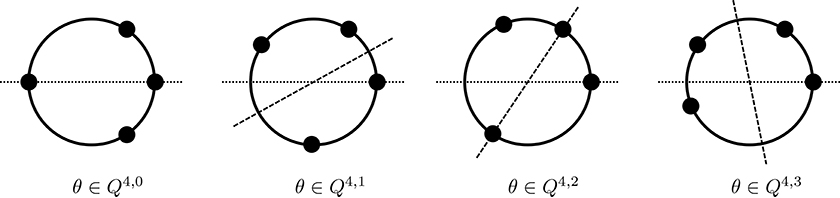
Figure 7. Configurations of phases of four oscillators that are invariant under time-reversal. Phases 0 = θ1 < θ2 < θ3 < θ4 are aligned anticlockwise around the circle. Reflection along the dashed line for QN, q corresponds to the action of time-reversal symmetry .
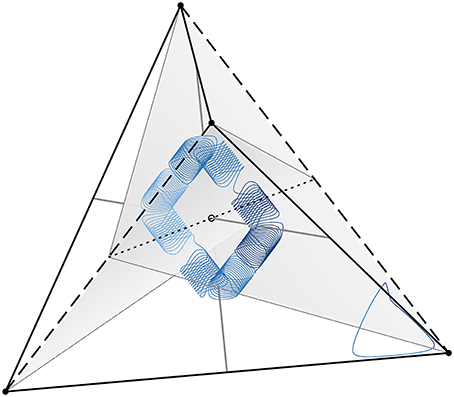
Figure 8. For N = 4 oscillators, the points of constrain the dynamics in for even coupling functions. As in Figure 1D, the faces of are points of S2 isotropy and black lines correspond to points of isotropy S3 (solid), S2 × S2 (dashed), and ℤ2 (dotted). The points in are depicted in gray: Q4, 0, Q4, 2 (thick gray lines), Q4, 1, Q4, 3 (planes and thin gray lines that depict points with S2 isotropy within). Trajectories (blue lines) for two initial conditions are plotted for the coupling function (Equation 43) with coefficients a1 = −0.5, a2 = −0.5, a3 = −0.25, a4 = 10. The shading of the trajectories indicates in which of the four connected subsets a point lies and changes of color correspond to intersections of the trajectories with Q4, 1 and Q4, 3. Note that the trajectories intersect Q4, 1 and Q4, 3 in exactly two points. For this choice of coupling function a higher order Fourier component dominates as in Figure 6C leading to the “spiraling” motion of the trajectory; details will be discussed elsewhere.
We give equations for fixed points in Q4, 0. In fact, any equilibrium within for N = 4 oscillators has to be neutrally stable after reducing the phase-shift symmetry; the linearization around equilibria with time-reversing symmetry for a three dimensional system will have one pair of real or pure imaginary eigenvalues and one zero eigenvalue. Introducing phase difference variables ψk = θk − θ1 for Q4, 0, we have ψ3 = π, ψ4 = 2π − ψ2. The vector field with components is given by
which has eigenvalues
These simplify if some harmonics of the coupling function g vanish: if the coupling function is π-periodic, g(ϕ + π) = g(ϕ), then Equation (49) yields
and if g(ϕ + π) = −g(ϕ) we obtain
implying that neutrally stable periodic orbits arise nearby.
Note that along Q4, 0. The linearization of Fψ at an equilibrium (0, ψ⋆, π, 2π − ψ⋆) is
Similarly, one can calculate equilibria in Q4, 3 where we have ψ4 = ψ2 + ψ3. For these points, the dynamics are given by
Note that the vector field vanishes in the ψ4 direction along Q4, 3. Points are equilibria if
Similarly calculating the eigenvalues, we find
and the eigenvector for λ = 0 is given by
Since g is even, there are solutions to the fixed point (Equation 51) that are independent of g. The arguments being equal, , q ∈ ℤ, implies , q ∈ ℤ and arbitrary . If the sign of the arguments is opposite, we have , q ∈ ℤ which implies , q ∈ ℤ. The condition defines a line of equilibria given by
which are points of ℤ2 isotropy in . Note that the eigenvector v0 of the trivial eigenvalue, Equation (53), points along L−. Moreover, the remaining two eigenvalues evaluate to
If some harmonics of the coupling function g vanish they take either real or imaginary values for all points in L−: if the coupling function is π-periodic, g(ϕ + π) = g(ϕ), L− is an continuum of saddles since
If g(ϕ + π) = −g(ϕ) we obtain
implying that neutrally stable periodic orbits arise close to L−.
Similarly, in the second case where the sign of the arguments is opposite, consider which yields a continuum of equilibria
which are points of S2 × S2 isotropy on ∂. Again, the eigenvector v0 corresponding to the neutrally stable direction points along L+. The remaining eigenvalues are given by
yielding a family of saddles. The stable and unstable manifolds lie in boundary faces of with S2 isotropy. They can intersect again in Q4, 1 which intersects the boundary faces adjacent to L+ in a line.
While the equilibria studied above exist for any choice of even coupling function g, there may be further equilibria that organize the dynamics. First, the Equations (47), (51) may have more equilibria that depend on the coupling function chosen. As these lie in they have symmetric stability properties. Second, the equilibria that are not contained in appear to play an important role and yield a mechanism that could give rise to complex heteroclinic networks in the system. For example, assume that θ⋆ ∈ \ is a hyperbolic equilibrium with trivial isotropy. Since the vector field is divergence free, the equilibrium has to be a saddle. Suppose that θ⋆ has one-dimensional stable and two-dimensional unstable manifold. The action of symmetries and time-reversal implies that there are N symmetric copies of θ⋆. At the same time, there are N copies with inverse stability properties that are given by the group orbit of . An intersection of the unstable manifold of θ⋆ with Q4, 1 or Q4, 3 yields a heteroclinic connection to an equilibrium related by the time-reversal symmetry. Such a heteroclinic connection may have trivial isotropy (given the way Q4, 1 and Q4, 3 subdivide the CIR into connected components) or nontrivial isotropy, depending on where this intersection takes place. In this way, a network between the (symmetrically and reversing symmetry related) copies of θ⋆ may be formed.
5. Discussion
5.1. Even Coupling and Integrability
As noted in Equation (41) for N = 3 and arbitrary even coupling function, there is N − 2 = 1 constant of the motion, in agreement with the case for Kuramoto coupling [15]. It is natural to consider whether there are N − 2 independent constants of the motion for N = 4 and arbitrary even coupling function. If this was the case, the only invariant sets would be two frequency quasiperiodicity. Although Watanabe and Strogatz [15] and the presence of time-reversal symmetries might hints this might be the case, we present evidence there is at most one integral of the motion for N = 4.
In particular, for N = 4 and the states with S2 isotropy on the boundary of , Figure 9 demonstrates that for the case N = 4 and even coupling functions with up to four harmonics of the form (Equation 43) are not fully integrable. In cases (c), (d) of the Figure, we argue there are no nontrivial smooth integrals of the motion within the S2 subspace, owing to the appearance of sink/source pairs. We only find such evidence of nonintegrable behavior if c3 and c4 are non both zero: if c3 and c4 are both zero (Equation 43) (only two harmonics) then there are apparently no equilibria within S2 that are not fixed by a time reversal symmetry and the phase portraits are consistent with the presence of a smooth constant of the motion.
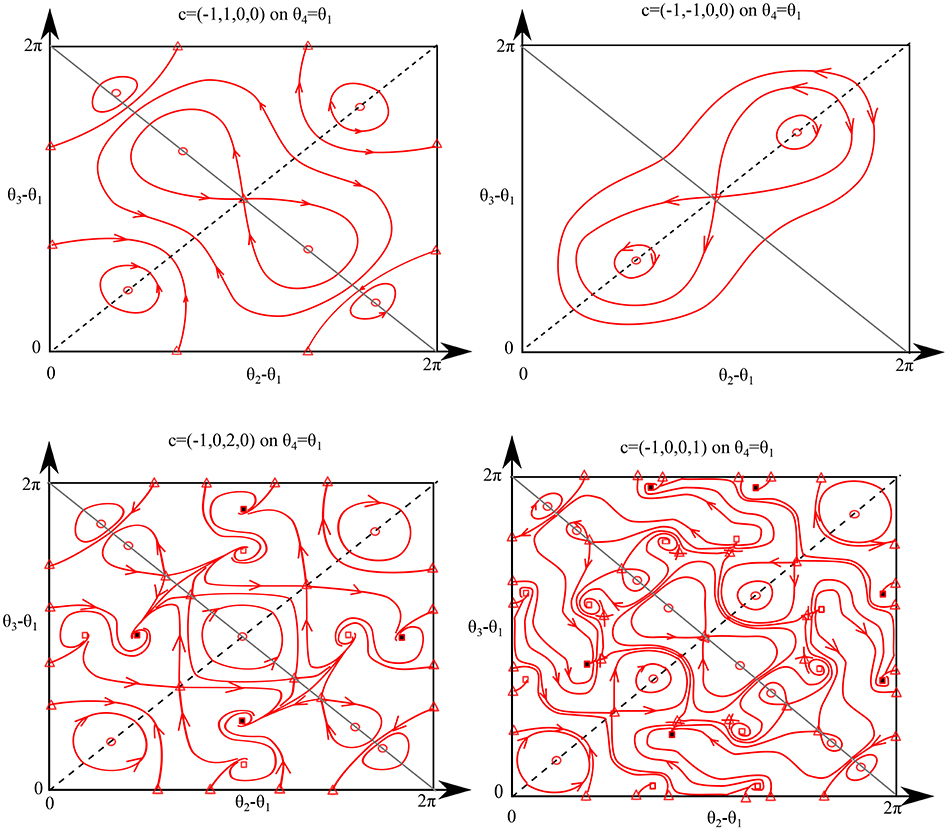
Figure 9. Phase portraits for N = 4 oscillators show a wide range of continua of heteroclinic cycles on the boundary of . Here we show a face of the CIR with S2 isotropy, assuming even g with the first four harmonics given by Equation (43). Dashed black lines are points with S2 × S2 isotropy foliated with fixed points and gray lines indicate . For equilibria, triangles are saddles, circles are centers, open squares are sources, and filled squares are sinks; these points are degenerate on the dashed line with S2 × S2 isotropy which corresponds to L+ with transversal stability given by Equation (55). Observe that four our choice of c1, c2, all equilibria lie within if c3 = c4 = 0, but there are sink/source pairs (indicating lack of integrability) for cases where one of them is non-zero.
It is still possible that there is one integral of the motion for the case N = 4 and general even coupling, as long as this integral is zero on the boundary of the canonical invariant region, and the trajectory shown in Figure 8 is consistent with this.
5.2. Open Questions
We finish by highlighting some open questions raised in this paper. Firstly, we note that addition of the second harmonic does unfold many degeneracies, though not all. We note that there may be some that are still present for (Equation 1) even for coupling functions with an infinite number of harmonics present, and these will disappear on considering more general coupling that is not of “pairwise” type (see [8]). There seems to be a subtle interplay of the order N, the symmetries of g and the number of harmonics L that determine the dynamics.
Extending a bifurcation analysis to higher N will be harder than extending to higher L, but the latter seems worthwhile especially if it is possible to determine the location of global bifurcations. We do extend the bifurcation analysis here in part analytically, using the special form of the coupling function to write the bifurcations of two-cluster in polynomial form. Potentially this can be extended to more general cluster states, though at the expense of ever more complex expressions. As an alternative approach, rather than doing a bifurcation analysis for fixed L, one could conversely ask whether some harmonics are crucial for specific bifurcations to occur.
The dynamics for the case of an even coupling function shows remarkable subtlety. Numerical experiments show a variety of periodic orbits which can be quite complicated in examples of even coupling functions where a higher harmonic dominates; cf. Figure 8. Although we demonstrate in the previous section that one cannot expect there to be fully integrability with N − 2 independent constants of the motion [15, Theorem, p. 249], there may well be one constant of the motion in the general even coupling case which we have not yet been able to determine.
For even coupling we demonstrate for N = 3, 4 that the set of phases with time-reversal symmetry within the canonical invariant region is a nontrivial (typically noninvariant) set that organizes the dynamics. Complicated dynamics, such as chimera states [23] and chaotic dynamics [22] (and as a consequence also the chaotic weak chimeras constructed in Bick and Ashwin [33]), typically arise in systems for small perturbations away from a system with time-reversal symmetry. We anticipate that understanding these heteroclinic networks in greater detail will shed light on how complicated arise in networks of coupled phase oscillators. Naturally, the more equilibria there are, the more intricate the heteroclinic network can be. Thus, deriving conditions for the existence of equilibria depending on the coupling function seems like a first step to understand the dynamics for even coupling functions g.
Author Contributions
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
PA gratefully acknowledges the financial support of the EPSRC via grant EP/N014391/1. CB gratefully acknowledges financial support from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007–2013) under REA grant agreement no. 626111.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fams.2016.00007
Footnotes
1. ^Note that for N > 4 there are points with ℤk ⊂ ℤN isotropy that are not in .
References
1. Winfree A. T. The Geometry of Biological Time, 2nd Edn. New York, NY: Springer (2001). doi: 10.1007/978-1-4757-3484-3
2. Kuramoto Y. Chemical Oscillations, Waves and Turbulence. Berlin: Springer-Verlag (1984). doi: 10.1007/978-3-642-69689-3
3. Kuramoto Y. Self-entrainment of a population of coupled non-linear oscillators. In: Araki H, editor. International Symposium on Mathematical Problems in Theoretical Physics, Lecture Notes in Physics. Berlin: Springer-Verlag (1975). p. 420–422. doi: 10.1007/BFb0013365
4. Ashwin P, Coombes S, Nicks R. Mathematical frameworks for oscillatory network dynamics in neuroscience. J Math Neurosci. (2016) 6:1–92. doi: 10.1186/s13408-015-0033-6
5. Acebrón J, Bonilla L, Pérez Vicente C, Ritort F, Spigler R. The Kuramoto model: a simple paradigm for synchronization phenomena. Rev Mod Phys. (2005) 77:137–85. doi: 10.1103/RevModPhys.77.137
6. Strogatz SH. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Phys D (2000) 143:1–20. doi: 10.1016/S0167-2789(00)00094-4
7. Ullner E, Politi A. Self-sustained irregular activity in an ensemble of neural oscillators. Phys Rev X (2016) 6:011015. doi: 10.1103/PhysRevX.6.011015
8. Ashwin P, Rodrigues A. Hopf normal form with SN symmetry and reduction to systems of nonlinearly coupled phase oscillators. Phys D (2016) 325:14–24. doi: 10.1016/j.physd.2016.02.009
9. Ashwin P, Swift JW. The dynamics of n weakly coupled identical oscillators. J Nonlin Sci. (1992) 2:69–108. doi: 10.1007/BF02429852
10. Brown E, Holmes P, Moehlis J. Globally coupled oscillator networks. In: Perspectives and Problems in Nonlinear Science: A Celebratory Volume in Honor of Larry Sirovich, eds E. Kaplan, J. E. Marsden, and K. R. Sreenivasan (New York, NY: Springer) (2003). p. 183–215. doi: 10.1007/978-0-387-21789-5_5
11. Golubitsky M, Schaeffer DG, Stewart IN. Singularities and Groups in Bifurcation Theory, Vol. II. New York, NY: Springer-Verlag (1988). doi: 10.1007/978-1-4612-4574-2
13. Lamb JSW, Roberts JAG. Time-reversal symmetry in dynamical systems: a survey. Phys D (1998) 112:1–39. doi: 10.1016/S0167-2789(97)00199-1
14. Sakaguchi H, Kuramoto Y. A soluble active rotator model showing phase transitions via mutual entrainment. Prog Theor Phys. (1986) 76:576–81. doi: 10.1143/PTP.76.576
15. Watanabe S, Strogatz SH. Constants of motion for superconducting Josephson arrays. Phys D (1994) 74:197–253. doi: 10.1016/0167-2789(94)90196-1
16. Kori H, Kuramoto Y, Jain S, Kiss IZ, Hudson J. Clustering in globally coupled oscillators near a Hopf bifurcation: theory and experiments. Phys Rev E (2014) 89:062906. doi: 10.1103/PhysRevE.89.062906
17. Ashwin P, Burylko O, Maistrenko Y. Bifurcation to heteroclinic cycles and sensitivity in three and four coupled phase oscillators. Phys D (2008) 237:454–66. doi: 10.1103/PhysRevE.89.062906
18. Hansel D, Mato G, Meunier C. Clustering and slow switching in globally coupled phase oscillators. Phys Rev E (1993) 48:3470–77. doi: 10.1103/PhysRevE.48.3470
19. Ashwin P, Orosz G, Wordsworth J, Townley S. Dynamics on networks of clustered states for globally coupled phase oscillators. SIAM J Appl Dyn Syst. (2007) 6:728–58. doi: 10.1137/070683969
20. Daido H. Onset of cooperative entrainment in limit-cycle oscillators with uniform all-to-all interactions: bifurcation of the order function. Phys D (1996) 91:24–66.
21. Bick C. Chaos and Chaos Control in Network Dynamical Systems. PhD dissertation, Georg-August-Universität Göttingen (2012).
22. Bick C, Timme M, Paulikat D, Rathlev D, Ashwin P. Chaos in symmetric phase oscillator networks. Phys Rev Lett. (2011) 107:244101. doi: 10.1103/PhysRevLett.107.244101
23. Abrams DM, Strogatz SH. Chimera states for coupled oscillators. Phys Rev Lett. (2004) 93:174102. doi: 10.1103/PhysRevLett.93.174102
24. Panaggio MJ, Abrams DM. Chimera states: coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity (2015) 28:R67–87. doi: 10.1088/0951-7715/28/3/R67
25. Laing CR. The dynamics of chimera states in heterogeneous Kuramoto networks. Phys D (2009) 238:1569–88. doi: 10.1016/j.physd.2009.04.012
26. Burylko O, Pikovsky A. Desynchronization transitions in nonlinearly coupled phase oscillators. Phys D (2011) 240:1352–61. doi: 10.1016/j.physd.2011.05.016
27. Orosz G, Moehlis J, Ashwin P. Designing the dynamics of globally coupled oscillators. Prog Theor Phys. (2009) 122:611–30. doi: 10.1143/PTP.122.611
29. Hoppensteadt FC, Izhikevich EM. Weakly Connected Neural Networks, volume 126 of Applied Mathematical Sciences. New York, NY: Springer (1997). doi: 10.1007/978-1-4612-1828-9
30. Devaney RL. Reversible diffeomorphisms and flows. Trans Am Math Soc. (1976) 218:89–113. doi: 10.1090/S0002-9947-1976-0402815-3
31. Golubitsky M, Krupa M, Lim C. Time-reversibility and particle sedimentation. SIAM J Appl Math. (1991) 51:49–72. doi: 10.1137/0151005
32. Pikovsky A, Rosenau P. Phase compactons. Phys D (2006) 218:56–69. doi: 10.1016/j.physd.2006.04.015
Keywords: phase oscillator, symmetry breaking, heteroclinic orbits, time reversal symmetry, Kuramoto network, bifurcation analysis
Citation: Ashwin P, Bick C and Burylko O (2016) Identical Phase Oscillator Networks: Bifurcations, Symmetry and Reversibility for Generalized Coupling. Front. Appl. Math. Stat. 2:7. doi: 10.3389/fams.2016.00007
Received: 10 March 2016; Accepted: 02 June 2016;
Published: 21 June 2016.
Edited by:
Laura Gardini, University of Urbino, ItalyReviewed by:
Oleksandr Popovych, Jülich Research Centre, GermanyTomasz Kapitaniak, Lodz University of Technology, Poland
Copyright © 2016 Ashwin, Bick and Burylko. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter Ashwin, cC5hc2h3aW5AZXhldGVyLmFjLnVr;
Christian Bick, Qy5CaWNrQGV4ZXRlci5hYy51aw==;
Oleksandr Burylko, YnVyaWxrb0BpbWF0aC5raWV2LnVh
 Peter Ashwin
Peter Ashwin Christian Bick
Christian Bick Oleksandr Burylko
Oleksandr Burylko