- The Department of Mathematics and Computer Science, University of Missouri–St. Louis, St. Louis, MO, United States
A tree-based method for regression is proposed. In a high dimensional feature space, the method has the ability to adapt to the lower intrinsic dimension of data if the data possess such a property so that reliable statistical estimates can be performed without being hindered by the “curse of dimensionality.” The method is also capable of producing a smoother estimate for a regression function than those from standard tree methods in the region where the function is smooth and also being more sensitive to discontinuities of the function than smoothing splines or other kernel methods. The estimation process in this method consists of three components: a random projection procedure that generates partitions of the feature space, a wavelet-like orthogonal system defined on a tree that allows for a thresholding estimation of the regression function based on that tree and, finally, an averaging process that averages a number of estimates from independently generated random projection trees.
1. Introduction
We consider the problem of estimating the unknown function in the model:
with a sample (xi, yi), i = 1, …, n, where ε is a random variable with E(ε) = 0 and Var(ε) = σ2. We are mainly interested in the case where the dimension p of the feature variable X is large, either relative to the sample size n of data or in itself, although the method of this paper also applies well to lower dimensional cases. When p is large, we assume that the domain of the function f is actually restricted to a much lower dimensional but unknown sub-manifold of ℝp. We refer to the dimension of this sub-manifold as the intrinsic dimension of the regression problem.
An important question to ask in this regression setting is that without having to learn the sub-manifold first, can one find an estimator for f that automatically adapts to the intrinsic low dimensional structure of data in the sense that it can still provide efficient and reliable estimates, without being hindered by the “curse of dimensionality” [1, 2] due to the large p? Bickel and Li [3] provide an affirmative answer to this question by showing that local polynomial regressions can achieve such a property under regularity conditions so that the decay of the prediction error in sample size depends only on the intrinsic dimension rather than p.
It turns out that the local polynomial regression is not the only approach that is capable of being adaptive to the intrinsic dimension of data. This is a more general phenomenon. Tree-based methods are useful and efficient alternatives and can be computationally more efficient. A work of Binev et al. [4, 5] provides arguments implying that certain tree-based approximations are adaptive. Later, Dasgupta and Freund [6] and Kpotufe and Dasgupta [7] demonstrate explicitly such adaptability for their random projection trees when the intrinsic dimension is defined to be the so-called doubling dimension. A tree-based regression [7–11] is to partition recursively the feature space ℝp into finer and finer subsets and then estimate f locally within each finest subset. Such a process has a naturally hierarchical tree structure. The corresponding tree is called a partitioning tree. An extension of the tree methods is the random-forest approach [8]. In this approach, an average of individual tree estimates based on bootstrap samples is used. In addition to the adaptive property, Dasgupta et al. [6] and Kpotufe and Dasgupta [7] argue that tree methods can be computationally more efficient than kernel smoothing methods, including the local polynomial regressions, or k-nearest neighbor methods, because while it takes only O(logn) steps, the height of a balanced tree, for a tree method to reach to a prediction, it takes Ω(n) for a kernel-type method and Ω(n1/2) for a k-nearest neighbor method to obtain a prediction.
We note that most of the tree-based regression methods depend exclusively on the means of yi's over the partitioning subsets in constructing their partitioning trees, and use the means of the tree leaves for final estimates. While such estimates can be MLEs of the corresponding sampling distributions, they need not be optimal in terms of minimax theory [12]. Better nonparametric estimates can often be obtained through shrinkage and thresholding of the mean values. Some recent developments provide a framework for a wavelet-like representation and analysis for tree-structure data. These methods adapt naturally to the shrinkage and thresholding processes in estimation. The unbalanced Haar orthogonal systems (also called the Haar-type wavelet orthogonal systems) on a given tree were constructed by several authors [13–15]. We note that the unbalanced Haar wavelets were first constructed in Mitrea [16] for dyadic cubes in ℝp and were later generalized in Girardi and Sweldens [15] to more general trees.
With the background above, we propose in this paper to integrate the wavelet-like analysis on trees with some efficient tree partitioning method so that an estimator for f that has the ability of adapting to the intrinsic low dimension of data can be obtained. However, our numerical experiments show that a simple combination of those ideas does not work well. Note that the ideas and results discussed above are mostly theoretical. There is little discussion in the literature on the actual numerical performance of those approaches. For example, the partition methods discussed in Binev et al. [4, 5], while possessing very nice analytical properties (the rates of convergence), would have a computational complexity that grows exponentially in p. Our numerical experiments also indicate that, when compared to the standard methods like random-forest, support vector machines, or even classical CART, the random projection tree regression of Dasgupta et al. [6] and Kpotufe and Dasgupta [7] or a wavelet soft-thresholding method based on trees generated through various partitioning procedures, including CART and random projection, do not show much, if any, significant improvements in terms of prediction error. A better approach is needed in order to fulfill the theoretical potential of these ideas. We propose a regression estimator in this paper that mitigates the difficulties. Our focus in this paper is mainly the methodology.
We only consider binary trees in this paper. The same ideas can be easily applied to more general trees. The tree-based estimator proposed here consists of three components. The first component is a partitioning algorithm. In principle any reasonable binary classifier, supervised or un-supervised, can be a candidate. The random projection algorithm of Dasgupta et al. [6] and Kpotufe and Dasgupta [7] or uniform partition of Binev et al. [4, 5] are un-supervised. For the kind of data we have, we however prefer supervised classifiers so that the information from yi's can be utilized. We propose one such classifier below. The second component is a wavelet-like tree-based estimation process that incorporates thresholding and shrinkage operations. It turns out that this can be done in a statistically rather intuitive manner. The final component, a necessary and crucial one, is an averaging process, taking the average of the estimates across several independently generated partitioning trees on the same training data. This averaging process is different from that of a random-forest. In random-forest, the average is taken over bootstrapped samples, and our experiments indicate that it does not work well in some problems. We will call our method “averaging random tree regression.”
While proposed as a computationally feasible algorithm for regression with low intrinsic dimensional data, our method also possesses other good properties. This estimator is to be compared through numerical experiments to some standard non-parametric estimators using higher dimensional data. We will also compare it in a low dimensional setting to a smoothing spline and random-forest. In low dimensional experiments, we observe that the proposed estimator is capable producing visually smoother estimates than CART-based estimators and, at the same time, being much more sensitive than a smoothing spline estimator to discontinuities of f, as it would be expected.
This paper is organized as follows. Section 2 gives a detailed description of the regression method and demonstrates some interesting features of the method. Section 3 gives some examples of our method. Section 4 provides a formulation of the method in terms of wavelet-like multilevel analysis on a tree. It includes a formal description of decomposition and reconstruction algorithms for the soft-thresholding estimation and an analytical study that establishes properties necessary for the thresholding method to work.
2. The Averaging Random Tree Regression
Suppose a dataset is given. Let and . For any subset , we will write ȳB for the mean of yis in B: , where nB denotes the size of B. Our tree-based method consists of three parts. We give a description for each of them below.
2.1. A Classifier for Space Partition and the Partitioning Tree
We first need a binary classifier which acts on the subsets of and partitions any given subset of at least two points into two finer subsets based on some classification criterion. Note that the partitioning method of the classical CART regression can certainly be one of such classifiers, but it can be computationally inefficient for higher dimensional data. Here we propose a different classifier based on the combination of an extension of the random projection proposed in Dasgupta and Freund [6] and Kpotufe and Dasgupta [7] and the idea of minimum sum of squares criterion of CART. The original random projection partition method do not utilize any information from yi's. This is a weakness of that method and we try to avoid it in the current approach. The idea is to choose among several random projection partitions the one that has the least mean square error for yi's. The partitioning classifier works as follows.
Let M be a preset integer number. For any subset A of with r points, we generate M unit directional vectors v1, …, vM in ℝp from a priori distribution (an uniform distribution for example). For each vj, j = 1, …M, we project all the p-dimensional points x in A onto this unit vector to obtain a set of r scalars . Let mvj be the median of these scalars. Let
If there are one or more xi ∈ A, i = 1, …, r ≥ 1 such that , we split these points randomly with equal probability into subsets of ⌊r⌋ (floor of r) and ⌈r⌉ (ceiling of r) points and assign the subsets with equal probability to AL, j or AR, j and still denote these subsets as AL, j and AR, j. In this way we obtain the partition A = AL, j ∪AR, j. Next we find the sum of squares for this directional vector vj:
We determine the vector v ∈ {v1, …, vM} with the smallest S(vj) value:
and choose the corresponding partitioning subsets AL and AR as the final partition of A and let mv be the corresponding dividing median. Let us denote the above process of obtaining a binary partition for a set A as
where M is an adjustable parameter. Clearly, the outcomes of πM are random, depending on realizations of the random vectors v1, …, vM. The reason for using median as the splitting point for partition is to keep the corresponding partition tree balanced. A balanced tree possesses some nice analytical properties for wavelet-like analysis on the tree, as we will see later.
With the partitioning classifier πM, we construct recursively a partitioning tree so that each node in the tree is a subset of and the children nodes are partitioning subsets of their parent nodes. In other words, we set the root of to be the whole point set and, starting from the root, we keep partitioning each node into two children nodes with about the same size until a node becomes a singleton set. The leaves of are singleton sets of .
In this construction, each non-leaf node is associated with a pair (v, mv) of a unit directional vector and the corresponding dividing median. All the pairs are pre-calculated and stored, and will serve as the parameters for partitioning the whole feature space ℝp. The space ℝp can now be partitioned into disjoint regions identified by the leaves of as follows. To begin with, we classify every point x ∈ ℝp as an “ point.” Next, for any x ∈ ℝp, if it is already classified as an “A point” for some tree node of at least two points and if πM(A) = {AL, AR, v, mv}, we calculate the projection of x onto v and then classify x further as either an “AL point” if , or an “AR point” if . In the case of , we classify x with equal probability into either AL or AR. This classification process goes on and will eventually classify x into one and only one of the leaf nodes. If x is ultimately classified as a leaf node “{xi} point” for some , we write . For every , let
Then Ai, i = 1, …, n forms a partition of ℝp according to the partitioning tree .
These trees are maximal trees. In order to preserve more local features of f in data, we do not prune them like CART. In fact, a default pruning process in CART destroys its ability to be adaptive to the intrinsic low dimension of data. On the other hand, as an implementation issue, if all yis in a node A have very close values so that S(vj) is small in all M selected directions, we can stop splitting this node and treat it as a leaf and use the mean of yis as the y-value for this node. All computations below can still be carried out without change. The overfitting issue caused by a large tree will be addressed in the last step of our estimation process to be described later.
2.2. A Multiscale Soft-Thresholding Estimate of f(Xi)
As we will see in section 4, the procedure described below is actually a modified version of a common wavelet denoising process with an unbalanced Haar wavelet on a tree. But since this process can also be described in a statistically more intuitive manner with simpler notations, we give the following algorithmic description first.
Suppose a partitioning tree is obtained. A hierarchical representation of the data can be obtained according to the tree as follows. For each non-leaf node in the tree , we find the mean ȳA of the node and the difference of the means of its children nodes AL and AR:
If A is a leaf, we set dA = 0. The original data can now be represented with the set of the numbers
based on which regression estimates will be obtained.
To estimate , i = 1, …, n, we first apply a soft-thresholding operation with a given α ≥ 0 to dA for all the non-leaf nodes A according to the formula
Next, we calculate estimates ŷA of E(ȳA|X = x) for all nodes A of based on the data
as follows. We start with setting
For each node A, once ŷA is obtained, we calculate the estimates for its two children nodes, ŷAL and ŷAR, according to the formula:
and
Repeat this process until one reaches all the leaves. If A = {xi} is a leaf, we use
as an estimate of f (xi). We will write ŷi for ŷ{xi} for short below.
Note that, if α = 0 in (6), then for all nodes A and, as a consequence, ŷA = ȳA for all . To see this, we note that , and if we have ŷA = ȳA and , then
and
Also note that |AL| and |AR| are differed by at most 1 and therefore for large nodes, |AL|/|A| ≃ |AR|/|A| ≃ 1/2. The smoothing parameter α can be determined through cross-validation.
In the framework of wavelet analysis, are the wavelet coefficients and (7)–(8) is the fast wavelet reconstruction algorithm to be derived in section 4.
2.3. The Averaging Random Tree Regression
Now to estimate f (x) for any x ∈ ℝp, we can in principle use
In other words, a search along the tree (with O(log2 n) steps) will allow us to determined for each x ∈ ℝp which partitioning subset Ai, as defined in (4), it belongs to and then use ŷi as an estimate for f (x). However, despite some nice theoretical properties, this estimate itself doesn't perform very well in our simulation experiments. It turns out that a significant improvement can be achieved by an averaging procedure described below.
For a given integer K, we repeat the process described in Section 2.1 K times, independently, on the same data to obtain trees , k = 1, …, K. For each tree , we calculate estimates according to (9). Finally, we take the average
as the final estimate of f (x). Let's call this estimate an “Averaging Random Tree Regression” estimate, or ARTR estimate for short. This averaging step improves significantly the accuracy of the estimates for the regression function. The resulting estimates can be adaptive to lower intrinsic dimension of data. It can also be visually smoother than other tree-based regression methods in two or three dimensional cases even with piecewise constant Haar wavelets, and being sensitive to discontinuities at the same time. It also addresses efficiently the overfitting problem.
We summarize the process into the following steps:
1. Generate a partitioning tree according to classifier πM.
2. Obtain and dA = ȳAL − ȳAR for all non-leave nodes and AL, AR ∈ πM(A).
3. Obtain from based on (6) for a given α and ŷi, i = 1, …, n, through recursively applying (7) and (8).
4. Calculate the estimate of f using (9).
5. Repeat steps 1–4 K times and take the average according to (10).
There are three tuning parameters in this process: M, the number of random projection directions for each partition in generating a partitioning tree; K, the number of trees to generate for averaging; and α, a factor in the threshold for smoothing. Cross-validation can be used to choose the values of these parameters.
Simulation studies show that ARTR estimation outperforms some standard methods, as can be seen through the examples in the following subsection. Note that our averaging approach is similar in its appearance to but different in principle from that of the random forests. In fact, the random forests approach which averages tree estimates based on resampling dataset does not produce good results in our experiments. Formally, our estimate can be viewed as a kernel method which takes a weighted average of nearby data points to obtain an estimate.
3. Examples of Applications to Some Statistical Problems
We give three examples demonstrating potential applications of the ARTR method. In all computations below, we set the number of random projections for partitioning M = 10 and the number of partition trees for averaging K = 36.
Example 1: Regression on a Lower Intrinsic Dimensional Manifold
This example is about high dimensional regression where the values of predictors are actually from an embedded unknown sub-manifold with a much lower dimension. In our example, this sub-manifold is the surface of a two-dimensional “Swiss roll” given by the parametric equations: x1 = u cosu, x2 = usinu, x3 = v, for u, v ∈ [0, 4π]. The regression function is
and ε ~ N(0, 1). Our data do not contain exact values of (x1, x2, x3). Rather, all the 3-dimensional points are embedded isometrically (with an arbitrary and unknown isometric transformation) into the space ℝ4, 000. Therefore, each feature point is recorded as a p = 4, 000 dimensional point. We apply support vector machine regression (SVMR), random forests regression (RFR), extreme gradient boost regression (XGBR) with the parameter nrounds set to 100, our ART regression (ARTR) without averaging (K = 1) and with averaging (K = 36) to a training dataset of n = 1, 000 points and then apply the estimated models from these different methods to an independent testing dataset of 1,000 points. Predictions of the values for the function are obtained at these 1,000 testing points. The approximation error at a point x is the difference between the predicted value at x and the true value of the function at x. Table 1 shows the mean squared approximation errors in this computation. We see that in terms of the mean approximation errors, ARTR with K = 36 is better than SVMR, and significantly better than RFR or XGBR. We also see that without taking average, ARTR with K = 1 has the worse performance. In ARTR we have used α = 2.0.
Example 2: Discovering Mixtures in a Higher Dimensional Space
This is a higher dimensional example. The problem in this example can be described in more general terms as follows. Suppose S1 and S2 are two unknown lower dimensional sub-manifolds embedded in ℝp. Suppose that data are sampled from S1 ∪ S2 and that yi's sampled from S1 have distribution and yi's from S2 has distribution . In other words,
where ε ~ N(0, σ2). We ask, from the data can we discover that yi's are a mixture of two different distributions? We show that ARTR can achieve this while some standard method fails in the following experiment.
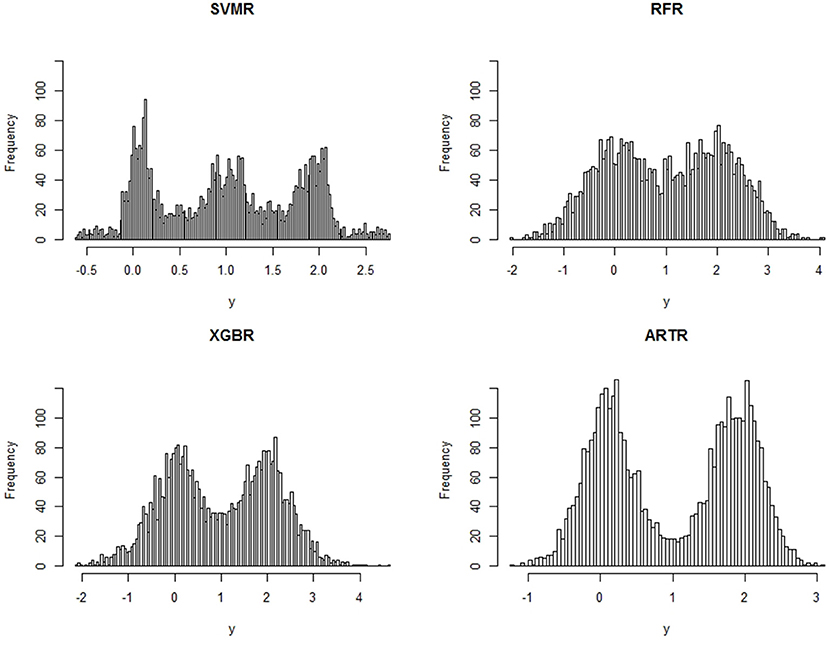
In this example, S1 and S2 are two intersecting unit 2-spheres embedded into a p = 6,000 dimensional space ℝ6,000. The centers of the 2-spheres are set to be 0.35 apart. We set μ1 = 0, μ2 = 2, and σ = 1. The data consists of n = 4, 000 sample points. A histogram of yi's would reveal no signs that yi are from a mixture of two distributions. Four different methods are applied to fit the data: SVMR, RFR, XGBR, all with the default settings in R packages “svm,” “randomForest,” and “xgboost” (nround=100), and our ART regression. Estimates ŷi of f(xi) are obtained from the methods and their histograms are displayed also in Figure 1. For the ARTR we choose K = 36 and α = 2.0.
We see from the histograms in Figure 1 that SVMR fails to recognize correctly the underlying lower dimensional structure of the data. It mistakenly treats the central region bounded by the intersection of the two spheres as the third region in which yi's have a mean value (μ1+μ2)/2 = 1. A much larger sample size is needed for SVMR to achieve a correct estimate, demonstrating the effect of the curse of dimensionality on the method. The RFR is capable of noticing the mixture and XGBR is better than RFR, but ARTR is clearly much more powerful than all others in detecting the mixture. This comparison between ARTR and RFR or XGBR supports the comment we make in the introduction section that a mean-based estimate can be significantly improved through shrinkage and thresholding operations.
The mean squared errors, calculated using ŷi, i = 1, …, 4, 000, and the true means μ1 = 0 and μ2 = 2, are listed in Table 2. It shows that ARTR has the smallest mean squared error among the four methods. We also notice that, while the mean squared error of SVMR is smaller than those of RFR or XGBR, the estimates from SVMR can be totally misleading.
Example 3: Smoothness and Sensitivity to Discontinuities
This is a two dimensional example to show smoothness and sensitivity to discontinuities of ARTR estimates. We do this through comparing ARTR to the thin plate splines (TPS) and random forests regression (RFR). The regression function we use is
with
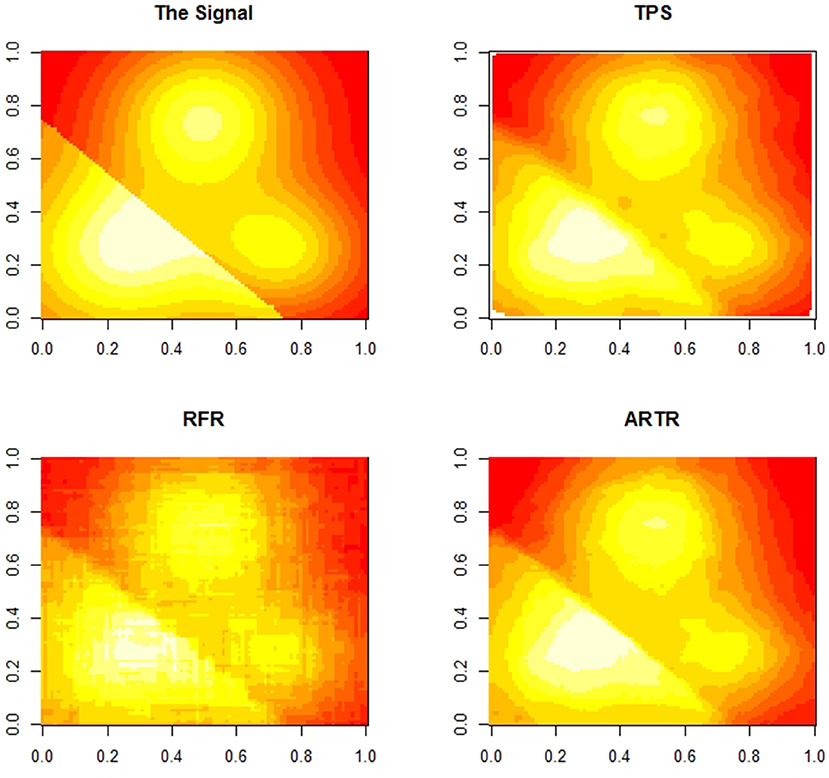
and ε ~ N(0, 1). An image of f (x) is given in Figure 2 (in these figures, the valleys are shown in red and the peaks are shown in white). The data consist of n = 4, 000 points with points in generated uniformly inside a two-dimensional unit square. Setting α = 2.0, we obtain ARTR estimates at 100 × 100 grid-points which is compared to the estimates at the same grid-points from the TPS and the RFR. In Figure 2, we observe that both TPS and ARTR produce smoother estimates than RFR does. Furthermore, the estimates from TPS and ARTR look more similar in local regions.
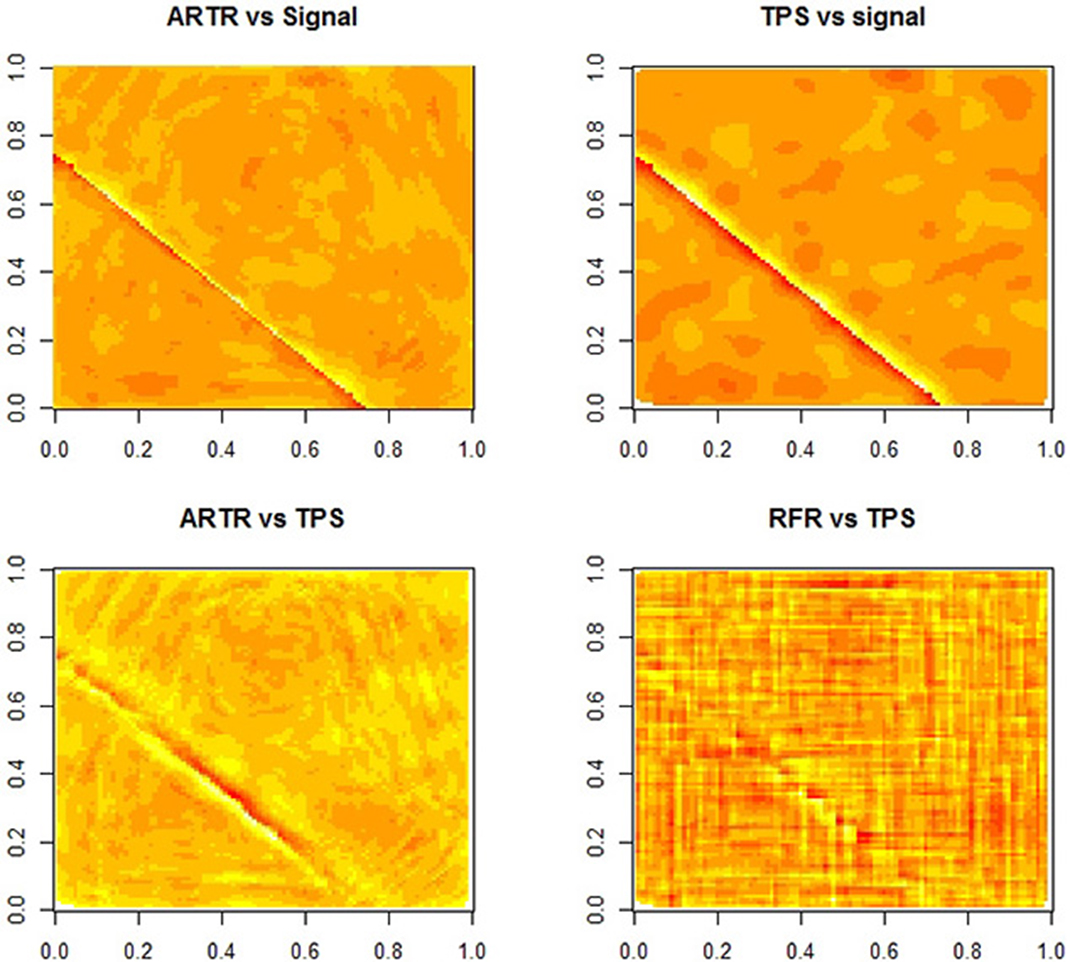
We note that the surface of the true regression function has a discontinuity line. Figure 3 provides a comparison among the three estimates. The two figures in the top row are the plots of errors from ARTR estimates and TPS estimates respectively. A difference between the two estimates along the discontinuity line is visible. The left plot in the second row of Figure 3 shows an even more significant difference. This figure displays a difference in sensitivity to discontinuities between the two methods. Note that, while such a property is what one would expect from a wavelet-type method, estimates from ARTR are smoother than those from a Haar-type wavelet. In contrast, the difference between the TPS estimates and the RFR estimates, while visible, is more noisy and less definite. Overall, ARTR performs best in this example. The “ARTR vs TPS” figure in Figure 3 suggests that one might even consider using such a figure, obtained completely from data, as a mean for detecting discontinuity of a noisy surface.
The mean squared approximation errors of the three methods from the same simulation computation are listed in Table 3. We see that in terms of approximation errors, ARTR is similar to (or slightly better than) TPS, and RFR is worse among the three.
4. Wavelet-Like Analysis on Trees
It is possible that the tree-based method proposed above be formulated and applicable within a more general context in which can be an arbitrary point set with a given partitioning tree . In particular, need not be a subset of ℝp. An important concept that makes an analysis possible for this setting is the tree metric [14] which characterizes the smoothness of the functions defined on in terms of their tree wavelet coefficients. In this section we first give a formal description of a Haar wavelet-like orthogonal system on the tree , then we present a fast-algorithm for decomposition and reconstruction of functions defined on according to the tree . This algorithm includes the algorithm in section 2 as a special case. The discussion below is for more general trees for which a leaf node can have more than one point and in this case the corresponding y-value is the average of yis in the node.
4.1. Wavelet-Like Orthogonal Systems on
Without loss of generality, we can assume that the binary partitioning tree has L levels, with the root at level 0 and all the leaves at level L. This would be exactly the case for a tree constructed in the previous section if consists of 2L points. To achieve this for an arbitrary and tree , if A is a node of the tree at level ℓ < L which is a leaf node, we simply define its offspring at level ℓ+1 to be the node itself.
For each ℓ = 0, 1, …, L, we index all the nodes in at level ℓ with an index set Iℓ and let Pℓ be the set of these nodes :
Then Pℓ forms a partition of : Aℓ, i ∩ Aℓ, j = ∅ for i ≠ j and . Further more, Pℓ + 1 is a refinement of Pℓ with
for some if |Aℓ, j| > 1, and
for some if |Aℓ, j| = 1. With these notations, is the root and AL, j, j ∈ IL are the leaves of .
A wavelet-like orthogonal system can now be defined on as follows. Let
be the space of all functions defined on equipped with the inner product:
Let ν be the empirical probability measure of X induced by the set of sample feature points:
with the understanding that ν depends on the sample size n. For a function f on , then
is just .
An orthogonal system on V with respect to the inner product in (12) can now be constructed based on the partitioning tree . The following describes the construction of Haar-type wavelets on , [13–15].
For each ℓ = 0, …, L and Pℓ = {Aℓ, j:j ∈ Iℓ}, let
Clearly, we have Vℓ ⊂ Vℓ + 1.
Let ϕℓ, j, 0 ≤ ℓ ≤ L and j ∈ Iℓ, be functions on defined by
For each ℓ, 0 ≤ ℓ ≤ L−1, let Jℓ ⊂ Iℓ denote the index set for those nodes Aℓ, j with |Aℓ, j| > 1. For each j ∈ Jℓ, with , let ψℓ, j be functions defined by
Then we have
Denote
The fact Vℓ = span{ϕℓ, j : j ∈ Iℓ} and the orthogonality of ϕℓ, j and ψℓ, j imply that Wℓ ⊂ Vℓ+1 and Vℓ ⊥ Wℓ. In addition, by a direct calculation, we have, for Aℓ, j, , and as related in (11) and j ∈ Jℓ,
which implies that Vℓ+1 ⊆ Vℓ + Wℓ. Therefore, Wℓ is the orthogonal complement of Vℓ in Vℓ+1, i.e., , where ⊕⊥ denotes the orthogonal sum. Hence
and finally
From (16), we see for ℓ ≠ ℓ′. Hence ψℓ, j, 0 ≤ ℓ ≤ L − 1, j ∈ Jℓ are orthogonal to each other. More precisely, we have
for all , where
We summarize this into the following theorem.
Theorem 1. The system of Haar-type wavelets
together with ϕ0, 0(x) ≡ 1 form an orthogonal basis of VL. More precisely, VL can be decomposed as (16) with f ∈ VL represented as
where is given by (17).
Since VL = V, (19) is a representation of all functions f on .
4.2. Fast Multiresolution Algorithm For Wavelet Transform
The orthogonal system we discussed above allows for a fast algorithm for computing wavelet coefficients 〈f, ψℓ, j〉.
Let f ∈ VL be the input data given by
with aL, j : = n〈f, ϕL, j〉/|AL, j| = the average value of f (x) at the leave node AL, j.
From
and that for any L0 with 0 ≤ L0 ≤ L − 1, ϕL0, i, ψℓ, j, L0 ≤ ℓ ≤ L − 1, i ∈ IL0, j ∈ Jℓ form an orthogonal basis for VL, we know that f ∈ VL can also be represented as
where , and the wavelet coefficients dℓ, j are given by
A multiscale fast algorithm to compute the wavelet coefficients can be obtained based on the refinement of the scaling function ϕℓ, j. Next, let us look at the decomposition algorithm for calculating aL−1, j, dL−1, j from aL, j, and the reconstruction algorithm for recovering aL, j from aL−1, j, dL−1, j.
Clearly, if k ∈ IL−1\JL−1, then , where is such an index that . Next we consider k ∈ JL−1, and let and be two children of AL−1, k. From (20), (21), the orthogonality of ϕL−1, j, ψL−1, j and the fact supp, we have
With , we have
Similarly, we have
Thus, we have
Combining these calculations, we obtain the following decomposition algorithm
One can obtain as above by the refinement of ϕL, j: and the orthogonality of ϕL, j the following reconstruction algorithm (which can also be obtained directly from the above decomposition algorithm):
We can obtain the algorithms in the same way for all other aℓ, k, dℓ, k. To summarize, we have the following theorem.
Theorem 2. Let aℓ, k, dℓ, k be coefficients of f ∈ VL with the wavelet expansion. Then for every non-leave node Aℓ−1, k, k ∈ Jℓ−1, and its children nodes and , where 1 ≤ ℓ ≤ L, we have the decomposition algorithm:
and the reconstruction algorithm:
It can be easily verified that here aℓ, k is exactly the mean of f (xi)'s over the subset Aℓ, k and dℓ, k is the difference of the means of f (xi) over the children subsets and , respectively. This justifies (5), (7), and (8) without shrinking.
After the wavelet coefficients dℓ, k are thresholded with
for some α > 0, the estimation of f (x) is obtained:
A fast algorithm to evaluate the estimation can be given as follows.
Set â0, 0 = a0.0 = 〈f, ϕ0, 0〉. Assume âℓ−1, k for k ∈ Iℓ−1 have been obtained. Define âℓ, k for k ∈ Iℓ as follows. If k ∉ Jℓ−1, then the corresponding node Aℓ−1, k is a leaf node, and let , where k′ is the index such that . If k ∈ Jℓ−1, then the corresponding node Aℓ−1, k has two children, denoted by and , and we define
Theorem 3. Let âL, j, j ∈ IL be the scalars defined above iteratively with ℓ = 1, 2, ⋯ , L and let in be the estimation for f (x) given in (25). Then . More precisely, in (25) can be represented as
Clearly, (26) is actually the wavelet reconstruction algorithm (23). Thus we can use a fast algorithm to evaluate .
The representation (27) for defined by (25) can be proved easily by applying the following claim.
Claim 1. For k ∈ Jℓ−1 with , where 1 ≤ ℓ ≤ L, we have
Proof of Calim 1: By the definitions of ϕℓ−1, k(x) and ψℓ−1, k(x), we have
as desired. □
Observe that (26) is the algorithm (7) and (8) we use in section 2, and (27) is the representation (9) we also use in section 2 for estimation of f (x).
5. Discussion
The regression method discussed in this paper is based on a tree-based representation of data and a wavelet-like multiscale analysis. The tree-based representation organizes data into hierarchically related partitioning subsets of feature points together with the differences of means of the response variables over the partitioning children subsets. With this representation, a wavelet soft-thresholding and reconstruction procedure allow us to fit the data into the tree-structure. For normal data, the soft-thresholding is equivalent to shrink a t-confidence interval about the origin to the origin on the real-line.
Through the examples (section 3), we see that this tress regression method can be an effective alternative to CART, random-forest, smoothing splines, or support vector machines in various circumstances. Its ability of being adaptive to intrinsic low dimension of data allows it to detect some hidden features of data, as is shown in Example 2, when the standard methods like support vector machine fail to archive this. It outperforms another popular tree-based method, random-forest in terms of prediction error in our regression example (Example 1) in high dimensional feature space with low intrinsic dimension of data. When applied to lower dimensional data (Example 3), it again shows lower prediction error than CART or random-forest, and outperforms other smoothing method when regression function has discontinuities.
Other partitioning trees could be used in subsection 2.1. Rules for stopping further splitting a node can also be considered, provided that the local structures of the regression function in data can be optimally preserved. Another feature of this regression is that, unlike a standard wavelet analysis, the unbalanced Haar orthogonal system here is data dependent.
For large and high dimensional datasets, our method takes significantly more computation time than the other algorithms we used in our examples above. How to improve the speed of computation in our method is a challenge. One possible direction in searching for a faster algorithm is to use smaller and random subsets of the features for splitting each node in growing a tree.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
The work was partially supported by Simons Foundation (Grant No. 353185).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
2. Stone CJ. Optimal global rates of convergence for nonparametric regression. Ann Stat. (1982) 10:1040–53.
3. Bickel P, Li B. Local polynomial regression on unknown manifolds. In: Liu R, Strawderman W, Zhang CH. Complex Datasets and Inverse Problems: Tomography, Networks, and Beyond. IMS Lecture Notes Monograph Series. Vol. 54. Bethesda, MD: Institute of Mathematical Statistics (2007). p. 177–86.
4. Binev P, Cohen A, Dahmen W, DeVore R, Temlyakov V. Universal algorithms for learning theory part I: piecewise constant functions. J Mach Learn Res. (2005) 6:1297–321.
5. Binev P, Cohen A, Dahmen W, DeVore R. Universal algorithms for learning theory part II: piecewise polynomial functions. Construct Approx. (2007) 26:127–52. doi: 10.1007/s00365-006-0658-z
6. Dasgupta S, Freund Y. Random projection trees and low dimensional manifolds. In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing. New York, NY (2008) p. 537–46.
7. Kpotufe S, Dasgupta S. A tree-based regressor that adapts to intrinsic dimension. J Comput Syst Sci. (2012) 78:1496–515. doi: 10.1016/j.jcss.2012.01.002
9. Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Belmont, CA: Wadsworth (1984).
10. Loh WY. Fifty years of classification and regression trees. Int Stat Rev. (2014) 82:329–48. doi: 10.1111/insr.12016
11. Morgan JN, Sonquist JA. Problems in the analysis of survey data, and a proposal. J Am Stat Assoc. (1963) 58:415–34.
13. Chui CK, Filbir F, Mhaskar HN. Representation of functions on big data: graphs and trees. Appl Comput Harmon Anal. (2015) 38:489–509. doi: 10.1016/j.acha.2014.06.006
14. Gavish M, Nadler B, Coifman RR. Multiscale wavelets on trees, graphs and high dimensional data: theory and applications to semi supervised learning. In: Proceedings of the 27th International Conference on Machine Learning. Haifa (2010). p. 367–74.
15. Girardi M, Sweldens W. A new class of unbalanced Haar wavelets that form an unconditional basis for Lp on general measure spaces. J Fourier Anal Appl. (1997) 3:457–74.
Keywords: regression, non-linear, high dimension data, tree methods, multiscale (MS) modeling, manifold learning
Citation: Cai H and Jiang Q (2018) A Tree-Based Multiscale Regression Method. Front. Appl. Math. Stat. 4:63. doi: 10.3389/fams.2018.00063
Received: 07 October 2018; Accepted: 07 December 2018;
Published: 21 December 2018.
Edited by:
Xiaoming Huo, Georgia Institute of Technology, United StatesReviewed by:
Don Hong, Middle Tennessee State University, United StatesShao-Bo Lin, Wenzhou University, China
Copyright © 2018 Cai and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haiyan Cai, caih@umsl.edu
 Haiyan Cai
Haiyan Cai Qingtang Jiang
Qingtang Jiang