- 1BioMedicine Design, Pfizer Worldwide R&D, Cambridge, MA, United States
- 2BioMedicine Design, Pfizer Worldwide R&D, Andover, MA, United States
Quantitative modeling is increasingly utilized in the drug discovery and development process, from the initial stages of target selection, through clinical studies. The modeling can provide guidance on three major questions–is this the right target, what are the right compound properties, and what is the right dose for moving the best possible candidate forward. In this manuscript, we present a site-of-action modeling framework which we apply to monoclonal antibodies against soluble targets. We give a comprehensive overview of how we construct the model and how we parametrize it and include several examples of how to apply this framework for answering the questions postulated above. The utilities and limitations of this approach are discussed.
Introduction
Modeling and simulation tools have become an essential part of the drug development process (Norris et al., 2000; Lalonde et al., 2007; Barrett et al., 2008; Edginton et al., 2008; Mager and Jusko, 2008; Rajman, 2008; Jones et al., 2009; Allerheiligen, 2010; van der Graaf and Benson, 2011; Zhao et al., 2011; Jones et al., 2012a; Knight-Schrijver et al., 2016; Danhof et al., 2018; Nijsen et al., 2018). Applying quantitative analyses early in the drug discovery can be very informative for selecting and de-selecting those programs with the best/least chance of clinical success. Traditional pharmacokinetics/pharmacodynamics (PKPD) models, while still widely utilized (Meibohm and Derendorf, 1997; Derendorf and Meibohm, 1999; Rajman, 2008), have gradually given place to increased mechanistic modeling complexity, with the intent to achieve higher predictive accuracy and mechanistic insights. These mechanistic modeling techniques include systems biology (SB) (Kitano, 2005; Kohl et al., 2010; Benson et al., 2011), quantitative systems pharmacology (QSP) (Hopkins, 2008; Allerheiligen, 2010; van der Graaf and Benson, 2011; van der Graaf, 2012; Jusko, 2013; Rogers et al., 2013; Peterson and Riggs, 2015; Knight-Schrijver et al., 2016; Danhof et al., 2018; Nijsen et al., 2018; Cucurull-Sanchez et al., 2019), and physiologically based pharmacokinetics (PBPK) (Baxter et al., 1994; Andersen, 1995; Baxter et al., 1995; Hoang, 1995; Arundel, 1997; Blakey et al., 1997; Nestorov et al., 1998; Grass and Sinko, 2002; Aarons, 2005; Jones et al., 2006a; Jones et al., 2006b; Cai et al., 2006; Barton et al., 2007; Nestorov, 2007; Edginton et al., 2008; Loizou et al., 2008; Jones et al., 2009; Chabot et al., 2011; Jones et al., 2011; Jones et al., 2012a; Jones et al., 2012b; Bouzom et al., 2012; Huang and Rowland, 2012; Rostami-Hodjegan et al., 2012; Shah and Betts, 2012; Zhao et al., 2012; Jones et al., 2013). Traditional empirical PKPD models are useful in predicting dosing and estimating pharmacology/efficacy in later stage clinical development and translation from pre-clinical animal models to humans. However, an extensive amount of pre-clinical PKPD data is needed to utilize them which limits their ability to be used to make early pre-clinical recommendations, before lead candidates are defined. In contrast, the mechanistic models, while often complex and computationally intensive, appear more suitable for overall disease and molecule modality recommendations.
Early stage biologics drug discovery programs concern themselves with three main questions: (1) is the proposed target biologically relevant and is hitting the target feasible; (2) what are the drug characteristics that would allow for biomarker modulation or efficacy; (3) what is the efficacious dose in humans? These three questions can be summarized as three components to each project: right target, right compound, right dose. Considering the high number of potential new targets, a flexible mechanistic modeling framework is needed that can be used to perform sensitivity analysis on a discrete number of parameters. This approach would quickly pinpoint gaps in knowledge that can be tested experimentally and make timely recommendations for each of the three components of project development. Therefore, for this purpose, one needs a model that is on the spectrum of complexity somewhere between the traditional PKPD and the multiscale systems biology models. We propose a site-of-action (SoA) model for assisting in the discovery and development of biologics.
The site-of-action model extends a two compartment PKPD model by including the mechanistic interactions of the drug and its target (e.g., binding, unbinding and drug-target complex clearance), the relevant properties of the target, as well as a separate compartment that models the tissues in which the disease progresses (a so-called site of action) (Brodfuehrer et al., 2014). Such a model can be implemented rapidly since it captures only the relevant biology and is expressed through a discrete number of differential equations, variables, and parameters, which allows for extensive sensitivity analysis to identify the important parameters and biological assumptions that need to be investigated further. Hence, this model should be considered a starting point from which to build out specific models of the biology of different targets, its main utility being in early stage projects.
A previous iteration of the model has been described by Tiwari et al. 2016a and used for assessing sensitivity of the projected target neutralization to target concentrations (Tiwari et al., 2016a) and antibody affinity (Tiwari, et al, 2017). The current iteration makes minor changes to the old model structure and goes into more detail in explaining the reasons for certain modeling and parameter value choices. We have implemented this approach successfully since, and, beyond the theoretical treatment in Tiwari et al. 2016a, in Applications of SoA Model Methodology of this manuscript will be demonstrating its utility by several real-world examples. The modeling work is highly dependent on robust assays to inform the parametrization of the model (biomeasures), which is yet another important expansion to the work presented in Tiwari et al. 2016a. We have listed the typical assays and input data used in the Target Parameters section. For the purposes of this article, we will focus on soluble targets. Membrane targets deserve to be covered in a separate manuscript, both in terms of the modeling approach, as well as in terms of utilizing the range of biomeasure assays and tools for supporting the modeling efforts.
Model Structure and Methods of Parametrization
The model is an extension of a drug-target mechanistic binding two-compartment model that accounts for the relevant disease tissue, which is referred to as site of action (SoA). Free plasma drug (with concentration
where
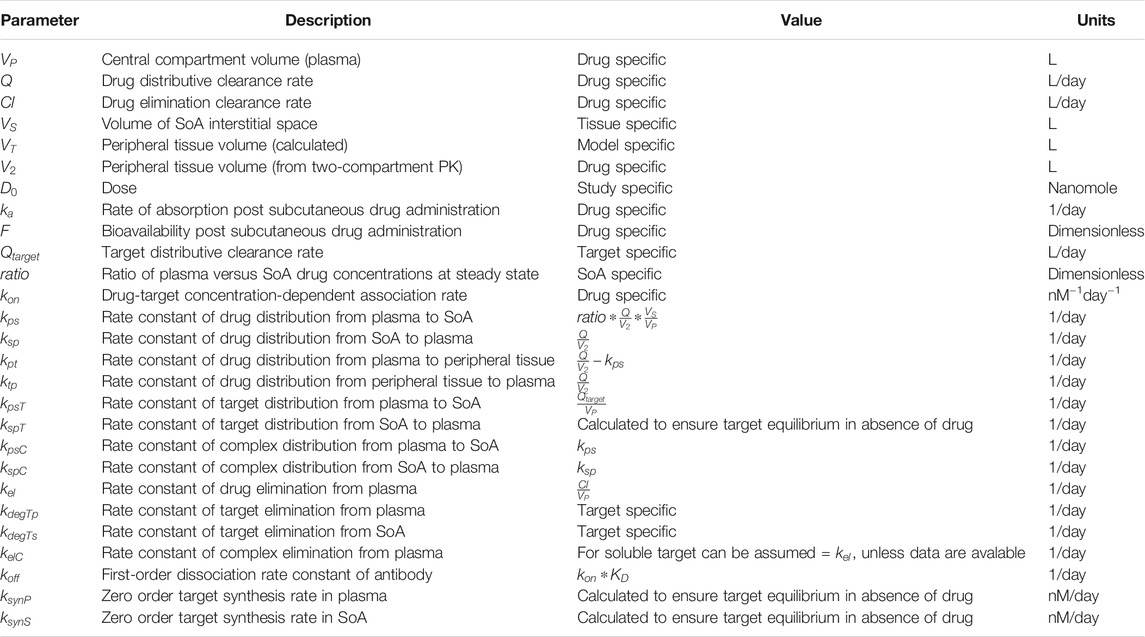
A schematic of the modeling reactions is shown in Figure 1. Table 1 lists the variables and parameters contained in the system of differential equations, with explanations.
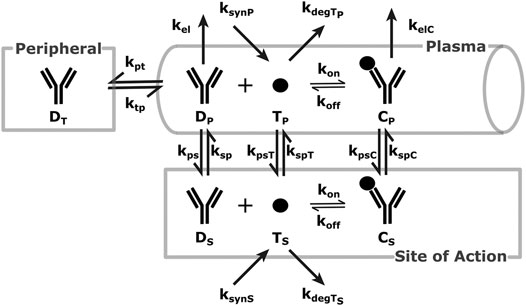
FIGURE 1. SoA Model Scheme: A diagram describing the distribution and elimination of the mAb (denoted by D), synthesis, distribution and elimination of the target (denoted by T) and the interactions between the mAb and target and the distribution and elimination of the resulting mAb:target complex (denoted by C). Subscripts describe the compartments - p for plasma, t for peripheral tissues, s for the site of action. Detailed descriptions of all variables and parameters are in Model Structure and Methods of Parametrization and Table 1.
The initial conditions of the variables above appear with a 0 after the subscript:
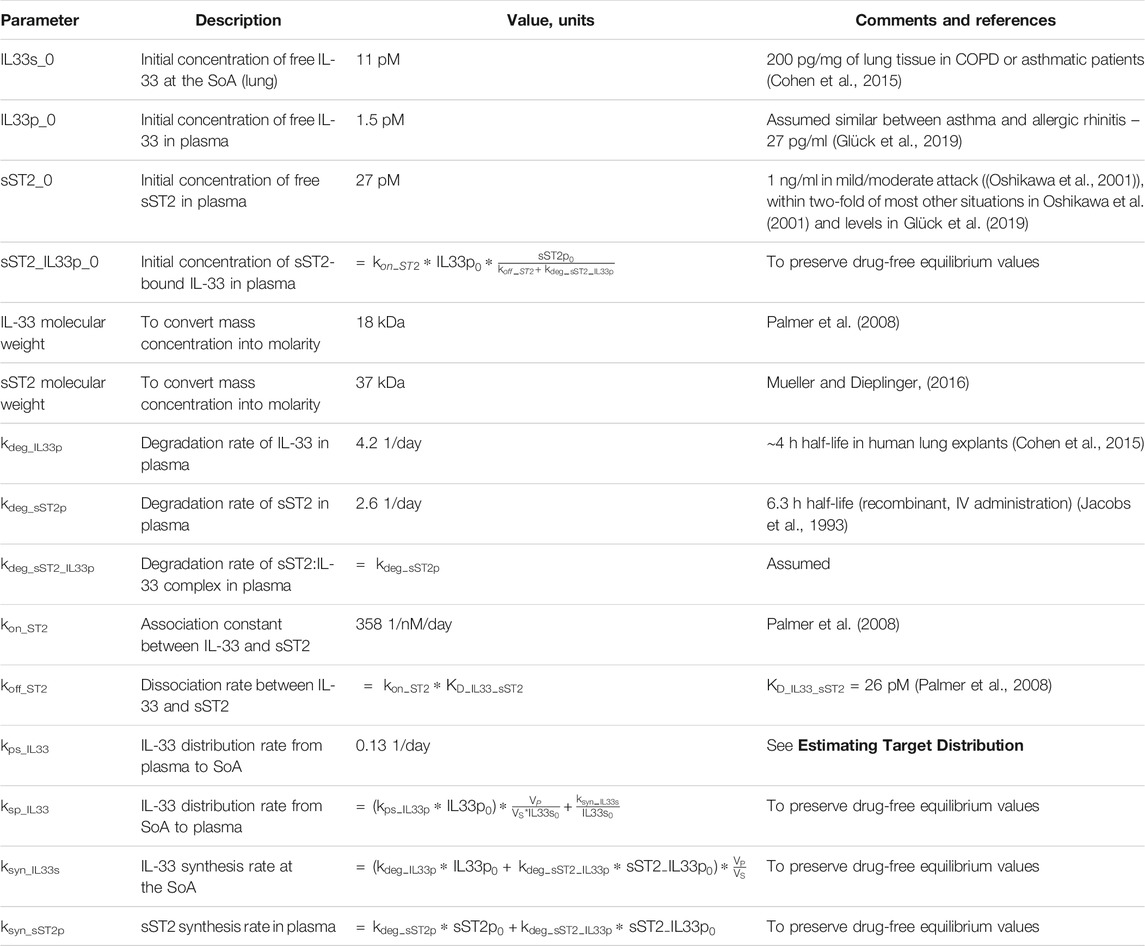
Table 2 presents the value of
Parameter Determination
The next few sections will discuss how the different parameters are estimated and suggest typical assumptions for their values. Initial parametrization of the model may be obtained from the literature or data repositories. However, when such information is unavailable, experimental determination of key model parameters may be required. Some of the experimental methods discussed here may not be applicable, appropriate, or even possible for particular targets. A conversation among modelers, biologists, and biomeasure analysts would determine the most appropriate path to appropriate parametrization of the model.
Drug Distribution Parameters
Monoclonal antibody (mAb) PK typically shows biphasic behavior and such data can be modeled using two-compartmental models, resulting in the estimation of 4 PK parameters (e.g.,
The following method can account for any ratio deemed appropriate for the particular project.
The calculations for the drug distribution constants presented here have two simultaneous aims: to retain mAb plasma PK and maintain the average concentration ratio (expressed as the parameter
where
There is an important distinction between
Binding Parameters
If
For variables
Target Parameters
The target related parameters are turnover (half-life or degradation rate), synthesis rate, concentrations (both in plasma and the SoA) and distribution rate (between the plasma and the SoA).
Estimating Target Concentrations
There are many published methods or approaches for measuring target levels both in serum and tissue (Becker and Hoofnagle, 2012), including ligand binding assays and mass spectrometry. A preferred approach, as previously highlighted due to its enhanced specificity and selectivity, is protein or peptide immunoaffinity liquid chromatography tandem mass spectrometry (IA LC-MS/MS). The method requires selection of optimal capture reagents, calibration standards and surrogate peptides for detection. In this method, proteins and/or trypsin digested peptides are enriched by anti-protein or anti-peptide antibodies or a sequential combination of both approaches. The enriched peptides are quantified using detection by nanoflow LC-MS/MS. A detailed description of this method can be found in Palandra et al. (2013) and Neubert et al. (2020). The addition of a stable isotope-labeled synthetic version of the surrogate peptide(s) prior to protein digestion reduces variables and quantitation relative to the chosen protein calibrator can be achieved. The mass spectrometric response of the endogenous peptide is compared to the analogous response for the labelled peptide in all samples, including calibrators, thereby normalizing for digestion efficiency and matrix suppression differences between the samples (Bantscheff et al., 2007). Examples of well designed, fit for purpose, sequential protein and tryptic peptide IA-LC-MS can achieve lower limit of quantitation (LLOQ) of sub 10 pg/ml (Neubert et al., 2013; Palandra et al., 2013), while protein IA and peptide IA only approaches are typically capable of achieving sub 100 pg/ml LLOQ (McAvoy et al., 2014; Zhao et al., 2018; Shuford et al., 2020).
Target expression levels vary widely depending on their biological function, disease state, tissue localization, and many other factors. For example, the growth and differentiation factor 8 (GDF-8), is present in circulation at very high expression levels of approximately 7 ng/ml in adult humans owing to its function in regulating muscle mass (Palandra et al., 2016). While targets like Interleukin-21 are not detected in human serum and can only be measured in certain human tissues such as colon tissue at an average concentration of 1 ng/g (Palandra et al., 2013). The alarmin cytokine, Interleukin-33 (IL-33) is present in circulation at approximately 20–100 pg/ml (Artru et al., 2020) and in many tissues at very elevated concentrations (200 ng/g in the lung (Cohen et al., 2015)) owing to its ubiquitous presence in the nucleus of all producing human cells. When the concentrations in a tissue homogenate are measured, the concentrations that are provided need to be adjusted for the interstitial volume of the analyzed tissue before being applied in the SoA model. Again, other methodologies have been used in some cases as driven by the protein and analytical complexities.
Estimating Target Turnover
While traditionally radio-labelling methods have been used for estimating turnover, methods based on in-vivo stable isotope labelling and proteomics have been established to measure physiologically relevant turnover (Bateman et al., 2006; Lindwall et al., 2006; Doherty and Whitfield, 2011; Hinkson and Elias, 2011; Lassman et al., 2014; Larance and Lamond, 2015). One of the preferred methods uses immunoaffinity enrichment of the target proteins from a stable isotope labeled amino acid tracer pulse-chase study, either from preclinical or clinical studies. Tracer incorporation in a surrogate peptide sequence is then measured by targeted mass spectrometry. The workflow and details of the study have been published (Farrokhi et al., 2018a). Once data is available for both the tracer levels and its incorporation in the protein of interest, the turnover rate is estimated using a series of models that account for the tracer’s incorporation, as well as the known biological properties of the protein of interest (e.g., a shed receptor in the tissue vs cytokine released primarily in plasma). An earlier version of these models was used in Farrokhi et al. 2018a These assays are confined by the time limitations in pulse-chase durations (multiple hours or a few days) in in vivo studies and accurate measurement of slow turnover rates (i.e., multiple days or weeks) are not feasible or are estimated from extrapolation. Also, in some cases, measurements are not feasible due to low concentrations of the target protein. Other methodologies have also been published in the literature, (Bateman et al., 2006; Lindwall et al., 2006; Doherty and Whitfield, 2011; Hinkson and Elias, 2011; Lassman et al., 2014; Larance and Lamond, 2015), but they are likely to experience similar limitations. Physiological target turnover measurements in human is limited to only the soluble targets and turnover in SoA is estimated from soluble target when possible.
Target Synthesis Rate
Generally, once information about the target’s concentrations and turnover are available, the synthesis is calculated assuming that in the absence of drug the system is at steady state. The rate constant for target distribution from the plasma to the site of action (
Target steady state concentration in plasma prior to drug administration is defined by:
Target steady state concentration at the SoA prior to drug administration is defined by:
Total target synthesis in the human body (in amount, nanomoles) is defined as:
It is rare that one has information about the ratio between target synthesis in plasma versus the SoA. This ratio is generally assumed taking into account what is known about the biology. For the remainder of this section and for the purpose of equations and calculations, the fraction of total synthesis in the SoA is captured by the parameter
Estimating Target Distribution
While drug distribution constants can be calculated from the PK and Eqs 8–10 above, target rates of distribution are largely unknown. We fix
At an exploratory stage, we use a parameter value for
Since these approaches have not be largely validated and adopted, one is advised to employ sensitivity analysis regarding target distribution parameters.
If
Applications of Site-of-Action Model Methodology
This section provides four examples of application of the SoA modeling structure to soluble targets. The examples are divided into the three main categories for successful use of translational modeling and simulation: right target, right compound, and right dose.
Right Target
In the pre-clinical space, especially in early project stages, it is appropriate to conduct feasibility analysis. At this stage, a successful assessment is both one that progresses a target as a part of the portfolio and eventually into the clinic, as well as one that shows that a target is infeasible from a clinical utility standpoint. Such analyses are performed to determine whether sufficient levels of target coverage can be achieved via neutralization with a monoclonal antibody and should not be confused with determining whether the target is “right” from a disease standpoint. Often these analyses are done with just in-vitro functional assays, whose utility is limited - they capture a narrow aspect of the biology and may be done in the pre-portfolio stage. Once the project is part of the portfolio, we recommend a more thorough analysis with a SoA model since more resources for modeling and biomeasures/biomarkers are available. In many cases, the required levels of target coverage for efficacy are unknown so a threshold is set, depending on the disease, competitive landscape, and other factors, often at >90% or >99% target neutralization. If the required coverage for pharmacology cannot be achieved at a commercially viable dose, project termination is recommended.
Osteopontin Example
The first example in this section is an example of the latter-targeting osteopontin for rheumatoid arthritis (RA). Osteopontin is a secreted protein from a plethora of cells, that has been implicated in a variety of biological functions, from inflammation and fibrosis, to tumorigenesis and metastasis (Ashkar et al., 2000; Lund et al., 2013; Wang et al., 2014; Liu et al., 2015; Clemente et al., 2016). The goal of the work was to assess feasibility in suppressing osteopontin for the treatment of RA. A full SoA model was not utilized in this case because, as you will see, plasma levels of osteopontin were high enough to sufficiently inform feasibility, without the need for further modeling complexity. Target turnover was estimated using a human D3-leucine pulse-chase study similar to discussed in Estimating Target Turnover. Target serum concentrations were measured using a nano flow liquid chromatography-tandem mass spectrometry method similar to discussed in Estimating Target Concentrations. Mean serum concentrations were measured at around 10 nM and half-life was estimated at around 10 min. The scenarios presented here assume a mAb interacting with a soluble target and PK parameters for the drug are in Table 3. For the purpose of the example, to assess the degree of target coverage (free target reduction) in plasma, two dosing regimens were explored – 300 mg SC and 1,000 mg IV, both every week. These are not commercially viable doses for RA but were selected to explore the maximum attainable coverage with a monoclonal antibody targeting osteopontin. The effect of antibody affinity on target coverage was simulated using
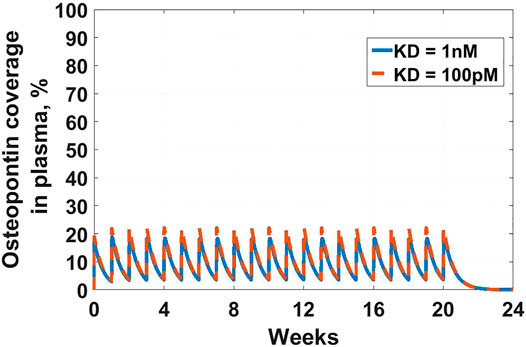
FIGURE 2. Osteopontin coverage in plasma: Shows the projected neutralization of osteopontin after mAb administration as described in Osteopontin Example. Simulated dose is 300 mg SC Q1W, with two antibody affinities –
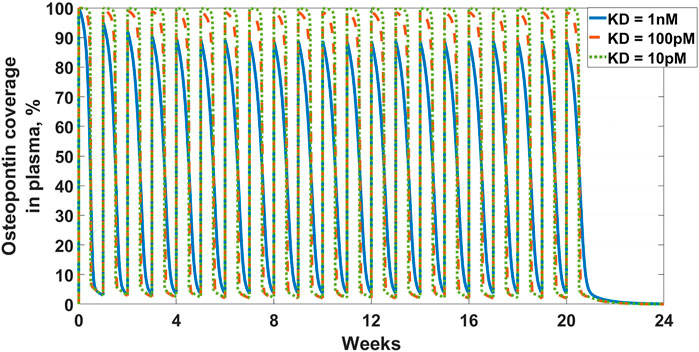
FIGURE 3. Osteopontin coverage in plasma: Shows the projected neutralization of osteopontin after mAb administration as described in Osteopontin Example. Simulated dose is 1,000 mg IV Q1W, with three antibody affinities –
IL-33 Example
Another feasibility example is IL-33. IL-33 is an alarmin, member of the IL-1 cytokine family, released by cells at the barrier surfaces (i.e., keratinocytes and airways epithelial cells) after disruption in the barrier function by pathogens, tissue injury, and cell death, and has been associated with atopic dermatitis and asthma (Saluja et al., 2015; Saluja et al., 2016). Asthma is the disease of choice for this example, therefore the SoA is lung. IL-33 signals through binding to ST2 and then forming a heterodimer with the IL-1 receptor (Saluja et al., 2015; Saluja et al., 2016; Griesenauer and Paczesny, 2017). ST2 can also be found in soluble form (sST2), which is a scavenger for IL-33 and constraints its signaling properties (Griesenauer and Paczesny, 2017). For the purpose of this example, our antibody competes with sST2 for binding to IL-33 in plasma. A scheme and description of the model is shown in Figure 4. The antibody binds IL-33 both in plasma and at the SoA. The distribution of the drug to the SoA and the periphery as well as assumptions regarding the mAb:IL-33 complex have been described earlier (see Drug Distribution Parameters). The target-related parameters and references used are described in Table 4. The mAb related parameters are described in Table 3 and Binding Parameters.
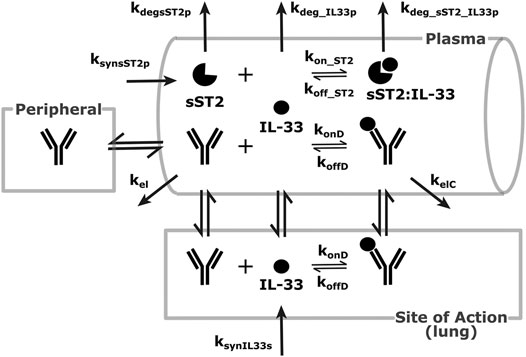
FIGURE 4. Modeling scheme of an anti-IL-33 mAb. The general processes are similar to the default scheme described in Figure 1, with several details adapted to the IL-33 scenario. IL-33 is synthesized at the SoA (lung) and distributes to the plasma. There, it can bind sST2 or get eliminated. sST2 is synthesized and eliminated in plasma only. The sST2:IL-33 complex clears in the plasma.
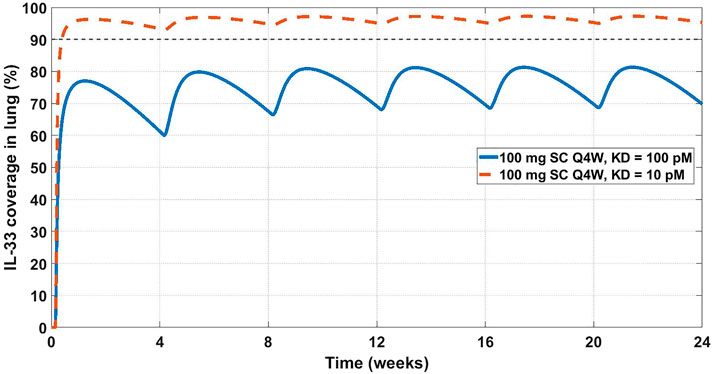
FIGURE 5. Projected IL-33 neutralization in the lung at 100 mg SC Q4W dosing at 10 pM (dashed orange line) and 100 pM (solid blue line) drug affinities. The 90% coverage line (dashed grey) is emphasized for convenience. The model projects that a 10 pM affinity would achieve 90% IL-33 neutralization in the lung.
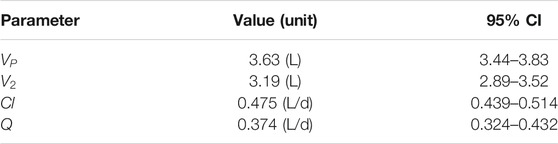
TABLE 4. GSK3050002 two-compartment PK parameters (Bouma et al., 2017).
This early-stage feasibility analysis omits several potentially important aspects of the biology of IL-33, e.g., quick inactivation due to oxidation and proteolytic activities, and synthesis in cellular nucleus and release under inflammatory conditions (Cohen et al., 2015; Saluja et al., 2015; Griesenauer and Paczesny, 2017; Scott et al., 2018). The former can increase the apparent clearance of active IL-33 and both properties can skew the measurements of active free IL-33 in plasma and tissue. Also, considering the tight binding of IL-33 to sST2, further considerations can be made regarding the expression of membrane ST2 in the lung and the antibody’s interaction with the target in a full receptor:target interaction mechanistic modeling system. Potentially, a competing vs non-competing epitope may be important for enhancing target neutralization, which could be evaluated at the next stage of mechanistic modeling - right molecule. Several anti-IL-33 molecules have already been in the clinic, and a couple have shown positive results in asthma (Anaptysbio, 2014; Regeneron Pharmaceuticals, 2019), validating the model’s conclusions.
Right Compound
Once feasibility has been established, the team delves deeper into assessing the molecular properties of the antibody necessary to neutralize the target. Most of the pharmacokinetic properties would depend on molecular assessment and there are currently few models that connect antibody molecular assessment and pharmacokinetics (Jones et al., 2019; Jones et al., 2020). Predominantly, modelers can assist the engineering team with projecting what antibody binding affinity is needed for the required level of neutralization (coverage). We use the next example of a clinical compound, to assess whether the mechanism was tested adequately and what affinity is required for improved target neutralization at a commercially viable dose.
Chemokine (C-C motif) ligand 20 (CCL20) is a chemoattractant for lymphocytes and dendritic cells in a variety of mucosal tissues (Schutyser et al., 2003). GSK3050002 is an anti-CCL20 monoclonal antibody that was tested in healthy volunteers (Bouma et al., 2017). The data presented in the study was drug, drug:target complex, and free target concentrations both in serum and in skin blister. The drug did not appear to inhibit monocytes and granulocytes activity in the skin blister model, so we decided to test whether a higher affinity antibody would be predicted to achieve higher and more sustained target coverage at the skin. For this purpose, a SoA model was constructed with skin as the SoA with the assumption that CCL20 was synthesized in the skin only and eliminated in the plasma only. Interstitial skin volume was assumed to be 1.125 L (Shah and Betts, 2012). Two-compartment PK model parameters (Table 4),
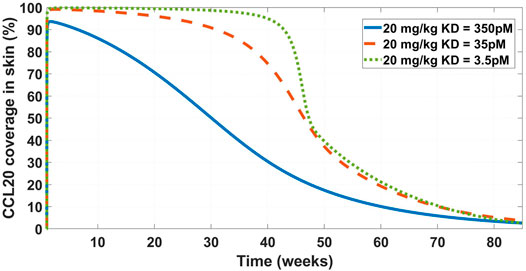
FIGURE 6. Model projected CCL20 coverage in the skin after administration of 20 mg/kg IV bolus dose of GSK3050002. Three mAb affinity scenarios were modeled – 350 pM (solid blue line), 35 pM (dashed orange line), and 3.5 pM (dotted green line). The low coverage at the base
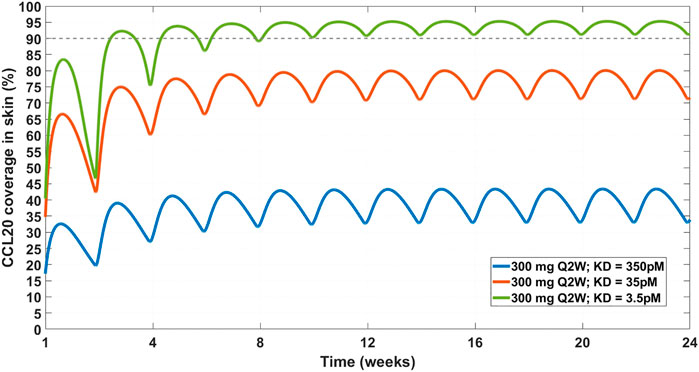
FIGURE 7. Projected CCL20 coverage in the skin at 300 mg SC Q2W dosing regimen and varying affinity. Three affinity scenarios were simulated – 350 pM (solid blue line), 35 pM (solid orange line), and 3.5 pM (solid green line). Thin dashed grey line indicates 90% coverage, which is emphasized for convenience. The model projects that a 3.5 pM affinity is required for achieving 90% CCL20 coverage in the skin.
While the general conclusion may still hold, several assumptions affect the results of the model. Some, like the synthesis of CCL20 in the skin, are reasonable given that the disease of interest is atopic dermatitis. The SoA:plasma ratio was assumed similar to the one found in IL-33 (see Table 5). That ratio would be target-dependent and potentially sensitivity analysis would need to be done to fully evaluate.
Right Dose
Once drug properties have been established, modeling is utilized to project a clinical efficacious dose in different patient populations. This step is important both from standpoint of selecting doses for toxicology studies and assisting in dose selection for first-in-human studies. This particular example is a retrospective analysis of the clinical compound IMA-026, an antagonist monoclonal antibody against IL-13 (Gauvreau et al., 2011; Kasaian et al., 2011; Tiwari et al., 2016b). IL-13 is a cytokine with demonstrated role in many inflammatory diseases, including asthma. IMA-026 is an M1 type anti-IL-13 antibody (May and Fung, 2015), which blocks IL-13 from interaction with its receptors - IL13Rα1 (signaling receptor) and IL13Rα2 (decoy receptor) (Chandriani et al., 2014). IMA-026 data in healthy volunteers (NCT00517348) has been analyzed before (Tiwari et al., 2016b), where initial IL-13 concentrations, drug affinity, and target turnover were estimated. However, we demonstrate here that the accumulation of total plasma concentration of IL-13 can be obtained without fitting any parameters by using literature references (target turnover), pre-clinical observations (drug affinity), and relevant clinical data (PK and initial target concentrations). IL-13 target turnover was estimated to be around 20 min in mice (Khodoun et al., 2007), drug
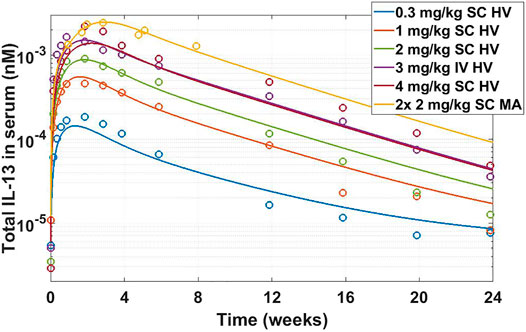
FIGURE 8. Total IL-13 accumulation after IMA-026 administration in Phase I trial - model simulations vs published data. Different color solid lines correspond to different doses, open circles with corresponding colors are clinical data. Labels: SC, subcutaneous; IV, intravenous; HV, healthy volunteers; MA, mild asthmatics. The model reasonably captures the behavior using internal affinity measures, previously published target data, and published PK parameters for IMA-026, without fitting any parameters.
The SoA model estimated that after 2 weeks dosing of 2 mg/kg SC Q1W the drug reached only around 8% target suppression at the site of action, while 8 weeks of dosing of 30 mg/kg SC Q1W would have achieved close to 90% coverage (Figure 9). Ultimately IMA-026 was abandoned since it did not show efficacy (Gauvreau et al., 2011). However, had data supporting an SoA model been available at time of the study conception, it could have projected the low coverage at 2 mg/kg and suggested either a longer duration study or a more appropriate dose for testing the mechanism. Likely, if SoA modeling had been available even earlier, an affinity maturation campaign could have been initiated to increase the affinity above 1 nM since a dose of 30 mg/kg Q1W is not commercially feasible. Suggestions for increased dose or improved affinity are corroborated by a crowd of anti-IL-13 monoclonal antibodies that have subsequently shown moderate to low efficacy in asthma (Gauvreau et al., 2011; Noonan et al., 2013; van Hartingsveldt et al., 2013; De Boever et al., 2014; Hanania et al., 2016), indicating the difficulty of achieving complete neutralization of IL-13 and/or its role as a standalone mechanism in the disease. The only anti-IL-13 mAb that has been in Phase 3 for asthma is lebrikizumab, with reported affinity of <10 pM (Ultsch et al., 2013). Lebrikizumab is currently in development for atopic dermatitis with positive results (Guttman-Yassky et al., 2020). Tralokinumab, whose affinity is reported at 58 pM (Popovic et al., 2017), has been approved for treatment of atopic dermatitis (LEO Pharma announces, 2021). The success and high affinity of both mAbs validate the model’s conclusions.
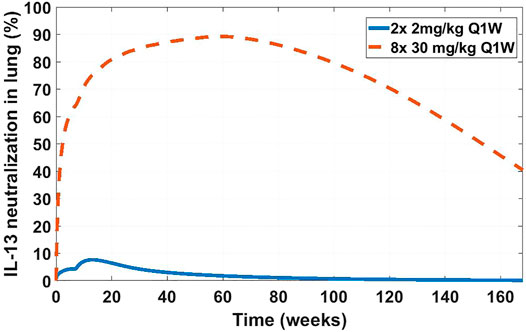
FIGURE 9. Projected IL-13 neutralization in lung at two dosing schedules for IMA-026. Two doses of 2 mg/kg a week apart (solid blue line) was the clinically tested dose in asthma patients (NCT00725582). Eight doses of 30 mg/kg a week apart (dashed orange line) is a hypothetical clinical dose at which the projected IMA-026 coverage reaches close to 90% IL-13 neutralization in the lung. Modeling suggests that the mechanism of IL-13 neutralization was likely untested in the clinic due to low tested dose, which is projected to result in low coverage.
Discussion
We have presented a three compartment mechanistic model that extends a typical two-compartment model by adding a site of action - a representation of the interstitial volume of the tissue where the interactions of the protein target with the drug are expected to contribute to disease modulation. The modeling is performed through a system of ordinary differential equations and is a mechanistic representation of the interaction of the drug with the target. The framework can be used for constructing a fit-for-purpose model to evaluate whether a target is biologically relevant and hitting the target is feasible (right target), guide drug properties for sufficient target engagement (right compound) and inform the necessary doses for achieving the degree of target engagement required for efficacy in the clinic (right dose). While the case studies described were categorized into examples of each of these three questions, these questions are inter-linked and in practice the modelling approach addresses all three if used at an appropriate stage of the drug discovery process. Ideally at project inception, a model should be generated to explore feasibility, affinity, and PK requirements for a desired dose level. Such an approach allows drug companies to focus on programs with the highest chance of success and limit the “wasted” resources on those which are more likely to fail. Hence, our proposal is to utilize this model in the early stages of drug discovery and, if possible, validate with clinical data.
The main feature of the SoA modeling approach is its flexibility. Depending on the target, a modeler can include any number of SoA compartments, ranging from zero to including every main tissue in the human body. Along with the system of equations, we suggest two key biomeasures: target concentrations and turnover, which represent essential parameters in early stage pre-clinical work. This is evident in the examples we presented - osteopontin could not be covered at any reasonable dose or affinity because of its high abundance and turnover; IL-33 needed high affinity for high neutralization but was deemed feasible due to relatively low expression and slow turnover; CCL20 also needed high affinity and a high dose to neutralize due to fast turnover. Different targets have different associated biology and will require different strategies to overcome difficulties in neutralizing them. Hence, while for the purpose of this discussion we are focused on the modeling structure, a capable biomarkers/biomeasures group is essential for the translational research effort.
Within the SoA model framework one can implement a variety of biological complexities: downstream or upstream biomarkers, different cell types, ligand-receptor binding, etc. The SoA model facilitates their implementations but one must weigh the complexity of the model versus the questions it tries to answer. The SoA modeling approach is not appropriate for a full disease model, for that goal a more complex QSP implementation would be appropriate. The SoA model is also not a physiologically based pharmacokinetics (PBPK) model - if the distribution of the drug in the whole body is important for the project, a PBPK model would likely be the appropriate tool.
The SoA model, as presented here, is fit for mAb modeling with its representation of mechanistic target binding and unbinding. The model can be adjusted and has been utilized to incorporate different molecular modalities - pegylated Fab fragments, bispecific antibodies, etc.
The examples in the manuscript are focused on soluble targets, which simplified some aspects of the presentation. Membrane-bound targets often present different challenges from modeling standpoint (i.e., target-mediated drug disposition, shedding of the membrane target) and relevant biomarker and biomeasures assays (i.e., number of receptors per cell, quantifying receptor internalization). These aspects can be described in a separate manuscript but there are excellent discussions on the topic, among which Aston et al. 2011 and Grimm 2009.
There are a number of shortcomings to the SoA modeling platform. The peripheral compartment may be underutilized - the model as presented here does not include target expression and turnover in the peripheral compartment or drug:target complex distribution in and out of the peripheral compartment. The method of fixing the ratio of drug concentration in plasma vs. the SoA assumes similar distribution to other previously measured antibodies. The rate of distribution of the drug into the SoA may have an effect on the target neutralization, and here it is calculated. Some of the mathematical methods may lead to non-physiological rates in order to preserve the measured concentrations at steady state. For example, the use of target distribution fixes the rate of distribution from plasma to the SoA and calculates the rate of distribution from the SoA into the plasma when assuming that the target is only synthesized in the SoA. This can lead to non-physiological differences in the plasma:SoA back and forth distribution rates. The very assumptions of target synthesis and distribution can alter the estimate of target suppression. However, despite these potential caveats of the base SoA model described in this manuscript, it is possible to adapt the framework to capture the relevant biological mechanisms as appropriate so that the sought physiological modulation can be described more accurately. Therefore, all the assumptions and calculations presented in this manuscript are just the most current iterations of ideas and are subject to scrutiny in the face of new facts and better representations.
As with all models, this framework requires validation. Early decisions can be made with sparse data and limited measurements but in order to improve confidence in the modeling results, ideally, measurements of key dynamics behaviors predicted by the model (longitudinal measurements of target engagement, free or total target levels, etc.) in relevant species with the candidate molecule or a suitable surrogate are needed for model validation. Furthermore, a retrospective validation using clinical data (external clinical data can also inform the pre-clinical model) should be performed when data is available in order to bridge the gap between theoretical and practical model projections. Some aspects of these validations include clinically-relevant disease-dependent level of target neutralization, distribution of the mAb into various types of SoA, or evaluation of the pre-clinical affinity biomeasures or functional assays and their translatability to the clinical setting. Not every project needs a site-of-action or a quantitative systems pharmacology model for successful translation from discovery to development. For the ones where understanding of the underlying pharmacology is limited, a simple exposure-response approach may be sufficient.
Conclusion
Ultimately, the SoA platform model is a useful framework that has allowed us to inform the progression of many successful mAb programs. In particular, we have used the model to determine the doability of targets, drug requirements for “best in class” mAbs and dosing regimens to achieve required levels of target coverage to demonstrate efficacy. This modeling approach is fully integrated in the drug discovery process with the ability to make decisions believed to be high.
Data Availability Statement
Publicly available datasets were analyzed in this study. Available data is referenced in the article (literature references only).
Author Contributions
HJ and GK conceived the concept. GK, JC, JN, and MR conducted the modeling research. HN, JP, VF, and JJ conducted the biomeasures research. RW and HJ supervised the research and manuscript. GK wrote the manuscript with support and contributions from all other authors.
Conflict of Interest
All authors are current or former employees of Pfizer Inc.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbinf.2021.731340/full#supplementary-material.
References
Aarons, L. (2005). Physiologically Based Pharmacokinetic Modelling: a Sound Mechanistic Basis Is Needed. Br. J. Clin. Pharmacol. 60 (6), 581–583. doi:10.1111/j.1365-2125.2005.02560.x
Allerheiligen, S. R. (2010). Next-generation Model-Based Drug Discovery and Development: Quantitative and Systems Pharmacology. Clin. Pharmacol. Ther. 88 (1), 135–137. doi:10.1038/clpt.2010.81
An, B., Zhang, M., Pu, J., Qu, Y., Shen, S., Zhou, S., et al. (2020). Toward Accurate and Robust Liquid Chromatography-Mass Spectrometry-Based Quantification of Antibody Biotherapeutics in Tissues. Anal. Chem. 92 (22), 15152–15161. doi:10.1021/acs.analchem.0c03620
Anaptysbio, I. (2014). Etokimab. Available from: https://www.anaptysbio.com/pipeline/etokimab/.
Andersen, M. E. (1995). Physiologically Based Pharmacokinetic (PB-PK) Models in the Study of the Disposition and Biological Effects of Xenobiotics and Drugs. Toxicol. Lett. 82-83, 341–348. doi:10.1016/0378-4274(95)03487-0
Artru, F., Bou Saleh, M., Maggiotto, F., Lassailly, G., Ningarhari, M., Demaret, J., et al. (2020). IL-33/ST2 Pathway Regulates Neutrophil Migration and Predicts Outcome in Patients with Severe Alcoholic Hepatitis. J. Hepatol. 72 (6), 1052–1061. doi:10.1016/j.jhep.2019.12.017
Ashkar, S., Weber, G. F., Panoutsakopoulou, V., Sanchirico, M. E., Jansson, M., Zawaideh, S., et al. (2000). Eta-1 (Osteopontin): an Early Component of Type-1 (Cell-mediated) Immunity. Science 287 (5454), 860–864. doi:10.1126/science.287.5454.860
Aston, P. J., Derks, G., Raji, A., Agoram, B. M., and van der Graaf, P. H. (2011). Mathematical Analysis of the Pharmacokinetic-Pharmacodynamic (PKPD) Behaviour of Monoclonal Antibodies: Predicting In Vivo Potency. J. Theor. Biol. 281 (1), 113–121. doi:10.1016/j.jtbi.2011.04.030
Banks, R. E., Forbes, M. A., Patel, P. M., Storr, M., Hallam, S., Clarke, D., et al. (2000). Subcutaneous Administration of Recombinant Glycosylated Interleukin 6 in Patients with Cancer: Pharmacokinetics, Pharmacodynamics and Immunomodulatory Effects. Cytokine 12 (4), 388–396. doi:10.1006/cyto.1999.0556
Bantscheff, M., Schirle, M., Sweetman, G., Rick, J., and Kuster, B. (2007). Quantitative Mass Spectrometry in Proteomics: a Critical Review. Anal. Bioanal. Chem. 389 (4), 1017–1031. doi:10.1007/s00216-007-1486-6
Barrett, J. S., Fossler, M. J., Cadieu, K. D., and Gastonguay, M. R. (2008). Pharmacometrics: a Multidisciplinary Field to Facilitate Critical Thinking in Drug Development and Translational Research Settings. J. Clin. Pharmacol. 48 (5), 632–649. doi:10.1177/0091270008315318
Barton, H. A., Chiu, W. A., Setzer, R. W., Andersen, M. E., Bailer, A. J., Bois, F. Y., et al. (2007). Characterizing Uncertainty and Variability in Physiologically Based Pharmacokinetic Models: State of the Science and Needs for Research and Implementation. Toxicol. Sci. 99 (2), 395–402. doi:10.1093/toxsci/kfm100
Bateman, R. J., Munsell, L. Y., Morris, J. C., Swarm, R., Yarasheski, K. E., and Holtzman, D. M. (2006). Human Amyloid-Beta Synthesis and Clearance Rates as Measured in Cerebrospinal Fluid In Vivo. Nat. Med. 12 (7), 856–861. doi:10.1038/nm1438
Baxter, L. T., Zhu, H., Mackensen, D. G., Butler, W. F., and Jain, R. K. (1995). Biodistribution of Monoclonal Antibodies: Scale-Up from Mouse to Human Using a Physiologically Based Pharmacokinetic Model. Cancer Res. 55 (20), 4611–4622.
Baxter, L. T., Zhu, H., Mackensen, D. G., and Jain, R. K. (1994). Physiologically Based Pharmacokinetic Model for Specific and Nonspecific Monoclonal Antibodies and Fragments in normal Tissues and Human Tumor Xenografts in Nude Mice. Cancer Res. 54 (6), 1517–1528.
Becker, J. O., and Hoofnagle, A. N. (2012). Replacing Immunoassays with Tryptic Digestion-Peptide Immunoaffinity Enrichment and LC-MS/MS. Bioanalysis 4 (3), 281–290. doi:10.4155/bio.11.319
Benson, N., Cucurull-Sanchez, L., Demin, O., Smirnov, S., and van der Graaf, P-H. (2011). Reducing Systems Biology to Practice in Pharmaceutical Company Research; Selected Case Studies. Adv. Exp. Med. Biol., 736, 607–615. doi:10.1007/978-1-4419-7210-1_36
Betts, A., Keunecke, A., van Steeg, T. J., van der Graaf, P. H., Avery, L. B., Jones, H., et al. (2018). Linear Pharmacokinetic Parameters for Monoclonal Antibodies Are Similar within a Species and across Different Pharmacological Targets: A Comparison between Human, Cynomolgus Monkey and hFcRn Tg32 Transgenic Mouse Using a Population-Modeling Approach. MAbs 10, 751–764. doi:10.1080/19420862.2018.1462429
Blakey, G. E., Nestorov, I. A., Arundel, P. A., Aarons, L. J., and Rowland, M. (1997). Quantitative Structure-Pharmacokinetics Relationships: I. Development of a Whole-Body Physiologically Based Model to Characterize Changes in Pharmacokinetics across a Homologous Series of Barbiturates in the Rat. J. Pharmacokinet. Biopharm. 25 (3), 277–312. doi:10.1023/a:1025771608474
Bouma, G., Zamuner, S., Hicks, K., Want, A., Oliveira, J., Choudhury, A., et al. (2017). CCL20 Neutralization by a Monoclonal Antibody in Healthy Subjects Selectively Inhibits Recruitment of CCR6+ Cells in an Experimental Suction Blister. Br. J. Clin. Pharmacol. 83 (9), 1976–1990. doi:10.1111/bcp.13286
Bouzom, F., Ball, K., Perdaems, N., and Walther, B. (2012). Physiologically Based Pharmacokinetic (PBPK) Modelling Tools: How to Fit with Our Needs?. Biopharm. Drug Dispos 33 (2), 55–71. doi:10.1002/bdd.1767
Brodfuehrer, J., Rankin, A., Edmonds, J., Keegan, S., Andreyeva, T., Lawrence-Henderson, R., et al. (2014). Quantitative Analysis of Target Coverage and Germinal Center Response by a CXCL13 Neutralizing Antibody in a T-dependent Mouse Immunization Model. Pharm. Res. 31 (3), 635–648. doi:10.1007/s11095-013-1185-2
Cai, H., Stoner, C., Reddy, A., Freiwald, S., Smith, D., Winters, R., et al. (2006). Evaluation of an Integrated In Vitro-In Silico PBPK (Physiologically Based Pharmacokinetic) Model to Provide Estimates of Human Bioavailability. Int. J. Pharm. 308 (1-2), 133–139. doi:10.1016/j.ijpharm.2005.11.002
Chabot, J. R., Dettling, D. E., Jasper, P. J., and Gomes, B. C. (2011). Comprehensive Mechanism-Based Antibody Pharmacokinetic Modeling. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2011, 4318–4323. doi:10.1109/IEMBS.2011.6091072
Chandriani, S., DePianto, D. J., N'Diaye, E. N., Abbas, A. R., Jackman, J., Bevers, J., et al. (2014). Endogenously Expressed IL-13Rα2 Attenuates IL-13-mediated Responses but Does Not Activate Signaling in Human Lung Fibroblasts. J. Immunol. 193 (1), 111–119. doi:10.4049/jimmunol.1301761
Clemente, N., Raineri, D., Cappellano, G., Boggio, E., Favero, F., Soluri, M. F., et al. (2016). Osteopontin Bridging Innate and Adaptive Immunity in Autoimmune Diseases. J. Immunol. Res. 2016, 7675437. doi:10.1155/2016/7675437
Cohen, E. S., Scott, I. C., Majithiya, J. B., Rapley, L., Kemp, B. P., England, E., et al. (2015). Oxidation of the Alarmin IL-33 Regulates ST2-dependent Inflammation. Nat. Commun. 6 (1), 8327. doi:10.1038/ncomms9327
Creaven, P. J., Plager, J. E., Dupere, S., Huben, R. P., Takita, H., Mittelman, A., et al. (1987). Phase I Clinical Trial of Recombinant Human Tumor Necrosis Factor. Cancer Chemother. Pharmacol. 20 (2), 137–144. doi:10.1007/BF00253968
Cucurull-Sanchez, L., Chappell, M. J., Chelliah, V., Amy Cheung, S. Y., Derks, G., Penney, M., et al. (2019). Best Practices to Maximize the Use and Reuse of Quantitative and Systems Pharmacology Models: Recommendations from the United Kingdom Quantitative and Systems Pharmacology Network. CPT Pharmacometrics Syst. Pharmacol. 8 (5), 259–272. doi:10.1002/psp4.12381
Danhof, M., Klein, K., Stolk, P., Aitken, M., and Leufkens, H. (2018). The Future of Drug Development: the Paradigm Shift towards Systems Therapeutics. Drug Discov. Today 23 (12), 1990–1995. doi:10.1016/j.drudis.2018.09.002
De Boever, E. H., Ashman, C., Cahn, A. P., Locantore, N. W., Overend, P., Pouliquen, I. J., et al. (2014). Efficacy and Safety of an anti-IL-13 mAb in Patients with Severe Asthma: a Randomized Trial. J. Allergy Clin. Immunol. 133 (4), 989–996. doi:10.1016/j.jaci.2014.01.002
Derendorf, H., and Meibohm, B. (1999). Modeling of Pharmacokinetic/Pharmacodynamic (PK/PD) Relationships: Concepts and Perspectives. Pharm. Res. 16 (2), 176–185. doi:10.1023/a:1011907920641
Dirks, N. L., and Meibohm, B. (2010). Population Pharmacokinetics of Therapeutic Monoclonal Antibodies. Clin. Pharmacokinet. 49 (10), 633–659. doi:10.2165/11535960-000000000-00000
Doherty, M. K., and Whitfield, P. D. (2011). Proteomics Moves from Expression to Turnover: Update and Future Perspective. Expert Rev. Proteomics 8 (3), 325–334. doi:10.1586/epr.11.19
Edginton, A. N., Theil, F. P., Schmitt, W., and Willmann, S. (2008). Whole Body Physiologically-Based Pharmacokinetic Models: Their Use in Clinical Drug Development. Expert Opin. Drug Metab. Toxicol. 4 (9), 1143–1152. doi:10.1517/17425255.4.9.1143
Farrokhi, V., Chabot, J. R., Neubert, H., and Yang, Z. (2018). Assessing the Feasibility of Neutralizing Osteopontin with Various Therapeutic Antibody Modalities. Sci. Rep. 8 (1), 7781. doi:10.1038/s41598-018-26187-w
Farrokhi, V., Chen, X., and Neubert, H. (2018). Protein Turnover Measurements in Human Serum by Serial Immunoaffinity LC-MS/MS. Clin. Chem. 64 (2), 279–288. doi:10.1373/clinchem.2017.272922
Foote, J., and Eisen, H. N. (1995). Kinetic and Affinity Limits on Antibodies Produced during Immune Responses. Proc. Natl. Acad. Sci. U S A. 92 (5), 1254–1256. doi:10.1073/pnas.92.5.1254
Gauvreau, G. M., Boulet, L. P., Cockcroft, D. W., Fitzgerald, J. M., Carlsten, C., Davis, B. E., et al. (2011). Effects of Interleukin-13 Blockade on Allergen-Induced Airway Responses in Mild Atopic Asthma. Am. J. Respir. Crit. Care Med. 183 (8), 1007–1014. doi:10.1164/rccm.201008-1210OC
Glück, J., Rymarczyk, B., Jura-Szołtys, E., and Rogala, B. (2019). Serum Levels of Interleukin 33 and its Receptor ST2 in Patients Treated with Subcutaneous Allergen Immunotherapy in Intermittent Allergic Rhinitis. Cent. Eur. J. Immunol. 44 (2), 214–217.
Grass, G. M., and Sinko, P. J. (2002). Physiologically-based Pharmacokinetic Simulation Modelling. Adv. Drug Deliv. Rev. 54 (3), 433–451. doi:10.1016/s0169-409x(02)00013-3
Griesenauer, B., and Paczesny, S. (2017). The ST2/IL-33 Axis in Immune Cells during Inflammatory Diseases. Front. Immunol. 8, 475. doi:10.3389/fimmu.2017.00475
Grimm, H. P. (2009). Gaining Insights into the Consequences of Target-Mediated Drug Disposition of Monoclonal Antibodies Using Quasi-Steady-State Approximations, J. Pharmacokinet. Pharmacodyn, 36, 1573–8744. doi:10.1007/s10928-009-9129-5
Guttman-Yassky, E., Blauvelt, A., Eichenfield, L. F., Paller, A. S., Armstrong, A. W., Drew, J., et al. (2020). Efficacy and Safety of Lebrikizumab, a High-Affinity Interleukin 13 Inhibitor, in Adults with Moderate to Severe Atopic Dermatitis: A Phase 2b Randomized Clinical Trial. JAMA Dermatol. 156 (4), 411–420. doi:10.1001/jamadermatol.2020.0079
Hanania, N. A., Korenblat, P., Chapman, K. R., Bateman, E. D., Kopecky, P., Paggiaro, P., et al. (2016). Efficacy and Safety of Lebrikizumab in Patients with Uncontrolled Asthma (LAVOLTA I and LAVOLTA II): Replicate, Phase 3, Randomised, Double-Blind, Placebo-Controlled Trials. Lancet Respir. Med. 4 (10), 781–796. doi:10.1016/S2213-2600(16)30265-X
Hinkson, I. V., and Elias, J. E. (2011). The Dynamic State of Protein Turnover: It's about Time. Trends Cel Biol. 21 (5), 293–303. doi:10.1016/j.tcb.2011.02.002
Hoang, K. (1995). Physiologically Based Pharmacokinetic Models: Mathematical Fundamentals and Simulation Implementations. Toxicol. Lett. 79 (1-3), 99–106. doi:10.1016/0378-4274(95)03361-n
Hopkins, A. L. (2008). Network Pharmacology: the Next Paradigm in Drug Discovery. Nat. Chem. Biol. 4 (11), 682–690. doi:10.1038/nchembio.118
Huang, S. M., and Rowland, M. (2012). The Role of Physiologically Based Pharmacokinetic Modeling in Regulatory Review. Clin. Pharmacol. Ther. 91 (3), 542–549. doi:10.1038/clpt.2011.320
Jacobs, C. A., Beckmann, M. P., Mohler, K., Maliszewski, C. R., Fanslow, W. C., and Lynch, D. H. (1993). Pharmacokinetic Parameters and Biodistribution of Soluble Cytokine Receptors. Int. Rev. Exp. Pathol. 34 Pt B, 123–135. doi:10.1016/b978-0-12-364935-5.50013-4
Janeway, C. A., and Walport, M. (2001). Immunobiology: The Immune System in Health and Disease. 5th ed. New York: Garland Science.
Jones, H. M., Barton, H. A., Lai, Y., Bi, Y. A., Kimoto, E., Kempshall, S., et al. (2012). Mechanistic Pharmacokinetic Modeling for the Prediction of Transporter-Mediated Disposition in Humans from sandwich Culture Human Hepatocyte Data. Drug Metab. Dispos 40 (5), 1007–1017. doi:10.1124/dmd.111.042994
Jones, H. M., Dickins, M., Youdim, K., Gosset, J. R., Attkins, N. J., Hay, T. L., et al. (2012). Application of PBPK Modelling in Drug Discovery and Development at Pfizer. Xenobiotica 42 (1), 94–106. doi:10.3109/00498254.2011.627477
Jones, H. M., Gardner, I. B., Collard, W. T., Stanley, P. J., Oxley, P., Hosea, N. A., et al. (2011). Simulation of Human Intravenous and Oral Pharmacokinetics of 21 Diverse Compounds Using Physiologically Based Pharmacokinetic Modelling. Clin. Pharmacokinet. 50 (5), 331–347. doi:10.2165/11539680-000000000-00000
Jones, H. M., Gardner, I. B., and Watson, K. J. (2009). Modelling and PBPK Simulation in Drug Discovery. AAPS J. 11 (1), 155–166. doi:10.1208/s12248-009-9088-1
Jones, H. M., Mayawala, K., and Poulin, P. (2013). Dose Selection Based on Physiologically Based Pharmacokinetic (PBPK) Approaches. AAPS J. 15 (2), 377–387. doi:10.1208/s12248-012-9446-2
Jones, H. M., Parrott, N., Jorga, K., and Lavé, T. (2006). A Novel Strategy for Physiologically Based Predictions of Human Pharmacokinetics. Clin. Pharmacokinet. 45 (5), 511–542. doi:10.2165/00003088-200645050-00006
Jones, H. M., Parrott, N., Ohlenbusch, G., and Lavé, T. (2006). Predicting Pharmacokinetic Food Effects Using Biorelevant Solubility media and Physiologically Based Modelling. Clin. Pharmacokinet. 45 (12), 1213–1226. doi:10.2165/00003088-200645120-00006
Jones, H. M., Tolsma, J., Zhang, Z., Jasper, P., Luo, H., Weber, G. L., et al. (2020). A Physiologically-Based Pharmacokinetic Model for the Prediction of "Half-Life Extension" and "Catch and Release" Monoclonal Antibody Pharmacokinetics. CPT Pharmacometrics Syst. Pharmacol. 9 (9), 534–541. doi:10.1002/psp4.12547
Jones, H. M., Zhang, Z., Jasper, P., Luo, H., Avery, L. B., King, L. E., et al. (2019). A Physiologically-Based Pharmacokinetic Model for the Prediction of Monoclonal Antibody Pharmacokinetics from In Vitro Data. CPT Pharmacometrics Syst. Pharmacol. 8 (10), 738–747. doi:10.1002/psp4.12461
Jusko, W. J. (2013). Moving from Basic toward Systems Pharmacodynamic Models. J. Pharm. Sci. 102 (9), 2930–2940. doi:10.1002/jps.23590
Kasaian, M. T., Raible, D., Marquette, K., Cook, T. A., Zhou, S., Tan, X. Y., et al. (2011). IL-13 Antibodies Influence IL-13 Clearance in Humans by Modulating Scavenger Activity of IL-13Rα2. J. Immunol. 187 (1), 561–569. doi:10.4049/jimmunol.1100467
Khodoun, M., Lewis, C. C., Lewis, C., Yang, J. Q., Orekov, T., Potter, C., et al. (2007). Differences in Expression, Affinity, and Function of Soluble (s)IL-4Ralpha and sIL-13Ralpha2 Suggest Opposite Effects on Allergic Responses. J. Immunol. 179 (10), 6429–6438. doi:10.4049/jimmunol.179.10.6429
Kitano, H. (2005). International Alliances for Quantitative Modeling in Systems Biology. Mol. Syst. Biol. 1, 2005–0007. doi:10.1038/msb4100011
Knight-Schrijver, V. R., Chelliah, V., Cucurull-Sanchez, L., and Le Novère, N. (2016). The Promises of Quantitative Systems Pharmacology Modelling for Drug Development. Comput. Struct. Biotechnol. J. 14, 363–370. doi:10.1016/j.csbj.2016.09.002
Kohl, P., Crampin, E. J., Quinn, T. A., and Noble, D. (2010). Systems Biology: an Approach. Clin. Pharmacol. Ther. 88 (1), 25–33. doi:10.1038/clpt.2010.92
Kroegel, C., Julius, P., Matthys, H., Virchow, J. C., and Luttmann, W. (1996). Endobronchial Secretion of Interleukin-13 Following Local Allergen challenge in Atopic Asthma: Relationship to Interleukin-4 and Eosinophil Counts. Eur. Respir. J. 9 (5), 899–904. doi:10.1183/09031936.96.09050899
Lalonde, R. L., Kowalski, K. G., Hutmacher, M. M., Ewy, W., Nichols, D. J., Milligan, P. A., et al. (2007). Model-based Drug Development. Clin. Pharmacol. Ther. 82 (1), 21–32. doi:10.1038/sj.clpt.6100235
Larance, M., and Lamond, A. I. (2015). Multidimensional Proteomics for Cell Biology. Nat. Rev. Mol. Cel Biol. 16, 269–280. doi:10.1038/nrm3970
Lassman, M. E., McAvoy, T., Lee, A. Y., Chappell, D., Wong, O., Zhou, H., et al. (2014). Practical Immunoaffinity-Enrichment LC-MS for Measuring Protein Kinetics of Low-Abundance Proteins. Clin. Chem. 60 (9), 1217–1224. doi:10.1373/clinchem.2014.222455
Leo Pharma announces, European Commission Approval of Adtralza® (Tralokinumab) as the First and Only Treatment Specifically Targeting IL-13 for Adults with Moderate-To-Severe Atopic Dermatitis [press release]. 2021.
Li, Z., Krippendorff, B. F., and Shah, D. K. (2017). Influence of Molecular Size on the Clearance of Antibody Fragments. Pharm. Res. 34 (10), 2131–2141. doi:10.1007/s11095-017-2219-y
Lindwall, G., Hsieh, E. A., Misell, L. M., Chai, C. M., Turner, S. M., and Hellerstein, M. K. (2006). Heavy Water Labeling of Keratin as a Non-invasive Biomarker of Skin Turnover In Vivo in Rodents and Humans. J. Invest. Dermatol. 126 (4), 841–848. doi:10.1038/sj.jid.5700189
Liu, Y., Cao, L., Chen, R., Zhou, X., Fan, X., Liang, Y., et al. (2015). Osteopontin Promotes Hepatic Progenitor Cell Expansion and Tumorigenicity via Activation of β-Catenin in Mice. Stem Cells 33 (12), 3569–3580. doi:10.1002/stem.2072
Loizou, G., Spendiff, M., Barton, H. A., Bessems, J., Bois, F. Y., d'Yvoire, M. B., et al. (2008). Development of Good Modelling Practice for Physiologically Based Pharmacokinetic Models for Use in Risk Assessment: the First Steps. Regul. Toxicol. Pharmacol. 50 (3), 400–411. doi:10.1016/j.yrtph.2008.01.011
Lund, S. A., Wilson, C. L., Raines, E. W., Tang, J., Giachelli, C. M., and Scatena, M. (2013). Osteopontin Mediates Macrophage Chemotaxis via α4 and α9 Integrins and Survival via the α4 Integrin. J. Cel Biochem. 114 (5), 1194–1202. doi:10.1002/jcb.24462
Mager, D. E., and Jusko, W. J. (2008). Development of Translational Pharmacokinetic-Pharmacodynamic Models. Clin. Pharmacol. Ther. 83 (6), 909–912. doi:10.1038/clpt.2008.52
May, R. D., and Fung, M. (2015). Strategies Targeting the IL-4/IL-13 Axes in Disease. Cytokine 75 (1), 89–116. doi:10.1016/j.cyto.2015.05.018
McAvoy, T., Lassman, M. E., Spellman, D. S., Ke, Z., Howell, B. J., Wong, O., et al. (2014). Quantification of Tau in Cerebrospinal Fluid by Immunoaffinity Enrichment and Tandem Mass Spectrometry. Clin. Chem. 60 (4), 683–689. doi:10.1373/clinchem.2013.216515
Meibohm, B., and Derendorf, H. (1997). Basic Concepts of Pharmacokinetic/pharmacodynamic (PK/PD) Modelling. Int. J. Clin. Pharmacol. Ther. 35 (10), 401–413.
Mueller, T., and Dieplinger, B. (2016). Soluble ST2 and Galectin-3: What We Know and Don't Know Analytically. EJIFCC 27 (3), 224–237.
Nestorov, I. (2007). Whole-body Physiologically Based Pharmacokinetic Models. Expert Opin. Drug Metab. Toxicol. 3 (2), 235–249. doi:10.1517/17425255.3.2.235
Nestorov, I. A., Aarons, L. J., Arundel, P. A., and Rowland, M. (1998). Lumping of Whole-Body Physiologically Based Pharmacokinetic Models. J. Pharmacokinet. Biopharm. 26 (1), 21–46. doi:10.1023/a:1023272707390
Neubert, H., Muirhead, D., Kabir, M., Grace, C., Cleton, A., and Arends, R. (2013). Sequential Protein and Peptide Immunoaffinity Capture for Mass Spectrometry-Based Quantification of Total Human β-nerve Growth Factor. Anal. Chem. 85 (3), 1719–1726. doi:10.1021/ac303031q
Neubert, H., Shuford, C. M., Olah, T. V., Garofolo, F., Schultz, G. A., Jones, B. R., et al. (2020). Protein Biomarker Quantification by Immunoaffinity Liquid Chromatography-Tandem Mass Spectrometry: Current State and Future Vision. Clin. Chem. 66 (2), 282–301. doi:10.1093/clinchem/hvz022
Nijsen, M. J. M. A., Wu, F., Bansal, L., Bradshaw-Pierce, E., Chan, J. R., Liederer, B. M., et al. (2018). Preclinical QSP Modeling in the Pharmaceutical Industry: An IQ Consortium Survey Examining the Current Landscape. CPT Pharmacometrics Syst. Pharmacol. 7 (3), 135–146. doi:10.1002/psp4.12282
Noonan, M., Korenblat, P., Mosesova, S., Scheerens, H., Arron, J. R., Zheng, Y., et al. (2013). Dose-ranging Study of Lebrikizumab in Asthmatic Patients Not Receiving Inhaled Steroids. J. Allergy Clin. Immunol. 132 (3), 567–e12. doi:10.1016/j.jaci.2013.03.051
Norris, D. A., Leesman, G. D., Sinko, P. J., and Grass, G. M. (2000). Development of Predictive Pharmacokinetic Simulation Models for Drug Discovery. J. Control. Release 65 (1-2), 55–62. doi:10.1016/s0168-3659(99)00232-1
Oshikawa, K., Kuroiwa, K., Tago, K., Iwahana, H., Yanagisawa, K., Ohno, S., et al. (2001). Elevated Soluble ST2 Protein Levels in Sera of Patients with Asthma with an Acute Exacerbation. Am. J. Respir. Crit. Care Med. 164 (2), 277–281. doi:10.1164/ajrccm.164.2.2008120
Owen, S. G., Francis, H. W., and Roberts, M. S. (1994). Disappearance Kinetics of Solutes from Synovial Fluid after Intra-articular Injection. Br. J. Clin. Pharmacol. 38 (4), 349–355. doi:10.1111/j.1365-2125.1994.tb04365.x
Palandra, J., Finelli, A., Zhu, M., Masferrer, J., and Neubert, H. (2013). Highly Specific and Sensitive Measurements of Human and Monkey Interleukin 21 Using Sequential Protein and Tryptic Peptide Immunoaffinity LC-MS/MS. Anal. Chem. 85 (11), 5522–5529. doi:10.1021/ac4006765
Palandra, J., Quazi, A., Fitz, L., Rong, H., Morris, C., and Neubert, H. (2016). Quantitative Measurements of GDF-8 Using Immunoaffinity LC-MS/MS. Proteomics Clin. Appl. 10 (5), 597–604. doi:10.1002/prca.201500112
Palmer, G., Lipsky, B. P., Smithgall, M. D., Meininger, D., Siu, S., Talabot-Ayer, D., et al. (2008). The IL-1 Receptor Accessory Protein (AcP) Is Required for IL-33 Signaling and Soluble AcP Enhances the Ability of Soluble ST2 to Inhibit IL-33. Cytokine 42 (3), 358–364. doi:10.1016/j.cyto.2008.03.008
Peterson, M. C., and Riggs, M. M. (2015). FDA Advisory Meeting Clinical Pharmacology Review Utilizes a Quantitative Systems Pharmacology (QSP) Model: A Watershed Moment?. CPT Pharmacometrics Syst. Pharmacol. 4 (3), e00020–92. doi:10.1002/psp4.20
A Multi-Compartmental Model Generally Applicable to Physiologically-Based Pharmacokinetics,”P. H. Arundel in 3rd IFAC Symposium; Modelling and Control in Biomedial Systems (UK: University of Warwick).
Popovic, B., Breed, J., Rees, D. G., Gardener, M. J., Vinall, L. M., Kemp, B., et al. (2017). Structural Characterisation Reveals Mechanism of IL-13-Neutralising Monoclonal Antibody Tralokinumab as Inhibition of Binding to IL-13Rα1 and IL-13Rα2. J. Mol. Biol. 429 (2), 208–219. doi:10.1016/j.jmb.2016.12.005
Poulin, P., and Theil, F. P. (2002). Prediction of Pharmacokinetics Prior to In Vivo Studies. 1. Mechanism-Based Prediction of Volume of Distribution. J. Pharm. Sci. 91 (1), 129–156. doi:10.1002/jps.10005
Rajman, I. (2008). PK/PD Modelling and Simulations: Utility in Drug Development. Drug Discov. Today 13 (7), 341–346. doi:10.1016/j.drudis.2008.01.003
Regeneron Pharmaceuticals, I. (2019). Regeneron and Sanofi Announce Positive Topline Phase 2 Results for IL-33 Antibody in Asthma June 21, 2019. Available from: https://investor.regeneron.com/news-releases/news-release-details/regeneron-and-sanofi-announce-positive-topline-phase-2-results/ (Acessed on June 21, 2019).
Rogers, M., Lyster, P., and Okita, R. (2013). NIH Support for the Emergence of Quantitative and Systems Pharmacology. CPT: Pharmacometrics Syst. Pharmacol. 2 (4), 37. doi:10.1038/psp.2013.13
Rostami-Hodjegan, A., Tamai, I., and Pang, K. S. (2012). Physiologically Based Pharmacokinetic (PBPK) Modeling: it Is Here to Stay!. Biopharm. Drug Dispos 33 (2), 47–50. doi:10.1002/bdd.1776
Saluja, R., Khan, M., Church, M. K., and Maurer, M. (2015). The Role of IL-33 and Mast Cells in Allergy and Inflammation. Clin. Transl Allergy 5 (1), 33. doi:10.1186/s13601-015-0076-5
Saluja, R., Zoltowska, A., Ketelaar, M. E., and Nilsson, G. (2016). IL-33 and Thymic Stromal Lymphopoietin in Mast Cell Functions. Eur. J. Pharmacol. 778, 68–76. doi:10.1016/j.ejphar.2015.04.047
Schutyser, E., Struyf, S., and Van Damme, J. (2003). The CC Chemokine CCL20 and its Receptor CCR6. Cytokine Growth Factor. Rev. 14 (5), 409–426. doi:10.1016/s1359-6101(03)00049-2
Scott, I. C., Majithiya, J. B., Sanden, C., Thornton, P., Sanders, P. N., Moore, T., et al. (2018). Interleukin-33 Is Activated by Allergen- and Necrosis-Associated Proteolytic Activities to Regulate its Alarmin Activity during Epithelial Damage. Sci. Rep. 8 (1), 3363. doi:10.1038/s41598-018-21589-2
Shah, D. K., and Betts, A. M. (2013). Antibody Biodistribution Coefficients: Inferring Tissue Concentrations of Monoclonal Antibodies Based on the Plasma Concentrations in Several Preclinical Species and Human. MAbs 5 (2), 297–305. doi:10.4161/mabs.23684
Shah, D. K., and Betts, A. M. (2012). Towards a Platform PBPK Model to Characterize the Plasma and Tissue Disposition of Monoclonal Antibodies in Preclinical Species and Human. J. Pharmacokinet. Pharmacodyn 39 (1), 67–86. doi:10.1007/s10928-011-9232-2
Shuford, C. M., Johnson, J. S., Thompson, J. W., Holland, P. L., Hoofnagle, A. N., and Grant, R. P. (2020). More Sensitivity Is Always Better: Measuring Sub-clinical Levels of Serum Thyroglobulin on a µLC-MS/MS System. Clin. Mass Spectrom. 15, 29–35. doi:10.1016/j.clinms.2020.01.001
Tang, Y., Zeng, X., and Liang, J. (2010). Surface Plasmon Resonance: An Introduction to a Surface Spectroscopy Technique. J. Chem. Educ. 87 (7), 742–746. doi:10.1021/ed100186y
Tiwari, A., Abraham, A. K., Harrold, J. M., Zutshi, A., and Singh, P. (2017). Optimal Affinity of a Monoclonal Antibody: Guiding Principles Using Mechanistic Modeling, AAPS J., 19, 1550–7416. doi:10.1208/s12248-016-0004-1
Tiwari, A., Kasaian, M., Heatherington, A. C., Jones, H. M., and Hua, F. (2016). A Mechanistic PK/PD Model for Two anti-IL13 Antibodies Explains the Difference in Total IL-13 Accumulation Observed in Clinical Studies. MAbs 8 (5), 983–990. doi:10.1080/19420862.2016.1172151
Tiwari, A., Luo, H., Chen, X., Singh, P., Bhattacharya, I., Jasper, P., et al. (2016). Assessing the Impact of Tissue Target Concentration Data on Uncertainty in In Vivo Target Coverage Predictions. CPT Pharmacometrics Syst. Pharmacol. 5 (10), 565–574. doi:10.1002/psp4.12126
Ultsch, M., Bevers, J., Nakamura, G., Vandlen, R., Kelley, R. F., Wu, L. C., et al. (2013). Structural Basis of Signaling Blockade by Anti-IL-13 Antibody Lebrikizumab. J. Mol. Biol. 425 (8), 1330–1339. doi:10.1016/j.jmb.2013.01.024
van der Graaf, P. H., and Benson, N. (2011). Systems Pharmacology: Bridging Systems Biology and Pharmacokinetics-Pharmacodynamics (PKPD) in Drug Discovery and Development. Pharm. Res. 28 (7), 1460–1464. doi:10.1007/s11095-011-0467-9
van der Graaf, P. H. (2012). CPT: Pharmacometrics and Systems Pharmacology. CPT Pharmacometrics Syst. Pharmacol. 1 (9), e8–e. doi:10.1038/psp.2012.8
van Hartingsveldt, B., Nnane, I. P., Bouman-Thio, E., Loza, M. J., Piantone, A., Davis, H. M., et al. (2013). Safety, Tolerability and Pharmacokinetics of a Human Anti-interleukin-13 Monoclonal Antibody (CNTO 5825) in an Ascending Single-Dose First-In-Human Study. Br. J. Clin. Pharmacol. 75 (5), 1289–1298. doi:10.1111/j.1365-2125.2012.04477.x
Vugmeyster, Y., DeFranco, D., Szklut, P., Wang, Q., and Xu, X. (2010). Biodistribution of [125I]-Labeled Therapeutic Proteins: Application in Protein Drug Development beyond Oncology. J. Pharm. Sci. 99 (2), 1028–1045. doi:10.1002/jps.21855
Vugmeyster, Y., Szklut, P., Tchistiakova, L., Abraham, W., Kasaian, M., and Xu, X. (2008). Preclinical Pharmacokinetics, Interspecies Scaling, and Tissue Distribution of Humanized Monoclonal anti-IL-13 Antibodies with Different IL-13 Neutralization Mechanisms. Int. Immunopharmacol 8 (3), 477–483. doi:10.1016/j.intimp.2007.12.004
Wang, X., Lopategi, A., Ge, X., Lu, Y., Kitamura, N., Urtasun, R., et al. (2014). Osteopontin Induces Ductular Reaction Contributing to Liver Fibrosis. Gut 63 (11), 1805–1818. doi:10.1136/gutjnl-2013-306373
Wani, T. A., Zargar, S., Wakil, S. M., and Darwish, I. A. (2016). New Analytical Application of Antibody-Based Biosensor in Estimation of Thyroid-Stimulating Hormone in Serum. Bioanalysis 8 (7), 625–632. doi:10.4155/bio-2015-0034
Zhang, T. T., Ma, J., Durbin, K. R., Montavon, T., Lacy, S. E., Jenkins, G. J., et al. (2019). Determination of IL-23 Pharmacokinetics by Highly Sensitive Accelerator Mass Spectrometry and Subsequent Modeling to Project IL-23 Suppression in Psoriasis Patients Treated with Anti-IL-23 Antibodies. AAPS J. 21 (5), 82. doi:10.1208/s12248-019-0352-8
Zhao, P., Rowland, M., and Huang, S. M. (2012). Best Practice in the Use of Physiologically Based Pharmacokinetic Modeling and Simulation to Address Clinical Pharmacology Regulatory Questions. Clin. Pharmacol. Ther. 92 (1), 17–20. doi:10.1038/clpt.2012.68
Zhao, P., Zhang, L., Grillo, J. A., Liu, Q., Bullock, J. M., Moon, Y. J., et al. (2011). Applications of Physiologically Based Pharmacokinetic (PBPK) Modeling and Simulation during Regulatory Review. Clin. Pharmacol. Ther. 89 (2), 259–267. doi:10.1038/clpt.2010.298
Keywords: site of action, PKPD, QSP, modeling and simulation, LC-MS
Citation: Kapitanov GI, Chabot JR, Narula J, Roy M, Neubert H, Palandra J, Farrokhi V, Johnson JS, Webster R and Jones HM (2021) A Mechanistic Site-Of-Action Model: A Tool for Informing Right Target, Right Compound, And Right Dose for Therapeutic Antagonistic Antibody Programs. Front. Bioinform. 1:731340. doi: 10.3389/fbinf.2021.731340
Received: 02 July 2021; Accepted: 23 August 2021;
Published: 03 September 2021.
Edited by:
Morgan Craig, University of Montreal, CanadaReviewed by:
Yanguang Cao, University of North Carolina at Chapel Hill, United StatesPatrick Glassman, University of Pennsylvania, United States
Copyright © 2021 Kapitanov, Chabot, Narula, Roy, Neubert, Palandra, Farrokhi, Johnson, Webster and Jones. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Georgi I. Kapitanov, Z2VvcmdpLmthcGl0YW5vdkBwZml6ZXIuY29t
 Georgi I. Kapitanov
Georgi I. Kapitanov Jeffrey R. Chabot1
Jeffrey R. Chabot1 Mahua Roy
Mahua Roy Hendrik Neubert
Hendrik Neubert Vahid Farrokhi
Vahid Farrokhi