- 1The Division of Computer Science, Texas Woman’s University, Denton, TX, United States
- 2The Department of Computer Science, The University of Texas Rio Grande Valley, Edinburg, TX, United States
Introduction: Accurate prediction of protein-protein interactions (PPIs) is crucial for understanding cellular functions and advancing the development of drugs. While existing in-silico methods leverage direct sequence embeddings from Protein Language Models (PLMs) or apply Graph Neural Networks (GNNs) to 3D protein structures, the main focus of this study is to investigate less computationally intensive alternatives. This work introduces a novel framework for the downstream task of PPI prediction via link prediction.
Methods: We introduce a two-stage graph representation learning framework, ProtGram-DirectGCN. First, we developed ProtGram, a novel approach that models a protein's primary structure as a hierarchy of globally inferred n-gram graphs. In these graphs, residue transition probabilities, aggregated from a large sequence corpus, define the edge weights of a directed graph of paired residues. Second, we propose a custom directed graph convolutional neural network, DirectGCN, which features a unique convolutional layer that processes information through separate path-specific (incoming, outgoing, undirected) and shared transformations, combined via a learnable gating mechanism. DirectGCN is applied to the ProtGram graphs to learn residue-level embeddings, which are then pooled via an attention mechanism to generate protein-level embeddings for the prediction task.
Results: The efficacy of the DirectGCN model was first established on standard node classification benchmarks, where its performance is comparable to that of established methods on general datasets, while demonstrating specialization for complex, directed, and dense heterophilic graph structures. When applied to PPI prediction, the full ProtGram-DirectGCN framework achieves robust predictive power despite being trained on limited data.
Discussion: Our results suggest that a globally inferred, directed graph-based representation of sequence transitions offers a potent and computationally distinct alternative to resource-intensive PLMs for the task of PPI prediction. Future work will involve testing ProtGram-DirectGCN on a wider range of bioinformatics tasks.
1 Introduction
Protein-protein interactions (PPIs) form a network of physical contacts and functional associations mediated by molecular bonds. These interactions are the basis for cellular processes and are collectively referred to as the cellular interactome. Therefore, understanding the underlying mechanisms by predicting valid interactions between proteins is the foundation for many in-vitro biomedical endeavors, such as understanding disease mechanisms, drug development and repurposing, and the potential development of futuristic biotechnologies (Vidal et al., 2011; Scott et al., 2016). In-vitro protein interaction prediction methods, including Yeast-2-Hybrid screening, co-immunoprecipitation followed by mass spectrometry and affinity purification, have been used to infer empirical evidence of protein association. However, these methods are usually prone to a high rate of false positives and false negatives (Rao et al., 2014).
Computational methods, also known as in-silico and data-driven approaches, have been adopted in life sciences research since at least the seventies (Wodak and Janin, 1978). In-silico methods help alleviate several of the significant challenges of the in-vitro methods mentioned above. The initial stages of drug discovery are heavily based on identifying and confirming valid drug targets, often proteins. This activity is typically protracted, resource-intensive, and time-consuming. Subsequent in-vitro screening of drug candidates against potential targets cannot be done efficiently until a validated list of candidate proteins is established. Delays in this upstream target identification task lead to delays in the beginning of extensive in-vitro studies (Scannell et al., 2012). Therefore, in-silico methods, mainly relying on the predictive power of complex machine learning models, are not meant to replace in-vitro methods. Instead, they are integrated into the workflow to create a potential pool of valid interactions waiting for wet lab filtering and confirmation, eventually and evidently speeding up the process (Vidal et al., 2011).
Recent advancements in machine learning, neural networks, and deep learning approaches have enabled the automation of feature extraction. In addition to embeddings of biological entities into a real vector space, where meaningful algebraic operations can be performed on the learned vectors representing individual residues or proteins. The advent of the transformer architecture (Vaswani et al., 2017) has surpassed sequence-to-sequence models, particularly recurrent neural networks (RNNs) like the Long Short-Term Memory (LSTM) model (Hochreiter and Schmidhuber, 1997). These models have been relied on in protein sequence modeling and representation learning (Cho et al., 2014). The input protein sequence is usually tokenized at different levels or granularity, such as representing single amino acids as words or a group of residues as k-mers (Guo et al., 2008). These models, although efficient in processing short-term dependencies, have demonstrated a limited understanding of context incorporation in language modeling. Though, that contextual understanding has had glimpses in non-recurrent language-based neural networks like Word2Vec (Mikolov et al., 2013), where the goal becomes incorporating context via a binary negative loss function that classifies in and out of context window words to the current word. The introduction of the attention mechanism and the transformer architecture, combining both sequence-to-sequence modeling and contextual encoding (Vaswani et al., 2017), has increased the predictive power of language models by orders of magnitude on multiple tasks. Subsequently that has contributed to the proliferation of different designs and architectures like BERT (encoder only) (Devlin et al., 2019), T5 (encoder-decoder) (Raffel et al., 2023), and GPT (decoder only) (Brown et al., 2020). That, however, comes at a significant computational and environmental cost, due to the increased reliance on training data for these models, as well as the near-linear correlation between a model’s predictive power and the number of parameters present in the network.
Transformer-based architectures have had great success in adoption in domain-specific tasks via fine-tuning; for example, BioBERT (Lee et al., 2020) fine-tunes BERT over the corpus of PubMed metadata and available full-text on multiple tasks. One of the tasks is biological named entity recognition and extraction for names of diseases, genes, proteins, species, and drugs. The protein embeddings extracted from BioBERT can provide encoded contextual meaning in downstream tasks, such as protein interaction prediction or gene identification. In drug development, particularly in protein-protein interaction prediction (PPI), advanced models have been applied at multiple levels. For example, in reinforcement learning, a prominent recent advancement is Google’s AlphaFold (Jumper et al., 2021). This complex model aims to predict protein 3D structures from primary sequences, a central challenge in biomedical informatics known as protein folding prediction. Predicted 3D structures are often utilized in frameworks that aim to predict protein interactions from all levels of protein structure representation via combining features from the primary, secondary, and tertiary structures in addition to topological features from protein-protein interaction networks (Zhou et al., 2022; Jha et al., 2022). However, the most common approaches in in-silico PPI prediction are primary structure sequence-based methods, where the sequential one-dimensional nature of individual amino acids and residue-level representations lend themselves to modern language modeling. The core lies in the context encoded in the transition probabilities between residues due to the relative simplicity of the input data.
Protein sequences can be conceptualized as a sequence of amino acids (or peptides), analogous to sentences being sequences of words. This analogy allows for the application of large language modeling techniques. For instance, ProtBert (Elnaggar et al., 2022) applies the BERT architecture (Devlin et al., 2019) to primary protein structures, yielding accurate models on downstream tasks that generate protein-level vector representations at the residue and protein levels. Moreover, work like (Sledzieski et al., 2021) D-SCRIPT relies on a PLMs to predict spatial protein interaction contact maps. The model was evaluated on per organism protein-based PPI prediction task yielding positive results. Building on these results, the model provides functionally informative predictions and yields more coherent gene clusters. The predicted contact maps significantly overlap with the true 3D structure contacts, despite being trained solely on sequence data. The common aspect of all of these models is that; first the output embeddings is typically pooled to produce per-protein embeddings that capture sequential features enabling higher predictive power in downstream tasks (Elnaggar et al., 2022). Second, primary structure sequences themselves appear to encode more than the obvious, even with relatively limited data availability.
However, even the most advanced modern approaches have had several problems.
• The limited context window size must be larger to capture longer-range dependencies beyond the immediate neighborhood which significantly increases their need for labeled training data.
• Increasing the number of layers, blocks and attention heads can lead to a significant (potentially exponential) increase in the number of parameters, demanding more computational resources.
• The models are generally highly sensitive to training data quality, diversity, volume and availability.
Here, we propose a novel approach to modeling protein primary structure sequences that partially overcomes some of these limitations. We cast the sequences as random walks sampled according to transition probabilities within a directed n-gram graph
Our approach overcomes the need for a context window (Elnaggar et al., 2022) where the computational limitations that contribute to limited context windows are only applied to a limited dense graph of n-grams. The first-order neighborhood of a spectral graph convolution operator approximation (Kipf and Welling, 2017) has a limited effect on the output compared to the sizes of a well-capturing context window in a large language model. In addition this approach in modeling the sequences reduces the number of parameters significantly as the directed graph convolution network operates on a limited unique vocab nodes. In addition to the ability to learn complex encoding from limited training data as the n-gram graph with different levels can act as a data augmentation mechanism if full sequence databases are not available. In addition this bottom-up approach ensures that the limitations are only applied to the lowest level of representation where reducing noise at that level reverberates at higher n-gram level, in addition to overcoming the need for intensive computational power.
From a biological standpoint the specific transition sequence of amino acids via their side chains or R groups determines how a polypeptide chain will fold. Hydrogen bonds, ionic bonds, and hydrophobic interactions generally drive the folding. And in the process, the local secondary structure, including alpha and beta helices, eventually creates binding sites essential for forming subunit proteins or interacting with other molecules. Hence, our intuition is that the primary structure sequences and the transition frequencies between residues holds enough signal power that can inform downstream not only the 3D tertiary structure of the protein but also tell the possible interactions with other proteins or the quaternary structure (Dill and MacCallum, 2012; Perkins et al., 2010; Anfinsen, 1973).
Accordingly we hypothesize that the global directed dense graph of n-grams
Here we are trying to answer the following research questions:
• Does learning representations of proteins from the embedded, inferred directed graph of n-grams
• Is our
• What is the predictive power of our hierarchical feature based n-gram representation
• Is the performance of the
2 Methods
This section details the design, development, and evaluation of our model
2.1
Our approach treats individual proteins, identified via the comprehensive database UniProt (Consortium, 2023), as distinct entities. These proteins form the nodes
The conditional probabilities are estimated from a large corpus based on the frequency of k-gram occurrences:
where
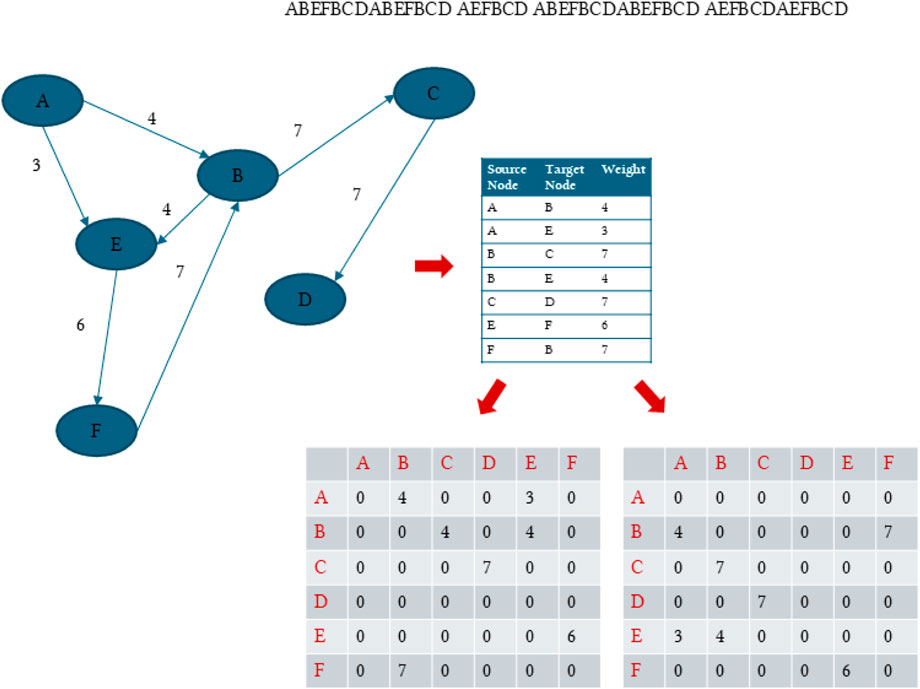
Figure 1. An example of dummy sequences separated by a space indicating multiple proteins. The figure shows how the transitions between the residues or characters are conceptualized as a directed, weighted, dense graph where the weights are the transition frequencies calculated as counts or probabilities. In addition, the figure shows how we split the directed adjacency into an
Our custom Directed Graph Convolutional Network
Standard GCNs are primarily for undirected graphs assuming symmetric adjacencies. However multiple works have explored applying GCNs to directed graphs for a complete review of directed GCN methods please see the Supplementary Material. Our
2.2
2.2.1 Propagation matrix formulation
The graph structure is initially captured by a raw weighted adjacency matrix
The final propagation matrix
where the square operations are element-wise and
2.2.2 Propagation layer
Given node features
Similarly, for the outgoing path:
And for the undirected path, using a standard symmetrically normalized adjacency matrix
In addition we model the idea of positional encoding which ensures that the model has some notion of time and sequence. We do that by adding a non transformed learnable embeddings layer that gives each node (n-gram) its positional identity:
where
where
where
2.2.3 Model architecture
The full
• Input Layer: The initial node features for the n-grams,
• Hidden Layers: The model stacks
• Output Layer: The output of the final hidden layer,
A
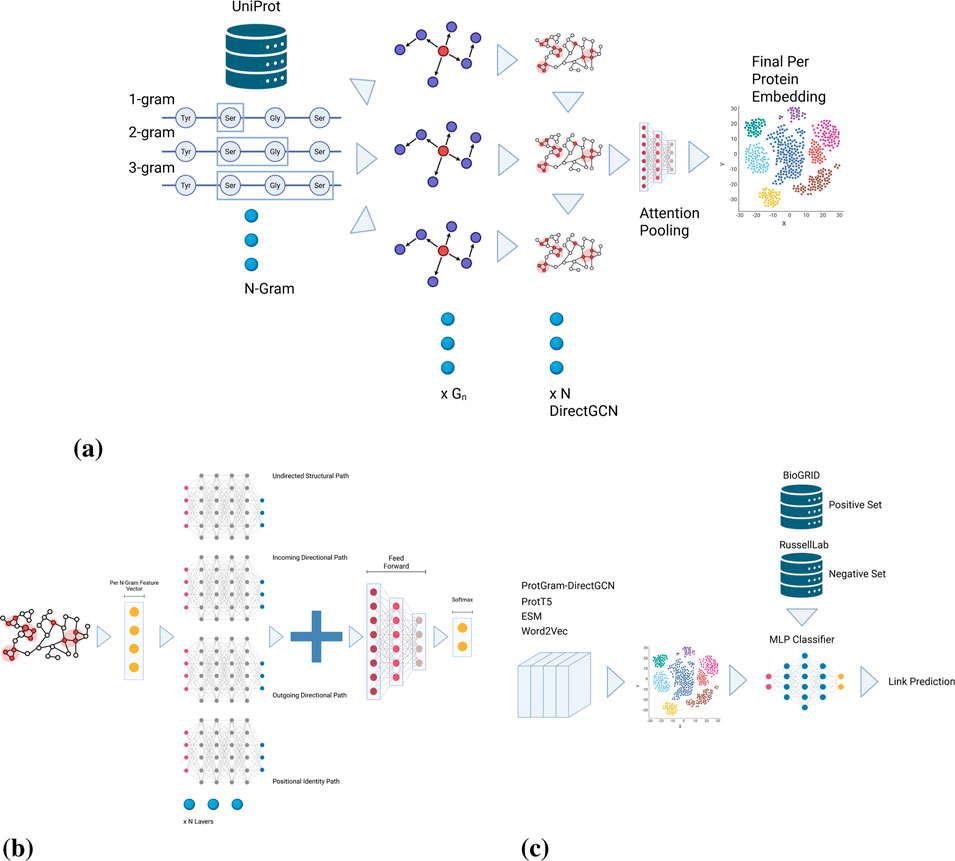
Figure 2.
3 Experiments
This section outlines the experimental design employed to evaluate the proposed
3.1 Materials
Our approach in this investigation is to minimize any cleaning or modification of publicly available datasets before running our main computational pipeline. UniProt-SPROT (current state) and UniRef50 (future work) are our main sources of protein sequences. All sequences are cleaned only after an official, validated, automated download. In this context, “prior processing” refers specifically to any data cleaning or manipulation done before the computational pipeline starts. In contrast, “preprocessing” refers to steps such as tokenization and the removal of special characters from sequences, which occur immediately before the main pipeline and as part of it. Sequence cleaning is dynamic; when a pipeline component requests sequence data, the raw FASTA file is read and any character not representing one of the 20 standard amino acids (A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y), in addition to an added separator token between individual sequences, is filtered out. This standardizes the alphabet for all downstream models. Sequence lengths are capped at 10,000 characters to fit in memory and on the GPU during training. Tokenization, or preprocessing, occurs on the fly for all models tested, including our own. For PPI ground truth we apply automated preprocessing to positive and negative ground truth links. Positive links are automatically downloaded from BioGRID (Oughtred et al., 2021), and negative links are obtained from Trabuco et al. (2012). Identifiers from these raw datasets are converted to canonical UniProtKB IDs using a mapping database built directly from the official UniProt ID mapping database. The standardized interaction pairs are saved in Parquet format and serve as the definitive ground truth for all evaluation tasks. Further preparation details are in the Supplementary Material.
3.1.1 Construction of hierarchical
The primary dataset for our methodology is a hierarchy of global n-gram graphs,
• Corpus: We used the curated and reviewed UniProt Swiss-Prot dataset, containing 573,230 protein sequences. Larger and more diverse sequence files liek UniRef50 and UniRef100 and PDB are in our plans to train our model on.
• Graph Construction: For each n-gram level from
3.2 Intrinsic evaluation of
To establish the general graph representation learning capabilities of the
• Datasets: We selected standard GNN benchmark datasets for the intrinsic evaluation: Karate Club, Cora, CiteSeer, PubMed, Cornell, Texas, and Wisconsin. All of the datasets where downloaded from the official PyTorch Geometric repository. For each dataset, we evaluated performance on their original edges (potentially directed). See Table 2.
• Task & Setup: The task was semi-supervised node classification relying on a fixed 10%/10%/80% train/validation/test split. All models were trained for 300 epochs using the Adam optimizer with a fixed 2 layer and layer norm architecture.
• Baseline Models: Graph Convolutional Network (GCN) (Kipf and Welling, 2017), Graph Attention Network (GAT) (Veličković et al., 2018), GraphSAGE (Hamilton et al., 2018), Graph Isomorphism Network (GIN) (Xu et al., 2019), and DirGNN (Rossi et al., 2023).
• Results: The goal of this evaluation was to validate
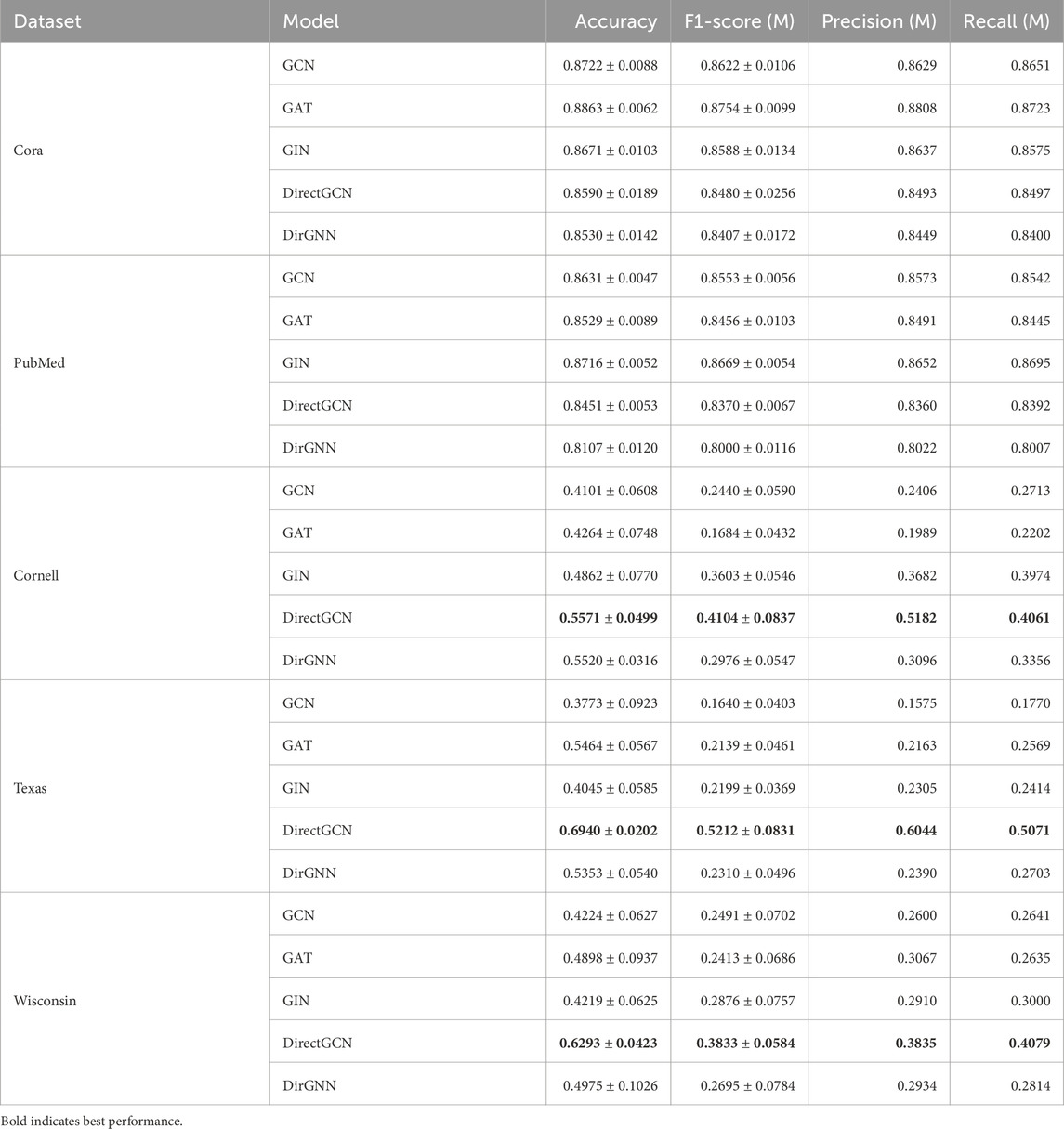
Table 3. Model performance on directed datasets. Accuracy and F1-Score are reported as
3.3 Learning N-gram embeddings from
The constructed
• Next-Node Prediction as a Self-Supervised Task: For each n-gram node
• Hierarchical Training: The training process is hierarchical. For the base level (
• Implementation Details: The model for each level
3.4 Protein-protein interaction (PPI) prediction as link prediction
• Protein-Level Embeddings Generation via Attention Pooling: A single, fixed-size feature vector is generated for each protein in the UniProt dataset. This is achieved by taking the sequence of each protein, identifying all of its constituent n-grams, retrieving their learned embeddings from the final
In this step, we use self-attention to create a single embedding vector for a protein from its n-gram embeddings (also called residue embeddings). Each n-gram determines its importance within context and receives a unique attention weight, so n-grams matching the protein’s syntax have greater influence. This lets the model focus on the most relevant sequence parts. Attention pooling is particularly suited for protein sequences, as it highlights structural motifs that affect binding sites, discussed further in Section 4.2.
We compute attention scores as follows:
• Let the set of n-gram embedding vectors for a protein be
• First, we calculate the average of all n-gram embeddings for the protein. This vector, called the context vector, represents the typical pattern or summary of the entire protein sequence. The context vector guides the model in determining which n-grams are most relevant in the protein’s context. The context vector
• Then we score each n-gram vector by its dot product with the context vector
• The final weights
• We next compute the weighted average of the n-gram embeddings using the attention weights. This produces the final, attention-pooled per-protein embedding vector. The final per-protein embeddings is the weighted sum of the n-gram vectors, each scaled by its attention weight:
• This final vector,
• PPI Datasets: A benchmark PPI dataset is compiled automatically using known positive interactions from the BioGRID database (Oughtred et al., 2021) and high-quality negative interactions (non-interacting pairs) from the experimentally-derived Russell Lab datasets (Trabuco et al., 2012). This ensures a robust and biologically relevant evaluation set.
• Link Prediction Model: A standard Multi-Layer Perceptron (MLP) was used as the binary classifier. For a pair of proteins
• Evaluation and Baselines: The model’s performance is rigorously assessed using a 5-fold stratified cross-validation scheme to ensure that results are robust and not dependent on a single random data split. We measure performance using a suite of standard binary classification and ranking metrics, including Area Under the ROC Curve (AUC), F1-Score, Precision, Recall. To contextualize our results, we compare the performance of our
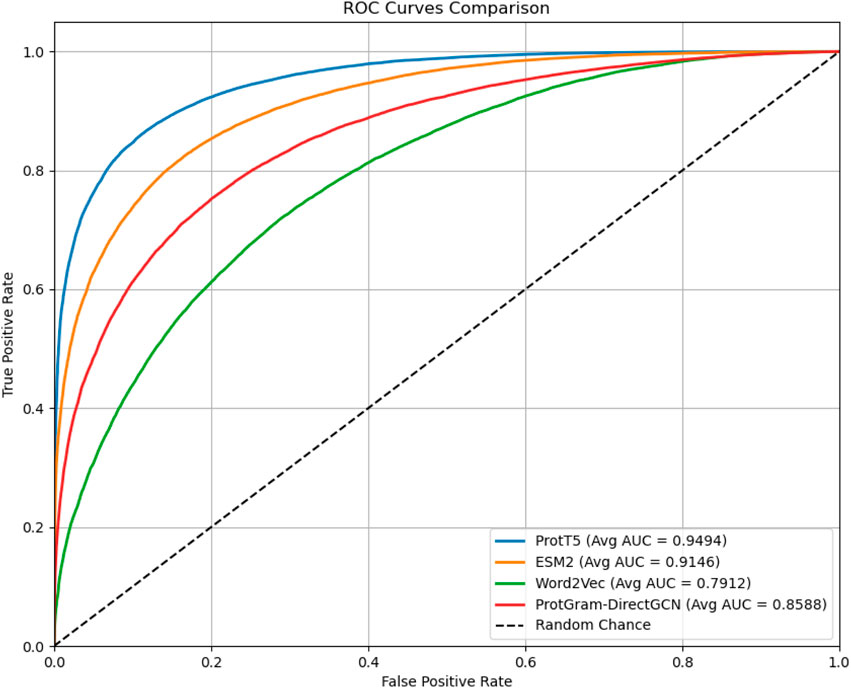
Figure 3. The plot displays the Receiver Operating Characteristic (ROC) curves comparing the performance of protein embeddings generated by the proposed
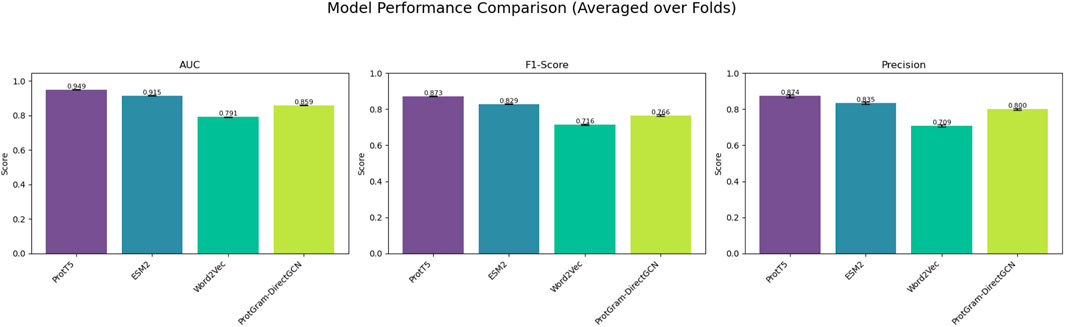
Figure 4. The figure illustrates the models’ performance metrics reflecting the results in Table 4.
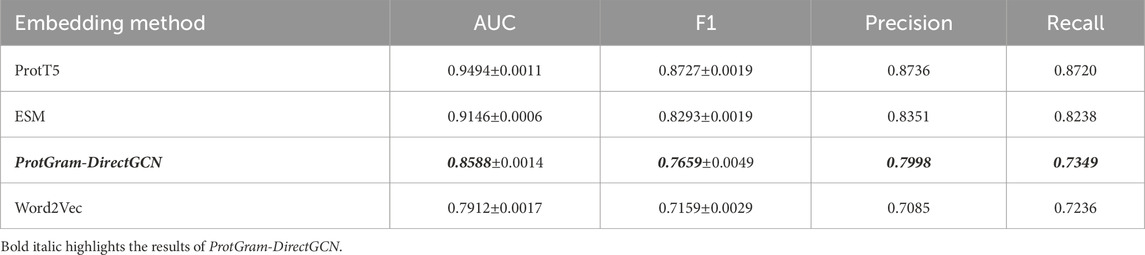
Table 4. Performance comparison of protein embeddings on PPI link prediction (averaged over 5 folds).
3.5 Ablation study of
Here we are going to understand the properties of the n-gram graph and its generated residue representation by training the model on a subset of the available sequence data on different model configuration. This step is crucial as the smallest pertubation in the data or the model affect the final per protein embeddings due to the hierarchical nature of the model.
The
• No Gating: The lack of gating has shown a consistent reduction in predictive power, with AUC scores closer to
• Scalar Gating: With scalar gating, AUC modestly increases with n. Notably,
• Vector Gating: For vector gating, the AUC increases from n1 (0.6376) to n2 (0.6616), then drops at n3 (0.6367). F1 shows a similar trend. Increasing n from 1 to 2 brings improvement, but going to 3 does not consistently help. This underlines diminishing returns for higher-order n-grams in low-data settings. The transition from 1-g to 2-g often enhances both gating types. Moving from 2-g to 3-g, however, can result in a decrease in performance. The best n-gram level varies by task or dataset, and higher n may require adjustments to the model or training.
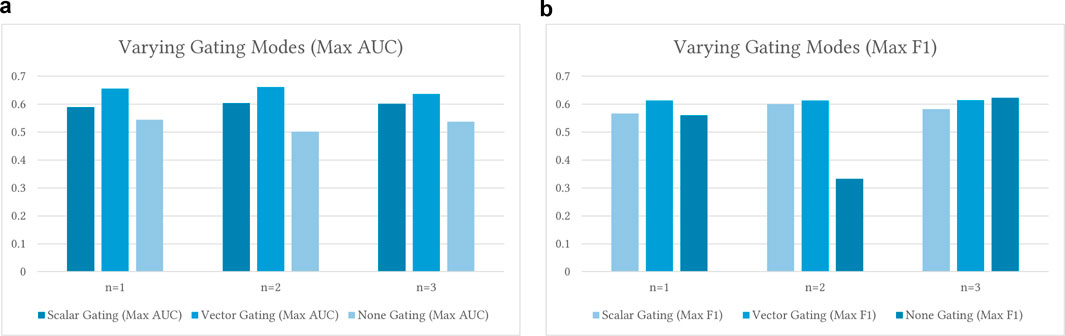
Figure 5. Ablation results for varying gating modes versus different n-gram levels when training
Overall, vector gating consistently outperforms scalar gating across all n-gram levels and test settings. Here, ”vector gating” refers to the use of node-specific, learnable gating vectors (the coefficients
Altogether, these findings demonstrate that
4 Discussion
This study introduced and evaluated a novel
4.1 Summary of findings
Our experimental evaluations spanned several stages: validating the core
• Evaluation of
• Evaluation of
• Evaluation of
• Comparison with ProtT5, ESM and Word2Vec Embeddings: The comparison with ProtT5 and ESM embeddings which are generted by the very powerful high capacity T5 encoder-decoder transformer model that is trained on the more comprehensive UniRef50 dataset is not meant as a head-to-head comparison. But rather as a demonstration that hefty transformer architectures for specialized tasks like PPI prediction can be contended with models that capture the underlying dynamics without having to rely on long context windows and demanding computational resources needs. The long range dependencies captured by ProtT5 and ESM are the reason why it is an efficient feature extractor for proteins. Yet those same dynamics can be captured from a lower level faint signal such as the simple transition directed graph of amino acids without long context windows. ProtT5, ESM and
4.2 Biological significance
PPI prediction is a bedrock in drug development, understanding drug efficacy, and many other crucial biomedical fields. Figure 6 displays the computed attention maps at
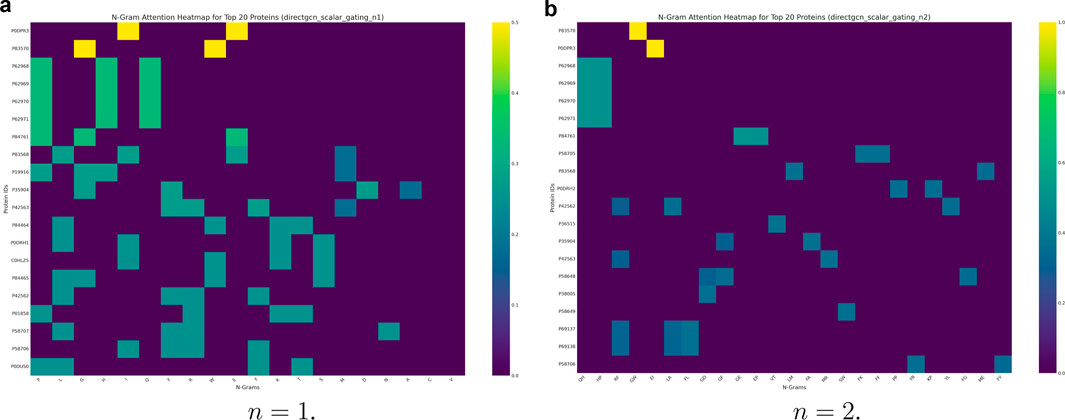
Figure 6. The attention pooling results described in Section 3.4 highlight attention scores after pooling residue-level (n-gram) embeddings to protein-level embeddings. These heatmaps are generated by identifying n-gram attention weights for proteins with the highest overall variance in attention. The X-axis of such a heatmap represents various n-grams, and the Y-axis represents specific protein IDs, with the color intensity in each cell indicating the attention score assigned to a particular n-gram within a given protein. (a)
The
The
By identifying these lead residues and sequence motifs that contribute significantly to the model’s predictions, the attention heatmaps can guide hypothesis generation for experimental testing. They can also accelerate the functional annotation of uncharacterized proteins (which we removed in our data preprocessing). Biologists could use these highlighted n-grams to design targeted experiments. For example, they might conduct site-directed mutagenesis to validate their functional role in protein interactions.
One motivation behind
4.3 Limitations
While this study presents promising results, several limitations should be acknowledged:
• Due to computational constraints,
• Initial features for 1-g nodes in
• Simple attention pooling was used to generate protein-level embeddings. More advanced pooling mechanisms were not exhaustively explored and might yield improved representations.
• The evaluation was centered on PPI link prediction, hence the utility of embeddings for additional tasks remains to be explored.
• While the design of
• The PPI link prediction task relies on the Russell Lab negative dataset (Trabuco et al., 2012), which, while experimentally grounded, has inherent assumptions and potential biases based on Yeast two-Hybrid limitations. The choice of negative samples can significantly impact the reported performance of PPI prediction.
• The current framework primarily relies on sequence-derived information for constructing
4.4 Future work
The findings and limitations of this study open several avenues for future research. First, future iterations will explore constructing
Finally, its worth mentioning that a notable class of modern PPI prediction methods leverages 3D structural information, either from experimental sources or high-fidelity predictions from models like AlphaFold2 (Jumper et al., 2021). These geometric deep learning approaches, such as GearNet and GVP-GNN, have demonstrated state-of-the-art performance by directly encoding the physical and chemical properties of protein surfaces. While these methods are powerful, their applicability is contingent on the availability of accurate structural data. Our work, with
5 Conclusion
This paper introduces a novel approach for protein representation learning, which has been shown to enable in-silico PPI prediction via a simpler yet expressive learning model. The method focuses on a novel data model that infers hierarchical global n-gram graphs from protein sequences namely
Data availability statement
The datasets and materials used in this study are available publicly at https://www.russelllab.org/negatives/ and https://downloads.thebiogrid.org/BioGRID. In addition codes for this study can be found at https://github.com/iebeid/ProtGram-DirectGCN/tree/v2.
Author contributions
IE: Conceptualization, Methodology, Project administration, Software, Writing – original draft, Writing – review and editing. HT: Methodology, Software, Validation, Writing – original draft, Writing – review and editing. PG: Data curation, Visualization, Writing – original draft, Writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that Generative AI was used in the creation of this manuscript. Code debugging, grammar checks for manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbinf.2025.1651623/full#supplementary-material
References
Anfinsen, C. B. (1973). Principles that govern the folding of protein chains. Science 181, 223–230. doi:10.1126/science.181.4096.223
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefebvre, E. (2008). Fast unfolding of communities in large networks. J. Stat. Mech. 2008, P10008. doi:10.1088/1742-5468/2008/10/p10008
Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., et al. (2020). Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 33, 1901. doi:10.48550/arXiv.2005.14165
Chiang, W.-L., Liu, X., Si, S., Li, Y., Bengio, S., and Hsieh, C. J. (2019). “Cluster-GCN: an efficient algorithm for training deep and large graph convolutional networks,” Proc. 25th ACM SIGKDD Int. Conf. Knowl. Discov. & Data Min. 19. New York, NY, USA: Association for Computing Machinery, 257–266. doi:10.1145/3292500.3330925
Cho, K., van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). “Learning phrase representations using RNN encoder–decoder for statistical machine translation,” in Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP). Editors A. Moschitti, B. Pang, and W. Daelemans (Doha, Qatar: Association for Computational Linguistics), 1724–1734. doi:10.3115/v1/D14-1179
Consortium, T. U., Martin, M. J., Orchard, S., Magrane, M., Ahmad, S., Alpi, E., et al. (2023). UniProt: the universal protein knowledgebase in 2023. Nucleic Acids Res. 51, D523–d531. doi:10.1093/nar/gkac1052
Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2019). “BERT: pre-Training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 conference of the north American chapter of the association for computational linguistics: human language technologies, volume 1 (long and short papers) (Minneapolis, Minnesota: Association for Computational Linguistics), 4171–4186. doi:10.18653/v1/N19-1423
Dill, K. A., and MacCallum, J. L. (2012). The protein-folding problem, 50 years on. science 338, 1042–1046. doi:10.1126/science.1219021
Elnaggar, A., Heinzinger, M., Dallago, C., Rehawi, G., Wang, Y., Jones, L., et al. (2022). ProtTrans: toward understanding the language of life through self-supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 44, 7112–7127. doi:10.1109/tpami.2021.3095381
Guo, Y., Yu, L., Wen, Z., and Li, M. (2008). Using support vector machine combined with auto covariance to predict protein-protein interactions from protein2 sequences. Ex. Class. ML (SVM) feature Discuss. 3, e47. doi:10.1093/nar/gkn159
Hamilton, W. L., Ying, R., and Leskovec, J. (2018). Inductive representation learning on large graphs. doi:10.48550/arXiv.1706.02216
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Jeh, G., and Widom, J. (2002). “SimRank: a measure of structural-context similarity,” in Proceedings of the eighth ACM SIGKDD international conference on knowledge discovery and data mining (New York, NY, USA: Association for Computing Machinery), 538–543. doi:10.1145/775047.775126
Jha, K., Saha, S., and Singh, H. (2022). Prediction of protein–protein interaction using graph neural networks. Sci. Rep. 12, 8360. doi:10.1038/s41598-022-12201-9
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589. doi:10.1038/s41586-021-03819-2
Kipf, T. N., and Welling, M. (2017). Semi-supervised classification with graph convolutional networks. arXiv:1609.02907 [cs.LG]. doi:10.48550/arXiv.1609.02907
Lee, J., Yoon, W., Kim, S., Kim, D., Kim, S., So, C. H., et al. (2020). BioBERT: a pre-trained biomedical language representation model for biomedical text mining. Bioinformatics 36, 1234–1240. doi:10.1093/bioinformatics/btz682
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. (2013). “Distributed representations of words and phrases and their compositionality,” in Advances in neural information processing systems, 26. Red Hook, NY, United States: Curran Associates, Inc.
Oughtred, R., Rust, J., Chang, C., Breitkreutz, B., Stark, C., Willems, A., et al. (2021). The BioGRID database: a comprehensive biomedical resource of curated protein, genetic, and chemical interactions. Protein Sci. 30, 187–200. doi:10.1002/pro.3978
Perkins, J. R., Diboun, I., Dessailly, B. H., Lees, J. G., and Orengo, C. (2010). Transient protein-protein interactions: structural, functional, and network properties. Structure 18, 1233–1243. doi:10.1016/j.str.2010.08.007
Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., et al. (2023). Exploring the limits of transfer learning with a unified text-to-text transformer. doi:10.48550/arXiv.1910.10683
Rao, V. S., Srinivas, K., Sujini, G. N., and Kumar, G. N. S. (2014). Protein-protein interaction detection: methods and analysis. Int. J. Proteomics 2014, 1–12. doi:10.1155/2014/147648
Rao, R., Meier, J., Sercu, T., Ovchinnikov, S., and Kondor, R. (2020). “Transformer protein language models are unsupervised structure learners,” in International conference on learning representations.
Rossi, E., Charpentier, B., Di Giovanni, F., Olsen, J. H. G., Stenetorp, P., and Riedel, S. (2023). Edge directionality improves learning on heterophilic graphs
Scannell, J. W., Blanckley, A., Boldon, H., and Warrington, B. (2012). Diagnosing the decline in pharmaceutical R&D efficiency. Nat. Rev. Drug Discov. 11, 191–200. doi:10.1038/nrd3681
Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M., and Monfardini, G. (2009). The graph neural network model. IEEE Trans. Neural Netw. 20, 61–80. doi:10.1109/tnn.2008.2005605
Scott, D. E., Bayly, A. R., Abell, C., and Skidmore, J. (2016). Small molecules, big targets: drug discovery faces the protein–protein interaction challenge. Nat. Rev. Drug Discov. 15, 533–550. doi:10.1038/nrd.2016.29
Sledzieski, S., Singh, R., Cowen, L., and Berger, B. (2021). D-SCRIPT translates genome to phenome with sequence-based, structure-aware, genome-scale predictions of protein-protein interactions. cels 12, 969–982.e6. doi:10.1016/j.cels.2021.08.010
Trabuco, L. G., Betts, M. J., and Russell, R. B. (2012). Negative protein–protein interaction datasets derived from large-scale two-hybrid experiments. Methods 58, 343–348. doi:10.1016/j.ymeth.2012.07.028
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. arXiv:1706.03762. doi:10.48550/arXiv.1706.03762
Veličković, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., and Bengio, Y. (2018). Graph attention networks. arXiv:1710.10903 [stat.ML]. doi:10.48550/arXiv.1710.10903
Vidal, M., Cusick, M. E., and Barabási, A.-L. (2011). Interactome networks and human disease. Cell 144, 986–998. doi:10.1016/j.cell.2011.02.016
Wodak, S. J., and Janin, J. (1978). Computer analysis of protein-protein interaction. J. Mol. Biol. 124, 323–342. doi:10.1016/0022-2836(78)90302-9
Xu, K., Hu, W., Leskovec, J., and Jegelka, S. (2019). How powerful are graph neural networks? arXiv:1810.00826. doi:10.48550/arXiv.1810.00826
Keywords: uniprot, biogrid, russellab, graph theory, graph representation learning, graph neural networks, graph convolution networks, link prediction
Citation: Ebeid IA, Tang H and Gu P (2025) Inferred global dense residue transition graphs from primary structure sequences enable protein interaction prediction via directed graph convolutional neural networks. Front. Bioinform. 5:1651623. doi: 10.3389/fbinf.2025.1651623
Received: 22 June 2025; Accepted: 22 September 2025;
Published: 22 October 2025.
Edited by:
Adam Yongxin Ye, Boston Children’s Hospital and Harvard Medical School, United StatesReviewed by:
Yao He, Broad Institute, United StatesWanying Dou, Northwestern University, United States
Copyright © 2025 Ebeid, Tang and Gu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Islam Akef Ebeid, aWViZWlkQHR3dS5lZHU=
 Islam Akef Ebeid
Islam Akef Ebeid Haoteng Tang
Haoteng Tang Pengfei Gu2
Pengfei Gu2