Material models and properties in the finite element analysis of knee ligaments: a literature review

Knee ligaments are elastic bands of soft tissue with a complex microstructure and biomechanics, which are critical to determine the kinematics as well as the stress bearing behavior of the knee joint. Their correct implementation in terms of material models and properties is therefore necessary in the development of finite element models of the knee, which has been performed for decades for the investigation of both its basic biomechanics and the development of replacement implants and repair strategies for degenerative and traumatic pathologies. Indeed, a wide range of element types and material models has been used to represent knee ligaments, ranging from elastic unidimensional elements to complex hyperelastic three-dimensional structures with anatomically realistic shapes. This paper systematically reviews literature studies, which described finite element models of the knee, and summarizes the approaches, which have been used to model the ligaments highlighting their strengths and weaknesses.

Introduction

Numerical methods have been used for decades for the simulation of the biomechanical behavior of the knee joint. Starting from the earliest analytical or numerical models solved by in-house computer programs (Crowninshield et al., 1976; Wismans et al., 1980; Hefzy and Grood, 1983), the complexity of the kinematics and of the capacity of the knee joint to withstand high loads while allowing for a high mobility of the joint have always challenged and fascinated the scientific community. Modern finite element models are usually based on magnetic resonance imaging (MRI) and/or computed tomography (CT) scans and possess a high degree of anatomical realism (e.g., Pena et al., 2006; Kazemi and Li, 2014). Besides the simulation of the intact joint, models are widely used for the prediction of the effects of degenerative pathologies, traumatic events as well as surgical repair and replacement strategies (e.g., Yoon et al., 2010; Fitzpatrick et al., 2014; Innocenti et al., 2014).

Although the geometrical accuracy of the three-dimensional reconstruction, which can be achieved relatively easily, the development of an accurate finite element model of the knee joint is still a complex task. The ligaments of the knee are among the most complicated structures to simulate and at the same time most critical in determining the biomechanics of the joint. Indeed, ligaments have peculiar mechanical characteristics (described in detail below), which present technical challenges to researchers. Furthermore, valid and trusted values of the material properties obtained with experimental mechanical testing are needed in order to have a realistic response of the joint as predicted by the numerical models.

A wide range of different approaches to these challenges has been presented in the literature, and is the subject of the present review. After a summary of the main anatomical and biomechanical properties of the knee ligaments, we present a systematic review of the literature aimed to cover: (1) the type of elements, which have been used to simulate the knee ligaments; (2) the constitutive material laws employed in published studies; and (3) the original data sources, e.g., from in vitro mechanical testing of isolated ligaments, which have been used in the development and validation of the models.

Functional Anatomy and Biomechanics of the Knee Ligaments

Similar to other biological soft tissues, the ligaments of the knee (Figure 1) and other articular joints are constituted by a water-rich ground substance reinforced with collagen fibers (Daniel et al., 1990). The ground substance contains proteoglycans, which together with hyaluronic acid are able to attract water from the external environment, creating a kind of gel (Daniel et al., 1990). The capability of the matrix to capture water molecules and therefore to maintain a high water content even when stretched, results in the assumption of incompressibility of the tissue, which is incorporated in most constitutive models (Weiss and Gardiner, 2001; Weiss et al., 2005).

FIGURE 1

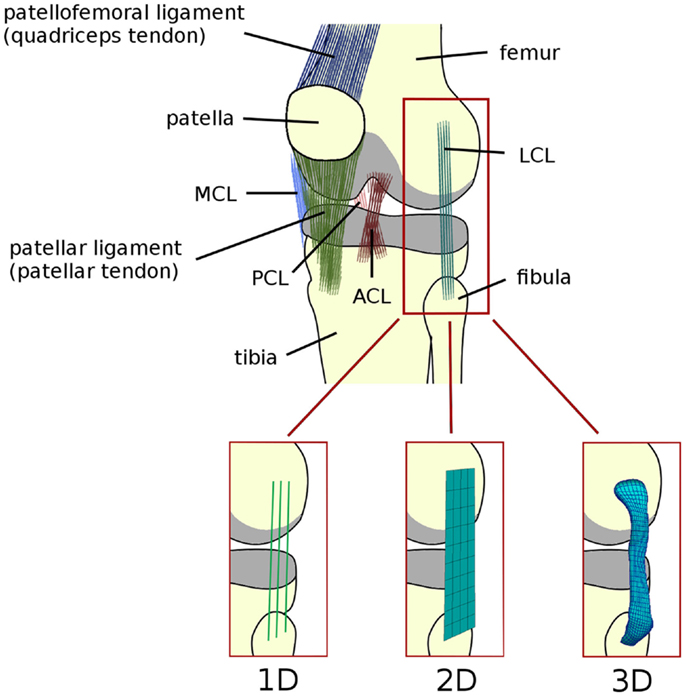
Figure 1. Schematic representation of the anatomy of the knee joint, depicting the ligaments (ACL, anterior cruciate ligament; PCL, posterior cruciate ligament; MCL, medial collateral ligament; LCL, lateral collateral ligament). Articular cartilage is shown in gray. Alternative names commonly used for the patellofemoral and patellar ligaments are reported in brackets. Schematic representations of 1D (springs, trusses, and beams), 2D (shell and membrane), and 3D elements (solid) used to model the knee ligaments are shown.

The matrix also contains a moderate number of fibroblasts, which are responsible for synthesizing collagen molecules, and constitute the fibers providing the tensional stiffness and resistance to the tissue (Nimni, 1983). The collagen skeleton of ligaments is a hierarchical structure, which includes microfibrils organized in fibrils or fascicles. In the unloaded configurations, collagen fibrils are crimped, i.e., arranged in a helical or waveform pattern (Diamant et al., 1972; Comninou and Yannas, 1976). When the ligament is stretched, the crimping progressively disappears as the fibrils become aligned with the loading direction. This structure gives the ligament a characteristic force–elongation curve, which can be subdivided in two zones: (1) a toe region with low stiffness and non-linear response, in which the fibrils lose their crimping; (2) a higher stiffness region in which the curve is almost linear, which corresponds to the stretching of the collagen fibrils (Trent et al., 1976; Weiss and Gardiner, 2001) (Figure 2). This behavior is well represented by the constitutive models, which were developed for the numerical simulation of the biomechanics of the knee joint, which are described below.

FIGURE 2

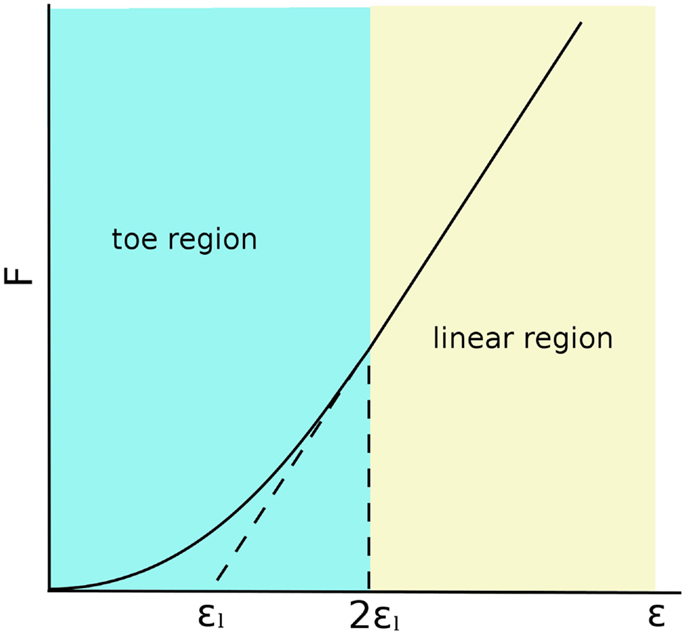
Figure 2. Force–strain behavior of a generic ligament following the model described by Blankevoort et al. (1991a). 2ε_l is the threshold strain, which indicates the change from the toe to the linear regions.

Review Methods

A Pubmed search with keywords “finite element” and “knee” was performed. The retrieved abstracts were then screened in order to determine, which papers were fulfilling the following inclusion criteria: (1) the paper describes a finite element model of the human lower limb, of the knee or of isolated knee ligaments; (2) the paper reports the material properties assigned to the knee ligaments or at least a reference to a literature source. Precedence was given to models of the entire knee joint and not on isolated ligaments; however, the latter papers were not excluded if retrieved by the aforementioned Pubmed search. Multibody models (i.e., based on rigid body dynamics) were not considered if not referenced by other finite element studies, for the sake of simplicity. When necessary, the full text of the retrieved papers was also screened. The reference lists of the papers were then analyzed in order to retrieve additional relevant papers, which had not been identified by the Pubmed search. The results of this systematic search were then subdivided into those showing a one-dimensional (1D) model of the knee ligaments, and those reporting two-dimensional (2D, surface elements), or three-dimensional (3D, solid elements) models.

Subsequently, the literature search was deepened in order to identify the original sources of the material properties, either based on assumptions, in vitro or in vivo measurements. Citation graphs tracking the origin of the material property values were created, specifically for the 1D and for the 2D–3D models (Figures 3 and 4).

FIGURE 3

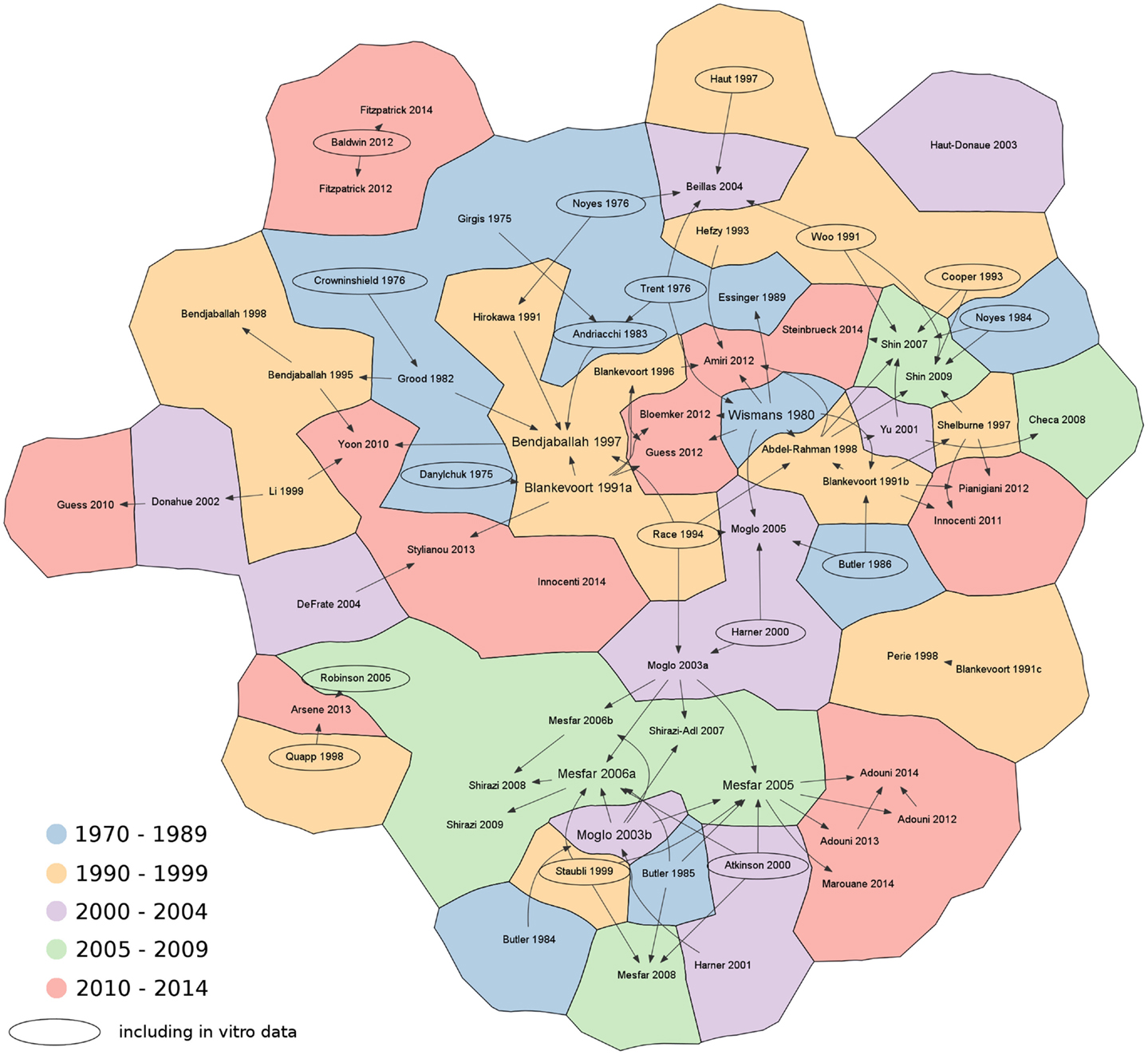
Figure 3. Citation chart showing the sources of each paper retrieved in the literature using 1D elements to represent the knee ligaments. Arrows indicate the papers used as reference for the material properties of the ligaments. Studies including in vitro data are highlighted with an oval border. For the sake of brevity, only the name of the first author is shown. References not reported in the main text: Abdel-Rahman and Hefzy, 1998; Adouni and Shirazi-Adl, 2013; Adouni and Shirazi-Adl, 2014; Adouni et al., 2012; Andriacchi et al., 1983; Arsene and Gabrys, 2013; Beillas et al., 2004; Blankevoort and Huiskes, 1996; Blankevoort et al., 1991c; Cooper et al., 1993; Danylchuk, 1975; DeFrate et al., 2004; Donahue et al., 2002; Essinger et al., 1989; Grood and Hefzy, 1982; Guess et al., 2010; Harner et al., 2000; Haut and Haut, 1997; Haut Donahue et al., 2003; Innocenti et al., 2011; Li et al., 1999; Marouane et al., 2014; Mesfar and Shirazi-Adl, 2006a; Mesfar and Shirazi-Adl, 2006b; Mesfar and Shirazi-Adl, 2008; Moglo and Shirazi-Adl, 2003a; Moglo and Shirazi-Adl, 2003b; Moglo and Shirazi-Adl, 2005; Noyes et al., 1984; Perie and Hobatho, 1998; Pianigiani et al., 2012; Robinson et al., 2005; Shelburne and Pandy, 1997; Shirazi and Shirazi-Adl, 2009; Shirazi et al., 2008; Shirazi-Adl and Mesfar, 2007; Stylianou et al., 2013.

FIGURE 4

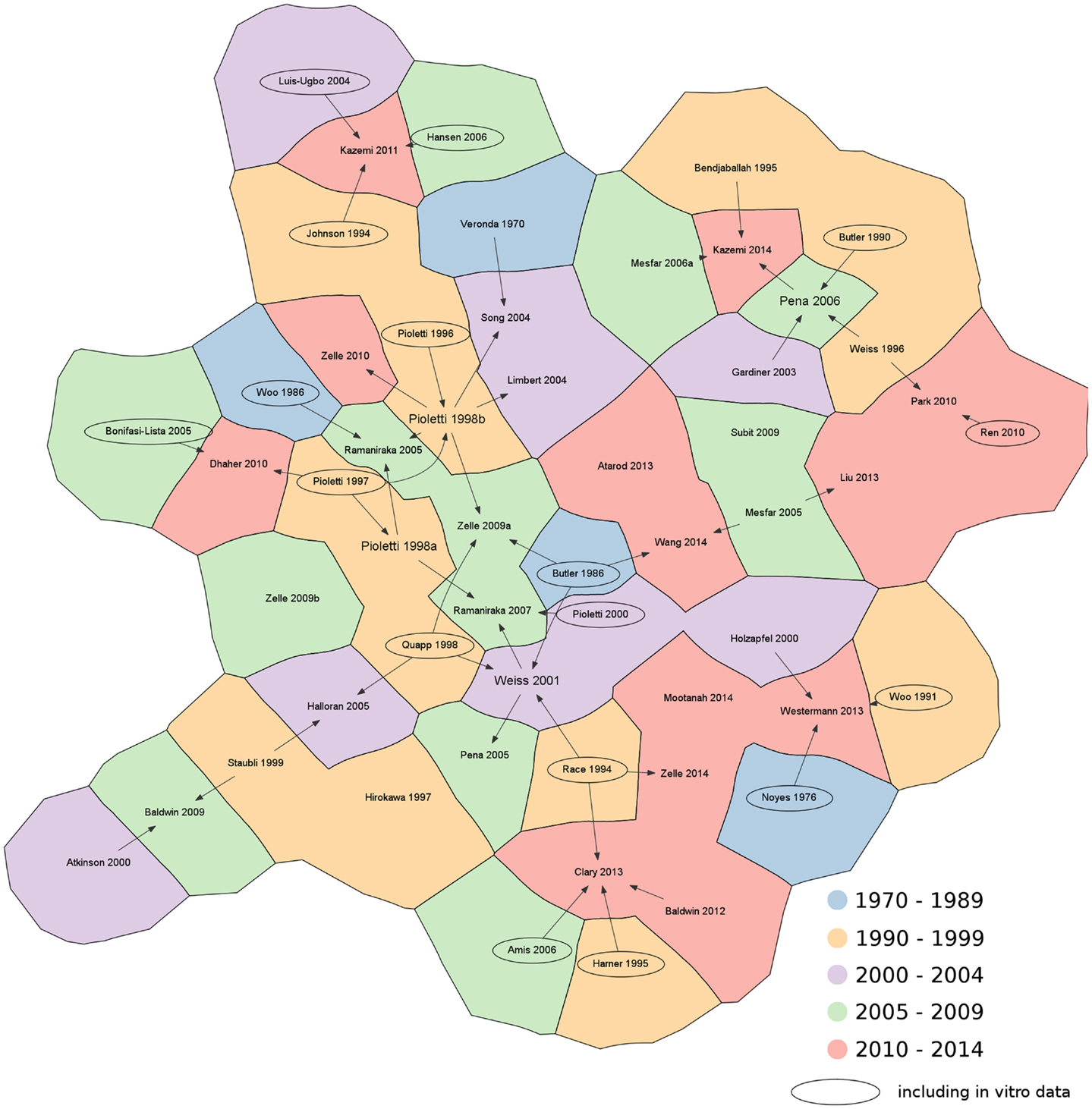
Figure 4. Citation chart showing the sources of each paper retrieved in the literature using 2D and 3D elements to represent the knee ligaments. Arrows indicate the papers used as reference for the material properties of the ligaments. Studies including in vitro data are highlighted with an oval border. For the sake of brevity, only the name of the first author is shown. References not reported in the main text: Amis et al., 2006; Atarod et al., 2013; Bonifasi-Lista et al., 2005; Butler et al., 1990; Dhaher et al., 2010; Hansen et al., 2006; Hirokawa and Tsuruno, 1997; Johnson et al., 1994; Louis-Ugbo et al., 2004; Mesfar and Shirazi-Adl, 2006a; Park et al., 2010; Pioletti et al., 1996; Ren et al., 2010; Subit et al., 2009; Wang et al., 2014.

Results of the Literature Review

The first Pubmed search retrieved 650 items. After screening, 69 relevant papers were selected. The analysis of the references returned nine additional relevant papers. Several papers used values of the material properties retrieved from other modeling studies, and did not provide citations to the original data sources. Based on the detailed analysis of the literature, 18 papers reporting in vitro data about mechanical testing of the knee ligaments were identified as the original sources of the material properties. For the sake of clarity, the retrieved studies were subdivided in papers using 1D elements to represent the knee ligaments and those using elements with higher dimensionality (2D, 3D).

1D Models

Line elements such as springs, trusses, and beams are frequently used to model the mechanical role of the ligaments in the knee joint (Figure 1). Bundles of line elements, which cover approximately the insertion areas of the ligaments are the most common solution (e.g., Bendjaballah et al., 1995), but single elements to describe each ligamental bundle were also used (Yu et al., 2001). The first mechanical tests conducted in the 70s (Girgis et al., 1975; Trent et al., 1976) showed a clear non-linearity of the force–elongation curves of all knee ligaments. Based on these observations, early numerical models of the knee joint used elements able to represent non-linear force–strain or force–elongation behaviors, e.g., quadratic (Wismans et al., 1980) or quadratic in the toe region and linear afterward (Blankevoort et al., 1991a). This behavior can be formulated as follows (Figure 2):

$\begin{array}{cc}f=\frac{1}{4}k\frac{{\mathrm{\epsilon }}^2}{{\mathrm{\epsilon }}_l},\hfill & 0\le \mathrm{\epsilon }\le 2{\mathrm{\epsilon }}_l\hfill \\ f=k\left(\mathrm{\epsilon }-{\mathrm{\epsilon }}_l\right),\hfill & \mathrm{\epsilon }>2{\mathrm{\epsilon }}_l\hfill \\ f=0,\hfill & \mathrm{\epsilon }<0\hfill \\ \hfill \end{array}$ (1)

where f is the axial force sustained by the ligament, k is a stiffness parameter, ε is the strain, and 2ε_l is the threshold strain, which indicates the change from the toe to the linear regions. In both cases, the elements representing the ligaments were able to sustain only tensile loads, and offered no resistance to compression or shear. In some papers (Yu et al., 2001; Checa et al., 2008), the force–strain behavior expressed in Eq. 1. has been modified as follows:

$\begin{array}{cc}f=k1{\left(L-L_0\right)}^2,\hfill & 0\le \mathrm{\epsilon }\le 2{\mathrm{\epsilon }}_l\hfill \\ f=k2\left(L-\left(1+{\mathrm{\epsilon }}_l\right)L_0\right),\hfill & \mathrm{\epsilon }>2{\mathrm{\epsilon }}_l\hfill \\ f=0,\hfill & \mathrm{\epsilon }<0\hfill \\ \hfill \end{array}$ (2)

where L is the current length of the ligament, L₀ is its slack length, and k1 and k2 are two stiffness parameters describing the toe and the linear regions, respectively. Linearized forms of Eqs 2 were also used (Shin et al., 2007):

$\begin{array}{cc}f=\frac{k_l}{2}\left(L-L_0\right),\hfill & 0\le \mathrm{\epsilon }\le 2{\mathrm{\epsilon }}_l\hfill \\ f=k_l\left(L-\left(1+{\mathrm{\epsilon }}_l\right)L_0\right),\hfill & \mathrm{\epsilon }>2{\mathrm{\epsilon }}_l\hfill \\ f=0,\hfill & \mathrm{\epsilon }<0\hfill \\ \hfill \end{array}$ (3)

where k_l is a linear stiffness parameter. Care should be taken in the comparison of the stiffness parameters k, k1, and k2 and k_l since they are expressed in different units.

These formulations are still widely used to model the ligaments in 1D (Table 1). It should be noted that the values of the material properties listed in Table 1 show considerable variability, especially regarding the reference strain. In some cases, the authors only stated the use of non-linear elements without any additional information on the constitutive equations (Shin et al., 2009; Yoon et al., 2010). In contrast, the use of linear 1D elements appears to be very limited in simulation studies (Shin et al., 2007; Innocenti et al., 2014; Steinbruck et al., 2014).

TABLE 1

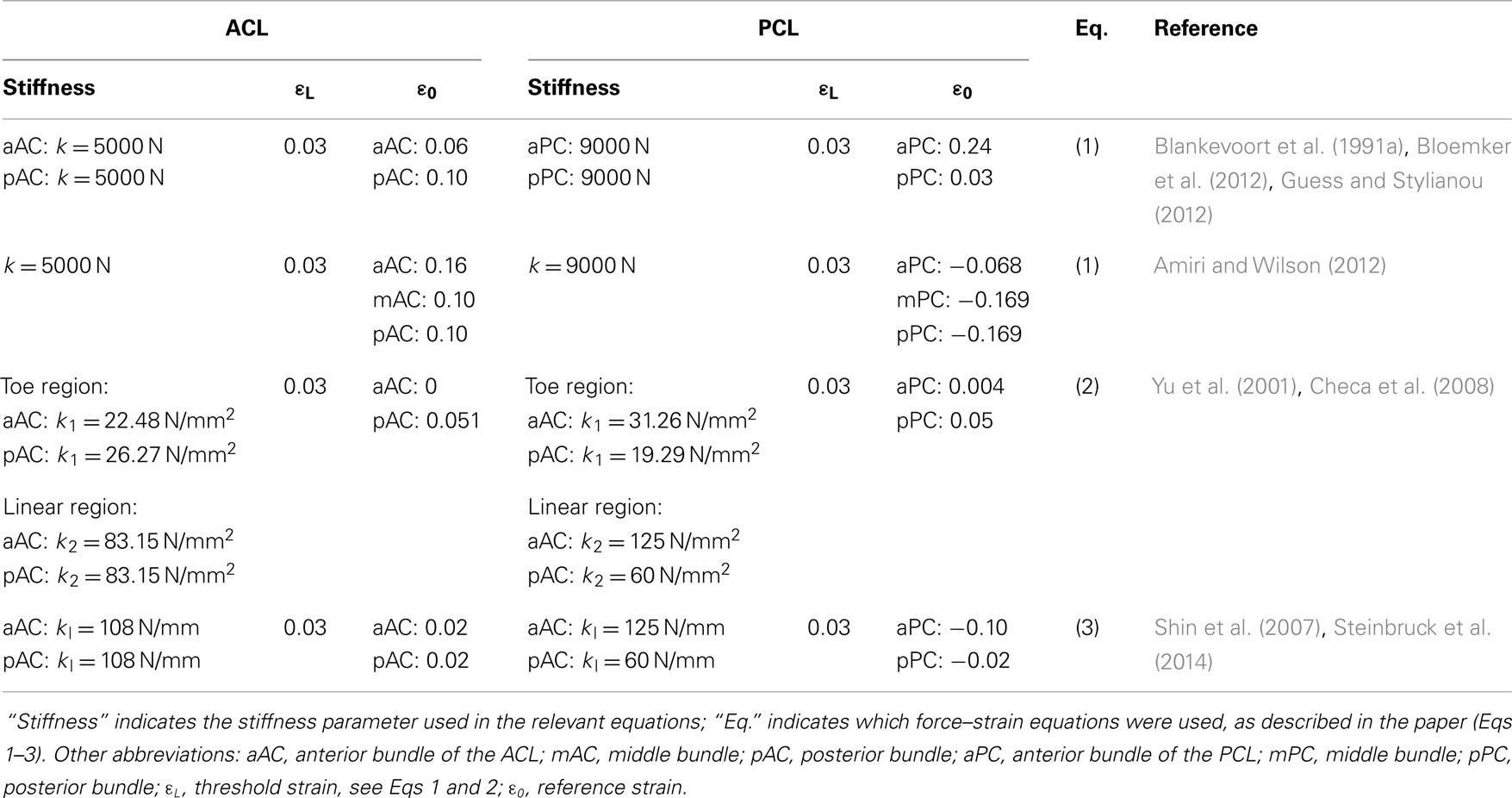
Table 1. Material properties used to model the non-linear behavior of the ACL and PCL with non-linear 1D elements.

Knee extension is usually considered as the reference state from which different motions can be simulated. In this state, the ligaments are strained and therefore already sustaining a tensile load (Daniel et al., 1990). Reference strains, also called pre-strains, are difficult to estimate experimentally, and assumptions were often made in order to circumvent this problem and to correctly simulate the initial state of knee extension (Wismans et al., 1980). Blankevoort et al. (1991a) used an iterative approach in order to minimize the differences between the predicted and experimentally measured flexion motions by altering the values of the reference strains of the ligaments. These data were used as a reference in a whole series of papers published by the École Polytechnique de Montréal (e.g., Mesfar and Shirazi-Adl, 2005). Another approach based on optimization to fit in vitro results was used by Baldwin et al. (2012) and served as basis for subsequent papers by the same research group (Fitzpatrick et al., 2012, 2013, 2014). Experimental measurements and sensitivity analyses about the reference strains were also performed (Bertozzi et al., 2007; Bloemker et al., 2012).

The ligaments of the knee do not only exert forces on the insertion areas in the direction connecting the insertion and origin, but exhibit wrapping behavior between themselves [anterior cruciate ligament (ACL) and posterior cruciate ligament (PCL)] or with bones [medial collateral ligament (MCL) with tibia and MCL with femur]. This behavior limits the accuracy of simple line elements to model these three ligaments if special techniques to simulate wrapping are not employed. Based on the analytical model proposed by Hefzy and Grood (1983), Blankevoort and Huiskes (1991b) first integrated the simulation of the MCL–tibia wrapping in a finite element model. The tibial surface was modeled as a curve in space upon which a moving contact point with the MCL was defined. The MCL was then divided into two line elements passing through the contact point. Similar approaches were used afterward (Bendjaballah et al., 1997, 1998), but the vast majority of papers employing 1D elements to model the ligaments neglected this phenomenon. In some specific cases in which wrapping markedly changes the force distribution and direction (e.g., when the valgus laxity is of interest), this limitation may significantly limit the accuracy of the results. However, the general effect of neglecting ligament wrapping was estimated to be not dramatic in other cases (Blankevoort and Huiskes, 1991b).

During the literature search and review, 14 in vitro papers were identified as reference for the material properties of the knee ligaments (Figure 3). The series of papers from the group of Butler and coworkers (Noyes and Grood, 1976; Butler et al., 1984, 1985, 1986) and the more recent paper by Race and Amis (1994) are worthy of note. Experimental data about the cruciate and collateral ligaments were also published by another research group (Woo et al., 1986, 1991; Harner et al., 1995, 2001). Experimental sources often cited were also Atkinson et al. (2000) and Staubli et al. (1999) regarding the patellar and patellofemoral ligaments.

It should be noted that in many finite element papers, the values of the material properties were retrieved from previous numerical studies, without direct references to experimental studies. A preference toward source papers, which explicitly showed values of the stiffness parameters and reference strain of the ligaments (such as Wismans et al., 1980 and Blankevoort et al., 1991a), is clearly seen in Figure 3. As a matter of fact, these studies refer to a small set of old experimental tests, which were shown already by Blankevoort et al. (1991a) to be rather inconsistent or inaccurate. Besides, values of the material properties used in previous models showed considerable variability (Table 1), thus making further questionable the model predictions and the comparability of data obtained with different models. We therefore recommend that authors of numerical models of the knee concentrating on the ligaments should not only focus on a single source of data, but perform a wider literature search as well and take into consideration also newer experimental datasets such as e.g., those reported by Race and Amis (1994) and Harner et al. (1995). It should be noted that the use of consolidated and valid sources for the material properties does not eliminate the need for a proper model validation.

2D–3D Models

The most intuitive way to include the ligaments in a 3D model of the knee is by using solid elements (Figure 1). Indeed, MRI scans in combination with 3D reconstruction software offer an accessible way to create detailed models of the joint including the geometry of the ligaments as well as their insertion sites for the specific patient. MRI scans can also be easily combined with CT, which offers high resolution imaging of the bony structures, by means of registration software. This approach also facilitates the simulation of ligament wrapping by the use of surface-to-surface contact, which is implemented in most free and commercial finite element packages. The accuracy of the simulation of stresses that are not purely tensional, such as those arising due to contact with bone and those close to the insertion areas, is also improved (Weiss and Gardiner, 2001).

However, ligaments have a peculiar mechanical behavior, being strongly anisotropic and not able to sustain compression, which makes their simulation with solid elements less attractive if compared to line elements. The pre-strain in the reference state is also more challenging to be simulated using solid elements. One approach in between, which combines the ease of implementation of the 1D elements and the anatomical realism of the 3D elements, is to embed springs or trusses in a 3D matrix having a simple constitutive law, such as linear isotropic elasticity or neo-Hooke hyperelasticity. This approach was used in some previous studies, especially employing 2D (surface) elements such as shells or membranes reinforced with non-linear line elements to accomplish the anisotropy of the ligaments (Halloran et al., 2005; Baldwin et al., 2009; Zelle et al., 2009a,b, 2010, 2014; Clary et al., 2013).

Simple continuum material models that do not take into account the anisotropy of the ligamentous tissue, namely hyperelastic neo-Hooke (Mootanah et al., 2014) or Mooney–Rivlin materials (Liu and Zhang, 2013) were also used. However, anisotropic hyperelastic continuum models are more often employed. Only one paper (Westermann et al., 2013) employed an anisotropic hyperelastic model directly available in a finite element package, the Holzapfel–Gasser–Ogden model (Holzapfel et al., 2000; Gasser et al., 2006) implemented in ABAQUS (Simulia, Providence, RI, USA).

Constitutive models were also purposely developed to model biological soft tissues. The Veronda–Westmann model published in 1970 (Veronda and Westmann, 1970) provides an exponential stress–strain relationship and is conveniently available in open-source finite element software FEBio (Maas et al., 2012), but is limited to the isotropic behavior in its conventional formulation. This model was implemented in MARC (MSC Software, Newport Beach, CA, USA) for the simulation of the ACL (Song et al., 2004).

Pioletti and coworkers (Pioletti et al., 1998a,b; Pioletti and Rakotomanana, 2000) developed a hyperelastic, incompressible, and viscoelastic isotropic law, which was used in following works of the group (Ramaniraka et al., 2005, 2007). In this formulation, the elastic part is based on the isotropic Veronda–Westmann material law and the novelty is mainly constituted by the viscous behavior. However, in two papers (Ramaniraka et al., 2007 and Ramaniraka et al., 2005) this constitutive law was used to perform static analyses, and therefore did not exploit its viscoelastic capabilities.

A model which was widely used in the following publications was presented by Weiss et al. (1996), and describes an incompressible, fiber-reinforced material able to simulate large displacements. This material model was designed to closely fit the response of the biological soft tissues, especially ligaments, based on experimental data (Quapp and Weiss, 1998). Within this model, pre-strain was also simulated by the same group (Gardiner and Weiss, 2003) by performing an initial unloaded step to search for the reference configuration. The material model is available in FEBio in two forms, in which the matrix is either a Mooney–Rivlin or a Veronda–Westmann material. Peña and coworkers implemented the same model in ABAQUS by means of a Fortran user subroutine (UMAT) (Pena et al., 2005, 2006). A similar material formulation expanded to incorporate fluid flow (poroelasticity) and viscoelasticity was implemented in ABAQUS by Kazemi and coworkers (Kazemi et al., 2011; Kazemi and Li, 2014) by means of a UMAT and was used to investigate the creep behavior of the knee joint. Limbert et al. (2004) focused their attention to the possibility of simulating pre-strain in a ligament, and developed an anisotropic, fiber-reinforced incompressible hyperelastic material formulation in which an additional load step to calculate the reference configuration due to pre-strain is not necessary. To our knowledge, this material model has not yet been employed in other studies.

The analysis of the data sources used for the choice of the values of the material properties for 3D models showed similar results to those for the 1D models (Figure 4). Experimental sources (e.g. Butler et al., 1986; Woo et al., 1991; Race and Amis, 1994; Quapp and Weiss, 1998) were widely cited. The research group of Pioletti and coworkers (Pioletti, 1997; Pioletti and Rakotomanana, 2000) presented additional in vitro results, which have been widely used not only by the same group, but also in other papers (Limbert et al., 2004; Zelle et al., 2009a, 2010) to provide experimental evidence. With respect to previous data, these experimental tests also provided time-dependent results obtained at different strain rates, which would be useful in the implementation of dynamic models of the knee. In contrast to the 1D models, key references cited by a high number of papers (such as Wismans et al., 1980; Blankevoort et al., 1991a) could not be identified.

Choice of Appropriate Elements and Material Models

The approaches used to simulate the mechanical behavior and role of the ligaments of the knee range from very simple (e.g. linear beams and springs) to complex models (e.g., anisotropic hyperelastic 3D materials, or biphasic formulations). The user planning to develop a computational model of the knee has therefore a wide range of possible choices, which should be evaluated according to the research questions and the desired applications of the model.

Weiss and Gardiner (2001) distinguished between microstructural models, which represent the mechanical role of each component of the ligamentous tissue, and phenomenological models, which simulate the global material behavior without directly referring to the tissue composition, therefore without a direct physical interpretation. The latter models are the focus of the present paper, and are the solution of choice for most models aimed to study the knee kinematics and load bearing, total or partial knee replacements, meniscus, and even ligament reconstruction and grafting.

Line elements have the distinct advantages of an easy implementation, a low computational cost and the possibility to exactly replicate non-linear force–elongation curves from experimental tests as well as pre-strain. Viscoelastic behavior can be also easily modeled, if required. As mentioned above, disadvantages include the lack of information about the behavior in the transverse plane and the need for special techniques to simulate ligament wrapping. Nevertheless, non-linear 1D elements are still a recommended choice and a commonly used method for the simulation of the global behavior of the knee and for total as well as unicompartmental knee replacements.

Solid elements offer a better anatomical realism and overcome the limitations in the simulation of wrapping. Besides, they have the potential to predict quantities not accessible with the used of 1D elements such as local strains and accurate load transfer between ligaments and surrounding tissues, which may be of interest for specific applications. However, their inherent higher complexity may lead to high computational costs, difficulties in the validation and evaluation of the results, and in some cases to the use of oversimplified material constitutive models, which should be avoided. We recommend their use only when the focus of the study is the biomechanics of the ligament itself, its interaction with the surrounding tissues or other complex research questions in which a correct 3D representation of the behavior of the ligament is required in order to obtain an accurate answer. It should be noted that, depending on the specific application, other anatomical structures such as menisci and articular cartilage may have a high significance in the determination of the results, and should therefore be modeled and validated properly.

Verification and Validation

Two key aspects for the development of numerical models of articular joints such as the knee are the verification and the validation. Even if these terms are sometimes used with similar meanings, as effectively synthesized by Roarche (1998) and Viceconti et al. (2005), verification is about solving the equations right, and validation is about solving the right equations. For the specific case of biomechanical simulation of the knee joint with commercial finite element software, verification is usually limited to the choice of an appropriate mesh density, the plausibility analysis of the solution of the contact problems and the check of the convergence of the iterative solution.

Validation is mostly performed by comparison of the results with controlled in vitro experiments. Experimental set-ups like the Oxford rig (Zavatsky, 1997) or the Kansas Knee Simulator (Maletsky and Hillberry, 2005) allow for the application of physiological loads and motions, and for the measurement of the resulting kinematics, which can then be compared with the numerical predictions. However, these experimental methods do not offer easy access to local variables such as strains in the ligaments, and therefore allow only for a partial validation of the numerical models. The use of sophisticated sensors such as differential variable reluctance transducers (DVRTs) (e.g., in Withrow et al., 2006) or optical strain measurements (e.g., in Freutel et al., 2014) offer a partial solution to this limitation, at the price of a higher level of complexity of the experimental set-up.

An alternative, indirect way to perform validation is by comparison with available data, such as data from literature or from previous experiments (Henninger et al., 2010). In this case, the user has no direct control on the experiments and on their quality and degree of variability. For this reason, validation against purposely performed experiments is generally preferred to indirect validation (Henninger et al., 2010).

Similarly to the choice of the most appropriate constitutive model described above, the design of a correct validation procedure is mainly based on the scope of the desired applications and on the output variables of interest (Viceconti et al., 2005; Henninger et al., 2010). For example, if the aim of the study is the evaluation of the kinematics of a total knee replacement, a comparison of the predictions with experimental kinematical data may be sufficient. However, a model validated in such a way would not be adequate for the evaluation of local strains in the MCL, which would require a model specifically validated for the mechanical behavior of the single ligament.

Future Developments

A number of topics concerning the biomechanics of the knee ligaments remain poorly understood. Fluid flow during deformation of the ligaments is one of these. Following the studies of the transient mechanics and mechanobiology of the intervertebral disk (e.g., Schroeder et al., 2006), models including osmotic swelling due to the presence of proteoglycans would allow for a more accurate prediction of their time-dependent response and the overcoming of the incompressibility assumption. However, experimental data about permeability for the ligamentous tissue is actually lacking (Weiss et al., 2005).

Another aspect which is poorly investigated is the simulation of ligament failure and injury. With current commercial software, anatomically realistic 3D models able to accurately simulate local strains could be easily enriched in order to predict crack initiation and propagation by the use of extended finite element methods (XFEM) (Moës et al., 1999). However, data available about ligament failure only concern uniaxial tension along the main axis of the ligament, and are therefore not sufficient for the development of adequate failure criteria to be implemented with XFEM (Weiss et al., 2005).

Conclusion

The use of numerical models for the biomechanical simulation of the knee joint in healthy and pathological conditions and following repair surgeries or implantation of prostheses appears to be wide and consolidated. The ligaments, especially ACL and PCL, have been the focus of studies from the earliest models onward (e.g., Wismans et al., 1980) due to their high biomechanical importance in both knee kinematics and load bearing. The increase in computational power of modern computers and the wide availability of advanced non-linear finite element packages, including software free of charge for academic use (e.g., FEBio) will likely broaden the use of 3D elements for the ligaments with respect to 1D solutions. We recommend the authors to consider all the unique aspects of the biomechanics of the ligaments, such as non-linearity, anisotropy, pre-strain, and wrapping, and to select the most appropriate modeling approach based on the specific application, especially when 3D elements are used.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abdel-Rahman, E. M., and Hefzy, M. S. (1998). Three-dimensional dynamic behaviour of the human knee joint under impact loading. Med. Eng. Phys. 20, 276–290. doi: 10.1016/S1350-4533(98)00010-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Adouni, M., and Shirazi-Adl, A. (2013). Consideration of equilibrium equations at the hip joint alongside those at the knee and ankle joints has mixed effects on knee joint response during gait. J. Biomech. 46, 619–624. doi:10.1016/j.jbiomech.2012.09.035

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Adouni, M., and Shirazi-Adl, A. (2014). Partitioning of knee joint internal forces in gait is dictated by the knee adduction angle and not by the knee adduction moment. J. Biomech. 47, 1696–1703. doi:10.1016/j.jbiomech.2014.02.028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Adouni, M., Shirazi-Adl, A., and Shirazi, R. (2012). Computational biodynamics of human knee joint in gait: from muscle forces to cartilage stresses. J. Biomech. 45, 2149–2156. doi:10.1016/j.jbiomech.2012.05.040

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Amiri, S., and Wilson, D. R. (2012). A computational modeling approach for investigating soft tissue balancing in bicruciate retaining knee arthroplasty. Comput. Math. Methods Med. 2012, 652865. doi:10.1155/2012/652865

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Amis, A. A., Gupte, C. M., Bull, A. M., and Edwards, A. (2006). Anatomy of the posterior cruciate ligament and the meniscofemoral ligaments. Knee Surg. Sports Traumatol. Arthrosc. 14, 257–263. doi:10.1007/s00167-005-0686-x

CrossRef Full Text | Google Scholar

Andriacchi, T. P., Mikosz, R. P., Hampton, S. J., and Galante, J. O. (1983). Model studies of the stiffness characteristics of the human knee joint. J. Biomech. 16, 23–29. doi:10.1016/0021-9290(83)90043-X

CrossRef Full Text | Google Scholar

Arsene, C. T., and Gabrys, B. (2013). Probabilistic finite element predictions of the human lower limb model in total knee replacement. Med. Eng. Phys. 35, 1116–1132. doi:10.1016/j.medengphy.2012.11.011

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Atarod, M., Rosvold, J. M., Kazemi, M., Li, L., Frank, C. B., and Shrive, N. G. (2013). Inter-insertional distance is a poor correlate for ligament load: analysis from in vivo gait kinetics data. J. Biomech. 46, 2264–2270. doi:10.1016/j.jbiomech.2013.06.023

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Atkinson, P., Atkinson, T., Huang, C., and Doane, R. (2000). “A comparison of the mechanical and dimensional properties of the human medial land lateral patellofemoral ligaments,” in 46th Annual Meeting of the Orthopaedic Research Society, Orlando, FL.

Google Scholar

Baldwin, M. A., Clary, C., Maletsky, L. P., and Rullkoetter, P. J. (2009). Verification of predicted specimen-specific natural and implanted patellofemoral kinematics during simulated deep knee bend. J. Biomech. 42, 2341–2348. doi:10.1016/j.jbiomech.2009.06.028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Baldwin, M. A., Clary, C. W., Fitzpatrick, C. K., Deacy, J. S., Maletsky, L. P., and Rullkoetter, P. J. (2012). Dynamic finite element knee simulation for evaluation of knee replacement mechanics. J. Biomech. 45, 474–483. doi:10.1016/j.jbiomech.2011.11.052

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Beillas, P., Papaioannou, G., Tashman, S., and Yang, K. H. (2004). A new method to investigate in vivo knee behavior using a finite element model of the lower limb. J. Biomech. 37, 1019–1030. doi:10.1016/j.jbiomech.2003.11.022

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bendjaballah, M. Z., Shirazi-Adl, A., and Zukor, D. J. (1995). Biomechanics of the human knee joint in compression: reconstruction, mesh generation and finite element analysis. Knee 2, 69. doi:10.1016/0968-0160(95)00018-K

CrossRef Full Text | Google Scholar

Bendjaballah, M. Z., Shirazi-Adl, A., and Zukor, D. J. (1997). Finite element analysis of human knee joint in varus-valgus. Clin. Biomech. (Bristol, Avon) 12, 139–148. doi:10.1016/S0268-0033(97)00072-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bendjaballah, M. Z., Shirazi-Adl, A., and Zukor, D. J. (1998). Biomechanical response of the passive human knee joint under anterior-posterior forces. Clin. Biomech. (Bristol, Avon) 13, 625–633. doi:10.1016/S0268-0033(98)00035-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bertozzi, L., Stagni, R., Fantozzi, S., and Cappello, A. (2007). Knee model sensitivity to cruciate ligaments parameters: a stability simulation study for a living subject. J. Biomech. 40(Suppl. 1), S38–S44. doi:10.1016/j.jbiomech.2007.02.018

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Blankevoort, L., and Huiskes, R. (1991b). Ligament-bone interaction in a three-dimensional model of the knee. J. Biomech. Eng. 113, 263–269. doi:10.1115/1.2894883

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Blankevoort, L., and Huiskes, R. (1996). Validation of a three-dimensional model of the knee. J. Biomech. 29, 955–961. doi:10.1016/0021-9290(95)00149-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Blankevoort, L., Kuiper, J. H., Huiskes, R., and Grootenboer, H. J. (1991a). Articular contact in a three-dimensional model of the knee. J. Biomech. 24, 1019–1031. doi:10.1016/0021-9290(91)90019-J

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Blankevoort, L., Huiskes, R., and de Lange, A. (1991c). Recruitment of knee joint ligaments. J. Biomech. Eng. 113, 94–103. doi:10.1115/1.2894090

CrossRef Full Text | Google Scholar

Bloemker, K. H., Guess, T. M., Maletsky, L., and Dodd, K. (2012). Computational knee ligament modeling using experimentally determined zero-load lengths. Open Biomed. Eng. J. 6, 33–41. doi:10.2174/1874230001206010033

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bonifasi-Lista, C., Lake, S. P., Small, M. S., and Weiss, J. A. (2005). Viscoelastic properties of the human medial collateral ligament under longitudinal, transverse and shear loading. J. Orthop. Res. 23, 67–76. doi:10.1016/j.orthres.2004.06.002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Butler, D. L., Grood, E. S., Noyes, F. R., and Sodd, A. N. (1985). On the interpretation of our anterior cruciate ligament data. Clin. Orthop. Relat. Res. 196, 26–34.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Butler, D. L., Grood, E. S., Noyes, F. R., Zernicke, R. F., and Brackett, K. (1984). Effects of structure and strain measurement technique on the material properties of young human tendons and fascia. J. Biomech. 17, 579–596. doi:10.1016/0021-9290(84)90090-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Butler, D. L., Kay, M. D., and Stouffer, D. C. (1986). Comparison of material properties in fascicle-bone units from human patellar tendon and knee ligaments. J. Biomech. 19, 425–432. doi:10.1016/0021-9290(86)90019-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Butler, D. L., Sheh, M. Y., Stouffer, D. C., Samaranayake, V. A., and Levy, M. S. (1990). Surface strain variation in human patellar tendon and knee cruciate ligaments. J. Biomech. Eng. 112, 38–45. doi:10.1115/1.2891124

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Checa, S., Taylor, M., and New, A. (2008). Influence of an interpositional spacer on the behaviour of the tibiofemoral joint: a finite element study. Clin. Biomech. (Bristol, Avon) 23, 1044–1052. doi:10.1016/j.clinbiomech.2008.04.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Clary, C. W., Fitzpatrick, C. K., Maletsky, L. P., and Rullkoetter, P. J. (2013). The influence of total knee arthroplasty geometry on mid-flexion stability: an experimental and finite element study. J. Biomech. 46, 1351–1357. doi:10.1016/j.jbiomech.2013.01.025

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Comninou, M., and Yannas, I. V. (1976). Dependence of stress-strain nonlinearity of connective tissues on the geometry of collagen fibers. J. Biomech. 9, 427–433. doi:10.1016/0021-9290(76)90084-1

CrossRef Full Text | Google Scholar

Cooper, D. E., Deng, X. H., Burstein, A. L., and Warren, R. F. (1993). The strength of the central third patellar tendon graft. A biomechanical study. Am. J. Sports Med. 21, 818–823. discussion 823-4, doi:10.1177/036354659302100610

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Crowninshield, R., Pope, M. H., and Johnson, R. J. (1976). An analytical model of the knee. J. Biomech. 9, 397–405. doi:10.1016/0021-9290(76)90117-2

CrossRef Full Text | Google Scholar

Daniel, D. M., Akeson, W. H., and O’Connor, J. J. (1990). Knee Ligaments: Structure, Function, Injury and Repair. New York, NY: Raven Press.

Google Scholar

Danylchuk, K. (1975). Studies on the Morphometric and Biomechanical Characteristica of Ligaments of the Knee Joint. M.Sc. thesis, University of Western Ontario, London, ON.

Google Scholar

DeFrate, L. E., Gill, T. J., and Li, G. (2004). In vivo function of the posterior cruciate ligament during weightbearing knee flexion. Am. J. Sports Med. 32, 1923–1928. doi:10.1177/0363546504264896

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Dhaher, Y. Y., Kwon, T. H., and Barry, M. (2010). The effect of connective tissue material uncertainties on knee joint mechanics under isolated loading conditions. J. Biomech. 43, 3118–3125. doi:10.1016/j.jbiomech.2010.08.005

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Diamant, J., Keller, A., Baer, E., Litt, M., and Arridge, R. G. (1972). Collagen; ultrastructure and its relation to mechanical properties as a function of ageing. Proc. R. Soc. Lond. B Biol. Sci. 180, 293–315. doi:10.1098/rspb.1972.0019

CrossRef Full Text | Google Scholar

Donahue, T. L., Hull, M. L., Rashid, M. M., and Jacobs, C. R. (2002). A finite element model of the human knee joint for the study of tibio-femoral contact. J. Biomech. Eng. 124, 273–280. doi:10.1115/1.1470171

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Essinger, J. R., Leyvraz, P. F., Heegard, J. H., and Robertson, D. D. (1989). A mathematical model for the evaluation of the behaviour during flexion of condylar-type knee prostheses. J. Biomech. 22, 1229–1241. doi:10.1016/0021-9290(89)90225-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fitzpatrick, C. K., Clary, C. W., and Rullkoetter, P. J. (2012). The role of patient, surgical, and implant design variation in total knee replacement performance. J. Biomech. 45, 2092–2102. doi:10.1016/j.jbiomech.2012.05.035

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fitzpatrick, C. K., Kim, R. H., Ali, A. A., Smoger, L. M., and Rullkoetter, P. J. (2013). Effects of resection thickness on mechanics of resurfaced patellae. J. Biomech. 46, 1568–1575. doi:10.1016/j.jbiomech.2013.03.016

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fitzpatrick, C. K., Komistek, R. D., and Rullkoetter, P. J. (2014). Developing simulations to reproduce in vivo fluoroscopy kinematics in total knee replacement patients. J. Biomech. 47, 2398–2405. doi:10.1016/j.jbiomech.2014.04.024

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Freutel, M., Seitz, A. M., Ignatius, A., and Dürselen, L. (2014). Influence of partial meniscectomy on attachment forces, superficial strain and contact mechanics in porcine knee joints. Knee Surg. Sports Traumatol. Arthrosc. doi:10.1007/s00167-014-2951-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gardiner, J. C., and Weiss, J. A. (2003). Subject-specific finite element analysis of the human medial collateral ligament during valgus knee loading. J. Orthop. Res. 21, 1098–1106. doi:10.1016/S0736-0266(03)00113-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gasser, T. C., Ogden, R. W., and Holzapfel, G. A. (2006). Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3, 15–35. doi:10.1098/rsif.2005.0073

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Girgis, F. G., Marshall, J. L., and Monajem, A. (1975). The cruciate ligaments of the knee joint. Anatomical, functional and experimental analysis. Clin. Orthop. Relat. Res. 106, 216–231. doi:10.1097/00003086-197501000-00033

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Grood, E. S., and Hefzy, M. S. (1982). An analytical technique for modeling knee joint stiffness – part I: ligamentous forces. J. Biomech. Eng. 104, 330–337. doi:10.1115/1.3138367

CrossRef Full Text | Google Scholar

Guess, T. M., and Stylianou, A. (2012). Simulation of anterior cruciate ligament deficiency in a musculoskeletal model with anatomical knees. Open Biomed. Eng. J. 6, 23–32. doi:10.2174/1874230001206010023

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Guess, T. M., Thiagarajan, G., Kia, M., and Mishra, M. (2010). A subject specific multibody model of the knee with menisci. Med. Eng. Phys. 32, 505–515. doi:10.1016/j.medengphy.2010.02.020

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Halloran, J. P., Petrella, A. J., and Rullkoetter, P. J. (2005). Explicit finite element modeling of total knee replacement mechanics. J. Biomech. 38, 323–331. doi:10.1016/j.jbiomech.2004.02.046

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hansen, P., Bojsen-Moller, J., Aagaard, P., Kjaer, M., and Magnusson, S. P. (2006). Mechanical properties of the human patellar tendon, in vivo. Clin. Biomech. (Bristol, Avon) 21, 54–58. doi:10.1016/j.clinbiomech.2005.07.008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Harner, C. D., Vogrin, T. M., Höher, J., Ma, C. B., and Woo, S. L. (2000). Biomechanical analysis of a posterior cruciate ligament reconstruction. Deficiency of the posterolateral structures as a cause of graft failure. Am. J. Sports Med. 28, 32–39.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Harner, C. D., Vogrin, T. M., and Woo, S. L. (2001). The Posterior Cruciate Ligament Injuries. Heidelberg: Springer.

Google Scholar

Harner, C. D., Xerogeanes, J. W., Livesay, G. A., Carlin, G. J., Smith, B. A., Kusayama, T., et al. (1995). The human posterior cruciate ligament complex: an interdisciplinary study. Ligament morphology and biomechanical evaluation. Am. J. Sports Med. 23, 736–745. doi:10.1177/036354659502300617

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Haut, T. L., and Haut, R. C. (1997). The state of tissue hydration determines the strain-rate-sensitive stiffness of human patellar tendon. J. Biomech. 30, 79–81. doi:10.1016/S0021-9290(96)00108-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Haut Donahue, T. L., Hull, M. L., Rashid, M. M., and Jacobs, C. R. (2003). How the stiffness of meniscal attachments and meniscal material properties affect tibio-femoral contact pressure computed using a validated finite element model of the human knee joint. J. Biomech. 36, 19–34. doi:10.1016/S0021-9290(02)00305-6

CrossRef Full Text | Google Scholar

Hefzy, M. S., and Grood, E. S. (1983). An analytical technique for modeling knee joint stiffness – part II: ligamentous geometric nonlinearities. J. Biomech. Eng. 105, 145–153. doi:10.1115/1.3138398

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Henninger, H. B., Reese, S. P., Anderson, A. E., and Weiss, J. A. (2010). Validation of computational models in biomechanics. Proc. Inst. Mech. Eng. H 210, 801–812. doi:10.1243/09544119JEIM649

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hirokawa, S., and Tsuruno, R. (1997). Hyper-elastic model analysis of anterior cruciate ligament. Med. Eng. Phys. 19, 637–651. doi:10.1016/S1350-4533(96)00077-X

CrossRef Full Text | Google Scholar

Holzapfel, G. A., Gasser, T. C., and Ogden, R. W. (2000). A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 61, 1–48. doi:10.1023/A:1010835316564

CrossRef Full Text | Google Scholar

Innocenti, B., Bilgen, O. F., Labey, L., van Lenthe, G. H., Sloten, J. V., and Catani, F. (2014). Load sharing and ligament strains in balanced, overstuffed and understuffed UKA. A validated finite element analysis. J. Arthroplasty 29, 1491–1498. doi:10.1016/j.arth.2014.01.020

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Innocenti, B., Pianigiani, S., Labey, L., Victor, J., and Bellemans, J. (2011). Contact forces in several TKA designs during squatting: a numerical sensitivity analysis. J. Biomech. 44, 1573–1581. doi:10.1016/j.jbiomech.2011.02.081

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Johnson, G. A., Tramaglini, D. M., Levine, R. E., Ohno, K., Choi, N. Y., and Woo, S. L. (1994). Tensile and viscoelastic properties of human patellar tendon. J. Orthop. Res. 12, 796–803. doi:10.1002/jor.1100120607

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kazemi, M., and Li, L. P. (2014). A viscoelastic poromechanical model of the knee joint in large compression. Med. Eng. Phys. 36, 998–1006. doi:10.1016/j.medengphy.2014.04.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kazemi, M., Li, L. P., Savard, P., and Buschmann, M. D. (2011). Creep behavior of the intact and meniscectomy knee joints. J. Mech. Behav. Biomed. Mater. 4, 1351–1358. doi:10.1016/j.jmbbm.2011.05.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Li, G., Gil, J., Kanamori, A., and Woo, S. L. (1999). A validated three-dimensional computational model of a human knee joint. J. Biomech. Eng. 121, 657–662. doi:10.1115/1.2800871

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Limbert, G., Taylor, M., and Middleton, J. (2004). Three-dimensional finite element modelling of the human ACL: simulation of passive knee flexion with a stressed and stress-free ACL. J. Biomech. 37, 1723–1731. doi:10.1016/j.jbiomech.2004.01.030

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Liu, X., and Zhang, M. (2013). Redistribution of knee stress using laterally wedged insole intervention: finite element analysis of knee-ankle-foot complex. Clin. Biomech. (Bristol, Avon) 28, 61–67. doi:10.1016/j.clinbiomech.2012.10.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Louis-Ugbo, J., Leeson, B., and Hutton, W. C. (2004). Tensile properties of fresh human calcaneal (Achilles) tendons. Clin. Anat. 17, 30–35. doi:10.1002/ca.10126

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Maas, S. A., Ellis, B. J., Ateshian, G. A., and Weiss, J. A. (2012). FEBio: finite elements for biomechanics. J. Biomech. Eng. 134, 011005. doi:10.1115/1.4005694

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Maletsky, L. P., and Hillberry, B. M. (2005). Simulating dynamic activities using a five-axis knee aimulator. J. Biomech. Eng. 127, 123–133. doi:10.1115/1.1846070

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marouane, H., Shirazi-Adl, A., Adouni, M., and Hashemi, J. (2014). Steeper posterior tibial slope markedly increases ACL force in both active gait and passive knee joint under compression. J. Biomech. 47, 1353–1359. doi:10.1016/j.jbiomech.2014.01.055

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mesfar, W., and Shirazi-Adl, A. (2005). Biomechanics of the knee joint in flexion under various quadriceps forces. Knee 12, 424–434. doi:10.1016/j.knee.2005.03.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mesfar, W., and Shirazi-Adl, A. (2006a). Knee joint mechanics under quadriceps – hamstrings muscle forces are influenced by tibial restraint. Clin. Biomech. (Bristol, Avon) 21, 841–848. doi:10.1016/j.clinbiomech.2006.04.014

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mesfar, W., and Shirazi-Adl, A. (2006b). Biomechanics of changes in ACL and PCL material properties or prestrains in flexion under muscle force-implications in ligament reconstruction. Comput. Methods Biomech. Biomed. Engin. 9, 201–209. doi:10.1080/10255840600795959

CrossRef Full Text | Google Scholar

Mesfar, W., and Shirazi-Adl, A. (2008). Knee joint biomechanics in open-kinetic-chain flexion exercises. Clin. Biomech. (Bristol, Avon) 23, 477–482. doi:10.1016/j.clinbiomech.2007.11.016

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moës, N., Dolbow, J., and Belytschko, T. (1999). A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46, 131–150. doi:10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.3.CO;2-A

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moglo, K. E., and Shirazi-Adl, A. (2003a). On the coupling between anterior and posterior cruciate ligaments, and knee joint response under anterior femoral drawer in flexion: a finite element study. Clin. Biomech. (Bristol, Avon) 18, 751–759. doi:10.1016/S0268-0033(03)00140-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moglo, K. E., and Shirazi-Adl, A. (2003b). Biomechanics of passive knee joint in drawer: load transmission in intact and ACL-deficient joints. Knee 10, 265–276. doi:10.1016/S0968-0160(02)00135-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moglo, K. E., and Shirazi-Adl, A. (2005). Cruciate coupling and screw-home mechanism in passive knee joint during extension – flexion. J. Biomech. 38, 1075–1083. doi:10.1016/j.jbiomech.2004.05.033

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mootanah, R., Imhauser, C. W., Reisse, F., Carpanen, D., Walker, R. W., Koff, M. F., et al. (2014). Development and validation of a computational model of the knee joint for the evaluation of surgical treatments for osteoarthritis. Comput. Methods Biomech. Biomed. Engin. 17, 1502–1517. doi:10.1080/10255842.2014.899588

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Nimni, M. E. (1983). Collagen: structure, function, and metabolism in normal and fibrotic tissues. Semin. Arthritis Rheum. 13, 1–86. doi:10.1016/0049-0172(83)90024-0

CrossRef Full Text | Google Scholar

Noyes, F. R., Butler, D. L., Grood, E. S., Zernicke, R. F., and Hefzy, M. S. (1984). Biomechanical analysis of human ligament grafts used in knee-ligament repairs and reconstructions. J. Bone Joint Surg. Am. 66, 344–352.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Noyes, F. R., and Grood, E. S. (1976). The strength of the anterior cruciate ligament in humans and Rhesus monkeys. J. Bone Joint Surg. Am. 58, 1074–1082.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Park, H. S., Ahn, C., Fung, D. T., Ren, Y., and Zhang, L. Q. (2010). A knee-specific finite element analysis of the human anterior cruciate ligament impingement against the femoral intercondylar notch. J. Biomech. 43, 2039–2042. doi:10.1016/j.jbiomech.2010.03.015

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pena, E., Calvo, B., Martinez, M. A., and Doblare, M. (2006). A three-dimensional finite element analysis of the combined behavior of ligaments and menisci in the healthy human knee joint. J. Biomech. 39, 1686–1701. doi:10.1016/j.jbiomech.2005.04.030

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pena, E., Calvo, B., Martinez, M. A., Palanca, D., and Doblare, M. (2005). Finite element analysis of the effect of meniscal tears and meniscectomies on human knee biomechanics. Clin. Biomech. (Bristol, Avon) 20, 498–507. doi:10.1016/j.clinbiomech.2005.01.009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Perie, D., and Hobatho, M. C. (1998). In vivo determination of contact areas and pressure of the femorotibial joint using non-linear finite element analysis. Clin. Biomech. (Bristol, Avon) 13, 394–402. doi:10.1016/S0268-0033(98)00091-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pianigiani, S., Chevalier, Y., Labey, L., Pascale, V., and Innocenti, B. (2012). Tibio-femoral kinematics in different total knee arthroplasty designs during a loaded squat: a numerical sensitivity study. J. Biomech. 45, 2315–2323. doi:10.1016/j.jbiomech.2012.06.014

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pioletti, D. P., Rakotomanana, L., Benvenuti, J. F., and Leyvraz, P. F. (1998a). “Finite element model of the human anterior cruciate ligament”, in Computer Methods in Biomechanics and Biomedical Engineering, (Amsterdam: Gordon and Breach Science Publishers), 561–568.

Google Scholar

Pioletti, D. P., Rakotomanana, L. R., Benvenuti, J. F., and Leyvraz, P. F. (1998b). Viscoelastic constitutive law in large deformations: application to human knee ligaments and tendons. J. Biomech. 31, 753–757. doi:10.1016/S0021-9290(98)00077-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pioletti, D. P., Rakotomanana, L., Gilliéron, C., Leyvraz, P. F., and Benvenuti, J. F. (1996). “Nonlinear viscoelasticity of the ACL: experiments and theory,” in Computer Methods in Biomechanics and Biomedical Engineering, eds J. Middleton, M. L. Jones, and G. N. Pande (Amsterdam: Gordon and Breach Science Publishers), 271–280.

Google Scholar

Pioletti, D. P., and Rakotomanana, L. R. (2000). Non-linear viscoelastic law for soft biological tissues. Eur. J. Mech. 19, 749–759. doi:10.1016/S0997-7538(00)00202-3

CrossRef Full Text | Google Scholar

Pioletti, D. P. (1997). Viscoelastic Properties of Soft Tissues: Application to Knee Ligaments and Tendons. Ph.D., Dissertation, Ecole Polytechnique Federale de Lausanne, Lausanne.

Google Scholar

Quapp, K. M., and Weiss, J. A. (1998). Material characterization of human medial collateral ligament. J. Biomech. Eng. 120, 757–763. doi:10.1115/1.2834890

CrossRef Full Text | Google Scholar

Race, A., and Amis, A. A. (1994). The mechanical properties of the two bundles of the human posterior cruciate ligament. J. Biomech. 27, 13–24. doi:10.1016/0021-9290(94)90028-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ramaniraka, N. A., Saunier, P., Siegrist, O., and Pioletti, D. P. (2007). Biomechanical evaluation of intra-articular and extra-articular procedures in anterior cruciate ligament reconstruction: a finite element analysis. Clin. Biomech. (Bristol, Avon) 22, 336–343. doi:10.1016/j.clinbiomech.2006.10.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ramaniraka, N. A., Terrier, A., Theumann, N., and Siegrist, O. (2005). Effects of the posterior cruciate ligament reconstruction on the biomechanics of the knee joint: a finite element analysis. Clin. Biomech. (Bristol, Avon) 20, 434–442. doi:10.1016/j.clinbiomech.2004.11.014

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ren, Y., Ahn, C., Park, H. S., Fung, D. T., and Zhang, L. (2010). “Testing for material properties of the human anterior cruciate ligament,” in 3rd Annual Meeting of the American Society of Biomechanics, Pennsylvania, USA.

Google Scholar

Roarche, P. J. (1998). Verification and Validation in Computational Science and Engineering. Albuquerque, NM: Hermosa Publishers.

Google Scholar

Robinson, J. R., Bull, A. M., and Amis, A. A. (2005). Structural properties of the medial collateral ligament complex of the human knee. J. Biomech. 38, 1067–1074. doi:10.1016/j.jbiomech.2004.05.034

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Schroeder, Y., Wilson, W., Huyghe, J. M., and Baaijens, F. P. (2006). Osmoviscoelastic finite element model of the intervertebral disc. Eur. Spine J. 15(Suppl. 3), S361–S371. doi:10.1007/s00586-006-0110-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shelburne, K. B., and Pandy, M. G. (1997). A musculoskeletal model of the knee for evaluating ligament forces during isometric contractions. J. Biomech. 30, 163–176. doi:10.1016/S0021-9290(96)00119-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shin, C. S., Chaudhari, A. M., and Andriacchi, T. P. (2007). The influence of deceleration forces on ACL strain during single-leg landing: a simulation study. J. Biomech. 40, 1145–1152. doi:10.1016/j.jbiomech.2006.05.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shin, C. S., Chaudhari, A. M., and Andriacchi, T. P. (2009). The effect of isolated valgus moments on ACL strain during single-leg landing: a simulation study. J. Biomech. 42, 280–285. doi:10.1016/j.jbiomech.2008.10.031

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shirazi, R., and Shirazi-Adl, A. (2009). Analysis of partial meniscectomy and ACL reconstruction in knee joint biomechanics under a combined loading. Clin. Biomech. (Bristol, Avon) 24, 755–761. doi:10.1016/j.clinbiomech.2009.07.005

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shirazi, R., Shirazi-Adl, A., and Hurtig, M. (2008). Role of cartilage collagen fibrils networks in knee joint biomechanics under compression. J. Biomech. 41, 3340–3348. doi:10.1016/j.jbiomech.2008.09.033

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shirazi-Adl, A., and Mesfar, W. (2007). Effect of tibial tubercle elevation on biomechanics of the entire knee joint under muscle loads. Clin. Biomech. (Bristol, Avon) 22, 344–351. doi:10.1016/j.clinbiomech.2006.11.003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Song, Y., Debski, R. E., Musahl, V., Thomas, M., and Woo, S. L. (2004). A three-dimensional finite element model of the human anterior cruciate ligament: a computational analysis with experimental validation. J. Biomech. 37, 383–390. doi:10.1016/S0021-9290(03)00261-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Staubli, H. U., Schatzmann, L., Brunner, P., Rincon, L., and Nolte, L. P. (1999). Mechanical tensile properties of the quadriceps tendon and patellar ligament in young adults. Am. J. Sports Med. 27, 27–34.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Steinbruck, A., Woiczinski, M., Weber, P., Muller, P. E., Jansson, V., and Schroder, C. (2014). Posterior cruciate ligament balancing in total knee arthroplasty: a numerical study with a dynamic force controlled knee model. Biomed. Eng. Online 13, 91. doi:10.1186/1475-925X-13-91

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Stylianou, A. P., Guess, T. M., and Kia, M. (2013). Multibody muscle driven model of an instrumented prosthetic knee during squat and toe rise motions. J. Biomech. Eng. 135, 041008. doi:10.1115/1.4023982

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Subit, D., Chabrand, P., and Masson, C. (2009). A micromechanical model to predict damage and failure in biological tissues. Application to the ligament-to-bone attachment in the human knee joint. J. Biomech. 42, 261–265. doi:10.1016/j.jbiomech.2008.10.028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Trent, P. S., Walker, P. S., and Wolf, B. (1976). Ligament length patterns, strength, and rotational axes of the knee joint. Clin. Orthop. Relat. Res. 117, 263–270.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Veronda, D. R., and Westmann, R. A. (1970). Mechanical characterization of skin-finite deformations. J. Biomech. 3, 111–124. doi:10.1016/0021-9290(70)90055-2

CrossRef Full Text | Google Scholar

Viceconti, M., Olsen, S., Nolte, L. P., and Burton, K. (2005). Extracting clinically relevant data from finite element simulations. Clin. Biomech. (Bristol, Avon) 20, 451–454. doi:10.1016/j.clinbiomech.2005.01.010

CrossRef Full Text | Google Scholar

Wang, Y., Fan, Y., and Zhang, M. (2014). Comparison of stress on knee cartilage during kneeling and standing using finite element models. Med. Eng. Phys. 36, 439–447. doi:10.1016/j.medengphy.2014.01.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Weiss, J. A., Bradley, N. M., and Govindjeed, S. (1996). Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput. Methods Appl. Mech. Eng. 135, 107–128. doi:10.1016/0045-7825(96)01035-3

CrossRef Full Text | Google Scholar

Weiss, J. A., and Gardiner, J. C. (2001). Computational modeling of ligament mechanics. Crit. Rev. Biomed. Eng. 29, 303–371. doi:10.1615/CritRevBiomedEng.v29.i3.20

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Weiss, J. A., Gardiner, J. C., Ellis, B. J., Lujan, T. J., and Phatak, N. S. (2005). Three-dimensional finite element modeling of ligaments: technical aspects. Med. Eng. Phys. 27, 845–861. doi:10.1016/j.medengphy.2005.05.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Westermann, R. W., Wolf, B. R., and Elkins, J. M. (2013). Effect of ACL reconstruction graft size on simulated Lachman testing: a finite element analysis. Iowa Orthop. J. 33, 70–77.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Wismans, J., Veldpaus, F., Janssen, J., Huson, A., and Struben, P. (1980). A three-dimensional mathematical model of the knee-joint. J. Biomech. 13, 677–685. doi:10.1016/0021-9290(80)90354-1

CrossRef Full Text | Google Scholar

Withrow, T. J., Huston, L. J., Wojtys, E. M., and Ashton-Miller, J. A. (2006). The relationship between quadriceps muscle force, knee flexion, and anterior cruciate ligament strain in an in vitro simulated jump landing. Am. J. Sports Med. 34, 269–274. doi:10.1177/0363546505280906

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Woo, S. L., Hollis, J. M., Adams, D. J., Lyon, R. M., and Takai, S. (1991). Tensile properties of the human femur-anterior cruciate ligament-tibia complex. The effects of specimen age and orientation. Am. J. Sports Med. 19, 217–225. doi:10.1177/036354659101900303

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Woo, S. L., Orlando, C. A., Gomez, M. A., Frank, C. B., and Akeson, W. H. (1986). Tensile properties of the medial collateral ligament as a function of age. J. Orthop. Res. 4, 133–141. doi:10.1002/jor.1100040201

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Yoon, K. H., Kim, Y. H., Ha, J. H., Kim, K., and Park, W. M. (2010). Biomechanical evaluation of double bundle augmentation of posterior cruciate ligament using finite element analysis. Clin. Biomech. (Bristol, Avon) 25, 1042–1046. doi:10.1016/j.clinbiomech.2010.07.014

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Yu, C. H., Walker, P. S., and Dewar, M. E. (2001). The effect of design variables of condylar total knees on the joint forces in step climbing based on a computer model. J. Biomech. 34, 1011–1021. doi:10.1016/S0021-9290(01)00060-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zavatsky, A. B. (1997). A kinematic-freedom analysis of a flexed-knee-stance testing rig. J. Biomech. 30, 277–280. doi:10.1016/S0021-9290(96)00142-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zelle, J., Heesterbeek, P. J., De Waal Malefijt, M., and Verdonschot, N. (2010). Numerical analysis of variations in posterior cruciate ligament properties and balancing techniques on total knee arthroplasty loading. Med. Eng. Phys. 32, 700–707. doi:10.1016/j.medengphy.2010.04.013

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zelle, J., van de Groes, S. A., de Waal Malefijt, M. C., and Verdonschot, N. (2014). Femoral loosening of high-flexion total knee arthroplasty: the effect of posterior cruciate ligament retention and bone quality reduction. Med. Eng. Phys. 36, 318–324. doi:10.1016/j.medengphy.2013.11.015

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zelle, J., Van der Zanden, A. C., De Waal Malefijt, M., and Verdonschot, N. (2009a). Biomechanical analysis of posterior cruciate ligament retaining high-flexion total knee arthroplasty. Clin. Biomech. (Bristol, Avon) 24, 842–849. doi:10.1016/j.clinbiomech.2009.08.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zelle, J., Barink, M., De Waal Malefijt, M., and Verdonschot, N. (2009b). Thigh-calf contact: does it affect the loading of the knee in the high-flexion range? J. Biomech. 42, 587–593. doi:10.1016/j.jbiomech.2008.12.015

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar