- 1Department of Mechanical Engineering, The University of Texas at Austin, Austin, TX, USA
- 2Pathokinesiology Laboratory, Rancho Los Amigos National Rehabilitation Center, Downey, CA, USA
- 3Rehabilitation Engineering, Rancho Los Amigos National Rehabilitation Center, Downey, CA, USA
Studies of manual wheelchair propulsion often assume bilateral symmetry to simplify data collection, processing, and analysis. However, the validity of this assumption is unclear. Most investigations of wheelchair propulsion symmetry have been limited by a relatively small sample size and a focus on a single propulsion condition (e.g., level propulsion at self-selected speed). The purpose of this study was to evaluate bilateral symmetry during manual wheelchair propulsion in a large group of subjects across different propulsion conditions. Three-dimensional kinematics and handrim kinetics along with spatiotemporal variables were collected and processed from 80 subjects with paraplegia while propelling their wheelchairs on a stationary ergometer during three different conditions: level propulsion at their self-selected speed (free), level propulsion at their fastest comfortable speed (fast), and propulsion on an 8% grade at their level, self-selected speed (graded). All kinematic variables had significant side-to-side differences, primarily in the graded condition. Push angle was the only spatiotemporal variable with a significant side-to-side difference, and only during the graded condition. No kinetic variables had significant side-to-side differences. The magnitudes of the kinematic differences were low, with only one difference exceeding 5°. With differences of such small magnitude, the bilateral symmetry assumption appears to be reasonable during manual wheelchair propulsion in subjects without significant upper-extremity pain or impairment. However, larger asymmetries may exist in individuals with secondary injuries and pain in their upper extremity and different etiologies of their neurological impairment.
Introduction
Manual wheelchair propulsion is commonly assumed to be a symmetric task. The rationale for this assumption is that any asymmetry, combined with the uncoupled nature of the wheels, would make straight-line propulsion difficult (e.g., de Groot et al., 2002). Resulting steering corrections could lead to increased energy cost and other unfavorable effects (e.g., Vegter et al., 2013a), and therefore experienced manual wheelchair users likely develop symmetrical propulsion mechanics over time.
However, the prevalence of the symmetry assumption has also been influenced by the limitations in available data collection systems. Early single-camera systems only allowed the measurement of unilateral kinematics that were usually restricted to the sagittal plane (e.g., Sanderson and Sommer, 1985; Masse et al., 1992; Veeger et al., 1992). Experimental set-ups involving mirrors and/or an additional camera allowed measurement of frontal plane kinematics and the calculation of 3D kinematics (e.g., van der Woude et al., 1989; Veeger et al., 1989; Goosey et al., 1998). The collection of bilateral 3D kinematics (e.g., Rao et al., 1996; Shimada et al., 1998) eventually became standard with the proliferation of multi-camera systems. By this time, instrumented wheels and other devices that allow the measurement of handrim kinetics had also been developed (e.g., Asato et al., 1993; Rodgers et al., 1994; Wu et al., 1998). However, many current laboratories are equipped with only one instrumented wheel due to the high cost of these devices (e.g., Hurd et al., 2008a). Thus, bilateral measurements often require multiple trials in which the instrumented wheel is switched back and forth between sides, effectively doubling the time and effort necessary for data collection.
Even with bilateral data collection, studies often do not report results for both sides, but elect to either average the data across both limbs (e.g., Boninger et al., 2000) or select only one limb for analysis (e.g., Finley et al., 2004; Mercer et al., 2006; Gagnon et al., 2014). Among the studies that have examined side-to-side differences in propulsion mechanics, there is a lack of consensus regarding the presence of asymmetry. Some studies have suggested that there is no significant asymmetry in kinematic (e.g., Goosey and Campbell, 1998), kinetic (e.g., Hurd et al., 2008b), or spatiotemporal (e.g., de Groot et al., 2002) variables. However, others have found significant side-to-side differences in similar propulsion variables (Hurd et al., 2008a; Stephens and Engsberg, 2010). The lack of statistically significant differences in most previous studies may be due to small sample sizes (n ≤ 20). In addition, studies have suggested that asymmetry may be present in specific individuals even if it is not detectable when comparing side-to-side group averages (e.g., Koontz et al., 2001; Schnorenberg et al., 2014).
Another limitation of previous studies is most have only examined side-to-side differences during one propulsion condition (e.g., level propulsion at self-selected speed). However, recent studies have suggested that the level of asymmetry may be influenced by the terrain (Hurd et al., 2008a, 2009). The purpose of this study was to evaluate bilateral symmetry during manual wheelchair propulsion in a large number of subjects across different propulsion conditions. These results have important implications for experimental setups in future analyses of wheelchair propulsion mechanics.
Materials and Methods
Subjects
Symmetry data were collected and analyzed from 80 individuals with paraplegia who were free of shoulder pain and used a manual wheelchair at least 50% of the time for community mobility (74 men, 6 women; age: 37.0 ± 9.9 years; time from injury: 9.0 ± 6.6 years; height: 1.72 ± 0.09 m; mass: 74.5 ± 16.9 kg). Dominant side was self-reported by each subject (74 right-handed, 6 left-handed). The participants were recruited from outpatient clinics at Rancho Los Amigos National Rehabilitation Center and provided written informed consent in accordance with the Institutional Review Board.
Data Collection
Participants propelled their wheelchair on a stationary ergometer (Figure 1) during three conditions (e.g., Lighthall-Haubert et al., 2009): level propulsion at their self-selected speed (free), level propulsion at their fastest comfortable speed (fast), and propulsion on an 8% grade at their level self-selected speed (graded). Subjects acclimated to each condition until they felt comfortable (at least 30 s of propulsion) and a 10-s trial was recorded for each condition. Data were collected separately from both the dominant and non-dominant sides, with the side tested first randomly selected. Three-dimensional handrim kinetics were collected using an instrumented handrim (SmartWheel; Three Rivers Holdings, Mesa, AZ, USA). Trunk, ipsilateral upper extremity, and wheel kinematics were collected using a CODA motion analysis system (Charnwood Dynamics Ltd., Leicestershire, UK) with 15 active markers placed on landmarks on the body and the wheel (Figure 1).
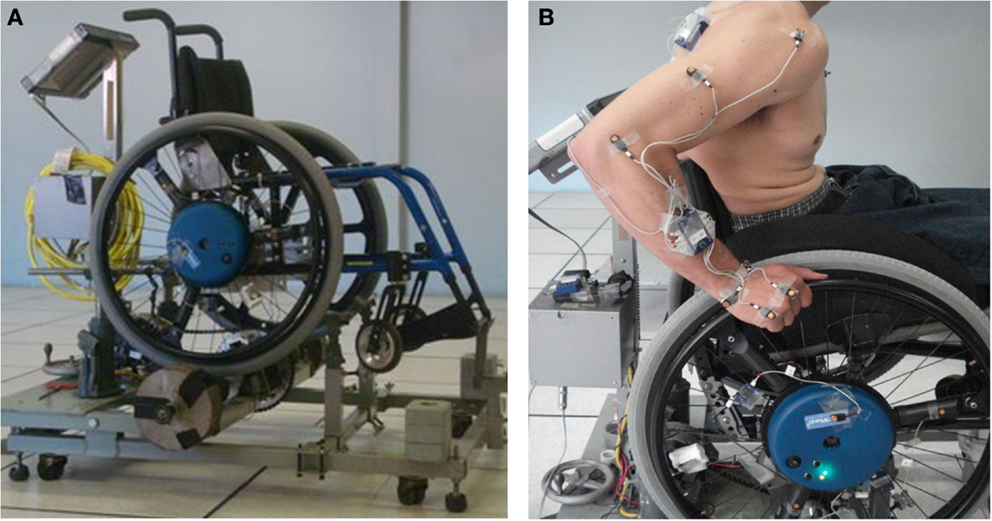
Figure 1. Experimental setup: (A) Manual wheelchair ergometer consisting of supporting frame, controlling computer and split rollers. (B) Subject on ergometer with markers affixed to the body and wheel.
Data Processing
Kinematic and kinetic data were processed in Visual3D (C-Motion, Inc., Germantown, MD, USA) using a low-pass, fourth-order, zero-lag Butterworth filter with cutoff frequencies of 8 and 10 Hz, respectively. A threshold of 1 Nm for the moment about the wheel axle was used to indicate the beginning and end of the push and recovery phases. Shoulder plane-of-elevation, shoulder elevation angle, shoulder internal-external rotation, elbow flexion-extension, and forearm pronation-supination angles were determined in accordance with International Society of Biomechanics recommendations (Wu et al., 2005). Range of motion values (ROMs) for these angles, peak and average tangential and resultant forces, fraction of effective force, cycle time, push percentage, and push angle were then calculated for each cycle and averaged across cycles for each subject during each condition (Table 1).
In addition, the third metacarpophalangeal joint center (MCP3) was located using a previously described method (Rao et al., 1996), and the MCP3 path was projected onto the plane of the handrim and averaged across cycles, resulting in a closed curve that details the full-cycle hand path or hand pattern (e.g., Figure 2; Boninger et al., 2002). Two objective, quantitative parameters were then calculated to characterize the hand pattern: net radial thickness (NRT) (a measurement of the displacement of the hand above the handrim) and total radial thickness (TRT) (a measurement of the distance between the hand and the handrim). For a detailed description of these parameters (NRT, TRT), see Slowik et al. (under review).
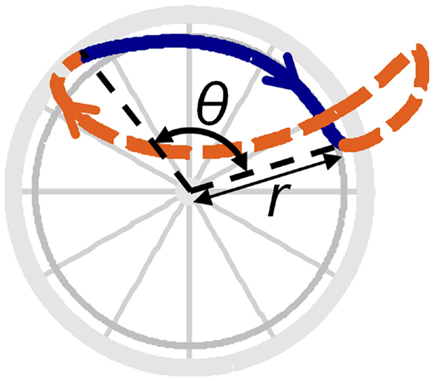
Figure 2. Hand pattern variable definitions. The solid line denotes the hand path during push phase, while the dashed line denotes the hand path during recovery phase. The handrim radius is denoted by the variable r and push angle is denoted by θ.
Statistical Analyses
To determine if there was asymmetry in any of the measured variables, statistical analyses were performed in SPSS (IBM Corp., Armonk, NY, USA) using two-factor (condition, side) repeated measures ANOVAs with a Huynh–Feldt correction in the case of non-sphericity. The condition factor consisted of three levels (free, fast, and graded) and the side factor consisted of two levels (dominant and non-dominant). If there was a significant interaction effect, pairwise comparisons were performed using paired t-tests with a Bonferroni adjustment for multiple comparisons. The unadjusted threshold for statistical significance for all analyses was set at α = 0.05. Condition main effects were not reported.
Results
Joint Kinematics
Almost all significant side-to-side differences occurred in the kinematic variables (Table 2). Elevation plane ROM had a significant interaction effect, particularly due to a larger dominant side value in the graded condition (condition*side interaction effect, p = 0.006; graded, dominant to non-dominant pairwise comparison, p = 0.014). Elevation angle ROM was larger on the dominant side than the non-dominant side (side main effect, p = 0.015). Shoulder rotation ROM was larger on the dominant side, particularly due to a larger dominant side value in the graded condition (side main effect, p = 0.007; condition*side effect, p = 0.002; graded, dominant to non-dominant pairwise comparison, p < 0.001). Elbow flexion ROM was larger on the dominant side than the non-dominant side (side main effect, p = 0.044). Forearm pronation ROM had a significant interaction effect, particularly due to a larger dominant side value in the graded condition (condition*side effect, p < 0.001; graded, dominant to non-dominant pairwise comparison, p < 0.001).
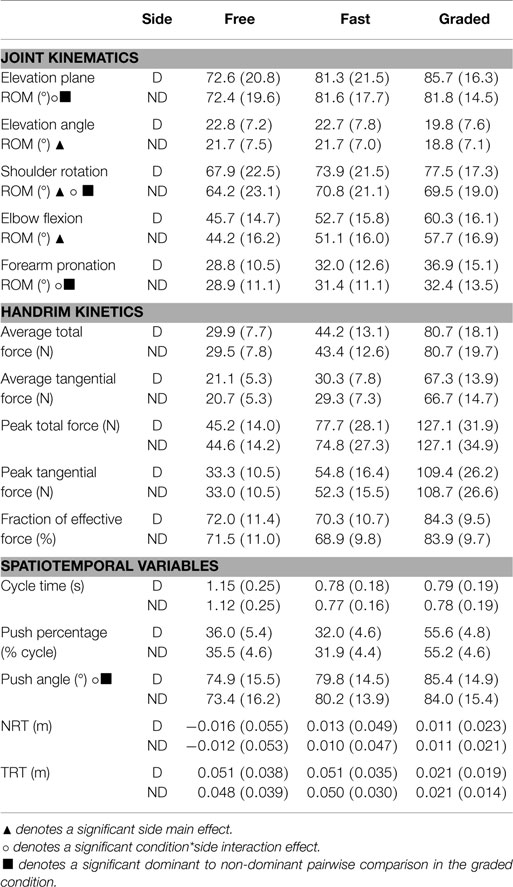
Table 2. Mean (SD) values for examined propulsion variables. D indicates a dominant side value and ND indicates a non-dominant side value.
There were no other side main effects or interaction effects, and all differences were <5° except for shoulder rotation ROM during the graded condition (8°).
Handrim Kinetics
There were no significant side main effects or interaction effects in any of the kinetic variables.
Spatiotemporal Variables
Push angle had a significant interaction effect, particularly due to a larger dominant side value in the graded condition (condition*side effect, p = 0.025; graded, dominant to non-dominant pairwise comparison, p = 0.033). There were no other significant side main effects or interaction effects in the spatiotemporal variables.
Discussion
The results suggest that low levels of asymmetry may exist in manual wheelchair propulsion, and that these levels may increase in the graded condition when the demand on the upper extremity is increased. However, we did not find any statistically significant side-to-side differences in any of the kinetic variables, and only one spatiotemporal variable (push angle) showed a significant side-to-side difference. We did find significant side-to-side differences in the joint ROMs, with dominant side values larger than those of the non-dominant side. However, the mean differences were small, with only one difference being larger than 5°. In addition, side-to-side differences were often smaller than differences between individuals or between conditions. Thus, while the comparisons showed statistical significance, the clinical significance of these differences is likely not high.
The magnitudes of the side-to-side differences were similar to those reported by others. An early study investigating racing propulsion (Goosey and Campbell, 1998) reported a non-significant mean difference of approximately 2° in the elbow flexion ROM in a sample of seven experienced wheelchair users. Others investigated standard handrim propulsion and reported non-significant mean differences of <1 N in peak and average handrim forces in 20 experienced wheelchair users (Koontz et al., 2001). Another group performed a series of three studies (Hurd et al., 2008a,b, 2009), examining side-to-side differences in kinetic and temporal variables for standard handrim propulsion on different terrains (12–14 experienced wheelchair users). All studies showed similar magnitudes of differences to the present study. Using similar statistical methods (i.e., repeated measures ANOVAs and/or paired t-tests), Hurd et al. (2008b, 2009) found only a single significant side-to-side difference (in average instantaneous power for propulsion on aggregate concrete). The third study (Hurd et al., 2008a) utilized a symmetry index and suggested that statistically significant levels of asymmetry were present for all investigated variables and terrains.
The lack of consensus regarding symmetry differences is likely due to a combination of different sample sizes and statistical methods. The present study may have been able to find statistical significance where others had not due to the large sample size (n = 80). In addition, while symmetry indices have been utilized in the study of gait (e.g., Sadeghi et al., 2000) and have potential in the analysis of manual wheelchair propulsion, the particular symmetry index used by Hurd et al. (2008a) disregarded the direction of asymmetries by taking the absolute value of observed differences, which resulted in only positive values. The difference between their symmetry index and the one that they attempted to replicate (Kaufman et al., 1996) may have led to an overestimation of the across-subjects mean levels of asymmetry. It is unlikely that dominant side data will be identical to the non-dominant side data for any single subject, and any small side-to-side differences that otherwise may have been neutralized across subjects (including those due to normal levels of experimental uncertainty and motion variability) were instead preserved by examining the absolute value.
The results of this study, in combination with previous results in the literature, suggest that the assumption of symmetry is reasonable when analyzing wheelchair propulsion in groups of subjects without secondary injury or pain in their upper extremities. However, our study only included data from subjects with paraplegia, so our conclusions may not be generalizable to other patient populations. A previous study found more asymmetry in propulsion biomechanics in individuals with multiple sclerosis than in individuals with spinal cord injury and able-bodied subjects (Fay et al., 2004), thus reinforcing the need to consider symmetry in the context of specific populations. In addition, it may not be appropriate to assume symmetry in the study of individual subjects as larger asymmetries may be present in individual subject data than in group-averaged data (e.g., Koontz et al., 2001; Schnorenberg et al., 2014), a finding that is also confirmed in our data. Individuals were found to have larger asymmetries than the group average. Studies should also be careful in assuming symmetry for propulsion during more strenuous conditions as we found the largest levels of asymmetry in the graded condition and a previous study concluded that asymmetry increased when propelling over outdoor terrain compared to laboratory terrain (Hurd et al., 2008a).
A potential limitation of this study is that only one instrumented wheel was used during data collection. As a result, dominant and non-dominant variables were recorded during separate trials. However, potential systematic differences between trials (e.g., fatigue effects) were minimized by randomly selecting the trial order. While any remaining systematic differences between trials could lead to overestimation of asymmetry, we still only found low levels. In addition, the alternative of using two instrumented wheels during a single trial is not without its own limitations. The side-to-side mean differences in kinetic variables that we observed were smaller than the documented accuracy and precision of instrumented wheels (e.g., Cooper et al., 1997; Wu et al., 1998; Guo et al., 2011). Even after calibration, there can be small differences between measurements from individual wheels, which are supported by a recent study that found differences between individual measurement wheels during a single trial were larger than single wheel differences between trials (Vegter et al., 2013b).
Another potential limitation is that subjects did not propel the wheelchair overground, but instead used a stationary ergometer set up to replicate overground propulsion. Although ergometers are unable to perfectly replicate overground propulsion, they do provide controlled conditions for data collection and have been shown to produce steady-state propulsion mechanics consistent with overground data (e.g., Koontz et al., 2001). However, propulsion on an ergometer is less constrained compared to overground propulsion. While the average power delivered to each handrim must be equivalent during straight-line overground propulsion, no such steering requirement exists for ergometer propulsion (e.g., de Groot et al., 2005). However, this limitation would likely lead to an overestimation of asymmetry, so the use of an ergometer likely did not alter the study conclusions.
In summary, our results support the assumption of symmetry in manual wheelchair propulsion for studies that analyze groups of subjects without significant upper extremity pain or impairment. Small asymmetries likely exist in propulsion variables, and these may increase when propelling under more strenuous conditions. Thus, the validity of the symmetry assumption should be carefully considered in light of the specific research aims and methods.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported by NIH Grant R01 HD049774 and a National Science Foundation Graduate Research Fellowship under Grant DGE-1110007.
References
Asato, K. T., Cooper, R. A., Robertson, R. N., and Ster, J. F. (1993). SMARTWheels: development and testing of a system for measuring manual wheelchair propulsion dynamics. IEEE Trans. Biomed. Eng. 40, 1320–1324. doi: 10.1109/10.250587
Boninger, M. L., Baldwin, M., Cooper, R. A., Koontz, A., and Chan, L. (2000). Manual wheelchair pushrim biomechanics and axle position. Arch. Phys. Med. Rehabil. 81, 608–613. doi:10.1016/S0003-9993(00)90043-1
Boninger, M. L., Souza, A. L., Cooper, R. A., Fitzgerald, S. G., Koontz, A. M., and Fay, B. T. (2002). Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Arch. Phys. Med. Rehabil. 83, 718–723. doi:10.1053/apmr.2002.32455
Cooper, R. A., Robertson, R. N., VanSickle, D. P., Boninger, M. L., and Shimada, S. D. (1997). Methods for determining three-dimensional wheelchair pushrim forces and moments: a technical note. J. Rehabil. Res. Dev. 34, 162–170.
de Groot, S., Veeger, D. H., Hollander, A. P., and Van der Woude, L. H. (2002). Wheelchair propulsion technique and mechanical efficiency after 3 weeks of practice. Med. Sci. Sports Exerc. 34, 756–766. doi:10.1097/00005768-200205000-00005
de Groot, S., Veeger, H. E., Hollander, A. P., and van der Woude, L. H. (2005). Influence of task complexity on mechanical efficiency and propulsion technique during learning of hand rim wheelchair propulsion. Med. Eng. Phys. 27, 41–49. doi:10.1016/j.medengphy.2004.08.007
Fay, B. T., Boninger, M. L., Fitzgerald, S. G., Souza, A. L., Cooper, R. A., and Koontz, A. M. (2004). Manual wheelchair pushrim dynamics in people with multiple sclerosis. Arch. Phys. Med. Rehabil. 85, 935–942. doi:10.1016/j.apmr.2003.08.093
Finley, M. A., Rasch, E. K., Keyser, R. E., and Rodgers, M. M. (2004). The biomechanics of wheelchair propulsion in individuals with and without upper-limb impairment. J. Rehabil. Res. Dev. 41, 385–394. doi:10.1682/JRRD.2004.03.0385
Gagnon, D. H., Babineau, A. C., Champagne, A., Desroches, G., and Aissaoui, R. (2014). Pushrim biomechanical changes with progressive increases in slope during motorized treadmill manual wheelchair propulsion in individuals with spinal cord injury. J. Rehabil. Res. Dev. 51, 789–802. doi:10.1682/JRRD.2013.07.0168
Goosey, V. L., and Campbell, I. G. (1998). Symmetry of the elbow kinematics during racing wheelchair propulsion. Ergonomics 41, 1810–1820. doi:10.1080/001401398185983
Goosey, V. L., Campbell, I. G., and Fowler, N. E. (1998). The relationship between three-dimensional wheelchair propulsion techniques and pushing economy. J. Appl. Biomech. 14, 412–427.
Guo, L., Kwarciak, A. M., Rodriguez, R., Sarkar, N., and Richter, W. M. (2011). Validation of a biofeedback system for wheelchair propulsion training. Rehabil. Res. Pract. 2011, 590780. doi:10.1155/2011/590780
Hurd, W. J., Morrow, M. M., Kaufman, K. R., and An, K. N. (2008a). Biomechanic evaluation of upper-extremity symmetry during manual wheelchair propulsion over varied terrain. Arch. Phys. Med. Rehabil. 89, 1996–2002. doi:10.1016/j.apmr.2008.03.020
Hurd, W. J., Morrow, M. M., Kaufman, K. R., and An, K. N. (2008b). Influence of varying level terrain on wheelchair propulsion biomechanics. Am. J. Phys. Med. Rehabil. 87, 984–991. doi:10.1097/PHM.0b013e31818a52cc
Hurd, W. J., Morrow, M. M., Kaufman, K. R., and An, K. N. (2009). Wheelchair propulsion demands during outdoor community ambulation. J. Electromyogr. Kinesiol. 19, 942–947. doi:10.1016/j.jelekin.2008.05.001
Kaufman, K. R., Miller, L. S., and Sutherland, D. H. (1996). Gait asymmetry in patients with limb-length inequality. J. Pediatr. Orthop. 16, 144–150. doi:10.1097/01241398-199603000-00002
Koontz, A. M., Cooper, R. A., and Boninger, M. L. (2001). An autoregressive modeling approach to analyzing wheelchair propulsion forces. Med. Eng. Phys. 23, 285–291. doi:10.1016/S1350-4533(00)00082-5
Lighthall-Haubert, L., Requejo, P. S., Mulroy, S. J., Newsam, C. J., Bontrager, E., Gronley, J. K., et al. (2009). Comparison of shoulder muscle electromyographic activity during standard manual wheelchair and push-rim activated power assisted wheelchair propulsion in persons with complete tetraplegia. Arch. Phys. Med. Rehabil. 90, 1904–1915. doi:10.1016/j.apmr.2009.05.023
Masse, L. C., Lamontagne, M., and O’Riain, M. D. (1992). Biomechanical analysis of wheelchair propulsion for various seating positions. J. Rehabil. Res. Dev. 29, 12–28. doi:10.1682/JRRD.1992.07.0012
Mercer, J. L., Boninger, M., Koontz, A., Ren, D., Dyson-Hudson, T., and Cooper, R. (2006). Shoulder joint kinetics and pathology in manual wheelchair users. Clin. Biomech. (Bristol, Avon) 21, 781–789. doi:10.1016/j.clinbiomech.2006.04.010
Rao, S. S., Bontrager, E. L., Gronley, J. K., Newsam, C. J., and Perry, J. (1996). Three-dimensional kinematics of wheelchair propulsion. IEEE Trans. Rehabil. Eng. 4, 152–160. doi:10.1109/86.536770
Rodgers, M. M., Gayle, G. W., Figoni, S. F., Kobayashi, M., Lieh, J., and Glaser, R. M. (1994). Biomechanics of wheelchair propulsion during fatigue. Arch. Phys. Med. Rehabil. 75, 85–93.
Sadeghi, H., Allard, P., Prince, F., and Labelle, H. (2000). Symmetry and limb dominance in able-bodied gait: a review. Gait Posture 12, 34–45. doi:10.1016/S0966-6362(00)00070-9
Sanderson, D. J., and Sommer, H. J. III (1985). Kinematic features of wheelchair propulsion. J. Biomech. 18, 423–429. doi:10.1016/0021-9290(85)90277-5
Schnorenberg, A. J., Slavens, B. A., Wang, M., Vogel, L. C., Smith, P. A., and Harris, G. F. (2014). Biomechanical model for evaluation of pediatric upper extremity joint dynamics during wheelchair mobility. J. Biomech. 47, 269–276. doi:10.1016/j.jbiomech.2013.11.014
Shimada, S. D., Robertson, R. N., Boninger, M. L., and Cooper, R. A. (1998). Kinematic characterization of wheelchair propulsion. J. Rehabil. Res. Dev. 35, 210–218.
Stephens, C. L., and Engsberg, J. R. (2010). Comparison of overground and treadmill propulsion patterns of manual wheelchair users with tetraplegia. Disabil. Rehabil. Assist. Technol. 5, 420–427. doi:10.3109/17483101003793420
van der Woude, L. H., Veeger, D. J., Rozendal, R. H., and Sargeant, T. J. (1989). Seat height in handrim wheelchair propulsion. J. Rehabil. Res. Dev. 26, 31–50.
Veeger, D., van der Woude, L. H., and Rozendal, R. H. (1989). The effect of rear wheel camber in manual wheelchair propulsion. J. Rehabil. Res. Dev. 26, 37–46.
Veeger, H. E., Lute, E. M., Roeleveld, K., and van der Woude, L. H. (1992). Differences in performance between trained and untrained subjects during a 30-s sprint test in a wheelchair ergometer. Eur. J. Appl. Physiol. Occup. Physiol. 64, 158–164. doi:10.1007/BF00717954
Vegter, R., de Groot, S., Lamoth, C., Veeger, D., and Van der Woude, L. (2013a). Initial skill acquisition of handrim wheelchair propulsion: a new perspective. IEEE Trans. Neural. Syst. Rehabil. Eng. 22, 104–113. doi:10.1109/TNSRE.2013.2280301
Vegter, R. J. K., Lamoth, C. J., de Groot, S., Veeger, D. H. E. J., and van der Woude, L. H. V. (2013b). Variability in bimanual wheelchair propulsion: consistency of two instrumented wheels during handrim wheelchair propulsion on a motor driven treadmill. J. Neuroeng. Rehabil. 10, 9. doi:10.1186/1743-0003-10-9
Wu, G., van der Helm, F. C., Veeger, H. E., Makhsous, M., Van Roy, P., Anglin, C., et al. (2005). ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion – part II: shoulder, elbow, wrist and hand. J. Biomech. 38, 981–992. doi:10.1016/j.jbiomech.2004.05.042
Keywords: asymmetry, side-to-side differences, hand dominance, speed, graded, biomechanics
Citation: Soltau SL, Slowik JS, Requejo PS, Mulroy SJ and Neptune RR (2015) An investigation of bilateral symmetry during manual wheelchair propulsion. Front. Bioeng. Biotechnol. 3:86. doi: 10.3389/fbioe.2015.00086
Received: 23 April 2015; Accepted: 25 May 2015;
Published: 11 June 2015
Edited by:
Alireza Mashaghi, Delft University of Technology, NetherlandsReviewed by:
Glen Lichtwark, The University of Queensland, AustraliaKatherine Saul, North Carolina State University, USA
Copyright: © 2015 Soltau, Slowik, Requejo, Mulroy and Neptune. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Richard R. Neptune, Department of Mechanical Engineering, The University of Texas at Austin, 204 E. Dean Keeton Street, Stop C2200, Austin, TX 78712, USA,cm5lcHR1bmVAbWFpbC51dGV4YXMuZWR1
 Shelby L. Soltau
Shelby L. Soltau Jonathan S. Slowik
Jonathan S. Slowik Philip S. Requejo
Philip S. Requejo Sara J. Mulroy2
Sara J. Mulroy2 Richard R. Neptune
Richard R. Neptune