- 1Department of Mechanical Engineering, University of Maryland College Park, College Park, MD, USA
- 2Department of Anesthesiology, Pharmacology and Therapeutics, The University of British Columbia, Vancouver, BC, Canada
The goal of this study is to derive a minimally complex but credible model of respiratory CO2 gas exchange that may be used in systematic design and pilot testing of closed-loop end-tidal CO2 controllers in mechanical ventilation. We first derived a candidate model that captures the essential mechanisms involved in the respiratory CO2 gas exchange process. Then, we simplified the candidate model to derive two lower-order candidate models. We compared these candidate models for predictive capability and reliability using experimental data collected from 25 pediatric subjects undergoing dynamically varying mechanical ventilation during surgical procedures. A two-compartment model equipped with transport delay to account for CO2 delivery between the lungs and the tissues showed modest but statistically significant improvement in predictive capability over the same model without transport delay. Aggregating the lungs and the tissues into a single compartment further degraded the predictive fidelity of the model. In addition, the model equipped with transport delay demonstrated superior reliability to the one without transport delay. Further, the respiratory parameters derived from the model equipped with transport delay, but not the one without transport delay, were physiologically plausible. The results suggest that gas transport between the lungs and the tissues must be taken into account to accurately reproduce the respiratory CO2 gas exchange process under conditions of wide-ranging and dynamically varying mechanical ventilation conditions.
Introduction
It is anticipated that autonomous closed-loop controlled mechanical ventilators will be increasingly used in the future to enhance the safety of mechanical ventilation. Automation will enable standardized treatment protocols as well as fill the gap between the increasing demands versus the limited number of respiratory experts. First, it is estimated that the failure to use recommended respiratory interventions in the intensive care unit (ICU) results in 170,000 preventable deaths per year in US (Pronovost et al., 2004). Thus, closed-loop-controlled mechanical ventilators can be an attractive option to translate the research knowledge into clinical practice via automatic knowledge transfer, which can potentially reduce errors, inappropriate interventions, and heterogeneity of knowledge and practice. Second, the number of prolonged mechanical ventilations (>96 h) was projected to have more than doubled in 2020 compared with that in 2000 (Zilberberg et al., 2008). It was also forecasted that the shortage of medical personnel with expertise in mechanical ventilation will begin in 2007 and will worsen thereafter (Angus et al., 2000). In this regard, autonomous and closed-loop-controlled mechanical ventilators can be a viable solution to guarantee quality care without exacerbating the medical personnel’s workload.
Despite their promising potential, closed-loop mechanical ventilation controllers have not yet penetrated, at least as much as anticipated, into clinical practice. This may be attributed to many reasons [such as conservatism and inertia (Cabana et al., 1999; Dent and Goldberg, 1999; Rubenfeld et al., 2004)], but a critical challenge may have been the concerns raised on the safety of these autonomous systems. Indeed, proving the validity and safety of closed-loop-controlled mechanical ventilators in preclinical testing is not trivial (see the limited number of subjects used in the testing of closed-loop mechanical ventilation controllers reported in the literature summarized in Table 1). In fact, even the new modes available in the commercialized mechanical ventilators [such as PAV (Younes, 2002), NAVA (Sinderby et al., 1999), ASV (Laubscher et al., 1994), and SmartCare™ (Dojat et al., 1992)] have not been extensively evaluated (Verbrugghe and Jorens, 2011; Cordioli et al., 2013; Rose et al., 2013).
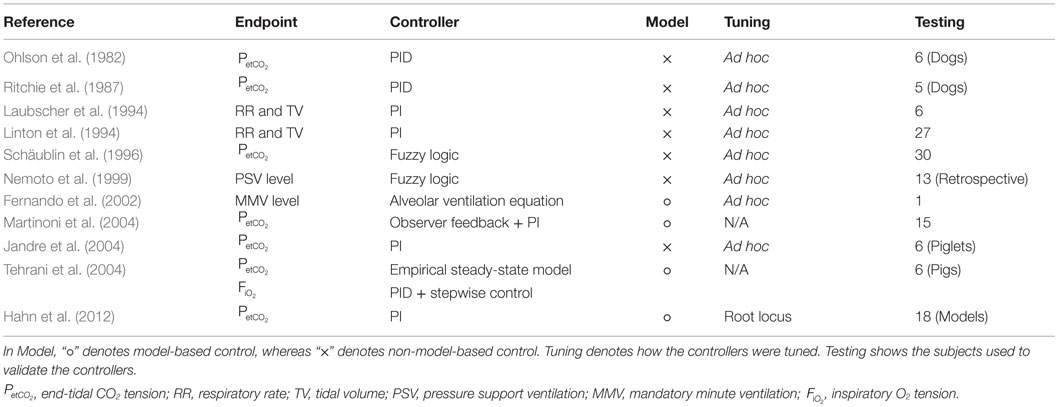
Table 1. Preclinical testing of closed-loop mechanical ventilation controllers reported in the literature.
Mathematical models of physiologic system have been promoted as viable alternative to preclinical testing. Indeed, computational models may potentially be widely used to examine and assess the safety of a range of medical devices and systems, as suggested by the guidance document recently released by the U.S. Food and Drug Administration (FDA) on the reporting of computational modeling studies in the medical device submissions (CDRH and FDA, 2014). To rigorously assess the safety, efficacy and robustness of closed-loop mechanical ventilation controllers, a mathematical model of respiratory physiology is required that possesses several desired characteristics: (1) it must reproduce a realistic respiratory response to mechanical ventilation with accuracy for trustworthy assessment of mechanical ventilation controllers, (2) it must be low-order with minimum number of parameters for tractability in controller design and testing, and (3) it must be physiologically transparent to streamline the interpretation of the testing results. However, models of respiratory physiology reported in today’s literature do not fulfill all these characteristics. Most importantly, existing models are typically too complex to be used in Monte-Carlo simulation-based testing (Chiari et al., 1997; Anderson et al., 2003; Wolf and Garner, 2007; Cheng et al., 2010).
In pursuit of the ultimate goal of realizing a computational model of respiratory physiology applicable to the design and testing of closed-loop mechanical ventilation controllers, the goal of this study is to derive a minimally complex but credible model of respiratory CO2 gas exchange that may be used in systematic design and pilot testing of closed-loop end-tidal CO2 controllers in mechanical ventilation. We first derived a candidate model that captures the essential mechanisms involved in the respiratory CO2 gas exchange process. Then, we simplified the candidate model to derive two lower-order candidate models. We compared these candidate models for predictive capability and reliability using experimental data collected from 25 pediatric subjects undergoing dynamically varying mechanical ventilation during surgical procedures.
This paper is organized as follows. Section 2 outlines the model structure, its data-based modeling procedure, and the comparative analysis approaches. Section 3 describes the experimental data and data analysis methods. Section 4 presents and discusses the results. Section 5 concludes the paper with future directions.
Respiratory Co2 Gas Exchange Model
Model Structure Selection
Respiratory CO2 gas exchange process during mechanical ventilation involves the lungs, arteries, and veins as well as body tissues (Grodins et al., 1954; Khoo et al., 1982; Batzel and Tran, 2000) (Figure 1). CO2 gas is produced in the tissues as a consequence of metabolism and is subsequently transported to the lungs via venous blood (whose CO2 tension is thus relatively high). CO2 gas is then excreted in the lungs by alveolar ventilation. The arterial blood, whose CO2 tension is relatively lower than the venous blood, is delivered back to the tissues to collect CO2 from them.
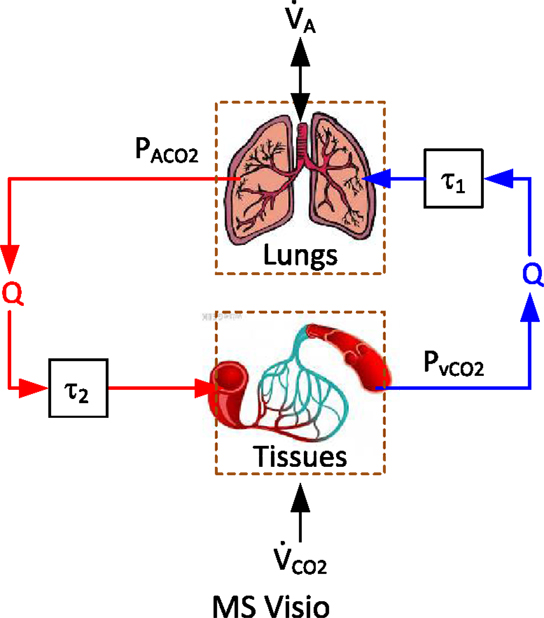
Figure 1. Essential components in respiratory CO2 gas exchange process: the lungs, arteries and veins, and the body tissues.
In this study, we model the lungs and the tissues as homogeneous compartments, while approximate the delivery of CO2 gas between them via arteries and veins as pure transport delays. The CO2 tension in the lungs (alveolar CO2 tension) is determined by the balance between CO2 supply from the venous blood and CO2 removal by the alveoli. The amount of CO2 gas supplied from the venous blood to the lungs depends on the difference between alveolar versus mixed venous CO2 concentrations as well as cardiac output (Q), while the amount of excreted CO2 gas is determined by alveolar CO2 tension and alveolar ventilation . Therefore, the rate of change in can be written as follows:
where VL is the effective lung volume, is the CO2 tension in the inspired air, τ1 is the transport delay between the tissues and the lungs, and λ = 863 mmHg lBTPS/lSTPD. The CO2 tension in the tissues is determined by the production of CO2 due to the body’s metabolic activity and its removal from the tissues via arterial blood. The amount of CO2 gas removed from the tissues depends on the difference between versus as well as Q. Therefore, the rate of change in can be written as follows:
where VB is effective tissue volume in the body and τ2 is the transport delay between the heart and the tissues. By assuming that CO2 concentration and tension are related to each other via the Henry’s law (Khoo et al., 1982; Lumb, 2005):
where α = 0.0065 lSTPD/mmHg l, β = 0.244 lSTPD/l, Eqs 1 and 2 are reduced to the following with and as state variables:
Finally, denoting , , and , and noting that , yields the following state variable representation that dictates the respiratory gas exchange process during mechanical ventilation:
where , , , and and the transport delays are the unknowns to be derived from the data. It is noted that Q and are regarded as constants (see Limitation and Future Perspectives for details).
We intend to conduct data-based modeling using minute ventilation and end-tidal CO2 tension data. To this aim, we assume that (1) (i.e., negligible dead space ventilation; see Limitation and Future Perspectives for details) and (2) (Burton, 1966; Coles et al., 1973; Ritchie et al., 1987; Williams and Babb, 1997; Brunner, 2002) (see Limitation and Future Perspectives for details). Since Eq. 5 cannot be identified solely based on and because x2 is not accessible, it is re-formulated into the following regression on 1:
where , , τ = τ1 + τ2, and . Note that only τ, but not τ1 and τ2 individually, appears in Eq. 6 because only x1 is measured. Both and data are given by discrete-time sequences. Thus, the regression Eq. 6 is discretized using the forward difference approximation (Nakamura, 1993) (this model is called M3 hereafter):
where Ts is sampling interval and τ is restricted to positive integers to be compatible with the discretization. Since the regression vector in Eq. 7 can be constructed solely based on x1 and u, and τ may be identified by fitting Eq. 6 to and .
We considered two avenues in deriving lower-order models from Eq. 4. First, noting that transport delays were not taken into account in many previous studies [see, e.g., Melo et al. (1993), Olofsen et al. (2010), Wang et al. (2010), and Karbing et al. (2011) versus Grodins et al. (1967), Khoo et al. (1982), Batzel and Tran (2000), Beda et al. (2010), and Dunn and Whiteley (2010)], a lower-order model was derived by neglecting τ in Eq. 4. This results in the following regression model (called M2 hereafter):
where . Second, Eq. 8 can be further simplified by aggregating the compartments associated with the lungs and the tissues. If we assume that gas exchange and metabolism occur in a single compartment representing the lungs and the tissues altogether, the following regression model results from Eq. 4 by setting x1 = x2 and τ1 = τ2 = 0, and then combining the two equations in Eq. 4 (called M1 hereafter):
where .
Model Identification
Since Eq. 7 is a pseudo-linear regression model due to the dependence of the regression vector ψ3 on τ, it cannot be solved via standard linear least-squares method. In addition, its parameter vector Ω3 contains the products of unknowns θ1θ3, θ2θ3, and θ2θ4, which presents a challenge in deriving θi, i = 1, …, 4 from Ω3 uniquely. Further, standard least-squares method is not ideal in maximizing the predictive capability since it minimizes one-step-ahead prediction error instead of pure (i.e., infinite-step-ahead) prediction error. To cope with these challenges, we identified Θ and τ by solving the following optimization problem:
where {Θ*,τ*} is the set of optimal model parameters, N is the number of data samples used to solve Eq. 10, x1(k) is the data at sample time k, while is the model-predicted derived from Eq. 7 by
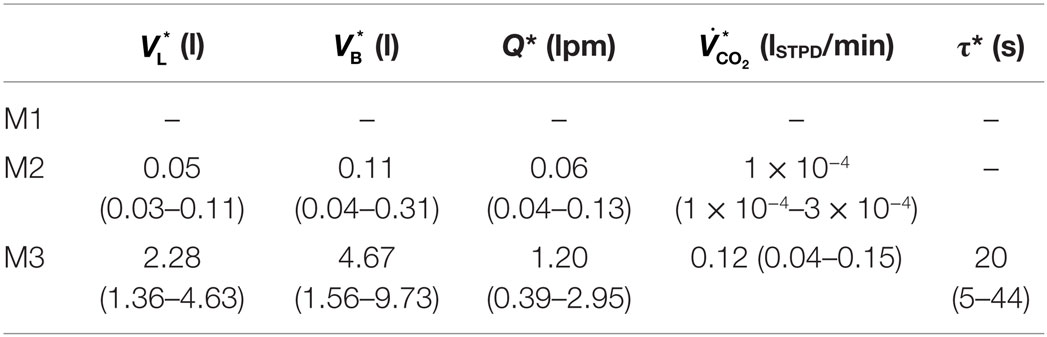
where is ψ3 computed using ’s, u(k)’s, and Ω3 = Ω3(Θ). Once Θ is determined, the physical respiratory parameters can be derived as follows. First, VL is derived as . Second, Q is derived as . Third, VB is derived as . Finally, is derived as . Thus, VL, VB, Q, and can be uniquely derived from Θ.
The parameters in M1 and M2 can be determined by solving optimization problems similar to Eq. 10 in order to maximize predictive capability, so that an objective comparison can be made on the three candidate models.
Comparative Model Analysis
The three candidate models were compared in terms of predictive capability and reliability. First, the predictive capability was measured in terms of the root-mean-squared error (RMSE) between data [x1(k)] versus model-predicted (; note that τ* = 0 for M1 and M2):
Second, the reliability was measured in terms of the asymptotic variance (Ljung, 1999), which represents the expected parametric variance estimated by the prediction error and the parametric sensitivity:
where is the prediction error variance associated with , and SN(Θ*) is the inverse sensitivity covariance matrix. Finally, the Akaike’s Information Criterion (AIC) (Burnham and Anderson, 1998) was used to compare the overall quality of the candidate models by rewarding the predictive capability and penalizing the model complexity simultaneously:
where K is the number of parameters in the model. The first term in Eq. 14 denotes the predictive capability (i.e., the goodness of fit), while the second term reflects the model complexity. The third term is to compensate for finite sample size (Burnham and Anderson, 1998).
Methods
Experimental Data
The and data used in this study were extracted from a large and anonymized physiologic database, which was constructed out of a standardized set of clinical data collected as part of a larger investigation which was approved by the Children’s and Women’s Health Centre of British Columbia. We selected 25 anonymous pediatric subjects receiving pressure-controlled mechanical ventilation during a surgical procedure. These subjects were selected based on the evidence of a large change in the ventilation setting made by the caregivers, manifested by their variability in respiratory rate (RR), peak inspiratory pressure, and I:E ratio (the ratio between inspiratory time versus expiratory time), rendering the corresponding data appropriate for data-based modeling analysis. The data were collected as trend values every 5 s using a standard respiratory module (M-CAiOVX, Datex-Ohmeda, Finland) and then saved via a custom-built, centrally located data collection software.
Data Analysis
The and data thus recorded were used to solve the optimization problems (e.g., Eq. 10 for M3) to derive the candidate models for each subject. A constrained optimization routine in MATLAB’s Optimization Toolbox was used. Multiple initial parameter values were employed to assure that the solution converged to the global minimum. The model-predicted was produced by applying and the requisite initial conditions on to Eq. 11. In deriving M3, the optimization problem was repetitively solved while the value of τ was varied via exhaustive search within a domain that was specified a priori based on the physiologically relevant values reported in the literature [see, e.g., Khoo et al. (1982) and Batzel and Tran (2000)]. In this way, multiple candidate solution sets (i.e., {Θ*,τ*}) were derived for different τ. Then, the optimal solution set was determined as the one associated with the minimum J value.
Once the optimal data-based models (M1, M2, and M3) corresponding to the 25 subjects were derived and the corresponding model-predicted produced, the candidate models associated with each subject were compared with each other using RMSE, asymptotic variance and AIC, which were computed by Eqs 12–14, respectively. The number of data samples that was used to compute RMSE, asymptotic variance, and AIC was dependent on subjects, since the amount of data available from each subject was different (see Table 2). The significance in difference among the candidate models was assessed as follows. First, the difference in predictive capability was analyzed using the paired t-test. Second, the difference in reliability associated with each element in was analyzed by applying the paired t-test to the asymptotic variance corresponding to each element in Θ*. The difference was regarded as significant in case p < 0.05. Third, in comparing the candidate models by AIC, the frequency in which M1, M2, and M3 attained the minimum AIC values was counted across the 25 subjects in order to assess how many times each of the candidate models was suggested as the best model among them.

Table 2. The range of , , mechanical ventilation settings, and the data length, shown in terms of median [interquartile range (IQR)].
Results and Discussion
A parsimonious and credible model of respiratory mechanics and physiology may expedite the design, analysis, testing, and deployment of closed-loop mechanical ventilation controllers. As an initial step toward such a computational model, the goal of this study was to derive a minimally complex and credible respiratory CO2 gas exchange model applicable to the design and pilot testing of closed-loop end-tidal CO2 controllers during mechanical ventilation. The novelty of this study is that we have rigorously compared respiratory CO2 gas exchange models with different degrees of complexity. We have evaluated the reliability and physiologic transparency of the respiratory parameters as well as the model accuracy in reproducing the relationship between minute ventilation and end-tidal CO2, which may offer unique value to the data-based computational modeling of respiratory physiology.
Data
On the average, 24.4 min length of data was available from each subject (Table 2). The ventilation settings were largely altered to yield considerable changes in and , as evidenced by Table 2 and Figure 2. In particular, Figure 2 shows that more than 30% change in (from its within-subject mean value) was made in 24 subjects, resulting in more than 29% change in in those subjects (again, from its within-subject mean value).
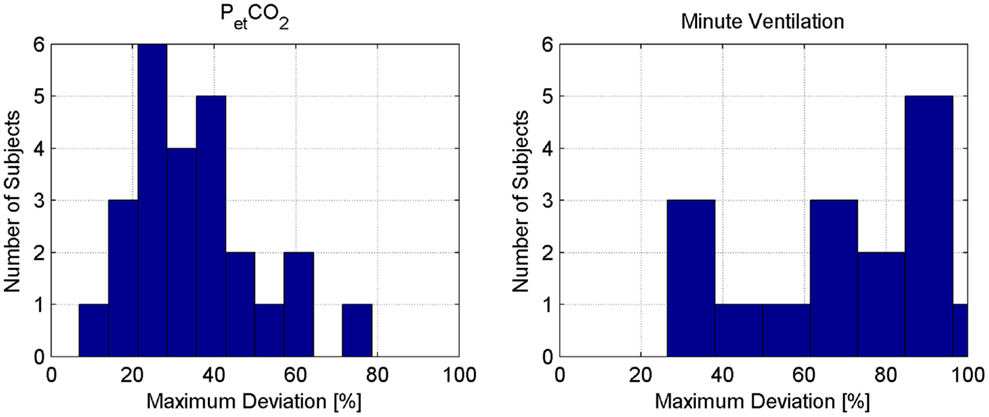
Figure 2. Distribution of the maximum percentage deviation of and from their respective within-subject mean values.
Predictive Capability and Reliability
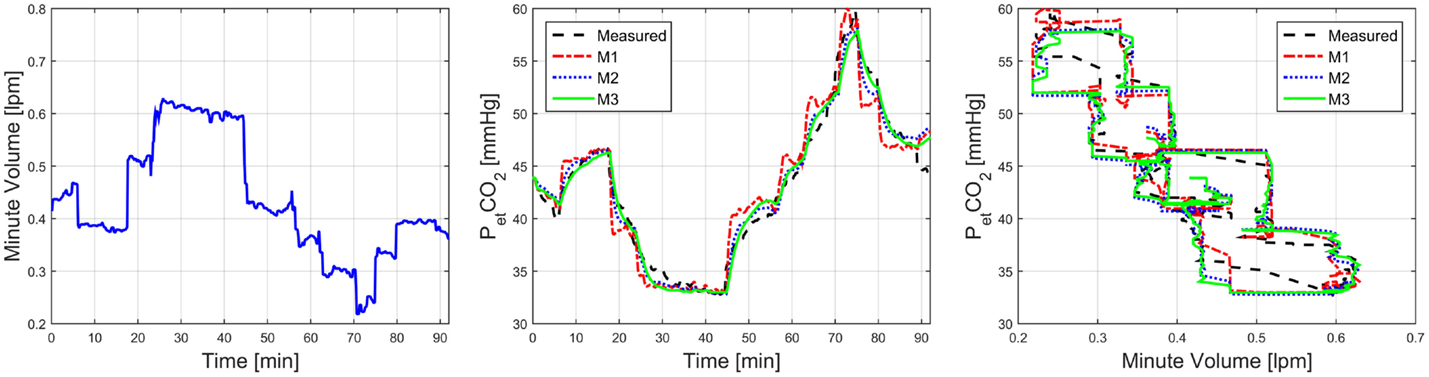
Overall, the two-compartment models (M2 and M3) exhibited superior predictive accuracy than their one-compartment counterpart (M1). Compared with M1, M2, and M3 achieved 35 and 45% reductions in RMSE, respectively, which were statistically significant (Table 3). A representative model-predicted in response to is shown in Figure 3. In this subject, both RR (7–13 1/min) and tidal volume (TV; 31.2–56.9 ml/min) were varied to yield a large change in and . This example indicates that M2 and M3 can reproduce the relationship between and with high fidelity, whereas M1 clearly exhibits deficiency. Due to its largely degraded predictive capability compared with M2 and M3, the remaining investigation was devoted to the comparison between M2 and M3.
The asymptotic variance (expressed as asymptotic standard variation) associated with , , and was reasonably small in both M2 and M3, which suggests that these parameters were adequately identified. Considering that , , and are made up of , , and Q* (which are closely related to the time constants associated with x1 and x2), reliable determination of these parameters may be attributed to the dynamic, widely varying that resulted in informative transient components in the response. On the other hand, the asymptotic variance associated with was relatively large for both M2 and M3. This may be at least in part attributed to the underlying assumption in these models that is constant. Indeed, considering that where can be reliably derived from and , uncertainty in may arise from . This interpretation is in fact supported by the examination of SN(Θ*) in Eq. 13. For all the 25 subjects, we found that the smallest eigenvalue of the sensitivity covariance matrix associated with M2 and M3 was consistently aligned with the direction of , which means that is more sensitive to , , and than . The reason for the small sensitivity of to may be because the corresponding regressor element is constant (i.e., 1), whereas the rest of the elements in ψ2 and ψ3 are widely varying. It may thus be concluded that the relatively large asymptotic variance associated with is caused by the lack of excitation in its direction by the data, which is essentially due to the assumption that is constant.
The analysis of AIC suggested that M3 is overall superior to M1 and M2, while M2 is superior to M1. The AIC results indicate that transport delay plays a crucial role in reproducing the respiratory gas exchange process under dynamically varying mechanical ventilation conditions.
Physiologic Transparency
The respiratory parameters derived for M2 were largely different from those for M3 with statistical significance (see Table 4). Compared with the respiratory parameter values for adults reported in the literature, the respiratory parameters derived for M3 appeared to be more physiologically plausible than those associated with M2. In particular, the median values of , , Q*, and derived for M3 were approximately 72, 31, 22, and 46% of the typical adult values, which appears to be at least qualitatively reasonable considering that the data used in this study were acquired from pediatric subjects.1 In contrast, the respiratory parameter values derived for M2 were unacceptably small to be physiologically realistic. Further investigation of the models showed that the predictive accuracy of M3 drastically deteriorated when its transport delay was set to 0 (much worse than M2), which suggests that the parameters derived for M2 were actually optimized reasonably well to minimize the prediction error in the absence of transport delay. Therefore, the above observation is an additional evidence to support that wide-ranging changes in mechanical ventilation settings result in emphasized transient responses in that may not be captured without transport delay.
The range of the respiratory parameters derived for M3 were wide; the interquartile ranges (IQRs) of , , Q*, and were approximately 143, 175, 213, and 92% of the respective median values. The results suggest that the subjects were associated with a wide-ranging respiratory variability, though the validity of the absolute values of the respiratory parameters cannot be established. The fact that our model could reproduce the responses of all these subjects without any a priori knowledge of these subjects is notable, because its governing Eq. 5 was derived by explicitly considering physiologic principles rather than to simply fit the data. In sum, the ability to derive subject-specific respiratory parameters suited to each subject is the strength of our model.
Limitation and Future Perspectives
This study has a number of limitations that need to be addressed in follow-up studies.
First, the lungs of the subjects analyzed in this study were mostly normal without any lung disease. Therefore, the validity of our model in subjects with respiratory pathophysiology has yet to be evaluated. It may be that our model needs to be expanded to include more physiologic mechanisms relevant to accurately reproduce the CO2 gas exchange phenomena in the presence of lung diseases. Future work must make improvements to our model to develop and validate minimally complex lumped-parameter models of respiratory CO2 gas exchange that can be used for both normal and pathologic conditions.
Second, the subjects examined in this study were subject to different anesthesia protocols and surgical procedures. This may not alter the conclusion regarding the validity of our model, because the model could yield physiologically plausible respiratory parameter values that accurately reproduced the data in all the subjects examined in this study. However, the values of the respiratory parameters associated with each subject may have been modestly affected in different ways to capture the influence of different anesthesia protocols and surgical procedures. To solidly establish the validity of our model, it must be tested against data collected under strictly standardized protocols.
Third, several key mechanisms in the model were simplified. For example, CO2 production and cardiac output were assumed constant in the model presented in this study. Noting that the subjects were undergoing surgical procedures, it may be reasonable to assume that CO2 production and cardiac output were stable due to the effect of anesthesia and the end-tidal CO2 was varied mainly by the change in the mechanical ventilator settings. However, it is possible that CO2 production and cardiac output may have changed, which may in turn have had an influence on the model parameters. The validity of the model presented in this study may be limited in subjects undergoing a large change in CO2 production and/or cardiac output. The models in this study also assumed negligible dead space ventilation and pulmonary shunt because accurate subject-specific estimation of dead space ventilation and pulmonary shunt solely based on minute ventilation and end-tidal CO2 data is in general challenging. Though the subjects examined in this study were all healthy, even healthy subjects have non-zero dead space, which may further increase under anesthesia despite the mechanical ventilation. Thus, this assumption may have had an influence on the values of the model parameters. In addition, this assumption may be far less justified in subjects with lung disease, limiting the applicability of our model. Thus, our model must be improved to explicitly incorporate dead space ventilation and pulmonary shunt.
Fourth, the models presented in this study are continuous ventilation models. As such, the tidal nature of breathing was not explicitly incorporated in the models. It has been suggested that tidal ventilation models explicitly incorporating the discontinuity in breathing due to inspiratory and expiratory phases are more desirable than continuous ventilation models when attempting to obtain a rigorous and comprehensive understanding of physiology and pathophysiology in respiratory gas exchange during mechanical ventilation [see, e.g., Hahn and Farmery (2003)] and the references therein]. The model presented in this work was able to reproduce the end-tidal CO2 response to minute ventilation. On the other hand, the validity and utility of this model beyond end-tidal CO2 (e.g., the relationship between x2 and mixed venous CO2 concentration) still need to be investigated. In this regard, care must be taken in using this model in analyzing responses to mechanical ventilation other than end-tidal CO2. At the same time, efforts to extend our continuous ventilation model to include tidal nature of breathing may also be rewarding.
Finally, the model presented in this study did not incorporate oxygen (O2) gas exchange. Considering that the primary objective of mechanical ventilation therapy is to achieve adequate arterial oxygenation, a truly viable computational model of respiratory physiology for mechanical ventilation beyond closed-loop end-tidal CO2 control must incorporate O2 dynamics. Future work must be conducted to expand our CO2 gas exchange model to enable the reproduction of both O2 and CO2 responses to mechanical ventilation.
Conclusion and Future Work
In our effort to derive a minimally complex, high-fidelity, and transparent data-based respiratory physiology model applicable to the design and pilot testing of closed-loop end-tidal CO2 controllers, we conducted a comparative data-based modeling analysis of the respiratory CO2 gas exchange process. It was shown that a two-compartment model with transport delay was able to accurately reproduce the end-tidal CO2 tension response to dynamically varying minute ventilation challenge in human subjects. Future work will include further investigation of the model as well as the design of model-based closed-loop end-tidal CO2 controllers.
Author Contributions
All authors listed have made substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This material is based upon work supported in part by the Office of Naval Research (ONR) under Grant No. N000141410591. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the ONR.
Footnote
- ^The weights of the pediatric subjects were not available in the anonymized data. However, the median size of the subjects may be estimated by comparing the values of and TV in Table 2 with those of typical adult values. For example, the median of 2.24 lpm is approximately 36.3% of the typical adult value of 6.16 lpm (TV 8.0 ml kg × weight 70 kg × RR 11 m), which is compatible to 72, 31, 22, and 46% of the typical adult values associated with , , Q, and , respectively.
References
Anderson, J. C., Babb, A. L., and Hlastala, M. P. (2003). Modeling soluble gas exchange in the airways and alveoli. Ann. Biomed. Eng. 31, 1402–1422. doi:10.1114/1.1630600
Angus, D. C., Kelley, M. A., Schmitz, R. J., White, A., and Popovich, J. Jr. (2000). Current and projected workforce requirements for care of the critically ill and patients with pulmonary disease: can we meet the requirements of an aging population? JAMA 284, 2762–2770. doi:10.1001/jama.284.21.2762
Batzel, J. J., and Tran, H. T. (2000). Modeling instability in the control system for human respiration: applications to infant non-REM sleep. Appl. Math. Comput. 110, 1–51. doi:10.1016/S0096-3003(99)00112-5
Beda, A., Jandre, F. C., and Giannella-Neto, A. (2010). A numerical model of the respiratory modulation of pulmonary shunt and PaO2 oscillations for acute lung injury. Ann. Biomed. Eng. 38, 993–1006. doi:10.1007/s10439-009-9862-3
Brunner, J. X. (2002). History and principles of closed-loop control applied to mechanical ventilation. Neth. J. Crit. Care 6, 6–9. doi:10.1186/cc1810
Burnham, K. P., and Anderson, D. R. (1998). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. New York: Springer-Verlag.
Burton, G. W. (1966). The value of carbon dioxide monitoring during anaesthesia. Anaesthesia 21, 173–183. doi:10.1111/j.1365-2044.1966.tb02573.x
Cabana, M. D., Rand, C. S., Powe, N. R., Wu, A. W., Wilson, M. H., Abboud, P. A. C., et al. (1999). Why don’t physicians follow clinical practice guidelines? A framework for improvement. JAMA 282, 1458–1465. doi:10.1001/jama.282.15.1458
CDRH, FDA. (2014). Reporting of Computational Modeling Studies in Medical Device Submissions – Draft Guidance for Industry and Food and Drug Administration Staff. Rockville: Food and Drug Administration. Available at: http://www.fda.gov/downloads/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/UCM381813.pdf
Cheng, L., Ivanova, O., Fan, H. H., and Khoo, M. C. (2010). An integrative model of respiratory and cardiovascular control in sleep-disordered breathing. Respir. Physiol. Neurobiol. 174, 4–28. doi:10.1016/j.resp.2010.06.001
Chiari, L., Avanzolini, G., and Ursino, M. (1997). A comprehensive simulator of the human respiratory system: validation with experimental and simulated data. Ann. Biomed. Eng. 25, 985–999. doi:10.1007/BF02684134
Coles, J. R., Brown, W. A., and Lampard, D. G. (1973). Computer control of respiration and anaesthesia. Med. Biol. Eng. 11, 262–267. doi:10.1007/BF02475535
Cordioli, R. L., Akoumianaki, E., and Brochard, L. (2013). Nonconventional ventilation techniques. Curr. Opin. Crit. Care 19, 31–37. doi:10.1097/MCC.0b013e32835c517d
Dent, E. B., and Goldberg, S. G. (1999). Challenging “resistance to change”. J. Appl. Behav. Sci. 35, 25–41. doi:10.1177/0021886399351003
Dojat, M., Brochard, L., Lemaire, F., and Harf, A. (1992). A knowledge-based system for assisted ventilation of patients in intensive care units. Int. J. Clin. Monit. Comput. 9, 239–250. doi:10.1007/BF01133619
Dunn, S. J., and Whiteley, J. P. (2010). Modeling alveolar volume changes during periodic breathing in heterogeneously ventilated lungs. Ann. Biomed. Eng. 38, 2988–2999. doi:10.1007/s10439-010-0034-2
Fernando, T., Cade, J., and Packer, J. (2002). Automatic control of arterial carbon dioxide tension in mechanically ventilated patients. IEEE Trans. Inf. Technol. Biomed. 6, 269–276. doi:10.1109/TITB.2002.806084
Grodins, F. S., Buell, J., and Bart, A. J. (1967). Mathematical analysis and digital simulation of the respiratory control system. J. Appl. Physiol. 22, 260–276.
Grodins, F. S., Gray, J. S., Schroeder, K. R., Norins, A. L., and Jones, R. W. (1954). Respiratory responses to CO2 inhalation. A theoretical study of a nonlinear biological regulator. J. Appl. Physiol. 7, 283–308.
Hahn, C. E. W., and Farmery, A. D. (2003). Gas exchange modelling: no more gills, please. Br. J. Anaesth. 91, 2–15. doi:10.1093/bja/aeg142
Hahn, J. O., Dumont, G. A., and Ansermino, J. M. (2012). System identification and closed-loop control of end-tidal CO2 in mechanically ventilated patients. IEEE Trans. Inf. Technol. Biomed. 16, 1176–1184. doi:10.1109/TITB.2012.2204067
Jandre, F. C., Pino, A. V., Lacorte, I., Neves, J. H. S., and Giannella-Neto, A. (2004). A closed-loop mechanical ventilation controller with explicit objective functions. IEEE Trans. Biomed. Eng. 51, 823–831. doi:10.1109/TBME.2004.826678
Karbing, D. S., Kjærgaard, S., Andreassen, S., Espersen, K., and Rees, S. E. (2011). Minimal model quantification of pulmonary gas exchange in intensive care patients. Med. Eng. Phys. 33, 240–248. doi:10.1016/j.medengphy.2010.10.007
Khoo, M. C., Kronauer, R. E., Strohl, K. P., and Slutsky, A. S. (1982). Factors inducing periodic breathing in humans – a general model. J. Appl. Physiol. 53, 644–659.
Laubscher, T. P., Heinrichs, W., Weiler, N., Hartmann, G., and Brunner, J. X. (1994). An adaptive lung ventilation controller. IEEE Trans. Biomed. Eng. 41, 51–59. doi:10.1109/10.277271
Linton, D. M., Potgieter, P. D., Davis, S., Fourie, A. T., Brunner, J. X., and Laubscher, T. P. (1994). Automatic weaning from mechanical ventilation using an adaptive lung ventilation controller. Chest 106, 1843–1850. doi:10.1378/chest.106.6.1843
Ljung, L. (1999). System Identification: Theory for the User. Upper Saddle River, NJ: Prentice-Hall.
Lumb, A. B. (2005). Nunn’s Applied Respiratory Physiology, 6th Edn. Edinburgh; Philadelphia, PA: Elsevier.
Martinoni, E. P., Pfister, C. A., Stadler, K. S., Schumacher, P. M., Leibundgut, D., Bouillon, T., et al. (2004). Model-based control of mechanical ventilation: design and clinical validation. Br. J. Anaesth. 92, 800–807. doi:10.1093/bja/aeh145
Melo, M. F., Loeppky, J. A., Caprihan, A., and Luft, U. C. (1993). Alveolar ventilation to perfusion heterogeneity and diffusion impairment in a mathematical model of gas exchange. Comput. Biomed. Res. 26, 103–120. doi:10.1006/cbmr.1993.1007
Nemoto, T., Hatzakis, G. E., Thorpe, C. W., Olivenstein, R., Dial, S., and Bates, J. H. (1999). Automatic control of pressure support mechanical ventilation using fuzzy logic. Am. J. Respir. Crit. Care Med. 160, 550–556. doi:10.1164/ajrccm.160.2.9809013
Ohlson, K. B., Westenskow, D. R., and Jordan, W. S. (1982). A microprocessor based feedback controller for mechanical ventilation. Ann. Biomed. Eng. 10, 35–48. doi:10.1007/BF02584213
Olofsen, E., Boom, M., Nieuwenhuijs, D., Sarton, E., Teppema, L., Aarts, L., et al. (2010). Modeling the non-steady state respiratory effects of remifentanil in awake and propofol-sedated healthy volunteers. Anesthesiology 112, 1382–1395. doi:10.1097/ALN.0b013e3181d69087
Pronovost, P. J., Rinke, M. L., Emery, K., Dennison, C., Blackledge, C., and Berenholtz, S. M. (2004). Interventions to reduce mortality among patients treated in intensive care units. J. Crit. Care 19, 158–164. doi:10.1016/j.jcrc.2004.07.003
Ritchie, R. G., Ernst, E. A., Pate, B. L., Pearson, J. D., and Sheppard, L. C. (1987). Closed-loop control of an anesthesia delivery system: development and animal testing. IEEE Trans. Biomed. Eng. 6, 437–443. doi:10.1109/TBME.1987.326078
Rose, L., Schultz, M. J., Cardwell, C. R., Jouvet, P., McAuley, D. F., and Blackwood, B. (2013). Automated versus non-automated weaning for reducing the duration of mechanical ventilation for critically ill adults and children. Cochrane Database Syst. Rev. 6, CD009235. doi:10.1002/14651858.CD009235.pub2
Rubenfeld, G. D., Cooper, C., Carter, G., Thompson, B. T., and Hudson, L. D. (2004). Barriers to providing lung-protective ventilation to patients with acute lung injury. Crit. Care Med. 32, 1289–1293. doi:10.1097/01.CCM.0000127266.39560.96
Schäublin, J., Derighetti, M., Feigenwinter, P., Petersen-Felix, S., and Zbinden, A. M. (1996). Fuzzy logic control of mechanical ventilation during anaesthesia. Br. J. Anaesth. 77, 636–641. doi:10.1093/bja/77.5.636
Sinderby, C., Navalesi, P., Beck, J., Skrobik, Y., Comtois, N., Friberg, S., et al. (1999). Neural control of mechanical ventilation in respiratory failure. Nat. Med. 5, 1433–1436. doi:10.1038/71012
Tehrani, F., Rogers, M., Lo, T., Malinowski, T., Afuwape, S., Lum, M., et al. (2004). A dual closed-loop control system for mechanical ventilation. J. Clin. Monit. Comput. 18, 111–129. doi:10.1023/B:JOCM.0000032744.99885.38
Verbrugghe, W., and Jorens, P. G. (2011). Neurally adjusted ventilatory assist: a ventilation tool or a ventilation toy? Respir. Care 56, 327–335. doi:10.4187/respcare.00775
Wang, A., Mahfouf, M., Mills, G. H., Panoutsos, G., Linkens, D. A., Goode, K., et al. (2010). Intelligent model-based advisory system for the management of ventilated intensive care patients. Part II: advisory system design and evaluation. Comput. Methods Programs Biomed. 99, 208–217. doi:10.1016/j.cmpb.2010.03.009
Williams, J. S., and Babb, T. G. (1997). Differences between estimates and measured during rest and exercise in older subjects. J. Appl. Physiol. 83, 312–316.
Wolf, M. B., and Garner, R. P. (2007). A mathematical model of human respiration at altitude. Ann. Biomed. Eng. 35, 2003–2022. doi:10.1007/s10439-007-9361-3
Younes, M. (2002). “Proportional assist ventilation,” in Mechanical Ventilation and Weaning, eds M. D. Jordi Mancebo, M. D. Alvar Net, and M. D. Laurent Brochard (Berlin; Heidelberg: Springer), 39–73.
Keywords: respiratory CO2 gas exchange, data-based modeling, closed-loop mechanical ventilation control
Citation: Kim C-S, Ansermino JM and Hahn J-O (2016) A Comparative Data-Based Modeling Study on Respiratory CO2 Gas Exchange during Mechanical Ventilation. Front. Bioeng. Biotechnol. 4:8. doi: 10.3389/fbioe.2016.00008
Received: 10 August 2015; Accepted: 20 January 2016;
Published: 03 February 2016
Edited by:
Timothy W. Secomb, University of Arizona, USAReviewed by:
William Andrew Pruett, University of Mississippi Medical Center, USATuhin K. Roy, Mayo Clinic, USA
Copyright: © 2016 Kim, Ansermino and Hahn. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jin-Oh Hahn, amhhaG4xMkB1bWQuZWR1
 Chang-Sei Kim
Chang-Sei Kim J. Mark Ansermino
J. Mark Ansermino Jin-Oh Hahn
Jin-Oh Hahn