- Fachinstitut für Theoretische Biologie (ITB), Institut für Biologie, Humboldt-Universität zu Berlin, Berlin, Germany
Oxygenic photosynthesis dominates global primary productivity ever since its evolution more than three billion years ago. While many aspects of phototrophic growth are well understood, it remains a considerable challenge to elucidate the manifold dependencies and interconnections between the diverse cellular processes that together facilitate the synthesis of new cells. Phototrophic growth involves the coordinated action of several layers of cellular functioning, ranging from the photosynthetic light reactions and the electron transport chain, to carbon-concentrating mechanisms and the assimilation of inorganic carbon. It requires the synthesis of new building blocks by cellular metabolism, protection against excessive light, as well as diurnal regulation by a circadian clock and the orchestration of gene expression and cell division. Computational modeling allows us to quantitatively describe these cellular functions and processes relevant for phototrophic growth. As yet, however, computational models are mostly confined to the inner workings of individual cellular processes, rather than describing the manifold interactions between them in the context of a living cell. Using cyanobacteria as model organisms, this contribution seeks to summarize existing computational models that are relevant to describe phototrophic growth and seeks to outline their interactions and dependencies. Our ultimate aim is to understand cellular functioning and growth as the outcome of a coordinated operation of diverse yet interconnected cellular processes.
1. Introduction
Almost all life on our planet ultimately depends on harvesting the light energy provided by the sun and the subsequent conversion of atmospheric CO2 and other inorganic nutrients into the building blocks of life. As one of the key inventions in evolution, oxygenic photosynthesis has transformed life on Earth and dominates the Earth’s primary productivity today (Lane, 2002; Morton, 2009). Beyond their evolutionary and ecological importance, phototrophic organisms are an essential resource for humankind and provide almost all food, feed, and fiber required to sustain human life on this planet with more than 7 billion inhabitants. Many of our strategies to master the challenges of the 21st century will inevitably rely on the growth of phototrophic organisms. Making better use of the sun’s light energy while avoiding past mistakes of industrial agriculture related to water usage, energy expenditure, eutrophication, and land use are necessary steps for a sustainable future.
Phototrophic microorganisms, in particular cyanobacteria, hold great promise as a renewable resource. Cyanobacteria are able to grow with high yield under adverse conditions and their cultivation does not rely on traditional farmland or fresh water. To make use of the biotechnological potential of cyanobacteria, however, requires further understanding of the organization of phototophic growth. While many aspects of phototrophic growth are well known and many details of photosynthetic functioning have been unraveled by decades of active research, it still remains a considerable challenge to understand the individual cellular processes in the context of a living cell.
To this end, the construction of computational models of cellular processes offers the possibility to investigate the emergent properties that arise from interacting processes. Corresponding to the path of experimental research, however, to date almost all computational models involving cyanobacterial functioning and growth focus on the inner workings of individual processes, such as the path of electrons in photosystem II or the functioning of the circadian clock. But phototrophic growth is an organismic property. It is not so much an individual process that gives rise to cellular growth, rather it is the interplay of individual processes that bears reproduction and growth of living cells.
In this contribution, we seek to provide an overview on processes relevant to cyanobacterial growth and summarize the available computational models thereof. Our aim is not encyclopedic, that is, we do not aim for a comprehensive account of all available models. Rather, we seek to focus on representative models that may contribute to our understanding of the functioning of a cell as a whole. Our focus are also not the, albeit important, minutiae of individual processes and models, but rather how they can be collated into a coherent whole. Our starting point is a set of existing computational descriptions of cellular processes and their possible interactions. Our ultimate goal is to describe cellular adaptation, cellular resource allocation, and phototrophic growth in complex environments. Or, as more eloquently put by Neidhardt (1999) already more than 15 years ago: “We must solve the cell. That is, we must do our best to design a computer-based model that can predict overall cell behavior for steady states of growth and for transitions between steady states. The model will at first be crude, inaccurate, and a complete failure at some tasks. With increasing refinement based on additional experimental data, the model should gradually improve. Importantly, the model will guide experimental inquiry by indicating areas of inadequate, insufficient, or incorrect information. Vitally, it is only through such modeling of whole-system behavior—that is, of growth—that one will learn how near and how far our knowledge takes us toward understanding the living cell.”
Our premise is that sophisticated computational models are already available for many of the processes that underlie phototrophic growth. Modeling their interactions, however, is still no trivial task. First, most models focus on the inner workings of the processes they describe—and therefore often do not describe key variables that govern the interaction with other processes. Second, the various subprocesses and time scales involved in a computational description of phototrophic growth typically require the use of different mathematical and computational concepts, which cannot always be easily reconciled within a single computational description. We seek to summarize these different computational descriptions and aim to highlight common variables and interactions. Importantly, we do not necessarily aim at a single unified model that encompassed all aspects of a growing cell. Rather, we argue for a modular approach—a growing set of models that describe aspects of cyanobacterial growth on different temporal and spatial scales. Depending on the research question, and the temporal and spatial scales involved in this particular research question, different descriptions of cyanobacterial functioning may be chosen—and utilized to derive the emergent properties of cellular growth by putting the parts together.
2. Modeling Phototrophic Growth: An Overview
Cellular growth is an organismic process that arises from a coordinated interplay of cellular functions. In the following, we briefly describe the key processes relevant to cyanobacterial functioning and growth in complex environments. An overview is provided in Figure 1.
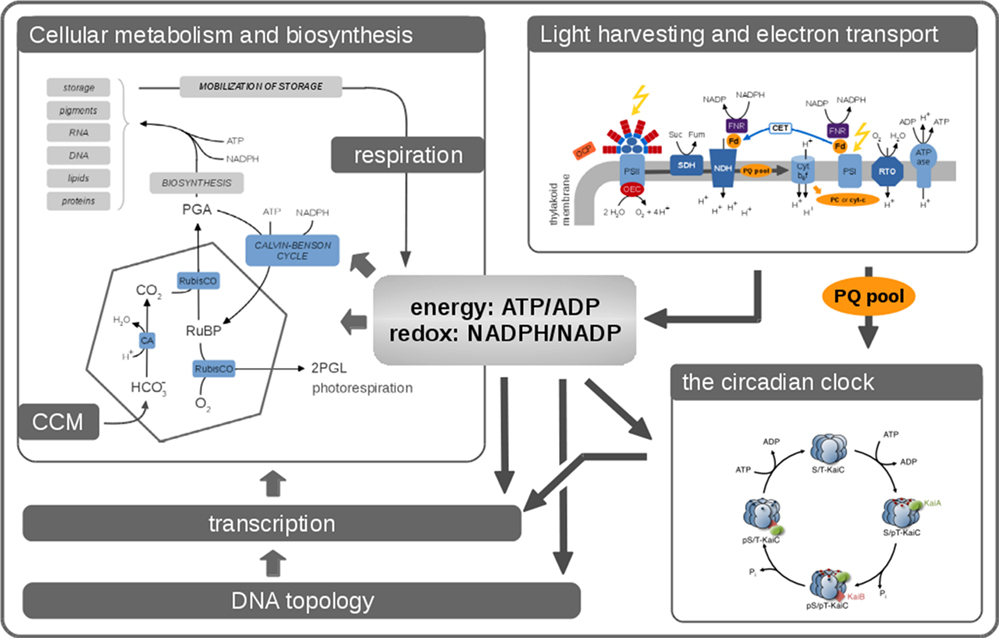
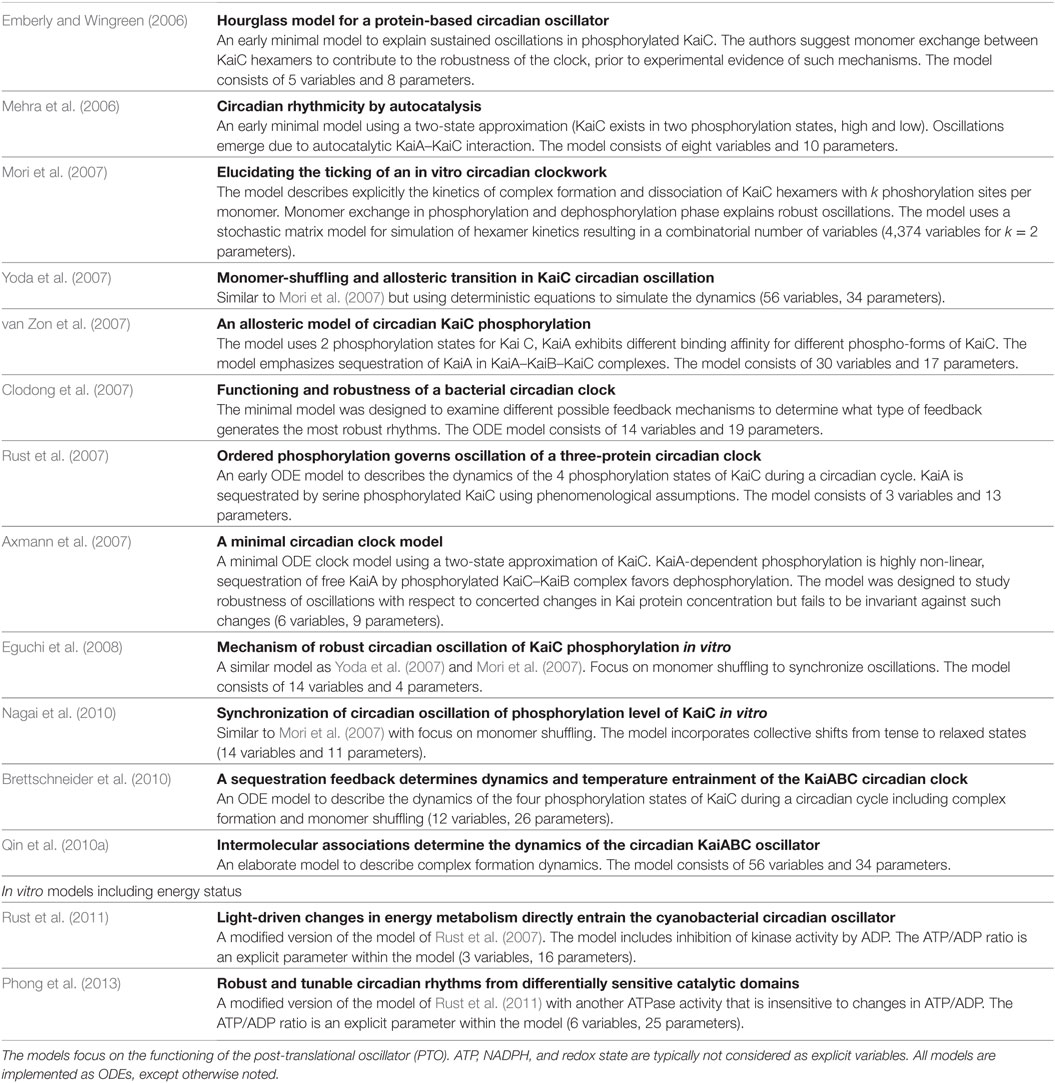
Figure 1. Phototrophic growth is an emergent property that arises from interacting cellular processes. Cellular growth can be described by considering these processes as interacting modules. Many aspects related to cellular growth are reasonably well understood, and detailed computational models already exist. Nonetheless, it remains a considerable challenge to integrate these diverse models into a coherent whole. In this contribution, we seek to describe the processes that are relevant for cyanobacterial functioning and growth. Key aspects are the photosynthetic light reactions, providing energy and reductants for cellular metabolism, cellular respiration in the absence of light, CO2-concentrating mechanisms (CCMs), transcription, and global energy-induced changes in DNA topology, as well as the circadian clock and its integration into diverse layers of cellular regulation.
Survival and growth of (most) cyanobacteria begins with the absorption of photons facilitated by large light-harvesting antennae, the phycobilisomes, and chlorophyll a. The energy harvested from sunlight drives water splitting at photosystem II (PSII). Electrons, derived from water, are provided to the electron transport chain (ETC) and molecular oxygen is released as the byproduct of photosynthesis.
The ETC consists of a number of large protein complexes, mostly located in the thylakoid membrane. Electrons are transferred along the ETC, ultimately resulting in the regeneration of adenosine triphosphate (ATP) and reduced nicotinamide adenine dinucleotide phosphate (NADPH) as energy carrier and reductant, respectively. The functioning of the photosystems and the ETC are complex biophysical processes and objects of intense research. The respective processes are characterized by fast time scales and transitions between a large number of possible states. While a number of detailed computational models of these processes are available, often with a focus on photosystem II, the respective models typically do not describe regeneration of ATP and NADPH, and hence are not straightforwardly connected to other cellular functions.
The ATP and NADPH regenerated by the photosynthetic light reactions play a crucial role for almost all other cellular processes. Beyond their role as energy donor and reductant, they also serve as important signaling compounds to convey information about the intracellular state. Regenerated ATP and NADPH are utilized to assimilate atmospheric carbon dioxide (CO2). Cyanobacteria possess mechanisms to concentrate inorganic carbon in the vicinity of the CO2-fixing enzyme, the ribulose-1,5-bisphosphate carboxylase/oxygenase (RuBisCO), making use of bacterial microcompartments known as carboxysomes. Compared to the light reactions, the relevant time scales of the so-called dark reactions are significantly slower. Modeling of CO2-concentrating mechanisms (CCMs) typically involves consideration of diffusion and spatial structure.
The carbon assimilated by the enzyme RuBisCO serves as a substrate to synthesize new cell components, including storage compounds and substrates for cellular respiration. Cellular metabolism involves several hundreds of biochemical reactions, catalyzed by enzymes, as well as spontaneous interconversions, transport, and diffusion processes. From a computational perspective, a description of cellular metabolism must involve several spatial and temporal scales. Detailed models for the action of individual enzymes, such as RuBisCO, exist, based on detailed enzyme mechanisms and elementary reaction steps. Pathways are typically described by combining, often approximative, kinetics of the involved enzymes into larger kinetic models, described by ordinary differential equations (ODEs).
While current kinetic models of metabolism rarely involve more than a few dozen compounds, cellular metabolism is increasingly analyzed using large-scale metabolic reconstructions and constraint-based computational methods. Metabolic network reconstructions are based upon the predicted gene content deduced from genomic DNA and aim to provide an unbiased and comprehensive account of all interconversions of small molecules inside a single cell or a compartment. Unlike kinetic models, metabolic reconstructions only make use of the stoichiometric properties of the respective interconversions, and manually curated reconstructions have been reported for a number of cyanobacteria (Knoop et al., 2010, 2013; Montagud et al., 2010; Nogales et al., 2012; Saha et al., 2012; Vu et al., 2012; Yoshikawa et al., 2015). Highly efficient computational methods exist that allow for the analysis of networks that consist of several hundreds of biochemical reactions and other molecular interconversions. These computational methods, however, are challenging to reconcile and integrate into more traditional enzyme kinetic models of metabolism.
In addition to the photosynthetic light reactions and cellular metabolism, cyanobacterial functioning also involves a large number of regulatory processes. Most prominent is the cyanobacterial circadian clock. Unique among all known prokaryotes, cyanobacteria possess a true circadian clock, a self-sustained oscillator that is entrained to an external zeitgeber. Since its discovery in the late 1980s, the cyanobacterial circadian clock has been an object of intense research (Pattanayak and Rust, 2014). Early research, however, was mostly focused on the inner workings of the clock, the molecular details of the core clock, and its input pathways. Only recently, interactions between the clock and metabolism and the question how the clock functions within a broader cellular context have been addressed in more detail (Pattanayak and Rust, 2014; Diamond et al., 2015; Shultzaberger et al., 2015).
Correspondingly, a number of quantitative computational models exist that describe the mechanistic details of the cyanobacterial clock, as well as its entrainment to environmental cues—but as yet only few of these models allow for a straightforward integration into a broader cellular context. While there is increasing evidence how the clock is influenced by, and itself influences, photosynthetic light reactions and metabolism, via sensing metabolic activity (Pattanayak et al., 2015) and redox state (Kim et al., 2012) and controlling transcription regulation, the precise evolutionary role of the clock remains insufficiently understood. Elucidating how the circadian clock interacts with other cellular processes and to integrate models of the cyanobacterial circadian clock into a broader cellular context, with the aim to understand how timing mechanisms affect cellular fitness, is a timely question for further computational research.
Energy metabolism and growth, like all cellular processes, are also dependent on the transcriptional and translational machinery. The transcriptional landscape of commonly cultivated cyanobacteria, such as Synechocystis sp. PCC 6803, is increasingly known (Kopf et al., 2014) and a number of studies investigated transcriptional rhythms in the presence of light–dark phases (Lehmann et al., 2013; Beck et al., 2014). Of particular interest is also the role of small regulatory RNA (sRNA) to coordinate cellular processes. For several cyanobacterial strains, most notably Synechocystis sp. PCC 6803, substantial sRNA transcription, intragenic transcripts, and antisense transcripts have been reported (Kopf and Hess, 2015). While generic computational models for various possible role of regulatory RNA exist (Legewie et al., 2008), these are currently not integrated within larger computational efforts to understand growth properties and adaptation of cyanobacteria.
As a key driver of cellular functioning and growth, global gene expression is believed to be under direct control of the circadian oscillator, mediated by the topological properties of the cyanobacterial chromosomes. It was shown that the superhelicity of the DNA undergoes rhythmic changes that drive global changes in gene expression (Woelfle et al., 2007; Vijayan et al., 2009). It is further known that the rate of transcription also depends on the local supercoiling status of DNA. Vice versa, supercoiling depends on the cellular energy status, since the extent of supercoiling achieved by the DNA gyrase is strongly dependent on ATP hydrolysis. For heterotrophic organisms, specifically Escherichia coli, these observations have led to the proposal of homeostatic control and a feedback loop between the intracellular ATP/ADP ratio, DNA supercoiling, transcription, and again changes in the ATP/ADP ratio (Wijker et al., 1995). Closely related ideas have been put forward in the context of ultradian rhythms in yeast where global partitioning of anabolism and catabolism might be mediated by ATP feedback loop on chromatin architecture (Amariei et al., 2013). In the case of cyanobacteria, a global feedback between cellular energy state, DNA supercoiling, and transcription might mediate between global transcription rhythms, the light reactions as the source of cellular energy, and the circadian clock. Such global feedbacks are currently not explicitly considered in models of cyanobacterial growth and are challenging to implement because of the diverse layers of cellular regulation involved.
Parallel to the efforts of molecular biology to understand the mechanistic and biophysical basis of the processes involved in phototrophic growth, there is a rich history of phenomenological phytoplanktonic growth models. Phenomenological growth formulations are typically employed in models of marine ecosystems and food webs, as well as biogeochemical models to understand the global response of ecosystems to environmental changes. Phenomenological growth models often employ Monod-type equations to describe uptake of a limiting nutrient. Following the early work of Droop (1968), also more sophisticated approaches exist to describe variable internal quotas, see Droop (1983) for an overview. The dynamics of simple phytoplankton growth models are typically based on empirical parameter fitting, rather than an outcome of the underlying cell physiology, and involve strong simplifications, such as using a constant carbon-to-nitrogen (C:N) stoichiometry and absence of photoacclimation (Ayata et al., 2013). It has been pointed out that a major shortcoming of such models is their limited ability to produce true emergence in marine ecosystem models (Allen and Polimene, 2011). Specifically, these models do not evolve to new states not already incorporated in their formulation that makes them unsuitable to properly predict ecosystem changes under changing environmental conditions. As argued by Allen and Polimene (2011), the path forward is to place more emphasis on the underlying intracellular processes—resulting in physiological growth formulations that allow for trade-offs between resource allocations of physiological activities, and hence the possibility to produce biogeochemical and ecological dynamics as emergent properties. Preliminary models, albeit still limited, that combine a detailed description of photosynthesis and phytoplankton growth are already available (Kroon and Thoms, 2006).
In the following, we seek to discuss selected computational models related to cyanobacterial functioning and growth in more detail. Our view is that cyanobacterial physiology depends on interacting cellular processes that can be interpreted as functional “modules”, such as the photosynthetic light reactions and the ETC, carbon uptake mechanisms, cellular metabolism, the circadian clock, as well as the transcriptional and translational machinery and its regulation. For many of these modules, reasonable computational descriptions already exist, whereas other processes, for example, the coordination of cell cycle events in relation to metabolism (Asato, 2005, 2006), have not yet been subject to computational studies.
Our aim is to highlight the common variables and known interactions between the processes relevant to cyanobacterial functioning and growth. In this respect, a particular challenge is the wide range of computational approaches and methods used. Models of cellular processes may take many forms, ranging from spatial versus non-spatial, stochastic versus deterministic, population level versus single cell level, and continuous versus discrete descriptions. See Figure 2 for an overview. Notwithstanding the technical challenges, we believe that the integration of different aspects of cellular growth, and their respective computational representation, is a prerequisite toward understanding the living cell. We seek to understand how phototrophic growth functions and how it is regulated. How does the coordination of physiological functions work in order to synthesize the right macromolecules at the right time? Which level of detail is required to describe cellular growth? What are the variables and time scales involved?
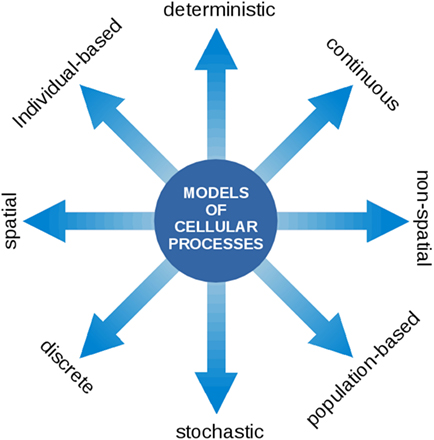
Figure 2. Models of cellular processes are highly diverse and may involve a wide range of computational concepts and methodologies. At the core of the modeling process is a translation of a biological processes into a formal (mathematical) language. Once this translation is established, the model can be interrogated using the tools of mathematical and computational analysis. The most prevalent representations of cellular processes described in this contribution make use of deterministic ordinary differential equations (ODEs) to describe the time-dependent dynamics of continuous intracellular concentrations, typically on the population level. In the following, such models are denoted as kinetic models and may either make use of heuristic approximate rate equations or rate equations derived from explicit biochemical mechanisms. Models of CCMs typically involve a spatial component and originate from a description based on partial differential equations (PDEs). Models of the light reactions frequently describe transitions between discrete states that occur with a certain state-dependent probability. Flux balance models consists of a set of linear relationships (linear inequality constraints) between variables and make use of linear programing (LP), a method to identify the optimum of a linear objective function. For a more detailed overview on model types, see also Steuer and Junker (2009).
3. Models of the Photosynthetic Light Reactions
Phototrophic growth begins with the absorption of light and its conversion into chemical energy. Despite a number of open questions and the need for further research, many of the fundamental properties of oxygenic photosynthesis have been elucidated in the past century. Owing to the fact that cyanobacteria are the evolutionary ancestors of modern-day chloroplasts, the organization of their photosynthetic ETC is essentially identical to that in algae and green plants (Vermaas, 2001).
In most cyanobacteria, light harvesting is facilitated by large antenna complexes, the phycobilisomes. Phycobilisomes are attached to the cytoplasmic surface of the thylakoid membrane (Mullineaux, 2014). The detailed composition of phycobilisomes is strain specific and depends on light quality, denoted as complementary chromatic adaptation. The energy absorbed by the phycobilisomes is transferred to either photosystem II or photosystem I, or dissipated as heat or fluorescence. The protein complexes of the photosynthetic ETC are embedded within the thylakoid membrane. The key proteins complexes responsible for photosynthetic electron transport are Photosystem II (PSII), the Cytochrome b6f complex (Cytb6f), Photosystem I (PSI), and ATP synthase (ATPase). See Figure 3 for an overview.
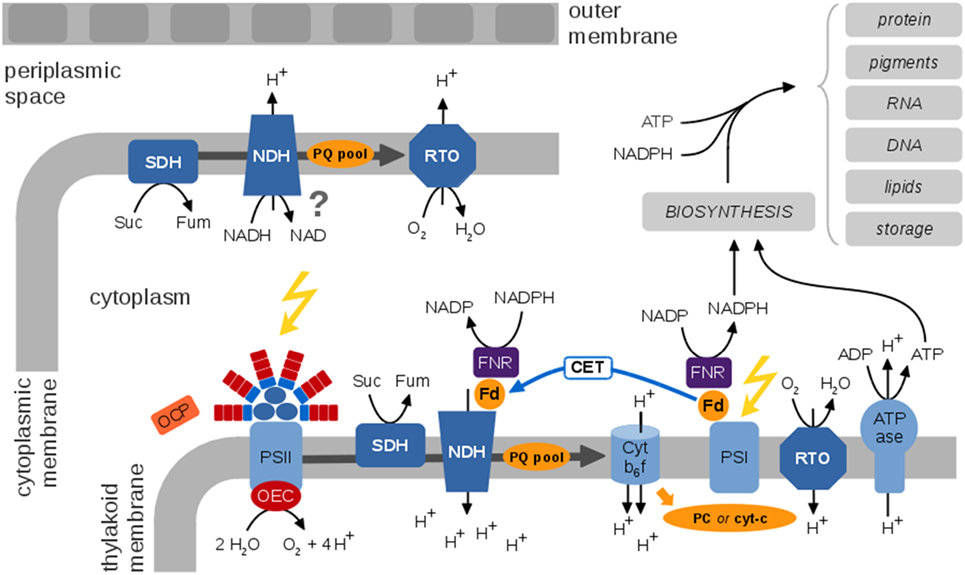
Figure 3. A generic view of the cyanobacterial electron transport chains (ETCs), species-specific differences are neglected. Cyanobacterial photosynthetic and respiratory ETCs share common components. The protein complexes of the photosynthetic ETC are embedded within the thylakoid membrane enclosing the thylakoid lumen. Key protein complexes are photosystem II (PSII), with the oxygen-evolving complex (OEC), the cytochrome b6f complex (Cytb6f), photosystem I (PSI), and the ATP synthase (ATPase). Cyclic electron transport involves the NDH complex and is still insufficiently understood. The Orange Carotenoid Protein (OCP) is a light sensor and energy quencher that interacts with the phycobilisomes to decrease energy arriving to the photosynthetic reaction centers (Kirilovsky and Kerfeld, 2013). The thylakoid membrane also contains respiratory components, in particular the succinate dehydrogenase (SDH), NADPH dehydrogenase (NDH), and a respiratory terminal oxidase (RTO). It has been suggested that ferredoxin (Fd) transfers electrons from NADPH to NDH-1 via the Fd-NADP+-reductase (FNR) (Ma and Ogawa, 2015). The cytoplasmic membrane contains a rudimentary respiratory electron transport chain; functional details and localization of putative components are largely unknown. Photosynthetic ETCs result in regeneration of ATP and NADPH for cellular synthesis and growth. A residual respiratory activity persists also in the presence of light. The photosynthetic and respiratory ETCs are subject to multiple alternative electron pathways (not shown) that act as “electron valves” to prevent overreduction of the ETC (Mullineaux, 2014).
PSII splits water and reduces the plastoquinone (PQ) pool. The latter mediates the transport of electrons from PSII to Cytb6f. At Cytb6f, electrons are transferred to a soluble electron carrier on the luminal side of the thylakoid membrane, either plastocyanine (PC) or cytochrome-c (cyt-c). At PSI, electrons are transferred to ferredoxin and eventually to NAPDH using light-induced excitation of the PSI reaction center (linear electron transport, LET). Alternatively, electrons from the excited PSI state can be transferred back to PQ and Cytb6f (cyclic electron transport, CET), details of CET are still under debate and insufficiently understood. Photosynthetic electron flow results in a protein gradient across the thylakoid membrane that drives regeneration of ATP by the ATPase.
Unique to cyanobacteria, as opposed to plants and microalgae, is the combination of oxygenic photosynthesis and respiration in the same membrane system using intersecting ETCs and common components (Vermaas, 2001). The respiratory ETC involves the succinate dehydrogenase (SDH), the NADPH dehydrogenase (NDH-1), and terminal oxidases. The PQ pool, the Cytb6f complex, and PC (or cyt-c) as soluble electron carrier are involved in respiratory as well as photosynthetic electron transport. While photosynthesis exclusively takes place in the thylakoid membrane, a rudimentary respiratory chain is also present in the plasma membrane (Schultze et al., 2009).
From a computational perspective, photosynthesis in cyanobacteria and microalgae can be described on different levels of complexity. Basic models are closely related to overall growth models in ecology—and typically to reproduce the production of oxygen and the photosynthesis–irradiance (PI) curve of cyanobacteria and microalgae. Early models were derived by Crill (1977), Megard et al. (1984), Eilers and Peeters (1988), and Zonneveld (1998) among others. These models make use of a highly simplified photosynthetic factory or photosynthetic unit (PSU) that encompasses PSII, PSI, and the ETCs. See Figure 4 for an example. The resulting differential equations for the dependency of photosynthesis on light intensity can often be solved analytically, with a solution analogous to the Haldane equation—an enzyme kinetic equation that was derived for substrates with inhibitory effects at high concentrations. Simple three-state models are suitable to describe basic features of photoinhibition and the PSII repair cycle (Tyystjärvi et al., 1994). In later iterations, the parameters of the basic three-state model were augmented with a more mechanistic interpretation (Han, 2001, 2002), and the models were extended to describe the effects of intermittent light (Rubio et al., 2003). Recently, a basic three-state model was also applied to describe the kinetics of non-photochemical quenching (NPQ), induced by an orange cartenoid protein (OCP), in cyanobacteria (Gorbunov et al., 2011). To this day, simple three-state models remain relevant to describe overall photosynthetic activity, in particular in bulk models to assess productivity in photobioreactors and related industrial application (Nedbal et al., 2010; Bernard, 2011). With respect to understanding interactions between cellular processes, a drawback of highly simplified growth models is their insufficient representation of intracellular parameters, such as no explicit PQ pool, no explicit regeneration of ATP and NADPH, and lack of alternative electron transport.
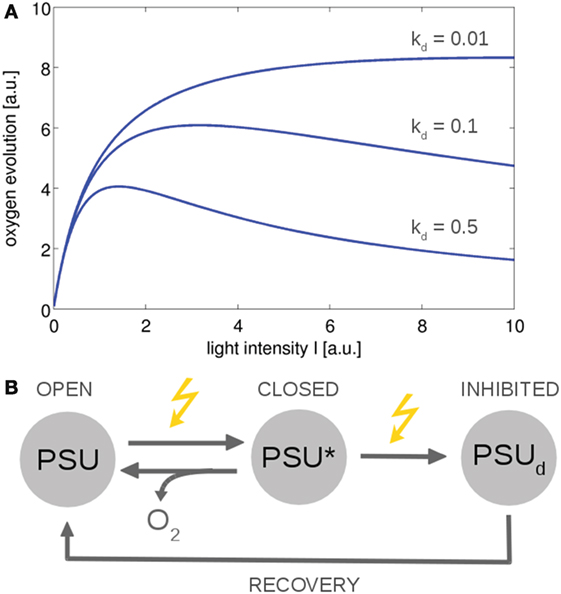
Figure 4. The photosynthesis–irradiance (PI) curve for a minimal model of photosynthesis (Han, 2002). The ETC is described by a photosynthetic unit (PSU) that exists in an open or reactive state. After being subjected to light, the PSU transits to a closed or activated state (PSU*). Excessive absorption results in photodamage and an inhibited state PSUd with rate constant kd. (A) Using simple ODEs based on mass action kinetics results in typical PI curves. The overall functional form is similar to the Haldane equation, an equation derived for enzymes whose substrates have an inhibitory effect at higher concentrations. (B) The reaction scheme. Similar models can describe non-photochemical quenching in which the damaged state corresponds to a quenching state (indirectly) activated by light (Gorbunov et al., 2011). All values are reported in arbitrary units (a.u.). The ODEs used to generate the figure are provided in the Appendix.
Beyond overall bulk models of photosynthesis, there is a significant history of biophysical models to understand oxygen evolution and chlorophyll fluorescence transients, often with a focus on PSII, as well as to understand specific properties, such as energy distribution in the photosynthetic apparatus (Butler and Strasser, 1977; Butler, 1978) or, more recently, excitation transfer in the PSII membrane (Amarnath et al., 2016). Early kinetic models were described by Mar and Govindjee (1972), a more elaborate model was put forward by Holzwarth et al. (2006) and later analyzed by Nedbal et al. (2007). Further elaborate models of this kind were developed by Lazár (2003) and Zhu et al. (2005). The former was refined and extended by Jablonský and Lazár (2008); different approaches were later compared by the same authors (Lazár and Jablonský, 2009). Common to these models is a focus on chlorophyll fluorescence emission, and to a lesser extent oxygen evolution, as the main output variables. While relevant for biophysical research, the respective models cannot be straightforwardly integrated into more comprehensive models of phototrophic growth, due to the focus on fast time scales and specific output variables. We note that the interpretation of results obtained from pulse-amplitude modulated (PAM) fluorimetry significantly differs between cyanobacteria and plants (Schuurmans et al., 2015; Acuña et al., 2016), with modeling approaches focusing almost exclusively on the latter.
Models that explicitly describe the photosynthetic electron transport chain and subsequent reactions, in addition to PSII, are more suitable to integrate into the context of a living cell. To this end, a small number of models exist (Berry and Rumberg, 2000; Vershubskii et al., 2014), typically based on ODEs. An elaborate model of this type was proposed by Laisk et al. (2006), developed to understand the photosynthetic process from light absorption to sucrose synthesis. The model neglects many of the detailed biophysical properties of earlier models (Zhu et al., 2005), such as an explicit representation of the s-states that describe the cyclic reactions of the oxygen-evolving complex (Kok et al., 1970). The model instead provides a combination of whole chain electron transport and carbon assimilation processes, including non-photochemical quenching, chlorophyll fluorescence, and (albeit simplified) photorespiration. Using a similar approach, Zhu et al. (2013) described a detailed dynamic model of leaf photosynthesis, based on ODEs, from light capture to carbon assimilation, and incorporates the previous partial model of the same authors (Zhu et al., 2007) augmented by additional reactions of the ETC. Both models focus on C3 plant metabolism, but similar approaches are feasible for cyanobacteria.
Importantly, both models provide a sufficient level of detail to interface with other cellular processes and include ATP regeneration and reduction of NADPH, photorespiration, alternative electron transport, as well as an explicit representation of the PQ pool and lumenal pH. Owing to the focus on plant C3 metabolism, neither of the models describe peculiarities of cyanobacteria, such as shared components between the photosynthetic and respiratory ETC and the resulting differences in regulation.
Selected models of the ETC and the photosynthetic light reactions are summarized in Table 1. Main challenges for the development of corresponding models for cyanobacteria are to incorporate the respiratory ETC, as well as to incorporate the specific alternative electron sinks of cyanobacteria. As an interface to other cellular processes, discussed below, a model of the cyanobacterial ETC should include regulatory switches in cyanobacterial photosynthesis, regulation of light harvesting including regulation of the orange carotenoid protein, state transitions that control the relative energy transfer from phycobilisomes to PSII versus PSI, and alternative electron sinks that serve as “electron valves” and prevent overreduction of the ETC, among other features that are relevant for cyanobacterial functioning and growth (Mullineaux, 2014). Relevant exchange variables are ATP and NADPH regeneration, the state of the PQ pool, leakage of reactive oxygen species (ROS), and oxidation of metabolites for cellular respiration.

Table 1. Selected models of the photosynthetic light reactions and the electron transport chain (ETC) in plants and cyanobacteria.
4. Kinetic Models of Cellular Metabolism
The energy harvested by the photosynthetic light reactions drives the assimilation of inorganic carbon and the synthesis of storage compounds and building blocks for cellular growth. Photoautotrophic metabolism involves the uptake of inorganic carbon facilitated by CO2-concentrating mechanisms (CCMs), assimilation of CO2 by RuBisCO, and the subsequent synthesis of cellular building blocks mediated by a network of metabolic reactions. Computational concepts used to describe cyanobacterial metabolism have been discussed previously (Steuer et al., 2012), here we focus on the integration of such descriptions into integrative models of phototrophic growth. In particular, models of metabolism are highly diverse and span multiple orders of magnitude with respect to the time scales and number of variables involved. As highlighted previously (Steuer and Junker, 2009), no single universal computational methodology exists that is suitable to describe all relevant aspects of metabolic functioning. Rather, a hierarchy of computational approaches exists, ranging from detailed kinetic models of individual enzymatic reactions, based on ODEs, to large-scale stoichiometric reconstructions that are evaluated using constraint-based analysis.
The basic building blocks of metabolism are the actions of individual enzymes and their respective reaction mechanisms. Computational modeling of enzyme kinetics is well understood (Steuer and Junker, 2009; Sauro, 2014), even though specific reaction mechanisms and atom transition maps are not yet comprehensively available and must be confirmed on an individual per-reaction basis. Detailed kinetic models of key reactions have been proposed in the literature, most notably for RuBisCO, the key enzyme of the Calvin–Benson cycle (Witzel et al., 2010). Following the rules for overall rate equations of enzyme kinetic mechanisms, multiple reaction steps can be integrated into larger models of cellular pathways. Corresponding detailed kinetic models of metabolic pathways exist since the late 1950s, see Steuer and Junker (2009) for a review, and several kinetic pathway models have since been proposed for phototrophic plant metabolism. Of particular interest is the Calvin–Benson cycle and the adjacent carbon metabolism. Among the first computational descriptions of phototrophic C3 carbon metabolism were the models proposed by Milstein and Bremermann (1979) and Hahn (1984). The former involves 17 first-order ODEs and 22 parameters. The latter involves 19 state variables and describes the dynamics of Calvin–Benson cycle intermediates, as well as parts of sucrose and starch metabolism. The model was later extended to include photorespiration (Hahn, 1987), and simplified representations were considered (Hahn, 1991). The latter analysis demonstrated that also smaller models are able to reproduce the observed dynamics. Both models, as well as the model of Laisk and Walker (1986), are largely based on mass action kinetics, rather than derived enzyme kinetic equations for kinetic mechanisms. Parallel to the development of detailed kinetic models of core carbon metabolism, a number of biochemical models of photosynthetic CO2 assimilation have been developed that focus on plant-specific properties, such as gas exchange and stomatal conductance, often also incorporating aspects of carbon reduction, see Farquhar et al. (1980) for an influential early example. Likewise, a significant number of models were developed to investigate the origin of photosynthetic oscillations (Giersch, 1986; Laisk and Walker, 1986; Laisk et al., 1989; Rovers and Giersch, 1995), see Roussel and Igamberdiev (2011) for a recent review.
The prototype of most current enzyme kinetic models of the Calvin–Benson cycle was proposed by Pettersson and Ryde-Pettersson (1988). The model is based on mechanistic non-linear enzyme kinetic rate equations, implemented as ODEs, together with equilibrium mass-action ratios. The model describes the dynamics of the Calvin-Benson cycle under conditions of light and CO2 saturation. The parameterization of the model involved approximately 50 kinetic parameters, sourced from the literature across several plant species. The model of Pettersson and Ryde-Pettersson (1988), like many current and past kinetic models, is therefore not necessarily a model of a single plant species, but must be considered as a prototype model that describes several generic aspects of plant leaf C3 metabolism. The model was later adapted to investigate further aspects of metabolic regulation in phototrophic metabolism (Poolman et al., 2000, 2001), and extended by Zhu et al. (2007) to investigate the reallocation of enzymes of photosynthetic carbon metabolism with respect to optimal nitrogen and protein investment. These models also served as a blueprint for the first detailed kinetic models of cyanobacterial core carbon metabolism. Jablonský et al. (2013) proposed a modified version of the model of Zhu et al. (2007), adapted to describe the cyanobacterium Synechococcus elongatus PCC 7942, to investigate the functional consequences of isoenzymes. The majority of parameters were retained from the original models. The model was later refined (Jablonský et al., 2014) to explain the metabolic regulation of primary carbon metabolism, also incorporating transcriptional data as a constraint for model dynamics. Most recently, a kinetic model of the central carbon metabolism of the cyanobacterium Synechocystis sp. PCC 6803 was developed to investigate the role of isozymes on metabolic network homeostasis with respect to changes in gene expression induced by different CO2 conditions (Jablonský et al., 2016). In particular, a comparison of model properties indicated that the higher number of isozymes present in the Synechocystis sp. PCC 6803 genome compared to the (smaller) genome of Synechococcus elongatus PCC 7942 may correspond to a shift of metabolic regulatory strategies from transcriptional control in latter toward post-transcriptional control in the former (Jablonský et al., 2016).
From computational perspective, the kinetic models considered above share several features relevant to the integration into multiscale models of phototrophic growth. In each case, the dynamics of the concentrations of metabolic intermediates are described by ordinary differential equations (ODEs). Rate equations are derived from enzyme kinetic mechanisms, and implemented using (usually reversible) non-linear Michaelis–Menten type functions. The rate equations consider allosteric regulations, as well as other post-translational mechanisms, as far as such interactions are known. The light reactions are typically highly simplified. In the model of Pettersson and Ryde-Pettersson (1988) and its later adaptations, ATP is provided by a single overall reaction (an ATP synthetase) that can be modulated according to light intensity. The concentrations of NADP+ and NADPH are assumed to be constant. Likewise, enzyme amounts are represented by external parameters, the respective values are part of the maximal reaction velocities Vmax. Table 2 lists selected kinetic models of central carbon metabolism and the Calvin–Benson cycle. We conjecture that such models provide a reasonable account of metabolite dynamics on short and medium time scales (minutes to few hours) and to metabolic adaptations to brief periods of darkness. As yet, the construction of kinetic models to adequately represent changes in day/night metabolism remains a considerable challenge.
The key factors to integrate models of core carbon metabolism into overall models of phototrophic growth requires an explicit representation of energy (ATP) and redox state (NADPH/NADP+) as dynamic variables that allow coupling to the ETC. In this respect, first steps have been made for plant metabolism. The models of Laisk et al. (2006) and Zhu et al. (2013) both integrate the photosynthetic light reactions with a detailed representation of the core C3 carbon metabolism, including photorespiration. Such models provide a framework for guiding engineering efforts and allow for a description of photosynthesis and carbon fixation in response to, for example, changes in photon flux density.
Beyond the integration of light capture and carbon metabolism, significant challenges remain. Allosteric post-translation regulation only covers small to medium time scales. No current kinetic model provides a description of diurnal changes in metabolism and the corresponding switch from carbon assimilation to the mobilization of storage compounds. In addition to redox regulation, such switches are likely to require the inclusion of additional hierarchies of cellular regulation, in particular transcription and possibly regulation by the circadian clock. Switches in metabolic modes are of particular relevance for cyanobacterial metabolism and growth, as they lack the compartmentation of eukaryotic algae and plants. Likewise, current models focus on carbon metabolism and its regulation, limitation of other macronutrients like phosphorus or nitrogen is typically not considered. Nonetheless, in particular with respect to nitrogen, kinetic models can be expected to provide insight into the role of certain metabolites, such as 2-oxoglutarate (2-OG), as signaling compounds (Fokina et al., 2010).
A major obstacle for detailed kinetic models also remains the scarcity of enzyme kinetic data. The construction of kinetic models requires detailed knowledge of enzyme kinetic parameters—with typically 4–5 parameters per reaction, including the Michaelis–Menten parameters KM for substrates and products, as well as thermodynamic equilibrium values Keq and the specific catalytic activities of enzymes. Even metabolic pathways of moderate size, such as the Calvin–Benson cycle and adjacent reaction, typically consist of 20–30 enzymatic reactions. Therefore, the construction of larger kinetic models, while feasible from a computational point of view, is primarily limited by data availability and data reliability (Srinivasan et al., 2015). To some extent, the scarcity of information about kinetic parameters can be alleviated by explicitly accounting for uncertainty in kinetic models of metabolism—suitable approaches have been proposed recently (Wang et al., 2004; Steuer et al., 2006; Tran et al., 2008; Steuer and Junker, 2009; Murabito et al., 2014) but are not yet widely applied in models of phototrophic growth.
5. Models of Carbon-Concentrating Mechanisms
A characteristic feature of cyanobacterial growth is the use of CO2-concentrating mechanisms (CCMs) to facilitate the uptake and acquisition of inorganic carbon. CCMs allow cyanobacteria to raise the local concentration of CO2 in the vicinity of the carboxylating enzyme RuBisCO, and thereby overcome the comparatively low affinity of RuBisCO for CO2 and depress the competitive oxygenation reaction (photorespiration). Cyanobacterial CCMs typically make use of dedicated microcompartments, the carboxysomes, that separate the assimilation of CO2 by RuBisCO from the rest of the cell. The CCMs of cyanobacteria relies on a number of components. The respective mechanisms are reasonably well understood (Kaplan and Reinhold, 1999; Price et al., 2008; Burnap et al., 2015), see Figure 5 for a schematic depiction, and the requirement of a quantitative mathematical analysis has recently been highlighted (Mangan and Brenner, 2014). The efficiency of the cyanobacterial CCMs can be characterized by the ratio between the apparent whole-cell affinity for extracellular CO2 and the respective affinity for CO2 of the carboxylating enzyme RuBisCO—with ratios up to 1,000 reported in the literature (Burnap et al., 2015). While many components of the CCMs are constitutively expressed, the expression of specific uptake systems is differentially regulated depending on environmental parameters, in particular light intensity and the availability of inorganic carbon (Ci) (Kaplan and Reinhold, 1999; Burnap et al., 2015).
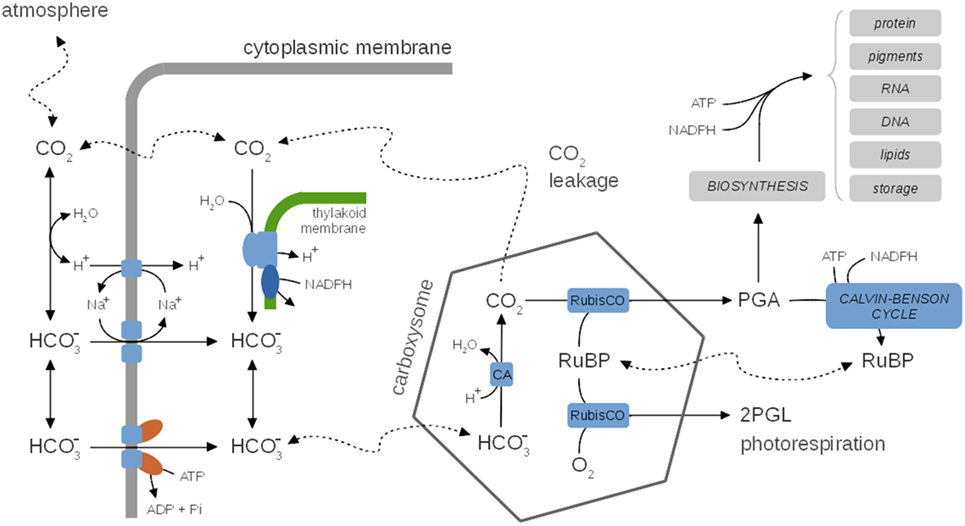
Figure 5. A generic representation of cyanobacterial CO2-concentrating mechanisms (CCM), species-specific differences are neglected. Inside, the carboxysome bicarbonate is rapidly converted to CO2 via the carbonic anhydrase (CA). CCMs thereby facilitate a CO2 gradient to increase the local concentration of CO2 in the vicinity of RuBisCO and depress photorespiration. Several uptake mechanisms for exist, including ABC-type high affinity transporters and Na+/ symporters. The activity of CCMs, including expression of several components, is modulated by environmental parameters, in particular CO2 availability. CO2 leaking from the carboxysomes may diffuse into the medium or is partly converted back to (carbon cycling) at the thylakoid membrane using insufficiently understood mechanisms. CCMs utilize cellular energy and might be involved in dissipating excess light energy and play a role in the maintenance of internal pH. Hence, CCMs are integrally tied to cellular metabolism and growth. See Table 3 for selected computational models of CCMs.
In addition to their important function to enhance the local CO2 concentration and depressing photorespiration, CCMs may also be involved in dissipating excess light energy (Xu et al., 2008) and might play a role in pH homeostasis. Despite this tight integration with carbon metabolism, none of the current kinetic models of carbon metabolism explicitly accounts for CCMs. Nonetheless, a number of quantitative models of CCMs are available that can be readily incorporated into models of cyanobacterial growth. See Table 3 for selected computational models of CCMs. Early models focus either on simple equations for CO2 and (bicarbonate) flux into and out of the cell (Badger et al., 1985), as well as on arguments based on reaction–diffusion equations (Reinhold et al., 1987, 1991). These models were refined further to include explicit representations of the carboxysomes. Specifically, the model of Fridlyand et al. (1996) considers the various CO2 or fluxes between medium, periplasmic space, cytoplasm and carboxysomes using derived values for geometric parameters, and permeability and diffusion coefficients. The model also considers the energetic consequences of scavenging CO2 that leaks back into the cytoplasm. Models can be adopted to specific cyanobacterial strains, such as the model of Hopkinson et al. (2014) for Prochlorococcus spp. MED4. Two recent quantitative models of CCM functioning are available (Clark et al., 2014; Mangan and Brenner, 2014). Both models are based on reaction–diffusion equations that are solved for highly simplified spatial topologies (spherical cells), but otherwise make use of partially divergent assumptions. The focus of Clark et al., 2014 are interspecies differences and a hypothetical carboxysome-free mutant that is of interest in industrial settings with elevated CO2 supply. The model assumes that the carboxysome walls are impermeable to CO2. The model of Mangan and Brenner (2014) assumed that carboxysome permeability is identical for and CO2 and the model explores the range of best parameter values that give rise to a functional and effective CCM. While carboxysome permeability has not yet been measured directly, Mangan and Brenner (2014) concluded that optimal parameter values indeed exist, and transport rates and concentrations derived for these optimal values are in good agreement with known experimental data. Very recently, the model was extended to incorporate the effect of intracellular pH as a key physiological parameter that governs the composition of the Ci pool (Mangan et al., 2016). The “pH-aware” model highlights the utility of quantitative models to evaluate the energetic costs of Ci accumulation for CCMs.
While current models of the CCM do consider the optimality and functioning of CCMs under different intracellular and environmental conditions, they typically do not incorporate explicit models of cellular growth or other cellular mechanisms. However, the high energy demand of Ci transport, either by direct hydrolysis of one ATP per bicarbonate, or indirectly via the costs of ion transport, the costs of synthesizing carboxysome shell proteins, as well as the significant impact of CCMs on the efficiency of carbon assimilation suggest that further integration of models of CCMs into a broader context of cellular functioning is worthwhile to understand the trade-offs and interactions between energy investment, CCM utilization, carbon assimilation, and growth.
6. Large-Scale Models of Cyanobacterial Metabolism
Beyond kinetic models of central carbon metabolism, metabolic networks are increasingly described using large-scale stoichiometric reconstructions (Steuer et al., 2012). Metabolic reconstructions aim to provide a comprehensive account of all possible interconversions of small molecules within a given cell or compartment, including enzymatic reactions as well as non-catalyzed (spontaneous) interconversions, transport reactions, and diffusion. Metabolic reconstructions are derived from annotated genomes with subsequent steps of manual curation and gap filling, see Knoop et al. (2010), Steuer et al. (2012), and Knoop et al. (2013) for recent examples. The description typically involves only knowledge about the stoichiometry of interconversions; knowledge about kinetic parameters (such as Michaelis–Menten parameters) or allosteric regulation is not required.
Nonetheless, large-scale stoichiometric models of bacterial metabolism are highly predictive (McCloskey et al., 2013). The predictive power derives from the fact that the fluxes through enzymatic reactions are not independent. Constraint-based computational methods rely on the fact that under steady-state conditions most intracellular metabolites do not accumulate. The rate of synthesis of any non-accumulating metabolite must therefore approximately equal the rate of consumption of this metabolite. Similar arguments also hold for diurnal metabolism: if, after a full diurnal cycle, the concentration of a given intracellular metabolite is approximately equal to its initial value, then the total flux of synthesis reactions and the total flux of consuming reactions must be approximately equal. The condition of flux balance puts significant constraints on the feasible flux space. Predictions about specific flux solutions are then typically based on assumptions about metabolic optimality. That is, among all feasible flux solutions, constraint-based methods seek to identify a solution that maximizes a given objective function, such as the maximal yield of biomass for a given light input—motivated by the fact that a similar selection might take place during evolution. Predictions from large-scale stoichiometric models are therefore not mechanistic, that is, they are not derived from knowledge about biophysical or biochemical interactions. Rather, predictions are derived from how metabolism ought to behave given the assumption that metabolic functioning fulfills certain evolutionary optimality principles.
Computationally, the analysis of large-scale stoichiometric reconstructions is based on methods of linear programing (LP) and is computationally feasible also for networks consisting of several thousands of reactions. The strength of stoichiometric models and constraint-based analysis are questions such as the following: What is the maximal growth yield for a given light or carbon input? Which set of enzymes is essential for the synthesis of certain biomass components? How many distinct biochemical paths exist for the synthesis of certain biomass components and how do these pathways differ with respect to cellular energy expenditure and cofactor utilization? Due to the specific computational methodology, however, a direct integration of large-scale stoichiometric models into kinetic models of metabolism remains challenging. Various extensions toward incorporating dynamics have been proposed (Mahadevan et al., 2002; Kim et al., 2008; Feng et al., 2012; Antoniewicz, 2013), and extensive efforts are undertaken to bridge the gap between kinetic and stoichiometric models (Steuer, 2007; Steuer and Junker, 2009; Chakrabarti et al., 2013; Srinivasan et al., 2015).
Detailed stoichiometric reconstructions are available for several cyanobacterial strains (Knoop et al., 2010, 2013; Montagud et al., 2010; Hamilton and Reed, 2012; Nogales et al., 2012; Saha et al., 2012; Vu et al., 2012; Mueller et al., 2013; Maarleveld et al., 2014; Yoshikawa et al., 2015)—typically consisting of several hundred enzymatic interconversions and accounting for all known pathways related to central metabolism and the synthesis of key biomass components. See Table 4 for selected examples of metabolic reconstructions. Such large-scale reconstructions are valuable tools to derive consistent equations for the (maximal) growth yield with respect to light input, to derive core models of reaction pathways, and to make predictions about maximal product yield in biotechnological applications (Zavřel et al., 2016). In particular, large-scale reconstructions also enable a semiautomated extraction of meaningful core models to facilitate the construction of smaller kinetic models (Erdrich et al., 2015). Analysis of the respective networks, however, is often confined to either a constant light environment, or to heterotrophic growth on extracellular carbon sources. Only recently stoichiometric analysis of phototrophic metabolism explicitly described different phases of light availability. For example, Knoop et al. (2013) simulated biomass synthesis fluxes over a full diurnal cycle, Muthuraj et al. (2013) used dynamic FBA (dFBA) to capture light-dark metabolism over discretized time intervals, Knies et al. (2015) considered storage metabolites that accumulate and are consumed over a diurnal cycle using a reconstruction of the unicellular alga Emiliania huxleyi, Cheung et al. (2014) described a flux balance model that captures interactions between light and dark metabolism in C3 and CAM leaves, and Baroukh et al. (2014) proposed a novel dynamic modeling framework to describe carbon metabolism of unicellular microalgae.
Beyond conventional FBA and related constraint-based methods, there has been increasing interest to evaluate cellular metabolism in terms of a cellular “protein economy” (Molenaar et al., 2009) and to study trade-offs in cellular resource allocation (Goel et al., 2012; Müller et al., 2015)—a theme where, as noted by Schaechter (2015), the bacterial growth physiology of old is connected to the systems biology of today (Stouthamer, 1973; Neidhardt et al., 1990). As one of the first applications involving cyanobacteria, Burnap (2015) formulated a model of autotrophic growth in terms of allocating protein resources among core functional groups, such as the ETC, light-harvesting antennae, and ribosomes. Along similar lines, Rügen et al. (2015) formulated a self-consistent autocatalytic model of phototrophic growth. The model is based on the observation that the macromolecules that constrain cellular growth, including the components of the ETC, metabolic enzymes, and ribosomes, are itself products of metabolism. Phototrophic growth can therefore be formulated as a time-dependent linear optimization problem, such that optimal growth entails a time-dependent allocation of resources during a full diurnal cycle. The approach of Rügen et al. (2015), denoted as conditional FBA, results in dynamic time courses for all involved reaction fluxes, as well as changes in biomass composition over a diurnal cycle. Similar to conventional FBA, models of this kind are not based on mechanistic insight, but rather seek to evaluate the optimality of resource allocation during phototrophic growth. It is expected that methods and applications that go beyond conventional FBA and involve spatial and temporal metabolic modeling based on genome-scale reconstructions of microbial metabolism will play an increasingly important role (Henson, 2015).
7. Models of the Cyanobacterial Clock
In addition to the biochemistry of metabolism, phototrophic growth is highly dependent on regulatory networks to coordinate growth and to relay environmental information. To this end, of particular relevance is the cyanobacterial circadian clock—discovered in the late 1980s and unique among prokaryotes (Pattanayak and Rust, 2014). The cyanobacterial clock consists of an interrelated network of multifunctional components functioning in timekeeping, input and/or output mechanisms. Synechococcus elongatus PCC 7942 is the cyanobacterium whose clock is currently best studied. The core oscillator comprises only three proteins: KaiA, KaiB, and KaiC (Ishiura et al., 1998). KaiC exhibits an intrinsic kinase, dephosphorylation, and ATPase activity (Nishiwaki et al., 2004; Terauchi et al., 2007; Egli et al., 2012; Nishiwaki and Kondo, 2012). In complex with KaiA and KaiB, KaiC undergoes circadian Thr/Ser phosphorylation (Nakajima et al., 2005; Nishiwaki et al., 2007; Rust et al., 2007) (Figure 6). KaiA promotes and KaiB represses phosphorylation of KaiC (Iwasaki et al., 2002; Kitayama et al., 2003; Xu et al., 2003). The ATPase activity of KaiC is extremely weak (only 15 ATP molecules are consumed per day) and slow, determining the about 24-h period of the clock (Terauchi et al., 2007; Abe et al., 2015; Chang et al., 2015). The circadian rhythm of KaiC phosphorylation runs without transcription–translation and can even operate in a test tube (Nakajima et al., 2005; Tomita et al., 2005). In vivo, the KaiABC protein system works as a post-translational oscillator (PTO).
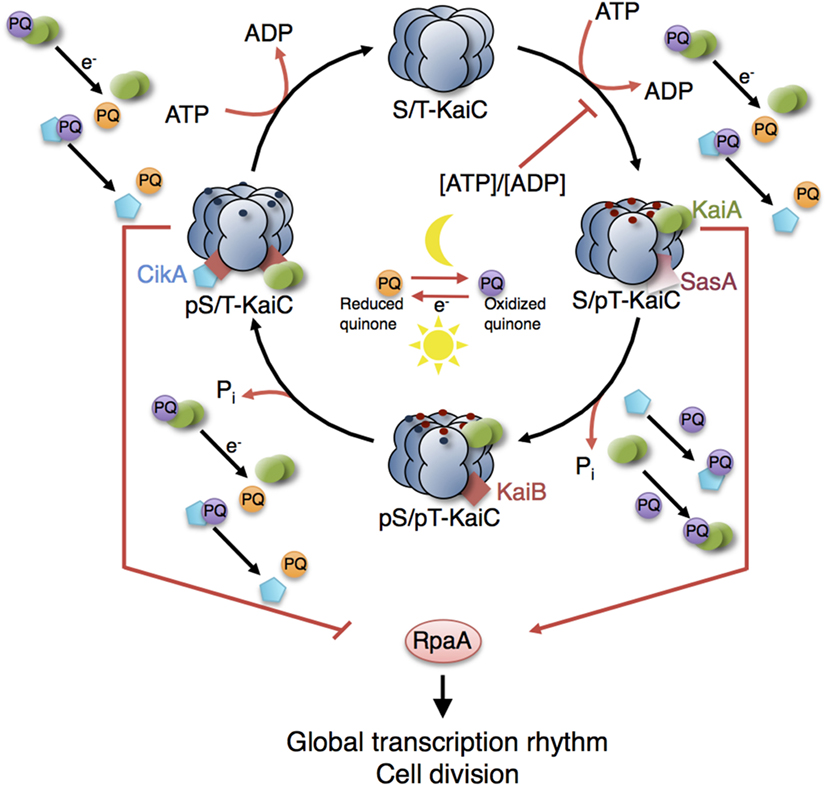
Figure 6. Model of the circadian clock and putative interaction sites with other metabolic processes. The KaiC phosphorylation cycle and the KaiABC complex formation are dependent on ATP. Cellular metabolic signals encoded in the ATP/ADP ratio have a direct effect on the core clock by modulating the KaiC’s kinase activity (Rust et al., 2011; Pattanayak et al., 2015). Increasing ADP levels at night reset the phase of oscillation by inhibiting further KaiC phosphorylation. Oxidation and reduction of plastoquinone (PQ) are controlled by photosynthetic electron transport during the day and by electrons derived from the respiratory ETC in the night. At the transition from day into night, quinones become transiently oxidized capturing KaiA and CikA (Kim et al., 2012). The aggregation of KaiA stops KaiC phosphorylation. The core circadian clock generates rhythms in gene expression and cell division via the global transcriptional factor RpaA. During the day, the physical interaction of SasA with KaiC promotes phosphotransfer to RpaA so that RpaA becomes active. During the night, the physical interaction of CikA with the KaiBC complex inhibits phosphorylation of RpaA so that RpaA becomes inactive (Gutu and OShea, 2013). Red and blue dots are phosphates at KaiC phosphorylation sites Thr432 and Ser431. Red arrows represent interactions with ATP, ADP, and oxidized quinones related to metabolic processes of phototrophic growth. The role of other input components (e.g., LdpA) and output components (e.g., LabA, RpaB) as well as the location of the quinones in the thylakoid membranes are not shown. See Table 5 (in vitro) and Table 6 (in vivo) for selected models of the cyanobacterial circadian clock.
The KaiC phosphorylation rhythm has widely been studied in systems biology, and hence, a variety of mathematical models have been put forward. The first models were rather minimal to explain how sustained oscillations in phosphorylation of KaiC occur, including no intermediate steps of phosphorylation, introducing feedbacks on KaiC phosphorylation or assuming hypothetical states of KaiA, KaiB, and KaiC (Emberly and Wingreen, 2006; Kurosawa et al., 2006; Mehra et al., 2006; Axmann et al., 2007; Mori et al., 2007). Emberly and Wingreen (2006) were the first who showed theoretically that monomer shuffling between KaiC hexamers at specific clock times could explain the robustness and resilience of the circadian clock—a hypothesis stated prior to experimental evidence. Different variations of the concept, monomer shuffling, have afterward been modeled by other groups (Kageyama et al., 2006; Mehra et al., 2006; Mori et al., 2007; Yoda et al., 2007; Eguchi et al., 2008; Nagai et al., 2010). Another hypothesis of how synchrony within the Kai oscillator could be achieved stresses KaiA sequestration into KaiABC complexes (Kurosawa et al., 2006; Clodong et al., 2007; Rust et al., 2007; van Zon et al., 2007; Brettschneider et al., 2010). The consensus view has emerged that both mechanisms work in concert (Qin et al., 2010a). See Table 5 (in vitro) and Table 6 (in vivo) for selected models of the cyanobacterial circadian clock.
Recent studies have increased our understanding of how the core oscillator is integrated with input pathways and output pathways, which enable the clock to synchronize (“entrain”) to the 24-h period of the environment and to transmit temporal information to downstream processes resulting in circadian rhythms in cellular physiology. Clock input cues involve the cellular ATP/ADP ratio, which has a direct effect on the core clock by modulating the KaiCs kinase activity (Rust et al., 2011). In particular, an increase in the ADP levels, occurring when cells are placed into darkness, inhibits further KaiC phosphorylation and thus resets the phase of oscillation to synchronize to the metabolic state of the cell. By simulating various ATP/ADP ratios that mimic different night phases, Rust et al. (2011) could recreate phase shifts in the core oscillator as seen in vitro and in vivo. For their theoretical analysis, the authors modified a previous mathematical model of the circadian clock, which was based on the rates of phosphorylation and dephosphorylation at Thr432 and Ser431 (Rust et al., 2007). In the refined model, the KaiA-dependent kinase rates were now additionally modulated by the ratio of ATP to ATP + ADP. This model was again adapted to account for an additional ATPase activity experimentally found in the CI subunit of KaiC and required for binding of KaiB to Ser-phosphorylated KaiC (Phong et al., 2013). The KaiBC complex formation was shown to depend on an ATPase, but whose activity was insensitive to changes in the cellular ATP/ADP ratio—in contrast to the ATPase in the CII subunit of KaiC (responsible for the Thr/Ser phosphorylation reactions). The results of the combined modeling and experimental study (Phong et al., 2013) suggest that these two differently sensitive catalytic domains are responsible for the capability of the clock to receive input signals while preserving circadian rhythmicity. Depending on the specific question under investigation, both entrainment models could relatively straightforwardly be integrated with other modules of cyanobacterial physiology, with ATP as key to coupling (e.g., light reactions). Another model version already exists, which additionally accounts for the transcription and translation of clock genes as well as the feedback to the core oscillator but needs to be extended to include interactions with other cellular parameters such as the ATP/ADP ratio (Teng et al., 2013). The mathematical clock model proposed by Brettschneider et al. (2010) could equally be envisaged for the integration into larger models of phototrophic growth. The core oscillator is modeled by a larger set of ODEs (12 ODEs; for comparison, 3 ODEs in Rust et al. (2007) but includes hexamerization of KaiC, monomer shuffling, and assembly and disassembly of KaiAC, KaiBC, and KaiABC complexes. Here also, an extended model (15 ODEs) coupled to a transcription–translation circuit has been proposed (Hertel et al., 2013). Inhibition of KaiCs’ kinase activity by ADP can be incorporated into the model.
Sensing the decrease in the ATP/ADP ratio during night is assumed to allow the clock to infer the length of night (Rust et al., 2011). In two biochemical studies, Pattanayak et al. uncovered a further connection between the clock and cellular metabolism: metabolic rhythms produced by the clock (such as rhythms in glycogen abundance, which go along with changing levels of ATP/ADP) feed back to the core oscillator. These rhythms are very likely the main driving force of the clock, allowing the cells to anticipate the onset of darkness in advance (Pattanayak et al., 2014, 2015). In addition, the clock seems to be able to anticipate nightfall through the plastoquinone pool, which is part of the ETC. In particular, the plastoquinone pool embedded within the thylakoid membrane becomes transiently oxidized at the transition from day into night and binding of PQ to KaiA causing aggregation and decay that, in turn, reduces the positive effect of KaiA on KaiC phosphorylation (Wood et al., 2010; Kim et al., 2012). Other redox-sensitive input components such as CikA (circadian input kinase) and LdpA (light-dependent period A) have been identified, which reset or modulate the phase of KaiC phosphorylation cycle [reviewed by Mackey et al. (2011)]. Figure 6 provides a schematic of possible sites of interactions. Mathematical models describing the interconnections at the molecular level have yet to be developed.
The cyanobacterial circadian clock results in genome-wide gene expression rhythms and regulates cell cycle progression relaying information via a two-component system that comprised SasA (Synechococcus adaptive sensor A) and RpaA (regulator of phycobilisome association A) (Liu et al., 1995; Mori et al., 1996; Takai et al., 2006; Dong et al., 2010). Rhythms of chromosome compaction and DNA topology (highly correlated with gene expression rhythms) do not hinge on SasA, pointing to the existence of other output pathways (Smith and Williams, 2006; Woelfle et al., 2007; Vijayan et al., 2009). In the positive transcriptional pathway, SasA interacts physically with KaiC and acts as a kinase toward RpaA (Takai et al., 2006; Gutu and OShea, 2013). In the course of a circadian cycle, KaiB displaces SasA from KaiC and KaiA becomes sequestered, switching KaiC into autodephosphorylation mode (Figure 6). The negative transcriptional output involves LabA (low amplitude and bright), CikA, and the transcriptional factor RpaB (regulator of phycobilisome associated B)—all three repressing the activity of RpaA (Taniguchi et al., 2007; Gutu and OShea, 2013; Espinosa et al., 2015). CikA, with its dual role in input and output pathways, plays a special role. As an output component, CikA competes with KaiA for binding to KaiB (Gutu and OShea, 2013; Chang et al., 2015). The binding of CikA to the KaiBC complex activates the phosphatase activity of CikA toward RpaA (Gutu and OShea, 2013) (Figure 6). RpaA, as both a circadian transcriptional activator and a repressor, drives global gene expression rhythms. The transcriptional output includes the regulation of clock genes, forming a transcription–translation feedback loop (TTFL) to the core oscillator (Ishiura et al., 1998). Since we are just beginning to understand the mechanistic details of the TTFL, the existing mathematical models are still highly simplified, using phenomenological assumptions as to how RpaA (Zwicker et al., 2010) or specific phospho-forms of KaiC control transcription of the kaiBC gene cluster (Miyoshi et al., 2007; Qin et al., 2010b; Hertel et al., 2013; Teng et al., 2013). These models reproduce the most important experimental results, although Miyoshi et al. (2007) assumed hypothetical states for KaiA, KaiB, and KaiC inconsistent with experiments. Due the relatively small numbers of variables and parameters, the ODE models of Teng et al. (2013) and Hertel et al. (2013) might be most suitable for use in larger models of phototrophic growth but require additional modifications that account for the most recent experimental findings.
8. Regulation of Gene Expression in Cyanobacteria
In Synechococcus elongatus PCC 7942, the KaiC phosphorylation cycle targets the general transcription apparatus and thereby regulates 30–100% of the transcriptome in circadian fashion, depending on the experimental setup (Liu et al., 1995; Nakahira et al., 2004; Ito et al., 2009; Vijayan et al., 2009; Lehmann et al., 2013). The transcriptional output is regulated by multiple factors such as circadian changes in chromosomal compaction/decompaction (Smith and Williams, 2006) involving oscillations in DNA supercoiling (Woelfle et al., 2007) as well as biochemical cascade pathways that converge to globally acting transcription factors, RpaA and RpaB and so far unknown factors (Taniguchi et al., 2007; Gutu and OShea, 2013; Paddock et al., 2013; Espinosa et al., 2015). Furthermore, it is now clear that small non-protein-coding RNAs (<200 nucleotides) play as both positive and negative regulators crucial roles in gene expression of cyanobacteria (Georg and Hess, 2011). By base-pairing with the target mRNA, small RNA molecules interfere with the ribosome binding site or other sequence stretches, and consequently alter mRNA translation and stability. This mode of regulation might explain why the proportion of cyclic proteins in diverse cyanobacteria is rather uncorrelated to that found in microarray studies (Stöckel et al., 2011; Waldbauer et al., 2012; Guerreiro et al., 2014), because not only transcriptional but also post-transcriptional (small RNA-mediated) mechanisms might be active and modulate or fine-tune the dynamics of regulatory networks. Synechocystis sp. PCC 6803 possesses a large number of small non-coding RNAs, and antisense RNAs influence at least 26% of all gene transcripts in this cyanobacterium. There are several hints that the non-coding RNAs fulfill important functions in light–dark acclimation (Georg et al., 2009; Mitschke et al., 2011). A specific functional role could be clarified for some of the antisense RNAs, e.g., IsrR (Dühring et al., 2006; Legewie et al., 2008), as-flv4 (Eisenhut et al., 2012), or PsbAR2 and PsbAR3 mRNA (Sakurai et al., 2012). Yet, many identified RNA regulators still await elucidation of their functional relevance.
9. Conclusion: Putting the Parts Together
Almost all cellular functions have evolved in the context of constraints and trade-offs that can only be understood if the respective cellular and environmental context is taken into account. To this end, the construction of computational models of cellular processes not only allows us to study the inner workings of selected processes but also allows us to investigate the emergent properties that arise from interactions between these processes. The trade-offs and interrelations within phototrophic growth are manifold: the energy required for cellular growth is derived from the photosynthetic light reactions, which themselves are a major source of reactive oxygen species (ROS) and therefore require careful balance between different electron transport pathways and alternative electron “valves”. CCMs use energy and have implications for the efficiency of carbon assimilation. The cellular ATP/ADP ratio and the oxidized PQ pool relays information to the circadian clock, which affects transcriptional output and hence metabolic activity. Metabolism itself depends on cellular energy and redox potential—and must be appropriately coordinated to synthesize the right metabolites at the right time. The availability of ribosomes and amino acids, which are itself products of metabolism, affects the rates of translation of new proteins—which must be coordinated to account for damage, stability, and turnover times of proteins. In particular, the components of PSII complexes themselves are dependent on environmental conditions due to photodamage caused by ROS (Yao et al., 2012).
Many if not most of these interactions and trade-offs are still insufficiently understood. An important example is the action and the evolutionary benefit of the circadian clock. While many if not most prokaryotes live in environments with periodic diurnal cycles of light, temperature, and humidity, only cyanobacteria are known to possess a bona fide circadian clock. While the competitive advantage of a circadian clock in a periodic environment has been demonstrated experimentally for cyanobacteria (Woelfle et al., 2004), the precise adaptive value and the selective pressure resulting the evolution of a clock remains only partially understood. Reasoning about the possible fitness implications of a circadian clock necessarily involves considering the organisms as a whole, as exemplified in the “escape from light” hypothesis that circadian rhythmicity arose from the need to protect the organism’s DNA from ultraviolet (UV) radiation, at the time unfiltered by the Earth’s early atmosphere (Hut and Beersma, 2011; Lück and Westermark, 2016). A quantitative evaluation of such a hypothesis requires to contrast the energetic cost of the circadian clock with its benefits for survival and growth—a task where advanced computational models will allow for an increasingly quantitative evaluation.
While, as outlined in this contribution, a large number of computational models related to phototrophic growth are already available, also many important cellular processes are still insufficiently described. An important example is the coordination of cellular growth in response to transient darkness, starvation, or stress conditions. Only recently, iconic pathways, such as the stringent response, have been shown to be active also in cyanobacteria and to mediate a coordinated transcriptional and translational reaction to (transient) periods of darkness (Hood et al., 2016). Likewise, knowledge about the molecular and physiological mechanisms involved in the transition of cyanobacterial cells from a resting state to an active vegetative state is still incomplete (Klotz et al., 2016)—albeit crucial to understand what mechanisms causes a cyanobacterial cell to divert resources away from growth and division and toward survival until environmental conditions improve. Also, only little is known concerning the coordination of cellular metabolism with cell cycle events (Asato, 2005, 2006). In particular, cell size control and size homeostasis in bacteria is still not fully understood, with conceptual models dating back to the work of Donachie (1968). Recent work on E. coli and B. subtilis favored the “ädder” model, in which the size added between birth and division is constant for a given growth condition—as opposed to the “sizer,” in which the cell actively monitors cell size, and “timer” model, in which the cell grows for a specific time before division (Taheri-Araghi et al., 2015). Corresponding studies for cyanobacteria are not yet available. Recent data have indicated that there is coupling between circadian oscillator and the cell cycle, specifically that cell cycle progression in some cyanobacteria slows during specific circadian intervals (Dong et al., 2010; Yang et al., 2010)—posing timely questions for further computational research and necessitating integrative modules of cyanobacterial growth.
Overall, there is increasing interest in whole-cell models to understand cellular trade-offs and functions in the context of a living cells. The construction of integrative computational models to predict phenotype from genotype has gained momentum with a first whole-cell model of the life cycle of the human pathogen Mycoplasma genitalium—based on a subdivision of cell functionality into modules (Karr et al., 2012). A similar effort was already undertaken for cyanobacteria to explain fitness advantage conveyed by a circadian clock (Hellweger, 2010)—an approach that can be regarded as a prototype for the path outlined in this contribution.
Distinct from other approaches to whole-cell models, however, we argue that it is unlikely that a single universal model—a model that spans all scales from intracellular to intercellular to properties of ecosystems—will fulfill all requirements needed to describe cellular growth. Rather, we envision a modular approach. Depending on the research question, different temporal and spatial scales must be considered. The task is then to derive an appropriate representation of cellular processes that accounts for the spatial and temporal scales involved. The derived submodels should be consistent with more fine-grained representation and their construction must be informed by knowledge how processes interact and which trade-offs are relevant for a specific research question. We note that, besides the biological challenges, such a strategy also entails major computational challenges. As yet, the annotation of computational models is often poor. That is, the biochemical identity of model variables is not defined in a computer-readable format, and hence, merging of models typically requires extensive manual curation (Krause et al., 2010). While standardized exchange formats for computational models, such as the Systems Biology Markup Language, SBML (Hucka et al., 2003), are available for more than a decade, they are not commonly applied outside the Systems Biology community. For example, as yet, none of the models of the cyanobacterial circadian clock are available from the BioModels database—a major resource for computational models of biological processes (Li et al., 2010). In addition, only few computational tools allow for the integration of different modeling concepts, such as constraint-based and kinetic models.
Notwithstanding these challenges in computational methodology, we expect a growing library of models related to cyanobacterial growth that can inform and guide research how phototrophic organisms, such as cyanobacteria, adapt to complex environments. These models must increasingly adhere to common standards and should be made available on open platforms, such as the BioModels database (Li et al., 2010) and e-cyanobacterium.org (Klement et al., 2013). Given the recent advances in model development and annotation, computational modeling will undoubtedly play a key role in understanding trade-offs and adaptations in cyanobacteria. In the beginning, integrated models of cyanobacterial growth will be still idealistic, crude, and most certainly incomplete. But, again referring to Neidhardt (1999), “it is only through such modeling of whole-system behavior—that is, of growth—that one will learn how near and how far our knowledge takes us toward understanding the living cell.”
Author Contributions
SW and RS conducted the research and wrote the article. Both authors approved the final manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Jiří Jablonský for discussing his work on modeling phtosynthetic light reactions and carbon metabolism, as well as Robert L. Burnap for comments and sharing insight about cyanobacterial physiology and growth.
Funding
This work is a contribution from the research grant CyanoGrowth funded by the German Federal Ministry of Education and Research as part of the e:Bio Innovationswettbewerb Systembiologie [e:Bio systems biology innovation competition] initiative (reference: FKZ 0316192).
References
Abe, J., Hiyama, T. B., Mukaiyama, A., Son, S., Mori, T., Saito, S., et al. (2015). Atomic-scale origins of slowness in the cyanobacterial circadian clock. Science 349, 312–316. doi:10.1126/science.1261040
Acuña, A. M., Snellenburg, J. J., Gwizdala, M., Kirilovsky, D., van Grondelle, R., and van Stokkum, I. H. M. (2016). Resolving the contribution of the uncoupled phycobilisomes to cyanobacterial pulse-amplitude modulated (PAM) fluorometry signals. Photosynth. Res. 127, 91–102. doi:10.1007/s11120-015-0141-x
Allen, J. I., and Polimene, L. (2011). Linking physiology to ecology: towards a new generation of plankton models. J. Plankton Res. 33, 989–997. doi:10.1093/plankt/fbr032
Amariei, C., Machné, R., Sasidharan, K., Gottstein, W., Tomita, M., Soga, T., et al. (2013). The dynamics of cellular energetics during continuous yeast culture. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2013, 2708–2711. doi:10.1109/EMBC.2013.6610099
Amarnath, K., Bennett, D. I. G., Schneider, A. R., and Fleming, G. R. (2016). Multiscale model of light harvesting by photosystem II in plants. Proc. Natl. Acad. Sci. U.S.A. 113, 1156–1161. doi:10.1073/pnas.1524999113
Antoniewicz, M. R. (2013). Dynamic metabolic flux analysis–tools for probing transient states of metabolic networks. Curr. Opin. Biotechnol. 24, 973–978. doi:10.1016/j.copbio.2013.03.018
Asato, Y. (2005). Control of ribosome synthesis during the cell division cycles of E. coli and Synechococcus. Curr. Issues Mol. Biol. 7, 109–117.
Asato, Y. (2006). Perspectives in the coordinate regulation of cell cycle events in Synechococcus. Curr. Issues Mol. Biol. 8, 91–95.
Axmann, I. M., Legewie, S., and Herzel, H. (2007). “A minimal circadian clock model,” in Genome Inform, Vol. 18 (World Scientific), 54–64.
Ayata, S.-D., Levy, M., Aumont, O., Sciandra, A., Sainte-Marie, J., Tagliabue, A., et al. (2013). Phytoplankton growth formulation in marine ecosystem models: should we take into account photo-acclimation and variable stoichiometry in oligotrophic areas? J. Mar. Syst. 125, 29–40. doi:10.1016/j.jmarsys.2012.12.010
Badger, M. R., Bassett, M., and Comins, H. N. (1985). A model for HCO(3) accumulation and photosynthesis in the cyanobacterium Synechococcus sp: theoretical predictions and experimental observations. Plant Physiol. 77, 465–471. doi:10.1104/pp.77.2.465
Baroukh, C., Muoz-Tamayo, R., Steyer, J.-P., and Bernard, O. (2014). DRUM: a new framework for metabolic modeling under non-balanced growth. Application to the carbon metabolism of unicellular microalgae. PLoS ONE 9:e104499. doi:10.1371/journal.pone.0104499
Beck, C., Hertel, S., Rediger, A., Lehmann, R., Wiegard, A., Kölsch, A., et al. (2014). Daily expression pattern of protein-encoding genes and small noncoding RNAs in Synechocystis sp. strain PCC 6803. Appl. Environ. Microbiol. 80, 5195–5206. doi:10.1128/AEM.01086-14
Bernard, O. (2011). Hurdles and challenges challenges for modelling and control of microalgae for CO2 mitigation and biofuel production. J. Process Control 21, 1378–1389. doi:10.1016/j.jprocont.2011.07.012
Berry, S., and Rumberg, B. (2000). Kinetic modeling of the photosynthetic electron transport chain. Bioelectrochemistry 53, 35–53. doi:10.1016/S0302-4598(00)00108-2
Brettschneider, C., Rose, R. J., Hertel, S., Axmann, I. M., Heck, A. J., and Kollmann, M. (2010). A sequestration feedback determines dynamics and temperature entrainment of the KaiABC circadian clock. Mol. Syst. Biol. 6, 389. doi:10.1038/msb.2010.44
Burnap, R. L. (2015). Systems and photosystems: cellular limits of autotrophic productivity in cyanobacteria. Front. Bioeng. Biotechnol. 3:1. doi:10.3389/fbioe.2015.00001
Burnap, R. L., Hagemann, M., and Kaplan, A. (2015). Regulation of CO2 concentrating mechanism in cyanobacteria. Life (Basel) 5, 348–371. doi:10.3390/life5010348
Butler, W. L. (1978). Energy distribution in the photochemical apparatus of photosynthesis. Ann. Rev. Plant Physiol. 29, 345–378. doi:10.1146/annurev.pp.29.060178.002021
Butler, W. L., and Strasser, R. J. (1977). Tripartite model for the photochemical apparatus of green plant photosynthesis. Proc. Natl. Acad. Sci. U.S.A. 74, 3382–3385. doi:10.1073/pnas.74.8.3382
Chakrabarti, A., Miskovic, L., Soh, K. C., and Hatzimanikatis, V. (2013). Towards kinetic modeling of genome-scale metabolic networks without sacrificing stoichiometric, thermodynamic and physiological constraints. Biotechnol. J. 8, 1043–1057. doi:10.1002/biot.201300091
Chang, Y.-G., Cohen, S. E., Phong, C., Myers, W. K., Kim, Y.-I., Tseng, R., et al. (2015). A protein fold switch joins the circadian oscillator to clock output in cyanobacteria. Science 349, 324–328. doi:10.1126/science.1260031
Cheung, C. Y. M., Poolman, M. G., Fell, D. A., Ratcliffe, R. G., and Sweetlove, L. J. (2014). A diel flux balance model captures interactions between light and dark metabolism during day-night cycles in C3 and crassulacean acid metabolism leaves. Plant Physiol. 165, 917–929. doi:10.1104/pp.113.234468
Clark, R. L., Cameron, J. C., Root, T. W., and Pfleger, B. F. (2014). Insights into the industrial growth of cyanobacteria from a model of the carbon-concentrating mechanism. AIChE J. 60, 12691277. doi:10.1002/aic.14310
Clodong, S., Dühring, U., Kronk, L., Wilde, A., Axmann, I., Herzel, H., et al. (2007). Functioning and robustness of a bacterial circadian clock. Mol. Syst. Biol. 3, 90. doi:10.1038/msb4100128
Crill, P. A. (1977). The photosynthesis-light curve: a simple analog model. J. Theor. Biol. 64, 503–516. doi:10.1016/0022-5193(77)90284-3
Diamond, S., Jun, D., Rubin, B. E., and Golden, S. S. (2015). The circadian oscillator in Synechococcus elongatus controls metabolite partitioning during diurnal growth. Proc. Natl. Acad. Sci. U.S.A. 112, E1916–E1925. doi:10.1073/pnas.1504576112
Donachie, W. D. (1968). Relationship between cell size and time of initiation of DNA replication. Nature 219, 1077–1079. doi:10.1038/2191077a0
Dong, G., Yang, Q., Wang, Q., Kim, Y.-I., Wood, T. L., Osteryoung, K. W., et al. (2010). Elevated ATPase activity of KaiC applies a circadian checkpoint on cell division in Synechococcus elongatus. Cell 140, 529–539. doi:10.1016/j.cell.2009.12.042
Droop, M. R. (1968). Vitamin B12 and marine ecology. IV. The kinetics of uptake, growth and inhibition in Monochrysis lutheri. J. Mar. Biol. Assoc. U.K. 48, 689–733. doi:10.1017/S0025315400019238
Droop, M. R. (1983). 25 years of algal growth kinetic: a personal view. Botanica Marina XXVI, 99–112.
Dühring, U., Axmann, I. M., Hess, W. R., and Wilde, A. (2006). An internal antisense RNA regulates expression of the photosynthesis gene isiA. Proc. Natl. Acad. Sci. U.S.A. 103, 7054–7058. doi:10.1073/pnas.0600927103
Ebenhöh, O., Houwaart, T., Lokstein, H., Schlede, S., and Tirok, K. (2011). A minimal mathematical model of nonphotochemical quenching of chlorophyll fluorescence. BioSystems 103, 196–204. doi:10.1016/j.biosystems.2010.10.011
Egli, M., Mori, T., Pattanayek, R., Xu, Y., Qin, X., and Johnson, C. H. (2012). Dephosphorylation of the core clock protein KaiC in the cyanobacterial KaiABC circadian oscillator proceeds via an ATP synthase mechanism. Biochemistry 51, 1547–1558. doi:10.1021/bi201525n
Eguchi, K., Yoda, M., Terada, T. P., and Sasai, M. (2008). Mechanism of robust circadian oscillation of KaiC phosphorylation in vitro. Biophys. J. 95, 1773–1784. doi:10.1529/biophysj.107.127555
Eilers, P. H. C., and Peeters, J. C. H. (1988). A model for the relationship between light intensity and the rate of photosynthesis. Ecol. Model. 42, 199–215. doi:10.1016/0304-3800(88)90057-9
Eisenhut, M., Georg, J., Klähn, S., Sakurai, I., Mustila, H., Zhang, P., et al. (2012). The antisense RNA As1_flv4 in the cyanobacterium Synechocystis sp. PCC 6803 prevents premature expression of the flv4-2 operon upon shift in inorganic carbon supply. J. Biol. Chem. 287, 33153–33162. doi:10.1074/jbc.M112.391755
Emberly, E., and Wingreen, N. S. (2006). Hourglass model for a protein-based circadian oscillator. Phys. Rev. Lett. 96, 038303. doi:10.1103/PhysRevLett.96.038303
Erdrich, P., Steuer, R., and Klamt, S. (2015). An algorithm for the reduction of genome-scale metabolic network models to meaningful core models. BMC Syst. Biol. 9:48. doi:10.1186/s12918-015-0191-x
Espinosa, J., Boyd, J. S., Cantos, R., Salinas, P., Golden, S. S., and Contreras, A. (2015). Cross-talk and regulatory interactions between the essential response regulator RpaB and cyanobacterial circadian clock output. Proc. Natl. Acad. Sci. U.S.A. 112, 2198–2203. doi:10.1073/pnas.1424632112
Farquhar, G. D., von Caemmerer, S., and Berry, J. A. (1980). A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90. doi:10.1007/BF00386231
Feng, X., Xu, Y., Chen, Y., and Tang, Y. J. (2012). Integrating flux balance analysis into kinetic models to decipher the dynamic metabolism of Shewanella oneidensis mr-1. PLoS Comput. Biol. 8:e1002376. doi:10.1371/journal.pcbi.1002376
Fokina, O., Chellamuthu, V.-R., Forchhammer, K., and Zeth, K. (2010). Mechanism of 2-oxoglutarate signaling by the Synechococcus elongatus PII signal transduction protein. Proc. Natl. Acad. Sci. U.S.A. 107, 19760–19765. doi:10.1073/pnas.1007653107
Fridlyand, L., Kaplan, A., and Reinhold, L. (1996). Quantitative evaluation of the role of a putative CO2-scavenging entity in the cyanobacterial CO2-concentrating mechanism. BioSystems 37, 229–238. doi:10.1016/0303-2647(95)01561-2
Georg, J., and Hess, W. R. (2011). cis-Antisense RNA, another level of gene regulation in bacteria. Microbiol. Mol. Biol. Rev. 75, 286–300. doi:10.1128/MMBR.00032-10
Georg, J., Voß, B., Scholz, I., Mitschke, J., Wilde, A., and Hess, W. R. (2009). Evidence for a major role of antisense RNAs in cyanobacterial gene regulation. Mol. Syst. Biol. 5, 305. doi:10.1038/msb.2009.63
Giersch, C. (1986). Oscillatory response of photosynthesis in leaves to environmental perturbations: a mathematical model. Arch. Biochem. Biophys. 245, 263–270. doi:10.1016/0003-9861(86)90213-4
Goel, A., Wortel, M. T., Molenaar, D., and Teusink, B. (2012). Metabolic shifts: a fitness perspective for microbial cell factories. Biotechnol. Lett. 34, 2147–2160. doi:10.1007/s10529-012-1038-9
Gorbunov, M. Y., Kuzminov, F. I., Fadeev, V. V., Kim, J. D., and Falkowski, P. G. (2011). A kinetic model of non-photochemical quenching in cyanobacteria. Biochim. Biophys. Acta 1807, 1591–1599. doi:10.1016/j.bbabio.2011.08.009
Guerreiro, A. C., Benevento, M., Lehmann, R., van Breukelen, B., Post, H., Giansanti, P., et al. (2014). Daily rhythms in the cyanobacterium Synechococcus elongatus probed by high-resolution mass spectrometry-based proteomics reveals a small defined set of cyclic proteins. Mol. Cell. Proteomics 13, 2042–2055. doi:10.1074/mcp.M113.035840
Gutu, A., and OShea, E. K. (2013). Two antagonistic clock-regulated histidine kinases time the activation of circadian gene expression. Mol. Cell 50, 288–294. doi:10.1016/j.molcel.2013.02.022
Hahn, B. D. (1987). A mathematical model of photorespiration and photosynthesis. Ann. Bot. 60, 157–169.
Hahn, B. D. (1991). Photosynthesis and photorespiration: modelling the essentials. J. Theor. Biol. 151, 123–139. doi:10.1016/S0022-5193(05)80147-X
Hamilton, J. J., and Reed, J. L. (2012). Identification of functional differences in metabolic networks using comparative genomics and constraint-based models. PLoS ONE 7:e34670. doi:10.1371/journal.pone.0034670
Han, B. P. (2001). Photosynthesis-irradiance response at physiological level: a mechanistic model. J. Theor. Biol. 213, 121–127. doi:10.1006/jtbi.2001.2413
Han, B.-P. (2002). A mechanistic model of algal photoinhibition induced by photodamage to photosystem-II. J. Theor. Biol. 214, 519–527. doi:10.1006/jtbi.2001.2468
Hellweger, F. L. (2010). Resonating circadian clock enhance fitness in cyanobacteria in silico. Ecol. Model. 221, 1620–1629. doi:10.1016/j.ecolmodel.2010.03.015
Henson, M. A. (2015). Genome-scale modelling of microbial metabolism with temporal and spatial resolution. Biochem. Soc. Trans. 43, 1164–1171. doi:10.1042/BST20150146
Hertel, S., Brettschneider, C., and Axmann, I. M. (2013). Revealing a two-loop transcriptional feedback mechanism in the cyanobacterial circadian clock. PLoS Comput. Biol. 9:e1002966. doi:10.1371/journal.pcbi.1002966
Holzwarth, A. R., Müller, M. G., Reus, M., Nowaczyk, M., Sander, J., and Rögner, M. (2006). Kinetics and mechanism of electron transfer in intact photosystem II and in the isolated reaction center: pheophytin is the primary electron acceptor. Proc. Natl. Acad. Sci. U.S.A. 103, 6895–6900. doi:10.1073/pnas.0505371103
Hood, R. D., Higgins, S. A., Flamholz, A., Nichols, R. J., and Savage, D. F. (2016). The stringent response regulates adaptation to darkness in the cyanobacterium Synechococcus elongatus. Proc. Natl. Acad. Sci. U.S.A 113, E4867–E4876. doi:10.1073/pnas.1524915113
Hopkinson, B. M., Young, J. N., Tansik, A. L., and Binder, B. J. (2014). The minimal CO2-concentrating mechanism of Prochlorococcus spp. MED4 is effective and efficient. Plant Physiol. 166, 2205–2217. doi:10.1104/pp.114.247049
Hucka, M., Finney, A., Sauro, H. M., Bolouri, H., Doyle, J. C., Kitano, H., et al. (2003). The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 19, 524–531. doi:10.1093/bioinformatics/btg015
Hut, R. A., and Beersma, D. G. M. (2011). Evolution of time-keeping mechanisms: early emergence and adaptation to photoperiod. Philos. Trans. R. Soc. Lond. B Biol. Sci. 366, 2141–2154. doi:10.1098/rstb.2010.0409
Ishiura, M., Kutsuna, S., Aoki, S., Iwasaki, H., Andersson, C. R., Tanabe, A., et al. (1998). Expression of a gene cluster kaiABC as a circadian feedback process in cyanobacteria. Science 281, 1519–1523. doi:10.1126/science.281.5382.1519
Ito, H., Mutsuda, M., Murayama, Y., Tomita, J., Hosokawa, N., Terauchi, K., et al. (2009). Cyanobacterial daily life with Kai-based circadian and diurnal genome-wide transcriptional control in Synechococcus elongatus. Proc. Natl. Acad. Sci. U.S.A. 106, 14168–14173. doi:10.1073/pnas.0902587106
Iwasaki, H., Nishiwaki, T., Kitayama, Y., Nakajima, M., and Kondo, T. (2002). KaiA-stimulated KaiC phosphorylation in circadian timing loops in cyanobacteria. Proc. Natl. Acad. Sci. U.S.A. 99, 15788–15793. doi:10.1073/pnas.222467299
Jablonský, J., Hagemann, M., Schwarz, D., and Wolkenhauer, O. (2013). Phosphoglycerate mutases function as reverse regulated isoenzymes in Synechococcus elongatus PCC 7942. PLoS ONE 8:e58281. doi:10.1371/journal.pone.0058281
Jablonský, J., and Lazár, D. (2008). Evidence for intermediate S-states as initial phase in the process of oxygen-evolving complex oxidation. Biophys. J. 94, 2725–2736. doi:10.1529/biophysj.107.122861
Jablonský, J., Papacek, S., and Hagemann, M. (2016). Different strategies of metabolic regulation in cyanobacteria: from transcriptional to biochemical control. Sci. Rep. 6, 33024. doi:10.1038/srep33024
Jablonský, J., Schwarz, D., and Hagemann, M. (2014). Multi-level kinetic model explaining diverse roles of isozymes in prokaryotes. PLoS ONE 9:e105292. doi:10.1371/journal.pone.0105292
Jablonský, J., Susila, P., and Lazár, D. (2008). Impact of dimeric organization of enzyme on its function: the case of photosynthetic water splitting. Bioinformatics 24, 2755–2759. doi:10.1093/bioinformatics/btn530
Kageyama, H., Nishiwaki, T., Nakajima, M., Iwasaki, H., Oyama, T., and Kondo, T. (2006). Cyanobacterial circadian pacemaker: Kai protein complex dynamics in the KaiC phosphorylation cycle in vitro. Mol. Cell 23, 161–171. doi:10.1016/j.molcel.2006.05.039
Kaplan, A., and Reinhold, L. (1999). CO2 concentrating mechanisms in photosynthetic microorganisms. Annu. Rev. Plant Physiol. Plant Mol. Biol. 50, 539–570. doi:10.1146/annurev.arplant.50.1.539
Karr, J. R., Sanghvi, J. C., Macklin, D. N., Gutschow, M. V., Jacobs, J. M., Bolival, B. Jr., et al. (2012). A whole-cell computational model predicts phenotype from genotype. Cell 150, 389–401. doi:10.1016/j.cell.2012.05.044
Kim, J. I., Varner, J. D., and Ramkrishna, D. (2008). A hybrid model of anaerobic E. coli GJT001: combination of elementary flux modes and cybernetic variables. Biotechnol. Prog. 24, 993–1006. doi:10.1002/btpr.73
Kim, Y.-I., Vinyard, D. J., Ananyev, G. M., Dismukes, G. C., and Golden, S. S. (2012). Oxidized quinones signal onset of darkness directly to the cyanobacterial circadian oscillator. Proc. Natl. Acad. Sci. U.S.A. 109, 17765–17769. doi:10.1073/pnas.1216401109
Kirilovsky, D., and Kerfeld, C. A. (2013). The orange carotenoid protein: a blue-green light photoactive protein. Photochem. Photobiol. Sci. 12, 1135–1143. doi:10.1039/c3pp25406b
Kitayama, Y., Iwasaki, H., Nishiwaki, T., and Kondo, T. (2003). KaiB functions as an attenuator of KaiC phosphorylation in the cyanobacterial circadian clock system. EMBO J. 22, 2127–2134. doi:10.1093/emboj/cdg212
Klement, M., Safranek, D., Ded, T., Pejznoch, A., Nedbal, L., Steuer, R., et al. (2013). A comprehensive web-based platform for domain-specific biological models. ENTCS 299, 61–67. doi:10.1016/j.entcs.2013.11.006
Klotz, A., Georg, J., Bučinská, L., Watanabe, S., Reimann, V., Januszewski, W., et al. (2016). Awakening of a dormant cyanobacterium from nitrogen chlorosis reveals a genetically determined program. Curr. Biol. 26, 2862–2872. doi:10.1016/j.cub.2016.08.054
Knies, D., Wittmüß, P., Appel, S., Sawodny, O., Ederer, M., and Feuer, R. (2015). Modeling and simulation of optimal resource management during the diurnal cycle in Emiliania huxleyi by genome-scale reconstruction and an extended flux balance analysis approach. Metabolites 5, 659–676. doi:10.3390/metabo5040659
Knoop, H., Gründel, M., Zilliges, Y., Lehmann, R., Hoffmann, S., Lockau, W., et al. (2013). Flux balance analysis of cyanobacterial metabolism: the metabolic network of Synechocystis sp. PCC 6803. PLoS Comput. Biol. 9:e1003081. doi:10.1371/journal.pcbi.1003081
Knoop, H., Zilliges, Y., Lockau, W., and Steuer, R. (2010). The metabolic network of Synechocystis sp. PCC 6803: systemic properties of autotrophic growth. Plant Physiol. 154, 410–422. doi:10.1104/pp.110.157198
Kok, B., Forbush, B., and McGloin, M. (1970). Cooperation of charges in photosynthetic O2 evolution-I. A linear four step mechanism. Photochem. Photobiol. 11, 457475. doi:10.1111/j.1751-1097.1970.tb06017.x
Kopf, M., and Hess, W. R. (2015). Regulatory RNAs in photosynthetic cyanobacteria. FEMS Microbiol. Rev. 39, 301–315. doi:10.1093/femsre/fuv017
Kopf, M., Klähn, S., Scholz, I., Matthiessen, J. K. F., Hess, W. R., and Voß, B. (2014). Comparative analysis of the primary transcriptome of Synechocystis sp. PCC 6803. DNA Res. 21, 527–539. doi:10.1093/dnares/dsu018
Krause, F., Uhlendorf, J., Lubitz, T., Schulz, M., Klipp, E., and Liebermeister, W. (2010). Annotation and merging of SBML models with semanticSBML. Bioinformatics 26, 421–422. doi:10.1093/bioinformatics/btp642
Kroon, B. M. A., and Thoms, S. (2006). From electron to biomass: a mechanistic model to describe phytoplankton photosynthesis and steady-state growth rates. J. Phycol. 42, 593–609. doi:10.1111/j.1529-8817.2006.00221.x
Kurosawa, G., Aihara, K., and Iwasa, Y. (2006). A model for the circadian rhythm of cyanobacteria that maintains oscillation without gene expression. Biophys. J. 91, 2015–2023. doi:10.1529/biophysj.105.076554
Laisk, A., Eichelmann, H., and Oja, V. (2006). C3 photosynthesis in silico. Photosynth. Res. 90, 45–66. doi:10.1007/s11120-006-9109-1
Laisk, A., Eichelmann, H., Oja, V., Eatherall, A., and Walker, D. A. (1989). A mathematical model of the carbon metabolism in photosynthesis. difficulties in explaining oscillations by fructose 2,6-bisphosphate regulation. Proc. R. Soc. Lond. B 237, 389–415. doi:10.1098/rspb.1989.0057
Laisk, A., and Walker, D. A. (1986). Control of phosphate turnover as a rate-limiting factor and possible cause of oscillations in photosynthesis: a mathematical model. Proc. R. Soc. Lond. B 227, 281–302. doi:10.1098/rspb.1986.0024
Lazár, D. (2003). Chlorophyll a fluorescence rise induced by high light illumination of dark-adapted plant tissue studied by means of a model of photosystem II and considering photosystem II heterogeneity. J. Theor. Biol. 220, 469–503. doi:10.1006/jtbi.2003.3140
Lazár, D., and Jablonský, J. (2009). On the approaches applied in formulation of a kinetic model of photosystem II: different approaches lead to different simulations of the chlorophyll alpha fluorescence transients. J. Theor. Biol. 257, 260–269. doi:10.1016/j.jtbi.2008.11.018
Legewie, S., Dienst, D., Wilde, A., Herzel, H., and Axmann, I. M. (2008). Small RNAs establish delays and temporal thresholds in gene expression. Biophys. J. 95, 3232–3238. doi:10.1529/biophysj.108.133819
Lehmann, R., Machné, R., Georg, J., Benary, M., Axmann, I., and Steuer, R. (2013). How cyanobacteria pose new problems to old methods: challenges in microarray time series analysis. BMC Bioinformatics 14:133. doi:10.1186/1471-2105-14-133
Li, C., Donizelli, M., Rodriguez, N., Dharuri, H., Endler, L., Chelliah, V., et al. (2010). Biomodels database: an enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 4:92. doi:10.1186/1752-0509-4-92
Liu, Y., Tsinoremas, N. F., Johnson, C. H., Lebedeva, N. V., Golden, S. S., Ishiura, M., et al. (1995). Circadian orchestration of gene expression in cyanobacteria. Genes Dev. 9, 1469–1478. doi:10.1101/gad.9.12.1469
Lück, S., and Westermark, P. O. (2016). Circadian mRNA expression: insights from modeling and transcriptomics. Cell Mol. Life Sci. 73, 497–521. doi:10.1007/s00018-015-2072-2
Ma, W., and Ogawa, T. (2015). Oxygenic photosynthesis-specific subunits of cyanobacterial NADPH dehydrogenases. IUBMB Life 67, 3–8. doi:10.1002/iub.1341
Maarleveld, T. R., Boele, J., Bruggeman, F. J., and Teusink, B. (2014). A data integration and visualization resource for the metabolic network of Synechocystis sp. PCC 6803. Plant Physiol. 164, 1111–1121. doi:10.1104/pp.113.224394
Mackey, S. R., Golden, S. S., and Ditty, J. L. (2011). The itty-bitty time machine: genetics of the cyanobacterial circadian clock. Adv. Genet. 74, 13. doi:10.1016/B978-0-12-387690-4.00002-7
Mahadevan, R., Edwards, J. S., and Doyle, F. J. III (2002). Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys. J. 83, 1331–1340. doi:10.1016/S0006-3495(02)73903-9
Mangan, N., and Brenner, M. (2014). Systems analysis of the CO2 concentrating mechanism in cyanobacteria. eLife 3:e02043. doi:10.7554/eLife.02043
Mangan, N. M., Flamholz, A., Hood, R. D., Milo, R., and Savage, D. F. (2016). pH determines the energetic efficiency of the cyanobacterial CO2 concentrating mechanism. Proc. Natl. Acad. Sci. U.S.A. 113, E5354–E5362. doi:10.1073/pnas.1525145113
Mar, T., and Govindjee (1972). Kinetic models of oxygen evolution in photosynthesis. J. Theor. Biol. 36, 427–446. doi:10.1016/0022-5193(72)90001-X
McCloskey, D., Palsson, B. O., and Feist, A. M. (2013). Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol. Syst. Biol. 9, 661. doi:10.1038/msb.2013.18
Megard, R. O., Tonkyn, D. W., and Senft, W. H. (1984). Kinetics of oxygenic photosynthesis in plankton algae. J. Plankton Res. 6, 325–337. doi:10.1093/plankt/6.2.325
Mehra, A., Hong, C. I., Shi, M., Loros, J. J., Dunlap, J. C., and Ruoff, P. (2006). Circadian rhythmicity by autocatalysis. PLoS Comput. Biol. 2:e96. doi:10.1371/journal.pcbi.0020096
Milstein, J., and Bremermann, H. J. (1979). Parameter identification of the Calvin photosynthetic cycle. J. Math. Biol. 7, 99–116. doi:10.1007/BF00276924
Mitschke, J., Georg, J., Scholz, I., Sharma, C. M., Dienst, D., Bantscheff, J., et al. (2011). An experimentally anchored map of transcriptional start sites in the model cyanobacterium Synechocystis sp. PCC 6803. Proc. Natl. Acad. Sci. U.S.A. 108, 2124–2129. doi:10.1073/pnas.1015154108
Miyoshi, F., Nakayama, Y., Kaizu, K., Iwasaki, H., and Tomita, M. (2007). A mathematical model for the Kai-protein-based chemical oscillator and clock gene expression rhythms in cyanobacteria. J. Biol. Rhythms 22, 69–80. doi:10.1177/0748730406295749
Molenaar, D., van Berlo, R., de Ridder, D., and Teusink, B. (2009). Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 5, 323. doi:10.1038/msb.2009.82
Montagud, A., Navarro, E., Fernandez de Cordoba, P., Urchueguia, J. F., and Patil, K. R. (2010). Reconstruction and analysis of genome-scale metabolic model of a photosynthetic bacterium. BMC Syst. Biol. 4:156. doi:10.1186/1752-0509-4-156
Mori, T., Binder, B., and Johnson, C. H. (1996). Circadian gating of cell division in cyanobacteria growing with average doubling times of less than 24 hours. Proc. Natl. Acad. Sci. U.S.A. 93, 10183–10188. doi:10.1073/pnas.93.19.10183
Mori, T., Williams, D. R., Byrne, M. O., Qin, X., Egli, M., Mchaourab, H. S., et al. (2007). Elucidating the ticking of an in vitro circadian clockwork. PLoS Biol. 5:e93. doi:10.1371/journal.pbio.0050093
Mueller, T. J., Berla, B. M., Pakrasi, H. B., and Maranas, C. D. (2013). Rapid construction of metabolic models for a family of cyanobacteria using a multiple source annotation workflow. BMC Syst. Biol. 7:142. doi:10.1186/1752-0509-7-142
Müller, S., Regensburger, G., and Steuer, R. (2015). Resource allocation in metabolic networks: kinetic optimization and approximations by FBA. Biochem. Soc. Trans. 43, 1195–1200. doi:10.1042/BST20150156
Mullineaux, C. W. (2014). Electron transport and light-harvesting switches in cyanobacteria. Front. Plant Sci. 5:7. doi:10.3389/fpls.2014.00007
Murabito, E., Verma, M., Bekker, M., Bellomo, D., Westerhoff, H. V., Teusink, B., et al. (2014). Monte-Carlo modeling of the central carbon metabolism of Lactococcus lactis: insights into metabolic regulation. PLoS ONE 9:e106453. doi:10.1371/journal.pone.0106453
Muthuraj, M., Palabhanvi, B., Misra, S., Kumar, V., Sivalingavasu, K., and Das, D. (2013). Flux balance analysis of Chlorella sp. FC2 IITG under photoautotrophic and heterotrophic growth conditions. Photosynth. Res. 118, 167–179. doi:10.1007/s11120-013-9943-x
Nagai, T., Terada, T. P., and Sasai, M. (2010). Synchronization of circadian oscillation of phosphorylation level of KaiC in vitro. Biophys. J. 98, 2469–2477. doi:10.1016/j.bpj.2010.02.036
Nakahira, Y., Katayama, M., Miyashita, H., Kutsuna, S., Iwasaki, H., Oyama, T., et al. (2004). Global gene repression by KaiC as a master process of prokaryotic circadian system. Proc. Natl. Acad. Sci. U.S.A. 101, 881–885. doi:10.1073/pnas.0307411100
Nakajima, M., Imai, K., Ito, H., Nishiwaki, T., Murayama, Y., Iwasaki, H., et al. (2005). Reconstitution of circadian oscillation of cyanobacterial KaiC phosphorylation in vitro. Science 308, 414–415. doi:10.1126/science.1108451
Nedbal, L., Cerveny, J., Keren, N., and Kaplan, A. (2010). Experimental validation of a nonequilibrium model of CO2 fluxes between gas, liquid medium, and algae in a flat-panel photobioreactor. J. Ind. Microbiol. Biotechnol. 37, 1319–1326. doi:10.1007/s10295-010-0876-5
Nedbal, L., Cerveny, J., Rascher, U., and Schmidt, H. (2007). E-photosynthesis: a comprehensive modeling approach to understand chlorophyll fluorescence transients and other complex dynamic features of photosynthesis in fluctuating light. Photosynth. Res. 93, 223–234. doi:10.1007/s11120-007-9178-9
Neidhardt, F. C. (1999). Bacterial growth: constant obsession with dN/dt. J. Bacteriol. 181, 7405–7408.
Neidhardt, F. C., Ingraham, J. L., and Schaechter, M. (1990). Physiology of the Bacterial Cell: A Molecular Approach. Sunderland, MA: Sinauer Associates, Inc.
Nishiwaki, T., and Kondo, T. (2012). Circadian autodephosphorylation of cyanobacterial clock protein KaiC occurs via formation of ATP as intermediate. J. Biol. Chem. 287, 18030–18035. doi:10.1074/jbc.M112.350660
Nishiwaki, T., Satomi, Y., Kitayama, Y., Terauchi, K., Kiyohara, R., Takao, T., et al. (2007). A sequential program of dual phosphorylation of KaiC as a basis for circadian rhythm in cyanobacteria. EMBO J. 26, 4029–4037. doi:10.1038/sj.emboj.7601832
Nishiwaki, T., Satomi, Y., Nakajima, M., Lee, C., Kiyohara, R., Kageyama, H., et al. (2004). Role of KaiC phosphorylation in the circadian clock system of Synechococcus elongatus PCC 7942. Proc. Natl. Acad. Sci. U.S.A. 101, 13927–13932. doi:10.1073/pnas.0403906101
Nogales, J., Gudmundsson, S., Knight, E. M., Palsson, B. O., and Thiele, I. (2012). Detailing the optimality of photosynthesis in cyanobacteria through systems biology analysis. Proc. Natl. Acad. Sci. U.S.A. 109, 2678–2683. doi:10.1073/pnas.1117907109
Paddock, M. L., Boyd, J. S., Adin, D. M., and Golden, S. S. (2013). Active output state of the Synechococcus Kai circadian oscillator. Proc. Natl. Acad. Sci. U.S.A. 110, E3849–E3857. doi:10.1073/pnas.1315170110
Pattanayak, G., and Rust, M. J. (2014). The cyanobacterial clock and metabolism. Curr. Opin. Microbiol. 18, 90–95. doi:10.1016/j.mib.2014.02.010
Pattanayak, G. K., Lambert, G., Bernat, K., and Rust, M. J. (2015). Controlling the cyanobacterial clock by synthetically rewiring metabolism. Cell Rep. 13, 2362–2367. doi:10.1016/j.celrep.2015.11.031
Pattanayak, G. K., Phong, C., and Rust, M. J. (2014). Rhythms in energy storage control the ability of the cyanobacterial circadian clock to reset. Curr. Biol. 24, 1934–1938. doi:10.1016/j.cub.2014.07.022
Pettersson, G., and Ryde-Pettersson, U. (1988). A mathematical model of the Calvin photosynthesis cycle. Eur. J. Biochem. 175, 661–672. doi:10.1111/j.1432-1033.1988.tb14242.x
Phong, C., Markson, J. S., Wilhoite, C. M., and Rust, M. J. (2013). Robust and tunable circadian rhythms from differentially sensitive catalytic domains. Proc. Natl. Acad. Sci. U.S.A. 110, 1124–1129. doi:10.1073/pnas.1212113110
Poolman, M. G., Fell, D. A., and Thomas, S. (2000). Modelling photosynthesis and its control. J. Exp. Bot. 51 Spec No, 319–328. doi:10.1093/jexbot/51.suppl_1.319
Poolman, M. G., Olcer, H., Lloyd, J. C., Raines, C. A., and Fell, D. A. (2001). Computer modelling and experimental evidence for two steady states in the photosynthetic Calvin cycle. Eur. J. Biochem. 268, 2810–2816. doi:10.1046/j.1432-1327.2001.02153.x
Price, G. D., Badger, M. R., Woodger, F. J., and Long, B. M. (2008). Advances in understanding the cyanobacterial CO2-concentrating-mechanism (CCM): functional components, Ci transporters, diversity, genetic regulation and prospects for engineering into plants. J. Exp. Bot. 59, 1441–1461. doi:10.1093/jxb/erm112
Qin, X., Byrne, M., Mori, T., Zou, P., Williams, D. R., Mchaourab, H., et al. (2010a). Intermolecular associations determine the dynamics of the circadian KaiABC oscillator. Proc. Natl. Acad. Sci. U.S.A. 107, 14805–14810. doi:10.1073/pnas.1002119107
Qin, X., Byrne, M., Xu, Y., Mori, T., and Johnson, C. H. (2010b). Coupling of a core post-translational pacemaker to a slave transcription/translation feedback loop in a circadian system. PLoS Biol. 8:1310. doi:10.1371/journal.pbio.1000394
Reinhold, L., Kosloff, R., and Kaplan, A. (1991). A model for inorganic carbon fluxes and photosynthesis in cyanobacterial carboxysomes. Can. J. Bot. 69, 984–988. doi:10.1139/b91-126
Reinhold, L., Zviman, M., and Kaplan, A. (1987). Inorganic Carbon Fluxes and Photosynthesis in Cyanobacteria – A Quantitative Model. Netherlands: Progress in Photosynthesis Research, Springer, 289–293.
Roussel, M. R., and Igamberdiev, A. U. (2011). Dynamics and mechanisms of oscillatory photosynthesis. BioSystems 103, 230–238. doi:10.1016/j.biosystems.2010.07.020
Rovers, W., and Giersch, C. (1995). Photosynthetic oscillations and the interdependence of photophosphorylation and electron transport as studied by a mathematical model. BioSystems 35, 63–73. doi:10.1016/0303-2647(94)01481-L
Rubio, F. C., Camacho, F. G., Sevilla, J. M. F., Chisti, Y., and Grima, E. M. (2003). A mechanistic model of photosynthesis in microalgae. Biotechnol. Bioeng. 81, 459–473. doi:10.1002/bit.10492
Rügen, M., Bockmayr, A., and Steuer, R. (2015). Elucidating temporal resource allocation and diurnal dynamics in phototrophic metabolism using conditional FBA. Sci. Rep. 5, 15247. doi:10.1038/srep15247
Rust, M. J., Golden, S. S., and OShea, E. K. (2011). Light-driven changes in energy metabolism directly entrain the cyanobacterial circadian oscillator. Science 331, 220–223. doi:10.1126/science.1197243
Rust, M. J., Markson, J. S., Lane, W. S., Fisher, D. S., and O’Shea, E. K. (2007). Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science 318, 809–812. doi:10.1126/science.1148596
Saha, R., Verseput, A. T., Berla, B. M., Mueller, T. J., Pakrasi, H. B., and Maranas, C. D. (2012). Reconstruction and comparison of the metabolic potential of cyanobacteria Cyanothece sp. ATCC 51142 and Synechocystis sp. PCC 6803. PLoS ONE 7:e48285. doi:10.1371/journal.pone.0048285
Sakurai, I., Stazic, D., Eisenhut, M., Vuorio, E., Steglich, C., Hess, W. R., et al. (2012). Positive regulation of psbA gene expression by cis-encoded antisense RNAs in Synechocystis sp. PCC 6803. Plant Physiol. 160, 1000–1010. doi:10.1104/pp.112.202127
Sauro, H. M. (2014). Enzyme Kinetics for Systems Biology (Version 1.06), 2nd Edn. Ambrosius Publishing.
Schaechter, M. (2015). A brief history of bacterial growth physiology. Front. Microbiol. 6:289. doi:10.3389/fmicb.2015.00289
Schultze, M., Forberich, B., Rexroth, S., Dyczmons, N. G., Roegner, M., and Appel, J. (2009). Localization of cytochrome b6f complexes implies an incomplete respiratory chain in cytoplasmic membranes of the cyanobacterium Synechocystis sp. PCC 6803. Biochim. Biophys. Acta 1787, 1479–1485. doi:10.1016/j.bbabio.2009.06.010
Schuurmans, R. M., van Alphen, P., Schuurmans, J. M., Matthijs, H. C. P., and Hellingwerf, K. J. (2015). Comparison of the photosynthetic yield of cyanobacteria and green algae: different methods give different answers. PLoS ONE 10:e0139061. doi:10.1371/journal.pone.0139061
Shastri, A. A., and Morgan, J. A. (2005). Flux balance analysis of photoautotrophic metabolism. Biotechnol. Prog. 21, 1617–1626. doi:10.1021/bp050246d
Shultzaberger, R. K., Boyd, J. S., Diamond, S., Greenspan, R. J., and Golden, S. S. (2015). Giving time purpose: the Synechococcus elongatus clock in a broader network context. Annu. Rev. Genet. 49, 485–505. doi:10.1146/annurev-genet-111212-133227
Smith, R. M., and Williams, S. B. (2006). Circadian rhythms in gene transcription imparted by chromosome compaction in the cyanobacterium Synechococcus elongatus. Proc. Natl. Acad. Sci. U.S.A. 103, 8564–8569. doi:10.1073/pnas.0508696103
Srinivasan, S., Cluett, W. R., and Mahadevan, R. (2015). Constructing kinetic models of metabolism at genome-scales: a review. Biotechnol. J. 10, 1345–1359. doi:10.1002/biot.201400522
Steuer, R. (2007). Computational approaches to the topology, stability and dynamics of metabolic networks. Phytochemistry 68, 2139–2151. doi:10.1016/j.phytochem.2007.04.041
Steuer, R., Gross, T., Selbig, J., and Blasius, B. (2006). Structural kinetic modeling of metabolic networks. Proc. Natl. Acad. Sci. U.S.A. 103, 11868–11873. doi:10.1073/pnas.0600013103
Steuer, R., and Junker, B. H. (2009). “Computational models of metabolism: stability and regulation in metabolic networks,” in Advances in Chemical Physics, Vol. 142, ed. S. A. Rice (Hoboken, NJ: John Wiley & Sons, Inc).
Steuer, R., Knoop, H., and Machné, R. (2012). Modelling cyanobacteria: from metabolism to integrative models of phototrophic growth. J. Exp. Bot. 63, 2259–2274. doi:10.1093/jxb/ers018
Stöckel, J., Jacobs, J. M., Elvitigala, T. R., Liberton, M., Welsh, E. A., Polpitiya, A. D., et al. (2011). Diurnal rhythms result in significant changes in the cellular protein complement in the cyanobacterium Cyanothece 51142. PLoS ONE 6:e16680. doi:10.1371/journal.pone.0016680
Stouthamer, A. H. (1973). A theoretical study on the amount of ATP required for synthesis of microbial cell material. Antonie Van Leeuwenhoek 39, 545–565. doi:10.1007/BF02578899
Taheri-Araghi, S., Bradde, S., Sauls, J. T., Hill, N. S., Levin, P. A., Paulsson, J., et al. (2015). Cell-size control and homeostasis in bacteria. Curr. Biol. 25, 385–391. doi:10.1016/j.cub.2014.12.009
Takai, N., Nakajima, M., Oyama, T., Kito, R., Sugita, C., Sugita, M., et al. (2006). A KaiC-associating SasA-RpaA two-component regulatory system as a major circadian timing mediator in cyanobacteria. Proc. Natl. Acad. Sci. U.S.A. 103, 12109–12114. doi:10.1073/pnas.0602955103
Taniguchi, Y., Katayama, M., Ito, R., Takai, N., Kondo, T., and Oyama, T. (2007). labA: a novel gene required for negative feedback regulation of the cyanobacterial circadian clock protein KaiC. Genes Dev. 21, 60–70. doi:10.1101/gad.1488107
Teng, S.-W., Mukherji, S., Moffitt, J. R., De Buyl, S., and Oshea, E. K. (2013). Robust circadian oscillations in growing cyanobacteria require transcriptional feedback. Science 340, 737–740. doi:10.1126/science.1230996
Terauchi, K., Kitayama, Y., Nishiwaki, T., Miwa, K., Murayama, Y., Oyama, T., et al. (2007). ATPase activity of KaiC determines the basic timing for circadian clock of cyanobacteria. Proc. Natl. Acad. Sci. U.S.A. 104, 16377–16381. doi:10.1073/pnas.0706292104
Tomita, J., Nakajima, M., Kondo, T., and Iwasaki, H. (2005). No transcription-translation feedback in circadian rhythm of KaiC phosphorylation. Science 307, 251–254. doi:10.1126/science.1102540
Tran, L. M., Rizk, M. L., and Liao, J. C. (2008). Ensemble modeling of metabolic networks. Biophys. J. 95, 5606–5617. doi:10.1529/biophysj.108.135442
Tyystjärvi, E., Mäenpää, P., and Aro, E. M. (1994). Mathematical modelling of photoinhibition and photosystem II repair cycle. I. Photoinhibition and D1 protein degradation in vitro and in the absence of chloroplast protein synthesis in vivo. Photosynth. Res. 41, 439–449. doi:10.1007/BF02183046
van Zon, J. S., Lubensky, D. K., Altena, P. R., and ten Wolde, P. R. (2007). An allosteric model of circadian KaiC phosphorylation. Proc. Natl. Acad. Sci. U.S.A. 104, 7420–7425. doi:10.1073/pnas.0608665104
Vermaas, W. (2001). “Photosynthesis and respiration in cyanobacteria,” in eLS (John Wiley & Sons, Ltd).
Vershubskii, A. V., Mishanin, V. I., and Tikhonov, A. N. (2014). Modeling of the photosynthetic electron transport regulation in cyanobacteria. Biochem. Moscow Suppl. Ser. A 8, 262. doi:10.1134/S199074781402007X
Vijayan, V., Zuzow, R., and O’Shea, E. K. (2009). Oscillations in supercoiling drive circadian gene expression in cyanobacteria. Proc. Natl. Acad. Sci. U.S.A. 106, 22564–22568. doi:10.1073/pnas.0912673106
Vu, T. T., Stolyar, S. M., Pinchuk, G. E., Hill, E. A., Kucek, L. A., Brown, R. N., et al. (2012). Genome-scale modeling of light-driven reductant partitioning and carbon fluxes in diazotrophic unicellular cyanobacterium Cyanothece sp. ATCC 51142. PLoS Comput. Biol. 8:e1002460. doi:10.1371/journal.pcbi.1002460
Waldbauer, J. R., Rodrigue, S., Coleman, M. L., and Chisholm, S. W. (2012). Transcriptome and proteome dynamics of a light-dark synchronized bacterial cell cycle. PLoS ONE 7:e43432. doi:10.1371/journal.pone.0043432
Wang, L., Birol, I., and Hatzimanikatis, V. (2004). Metabolic control analysis under uncertainty: framework development and case studies. Biophys. J. 87, 3750–3763. doi:10.1529/biophysj.104.048090
Wijker, J. E., Jensen, P. R., Snoep, J. L., Vaz Gomes, A., Guiral, M., Jongsma, A. P., et al. (1995). Energy, control and DNA structure in the living cell. Biophys. Chem. 55, 153–165. doi:10.1016/0301-4622(94)00148-D
Witzel, F., Götze, J., and Ebenhöh, O. (2010). Slow deactivation of ribulose 1,5-bisphosphate carboxylase/oxygenase elucidated by mathematical models. FEBS J. 277, 931–950. doi:10.1111/j.1742-4658.2009.07541.x
Woelfle, M. A., Ouyang, Y., Phanvijhitsiri, K., and Johnson, C. H. (2004). The adaptive value of circadian clocks: an experimental assessment in cyanobacteria. Curr. Biol. 14, 1481–1486. doi:10.1016/j.cub.2004.08.023
Woelfle, M. A., Xu, Y., Qin, X., and Johnson, C. H. (2007). Circadian rhythms of superhelical status of DNA in cyanobacteria. Proc. Natl. Acad. Sci. U.S.A. 104, 18819–18824. doi:10.1073/pnas.0706069104
Wood, T. L., Bridwell-Rabb, J., Kim, Y.-I., Gao, T., Chang, Y.-G., LiWang, A., et al. (2010). The KaiA protein of the cyanobacterial circadian oscillator is modulated by a redox-active cofactor. Proc. Natl. Acad. Sci. U.S.A. 107, 5804–5809. doi:10.1073/pnas.0910141107
Xu, M., Bernt, G., Singh, A., Mi, H., Rgner, M., Pakrasi, H. B., et al. (2008). Properties of mutants of Synechocystis sp. strain PCC 6803 lacking inorganic carbon sequestration systems. Plant Cell Physiol. 49, 1672–1677. doi:10.1093/pcp/pcn139
Xu, Y., Mori, T., and Johnson, C. H. (2003). Cyanobacterial circadian clockwork: roles of KaiA, KaiB and the kaiBC promoter in regulating KaiC. EMBO J. 22, 2117–2126. doi:10.1093/emboj/cdg168
Yang, Q., Pando, B. F., Dong, G., Golden, S. S., and van Oudenaarden, A. (2010). Circadian gating of the cell cycle revealed in single cyanobacterial cells. Science 327, 1522–1526. doi:10.1126/science.1181759
Yao, D. C. I., Brune, D. C., and Vermaas, W. F. J. (2012). Lifetimes of photosystem I and II proteins in the cyanobacterium Synechocystis sp. PCC 6803. FEBS Lett. 586, 169–173. doi:10.1016/j.febslet.2011.12.010
Yoda, M., Eguchi, K., Terada, T. P., and Sasai, M. (2007). Monomer-shuffling and allosteric transition in KaiC circadian oscillation. PLoS ONE 2:e408. doi:10.1371/journal.pone.0000408
Yoshikawa, K., Aikawa, S., Kojima, Y., Toya, Y., Furusawa, C., Kondo, A., et al. (2015). Construction of a genome-scale metabolic model of Arthrospira platensis NIES-39 and metabolic design for cyanobacterial bioproduction. PLoS ONE 10:e0144430. doi:10.1371/journal.pone.0144430
Zavřel, T., Červený, J., Knoop, H., and Steuer, R. (2016). Optimizing cyanobacterial product synthesis: meeting the challenges. Bioengineered 7, 490–496. doi:10.1080/21655979.2016.1207017
Zhang, S., and Bryant, D. A. (2011). The tricarboxylic acid cycle in cyanobacteria. Science 334, 1551–1553. doi:10.1126/science.1210858
Zhu, X.-G., de Sturler, E., and Long, S. P. (2007). Optimizing the distribution of resources between enzymes of carbon metabolism can dramatically increase photosynthetic rate: a numerical simulation using an evolutionary algorithm. Plant Physiol. 145, 513–526. doi:10.1104/pp.107.103713
Zhu, X.-G., Govindjee, Baker, N. R., deSturler, E., Ort, D. O., and Long, S. P. (2005). Chlorophyll a fluorescence induction kinetics in leaves predicted from a model describing each discrete step of excitation energy and electron transfer associated with photosystem II. Planta 223, 114–133. doi:10.1007/s00425-005-0064-4
Zhu, X.-G., Wang, Y., Ort, D. R., and Long, S. P. (2013). e-Photosynthesis: a comprehensive dynamic mechanistic model of C3 photosynthesis: from light capture to sucrose synthesis. Plant Cell Environ. 36, 1711–1727. doi:10.1111/pce.12025
Zonneveld, C. (1998). Photoinhibition as affected by photoacclimation in phytoplakton: a model approach. J. Theor. Biol. 193, 115–123. doi:10.1006/jtbi.1998.0688
Zwicker, D., Lubensky, D. K., and ten Wolde, P. R. (2010). Robust circadian clocks from coupled protein-modification and transcription–translation cycles. Proc. Natl. Acad. Sci. U.S.A. 107, 22540–22545. doi:10.1073/pnas.1007613107
Appendix
The differential equations that define the model shown in Figure 4 are d[PSU*]/dt = v1 − v2 − vd and d[PSUd]/dt = vd − vr, together with the conservation relationship [PSU] + [PSU*] + [PSUd] = [PSUtotal]. The reactions rates describe the activation of the photosynthetic unit (PSU), v1 = k1⋅I⋅[PSU], the return to the open state, v2 = k2⋅[PSU*], the transition to a photodamaged state, vd = kd⋅I⋅[PSU*], and the recovery, vr = kr⋅[PSUd]. The rate of activation, v1, and photodamage, vd, both depend on the light intensity, I (with kd ≪ k1). Parameters used are k1 = 10.0, k2 = 10.0, kr = 1.0, [PSUtotal] = 1.0, and kd as indicated in Figure 4. The rate of oxygen evolution (v2) obtained from an (analytical) steady-state solution of the ODEs is shown. Parameters are arbitrary and do not reflect actual values found in cyanobacteria.
Keywords: photosynthesis, cyanobacteria, whole-cell models, flux balance analysis (FBA), circadian clock, CO2-concentrating mechanisms (CCMs), network reconstruction, metabolism
Citation: Westermark S and Steuer R (2016) Toward Multiscale Models of Cyanobacterial Growth: A Modular Approach. Front. Bioeng. Biotechnol. 4:95. doi: 10.3389/fbioe.2016.00095
Received: 18 February 2016; Accepted: 09 December 2016;
Published: 26 December 2016
Edited by:
Alberto Marin-Sanguino, Technische Universität München, GermanyReviewed by:
Monika Heiner, Brandenburg University of Technology, GermanyGanesh Sriram, University of Maryland College Park, USA
Copyright: © 2016 Westermark and Steuer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ralf Steuer, cmFsZi5zdGV1ZXJAaHUtYmVybGluLmRl
 Stefanie Westermark
Stefanie Westermark Ralf Steuer
Ralf Steuer