Estimation of Trunk Muscle Forces Using a Bio-Inspired Control Strategy Implemented in a Neuro-Osteo-Ligamentous Finite Element Model of the Lumbar Spine

Introduction

Low back pain (LBP) as the leading cause for work loss and years lived with disability emerges also as the most common and costliest problem in occupational musculoskeletal disorders (Clark and Horton, 2018; Hartvigsen et al., 2018). In the United States alone, the annual cost of LBP was estimated at ∼$200 billion in 2006 (Katz, 2006). This asserts the important role of biomechanical investigations to mitigate and manage the associated risk of injury through quantitative assessment of the mechanical loads on the spine during various daily and occupational activities. In the absence of adequate non-invasive in vivo measurement techniques, a number of musculoskeletal spine models, with different degrees of complexities, have been developed to estimate the internal loads in the active-passive structures of the trunk (Dreischarf et al., 2016; Ghezelbash et al., 2020). Due to the large number of trunk muscles spanning the intervertebral joints, the available equations are insufficient to solve this mechanically indeterminate system toward a unique solution, i.e., joint kinetics redundancy. The kinematic redundancies in the multi-joint spinal column, while providing flexibility in performing a specific task, add further complexity to the motor control strategies (Parnianpour, 2013). They can be viewed as the abundance to manage the conflicting objectives due to alterations in the environmental conditions and/or changes in task demand priorities (Latash et al., 2010).

Two distinct approaches are generally used to resolve the redundancies in such musculoskeletal models: inverse (e.g., equilibrium- and equilibrium-stability-based) and forward (e.g., control-based) dynamic. Equilibrium-based models leverage the available kinematics and governing equilibrium equations at various levels/joints/directions, and employ an optimization algorithm [often combined with limited recording of surface muscle electromyography (EMG)], to compute muscle forces and internal loads (Cholewicki and McGill, 1996; Parnianpour et al., 1997; Sparto and Parnianpour, 1998; Gagnon et al., 2011; Mohammadi et al., 2015; Dreischarf et al., 2016). In these models, the system, maintains equilibrium (static and/or dynamic) with no attention to crucial stability requirements. Imposing stability, in addition to the equilibrium, has led to the development of multi-criteria equilibrium-stability-based models, in which the kinetics redundancy can once again be resolved either by using an optimization/control theory-based algorithm (Hemami and Katbab, 1982; Granata and Orishimo, 2001; Zeinali-Davarani et al., 2008; Vakilzadeh et al., 2011; Hajihosseinali et al., 2014), or an EMG-driven algorithm (Samadi and Arjmand, 2018). The stability criterion in these models is typically investigated through the positive definiteness of the Hessian matrix of the system’s potential energy (Crisco and Panjabi, 1991; Cholewicki and McGill, 1996; Shirazi-Adl et al., 2005), or equivalently by the eigenvalues of the dynamic system (Hemami and Katbab, 1982; Bazrgari et al., 2008, 2009; Zeinali-Davarani et al., 2008; Shahvarpour et al., 2015). In general, considering stability requirements when calculating trunk muscle forces yields stronger correlation between predicted muscle activation and experimentally measured EMG data (Granata and Orishimo, 2001; Hajihosseinali et al., 2014; Samadi and Arjmand, 2018).

Unlike the inverse dynamics approaches, forward control-based dynamic models assign forces to muscles, either individually or synergistically grouped, in alignment with the central nervous system’s (CNS) neural control strategies applied in trunk movements. The controller used in these models commonly adjusts muscle forces in search of target postural trajectories, while maintaining dynamic equilibrium and stability requirements (Dariush et al., 1998). Predictions of control-based models have been successfully validated against EMG data (Sedighi et al., 2011; Nasseroleslami et al., 2014). Due to the challenging geometrical complexity and intricate multi-joint structures in the human trunk, previous control-based models have mainly simplified the upper trunk as an inverted pendulum with a single ball-and-socket (spherical) joint fixed at its base [i.e., the lumbosacral (L5/S1) junction]. This approach neglects relative deformations at the upper levels, translational degrees of freedom (DoFs), and changes in the centers of rotation (CoRs) under varying motions/loading conditions (Nasseroleslami et al., 2014). Recent investigations have demonstrated the variable effects of both the joint positioning (Ghezelbash et al., 2018) and joint translational DoFs (Cashaback et al., 2013; Ghezelbash et al., 2015) on the kinematics, as well as, muscle forces and spinal loads. While a control-based model of the whole body is used to provide more geometrical details, it is based on multi-body simulations of the spine thus neglecting the intervertebral joint complexities (Rupp et al., 2015). Up to date, however, only one control-based FE model of the entire body included translational DoFs (with movement restricted to the sagittal plane), while using a simplistic proportional-integral-derivative (PID) controller, to determine muscle activations (Östh, 2010; Andersson, 2013). To provide more geometrical details, deformable elements, based on fitting a curve on the forces and moments previously obtained by a finite element model of the intervertebral disc, were added to the multi-body model of the lumbar spine; again neglecting the intervertebral joint complexities (Karajan et al., 2013, 2014; Rupp et al., 2015). Moreover, a previous study included active muscle models in a reduced musculoskeletal finite element model of the lumbar spine to explore possible functional relationships between muscle function and intervertebral disc condition (Toumanidou and Noailly, 2015).

The objectives of the present study are as follows:

(1) To develop a novel 2D beam-column control-based model of the lumbar spine and compare its muscle force predictions with an existing geometrically matched equilibrium-based model (Patwardhan et al., 2001). The model incorporate (1) the DoFs at all levels of the spine [via implementing the controller in a finite element model of plant (passive spine)] thus also approximating changes in the joint CoRs, (2) force-length and force-velocity relationships in muscles using a Hill-based muscle model (Zajac, 1989), and (3) a bio-inspired control strategy to estimate muscle forces using fuzzy neuro-controllers with an emotional learning algorithm that adequately mimics the adaptive mechanism of the CNS. The controller minimizes kinematic deviations between actual and target postures, while calculating muscle activations by penalizing the controller unit for muscle activation level (Nasseroleslami et al., 2014).

(2) To investigate, using the foregoing control-based finite element model, the follower load (FL) concept as suggested in the geometrically matched equilibrium-based model (Patwardhan et al., 2001). In that model, the muscle forces were estimated based on the premise that the resultant compressive load on the spine behaves as a follower load (FL) (i.e., a load that follows the curvature of the lumbar spine, at all lumbar levels and postures), thus providing inherent spinal stability, as observed in in vitro studies. This strategy implicitly leverages the stability requirement by minimizing horizontal translations/rotations along the spine. We hypothesize that our control strategy (selected to mimic the role of the CNS in resolving the kinetic redundancy) automatically leads to trunk muscle forces consistent with a FL on the spine, thereby maximizing the mechanical stability of the spine. This suggests that the controller used in our model would learn to activate muscles in a manner that not only minimizes the kinematic deviations, but also the destabilizing shear forces and moments.

(3) To investigate the effect of external load magnitude on the trunk muscle activation patterns. It is hypothesized that the predicted pattern of muscle activation is scaled with the external load magnitude, thus providing evidence for a synergistic activation.

Materials and Methods

Geometry and Musculature of the Lumbar Spine Model

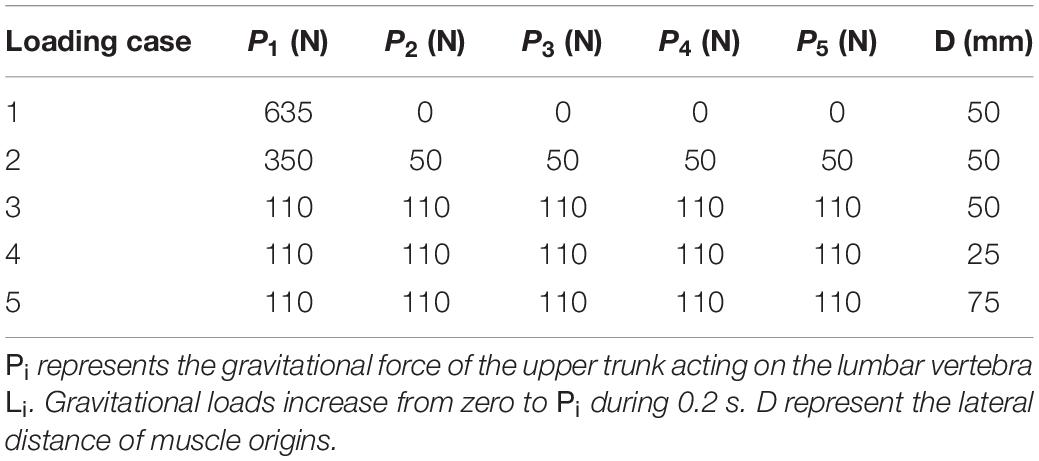
For the sake of comparison and hypothesis testing, the geometry of our deformable beam-column model of the lumbar spine and musculature were selected to be identical to those introduced in a previous work (Patwardhan et al., 2001). A simple 2D model of the lumbar spine, as a continuous elastic beam-column in the frontal plane, was constructed in LS-DYNA^® (Livermore Software Technology Corporation, Livermore, CA, United States) (Figure 1). Five distinct pairs of muscles were attached to a fixed base (representing the pelvis/sacrum) of the deformable beam at various L1–L5 lumbar levels. The simulation at the steady-state condition was quasi-static; upper body masses and inertias were hence neglected. The gravitational effect of masses was, however, accounted for by either a concentrated force at the L1 or distributed forces at various nodes (Table 1). The exact beam geometry, flexural rigidity (EI = 1.9 Nm²), and coordinates of upper/lower muscle insertions were all adopted from earlier work (Table 2; Patwardhan et al., 2001). The cross sectional area of the column was assumed constant at 1225 mm². The model was fixed at the sacrum (lower node) and restricted elsewhere to solely move in the frontal plane. The lumbar spine model consisted of five Hughes-Liu beam elements. The Hughes-Liu beam is a degenerated 8-node solid element (linear displacement and rotation field) with high computational efficiency and robustness (Hallquist, 2006). Sensitivity of the model predictions to the number of beam elements in the model (i.e., mesh refinement) was verified.

FIGURE 1

Figure 1. Geometry and musculature of the lumbar spine model in a laterally flexed posture in the frontal plane (Patwardhan et al., 2001).

TABLE 1

Table 1. Simulation cases.

TABLE 2

Table 2. Nodal coordinates of the deformed lumbar spine model (see Figure 1).

Hill’s Muscle Model

A Hill muscle model (Zajac, 1989) is used as follows:

$$F=f_{\mathit{max}}(\mathrm{\alpha }.f_l\left(l\right).f_v\left(\stackrel{.}{l}\right)+f_p\left(l\right))(1)$$

$$f_l\left(l\right)=5.1-29\left(\frac{l}{l_0}\right)+56{\left(\frac{l}{l_0}\right)}^2-41{\left(\frac{l}{l_0}\right)}^3+10{\left(\frac{l}{l_0}\right)}^4(2)$$

$$f_v(\stackrel{.}{l})=\frac{0.1433}{0.1074+\exp \left(-1.409\sinh \left(3.2\frac{\stackrel{\_}{l}}{{\stackrel{\_}{l}}_{\mathit{max}}}+1.6\right)\right)}(3)$$

$$f_p\left(l\right)=\exp \left(-10.671+7.675\frac{l}{l_0}\right)(4)$$

In the above equations, F, f _l (l) (Nussbaum and Chaffin, 1998), f_v⁢(l) (Hatze, 1977), and f_p(l) (McGill and Norman, 1986) are muscle force, as well as force-length, force-velocity and passive force-length relationships, respectively. Moreover, f_max, α, l, $\stackrel{.}{l}$, l₀, ${\stackrel{.}{l}}_{\mathit{max}}$ represent muscle maximum force, muscle activation level, muscle length, muscle velocity, muscle resting length and maximum muscle velocity, respectively. The value of ${\stackrel{.}{l}}_{\mathit{max}}=\frac{l_0}{0.1s}$ is assumed in this study (Zajac, 1989). f_max is assumed to be 800 N in all muscles. In muscles, the damping is represented intrinsically by the force-velocity relationship (Eq. 3), while the stiffness alters with the current length according to the force-length relationships (Eqs. 2 and 4). Inspection of the Hill type muscle response used (Eq. 1) reveals that the muscle activation affects the system response by modulating the muscle force and stiffness (Hogan, 1990). The spine structural stiffness matrix consists of contributions from both active and passive systems.

Controller

One single-input and single-output (SISO) controller for each muscle was used to control the continuous beam model. The main idea behind the control structure assumes that each pair of bilateral muscles attached to a particular point increases the active stiffness at that point. The SISO controller used in this study is a fuzzy neuro-controller whose weights are tuned according to two critic signals (Figure 2; Lucas et al., 2004). The purpose of the controller is to minimize the general error function displayed below (Eq. 5) with the steepest descent algorithm:

FIGURE 2

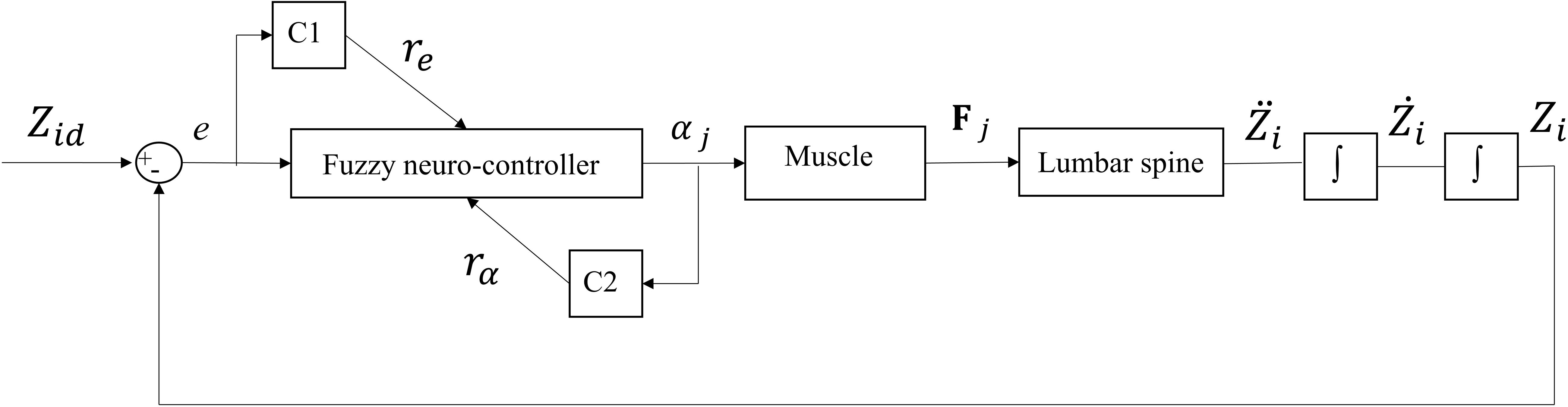
Figure 2. Feedback control loop with SISO fuzzy neuro-controller unit. C1 and C2 are the critics of the system that generate $r_e=h_{1}e+h_2\stackrel{.}{e}+h_3\int e$ and r_α = abs(α), respectively. α_j is the level of activation of muscle (j) attached to L_i and e is the difference between desired (Z_id) and actual (Z_i) Z-coordinate of the node L_i (Figure 1).

$$E=E_e+E_{\mathrm{\alpha }}=\frac{1}{2}{k}_e{\left(h_{1}e+h_2\stackrel{.}{e}+h_3\int e\right)}^2+\frac{1}{2}{k}_{\mathrm{\alpha }}{\left(\mathit{abs}\left(\mathrm{\alpha }\right)\right)}^2(5)$$

In the above equation, e, $\stackrel{.}{e}$, and ∫erepresent the error (difference between the actual and target kinematics), error rate, and the integral of error, where h₁, h₂, and h₃ represent error, error rate and error integral coefficients. Moreover, k_e and k_α represent the weighting functions for the priority of the error signal components. α is the level of muscle activation (between 0 and 1). As can be seen in Eq. 5, the error function consists of two parts E_eand E_α,whereE_erepresents the kinematics error, while E_αpenalizes the controller for the control activation signal and plays an essential role in resolving the system redundancy in terms of muscle forces (Nasseroleslami et al., 2014). The above cost function is defined for each muscle, where the error terms are based on the Z-coordinates of the nodes to which muscles are attached. Eq. (6), formulated below, is defined as the Jacobian of the SISO controller. In MIMO applications, it is necessary to calculate the exact value of the Jacobian. However, in SISO systems, only the sign of the Jacobian is sufficient for control (Nasseroleslami et al., 2014). The overall weight tuning rule can be calculated from Eq. 7.

$$j=\frac{\partial Z}{\partial \mathrm{\alpha }}(6)$$

$$\mathrm{\Delta }{w}_i=-\eta .\frac{\partial E}{\partial w_i}(7)$$

Where w_i is the ith neuron weight of the neural controller and η (learning rate) represents the rate of change in weights. Finally, by using the chain derivative rule and combining the relevant equations, Eq. (7) is rewritten as Eq. (10):

$$\frac{\partial E_e}{\partial w_i}=\frac{\partial E_e}{\partial r_e}.\frac{\partial r_e}{\partial Z}.\frac{\partial Z}{\partial \mathrm{\alpha }}.\frac{\partial \mathrm{\alpha }}{\partial w_i}=-k_e.h_1.r_e.j.\frac{\partial \mathrm{\alpha }}{\partial w_i}(8)$$

$$\frac{\partial E_{\mathrm{\alpha }}}{\partial w_i}=\frac{\partial E_{\mathrm{\alpha }}}{\partial r_{\mathrm{\alpha }}}.\frac{\partial r_{\mathrm{\alpha }}}{\partial \mathrm{\alpha }}.\frac{\partial \mathrm{\alpha }}{\partial w_i}=k_{\mathrm{\alpha }}.\mathit{sgn}(\mathrm{\alpha }).r_{\mathrm{\alpha }}.\frac{\partial \mathrm{\alpha }}{\partial w_i}(9)$$

$$\mathrm{\Delta }{w}_i=\eta (k_e.h_1.r_e.j-k_{\mathrm{\alpha }}.r_{\mathrm{\alpha }}).\frac{\partial \mathrm{\alpha }}{\partial w_i}(10)$$

In these equations, $r_e=h_{1}e+h_2\stackrel{.}{e}+h_3\int e$and r_α = abs(α). h₁, h₂, h₃, k_α, are assumed as 2, 2, 2, and 0.2, respectively.k_e = 15, 7, 2.5, 1, and 0.1 for levels L1 through L5, respectively. Each muscle is considered as a SISO controller, thus the Jacobian sign would be adequate for control. Each controller-muscle unit minimizes the kinematic error of the node to which it is attached while minimizing its muscle activation. Initial muscle activations were neglected as the muscle forces were adjusted through a feedback strategy.

Simulations

A total of five simulations (loading cases 1–5), based on the external load distributions and lateral distances of the muscle origins, were considered in this study (Patwardhan et al., 2001; Table 1). Gravitational loads attained their values in 0.2 s. All simulation cases were modeled with and without the muscle/controller. Identical boundary conditions were considered for all simulated cases. The purpose of the controller in this study (i.e., target posture), was to maintain the primary Z-coordinates (minimize lateral deviations between the target and actual positions to remain bounded within 2 mm during the learning process) of the beam, as specified in Table 2. It is noteworthy that the foregoing restrictions on the lateral translations automatically limit any changes in the nodal lateral rotations. The vertical (X direction) displacement of the beam as well as the orientation of the vertebrae were left free to change under the external loads and muscle forces. In addition, in order to investigate the effect of the external load magnitude on the pattern of trunk muscle activations in loading case 2 (Table 1), the muscle forces were recalculated for different external vertical loads (150-750 N) applied at the L1 level.

Results

Comparison With the Matched Equilibrium-Based Model

In the absence of any controller (i.e., without any muscle activation), the simulated system, expectedly, exhibited large deformations and became unstable. In all five loading cases (Table 1), the controllers in the model successfully learned, over time, to maintain the model close to the target kinematics at equilibrium under the estimated muscle exertions and applied external loads (Figure 3). The actual and target nodal Z-coordinates were different by <0.2 mm during the steady-state condition after 20 s. Initially in the transient period, when the controller was not fully trained, the model deviated slightly (Figure 3) from its target kinematics, and the muscle forces substantially increased. By training the controller, the muscle forces subsequently considerably decreased, and the model reached its steady state. In all five loading conditions, the controllers unilaterally activated only one muscle at each level (i.e., no coactivation). As compared to the matched equilibrium-based model mentioned earlier (Patwardhan et al., 2001), our model predicted similar patterns for muscle forces (i.e., the muscles were activated unilaterally, and their forces decreased going downwards from the upper levels, although generally at lower values (RMSE = ∼41, 16, 12, 44, and 9 N for loading cases 1 through 5, with an overall normalized (to mean) RMSE of 121% for all loading cases) (Figure 4). Consequently, our control-based model predicted smaller compressive loads as compared to its matched equilibrium-based model (Patwardhan et al., 2001; Table 3). However, the equilibrium-based model predicted near zero shear loads in keeping with its own strategy to use the joint reaction forces as an FL (Table 3).

FIGURE 3

Figure 3. Error, error rate, and muscle forces at different lumbar levels vs. time (up to 0.5 s) for the loading case 1 (with controllers and muscles). Gravitational loads increase from zero to P_i (see Table 1) during 0.2 s. The controller tries to maintain the primary Z-coordinates of beam (Table 2) with a penalty on muscle activation level. For the sake of a clarified visualization, the horizontal axis is cut at 0.5 s while the convergence occurs at ∼20 s.

FIGURE 4

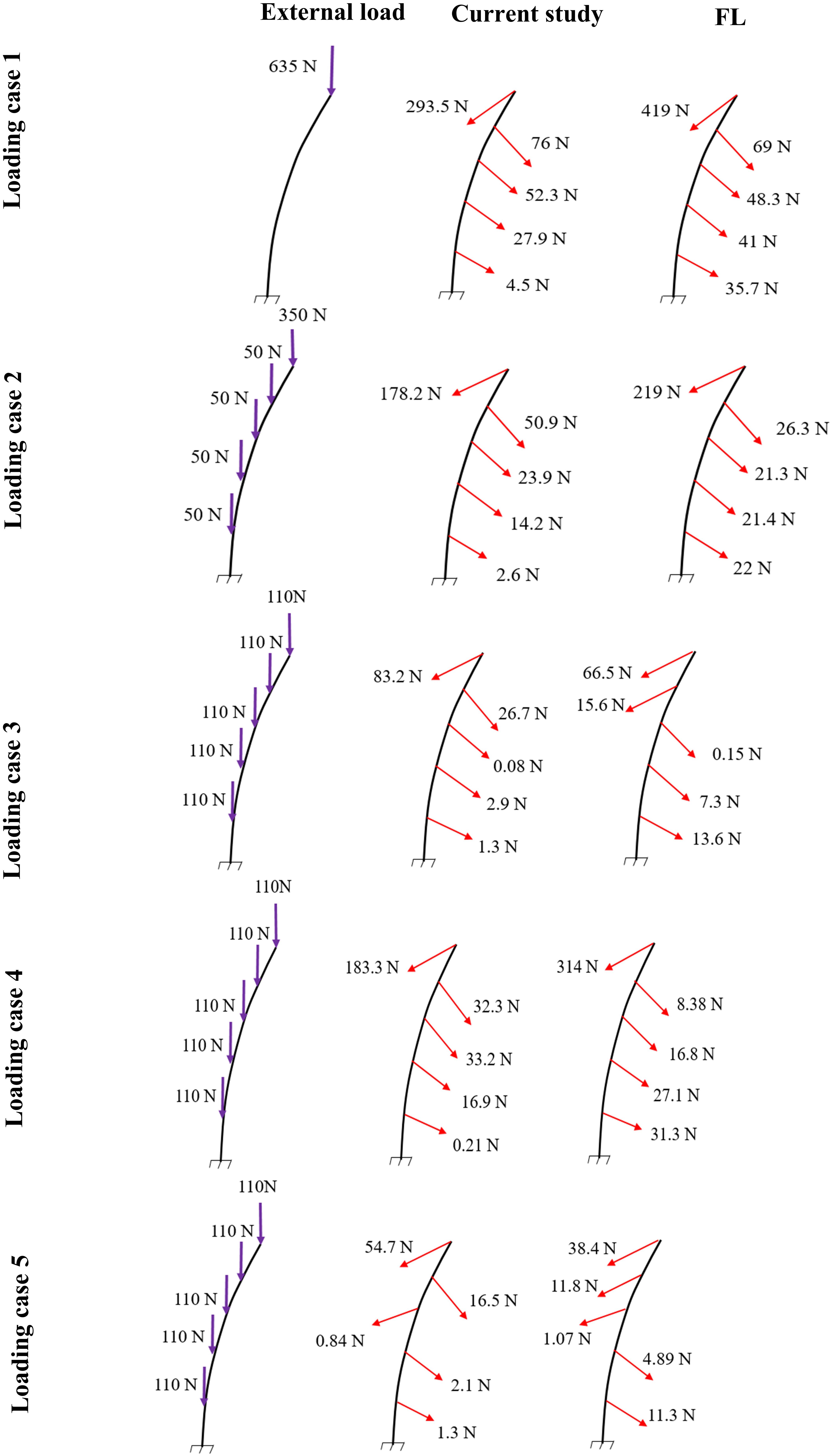
Figure 4. Predicted muscle forces in the current study (middle) as compared to those predicted by a matched equilibrium-based model (Patwardhan et al., 2001) (right) for different loading cases (left) (Table 1).

TABLE 3

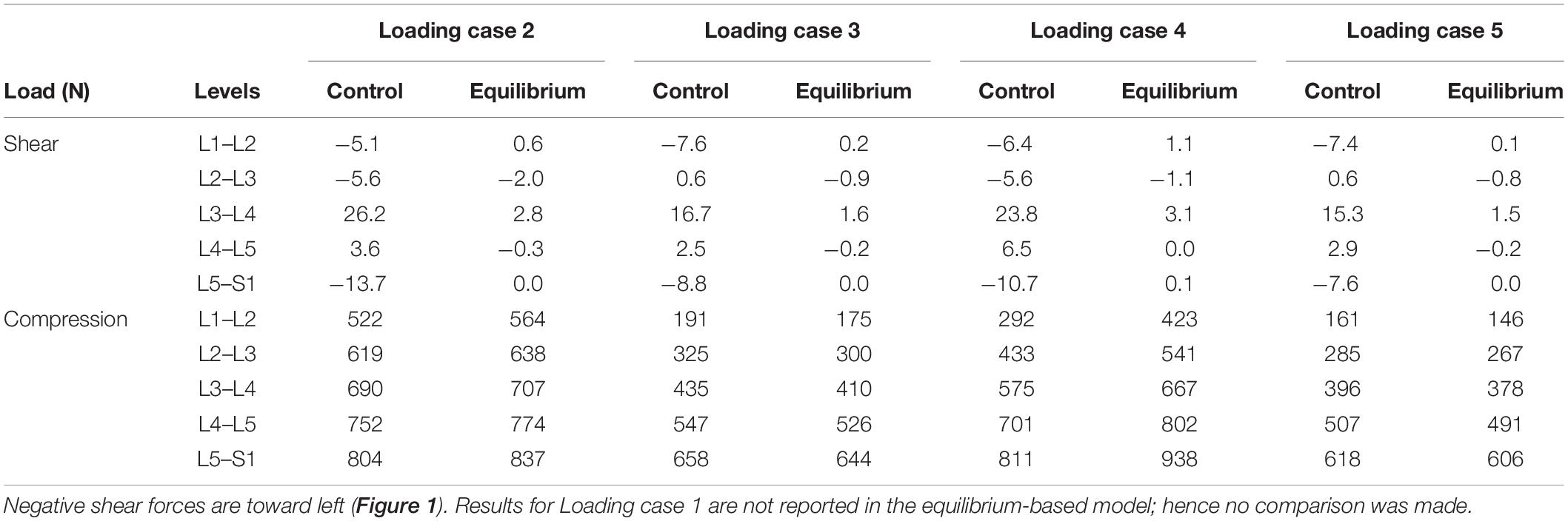
Table 3. Predicted spinal loads (compression and shear) in the current control-based model as compared to those predicted by a matched equilibrium-based model (Patwardhan et al., 2001) for different loading cases (Table 1).

Follower Load (FL) Hypothesis

By minimizing the errors between the actual and target nodal Z-coordinates, the control-based model, predicted muscle forces that also generated a near FL on the spine (Figure 5). Regardless of the loading case, the angle between the resultant force on the lumbar spine in our model and an optimal hypothetical FL remained <3°.

FIGURE 5

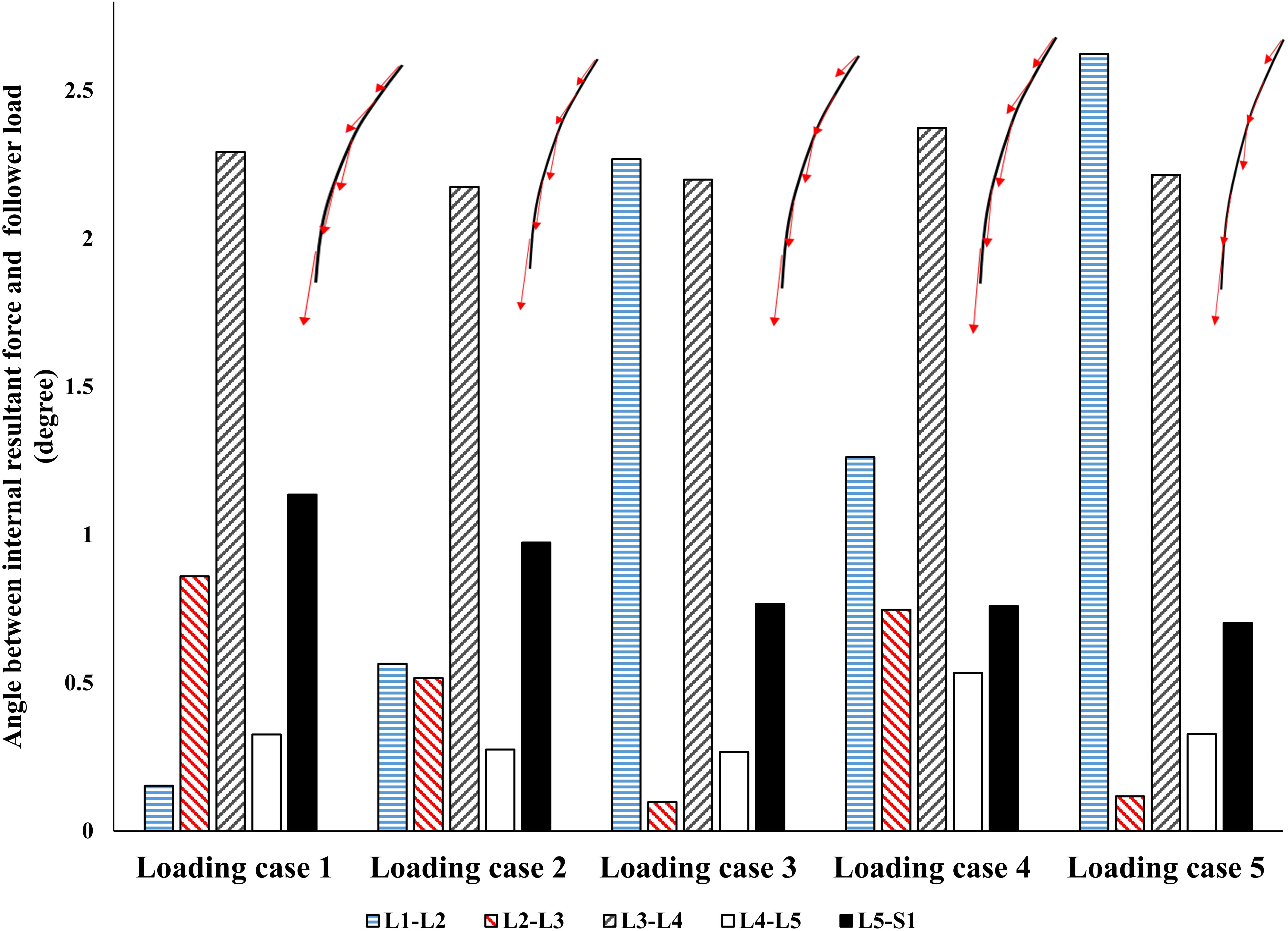
Figure 5. The absolute value of angle between the resultant force on the spine and a hypothetical follower load (FL).

Effect of External Load on Muscle Activations

The controllers activated the trunk muscles unilaterally (no bilateral co-activation) regardless of the magnitude of the external loads (Figure 6). Both models produced similar, although not identical activation patterns in the five loading cases. Variation of the muscle forces with the magnitude of external loading within the range simulated at the L1 was found linear.

FIGURE 6

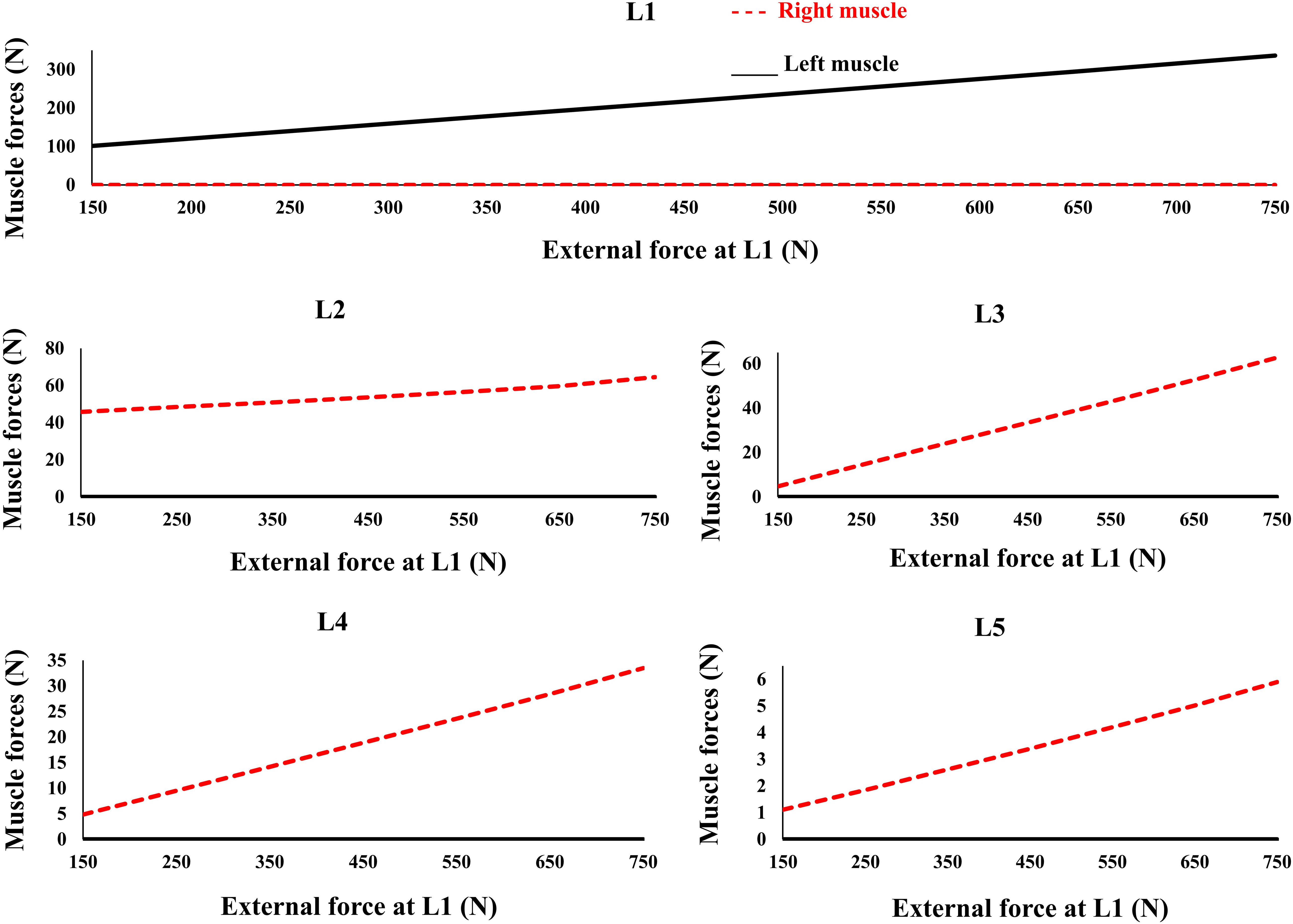
Figure 6. Predicted muscle forces for different external compressive loads acting on the L1 and the distributed loads of 50 N at the L2 to L5 similar to loading Case 2 (Table 1). External force increases from zero to its final value in 0.2 s.

Discussion

This study developed a novel geometrically simple control-based model of the lumbar spine and compared its predictions for a slightly bent posture in the frontal plane with those of a geometrically matched equilibrium-based model (Patwardhan et al., 2001). Moreover, the FL concept suggested as an input constraint in the matched equilibrium-based model, as well as, the effect of changes in the externally applied loads on muscle forces, were investigated. The present learning algorithm is classified as a reinforcement-based one, where the controller tends to decrease the defined cost function based on the critic’s signals (Figure 2). The findings indicated that, similar to the equilibrium-based model, the fuzzy neuro-controllers balanced the spine at a given deformed posture using a unilateral muscle force pattern, albeit with generally smaller muscle forces (the sums of muscle forces in our model were smaller by ∼ 159, 40, −11, 132, and −8 N for loading cases 1 through 5, and hence, the L5-S1 compression forces were smaller by ∼ 145, 33, −14, 127, and −12 N for loading cases 1 through 5, respectively). This unilateral muscle activation pattern did not change with the variation of the magnitude of external loads (i.e., the spine was balanced by the controllers without bilateral coactivations). Moreover, for the loading conditions at a slightly laterally bent posture (i.e., quiet standing posture) considered in this study, and consistent with the objective function, the controllers activated the muscles such that the net load on the lumbar spine approached an ideal FL condition. In the future, our control-based approach will be applied to our 3D musculoskeletal model of the spine (Arjmand and Shirazi-Adl, 2006) while simulating various physiological tasks. This model incorporates a realistic geometry of the spine, including ∼80 thoracolumbar muscles, and 6 degrees-of-freedom intervertebral joint with non-linear passive properties. The controllers will aim to determine optimal muscle forces accounting for all the degrees-of-freedom in all anatomical planes. In particular, it would also be interesting to simulate, amongst others, some passive-active injuries and pathological conditions (e.g., altered passive stiffness-muscle coordination/muscle areas).

Interpretations

Application of the external loads in 0.2 s resulted in an increase in the initial position and velocity beyond those in the target condition (Figure 3). In response, and to maintain equilibrium and stability, the controllers bilaterally and significantly activated the muscles at all levels. Following a transient period with large fluctuations, the controllers succeeded in reducing the errors, such that at the final steady state conditions, the velocity errors completely disappeared, while the position errors diminished to less than 1 mm (Figure 3). At this final static configuration, and in agreement with the matched equilibrium-based model, the controllers activated the muscles unilaterally with no coactivation to balance the spine (Figure 4). The only difference between the two models was observed in loading cases 3 and 5, during which the unilaterally opposite muscles were activated at the L2 level (Figure 4). The control-based model generally balanced the external loads at smaller muscle forces (differences reached ∼159, 40, −11, 132, and −8 N for loading cases 1 through 5). This in in alignment with objective functions minimizing the sum of linear, squared, or cubed muscle forces/stresses, commonly considered in optimization-driven models. While at some levels in the loading cases 3 and 5, our model predicted larger muscular forces, as compared to its matched equilibrium-based model, the sums of muscle forces in these loading conditions, were only moderately larger (11 and 12% increase for loading case 3 and 5, respectively) (Table 3 and Figure 4). This suggests that the cost function used by the CNS to assign forces to muscles may additionally depend on loading conditions and posture. It is to be noted that even smaller total (resultant) spinal loads were estimated in our model when compared to the equilibrium-based model. This highlights the crucial role of our controller (Eq. 5).

Interestingly, without imposing any constraints on the magnitude or direction of muscle or reaction forces in the lumbar spine, a near FL condition was found in various cases (Figure 5). This was in agreement with the matched equilibrium-based model, which constrained activation in muscles to generate an FL on the spine at all levels. It appears, therefore, that the controllers (i.e., the CNS) learned to balance and stabilize the spine by generating conditions approaching that under an FL. This is also in agreement with findings from another detailed musculoskeletal equilibrium-based model of the spine, in which the muscle forces were predicted to create compressive FLs on the spine during a quiet standing posture (Han et al., 2011). The outcome in internal loading is also consistent with the minimization of changes in horizontal translations. Moreover, unlike the equilibrium-based model which predicted no shear loads on the spine, small spinal shear loads were predicted in our model (Table 3). The structure and nature of the constitutive components of the objective function in our model (Eq. 5) allow for diverse simulation possibilities to explore the competing goals of the system toward emulating the sophisticated physiological system and its intricate strategies. The addition of more state variables can be another intriguing motivation for future investigation.

The recruitment of trunk muscles has been shown to be strongly direction dependent (Nussbaum et al., 1995; Hadizadeh et al., 2014; Sedaghat-Nejad et al., 2015; Eskandari et al., 2016). In quasi-static conditions the emergent synergies responsible for a direction of external load will be linearly scaled. The invariance in set of activated muscles under varying magnitude of external load (Figure 6) is in line with the theories of using muscle synergy in multiple muscle systems across the cost functions (Moghadam et al., 2013; Eskandari et al., 2016). Future studies must test this in more physiological models with realistic posture/loading and non-linear properties. Future studies can also benefit by incorporating more physiologically based detailed architectural/geometrical muscle models and structure/function data obtained from neuroimaging studies.

Limitations

This model was idealized in terms of the geometry of the active-passive tissues, material properties, and loading conditions in the frontal plane, as we primarily aimed to (1) implement a novel bio-inspired control strategy that mimics the adaptive mechanism of the CNS and (2) compare its predictions with an existing matched equilibrium-based model. As the current model was idealized based on simplifying assumptions in terms of the geometry of the spine, loading, boundary conditions, and musculature, caution should be exercised when extrapolating results to clinical applications. The maximal force in all muscles was considered to be 800 N, in order to accommodate large fluctuations in muscle forces during the transient period (Figure 3). In the final steady-state, however, much smaller muscular forces were estimated (Figure 4). Non-zero muscle pre-activation values (initial values) could subdue the fluctuations observed in the transient state. While the stability was not formally examined in our model, different perturbations (e.g., the addition of a moment at the L1 and the reduction of Young’s modulus of the beams; Nasseroleslami et al., 2014) did not cause instability, as the controllers prevented large deformations and maintained the final steady-state position. For example, Figure 7 depicts the model response under a perturbation, where the addition and removal of a 100 N load to impose external compression of 635 N at L1 for a duration of 0.5 s, caused the muscle force to appropriately rise and fall, respectively, to maintain the required objective posture (Z coordinates). The error terms, which approached nil at the end of the 20 s simulation, are not shown in Figure 7 for clarity. The closed loop response could include multiple loops with varying gains and time delays (Zeinali-Davarani et al., 2008). We have neither considered the spindle nor the reflexive responses in the feedback loop, and we have not used an internal model to assist with the initial exploration of activation selection (Dariush et al., 1998; Shadmehr and Mussa-Ivaldi, 2012), all warranting future investigation. The objective function should be designed considering stability in the Lyapunov sense, while setting the performance criterion to maintain the system within the safe normal physiological limits of the passive and active spinal structures. This provides an envelope with margins of safety to avoid pain, discomfort, muscle fatigue, instability and ultimately failure/injury.

FIGURE 7

Figure 7. External compressive force, error, error rate and muscle forces at L1 vs. time (up to 2.2 s) for the loading case 1 under application of −100 N and 100 N vertical force at L1 during [0.5 s, 1 s] and [1.5 s, 2 s] time intervals, respectively, in order to model perturbations (with controllers and muscles). The controller tries to maintain the primary Z-coordinates of beam (Table 2) with a penalty on muscle activation level.

Conclusion

This work presents a new method to estimate muscle forces using a control-based FE model of the lumbar spine. The model incorporates a control strategy that mimics the adaptive mechanism of the CNS to adjust muscle forces. Steady state muscle forces have similar patterns to a geometrically matched equilibrium-based model and spine reaction forces resemble a FL on the spine. Additionally, controllers linearly scale muscle forces in a specific loading condition with varying magnitude of external load. The phenomenon of FL is the predicted behavior of this adaptive neuro-fuzzy control system and not the explicit objective of the mathematical theory or conjecture. That creates a fertile paradigm to consider clinical ideas (i.e., spinal injuries and/or fusion) to be investigated in future studies with a more detailed architecture for muscles under more general loading conditions during daily activities at work, leisure and sport.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed above have made substantial contributions to the conception and design of the study, analysis and interpretation of data, preparing the manuscript, and have read the final approval of the version to be submitted and listed on the title page have read the manuscript and also attest to the validity and legitimacy of the data and its interpretation, and agreed to its submission.

Funding

This work was supported by grants from the Sharif University of Technology (Tehran, Iran).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Assistance of Mr. Mohammad Shahiri in model simulation is greatly appreciated.

References

Andersson, S. (2013). Active Muscle Control in Human Body Model Simulations: Implementation of a Feedback Control Algorithm with Standard Keywords in LS-DYNA. M. Sc. Thesis, Chalmers University of Technology, Göteborg.

Google Scholar

Arjmand, N., and Shirazi-Adl, A. (2006). Model and in vivo studies on human trunk load partitioning and stability in isometric forward flexions. J. Biomech. 39, 510–521. doi: 10.1016/j.jbiomech.2004.11.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazrgari, B., Shirazi-Adl, A., and Parnianpour, M. (2009). Transient analysis of trunk response in sudden release loading using kinematics-driven finite element model. Clin. Biomech. 24, 341–347. doi: 10.1016/j.clinbiomech.2009.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazrgari, B., Shirazi-Adl, A., Trottier, M., and Mathieu, P. (2008). Computation of trunk equilibrium and stability in free flexion–extension movements at different velocities. J. Biomech. 41, 412–421. doi: 10.1016/j.jbiomech.2007.08.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Cashaback, J. G., Potvin, J. R., and Pierrynowski, M. R. (2013). On the derivation of a tensor to calculate six degree-of-freedom, musculotendon joint stiffness: implications for stability and impedance analyses. J. Biomech. 46, 2741–2744. doi: 10.1016/j.jbiomech.2013.07.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Cholewicki, J., and McGill, S. M. (1996). Mechanical stability of the in vivo lumbar spine: implications for injury and chronic low back pain. Clin. Biomech. 11, 1–15. doi: 10.1016/0268-0033(95)00035-6

CrossRef Full Text | Google Scholar

Clark, S., and Horton, R. (2018). Low back pain: a major global challenge. The Lancet 391, 2295–2388. doi: 10.1016/S0140-6736(18)30725-6

CrossRef Full Text | Google Scholar

Crisco, J. J. III, and Panjabi, M. M. (1991). The intersegmental and multisegmental muscles of the lumbar spine: a biomechanical model comparing lateral stabilizing potential. Spine 16, 793–799. doi: 10.1097/00007632-199107000-00018

PubMed Abstract | CrossRef Full Text | Google Scholar

Dariush, B., Parnianpour, M., and Hemami, H. (1998). Stability and a control strategy of a multilink musculoskeletal model with applications in FES. IEEE Trans. Biomed. Eng. 45, 3–14. doi: 10.1109/10.650346

CrossRef Full Text | Google Scholar

Dreischarf, M., Shirazi-Adl, A., Arjmand, N., Rohlmann, A., and Schmidt, H. (2016). Estimation of loads on human lumbar spine: a review of in vivo and computational model studies. J. Biomech. 49, 833–845. doi: 10.1016/j.jbiomech.2015.12.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Eskandari, A. H., Sedaghat-Nejad, E., Rashedi, E., Sedighi, A., Arjmand, N., and Parnianpour, M. (2016). The effect of parameters of equilibrium-based 3-D biomechanical models on extracted muscle synergies during isometric lumbar exertion. J. Biomech. 49, 967–973. doi: 10.1016/j.jbiomech.2015.12.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Gagnon, D., Arjmand, N., Plamondon, A., Shirazi-Adl, A., and Larivière, C. (2011). An improved multi-joint EMG-assisted optimization approach to estimate joint and muscle forces in a musculoskeletal model of the lumbar spine. J. Biomech. 44, 1521–1529. doi: 10.1016/j.jbiomech.2011.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghezelbash, F., Arjmand, N., and Shirazi-Adl, A. (2015). Effect of intervertebral translational flexibilities on estimations of trunk muscle forces, kinematics, loads, and stability. Comput. Methods Biomech. Biomed. Engin. 18, 1760–1767. doi: 10.1080/10255842.2014.961440

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghezelbash, F., Eskandari, A. H., Shirazi-Adl, A., Arjmand, N., El-Ouaaid, Z., and Plamondon, A. (2018). Effects of motion segment simulation and joint positioning on spinal loads in trunk musculoskeletal models. J. Biomech. 70, 149–156. doi: 10.1016/j.jbiomech.2017.07.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghezelbash, F., Schmidt, H., Shirazi-Adl, A., and El-Rich, M. (2020). Internal load-sharing in the human passive lumbar spine: review of in vitro and finite element model studies. J. Biomech. 102:109441. doi: 10.1016/j.jbiomech.2019.109441

PubMed Abstract | CrossRef Full Text | Google Scholar

Granata, K. P., and Orishimo, K. F. (2001). Response of trunk muscle coactivation to changes in spinal stability. J. Biomech. 34, 1117–1123. doi: 10.1016/S0021-9290(01)00081-1

CrossRef Full Text | Google Scholar

Hadizadeh, M., Mousavi, S. J., Sedaghatnejad, E., Talebian, S., and Parnianpour, M. (2014). The effect of chronic low back pain on trunk accuracy in a multidirectional isometric tracking task. Spine 39, E1608–E1615. doi: 10.1097/BRS.0000000000000628

PubMed Abstract | CrossRef Full Text | Google Scholar

Hajihosseinali, M., Arjmand, N., Shirazi-Adl, A., Farahmand, F., and Ghiasi, M. S. (2014). A novel stability and kinematics-driven trunk biomechanical model to estimate muscle and spinal forces. Med. Eng. Phys. 36, 1296–1304. doi: 10.1016/j.medengphy.2014.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Hallquist, J. O. (2006). LS-DYNA Theory Manual. Livermore Software Technology Corporation 3, 25–31.

Google Scholar

Han, K. S., Rohlmann, A., Yang, S. J., Kim, B. S., and Lim, T. H. (2011). Spinal muscles can create compressive follower loads in the lumbar spine in a neutral standing posture. Med. Eng. Phys. 33, 472–478. doi: 10.1016/j.medengphy.2010.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartvigsen, J., Hancock, M. J., Kongsted, A., Louw, Q., Ferreira, M. L., Genevay, S., et al. (2018). What low back pain is and why we need to pay attention. Lancet 391, 2356–2367. doi: 10.1016/S0140-6736(18)30480-X

CrossRef Full Text | Google Scholar

Hatze, H. (1977). A myocybernetic control model of skeletal muscle. Biol. Cybern. 25, 103–119. doi: 10.1007/BF00337268

PubMed Abstract | CrossRef Full Text | Google Scholar

Hemami, H., and Katbab, A. (1982). Constrained inverted pendulum model for evaluating upright postural stability. J. Dyn. Syst. Meas. Control 104, 343–349. doi: 10.1115/1.3139720

CrossRef Full Text | Google Scholar

Hogan, N. (1990). “Mechanical impedance of single-and multi-articular systems,” in Multiple Muscle Systems, eds J. M. WintersSavio and L.-Y. Woo (Berlin: Springer), 149–164. doi: 10.1007/978-1-4613-9030-5_9

CrossRef Full Text | Google Scholar

Karajan, N., Otto, D., Oladyshkin, S., and Ehlers, W. (2014). Application of the polynomial chaos expansion to approximate the homogenised response of the intervertebral disc. Biomech. Model. Mechanobiol. 13, 1065–1080. doi: 10.1007/s10237-014-0555-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Karajan, N., Röhrle, O., Ehlers, W., and Schmitt, S. (2013). Linking continuous and discrete intervertebral disc models through homogenisation. Biomech. Model. Mechanobiol. 12, 453–466. doi: 10.1007/s10237-012-0416-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz, J. N. (2006). Lumbar disc disorders and low-back pain: socioeconomic factors and consequences. JBJS 88, 21–24. doi: 10.2106/JBJS.E.01273

PubMed Abstract | CrossRef Full Text | Google Scholar

Latash, M. L., Levin, M. F., Scholz, J. P., and Schöner, G. (2010). Motor control theories and their applications. Medicina 46, 382–392. doi: 10.3390/medicina46060054

CrossRef Full Text | Google Scholar

Lucas, C., Fatourechi, M., Famil Khalili, G., Abdi, J., and Khaki-Sedigh, A. (2004). Control of multivariable systems based on emotional temporal difference learning controller. Int. J. Eng. 17, 363–376.

Google Scholar

McGill, S. M., and Norman, R. W. (1986). Partitioning of the L4-L5 dynamic moment into disc, ligamentous, and muscular components during lifting. Spine 11, 666–678. doi: 10.1097/00007632-198609000-00004

PubMed Abstract | CrossRef Full Text | Google Scholar

Moghadam, M. N., Aminian, K., Asghari, M., and Parnianpour, M. (2013). How well do the muscular synergies extracted via non-negative matrix factorisation explain the variation of torque at shoulder joint? Comput. Methods Biomech. Biomed. Engin 16, 291–301. doi: 10.1080/10255842.2011.617705

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, Y., Arjmand, N., and Shirazi-Adl, A. (2015). Comparison of trunk muscle forces, spinal loads and stability estimated by one stability-and three EMG-assisted optimization approaches. Med. Eng. Phys. 37, 792–800. doi: 10.1016/j.medengphy.2015.05.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Nasseroleslami, B., Vossoughi, G., Boroushaki, M., and Parnianpour, M. (2014). Simulation of movement in three-dimensional musculoskeletal human lumbar spine using directional encoding-based neurocontrollers. J. Biomech. Eng. 136:091010. doi: 10.1115/1.4027664

CrossRef Full Text | Google Scholar

Nussbaum, M. A., and Chaffin, D. B. (1998). Lumbar muscle force estimation using a subject-invariant 5-parameter EMG-based model. J. Biomech. 31, 667–672. doi: 10.1016/S0021-9290(98)00055-4

CrossRef Full Text | Google Scholar

Nussbaum, M. A., Chaffin, D. B., and Martin, B. J. (1995). A back-propagation neural network model of lumbar muscle recruitment during moderate static exertions. J. Biomech. 28, 1015–1024. doi: 10.1016/0021-9290(94)00171-Y

CrossRef Full Text | Google Scholar

Östh, J. (2010). Active Muscle Responses in a Finite Element Human Body Model. Lic. Eng Thesis, Chalmers University of Technology, Göteborg.

Google Scholar

Parnianpour, M., Wang, J. L., Shirazi-Adl, A., Sparto, P., and Wilke, H. J. (1997). The effect of variations in trunk models in predicting muscle strength and spinal loading. J. Musculoskelet. Res. 1, 55–69. doi: 10.1142/S0218957797000086

CrossRef Full Text | Google Scholar

Parnianpour, M. (2013). “Computational models for trunk trajectory planning and load distribution: a test-bed for studying various clinical adaptation and motor control strategies of low back pain patients,” in Spinal Control, eds Hodges, P. W., Cholewicki, J., and Van Dieën, J. H. (Amsterdam: Elsevier), 17–29. doi: 10.1016/b978-0-7020-4356-7.00003-3

CrossRef Full Text | Google Scholar

Patwardhan, A. G., Meade, K. P., and Lee, B. (2001). A frontal plane model of the lumbar spine subjected to a follower load: implications for the role of muscles. J. Biomech. Eng. 123, 212–217. doi: 10.1115/1.1372699

CrossRef Full Text | Google Scholar

Rupp, T. K., Ehlers, W., Karajan, N., Günther, M., and Schmitt, S. (2015). A forward dynamics simulation of human lumbar spine flexion predicting the load sharing of intervertebral discs, ligaments, and muscles. Biomech. Model. Mechanobiol. 14, 1081–1105. doi: 10.1007/s10237-015-0656-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Samadi, S., and Arjmand, N. (2018). A novel stability-based EMG-assisted optimization method for the spine. Med. Eng. Phys. 58, 13–22. doi: 10.1016/j.medengphy.2018.04.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Sedaghat-Nejad, E., Mousavi, S. J., Hadizadeh, M., Narimani, R., Khalaf, K., Campbell-Kyureghyan, N., et al. (2015). Is there a reliable and invariant set of muscle synergy during isometric biaxial trunk exertion in the sagittal and transverse planes by healthy subjects? J. Biomech. 48, 3234–3241. doi: 10.1016/j.jbiomech.2015.06.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Sedighi, A., Sadati, N., Nasseroleslami, B., Khorsand Vakilzadeh, M., Narimani, R., and Parnianpour, M. (2011). “Control of human spine in repetitive sagittal plane flexion and extension motion using a CPG based ANN approach,” in 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, 8146–8149.

Google Scholar

Shadmehr, R., and Mussa-Ivaldi, S. (2012). Biological Learning and Control: How the Brain Builds Representations, Predicts Events, and Makes Decisions. Cambridge, MA: MIT Press.

Google Scholar

Shahvarpour, A., Shirazi-Adl, A., Larivière, C., and Bazrgari, B. (2015). Computation of trunk stability in forward perturbations—Effects of preload, perturbation load, initial flexion and abdominal preactivation. J. Biomech. 48, 716–720. doi: 10.1016/j.jbiomech.2015.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Shirazi-Adl, A., El-Rich, M., Pop, D. G., and Parnianpour, M. (2005). Spinal muscle forces, internal loads and stability in standing under various postures and loads—application of kinematics-based algorithm. Eur. Spine J. 14, 381–392. doi: 10.1007/s00586-004-0779-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sparto, P. J., and Parnianpour, M. (1998). Estimation of trunk muscle forces and spinal loads during fatiguing repetitive trunk exertions. Spine 23, 2563–2573. doi: 10.1097/00007632-199812010-00011

PubMed Abstract | CrossRef Full Text | Google Scholar

Toumanidou, T., and Noailly, J. (2015). Musculoskeletal modeling of the lumbar spine to explore functional interactions between back muscle loads and intervertebral disk multiphysics. Front. Bioeng. Biotechnol. 3:111. doi: 10.3389/fbioe.2015.00111

PubMed Abstract | CrossRef Full Text | Google Scholar

Vakilzadeh, M. K., Sedighi, A., Salarieh, H., Asghari, M., and Parnianpour, M. (2011). A computation tool to simulate trunk motion and predict muscle activation by assigning different weights to physical and physiological criteria. J. Med. Imaging Health Inform. 1, 231–237. doi: 10.1166/jmihi.2011.1033

CrossRef Full Text | Google Scholar

Zajac, F. E. (1989). Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 17, 359–411.

Google Scholar

Zeinali-Davarani, S., Hemami, H., Barin, K., Shirazi-Adl, A., and Parnianpour, M. (2008). Dynamic stability of spine using stability-based optimization and muscle spindle reflex. IEEE Trans. Neural. Syst. Rehabil. Eng. 16, 106–118. doi: 10.1109/TNSRE.2007.906963

PubMed Abstract | CrossRef Full Text | Google Scholar