- 1School of Automation Engineering, Northeast Electric Power University, Jilin, China
- 2School of Computer Science, Northeast Electric Power University, Jilin, China
- 3College of Mechanical and Electric Engineering, Changchun University of Science and Technology, Changchun, China
- 4School of Computer Science, Northwestern Polytechnical University, Xi’an, China
- 5School of Biomedical Engineering and Brain and Mind Center, University of Sydney, Sydney, NSW, Australia
Recognition accuracy and response time are both critically essential ahead of building the practical electroencephalography (EEG)-based brain–computer interface (BCI). However, recent approaches have compromised either the classification accuracy or the responding time. This paper presents a novel deep learning approach designed toward both remarkably accurate and responsive motor imagery (MI) recognition based on scalp EEG. Bidirectional long short-term memory (BiLSTM) with the attention mechanism is employed, and the graph convolutional neural network (GCN) promotes the decoding performance by cooperating with the topological structure of features, which are estimated from the overall data. Particularly, this method is trained and tested on the short EEG recording with only 0.4 s in length, and the result has shown effective and efficient prediction based on individual and groupwise training, with 98.81% and 94.64% accuracy, respectively, which outperformed all the state-of-the-art studies. The introduced deep feature mining approach can precisely recognize human motion intents from raw and almost-instant EEG signals, which paves the road to translate the EEG-based MI recognition to practical BCI systems.
1 Introduction
Recently, the brain–computer interface (BCI) has played a promising role in assisting and rehabilitating patients from paralysis, epilepsy, and brain injuries via interpreting neural activities to control the peripherals (Bouton et al., 2016; Schwemmer et al., 2018). Among the noninvasive brain activity acquisition systems, electroencephalography (EEG)-based BCI has gained extensive attention recently given its higher temporal resolution and portability. Hence, it has been popularly employed to assist the recovery of patients from motor impairments, e.g., amyotrophic lateral sclerosis (ALS), spinal cord injury (SCI), or stroke survivors (Daly and Wolpaw, 2008; Pereira et al., 2018). Specifically, researchers have focused on the recognition of motor imagery (MI) based on EEG and translating brain activities into specific motor intentions. In such a way, users can further manipulate external devices or exchange information with the surroundings (Pereira et al., 2018). Although researchers have developed several MI-based prototype applications, there is still space for improvement before the practical clinical translation could be promoted (Schwemmer et al., 2018; Mahmood et al., 2019). De facto, to achieve effective and efficient control via only MI, both precise EEG decoding and quick response are eagerly expected. However, few existing works of literature are competent in both perspectives. In this study, we explore the possibility of a deep learning framework to tackle the challenge.
1.1 Related Work
Lately, deep learning (DL) has attracted increasing attention in many disciplines because of its promising performance in classification tasks (LeCun et al., 2015). A growing number of works have shown that DL will play a pivotal role in the precise decoding of brain activities (Schwemmer et al., 2018). Especially, recent works have been carried out on EEG motion intention detection. A primary current focus is to implement the DL-based approach to decode EEG MI tasks, which have attained promising results (Lotte et al., 2018). Due to the high temporal resolution of EEG signals, methods related to the recurrent neural network (RNN) (Rumelhart et al., 1986), which can analyze time-series data, were extensively applied to filter and classify EEG sequences, i.e., time points (Güler et al., 2005; Wang P et al., 2018; Luo et al., 2018; Zhang T et al., 2018; Zhang X et al., 2018). In reference to Zhang T et al. (2018), a novel RNN framework with spatial and temporal filtering was put forward to classify EEG signals for emotion recognition and achieved 95.4% accuracy for three classes with a 9-s segment as a sample. Yang et al. also proposed an emotion recognition method using long short-term memory (LSTM) (Yang J et al., 2020). Wang et al. and Luo et al. performed LSTM (Hochreiter and Schmidhuber, 1997) to handle signals of time slices and achieved 77.30% and 82.75% accuracy, respectively (Wang P et al., 2018; Luo et al., 2018). Zhang X et al. (2018) presented attention-based RNN for EEG-based person identification, which attained 99.89% accuracy for eight participants at the subject level with 4-s signals as a sample. LSTM was also employed in some medical fields, such as seizure detection (Hu et al., 2020), with the recorded EEG signals. However, it can be found that in these studies, signals over experimental duration were recognized as samples, which resulted in a slow responsive prediction.
Apart from RNN, the convolutional neural network (CNN) (Fukushima, 1980; LeCun et al., 1998) has been performed to decode EEG signals as well (Dose et al., 2018; Hou et al., 2020). Hou et al. proposed ESI and CNN and achieved competitive results, i.e., 94.50% and 96.00% accuracy at the group and subject levels, respectively, for four-class classification. What is more, by combining CNN with the graph theory, the graph convolutional neural network (GCN) (Bruna et al., 2014; Henaff et al., 2015; Duvenaud et al., 2015; Niepert et al., 2016; Defferrard et al., 2016) approach was presented lately, taking consideration of the functional topological relationship of EEG electrodes (Wang XH et al., 2018; Song et al., 2018; Zhang T et al., 2019; Wang et al., 2019). In reference to Wang XH et al. (2018) and Zhang T et al. (2019), a GCN with a broad learning approach was proposed and attained 93.66% and 94.24% accuracy, separately, for EEG emotion recognition. Song et al. and Wang et al. introduced dynamical GCN (90.40% accuracy) and phase-locking value-based GCN (84.35% accuracy) to recognize different emotions (Song et al., 2018; Wang et al., 2019). A highly accurate prediction has been accomplished via the GCN model. Few researchers have investigated the approach in the area of EEG MI decoding.
1.2 Contribution of This Paper
Toward accurate and fast MI recognition, an attention-based BiLSTM–GCN was introduced to mine the effective features from raw EEG signals. The main contributions were summarized as follows:
i) As far as we know, this work was the first that combined BiLSTM with the GCN to decode EEG tasks.
ii) The attention-based BiLSTM successfully derived relevant features from raw EEG signals. Followed by the GCN model, it enhanced the decoding performance by considering the internal topological structure of features.
iii) The proposed feature mining approach managed to decode EEG MI signals with stably reproducible results yielding remarkable robustness and adaptability that deals with the considerable intertrial and intersubject variability.
1.3 Organization of This Paper
The rest of this paper was organized as follows. The preliminary knowledge of the BiLSTM, attention mechanism, and GCN was introduced in the Methodology section, which was the foundation of the presented approach. In the Results and Discussion section, experimental details and numerical results were presented, followed by the conclusion in the Conclusion section.
2 Methodology
2.1 Pipeline Overview
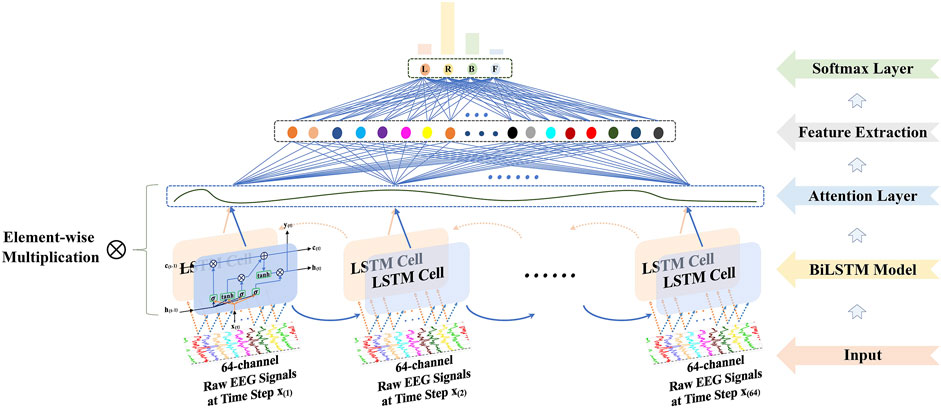
The framework of the proposed method is presented in Figure 1.
i) The 64-channel raw EEG signals were acquired via the BCI 2000, and then the 4-s (experimental duration) signals were sliced into 0.4-s segments over time, where the dimension of each segment was 64 channels × 64 time steps.
ii) The attention-based BiLSTM was put forward to filter 64-channel (spatial information) and 0.4-s (temporal information) raw EEG data and derived features from the fully connected neurons.
iii) The Pearson, adjacency, and Laplacian matrices of overall features were introduced sequentially to represent the topological structure of features, i.e., as a graph. Followed by the features and its corresponding graph representation as the input, the GCN model was performed to classify four-class MI tasks.
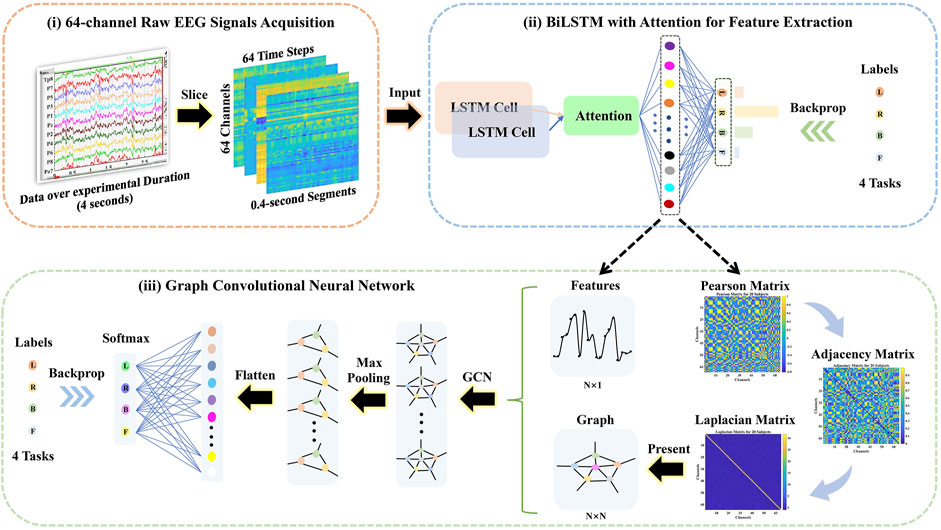
FIGURE 1. The schematical overview consisted of the 64-channel raw electroencephalography (EEG) signal acquisition, the bidirectional long short-term memory (BiLSTM) with the attention model for feature extraction, and the graph convolutional neural network (GCN) model for classification.
2.2 Bidirectional Long Short Term Memory With Attention
2.2.1 Bidirectional Long Short Term Memory Model
RNN-based approaches have been extensively applied to analyze EEG time-series signals. An RNN cell, though alike a feedforward neural network, has connections pointing backward, which sends its output back to itself. The learned features of an RNN cell at time step t are influenced by not only the input signals x(t) but also the output (state) at time step t − 1. This design mechanism dictates that RNN-based methods can handle sequential data, e.g., time point signals, by unrolling the network through time. The LSTM and gated recurrent unit (GRU) (Cho et al., 2014) are the most popular variants of the RNN-based approaches. In theProposed approachsection, the paper compared the performance of the welcomed models experimentally, and the BiLSTM with attention displayed in Figure 2 outperformed others due to better detection of the long-term dependencies of raw EEG signals.
As illustrated in Figure 2, three kinds of gates manipulate and control the memories of EEG signals, namely, the input gate, forget gate, and output gate. Demonstrated by the i(t), the input gate partially stores the information of x(t) and controls which part of it should be added to the long-term state c(t). The forget gate controlled by the f(t) decides which piece of the c(t) should be overlooked. The output gate, controlled by o(t), allows which part of the information from c(t) should be outputted, denoted as y(t), known as the short-term state h(t). Manipulated by the above gates, two kinds of states are stored. The long-term state c(t) travels through the cell from left to right, dropping some memories at the forget gate and adding something new from the input gate. After that, the information passes through a nonlinear activation function, tanh activation function usually, and then it is filtered by the output gate. In such a way, the short-term state h(t) is produced.
Eqs. 1–6 describe the procedure of an LSTM cell, where W and b are the weights and biases for different layers to store the memory and learn a generalized model, and σ is a nonlinear activation function, i.e., sigmoid function used in the experiments. For bidirectional LSTM, BiLSTM for short, the signals x(t) are inputted from left to right for the forward LSTM cell. What is more, they are reversed and inputted into another LSTM cell, the backward LSTM. Thus, there are two output vectors, which store much more comprehensive information than a single LSTM cell. Then they are concatenated as the final output of the cell.
2.2.2 Attention Mechanism
The attention mechanism, imitated from the human vision, has a vital part to play in the field of computer vision (CV), natural language processing (NLP), and automatic speech recognition (ASR) (Bahdanau et al., 2014; Chorowski et al., 2015; Xu et al., 2015; Yang et al., 2016). Not all the signals contribute equally toward the classification. Hence, an attention mechanism s(t) is jointly trained as a weighted sum of the output of the BiLSTM with attention based on the weights.
u(t) is a fully connected (FC) layer for learning features of y(t), followed by a softmax layer which outputs a probability distribution α(t). Ww, uw, and bw denote trainable weights and biases, respectively. It selects and extracts the most significant temporal and spatial information from y(t) by multiplying α(t) with regard to the contribution to the decoding tasks.
2.3 Graph Convolutional Neural Network
2.3.1 Graph Convolution
In the graph theory, a graph is presented by the graph Laplacian L. It is computed by the degree matrix D minus the adjacency matrix A, i.e., L = D − A. In this work, Pearson’s matrix P was utilized to measure the inner correlations among features.
where X and Y are two variables regarding different features, ρX,Y is their correlation, σX and σY are the standard deviations, and μX and μY are the expectations. Besides, the adjacency matrix A is recognized as:
where |P| is the absolute of Pearson’s matrix P, and
Then the normalized graph Laplacian is computed as:
It is then decomposed by the Fourier basis
in which gθ is a nonparametric filter. Specifically, the operation is as follows:
in which
2.3.2 Graph Pooling
The graph pooling operation can be achieved via the Graclus multilevel clustering algorithm, which consists of node clustering and one-dimensional pooling (Dhillon et al., 2007). A greedy algorithm was implemented to compute the successive coarser of a graph and minimize the clustering objective, from which the normalized cut was chosen (Shi and Malik, 2000). Through such a way, meaningful neighborhoods on graphs were acquired. Defferrard et al. (2016) proposed to carry out a balanced binary tree to store the neighborhoods, and a one-dimensional pooling was then applied for precise dimensionality reduction.
2.4 Proposed Approach
The presented approach was a combination of the attention-based BiLSTM and the GCN, as illustrated in Figure 1. The BiLSTM with the attention mechanism was presented to derive relevant features from raw EEG signals. During the procedure, features were obtained from neurons at the FC layer. In Figure 3, we demonstrated the topological connections of the Subject Nine’s features via the Pearson Matrix, Absolute Pearson Matrix, Adjacency Matrix, and Laplacian Matrix. The GCN was then applied to classify the extracted features. It was the combination of two models that promoted and enhanced the decoding performance by a significant margin compared with existing studies. Details were provided in the following.
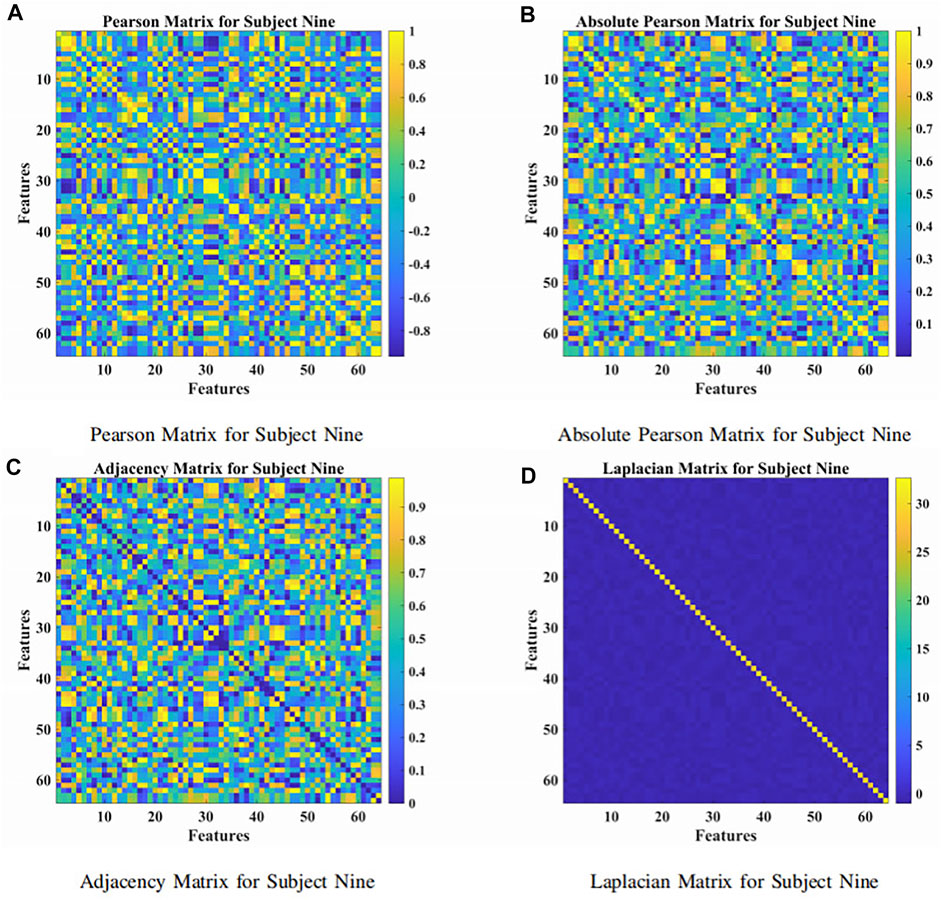
FIGURE 3. The Pearson, absolute Pearson, adjacency, and Laplacian matrices for subject nine. (A) Pearson matrix for subject nine. (B) Absolute Pearson matrix for subject nine. (C) Adjacency matrix for subject nine. (D) Laplacian matrix for subject nine.
First of all, an optimal RNN-based model was explored to obtain relevant features from raw EEG signals. As shown in Figure 4, in this work, the BiLSTM with the attention model was best performed, which achieved 77.86% global average accuracy (GAA). The input size x(t) of the model was 64, denoting 64 channels (electrodes) of raw EEG signals. The maximum time t was chosen as 64, which was a 0.4-s segment. According to Figures 4A, B, higher accuracy has been obtained while increasing the number of cells of the BiLSTM model. It should, however, be noted in Figure 3F that when there were more than 256 cells, the loss showed an upward trend, which indicated the concern of overfitting due to the increment of the model complexity. As a result, 256 LSTM cells (76.67% GAA) were chosen to generalize the model. Meanwhile, it was apparent that, in Figure 4C, as for the linear size of the attention weights, the majority of the choices did not make a difference. Thus, eight neurons, with 79.40% GAA, were applied during the experiments empirically. Comparing Figures 4D, H, it showed that a compromise solution should be applied, which took into consideration both performance and input size of the GCN. As a result, a linear size of 64 (76.73% GAA) was utilized at the FC layer.
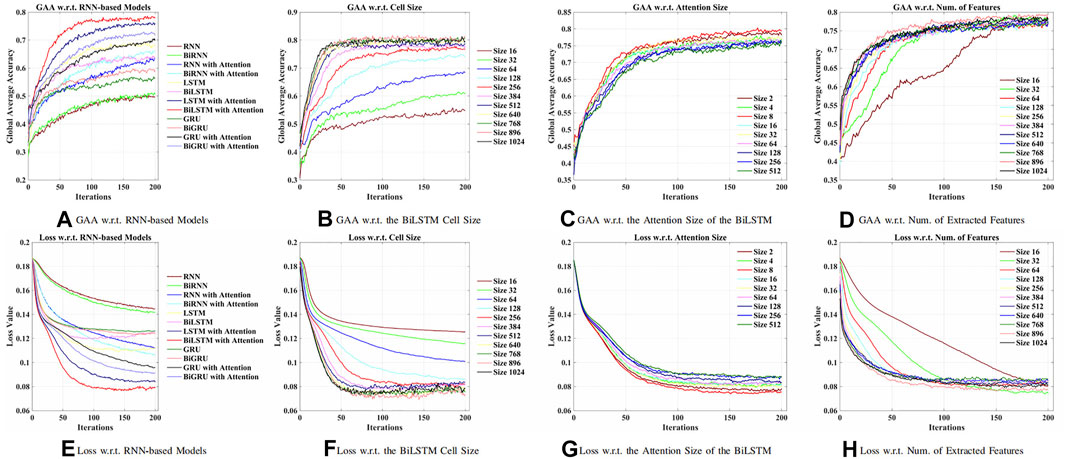
FIGURE 4. Comparison of models and hyperparameters w.r.t. the recurrent neural network (RNN)-based methods for feature extraction. (A) Global average accuracy (GAA) w.r.t. RNN-based models. (B) GAA w.r.t. BiLSTM cell size. (C) GAA w.r.t. attention size of the BiLSTM. (D) GAA w.r.t. the number of the extracted features. (E) Loss w.r.t. RNN-based models. (F) Loss w.r.t. BiLSTM cell size. (G) Loss w.r.t. attention size of the BiLSTM. (H) Loss w.r.t. the number of the extracted features.
Besides, to prevent overfitting, a 25% dropout (Srivastava et al., 2014) for the BiLSTM and FC layer was implemented. The model carried out batch normalization (BN) (Ioffe and Szegedy, 2015) for the FC layer, which was activated by the softplus function (Hahnloser et al., 2000). The L2 norm with the 1 × 10−7 coefficient was applied to the Euclidean distance as the loss function. A total of 1,024 batch sizes were used to maximize the usage of GPU resources. The 1 × 10−4 learning rate was applied to the Adam optimizer (Kingma and Ba, 2014).
Furthermore, the second-order Chebyshev polynomial was applied to approximate convolutional filters in the experiments. The GCN consisted of six graph convolutional layers with 16, 32, 64, 128, 256, and 512 filters, respectively, each followed by a graph max-pooling layer, and a softmax layer derived the final prediction.
In addition, for the GCN model, before the nonlinear softplus activation function, BN was utilized at all of the layers except the final softmax. The 1 × 10−7 L2 norm was added to the loss function, which was a cross-entropy loss. Stochastic gradient descent (Zhang, 2004) with 16 batch sizes was optimized by the Adam (1 × 10−7 learning rate).
All the experiments above were performed and implemented by the Google TensorFlow (Abadi et al., 2016) 1.14.0 under NVIDIA RTX 2080ti and CUDA10.0.
3 Results and Discussion
3.1 Description of the Dataset
The data collected from the EEG Motor Movement/Imagery Dataset (Goldberger et al., 2000) was employed in this study. Numerous EEG trials were acquired from 109 participants performing four MI tasks, i.e., imagining the left fist (L), the right fist (R), both fists (B), and both feet (F) (21 trials per task). Each trial is a 4-s experiment duration (160 Hz sample rate) with one single task (Hou et al., 2020). In this work, a 0.4-s temporal segment of 64 channel signals, i.e., 64 channels × 64 time points, was regarded as a sample. In the Groupwise prediction section, we used a group of 20 subject data (S1 − S20) to train and validate our method. The 10-fold cross-validation was carried out. Further, 50 subjects (S1 − S50) were selected to verify the repeatability and stability of our approach. In the Subject-specific adaptation section, the dataset of individual subjects (S1 − S10) was utilized to perform subject-level adaptation. For all the experiments, the dataset was randomly divided into 10 parts, where 90% was the training set, and the remaining 10% was regarded as the test set. In the Groupwise prediction section, the above procedure has been carried out 10 times. Thus, it left us 10 results of 10-fold cross-validation.
3.2 Groupwise Prediction
It was suggested that intersubject variability remains one of the concerns for interpreting EEG signals (Tanaka, 2020). First, a small group size (20 subjects) was adopted for groupwise prediction. In Figure 4A, 63.57% GAA was achieved by the BiLSTM model. After applying the attention mechanism, it enhanced the decoding performance, which accomplished 77.86% GAA (14.29% improvement). Further, we employed an attention-based BiLSTM–GCN model in this work. It attained 94.64% maximum GAA (Hou et al., 2020) (31.07% improvement compared with the BiLSTM model) and 93.04% median accuracy from 10-fold cross-validation. Our method promoted the classification capability under subject variability and variations by taking the topological relationship of relevant features into consideration. Meanwhile, as illustrated in Figure 5A, the median values of GAA, kappa, precision, recall, and F1 score were 93.04%, 90.71%, 93.02%, 93.01%, and 92.99%, respectively. To the knowledge of the authors, the proposed method has achieved the best state-of-the-art performance in group-level prediction. Besides, remarkable results of 10-fold cross-validation have verified the repeatability and stability. Furthermore, the confusion matrix of test one (94.64% GAA) was given in Figure 5B. Accuracies of 91.69%, 92.11%, 94.48%, and 100% were obtained for each task. It can be observed that our method was unprecedentedly effective and efficient in detecting human motion intents from raw EEG signals.
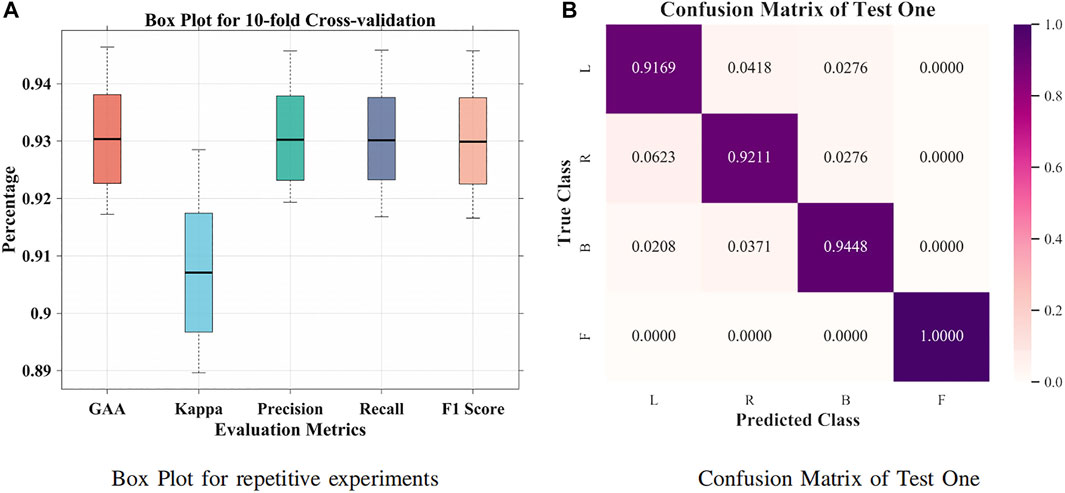
FIGURE 5. Box plot and confusion matrix for 10-fold cross-validation. (A) Box plot for repetitive experiments. (B) Confusion matrix for test one.
By grouping signals from additional 30 subjects (in total 50 subjects), the robustness of the method has been validated in Figure 6.
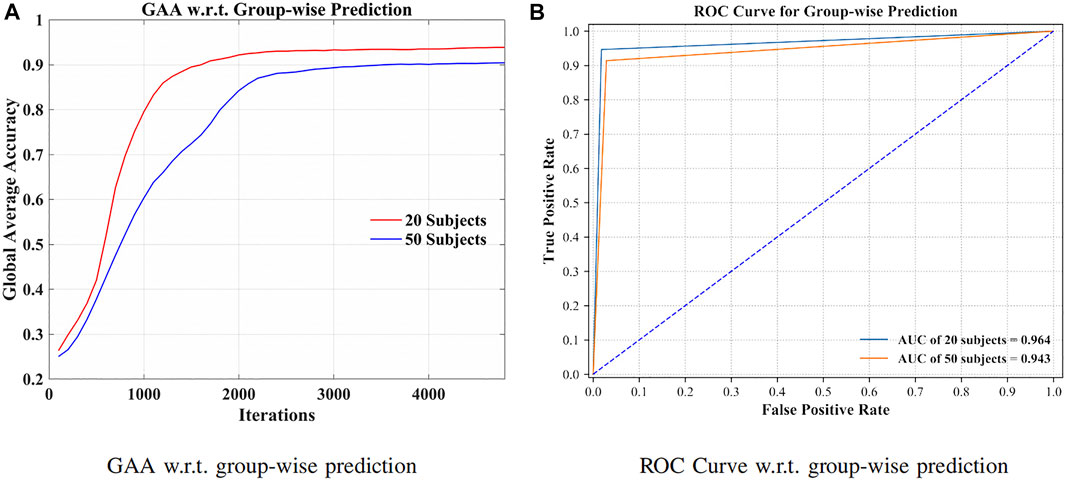
FIGURE 6. GAA and receiver operating characteristic curve (ROC curve) for 20 and 50 subjects, separately. (A) GAA w.r.t. groupwise prediction. (B) ROC curve w.r.t. groupwise prediction.
Toward practical EEG-based BCI applications, it is essential to develop a robust model to counter serious individual variability (Tanaka, 2020). Figure 6A illustrates the GAA of our method through iterations. As listed in Figure 6B, we can see that 94.64% and 91.40% GAA were obtained with regard to the group of 20 and 50 subjects, respectively. The area under the curves (AUCs) were 0.964 and 0.943. Indicated by the above results, the presented approach can successfully filter the distinctions of signals, even though the dataset was extended. In other words, by increasing the intersubject variability, the robustness and effectiveness of the method were evaluated.
The comparison of groupwise evaluation was demonstrated, measured by the maximum of GAA (Hou et al., 2020) during experiments (Ma et al., 2018; Hou et al., 2020). Here, we compared the performance of several state-of-the-art methods in Table 1.
Table 1 lists the performance of related methods. Hou et al. achieved competitive results. However, our method obtained higher performance (0.14% accuracy improvement) even with doubling the number of subjects. It can be found that our approach has outperformed those by giving the highest accuracy of decoding EEG MI signals.
3.3 Subject-Specific Adaptation
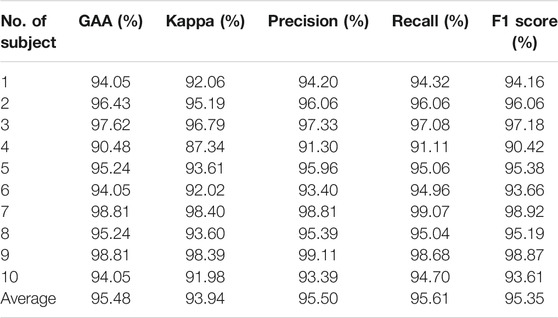
The performance of individual adaptation has witnessed a flourishing increment (Dose et al., 2018; Amin et al., 2019; Zhang R et al., 2019; Ji et al., 2019; Ortiz-Echeverri et al., 2019; Sadiq et al., 2019; Taran and Bajaj, 2019; Hou et al., 2020). The results of our method on subject-level adaptation have been reviewed in Table 2, and we compared the results in Table 3.
Results are given in Table 2, from which the highest GAA was 98.81% achieved by subjects S7 and S9, and the lowest was 90.48% by S4. On average, the presented approach can handle the challenge of subject-specific adaptation. It achieved competitive results, with an average accuracy of 95.48%. Moreover, Cohen’s kappa coefficient (kappa), precision, recall, and F1 score were 93.94%, 95.50%, 95.61%, and 95.35%, respectively. The promising results above indicated that the introduced method filtered raw EEG signals and succeeded in classifying MI tasks.
As can be seen from Figure 7A, the model has been shown to converge for the subject-specific adaptation. The receiver operating characteristic curve (ROC curve) with its corresponding AUC is visible in Figure 7B.
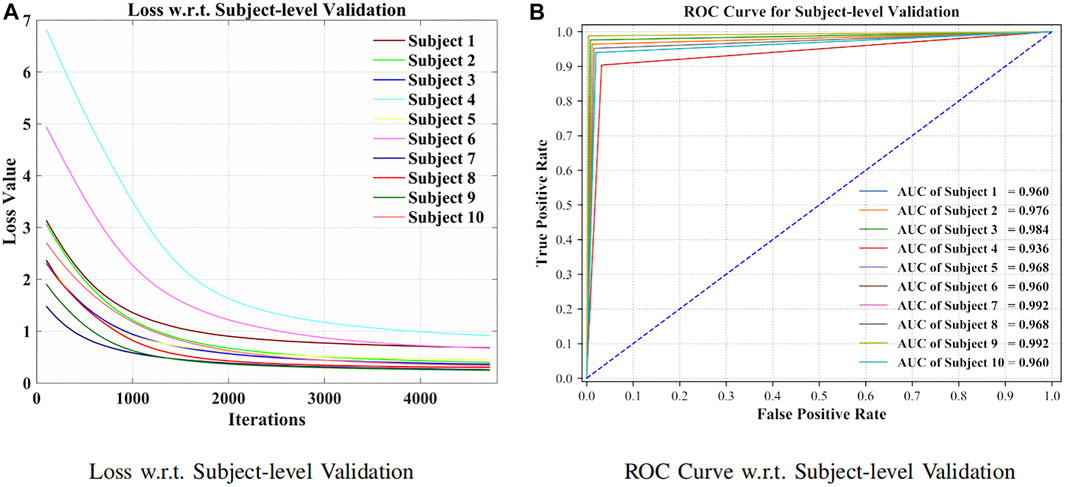
FIGURE 7. Loss and ROC curve for subject-level evaluation. (A) Loss w.r.t. subject-level validation. (B) ROC curve w.r.t. subject-level validation.
The comparison of subject-level prediction was put forward between the presented approach and the competitive models (Dose et al., 2018; Amin et al., 2019; Zhang R et al., 2019; Ji et al., 2019; Ortiz-Echeverri et al., 2019; Sadiq et al., 2019; Taran and Bajaj, 2019; Hou et al., 2020). The attention-based BiLSTM–GCN approach has achieved highly accurate results, which suggested robustness and effectiveness toward EEG signal processing, as shown in Table 3.
The presented approach has improved classification accuracy and obtained state-of-the-art results. The reason for the outstanding performance was that the attention-based BiLSTM model managed to extract relevant features from raw EEG signals. The followed GCN model successfully classified features by cooperating with the topological relationship of overall features.
4 Conclusion
To address the challenge of intertrial and intersubject variability in EEG signals, an innovative approach of attention-based BiLSTM–GCN was proposed to accurately classify four-class EEG MI tasks, i.e., imagining the left fist, the right fist, both fists, and both feet. First of all, the BiLSTM with the attention model succeeded in extracting relevant features from raw EEG signals. The followed GCN model intensified the decoding performance by cooperating with the internal topological relationship of relevant features, which were estimated from Pearson’s matrix of the overall features. Besides, results provided compelling evidence that the method has converged to both the subject-level and groupwise predictions and achieved the best state-of-the-art performance, i.e., 98.81% and 94.64% accuracy, respectively, for handling individual variability, which were far ahead of existing studies. The 0.4-s sample size was proven effective and efficient in prediction compared with the traditional 4-s trial length, which means that our proposed framework can provide a time-resolved solution toward fast response. Results on a group of 20 subjects were derived by 10-fold cross-validation, indicating repeatability and stability. The proposed method is predicted to advance the clinical translation of the EEG MI-based BCI technology to meet the diverse demands, such as of paralyzed patients. In summary, the unprecedented performance with the highest accuracy and time-resolved prediction were fulfilled via the introduced feature mining approach.
In addition, the proposed method in this paper could be potentially applied in relevant practical directions, such as digital neuromorphic computing to assist movement disorder (Yang et al., 2018; Yang et al., 2019; Yang S et al., 2020; Yang et al., 2021).
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.physionet.org/content/eegmmidb/1.0.0/.
Author Contributions
YH conceived and designed the research. SJ and XL collected the data and conducted the research. SZ, TC, FW, and JL interpreted the results. All authors contributed to the writing and revisions.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank the Brain Team at Google for developing TensorFlow. We further acknowledge PhysioNet for open-sourcing the EEG Motor Movement/Imagery Dataset to promote the research.
References
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., et al. (2016). “Tensorflow: A System for Large-Scale Machine Learning,” in 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI-16), Savannah, GA, November 2–4, 2016, 265–283.
Amin, S. U., Alsulaiman, M., Muhammad, G., Bencherif, M. A., and Hossain, M. S. (2019). Multilevel Weighted Feature Fusion Using Convolutional Neural Networks for Eeg Motor Imagery Classification. IEEE Access 7, 18940–18950. doi:10.1109/access.2019.2895688
Bahdanau, D., Cho, K., and Bengio, Y. (2014). “Neural Machine Translation by Jointly Learning to Align and Translate,” in International Conference on Learning Representations, San Diego, CA, May 7–9, 2015.
Bouton, C. E., Shaikhouni, A., Annetta, N. V., Bockbrader, M. A., Friedenberg, D. A., Nielson, D. M., et al. (2016). Restoring Cortical Control of Functional Movement in a Human with Quadriplegia. Nature 533, 247–250. doi:10.1038/nature17435
Bruna, J., Zaremba, W., Szlam, A., and Lecun, Y. (2014). “Spectral Networks and Locally Connected Networks on Graphs,” in International Conference on Learning Representations (ICLR2014), Banff, AB, April 14–16, 2014.
Cho, K., van Merrienboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). “Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation,” in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, October 25–29, 2014 (Doha, Qatar: Association for Computational Linguistics), 1724–1734. doi:10.3115/v1/D14-1179
Chorowski, J. K., Bahdanau, D., Serdyuk, D., Cho, K., and Bengio, Y. (2015). “Attention-based Models for Speech Recognition,” in Advances in Neural Information Processing Systems (Montreal, QC: Association for Computing Machinery (ACM)), 577–585.
Daly, J. J., and Wolpaw, J. R. (2008). Brain-computer Interfaces in Neurological Rehabilitation. Lancet Neurol. 7, 1032–1043. doi:10.1016/s1474-4422(08)70223-0
Defferrard, M., Bresson, X., and Vandergheynst, P. (2016). “Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering,” in Advances in Neural Information Processing Systems (Barcelona, Spain: Association for Computing Machinery (ACM)), 3844–3852.
Dhillon, I. S., Guan, Y., and Kulis, B. (2007). Weighted Graph Cuts without Eigenvectors a Multilevel Approach. IEEE Trans. Pattern Anal. Machine Intell. 29, 1944–1957. doi:10.1109/tpami.2007.1115
Dose, H., Møller, J. S., Iversen, H. K., and Puthusserypady, S. (2018). An End-To-End Deep Learning Approach to Mi-Eeg Signal Classification for Bcis. Expert Syst. Appl. 114, 532–542. doi:10.1016/j.eswa.2018.08.031
Duvenaud, D. K., Maclaurin, D., Iparraguirre, J., Bombarell, R., Hirzel, T., Aspuru-Guzik, A., et al. (2015). “Convolutional Networks on Graphs for Learning Molecular Fingerprints,” in Advances in Neural Information Processing Systems (Montreal, QC: Association for Computing Machinery (ACM)), 3844–3852.
Fukushima, K. (1980). Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. Biol. Cybernet. 36, 193–202. doi:10.1007/bf00344251
Goldberger, A. L., Amaral, L. A., Glass, L., Hausdorff, J. M., Ivanov, P. C., Mark, R. G., et al. (2000). Physiobank, Physiotoolkit, and Physionet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 101, e215–20. doi:10.1161/01.cir.101.23.e215
Güler, N. F., Übeyli, E. D., and Güler, I. (2005). Recurrent Neural Networks Employing Lyapunov Exponents for Eeg Signals Classification. Expert Syst. Appl. 29, 506–514. doi:10.1016/j.eswa.2005.04.011
Hahnloser, R. H. R., Sarpeshkar, R., Mahowald, M. A., Douglas, R. J., and Seung, H. S. (2000). Digital Selection and Analogue Amplification Coexist in a Cortex-Inspired Silicon Circuit. Nature 405, 947–951. doi:10.1038/35016072
Hammond, D. K., Vandergheynst, P., and Gribonval, R. (2011). Wavelets on Graphs via Spectral Graph Theory. Appl. Comput. Harmonic Anal. 30, 129–150. doi:10.1016/j.acha.2010.04.005
Henaff, M., Bruna, J., and LeCun, Y. (2015). Deep Convolutional Networks on Graph-Structured Data. New York, NY: arXiv. arXiv preprint arXiv:1506.05163.
Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Hou, Y., Zhou, L., Jia, S., and Lun, X. (2020). A Novel Approach of Decoding EEG Four-Class Motor Imagery Tasks via Scout ESI and CNN. J. Neural Eng. 17, 016048. doi:10.1088/1741-2552/ab4af6
Hu, X., Yuan, S., Xu, F., Leng, Y., Yuan, K., and Yuan, Q. (2020). Scalp Eeg Classification Using Deep Bi-lstm Network for Seizure Detection. Comput. Biol. Med. 124, 103919. doi:10.1016/j.compbiomed.2020.103919
Ioffe, S., and Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Lille, France: arXiv.
Ji, N., Ma, L., Dong, H., and Zhang, X. (2019). Eeg Signals Feature Extraction Based on Dwt and Emd Combined with Approximate Entropy. Brain Sci. 9, 201. doi:10.3390/brainsci9080201
Kingma, D. P., and Ba, J. (2014). Adam: A Method for Stochastic Optimization. San Diego, CA: arXiv. arXiv preprint arXiv:1412.6980.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based Learning Applied to Document Recognition. Proc. IEEE 86, 2278–2324. doi:10.1109/5.726791
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539
Lotte, F., Bougrain, L., Cichocki, A., Clerc, M., Congedo, M., Rakotomamonjy, A., et al. (2018). A Review of Classification Algorithms for EEG-Based Brain-Computer Interfaces: a 10 Year Update. J. Neural Eng. 15, 031005. doi:10.1088/1741-2552/aab2f2
Luo, T.-j., Zhou, C.-l., and Chao, F. (2018). Exploring Spatial-Frequency-Sequential Relationships for Motor Imagery Classification with Recurrent Neural Network. BMC Bioinformatics 19, 344. doi:10.1186/s12859-018-2365-1
Ma, X., Qiu, S., Du, C., Xing, J., and He, H. (2018). Improving Eeg-Based Motor Imagery Classification via Spatial and Temporal Recurrent Neural Networks. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2018, 1903–1906. doi:10.1109/EMBC.2018.8512590
Mahmood, M., Mzurikwao, D., Kim, Y.-S., Lee, Y., Mishra, S., Herbert, R., et al. (2019). Fully Portable and Wireless Universal Brain-Machine Interfaces Enabled by Flexible Scalp Electronics and Deep Learning Algorithm. Nat. Mach Intell. 1, 412–422. doi:10.1038/s42256-019-0091-7
Niepert, M., Ahmed, M., and Kutzkov, K. (2016). “Learning Convolutional Neural Networks for Graphs,” in International Conference on Machine Learning, New York, NY, June 19–24, 2016, 2014–2023.
Ortiz-Echeverri, C. J., Salazar-Colores, S., Rodríguez-Reséndiz, J., and Gómez-Loenzo, R. A. (2019). A New Approach for Motor Imagery Classification Based on Sorted Blind Source Separation, Continuous Wavelet Transform, and Convolutional Neural Network. Sensors 19, 4541. doi:10.3390/s19204541
Pereira, J., Sburlea, A. I., and Müller-Putz, G. R. (2018). Eeg Patterns of Self-Paced Movement Imaginations towards Externally-Cued and Internally-Selected Targets. Sci. Rep. 8, 13394. doi:10.1038/s41598-018-31673-2
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning Representations by Back-Propagating Errors. Nature 323, 533–536. doi:10.1038/323533a0
Sadiq, M. T., Yu, X., Yuan, Z., Fan, Z., Rehman, A. U., Li, G., et al. (2019). Motor Imagery Eeg Signals Classification Based on Mode Amplitude and Frequency Components Using Empirical Wavelet Transform. IEEE Access 7, 127678–127692. doi:10.1109/access.2019.2939623
Schwemmer, M. A., Skomrock, N. D., Sederberg, P. B., Ting, J. E., Sharma, G., Bockbrader, M. A., et al. (2018). Meeting Brain-Computer Interface User Performance Expectations Using a Deep Neural Network Decoding Framework. Nat. Med. 24, 1669–1676. doi:10.1038/s41591-018-0171-y
Jianbo Shi, J., and Malik, J. (2000). Normalized Cuts and Image Segmentation. IEEE Trans. Pattern Anal. Machine Intell. 22, 888–905. doi:10.1109/34.868688
Song, T., Zheng, W., Song, P., and Cui, Z. (2018). Eeg Emotion Recognition Using Dynamical Graph Convolutional Neural Networks. IEEE Trans. Affective Comput 11, 532–541. doi:10.1109/TAFFC.2018.2817622
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a Simple Way to Prevent Neural Networks from Overfitting. J. Machine Learn. Res. 15, 1929–1958.
Tanaka, H. (2020). Group Task-Related Component Analysis (Gtrca): a Multivariate Method for Inter-trial Reproducibility and Inter-subject Similarity Maximization for Eeg Data Analysis. Sci. Rep. 10, 84–17. doi:10.1038/s41598-019-56962-2
Taran, S., and Bajaj, V. (2019). Motor Imagery Tasks-Based Eeg Signals Classification Using Tunable-Q Wavelet Transform. Neural Comput. Applic. 31, 6925–6932. doi:10.1007/s00521-018-3531-0
Wang, Z., Tong, Y., and Heng, X. (2019). Phase-locking Value Based Graph Convolutional Neural Networks for Emotion Recognition. IEEE Access 7, 93711–93722. doi:10.1109/access.2019.2927768
Wang P, P., Jiang, A., Liu, X., Shang, J., and Zhang, L. (2018). Lstm-based Eeg Classification in Motor Imagery Tasks. IEEE Trans. Neural Syst. Rehabil. Eng. 26, 2086–2095. doi:10.1109/tnsre.2018.2876129
Wang XH, X. H., Zhang, T., Xu, X.-m., Chen, L., Xing, X.-f., and Chen, C. P. (2018). “Eeg Emotion Recognition Using Dynamical Graph Convolutional Neural Networks and Broad Learning System,” in 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, December 3–6, 2018 (IEEE), 1240–1244. doi:10.1109/bibm.2018.8621147
Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., et al. (2015). “Show, Attend and Tell: Neural Image Caption Generation with Visual Attention,” in International Conference on Machine Learning, Lille, France, July 7–9, 2015, 2048–2057.
Yang, Z., Yang, D., Dyer, C., He, X., Smola, A., and Hovy, E. (2016). “Hierarchical Attention Networks for Document Classification,” in Proceedings of the 2016 conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, June 13–15, 2016, 1480–1489. doi:10.18653/v1/n16-1174
Yang, S., Wei, X., Deng, B., Liu, C., Li, H., and Wang, J. (2018). Efficient Digital Implementation of a Conductance-Based Globus Pallidus Neuron and the Dynamics Analysis. Physica A Stat. Mech. Appl. 494, 484–502. doi:10.1016/j.physa.2017.11.155
Yang, S., Deng, B., Wang, J., Liu, C., Li, H., Lin, Q., et al. (2019). Design of Hidden-Property-Based Variable Universe Fuzzy Control for Movement Disorders and its Efficient Reconfigurable Implementation. IEEE Trans. Fuzzy Syst. 27, 304–318. doi:10.1109/tfuzz.2018.2856182
Yang, S., Wang, J., Deng, B., Azghadi, M. R., and Linares-Barranco, B. (2021). Neuromorphic Context-dependent Learning Framework with Fault-Tolerant Spike Routing. IEEE Trans. Neural Netw. Learn. Syst., 1–15. doi:10.1109/tnnls.2021.3084250
Yang J, J., Huang, X., Wu, H., and Yang, X. (2020). Eeg-based Emotion Classification Based on Bidirectional Long Short-Term Memory Network. Proced. Comput. Sci. 174, 491–504. doi:10.1016/j.procs.2020.06.117
Yang S, S., Deng, B., Wang, J., Li, H., Lu, M., Che, Y., et al. (2020). Scalable Digital Neuromorphic Architecture for Large-Scale Biophysically Meaningful Neural Network with Multi-Compartment Neurons. IEEE Trans. Neural Netw. Learn. Syst. 31, 148–162. doi:10.1109/tnnls.2019.2899936
Zhang R, R., Zong, Q., Dou, L., and Zhao, X. (2019). A Novel Hybrid Deep Learning Scheme for Four-Class Motor Imagery Classification. J. Neural Eng. 16, 066004. doi:10.1088/1741-2552/ab3471
Zhang T, T., Zheng, W., Cui, Z., Zong, Y., and Li, Y. (2018). Spatial-Temporal Recurrent Neural Network for Emotion Recognition. IEEE Trans. Cybern. 49, 839–847. doi:10.1109/TCYB.2017.2788081
Zhang T, T., Wang, X., Xu, X., and Chen, C. P. (2019). Gcb-net: Graph Convolutional Broad Network and its Application in Emotion Recognition. IEEE Trans. Affective Comput, 1. doi:10.1109/taffc.2019.2937768
Zhang X, X., Yao, L., Kanhere, S. S., Liu, Y., Gu, T., and Chen, K. (2018). Mindid: Person Identification from Brain Waves through Attention-Based Recurrent Neural Network. Proc. ACM Interactive Mobile Wearable Ubiquitous Tech. 2, 149. doi:10.1145/3264959
Keywords: brain–computer interface (BCI), electroencephalography (EEG), motor imagery (MI), bidirectional long short-term memory (BiLSTM), graph convolutional neural network (GCN)
Citation: Hou Y, Jia S, Lun X, Zhang S, Chen T, Wang F and Lv J (2022) Deep Feature Mining via the Attention-Based Bidirectional Long Short Term Memory Graph Convolutional Neural Network for Human Motor Imagery Recognition. Front. Bioeng. Biotechnol. 9:706229. doi: 10.3389/fbioe.2021.706229
Received: 07 May 2021; Accepted: 30 December 2021;
Published: 11 February 2022.
Edited by:
Fernando Corinto, Politecnico di Torino, ItalyReviewed by:
Shuangming Yang, Tianjin University, ChinaDeliang Fan, Arizona State University, United States
Copyright © 2022 Hou, Jia, Lun, Zhang, Chen, Wang and Lv. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shuyue Jia, c2h1eXVlakBpZWVlLm9yZw==
 Yimin Hou
Yimin Hou Shuyue Jia
Shuyue Jia Xiangmin Lun
Xiangmin Lun Shu Zhang
Shu Zhang Tao Chen
Tao Chen Fang Wang
Fang Wang Jinglei Lv
Jinglei Lv