- 1School of Biomedical Engineering, Capital Medical University, Beijing, China
- 2Beijing Key Laboratory of Fundamental Research on Biomechanics in Clinical Application, Capital Medical University, Beijing, China
- 3School of Sport Sciences, Beijing Sport University, West Lafayette, IN, United States
- 4Fashion Accessory Art and Engineering College, Beijing Institute Of Fashion Technology, Beijing, China
- 5College of Health and Human Sciences, Purdue University, West Lafayette, IN, United States
- 6Anta Sports Science Laboratory, Xiamen, China
- 7China Institute of Sport and Health Science, Beijing Sport University, Beijing, China
Large and repeated impacts on the heel during running are among the primary reasons behind runners’ injuries. Reducing plantar pressure can be conducive to reducing running injury and improving running performance and is primarily achieved by modifying the design parameters of running shoes. This study examines the effect of design parameters of running shoes (i.e., heel-cup, insole material, midsole material, and insole thickness) on landing peak plantar pressure and determines the combination of different parameters that optimize cushion effects by employing the Taguchi method. We developed the foot–shoe finite element (FE) model through reverse engineering. Model assembly with different design parameters was generated in accordance with the Taguchi method orthogonal table. The effectiveness of the model was verified using the static standing model in Ansys. The significance and contribution of different design parameters, and the optimal design to reduce plantar pressure during landing, were determined using the Taguchi method. In the descending order of percentage contribution was a conforming heel-cup (53.18%), insole material (25.89%), midsole material (7.81%), and insole thickness (2.69%). The more conforming heel-cup (p < 0.001) and softer insole (p = 0.001) reduced the heel pressure during landing impact. The optimal design of running shoe in this study was achieved with a latex insole, a 6 mm insole thickness, an Asker C-45 hardness midsole, and a 100% conforming heel-cup. The conforming heel-cup and the insole material significantly affected the peak plantar pressure during heel landing. The implementation of a custom conforming heel-cup is imperative for relieving high plantar pressure for long-distance heel-strike runners.
Introduction
Between 37 and 56% of runners suffer running injuries at least once a year (Van Mechelen, 1992), frequently resulting from hard landings and repeated impact (Torg et al., 1974; Andréasson and Peterson, 1986; Pine, 1991; Nigg and Wakeling, 2001). Over 75% of long-distance runners primarily perform heel landing when running at a medium speed (Kerr, 1983; Hasegawa et al., 2007). Rapid deceleration following heel contact exerts significant instantaneous ground reaction forces (GRFs) on the heel (Denoth, 1986), which lead to the increased risk of injuries compared to forefoot running (Sanzén et al., 1986; Willems et al., 2006; Song et al., 2013). It has been demonstrated that excessive impact force is predictive of a wide variety of running injuries (Milner et al., 2006; Pohl et al., 2009; Zadpoor and Nikooyan, 2011; Bredeweg et al., 2013; Chan et al., 2018). Therefore, reducing the impact load through the redistribution of plantar foot pressure has been an important target during the design of running shoes.
To redistribute plantar foot pressure (Cheung and Zhang, 2005; Peng et al., 2022), several shoe parameters were modified in terms of their shape and material of the midsole and insole (Actis et al., 2008; Antunes et al., 2008; Cheung and Zhang, 2008). Conventional methods of determining these parameters required an extensive research and development cycle. The finite element (FE) method facilitated the efficient evaluation of different designs and material parameters of the running shoe without the prerequisite of fabricating it and replicating subject trials (Cheung and Zhang, 2008), representing a time- and labor-saving solution to the cycle (Hannah et al., 2016; Peng et al., 2022). Previous FE analyses indicated that the arch-conforming shape (Cheung and Zhang, 2008; Peng et al., 2022), insole thickness (Chatzistergos et al., 2015), insole and midsole material (Cheung and Zhang, 2008; Chatzistergos et al., 2015; Peng et al., 2022), and insole lateral wedge angle (Peng et al., 2022) were conducive to reducing the plantar pressure during static standing. While some studies investigated the shoe design factors on plantar pressure during standing, their contribution to reducing heel impact forces during running remains unclear.
Previous studies on the plantar pressure distribution of landing the foot during running employed either a vertical landing model or a partial foot and insole model. However, the impact area and foot kinematics of heel landing during running differ significantly from static standing or vertical landing. Therefore, models for vertical landing (Goske et al., 2006; Cho et al., 2009) or an incomplete FE model (Goske et al., 2006; Fontanella et al., 2013; Hannah et al., 2016; Drougkas et al., 2018) limit the accuracy of simulation results and systematic investigation of the heel impact in response to various running design combinations. To the best of our knowledge, this is the first study to explore plantar pressure with a complete foot–shoe FE model during heel landing. The complexity of the FE foot–shoe model limits the study of heel landing. Several simplified or incomplete FE models were proposed for studying heel landing. For instance, grounded midsole (Fontanella et al., 2013; Nonogawa et al., 2020) or midsole foot bonding (Hannah et al., 2016) provides different boundary conditions for landing in shoes. Hence, a complete foot–shoe FE model for authentic shoes available for purchase is required to effectively simulate heel impact.
The evaluation of different multiple factor designs and level combinations for running shoes can be time-consuming and costly with conventional testing methods (Rao et al., 2008). A multi-factor and multi-level experimental method in accordance with the orthogonal array, known as the Taguchi method, is a statistical method for FE analysis (Dar et al., 2002; Rao et al., 2008). This allows a balanced comparison of levels of any factor with less effort (Cheung and Zhang, 2008), and has been extensively used to investigate the sensitivity of the design parameters in FE models (Cheung and Zhang, 2008; Zhang et al., 2020; Peng et al., 2022).
The aim of the present study was to determine how to lower the peak plantar heel pressure with different shoe parameter combinations based on a complete foot–shoe FE model developed through reverse engineering (Jeng et al., 2012) and the Taguchi method. We hypothesized that all design parameters significantly affect the peak plantar pressure and that there exists an optimal combination to minimize it.
Materials and methods
To simulate the rearfoot strike in running and estimate the effect of different shoe design parameters on plantar pressure, we scanned the foot and shoe from a single individual and constructed the FE model through reverse engineering. We set the boundary conditions using running kinematics and kinetic data from the model participant. Finally, we employed the statistics-based Taguchi method (Peng et al., 2022) to investigate the effect of different design feature combinations of running shoes on plantar pressure, including conforming heel-cup, insole material, midsole material, and insole thickness. The workflow is depicted in Figure 1.
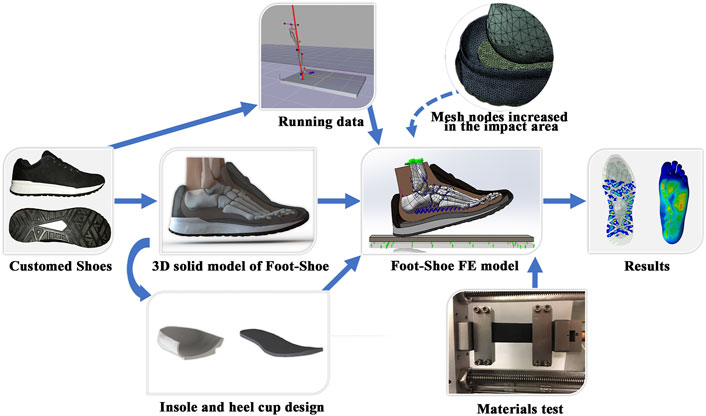
FIGURE 1. Overview of the foot–shoe FE model. The 3D solid model of foot–shoe is based on custom shoes. Different insole and heel-cups were designed in SOLIDWORKS, and various midsole and insole materials were tested. Kinematic and kinetic running data were collected and input as boundary conditions, and mesh nodes in the impact area were increased to obtain smooth prediction results.
Reverse engineering data acquisition
A foot–shoe CT scan was obtained from a model participant (25 year old, male, height: 168 cm, weight: 67 kg) wearing custom running shoes (size: US 41, insole and midsole material: ethylene-vinyl acetate (EVA), insole hardness: Asker C-45, midsole hardness: Asker C-60, outsole material: rubber). This study was approved by the Institutional Review Board of Beijing Sport University (Number: 2021176H). CT images were scanned at 1.25-mm intervals from the participant’s right foot in a weight-off position.
Kinematic and kinetic data acquisition
The participant performed five heel-strike running trials while wearing the shoes on a 20-m runway. The running speed was maintained at 3.8 ± 0.2 m/s using a timing system (300-series, Newtest oy, Oulu, Finland). Four force plates (9281CA, Kistler, Zürich, Switzerland) were embedded in the middle of the runway, sampling at 1000 Hz. Foot contact with the ground occurred within one of the force plates for all five trials. Lower limb kinematics were tracked with 19 retroreflective markers based on the modified Helen Hayes model (Vaughan et al., 1999) at 200 Hz using an eight-camera motion capture system (Raptor-4, Motion analysis, Rohnert Park, CA, United States). Gait biomechanical variables (e.g., GRF, foot–ground angle, net ankle joint force, ankle dorsiflexion moment) were obtained at the instant of vertical impact peak force for each trial (Willems et al., 2005). Plantar and outsole pressures of natural standing were collected synchronously using Footscan (V9 essentials, Rsscan, Beringen, Belgium) and Pedar Insole (Pedar-x, novel, Munich, Germany).
Material properties
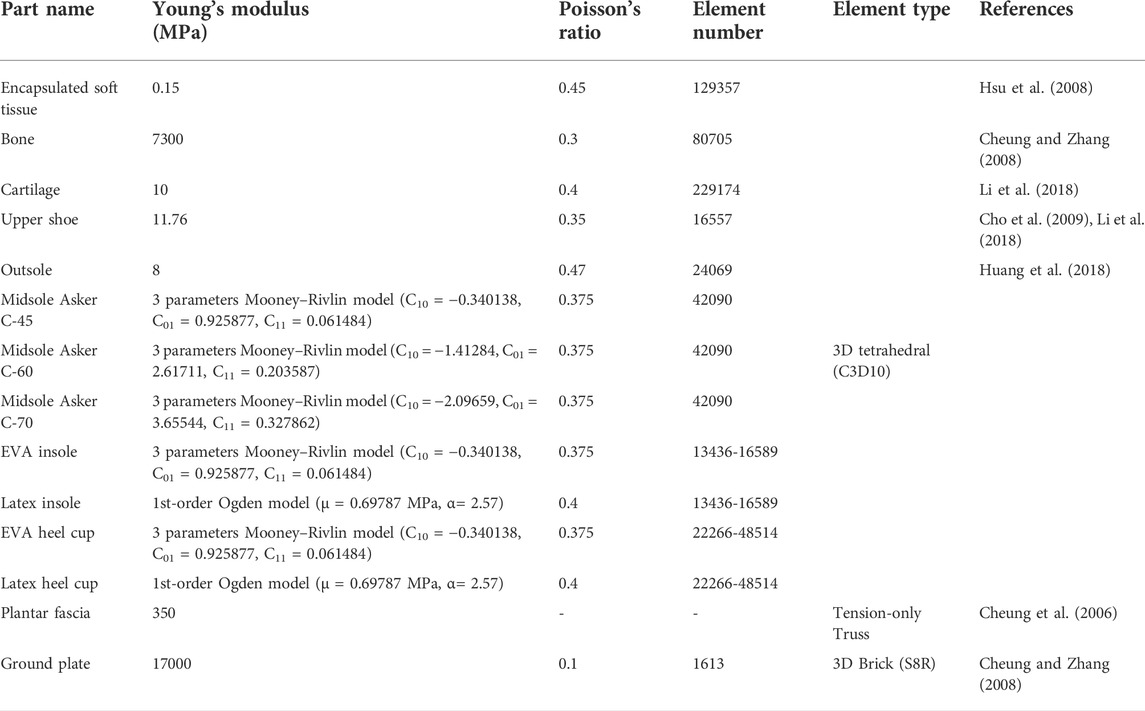
The material properties of shoe midsole and insole materials were tested, using custom size EVA and Latex materials. Three separate EVA materials (7.5 cm long, 2 cm wide, 5 mm thick) with different hardnesses (Asker C-45, 60, and 70) were tested using a MicroTester (eXpert 4000, ADMET, Norwood, MA, United States). The latex material (7.5 cm long, 2 cm wide, and 1 cm thick) was tested using a push–pull tester (HPH, Handpi LLC, Yueqing, Zhejiang, China). The respective material was tested three times, and the results of uniaxial tension with a testing speed of 1 mm/s and strain were recorded. The stress–strain curve and Poisson’s ratio were obtained for each tested material. The stress–strain curve was used as input parameters for Mooney–Rivlin or Ogden hyper-elastic material models simulated in the FE analysis (Table 1).
Full foot–shoe finite element model construction
To build the foot–shoe structural model, we reconstructed the foot (bones, encapsulated soft tissues) and shoe geometries (upper, insole, midsole, and outsole) from the CT scans in Mimics (Version 10.0, Materialise, Leuven, Belgium), smoothed in Geomagic (Version 2015, 3D Systems, Research Triangle Park, NC, United States) and assembled in SOLIDWORKS (Version 2018; SolidWorks Corp., Waltham, MA, United States).
Because cartilage and ligaments cannot be recognized from CT scans, cartilage was rebuilt in SOLIDWORKS based on anatomical locations (Human Anatomy Atlas, Visible Body, Newton, MA, United States). The middle and distal ends of the fifth metatarsal were fused because the latter was relatively small. The different insole and heel-cup shapes were designed in SOLIDWORKS, and the heel-cup and the insole were segmented, whereas the materials used for the heel-cup and the insole in one analysis remained unchanged. Lastly, a ground plate was built into the FE model to simulate ground support (Figure 1).
Similarly, foot ligaments (including the plantar fascial) were simulated using tension-only springs, in Ansys (Version 19.0, ANSYS, Canonsburg, PA, United States), and the resultant stiffness data were between 39.1 and 650 N/mm (Siegler et al., 1988; Cheung et al., 2006; Hoefnagels et al., 2007). Table 1 lists the part and element information in the foot–shoe model (Table 1). We used the bonded contact between the bone, encapsulated soft tissues, and cartilage elements, thus adding frictional contact to potential contact surfaces with cavities (friction coefficient μ = 0.6) (Cheung et al., 2005).
To increase the accuracy of the analysis and obtain higher solution convergence, a local mesh refinement was carried out on the heel region to accommodate the simulation of heel impact. The remaining components were automatically generated using the software in accordance with size. The mesh size of the ground plate was 5 mm. The mesh size of the feet and shoes was 2–10 mm following refinement.
The final foot model consisted of 29 bony segments, 69 ligaments, and 15 cartilage segments embedded in a volume of encapsulated soft tissues. The shoe model consisted of an upper, a heel cup, insole, midsole, and an outsole (Figure 2). The entirety of the tetrahedral elements was present in our model with acceptable quality in mesh control. The skewness value was 0.36 ± 0.21, where 0 corresponds to an equilateral tetrahedral element (Ansys, 2013). The aspect ratio was 2.22 ± 1.37, which represents relatively good mesh quality (Drougkas et al., 2018).
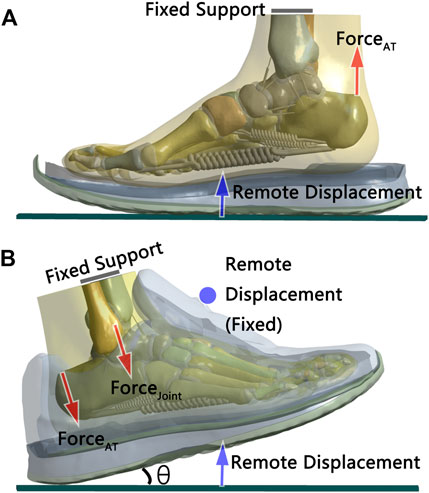
FIGURE 2. FE model and boundary set-up for (A) static standing and (B) rearfoot striking. “θ” represented the foot strike angle between the shoe model and ground plate.
Static stand load and boundary conditions
Our FE model was validated through static standing (i.e., validation model; Figure 2A). To simulate standing and landing, nonlinear large deformation quasi-static contact analysis was employed in this model. The shoe’s upper was removed to simplify the static stand model calculation. Bonded contact was used between the insole and midsole and between the midsole and outsole. Frictional contact (μ = 0.6) was used between the foot and insole and between the outsole and the ground plate.
While the upper surface of the tibia and fibula was fixed and restrained, the ground plate could move in a vertical direction and simulate the GRF loading. The ground plate was set to come into contact with the outsole first (GRF = 0) and then start to simulate in two steps. During the first step, the Achilles tendon force (ForceAT) was set to be applied at the instant of ground plate contact and increase until 1/4 of the participant’s weight was applied, after exactly 1 s. For the second step, while the tendon force stayed constant, the ground plate started to move upward and the GRF loading increased. Once the vertical GRF reached half of the participant’s weight, the simulation was complete, at which point the plantar pressure data were collected.
Heel-strike load and boundary conditions
Across-trial averages of the gait parameters of the model participant were used to simulate the heel strike load. In addition, the across-trial average of ankle dorsiflexion moment of the model participant was introduced into the model by applying an equivalent Achilles tendon force (Novacheck, 1998; Morales-Orcajo et al., 2018).
Boundary conditions were specified with respect to model constraint, type of contact, foot strike angle, and ways to apply external forces (Figure 2B). The upper surface of the tibia and fibula was assumed fixed and restrained in this model. “Remote displacement” was applied at the tongue loop of the shoe; this setting allowed for deformation and movement of the shoe materials around the tongue loop. Similar to the static stand model, there was a bonded contact between the insole and midsole and between the midsole and outsole; frictional contact (μ = 0.6) was used between the foot with the insole and upper and between the outsole and the ground plate. The ground plate was set to form the initial foot strike angle (i.e., obtained from the average running trials) and came into contact with the outsole first and then the external force was loaded in steps. In the first step, the net ankle joint force (ForceJoint) was applied to the top of the talus for 1 s and then maintained for 3 s to simulate the landing inertia force. For the second step, the Achilles tendon force was applied for 1–2 s and then maintained for 3 s. For the third step, the continuous displacement load was applied through the plate for 2–3 s until the force on the plate reached the same GRF value obtained from the trials. Nonlinear large deformation quasi-static contact analysis was employed in this model.
Parametric analysis by the Taguchi method
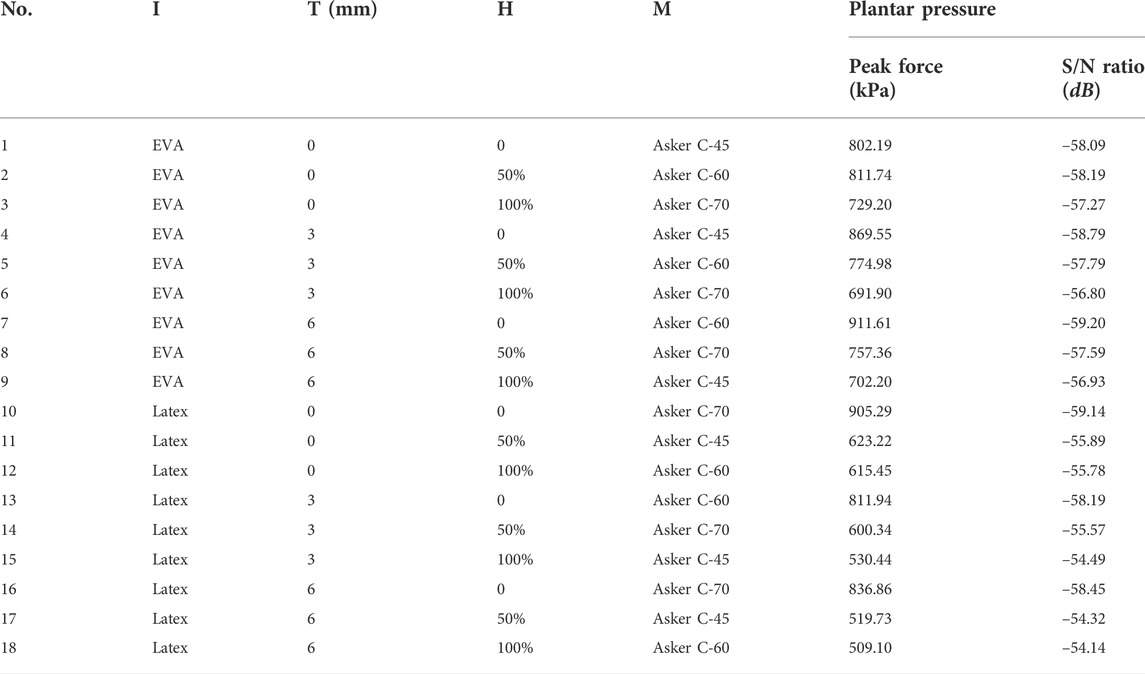
There were four design factors: the midsole hardness (M, 3 levels), the insole material (I, 2 levels), the insole thickness (Fontanella et al., 2013) (T, 3 levels), and a conforming heel-cup (Goske et al., 2006) (H, 3 levels). Detailed combinations are listed in Table 2, demonstrating a total of 54 possible combinations.
We used the statistics-based Taguchi method to optimize design parameters with a reduced number of simulations. We conducted 18 simulations to calculate the effect of design factors based on the orthogonal array L18 (21 × 33) generated by Minitab (Version 17.0, Minitab, LLC, State College, PA, United States). After that, if the optimal design combination was not present within the 18 simulations, a further simulation was conducted to perform the best cushioning combination in this study. Thus, the peak pressure of the rearfoot was predicted through at least 18 FE analyses. The mean effect of the respective level of the four design factors on the mechanical responses was computed using Minitab. Considering that our goal was reduced plantar pressure, Taguchi’s “the smaller the better” signal-to-noise (S/N ratio) calculation was employed to measure simulation outcome. An analysis of variance (ANOVA) was performed, which calculated the effect of the design factors to determine the sensitivity of the respective design parameters (Rao et al., 2008; Peng et al., 2022). For the interpretation of statistical analyses, p < 0.05 indicates a statistically significant difference.
Results
Boundary condition results from running trials
The results of five running trials were analyzed and averaged: GRF was 1149 N, foot strike angle was 14°, ForceJoint was -802 N, and ankle dorsiflexion moment was 10 N/m. After dividing the moment by the arm of the Achilles tendon, ForceAT was –186 N.
Experimental validation
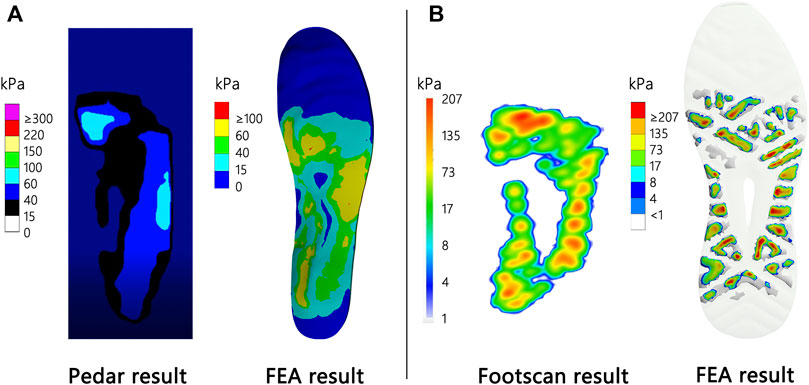
Figure 3 shows the plantar and outsole pressure results with pressure systems and the results predicted with the FE model.
As depicted in Figure 3A, the peak plantar pressure was 95 kPa, i.e., 5 kPa less than the FE result. As revealed by the results, the main pressure positions of the plantar were distributed at the 1st and 2nd metatarsophalangeal joints and the lateral longitudinal arch of the foot.
As depicted in Figure 3B, the peak of plantar pressure was 207 kPa, i.e., 9 kPa less than the FE result. From the distribution results, the main pressure positions of the outsole were distributed at the heel, metatarsal joint, and lateral longitudinal arch of the foot.
Plantar pressure
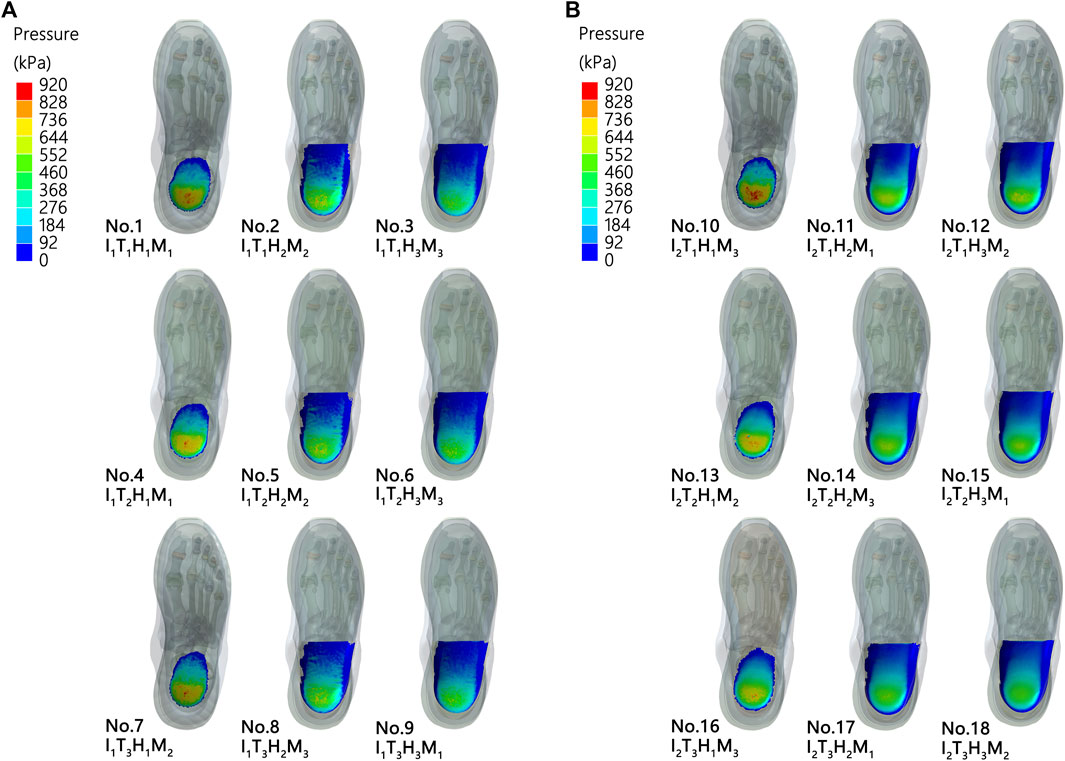
The results of the FE analyses for predicting the heel pressure distribution during landing are listed in Figure 4 and Table 3. The lowest peak pressure among the 18 simulations was simulation no. 18 (509.10 kPa, I2T3H3M1) and the highest was in simulation no. 7 (911.61 kPa, I2T3H3M1).
Taguchi method result
The signal-to-noise ratio results of plantar pressure are presented in Table 3. The highest signal-to-noise ratio among the 18 simulations was in simulation no. 18 (–54.14 dB, I2T3H3M1) and the lowest was in simulation no. 7 (–59.20 dB, I2T3H3M1).
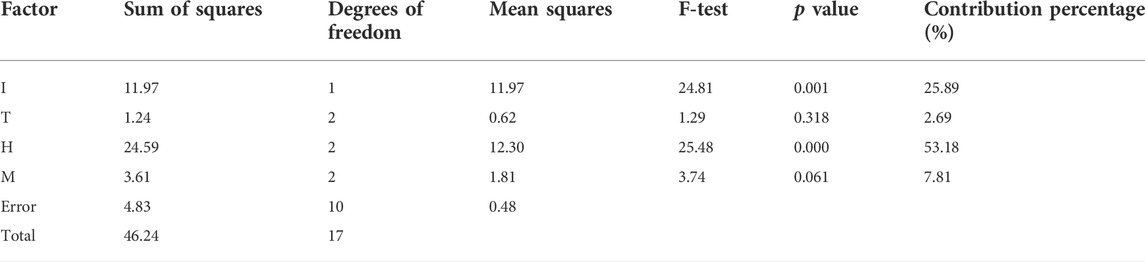
Among the four design factors, the use of a conforming heel-cup was identified as the critical design factor for peak heel pressure reduction (53.18%, p < 0.001). The insole material was the second most important factor for peak heel reduction (25.89%, p = 0.001). The descending order of percentage contribution was conforming heel-cup, insole material, midsole material, and insole thickness (Table 4).
The main effect plot further indicates the respective effects of each design factor on reducing heel pressure (Figure 5).
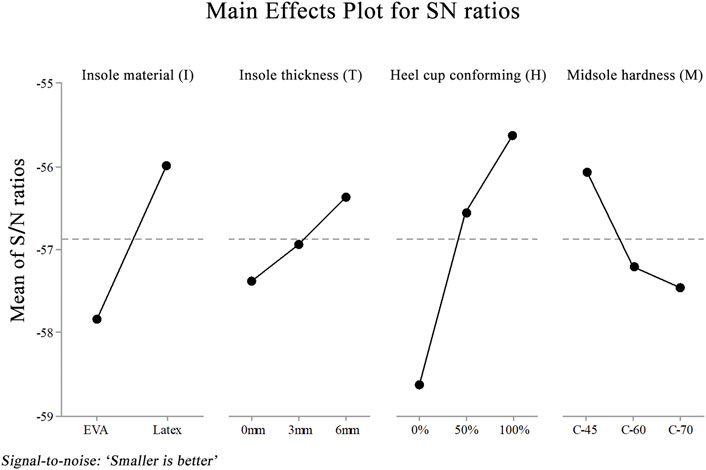
FIGURE 5. S/N graph for peak pressure. The X axis shows the different levels of each design factor. The Y axis shows the values of the S/N ratio.
Optimal combination
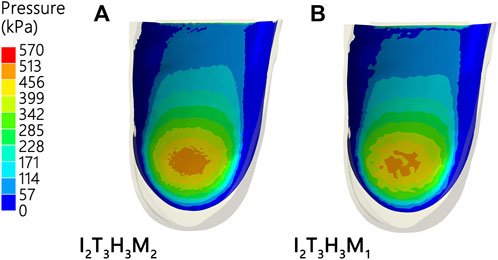
An optimal combination to reach the lowest planter pressure was predicted based on the Taguchi method, which consisted of I2T3H3M1 (Figure 6).
Table 5 presents a comparison of no. 18 (i.e., the best combination among the 18 simulations) with the optimal design result, which shows that the pressure for the optimal combination is a 9-kPa lower heel pressure than that in the no. 18 combination. Good agreement was observed between the prediction and the FE result under the optimal design, revealing that the peak force is lower than any of the peak force data presented in Table 3.
Discussion
This study investigated the influence of four factors of running shoe design in reducing plantar pressure during heel-strike running. The study adds to the current body of literature of FE analysis on the impact during running through a complete foot–shoe model instead of a partial model, as well as the testing of shoe parameters with the Taguchi method. The first hypothesis, that all design parameters significantly lower heel pressure, was partially supported, as only the conforming heel-cup and insole material were significant. The second hypothesis, that there is an optimal design to minimize peak heel pressure, was supported. The latex material, 6 mm insole, 100% conforming heel-cup, and midsole hardness of type Asker C-45 were identified as the optimal combination that maximally enhanced the cushioning ability upon heel landing. These findings contribute to a better and more efficient shoe design to reduce the risk of running injuries.
The comparison of FE-predicted pressure and experiment measurements during standing or walking was broadly used in foot finite model validation (Cheung and Zhang, 2008; Hsu et al., 2008; Yu et al., 2008; Yu et al., 2016; Li et al., 2018; Peng et al., 2021a). Our results of validation indicated that the FE-predicted pressure and force distribution have good agreement with results from the Pedar and the Footscan system. Our FE-predicted pressure was 4.3 and 5.3% higher than the Pedar and Footscan system, respectively. The error was less than 10% and acceptable (Zhang et al., 2020), explained by the fact that the higher number of nodes used in the FE model than the number of sensors in experimental measurements may increase the pressure result (Hsu et al., 2008; Yu et al., 2008; Li et al., 2018). Moreover, the optimum combination result from the Taguchi method showed a minimal difference to the FE-predicted results (0.3–1.8%; Table 5), indicating no hidden interaction effects in the FE model. Taken together, the foot–shoe FE model was considered accurate enough to investigate the design feature combinations.
We observed different effects of shoe design factors on peak heel pressure. In the descending order of effect were the conforming heel-cup, insole material, midsole hardness, and insole thickness. The conforming heel-cup result is consistent with previous studies (Bus et al., 2004; Tsung et al., 2004; Cheung and Zhang, 2008). The predicted results revealed that the conforming heel-cup achieved the highest contribution rate (53.18%) among the four design factors in the peak plantar pressure during heel contact. Furthermore, it significantly reduced the peak plantar pressure (p < 0.001). The 100% conforming heel-cup maximized the heel contact area and limited the deformation of plantar soft tissue (Chen et al., 2003; Goske et al., 2006) to achieve the effective dispersion of stress. The softer insole material significantly reduced the peak plantar pressure (p = 0.001), consistently with other studies using the static stand model (Goske et al., 2006; Cheung and Zhang, 2008; Luo et al., 2011). The insole material had a secondary contribution (25.89%) to the change in the peak plantar pressure, and the application of latex could significantly reduce the excessive heel pressure to a greater extent than does EVA, the latter being commonly used in various orthopedic insoles owing to its good deformability. The possible reason is that the use of latex materials significantly increases the strain of the insole and heel-cup when impacted. Specifically, the large strain of latex material increases the deceleration distance (Clarke et al., 1983; Kaelin et al., 1985; Bennrtt and Ker, 1990); the insole and the heel-cup together constitute a shock absorption buffer of nonlinear elastic material.
The result of midsole hardness was consistent with the thickness of the insole. Although neither of the parameters was significant, trends were observed. The contribution rate of the midsole hardness was 7.81% (p = 0.061). The softer the midsole, the lower the plantar pressure, as the former yields greater deformation to reduce the impact of ground reaction forces on the plantar. At present, the midsole hardness of running shoes on the market has usually been from type Asker C-38 to Asker C-70 (Table 6). Thus, changing the hardness has a limited effect on plantar pressure. More elastic midsole material under the same hardness must be considered by shoe manufacturers. The thicker the insole, the lower the plantar pressure (Birke et al., 1994; Linge and Klenerman, 1996; Cheung and Zhang, 2008). In contrast, no significant difference was observed (p = 0.318), and the lowest contribution (2.69%) was identified. Due to the application of the reverse engineering shoe model, the choice of insole thickness is limited, giving the insole thickness a smaller role in reducing plantar pressure than previously expected (Chatzistergos et al., 2015).
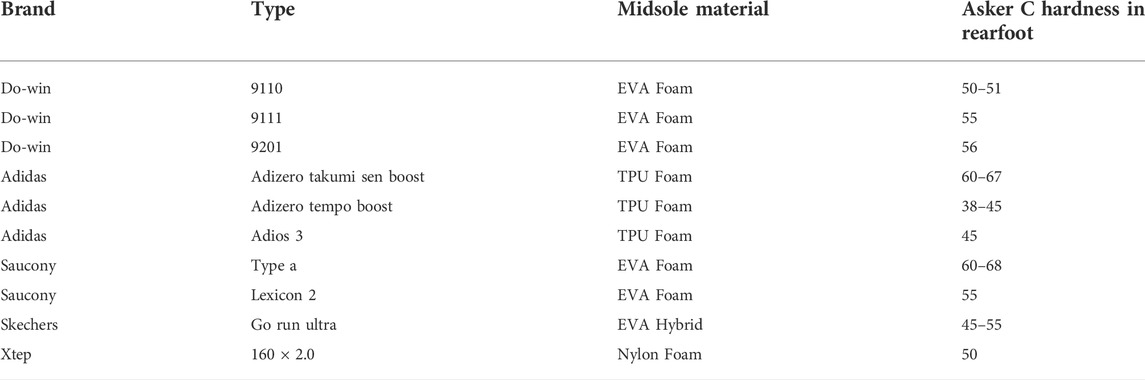
TABLE 6. Hardness characteristics of midsole materials of some sport shoes (Fu et al., 2021).
The optimal design combination obtained by the FE analysis was compared with the predicted value of the minimum plantar pressure in 18 combinations (Table 5; Figure 6). The peak plantar pressure (1.8%) and S/N ratio (0.3%) in the optimal design combination were reduced as compared with the no. 18 result. The FE results of the peak plantar pressure (Error: 1.54 kPa, 0.31%) and S/N ratio (Error: 0.02 dB, 0.03%) of the optimal design combination were basically consistent with the results predicted using the Taguchi method. We therefore suggest that the design factors of running shoes selected in this study are effective as well as the optimal design combination model calculated by the Taguchi method. The optimal design combination obtained by the Taguchi method significantly reduces the peak plantar pressure of heel landing in the selection of design parameters of running shoes.
The heel-cup conforming design is considered the critical factor for the reduction of plantar pressure, followed by the insole material. These two factors pertain to additional modifications that do not alter the structure of running shoes. The development of customized heel-cups and the selection of different insole materials are effective in the reducing peak plantar pressure during running. Compared to shoe midsole hardness and running surface modifications, a heel-cup conforming design is more cost- and time-efficient for reducing the damage caused by the repeated impact on the heel. For shoe manufacturers, modifying the midsole hardness and the insole thickness brings limited advantages, whereas this situation can be changed by replacing EVA materials with more elastic ones.
Our study has several limitations. The first limitation is the single test subject design, which limits the generalization of results. Considering the complexity of the shoe FE model, single subject studies are often used in existing foot-related FE studies (Chatzistergos et al., 2015; Wen-Ming et al., 2015; Hannah et al., 2016; Van Waerbeke et al., 2022), especially those involving the Taguchi method (Cheung and Zhang, 2008; Zhang et al., 2020; Anggoro et al., 2021; Peng et al., 2022). In the present study, we used a classical static standing FE model to verify the effectiveness of the model. A Taguchi verification experiment (Rao et al., 2008) was conducted to assess optimal combinations. Moreover, the high number of foot FE elements and the complete foot–shoe model contributed to model fidelity, which helps address external validity issues (Wong et al., 2021; Peng et al., 2022). The second limitation is that a restricted number of midsole factors were considered in this study. Different midsole materials, such as the carbon fiber insert and midsole structure (e.g., Nike Vaporfly 4% (Burns and Tam, 2020)), are available on the market. Future research must further consider these factors to accommodate changes in the design and function of running shoes. The third limitation is that our study simplified plantar fascia as five tension-only springs. Compared to studies that built the geometry of the plantar fascia (Peng et al., 2022; Van Waerbeke et al., 2022) and that considered the interaction between plantar fascia and the encapsulated soft tissue (Peng et al., 2021b), our FE model could only be applied and sustained load in the axial direction but not in the cross-sectional direction that may underestimate the stress of the fascia and the insertion points. The last limitation is that our study uses a quasi-static FE model, which is easier than a dynamic FE model, which could also account for the inertia, loading rate, viscoelasticity of materials, etc. Dynamic FE models have been exploited to investigate foot trauma (Shin et al., 2012; Wong et al., 2016; Chen et al., 2019). Due to the complexity of dynamic FE modeling and the multi-models needed to be constructed with the Taguchi method, rarely do FE studies consider both dynamic modeling and the Taguchi method. Future studies should consider discovering the relationship between shoe design factors and cushion effect from heel contact until toe off, which will result in the generation of shoe designs suitable for recommendation to shoe manufacturers.
Conclusion
To enhance the cushioning effect of running shoes during heel landing, a better conforming heel-cup and a softer insole should be considered. The results from this study suggest that runners who want to relieve plantar pressure should consider a custom insole with a conforming heel-cup.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by the Institutional Review Board Beijing Sport University (Number: 2021176H). The patients/participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
ZY, HL, FQ, and KZ conceived the experiment. XW facilitated patient recruitment and the CT scan. ZY reconstructed the model and conducted the FE analysis. ZZ and CC conducted the material and gait experiment and analysis. ZY and SY conducted the data analysis and wrote the article. All authors contributed to revising and editing this article.
Conflict of interest
ZZ was employed by the company Anta (China) Co., Ltd. Anta Sports Science Laboratory.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Actis, R. L., Ventura, L. B., Lott, D. J., Smith, K. E., Commean, P. K., Hastings, M. K., et al. (2008). Multi-plug insole design to reduce peak plantar pressure on the diabetic foot during walking. Med. Biol. Eng. Comput. 46 (4), 363–371. doi:10.1007/s11517-008-0311-5
Andréasson, G., and Peterson, L. (1986). Effects of shoe and surface characteristics on lower limb injuries in sports. Int. J. Sport Biomechanics 2 (3), 202–209. doi:10.1123/ijsb.2.3.202
Anggoro, P., Bawono, B., Jamari, J., Tauviqirrahman, M., and Bayuseno, A. (2021). Advanced design and manufacturing of custom orthotics insoles based on hybrid Taguchi-response surface method. Heliyon 7 (3), e06481. doi:10.1016/j.heliyon.2021.e06481
Ansys, I. (2013). ANSYS meshing user’s guide, Canonsburg, PA. Available at: https://www.academia.edu/27974461/ANSYS_Meshing_Users_Guide (Accessed August 31, 2022). Release 15.0 [Online].
Antunes, P., Dias, G. R., Coelho, A., Rebelo, F., and Pereira, T. (2008). Hyperelastic modelling of cork-polyurethane gel composites: Non-linear FEA implementation in 3D foot model. Mater. Sci. Forum Trans Tech Publ 587, 700–705. doi:10.4028/www.scientific.net/MSF.587-588.700()
Bennett, M. B., and Ker, R. F. (1990). The mechanical properties of the human subcalcaneal fat pad in compression. J. Anat. 171 (4), 131–138.
Birke, J. A., Foto, J. G., Deepak, S., and Watson, J. (1994). Measurement of pressure walking in footwear used in leprosy. Lepr. Rev. 65 (3), 262–271. doi:10.5935/0305-7518.19940026
Bredeweg, S. W., Kluitenberg, B., Bessem, B., and Buist, I. (2013). Differences in kinetic variables between injured and noninjured novice runners: A prospective cohort study. J. Sci. Med. Sport 16 (3), 205–210. doi:10.1016/j.jsams.2012.08.002
Burns, G. T., and Tam, N. (2020). Is it the shoes? A simple proposal for regulating footwear in road running. Br. J. Sports Med. 54 (8), 439–440. doi:10.1136/bjsports-2018-100480
Bus, S. A., Ulbrecht, J. S., and Cavanagh, P. R. (2004). Pressure relief and load redistribution by custom-made insoles in diabetic patients with neuropathy and foot deformity. Clin. Biomech. 19 (6), 629–638. doi:10.1016/j.clinbiomech.2004.02.010
Chan, Z. Y., Zhang, J. H., Au, I. P., An, W. W., Shum, G. L., Ng, G. Y., et al. (2018). Gait retraining for the reduction of injury occurrence in novice distance runners: 1-year follow-up of a randomized controlled trial. Am. J. Sports Med. 46 (2), 388–395. doi:10.1177/0363546517736277
Chatzistergos, P. E., Naemi, R., and Chockalingam, N. (2015). A method for subject-specific modelling and optimisation of the cushioning properties of insole materials used in diabetic footwear. Med. Eng. Phys. 37 (6), 531–538. doi:10.1016/j.medengphy.2015.03.009
Chen, T. L.-W., Wong, D. W.-C., Wang, Y., Lin, J., and Zhang, M. (2019). Foot arch deformation and plantar fascia loading during running with rearfoot strike and forefoot strike: A dynamic finite element analysis. J. Biomechanics 83, 260–272. doi:10.1016/j.jbiomech.2018.12.007
Chen, W.-P., Ju, C.-W., and Tang, F.-T. (2003). Effects of total contact insoles on the plantar stress redistribution: A finite element analysis. Clin. Biomech. 18 (6), S17–S24. doi:10.1016/s0268-0033(03)00080-9
Cheung, J. T.-M., An, K.-N., and Zhang, M. (2006). Consequences of partial and total plantar fascia release: A finite element study. Foot Ankle Int. 27 (2), 125–132. doi:10.1177/107110070602700210
Cheung, J. T.-M., Zhang, M., Leung, A. K.-L., and Fan, Y.-B. (2005). Three-dimensional finite element analysis of the foot during standing-a material sensitivity study. J. biomechanics 38 (5), 1045–1054. doi:10.1016/j.jbiomech.2004.05.035
Cheung, J. T., and Zhang, M. (2005). A 3-dimensional finite element model of the human foot and ankle for insole design. Arch. Phys. Med. Rehabil. 86 (2), 353–358. doi:10.1016/j.apmr.2004.03.031
Cheung, J. T., and Zhang, M. (2008). Parametric design of pressure-relieving foot orthosis using statistics-based finite element method. Med. Eng. Phys. 30 (3), 269–277. doi:10.1016/j.medengphy.2007.05.002
Cho, J. R., Park, S. B., Ryu, S. H., Kim, S. H., and Lee, S. B. (2009). Landing impact analysis of sports shoes using 3-D coupled foot-shoe finite element model. J. Mech. Sci. Technol. 23 (10), 2583–2591. doi:10.1007/s12206-009-0801-x
Clarke, T. E., Frederick, E. C., and Cooper, L. B. (1983). Effects of shoe cushioning upon ground reaction forces in running. Int. J. Sports Med. 4 (4), 247–251. doi:10.1055/s-2008-1026043
Dar, F. H., Meakin, J. R., and Aspden, R. M. (2002). Statistical methods in finite element analysis. J. biomechanics 35 (9), 1155–1161. doi:10.1016/s0021-9290(02)00085-4
Denoth, J. (1986). “Chapter: Load on the locomotor system and modelling,” in Biomechanics of Running Shoes, Editor B. Nigg (Champaign, IL: Human Kinetics Publishers), 63–116.
Drougkas, D., Karatsis, E., Papagiannaki, M., Chatzimoisiadis, S., Arabatzi, F., Maropoulos, S., et al. (2018). Gait-specific optimization of composite footwear midsole systems, facilitated through dynamic finite element modelling. Appl. Bionics Biomechanics 2018, 1–9. doi:10.1155/2018/6520314
Fontanella, C. G., Forestiero, A., Carniel, E. L., and Natali, A. N. (2013). Analysis of heel pad tissues mechanics at the heel strike in bare and shod conditions. Med. Eng. Phys. 35 (4), 441–447. doi:10.1016/j.medengphy.2012.06.008
Fu, F., Levadnyi, I., Wang, J., Xie, Z., Fekete, G., Cai, Y., et al. (2021). Effect of the construction of carbon fiber plate insert to midsole on running performance. Materials 14 (18), 5156. doi:10.3390/ma14185156
Goske, S., Erdemir, A., Petre, M., Budhabhatti, S., and Cavanagh, P. R. (2006). Reduction of plantar heel pressures: Insole design using finite element analysis. J. Biomechanics 39 (13), 2363–2370. doi:10.1016/j.jbiomech.2005.08.006
Hannah, I., Harland, A., Price, D., Schlarb, H., and Lucas, T. (2016). Evaluation of a kinematically-driven finite element footstrike model. J. Appl. Biomechanics 32 (3), 301–305. doi:10.1123/jab.2015-0002
Hasegawa, H., Yamauchi, T., and Kraemer, W. J. (2007). Foot strike patterns of runners at the 15-km point during an elite-level half marathon. J. Strength Cond. Res. 21 (3), 888–893. doi:10.1519/00124278-200708000-00040
Hoefnagels, E. M., Waites, M. D., Wing, I. D., Belkoff, S. M., and Swierstra, B. A. (2007). Biomechanical comparison of the interosseous tibiofibular ligament and the anterior tibiofibular ligament. Foot Ankle Int. 28 (5), 602–604. doi:10.3113/fai.2007.0602
Hsu, Y.-C., Gung, Y.-W., Shih, S.-L., Feng, C.-K., Wei, S.-H., Yu, C.-h., et al. (2008). Using an optimization approach to design an insole for lowering plantar fascia stress-a finite element study. Ann. Biomed. Eng. 36 (8), 1345–1352. doi:10.1007/s10439-008-9516-x
Huang, Q., Mingyu, H., Bo, X., Jianxin, W., and Jin, Z. (2018). Feasibility of application of finite element method in shoe slip resistance test. Rev. Pielarie Incaltaminte 18 (2), 139–148. doi:10.24264/lfj.18.2.9
Jeng, Y.-R., Liu, D.-S., and Yau, H.-T. (2012). Designing experimental methods to predict the expansion ratio of EVA foam material and using finite element simulation to estimate the shoe expansion shape. Mat. Trans. 53 (9), 1685–1688. doi:10.2320/matertrans.m2012178
Kaelin, X., Denoth, J., Stacoff, A., and Stuessi, E. (1985). Cushioning during running-Material tests contra subject tests. J. Biomechanics 18 (7), 553. doi:10.1016/0021-9290(85)90826-7
Kerr, B. (1983). “Footstrike patterns in distance running,” in Biomechanical aspects of sport shoes and playing surfaces: Proceedings of the international symposium on biomechanical aspects of sport shoesand playing surfaces (Calgary: University Press), 135–142.
Li, Y., Leong, K. F., and Gu, Y. (2018). Construction and finite element analysis of a coupled finite element model of foot and barefoot running footwear. Proc. Institution Mech. Eng. Part P J. Sports Eng. Technol. 233 (3), 101–109. doi:10.1177/1754337118803540
Linge, K., and Klenerman, L. (1996). A preliminary objective evaluation of leprosy footwear using in-shoe pressure measurement. Acta Orthop. belg. 62 (14), 18–22.
Luo, G., Houston, V. L., Garbarini, M. A., Beattie, A. C., and Thongpop, C. (2011). Finite element analysis of heel pad with insoles. J. Biomechanics 44 (8), 1559–1565. doi:10.1016/j.jbiomech.2011.02.083
Milner, C. E., Ferber, R., Pollard, C. D., Hamill, J., and Davis, I. S. (2006). Biomechanical factors associated with tibial stress fracture in female runners. Med. Sci. Sports Exerc. 38 (2), 323–328. doi:10.1249/01.mss.0000183477.75808.92
Morales-Orcajo, E., Becerro de Bengoa Vallejo, R., Losa Iglesias, M., Bayod, J., and Barbosa de Las Casas, E. (2018). Foot internal stress distribution during impact in barefoot running as function of the strike pattern. Comput. Methods Biomechanics Biomed. Eng. 21 (7), 471–478. doi:10.1080/10255842.2018.1480760
Nigg, B. M., and Wakeling, J. M. (2001). Impact forces and muscle tuning: A new paradigm. Exerc. Sport Sci. Rev. 29 (1), 37–41. doi:10.1097/00003677-200101000-00008
Nonogawa, M., Takeuchi, K., and Azegami, H. (2020). Shape optimization of running shoes with desired deformation properties. Struct. Multidiscipl. Optim. 62 (3), 1535–1546. doi:10.1007/s00158-020-02560-0
Novacheck, T. F. (1998). The biomechanics of running. Gait posture 7 (1), 77–95. doi:10.1016/s0966-6362(97)00038-6
Peng, Y., Niu, W., Wong, D. W.-C., Wang, Y., Chen, T. L.-W., Zhang, G., et al. (2021a). Biomechanical comparison among five mid/hindfoot arthrodeses procedures in treating flatfoot using a musculoskeletal multibody driven finite element model. Comput. Methods Programs Biomed. 211, 106408. doi:10.1016/j.cmpb.2021.106408
Peng, Y., Wang, Y., Wong, D. W.-C., Chen, T. L.-W., Chen, S. F., Zhang, G., et al. (2022). Different design feature combinations of flatfoot orthosis on plantar fascia strain and plantar pressure: A muscle-driven finite element analysis with Taguchi method. Front. Bioeng. Biotechnol. 10, 853085. doi:10.3389/fbioe.2022.853085
Peng, Y., Wong, D. W.-C., Wang, Y., Chen, T. L.-W., Zhang, G., Yan, F., et al. (2021b). Computational models of flatfoot with three-dimensional fascia and bulk soft tissue interaction for orthosis design. Med. Nov. Technol. Devices 9, 100050. doi:10.1016/j.medntd.2020.100050
Pine, D. (1991). Artificial vs natural turf: Injury perceptions fan the debate. Physician Sportsmed. 19 (8), 125–128. doi:10.1080/00913847.1991.11702235
Pohl, M. B., Hamill, J., and Davis, I. S. (2009). Biomechanical and anatomic factors associated with a history of plantar fasciitis in female runners. Clin. J. Sport Med. 19 (5), 372–376. doi:10.1097/jsm.0b013e3181b8c270
Rao, R. S., Kumar, C. G., Prakasham, R. S., and Hobbs, P. J. (2008). The Taguchi methodology as a statistical tool for biotechnological applications: A critical appraisal. Biotechnol. J. Healthcare Nutrition Technol. 3 (4), 510–523. doi:10.1002/biot.200700201
Sanzén, L., Forsberg, A., and Westlin, N. (1986). Anterior tibial compartment pressure during race walking. Am. J. Sports Med. 14 (2), 136–138. doi:10.1177/036354658601400207
Shin, J., Yue, N., and Untaroiu, C. D. (2012). A finite element model of the foot and ankle for automotive impact applications. Ann. Biomed. Eng. 40 (12), 2519–2531. doi:10.1007/s10439-012-0607-3
Siegler, S., Block, J., and Schneck, C. D. (1988). The mechanical characteristics of the collateral ligaments of the human ankle joint. Foot Ankle 8 (5), 234–242. doi:10.1177/107110078800800502
Song, Q., Ding, Z., Mao, D., Zhang, C., Sun, W., Ding, Z., et al. (2013). “The biomechanics and injury risk factors during race walking,” in 31 international conference of Biomechanics in sports.()
Torg, J. S., Quedenfeld, T. C., and Landau, S. (1974). The shoe-surface interface and its relationship to football knee injuries. J. Sports Med. 2 (5), 261–269. doi:10.1177/036354657400200502
Tsung, B. Y., Zhang, M., Mak, A. F., and Wong, M. W. (2004). Effectiveness of insoles on plantar pressure redistribution. J. Rehabilitation Res. Dev. 41 (6), 767. doi:10.1682/jrrd.2003.09.0139
Van Mechelen, W. (1992). Running injuries. A review of the epidemiological literature. Sports Med. 14 (5), 320–335. doi:10.2165/00007256-199214050-00004
Van Waerbeke, C., Jacques, A., Berton, E., and Rao, G. (2022). Inter-strides variability affects internal foot tissue loadings during running. Sci. Rep. 12 (1), 4227. doi:10.1038/s41598-022-08177-1
Vaughan, C. L., Davis, B. L., and Jeremy, C. (1999). Dynamics of human gait. Cape Town: Kiboho Publishers.
Wen-Ming, C., Sung-Jae, L., and Lee, P. V. S. (2015). Plantar pressure relief under the metatarsal heads - therapeutic insole design using three-dimensional finite element model of the foot. J. Biomechanics 48 (4), 659–665. doi:10.1016/j.jbiomech.2014.12.043
Willems, T. M., De, C. D., Delbaere, K., Vanderstraeten, G., De, C. A., and Witvrouw, E. (2006). A prospective study of gait related risk factors for exercise-related lower leg pain. Gait Posture 23 (1), 91–98. doi:10.1016/j.gaitpost.2004.12.004
Willems, T., Witvrouw, E., Delbaere, K., De Cock, A., and De Clercq, D. (2005). Relationship between gait biomechanics and inversion sprains: A prospective study of risk factors. Gait posture 21 (4), 379–387. doi:10.1016/j.gaitpost.2004.04.002
Wong, D. W.-C., Chen, T. L.-W., Peng, Y., Lam, W.-K., Wang, Y., Ni, M., et al. (2021). An instrument for methodological quality assessment of single-subject finite element analysis used in computational orthopaedics. Med. Nov. Technol. Devices 11, 100067. doi:10.1016/j.medntd.2021.100067
Wong, D. W.-C., Niu, W., Wang, Y., and Zhang, M. (2016). Finite element analysis of foot and ankle impact injury: Risk evaluation of calcaneus and talus fracture. PloS one 11 (4), e0154435. doi:10.1371/journal.pone.0154435
Yu, J., Cheung, J. T.-M., Fan, Y., Zhang, Y., Leung, A. K.-L., and Zhang, M. (2008). Development of a finite element model of female foot for high-heeled shoe design. Clin. Biomech. 23, S31–S38. doi:10.1016/j.clinbiomech.2007.09.005
Yu, J., Wong, W. C., Zhang, H., Luo, Z. P., and Zhang, M. (2016). The influence of high-heeled shoes on strain and tension force of the anterior talofibular ligament and plantar fascia during balanced standing and walking. Med. Eng. Phys. 38 (10), 1152–1156. doi:10.1016/j.medengphy.2016.07.009
Zadpoor, A. A., and Nikooyan, A. A. (2011). The relationship between lower-extremity stress fractures and the ground reaction force: A systematic review. Clin. Biomech. 26 (1), 23–28. doi:10.1016/j.clinbiomech.2010.08.005
Keywords: rearfoot strike, shoe design, plantar pressure, finite element method, Taguchi method
Citation: Yang Z, Cui C, Wan X, Zheng Z, Yan S, Liu H, Qu F and Zhang K (2022) Design feature combinations effects of running shoe on plantar pressure during heel landing: A finite element analysis with Taguchi optimization approach. Front. Bioeng. Biotechnol. 10:959842. doi: 10.3389/fbioe.2022.959842
Received: 02 June 2022; Accepted: 15 August 2022;
Published: 13 September 2022.
Edited by:
Alexandros E. Tsouknidas, University of Western Macedonia, GreeceReviewed by:
Duo Wai-Chi Wong, Hong Kong Polytechnic University, Hong Kong SAR, ChinaMaria Papagiannaki, Aristotle University of Thessaloniki, Greece
Copyright © 2022 Yang, Cui, Wan, Zheng, Yan, Liu, Qu and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kuan Zhang, a3poYW5nQGNjbXUuZWR1LmNu
 Zihan Yang
Zihan Yang Chuyi Cui5
Chuyi Cui5 Songhua Yan
Songhua Yan Kuan Zhang
Kuan Zhang