- 1The Sixth Affiliated Hospital of Xinjiang Medical University, Urumqi, China
- 2The Affiliated Tumor Hospital of Xinjiang Medical University, Urumqi, China
- 3Shandong Public Health Clinical Center, Shandong University, Jinan, China
The dynamics of disc degeneration was analyzed to determine the effect of disc degeneration at the L4-L5 segment on the dynamic characteristics of the total lumbar spine. A three-dimensional nonlinear finite element model of the L1-S1 normal lumbar spine was constructed and validated. This normal model was then modified to construct two degeneration models with different degrees of degeneration (mild, moderate) at the L4-L5 level. Modal analysis, harmonic response analysis, and transient dynamics analysis were performed on the total lumbar spine when experiencing following compressive loading (500 N). As the degree of disc degeneration increased, the vibration patterns corresponding to the first three orders of the model’s intrinsic frequency were basically unchanged, with the first order being in the left-right lateral bending direction, the second order being in the forward-flexion and backward-extension direction, and the third order being in the axial stretching direction. The nucleus pulposus pressure peaks corresponding to the first order intrinsic frequency for the harmonic response analysis are all on the right side of the model, with sizes of 0.053 MPa, 0.061 MPa, and 0.036 MPa, respectively; the nucleus pulposus pressure peaks corresponding to the second order intrinsic frequency are all at the rear of the model, with sizes of 0.13 MPa, 0.087 MPa, and 0.11 MPa, respectively; and the nucleus pulposus pressure peaks corresponding to the third order intrinsic frequency are all at the front of the model, with sizes of 0.19 MPa, 0.22 MPa, and 0.22 MPa, respectively. The results of the transient analysis indicated that over time, the response curves of the healthy model, the mild model, and the moderate model all exhibited cyclic response characteristics. Intervertebral disc degeneration did not adversely affect the vibration characteristics of the entire lumbar spine system. Intervertebral disc degeneration significantly altered the dynamics of the degenerative segments and their neighboring normal segments. The process of disc degeneration gradually shifted the load from the nucleus pulposus to the annulus fibrosus when the entire lumbar spine was subjected to the same vibratory environment.
1 Introduction
Intervertebral disc degeneration is a progressive lesion that leads to changes in the geometry and biomechanical behavior of the disc, ultimately affecting its ability to transmit and distribute loads (Adams and Roughley, 2006). Lumbar disc degeneration is one of the most common causes of low back pain. Its causes are complex and multifactorial, including aging, abnormal mechanical loading and accidental injury (Luoma et al., 2000; Wilke et al., 2006; Diwan and Melrose, 2023). Early signs of disc degeneration include a decrease in the amount of water in the nucleus pulposus, which leads to a gradual change in the nucleus pulposus from a fluid to a solid state, as well as causing a decrease in disc height and swelling pressure (Urban and McMullin, 1988; Frobin et al., 2001; Benneker et al., 2005). As disc degeneration progresses, the increase in collagen in the nucleus pulposus leads to fibrosis, causing the nucleus pulposus to become rigid and the border between the annulus fibrosus and the nucleus pulposus to gradually blur (Adams, 2004; Inoue and Espinoza Orias, 2011). Changes in disc biochemistry and mechanical properties will inevitably affect spinal biomechanical properties.
For the lumbar spine, in a vibration environment, the stresses and strains in the lumbar spine tissues are equivalent to 2–3 times the size of the static load, and prolonged exposure to vibration may lead to degenerative changes in the lumbar joints of drivers. (Li et al., 2015; Taghizadeh-Alisaraei, 2017). Significant increase in disc stress and peak Von-Mises stress compared to normal disc (Li et al., 2017). Thus, overexposure to vibration is considered to be a major contributor to degenerative changes in the lumbar spine joints of drivers (Bovenzi and Betta, 1994; Jiang et al., 2021).
Numerous in vitro experimental studies have analyzed the effects of disc degeneration on the biomechanics of the spine, including the range of motion (ROM) of the lumbar spine (Mimura et al., 1994; Fujiwara et al., 2000a; Kettler et al., 2011), the small joint facet contact forces (Fujiwara et al., 2000b; Hicks et al., 2009), the intravertebral disc pressures (IDPs), and the distribution of stresses in the vertebral body (McNally and Adams, 1992; Johansson et al., 2017). For example, experimental studies by Mimura et al. (Mimura et al., 1994) and Kettler et al. (Kettler et al., 2011) found that the ROM of the degenerated segments during forward flexion-backward extension and left-right lateral bending decreases with increasing disc degeneration. Ruberne et al. (Ruberté et al., 2009) developed a finite element model of lumbar vertebrae L1-S1 with different degrees of degeneration in a single disc (L4-L5) and found that the peak Von-Mises stresses and tangential forces on the annulus fibrosus matrix of its adjacent segments during forward flexion-backward extension, right and left lateral bending, and axial torsion increase with increasing disc degeneration. However, these previous studies have mainly analyzed the effects of disc degeneration under static loading, and have not yet addressed the effects of disc degeneration on the biomechanical properties of the lumbar spine system in a vibration environment. Therefore, this study will focus on the effects of disc degeneration on the biomechanical properties of the lumbar spine system in a vibration environment.
2 Materials and methods
2.1 Geometric modeling
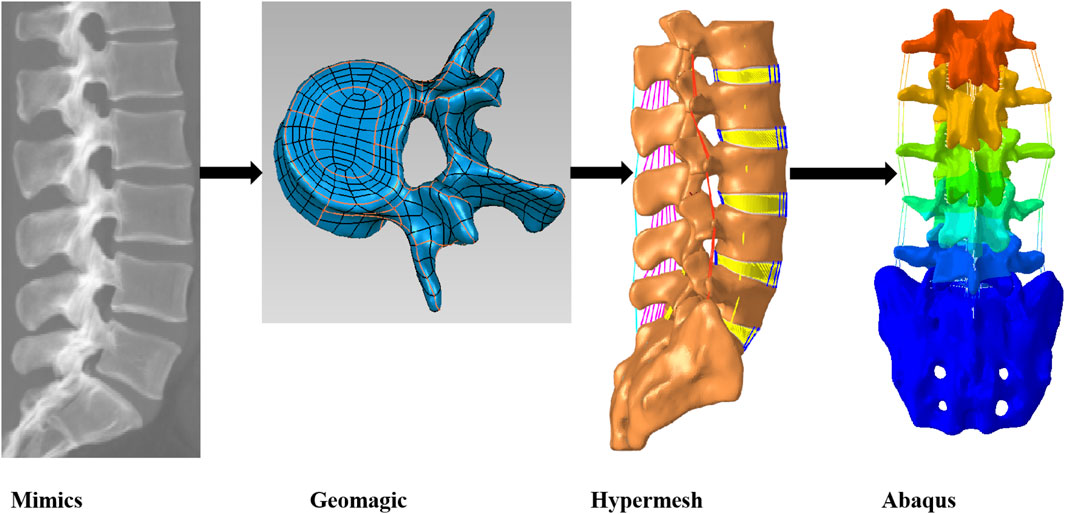
The volunteers for this study had detailed knowledge of the study and their written consent was obtained. The technical flow of this paper is shown in (Figure 1). A total of 511 DICOM images were acquired by CT from the upper edge of L1 to the sacrum with a slice spacing of 0.629 mm.Based on the CT scan dataset, a 3D geometric model of the lumbar spine was obtained by separating the target region and performing 3D reconstruction by setting a grayscale threshold and manually modifying it in Mimics 21.0 (Materialise, Belgium). The 3D model in Mimics software was exported in STL format to Geomagic Studio 12.0 (Geomagic, USA) for geometric routing and surface smoothing optimization, as well as reverse engineering to create the disc contour. Mesh delineation and material property assignment of the model was done in Hypermesh 2022 (Altair, USA), and finite element analysis calculations were performed using Abaqus 2021 (Simulia, USA) software.
2.2 Mesh delineation and material property assignment for finite element models
The complete nonlinear finite element model shown in (Figure 2) includes cortical bone, cancellous bone, posterior structures, intervertebral discs, endplates, and ligaments. Cortical bone and cancellous bone are considered orthogonal anisotropic materials (Schmidt et al., 2007). Cortical bone thickness and endplate thickness were both set to 1 mm and defined as C3D8R elements (Li et al., 2023). The endplate mesh is connected to the vertebral body and the intervertebral disc mesh by a co-nodal method. The intervertebral disc consists of the nucleus pulposus, the fibrous matrix and the annulus fibrosus, with the nucleus pulposus accounting for approximately 44% of the disc volume (Sengupta, 2017). The fibrous ring consists of 6 layers of T3D2 elements of decreasing rigidity from lateral to medial (Table 1). The ligaments included seven ligament models of the capsular ligament (CL), intertransverse ligament (ITL), supraspinous ligament (SL), interspinous ligament (ISL), ligamentum flavum (LF), anterior longitudinal ligament (ALL), and posterior longitudinal ligament (PLL), and the ligament was modeled as a tensile-only truss (Polikeit et al., 2003).
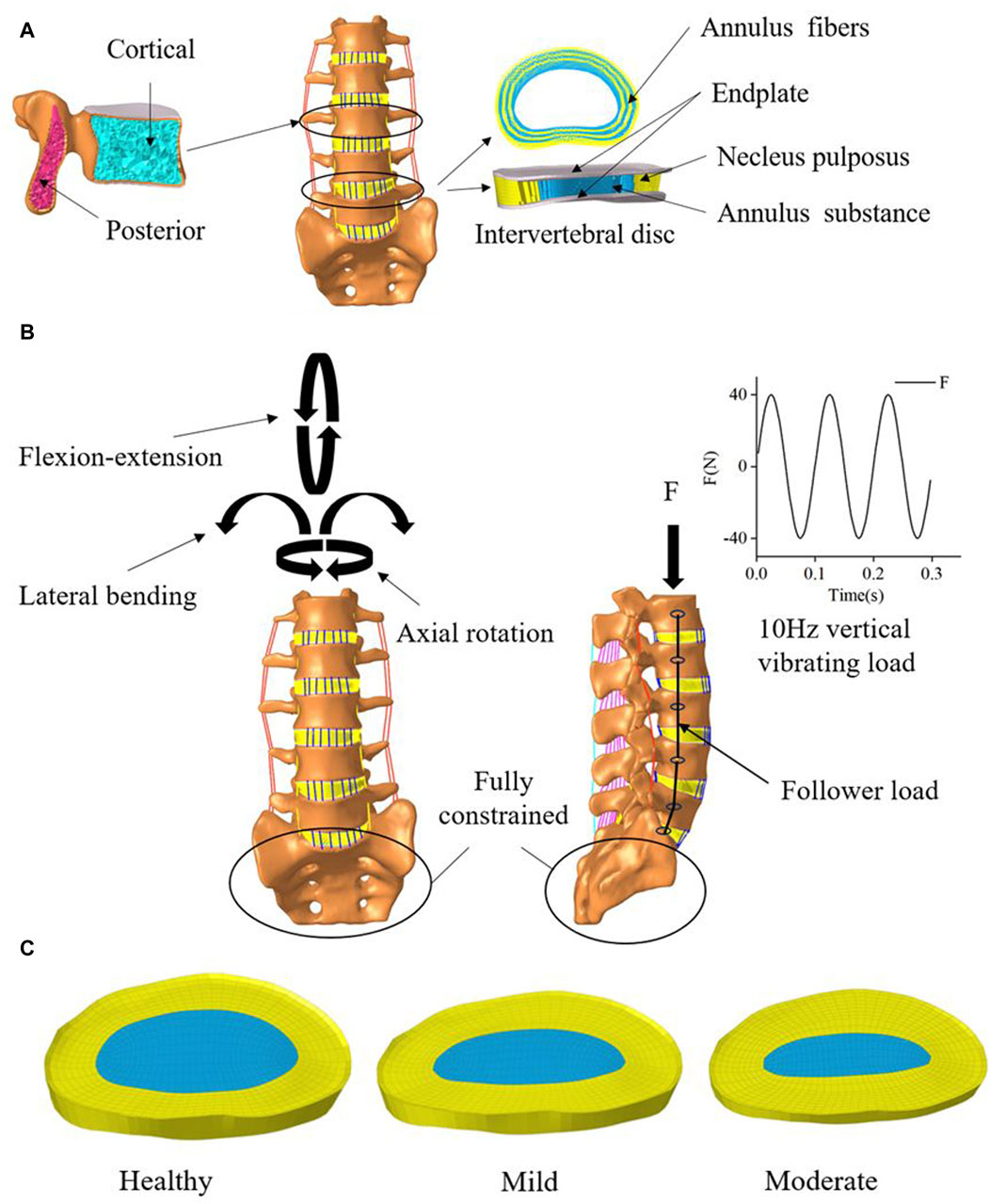
Figure 2. Mesh delineation and material property assignment for finite element models. (A) vertebral and Intervertebral disc model. (B) Boundary conditions (C) Intervertebral discs with 2 levels of degeneration.
2.3 Modeling of lumbar disc degeneration
In this study, On the basis of the established health model, two intervertebral discs with different degrees of degeneration were simulated. we modified two variables of disc morphology (disc height, nucleus pulposus area) and changed the material properties of the disc and adjacent endplates (Cai et al., 2020) as shown in Tables 2, 3. We constructed two models simulating mild and moderate lumbar degeneration at the L4-L5 level (Figure 2). The L4-L5 segment was chosen for disc degeneration simulation because the incidence of disc degeneration is higher in this segment (Ruberté et al., 2009).

Table 2. Changes in three variables of lumbar disc geometry morphology (Cai et al., 2020).

Table 3. Changes in material properties of lumbar intervertebral discs with different levels of degeneration (Cai et al., 2020).
2.4 Boundary conditions and contact settings
In this study, all the degrees of freedom at the bottom of S1 are fixed, a reference point is established at the upper surface of L1 and coupled to the upper surface node of L1. During the calibration and validation process, the ROM and the degree of deformation were calculated for pure torque loads (8 N-m flexural moment, 6 N-m transverse bending moment, 4 N-m rotational moment as in Figure 2) and 1200 N axial following loads. The accuracy of the normal model was verified by comparing the motions of each segment of the normal model with the previous sample data and finite element data (Renner et al., 2007; Park, Kim and Kim, 2013). In subsequent simulations, a following preload of 500 N was applied to the entire lumbar spine system (Figure 2) to simulate the upper body weight of the human body (Du et al., 2016). The model is then subjected to prestressed modal analysis, taking the first three orders of intrinsic frequency and mode of vibration below 30 Hz. Based on the modal analysis, the dynamic response of the healthy lumbar spine and disc degeneration lumbar spine under vibratory force excitation was further investigated. The modal steady-state dynamic analysis method was used to analyze the patient’s thoracolumbar sacral segment (L1-S1). Based on the modal analysis, the harmonic response analysis was performed using an equivalent damping ratio of 0.08. All degrees of freedom of the lower surface of the sacral vertebral body were fixed. A sinusoidal axial force of 40 N was applied to the upper surface of the vertebral body L1 with a frequency range of 0–30 Hz (Li et al., 2011). According to the modal analysis, the equivalent damping ratio for the transient analysis was also 0.08. All degrees of freedom of the lower surface of the sacral vertebral body were fixed. A sinusoidal axial force of 40N was applied to the upper surface of the vertebral body L1 (Figure 2) and the frequency was set to 10 Hz (Guo and Li, 2020).
3 Results
3.1 Model validation results
The current method of validating spine finite element models is mainly by comparing the ROM, mainly because the ROM of spine cadaveric specimens is easier to measure. As shown in the (Figure 3), the compression and ROM of each segment of the model are more consistent with Renner’s specimen experiment (Renner et al., 2007), which verifies the validity of the model.
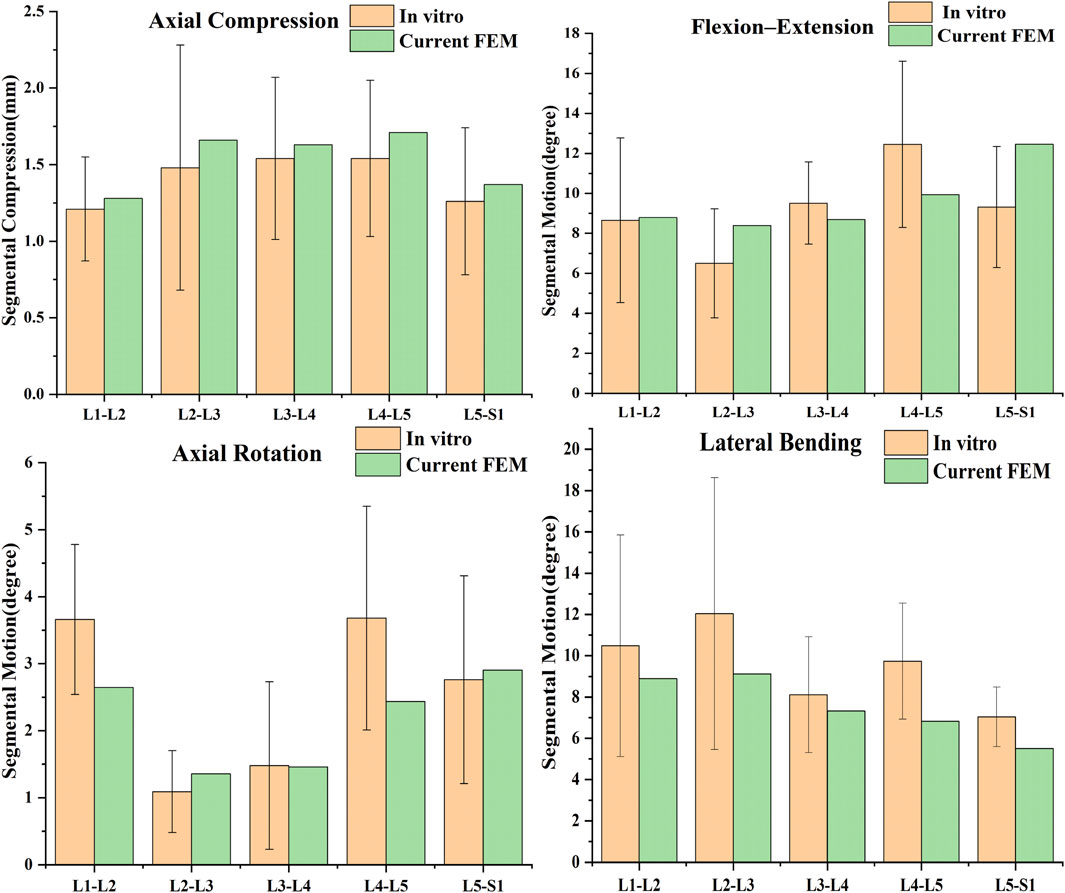
Figure 3. Comparison of predicted results by the current FE model with previous studies (Renner et al., 2007).
3.2 Modal analysis results
The results of the modal analysis showed (Figure 4) that the first order intrinsic frequency of the model increased from 1.16 Hz to 1.26 Hz–1.32 Hz for the healthy model to the mildly degenerating disc model and the moderately degenerating model, the second order intrinsic frequency of the model increased from 1.84 Hz to 1.93 Hz–1.97 Hz, and the third order intrinsic frequency of the model increased from 13.22 Hz to 13.44 Hz–13.7 Hz, the vibration patterns corresponding to the first three orders of the model’s intrinsic frequency are basically unchanged, with the first order being in the left-right lateral bending direction, the second order being in the forward-backward direction, and the third order being in the vertical direction.
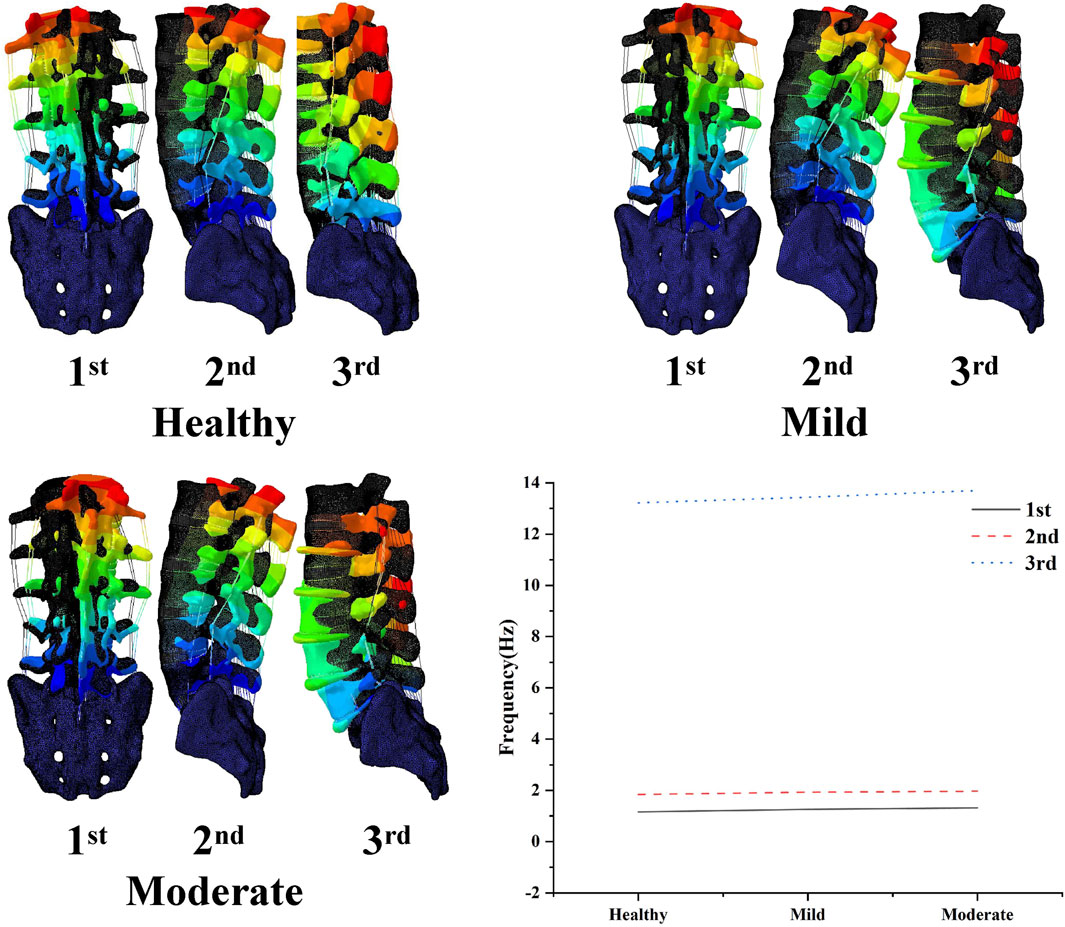
Figure 4. Variation of the first three orders of modal amplitude and resonance frequency of the lumbar spine model with different levels of degeneration.
3.3 Harmonic response analysis results
The results of the harmonic response analysis showed (Figure 5) that both the healthy and lumbar degeneration models showed varying degrees of wave crests at the displacement amplitudes corresponding to the first three orders of the intrinsic frequency, the displacement amplitude component of the healthy model at the first order intrinsic frequency is 0.14 mm maximum in the U1 direction, the displacement amplitude component at the second order intrinsic frequency has a maximum of 0.38 mm in the U2 direction, and the displacement amplitude component at the third order intrinsic frequency has a maximum of 0.26 mm in the U3 direction, the displacement amplitude component of the mildly degenerate model at the first order intrinsic frequency has a maximum of 0.15 mm in the U1 direction, the displacement amplitude component at the second order intrinsic frequency has a maximum of 0.24 mm in the U2 direction, and the displacement amplitude component at the third order intrinsic frequency has a maximum of 0.25 mm in the U3 direction, the displacement amplitude component of the moderately degenerate model at the first order intrinsic frequency has a maximum of 0.09 mm in the U1 direction, the displacement amplitude component at the second order intrinsic frequency has a maximum of 0.26 mm in the U2 direction, and the displacement amplitude component at the third order intrinsic frequency has a maximum of 0.26 mm in the U3 direction.
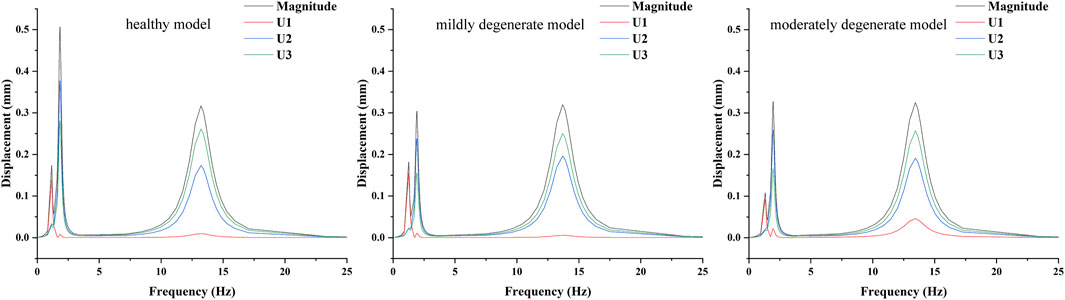
Figure 5. Mean displacement amplitude response curves of the nucleus pulposus fibrous ring at L4-L5 degenerative segments in lumbar spine models with different degrees of degeneration.
The disc pressures in the nucleus pulposus of the L4-L5 intervertebral disc corresponding to the three wave peaks in the harmonic response analysis are shown in (Figure 6), and the distribution of the amplitude of the disc pressures corresponding to the first three orders of the intrinsic frequency is basically the same for the healthy model and the mildly degenerated model and the moderately degenerated model, the maxima corresponding to the first order of the intrinsic frequency are to the right side of the model, with the sizes of 0.053 MPa, 0.061 MPa and 0.036 MPa; the maximum values corresponding to the second-order intrinsic frequency were all at the rear of the model, with sizes of 0.13 MPa, 0.087 MPa and 0.11 MPa; the maximum values corresponding to the third-order intrinsic frequency were all at the front of the model, with sizes of 0.19 MPa, 0.22 MPa and 0.22 MPa, respectively.
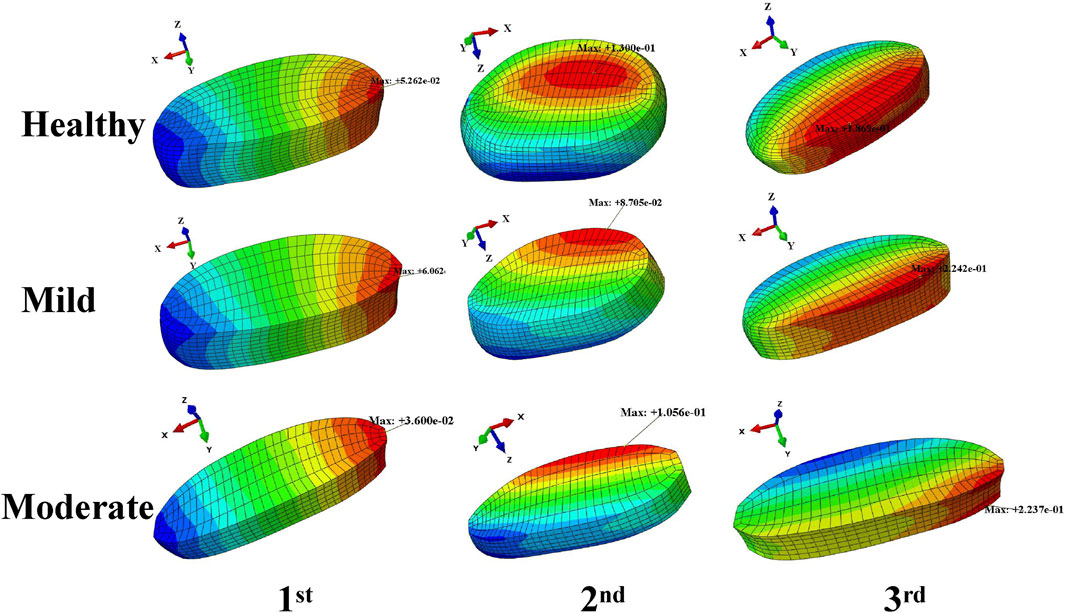
Figure 6. Distribution of medullary pressure at the peak of the displacement amplitude wave in the harmonic response analysis.
3.4 Transient analysis results
The results of the transient analysis indicated that the response curves of the healthy, mild degeneration, and moderate degeneration models exhibited cyclic response properties over time. The time-domain dynamic responses of all lumbar segments (L1-L2, L2-L3, L3-L4, L4-L5, and L5-S1) in L1-S1 for healthy, mild regression, and moderate regression as well as the results of the peak Von Mises stresses in the lumbar discs of L1-S1 under 10 Hz axial vibration loading are shown in (Figure 7). The results showed that the maximum values of the dynamic response curves of the nucleus pulposus in the L2-L3 and L4-L5 segments showed the same trend of change in the case of L4-L5 degeneration of the intervertebral discs, with the maximum pressure of the nucleus pulposus in the L2-L3 segment increasing from 0.56 MPa to 0.59 MPa and decreasing to 0.44 MPa, and that of the nucleus pulposus in the L4-L5 segment increasing from 0.55 MPa to 0.6 MPa and then decreased to 0.44 MPa, while the maximum pressure in the medulla in the L1-L2 and L3-L4 segments varied essentially the same, for example, the maximum pressure in the nucleus pulposus in the L1-L2 segment changed from 0.67 MPa to 0.67 MPa then decreased to 0.6 MPa. The peak Von-Mises stress in the L4-L5 intervertebral disc decreased from 0.54 MPa to 0.53 MPa and then increased to 0.63 MPa, and the peak Von-Mises stress in the healthy and mildly degenerated and moderately degenerated models of the L1-L2, L2-L3, and L3-L4 discs was basically unchanged, whereas the peak Von-Mises stress in the discs of the L5-S1 segments of the L5-S1 segment decreased sequentially from 0.66 MPa to 0.59 MPa–0.48 MPa. As the degree of deformation increases the degree of deformation of the fiber ring is decreasing in the anterior-posterior direction and the total displacement, the maximum displacement in the anterior-posterior direction decreases from 0.84 mm to 0.65 mm and then to 0.64 mm, and the total displacement decreases from 1.41 mm to 1.04 mm and finally to 1.0 mm.
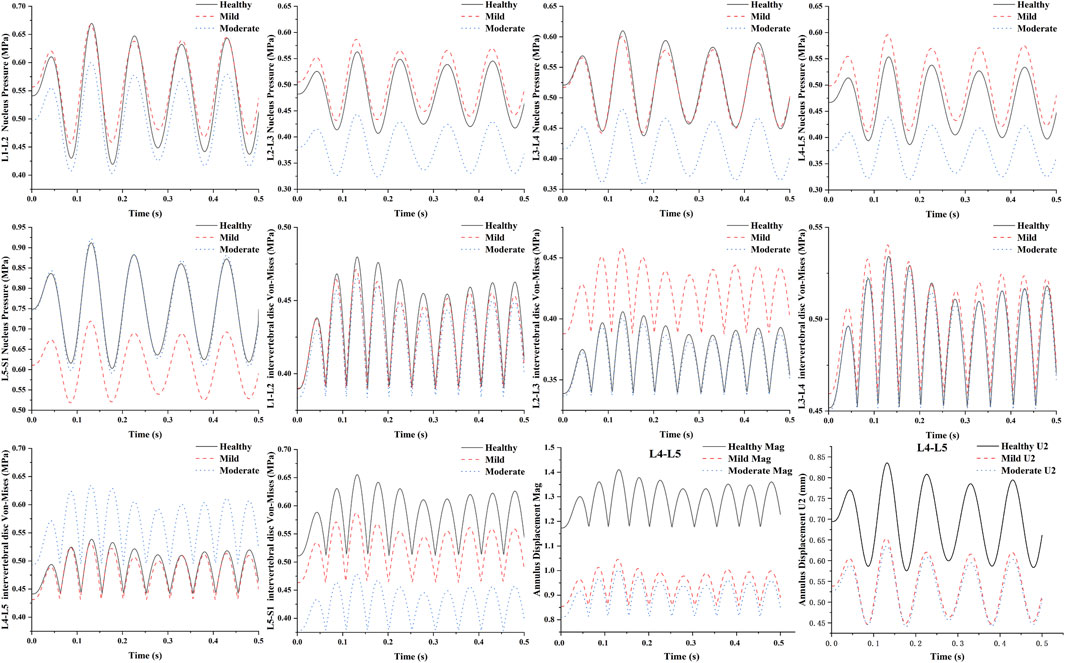
Figure 7. Time-domain dynamic response on L4-L5 lumbar segments with different degrees of degeneration under sinusoidal axial loading.
4 Discussion
In this study, a finite element model of the normal lumbar spine at the L1-S1 level was constructed based on CT images. The validity of the model was verified by comparing the finite element simulation data with previously published sample experimental data and previous finite element experimental data. A finite element model of the lumbar spine with mild versus moderate degeneration was developed by varying the geometry and material properties of the intervertebral disc at the L4-L5 segment. Three levels of intervertebral disc models were included, which included the nucleus pulposus, the material properties of the annulus fibrosus matrix and endplates, and changes in disc height parameters were more consistent with the pathologic changes of advanced disc degeneration. Using these models, we evaluated the effects of disc degeneration on vibration in the lumbar spine system.
For the degenerated L4-L5 segment, as the degree of L4-L5 disc degeneration increased, the results of the modal analysis simulation showed that the increase in the degree of single-segment disc degeneration resulted in a small increase in the low-order intrinsic frequency of the whole lumbar spine system, but the corresponding vibration patterns remained basically unchanged, with the first order being in the left-right lateral bending direction, the second order being in the forward flexion and posterior extension direction, and the third order being in the axial stretching direction. Overall, disc degeneration did not lead to a deterioration of the vibration characteristics of the entire lumbar spine system (Guo and Fan, 2017).
The results of the harmonic response analysis showed that the displacement of the annulus fibrosus in the degenerated L4-L5 lumbar segments was mainly larger in the U2 direction, with the max U2 decreasing from 0.38 mm to 0.24 mm and then increasing to 0.261 mm. With the increase in the magnitude of the disc degeneration, the pressure in the nucleus pulposus of the L4-L5 increased slightly and then decreased markedly, and the distribution of the pressure in the nucleus pulposus was basically the same, which indicated that the increase in the degree of disc degeneration would not change the distribution of the pressure in the nucleus pulposus of the degenerated discs but would change its carrying capacity. The increase in the degree of disc degeneration will not change the distribution of pressure in the nucleus pulposus of the degenerated disc, but it will change its carrying capacity, and it will make the maximum pressure in the nucleus pulposus of the intervertebral discs slightly increase by slight degeneration of the intervertebral discs, but with the increase of the magnitude of the degeneration the maximum pressure in the nucleus pulposus significantly decreases.
In this study, the amplitude of the dynamic response of the L4-L5 intramedullary pressure decreased significantly as the degree of disc degeneration increased, while the L4-L5 maximum von Mises stress increased with the degree of disc degeneration, which is consistent with the results of previous hydrostatic studies (Cai et al., 2020; Wang, Li, Huang, Xu and Fan, 2023). This phenomenon suggests that the load-bearing capacity of the nucleus pulposus continues to diminish and the load borne by the annulus fibrosus continues to increase as the degeneration increases, i.e., the total load of the disc is shifted from the nucleus pulposus to the annulus fibrosus. At the same time, in the normal segment of L5-S1, the maximum von Mises stress and intramedullary pressure also decreased with the increase of disc degeneration. The amplitude of vibratory displacement of the annulus fibrosus also decreased, which is consistent with previous studies (Guo and Fan, 2018).
There are some limitations to this study, first, the structure of the human lumbar spine is extraordinarily complex, which leads us to some simplifications and constraints in finite element analysis. This study did not consider the near circular arc contour of intervertebral discs in the sagittal plane (Cappetti, Naddeo, Naddeo and Solitro, 2015). We acknowledge that our model does not incorporate the poroelastic behavior of the IVD, nor does it capture the permeability of nutrients within the disc (Elmasry et al., 2017; Elmasry et al., 2018; Volz et al., 2022). The whole lumbar spine finite element model in this paper was developed based on the CT data of a single volunteer, and the differences in geometric morphology between individuals may lead to differences in kinetic properties. Second, due to the difficulty of accurately modeling the true geometry of the ligaments, we simplified them to one-dimensional linear truss units, and the vertebrae were simplified to orthotropic anisotropic materials. But variations in vertebral bone density arise due to differences in age, gender, and other factors among individuals, which affecting the mechanical performance of vertebrae (Al-Barghouthi et al., 2020; Garay et al., 2022). And although we employed follower load techniques to approximate the effects of muscles and mitigate their absence on the biomechanical properties of the lumbar spine, we acknowledge that this method cannot fully substitute for the actual function of muscles. In addition, this study did not measure the specific values of intervertebral disc protrusion and did not quantify the reduction of intervertebral foramen in intervertebral disc degeneration (Amirouche et al., 2015). Despite these simplifications and limitations, the study in this paper shows consistency with previous studies.
5 Conclusion
In this study, we investigated the vibrational biomechanical properties of patients with disc degeneration in the vertical direction from a kinetic point of view. Our study showed that disc degeneration did not lead to the deterioration of the vibrational properties of the whole lumbar spine system, and that disc degeneration significantly altered the changes in the kinetic properties of the degenerative segments and their neighboring normal segments, and that during the process of disc degeneration when the whole lumbar vertebrae were in the same vibrational environment, the disc loads gradually shifts toward the annulus fibrosus.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
XW: Writing–original draft, Writing–review and editing. WL: Data curation, Formal Analysis, Methodology, Validation, Writing–review and editing. YZ: Data curation, Formal Analysis, Methodology, Validation, Writing–review and editing. PM: Data curation, Formal Analysis, Methodology, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
We thank the volunteer for the participation and cooperation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adams, M. (2004). Biomechanics of back pain. Acupunct. Med. J. Br. Med. Acupunct. Soc. 22 (4), 178–188. doi:10.1136/aim.22.4.178
Adams, M., and Roughley, P. (2006). What is intervertebral disc degeneration, and what causes it? SPINE 31 (18), 2151–2161. doi:10.1097/01.brs.0000231761.73859.2c
Al-Barghouthi, A., Lee, S., Solitro, G. F., Latta, L., and Travascio, F. (2020). Relationships among bone morphological parameters and mechanical properties of cadaveric human vertebral cancellous bone. JBMR Plus 4 (5), e10351. doi:10.1002/jbm4.10351
Amirouche, F., Solitro, G. F., Siemionow, K., Drucker, D., Upadhyay, A., and Patel, P. (2015). Role of posterior elements in the disc bulging of a degenerated cervical spine. Int. J. Spine Surg. 9, 13. doi:10.14444/2013
Benneker, L., Heini, P., Anderson, S., Alini, M., and Ito, K. (2005). Correlation of radiographic and MRI parameters to morphological and biochemical assessment of intervertebral disc degeneration. Eur. spine J. official Publ. Eur. Spine Soc. Eur. Spinal Deformity Soc. Eur. Sect. Cerv. Spine Res. Soc. 14 (1), 27–35. doi:10.1007/s00586-004-0759-4
Bovenzi, M., and Betta, A. (1994). Low-back disorders in agricultural tractor drivers exposed to whole-body vibration and postural stress. Appl. Ergon. 25 (4), 231–241. doi:10.1016/0003-6870(94)90004-3
Cai, X.-Y., Sun, M.-S., Huang, Y., Liu, Z., Liu, C.-J., Du, C.-F., et al. (2020). Biomechanical effect of L<sub>4</sub>–L<sub>5</sub> intervertebral disc degeneration on the lower lumbar spine: a finite element study. Orthop. Surg. 12, 917–930. doi:10.1111/os.12703
Cappetti, N., Naddeo, A., Naddeo, F., and Solitro, G. F. (2015). Finite elements/Taguchi method based procedure for the identification of the geometrical parameters significantly affecting the biomechanical behavior of a lumbar disc. Comput. METHODS BIOMECHANICS Biomed. Eng. 19 (12), 1278–1285. doi:10.1080/10255842.2015.1128529
Diwan, A., and Melrose, J. (2023). Intervertebral disc degeneration and how it leads to low back pain. JOR Spine 6 (1), e1231. doi:10.1002/jsp2.1231
Du, C.-F., Yang, N., Guo, J., Huang, Y., and Zhang, C. (2016). Biomechanical response of lumbar facet joints under follower preload: a finite element study. BMC Musculoskelet. Disord. 17, 126. doi:10.1186/s12891-016-0980-4
Elmasry, S., Asfour, S., and Travascio, F. (2017). Effectiveness of pedicle screw inclusion at the fracture level in short-segment fixation constructs for the treatment of thoracolumbar burst fractures: a computational biomechanics analysis. Comput. METHODS BIOMECHANICS Biomed. Eng. 20 (13), 1412–1420. doi:10.1080/10255842.2017.1366995
Elmasry, S. S., Asfour, S. S., and Travascio, F. (2018). Finite element study to evaluate the biomechanical performance of the spine after Augmenting Percutaneous pedicle screw fixation with Kyphoplasty in the treatment of burst fractures. J. Biomechanical Eng. 140 (6). doi:10.1115/1.4039174
Frobin, W., Brinckmann, P., Kramer, M., and Hartwig, E. (2001). Height of lumbar discs measured from radiographs compared with degeneration and height classified from MR images. Eur. Radiol. 11 (2), 263–269. doi:10.1007/s003300000556
Fujiwara, A., Lim, T., An, H., Tanaka, N., Jeon, C., Andersson, G., et al. (2000a). The effect of disc degeneration and facet joint osteoarthritis on the segmental flexibility of the lumbar spine. SPINE 25 (23), 3036–3044. doi:10.1097/00007632-200012010-00011
Fujiwara, A., Tamai, K., An, H., Kurihashi, T., Lim, T., Yoshida, H., et al. (2000b). The relationship between disc degeneration, facet joint osteoarthritis, and stability of the degenerative lumbar spine. J. spinal Disord. 13 (5), 444–450. doi:10.1097/00002517-200010000-00013
Garay, R. S., Solitro, G. F., Lam, K. C., Morris, R. P., Albarghouthi, A., Lindsey, R. W., et al. (2022). Characterization of regional variation of bone mineral density in the geriatric human cervical spine by quantitative computed tomography. PLoS One 17 (7), e0271187. doi:10.1371/journal.pone.0271187
Guo, L., and Fan, W. (2017). The effect of single-level disc degeneration on dynamic response of the whole lumbar spine to vertical vibration. World Neurosurg. 105, 510–518. doi:10.1016/j.wneu.2017.06.008
Guo, L., and Fan, W. (2018). Dynamic response of the lumbar spine to whole-body vibration under a compressive follower preload. SPINE 43 (3), E143–E153. doi:10.1097/brs.0000000000002247
Guo, L., and Li, W. (2020). Finite element modeling and static/dynamic validation of thoracolumbar-pelvic segment. Comput. METHODS BIOMECHANICS Biomed. Eng. 23 (2), 69–80. doi:10.1080/10255842.2019.1699543
Hicks, G., Morone, N., and Weiner, D. (2009). Degenerative lumbar disc and facet disease in older adults: prevalence and clinical correlates. SPINE 34 (12), 1301–1306. doi:10.1097/BRS.0b013e3181a18263
Inoue, N., and Espinoza Orias, A. (2011). Biomechanics of intervertebral disk degeneration. Orthop. Clin. N. Am. 42 (4), 487–499. doi:10.1016/j.ocl.2011.07.001
Jiang, Q.-M., Ni, W., Zhang, X., Chen, P., Xu, L., and Yang, Y. (2021). Evaluation of tractor driving comfort according to the steering angle and speed using a virtual prototype. Proc. Institution Mech. Eng. Part D J. Automob. Eng. 235, 1191–1199. doi:10.1177/0954407020982867
Johansson, M., Jensen Stochkendahl, M., Hartvigsen, J., Boyle, E., and Cassidy, J. (2017). Incidence and prognosis of mid-back pain in the general population: a systematic review. Eur. J. pain London, Engl. 21 (1), 20–28. doi:10.1002/ejp.884
Kettler, A., Rohlmann, F., Ring, C., Mack, C., and Wilke, H. (2011). Do early stages of lumbar intervertebral disc degeneration really cause instability? Evaluation of an in vitro database. Eur. spine J. official Publ. Eur. Spine Soc. Eur. Spinal Deformity Soc. Eur. Sect. Cerv. Spine Res. Soc. 20 (4), 578–584. doi:10.1007/s00586-010-1635-z
Li, L., Shen, T., and Li, Y. (2017). A finite element analysis of stress distribution and disk displacement in response to lumbar rotation Manipulation in the Sitting and side-Lying Positions. J. Manip. PHYSIOLOGICAL Ther. 40 (8), 580–586. doi:10.1016/j.jmpt.2017.07.006
Li, W., Zhang, M., Lv, G. d., Han, Q., Gao, Y., Wang, Y., et al. (2015). Biomechanical response of the musculoskeletal system to whole body vibration using a seated driver model. Int. J. INDUSTRIAL ERGONOMICS 45, 91–97. doi:10.1016/j.ergon.2014.12.006
Li, X., Liu, Z., Dai, L., Zhong, G., and Zang, W. (2011). Dynamic response of the idiopathic scoliotic spine to axial cyclic loads. SPINE 36 (7), 521–528. doi:10.1097/BRS.0b013e3181d55fb0
Li, Y., Zhang, Y., Xu, P., Zheng, J., and Fan, Y. (2023). Biomechanics of brain tissue damage caused by fiber endoscope penetration in third ventriculostomy surgery. Comput. METHODS BIOMECHANICS Biomed. Eng., 1–11. doi:10.1080/10255842.2023.2262661
Luoma, K., Riihimäki, H., Luukkonen, R., Raininko, R., Viikari-Juntura, E., and Lamminen, A. (2000). Low back pain in relation to lumbar disc degeneration. SPINE 25 (4), 487–492. doi:10.1097/00007632-200002150-00016
McNally, D., and Adams, M. (1992). Internal intervertebral disc mechanics as revealed by stress profilometry. SPINE 17 (1), 66–73. doi:10.1097/00007632-199201000-00011
Mimura, M., Panjabi, M., Oxland, T., Crisco, J., Yamamoto, I., and Vasavada, A. (1994). Disc degeneration affects the multidirectional flexibility of the lumbar spine. SPINE 19 (12), 1371–1380. doi:10.1097/00007632-199406000-00011
Park, W., Kim, K., and Kim, Y. (2013). Effects of degenerated intervertebral discs on intersegmental rotations, intradiscal pressures, and facet joint forces of the whole lumbar spine. Comput. Biol. Med. 43 (9), 1234–1240. doi:10.1016/j.compbiomed.2013.06.011
Polikeit, A., Ferguson, S., Nolte, L., and Orr, T. (2003). Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur. spine J. official Publ. Eur. Spine Soc. Eur. Spinal Deformity Soc. Eur. Sect. Cerv. Spine Res. Soc. 12 (4), 413–420. doi:10.1007/s00586-002-0505-8
Renner, S. M., Natarajan, R. N., Patwardhan, A. G., Havey, R. M., Voronov, L. I., Guo, B., et al. (2007). Novel model to analyze the effect of a large compressive follower pre-load on range of motions in a lumbar spine. J. BIOMECHANICS 40 (6), 1326–1332. doi:10.1016/j.jbiomech.2006.05.019
Ruberté, L., Natarajan, R., and Andersson, G. (2009). Influence of single-level lumbar degenerative disc disease on the behavior of the adjacent segments--a finite element model study. J. BIOMECHANICS 42 (3), 341–348. doi:10.1016/j.jbiomech.2008.11.024
Schmidt, H., Heuer, F., Drumm, J., Klézl, Z., Claes, L., and Wilke, H.-J. (2007). Application of a calibration method provides more realistic results for a finite element model of a lumbar spinal segment. Clin. Biomech. 22 (4), 377–384. doi:10.1016/j.clinbiomech.2006.11.008
Sengupta, D. K. (2017). Clinical biomechanics of the spine. SPINE 42 (7), S3. doi:10.1097/brs.0000000000002019
Taghizadeh-Alisaraei, A. (2017). Analysis of annoying shocks transferred from tractor seat using vibration signals and statistical methods. Comput. Electron. Agric. 141, 160–170. doi:10.1016/j.compag.2017.07.020
Urban, J., and McMullin, J. (1988). Swelling pressure of the lumbar intervertebral discs: influence of age, spinal level, composition, and degeneration. SPINE 13 (2), 179–187. doi:10.1097/00007632-198802000-00009
Volz, M., Elmasry, S., Jackson, A. R., and Travascio, F. (2022). Computational modeling intervertebral disc Pathophysiology: a review. Front. Physiology 12, 750668. doi:10.3389/fphys.2021.750668
Wang, H., Li, N., Huang, H., Xu, P., and Fan, Y. (2023). Biomechanical effect of intervertebral disc degeneration on the lower lumbar spine. Comput. METHODS BIOMECHANICS Biomed. Eng. 26 (14), 1669–1677. doi:10.1080/10255842.2022.2129970
Wilke, H., Rohlmann, F., Neidlinger-Wilke, C., Werner, K., Claes, L., and Kettler, A. (2006). Validity and interobserver agreement of a new radiographic grading system for intervertebral disc degeneration: Part I. Lumbar spine. Eur. spine J. official Publ. Eur. Spine Soc. Eur. Spinal Deformity Soc. Eur. Sect. Cerv. Spine Res. Soc. 15 (6), 720–730. doi:10.1007/s00586-005-1029-9
Keywords: disc degeneration, lumbar spine, modal analysis, harmonic response analysis, time domain result
Citation: Wang X, Liu W, Zhao Y and Ma P (2024) The impact of disc degeneration on the dynamic characteristics of the lumbar spine: a finite element analysis. Front. Bioeng. Biotechnol. 12:1384187. doi: 10.3389/fbioe.2024.1384187
Received: 08 February 2024; Accepted: 17 April 2024;
Published: 01 May 2024.
Edited by:
Redha Taiar, Université de Reims Champagne-Ardenne, FranceReviewed by:
Francesco Travascio, University of Miami, United StatesWojciech Wolański, Silesian University of Technology, Poland
Copyright © 2024 Wang, Liu, Zhao and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pengcheng Ma, bWFwZW5nY2hlbmcwNTE4QDE2My5jb20=
†These authors have contributed equally to this work
 Xue Wang
Xue Wang Wei Liu2†
Wei Liu2†