Nonlinear Reactor Design Optimization With Embedded Microkinetic Model Information

1 Introduction

Multiscale modeling bridges scientific domains and accelerates innovation in diverse fields such as bioengineering (Mei et al., 2015; Alber et al., 2019), pharmaceuticals (Rim et al., 2009; Li et al., 2014; Clancy et al., 2016), material sciences (LLorca et al., 2011; Talebi et al., 2014; Vassaux et al., 2020), and chemical engineering (van der Hoef et al., 2006; Fermeglia and Pricl, 2009; Eugene et al., 2019). Various time-bridging approaches (Vlachos, 2005; Horstemeyer, 2009; Salciccioli et al., 2011b; Tsay and Baldea, 2019) enable tractable transfer of information across length and time scales. For example, top-down approaches (Fedder, 2000; Zhao et al., 2019) enable fast screening of materials through process optimization and inform inverse design of materials. Likewise, bottom-up approaches (Sinno, 2007; Boţan et al., 2015) can evaluate materials and devices in the context of optimized process systems and infrastructures.

Multiscale modeling plays a critical role in modernizing the energy economy including the responsible use of shale gas. In the United States, a surplus of ethylene and propylene (Sieminski, 2016) has dampened the demand for conventional natural gas liquids (NGL) and liquefied natural gas (LNG) processing (Goellner, 2012). Additionally, the distributed, stranded location of wells and their time-varying production rates (Tan and Barton, 2015; Kim et al., 2016; Yang and You, 2018) make traditional large-scale, capital-intensive processing facilities economically unfavorable (Wilczewski, 2015). These factors create opportunities for the development of modular (Tan and Barton, 2015; Kim et al., 2016), catalytic processes (Cantrell et al., 2016; He et al., 2018; Ridha et al., 2018) to transform shale gas into high-value hydrocarbons such as fuel (e.g., gasoline, diesel, jet) additives or other chemicals. Here, multiscale modeling is critical to resolving complex, interdependent decisions across the materials, unit operations, process, and infrastructure scales (Eugene et al., 2019). For example, computational chemistry (Breuil et al., 2015; Ko et al., 2020) and microkinetic (MK) (Terrell et al., 2019; Vernuccio et al., 2019) models for oligomerization reactions in catalytic upgrading of lighter olefins like ethylene and propylene help evaluate novel catalyst performance in silico in tandem with experiments. While these models inform molecular and materials design decisions, they have yet to be directly integrated with reactor and process models to assess viable design configurations and product portfolios.

Numerical tractability concerns (Mhadeshwar and Vlachos, 2005; Salciccioli et al., 2011a; Karst et al., 2015) limit the use of MK models for detailed reactor modeling, optimization, and design; engineers often use conversion or equilibrium models (e.g., Gibbs free energy minimization) for process design and optimization (Ridha et al., 2018; Yang and You, 2018). For complex reaction networks including oligomerization in natural gas upgrading, such simplified models may lead to inaccurate conclusions by not considering chemical kinetics.

Instead, three computational approaches—MK model reduction, machine learning surrogate models, and reduced-order kinetic (ROK) models—are emerging to embed the dominant kinetic information in macroscale calculations such as computational fluid dynamics or dynamic optimization while maintaining computational tractability (Jebahi et al., 2016). MK model reduction strategies, in particular, have received considerable attention; recent literature (Mhadeshwar and Vlachos, 2005; Salciccioli et al., 2011a; Karst et al., 2015; Partopour and Dixon, 2016; de Carvalho et al., 2018) has demonstrated model size reductions of up to 50% for single-product and small reaction networks with $\mathcal{O}(\mathrm{10})$ elementary reaction steps without significant loss of kinetic information. However, these strategies have yet to be demonstrated on complex reaction networks such as oligomerization that consider $\mathcal{O}(10^3)$ elementary reaction steps (Vernuccio et al., 2019) and multiple products. Machine learning approaches (Teske, 2014; Miriyala et al., 2016; Kotidis and Kontoravdi, 2020), on the other hand, use simulations or experimental data libraries to train neural networks and similar surrogate models to predict the reactor effluent. Although these approaches are not restricted by the MK model size, they require large amounts of data to train and lack the ability to emulate kinetic or thermodynamic behavior outside the range of validation (Miriyala et al., 2016) which can be problematic for reactor optimization. In contrast, ROK models (Jacob et al., 1976; Oliveira et al., 2010) are developed by lumping the MK reactant and product species into major products or product groups to reduce complexity; simplified reaction mechanisms are used to postulate rate laws using these pseudo-products. These models are computationally tractable due to the reduced model size while the kinetic form of the models enables considerably reliable process-scale extrapolations. This makes ROK models especially attractive for oligomerization reactor optimization. A major challenge, which we address in this paper, is how to postulate and select the rate laws used in ROK models.

In this paper, we propose a computationally tractable ROK modeling framework to incorporate MK simulation data into nonlinear reactor optimization for oligomerization in shale gas upgrading. Specifically, we answer the following questions: 1) what ROK model-form best emulates MK simulation data while remaining computationally tractable for dynamic optimization? and 2) what is the impact of ROK model-form and parametric uncertainties on reactor design optimization results? To address these questions, we postulate a library of ROK models based on literature (Oliveira et al., 2010) and MK modeling strategies (Vernuccio et al., 2019); using statistical quality of fit metrics, identifiability analysis, and sensitivity analysis, we determine that a previously proposed oligomerization kinetic model (Oliveira et al., 2010) does not emulate MK model simulations trends. We then demonstrate how the proposed ROK models enable tractable optimization of temperature zones in a packed bed reactor (PBR). Finally, we show that model-form uncertainty, e.g., choice of ROK model, does not impact the optimal temperature profile (decisions) but, dramatically impacts the predicted conversion (optimization objective) and surpasses the effect of parametric uncertainty propagation on the optimization results. To our knowledge, this paper is the first to build ROK models for multi-product oligomerization based on MK simulations and demonstrate tractable reactor design optimization.

The remainder of this paper is organized as follows. Section 3 reviews multiscale and lumped-rate kinetic modeling literature. Section 4 describes the proposed modeling and computational framework. Sections 5 and 6 present results for ROK model identification and reactor optimization, respectively. Finally, Section 7 discusses conclusions, limitations, and future work.

2 Literature Review

2.1 Multiscale Modeling in Reaction Engineering

Multiscale modeling accelerates materials engineering and discovery through in silico inverse design and optimization. At the microscopic scale, thermodynamic and kinetic parameters like enthalpy of formation, entropy, and activation energy of single atoms or molecules are estimated via ab initio calculations using density functional theory (DFT) (Parr, 1983) and molecular dynamics (MD) coupled with statistical mechanics. Other semi-empirical parameters such as pre-exponential factors are calculated using transition state theory (TST) (Pechukas, 1981). These parameters are then embedded into ordinary differential equations (ODEs) to represent elementary reaction rates. Using domain knowledge or Monte Carlo (MC) techniques, the ODEs are then combined to form MK models (Hansen et al., 2007) that describe elementary, surface-level chemistries of catalytic reactions (Prasad et al., 2010; Stamatakis and Vlachos, 2012; Stamatakis, 2014). At the macroscopic scale, tools such as continuum equations (Hadjiconstantinou and Patera, 1997), computational fluid dynamics (CFD) (Dixon and Nijemeisland, 2001), and mathematical reactor models (Rawlings and Ekerdt, 2002) are used to evaluate scale-appropriate mass and heat transfer correlations. Using these tools, scientists and engineers set material design targets for catalyst development and determine the value of additional data to reduce uncertainty. Detailed reactor and process design frameworks further enable advanced control (Murase et al., 1970; Elnashaie et al., 1988; Gentric et al., 1999; Abel et al., 2000; Hagh, 2003), reactor arrangement and configuration optimization (Hillestad, 2010; Rafiee and Hillestad, 2012, 2013; Manenti et al., 2014; Fischer and Freund, 2021), and reactor network optimization through superstructure optimization (Balakrishna and Biegler, 1992; Kokossis and Floudas, 1994; Lakshmanan and Biegler, 1996; Gong and You, 2018).

Several modeling frameworks have been proposed over the last 20 years for the multiscale development of catalytic processes. Molecular-scale tools such as quantum mechanics, molecular dynamics, and kinetic Monte Carlo (KMC) for property estimation, coupled with data science tools including parameter estimation and identifiability analysis form the basis for a “multiscale simulation ladder” (Vlachos et al., 2006). Raimondeau and Vlachos (2002) demonstrated the computational feasibility of multiscale simulations by generating data at the molecular level (MC simulations and other surface simulators) to fit models for macroscopic reactor modeling. Sutton et al. (2018) successfully established feedback loops between first-principles kinetic Monte Carlo (KMC) simulations and computational fluid dynamics (CFD) to extract chemical insights for rate-determining steps at the molecular-scale and optimal reactor operation mode at the process-scale. Their framework accurately predicts reactor-scale selectivity and conversion under unexplored conditions for the catalytic oxidation of carbon monoxide. Partopour and Dixon (2019) developed a multiscale approach for transient simulation of fixed bed reactors using CFD to study the overall transient behavior of the reactor as well as local effects such as species distribution inside the particles under dynamic conditions. Quiceno et al. (2006) incorporated the MK model for catalytic partial oxidation of methane over platinum catalyst into CFD models and were able to perfectly match experimental results from literature while Maestri et al. (2008) proposed a hierarchy of validated kinetic models for steam and dry reforming of methane starting from MK models to two-step reduced models fit for implementation in reactor design. More recently, Karst et al. (2015) and Partopour and Dixon (2016) used MK model reduction strategies to mitigate the computational demand associated with the incorporation of MK models in process-scale reactor design. These reduction strategies are reviewed in detail below. While these frameworks enable some multiscale design, they were demonstrated using relatively simple reaction networks such as methane reforming and water gas shift reaction that involve $\mathcal{O}(\mathrm{10})$ elementary steps; how to scale these approaches to more complex reaction systems with multiple products or $\mathcal{O}(10^3)$ steps remains an open question. Moreover, in-depth knowledge of both micro- and macro-scopic phenomena is required to successfully implement these modeling frameworks.

We now review three categories of approaches—MK model reduction, machine learning emulators, and ROK models—to incorporate MK information in macroscale models (Solle et al., 2017).

2.2 MK Model Reduction

The goal of MK model reduction is to create a simplified reaction network that emulates the predominant model trends (e.g., conversion) by combining and removing elementary reactions from the original (large) network. Sensitivity analysis followed by principal component analysis (PCA) (Wold et al., 1987) is the most widely-used strategy for MK model reduction in literature (Mhadeshwar and Vlachos, 2005; Salciccioli et al., 2011a; Karst et al., 2015; Partopour and Dixon, 2016; de Carvalho et al., 2018). In this method, the significance/importance of each elementary reaction step in the MK model is quantified using sensitivity matrices that record the change in MK model performance (e.g., conversion, product yield, selectivity) resulting from the one-at-a-time removal of the elementary steps from the model. PCA is then performed using the sensitivity matrix to eliminate the least sensitive elementary steps based on eigenvalue analysis from the network until a threshold is met. Recent successful applications of PCA-based MK model reduction include analysis of the MK model for water gas shift reaction on platinum catalyst consisting of 46 elementary steps (Mhadeshwar and Vlachos, 2005) and on nickel catalyst consisting of 19 reversible elementary steps (de Carvalho et al., 2018), ethylene hydrogenation and ethane hydrogenolysis MK model consisting of 32 reversible elementary steps (Salciccioli et al., 2011a), and partial ethylene oxidation MK model with 17 reversible steps (Partopour and Dixon, 2016). Karst et al. (2015) used the PCA-based approach followed by reaction pathway analysis to reduce the methane chemistry model from Maestri et al. (2009) from 41 elementary steps to 21 steps with an overall average error of 0.05% in predictions. The reduced-order model was then used to maximize the yield of hydrogen by optimizing the feed composition and reactor temperature profile and the results were validated to predict hydrogen production within 0.13% of the predictions obtained by simulating the MK model at the optimal conditions. Our work scales these approaches to multi-product systems with two orders of magnitude more elementary reaction steps.

Backward feature elimination (BFE) is another popular approach for MK model reduction. To start, BFE creates a library of candidate reduced MK models by sequentially removing a single reaction from the model in each step and recalibrating the reduced MK model using experimental data. The reduced MK models with the largest prediction errors are removed from the library and the process repeats until an acceptance criterion such as minimum model size or maximum prediction error is met. Often, simulated annealing or other heuristic search algorithms are then used to reparameterize the reduced MK models and minimize prediction error compared to the original MK model. Avşar (2017) used this approach to study carbon monoxide conversion from the water gas shift reaction on platinum consisting of 46 elementary steps. Although BFE yielded better-predicting reduced models with 5.8% lower root mean squared error (RMSE) compared to PCA in the study by Avşar (2017), the BFE approach cannot guarantee optimal reduction of MK models because it is a heuristic search.

Despite their potential advantages, PCA- and BFE-enabled MK model reduction strategies, so far, have only been applied to reaction networks consisting of 40–50 reaction rates, providing up to 50% reduction in model size without losing considerable model fidelity. In this work, we consider the HZSM-5-catalyzed propylene oligomerization reaction model fully described by Vernuccio et al. (2019), which contains 4,243 reactions, 2,345 net reaction rates, and 909 state variables (ODEs). These ODEs, defined as the partial pressure of each species with respect to the number of catalyst active sites along the reactor, were integrated using the double precision differential/algebraic sensitivity analysis code (DDASAC) solver (Warren, 1995) as an initial value problem. Each MK model integration takes a few minutes to complete. Additionally, large MK models are often sensitive to the initial operating conditions (Becerra et al., 2021), i.e., small perturbations in initial conditions can cause large changes in the output. Therefore, we anticipate a MK model embedded in process flowsheet with recycle loops would need to be integrated tens to hundreds of times to converge the flowsheet in sequential modular simulation environments (e.g., AspenPlus) which would make process simulation or optimization cumbersome and computationally intensive. Finally, the above-described MK model reduction methods are intrusive by nature and require nontrivial modifications to MK model/code to implement. For this reason, practitioners often prefer using modeling strategies, if possible, which require less software modifications and in-depth MK modeling expertise.

2.3 Machine Learning Emulators

Alternately, machine learning methods can be used to train surrogates such as polynomial regression models (Wang et al., 2018), artificial neural networks (ANNs) (Teske, 2014; Miriyala et al., 2016; Kotidis and Kontoravdi, 2020), or distribution models (Hutter et al., 2021) to emulate the behavior of MK models. For example, Wang et al. (2018) correlated combustion reaction data at different operating conditions using neural network surrogate models. They introduced constraints based on the proximity of model response to available data to avoid model extrapolation for data selection, experimental design, and property estimation. Miriyala et al. (2016) replaced the detailed kinetic model for polymerization with neural networks in multi-objective reactor optimization problems which reduced the number of function calls by up to 90% and, in turn, reduced the solution time. Recently, Bradley and Boukouvala (2021) successfully demonstrated up to 67% reduction in computation time without loss of prediction accuracy using a two-step approach for reaction kinetics parameter estimation. First, they trained neural ordinary differential equations (NODEs) to represent state derivative information and then used the NODEs for parameter estimation. These and similar results highlight two key benefits of surrogate models: they require limited knowledge of reaction kinetics and have the potential to improve computation time. However, model extrapolation using purely machine learning-based (surrogate) models remains challenging due to the absence of model physics (Von Stosch et al., 2014). Trust region methods are one way to overcome this limitation (Eason and Biegler, 2016). For example, Franzoi et al. (2021) use a trust region based adaptive sampling strategy to develop highly accurate multiple-input single-output (MISO) surrogate models to replace Arrhenius-form kinetics in the Williams-Otto optimization problem (Williams and Otto, 1960). Using this approach, they iteratively refined the surrogate model and performed optimization, ultimately obtaining solutions within 0.016% of the best known objective value.

Hybrid models are emerging to overcome the limitations of both first-principles and purely data-driven models. The seminal work of Psichogios and Ungar (1992) combines a first-principles model and ANNs to model the operation of a fedbatch reactor; the first-principles model emulated known reaction kinetics while the black-box ANN was used to model dynamic behavior arising from unknown interactions between living organisms. Since this seminal work, neural networks have remained the preferred form of surrogate that are coupled with some form of first-principles model in hybrid modeling (Qi et al., 1999; Zahedi et al., 2005; Mosavi et al., 2019; Bangi and Kwon, 2020). Von Stosch et al. (2014) provide a review of recent advances in coupling non-parametric surrogates and first-principles models. More recently, Yang et al. (2020) used a hybrid approach to combine a first-principles, rate-based model with neural network surrogate models that emulates fluid catalytic cracking reactions and improves prediction accuracy by 9% compared to stand-alone neural network models. Tsopanoglou and del Val (2021) combined mechanistic models for material balances and kinetics with neural network surrogate models for in situ bioprocess monitoring. De Jaegher et al. (2021) use neural differential equations to model colloid-membrane collisions, coupled with mechanistic models, to study fouling in electrodialysis membranes. The neural differential equations elucidate missing physics for ion-exchange membranes and motivate the need for further research towards developing fully-mechanistic models for membrane fouling. Foad et al. (2022) trained hybrid models—reduced-order model derived using PCA combined with a deep neural network (DNN)—to emulate the transient behavior of a nuclear reactor and were able to emulate the output power trajectory of the reactor with only 2% deviation. While hybrid models are promising, they are often demonstrated using reaction networks with only tens of reactions (Potočnik et al., 2003; Bhutani et al., 2006; Bayer et al., 2020).

2.4 ROK Model Development

ROK modeling strategies, a proven practice in literature (Jacob et al., 1976; Coxson, 1995; de Andrade Lima and Hodouin, 2005; Radmanesh et al., 2006; Oliveira et al., 2010), use a priori knowledge of the reaction mechanism such as the rate form (Laidler, 1984) to postulate and train first-principles based lumped-rate models. These models, once validated, can be extrapolated to make conversion and product distribution predictions. For example, Zong et al. (2010) proposed an ROK model for the heavy oil catalytic cracking and maximizing of iso-paraffins (MIP) process and validated the model using industrial data. In addition to predicting product distribution and product quality with 7.5% error, the validated model was able to predict expected kinetic behavior for the MIP process. Similarly, Ying et al. (2015) proposed an ROK for the catalytic methanol-to-olefins (MTO) process which, after calibration, predicted conversion of major olefins within 5% of experiments. More recently, Tsu et al. (2019) developed a library of candidate rate equations and used Monte Carlo algorithms to sample from the candidate equations to create kinetic models. Wang et al. (2021) demonstrated the tractability of ROK models in reactor design by embedding an ROK model for CaO-CO₂ carbonation in a bubbling bed reactor model; simulations indicated that the ROK model successfully emulate temperature, concentration, and particle size effects observed in laboratory experiments.

ROK models are especially useful for modeling multi-product reaction networks. Jacob et al. (1976) first presented the idea of developing ROK models for complex reaction networks such as fluid catalytic cracking (FCC) to obtain a more “fundamental basis” to relate feed composition and process variable effects to product distribution. Similarly, Tabak et al. (1986) proposed the use of ROK models to model and study catalytic oligomerization. Based on the simplified mechanism proposed by Tabak et al. (1986), Borges et al. (2007) and Oliveira et al. (2010) developed ROK models using rate expressions lumped by the carbon number of the species that are capable of emulating low conversion product distributions for ethylene, propylene, and butene oligomerization. Owing to their practical applicability towards modeling complex, multi-component chemical reaction systems, ROK models continue to be the preferred modeling strategy for systems such as catalytic cracking (Ebrahimi et al., 2018; Sani et al., 2018; Sun et al., 2018; John et al., 2019) and pyrolysis (Yan et al., 2019; Schubert et al., 2020; Zhang and Sarathy, 2021). Beyond modeling complex petrochemical processes, ROK models have also been developed for a variety of chemical processes including gold ore cyanidation (de Andrade Lima and Hodouin, 2005), biomass pyrolysis (Radmanesh et al., 2006), and solid fuel combustion (Moríñigo and Hermida-Quesada, 2016).

3 Methods

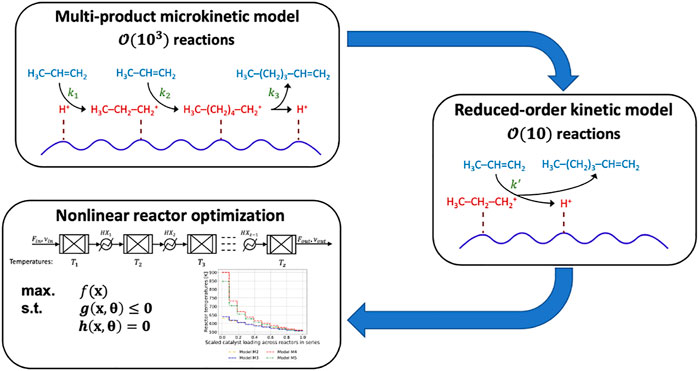
In this work, we propose the multiscale framework in Figure 1 to incorporate MK information into detailed oligomerization reactor design optimization calculations. Based on the size of the propylene oligomerization MK model (2,345 reaction rates and 909 species) developed by Vernuccio et al. (2019) and the limitations of existing model reduction strategies, we focus on ROK models. We start with the ROK model for propylene oligomerization from Oliveira et al. (2010). We then postulate a library of ROK models by progressively altering the model form to reflect MK model structure. We use weighted least-squares parameter estimation, sensitivity analysis, and identifiability analysis to determine which ROK models best emulate MK model behavior. Using the calibrated models, we solve temperature-staged reactor optimization problems and quantify the effects of parametric (i.e., aleatoric) and model-form (i.e., epistemic) uncertainties.

FIGURE 1

FIGURE 1. Proposed multiscale modeling framework for oligomerization reactor modeling and design optimization.

3.1 MK Model Simulation Data

We focus on the HZSM-5 catalyzed propylene oligomerization MK model developed by Vernuccio et al. (2019). The elementary steps in this model involve physisorption of a gas-phase olefin into the pores of the zeolite followed by protonation by a Brønsted acid site to form a reaction intermediate (carbenium ion or covalent alkoxide). The addition of a physisorbed olefin to a protonated intermediate results in the formation of a higher carbon number intermediate which finally deprotonates to form a heavier product olefin (Vernuccio et al., 2019). Following the formation of oligomers resulting from dimerization and subsequent oligomerization of the olefin monomer reactant (Sarazen et al., 2016), skeletal isomerization and cracking via β-scission occur, resulting in a mixture of olefins from ethylene to nonene. The reaction network for this model is developed using an automated network generator, NetGen (Broadbelt et al., 1994). The automated generation process for an oligomerization network is in principle infinite because of the nature of the oligomerization steps which lead to the formation of heavier species. However, the experimental data collected in Vernuccio et al. (2019) for model validation showed a negligible amount of C_>9 species in the low pressure regime. For this reason, the reaction network was limited to molecular species and reaction intermediates with carbon number lower or equal to 9. Vernuccio et al. (2019) track 909 species through 4,243 reactions and 2,345 net rates to model the formation of species with two to nine carbon atoms with a pure propylene feed (75% propylene and 25% inert). The kinetic parameters for each elementary step were estimated using transition state theory, Evans–Polanyi relationships, and thermodynamic data. Originally developed for low-pressure and low-conversions operations, the MK model assumes the rate of hydride transfer to be negligible and does not track conversions to aromatics and paraffins. This assumption is justified when the reaction system primarily includes small olefins with only few abstractable hydrogens. This prevents hydride transfer steps from occurring which in turn limits the production of paraffins. In order to verify the applicability of the MK model to higher pressure operations, we developed an extended version of the model which includes hydride transfer steps between molecular species and carbenium ions/alkoxides as well as cyclization steps which lead to the formation of C₅ and C₆ ring structures. This extended MK model, including 4,212 species and 23,086 reactions, is substantially larger and less manageable than the MK model adopted in this work and was used for verification purposes only. While the MK model from Vernuccio et al. (2019) takes a few minutes to integrate, the extended MK model takes almost 6 hours to integrate. However, Figure 2 shows that the selectivity for butene and heavier olefins is comparable between the 2 MK models. Therefore, to reduce computation costs, we consider the MK model from Vernuccio et al. (2019) as the “ground truth” model in this work.

FIGURE 2

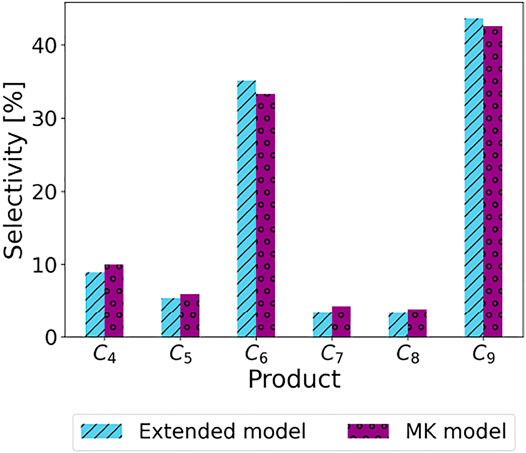
FIGURE 2. Product selectivity for butene and heavier olefins using MK (Vernuccio et al., 2019) and extended MK models at 10 bar feed pressure.

In this work, we use data generated by simulating the MK model (Vernuccio et al., 2019) in a PBR at high conversion range to reparametrize the ROK models. We divide data from 73 MK simulations into two groups: 1) 64 low pressure simulations at pressure 2.18 atm, temperatures 483–522 K, and space velocities 62 to 740 $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ previously published in Ganesh et al. (2020) and 2) nine high pressure simulations at pressures of 10–30 atm, temperatures of 523–573 K, and space velocity of 1123 $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$.

3.2 Library of ROK Models

We postulate a library of six candidate ROK models. Model M0 is a simple kinetic model with Arrhenius-form rate expressions. Model M1 is an ROK model adopted from literature (Oliveira et al., 2010). Model M2 updates the adsorption enthalpy chain length dependence and adsorption isotherm model from M1. Model M3 adds temperature dependence to the frequency factor from model M2. Models M4 and M5 add activation energy chain length dependence to models M2 and M3, respectively. The sequential structural changes introduced in the ROK models from M0 to M5 are intended to ultimately match the MK model structure presented by Vernuccio et al. (2019). In this paper, we use the phrase “functional form” to refer to the dependence of kinetic parameters on reaction conditions, including temperature and adsorption phenomena, and reactant characteristics, including chain length and chain symmetry.

3.2.1 Sets and Indices

First, we define the sets and indices necessary to describe the general reduced-order oligomerization reaction network:

Reaction type: $i\in \mathcal{I}=\{\mathrm{1,2}\}$

Number of carbon atoms: $j,n,\mathrm{o}\mathrm{r}m\in \mathcal{C}=\{\mathrm{2,3,4},\dots ,N\}$

where N denotes the number of carbon atoms in the largest olefin species considered in the reaction network. The two reaction types considered in the network are oligomerization (i = 1) and cracking (i = 2) leading to the transformation of olefins ranging from C₂H₄ to C_NH_2N. Whereas olefin isomers are accounted for as separate species in the MK model, in this work we have lumped all isomeric species together by carbon number.

3.2.2 Reactions

Let X_n (X_m or X_n+m) represent olefins with n (m or n + m) carbon atoms. In the forward oligomerization reaction, with rate constant $k_{i=1,n,m}^{\prime }$, light olefins combine to form heavier olefins. In the reverse cracking reaction, with rate constant $k_{i=2,n,m}^{\prime }$, heavier olefins break into lighter olefins.

$[{\mathrm{X}}_n\mathrm{Z}]+{\mathrm{X}}_m\underset{k_{i=2,n,m}^{\prime }}{\stackrel{k_{i=1,n,m}^{\prime }}{\rightleftharpoons }}[{\mathrm{X}}_{n+m}\mathrm{Z}]$

In the above reaction, Z refers to the catalyst active sites where the olefins are adsorbed before reacting with other gas-phase olefins. X_nZ represents the olefin attached to the catalyst active site Z and X_m represents the gas-phase olefin which combine to form X_n+mZ.

3.2.3 Rate Equation

We define the overall rate equation using r_n,m (mol min⁻¹g⁻¹) where n and m represent the number of carbon atoms in the reacting species.

$-r_{n,m}=k_{i=1,n,m}^{\prime }\cdot p_m\cdot p_n-k_{i=2,n,m}^{\prime }\cdot p_{n+m}\forall n+m\le N(1)$

The partial pressure of each species is denoted by p_j (or p_n, p_m, and p_n+m) where j (or n, m, and n + m) denotes the number of carbon atoms in the species molecule. The concentration of the adsorbed species is substituted with the partial pressure of the corresponding gas-phase species using adsorption isotherm relations (discussed later) contained in the rate constants $k_{i,n,m}^{\prime }$.

3.2.4 Rate Constants

We first defined a simple Arrhenius-form ROK model with the rate constant:

$k_{i,n,m}^{\prime }={\alpha }_{i,n+m}{\mathrm{e}}^{-E_{i,n+m}/RT},i\in \mathcal{I}(2)$

where α_i,n+m is the pre-exponential frequency factor and E_i,n+m is the aggregated activation energy for reaction type i involving olefins with carbon numbers n, m, and n + m.

Next, we considered an ROK model from Oliveira et al. (2010) originally developed to model olefin transformations at low conversion. The rate constants are given as:

$k_{i,n,m}^{\prime }=\omega k_{i,n,m}^0\cdot {\mathrm{e}}^{-E_{i,n,m}^{\prime }/RT},i\in \mathcal{I}(3)$

The pre-exponential frequency factor, $k_{i,n,m}^0$ is given by:

$k_{i,n,m}^0={\alpha }_i\cdot {\mathrm{e}}^{E_{i,n,m}^{\prime }{\beta }_i},i\in \mathcal{I}(4)$

Thus, Eq. 3 is re-written as:

$k_{i,n,m}^{\prime }=\omega {\alpha }_i^{\prime }{\mathrm{e}}^{E_{i,n,m}^{\prime }\left({\beta }_i-1/RT\right)},i\in \mathcal{I}(5)$

In Eqs 4, 5, ${\alpha }_i^{\prime }$ is the frequency factor and β_i is the compensation factor to relate $k_{i,n,m}^0$ and the activation energy $E_{i,n,m}^{\prime }$. In this work, the compensation factors are assumed to be constant (not fitted parameters). The rate constant in Vernuccio et al. (2019) does not consist of the compensation factor β_i and can be written using frequency factor ${\alpha }_i^{\prime \prime }$ as:

$k_{i,n,m}^{\prime }=\omega {\alpha }_i^{″}{\mathrm{e}}^{-E_{i,n,m}^{″}/RT},i\in \mathcal{I}(6)$

Next, we add temperature-dependence to the pre-exponential frequency factor in Eqs 5, 6 following Vernuccio et al. (2019) which gives Eqs 7, 8, respectively:

$k_{i,n,m}^{\prime }=\omega {\alpha }_i^{\prime \prime \prime }\frac{T}{T_{\mathit{ref}}}{\mathrm{e}}^{E_{i,n,m}^{\prime }\left({\beta }_i-1/RT\right)},i\in \mathcal{I}(7)$

$k_{i,n,m}^{\prime }=\omega {\alpha }_i^{⁗}\frac{T}{T_{\mathit{ref}}}{\mathrm{e}}^{-E_{i,n,m}^{″}/RT},i\in \mathcal{I}(8)$

In the above equations, ω is the adsorption isotherm constant used to relate the concentration of adsorbed species to the corresponding gas-phase partial pressures and T_ref = 298.15 K.

3.2.5 Activation Energies

We consider two functional forms to represent the carbon chain-length dependence of activation energies. The literature model (Oliveira et al., 2010) considers the following formula:

$E_{i,n,m}^{\prime }=\frac{{E^{\prime }}_i}{\tanh \left({\gamma }_i\cdot m\right)},i=1(9)$

$E_{i,n,m}^{\prime }=\frac{{E^{\prime }}_i\cdot \left(1+{\varphi }_i\cdot |n-m|\right)}{\tanh \left({\gamma }_i\cdot \left(n+m\right)\right)},i=2(10)$

where γ_i models the influence of chain length in reaction i and takes a different functional form for each reaction type. ϕ₂ models the influence of structure symmetry in activation energy calculation for cracking reactions (i = 2).

Vernuccio et al. (2019) use a linear relationship, Eq. 11, to calculate activation energies from heat of reactions ${\mathrm{\Delta }{H}_R}_{i,n,m}$.

$E_{i,n,m}^{″}=\left\{\begin{array}{c}{E}_0+{\kappa }_i\cdot {\mathrm{\Delta }{H}_R}_{i,n,m},\text{if}{\mathrm{\Delta }{H}_R}_{i,n,m}\le 0\hfill \\ E_0+\left(1-{\kappa }_i\right)\cdot {\mathrm{\Delta }{H}_R}_{i,n,m},\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}\right.(11)$

where E₀ is the intrinsic energy barrier and κ_i is the transfer coefficient for reaction type i; more exothermic reactions have κ_i values closer to 0 and more endothermic reactions have κ_i values closer to 1. The heats of reaction ${\mathrm{\Delta }{H}_R}_{i,n,m}$ are calculated from heats of formation ${\mathrm{\Delta }{H}_F}_j$ of reactant and product species following Eq. 12.

${\mathrm{\Delta }{H}_R}_{i,n,m}=\sum _{j\in \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{s}}{\mathrm{\Delta }{H}_F}_j-\sum _{j\in \mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{s}}{\mathrm{\Delta }{H}_F}_j(12)$

In this work, the heats of formation ${\mathrm{\Delta }{H}_F}_j$ are approximated using a linear combination of parameters δ, γ′, and species chain length j as shown in Eq. 13.

${\mathrm{\Delta }{H}_F}_j=\delta +j\cdot {\gamma }^{\prime }(13)$

3.2.6 Adsorption Isotherm Model

Oliveira et al. (2010) use a Langmuir isotherm to model adsorption:

$\omega =\frac{K_0{\mathrm{e}}^{-\mathrm{\Delta }H/RT}{C}_Z}{1+K_0{\mathrm{e}}^{-\mathrm{\Delta }H/RT}{P}_{\mathit{inlet}}}(14)$

here, K₀ is the adsorption equilibrium pre-exponential constant, C_Z is the total concentration of active sites in fresh catalyst, ΔH is the adsorption enthalpy, and P_inlet is the inlet reactor pressure.

Vernuccio et al. (2019) consider a linear adsorption isotherm model where the adsorption and desorption rates are written in the Arrhenius form and the activation energy for adsorption is assumed to be zero:

$k_{\mathit{ads, forward}}=A_F(15)$

$k_{\mathit{ads, backward}}=A_B{\mathrm{e}}^{-\mathrm{\Delta }{H}^{\prime }/RT}(16)$

here, k_{ads, forward} is the rate constant of adsorption, A_F is the adsorption frequency factor, k_{ads, backward} is the rate constant of desorption, A_B is the desorption frequency factor, and ΔH′ is the heat of desorption which is set equal to the heat of adsorption steps. Assuming equilibrium between the adsorption and desorption process:

$K_{\mathit{ads}}=\frac{k_{\mathit{ads, forward}}}{k_{\mathit{ads, backward}}}=\frac{A_F}{A_B{\mathrm{e}}^{-\mathrm{\Delta }{H}^{\prime }/RT}}(17)$

To simplify, we define λ to denote the log-transformed ratio of the pre-exponential rate constants:

$\omega =\lambda {\mathrm{e}}^{\mathrm{\Delta }{H}^{\prime }/RT},\lambda ={\log }_{\text{e}}\left(\frac{A_F}{A_B}\right)(18)$

3.2.7 Adsorption Enthalpy

Oliveira et al. (2010) assume the adsorption enthalpy is independent of the chain length of species being adsorbed. However, Vernuccio et al. (2019) use the chain length dependent adsorption enthalpy model from Nguyen et al. (2011):

$\mathrm{\Delta }{H}_j^{\prime }={\alpha }_{\mathit{ads}}+j{\beta }_{\mathit{ads}}(19)$

where α_ads and β_ads are characteristic parameters of the HZSM-5 zeolite framework that quantify the dispersive van der Waals interactions and local interactions with catalyst acid sites, respectively.

Based on the functional forms available to compute various kinetic parameters, we postulate six ROK models using a combination of Eqs 9-19. Table 1 presents the details of the functional form for ROK models M0 to M5.

TABLE 1

TABLE 1. Kinetic model library. M0 is the Arrhenius-form simple model with constant frequency factor and activation energy parameters (no correlations). M1 is the ROK model adopted from Oliveira et al. (2010). In M2 and M3, the adsorption enthalpy and adsorption isotherm models are updated. Unlike M2, M3 has a temperature-dependent frequency factor. In addition to the changes in M2 and M3, M4 and M5 have activation energies updated to match the MK model. Similar to M3, M5 has a temperature-dependent frequency factor while M4 does not.

Using the kinetic rate equations defined using Eq. 1 and Table 1, the rate of change of olefin partial pressures with normalized catalyst loading along a PBR is given by:

$\frac{d{p}_j}{d{m}_{\mathit{cat}}}=\frac{P{p}_{\text{inert}}}{SV{n}_{\mathit{cat}}{p_{\text{inert}}}_0}\sum _{n=2}^{j-2}\sum _{m=2}^{j-n}\left(-r_{n,m}\right)(20)$

where m_cat is the scaled catalyst mass along the length of the PBR, SV is the stream space velocity, n_cat is the number of moles of active site per gram of catalyst, P is the total pressure in the reactor, p_inert is the inert partial pressure, and ${p_{\text{inert}}}_0$ is the feed partial pressure of inerts. Supplementary Section S2 in the Supplementary Material derives Eq. 20.

3.3 Parameter Estimation

To calibrate parameters in each candidate model, we minimize a linear combination of the sum of squared errors (SSE) and sum of squared percent errors (SSPE) between olefins concentrations predicted by the MK and ROK models in a PBR:

$\begin{array}{cc}\hfill \underset{\begin{array}{c}\theta \end{array}}{\min }& \mathrm{S}\mathrm{S}\mathrm{E}+w\mathrm{S}\mathrm{S}\mathrm{P}\mathrm{E}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{w}\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\text{(1)}\hfill \\ \hfill & \mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{b}\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{P}\mathrm{B}\mathrm{R}\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{E}\mathrm{q}.(\mathrm{20})\hfill \\ \hfill & \mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{s}\hfill \end{array}(21)$

where w is the weight assigned to SSPE. θ is the vector estimated kinetic model parameters, which are defined as follows for models M0 through M5: θ₀ = [α_1,j, α_2,j, E_1,j, E_2,j] for all j ∈ {4, …, N}, θ₁ = [${\alpha }_1^{\prime }$, ${\alpha }_2^{\prime }$, γ₁, γ₂, ϕ₂, λ, ΔH′, $E_1^{\prime }$, $E_2^{\prime }$], θ₂ = [${\alpha }_1^{\prime }$, ${\alpha }_2^{\prime }$, γ₁, γ₂, ϕ₂, α_ads, β_ads, $E_1^{\prime }$, $E_2^{\prime }$], θ₃ = [${\alpha }_1^{\prime \prime \prime }$, ${\alpha }_2^{\prime \prime \prime }$, γ₁, γ₂, ϕ₂, α_ads, β_ads, $E_1^{\prime }$, $E_2^{\prime }$], θ₄ = [${\alpha }_1^{\prime \prime }$, ${\alpha }_2^{\prime \prime }$, γ′, δ, E₀, κ₁, κ₂, α_ads, β_ads], and θ₅ = [${\alpha }_1^{\prime \prime \prime \prime }$, ${\alpha }_2^{\prime \prime \prime \prime }$, γ′, δ, E₀, κ₁, κ₂, α_ads, β_ads]. Additionally, we analyze the effects of model scaling and objective function SSE formulation on model fit quality to choose the best modeling strategy. The formulation and details of this analysis are reported in Supplementary Material.

The models were implemented in Pyomo (Hart et al., 2017) and discretized using backward finite-difference scheme via Pyomo.DAE (Nicholson et al., 2018). The resulting regression problems were formulated using Pyomo.parmest (Klise et al., 2019) and contain 22,192 (M0), 23,214 (M1, M2, and M3), and 21,097 (M4 and M5) variables and 22,168 (M0), 23,205 (M1, M2, and M3), and 21,088 (M4 and M5) constraints. The problems were solved using with IPOPT (Wächter and Biegler, 2006) and the HSL linear solver MA27 (HSL).

3.4 Model Identifiability

Kinetic models are often only partially identifiable (Vajda et al., 1989). A model is said to be identifiable if there exists a unique set of model parameter values that produce a unique model response. Conversely, a model lacks identifiability if multiple distinct sets of model parameter values produce the same model response (Seber and Wild, 1989). In nonlinear regression problems, the model being reparameterized is not identifiable when the least-squares regression objective is flat in one or more directions (related to fitted parameters) and the Fisher Information Matrix (FIM), which is proportional to the reduced Hessian for the regression problem, is (near) singular. The FIM, M, is also approximately the inverse of the parameter covariance matrix, V. In this work, we ignore prior information (Franceschini and Macchietto, 2008) when approximating M as:

$\mathit{M}\left(\widehat{\mathit{\theta }},{\mathit{\varphi }}^{\prime }\right)\approx {\left[\mathit{V}\left(\widehat{\mathit{\theta }},{\mathit{\varphi }}^{\prime }\right)\right]}^{-1}(\mathrm{22a})$

$\mathit{M}\left(\widehat{\mathit{\theta }},{\mathit{\varphi }}^{\prime }\right)\approx \mathit{Q}\left(\widehat{\mathit{\theta }},{\mathit{\varphi }}^{\prime }\right)\cdot {{\mathbf{\Sigma }}_{\mathbf{p}}}^{-1}\cdot {\mathit{Q}}^T\left(\widehat{\mathit{\theta }},{\mathit{\varphi }}^{\prime }\right)(\mathrm{22b})$

$\begin{array}{ll}\hfill {\mathit{M}}_{u,u^{\prime }}\left(\widehat{\mathit{\theta }},{\mathit{\varphi }}^{\prime }\right)& \approx \sum _{j^{\prime }=1}^{N-1}\sum _{j^{″}=1}^{N-1}\sum _{mc=1}^{M_c}\sum _{m{c}^{\prime }=1}^{M_c}{q}_{\left(j^{\prime },mc\right),u}{\tilde{\sigma }}_{\left(j^{\prime },mc\right),\left(j^{″},m{c}^{\prime }\right)}{q}_{\left(j^{″},m{c}^{\prime }\right),u^{\prime }}\hfill \end{array}(\mathrm{22c})$

In Eq. 22, the FIM M is evaluated using nominal parameter valuesparameter values $\widehat{\mathit{\theta }}$ at operating conditions ϕ′. Recall, the parameter covariance matrix V represents the uncertainty in parameter estimates obtained from the least-squares regression problem. Classical nonlinear regression theory assumes the measurements are corrupted with random independently and identically distributed (i.i.d.) zero-mean observation uncertainty (Bates and Watts (1988)). Let the measurement covariance matrix Σ_p correspond to such multivariate Gaussian uncertainty. Furthermore, the sensitivity matrix Q contains the partial derivatives of each model prediction with respect to regressed model parameter. Thus, Eq. 22b is a first order approximation to propagate the measurement covariance Σ_p through the regressed model to obtain the parameter covariance V. Likewise, when the model residuals are small, Eq. 22b approximates the inverse of the reduced Hessian of the regression problem (Bard, 1974). Eq. 22c is the equivalent calculation expressed with summations. Here the pairs (j′, mc) and (j^″, mc’) index the partial pressures predicted by the model. Specifically, j′ and j^″ indicate the olefin species with carbon numbers j′ + 1 and j^″ + 1 (for example, j′ = 1 corresponds to ethylene). Likewise, mc and mc’ indicate discretization points along the reactor, in terms of scaled catalyst mass per Eq. 20, at which model responses are recorded. The regressed parameters are indexed by u and u′. ${\tilde{\sigma }}_{(j^{\prime },mc),(j^{\prime \prime },m{c}^{\prime })}$ is the element of the inverse of Σ_p that corresponds to the covariance between measurement (j′, mc) and (j^″, mc’). Likewise, q_(j′,mc),u corresponds to the element of Q for the sensitivity of model response p_j’ measured at point mc (or mc’) with respect to model parameter θ_u:

$q_{\left(j^{\prime },mc\right),u}={\left.\frac{\partial p_{j^{\prime },mc}}{\partial {\theta }_u}\right|}_{\widehat{\mathit{\theta }}}(23)$

These calculations are performed using the Pyomo.DOE package (Wang and Dowling, 2022). We approximate the inverse of the measurement uncertainties ${\tilde{\sigma }}_{(j^{\prime },mc),(j^{\prime \prime },m{c}^{\prime })}$ using the sum of squared residuals SSE from the regression problem in Eq. 21 as follows:

${\tilde{\sigma }}_{\left(j^{\prime },mc\right),\left(j^{″},m{c}^{\prime }\right)}\approx \left\{\begin{array}{cc}{\left(\frac{SSE}{N_D-N_{\theta }}\right)}^{-1}\hfill & j^{\prime }=j^{″}\text{and}mc=m{c}^{\prime }\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.(24)$

where N_D is the total number of data points used to calibrate the model and calculate SSE. N_θ is the total number of model parameters and defined in Table 1 for each ROK model.

If the FIM $\mathit{M}$ approximated using Eq. 22c is (near) singular, eigendecomposition of $\mathit{M}$, can be used to identify the direction of “sloppiness” (Chis et al., 2016), i.e., the parameter(s) which can assume multiple values without changing the model response and least-squares regression objective value.

$\mathit{M}=\mathit{U}\mathbf{\Lambda }{\mathit{U}}^T=\sum _{k=1}^{N_{\theta }}{\lambda }_k{\stackrel{˗}{\mathit{u}}}_k{\stackrel{˗}{\mathit{u}}}_k^T(25)$

In Eq. 25, FIM $\mathit{M}$ is decomposed into eigenvectors $\mathit{U}=[{\mathit{u}}_1,\dots ,{\mathit{u}}_{N_{\theta }}]$ and corresponding eigenvalues ${\lambda }_1,\dots ,{\lambda }_{N_{\theta }}$.¹$\mathbf{\Lambda }$ is a diagonal matrix with the eigenvalues on the diagonal. By definition, the eigenvectors ${\mathit{u}}_k\in {\mathbb{R}}^{1\times N_{\theta }}$ are unit vectors in the parameter space. Recall, the FIM $\mathit{M}$ is proportional to the reduced Hessian of the least-squares optimization problem. A (near-)zero eigenvalue indicates that the regression objective function has (near-)zero curvature in the direction of the corresponding eigenvector, which is a consequence of the model predictions being insensitive to perturbations in said direction. When interpreting the eigendecomposition, if ${\lambda }_k\approx 0$ and the corresponding ${\mathit{u}}_k$ predominantly points in the direction of a single parameter, said parameter is sloppy.

In this work, we use a sequential approach to identify ROK model sloppy parameters. In this approach, once a sloppy parameter is identified using Eq. 25, the parameter is removed as a decision variable from the regression problem and is fixed to a previously-obtained value that preserves model feasibility. Then the regression problem is re-solved, the FIM is recomputed for eigenvalue analysis, and the process is repeated until the FIM is no longer singular and the model is identifiable. This algorithm is further explained in Section 5.3.

Although an ill-posed model with sloppy parameters can be used for parameter estimation, the uncertainty in resulting parameter estimates is extremely large. Adding measurements (data) or removing (i.e., fixing) sloppy parameters as decision variables often makes the model identifiable and reduces the uncertainty of parameter estimates. This is a local analysis because $\mathit{M}$ is approximated at specific values of $\mathit{\theta }$ via Eq. 22; repeating the analysis at different values of $\mathit{\theta }$ may reveal different sloppy parameters.

3.5 Staged Reactor Design

Using the calibrated ROK models, we compute the optimal temperature profiles for a staged PBR. In place of one PBR with volume V, catalyst mass M_cat, and temperature T, we consider N_Z isothermal PBRs, each with catalyst loading M_cat/N_Z, in series with inter-stage cooling in the staged PBR design, as shown in Figure 3.

FIGURE 3

FIGURE 3. PBR divided into N_Z isothermal, equal-volume stages with heat exchangers for inter-stage cooling/heating. The dashed lines represent the presence of additional reactor and heat exchangers depending on the number of stages considered in the arrangement.

Following from the PBR governing equation, Eq. 20, the design equation for an olefin with j carbon atoms at each stage can be written as:

$N_Z{\left.\frac{d{p}_j}{d{m}_{\mathit{cat}}}\right|}_{T_z}-\frac{P{p}_{\text{inert}}}{SV{n}_{\mathit{cat}}{p_{\text{inert}}}_0}\sum _{n=2}^{j-2}\sum _{m=2}^{j-n}\left(-r_{n,m}\right){|}_{T_z}=0,\forall z\in \left\{1,\dots ,N_z\right\}(26)$

Under these assumptions, we propose a staged-PBR temperature optimization problem to maximize the formation of high-value olefins, with carbon numbers j_min to N:

$\begin{array}{cc}\hfill \underset{\begin{array}{c}{T}_z\end{array}}{\max }& \sum _{j_{\min }\le j\le N}{\left.p_j\right|}_{z=N_Z}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{d}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{E}\mathrm{q}.(\mathrm{26})\hfill \\ \hfill & \mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{b}\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\hfill \\ \hfill & \mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{s}\hfill \end{array}(27)$

In Eq. 27, the system operates at constant pressure and therefore, through ideal gas law, maximizing the partial pressure of select olefins maximizes the molar flow, i.e., formation of those olefins. The temperatures T_z for stages z ∈ {1, 2, …, N_z} are the design degrees of freedom. The number of reactors in series is varied while keeping the total available reactor volume constant. The problem is initialized using the 1-stage or previous best solution. For example, the 2-stage solution is used to initialize the 4-stage problem. Likewise, 1-, 3-, and 5-stage solutions are used to initialize the 5-, 6-, and 10-stage problems, respectively. The differential-algebraic equation (DAE) system was discretized along the reactor length using backward finite difference via Pyomo.DAE (Nicholson et al., 2018) and the resulting nonlinear optimization problem consists of 1,674 variables and N_z degrees of freedom. The problem is defined in Pyomo (Hart et al., 2017) and solved using IPOPT (Wächter and Biegler, 2006) with the HSL linear solver MA27 (HSL). Each optimization problem solved in under 14 seconds, including initialization.

The uncertainty in calibrated ROK model parameters induces uncertainty in the objective function of the staged reactor problem. We use the Uncertainty Propagation Toolbox in the IDAES-PSE framework (Lee et al., 2021) to propagate this parametric uncertainty through Eq. 28 using the following first-order error propagation formula (Rooney and Biegler, 2001):

$\text{Var}\left[f\left({\mathit{x}}^{\ast },\widehat{\mathit{\theta }}\right)\right]\approx \left(\frac{\partial f}{\partial \mathit{\theta }}+\frac{\partial f}{\partial \mathit{x}}\frac{\partial \mathit{x}}{\partial \mathit{\theta }}\right)\cdot \mathit{V}\cdot {\left(\frac{\partial f}{\partial \mathit{\theta }}+\frac{\partial f}{\partial \mathit{x}}\frac{\partial \mathit{x}}{\partial \mathit{\theta }}\right)}^T(28)$

In Eq. 28, V is the parameter covariance matrix calculated in Section 4.4, x^∗ is the optimal solution and $f({\mathit{x}}^{\ast },\widehat{\mathit{\theta }})$ is the corresponding objective function value for the staged reactor problem obtained using the parameters $\widehat{\mathit{\theta }}$. The nonlinear programming sensitivity code k_aug (Thierry, 2019) is used to calculate the gradients in Eq. 28.

4 Results: Model Calibration and Selection

4.1 Quality of Fit Metrics

To systematically train, evaluate, and compare ROK models from the library (Table 1), we performed weighted nonlinear regression (Eq. 21) using the MK simulation data described in Section 4.1. Table 2 reports quality of fits metrics R², mean squared error (MSE), mean absolute error (MAE), and mean squared logarithmic error (MSLE) for the six ROK model alternatives.

TABLE 2

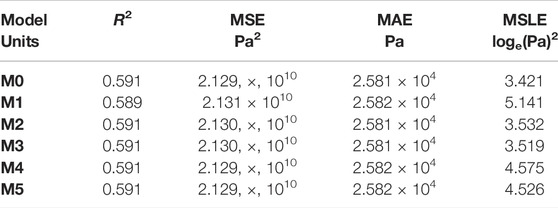
TABLE 2. Comparison of metrics R² (coefficient of determination), MSE (mean squared error) in Pa², MAE (mean absolute error) in Pa, and MSLE (mean squared logarithmic error) in log_e^(Pa)2

For ROK model training with MK simulation data, MSLE is the most informative metric. MK simulation data used to train the ROK models consists of olefin partial pressure values ranging from $\mathcal{O}({\mathrm{10}}^{-8})$ to $\mathcal{O}(10^7)$ Pa. As Table 2 shows, R², MSE, and MAE values for models M0 to M5 are almost identical and vary by less than 0.2%, 0.1%, and 0.05%, respectively, for the six candidate ROK models. The R², MSE, and MSE metrics, therefore, are most influenced by olefins with higher partial pressures (propylene, butene, pentene, and hexene); olefins with lower partial pressures (ethylene, heptene, octene, and nonene) do not significantly affect these metrics. Moreover, the geometrical interpretation of R² does not hold for nonlinear regression (Miaou et al., 1996; Spiess and Neumeyer, 2010). The species-wise MSE and MAE values for the remaining species are two and four orders of magnitude smaller, respectively, than the total values and, therefore, a log-scaled error metric such as MSLE is needed to assess model fit quality for olefins with low and high partial pressures. The MSLE values have the same order of magnitude for all olefin species, regardless of partial pressure. MSLE shows up to 33.5% difference in fit quality between the ROK models M5 (lowest MSLE) and M1 (highest MSLE). The MSLE of models M0, M2, and M3 are within 3% of each other and within 25% of models M4 and M5. The literature model M1, with its distinct kinetic functional forms (compared to the MK model as discussed in Section 4), has the largest MSLE value of all six ROK models which indicates it has the worst fit to MK simulation data. The fitted parameter values for the six ROK models are reported in Supplementary Tables S1-S6 in Supplementary Material. In ROK modeling literature, it is most common to qualitatively assess the quality of fit (Oliveira et al., 2010; Ying et al., 2015; Wang et al., 2021; Zhang and Sarathy, 2021) or report relative error metrics using experimental data (Radmanesh et al., 2006; Ebrahimi et al., 2018; Sani et al., 2018; Sun et al., 2018; John et al., 2019). In some cases, a metric such as R² (Yan et al., 2019) is reported, but it is challenging to meaningfully compare such fit metrics across different models and datasets.

Figures 4, 5 confirm that M1 fails to emulate MK model behavior and highlight the importance of model functional form and model assumptions (see Table 1). By virtue of having unique pre-exponential factor and activation energy values fitted for each olefin species and reaction type, M0 emulates MK simulations with similar accuracy as models M2 to M5. Although model M1 was extended to consider transformations up to nonene, instead of octene, the activation energy chain length dependence (Eqs. (9)-(10)), adsorption enthalpy (fixed), and adsorption isotherm model assumption (Eq. 14) are different compared to the MK model (Vernuccio et al., 2019); consequently, M1 struggles to emulate MK simulations. The introduction of adsorption enthalpy chain length dependence and change in adsorption isotherm model assumptions in models M2 to M5 (and additionally updated activation energy functional form of models M4 and M5), discussed in detail in Sections 4.2.6 and 4.2.7, respectively, and elaborated in Table 1, enable these models to capture MK model conversion trends and magnitudes better than model M1. As a result, Model M1 is not considered a viable model for MK model emulation and excluded from further analysis. There is also a significant gap between the conversions predicted by MK and ROK models M0 and M2 to M5. We hypothesize this is because the ROK models are missing some of the pertinent information (e.g., mathematical expressions in the rate law) and purpose model refinement as future work.

FIGURE 4

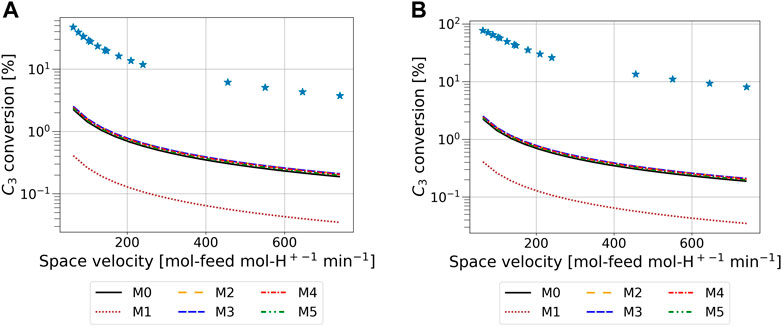
FIGURE 4. Propylene conversion from M0 to M5 with respect to space velocity at constant pressure (2.18 atm) and temperatures 483 K (A) and 522 K (B). The blue stars represent the MK model simulation data. The solid and dashed lines represent the reparameterized ROK model simulations. The lines for models M0 and M2 to M5 overlap each other.

FIGURE 5

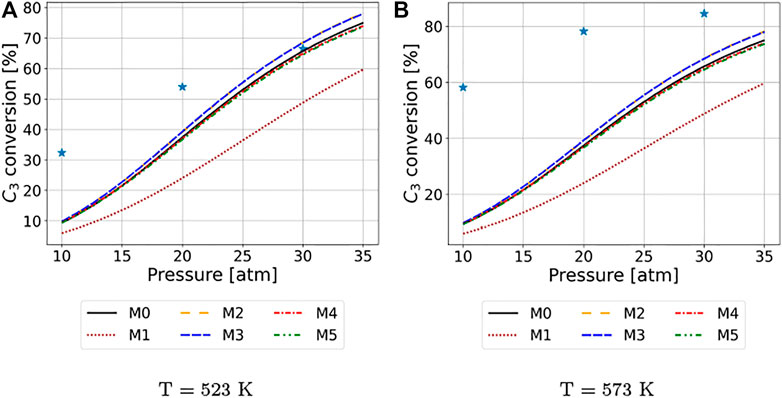
FIGURE 5. Propylene conversion from M0 to M5 with respect to pressure at constant space velocity (1123 $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$) and temperatures 523 K (A) and 573 K (B). The blue stars represent the MK model simulation data. The solid and dashed lines represent the reparameterized ROK model simulations. The lines for models M2 and M3 overlap each other and the lines for models M0, M4, and M5 overlap each other.

4.2 Sensitivity Analysis

Next, the calibrated ROK models were simulated with a mixed feed composition mirroring the Bakken shale basin (Ridha et al., 2018) and a reactor size estimated to create a space velocity of 25 $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ (which is reasonable for typical oligomerization reactors) over process-relevant temperatures of 473–1073 K and pressures of 2–40 atm.

Sensitivity analysis shown in Figure 6 indicates that models M3 to M5 are most reliable at process conditions. Since oligomerization is exothermic and the reverse cracking is endothermic, a higher conversion to heavier olefins is expected at lower temperatures and a lower conversion to heavier olefins is expected behavior at higher temperatures. Despite having a good in-sample fit, model M0 is unable to emulate this thermodynamic behavior; it demonstrates the opposite behavior by predicting higher conversions with increasing temperatures. Additionally, IPOPT struggles to converge material balances for the olefins at high temperatures and pressures (top-right corner of Figure 6A). The apparent good fit quality of M0 to MK simulation data, discussed previously, is, therefore, a result of over-parameterization of the ROK model. Referring back to Table 1, M0 is defined using pairwise unique activation energies and pre-exponential factors for each olefin species and reaction type (Eq. 2) and consists of 24 degrees of freedom (number of fitted parameters). This improves the fit quality of M0 to training data (MK simulations) but, leads to poor scaling with temperature and space velocity due to the lack of operating condition dependence of the parameters. Models M2 to M5, on the other hand, each consist of only nine fitted parameters but, capture oligomerization thermodynamics quite well (through the parametric dependencies on operating conditions) across the range of temperatures and pressures and predict maximum propylene conversion at temperatures below 600 K. However, IPOPT once again struggles to converge the olefin material balances in M2 and M3 at higher temperature and pressure conditions (top-right corner of Figure 6B). For models M0, M2, and M3, IPOPT also fails to converge the olefin material balances at higher temperatures and pressures. These convergence issues persist even with alternate model scaling strategies, which are discussed in Section 5.5 and Supplementary Section S1 of the Supporting Material. IPOPT converges successfully across the entire range of operating conditions analyzed for models M4 and M5.

FIGURE 6

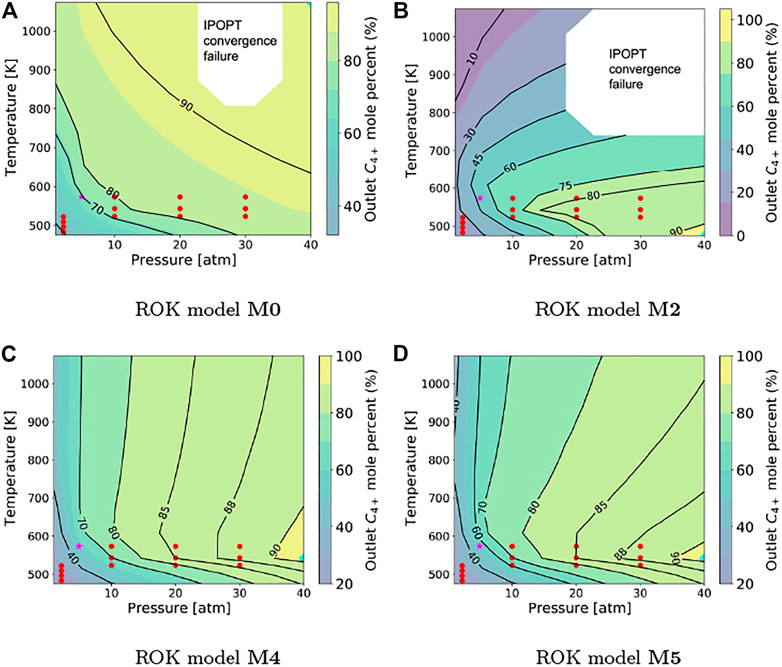
FIGURE 6. Propylene conversion to butene and heavier olefins between 473 K and 1073 K and 1 atm–40 atm using (A) M0, (B) M2 (M3 has similar countours to M2), (C) M4, and (D) M5. The red dots represent the temperature and pressure conditions at which MK data is available and was used to train the ROK models (although at different space velocities). The magenta star represents the temperature and pressure conditions suggested by Ridha et al. (2018) for process operations. The cyan-colored diamond represents the condition for maximum conversion. The white space, as labeled, represents the operating conditions at which IPOPT is unable to converge the olefin material balance for ROK models M0, M2, and M3 (similar to M2 but, not shown here).

4.3 Identifiability Analysis

Model identifiability analysis is important to properly characterize the uncertainty in estimated parameters. For models M2 to M5, one or more parameters are sloppy. We use the following sequential approach to identify and remove (fix) the sloppy model parameters:

1) Compute the FIM using Eq. 22

2) If the condition number of the FIM is smaller than $\mathcal{O}(10^8)$, STOP.

3) Perform an eigen decomposition of the FIM.

4) Fix the parameter with the largest contribution to the eigenvector that corresponds to the smallest eigenvalue.

5) (Optional) Refit the remaining parameters.

6) GOTO Step 1.

Using this procedure, we analyze model M5. We will use Eqs 29, 30, which are the expanded-form of the rate law from Eq. 8 and Table 1, to provide physical interpretations for the identifiability analysis results.

$\log \left(k_{1,n,m}^{\prime }\right)=\log \left({\alpha }_1^{⁗}\right)+\log \left(\frac{T}{T_{\mathit{ref}}}\right)+\frac{n{\beta }_{\mathit{ads}}+{\alpha }_{\mathit{ads}}-E_0+{\kappa }_1\left(\delta -\mathrm{\Delta }j{\gamma }^{\prime }\right)}{RT}(29)$

$\log \left(k_{2,n,m}^{\prime }\right)=\log \left({\alpha }_2^{⁗}\right)+\log \left(\frac{T}{T_{\mathit{ref}}}\right)+\frac{n{\beta }_{\mathit{ads}}+{\alpha }_{\mathit{ads}}-E_0-\left(1-{\kappa }_2\right)\left(\delta +\mathrm{\Delta }j{\gamma }^{\prime }\right)}{RT}(30)$

Identifiability Iteration 1 for M5: Without fixing any parameter, the condition number of the FIM is 3.49, ×, 10²¹. Supplementary Table S16 in Supplementary Material reports the eigen decomposition of the FIM for M5 with nine fitted parameters; these results show that parameter γ′ is sloppy. γ′ cannot be identified uniquely since Δj in Eqs 29, 30 denotes the change in number of C-atoms between reactants and products and, therefore, takes a value of zero (law of conservation).

Identifiability Iteration 2 for M5: With γ′ fixed, the condition number of the FIM decreases to 3.16 × 10¹⁸. With eight fitted parameters, the eigen decomposition reported in Supplememtary Table S17 in Supplementary Material shows δ is the next sloppy parameter. Referring to Eqs 29, 30, δ forms a bilinear combination with parameters κ₁ and κ₂. At most only one parameter in a bilinear combination can be uniquely estimated.

Identifiability Iteration 3 for M5: With γ′ and δ fixed (and seven remaining parameters), the condition number of the FIM decreases to 7.21 × 10¹⁷. The eigen decomposition reported in Supplementary Table S18 shows that E₀ is the next sloppy parameter. In Eqs 29, 30, E₀ forms a linear combination with two other fitted parameters—α_ads and κ_i from the bilinear term κ_iδ—out of which only one parameter can be estimated uniquely. E₀ is, therefore, fixed in this iteration.

Identifiability Iteration 4 for M5: With γ′, δ, and E₀ fixed, the condition number of the FIM decreased to 7.95 × 10¹⁶. Supplementary Table S19 reveals that κ₁ is the next sloppy parameter. Inspecting Eq. 29 shows that despite fixing E₀, κ₁ in the bilinear term κ₁δ forms a linear combination with α_ads (fitted parameter) and, therefore, could not be identified uniquely.

Identifiability Iteration 5 for M5: With γ′, δ, E₀, and κ₁ fixed, the condition number of the FIM decreased to 1.56 × 10⁶. Supplementary Table S20 in Supplementary Material shows the eigen decomposition. This is smaller than the threshold of $\mathcal{O}(10^8)$ and the identifiability analysis procedure is terminated.

Per Table 1, model M4 is structurally similar to M5. As expected, repeating the identifiability analysis also reveals γ′, δ, E₀, and κ₁ as the sloppy parameters for model M4. Fixing these parameters improved the condition number of the FIM from 2.55 × 10²¹ to 2.40, ×, 10⁶. For completeness, Supplementary Tables S11—S15 in Supplementary Material tabulate the eigenvalue analysis for model M4 in sequential order.

We performed similar analysis for M2 and M3. Fixing parameters ${\alpha }_1^{\prime }$ (M2) and ${\alpha }_1^{\prime \prime \prime }$ (M3) reduced the FIM condition numbers from 3.87 × 10⁹ to 1.47 × 10⁷ and 7.70, ×, 10⁹ to 1.30, ×, 10⁷, respectively. Supplementary Tables S7–S10 tabulate the eigenvalue analysis for models M2 and M3, respectively.

Recalibration of models M2 to M5 with sloppy parameters fixed does not affect model fit quality. This is because the presence of sloppy parameters reduces the confidence of parameter estimates without affecting the overall model fit quality. In this work, all results for models M2 to M5 were generated after fixing the sloppy parameters. As we will see in Section 6, the fixing of sloppy parameters to make models identifiable not only reduces parameter estimate uncertainties but, as a consequence, improves the confidence in results obtained using the updated models.

For identifiability analysis described above, we assume the measurement covariance matrices Σ_p are identity matrices times the following scalars: 9.47 × 10⁻⁴ atm² (M2), 9.46 × 10⁻⁴ atm² (M3), 9.93 × 10⁻⁴ atm² (M4), and 9.92 × 10⁻⁴ atm² (M5).

4.4 Product Distribution Predictions

Figure 7 shows that none of the ROK models, including M4 and M5, accurately recapitulate product distribution at both high and low pressures. The ROK models under-predict propylene conversion at low pressures (Figure 7A) and models M2 and M3 over-predict propylene conversion at high pressure (Figure 7B). Models M4 and M5, which have a low in-sample residual, match propylene conversions well only at high pressure but, over-predict the formation of nonene. The overproduction of C₉ species suggests that the flux of the MK model might be artificially truncated by the termination criterion adopted for the automated network generation. The exclusion of C_>9 from the reaction network results in an accumulation of C₉ species which are not allowed to further oligomerize. As a result, C₉ intermediates in the MK model are forced to deprotonate or generate smaller products via β-scission. It is worth noting that the number of species and reactions that are automatically generated for an oligomerization network increase exponentially as a function of the termination criterion (Vernuccio and Broadbelt, 2019). Thus, the inclusion of heavier species in the reaction mechanism would result in unmanageable models and impracticable computational costs.

FIGURE 7

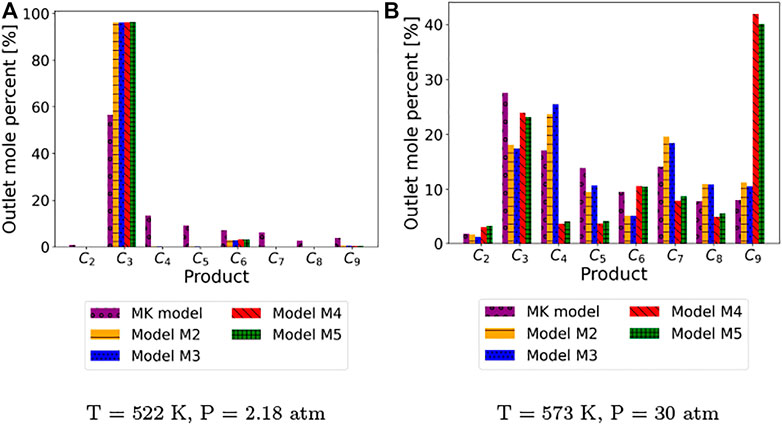
FIGURE 7. Product distribution by outlet mole percent at (A) low pressure operation and (B) high pressure operation. Indicated in magenta are the lumped product mole percents predicted by the MK model at the corresponding temperature and pressure conditions.

The differences observed in Figure 7 for low and high pressure operation can be also ascribed to the different MK model assumptions that were used to generate the low and high-pressure data. In order to investigate this aspect, we used the extended MK model described in 3.1 to simulate the oligomerization process at 523 K and 10–30 atm. Figure 8 shows a parity plot for the product selectivity calculated with the extended model and the MK model used in this work. At 10 atm, the rate of hydride transfer which leads to the formation of paraffins is negligible and the omission of the corresponding reactions from the MK model results in minor deviations from the model performance. However, at 20 and 30 atm, the presence of these additional reactions alters the rates of oligomerization and the product selectivity. Thus, the omission of hydride transfer, cyclization as well as aromatization steps, not included in the MK model for numerical tractability, has an impact on the overall model performance. Due to this implicit issue with the data source, the overall in-sample fit quality of the ROK models is a trade-off across the range of pressure conditions over which the models were calibrated. In addition to simplified chemistry, this trade-off makes it very challenging to train a “one-size-fits-all” ROK model.

FIGURE 8

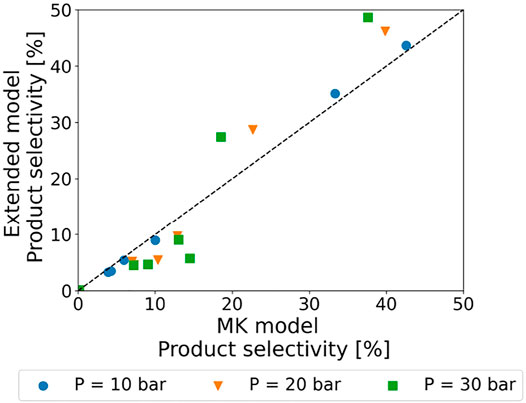
FIGURE 8. Parity plot to compare the selectivity for ethylene, butene, and heavier olefins at varying feed pressures using the extended MK model and the MK model used to validate the ROK models.

4.5 Objective Weight Sensitivity Analysis

Finally, we studied the effect of weight w in the objective of the optimization problem in Eq. 21. Supplementary Figure S2 in Supplementary Material shows the trade-off in SSE and SSPE with varying values of w. A weight w of 0.1 balances the trade-off and produces calibrated models that best emulate the entire product distribution (Supplementary Figure S3). Supplementary Figure S1 in Supplementary Material shows that ROK model predictions are robust to the choice of model scaling, i.e., partial pressures as shown in Eq. 1, or mole fractions as shown in Supplementary Equation S2. Supplementary Figure S2 in Supplementary Material shows that model fit for the ROK models is also robust to SSE objective function scaling options shown in Supplementary Equation S3,S4.

5 Results: Reactor Temperature Optimization

We now explore how ROK model selection impacts reactor design decisions, especially the temperature profile, using a mixed feed composition mirroring the Bakken shale basin (Ridha et al., 2018) and a total reactor size estimated to create a space velocity of 25 $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ with up to 10 temperature stages. Figure 9A shows the optimal temperature profiles obtained by resolving Eq. 27 using ROK models M2 to M5 for a 10-stage PBR. The monotonically decreasing temperatures across the PBRs in series shown in Figure 9A maximizes the production of heavier olefins. Surprisingly, ROK models M2 to M5 predict qualitatively-similar optimal temperature profiles despite the difference in quality of fit and conversion predictions shown in Figure 6. To understand this result, recall that the rates of oligomerization and cracking are temperature-sensitive. While forward exothermic oligomerization yields heavier (preferred) olefins, reverse endothermic cracking breaks down heavier olefins to lighter olefins. Therefore, a monotonically decreasing temperature profile improves the conversion to heavier olefins. Quantitatively, however, the profiles differ across the four ROK models. While the temperature decreases by 11% for M2 (630 K–562 K) and 13% for M3 (640 K–558 K) across the 10 stages, for models M4 and M5, the decrease is much larger at approximately 38% (900 K–560 K) and 35% (847 K–554 K), respectively. Additionally, the first stage temperature for M4 (900 K) is almost 43% higher than M2 (630 K) while the effluent temperature varies by less than 1% across all four models. From a process design perspective, despite the quantitative differences, the monotonically decreasing temperature profiles are a favorable outcome since the same temperature profile is desired for the reactor irrespective of ROK model choice to preserve the physical arrangement of the reactor and necessary heat exchangers.

FIGURE 9

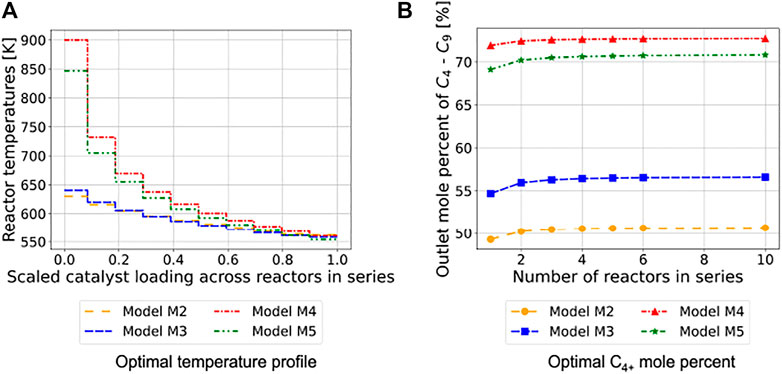
FIGURE 9. Optimization results from the staged reactor design calculations aimed at maximizing outlet mole percent of butene and heavier olefins (A) The optimal temperature profile across 10 staged isothermal PBRs for models M2 to M5. Each step in the plot corresponds to the temperature in a staged reactor. Catalyst loading is directly proportional to the volume of a PBR; the horizontal axis is presented in terms of scaled catalyst loading (similar to profiles generated across a PBR) and is indicative of the PBR stages from first to last (B) The optimal outlet mole percent of butene and heavier olefins obtained from the staged reactor calculations by resolving Eq. 28 for one to 6 and 10 stages.

Despite the similar temperature profiles, Figure 9B shows that the optimal staged-reactor outlet conversion varies significantly based on the choice of ROK model. Model M2 consistently predicts up to 22 mol% and 20 mol% less butene and heavier olefin production compared to models M4 and M5, respectively, across the different PBR staging configurations. This difference in the optimal effluent composition (i.e., objective function) reflects the effect of model-form uncertainty which may have significant consequences for both reactor design and the integrated shale gas conversion process. Interestingly, the yield of desired butene and heavier products increases by up to 2.5 mol% across all four ROK models as the number of isothermal PBRs in series increases. Moreover, the increase in yield diminishes beyond four temperature stages for all four ROK models.

Figure 10 further shows the effect of ROK model choice, i.e., model-form uncertainty, on the product distribution leaving the reactor. For models M2 and M3, lighter olefins (up to butene) are more preferred compared to models M4 and M5 which favor the formation of heavier olefins (pentene and higher). This behavior indicates that the ROK model-form affects the formation rate of specific olefins within the model. Recall, M2 and M3 incorporate chain length dependencies for activation energies via Eqs 9, 10, which are adapted from Oliveira et al. (2010). In contrast, M4 and M5 use chain length dependencies in Eqs 11—13, which are adapted from the MK model. These results highlight the impact of chemistry modeling choices, especially chain length dependencies, on optimal reactor design.

FIGURE 10

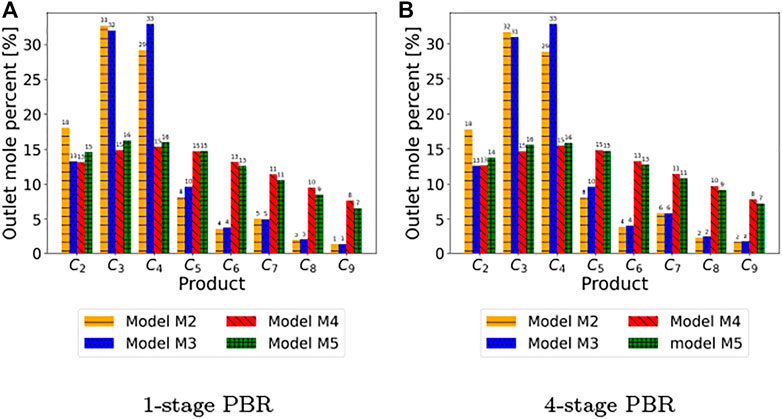
FIGURE 10. The optimal product distributions predicted using models M2 to M5. The outlet mole percent of each olefin species is reported above each bar (A) 1-stage PBR, special case of staged reactor design: traditional reactor temperature optimization (B) 4-stage PBR: when number of staged is increased beyond four, the cumulative outlet mole percent of butene and heavier olefins remains roughly the same. Thus, we have only shown the species-wise product distribution up to four stages here. The two plots show that the product distribution from models M2 and M3 are quite different from models M4 and M5.

Figure 11 shows the outlet composition when the temperature optimization problem in Eq. 27 is resolved for space velocities from 0.025 to 25,000 $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$ which correspond to laboratory and conventional gas-processing reactors, respectively. These optimization results demonstrate that models M2 to M5 exhibit the same sensitivity to changing space velocity and predict a decrease in outlet mole percentage of butene and heavier olefins as the space velocity is increased. Increasing space velocity decreases the residence time of the reacting feed in the reactor which reduces the extent of the reactions occurring and subsequent conversion to heavier olefins. However, the difference in product distribution predictions is persistent across the ROK models over the range of space velocities considered. Models M4 and M5 consistently predict a product outlet that is rich in pentene and heavier olefins compared to models M2 and M3. Thus, additional experiments, simulations, or both could be performed at these conditions to further distinguish between models M2 to M5. However, because the MK model has not been validated yet with high conversion laboratory data, this is left as future work. At this point, we can, therefore, conclude that models M2 to M5 emulate expected kinetic behavior over a wide range of space velocities despite differences in product distribution predictions.

FIGURE 11

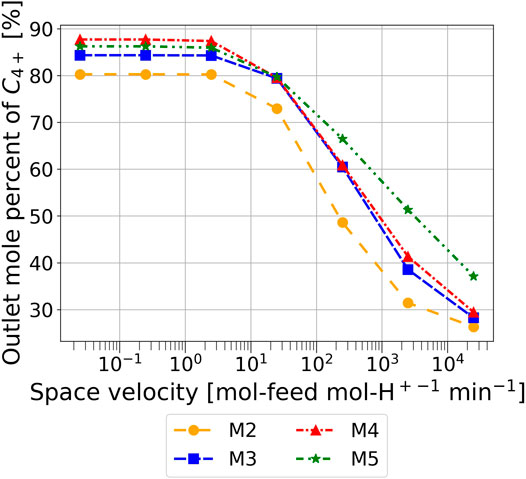
FIGURE 11. Outlet mole percent of butene and heavier olefins predicted at optimal temperature operation of a 4-stage PBR at different space velocities predicted by models M2 to M5.

We also find that parametric uncertainty induces less than a 9.9 mol% uncertainty in the optimized butene and heavier olefin production. Table 3 shows the results of propagating the parameter covariance matrix V defined in Eq. 22 through the 4-stage temperature optimization problem defined in Eq. 27. The reported standard deviations in the objective function were calculated using Eq. 28 for models M2 to M5 using V estimated with and without fixing sloppy parameters. As expected, fixing sloppy model parameters improves the confidence in optimal results by reducing parametric uncertainty even when the objective function value remains unaffected. Fixing sloppy parameters in models M2 and M3 leads to an almost 90% reduction in standard deviation of the objective function and increases the confidence in optimal decisions (as opposed to more conservative decisions obtained using models with sloppy parameters). Similarly, fixing of sloppy parameters in M4 and M5 facilitates confident decisions on par with sloppy-parameter-fixed M2 and M3. The standard deviation with unfixed sloppy parameters in M4 and M5 is extremely large because the covariance matrix (V) is near singular. These results are included for completeness, but we caution against over-interpretation.

TABLE 3

TABLE 3. Comparison of the effect of parametric uncertainty in models M2 to M5 on optimal conversion predictions to butene and heavier olefins. The Objective column lists the value of the optimization problem objective function. The following two columns list the standard deviation in predicted objective function values due to parametric uncertainties associated with the ROK models with sloppy parameters not fixed and sloppy parameters fixed, respectively.

Additionally, IPOPT required under 14 seconds on average to solve Eq. 27 using Macbook Pro 2020 with 1.4 GHz Quad-Core Intel Core i5 and 8 GB of RAM. We speculate this low computation time is sufficient to integrate the ROK model or reactor optimization problem into sequential modular or equation-oriented flowsheet optimization tools but, leave the analysis of an integrated process as future work.

6 Conclusion

This paper demonstrates ROK modeling strategies to embed multi-product MK modeling information into computationally tractable nonlinear reactor design optimization problems. We consider partial pressure data generated using the propylene oligomerization MK model from Vernuccio et al. (2019) that tracks the transformation of 909 species using 2,345 net reaction rates over HZSM-5 catalyst. We postulate a library of ROK models (see Table 1) and find that the candidate ROK models which most closely mimic MK model and its assumptions (e.g., similar chain length dependence) better emulate MK simulations. Statistical fit quality assessment shows that mean squared logarithmic error (MSLE) successfully quantifies the prediction quality for all olefin species (low and high partial pressures) and, therefore, is more informative compared to R², mean squared error (MSE), and mean absolute error (MAE). Through sensitivity analyses, we show that ROK models with temperature and olefin chain length dependencies that best mimic the MK model exhibit expected thermodynamic behavior for oligomerization and improved tractability across conditions relevant to gas-processing systems. Sequential model identifiability analysis shows that the candidate models contain one or more sloppy parameters which when fixed through a systematic eigenvalue analysis of the FIM, lead to more meaningful parametric uncertainty estimates. Next, we demonstrate nonlinear temperature optimization of a staged packed bed reactor (PBR) using a subset of the four best ROK models. We find that optimal temperature profiles are qualitatively-consistent and decrease monotonically. Quantitatively, the optimal temperature varies by up to 43% across ROK models at the first stage while the effluent temperature is within 1% for all four ROK models. The optimal design decisions are consistent across six orders of magnitude of space velocity and gives the qualitative insight that the optimal temperature profile in the staged-reactor configuration is monotonically decreasing. All four ROK models predict an increase in heavier olefin production of up to 2.5% for a 4-stage reactor configuration and show that there is limited benefit of adding more than four stages. We find that this model-form, i.e., epistemic, uncertainty results in butene and heavier olefins predicted varies up to 22% across ROK models. This is twice the impact of parametric uncertainty, which, approximated with a first-order propagation formula, resulted in a standard deviation in the objective of less than 9.9%. These results highlight the importance of accounting for both parametric and model-form uncertainties in multi-scale reactor and process design optimization.

This paper highlights several nuanced aspects of ROK model selection; there is no single “best-fit” model for all simulation conditions. Validation of MK models using high pressure experiments that track conversion to heavier olefins and paraffins, which is left as future work, can facilitate further extensions and discrimination between ROK models. Additionally, machine learning, hybrid, or distribution-emulating kinetic models should be explored to reconcile the difference in predictions between ROK and MK models. As future work, design of experiments can be deployed to maximize information gain from either MK simulations or laboratory kinetic characterization which, in turn, will enhance ROK model fit and prediction quality. Discrepancies in predicted conversion across ROK models indicate that reactor configuration (staging) and design (temperature profile) are not sufficient to balance epistemic (model-form) uncertainty introduced by the choice of ROK model. Instead, operational degrees of freedom in an integrated process design with ROK models need to be considered to mitigate ROK model-form uncertainty. The presented framework, which includes ROK model selection, regression and identifiability analysis, dynamic optimization, and uncertainty quantification and propagation steps, is generally applicable to all catalytic systems. Additionally, the specific model library proposed in this work can also be easily extended to consider oligomerization using other catalysts and other similar hydrocarbon conversion processes.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KG: Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualiziation, Writing - original draft; Writing—review and editing. SV: Microkinetic model building, Data generation, Data curation, Writing—review and editing. AD: Conceptualization, Funding acquisition, Project administration, Resources, Investigation, Methodology, Supervision, Writing—review and editing.

Funding

This work was supported primarily by the U.S. National Science Foundation under Cooperative Agreement No. EEC-1647722 with additional support from CBET-1941596. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge helpful and insightful discussions with Linda J. Broadbelt from the Department of Chemical and Biological Engineering at Northwestern University. We would like to acknowledge Jialu Wang at the University of Notre Dame for developing Pyomo.DOE and providing technical assistance with the Fisher information matrix calculations.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2022.898685/full#supplementary-material

References

Abel, O., Helbig, A., Marquardt, W., Zwick, H., and Daszkowski, T. (2000). Productivity Optimization of an Industrial Semi-Batch Polymerization Reactor Under Safety Constraints. J. Process Control 10, 351–362. doi:10.1016/S0959-1524(99)00049-9

CrossRef Full Text | Google Scholar

Alber, M., Buganza Tepole, A., Cannon, W. R., De, S., Dura-Bernal, S., Garikipati, K., et al. (2019). Integrating Machine Learning and Multiscale Modeling-Perspectives, Challenges, and Opportunities in the Biological, Biomedical, and Behavioral Sciences. npj Digit. Med. 2, 1–11. doi:10.1038/s41746-019-0193-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Avşar, E. (2017). Dimensionality Reduction for Predicting CO Conversion in Water Gas Shift Reaction Over Pt-Based Catalysts Using Support Vector Regression Models. Int. J. Hydrogen Energy 42, 23326–23333. doi:10.1016/j.ijhydene.2016.12.091

CrossRef Full Text | Google Scholar

Balakrishna, S., and Biegler, L. T. (1992). Constructive Targeting Approaches for the Synthesis of Chemical Reactor Networks. Ind. Eng. Chem. Res. 31, 300–312. doi:10.1021/ie00001a041

CrossRef Full Text | Google Scholar

Bangi, M. S. F., and Kwon, J. S.-I. (2020). Deep Hybrid Modeling of Chemical Process: Application to Hydraulic Fracturing. Comput. Chem. Eng. 134, 106696. doi:10.1016/j.compchemeng.2019.106696

CrossRef Full Text | Google Scholar

Bard, Y. (1974). Nonlinear Parameter Estimation. New York: Academic Press.

Google Scholar

Bates, D. M., and Watts, D. G. (1988). Nonlinear Regression Analysis and its Applications. New York: John Wiley & Sons.

Google Scholar

Bayer, B., Striedner, G., and Duerkop, M. (2020). Hybrid Modeling and Intensified DoE: An Approach to Accelerate Upstream Process Characterization. Biotechnol. J. 15, 2000121. doi:10.1002/biot.202000121

PubMed Abstract | CrossRef Full Text | Google Scholar

Becerra, A., Prabhu, A., Rongali, M. S., Velpur, S. C. S., Debusschere, B., and Walker, E. A. (2021). How a Quantum Computer Could Quantify Uncertainty in Microkinetic Models. J. Phys. Chem. Lett. 12, 6955–6960. doi:10.1021/acs.jpclett.1c01917

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhutani, N., Rangaiah, G. P., and Ray, A. K. (2006). First-Principles, Data-Based, and Hybrid Modeling and Optimization of an Industrial Hydrocracking Unit. Ind. Eng. Chem. Res. 45, 7807–7816. doi:10.1021/ie060247q

CrossRef Full Text | Google Scholar

Borges, P., Pinto, R. R., Lemos, M. A. N. D. A., Lemos, F., Védrine, J. C., Derouane, E. G., et al. (2007). Light Olefin Transformation Over ZSM-5 Zeolites A Kinetic Model for Olefin Consumption. Appl. Catal. A General 324, 20–29. doi:10.1016/j.apcata.2007.02.051

CrossRef Full Text | Google Scholar

Boţan, A., Ulm, F.-J., Pellenq, R. J.-M., and Coasne, B. (2015). Bottom-Up Model of Adsorption and Transport in Multiscale Porous Media. Phys. Rev. E 91, 032133. doi:10.1103/PhysRevE.91.032133

CrossRef Full Text | Google Scholar

Bradley, W., and Boukouvala, F. (2021). Two-Stage Approach to Parameter Estimation of Differential Equations Using Neural ODEs. Ind. Eng. Chem. Res. 60 (45), 16330–16344. doi:10.1021/acs.iecr.1c00552

CrossRef Full Text | Google Scholar

Breuil, P.-A. R., Magna, L., and Olivier-Bourbigou, H. (2015). Role of Homogeneous Catalysis in Oligomerization of Olefins : Focus on Selected Examples Based on Group 4 to Group 10 Transition Metal Complexes. Catal. Lett. 145, 173–192. doi:10.1007/s10562-014-1451-x

CrossRef Full Text | Google Scholar

Broadbelt, L. J., Stark, S. M., and Klein, M. T. (1994). Computer Generated Pyrolysis Modeling: On-The-Fly Generation of Species, Reactions, and Rates. Ind. Eng. Chem. Res. 33, 790–799. doi:10.1021/ie00028a003

CrossRef Full Text | Google Scholar

Cantrell, J., Bullin, J. A., McIntyre, G., Butts, C., and Cheatham, B. (2016). Economic Alternative for Remote and Stranded Natural Gas and Ethane in the US. URL: https://www.digitalrefining.com/article/1000990/economic-alternative-for-remote-and-stranded-natural-gas-and-ethane-in-the-us (Accessed January 5, 2022).

Google Scholar

Chis, O.-T., Villaverde, A. F., Banga, J. R., and Balsa-Canto, E. (2016). On the Relationship Between Sloppiness and Identifiability. Math. Biosci. 282, 147–161. doi:10.1016/j.mbs.2016.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Clancy, C. E., An, G., Cannon, W. R., Liu, Y., May, E. E., Ortoleva, P., et al. (2016). Multiscale Modeling in the Clinic: Drug Design and Development. Ann. Biomed. Eng. 44, 2591–2610. doi:10.1007/s10439-016-1563-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Coxson, P. G., Huesman, R. H., and Borland, L. (1995). Consequences of Using a Simplified Kinetic Model for Dynamic PET Data. J. Nucl. Med. 38, 660–667. URL: https://jnm.snmjournals.org/content/38/4/660.

Google Scholar

de Andrade Lima, L. R. P., and Hodouin, D. (2005). A Lumped Kinetic Model for Gold Ore Cyanidation. Hydrometallurgy 79, 121–137. doi:10.1016/j.hydromet.2005.06.001

CrossRef Full Text | Google Scholar

de Carvalho, T. P., Catapan, R. C., Oliveira, A. A. M., and Vlachos, D. G. (2018). Microkinetic Modeling and Reduced Rate Expression of the Water-Gas Shift Reaction on Nickel. Ind. Eng. Chem. Res. 57, 10269–10280. doi:10.1021/acs.iecr.8b01957

CrossRef Full Text | Google Scholar

De Jaegher, B., De Schepper, W., Verliefde, A., and Nopens, I. (2021). Enhancing Mechanistic Models with Neural Differential Equations to Predict Electrodialysis Fouling. Sep. Purif. Technol. 259, 118028. doi:10.1016/j.seppur.2020.118028

CrossRef Full Text | Google Scholar

Dixon, A. G., and Nijemeisland, M. (2001). CFD as a Design Tool for Fixed-Bed Reactors. Ind. Eng. Chem. Res. 40, 5246–5254. doi:10.1021/ie001035a

CrossRef Full Text | Google Scholar

Eason, J. P., and Biegler, L. T. (2016). A Trust Region Filter Method for Glass Box/Black Box Optimization. AIChE J. 62, 3124–3136. doi:10.1002/aic.15325

CrossRef Full Text | Google Scholar

Ebrahimi, A. A., Mousavi, H., Bayesteh, H., and Towfighi, J. (2018). Nine-Lumped Kinetic Model for VGO Catalytic Cracking; Using Catalyst Deactivation. Fuel 231, 118–125. doi:10.1016/j.fuel.2018.04.126

CrossRef Full Text | Google Scholar

Elnashaie, S. S., Abashar, M. E., and Al-Ubaid, A. S. (1988). Simulation and Optimization of an Industrial Ammonia Reactor. Ind. Eng. Chem. Res. 27, 2015–2022. doi:10.1021/ie00083a010

CrossRef Full Text | Google Scholar

Eugene, E. A., Phillip, W. A., and Dowling, A. W. (2019). Data Science-Enabled Molecular-To-Systems Engineering for Sustainable Water Treatment. Curr. Opin. Chem. Eng. 26, 122–130. doi:10.1016/j.coche.2019.10.002

CrossRef Full Text | Google Scholar

Fedder, G. K. (2000). “Top-Down Design of MEMS,” in 2000 International Conference on Modeling and Simulation of Microsystems-MSM 2000 and 2000 International Conference on Modeling and Simulation of Microsystems-MSM 2000 (San Diego: Citeseer), 7–10. URL: https://briefs.techconnect.org/wp-content/volumes/MSM2000/pdf/M1.02.pdf.

Google Scholar

Fermeglia, M., and Pricl, S. (2009). Multiscale Molecular Modeling in Nanostructured Material Design and Process System Engineering. Comput. Chem. Eng. 33, 1701–1710. doi:10.1016/j.compchemeng.2009.04.006

CrossRef Full Text | Google Scholar

Fischer, K. L., and Freund, H. (2021). Intensification of Load Flexible Fixed Bed Reactors by Optimal Design of Staged Reactor Setups. Chem. Eng. Process. - Process Intensif. 159, 108183. doi:10.1016/j.cep.2020.108183

CrossRef Full Text | Google Scholar

Foad, B., Elzohery, R., and Novog, D. R. (2022). Demonstration of Combined Reduced Order Model and Deep Neural Network for Emulation of a Time-Dependent Reactor Transient. Ann. Nucl. Energy 171, 109017. doi:10.1016/j.anucene.2022.109017

CrossRef Full Text | Google Scholar

Franceschini, G., and Macchietto, S. (2008). Model-Based Design of Experiments for Parameter Precision: State of the Art. Chem. Eng. Sci. 63, 4846–4872. doi:10.1016/j.ces.2007.11.034

CrossRef Full Text | Google Scholar

Franzoi, R. E., Kelly, J. D., Menezes, B. C., and Swartz, C. L. E. (2021). An Adaptive Sampling Surrogate Model Building Framework for the Optimization of Reaction Systems. Comput. Chem. Eng. 152, 107371. doi:10.1016/j.compchemeng.2021.107371

CrossRef Full Text | Google Scholar

Ganesh, H. S., Dean, D. P., Vernuccio, S., Edgar, T. F., Baldea, M., Broadbelt, L. J., et al. (2020). Product Value Modeling for a Natural Gas Liquid to Liquid Transportation Fuel Process. Ind. Eng. Chem. Res. 59, 3109–3119. doi:10.1021/acs.iecr.9b06673

CrossRef Full Text | Google Scholar

Gentric, C., Pla, F., Latifi, M. A., and Corriou, J. P. (1999). Optimization and Non-Linear Control of a Batch Emulsion Polymerization Reactor. Chem. Eng. J. 75, 31–46. doi:10.1016/S1385-8947(98)00116-8

CrossRef Full Text | Google Scholar

Goellner, J. (2012). Expanding the Shale Gas Infrastructure. Chem. Eng. Prog. 108, 49–52+59. URL: http://fscarbonmanagement.org/sites/default/files/cep/20120849.pdf.

Google Scholar

Gong, J., and You, F. (2018). A New Superstructure Optimization Paradigm for Process Synthesis with Product Distribution Optimization: Application to an Integrated Shale Gas Processing and Chemical Manufacturing Process. AIChE J. 64, 123–143. doi:10.1002/aic.15882

CrossRef Full Text | Google Scholar

Hadjiconstantinou, N. G., and Patera, A. T. (1997). Heterogeneous Atomistic-Continuum Representations for Dense Fluid Systems. Int. J. Mod. Phys. C 08, 967–976. doi:10.1142/S0129183197000837

CrossRef Full Text | Google Scholar

Hagh, B. (2003). Optimization of Autothermal Reactor for Maximum Hydrogen Production. Int. J. Hydrogen Energy 28, 1369–1377. doi:10.1016/S0360-3199(02)00292-6

CrossRef Full Text | Google Scholar

Hansen, A. G., van Well, W. J. M., and Stoltze, P. (2007). Microkinetic Modeling as a Tool in Catalyst Discovery. Top. Catal. 45, 219–222. doi:10.1007/s11244-007-0269-9

CrossRef Full Text | Google Scholar

Hart, W. E., Laird, C. D., Watson, J. P., Woodruff, D. L., Hackebeil, G. A., Nicholson, B. L., et al. (2017). Pyomo-Optimization Modeling in Python, Vol. 67. New York: Springer.

Google Scholar

He, T., Karimi, I. A., and Ju, Y. (2018). Review on the Design and Optimization of Natural Gas Liquefaction Processes for Onshore and Offshore Applications. Chem. Eng. Res. Des. 132, 89–114. doi:10.1016/j.cherd.2018.01.002

CrossRef Full Text | Google Scholar

Hillestad, M. (2010). Systematic Staging in Chemical Reactor Design. Chem. Eng. Sci. 65, 3301–3312. doi:10.1016/j.ces.2010.02.021

CrossRef Full Text | Google Scholar

Horstemeyer, M. F. (2009). “Multiscale Modeling: A Review,” in Practical Aspects of Computational Chemistry. Berlin, Germany: Springer, 87–135. doi:10.1007/978-90-481-2687-3_4

CrossRef Full Text | Google Scholar

HSL A Collection of Fortran Codes for Large-Scale Scientific Computation. URL: https://www.hsl.rl.ac.uk/. (Accessed January 5, 2022).

Google Scholar

Hutter, C., Stosch, M., Cruz Bournazou, M. N., and Butté, A. (2021). Knowledge Transfer Across Cell Lines Using Hybrid Gaussian Process Models with Entity Embedding Vectors. Biotech. Bioeng. 118, 4389–4401. doi:10.1002/bit.27907

CrossRef Full Text | Google Scholar

Jacob, S. M., Gross, B., Voltz, S. E., and Weekman, V. W.. (1976). A Lumping and Reaction Scheme for Catalytic Cracking. AIChE J. 22, 701–713. doi:10.1002/aic.690220412

CrossRef Full Text | Google Scholar

Jebahi, M., Dau, F., Charles, J.-L., and Iordanoff, I. (2016). Multiscale Modeling of Complex Dynamic Problems: An Overview and Recent Developments. Arch. Comput. Methods Eng. 23, 101–138. doi:10.1007/s11831-014-9136-6

CrossRef Full Text | Google Scholar

John, Y. M., Mustafa, M. A., Patel, R., and Mujtaba, I. M. (2019). Parameter Estimation of a Six-Lump Kinetic Model of an Industrial Fluid Catalytic Cracking Unit. Fuel 235, 1436–1454. doi:10.1016/j.fuel.2018.08.033

CrossRef Full Text | Google Scholar

Karst, F., Maestri, M., Freund, H., and Sundmacher, K. (2015). Reduction of Microkinetic Reaction Models for Reactor Optimization Exemplified for Hydrogen Production from Methane. Chem. Eng. J. 281, 981–994. doi:10.1016/j.cej.2015.06.119

CrossRef Full Text | Google Scholar

Kim, J., Seo, Y., and Chang, D. (2016). Economic Evaluation of a New Small-Scale LNG Supply Chain Using Liquid Nitrogen for Natural-Gas Liquefaction. Appl. Energy 182, 154–163. doi:10.1016/j.apenergy.2016.08.130

CrossRef Full Text | Google Scholar

Klise, K. A., Nicholson, B. L., Staid, A., and Woodruff, D. L. (2019). “Parmest: Parameter Estimation via Pyomo,” in Proceedings of the 9th International Conference on Foundations of Computer-Aided Process Design. Editors S.G. Muñoz, C.D. Laird, and M.J. Realff (New York: Elsevier), 41–46. Volume 47 of Computer Aided Chemical Engineering. doi:10.1016/B978-0-12-818597-1.50007-2

CrossRef Full Text | Google Scholar

Ko, J., Muhlenkamp, J. A., Bonita, Y., LiBretto, N. J., Miller, J. T., Hicks, J. C., et al. (2020). Experimental and Computational Investigation of the Role of P in Moderating Ethane Dehydrogenation Performance Over Ni-Based Catalysts. Ind. Eng. Chem. Res. 59, 12666–12676. doi:10.1021/acs.iecr.0c00908

CrossRef Full Text | Google Scholar

Kokossis, A. C., and Floudas, C. A. (1994). Optimization of Complex Reactor Networks-II. Nonisothermal Operation. Chem. Eng. Sci. 49, 1037–1051. doi:10.1016/0009-2509(94)80010-3

CrossRef Full Text | Google Scholar

Kotidis, P., and Kontoravdi, C. (2020). Harnessing the Potential of Artificial Neural Networks for Predicting Protein Glycosylation. Metab. Eng. Commun. 10, e00131. doi:10.1016/j.mec.2020.e00131

PubMed Abstract | CrossRef Full Text | Google Scholar

Laidler, K. J. (1984). The Development of the Arrhenius Equation. J. Chem. Educ. 61, 494. doi:10.1021/ed061p494

CrossRef Full Text | Google Scholar

Lakshmanan, A., and Biegler, L. T. (1996). Synthesis of Optimal Chemical Reactor Networks. Ind. Eng. Chem. Res. 35, 1344–1353. doi:10.1021/ie950344b

CrossRef Full Text | Google Scholar

Lee, A., Ghouse, J. H., Eslick, J. C., Laird, C. D., Siirola, J. D., Zamarripa, M. A., et al. (2021). The IDAES Process Modeling Framework and Model Library-Flexibility for Process Simulation and Optimization. Jnl Adv. Manuf. & Process 3, e10095. doi:10.1002/amp2.10095

CrossRef Full Text | Google Scholar

Li, Y., Stroberg, W., Lee, T.-R., Kim, H. S., Man, H., Ho, D., et al. (2014). Multiscale Modeling and Uncertainty Quantification in Nanoparticle-Mediated Drug/Gene Delivery. Comput. Mech. 53, 511–537. doi:10.1007/s00466-013-0953-5

CrossRef Full Text | Google Scholar

LLorca, J., González, C., Molina-Aldareguía, J. M., Segurado, J., Seltzer, R., Sket, F., et al. (2011). Multiscale Modeling of Composite Materials: A Roadmap Towards Virtual Testing. Adv. Mat. 23, 5130–5147. doi:10.1002/adma.201101683

CrossRef Full Text | Google Scholar

Maestri, M., Vlachos, D., Beretta, A., Groppi, G., and Tronconi, E. (2008). Steam and Dry Reforming of Methane on Rh: Microkinetic Analysis and Hierarchy of Kinetic Models. J. Catal. 259, 211–222. doi:10.1016/j.jcat.2008.08.008

CrossRef Full Text | Google Scholar

Maestri, M., Vlachos, D. G., Beretta, A., Groppi, G., and Tronconi, E. (2009). A C1microkinetic Model for Methane Conversion to Syngas on Rh/Al₂O₃. AIChE J. 55, 993–1008. doi:10.1002/aic.11767

CrossRef Full Text | Google Scholar

Manenti, F., Leon-Garzon, A. R., Ravaghi-Ardebili, Z., and Pirola, C. (2014). Systematic Staging Design Applied to the Fixed-Bed Reactor Series for Methanol and One-Step Methanol/Dimethyl Ether Synthesis. Appl. Therm. Eng. 70, 1228–1237. doi:10.1016/j.applthermaleng.2014.04.011

CrossRef Full Text | Google Scholar

Mei, Y., Abedi, V., Carbo, A., Zhang, X., Lu, P., Philipson, C., et al. (2015). Multiscale Modeling of Mucosal Immune Responses. BMC Bioinforma. 16, 1–14. doi:10.1186/1471-2105-16-S12-S2

CrossRef Full Text | Google Scholar

Mhadeshwar, A. B., and Vlachos, D. G. (2005). Is the Water-Gas Shift Reaction on Pt Simple? Catal. Today 105, 162–172. doi:10.1016/j.cattod.2005.04.003

CrossRef Full Text | Google Scholar

Miaou, S.-P., Lu, A., and Lum, H. S. (1996). Pitfalls of Using R2 to Evaluate Goodness of Fit of Accident Prediction Models. Transp. Res. Rec. 1542, 6–13. doi:10.1177/0361198196154200102

CrossRef Full Text | Google Scholar

Miriyala, S. S., Mittal, P., Majumdar, S., and Mitra, K. (2016). Comparative Study of Surrogate Approaches while Optimizing Computationally Expensive Reaction Networks. Chem. Eng. Sci. 140, 44–61. doi:10.1016/j.ces.2015.09.030

CrossRef Full Text | Google Scholar

Moríñigo, J. A., and Hermida-Quesada, J. (2016). Evaluation of Reduced-Order Kinetic Models for HTPB-Oxygen Combustion Using LES. Aerosp. Sci. Technol. 58, 358–368. doi:10.1016/j.ast.2016.08.027

CrossRef Full Text | Google Scholar

Mosavi, A., Shamshirband, S., Salwana, E., Chau, K.-W., and Tah, J. H. M. (2019). Prediction of Multi-Inputs Bubble Column Reactor Using a Novel Hybrid Model of Computational Fluid Dynamics and Machine Learning. Eng. Appl. Comput. Fluid Mech. 13, 482–492. doi:10.1080/19942060.2019.1613448

CrossRef Full Text | Google Scholar

Murase, A., Roberts, H. L., and Converse, A. O. (1970). Optimal Thermal Design of an Autothermal Ammonia Synthesis Reactor. Ind. Eng. Chem. Proc. Des. Dev. 9, 503–513. doi:10.1021/i260036a003

CrossRef Full Text | Google Scholar

Nguyen, C. M., De Moor, B. A., Reyniers, M.-F., and Marin, G. B. (2011). Physisorption and Chemisorption of Linear Alkenes in Zeolites: A Combined QM-Pot(MP2//B3LYP:GULP)-Statistical Thermodynamics Study. J. Phys. Chem. C 115, 23831–23847. doi:10.1021/jp2067606

CrossRef Full Text | Google Scholar

Nicholson, B., Siirola, J. D., Watson, J.-P., Zavala, V. M., and Biegler, L. T. (2018). pyomo.dae: A Modeling and Automatic Discretization Framework for Optimization with Differential and Algebraic Equations. Math. Prog. Comp. 10, 187–223. doi:10.1007/s12532-017-0127-0

CrossRef Full Text | Google Scholar

Oliveira, P., Borges, P., Pinto, R. R., Lemos, M. A. N. D. A., Lemos, F., Védrine, J. C., et al. (2010). Light Olefin Transformation Over ZSM-5 Zeolites with Different Acid Strengths - A Kinetic Model. Appl. Catal. A General 384, 177–185. doi:10.1016/j.apcata.2010.06.032

CrossRef Full Text | Google Scholar

Parr, R. G. (1983). Density Functional Theory. Annu. Rev. Phys. Chem. 34, 631–656. doi:10.1146/annurev.pc.34.100183.003215

CrossRef Full Text | Google Scholar

Partopour, B., and Dixon, A. G. (2019). Integrated Multiscale Modeling of Fixed Bed Reactors: Studying the Reactor Under Dynamic Reaction Conditions. Chem. Eng. J. 377, 119738. doi:10.1016/j.cej.2018.08.124

CrossRef Full Text | Google Scholar

Partopour, B., and Dixon, A. G. (2016). Reduced Microkinetics Model for Computational Fluid Dynamics (CFD) Simulation of the Fixed-Bed Partial Oxidation of Ethylene. Ind. Eng. Chem. Res. 55, 7296–7306. doi:10.1021/acs.iecr.6b00526

CrossRef Full Text | Google Scholar

Pechukas, P. (1981). Transition State Theory. Annu. Rev. Phys. Chem. 32, 159–177. doi:10.1146/annurev.pc.32.100181.001111

CrossRef Full Text | Google Scholar

Potočnik, P., Grabec, I., Šetinc, M., and Levec, J. (2003). “Hybrid Modeling of Kinetics for Methanol Synthesis,” in Soft Computing Approaches in Chemistry (Berlin: Springer), 297–315. doi:10.1007/978-3-540-36213-5_11

CrossRef Full Text | Google Scholar

Prasad, V., Karim, A. M., Ulissi, Z., Zagrobelny, M., and Vlachos, D. G. (2010). High Throughput Multiscale Modeling for Design of Experiments, Catalysts, and Reactors: Application to Hydrogen Production from Ammonia. Chem. Eng. Sci. 65, 240–246. doi:10.1016/j.ces.2009.05.054

CrossRef Full Text | Google Scholar

Psichogios, D. C., and Ungar, L. H. (1992). A Hybrid Neural Network-First Principles Approach to Process Modeling. AIChE J. 38, 1499–1511. doi:10.1002/aic.690381003

CrossRef Full Text | Google Scholar

Qi, H., Zhou, X.-G., Liu, L.-H., and Yuan, W.-K. (1999). A Hybrid Neural Network-First Principles Model for Fixed-Bed Reactor. Chem. Eng. Sci. 54, 2521–2526. doi:10.1016/S0009-2509(98)00523-5

CrossRef Full Text | Google Scholar

Quiceno, R., Pérez-Ramírez, J., Warnatz, J., and Deutschmann, O. (2006). Modeling the High-Temperature Catalytic Partial Oxidation of Methane Over Platinum Gauze: Detailed Gas-Phase and Surface Chemistries Coupled with 3D Flow Field Simulations. Appl. Catal. A General 303, 166–176. doi:10.1016/j.apcata.2006.01.041

CrossRef Full Text | Google Scholar

Radmanesh, R., Courbariaux, Y., Chaouki, J., and Guy, C. (2006). A Unified Lumped Approach in Kinetic Modeling of Biomass Pyrolysis. Fuel 85, 1211–1220. doi:10.1016/j.fuel.2005.11.021

CrossRef Full Text | Google Scholar

Rafiee, A., and Hillestad, M. (2013). Staging of the Fischer-Tropsch Reactor with a Cobalt-Based Catalyst. Chem. Eng. Technol. 36, a–n. doi:10.1002/ceat.201200700

CrossRef Full Text | Google Scholar

Rafiee, A., and Hillestad, M. (2012). Staging of the Fischer-Tropsch Reactor with an Iron Based Catalyst. Comput. Chem. Eng. 39, 75–83. doi:10.1016/j.compchemeng.2011.11.009

CrossRef Full Text | Google Scholar

Raimondeau, S., and Vlachos, D. G. (2002). Recent Developments on Multiscale, Hierarchical Modeling of Chemical Reactors. Chem. Eng. J. 90, 3–23. doi:10.1016/S1385-8947(02)00065-7

CrossRef Full Text | Google Scholar

Rawlings, J. B., and Ekerdt, J. G. (2002). Chemical Reactor Analysis and Design Fundamentals. Santa Barbara: Nob Hill Pub, LLC.

Google Scholar

Ridha, T., Li, Y., Gençer, E., Siirola, J., Miller, J., Ribeiro, F., et al. (2018). Valorization of Shale Gas Condensate to Liquid Hydrocarbons Through Catalytic Dehydrogenation and Oligomerization. Processes 6, 139. doi:10.3390/pr6090139

CrossRef Full Text | Google Scholar

Rim, J. E., Pinsky, P. M., and Van Osdol, W. W. (2009). Multiscale Modeling Framework of Transdermal Drug Delivery. Ann. Biomed. Eng. 37, 1217–1229. doi:10.1007/s10439-009-9678-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Rooney, W. C., and Biegler, L. T. (2001). Design for Model Parameter Uncertainty Using Nonlinear Confidence Regions. AIChE J. 47, 1794–1804. doi:10.1002/aic.690470811

CrossRef Full Text | Google Scholar

Salciccioli, M., Chen, Y., and Vlachos, D. G. (2011a). Microkinetic Modeling and Reduced Rate Expressions of Ethylene Hydrogenation and Ethane Hydrogenolysis on Platinum. Ind. Eng. Chem. Res. 50, 28–40. doi:10.1021/ie100364a

CrossRef Full Text | Google Scholar

Salciccioli, M., Stamatakis, M., Caratzoulas, S., and Vlachos, D. G. (2011b). A Review of Multiscale Modeling of Metal-Catalyzed Reactions: Mechanism Development for Complexity and Emergent Behavior. Chem. Eng. Sci. 66, 4319–4355. doi:10.1016/j.ces.2011.05.050

CrossRef Full Text | Google Scholar

Sani, A. G., Ebrahim, H. A., and Azarhoosh, M. J. (2018). 8-Lump Kinetic Model for Fluid Catalytic Cracking with Olefin Detailed Distribution Study. Fuel 225, 322–335. doi:10.1016/j.fuel.2018.03.087

CrossRef Full Text | Google Scholar

Sarazen, M. L., Doskocil, E., and Iglesia, E. (2016). Effects of Void Environment and Acid Strength on Alkene Oligomerization Selectivity. ACS Catal. 6, 7059–7070. doi:10.1021/acscatal.6b02128

CrossRef Full Text | Google Scholar

Schubert, T., Lechleitner, A., Lehner, M., and Hofer, W. (2020). 4-Lump Kinetic Model of the Co-Pyrolysis of LDPE and a Heavy Petroleum Fraction. Fuel 262, 116597. doi:10.1016/j.fuel.2019.116597

CrossRef Full Text | Google Scholar

Seber, G. A., and Wild, C. J. (1989). Nonlinear Regression. New York: John Wiley & Sons.

Google Scholar

Sieminski, A. (2016). Energy Information Administration. URL: https://www.eia.gov/pressroom/presentations/sieminski_06282016.pdf (Accessed January 5, 2022).

Google Scholar

Sinno, T. (2007). A Bottom-Up Multiscale View of Point-Defect Aggregation in Silicon. J. Cryst. Growth 303, 5–11. doi:10.1016/j.jcrysgro.2006.11.278

CrossRef Full Text | Google Scholar

Solle, D., Hitzmann, B., Herwig, C., Pereira Remelhe, M., Ulonska, S., Wuerth, L., et al. (2017). Between the Poles of Data-Driven and Mechanistic Modeling for Process Operation. Chem. Ing. Tech. 89, 542–561. doi:10.1002/cite.201600175

CrossRef Full Text | Google Scholar

Spiess, A.-N., and Neumeyer, N. (2010). An Evaluation of R2 as an Inadequate Measure for Nonlinear Models in Pharmacological and Biochemical Research: A Monte Carlo Approach. BMC Pharmacol. 10, 1–11. doi:10.1186/1471-2210-10-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Stamatakis, M. (2014). Kinetic Modelling of Heterogeneous Catalytic Systems. J. Phys. Condens. Matter 27, 013001. doi:10.1088/0953-8984/27/1/013001

PubMed Abstract | CrossRef Full Text | Google Scholar

Stamatakis, M., and Vlachos, D. G. (2012). Unraveling the Complexity of Catalytic Reactions via Kinetic Monte Carlo Simulation: Current Status and Frontiers. Acs Catal. 2, 2648–2663. doi:10.1021/cs3005709

CrossRef Full Text | Google Scholar

Sun, S., Meng, F., and Yan, H. (2018). A New Lumping Kinetic Model for Fluid Catalytic Cracking. Petroleum Sci. Technol. 36, 1951–1957. doi:10.1080/10916466.2018.1519576

CrossRef Full Text | Google Scholar

Sutton, J. E., Lorenzi, J. M., Krogel, J. T., Xiong, Q., Pannala, S., Matera, S., et al. (2018). Electrons to Reactors Multiscale Modeling: Catalytic CO Oxidation over RuO2. ACS Catal. 8, 5002–5016. doi:10.1021/acscatal.8b00713

CrossRef Full Text | Google Scholar

Tabak, S. A., Krambeck, F. J., and Garwood, W. E. (1986). Conversion of Propylene and Butylene Over ZSM-5 Catalyst. AIChE J. 32, 1526–1531. doi:10.1002/aic.690320913

CrossRef Full Text | Google Scholar

Talebi, H., Silani, M., Bordas, S. P. A., Kerfriden, P., and Rabczuk, T. (2014). A Computational Library for Multiscale Modeling of Material Failure. Comput. Mech. 53, 1047–1071. doi:10.1007/s00466-013-0948-2

CrossRef Full Text | Google Scholar

Tan, S. H., and Barton, P. I. (2015). Optimal Dynamic Allocation of Mobile Plants to Monetize Associated or Stranded Natural Gas, Part I: Bakken Shale Play Case Study. Energy 93, 1581–1594. doi:10.1016/j.energy.2015.10.043

CrossRef Full Text | Google Scholar

Terrell, E., Dellon, L. D., Dufour, A., Bartolomei, E., Broadbelt, L. J., and Garcia-Perez, M. (2019). A Review on Lignin Liquefaction: Advanced Characterization of Structure and Microkinetic Modeling. Ind. Eng. Chem. Res. 59, 526–555. doi:10.1021/acs.iecr.9b05744

CrossRef Full Text | Google Scholar

Teske, L. S. (2014). Integrating Rate Based Models into a Multi-Objective Process Design & Optimisation Framework Using Surrogate Models (Lausanne, Switzerland: EPFL). Technical Report. doi:10.5075/epfl-thesis-6302

CrossRef Full Text | Google Scholar

Thierry, D. (2019). Nonlinear Optimization Based Frameworks for Model Predictive Control, State-Estimation, Sensitivity Analysis, and Ill-Posed Problems (Pittsburgh: Carnegie Mellon University). Ph.D. thesis.

Tsay, C., and Baldea, M. (2019). 110th Anniversary: Using Data to Bridge the Time and Length Scales of Process Systems. Ind. Eng. Chem. Res. 58, 16696–16708. doi:10.1021/acs.iecr.9b02282

CrossRef Full Text | Google Scholar

Tsopanoglou, A., and Jiménez del Val, I. (2021). Moving Towards an Era of Hybrid Modelling: Advantages and Challenges of Coupling Mechanistic and Data-Driven Models for Upstream Pharmaceutical Bioprocesses. Curr. Opin. Chem. Eng. 32, 100691. doi:10.1016/j.coche.2021.100691

CrossRef Full Text | Google Scholar

Tsu, J., Díaz, V. H. G., and Willis, M. J. (2019). Computational Approaches to Kinetic Model Selection. Comput. Chem. Eng. 121, 618–632. doi:10.1016/j.compchemeng.2018.12.002

CrossRef Full Text | Google Scholar

Vajda, S., Rabitz, H., Walter, E., and Lecourtier, Y. (1989). Qualitative and Quantitative Identifiability Analysis of Nonlinear Chemical Kinetic Models. Chem. Eng. Commun. 83, 191–219. doi:10.1080/00986448908940662

CrossRef Full Text | Google Scholar

van der Hoef, M. A., Ye, M., van Sint Annaland, M., Andrews, A. T., Sundaresan, S., and Kuipers, J. A. M. (2006). Multiscale Modeling of Gas-Fluidized Beds. Adv. Chem. Eng. 31, 65–149. doi:10.1016/S0065-2377(06)31002-2

CrossRef Full Text | Google Scholar

Vassaux, M., Sinclair, R. C., Richardson, R. A., Suter, J. L., and Coveney, P. V. (2020). Toward High Fidelity Materials Property Prediction from Multiscale Modeling and Simulation. Adv. Theory Simul. 3, 1900122. doi:10.1002/adts.201900122

CrossRef Full Text | Google Scholar

Vernuccio, S., Bickel, E. E., Gounder, R., and Broadbelt, L. J. (2019). Microkinetic Model of Propylene Oligomerization on Brønsted Acidic Zeolites at Low Conversion. ACS Catal. 9, 8996–9008. doi:10.1021/acscatal.9b02066

CrossRef Full Text | Google Scholar

Vernuccio, S., and Broadbelt, L. J. (2019). Discerning Complex Reaction Networks Using Automated Generators. AIChE J. 65, e16663. doi:10.1002/aic.16663

CrossRef Full Text | Google Scholar

Vlachos, D. G. (2005). A Review of Multiscale Analysis: Examples from Systems Biology, Materials Engineering, and Other Fluid–Surface Interacting Systems. Adv. Chem. Eng. 30, 1–61. doi:10.1016/S0065-2377(05)30001-9

CrossRef Full Text | Google Scholar

Vlachos, D. G., Mhadeshwar, A. B., and Kaisare, N. S. (2006). Hierarchical Multiscale Model-Based Design of Experiments, Catalysts, and Reactors for Fuel Processing. Comput. Chem. Eng. 30, 1712–1724. doi:10.1016/j.compchemeng.2006.05.033

CrossRef Full Text | Google Scholar

Von Stosch, M., Oliveira, R., Peres, J., and Feyo de Azevedo, S. (2014). Hybrid Semi-Parametric Modeling in Process Systems Engineering: Past, Present and Future. Comput. Chem. Eng. 60, 86–101. doi:10.1016/j.compchemeng.2013.08.008

CrossRef Full Text | Google Scholar

Wächter, A., and Biegler, L. T. (2006). On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 106, 25–57. doi:10.1007/s10107-004-0559-y

CrossRef Full Text | Google Scholar

Wang, H., Li, Z., Li, Y., and Cai, N. (2021). Reduced-Order Model for CaO Carbonation Kinetics Measured Using Micro-Fluidized Bed Thermogravimetric Analysis. Chem. Eng. Sci. 229, 116039. doi:10.1016/j.ces.2020.116039

CrossRef Full Text | Google Scholar

Wang, J., and Dowling, A. W. (2022). Pyomo.DOE: An Open-Source Package for Model-Based Design of Experiments in Python. AIChE Journal. e17813. doi:10.1002/aic.17813

CrossRef Full Text | Google Scholar

Wang, J., Li, S., and Yang, B. (2018). Combustion Kinetic Model Development Using Surrogate Model Similarity Method. Combust. Theory Model. 22, 777–794. doi:10.1080/13647830.2018.1454607

CrossRef Full Text | Google Scholar

Warren, S. E. (1995). Double Precision Differential/Algebraic Sensitivity Analysis Code. version 00. URL: https://www.osti.gov/biblio/1230304 (Accessed January 5, 2022).

Google Scholar

Wilczewski, W. (2015). Growing US HGL Production Spurs Petrochemical Industry Investment. URL: https://www.eia.gov/todayinenergy/detail.php?id=19771 (Accessed January 5, 2022).

Google Scholar

Williams, T. J., and Otto, R. E. (1960). “A Generalized Chemical Processing Model for the Investigation of Computer Control,” in Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics. New York: IEEE, 79, 458–473. doi:10.1109/TCE.1960.6367296

CrossRef Full Text | Google Scholar

Wold, S., Esbensen, K., and Geladi, P. (1987). Principal Component Analysis. Chemom. Intelligent Laboratory Syst. 2, 37–52. doi:10.1016/0169-7439(87)80084-9

CrossRef Full Text | Google Scholar

Yan, T., Chen, K., Wang, L., Fang, T., Liu, Y., Zhang, Y., et al. (2019). A Six-Lumped Kinetic Model of Pyrolysis of Heavy Oil in Supercritical Methanol. Petroleum Sci. Technol. 37, 68–75. doi:10.1080/10916466.2018.1493501

CrossRef Full Text | Google Scholar

Yang, F., Dai, C., Tang, J., Xuan, J., and Cao, J. (2020). A Hybrid Deep Learning and Mechanistic Kinetics Model for the Prediction of Fluid Catalytic Cracking Performance. Chem. Eng. Res. Des. 155, 202–210. doi:10.1016/j.cherd.2020.01.013

CrossRef Full Text | Google Scholar

Yang, M., and You, F. (2018). Modular Methanol Manufacturing from Shale Gas: Techno‐Economic and Environmental Analyses of Conventional Large‐Scale Production versus Small‐Scale Distributed, Modular Processing. AIChE J. 64, 495–510. doi:10.1002/aic.15958

CrossRef Full Text | Google Scholar

Ying, L., Yuan, X., Ye, M., Cheng, Y., Li, X., and Liu, Z. (2015). A Seven Lumped Kinetic Model for Industrial Catalyst in DMTO Process. Chem. Eng. Res. Des. 100, 179–191. doi:10.1016/j.cherd.2015.05.024

CrossRef Full Text | Google Scholar

Zahedi, G., Elkamel, A., Lohi, A., Jahanmiri, A., and Rahimpor, M. R. (2005). Hybrid Artificial Neural Network-First Principle Model Formulation for the Unsteady State Simulation and Analysis of a Packed Bed Reactor for CO₂ Hydrogenation to Methanol. Chem. Eng. J. 115, 113–120. doi:10.1016/j.cej.2005.08.018

CrossRef Full Text | Google Scholar

Zhang, X., and Mani Sarathy, S. (2021). A Lumped Kinetic Model for High-Temperature Pyrolysis and Combustion of 50 Surrogate Fuel Components and Their Mixtures. Fuel 286, 119361. doi:10.1016/j.fuel.2020.119361

CrossRef Full Text | Google Scholar

Zhao, X., Liao, C., Ma, Y.-T., Ferrell, J. B., Schneebeli, S. T., and Li, J. (2019). Top-Down Multiscale Approach to Simulate Peptide Self-Assembly from Monomers. J. Chem. Theory Comput. 15, 1514–1522. doi:10.1021/acs.jctc.8b01025

PubMed Abstract | CrossRef Full Text | Google Scholar

Zong, G., Ning, H., Jiang, H., and Ouyang, F. (2010). The Lumping Kinetic Model for the Heavy Oil Catalytic Cracking MIP Process. Petroleum Sci. Technol. 28, 1778–1787. doi:10.1080/10916460903261749

CrossRef Full Text | Google Scholar

Nomenclature

Set and Indices

$\mathit{C}$ Set of number of car atoms in species

$\mathit{I}$ Set of type of reactions

N number of C-atoms in largest olefin species in reaction network

N_D Total number of datasets

N_θ Total number of parameters

N_Z Maximum number of PBR stages

i Index for type of reaction

j, n, m Indices for number of carbon atoms in an olefin species molecule

j′, j Model response indices for FIM calculations (j′, j^″ = j − 1)

k Index for eigenvalues and eigenvectors

mc, mc′ Indices for catalyst loading points along the length of the PBR where data is recorded

u, u′ Indices for elements in the parameter vector θ

z Index for number of temperature zones in staged PBR

Kinetic Model Variables and Parameters

α_i=1,n,m Frequency factor for oligomerization involving olefins with n, m, and n + m C-atoms in model M0, mol atm⁻² min⁻¹g⁻¹a.u.⁻¹

α_i=2,n,m Frequency factor for cracking involving olefins with n, m, and n + m C-atoms in model M0, mol atm⁻¹ min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=1}^{\prime }$ Frequency factor for oligomerization in models M1 and M2, mol atm⁻¹ min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=\mathbf{2}}^{\prime }$ Frequency factor for cracking in models M1 and M2, mol min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=1}^{\prime \prime }$ Frequency factor for oligomerization in model M4, mol atm⁻¹ min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=\mathbf{2}}^{\prime \prime }$ Frequency factor for cracking in model M4, mol min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=1}^{\prime \prime \prime }$ Frequency factor for oligomerization in model M3, mol atm⁻¹ min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=\mathbf{2}}^{\prime \prime \prime }$ Frequency factor for cracking in model M3, mol min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=\mathbf{1}}^{\prime \prime \prime \prime }$ Frequency factor for oligomerization in model M5, mol atm⁻¹ min⁻¹g⁻¹a.u.⁻¹

${\mathit{\alpha }}_{\mathit{i}=\mathbf{2}}^{\prime \prime \prime \prime }$ Frequency factor for cracking in model M5, mol min⁻¹g⁻¹a.u.⁻¹

α_ads Parameter to quantify dispersive Van der Waals interactions for models M2 to M5, J mol⁻¹

A_B Frequency factor of desorption for models M2 to M5, mol min⁻¹a.u.⁻¹g⁻¹

A_F Frequency factor of adsorption for models M2 to M5, mol min⁻¹atm⁻¹g⁻¹

β_i Compensation factor to relate pre-exponential rate constant and activation energies for reaction i in models M1 to M3, mol/J

β_ads Parameter to quantify local interactions of olefins with the acid site for models M2 to M5, J mol⁻¹

C_Z Concentration of active sites for model M1, a.u.

δ Standard heat of formation for olefins, J mol⁻¹

ΔH Enthalpy of adsorption for model M1, J mol⁻¹

ΔH′ Enthalpy of desorption for models M2 to M5, J mol⁻¹

${\mathit{\Delta }{\mathit{H}}_{\mathit{F}}}_j$ Heat of formation of olefin with j C-atoms, J mol⁻¹

${\mathit{\Delta }{\mathit{H}}_{\mathit{R}}}_{\mathit{i},\mathit{n},\mathit{m}}$ Heat of reaction for reaction i where olefins with n and m C-atoms react to produce olefin with n + m C-atoms, J mol⁻¹

E_i,n,m Activation energy for reaction i involving olefins with n, m, and n + m C-atoms in model M0, J mol⁻¹

${\mathit{E}}_{\mathit{i}}^{\prime }$ Chain length independent activation energy for reaction i in models M1 to M3, J mol⁻¹

${\mathit{E}}_{\mathit{i},\mathit{n},\mathit{m}}^{\prime }$ Chain length dependent activation energy for reaction i involving olefins with C-atoms n, m, and n + m in models M1 to M3, J mol⁻¹

${\mathit{E}}_{\mathit{i},\mathit{n},\mathit{m}}^{\prime \prime }$ Chain length dependent activation energy for reaction i involving olefins with C-atoms n, m, and n + m in models M4 and M5, J mol⁻¹

E₀ Intrinsic energy barrier for models M4 and M5, J mol⁻¹

F Total molar flow rate, mol min⁻¹

f_inert Inert molar flow rate, mol min⁻¹

f_j Molar flow rate of olefin with j C-atoms, mol min⁻¹

γ′ Coefficient for chain length dependence of heat of formation, J mol⁻¹

γ_i Parameter to model influence of chain length on activation energy of reaction i in models M1 to M3

k_{ads, backward} Rate constant of desorption for models M2 to M5, mol min⁻¹a.u.⁻¹g⁻¹

k_{ads, forward} Rate constant of adsorption for models M2 to M5, mol min⁻¹atm⁻¹g⁻¹

K₀ Langmuir adsorption equilibrium pre-exponential constant for model M1, atm⁻¹

${{\mathit{k}}^0}_{\mathit{i}=1,\mathit{n},\mathit{m}}$ Pre-exponential rate constant of oligomerization reaction of X_m+n olefin, mol min⁻¹atm⁻¹g⁻¹a.u.⁻¹

${{\mathit{k}}^0}_{\mathit{i}=2,\mathit{n},\mathit{m}}$ Pre-exponential rate constant of cracking reaction of X_m+n olefin, mol min⁻¹g⁻¹a.u.⁻¹

${\mathit{k}}_{\mathit{i}=1,\mathit{n},\mathit{m}}^{\prime }$ Rate constant of oligomerization reaction for C_m+n olefin, mol atm⁻² min⁻¹g⁻¹a.u.⁻¹

${\mathit{k}}_{\mathit{i}=2,\mathit{n},\mathit{m}}^{\prime }$ Rate constant of cracking reaction for C_m+n olefin, mol atm⁻¹ min⁻¹g⁻¹a.u.⁻¹

κ_i Transfer coefficient for reaction i in models M4 and M5

λ Log-transformed ratio of adsorption to desorption rate constants for models M2 to M5, a.u. atm⁻¹

M_cat Total mass of catalyst, g

m_cat Scaled differential mass of catalyst

n_cat Moles of active site per Gram of catalyst, mol g⁻¹

ν Volumetric flow rate of gas, m³ min⁻¹

ω Isotherm constant, a.u. atm⁻¹

P Total pressure inside reactor, atm

P_inlet Total inlet pressure, atm

p_inert Inert partial pressure, atm

${p_{\text{inert}}}_0$ Inlet inert partial pressure, atm

p_j Partial pressure of olefin with j carbon atoms, atm

${{\mathit{p}}_{\mathit{j}}}^{\mathit{obj}}$ Lumped partial pressure of olefins with j C-atoms predicted by MK model, atm

ϕ_i=2 Parameter to model influence of chain symmetry on activation energy of cracking in models M1 to M3

R Universal gas constant, m³ atm mol⁻¹ K⁻¹

r_i,n,m Rate of reaction type i for reaction of species with carbon numbers n and m, mol min⁻¹g⁻¹

ρ_cat Catalyst bulk density, g m⁻³

SV Space velocity, $\mathrm{m}\mathrm{o}\mathrm{l}-\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{l}-{{\mathrm{H}}^{+}}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$

T Reactor temperature, K

T_z Temperature of zth stage of staged PBR, K

V Reactor volume, m³

X_j Olefin species with j carbon atoms

X_jZ Olefin species X_j adsorbed on catalyst site Z

x_j Mole fraction of olefin with j C-atoms

${{\mathit{x}}_{\mathit{j}}}^{\mathit{obj}}$ Lumped mole fraction of olefins with j C-atoms predicted by MK model

Generic Variables and Parameters

Λ Matrix of eigenvalues

λ_k Eigenvalue

M Fisher information matrix

ϕ′ Vector of operating conditions

q_(j′,mc),u Sensitivity of model response (j′, mc) with respect to model parameter θ_u

Σ_p Measurement covariance matrix

${\tilde{\sigma }}_{({\mathit{j}}^{\prime },\mathit{m}\mathit{c}),({\mathit{j}}^{\prime \prime },\mathit{m}{\mathit{c}}^{\prime })}$ Element of ${\mathbf{\Sigma }}_{\mathit{p}}^{-1}$ corresponding to model responses (j′, mc) and (j^″, mc′)

$\widehat{\mathit{\theta }}$ Vector of nominal parameter values

U Matrix of eigenvectors

u_k Eigenvector

V Parameter covariance matrix