- 1EDF R&D SEQUOIA, Palaiseau, France
- 2Institute for Energy Engineering, Technische Universität Berlin, Berlin, Germany
With new materials, objectives or constraints, it becomes increasingly difficult to develop optimal processes using conventional heuristics-based or superstructure-based methods. Hence, data-driven alternatives have emerged recently, to increase creativity and accelerate the development of innovative technologies without requiring extensive industrial feedback. However, beyond these proof-of-concepts and the promise of automation they hold, a deeper understanding of the behaviour and use of these advanced algorithms by the process engineer is still needed. In this paper, we provide the first data-driven solution for designing supercritical CO2 power cycle for waste heat recovery, a challenging industrial use case with lack of consensus on the optimal layout from the field literature. We then examine the issue of artificial intelligence acceptance by the process engineer, and formulate a set of basic requirements to foster user acceptance - robustness, control, understanding of the results, small time-to-solution. The numerical experiments confirm the robustness of the method, able to produce optimal designs performing as well as a set of selected expert layouts, yet only from the specification of the unit operations (turbomachinery and heat exchangers). We provide tools to exploit the vast amount of generated data, with pattern mining techniques to extract heuristic rules, thereby explaining the decision-making process. As a result, this paper shows how the process engineer can interact with the data-driven design approaches, by refocusing on the areas of domain expertise, namely, definition and analysis of the physical problem.
1 Introduction
Spurred by remarkable algorithmic breakthroughs as well as improved data and hardware availability, the field of machine learning (ML) has reached a level of maturity enabling its integration in real-life systems. ML is thus more and more popular in many application areas and is used by engineers to make decisions in uncertain, complex, environments, although its full potential remains to be discovered (Venkatasubramanian, 2019; Schweidtmann et al., 2021). At the same time, the field of chemical engineering is undergoing an “unprecedented transition”, as coined by Venkatasubramanian, with multiple challenges ahead to enable the rise of sustainable technologies and processes: working with new materials, new optimization objectives under new constraints, typically environmental constraints, while meeting the market needs (Martín and Adams II, 2019). As a representative instance of an emerging, complex, process to design, this paper focuses on the synthesis of supercritical carbon dioxide (sCO2) power cycles for waste heat recovery, i.e., for converting the residual heat of an industrial facility into electricity using a so-called bottoming power cycle (Marchionni et al., 2020). Due to its thermodynamic properties, sCO2 is indeed being investigated to replace steam as a working fluid in the power industry, to increase the efficiency of the energy conversion while reducing the environmental cost (White et al., 2021). Waste heat recovery is one of the most promising applications of sCO2, with faster market penetration prospects in comparison to other capital intensive applications such as nuclear, Concentrated Solar Power, etc. (Wright et al., 2016; Brun et al., 2017; De Servi et al., 2019; Ma et al., 2020; Mussati et al., 2020; Soliman et al., 2021; Noaman et al., 2022). However, despite these recent research efforts, sCO2 cycles remain largely a theoretical topic with open challenges, including the application of the advanced exergy analysis (Morosuk and Tsatsaronis, 2015), and only a few small-scale experimental systems currently deployed worldwide (Yu et al., 2021).
Solving these challenges and developing commercially viable sCO2 cycles requires notably new systematic methodologies to perform process design (Yu et al., 2021). Shorter industrial feedback and limited domain knowledge make increasingly difficult the design of advanced processes with conventional approaches, whether they are based on heuristics or on mathematical programming (superstructure optimization, Mencarelli et al. (2020)). In general, the task can be formulated as a two-level problem, on one hand generating the topology (layout) of the process and on the other hand, evaluating the given flowsheet by optimizing its design variables for a given objective function (flowsheet evaluation). Superstructure modelling merges the two levels in a single-level problem, with a joint optimization of structural and design variables. Yet, both heuristics and superstructure-based approaches suffer from some common limitation for generating the layouts, relying heavily on field expertise to define the search space as a postulated set of alternative flowsheets to be optimized. New methods for optimal decision making in process engineering are therefore currently being searched for and the past few years have witnessed the emergence of a third option based on algorithmic strategies removing the need to start from a predefined flowsheet. Dating back to at least Nishida et al. (1981), this idea has been rising recently, with the advent of machine learning, artificial intelligence (AI) and powerful hardware. The distinctive feature of these methods is to address layout generation by only defining the set of available unit operations, without assuming any knowledge about how to combine them into a promising flowsheet. In this sense, we call them AI-based methods in the rest of this paper. Using machine learning in chemical and power engineering should thus ultimately help making optimal decisions and bringing creativity to build new designs (Schweidtmann et al., 2021).
Moreover, beyond the optimality of AI-based designs, addressed by an increasing number of algorithmic contributions, another key challenge received little attention from the literature: acceptance by the end-user, the process engineer. In complement to other methodological contributions, our goal is to give a broader perspective by investigating more closely how already-established AI techniques for layout generation can benefit the process engineer, to identify key bottlenecks and outline future research directions. Our contribution is two-fold. Firstly, whereas we observe a lack of consensus from the available domain literature on the design of the bottoming cycle for waste heat recovery, we propose the first data-driven solution to this problem with sCO2 bottoming cycles. Secondly, building on this complex use case, we extend the analysis by examining AI acceptance by the process engineer. We formulate a set of basic requirements - robustness, control, understanding the results and assessment of the cost -, propose a more comprehensive post-processing evaluation strategy and conduct additional experiments to provide a deeper understanding of how an engineer would interact with such systems.
The rest of this paper is organized as follows. Background on the problem, including a literature review of AI-based process design, is provided in Section 2. We describe then the chosen data-driven methodologies in Section 3. The results are presented, analyzed and discussed in Section 4. We conclude in Section 5.
2 Problem definition and literature review
2.1 Designing a waste heat recovery cycle with supercritical CO2
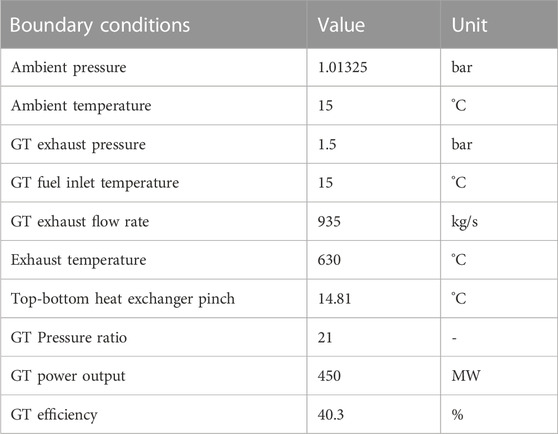
Use case description A brief description of the use case is provided in this section; more details are provided in the Supplementary Materials (Section 1). A combined cycle is selected as a waste heat recovery application where a bottoming power cycle is used to extract the exhaust gas exiting a topping gas turbine (GT). This configuration allows to produce up to 50% more electricity compared to a standalone GT with the same fuel source. In this study, supercritical CO2 (sCO2) power cycles are used as the bottoming technology, instead of the conventional steam Rankine cycle, due to their operation at supercritical pressures and temperatures allowing to reach higher efficiencies. In addition, sCO2 is two times denser than water/steam, resulting in smaller turbo-machinery and thus into relatively lower capital and operational expenditures (Brun et al., 2017; Noaman et al., 2022). The chosen topping cycle is a 450 MW heavy duty Siemens H-class gas turbine SGT5-8000H, representative of typical industrial conditions and previously investigated in (Blumberg et al., 2017). The corresponding boundary conditions are listed in Table 1, following the ISO conditions for environmental variables and fuel inlet temperature. Given this fixed topping cycle, the task is to provide an optimal design, i.e., a layout and its operating conditions, for the sCO2 bottoming cycle, to recover the waste heat exiting the gas turbine at 935 kg/s, 630°C, 1.5 bar. In this work, the synthesis problem is formulated as a bi-level optimization problem:
with Γ the discrete topological search space of bottoming cycle layouts, ΘG the continuous parameter space (operating conditions) of a layout G, F the fitness function. Solving Eq.1c by acting on the degrees of freedom θ of each component in a given layout G - full list in Table 2 - is called flowsheet evaluation. This formulation differs from state-of-the-art superstructure modelling, where Γ is restricted to a fixed subset of
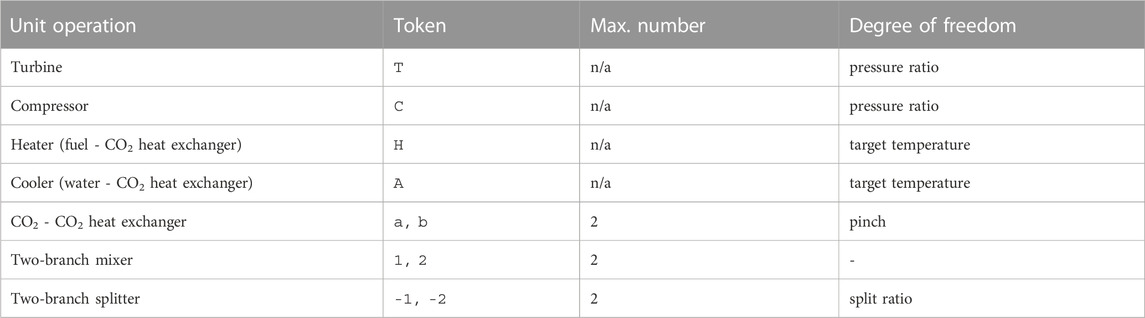
TABLE 2. Unit operations in sCO2 cycles, corresponding tokens in the string representation, maximum numbers of occurrence in the layout and the associated variable to be optimized for flowsheet evaluation.
Fitness function F The optimality of the proposed designs is assessed in terms of exergoeconomics fitness function, which combines cost functions with exergy analysis in a joint technical and economic accounting of the system’s efficiency gains. We describe briefly the computation of the overall exergoeconomic cost of a thermal system, and refer to the Supplementary Materials (Section 4), as well as Bejan et al. (1996) for more details and Noaman et al. (2019) for further insights on its application to sCO2 bottoming cycles.
The calculations are carried out in four main steps, namely, a) exergy analysis; b) economic analysis and then exergoeconomic costing c) at the component and d) the system levels. Step a) is a conventional analysis in terms of exergies of fuel and product, following Bejan et al. (1996). After having determined the exergy
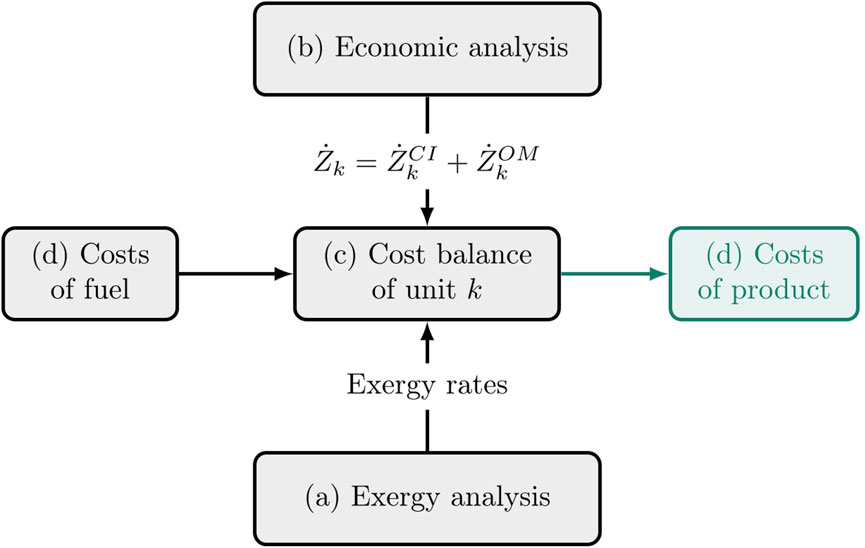
FIGURE 1. Exergoeconomic model of the kth unit component in the system, adapted from Bejan et al. (1996). After performing (a) an exergy analysis of all streams in the system and (b) an economic costing of all components, the exergoeconomic cost of product is computed from the cost of fuel, the capital investment costs
2.2 Expert vs. expert-free design
The problem of designing sCO2 bottoming cycles for waste heat recovery applications has been examined in the literature with thermodynamic expert analysis, e.g., by Wright et al. (2016); Persichilli et al. (2012); Khadse et al. (2018); Huck et al. (2016); Ayub et al. (2018); Thanganadar et al. (2019); Moroz et al. (2015a); Kimzey (2012); Moroz et al. (2015b); Kim et al. (2017). However, only a few of these studies use exergoeconomics to evaluate the performance of the designs. Overall, the available literature does not show a clear consensus for a collective conclusion about the design of the bottoming cycle, due to the diversity in the boundary conditions and to varying assumptions reported in every study, as illustrated, e.g., by Table 1 in (Yang et al., 2021).
Building-up on an extensive review omitted here for the sake of brevity, five layouts are thus selected and depicted in Figure 2 to represent the wide range of expert designs investigated in the literature. The sCO2 single recuperated cycle is the most basic layout that can be used for a bottoming application. The sCO2 partial heating layout offers high bottoming cycle performance with a slight added complexity compared to the single recuperated cycle layout. The triple heating sCO2 cycle represents the group of cycles found in the literature that use three simultaneous heaters to extract the thermal energy available in the flue gases exiting the topping gas turbine cycle. Then, the dual-rail sCO2 cycle is representative of the group of composite cycles, having shown high performances in bottoming applications. Lastly, the so-called cascade III cycle (dual-flow split with dual-expansion sCO2 cycle) is selected as it has shown the highest power output among the advanced cycle layouts category.
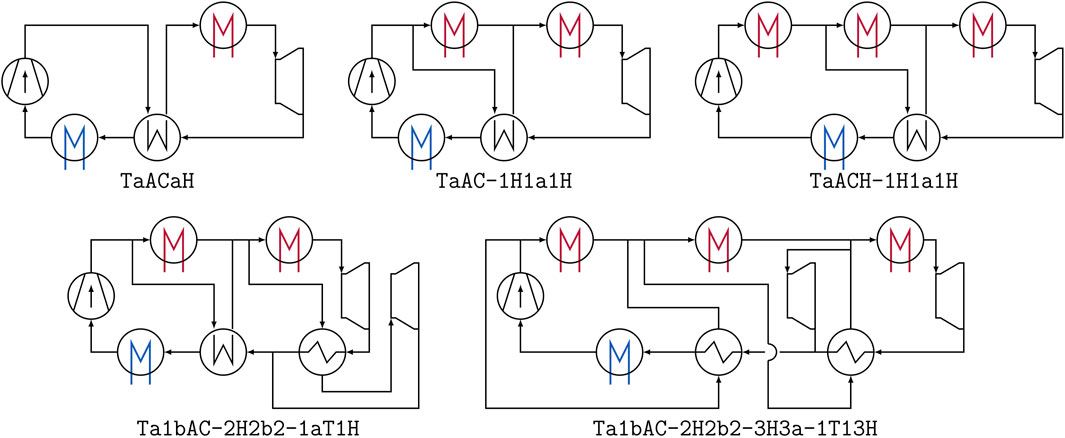
FIGURE 2. Five state-of-the-art expert layouts for sCO2 bottoming cycles, with their name in the string representation of Section 3.1.1: recuperation (TaACaH), partial heating (TaAC-1H1a1H), triple heating (TaACH-1H1a1H), cascade (Ta1bAC-2H2b2-1aT1H) and dual-rail (Ta1bAC-2H2b2-3H3a-1T13H).
If bottoming cycles for waste heat recovery have been designed by mathematical programming (superstructure modelling), they have to the best of our knowledge never been designed by AI-based methods for layout generation. Typical comparative studies, such as those conducted by Blumberg et al. (2017) or Manente and Fortuna. (2019) pre-define the bottoming layout, restricting themselves to less than five alternatives in general. Similarly, a representative contribution of superstructure modelling such as Yang et al. (2021) contains 16 alternative layouts. In the next section, we review key contributions of AI-based methods, that explore larger search spaces with no explicit definition by the designer.
2.3 AI-based process design
Most contributions in the AI-based process design literature adopt a reward-driven methodology, where the goal is to optimize the fitness function directly in the discrete topological space Γ of process layouts (Nabil et al., 2022). As a first example, Neveux. (2018) used Evolutionary Programming to iteratively generate processes by applying mutation operators. The approach is validated on a well-known reaction-separation problem, retrieving an optimal design in agreement with the literature. Since this first milestone, substantial efforts are being made to apply reinforcement learning (RL, Sutton and Barto. (2018)) to the task of process synthesis, where an agent interacts by trial-and-error with its environment, here the process structure, to maximize a desired reward function. To the best of our knowledge, Khan and Lapkin. (2020) and Midgley. (2020) were the first to frame the synthesis task as an RL problem. Midgley. (2020) applies a soft actor-critic agent to design distillation sequences. At each step of the incremental construction of the flowsheet, the agent decides whether or not to add a new column and determines then the best operating conditions. On the other hand, the value-based agent proposed by Khan and Lapkin. (2020) makes discrete (topological) and continuous (operating conditions) decisions to design simple processes. RL has also been applied by Plathottam et al. (2021) to solve the flowsheet evaluation problem (Eq.1c), for a fixed layout of a solvent extraction process.
Subsequent contributions improve the learning strategy. In the hierarchical RL framework by Khan and Lapkin (2022), a higher-level agent builds the global process flowsheet by connecting process sections, whereas a lower-level agent builds each section by choosing unit types and operating conditions, with discretized design variables. The method is tested to maximize the profit of a typical reaction-separation process, outperforming a baseline design. Another original RL approach is proposed by Göttl et al. (2022a). The problem is formulated as a competitive two-player game, two players taking turns to iteratively build a flowsheet better than their opponent’s. This mechanism allows Player 2 to be creative trying to outperform Player 1, whereas Player 1 applies the good recipes from Player 2 to win the game (Göttl et al., 2022b). Evaluated in terms of net present value, the agent performs as well as, sometimes better, than a benchmark design based on basic engineering rationale on a reaction-distillation process in a quaternary system without (Göttl et al., 2022a) or with recycling (Göttl et al., 2021; Göttl et al., 2022b). Finally, whereas other contributions used state vectors derived directly from the process flowsheet, Stops et al. (2022) apply a Graph Convolutional Network (Kipf and Welling, 2017) to automatically extract relevant topological and continuous features from the flowsheet seen as a directed colored graph, and summarize them in a fingerprint vector. This learned vector representation is used by a hierarchical RL algorithm performing both topological and design optimization levels in a hybrid discrete-continuous action space. The approach is tested on the methyl-acetate production use case, with four unit operations, including recycling to the feed stream, showing that the agent can quickly learn to produce good flowsheets.
There is thus a trend towards more advanced algorithmic RL strategies showing promising performances on relatively simple use cases. It remains however to investigate how well these algorithms would adapt to more complex use cases (nonlinear physics, involved unit operations, etc.), in terms of optimality of the results as well as computation cost, hyperparameter finetuning, etc. Besides, although a popular choice, it has been shown that RL requires careful validation in practice to strengthen the robustness of the results because of the inherent statistical uncertainty of the algorithms (Agarwal et al., 2021).
Alternatively to reward-driven design, another line of work much used in the literature of molecular design (Elton et al., 2019), consists in training a generative statistical model that learns the underlying distribution of a dataset of process samples, before biasing the distribution towards regions of high fitness values. Based on a string representation of the process, Nabil et al. (2019) use a recurrent neural network (RNN) to produce large pools of sCO2 power cycles for Concentrating Solar Power plants with optimal technical performances (thermal efficiency, shaft power). Oeing et al. (2022) used RNNs to predict the next equipment in linear sequences of six unit operations extracted from random walks in piping and instrumentation diagrams (P&IDs) seen as graphs. Similarly, based on a string representation and a small set of synthetic layouts, Vogel et al. (2022) train a Transformer model (Vaswani et al., 2017) to perform process flowsheet autocompletion. The model builds realistic flowsheets from empty or partial ones, without, however, optimizing their design variables towards a certain fitness function.
The results of Nabil et al. (2019) and Vogel et al. (2022) show that language models can learn the syntax of processes, i.e., generate strings corresponding to valid process flowsheets. Besides, unlike reward-driven methodologies, generative data-driven models can produce large amounts - in theory, infinitely many - of valid layouts with high values of the fitness function. However, their application to a complex industrial use case remains an open question. This leads us to formulate a first research question, asking what domain knowledge can be gained by an AI-based, expert-free, design method: (Q1) What are the key thermodynamic substructures that are required to obtain the best exergoeconomic fitness values for sCO2 waste heat recovery bottoming cycles?
2.4 Acceptance by the process engineer
AI often carries the implicit promise of automation, here by removing the need for expertise in process design to address (Q1). Nevertheless, a process engineer is likely to become the end-user of such tools, raising the issue of whether and how they would be employed. Building on the real-world use case introduced in Section 2.1, we propose to examine the acceptance of an AI-based design tool by a process engineer. Can a process engineer trust and use an AI-based design tool, or conversely, to what extent do current state-of-the-art AI-based process synthesis models facilitate technology acceptance by the designer?
The theoretical basis for analyzing user acceptance is the Technology Acceptance Model (Davis, 1989). It postulates that the intent to use a given technology is determined by two key beliefs, perceived usefulness (PU) and perceived ease of use (PEoU). PU is the degree to which a person believes that using a particular system would enhance their job performance: the AI-based design software is beneficial to the process engineer, allows solving complex problems and enhances quality. PEoU is the degree to which a person believes that using a particular system would be free of effort: the software does not require specific knowledge or training to be applied. Within this framework and based on studies in related domains (Ong et al., 2004; Mezhuyev et al., 2019; Sohn and Kwon, 2020), we hypothesize that:
1. The intention of adoption of an AI-based process design software is positively affected by three factors, namely, i) perceived usefulness, ii) perceived ease of use and iii) perceived control (the fact that using AI is entirely within the control of the process engineer);
2. PU is determined by performance and validity, automation, reasonable time to find a solution, scalability, robustness, ability to solve complex problems;
3. PEoU is determined by simplicity, no specific knowledge needed, short learning curve, definition of metrics, complexity of parameter tuning, difficulties in interpretability and predictability of the results.
Focusing on technical criteria, it follows that a process engineer asked to use AI-based design tools instead of well-known heuristics would need guarantees with respect to: (G1) the robustness of the method; (G2) how to control the model without expertise in AI; (G3) how to understand the results; (G4) the cost and limitations of the method. Whereas (G1) and (G3) are examined by answering (Q1), this leads us to formulate two other questions that we investigate in this paper, to respectively address (G2) and (G4) in the context of designing bottoming cycles for waste heat recovery:(Q2) What decisions or interactions should be made by the process engineer with no AI expertise to use such tools? How do they impact the final solution?
(Q3) What is the computational cost of data-driven synthesis methods applied to sCO2 power cycle design, and how to mitigate it? What are the other obstacles to data-driven methods?
3 Methods
Designing waste heat recovery bottoming cycles combines multiple levels of complexity, caused by the strongly nonlinear properties of supercritical CO2, the design of a cycle instead of a sequence, including bi-fluid heat exchangers, splitters and mixers as unit operations and the advanced strategies required to optimize the techno-economic fitness function. This section describes the model selected to address the research questions developed in Section 2.
3.1 Generative modelling
3.1.1 String representation
Choosing an adequate numerical, machine-readable, representation of a chemical process is a key component to machine learning based design (Aouichaoui et al., 2022; Wigh et al., 2022). Indeed, the representation, which should be concise, unambiguous and bijective, may impact the downstream machine learning or optimization task depending on whether, and how, it contains the critical structural information necessary to understand the underlying behaviour. On the other hand, multiple representations of chemical processes have emerged, in particular graphs (signal-flow graphs, P-Graphs (Friedler et al., 1992), etc.) or strings (SFILES, Simplified Flowsheet Input-Line Entry System, d’Anterroches and Gani. (2005)), and it remains an open question to determine which one is best suited to the task of process synthesis.
The compact string representation in Nabil et al. (2019) is designed for power cycles, modelling them as heterogeneous directed graphs, where process units (respectively, material streams) are the nodes of the graph (respectively, the edges). The nodes are labeled with unit types, whereas there is a single edge type, namely, CO2 stream. To ensure the uniqueness of the representation, a CO2-CO2 heat exchanger is represented by two nodes in the graph, for the hot and cold sides, respectively. The directed graph is then uniquely represented by a sequence of tokens (a word) chosen from the finite alphabet
For the sake of illustration, the expert layouts introduced in Section 2.2 and shown in Figure 2 are respectively mapped to TaACaH (recuperation), TaAC-1H1a1H (partial heating), TaACH-1H1a1H (triple heating), Ta1bAC-2H2b2-3H3a-1T13H (dual rail) and Ta1bAC-2H2b2-1aT1H (cascade).
3.1.2 Model architecture
New words, i.e., new power cycle layouts, are produced by training a statistical generative model. Similarly to, e.g., Gupta et al. (2018) for drug design, we use Recurrent Neural Networks (RNNs, Rumelhart et al. (1986); Williams and Zipser (1989)), and more specifically Long Short Term Memory networks (LSTMs, Hochreiter and Schmidhuber. (1997)), to learn the distribution of words representing power cycles. RNNs are the baseline neural networks for handling sequential data x = (x[1], x[2], …, x[n]) of varying length, such as text or time series, by introducing a memory cell that allows persistent information to be conveyed from one element of the sequence to the next. On the contrary, LSTM networks are a special form of RNN with additional interacting layers within a cell, designed to handle long-term dependencies - poorly captured by the vanilla RNN in practice - by controlling what information is transferred to the next cell.
We use the sequence-to-one architecture described by Nabil et al. (2019), to generate words one token at a time. The chosen model is a stack of two LSTM layers of 32 cells each, followed by a feedforward layer with
3.1.3 Training procedure
Generation of valid flowsheets In a first step, the LSTM model is trained to generate words that do correspond to thermodynamically valid process flowsheets, regardless of their fitness function. Starting from a set
In practice, the training set
Finetuning The aim of the finetuning procedure is the targeted generation of power cycles with small specific cost of electricity c < δ, where δ is a predefined threshold. This is achieved following the same procedure as for the pretraining step, except that i) all words in the training set
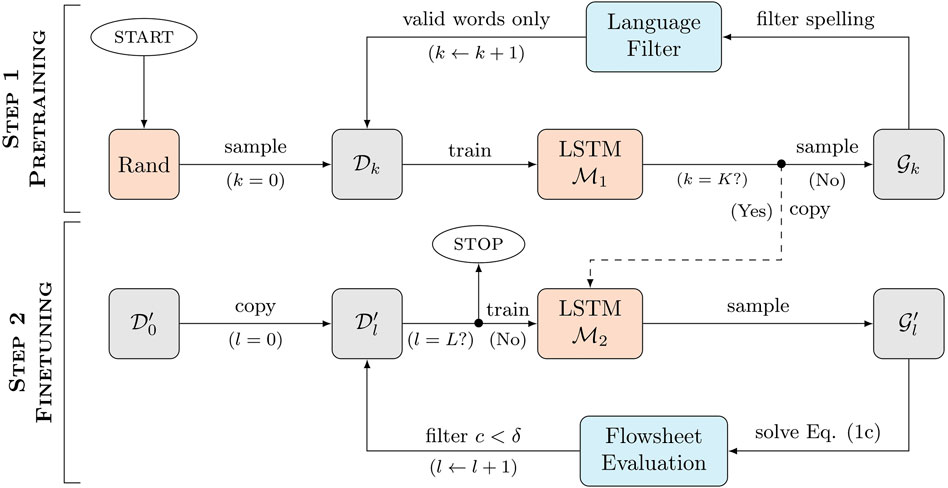
FIGURE 3. Training procedure of the data-driven model for process generation. In K iterations of Step 1 (pre-training), LSTM model
Regarding the lower-level problem of fitness evaluation of a layout generated by
with η < 1 the thermal efficiency, η0 the threshold for the minimum thermal efficiency,
All computations and models are implemented in Python 3.8, using the libraries CoolProp (Bell et al., 2014) for the thermodynamic properties, PyTorch 1.9.0 (Paszke et al., 2019) and Lightning 1.4.7 (Falcon, 2019) for the deep learning models, which are optimized using the Adam solver with a learning rate of 10–3. Because the discussion of the economic hypotheses leading to the optimal exergoeconomic cost is beyond the scope of this article, all results are presented in terms of specific cost normalized by a reference value. The design variables of the five expert layouts in Section 2.2 are optimized with PSO, the smallest value (best expert) serves as normalizing constant. The target performance is to reach costs c at most 9% more expensive than the best expert design, where this threshold is set arbitrarily.
3.2 Post-processing
The trained machine learning model outputs large pools of new layouts with high fitness values. To fully address (Q1), it remains however to determine how the process engineer can learn from the generated data. Whereas previous contributions focused on the analysis of a handful of layouts, we suggest to extend the analysis i) on one hand with word embeddings to visualize the search space Γ and the convergence towards optimal regions, for the sake of diagnostic, and ii) on the other hand, with pattern matching techniques, to extract knowledge under the form of new heuristic rules for the process designer.
Best flowsheet Extracting the best flowsheets from the set of layouts generated by the model is the first output of the method. The thermodynamics of these few designs are then analyzed manually, with domain knowledge, to assess their consistency.
Word embeddings We use vector embeddings to visualize words (power cycles). These vectors are obtained by first converting each word to a sequence of overlapping 3-g. Next, each 3-g is mapped to a vector of size 20 (size chosen arbitrarily in this study), using the state-of-the-art embedding model skip-gram by Mikolov et al. (2013a). skip-gram creates a lookup table, where the vector representation of each 3-g can be found and such that similar 3-g tend to be closer to each other in the vector space (syntactic regularities). Besides, the transformation also preserves semantic regularities by learning the context of each 3-g. See Mikolov et al. (2013a); Mikolov et al. (2013b)) for more details on this topic, and Asgari and Mofrad. (2015) for an application to biological sequences. The vector representation of a given power cycle is then the sum of the vectors representing its 3-g. It is finally projected onto a two-dimensional space by applying principal component analysis, thereby visualizing the search space explored by the model.
Model interpretability with frequent pattern mining We apply the last step of the methodology proposed by Zhang et al. (2019) to systematically compare the structures of the flowsheets by extracting multiple common sub-sequences within the words representing them. The first two steps in (Zhang et al., 2019) map a flowsheet into a unique string based on the SFILES format (d’Anterroches and Gani, 2005), with the objective of preserving unit types and the connection of the layout while discarding unit numbering information. The string representation described in this work in Section 3.1.1 is already well suited to this pattern mining task, where the only adjustment is to replace every heat exchangers by a single token (namely, a), and similarly for splitters (-1) and mixers 1). Hence, words for pattern matching are rewritten in the shorter alphabet
Once M is filled, zero values correspond to non-matching sequences whereas positive values correspond to matched characters and consecutive positive diagonal elements to matched sub-sequences. Since S[i, j] = 1, the length of a common sequence ending at characters x[i] and y[j], respectively, is M[i, j]. Finding common sub-sequences of a certain length consists thus in thresholding M. Besides, since the words correspond to cycles, we add a third step for filling M, by looking at the last value M[m, n]:
• if M[m, n] = 0, the last characters of x and y do not match, all sub-sequences are already identified;
• if M[m, n] > 0 and M[1, 1] > 0, then the common sub-sequences respectively ending at the last and starting at the first characters of x and y are joined to form one unique sequence.
The algorithm runs with a time complexity in4 Results and discussion
4.1 Results: optimization of the waste heat recovery bottoming cycle
Pretrained language model Model
Finetuning - language model After finetuning the pretrained model
Finetuning - fitness values The best expert is partial heating (TaAC-1H1a1H). The other expert costs are respectively 1.005 for triple heating, 1.013 for cascade, 1.017 for dual rail and 1.035 for recuperation. The best layouts generated by the finetuned model
The analysis of the best three layouts suggests that partial heating is an important thermodynamic substructure required to obtain small exergoeconomic cost for waste heat recovery. To confirm this conclusion and thoroughly examine our question (Q1), we apply the frequent pattern mining approach described in Section 3.2. We mined patterns respectively from a) the five expert designs; b) the 208 best and c) the 290 worst layouts from the finetuned LSTM model, each time with pairwise comparisons. The 20 most common patterns of length at least 3 are shown in Table 3.

TABLE 3. Most common patterns extracted from the expert, best and worst LSTM layouts, respectively. The substructures from the expert layouts and found as well in the LSTM designs are highlighted in bold.
Nine patterns are extracted from the expert layouts, ranging from simple widespread heuristics (e.g., aAC, i.e., cool and compress from after a heat exchanger, 1HTa, i.e., heat, expand and recuperate heat from after a mixer or -1H1a, i.e., partial heating and heat recovery) to longer and more specific rules such as aAC-1H1a1 (cool and compress, partial heating, heat recuperation) or -1H1a1HTaAC (combining partial heating, cool and compress, heat and expand, heat recuperation in a special layout). The patterns extracted from the poor layouts are almost always 3-g, with some simple heuristics being retrieved, e.g., aAC or ACH, but also other physically irrelevant patterns such as HTC (expand then compress) or CAH (cool then heat). It appears that the poor layouts are characterized by minor, random, changes to the simple Brayton cycle TACH from which they were built. On the contrary, more informative patterns are extracted from the best layouts. On one hand, the shorter sub-structures correspond to valid well-known thermodynamic knowledge (aAC, -1H1a, HTa, etc.) that were part of the expert designs. On the other hand, longer rules are also extracted, such as HTaAC, AC-1H1a or -1H1a1HT, and they correspond to more involved expert knowledge developing the idea of partial heating. In total, six out of the nine expert patterns appear in the 20 most common patterns of the best LSTM layouts.
Next, the histograms of the normalized exergoeconomic cost for layouts generated i) by the pretrained model (in blue) and ii) the finetuned model (in green) are displayed in Figure 5A. The vertical black line shows the target performance threshold, cycles on the left of this line are at most 9% more expensive than the best expert design. The histograms are shifted from right (blue) to left (green), i.e., the finetuned model is shifted to higher fitness (smaller cost) regions compared to the pretrained model. Hence, the finetuned model did learn to specialize on some specific patterns in the process layouts, as confirmed by the PCA plot of the word embeddings in Figures 5B,C, where the embeddings of the finetuned layouts only span one part of those of the non-finetuned model, discarding the upper region.

FIGURE 5. Performances of the finetuned LSTM model. (A) Histogram and estimated density of the normalized specific costs for bottoming cycles respectively sampled from the pretrained (blue) and finetuned (green) models
Intermediate conclusion The results illustrate the main advantage of data-driven process design, able to provide optimal designs and advanced insights on a new complex use case without building on years of domain research efforts. Additional results are provided in the Supplementary Materials (Section 2), in particular plots of the exergy efficiency, net shaft power output and thermal efficiency of the designs (Supplementary Figure S3). These insights are backed by a more systematic–although without guaranteeing exhaustiveness, as discussed in Section 4.2.3 nor global convergence of the PSO solver–exploration of the search space, thereby increasing the confidence of the process engineer in the AI-based solution. In particular, the behaviour of the model, as summarized per Table 3 and Figure 5Ais clearly accessible to a process engineer. The addition of the pattern mining methodology to analyze the outcome of the machine learning algorithm helps thus addressing the needs (G1) of robustness and (G3) of understanding the results: extracting coherent knowledge from a pool of hundreds of layouts suggests that the data-driven model robustly converges towards certain designs and provides a stronger explanation of the behaviour of the model, compared to a single optimal design.
4.2 Discussion and complementary experiments
4.2.1 Process engineer acceptance
We proceed to complementary analyses and experiments to investigate (Q2) in light of our use case. It is worth mentioning that the discussion of perceived usefulness and ease of use (PU and PEoU, see Section 2.4) is based on these experiments only; the conclusions should be further validated by behavioral studies as is standard practice in this field (e.g., Sohn and Kwon, 2020). To begin with, as the end-user of the AI-based tool, the process engineer is supposed not to have expertise in AI; the software should solve the use case based on the specified design choices and produces then an output. We assume thus that the role of the process engineer is to focus i) on design choices in the definition of the case study (before calling the AI module) and ii) on understanding and analyzing the output of the algorithm. Based on the results in Section 4.1, and consistently with promising other contributions (see Section 2.3), it appears reasonable to assume that a process design software based on such an AI-based model could meet the criterion of PU in terms of performance and ability to solve complex problems, and PEoU in terms of delivering explainable decisions and metrics accessible to a process engineer. This addresses ii), and we discuss now i).
Design choices - search space definition Firstly, the process designer should define the search space, in terms of unit operations and target performance. We experiment by training another model allowing up to two CO2 - CO2 heat exchangers, against one in Section 4.1. After generating 100,000 cycles from pretrained model
However, finetuning the model with up to two heat-exchangers collapsed to flowsheets almost all having at most a single heat exchanger, which was not the case before finetuning (34% of the cycles generated by the pretrained model have two heat exchangers). This emphasizes fitness evaluation as the main bottleneck of data-driven process synthesis methods, a fact we discuss in the next section.
Another aspect of the search space definition is the target performance, here at most 9% away from the best expert. During the finetuning of the model with at most one heat exchanger, the proportion of good layouts, reaching the target performance, saturates below 40% - see Supplementary Figure S2B in the Supplementary Materials. We extend the analysis below by comparing with the CSP use case from Nabil et al. (2019).
Design choices - Reward design A key decision made by the process engineer is the design of the fitness function, while avoiding the pitfall of including physical constraints without defining a de facto very small search space. Reward design heavily depends on the use case at study, hence requires domain knowledge. For instance, Stops et al. (2022) proposed a reward function for a reinforcement learning agent based on the net cash value and additional penalties to encourage space exploration. Khan and Lapkin. (2022) also identified reward engineering as a key step to drive the learning process. Here, we chose a cost function of the form of Eq. (2), where adding a penalty on technical criteria (thermal efficiency and heat recuperation ratio) helped discarding valid yet thermodynamically not promising layouts.
Insights from the comparison to the CSP study The above findings (Section 4.1) are consistent with the results reported by Nabil et al. (2019) for Concentrated Solar Power (CSP) cycles with at most one heat exchanger. In particular, their pretrained model produces 93.1% valid power cycles, of which 87% are unique, the novelty rate is 86%. Since the length of the CSP power cycles was left unbounded, against a limit of at most 20 units in this work, this confirms that narrower search spaces logically yields more specialized models. On the other hand, pretraining depends only on power cycle layout and not on the actual fitness function or boundary conditions, hence the similar validity rates. Regarding finetuning, the fitness function used by Nabil et al. (2019) is the product of the thermal efficiency and net shaft power output of the bottoming cycle, with a target performance threshold set at 48% of the best expert. They report a ratio of good layouts of 86%—against 45% in this paper–and the distribution of the technical fitness function of the layouts is heavily shifted towards the region of interest, as shown in Figure 6A. Yet, much less mass can be found above the demanding 9% threshold. Besides, we extract the 20 most frequent patterns from their best 200 technical layouts (see Supplementary Table S3 in Supplementary Materials). 13 patterns are 3-g and only 1 contains at least 5 tokens (ACaHT, a standard pattern), against respectively 7 and 8 in Table 3 in this paper. This confirms how the user-defined target performance impacts the metrics of the model: a looser target area yields a higher success ratio but a lower proportion of very good cycles and more generic, less specialized, libraries of layouts.
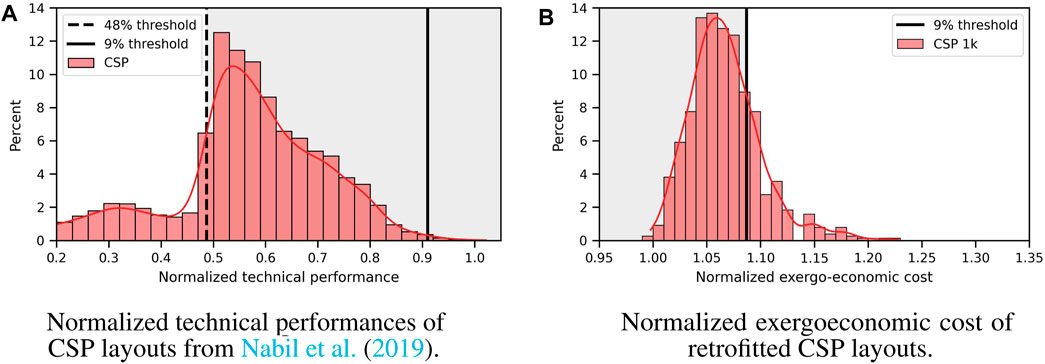
FIGURE 6. (A) Normalized technical performances of the layouts generated and optimized for a CSP use case in Nabil et al. (2019). (B) Normalized cost of these CSP layouts retrofitted to solve Eq. (1c) with exergoeconomic fitness function.
Intermediate conclusion The discussion and complementary results show how to understand the behaviour of the model depending on the design choices of process engineers, so that data-driven methods remain under their control (G2). Optimizing their use requires domain knowledge to formulate a good problem to solve, by constructing relevant reward functions and delimiting an appropriate search space. In this sense, perceived control of an AI-based model depends on the domain expertise of the process engineer, but could be improved by covering larger search spaces to avoid model collapse. Besides, the comparison to CSP shows that the model behaves similarly in both cases, with no parameter tuning, which benefits to the PEoU. It remains to investigate the performances for processes other than power cycles to confirm this fact. Finally, it can be observed that the model depends on the specific string representation described in Section 3.1.1: using a more generic format, such as SFILES (d’Anterroches and Gani, 2005) could help increase PEoU so that the end-user does not have to define a language for every use case.
4.2.2 Cost
Flowsheet evaluation and computation time In this work, finetuning the LSTM model required about
The typical solution to this problem consists in using a surrogate regression model, e.g., neural networks (Fahmi and Cremaschi, 2012) or kriging (Gorissen et al., 2010) - although the training of such models also requires large amount of data and therefore of fitness function evaluations (Fahmi and Cremaschi, 2012). The main limitation of surrogate modelling is that the strongly nonlinear behaviour of sCO2 might be locally inaccurately represented by the model, thereby potentially biasing the data generation process.
Mitigation strategy The computation time might be a limitation in an industrial context when one should carry out the entire optimization procedure for every new use case, e.g., when the fitness function changes (same physics but new objectives or constraints). However, one use case produces a large pool of layouts that could be reused (retrofitted) to alleviate the computational cost. Instead of solving Eqs (1a)–(1c) for every new sCO2 power cycle use case, we evaluate the following strategy: i) solve (1a)–(1c) for Use Case 1; ii) save the top n layouts according to the fitness of Use Case 1; iii) solve (1c) (flowsheet evaluation) on these K layouts, with the new fitness of Use Case 2.
We use the top n = 1, 000 layouts generated by Nabil et al. (2019) for sCO2 CSP cycles. The boundary conditions are also different, but the search space (number of heat exchangers, splitters, etc., allowed per cycle) is the same. These layouts are retrofitted to solve Eq.1c with fitness given by the exergoeconomic cost Eq. 2, instead of the product of the thermal efficiency and net shaft power output. The histogram of the normalized cost is shown in Figure 6B: the results are close to Figure 5A and the best layout performs as well as the best expert. The most frequent patterns mined from the best 200 layouts are different from those of the best CSP layouts for the technical fitness function (Supplementary Table S3), indicating that the good but not too specialized layouts in Nabil et al. (2019) contained enough information to be retrofitted for another use case. The computation time for these 1,000 layouts is 5.2 days,
4.2.3 Other challenges
The field of machine learning based process design is still nascent (Schweidtmann et al., 2021), in particular purely data-driven methods. Hence, from a methodological perspective, AI-based process design faces several challenges, in particular: initial dataset constitution, reward design, model architecture and finetuning strategy (Nabil et al., 2022). In the sequel, we discuss dataset constitution and search space exploration, based on the experiments carried out in this paper. The discussion of the latter two challenges is postponed to Section 3 of the Supplementary Materials.
Initial dataset The models used in this paper are trained to learn the underlying distribution of a dataset. To do so, they require large amount of data - for instance the models trained on the similar problem of molecular design are based on datasets with 105–106 samples (Elton et al., 2019). Such large datasets do not exist for process design, which limits their applicability. Observe on the other hand that the reward-driven process design literature discussed in Section 2.3, in particular reinforcement learning algorithms, does not need an initial training set since they are optimization procedures in the topological space of process layouts. As such, these methods are more straightforward to implement. In this work, we used a random generator to initialize the procedure and obtained good performances despite the smaller training size. Vogel et al. (2022) also built a synthetic generator, a Markov-chain process based on process design heuristics, training their data-driven flowsheet completion model on about 8,000 synthetic data.
Besides, the generative model is only as diverse as its training set is. This is confirmed by our experiments. Indeed, whereas the pretrained LSTM model
Exploration - exploitation tradeoffs More generally, this raises the issue of how the training set impacts the exploration of the search space and the creativity of the generative model, one of the six challenges identified by Schweidtmann et al. (2021) for machine learning in chemical engineering. Although our method does not provide guarantees in this regard, similarly to others, there are nevertheless a few hints that the model successfully extrapolated the initial random training set. We observed in Section 4.1 that the finetuned model successfully learned to combine process non-trivial substructures, not found within random layouts, into flowsheets that correspond to the state-of-the-art expert solutions, on this specific use case. The distribution of the flowsheet macroscopic properties, in Supplementary Figure S3 in Supplementary Materials, covers a wide range of values, showcasing the variety of generated designs beyond those of the known expert layouts. Hence, the model managed to find a successful path among several good alternatives. How to quantify the degree of exploration and creativity of such a model is an open research question that goes beyond the scope of this paper. We refer to Alaa et al. (2022) for a recent contribution on the topic.
Finally, we can draw a connection with Palowitch et al. (2022), who recently introduced GraphWorld, a generator of arbitrarily large populations of synthetic graphs, and showed that it could efficiently explore regions of the search space uncovered by standard benchmark data. This indicates that insights and successful results can be obtained starting from synthetic data only. Another promising track explores the opposite direction: Balhorn et al. (2022) suggest to scan the process design literature in order to build a digital process flowsheet dataset, not available as of writing time.
5 Conclusion
In this work, we propose to solve an industrial process design problem, of a supercritical CO2 bottoming cycle for waste heat recovery, providing the first data-driven solution to this use case. Confirming the findings of other studies, the model successfully proposes optimal designs without requiring any other expert knowledge than the definition of the unit operations. Most importantly, we demonstrate how a process engineer could benefit from such a tool by refocusing on his/her expertise i) in problem definition, through reward design and search space definition, and ii) in problem analysis, by incorporating the knowledge extracted from the model. We analyze the use case from the perspective of user acceptance. Backed by adequate post-processing strategies, we provide empirical evidence supporting the robustness of data-driven algorithms, their explainability and the ability to control their behaviour. We draw attention on the computational cost of generative models that can significantly impact the time-to-solution, hence the perceived usefulness, because of the costly lower-level optimization problem to solve for flowsheet evaluation.
Future research directions are multiple, both from the perspective of the use case and of the methodology. From the perspective of the use case, this work focused on the design of bottoming cycles for a fixed gas turbine, a natural extension would be to generate layouts of the entire combined cycle, bottom and top jointly. This task is harder to solve, due to an increased cost of flowsheet evaluation and to the introduction of a second component to the layout with a different material stream. Beyond this industrial use-case, AI-based process design is a recent field with multiple research questions to explore. The data-driven process generation investigated in this paper could also benefit from better optimization procedures, to improve the convergence towards high-fitness regions. More fundamentally, it remains to determine what is the best process representation, either string or graph. Promising results have been achieved on targeted undirected molecular graph generation, with models outperforming those based on strings, yet it remains to develop similar approaches for the generation of directed graphs representing process flowsheets. Finally, theoretical contributions analyzing the exploration of the search space could provide a better understanding of the behaviour of the generative model to the process designer.
Data availability statement
The datasets presented in this article are not readily available because of general EDF policy. Requests to access the datasets should be directed to dGFoYXIubmFiaWxAZWRmLmZy.
Author contributions
Use case conceptualization, MN and TM; AI-based methodology conceptualization, AI literature review, Python implementation, results analysis, visualization, discussion, TN; use case literature review, thermodynamic analyses, MN; writing–original draft preparation, TN and MN; writing–review and editing, TM; supervision, TM. All authors contributed to the article and approved the submitted version.
Funding
MN acknowledges the financial support of the Federal Ministry of Education and Research (BMBF) under the Transnational Education project (ID 57128418) of the German Academic Exchange Service (DAAD).
Conflict of interest
Author TN was employed by company EDF R&D SEQUOIA.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2023.1144115/full#supplementary-material
References
Agarwal, R., Schwarzer, M., Castro, P. S., Courville, A. C., and Bellemare, M. (2021). “Deep reinforcement learning at the edge of the statistical precipice,” in Advances in neural information processing systems. Editors M. Ranzato, A. Beygelzimer, Y. Dauphin, P. Liang, and J. W. Vaughan (Curran Associates, Inc), 29304–29320.
Alaa, A., Van Breugel, B., Saveliev, E. S., and van der Schaar, M. (2022). “How faithful is your synthetic data? Sample-level metrics for evaluating and auditing generative models,” in Proceedings of the 39th international conference on machine learning. Editors K. Chaudhuri, S. Jegelka, L. Song, C. Szepesvari, G. Niu, and S. Sabato (Baltimore, MD: PMLR), 290–306.
Aouichaoui, A. R., Fan, F., Mansouri, S. S., and Sin, J. A. G. (2022). Molecular representations in deep-learning models for chemical property prediction. Comput. Aided Chem. Eng. 49, 1591–1596. doi:10.1016/B978-0-323-85159-6.50265-7
Asgari, E., and Mofrad, M. R. (2015). Continuous distributed representation of biological sequences for deep proteomics and genomics. PLOS ONE 10, e0141287. doi:10.1371/journal.pone.0141287
Ayub, A., Sheikh, N. A., Tariq, R., Khan, M. M., and Invernizzi, C. M. (2018). Exergetic optimization and comparison of combined gas turbine supercritical co2 power cycles. J. Renew. Sustain. Energy 10, 044703. doi:10.1063/1.5038333
Balhorn, L. S., Gao, Q., Goldstein, D., and Schweidtmann, A. M. (2022). Flowsheet recognition using deep convolutional neural networks. Comput. Aided Chem. Eng. 49, 1567–1572. doi:10.1016/B978-0-323-85159-6.50261-X
Bejan, A., Tsatsaronis, G., and Moran, M. J. (1996). Thermal design and optimization. Hoboken, NJ: John Wiley & Sons.
Bell, I. H., Wronski, J., Quoilin, S., and Lemort, V. (2014). Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolprop. Industrial Eng. Chem. Res. 53, 2498–2508. doi:10.1021/ie4033999
Blumberg, T., Assar, M., Morosuk, T., and Tsatsaronis, G. (2017). Comparative exergoeconomic evaluation of the latest generation of combined-cycle power plants. Energy Convers. Manag. 153, 616–626. doi:10.1016/j.enconman.2017.10.036
Brun, K., Friedman, P., and Dennis, R. (2017). Fundamentals and applications of supercritical carbon dioxide (sCO2) based power cycles. Cambridge, United Kingdom: Woodhead publishing.
d’Anterroches, L., and Gani, R. (2005). Group contribution based process flowsheet synthesis, design and modelling. Fluid Phase Equilibria 228, 141–146. doi:10.1016/j.fluid.2004.08.018
Davis, F. D. (1989). Perceived usefulness, perceived ease of use, and user acceptance of information technology. MIS Q. 13, 319–340. doi:10.2307/249008
De Servi, C., Trabucchi, S., Der Stelt, T. C., Strobelt, F., Glos, S., Klink, W., et al. (2019). “Supercritical co2-based waste heat recovery systems for combined cycle power plants,” in 5th international seminar on ORC power systems: tech. rep. Editors S. Karellas, and E. Kakaras (Athens, Greece: The National Technical University of Athens (NTUA)).
Eberhart, R., and Kennedy, J. (1995). “A new optimizer using particle swarm theory,” in MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 04-06 October 1995 (IEEE), 39–43. doi:10.1109/MHS.1995.494215
Elton, D. C., Boukouvalas, Z., Fuge, M. D., and Chung, P. W. (2019). Deep learning for molecular design—a review of the state of the art. Mol. Syst. Des. Eng. 4, 828–849. doi:10.1039/C9ME00039A
Fahmi, I., and Cremaschi, S. (2012). Process synthesis of biodiesel production plant using artificial neural networks as the surrogate models. Comput. Chem. Eng. 46, 105–123. doi:10.1016/j.compchemeng.2012.06.006
Falcon, W. A. (2019). PyTorch lightning. Avaliable At: https://github.com/Lightning-AI/lightning.
Friedler, F., Tarjan, K., Huang, Y., and Fan, L. (1992). Graph-theoretic approach to process synthesis: axioms and theorems. Chem. Eng. Sci. 47, 1973–1988. doi:10.1016/0009-2509(92)80315-4
Gorissen, D., Couckuyt, I., Demeester, P., Dhaene, T., and Crombecq, K. (2010). A surrogate modeling and adaptive sampling toolbox for computer based design. J. Mach. Learn. Res. 11, 2051–2055. doi:10.5555/1756006.1859919
Göttl, Q., Grimm, D. G., and Burger, J. (2022a). Automated synthesis of steady-state continuous processes using reinforcement learning. Front. Chem. Sci. Eng. 16, 288–302. doi:10.1007/s11705-021-2055-9
Göttl, Q., Grimm, D. G., and Burger, J. (2022b). Using reinforcement learning in a game-like setup for automated process synthesis without prior process knowledge. Comput. Aided Chem. Eng. 49, 1555–1560. doi:10.1016/B978-0-323-85159-6.50259-1
Göttl, Q., Tönges, Y., Grimm, D. G., and Burger, J. (2021). Automated flowsheet synthesis using hierarchical reinforcement learning: proof of concept. Chem. Ing. Tech. 93, 2010–2018. doi:10.1002/cite.202100086
Gupta, A., Müller, A. T., Huisman, B. J., Fuchs, J. A., Schneider, P., and Schneider, G. (2018). Generative recurrent networks for de novo drug design. Mol. Inf. 37, 1700111. doi:10.1002/minf.201700111
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Huck, P., Freund, S., Lehar, M., and Peter, M. (2016). “Performance comparison of supercritical co2 versus steam bottoming cycles for gas turbine combined cycle applications,” in 5th international supercritical CO2 power cycle symposium (San Antonio, Texas: General Electric Company).
Khadse, A., Blanchette, L., Kapat, J., Vasu, S., Hossain, J., and Donazzolo, A. (2018). Optimization of supercritical co2 brayton cycle for simple cycle gas turbines exhaust heat recovery using genetic algorithm. J. energy Resour. Technol. 140, 63696. doi:10.1115/GT2017-63696
Khan, A. A., and Lapkin, A. A. (2022). Designing the process designer: hierarchical reinforcement learning for optimisation-based process design. Chem. Eng. Process. - Process Intensif. 180, 108885. doi:10.1016/j.cep.2022.108885
Khan, A. A., and Lapkin, A. A. (2020). Searching for optimal process routes: a reinforcement learning approach. Comput. Chem. Eng. 141, 107027. doi:10.1016/j.compchemeng.2020.107027
Kim, Y. M., Sohn, J. L., and Yoon, E. S. (2017). Supercritical co2 rankine cycles for waste heat recovery from gas turbine. Energy 118, 893–905. doi:10.1016/j.energy.2016.10.106
Kimzey, G. (2012). Development of a Brayton bottoming cycle using supercritical carbon dioxide as the working fluid. Tech. rep. Palo Alto, CA: Electric Power Research Institute. University Turbine Systems Research Program, Gas Turbine Industrial Fellowship.
Kipf, T. N., and Welling, M. (2017). “Semi-supervised classification with graph convolutional networks,” in 5th international conference on learning representations (Toulon, France: OpenReview.net).
Ma, Y., Morosuk, T., Luo, J., Liu, M., and Liu, J. (2020). Superstructure design and optimization on supercritical carbon dioxide cycle for application in concentrated solar power plant. Energy Convers. Manag. 206, 112290. doi:10.1016/j.enconman.2019.112290
Manente, G., and Fortuna, F. M. (2019). Supercritical CO2 power cycles for waste heat recovery: a systematic comparison between traditional and novel layouts with dual expansion. Energy Convers. Manag. 197, 111777. doi:10.1016/j.enconman.2019.111777
Marchionni, M., Bianchi, G., and Tassou, S. A. (2020). Review of supercritical carbon dioxide (sco2) technologies for high-grade waste heat to power conversion. SN Appl. Sci. 2, 611–613. doi:10.1007/s42452-020-2116-6
Martín, M., and Adams, T. A. (2019). Challenges and future directions for process and product synthesis and design. Comput. Chem. Eng. 128, 421–436. doi:10.1016/j.compchemeng.2019.06.022
Mencarelli, L., Chen, Q., Pagot, A., and Grossmann, I. E. (2020). A review on superstructure optimization approaches in process system engineering. Comput. Chem. Eng. 136, 106808. doi:10.1016/j.compchemeng.2020.106808
Mezhuyev, V., Al-Emran, M., Ismail, M. A., Benedicenti, L., and Chandran, D. A. (2019). The acceptance of search-based software engineering techniques: an empirical evaluation using the technology acceptance model. IEEE Access 7, 101073–101085. doi:10.1109/ACCESS.2019.2917913
Midgley, L. I. (2020). Deep reinforcement learning for process synthesis. arXiv preprint arXiv:2009.13265.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. (2013b). “Distributed representations of words and phrases and their compositionality,” in Advances in neural information processing systems. Editors C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Weinberger (Lake Tahoe, Nevada: Curran Associates, Inc), 3111–3119.
Morosuk, T., and Tsatsaronis, G. (2015). “Advanced exergy-based analyses applied to the supercritical co2 power cycles,” in Proceedings of the ASME2015 international mechanical engineering congress & exposition (IMECE2015) (Houston, TX, USA: American Society of Mechanical Engineers). doi:10.1115/IMECE2015-50527
Moroz, L., Burlaka, M., Rudenko, O., and Joly, C. (2015a). “Evaluation of gas turbine exhaust heat recovery utilizing composite supercritical co2 cycle,” in Proceedings of the international gas turbine congress (Tokyo, Japan: Spinger), 15–20.
Moroz, L., Pagur, P., Rudenko, O., Burlaka, M., and Joly, C. (2015b). “Evaluation for scalability of a combined cycle using gas and bottoming sco2 turbines,” in ASME power conference (Tokyo, Japan: Gas Turbine Society of Japan), V001T09A007. doi:10.1115/POWER2015-49439
Mussati, S. F., Morosuk, T., and Mussati, M. C. (2020). Superstructure-based optimization of vapor compression-absorption cascade refrigeration systems. Entropy 22, 428. doi:10.3390/e22040428
Nabil, T., Commenge, J. M., and Neveux, T. (2022). Generative approaches for the synthesis of process structures. Comput. Aided Chem. Eng. 49, 289–294. doi:10.1016/B978-0-323-85159-6.50048-8
Nabil, T., Le Moullec, Y., and Le Coz, A. (2019). “Machine learning based design of a supercritical co2 concentrating solar power plant,” in 3rd European conference on supercritical CO2 (sCO2) power systems 2019 (Paris, France: EU), 148–157. doi:10.17185/duepublico/48885
Neveux, T. (2018). Ab-initio process synthesis using evolutionary programming. Chem. Eng. Sci. 185, 209–221. doi:10.1016/j.ces.2018.04.015
Neveux, T., Addis, B., Castel, C., Piccialli, V., and Favre, E. (2022). A comparison of process synthesis approaches for multistage separation processes by gas permeation. Comput. Aided Chem. Eng. 51, 685–690. doi:10.1016/B978-0-323-95879-0.50115-6
Nishida, N., Stephanopoulos, G., and Westerberg, A. W. (1981). A review of process synthesis. AIChE J. 27, 321–351. doi:10.1002/aic.690270302
Noaman, M., Awad, O., Morosuk, T., Tsatsaronis, G., and Salomo, S. (2022). Identifying the market scenarios for supercritical co2 power cycles. J. Energy Resour. Technol. 144, 050906. doi:10.1115/1.4052543
Noaman, M., Saade, G., Morosuk, T., and Tsatsaronis, G. (2019). Exergoeconomic analysis applied to supercritical co2 power systems. Energy 183, 756–765. doi:10.1016/j.energy.2019.06.161
Oeing, J., Welscher, W., Krink, N., Jansen, L., Henke, F., and Kockmann, N. (2022). Using artificial intelligence to support the drawing of piping and instrumentation diagrams using dexpi standard. Digit. Chem. Eng. 4, 100038. doi:10.1016/j.dche.2022.100038
Ong, C. S., Lai, J. Y., and Wang, Y. S. (2004). Factors affecting engineers’ acceptance of asynchronous e-learning systems in high-tech companies. Inf. Manag. 41, 795–804. doi:10.1016/j.im.2003.08.012
Palowitch, J., Tsitsulin, A., Mayer, B., and Perozzi, B. (2022). “GraphWorld: fake graphs bring real insights for GNNs,” in Proceedings of the 28th ACM SIGKDD conference on knowledge discovery and data mining (New York, NY, USA: Association for Computing Machinery), 3691–3701. doi:10.1145/3534678.3539203
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). “Pytorch: an imperative style, high-performance deep learning library,” in Advances in neural information processing systems. Editors H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Vancouver, Canada: Curran Associates, Inc), 8024–8035.
Persichilli, M., Kacludis, A., Zdankiewicz, E., and Held, T. (2012). Supercritical co2 power cycle developments and commercialization: why sco2 can displace steam. Power-Gen India & Central Asia 2012, 19–21.
Plathottam, S. J., Richey, B., Curry, G., Cresko, J., and Iloeje, C. O. (2021). Solvent extraction process design using deep reinforcement learning. J. Adv. Manuf. Process. 3, e10079. doi:10.1002/amp2.10079
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi:10.1038/323533a0
Schweidtmann, A. M., Esche, E., Fischer, A., Kloft, M., Repke, J. U., Sager, S., et al. (2021). Machine learning in chemical engineering: a perspective. Chem. Ing. Tech. 93, 2029–2039. doi:10.1002/cite.202100083
Sohn, K., and Kwon, O. (2020). Technology acceptance theories and factors influencing artificial intelligence-based intelligent products. Telematics Inf. 47, 101324. doi:10.1016/j.tele.2019.101324
Soliman, H. R., Þórsson, B. J., Trevisan, S., and Guédez, R. (2021). “Utilizing industrial waste heat for power generation using sco2 cycle,” in 4th European sCO2 conference for energy systems 2021 (DuEPublico), 322–332. doi:10.17185/duepublico/73942
Stops, L., Leenhouts, R., Gao, Q., and Schweidtmann, A. M. (2022). Flowsheet synthesis through hierarchical reinforcement learning and graph neural networks. arXiv preprint arXiv:2207.12051.
Sutton, R. S., and Barto, A. G. (2018). Reinforcement learning: an introduction. Adaptive computation and machine learning series. 2 edn. Cambridge, MA: MIT press.
Thanganadar, D., Asfand, F., and Patchigolla, K. (2019). Thermal performance and economic analysis of supercritical carbon dioxide cycles in combined cycle power plant. Appl. Energy 255, 113836. doi:10.1016/j.apenergy.2019.113836
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention is all you need,” in Advances in neural information processing systems. Editors I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathanet al. (Long Beach, CA, USA: Curran Associates, Inc), 5998–6008.
Venkatasubramanian, V. (2019). The promise of artificial intelligence in chemical engineering: is it here, finally? AIChE J. 65, 466–478. doi:10.1002/aic.16489
Vogel, G., Balhorn, L. S., and Schweidtmann, A. M. (2022). Learning from flowsheets: a generative transformer model for autocompletion of flowsheets. arXiv preprint arXiv:2208.00859.
Weiland, N. T., Lance, B. W., and Pidaparti, S. R. (2019). “sCO2 power cycle component cost correlations from DOE data spanning multiple scales and applications,” in Proceedings of the ASME turbo expo 2019: turbomachinery technical conference and exposition (Phoenix, AZ, USA: ASME). doi:10.1115/GT2019-90493
White, M. T., Bianchi, G., Chai, L., Tassou, S. A., and Sayma, A. I. (2021). Review of supercritical co2 technologies and systems for power generation. Appl. Therm. Eng. 185, 116447. doi:10.1016/j.applthermaleng.2020.116447
Wigh, D. S., Goodman, J. M., and Lapkin, A. A. (2022). A review of molecular representation in the age of machine learning. WIREs Comput. Mol. Sci. 12, e1603. doi:10.1002/wcms.1603
Williams, R. J., and Zipser, D. (1989). A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1, 270–280. doi:10.1162/neco.1989.1.2.270
Wright, S. A., Davidson, C. S., and Scammell, W. O. (2016). “Thermo-economic analysis of four sco2 waste heat recovery power systems,” in Fifth international SCO2 symposium (San Antonio, TX: EU).
Yang, C., Deng, Y., Zhang, N., Zhang, X., He, G., and Bao, J. (2021). Optimal structure design of supercritical CO2 power cycle for gas turbine waste heat recovery: a superstructure method. Appl. Therm. Eng. 198, 117515. doi:10.1016/j.applthermaleng.2021.117515
Yu, A., Su, W., Lin, X., and Zhou, N. (2021). Recent trends of supercritical co2 brayton cycle: bibliometric analysis and research review. Nucl. Eng. Technol. 53, 699–714. doi:10.1016/j.net.2020.08.005
Keywords: process design, deep learning, structural optimization, pattern mining, combined cycle, supercritical CO2, exergoeconomics
Citation: Nabil T, Noaman M and Morosuk T (2023) Data-driven structural synthesis of supercritical CO2 power cycles. Front. Chem. Eng. 5:1144115. doi: 10.3389/fceng.2023.1144115
Received: 13 January 2023; Accepted: 02 October 2023;
Published: 16 October 2023.
Edited by:
Zukui Li, University of Alberta, CanadaReviewed by:
Jie Li, The University of Manchester, United KingdomAlexander William Dowling, University of Notre Dame, United States
Copyright © 2023 Nabil, Noaman and Morosuk. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tahar Nabil, dGFoYXIubmFiaWxAZWRmLmZy
 Tahar Nabil
Tahar Nabil Mohamed Noaman2
Mohamed Noaman2 Tatiana Morosuk
Tatiana Morosuk