An Agro-Pastoral Phenological Water Balance Framework for Monitoring and Predicting Growing Season Water Deficits and Drought Stress

Sharing simple ideas across a broad community of practitioners helps them to work together more effectively. For this reason, drought early warning systems spend a considerable effort on describing how hazards are detected and defined. Well-articulated definitions of drought provide a shared basis for collaboration, response planning, and impact mitigation. One very useful measure of agricultural drought stress has been the “Water Requirement Satisfaction Index” (WRSI). In this study, we develop a new, simpler metric of water requirement satisfaction, the Phenological Water Balance (PWB). We describe this metric, compare it to WRSI and yield statistics in a food-insecure region (east Africa), and show how it can be easily combined with analog-based rainfall forecasts to produce end-of-season estimates of growing season water deficits. In dry areas, the simpler PWB metric is very similar to the WRSI. In these regions, we show that the coupling between rainfall deficits and increased reference evapotranspiration amplifies the impacts of droughts. In wet areas, on the other hand, our new metric provides useful information about water excess—seasons that are so wet that they may not be conducive to good agricultural outcomes. Finally, we present a PWB-based forecast example, demonstrating how this framework can be easily used to translate assumptions about seasonal rainfall outcomes into predictions of growing season water deficits. Effective humanitarian relief efforts rely on early projections of these deficits to design and deploy appropriate targeted responses. At present, it is difficult to combine gridded satellite-gauge precipitation forecasts with climate forecasts. Our new metric helps overcome this obstacle. Future extensions could use the water requirement framework to contextualize other water supply indicators, like actual evapotranspiration values derived from satellite observations or hydrologic models.

Introduction

A central and successful tenet of the famine early warning community is the fact that impacts of water deficits are predictable—water deficits anticipate reductions in food access and availability. In the late 1970s and 1980s, plot-based studies by the Food and Agricultural Organization (FAO) identified crop water requirements (Doorenbos and Pruitt, 1977) and created the Water Requirement Satisfaction Index (WRSI) model (Frère and Popov, 1986) to estimate yield reductions based on the crop water balance and accumulated deficits. The WRSI framework quantifies the water required for optimal plant growth during four main growth stages, with the vegetative and grain-filling stages occurring when the crop water requirements are highest. The WRSI tracks increased crop water use—and crop water stress—, which occurs when the available soil moisture is less than the crop's water requirement. For regional crop monitoring, an important step forward in operational application of the WRSI was the combination of the WRSI formulation with gridded rainfall, reference evapotranspiration, and soil property data sets (Senay and Verdin, 2001, 2003; Verdin and Klaver, 2002). These models now provide a widely used foundation for tracking agricultural shocks in food-insecure countries. WRSI is actively used to support the Famine Early Warning Systems Network (FEWS NET) Food Security Outlook (FSO) process (Magadzire et al., 2017), in which FEWS NET scientists provide forward-looking assumptions that food security analysts use to estimate food-insecure populations (Funk et al., 2019b). In this study, we draw from some of the most useful aspects of the WRSI framework and consider how advancements in forecast weather and climate data can support new types of forward-looking crop and rangeland monitoring applications.

Over the past few decades, the food security community has increasingly taken advantage of the opportunities provided by climate science (Verdin et al., 2005). FEWS NET scientists use “staged” early warning systems that combine long-lead and short-lead climate and weather forecasts with high-resolution satellite observations, and hydrology and crop model simulations. The staged system accommodates the benefits and challenges from weather and climate information being produced by different communities, with disparate scales and statistical distributions, as well as the skill in long-lead time climate forecasts associated with major climate modes like the El Niño-Southern Oscillation and at short-lead time weather forecasts.

At the forefront of such efforts are climate services focused on producing “seamless” or “interoperable” sets of precipitation estimates that combine satellite observations, rain gauge archives, weather forecasts and climate outlooks—high-resolution grids that extend from the past into the future. A key aspect of such systems is that the statistical distributions of the rainfall predictions are similar to those of the observations. At weather time scales, the Climate Hazards Center (CHC) uses quantile mapping to produce high-resolution forecasts at weather time scales. At climate time scales, it is also common practice to identify analog seasons, which can also be used to generate high-resolution “forecasts” of future rainfall based on averages of observed blended satellite-gauge data. For example, in early November 2020, combinations of satellite-gauge observations, downscaled weather forecasts, and expectations based on climate analogs, were combined and presented in a Crop Monitor Alert¹ While these “Early Estimates” were fairly accurate², they only presented likely precipitation outcomes. To move closer to impacts associated with crop and rangeland water deficits, we explore simple combinations of Growing Season Precipitation (GSP) and estimates of crop and rangeland Water Requirements (WR). We use GSP and WR to define a simple “Phenological Water Balance” (PWB) metric.

WRSI tracking involves estimating, in mm, the amount of evapotranspiration required by the crop at each time step, which is typically a dekad, or 10-day increment³. This is the Water Requirement (WR). The WRSI estimates water supply, in mm per dekad, by using a “bucket” model of the soil column, parameterized using assumptions about crop phenology (e.g., rooting depth) and water holding capacity, to track soil moisture conditions throughout the growing season. The WRSI is the ratio of growing season actual evapotranspiration (AET) to the crop's water requirements (WR). This ratio quantifies the degree of crop water stress, ranging from no stress to enough stress to cause wilting (Smith, 1992; Senay and Verdin, 2003). The dekad is the most common time step used in WRSI modeling, and we use it here. Each month is divided into two 10-day dekads and a final dekad that contains the remainder of the days in each month.

The start of the growing season (SOS) commences when a location receives more than 25 mm of rain, and is followed by two dekads that total more than 20 mm of rain combined (AGRHYMET, 1996). Beginning with that first dekad, the WR component of the WRSI uses Length of Growing Period (LGP) assumptions and crop-stage-dependent coefficients (K_c) to adjust the Reference EvapoTranspiration (RefET) corresponding to the phenological cycle of healthy plant growth and photosynthesis during a growing season (WR = RefET × K_c). For context, Kc values greater than one indicate periods of the phenological cycle in which the crop has a greater upper limit to its atmospheric demand of moisture than the reference green-grass crop used in the calculation of the RefET data. This will be shown formulaically in Methods section, but can be described generally as follows. Plants emerge, and WR increases as they add biomass during their vegetative stage. Then, after a fixed fraction of the LGP, cereals enter a grain-filling phase. The energy, carbohydrates, and sugars obtained via photosynthesis are used to increase the size and quantity of grains. Finally, cereal crops enter a senescent stage associated with decreasing WR. The bucket model, driven with observed precipitation and RefET, estimates the amount of water available for extraction as AET. When there is always sufficient moisture available to meet the WR, the WRSI (AET÷WR) will be 100%, and there is no water deficit-related yield reduction. Large (~50%) seasonal water deficits will be associated with crop failure (Smith, 1992).

The PWB is simpler to calculate than the WRSI, easier to integrate with climate observations and forecasts, less impacted by potential biases associated with the input rainfall and RefET data sets, and unaffected by potential errors in the specification of soil conditions. Furthermore, unlike the WRSI, the PWB is not capped at 100%, and therefore provides more information about exceptionally wet conditions. This feature may support better assessments of adverse precipitation impacts in productive agriculture areas and could mean that PWB is better equipped for monitoring impacts of extreme precipitation events and destructive storms related to global climate change (Trenberth et al., 2003; Donat et al., 2016). Sub-Saharan Africa may be experiencing more extreme precipitation events, yet information is heavily under observed (Harrison et al., 2019).

The PWB indicator can be seen as a plant-smart form of Aridity Index (Zucca et al., 2012) or Standardized Precipitation Evaporation Index (SPEI) (Vicente-Serrano et al., 2010; Peng et al., 2020). We will explore the utility of the PWB framework for seasonal monitoring, scenario development (Husak et al., 2013), yield estimation, trend analyses, and national agricultural risk management. We will use seasonal precipitation as our water supply indicator, but the approach used here could easily be expanded to incorporate alternative variables, such as satellite or model-based estimates of AET or soil moisture, Normalized Difference Vegetation Index (NDVI) Values, etc. The temporal filtering provided by the WR framework could be used in conjunction with myriad supply-related inputs. These filtered inputs, furthermore, could then feed into more complex statistical or machine-learning-based estimation processes (e.g., Laudien et al., 2020).

This study seeks to demonstrate the utility of the PWB framework for seasonal monitoring, prediction, trend analyses, and risk management. In the sections below, we examine the following questions:

• Can the PWB be used, like the WRSI, to effectively detect agricultural and pastoral droughts? Can it provide insights into areas with high drought risk?

• How does the PWB compare with WRSI as a basis for estimating national and sub-national crop production in Kenya?

• Can the PWB framework be used to combine gridded satellite observations with weather and climate forecasts to produce mid-season outlooks of plant water stress?

The case study presented here focuses on east Africa during the boreal spring Long/Gu/Belg rainy season, providing an important context for our analyses. This region, which includes parts of Kenya, Somalia, and Ethiopia, is extremely food insecure, and prone to both severe droughts and flooding. While March–April–May is the core of this season, some regions may start earlier or end later. Data and Study Region section describes the data used and our study region, and Methods section lays out our methods. Examining the Utility of the PWB Framework for Monitoring Water Stress section, Examining the Utility of the PWB Framework as a Basis for Estimation of National and Sub-national Yields in Kenya section and, Examining the Utility of the PWB Framework as a Basis for Translating Integrated Rainfall Early Estimates into Assessments of Agro-pastoral Hazards section, then examine: (1) The utility of the PWB Framework for monitoring agro-pastoral drought; (2) The utility of the PWB framework as a basis for estimation national and sub-national yields in Kenya; and (3) The utility of the PWB framework as a basis for translating integrated rainfall observations and forecasts into assessments of agro-pastoral hazards. Discussion and Conclusion sections present some discussion and conclusions.

Data and Study Region

This study uses 1981–2020 0.1° Climate Hazards InfraRed Precipitation with Stations (CHIRPS) rainfall data (Funk et al., 2015b) and 0.1° Penman-Monteith-based RefET estimates produced by Michael Hobbins (Hobbins et al., 2016)⁴ Focusing on the east Africa boreal spring rainy season, the study uses the land cover designations, LGP, and crop types commonly used by the United States Geological Survey (USGS)'s Early Warning team⁵ to support FEWS NET. Three WRSI modeling frameworks have been combined to provide one synoptic overview of east Africa (Figure 1A). A “long rains” maize modeling framework describes crop-growing conditions across the general region. Within Ethiopia, settings for the “Belg” growing season augment this default. Finally, in drier regions, settings for rangeland are used to quantify outcomes in pastoral regions. This corresponds with the USGS's “Long rains, maize” WRSI framework⁶, “Croplands Belg”⁷, and “Long rains, rangeland” WRSI⁸ The long rains and Belg maize simulations use the same crop coefficients, but the Belg season has been customized for Ethiopia, with a different mask, LGP, and SOS values. Where available, Belg cropland parameters were used in place of the long rains values. In highland areas, the Belg LGP values can be long, 15+ dekads, representing the slow development of crops in cool high-elevation locations. The resulting composite map provides a snapshot of conditions over the entire region in a single view, aiding in the interpretation of individually modeled growing conditions and identification of conditions which may present food-insecurity issues.

FIGURE 1

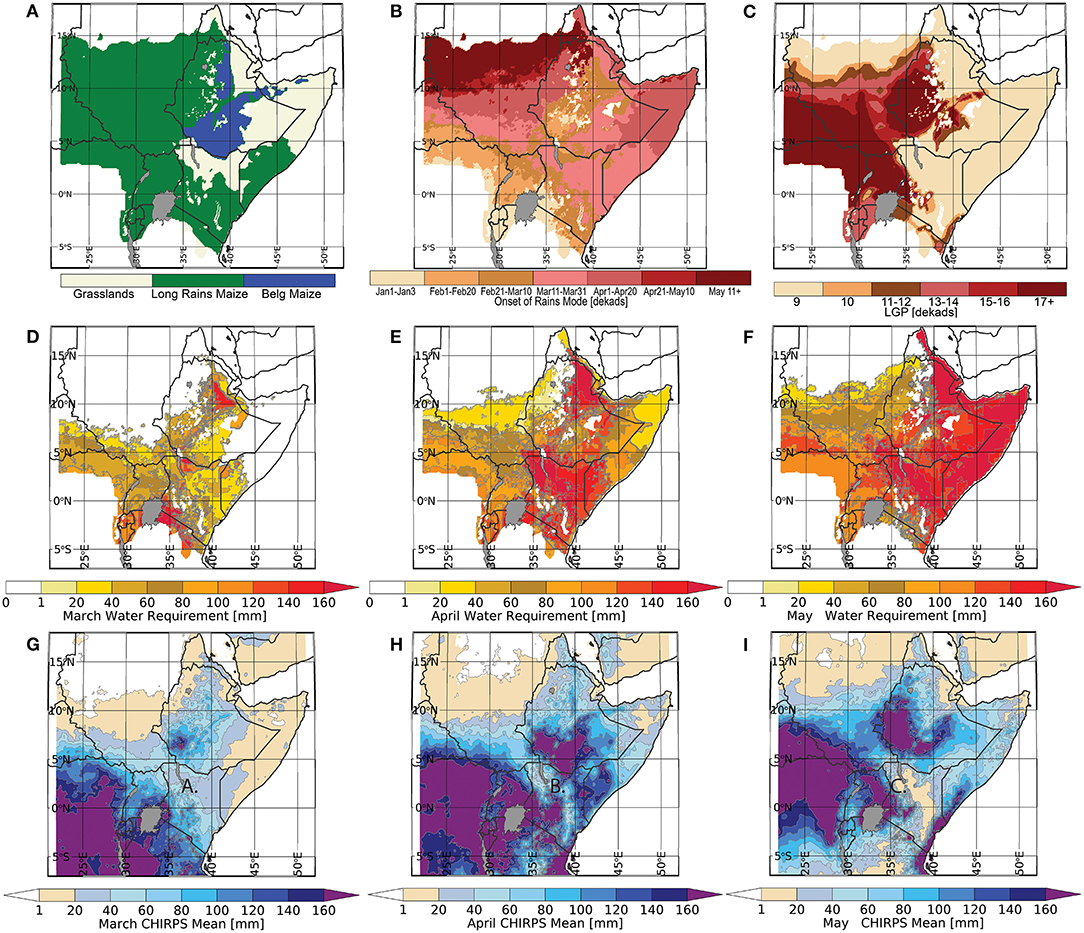
Figure 1. (A) The three crop classes used to calculate Water Requirements. (B) The most frequent (modal) SOS dekad used to define the start of the season. (C) Mean LGP values, in dekads. (D–F) Average monthly crop WR totals in mm. (G–I) Average monthly CHIRPS precipitation totals in mm.

The rangeland WRSI parameters are very different from the maize parameters. The SOS calculation uses a much-less stringent threshold: 10 mm in dekad one, followed by a total of just 5 mm in the next two dekads. The maximum Kc coefficients are substantially lower (0.75 as opposed to 1.2), and the LGP is set to a universal 7 dekads.

The next key modeling parameters used are modal estimates of SOS. Using 40 years of CHIRPS data, onset dates were calculated for each pixel, and then the most frequent SOS dekad (i.e., the mode) was identified (Figure 1B). In this pilot study, we use these fixed dates to begin every year's growing season. In practice, different dates could be identified every year. Implicit in the WRSI simulation system developed by the U.S. Geological Survey FEWS NET team⁹ This framework provides spatially detailed information about the dominant crop or pasture type, when we can expect the season to begin, and how the plant water requirements are expected to evolve over time.

Commencing with the SOS dekad, LGP values (Figure 1C) are then used to identify the end of a growing season. Static LGP values were originally developed by WRSI modelers at the U.S. Geological Survey (Senay and Verdin, 2001, 2003; Verdin and Klaver, 2002) based on climatological (long-term average) precipitation and RefET. Note that LGP will vary dramatically depending on geographical location. A common metric for estimating LGP is the number of consecutive dekads in which the precipitation is greater than one half of the reference evapotranspiration¹⁰ (FAO, 1978). In arid areas with low rainfall and high RefET, LGP values will be low (~7 dekads or 70 days). In these regions, plants have a very short window through which to receive adequate moisture to support growth. In moist, cool areas with high rainfall and low RefET, LGP values can be much larger. Corresponding growing seasons can extend beyond 18 dekads (180 days). In east Africa, longitude and altitude play a huge role in determining LGP. As seen in Figure 1C, many critical crop-growing regions tend to be located in spatially limited, high-mountain areas associated with the Rift Valley escarpments. Meanwhile, in most of Kenya, all of Somalia, and most of Ethiopia east of 38°E, the growing season is very short.

Taken together, the SOS, LGP, and K_c coefficients provide a simple yet powerful way to automatically filter environmental information in time. In data-sparse environments, such filtering can be extremely useful in a food-security setting. While we are often interested in the ultimate drivers of food access and availability shocks, such as food production deficits, in practice, we only have proximate indicators like precipitation, RefET, etc. The WR framework gives us a physically plausible way to interpret this information. This filtering can be used to augment statistical and machine-learning-based estimation approaches and support easy-to-implement decision support informatics.

As previously noted (Figure 1C), most of Kenya, all of Somalia, and most of Ethiopia east of 38°E have very short growing seasons. In many of these areas, RefET and WR increases substantially in April and May (Figures 1E,F), and precipitation drops in May (Figure 1I). This results in a short window for crop and pasture growth.

A few high-elevation areas with high rainfall and low RefET provide limited areas that can support highly productive crops. The interplay of water demand and water supply can be visualized using long-term averages for March, April, and May (Figures 1D–I). In March, both WR and GSP totals tend to be relatively low, as the season becomes established and the growing season begins. WR values increase dramatically in April, as K_c values increase and crops typically enter their vegetative stage. April typically represents the month of maximum rains in most eastern regions (east of 38°E). In May, WR values remain high, or even increase in this eastern region, as rains begin to subside and climatological RefET values intensify. This intensification and the inherently short eastern African March-April-May rainy season can make it hard to recover from late starts or early-to-mid season deficits.

Methods

Building on the standard FEWS NET crop phenology framework (Figures 1A–C), we introduce a simple agro-pastoral Phenological Water Balance (PWB), which is a form of tailored Aridity Index that takes into account the total amount of Growing Season Precipitation (GSP) and crop Water Requirements (WR) based on standard WRSI modeling practices. In this study, we use fixed SOS dates (Figure 1B). Beginning with each location's SOS date, and assuming a fixed LGP value at each pixel (Figure 1C), GSP values can be accumulated over each year's growing season's dekadal precipitation in mm (P_i).

$\begin{array}{ll}GSP={\displaystyle \sum _{i=SOS}^{SOS+LGP}}{P}_i& (1)\end{array}$

Equation (1) represents a simple measure of water supply. Borrowing directly from the WRSI framework, we can then estimate seasonal plant-specific WR values based on time-varying crop coefficients (K_c) and time-varying dekadal RefET values—equation (2). The WR values represent the amount of AET required by crops or fields to maintain maximum “water satisfaction.” As atmospheric water demand (RefET) increases, the optimal amount of AET increases as well. But WR also changes as plants grow. RefET formulations typically assume a well-watered, well-developed “reference” crop, like alfalfa, that efficiently transports water into the atmosphere. At the start of the season, at emergence, WR values will be much lower than this upper limit. Hence, K_c terms start low and increase during the vegetative stage. In cereal crops, the K_c terms typically stay high during grain filling, then drop rapidly as the plants senesce. Rangeland K_c terms typically stay high throughout the plant's short (70-day) growing season (Figure 1C). The time-varying K_c and RefET values can be combined to calculate season WR totals in mm.

$\begin{array}{ll}WR={\displaystyle \sum _{i=SOS}^{SOS+LGP}}K{c}_i\times RefE{T}_i& (2)\end{array}$

While powerful, WRSI results can be problematic when any of the core inputs are biased. Furthermore, because the WRSI requires sub-monthly rainfall data, it can be difficult to connect the WRSI framework with climate forecasts, climate change simulations, or historical gridded rainfall archives. Finally, WRSI does not provide information about extremely wet conditions.

Hence, we examine here the utility of combining the WR framework of the WRSI with a simpler PWB formulation:

$\begin{array}{ll}PWB=100\times \frac{GSP+\epsilon }{WR+\epsilon }& (3)\end{array}$

Whereas the WRSI estimates the ratio of AET and WR values, PWB examines the ratio of GSP and WR. A small value (10 mm in this study) is added to both the numerator and denominator to increase numerical stability in arid regions. This study will compare PWB results with those produced using the WRSI model, asking whether we can get reasonably comparable results using the simpler PWB framework.

Note also that the rainfall accumulations in the numerator of eq. 3 could be replaced by a host of other indicators, such as AET values from hydrologic models, like the FEWS NET Land Data Assimilation System (FLDAS) (McNally et al., 2017), hydrologic forecast systems (Arsenault et al., 2020), satellite-based energy balances (Senay et al., 2007, 2011; Anderson et al., 2011), or satellite-based vegetation or soil moisture observations (McNally et al., 2015). The WR framework, therefore, could be used to search for consilience across multiple data sets that relate to crop water supply.

Results

Examining the Utility of the PWB Framework for Monitoring Water Stress

This section begins by comparing PWB and WRSI values over east Africa. As Figures 2A,B reveal, the variance structure of WRSI and PWB is quite similar in drier, water-limited areas, where WR > GSP, but quite different in wetter areas, where WR < GSP. In the latter, the WRSI tends to saturate at or just below 100%, and the WRSI standard deviation rapidly tends to zero. In these regions, the PWB is allowed to have large values >100, and hence, has a larger amount of variability. In many water-limited areas, however, we find moderate-to-high correlations between the WRSI and PWB (Figure 2C).

FIGURE 2

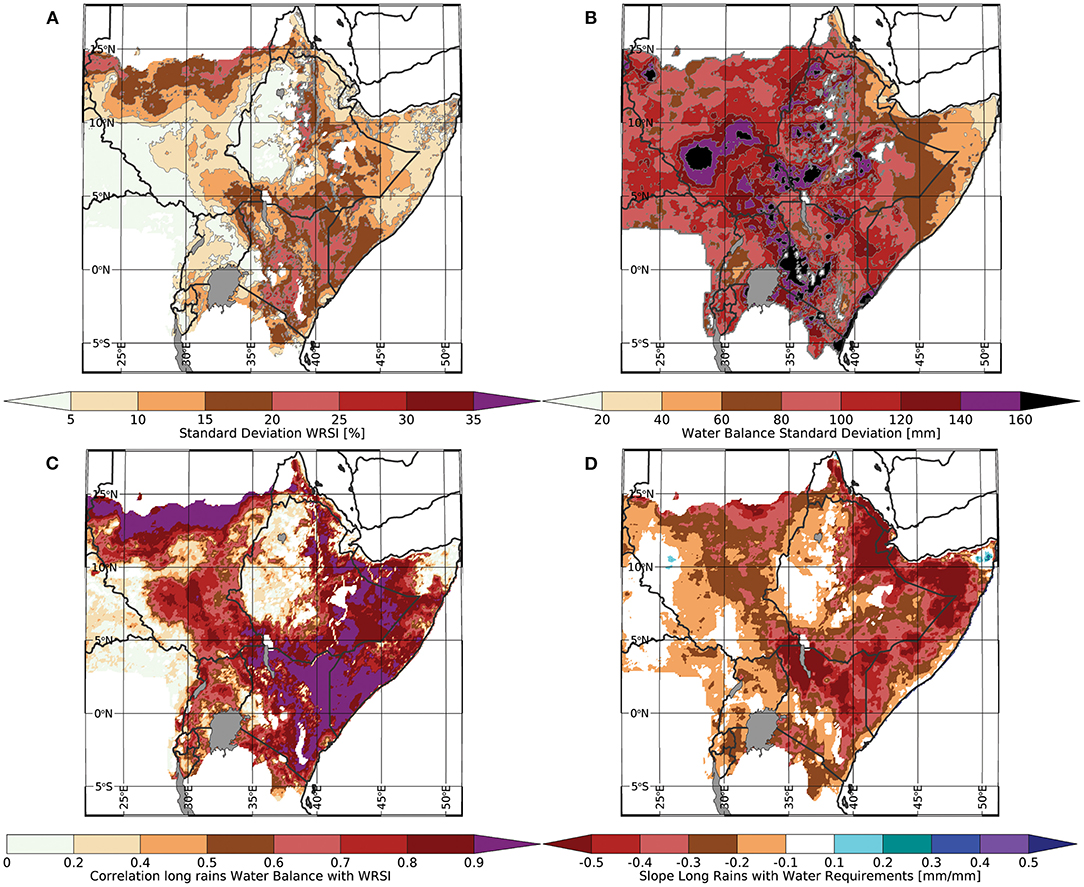
Figure 2. (A) Interannual WRSI standard deviation. (B) Interannual PWB standard deviation. (C) Interannual correlation between end-of-season WRSI and WB (D). Slope coefficients from regression between GSP and WR in units of mm per mm.

Note that there are potential advantages to both approaches. If the WRSI is perfectly calibrated with the correct soil properties, crop coefficients, plant phenology, and driven by accurate and low-bias precipitation and RefET data, then, presumably, WRSI values near 100 will be a reliable indicator of good yields. There are times and places, however, where these conditions are not met. In such cases, the simpler PWB approach might actually be more representative. Another interesting potential application of the PWB might be to explore negative impacts associated with very high PWB values. It seems plausible that when PWB values become very large, crops may experience waterlogging, reduced photosynthesis due to reduced sunlight, or other detrimental influences associated with extremely wet conditions. Extremely wet conditions will not register in WRSI simulations.

As one might expect, the overall correlation between the end-of-season WRSI and PWB is quite high in water-limited areas, where the standard deviation of the WRSI is high (Figure 2A). Stratifying these correlation grids by the standard deviation of the WRSI, we find that the mean WRSI-PWB correlations are 0.28, 0.59, 0.71, 0.83, and 0.87 when σ_WRSI ranges from >0 to <5, >5 to <10, >10 to <15, >15 to <20, and >20, respectively. Hence, the PWB and WRSI results are quite similar in water-limited regions.

The simplicity of the PWB framework makes it easy to explore and quantify the covariability of the supply (GSP) and demand terms (WR). This is valuable, because the Bouchet–Morton Complementary Relationship suggests that water-limited arid regions will exhibit a negative relationship between RefET and AET (Hobbins et al., 2012). Under arid conditions, reductions in AET drive increase in RefET through energy exchanges across the land-atmosphere interface (Hobbins et al., 2016). In contrast, in humid regions, radiation, not water availability, limits AET, and RefET will equal AET. In dry regions, the lack of AET means that the Earth's surface will need to rely on upward radiative and sensible heat energy fluxes. So as radiation increases, surface temperatures and RefET increase, and as RefET increases, AET tends to decrease. And as AET decreases, RefET increases.

Figure 2D displays an empirical regression slope grid, with GSP predicting WR. While we might expect an inverse relationship from first principles, the strong spatial coherence of these slope values is nonetheless striking. Particularly in arid pastoral regimes, we find slopes as low as −0.5 mm·mm⁻¹. This slope implies that a 50-mm rainfall deficit might be exacerbated by a 25 mm increase in WR. The magnitude of the plant water deficits would be magnified by 50%, from 50 to 75 mm. On a year-to-year basis, this helps explain why pasture conditions can collapse so rapidly in arid and semi-arid areas like southern and eastern Ethiopia, northern and eastern Kenya, and all of Somalia, where RefET or WR often increase with rainfall deficits.

According to the Complementary Relationship, one expects that the mean AET and RefET will converge in humid areas and diverge in water-limited areas, where AET decreases and RefET increases. What we see in Figure 2D is an important temporal expression of these interdependencies. In humid areas, AET should follow RefET, and we do not expect precipitation to strongly influence RefET. Regression coefficients in these regions are very low. In dry areas, wet and dry seasons will be associated with more or less clouds and cooler or warmer land surface conditions, which in turn strongly modulate RefET and WR.

In Figures 3, 4 we have plotted PWB and WRSI anomalies for four boreal spring seasons, as well as four prior signature drought years. While not identical, there is a high level of agreement between the PWB and WRSI anomaly figures. This suggests that very WRSI-like results may be derived from GSP and WR. The 2017, 2018, 2019, and 2020 seasons were selected because they provide a “whip-saw” example, with dramatic swings between dry and wet seasons. Both the PWB and WRSI display this sequence. But by construction, the unbounded PWB indicator provides more information about very wet conditions in humid areas. It is interesting to note that the PWB dry anomalies in 2017 and 2019 indicate more stress in some important areas, such as southern Somalia, the south-central highlands of Ethiopia, and central-western Kenya. The stronger and more extensive drought response of the PWB index maps can be seen even more clearly in plots of four very dry seasons: 1984, 1993, 2000, and 2009. In 1984 and 1993, tragic famines struck Ethiopia and Somalia, respectively. In 2000 and 2009, strong La Niña conditions and extremely warm west Pacific sea surface temperatures produced widespread droughts (Funk et al., 2018b). For these very dry years, in humid regions, the PWB anomalies suggest more widespread water deficits than the WRSI.

FIGURE 3

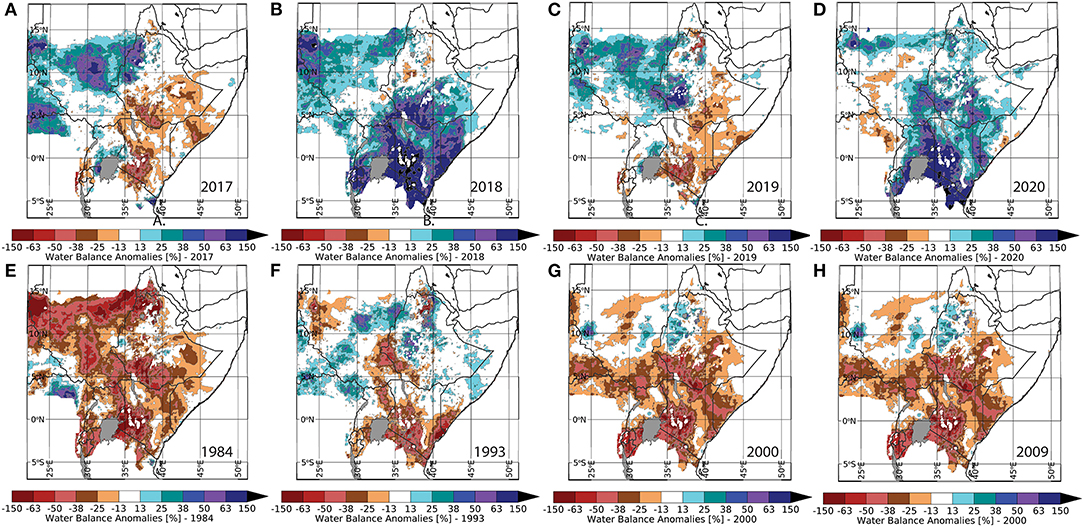
Figure 3. Seasonal PWB maps, expressed as percent anomalies from the long-term average, for the four most recent years (A 2017, B 2018, C 2019, D 2020) and four extremely dry prior years (E 1984, F 1993, G 2000, H 2009).

FIGURE 4

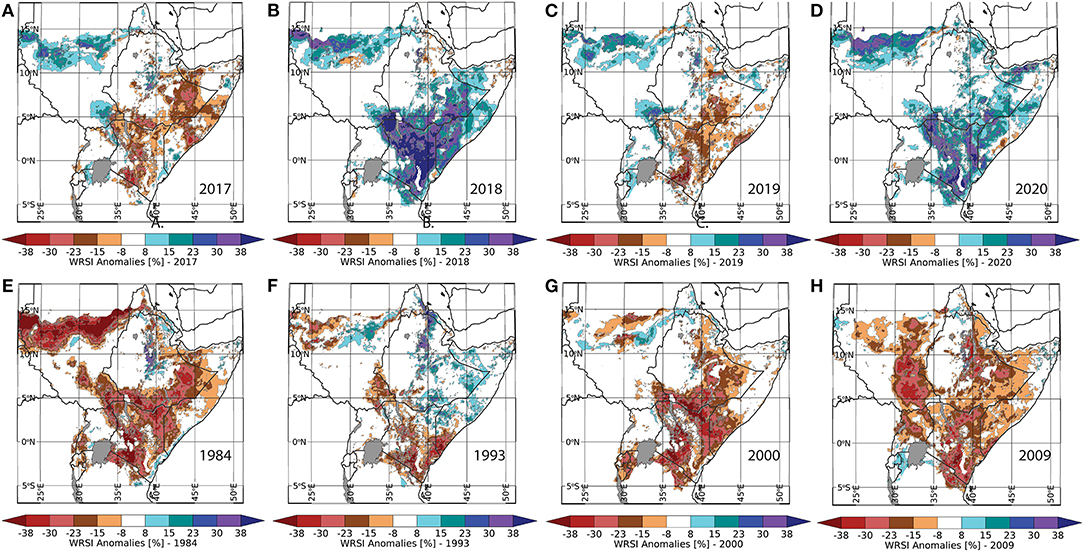
Figure 4. End-of-season WRSI anomalies for the four most recent years (A 2017, B 2018, C 2019, D 2020) and four extremely dry prior years (E 1984, F 1993, G 2000, H 2009).

Examining the Utility of the PWB Framework as a Basis for Estimation of National and Sub-national Yields in Kenya

We next turn to a comparison of WRSI and PWB values with national and sub-national maize yields for Kenya. Kenya has been selected because of its abundant crop data compared to other countries in the region. It should be noted, however, that this data is imperfect, given limited and changing crop survey capacities. Two sources of yield statistics were examined: (1) sub-national (county) level yields, obtained via the FEWS NET Data Warehouse, and (2) national yields obtained from the FAO's statistical archive (FAOSTAT). At the sub-national scale, we focused on 18 key agricultural counties¹¹. The PWB and WRSI time-series were very similar in 12 of these counties (R > 0.8). In four counties, correlations were 0.5–0.79. The remaining two counties had saturated WRSI (mean of >99%), resulting in no relationship between the two metrics.

Overall, the correlations between county-level yields and WRSI and PWB were relatively poor, with median correlations of 0.36 and 0.37, respectively. While far from impressive, these results do indicate that the performance of the WRSI and PWB were not statistically distinguishable. The WRSI did not perform better than the PWB.

We next turn to comparisons with national Kenyan FAOSTAT yields and spatially aggregated sub-national yields (Figure 5). For these comparisons, the PWB and WRSI were averaged over key cropping counties⁹. Scatterplots with national yields are shown in panels A and B, and sub-national results are plotted in C and D. Again, the statistical relationships are fairly weak, with national R² values ranging from 25 to 41%¹² In general, the scatterplots reveal more discrimination when PWB and WRSI averages are low. When PWB and WRSI are high, the values' relationships with yields are weak. But, when PWB and WRSI are <90 and 60%, respectively, we do find consistent below-normal yield outcomes. These seasons (1984, 1993, 2000, and 2009) are noted in Figure 5 and are mapped in Figure 3, Figure 4. The relationships with sub-national yields are somewhat stronger, with R² values of 41 and 37 percent. For both national and sub-national yields, there are low-yield seasons that have average WRSI and PWB values. It is not clear whether this is an issue with the yield statistics or a function of non-weather-related factors, such as conflict. While the PWB and WRSI performance is very similar, the PWB is substantially less complex to calculate, and less sensitive to parameterization.

FIGURE 5

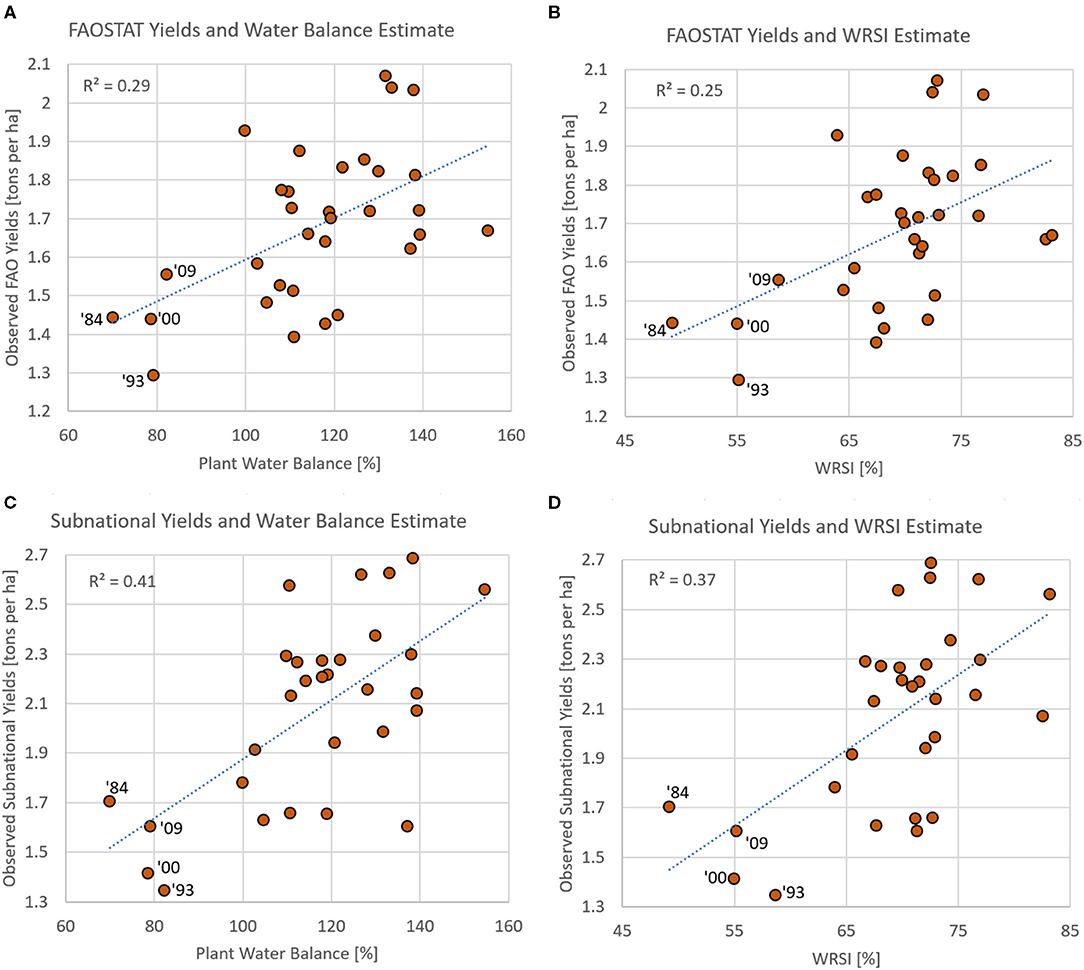
Figure 5. Comparisons (scatterplots) showing Kenyan FAOSTAT national yields (y-axis) and Plant Water Balance (A) and WRSI (B) (x-axis) in key crop-growing counties in Kenya. (C, D) Show similar results based on sub-national yields from these counties. The FAOSTAT time-series extends from 1982 to 2019, the sub-national yields extend from 1982 to 2016.

Figure 6 presents a time-series of national yields and standardized PWB values from Kenya's key cropping counties. One striking aspect of this time-series is the incredibly wet outcomes in 2018 and 2020. The actual PWB values for Kenya were 269 and 232%. The GSP totals far exceeded crop water requirements. The average WRSI time-series (not shown) presents a very different story, with 2018 and 2020 values of 89 and 87. While these values are extremes in both time-series, the physical implications of these values are quite distinct. A WRSI value of about 88 indicates good cropping conditions. A PWB value of about 250% may indicate issues associated with extremely wet conditions. Again, PWB and WRSI maps of these wet seasons (Figures 3, 4) demonstrate that the PWB better reflects the dynamic range of these extremely wet seasons. Plots of the GSP minus WR differences (not shown) are also useful from this perspective.

FIGURE 6

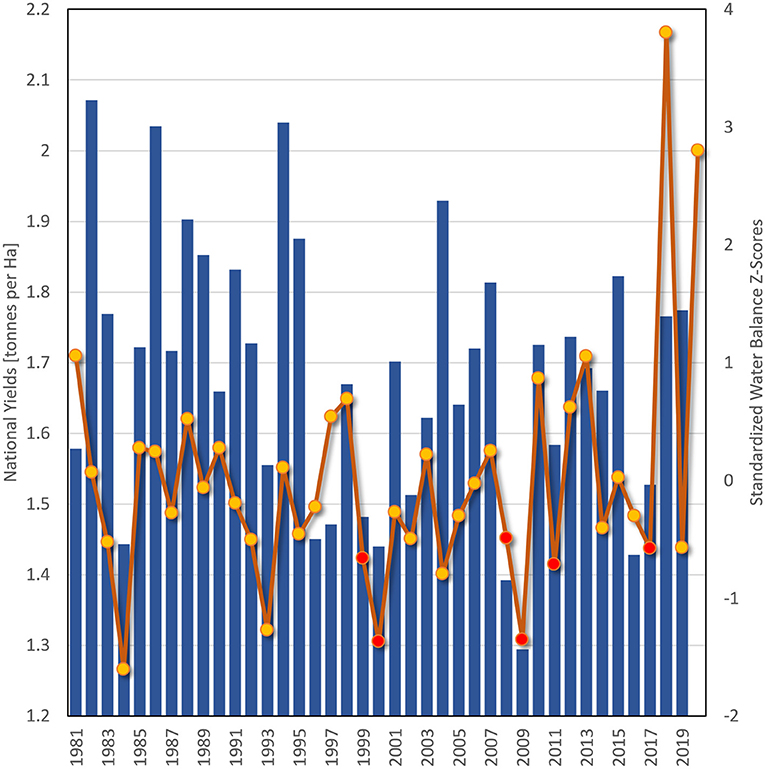
Figure 6. Time-series of FAOSTAT national Kenyan maize yields (blue bars) and PWB Z-scores for key crop-growing counties (orange line with dots).

It is worth noting that national yields appear quite static, i.e., they are not trending upward. At the same time, the population has grown rapidly, at about 3% per year. As we will explore, this has resulted in exceptionally low per-capita maize production values. But another striking feature of Figure 6 is the lack of extreme agro-hydrological deficits over the last 10 years—a period in which the number of people facing acute food insecurity has climbed dramatically. While 2011, 2014, 2016, 2017, and 2019 had below-average PWB values, the magnitude of these PWB deficits were relatively mild given the historical record, with standardized anomalies of about −0.7. Given that many of these seasons were associated with large humanitarian crises (Funk et al., 2018a), these results appear to indicate that non-weather drivers may be decreasing Kenyan resilience and adaptive capacity, so that relatively modest droughts appear associated with rather large increases in food insecurity.

What will happen when Kenya experiences another severe drought, a drought similar to 1984, 1993, 2000, or 2009? We will explore this question in more detail in Examining the Utility of the PWB Framework as a Basis for Translating Integrated Rainfall Early Estimates into Assessments of Agro-pastoral Hazards section.

Examining the Utility of the PWB Framework as a Basis for Translating Integrated Rainfall Early Estimates Into Assessments of Agro-Pastoral Hazards

We next describe how the PWB framework can be used to take advantage of integrated monitoring-forecast systems. For many years, the Climate Hazards Center has worked toward methods that support the combination of high-resolution gridded rainfall estimates (like CHIRPS) with weather and climate forecasts. The basic idea is that coarse resolution weather and climate information can be transformed such that it has statistical distributions similar to high-resolution, rapidly updated data streams, like CHIRPS. This makes these forecasts inter-operable with the observations. The ability to combine observations and predictions can be very powerful. In terms of hydrologic modeling, the NASA Hydrologic Forecast System (NHyFAS) (Arsenault et al., 2020) provides one good example of linking to-date conditions and forecasts to assess hydrologic conditions in the future. Here, we demonstrate how the PWB framework can be used to generate forecasts of agro-pastoral water deficits. This framework builds on two existing forecasting resources: (1) high-resolution CHIRPS-GEFS 1–15-day precipitation forecasts and (2) east African climate analog-based rainfall and RefET predictions.

CHIRPS-GEFS is a bias-corrected and downscaled version of National Center for Environmental Prediction Global Ensemble Forecast System (GEFS) precipitation forecasts (Hamill et al., 2013). Quantile matching is used to make GEFS forecasts spatially compatible with various CHIRPS products¹³ Daily rainfall forecasts are accumulated to create 5-, 10-, and 15-day totals. The rank-based quantile of these totals is then quantile-matched to the empirical distribution of CHIRPS rainfall for the corresponding period. The result of this quantile-matching scheme is that the average and variance of the CHIRPS data is approximately retained in the resulting CHIRPS-GEFS values.

The CHIRPS-GEFS forecast data product is a valuable resource for CHIRPS users, since it provides GEFS precipitation totals and anomalies that are compatible with the historical CHIRPS. This feature allows for the timely assessment of how the latest forecast could alter the current agro-climatological situation. The CHC Early Estimates provide routinely updated analyses that combine CHIRPS and CHIRPS-GEFS.

Climate analogs can provide longer lead (1–8 months) climate forecasts. Typically based on diagnostic drought analyses, the identification of analog seasons (historical seasons that may resemble current/predicted conditions) provides a simple but powerful means of leveraging the power and detail of high-resolution data sets and hydrologic and crop simulations. This can be especially powerful when combined with skillful long-lead climate forecasts of Pacific Sea surface temperatures, as exemplified by FEWS NET long-lead forecasts for eastern Africa. To support the FEWS NET FSO process, FEWS NET uses a staged approach (Funk et al., 2019b) that combines tailored 1–8 month climate forecasts, down-scaled weather predictinos, satellite observations and hydrologic simulations (McNally et al., 2017) and forecasts (Arsenault et al., 2020).

Following the disastrous 2011 famine in Somalia (Checchi and Robinson, 2013), the FEWS NET team carried out extensive research that focused on understanding and predicting east African droughts (Hoell and Funk, 2013a; Funk et al., 2014; Hoell et al., 2014; Shukla et al., 2014). While a full description of this work is beyond the scope of this paper, this research links climate change-enhanced La Niña conditions to sequential dry east African conditions in the October-to-December and March-to-May rainy seasons (Funk et al., 2018a, 2019a). While the best analog definitions vary by season, timing, and data source, variations of the West Pacific Gradient (WPG) (Hoell and Funk, 2013b) are used to identify strong-gradient La Niña seasons.

In eastern Africa, this approach, combined with the latest generation of climate forecast models, can provide surprisingly skillful forecasts at very long leads of 6 or more months. For the October-to-December season, many La Niña-related dry seasons can be identified as early as June^14,15 For the March-to-May season, September forecasts of strong La Niña-like Pacific Sea surface temperature gradients can be robust indicators of eastern east Africa droughts¹⁶ While these forecasts explain a relatively low amount of the overall variance (~40%), they do provide valuable advance notice of many sequential droughts. The September 2020 analysis identified 2017, 1999, 2011, 2008, 2014, and 2009 as analogs. The final update¹⁷ identified 1999, 2000, 2001, 2008, 2009, 2011, 2012, and 2017.

In May of 2021 (as we write), the eastern Horn faces a severe food crisis associated with poor late 2020 and early 2021 rainy seasons. The food security situation, already dire due to the combined influences of conflict in Ethiopia and Somalia, recurrent drought and flood shocks since 2016, persistently high inflation in Ethiopia, the COVID-19 pandemic, and the desert locust upsurge, is becoming worse.

Our focus here is to show how the PWB framework makes it relatively simple to “stack” three sources of information to provide spatially detailed forecasts of agro-pastoral risk—CHIRPS observations, CHIRPS-GEFS forecasts, and analog-based climate forecasts. In this example, we use CHIRPS observations through the 1st dekad of April (dekad 10), CHIRPS-GEFS forecasts for the second dekad of April, and then analog and average CHIRPS rainfall through the remainder of the season. In this last step, we use two different assumptions to finish out the season. We explore one scenario that assumes performance similar to the recent La Niña-like seasons, using the average of our analog seasons. We also examine a “normal” scenario that uses the 40-year (1981–2020) average of the CHIRPS archive.

Figure 7A shows the observed+CHIRPS-GEFS precipitation anomalies for the beginning of the 2021 growing season (dekads 1–10). To harmonize our results with those already presented, in this example, we have used, as above, a fixed climatological start of season (Figure 1B). Onset dates could vary from year to year in a more sophisticated operational implementation. Through dekad 10, much of the region had experienced rainfall deficits ranging from about −15 to more than −90 mm, with the largest deficits occurring in the Ethiopian highlands, northeastern Kenya, and southern Somalia. While these types of anomalies are known to frequently occur during recent La Niña-like seasons, the impact of elevated WR values during these events has not been examined. Growing season analog WR anomalies (Figure 7B) are actually fairly large (up to ~+50 mm), and, more importantly, the location of many of these increases are often in exceptionally dry areas of Kenya, Somalia, and Ethiopia. We can finish out the season by either assuming rainfall performance similar to our set of analogs (Figure 7C) or simple climatological averages (Figure 7D). The analog scenario is substantially more pessimistic, particularly for Kenya and Somalia, where late April and early May rains play a critical role in providing moisture for crops.

FIGURE 7

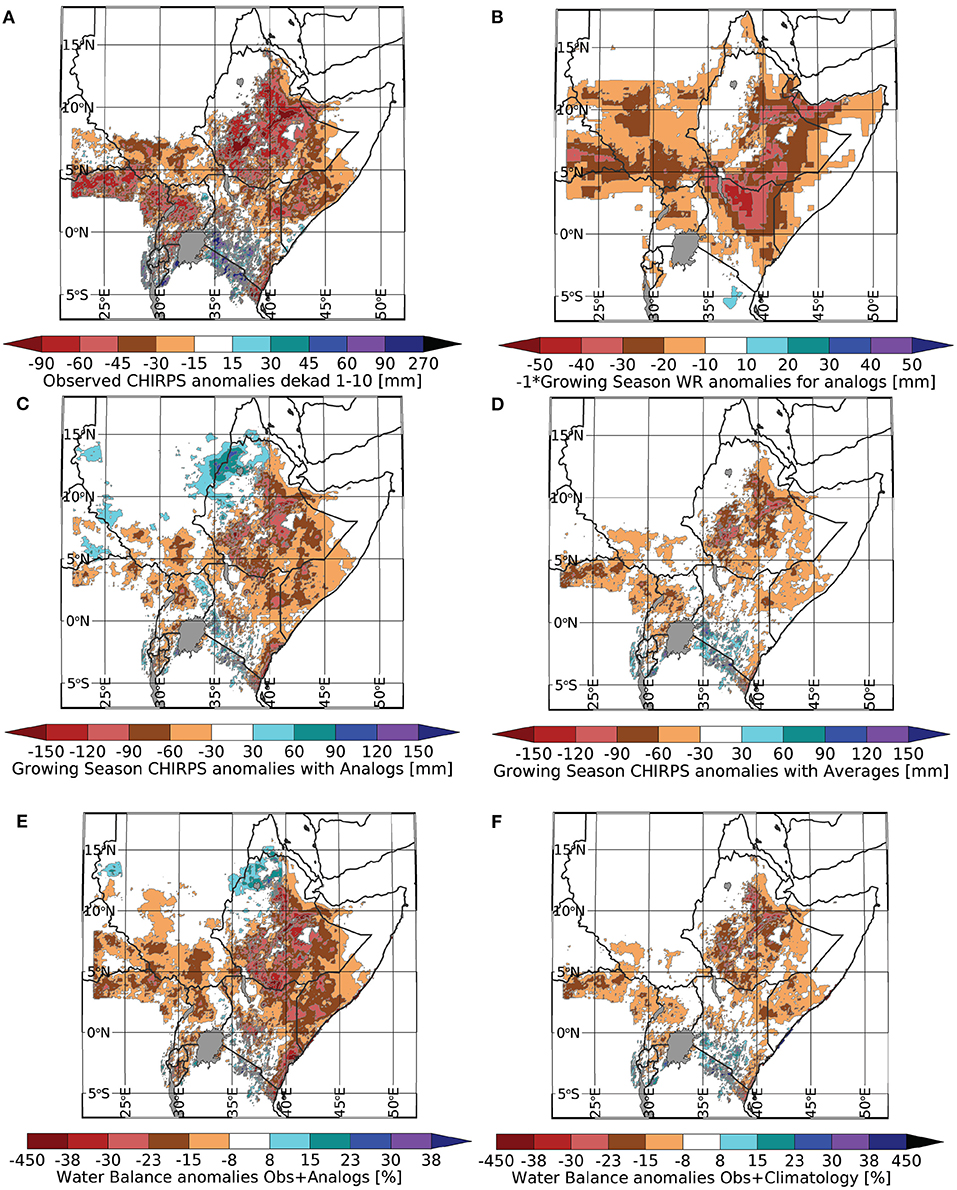
Figure 7. An Agro-Pastoral Outlook example for 2021. (A) Early season rainfall anomalies through dekad 10. (B) Average growing season WR anomalies for analog seasons. (C) 2021 GSP CHIRPS anomalies based on analogs for dekads 11–36. (D) Same but based on long-term averages. (E) The predicted end-of-season WB anomalies associated with the analog forecast assumption shown in (C). (F) The predicted end-of-season WB anomalies associated with the climatological forecast shown in (D). (C, D) All anomalies based on a 1981–2020 period of record.

Combining the analog-based GSP precipitation totals with analog season WR totals allows us to generate a mid-season analog PWB anomaly map (Figure 7E). We can use a similar calculation based on climatological WR calculations to create an “average” PWB projection (Figure 7F). While more sophisticated bootstrapping approaches could be used to generate scenarios (Husak et al., 2013), Figure 7E, F represent a reasonable way to transform CHIRPS-GEFS and climate analog assumptions into results bracketing likely agro-pastoral outcomes. Contrasting the pessimistic analog with the less-presumptive average scenario suggests that outcomes in Kenya and Somalia may be substantially less certain than in Ethiopia. In Ethiopia, in both the analog and average scenarios, substantial water stress appears across much of the country.

While space limitations prevent further elaboration here, the PWB framework does seem promising as a basis for developing predictive agro-pastoral outlooks. In addition to growing-season precipitation totals derived from observations, weather, and climate conditions, similar interoperable seamless RefET observations/prediction data streams could be developed. One-to-fifteen-day forecasts could be derived from the GEFS (Hamill et al., 2013). At climatic timescales, these forecasts could be derived from coupled ocean-atmosphere models (Shukla et al., 2017), predictive hydrologic modeling systems (Arsenault et al., 2020), or via constructed analogs (Pierce et al., 2014). Finally, it should be noted that these outlooks could also help capture potential disruptions associated with extreme precipitation. Using the WRSI phenology stages, for example, one can identify regions in the grain-filling stage and the associated optimal WR values. When the observed precipitation far exceeds these WR values, that may be a clear indicator of potential negative influences (e.g., flooding).

Discussion

In his classic book on Cultural Anthropology, Clifford Geertz explained how societies produce cultures that allow for coordinated behavior by effectively combining “models of ” the world and “models for” the world (Geertz, 1973). Models “of ” the world imitate or simulate the world as it is; they resemble our numerical models. Models “for” the world, however, are models “for” human behavior, behaviors that imply specific and coherent actions, actions informed by our models “of ” the world. This distinction was first introduced by Geertz (1973) as he described how conceptual frameworks supported coherent behavior among tribes in Southeast Asia (Geertz, 1973). Such considerations are relevant here because agricultural early warning systems, like the FEWS NET (www.fews.net) (Brown, 2008; Funk et al., 2019b) or the United States Drought Monitor (Svoboda et al., 2002) are also “cultures” — cultures, furthermore, distributed across space, multiple institutions, and even nations. Coherent, intelligent behavior in these systems requires shared and crisply defined “search patterns.” These patterns describe hazards, supporting consensus and early action, leading to emergent collaboration across a wide variety of factors. In this setting, models “of” the world provide information, while models “for” the world describe impacts and (re)actions (Funk et al., 2021).

Models “of” the world may provide synoptic observations of precipitation (Funk et al., 2015b; Huffman et al., 2020), soil moisture (Karthikeyan et al., 2017a,b), or actual evapotranspiration (Anderson et al., 2011; Senay et al., 2011, 2013). Complex numerical models “of” the world may offer detailed simulations and forecasts of land (Nijssen et al., 1997, 2014; McNally et al., 2017; Arsenault et al., 2020) and atmospheric (Hamill et al., 2013; Gelaro et al., 2017) conditions. In fact, every day, an ever-increasing torrent of such sources output more and more information.

Ironically, filtering and assimilating all of this information is increasingly challenging. But one long-standing and very effective “model for” impact assessment, which we have explored in this study, is crop WR. Here, we have revisited this widely used and effective concept, using an example situated in the boreal spring rain season of eastern Africa. We have described how this simple yet powerful framework can guide monitoring and prediction, providing “WRSI-like” results that are easier to calculate, more interoperable with rainfall forecasts, and potentially less sensitive to parameterization and potential biases and timing issues.

Clearly communicated definitions of drought (Wilhite and Glantz, 1985; Svoboda and Fuchs, 2016) provide a shared basis for collaboration, response planning, and impact mitigation. In the context of food security, the Integrated Phase Classification (IPC) system supports the evaluation of food security status across diverse cultural and socio-economic settings (Frankenberger and Verduijn, 2011). More specifically, FEWS NET uses a household food economy approach to develop food security scenarios¹⁸ that take into account a complex tableau of drivers. Many social factors—conflict, price shocks, micro and macro-economic conditions—drive food insecurity. But, especially in many arid and semi-arid regions, agricultural and pastoral water deficits create shocks to food access and availability.

In this paper, we have used the PWB framework to demonstrate WRSI-like performance across several important decision support contexts. In general, we found that the easy-to-calculate PWB index appears to perform very similarly to the WRSI in most locations. More detailed analyses based on crop stages could certainly be of value, and the WR framework could be used to filter other indicators of water supply or water stress. Satellite-observed soil moisture (Karthikeyan et al., 2017a,b) or actual evapotranspiration (Anderson et al., 2011; Senay et al., 2011, 2013) could be processed with WR framing, as could hydrologic model outputs (McNally et al., 2017; Arsenault et al., 2020).

The simplicity of the PWB makes it relatively straightforward to combine observations, weather forecasts, and climate analog predictions, as demonstrated in Examining the Utility of the PWB Framework as a Basis for Translating Integrated Rainfall Early Estimates into Assessments of Agro-pastoral Hazards section. Producing reasonably interoperable rainfall and RefET estimates, at high resolutions, based on satellite and station observations, reanalyses, weather models, and coupled global climate models is challenging on its own. The PWB provides a defensible way to combine such outputs, resulting in forward-looking assessments of crop water satisfaction. The example provided here focuses on combining Early Estimates and climate analog predictions (Examining the Utility of the PWB Framework as a Basis for Translating Integrated Rainfall Early Estimates into Assessments of Agro-Pastoral Hazards Section), but similar framing could be used with outputs from hydrologic forecast systems like NHyFAS. NHyFAS forecasts of AET and RefET could be translated into PWB forecasts, for example.

In addition to an expected opportunity to describe PWB-based impact assessments, we were also surprised by two specific aspects of this study: the very high level of covariability of WR and GSP in arid regions (Figure 2D) and the extremely high positive Kenyan PWB values in 2018 and 2020 (Figure 6). Both results indicate forms of climatic hazards. During dry seasons in arid regions, positive land surface feedbacks associated with low precipitation enhance RefET and WR values, increasing plant water stress. But during extremely wet seasons, like 2018 and 2020, the available water may far exceed plant needs in many areas, leading to increased runoff and potential waterlogging and flooding.

Conclusions

Simplicity can, at times, be revealing. Because the PWB simply uses accumulations of CHIRPS rainfall and WR, this framework makes it very easy to assess the covariability and relative contributions of water supply and atmospheric demand. Explicitly calculating and analyzing the WR provides valuable insights. Climatologically, late-season WR values make it hard to catch up from early season rainfall deficits (Figure 1). Interannually, the magnitude of WR increases and decreases in dry and wet seasons can be relatively large in arid regions, amplifying rainfall anomalies, and helping to support extreme outcomes (Figure 2D).

In conclusion, the PWB framework seems very useful for monitoring, prediction, trend analyses, and risk management applications. Future work will expand our analysis to more regions and develop more decision support-related analyses. In general, analyzing WR along with GSP provides valuable information by answering a simple question—was growing season precipitation inadequate, adequate, or much more than adequate? Spatially, this provides a picture of eastern east Africa as a relatively small set of cool, moist highland areas with seasons long enough to support agriculture.

Finally, we return to a simple but important result: the PWB provides results that are, for most water-limited areas, very similar to the WRSI. At the pixel scale, correlations were greater than 0.8 for all regions in which the standard deviation of WRSI was greater than 15. At the sub-national administrative unit, the median 1981–2020 PWB/WRSI correlations were 0.8, 0.93, and 0.82 in Kenya, Somalia, and Ethiopia, respectively. For our Kenya crop-growing counties, the correlation between regionally averaged PWB and WRSI was 0.85. These results suggest that the PWB can be a useful supplement to the more intensive WRSI modeling. When parameterized with accurate soil information and driven with accurate climate data, the WRSI should provide more accurate estimates that take into account soil moisture and sub-seasonal weather variability. But WRSI-like results can be obtained using GSP and WR. Similar analyses could incorporate other metrics of water supply, such as satellite or model-based estimates of AET. Both satellite and model-based estimates are likely to capture the complementary transitions as AET decreases and WR increases during periods of severe water stress.

In a world with increasingly extreme precipitation (Emori and Brown, 2005; Allan and Soden, 2008) and Indo-Pacific sea surface temperature volatility (Cai et al., 2013, 2015), East African agricultural advances are struggling to cope with climate change (Davenport et al., 2018). As the combination of population growth, declining rainfall and climate volatility create increasing food stress (Funk et al., 2005, 2015a; Funk and Brown, 2009), improved integrated drought early warning systems (Funk et al., 2007; Thomas et al., 2019, 2020; Funk and Shukla, 2020; Shukla et al., 2021) and improved drought risk management practices and policies (Pulwarty and Sivakumar, 2014; Wilhite and Pulwarty, 2017) can help east Africa manage risk and boost productivity. The PWB framework, discussed here, will provide a relatively simple means of connecting satellite observations with climate, weather and land surface model simulations, helping to support integrated early warning systems.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

Primary support for this work came from the National Aeronautics and Space Administration (NASA) GPM mission grant #80NSSC19K0686 and the United States Agency for International Development (USAID) cooperative agreement #72DFFP19CA00001 and the Famine Early Warning Systems Network.

Conflict of Interest

AM was employed by company SAIC Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^http://cropmonitor.org/documents/EWCM/reports/EarlyWarning_CropMonitor_202011.pdf.

2. ^https://blog.chc.ucsb.edu/?p=937.

3. ^Dekads break each month into two 10 day periods and one final dekad containing the remaining days in each month.

4. ^https://psl.noaa.gov/eddi/globalrefet/.

5. ^https://earlywarning.usgs.gov/fews/.

6. ^https://earlywarning.usgs.gov/fews/product/125.

7. ^https://earlywarning.usgs.gov/fews/product/124.

8. ^https://earlywarning.usgs.gov/fews/product/130.

9. ^https://earlywarning.usgs.gov/fews.

10. ^http://www.fao.org/nr/climpag/cropfor/lgp_en.asp.

11. ^Baringo, Elgeyo-Marakwet, Kajiado, Kiambu, Kirinyaga, Kwale, Laikipia, Lamu, Murang'a, Nakuru, Narok, Nyandarua, Nyeri, Taita Taveta, Tana River, Trans Nzoia, Uasin Gishu, Kilifi.

12. ^Please note that, in general, very few counties exhibited positive yield trends. In general, yield growth in Kenya is stagnant, and per capita cereal production is declining. https://www.usaid.gov/documents/1867/contrasting-kenyan-resilience-drought-2011-2017-full-report.

13. ^https://chc.ucsb.edu/data/chirps-gefs.

14. ^https://blog.chc.ucsb.edu/?p=937.

15. ^https://blog.chc.ucsb.edu/?p=757.

16. ^https://blog.chc.ucsb.edu/?p=880.

17. ^https://blog.chc.ucsb.edu/?p=946.

18. ^https://fews.net/sites/default/files/documents/reports/Guidance_Document_Scenario_Development_2018.pdf.

References

AGRHYMET (1996). Méthodologie de suivi des zones à risque. Niamey: AGRHYMET FLASH, Bulletin de Suivi de la Campagne Agricole au Sahel, Centre Regional AGRHYMET

Allan, R. P., and Soden, B. J. (2008). Atmospheric warming and the amplification of precipitation extremes. Science 321, 1481–1484. doi: 10.1126/science.1160787

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, M. C., Kustas, W. P., Norman, J. M., Hain, C. R., Mecikalski, J. R., Schultz, L., et al. (2011). Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 15, 223–239. doi: 10.5194/hess-15-223-2011

CrossRef Full Text | Google Scholar

Arsenault, K. R., Shukla, S., Hazra, A., Getirana, A., McNally, A., Kumar, S. V., et al. (2020). The NASA hydrological forecast system for food and water security applications. Bull. Am. Meteorol. Soc. 101, E1007–E1025. doi: 10.1175/BAMS-D-18-0264.1

CrossRef Full Text | Google Scholar

Brown, M. E. (2008). Famine Early Warning Systems and Remote Sensing Data. Berin: Springer Science and Business Media.

Google Scholar

Cai, W., Santoso, A., Wang, G., Yeh, S. W., An, S. I., Cobb, K. M., et al. (2015). ENSO and greenhouse warming. Nat. Clim. Change 5, 849–859. doi: 10.1038/nclimate2743

CrossRef Full Text | Google Scholar

Cai, W., Zheng, X. T., Weller, E., Collins, M., Cowan, T., Lengaigne, M., et al. (2013). Projected response of the Indian Ocean Dipole to greenhouse warming. Nat. Geosci. 6, 999–1007. doi: 10.1038/ngeo2009

CrossRef Full Text | Google Scholar

Checchi, F., and Robinson, W. C. (2013). Mortality among populations of southern and central Somalia affected by severe food insecurity and famine during 2010–2012. Washington, DC: FEWS NET.

Google Scholar

Davenport, F., Funk, C., and Galu, G. (2018). How will East African maize yields respond to climate change and can agricultural development mitigate this response? Clim. Change 147, 491–506. doi: 10.1007/s10584-018-2149-7

CrossRef Full Text | Google Scholar

Donat, M. G., Lowry, A. L., Alexander, L. V., O'Gorman, P. A., and Maher, N. (2016). More extreme precipitation in the world's dry and wet regions. Nat. Clim. Change 6:508. doi: 10.1038/nclimate2941

CrossRef Full Text | Google Scholar

Doorenbos, J., and Pruitt, W. O. (1977). Crop Water Requirements. Rome: FAO.

Google Scholar

Emori, S., and Brown, S. (2005). Dynamic and thermodynamic changes in mean and extreme precipitation under changed climate. Geophys. Res. Lett. 32:1–5. doi: 10.1029/2005GL023272

CrossRef Full Text | Google Scholar

FAO (1978). World Soil Resources Report 48/1. Rome: FAO.

Frankenberger, T. R., and Verduijn, R. (2011). Integrated Food Security Phase Classification (IPC). Rome: The Food and Agriculture Organization of the United Nations.

Google Scholar

Frère, M., and Popov, G. (1986). Early Agrometeorological Crop Yield Forecasting. Rome: The Food and Agriculture Organization of the United Nations.

Funk, C., Davenport, F., Eilerts, G., Nourey, N., and Galu, G. (2018a). Contrasting Kenyan Resilience to Food Insecurity: 2011 and 2017. USAID Special Report.

Funk, C., Harrison, L., Shukla, S., Pomposi, C., Galu, G., and Korecha, D. (2018b). Examining the role of unusually warm Indo-Pacific sea surface temperatures in recent African droughts. Quart J Roy Meteor Soc 144, 360–383. doi: 10.1002/qj.3266

CrossRef Full Text | Google Scholar

Funk, C., Hoell, A., Shukla, S., Bladé, I., Liebmann, B., Roberts, J. B., and Husak, G. (2014). Predicting East African spring droughts using Pacific and Indian Ocean sea surface temperature indices. Hydrol. Earth Syst. Sci. Discuss. 11, 3111–3136. doi: 10.5194/hessd-11-3111-2014

CrossRef Full Text | Google Scholar

Funk, C., Nicholson, S. E., Landsfeld, M., Klotter, D., Peterson, P., and Harrison, L. (2015a). The Centennial Trends Greater Horn of Africa precipitation dataset. Sci. Data 2:150050. doi: 10.1038/sdata.2015.50

PubMed Abstract | CrossRef Full Text

Funk, C., Pedreros, D., Nicholson, S., Hoell, A., Korecha, D., Galu, G., et al. (2019a). Examining the potential contributions of extreme 'Western V' sea surface temperatures to the 2017 March–June East African Drought. Bull. Am. Meteor. Soc. 100, S55–S60. doi: 10.1175/BAMS-D-18-0108.1

CrossRef Full Text | Google Scholar

Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., et al. (2015b). The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes. Sci. Data 2:150066. doi: 10.1038/sdata.2015.66

PubMed Abstract | CrossRef Full Text | Google Scholar

Funk, C., Senay, G., Asfaw, A., Verdin, J., Rowland, J., Michaelson, J., et al. (2005). Recent drought tendencies in Ethiopia and equatorial-subtropical eastern Africa. Vulnerability to Food Insecurity: Factor Identification and Characterization Report, F. NET, Ed., US Agency for International Development, 12.

Funk, C., and Shukla, S. (2020). Drought Early Warning and Forecasting: Theory and Practice. Elsevier. doi: 10.1016/B978-0-12-814011-6.00003-8

CrossRef Full Text | Google Scholar

Funk, C., Shukla, S., Thiaw, W. M., Rowland, J., Hoell, A., McNally, A., et al. (2019b). Recognizing the famine early warning systems network (FEWS NET): over 30 years of drought early warning science advances and partnerships promoting global food security. Bull. Am. Meteor. Soc. 14:13.

Google Scholar

Funk, C., Verdin, J. P., and Husak, G. (2007). Integrating observation and statistical forecasts over sub-Saharan Africa to support Famine Early Warning. 87th American Meteorological Society Annual Meeting, San Antonio, TX.

Google Scholar

Funk, C. C., and Brown, M. E. (2009). Declining global per capita agricultural production and warming oceans threaten food security. Food Sec. 1, 271–289. doi: 10.1007/s12571-009-0026-y

CrossRef Full Text | Google Scholar

Funk, C. C., Hoell, A., and Mitchell, D. (2021). Climate science advances to address 21st century weather and climate extremes. Front. Clim. 3:59. doi: 10.3389/fclim.2021.680291

CrossRef Full Text | Google Scholar

Geertz, C. (1973). The Interpretation of Cultures, Vol. 5019. New York, NY: Basic Books.

Google Scholar

Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., et al. (2017). The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 30, 5419–5454. doi: 10.1175/JCLI-D-16-0758.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamill, T. M., Bates, G. T., Whitaker, J. S., Murray, D. R., Fiorino, M., Galarneau Jr, T. J. et al. (2013). NOAA's second-generation global medium-range ensemble reforecast dataset. Bull. Am. Meteorol. Soc. 94, 1553–1565. doi: 10.1175/BAMS-D-12-00014.1

CrossRef Full Text | Google Scholar

Harrison, L., Funk, C., and Peterson, P. (2019). Identifying changing precipitation extremes in Sub-Saharan Africa with gauge and satellite products. Environ. Res. Lett. 14:085007. doi: 10.1088/1748-9326/ab2cae

CrossRef Full Text | Google Scholar

Hobbins, M., Wood, A., Streubel, D., and Werner, K. (2012). What drives the variability of evaporative demand across the conterminous United States? J. Hydrometeorol. 13, 1195–1214. doi: 10.1175/JHM-D-11-0101.1

CrossRef Full Text | Google Scholar

Hobbins, M. T., Wood, A., McEvoy, D. J., Huntington, J. L., Morton, C., Anderson, M., and Hain, C. (2016). The evaporative demand drought index. Part I: Linking drought evolution to variations in evaporative demand. J. Hydrometeorol. 17, 1745–1761. doi: 10.1175/JHM-D-15-0121.1

CrossRef Full Text | Google Scholar

Hoell, A., and Funk, C. (2013a). Indo-Pacific sea surface temperature influences on failed consecutive rainy seasons over eastern Africa. Clim. Dyn. 43, 1645–1660. doi: 10.1007/s00382-013-1991-6

CrossRef Full Text | Google Scholar

Hoell, A., and Funk, C. (2013b). The ENSO-related west pacific sea surface temperature gradient. J. Clim. 26, 9545–9562. doi: 10.1175/JCLI-D-12-00344.1

CrossRef Full Text | Google Scholar

Hoell, A., Funk, C., and Barlow, M. (2014). La Nina diversity and the forcing of Northwest Indian Ocean Rim teleconnections. Clim. Dyn. 42, 3289–3311. doi: 10.1007/s00382-013-1799-4

CrossRef Full Text | Google Scholar

Huffman, G. J., Bolvin, D. T., Braithwaite, D., Hsu, K. L., Joyce, R. J., Kidd, C., et al. (2020). “Integrated multi-satellite retrievals for the global precipitation measurement (GPM) mission (IMERG),” in Satellite Precipitation Measurement, eds K. C. Levizzani, D. Kirschbaum, C. Kummerow, K. Nakamura, and F. Turk (Cham: Springer), 343–354. doi: 10.1007/978-3-030-24568-9_19

CrossRef Full Text | Google Scholar

Husak, G. J., Funk, C. C., Michaelsen, J., Magadzire, T., and Goldsberry, K. P. (2013). Developing seasonal rainfall scenarios for food security early warning. Theor. Appl. Climatol. 114, 291–302. doi: 10.1007/s00704-013-0838-8

CrossRef Full Text | Google Scholar

Karthikeyan, L., Pan, M., Wanders, N., Kumar, D. N., and Wood, E. F. (2017a). Four decades of microwave satellite soil moisture observations: Part 1. A review of retrieval algorithms. Adv. Water Resour. 109, 106–120. doi: 10.1016/j.advwatres.2017.09.006

CrossRef Full Text | Google Scholar

Karthikeyan, L., Pan, M., Wanders, N., Kumar, D. N., and Wood, E. F. (2017b). Four decades of microwave satellite soil moisture observations: Part 2. Product validation and inter-satellite comparisons. Adv. Water Resour. 109, 236–252. doi: 10.1016/j.advwatres.2017.09.010

CrossRef Full Text | Google Scholar

Laudien, R., Schauberger, B., Makowski, D., and Gornott, C. (2020). Robustly forecasting maize yields in Tanzania based on climatic predictors. Sci. Rep. 10, 1–12. doi: 10.1038/s41598-020-76315-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Magadzire, T., Galu, G., and Verdin, J. (2017). How Climate Forecasts Strengthen Food Security. World Meteorological Organisation Bulletin—Special Issue on Water, World Meteorological Organisation.

McNally, A., Arsenault, K., Kumar, S., Shukla, S., Peterson, P., Wang, S., et al. (2017). A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 4:170012. doi: 10.1038/sdata.2017.12

PubMed Abstract | CrossRef Full Text | Google Scholar

McNally, A., Husak, G. J., Brown, M., Carroll, M., Funk, C., Yatheendradas, S., et al. (2015). Calculating crop water requirement satisfaction in the West Africa Sahel with remotely sensed soil moisture. J. Hydrometeorol. 16, 295–305. doi: 10.1175/JHM-D-14-0049.1

CrossRef Full Text | Google Scholar

Nijssen, B., Lettenmaier, D. P., Liang, X., Wetzel, S. W., and Wood, E. F. (1997). Streamflow simulation for continental-scale river basins. Water Resour. Res. 33, 711–724. doi: 10.1029/96WR03517

CrossRef Full Text | Google Scholar

Nijssen, B., Shukla, S., Lin, C., Gao, H., Zhou, T., Sheffield, J., et al. (2014). A prototype global drought information system based on multiple land surface models. J. Hydrometeorol. 15, 1661–1676. doi: 10.1175/JHM-D-13-090.1

CrossRef Full Text | Google Scholar

Peng, J., Dadson, S., Hirpa, F., Dyer, E., Lees, T., Miralles, D. G., et al. (2020). A pan-African high-resolution drought index dataset. Earth Syst. Sci. Data 12, 753–769. doi: 10.5194/essd-12-753-2020

CrossRef Full Text | Google Scholar

Pierce, D. W., Cayan, D. R., and Thrasher, B. L. (2014). Statistical downscaling using localized constructed analogs (LOCA). J. Hydrometeorol. 15, 2558–2585. doi: 10.1175/JHM-D-14-0082.1

CrossRef Full Text | Google Scholar

Pulwarty, R. S., and Sivakumar, M. V. (2014). Information systems in a changing climate: early warnings and drought risk management. Weather Clim. Extremes 3, 14–21. doi: 10.1016/j.wace.2014.03.005

CrossRef Full Text | Google Scholar

Senay, G., and Verdin, J. (2001). “Using a GIS-based water balance model to assess regional crop performance,” in Proceedings of the Fifth International Workshop on Application of Remote Sensing in Hydrology.

Senay, G. B., Bohms, S., Singh, R. K., Gowda, P. H., Velpuri, N. M., Alemu, H., and Verdin, J. P. (2013). Operational evapotranspiration mapping using remote sensing and weather datasets: a new parameterization for the SSEB approach. JAWRA J. Am. Water Resour. Assoc. 49, 577–591. doi: 10.1111/jawr.12057

CrossRef Full Text | Google Scholar

Senay, G. B., Budde, M., Verdin, J. P., and Melesse, A. M. (2007). A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 7, 979–1000. doi: 10.3390/s7060979

CrossRef Full Text | Google Scholar

Senay, G. B., Budde, M. E., and Verdin, J. P. (2011). Enhancing the simplified surface energy balance (SSEB) approach for estimating landscape ET: validation with the METRIC model. Agric. Water Manag. 98, 606–618. doi: 10.1016/j.agwat.2010.10.014

CrossRef Full Text | Google Scholar

Senay, G. B., and Verdin, J. (2003). Characterization of yield reduction in Ethiopia using a GIS-based crop water balance model. Can. J. Remote Sens. 29, 687–692. doi: 10.5589/m03-039

CrossRef Full Text | Google Scholar

Shukla, S., Funk, C., and Hoell, A. (2014). Using constructed analogs to improve the skill of March-April-May precipitation forecasts in equatorial East Africa. Environ. Res. Lett. 9:094009. doi: 10.1088/1748-9326/9/9/094009

CrossRef Full Text | Google Scholar

Shukla, S., Husak, G., Turner, W., Davenport, F., Funk, C., Harrison, L., and Krell, N. (2021). A slow rainy season onset is a reliable harbinger of drought in most food insecure regions in Sub-Saharan Africa. PLos ONE 16:e0242883. doi: 10.1371/journal.pone.0242883

PubMed Abstract | CrossRef Full Text | Google Scholar

Shukla, S., McEvoy, D., Hobbins, M., Husak, G., Huntington, J., Funk, C., et al. (2017). Examining the value of global seasonal reference evapotranspiration forecasts to support FEWS NET's food insecurity outlooks. J. Appl. Meteorol. Climatol. 56, 2941–2949. doi: 10.1175/JAMC-D-17-0104.1

CrossRef Full Text | Google Scholar

Smith, M. (1992). Expert Consultation on Revision of FAO Methodologies for Crop Water Requirements. Rome: FAO

Google Scholar

Svoboda, M., and Fuchs, B. (2016). Handbook of drought indicators and indices. Geneva: World Meteorological Organization. doi: 10.1201/b22009-11

CrossRef Full Text

Svoboda, M., LeComte, D., Hayes, M., Heim, R., Gleason, K., Angel, J., et al. (2002). The drought monitor. Bull. Am. Meteorol. Soc. 83, 1181–1190. doi: 10.1175/1520-0477-83.8.1181

CrossRef Full Text | Google Scholar

Thomas, E., Jordan, E., Linden, K., Mogesse, B., Hailu, T., Jirma, H., et al. (2020). Reducing drought emergencies in the Horn of Africa. Sci. Total Environ. 727:138772. doi: 10.1016/j.scitotenv.2020.138772

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, E. A., Needoba, J., Kaberia, D., Butterworth, J., Adams, E. C., Oduor, P., et al. (2019). Quantifying increased groundwater demand from prolonged drought in the East African Rift Valley. Sci. Total Environ. 666, 1265–1272. doi: 10.1016/j.scitotenv.2019.02.206

PubMed Abstract | CrossRef Full Text | Google Scholar

Trenberth, K. E., Dai, A., Rasmussen, R. M., and Parsons, D. B. (2003). The changing character of precipitation. Bull. Am. Meteorol. Soc. 84, 1205–1217. doi: 10.1175/BAMS-84-9-1205

CrossRef Full Text | Google Scholar

Verdin, J., Funk, C., Senay, G., and Choularton, R. (2005). Climate science and famine early warning. Philos. Trans. R. Soc. B 360, 2155–2168. doi: 10.1098/rstb.2005.1754

PubMed Abstract | CrossRef Full Text | Google Scholar

Verdin, J., and Klaver, R. (2002). Grid-cell-based crop water accounting for the famine early warning system. Hydrol. Process. 16, 1617–1630. doi: 10.1002/hyp.1025

CrossRef Full Text | Google Scholar

Vicente-Serrano, S. M., Beguería, S., and López-Moreno, J. I. (2010). A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 23, 1696–1718. doi: 10.1175/2009JCLI2909.1

CrossRef Full Text | Google Scholar

Wilhite, D., and Glantz, M. (1985). Understanding: the Drought Phenomenon: The Role of Definitions. Water Int. 10, 111–120. doi: 10.1080/02508068508686328

CrossRef Full Text | Google Scholar

Wilhite, D., and Pulwarty, R. S. (2017). Drought and Water Crises: Integrating Science, Management, and Policy. Boca Raton: CRC Press.

Google Scholar

Zucca, C., Della Peruta, R., Salvia, R., Sommer, S., and Cherlet, M. (2012). Towards a World desertification atlas. Relating and selecting indicators and data sets to represent complex issues. Ecol. Indic. 15, 157–170. doi: 10.1016/j.ecolind.2011.09.012

CrossRef Full Text | Google Scholar