- Department of Aerospace Engineering, University of Michigan, Ann Arbor, MI, United States
In this work, we study finite-time stability of hybrid systems with unstable modes. We present sufficient conditions in terms of multiple Lyapunov functions for the origin of a class of hybrid systems to be finite-time stable. More specifically, we show that even if the value of the Lyapunov function increases during continuous flow, i.e., if the unstable modes in the system are active for some time, finite-time stability can be guaranteed if the finite-time convergent mode is active for a sufficient amount of cumulative time. This is the first work on finite-time stability of hybrid systems using multiple Lyapunov functions. Prior work uses a common Lyapunov function approach, and requires the Lyapunov function to be decreasing during the continuous flows and non-increasing at the discrete jumps, thereby, restricting the hybrid system to only have stable modes, or to only evolve along the stable modes. In contrast, we allow Lyapunov functions to increase both during the continuous flows and the discrete jumps. As thus, the derived stability results are less conservative compared to the earlier results in the related literature, and in effect allow the hybrid system to have unstable modes.
1 Introduction
Stability of the equilibrium point or equilibrium set of switched and hybrid systems has been studied extensively in the literature. In Branicky (1998), the author introduces the concept of multiple Lyapunov functions to analyze stability of switched systems; since then, a lot of work has been done on the topic, see e.g., (Zhao and Hill, 2008); Zhao et al., 2012). In Zhao and Hill (2008), the authors relax the non-increasing condition on the Lyapunov functions used in (Branicky, 1998), by introducing the notion of generalized Lyapunov functions. They present necessary and sufficient conditions for Lyapunov and asymptotic stability (AS) of switched systems under arbitrary switching. Inspired by the results in (Branicky, 1998; Zhao and Hill, 2008), we study conditions for finite-time stability (FTS)1 of a class of hybrid systems, using multiple generalized Lyapunov functions. In contrast to AS, which pertains to convergence as time tends to infinity, FTS is a concept that requires convergence of solutions in finite time. FTS is a well-studied concept, motivated in part from a practical viewpoint due to properties such as convergence in finite time, as well as robustness with respect to disturbances (Ryan, 1991). In the seminal work (Bhat and Bernstein, 2000), the authors introduce necessary and sufficient conditions in terms of Lyapunov functions for continuous, autonomous systems to exhibit FTS.
FTS of switched and hybrid systems has gained popularity in the last few years. The authors in Liu et al. (2017) consider the problem of designing a controller for a linear switched system under delay and external disturbance with finite-time convergence. The authors in Li and Sanfelice (2019) present conditions in terms of a common Lyapunov function for FTS of hybrid systems. They require the value of the Lyapunov function to be decreasing during the continuous flow and non-increasing at the discrete jumps. The authors in Ríos et al. (2015) design an FTS state observer for switched systems via a sliding-mode technique under the assumption that each individual subsystem is observable on a domain. More recently, the authors in Zhang (2018) study FTS of homogeneous switched systems by introducing the concept of hybrid homogeneous degree, and relating negative homogeneity with FTS. They consider switched systems with an assumption that each subsystem possess a homogeneous Lyapunov function, and that the switching-intervals are constant.
In this paper, we develop sufficient conditions for FTS of a class of hybrid systems in terms of multiple Lyapunov functions. To the best of authors’ knowledge, this is the first work considering FTS of hybrid systems using multiple Lyapunov functions. We first define the notion of FTS for hybrid systems in a way that does not restrict each mode of the hybrid system to be FTS in itself. More specifically, we relax the requirement in (Zhao and Hill, 2008; Li and Sanfelice, 2019) that each Lyapunov function is non-increasing at the discrete jumps, and strictly decreasing during the continuous flow; instead, we allow the Lyapunov functions to increase both during the continuous flow and at the discrete jumps, and require that these increments are bounded. In this respect, we allow the hybrid system to have unstable modes while still guaranteeing FTS. In addition, we present a novel proof on the stability of the origin using multiple Lyapunov functions under the aforementioned relaxed conditions. As compared to Zhang (2018), in the current paper we do not assume that the subsystems are homogeneous or in strict feedback form. The main result is that if the origin is stable under arbitrary switching, and if there exists an FTS mode that is active for a sufficient cumulative time, then the origin of the resulting hybrid system is FTS. As thus, the results in Bhat and Bernstein (2000) on FTS of continuous systems are a special case of the proposed results. The paper also extends and generalizes the results of the authors’ prior work in (Garg and Panagou, 2021) where FTS of a class of switched system is studied.
The motivation of studying FTS using multiple Lyapunov functions comes from applications where the switching law is not under the user’s control authority, or where keeping the FTS mode active for a long period leads to undesirable behavior. As an example, consider a spacecraft that tracks a desired trajectory, with the on-board communication and the controller module requiring a certain minimum energy threshold to function. The charge-level of the spacecraft battery can be modeled as a hybrid system, where being in the path of sunlight would be an FTS mode, leading to increase in the charging level, and tracking the desired trajectory an unstable mode since it depletes the charge. Now, keeping the FTS mode active for a long duration might lead to the spacecraft losing track of its desired trajectory, and thus, the switching signal between the two modes cannot be designed arbitrarily. At the same time, FTS is desired so that the spacecraft can activate its communication module for crucial communications with the ground station and/or the control module to compute inputs for the next part of the journey. Thus, for the applications where the FTS mode cannot be kept active for all times, or the switching signal is not under user’s control, it is essential to study FTS under switching laws that allow the FTS mode to become inactive, and unstable modes to become active.
2 Finite-Time Stability of Hybrid Systems
2.1 Preliminaries
We denote by ‖ ⋅ ‖ the Euclidean norm of vector (⋅), |⋅| the absolute value if (⋅) is scalar and the length if (⋅) is a time interval. The set of non-negative reals is denoted by
Definition: A continuous function
• Class-
• Class-
Next, we review the notion of FTS. Consider the system:
where
Theorem 1: [Bhat and Bernstein (2000)].Suppose there exist a continuously differentiable, positive definite function
Then the origin is an FTS equilibrium.
We state the following Lemma before we proceed to the main results, which follows from (Zuo and Tie, 2016, Lemma 3.3).
Lemma 1:Letai ≥ bi ≥ 0 for alli ∈{1, 2, … , K} for some
2.2 Main Results
We consider the class of hybrid systems
where
Denote by
Assumption 1.The functionsfiare continuous for alli ∈Σfand the origin is the unique equilibrium point ofEq. 4.
The case when there exists a closed set
• it is absolutely continuous between any two jump instants and satisfies
• it satisfies x (t+) = g (x(t)), for all
Interested reader is referred to (Goebel et al., 2012, Chapter 2) for a detailed presentation on solution notion of hybrid systems. We assume that the solution of Eq. 4 exists for all t ≥ 0, and is non-Zeno2. Similar assumptions have been used in literature (e.g., Zhao and Hill, 2008; Li and Sanfelice, 2019; Sanfelice et al., 2007) in order to analyze stability properties of the origin of hybrid systems.
Next, we define the notion of FTS for hybrid systems. Note that a mode F ∈Σf is called an FTS subsystem or FTS mode if the origin of
Definition 1.The origin of the hybrid systemEq. 4is called LS, AS or FTS if there exists an open neighborhood
Before presenting the main result, we define the necessary notation. For each interval
Theorem 2.If there exist positive definite, continuous functionsVifor eachi ∈ΣfsatisfyingVi(x) ≤ α0 (‖x‖) for alli ∈Σf, where
1) There exists
2) There exists
3) There exists
4) There exist an FTS modeF ∈Σf, a positive definite, continuously differentiable Lyapunov functionVFand constantsc > 0, 0 < β < 1 such that
5) The accumulated duration
whereα = α0 + α1 + α2 + Nfα3,
Before presenting the proof, we provide an intuitive explanation of the conditions of Theorem 2 (see Figure 1).
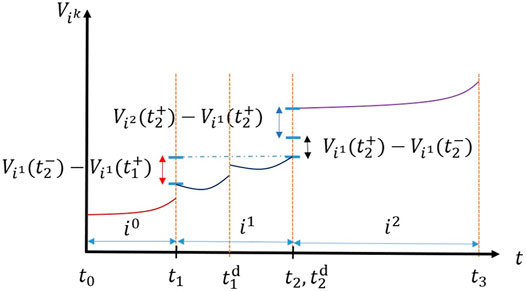
FIGURE 1. Conditions 1), 2) and 3) of Theorem 2 regarding the allowable changes in the values of the Lyapunov functions. The increments shown by blue, red and black double-arrows pertain to condition 1), 2) and 3), respectively.
• Note that since Vi’s are positive definite functions, there exists a class-
• Condition 1) means that the cumulative value of the differences between the consecutive Lyapunov functions at the switching instants of the dynamics of continuous flows (i.e., at switches of the signal σf) is bounded by a class-
• Condition 2) means that the cumulative increment in the values of the individual Lyapunov functions when the respective modes are active (evaluated before and after a discrete-jump at tk+1 and tk, respectively, if any) is bounded by a class-
• Eq. 7 in condition 3) means that the cumulative increment in the value of the Lyapunov function Vi is bounded by a class-
• Condition 4) means that there exists an FTS mode F ∈Σ and a Lyapunov function VF satisfying Eq. 2 for
• Condition 5) means that the FTS mode F is active for a sufficiently long cumulative time γ(‖x0‖) without any discrete jump occurring in that cumulative period.
Now we provide the proof of Theorem 2.
Proof. First we prove the stability of the origin under conditions (1–3). Let x0 ∈ D, where D is some open neighborhood of the origin. For all
where
for all
Since the functions Vi are positive definite, the sub-level sets di (c) are bounded for small c > 0, and hence, the function r is invertible. The inverse function cϵ = r−1 (ϵ) maps the radius ϵ > 0 to the value cϵ such that the sub-level sets di (cϵ) are contained in Bϵ for all i ∈Σf. For any given ϵ > 0, choose δ such that α(δ) ≤ (r−1 (ϵ)) > 0 so that Eq. 9 implies that for ‖x0‖ ≤ δ, we have
Next, we prove FTS of the origin when conditions (4–5) also hold. From Eq. 9, we have that
for all
for all
Using Eq. 10, we obtain that
Define
Using Lemma 1, we obtain that
From the analysis in the first part of the proof, we know that VF (x (t)) ≤ α (‖x0‖). Define
Hence, we have that
where the second inequality follows from (Zuo and Tie, 2016, Lemma 3.4). Define
Clearly,
which implies that
Estimation of time of activation
where M* is the solution of
Activation of the FTS mode: Intuitively, Theorem 2 can be interpreted as follows: if Lyapunov stability of the origin can be established for a given switching signal σf, then the presence of a switching signal and an FTS mode such that the latter is active for a sufficient amount of time
Comparison with earlier results: In contrast to (Zhao and Hill, 2008, Proposition 3.8), where the authors provided necessary and sufficient conditions for stability of switched system under Eq. 9 and non-increasing condition on the Lyapunov functions Vi during activation period, we proved stability of the origin with just Eq. 9. Compared to Li and Sanfelice (2019), our results are less conservative in the sense that the Lyapunov functions are allowed to increase during the continuous flows (per Eq. 6), as well as at the discrete jumps (per Eq. 7). In other words, we allow unstable modes to be present in the hybrid system while still guaranteeing FTS of the origin.
A note on construction of functionsVi: In practice, the conditions (1–3) in Theorem 2, or those presented in Zhao and Hill (2008) can be difficult to verify for a general class of hybrid systems involving non-linear subsystems. For a class of switched systems consisting of N − 1 linear modes and one FTS mode F, one can follow a procedure similar to (Zhao and Hill, 2008, Remark 3.21) to construct the functions μij to design the switching signal σf, as well as the Lyapunov candidates Vi for i ≠ F. The design procedure includes choosing quadratic functions μij = xTPijx and Vi = xTRix with Ri as positive definite matrices to formulate a linear matrix inequality (LMI) problem. For systems consisting of polynomial dynamics fi, one can formulate a sum-of-square (SOS) problem to find polynomial functions Vi, μij [see Parrilo (2000) for an overview of SOS programming and (Prajna et al., 2002) for methods of solving SOS problems]. The study of finding Lyapunov functions to assess stability for a general class of hybrid systems with nonlinear modes is an open field of research, and is out of scope of this work.
3 Simulations
We present an instance of the hybrid system Eq. 4 with five modes, where one mode is FTS, one is AS, and three are unstable. The simulation results have been obtained by discretizing the continuous-time dynamics using Euler discretization. We use a step size of dt = 10–3, and run the simulations till the norm of the states drops below 10–10. At this point we wish to emphasize that while the theoretical results hold for the continuous-time dynamics, and not for the implemented discretized dynamics, still the simulations reflect stable behavior that meets the theoretical bounds on the sufficiently long active time of the finite-time stable mode. Consider the hybrid system
with β = 0.98, where the fifth mode is FTS, and thus F = 5. Note that the states x1 and x2 change sign and increase in magnitude at the discrete jumps. The Lyapunov functions are defined as Vi(x) = xTPix, for i ∈{1, 2, 3, 4}, with
The switching signal is designed so that the Lyapunov candidates Vi satisfy conditions 1) and 3) of Theorem 2 (see Garg and Panagou, 2021) for a discussion on how a finite-time stabilizing switching signal can be designed). Mode 3 and 5, being stable, satisfy condition 2) with α2 = 0, and modes 1, 2 and 4, being active for a finite interval each time, satisfy condition 2) with α2 = k‖x0‖2 for some k > 0, and so α2 = k‖x0‖2 satisfy 2) for all the modes. It can be verified that f5 is homogeneous with degree of homogeneity d = α − 1 < 0. Thus, using (Bhat and Bernstein, 2005, Theorem 7.2), the origin is FTS under the system dynamics f5, and there exists a V5 satisfying Eq. 8; therefore, condition 4) is satisfied. Finally, the switching signal is designed so that mode five is active for a sufficient amount of time that satisfies condition 5).
Figure 2 illustrates the state trajectories x1 (t) and x2 (t). Note that the states change sign at the discrete jumps. Figure 3 depicts the norm of the state vector x (t) on log scale; note that ‖x (t)‖ is increasing while operating in unstable modes, and decreasing while operating in stable modes. As seen in the figures, the system states, starting from ‖x (0)‖ = 10, reach to a norm of ‖x (t)‖ ≤ 10–10 within first 90 s of the simulation. Finally, Figure 4 illustrates the evolution of the Lyapunov functions Vi with respect to time; note that the Lyapunov functions increase, as expected, at the times of the switches in σf, as well as during the continuous flows along the unstable modes 1, 2, and 4. The provided example demonstrates that the origin of the system is FTS even when one or more modes are unstable, if the FTS mode is active for a sufficient amount of time.
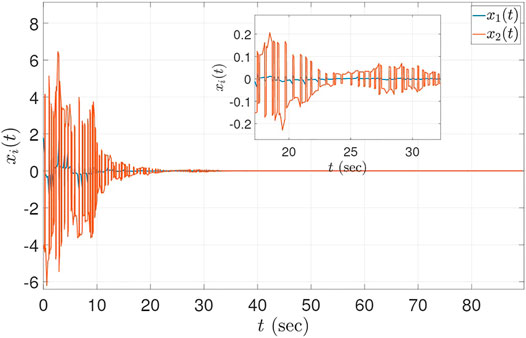
FIGURE 2. The evolution of x1 (t) and x2 (t) for hybrid system Eq. 19. The states can be seen switching signs during discrete jumps.
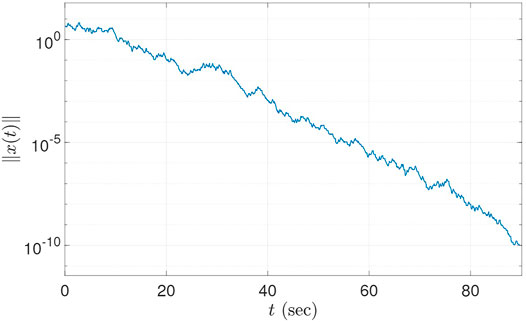
FIGURE 3. The evolution of ‖x (t)‖ for Eq. 19. The norm of the states reach a small neighborhood of the origin within a finite time.
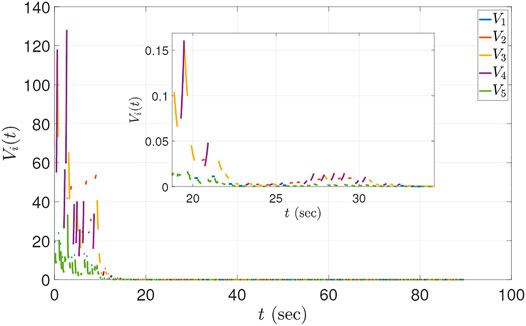
FIGURE 4. The evolution of the Lyapunov functions Vi (t) for t ∈ (0, 10) sec for Eq. 19. The Lyapunov functions for unstable modes (mode 2 and 4) increase when the respective modes are active.
4 Conclusions and Future Work
In this paper, we studied FTS of a class of hybrid systems. We showed that under some mild conditions on the bounds of the increase of the Lyapunov functions, if the FTS mode is active for a sufficient cumulative time, then the origin of the hybrid system is FTS. Our proposed method allows the individual Lyapunov functions to increase both during the continuous flows as well as at the discrete state jumps, i.e., it allows the hybrid system to have unstable modes.
Future research focuses on incorporating input and state constraints in the hybrid systems framework to model safety (in the sense of invariance of a safe set of states) and temporal requirements (in the sense of convergence to a set or to a point within an arbitrarily chosen time, if possible). More specifically, we would like to investigate how to impose convergence of the system trajectories in a finite time that can be a priori selected independent of the initial conditions, so that the overall framework can be used for the synthesis and analysis of controllers under spatiotemporal specifications.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
KG is responsible for the conceptualization, the simulation and the writing of this paper. DP is responsible for the funding acquisition, the conceptualization of the main idea and the revisions of the paper.
Funding
The authors would like to acknowledge the support of the Air Force Office of Scientific Research under award number FA9550-17-1-0284.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1With slight abuse of notation, we use FTS to denote the phrase “finite-time stability” or “finite-time stable”, depending on the context.
2A sufficient condition for the solutions of a switched or hybrid to exhibit non-Zeno behavior is that there is a non-zero dwell-time τ > 0 between any two switching instants [see (Liberzon, 2003)].
3Note that some authors use the time derivative condition, i.e., $\dot{V}_{i}\leq {\lambda} V_{i}$ with λ > 0, in place of condition 2), to allow growth of Vi, hence, requiring each Vi to be continuously differentiable.
References
Bhat, S. P., and Bernstein, D. S. (2000). Finite-time stability of continuous autonomous systems. SIAM J. Control. Optim. 38, 751–766. doi:10.1137/s0363012997321358
Bhat, S. P., and Bernstein, D. S. (2005). Geometric homogeneity with applications to finite-time stability. Math. Control. Signals Syst. 17, 101–127. doi:10.1007/s00498-005-0151-x
Branicky, M. S. (1998). Multiple Lyapunov functions and other analysis tools for switched and hybrid systems. IEEE Trans. Automat. Contr. 43, 475–482. doi:10.1109/9.664150
Fu, J., Ma, R., and Chai, T. (2015). Global finite-time stabilization of a class of switched nonlinear systems with the powers of positive odd rational numbers. Automatica 54, 360–373. doi:10.1016/j.automatica.2015.02.023
Garg, K., and Panagou, D. (2021). Finite-time stabilization of switched systems with unstable modes. IEEE Conference on Decision and Control. Submitted, under review (IEEE).
Goebel, R., Sanfelice, R. G., and Teel, A. R. (2012). Hybrid Dynamical Systems: Modeling, Stability, and Robustness. Princeton, New Jersey: Princeton University Press.
Khalil, H. K., and Grizzle, J. W. (2002). Nonlinear Systems, Vol. 3. Upper Saddle River, NJ): Prentice hall.
Li, Y., and Sanfelice, R. G. (2019). Finite time stability of sets for hybrid dynamical systems. Automatica 100, 200–211. doi:10.1016/j.automatica.2018.10.016
Lin, H., and Antsaklis, P. J. (2009). Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans. Automat. Contr. 54, 308–322. doi:10.1109/tac.2008.2012009
Liu, X., Ho, D. W. C., Song, Q., and Cao, J. (2017). Finite-/fixed-time robust stabilization of switched discontinuous systems with disturbances. Nonlinear Dyn. 90, 2057–2068. doi:10.1007/s11071-017-3782-9
Parrilo, P. A. (2000). Structured semidefinite programs and semialgebraic geometry methods in robustness and optimization. California: California Institute of Technology (Ph.D. thesis.
Peleties, P., and DeCarlo, R. (1991). Asymptotic stability of m-switched systems using lyapunov-like functions, 1991 American Control Conference (IEEE). 1679–1684. doi:10.23919/acc.1991.4791667
Prajna, S., Papachristodoulou, A., and Parrilo, P. A. (2002). Introducing SOSTOOLS: a general purpose sum of squares programming solver, 41st IEEE Conference on Decision and Control (IEEE). 741–746.
Ríos, H., Davila, J., and Fridman, L. (2015). “State estimation on switching systems via high-order sliding modes,” in Hybrid Dynamical Systems (Germany: Springer), 151–178. doi:10.1007/978-3-319-10795-0_6
Ryan, E. (1991). “Finite-time stabilization of uncertain nonlinear planar systems,” in Mechanics and Control (Germany: Springer), 406–414. doi:10.1007/bf02169426
Sanfelice, R. G., Goebel, R., and Teel, A. R. (2007). Invariance principles for hybrid systems with connections to detectability and asymptotic stability. IEEE Trans. Automat. Contr. 52, 2282–2297. doi:10.1109/tac.2007.910684
Wang, Y.-E., Karimi, H. R., and Wu, D. (2018). “Conditions for the stability of switched systems containing unstable subsystems,” in IEEE Transactions on Circuits and Systems II: Express Briefs. IEEE.
Zhang, B. (2018). On finite-time stability of switched systems with hybrid homogeneous degrees. Math. Probl. Eng. 2018, 1–7. doi:10.1155/2018/309698610.1155/2018/3096986
Zhao, J., and Hill, D. J. (2008). On stability, l2-gain and H∞ control for switched systems. Automatica 44, 1220–1232. doi:10.1016/j.automatica.2008.05.010
Zhao, X., Zhang, L., Shi, P., and Liu, M. (2012). Stability of switched positive linear systems with average dwell time switching. Automatica 48, 1132–1137. doi:10.1016/j.automatica.2012.03.008
Keywords: finite-time stability, hybrid systems, multiple lyapunov functions, lyapunov method, stability
Citation: Garg K and Panagou D (2021) Finite-Time Stability of Hybrid Systems With Unstable Modes. Front. Control. Eng. 2:707729. doi: 10.3389/fcteg.2021.707729
Received: 10 May 2021; Accepted: 19 July 2021;
Published: 02 August 2021.
Edited by:
Avimanyu Sahoo, Oklahoma State University, United StatesReviewed by:
Wei Ren, Catholic University of Louvain, BelgiumMohamad Kazem Shirani Faradonbeh, University of Georgia, United States
Copyright © 2021 Garg and Panagou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kunal Garg, a2dhcmdAdW1pY2guZWR1
 Kunal Garg
Kunal Garg Dimitra Panagou
Dimitra Panagou