Leader-Following Multi-Agent Coordination Control Accompanied With Hierarchical Q(λ)-Learning for Pursuit

In this paper, we investigate a pursuit problem with multi-pursuer and single evader in a two-dimensional grid space with obstacles. Taking a different approach to previous studies, this paper aims to address a pursuit problem in which only some pursuers can directly access the evader’s position. It also proposes using a hierarchical Q(λ)-learning with improved reward, with simulation results indicating that the proposed method outperforms Q-learning.

1 Introduction

Interest in pursuit problems and their applications has increased in recent years, facilitated by recent technological and computational advances. As a significant branch of the pursuit problem, multi-agent coordination pursuit has received much attention for its broad applications in military (Eklund et al., 2012), aerospace (Ye et al., 2020), autonomous vehicle fields (Vidal and Sastry, 2002), underwater vehicles (Qi and Cai, 2021), artificial intelligence (Haynes and Sen, 2006) and so on in the past decade.

In 1965, Isaacs first proposed the pursuit problem in a paper about differential games (Isaacs, 1965). From the view of control, the pursuit problem is an optimization problem with the minimum cost as the goal. In recent years, researchers have proposed many solutions to pursuit problems. Under the known agents’ dynamics or environments’ dynamics, pursuit problems have been addressed by finding analytical solutions (Shinar et al., 2009; Yan and Li, 2013; Beke and Kumbasar, 2018; Casini et al., 2019; Mejia et al., 2019). However, in practical engineering applications, it is hard to obtain an analytical solution of the pursuit problem. Hence, many learning algorithms, especially reinforcement learning, have been introduced into pursuit problems. Ishiwaka et al. (2003) studied a pursuit problem with four pursuers and one evader and employed reinforcement learning to complete the capture. Bilgin and Kadioglu-Urtis (2015) solved a pursuit problem with two pursuers and one stationary evader by employing Q(λ)-learning and verified the influence of learning rate and decay rate on simulation results. A pursuit problem with one evader whose goal is to reach its target while avoiding being captured by pursuers was investigated in Selvakumar and Bakolas (2020) by utilizing Min-Max Q-learning and matrix game theory. Noro et al. (2014) proposed signal learning with messages based on reinforcement learning to deal with a multi-agent pursuit problem. Additionally, Yu et al. (2020) presented a fully decentralized multi-agent reinforcement learning approach and applied it to the cooperative multi-robot pursuit problem successfully.

Pursuit problems can be divided into two categories. The first is a pursuit problem with a single evader, the other is a pursuit problem with multiple evaders. This paper focuses on a pursuit problem with a single evader in the presence of obstacles. In a typical pursuit problem, agents can be divided into evaders and pursuers. In most literature, researchers assume that all pursuers can obtain the position of the evader independently, so some effective and expensive detectors are needed for practical application. In this work, based on leader-following control, we divided the pursuers into leader pursuers and follower pursuers. Only leader pursuers can directly detect the position of the evader. We addressed the pursuit problem with reinforcement learning under the assumption that partial pursuers know the evader’s position. The contributions of this paper are summarized as follows:

• Leader-following control thought is adopted to solve the pursuit problem since it can reduce the cost of detectors.

• We propose the use of a hierarchical Q(λ)-learning with improved reward, as it has shown good performance for pursuit problems.

This paper is organized by defining the pursuit problem in Section 2. We then introduce Q(λ)-learning in Section 3. The proposed algorithm is described in Section 4 and the simulation experiments and results are shown in Section 5. Finally, Section 6 presents the conclusions of this study.

2 Our Pursuit Problem Setting

In this article, we mainly focus on a pursuit problem with a single evader. The environment of our pursuit problem is represented by a bounded two-dimensional grid map with obstacles, which are randomly distributed in the map and each obstacle occupies a cell. Obstacles cannot be occupied by agents.

Assuming that there are 2n pursuers, which include n leader pursuers and n follower pursuers in our map, each agent executes an action at each time step and moves in four main directions or remains in its current cell. Additionally, agents cannot cross the boundaries. For example, an agent can execute the 4 possible actions or remain in the current cell, when the agent in cell 5 of the simple map, as illustrated in Figure 1. Each cell can only be occupied by an agent or an obstacle. When several agents try to move to the same cell as part of the time step t + 1, the actions of these agents are canceled and the agents remain in the cell they inhabited at time step t.

FIGURE 1

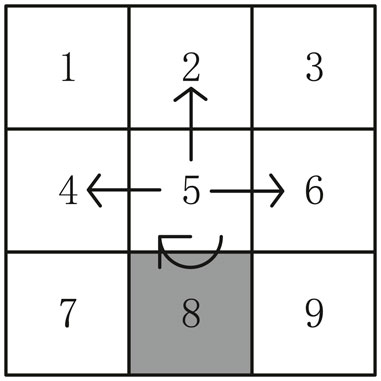
FIGURE 1. Possible actions (black arrows) for an agent in cell 5 of a sample map (cell 8 is an obstacle).

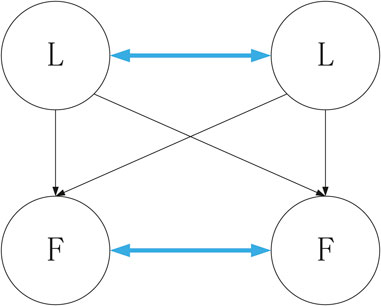
This pursuit problem assumes that only leader pursuers can directly detect the position of the evader. Leader pursuers can communicate with each other, and follower pursuers can also communicate with each other. Each leader pursuer sends its real-time position to all follower pursuers, so each follower pursuer knows all leader pursuers’ positions. The communication of a pursuit problem with two leader pursuers and two follower pursuers is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Communication of a pursuit problem with two leader pursuers and two follower pursuers.

2.1 Pursuit Groups

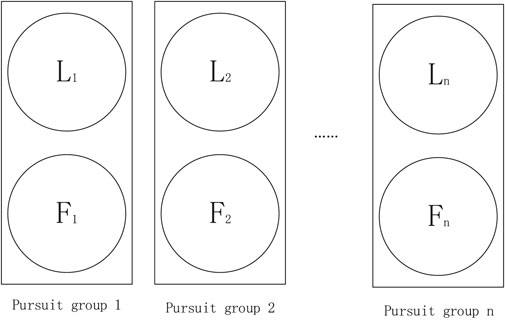
In this article, we assume that a leader pursuer can only be followed by one follower pursuer at the same time, and a follower pursuer can only choose one leader pursuer as its target to follow. Therefore, as illustrated in Figure 3, 2n pursuers can be divided into n pursuit groups, and each pursuit group has a leader pursuer and a follower pursuer. Furthermore, in Figure 3, L_i(i ∈ {1, 2, …, n}) is the target that F_i follows.

FIGURE 3

FIGURE 3. Pursuit groups.

In nature, small carnivores hunt large prey collectively. They usually encircle the prey first to prevent the prey from escaping. Then, when a large number of companions arrive, they hunt the prey together to ensure success. Similarly, in this paper, to ensure the success of the pursuit, we divided the pursuit into two stages: encirclement and capture.

2.2 Definition of Encirclement

We found that when the northwest cell and the southeast cell of the evader are occupied by the pursuers simultaneously, as shown in Figure 4A, or the northeast cell and the southwest cell are occupied by the pursuer simultaneously, for example, in the case of Figure 4B. We think the evader has been encircled. In our pursuit problem, at least two pursuers are required to encircle an evader. When the evader is encircled by the pursuers, it will always remain in its current cell.

FIGURE 4

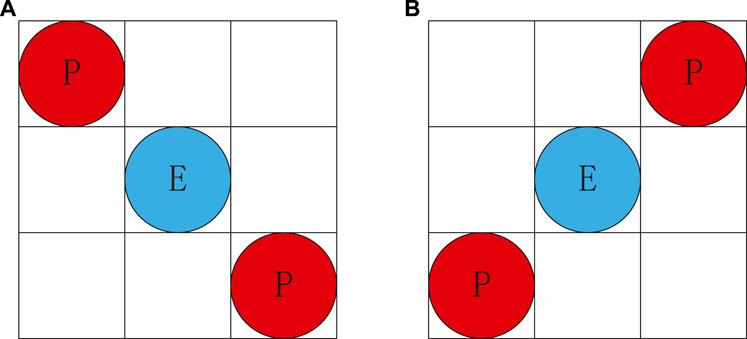
FIGURE 4. Definition of encirclement (red circles represent the pursuers and blue circles represents the evaders).

2.3 Definition of Capture

When the evader has been encircled and at least two cells of the evader’s north cell, the evader’s south cell, the evader’s east cell, and the evader’s west cell are occupied by the pursuers, the evader has been successfully captured. For example, in Figure 5, the evader in cell 5 has been encircled. The evader has been captured because cell 4 and cell 8 are also occupied by pursuers. Therefore, in our pursuit problem, at least four pursuers are required to capture an evader.

FIGURE 5

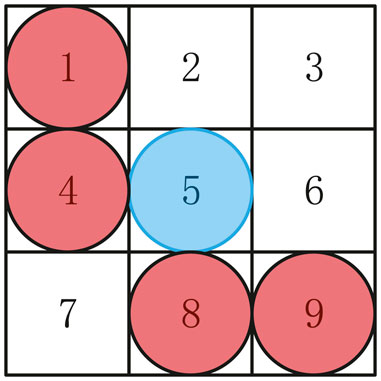
FIGURE 5. A simple case of capture (the evader in cell 5 has been encircled and cell 1, cell 4, cell 8, and cell 9 are occupied by pursuers).

3 Q(λ)-Learning

Q(λ)-learning is an improved Q-learning algorithm. As the foundation of Q(λ)-learning, Q-learning was first proposed by Watkins et al. (1992) and it is also known as single-step Q-learning. Due to its simple structure, single-step Q-learning has become a popular topic in reinforcement learning. Yet, Q-learning exhibits slow convergence. In order to accelerate convergence, Peng and Williams (1998) proposed Q(λ)-learning.

For accelerating the convergence, the eligibility trace is introduced into Q(λ)-learning. With the eligibility trace, Q(λ)-learning will look back further in time. For example, if the current reward is good, Q(λ)-learning not only updates the current state but also assigns some of the rewards to some of the previous states which drove the agent to be in a current state (Schwartz, 2014). The eligibility trace tracks a particular state that has been visited at last time and then assigns the current reward to recently visited states. A state that has not been visited for a long time is not eligible to get some of the current rewards. These requirements will greatly accelerate the convergence.

The eligibility trace of each state s (s ∈ S, s is the state of the agent and S is state space of the agent) at time step t is defined as e_t(s) and decays as λγ (0 ≤ λ ≤ 1, 0 ≤ γ ≤ 1). For the state that has just been accessed, its eligibility trace will increase by 1, so the eligibility trace is updated as (Schwartz, 2014)

$e_t\left(s\right)=\left\{\begin{array}{cc}\gamma \lambda e_{t-1}\left(s\right),\hfill & \text{if}s\ne s_t,\hfill \\ \gamma \lambda e_{t-1}\left(s\right)+1,\hfill & \text{if}s=s_t.\hfill \end{array}\right.(1)$

In Q(λ)-learning algorithm, the eligibility trace function becomes e(s, a), a is the action that was executed by agent. The eligibility trace of Q(λ)-learning is updated as

$e_t\left(s,a\right)=\left\{\begin{array}{cc}\gamma \lambda e_{t-1}\left(s,a\right),\hfill & \text{if}s\ne s_t,\hfill \\ \gamma \lambda e_{t-1}\left(s,a\right)+1,\hfill & \text{if}s=s_t,\hfill \end{array}\right.(2)$

and the prediction error is defined as

${\delta }_t=R_{t+1}+\gamma \max Q\left(s_{t+1},a_{t+1}\right)-Q\left(s_t,a_t\right),(3)$

where R_t+1 represents the immediate reward, γ is the discount factor, $a_t\in A_{s_t}$ and $A_{s_t}$ is an action set of the agent for the given state. In conventional Q-learning, we usually define the evaluation for each action at a given state as Q-value, and Q-values are stored in a state-action table, which is termed as Q-table. In Eq. 3, when the agent executes action a_t at a given state s_t, the Q-value of a_t is Q(s_t, a_t). The iterative equation for the Q-value takes as

$Q\left(s_t,a_t\right)=Q\left(s_t,a_t\right)+\alpha {\delta }_t{e}_t\left(s_t,a_t\right),(4)$

where α (0 ≤ α ≤ 1) is the learning rate. The Q(λ)-learning algorithm is described in Algorithm 1 (Schwartz, 2014).

Algorithm 1

4 The Proposed Algorithm

4.1 Coordination Multi-Agent Pursuit

In our research, since only partial pursuers can access the position of the evader, we assign different tasks to the pursuers according to their abilities. For the leader pursuers, because they can access the position of the evader, they are mainly responsible for encircling the evader to prevent the evader from escaping. For the follower pursuers, since the follower pursuers do not know the evader’s position, the follower pursuers are responsible for following the leader pursuers and assisting the leader pursuers to capture the evader after the evader is encircled.

4.1.1 Pursuit Groups Creation

In our pursuit problem, at least two leader pursuers are required to encircle an evader, and at least four pursuers are required to capture an evader. To minimize the total cost of the pursuit, in this article, two leader pursuers and two follower pursuers are selected to form two pursuit groups to participate in pursuit. The specific steps of pursuit groups creation are as follows.

Step 1. Initialize the position of evader x_e.

Step2. Initialize the positions of leader pursuers $x_{l_i}(i\in \{\mathrm{1,2},\dots ,n\})$ and the positions of follower pursuers $x_{f_j}(j\in \{\mathrm{1,2},\dots ,n\})$.

Step 3. Calculate the Euclidean distance $d_{l_{i}e}$ between the leader pursuer l_i and the evader and the distance matrix D_le

$D_{le}=\left(\begin{array}{c}\hfill d_{l_{1}e}\hfill \\ \hfill d_{l_{2}e}\hfill \\ \hfill ⋮\hfill \\ \hfill d_{l_{n}e}\hfill \end{array}\right),$

Step 4. Select two leader pursuers closest to the evader as L₁, L₂ to participate in the pursuit according to D_le.

Step 5. Calculate the Euclidean distance $d_{f_j{L}_k}(k\in \{\mathrm{1,2}\})$ between the follower pursuer f_j and the selected leader pursuer L_k and the distance matrix D_fL

$D_{fL}=\left(\begin{array}{cc}\hfill d_{f_1{L}_1}\hfill & \hfill d_{f_1{L}_2}\hfill \\ \hfill d_{f_2{L}_1}\hfill & \hfill d_{f_2{L}_2}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill d_{f_n{L}_1}\hfill & \hfill d_{f_n{L}_2}\hfill \end{array}\right),$

Step 6. Select a follower pursuer closest to L₁ as F₁ and select a follower pursuer closest to L₂ as F₂ according to D_fL.

Step 7. Solve the contradictions in the follower pursuers task assignment through negotiation, for example, if F₁ and F₂ are the same follower pursuer.

Step 8. The selected 2 leader pursuers and 2 follower pursuers form two pursuit groups.

4.1.2 Specific Task Assignment

The selected leader pursuers choose an encirclement pattern with the shortest distance from Figures 4A,B to encircle the evader and assign specific tasks through negotiation.

For the follower pursuers, they need to select a target cell to realize capture when the evader is encircled. According to the definition of capture, for each follower pursuer, we define a cell that has a common side with the follower pursuer’s target leader pursuers and is closest to the other leader pursuer as the possible target cell under the assumption that the evader is encircled. For example, in the case of Figure 6, the evader is encircled, if L₁ in cell 9, only cell 4, cell 8, cell 10, and cell 14 have a common side with L₁. For F₁, cell 8 and cell 14 are possible target cells, since cell 8 and cell 14 are closest to the other leader pursuers. The follower pursuer will select the nearest possible target cell as its final target cell.

FIGURE 6

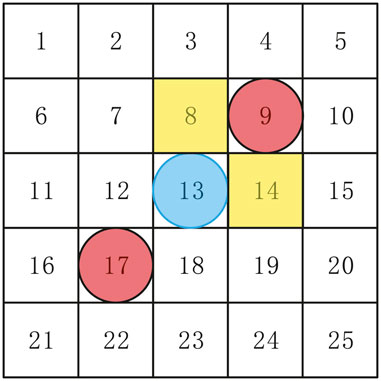
FIGURE 6. Possible target cells for the follower pursuer (red circles represent the leader pursuers, blue circle represents the evader and possible target cells are printed yellow).

4.2 Hierarchical Reinforcement Learning for Pursuit Problem

Hierarchical reinforcement learning is a widely utilized algorithm to solve the problem of “curse of dimensionality” (Botvinick, 2012). Decomposing the whole team task into some subtasks at different levels is the core idea of hierarchical reinforcement learning. Moreover, the policy, which is learned by an agent in a subtask, can also be utilized by other agents, so hierarchical reinforcement learning significantly accelerates the convergence. Option learning (Sutton et al., 1999) is one of the most popular hierarchical learning algorithms.

In option learning, option means closed-loop policies for taking action over a period of time. The option is a term for generalizing primitive actions and it consists of three elements: policy π, termination condition β and an initiation set ζ. Only if current state s ∈ ζ, an option $<\pi ,\beta ,\zeta >$ is available. While an option is adopted, actions are chosen according to policy π until the option ends. When the current option terminates, agents have the opportunity to select other options (Sutton et al., 1999).

In our research, we apply option learning to leader pursuers. We abstract each leader pursuer’s task into two options: O₁ and O₂. O₁ and O₂ are defined as follows.

• In O₁, approaching the evader quickly is the aim of the leader pursuer.

• In O₂, encircling the evader is the aim of the leader pursuer.

In this paper, there is only one evader in our pursuit problem, so leader pursuers can share learning experiences and update the policy together during O₁. When the leader pursuers in O₂, each leader pursuer will learn its policy separately. The internal policy π of O₁ and O₂ are unknown, and the internal policy of each option is learned with reinforcement learning respectively. By introducing hierarchical reinforcement learning, we have greatly improved the learning efficiency of leader pursuers.

4.3 Reward Improving

Q(λ)-learning and Q-Learning are all typical reward-guidance learning algorithms. Therefore, it is very significant to define rewards and penalties. The sparse reward is one of the most popular rewards nowadays due to its simple structure. Generally, the sparse reward is defined as follows

$R=\left\{\begin{array}{cc}{r}_1,\hfill & \text{Situation\hspace{0.17em}}1\text{,}\hfill \\ r_2,\hfill & \text{Situation\hspace{0.17em}}2\text{,}\hfill \\ -r_3,\hfill & \text{Situation\hspace{0.17em}}3\text{,}\hfill \\ \dots ,\hfill & \dots ,\hfill \end{array}\right.(5)$

where r_n⩾0 (n ∈ 1, 2, 3, …) and all rewards are constants. When dealing with some simple tasks, sparse reward exhibits a good performance. However, when the task is complex, the agent may achieve more penalties than rewards during training with sparse reward, which will reduce the learning efficiency and even hinder the agent from learning. In order to solve this problem, we alter the reward function. Different from the sparse reward, we designed an additional reward. The proposed reward is defined as follows

$R=r_c+r_a,(6)$

where r_c refers to sparse reward. r_c is defined as follows

$r_c=\left\{\begin{array}{cc}{r}_{c_1},\hfill & \text{Situation\hspace{0.17em}}1\text{,}\hfill \\ r_{c_2},\hfill & \text{Situation\hspace{0.17em}}2\text{,}\hfill \\ -r_{c_3},\hfill & \text{Situation\hspace{0.17em}}3\text{,}\hfill \\ \dots ,\hfill & \dots ,\hfill \end{array}\right.(7)$

where $r_{c_n}⩾0(n\in \mathrm{1,2,3},\dots )$ and all rewards are constants. Besides, r_a in Eq. 6 represents the additional reward and it is given by

$r_a=f\left(x\right),(8)$

where f(x) is a continuous function related to the distance x between agents.

4.4 Complete Algorithm

The complete algorithm is described in Algorithm 2.

Algorithm 1

5 Simulation Experiments and Results

5.1 Configuration of the Simulation Experiment Environment

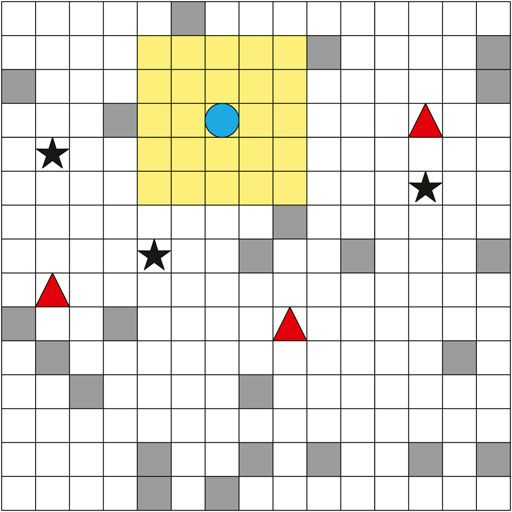
In our simulation experiment, we consider a bounded grid map of 15 × 15 cells with obstacles, which are randomly distributed in the map and each obstacle occupies a cell. There are 3 leader pursuers, 3 follower pursuers, and 1 evader on the map. The map is illustrated in Figure 7, where the red circles represent leader pursuers, the black stars represent follower pursuers, the blue circle represents the evader, and obstacles are printed grey.

FIGURE 7

FIGURE 7. Our pursuit problem environment.

5.2 Experimental Results and Analysis

5.2.1 Q-Learning and Hierarchical Q(λ)-Learning

In this section, Q-learning, Q(λ)-learning, hierarchical Q-learning, and hierarchical Q(λ)-learning are utilized to solve our pursuit problem respectively. In our experiment, Q-learning and Q(λ)-learning takes ϵ-greedy strategy as their action-selection strategy. The parameters are set in Table 1.

TABLE 1

TABLE 1. Parameters setting.

For leader pursuers, entering within 5 × 5 cells centered on the evader is defined as O₁. For example, in the case of Figure 7, when the evader in the current cell, entering within the yellow area is defined as O₁. In this section, the reward is defined as follows

$R=r_m+r_d+r_b,(9)$

where r_m is defined as follows

$r_m=\left\{\begin{array}{cc}-3,\hfill & \text{The\hspace{0.17em}distance\hspace{0.17em}between\hspace{0.17em}the\hspace{0.17em}leader\hspace{0.17em}pursuer}(\text{the}\hfill \\ \hfill & \text{follower\hspace{0.17em}pursuer})\text{\hspace{0.17em}and\hspace{0.17em}the\hspace{0.17em}evader\hspace{0.17em}}(\text{its\hspace{0.17em}target}\hfill \\ \hfill & \text{leader\hspace{0.17em}pursuer})\text{\hspace{0.17em}becomes\hspace{0.17em}longer,}\hfill \\ 0,\hfill & \text{Other\hspace{0.17em}conditions,}\hfill \end{array}\right.(10)$

r_d is given by

$r_d=\left\{\begin{array}{cc}100,\hfill & \text{The\hspace{0.17em}evader\hspace{0.17em}is\hspace{0.17em}captured\hspace{0.17em}successfully,}\hfill \\ 50,\hfill & \text{If\hspace{0.17em}the\hspace{0.17em}pursuer\hspace{0.17em}completes\hspace{0.17em}its\hspace{0.17em}own\hspace{0.17em}individual}\hfill \\ \hfill & \text{\hspace{0.17em}task,}\hfill \\ 0,\hfill & \text{Other\hspace{0.17em}conditions,}\hfill \end{array}\right.(11)$

r_b can be obtained by

$r_b=\left\{\begin{array}{cc}-5,\hfill & \text{If\hspace{0.17em}the\hspace{0.17em}pursuer\hspace{0.17em}attempts\hspace{0.17em}to\hspace{0.17em}cross\hspace{0.17em}boundary}\hfill \\ \hfill & \text{or\hspace{0.17em}collide\hspace{0.17em}with\hspace{0.17em}obstacle,}\hfill \\ 0,\hfill & \text{Other\hspace{0.17em}conditions.}\hfill \end{array}\right.(12)$

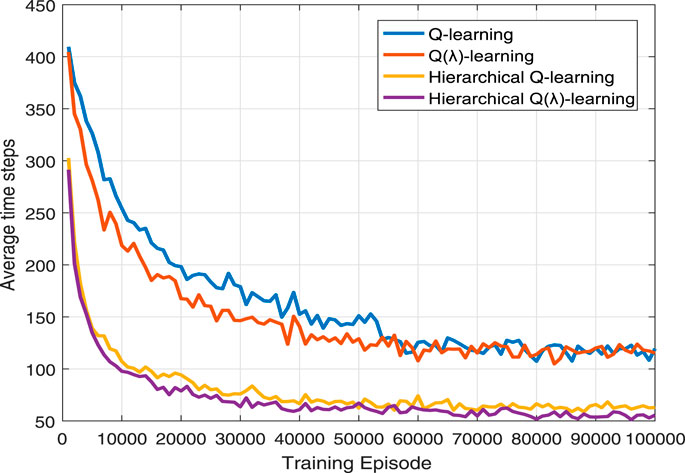
Every 1,000 episode, we record the average time steps it takes the pursuers to successfully capture the evader. The simulation results are illustrated in Figure 8 and Table 2 shows the average time steps for 100,000 episodes. By introducing the eligibility trace, learning results at any time step can immediately influence the policy and improve the learning efficiency. Compared with Q-learning, Q(λ)-learning greatly accelerates the convergence. Yet, Q(λ)-learning cannot significantly improve the convergence results. Because the hierarchical reinforcement learning greatly reduces the state set of the algorithm, the average time steps for the pursuers to capture the evader are significantly reduced. From Table 2, we can intuitively conclude that compared with Q-learning, hierarchical Q(λ)-learning can save 56.1% of average time steps.

FIGURE 8

FIGURE 8. Average time steps of four learning algorithms.

TABLE 2

TABLE 2. Average time steps for 100,000 episodes.

5.2.2 The Improved Reward

In this section, we verify the effectiveness of the improved reward and hierarchical Q(λ)-learning approach to solve our pursuit problem. Compared with the above simulation, we only replace r_m with r_a. r_a is defined as follows

$r_a=\left\{\begin{array}{cc}-3e^{d_{le}^2-d_{\mathit{max}}^2},\hfill & \text{If\hspace{0.17em}the\hspace{0.17em}pursuer\hspace{0.17em}is\hspace{0.17em}a\hspace{0.17em}leader\hspace{0.17em}pursuer,}\hfill \\ -3e^{d_{fl}^2-d_{\mathit{max}}^2},\hfill & \text{If\hspace{0.17em}the\hspace{0.17em}pursuer\hspace{0.17em}is\hspace{0.17em}a\hspace{0.17em}follower\hspace{0.17em}pursuer,}\hfill \end{array}\right.(13)$

where the theoretical maximum distance between two agents in our map is defined as d_max, d_le(1⩽d_le⩽d_max) is the distance between the leader pursuer and the evader, and d_fl(1⩽d_fl⩽d_max) refers to the distance between the follower pursuer and its target leader pursuer.

We also record the average time steps every 1, 000 episodes. Figure 9 shows the simulation results and Table 3 exhibits the average time steps for 100,000 episodes. Compared with sparse reward, the improved reward provides more reward signals for the pursuers during training and improves the learning efficiency of the pursuers. It can be seen from Table 3 that the improved reward can save 17.5% of average time steps in our pursuit problem.

FIGURE 9

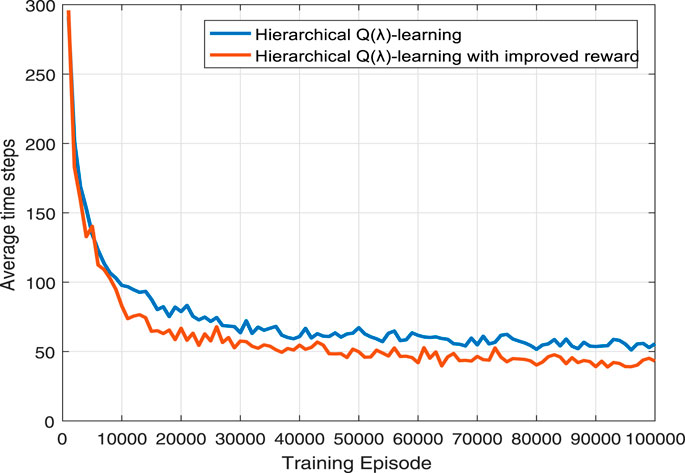
FIGURE 9. Average time steps of hierarchical Q(λ)-learning and hierarchical Q(λ)-learning with improved reward.

TABLE 3

TABLE 3. Average time steps for 100,000 episodes.

6 Conclusion

In this paper, we address a pursuit problem in a two-dimensional environment with obstacles. Different from previous literature, in the present study only a partial number of the pursuers know the evader’s position. We combine the thought of leader-following control and reinforcement learning to address the pursuit problem and present a hierarchical Q(λ)-learning with improved reward to accelerate the convergence. Our proposed method demonstrates better performance than Q-learning in the pursuit problem.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China under Grants 61973139 and 61473138, and the Fundamental Research Funds for the Central Universities under Grant JUSRP22014.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beke, A., and Kumbasar, T. (2020). Type-2 Fuzzy Logic-Based Linguistic Pursuing Strategy Design and its Deployment to a Real-World Pursuit Evasion Game. IEEE Trans. Cybern. 50, 211–221. doi:10.1109/TCYB.2018.2868405

PubMed Abstract | CrossRef Full Text | Google Scholar

Bilgin, A. T., and Kadioglu-Urtis, E. (2015). “An Approach to Multi-Agent Pursuit Evasion Games Using Reinforcement Learning,” in International Conference on Advanced Robotics, July 27-31, Turkey. ICAR. 164–169. doi:10.1109/ICAR.2015.7251450

CrossRef Full Text | Google Scholar

Botvinick, M. M. (2012). Hierarchical Reinforcement Learning and Decision Making. Curr. Opin. Neurobiol. 22, 956–962. doi:10.1016/j.conb.2012.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Casini, M., Criscuoli, M., and Garulli, A. (2019). A Discrete-Time Pursuit-Evasion Game in Convex Polygonal Environments. Syst. Control. Lett. 125, 22–28. doi:10.1016/j.sysconle.2018.12.008

CrossRef Full Text | Google Scholar

Eklund, J. M., Sprinkle, J., and Sastry, S. S. (2012). Switched and Symmetric Pursuit/evasion Games Using Online Model Predictive Control with Application to Autonomous Aircraft. IEEE Trans. Contr. Syst. Technol. 20, 604–620. doi:10.1109/tcst.2011.2136435

CrossRef Full Text | Google Scholar

Haynes, T., and Sen, S. (2006). Evolving Behavioral Strategies in Predators and Prey. Berlin: Springer. 113–126.

Google Scholar

Isaacs, R. (1965). Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization. New York, NY: John Wiley.

Google Scholar

Ishiwaka, Y., Sato, T., and Kakazu, Y. (2003). An Approach to the Pursuit Problem on a Heterogeneous Multiagent System Using Reinforcement Learning. Robotics Autonomous Syst. 43, 245–256. doi:10.1016/S0921-8890(03)00040-X

CrossRef Full Text | Google Scholar

Lopez, V. G., Lewis, F. L., Wan, Y., Sanchez, E. N., and Fan, L. (2020). Solutions for Multiagent Pursuit-Evasion Games on Communication Graphs: Finite-Time Capture and Asymptotic Behaviors. IEEE Trans. Automat. Contr. 65, 1911–1923. doi:10.1109/TAC.2019.2926554

CrossRef Full Text | Google Scholar

Noro, K., Tenmoto, H., and Kamiya, A. (2014). Signal Learning with Messages by Reinforcement Learning in Multi-Agent Pursuit Problem. Proced. Comp. Sci. 35, 233–240. doi:10.1016/j.procs.2014.08.103

CrossRef Full Text | Google Scholar

Peng, J., and Williams, R. J. (1996). Incremental Multi-step Q-Learning. Mach Learn. 22, 283–290. doi:10.1007/BF00114731

CrossRef Full Text | Google Scholar

Qi, X., and Cai, Z.-J. (2021). Cooperative Pursuit Control for Multiple Underactuated Underwater Vehicles with Time Delay in Three-Dimensional Space. Robotica 39, 1101–1115. doi:10.1017/S0263574720000922

CrossRef Full Text | Google Scholar

Schwartz, H. M. (2014). Multi-Agent Machine Learning: A Reinforcement Approach. Hoboken: John Wiley and Sons,Inc. doi:10.1002/9781118884614

CrossRef Full Text | Google Scholar

Selvakumar, J., and Bakolas, E. (2020). Min-max q-learning for multi-player pursuit-evasion games. arXiv: 2003.03727

Google Scholar

Shinar, J., Glizer, V. Y., and Turetsky, V. (2009). A Pursuit-Evasion Game with Hybrid Pursuer Dynamics. Eur. J. Control. 15, 665–684. doi:10.3166/ejc.15.665-684

CrossRef Full Text | Google Scholar

Sutton, R., Precup, D., and Singh, S. (1999). Between Mdps and Semi-mdps: A Framework for Temporal Abstraction in Reinforcement Learning. Artif. Intelligence 112, 181–211. doi:10.1016/s0004-3702(99)00052-1

CrossRef Full Text | Google Scholar

Vidal, R., and Sastry, S. (2002). Vision-based Detection of Autonomous Vehicles for Pursuit-Evasion Games. IFAC Proc. Volumes 35, 391–396. doi:10.3182/20020721-6-es-1901.01290

CrossRef Full Text | Google Scholar

Watkins, C. J. C. H., Dayan, P., and Dayan, P. (1992). Technical Note. Q-learning. Techn. Note 4, 55–68. doi:10.1007/978-1-4615-3618-5_4

CrossRef Full Text | Google Scholar

Yan, J., Guan, X.-p., Luo, X.-y., and Chen, C.-l. (2013). A Cooperative Pursuit-Evasion Game in Wireless Sensor and Actor Networks. J. Parallel Distributed Comput. 73, 1267–1276. doi:10.1016/j.jpdc.2013.05.009

CrossRef Full Text | Google Scholar

Ye, D., Shi, M., and Sun, Z. (2020). Satellite Proximate Pursuit-Evasion Game with Different Thrust Configurations. Aerospace Sci. Tech. 99, 105715. doi:10.1016/j.ast.2020.105715

CrossRef Full Text | Google Scholar

Yu, C., Yinzaho, D., Li, Y., and Chen, Y. (2020). Distributed Multi-Agent Deep Reinforcement Learning for Cooperative Multi-Robot Pursuit. J. Eng. 13, 499–504. doi:10.1049/joe.2019.1200

CrossRef Full Text | Google Scholar