- 1School of Mathematics and Physics Sciences, Anhui Jianzhu University, Hefei, China
- 2Institute of Mathematics, School of Mathematical Sciences, Nanjing Normal University, Nanjing, China
This paper investigates the robust consensus problem for heterogeneous second-order multi-agent systems with uncertain parameters. Based on the sliding mode control method, novel robust consensus protocols are designed for the linear multi-agent systems with uncertain parameters and a class of uncertain nonlinear multi-agent systems. Finally, numerical simulations are given to verify the effectiveness of the proposed protocols.
1 Introduction
A multi-agent system (MAS) is composed of many subsystems connected by a network, where each subsystem is called an agent. All the agents transmit state information via the interconnecting network and affect each other according to a control protocol. The research topics on multi-agent system theory include mathematical models, simulations, collective behavior analysis, protocol design and so on. Collective behavior analysis of multi-agent systems is an important issue of multi-agent system theory, which has a wide background on physics and engineering such as the self-organization of a colony, coordinated control of robots, synchronization of satellites, formation control of unmanned aerial vehicles (UAVs).
In recent years, many mathematical models of MASs have been widely studied and lots of research contributions have been published Ren and Atkins (2007); Ren and Beard (2005); Ren (2007); Liu and Guo (2008, 2009), including Vicsek model Liu and Guo (2008, 2009); Vicsek et al. (1995), Kuramoto model Kuramoto (1975), integrator multi-agent systems Olfati-Saber et al. (2007); Olfati-Saber and Murray (2004), general high-order linear multi-agent systems Ma and Zhang (2010) and nonlinear multi-agent systems Ren and Chen (2015). A protocol is an interaction rule that specifies the information exchange between an agent and its neighbours on the network. Consensus problem is just to design a protocol such that the states of agents reach consensus, which has been studied from several different perspectives in the existing literatures Olfati-Saber and Murray (2004)-Hou et al. (2009). In Olfati-Saber and Murray (2004); Tang et al. (2012); Xu et al. (2013), consensus protocols for the first order multi-agent systems are developed. While in Islam et al. (2018); Su et al. (2011); Yu et al. (2009), consensus protocols for the second order multi-agent systems are proposed.
For an actual system, it is usually difficult to get an exact mathematical model since uncertain parameters and external disturbances often exist. Thus it is significant to investigate this kind of multi-agent systems with agents having different dynamics and being affected by uncertainties and disturbances. Sliding mode control is an important technique in robust control field, whose main advantage lies in the robustness with respect to uncertainties and disturbances Utkin (1978, 1993); Utkin et al. (2009). At present, sliding mode technique has been used in multi-agent systems to control some collective behaviors. For solving finite-time consensus problem, sliding mode control method has been adopted in many cases Khoo et al. (2009, 2008); Cao et al. (2010); Yu and Long (2015). The well-known high-order sliding mode control is effective in diminishing the chattering phenomenon Levant (1993); Moreno and Osorio (2008) and has been used to solve some formation control problems Jia et al. (2007); Galzi and Shtessel (2006). In Zhang et al. (2017) and Islam et al. (2018), sliding mode control method has been used to solve some consensus problem of multi-agent systems with uncertainties. Some recent results on robust consensus can be seen in Xue et al. (2021) and Yu et al. (2021). In Xue et al. (2021), structured uncertainties are considered, and in Yu et al. (2021) adaptive sliding mode control is designed. In our recent paper Zhao and Zhu (2020), we have investigated a class of linear uncertain multi-agent systems. However, in Zhao and Zhu (2020), one has to solve linear matrix inequalities, and the nonlinear uncertain multi-agent systems have not been considered.
In this paper, we investigates the robust consensus problem for the heterogeneous uncertain second-order multi-agent systems based on sliding mode control. For the linear uncertain multi-agent systems, the uncertain parameters appear in both the state coefficients and the control coefficients. A similar result is obtained for a class of nonlinear multi-agent systems with uncertain parameters. Simulations show the effectiveness of the proposed protocols in realizing robust consensus.
2 Robust Consensus of the Linear Heterogeneous Second-Order Multi-Agent Systems
We consider the networked multi-agent system with the fixed topology
Suppose that each node of the digraph is a dynamic agent with dynamics.
where
The robust consensus problem is just to design a distributed feedback controller ui for each i = 1, 2, …, m such that the closed-loop system satisfies
for some kinds of uncertain parameters a1i, a2i, bi and external disturbances.
Assumption 1All of the uncertain parameters and the disturbances are uniformly bounded, i.e., there exist known positive constants η and δ such that
where b0 is a known constant and δ < ∣b0∣.
Theorem 1Consider the heterogeneous uncertain multi-agent system described by Eq. 2 and Eq. 3. If digraph
where
ProofFirst, we prove that the trajectory of the closed-loop system will stay in the sliding surfaces si = 0 (i = 1, 2, …, m) after a finite time. Let
By Eq. 7, it is easy to see
By Eq. 9, we have
From Eq. 11, one obtains that si(t) = 0 as
From Eq. 12 and Eq. 2, it follows that the dynamics limited on the sliding mode surfaces is described by
In Olfati-Saber and Murray (2004), the consensus of system (13) has been proved as follows: there exists a constant C, which is dependent on the initial states
Remark 1The proposed conditions are somewhat conservative since the designed controller depends on the bounds of the uncertain parameters. If the bounds are unknown, one can consider adopt adaptive control method. In many practical systems, there are errors in the measurement of parameters, but generally speaking the measurement accuracy of the instrument is known. Therefore, in this case the variation range of parameters in Assumption 1 can be accurately determined. Moreover, the boundary of disturbance signals needs to be obtained through experience and experiments.
3 Robust Consensus of a Class of Uncertain Nonlinear Multi-Agent Systems
In this section, we consider a kind of uncertain nonlinear multi-agent systems. Suppose that each node of the digraph has a nonlinear dynamics as follows:
where
Assumption 2For the uncertain nonlinear functions ai(xi, vi) and bi(xi, vi), there exists a known function L(xi, vi) satisfying
where bi (xi, vi) ≥ b0 for known constant b0 > 0.
Theorem 2For the uncertain nonlinear multi-agent system described by Eq. 14 and Eq. 15, If digraph
where
with a known constant β0 > 0 and
with any constant k > 0.
ProofLet
Applying Assumption 2, (17) and (18), we have
From Eq. 20, it follows that si(t) = 0 as
Remark 2In practice, the upper bound functions satisfying Assumption 2 are also needed to be designed via experience and experiments. The bound of nonlinearity is used to design the controller, which can lead to high-gain feedback. This is a disadvantage of our paper.
4 Simulations
Example 1Consider the multi-agent systems with the topology
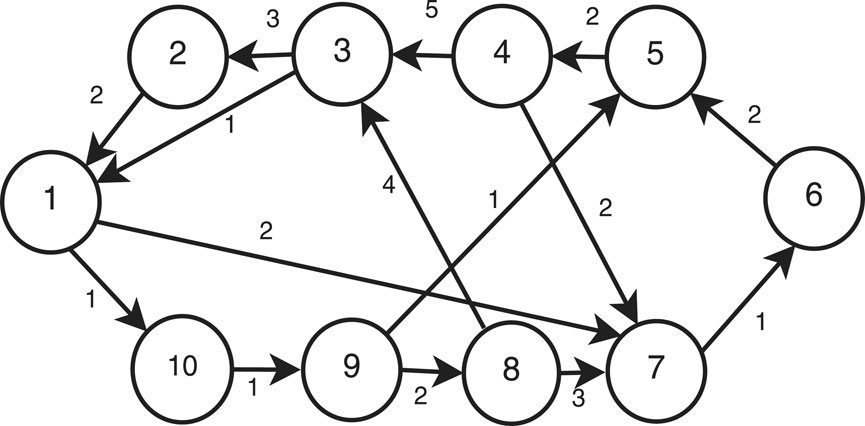
where i = 1, 2, …, 10. Let x = [x1, x2, …, x10] and v = [v1, v2, …, v10] be the position vector and the velocity vector of the multi-agent system. Let a1 = [a11, a12, …, a1,10], a2 = [a21, a22, …, a2,10] and b = [b1, b2, …, b10] be the uncertain parameters satisfying |aij| ≤ 0.3, |bi − 1| ≤ 0.3. Let w(t) = [w1(t), w2(t), …, w10] be composed of the disturbance signals satisfying |wi(t)| ≤ 0.3. By Figure 1, the adjacency matrix of
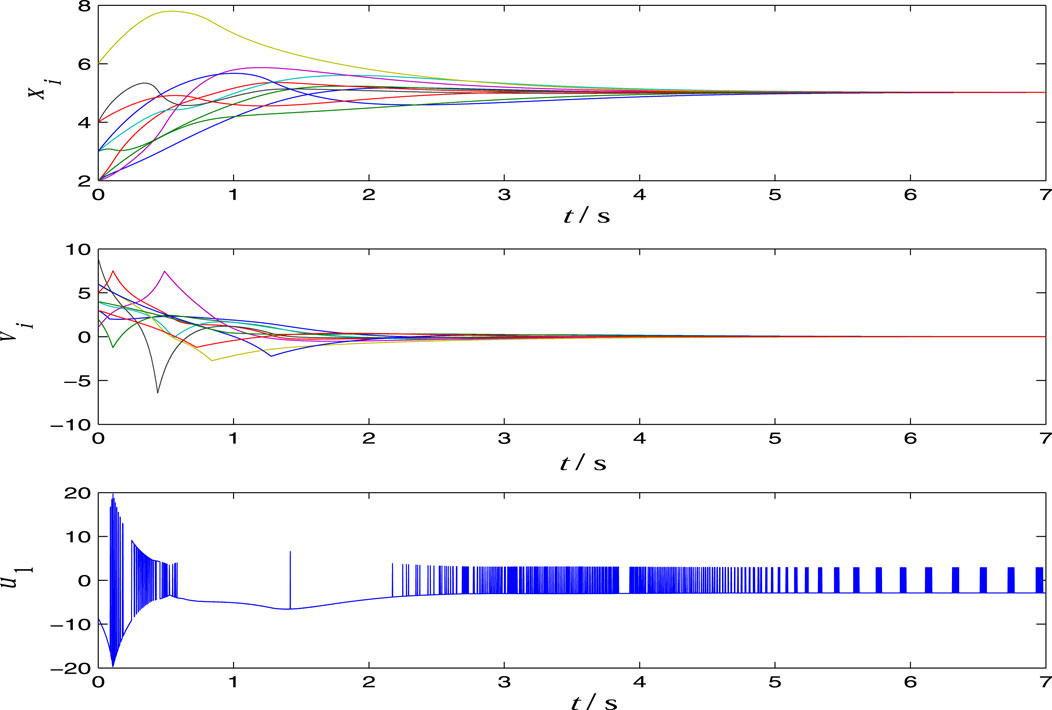
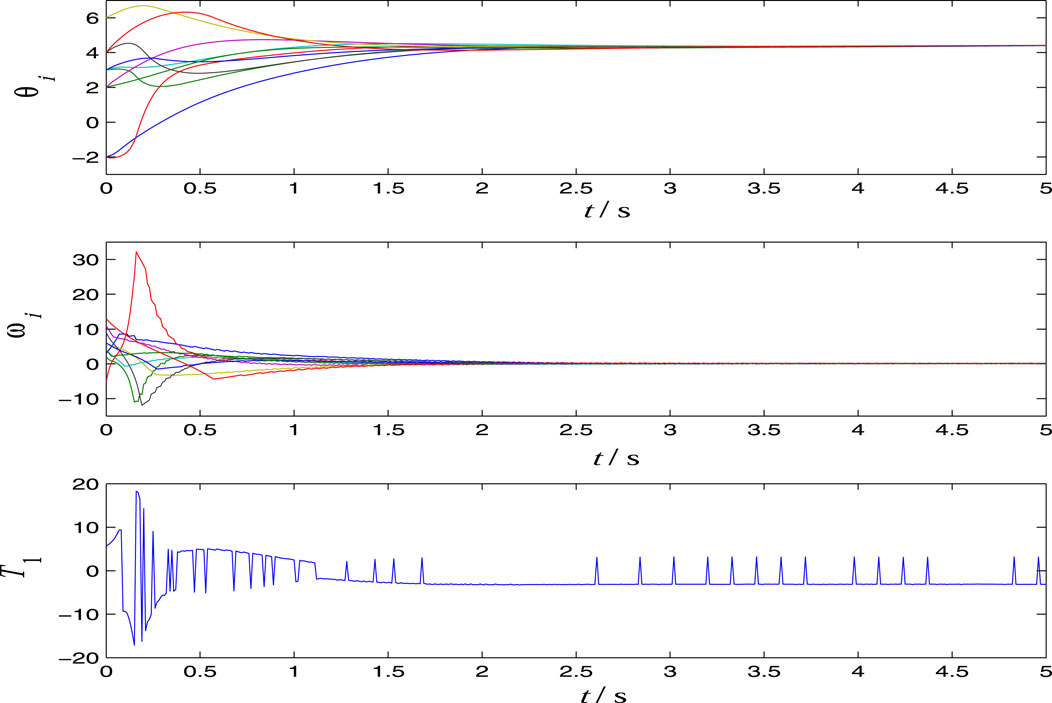
The controller is designed as (6)–(8) with η = δ = 0.3, k = 1, b0 = 1 and r = δ/b0 = 0.3. In order to show the robustness of the designed controller, we choose three groups of parameters and disturbance signals in the simulations. In Figure 2, the time response curves and the first control component are displayed with
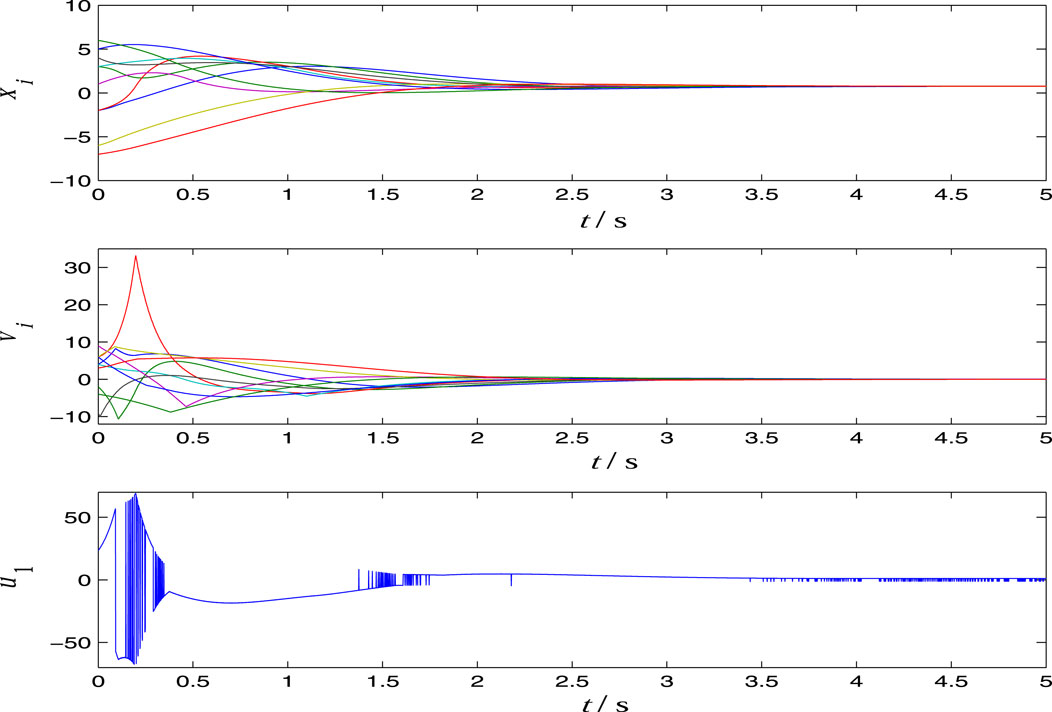
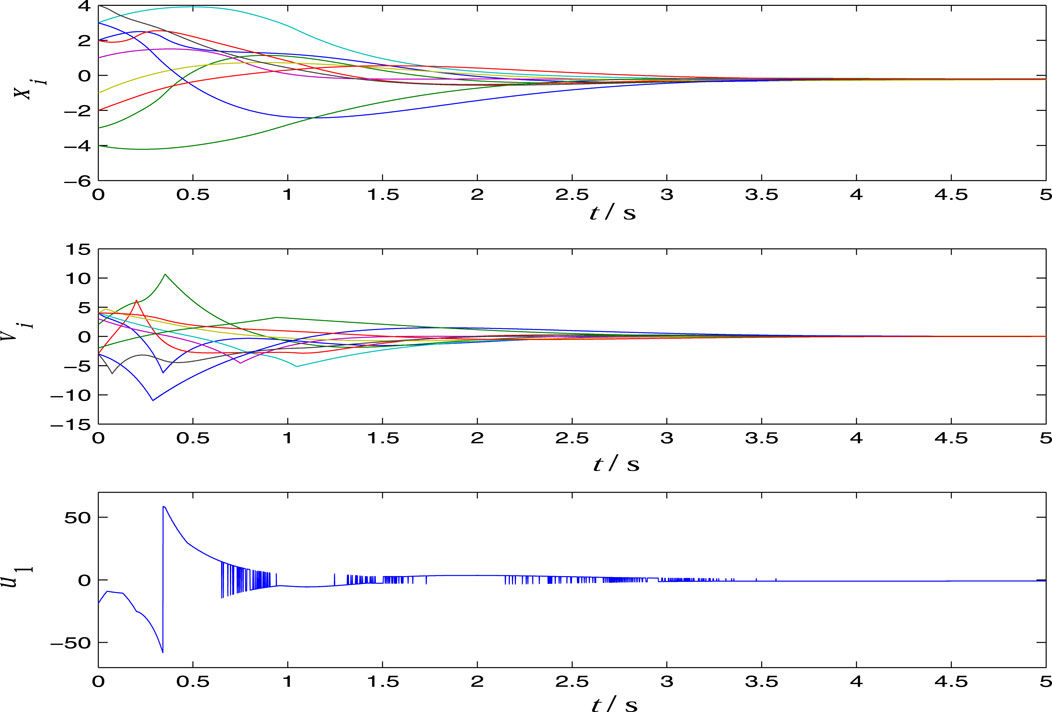
In the simulations shown in Figure 3 and Figure 4, we set
and
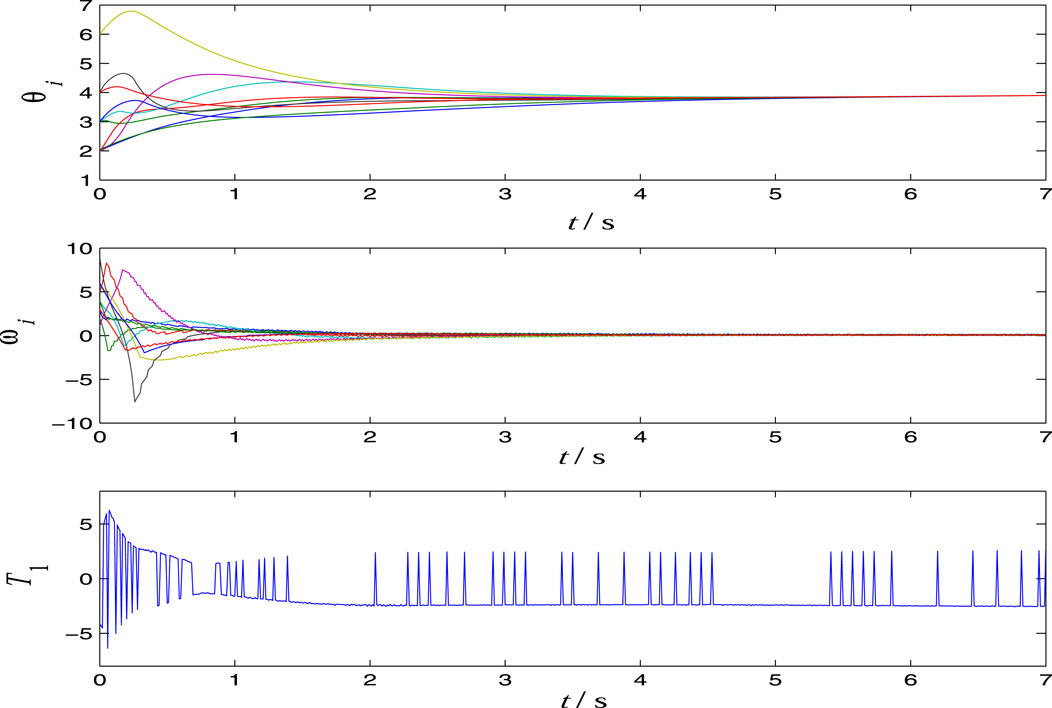
respectively. From Figure 2, Figure 3 and Figure 4, we see that the controller is robust for the parameters and disturbances. From the time response curves of u1(t), we see that the typical characteristic chattering phenomenon exists in the sliding mode control.
Example 2Consider a practical multi-agent system: a dynamical network composed of pendulums:
where θi, ωi, Ti, mi, and li are angular displacement, angular velocity, external torque, mass, and length of the ith pendulum, respectively. The constants k0 and g0 are coefficient of friction and acceleration due to the gravity, respectively. The known parameter information include 0.05 < mi < 0.2, 0.9 < li < 1.1, 0.01 < k0 < 0.05, and 9.8 < g0 < 9.9. By Theorem 2, we need to determine L (θi, ωi) satisfying Assumption 2. It is easy to check that
By Eq. 26, we let Li (θi, ωi) = 2.178| sin (θi)| + 0.0605|ωi|. Since
5 Conclusion
In this paper, we have investigated the robust consensus problem for the heterogeneous uncertain second order multi-agent systems based on sliding mode control. Novel robust consensus protocols have been proposed based on sliding mode control to realize the consensus. Numerical simulations have shown the effectiveness of the proposed protocols. The main disadvantage lies in the chattering phenomenon of the designed controller. How to reduce the chattering phenomenon will be discussed in our future research work.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is supported by Young Scholar Project of Anhui Jianzhu University under grant 2016XQZ08 and National Natural Science Foundation (NNSF) of China under Grants 61628302.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcteg.2021.744027/full#supplementary-material
References
Cao, Y., Ren, W., and Meng, Z. (2010). Decentralized Finite-Time Sliding Mode Estimators and Their Applications in Decentralized Finite-Time Formation Tracking. Syst. Control. Lett. 59, 522–529. doi:10.1016/j.sysconle.2010.06.002
Chen, T., Zhu, J., and Shi, Y. (2010). Leader-follower Coordination of Linear Time-Invariant Multi-Agent Systems. Dyn. Continuous, Discrete Impulsive Syst. Ser. B: Appl. Algorithms 17, 431–448.
Galzi, D., and Shtessel, Y. (2006). “Uav Formations Control Using High Order Sliding Modes,” in 2006 American Control Conference, June 14-16, 2006, Minneapolis, MN (IEEE), 4249–4254. doi:10.1109/acc.2006.1657386
Hou, Z.-G., Cheng, L., and Tan, M. (2009). Decentralized Robust Adaptive Control for the Multiagent System Consensus Problem Using Neural Networks. IEEE Trans. Syst. Man. Cybern. B 39, 636–647. doi:10.1109/tsmcb.2008.2007810
Islam, S., Khawli, T. A., Alzaabi, A., and Sunda-Meya, A. (2018). “Consensus Based Distributed Robust Adaptive Control for Second-Order Nonlinear Multi-Agent Systems with Uncertainty,” in The 2018 IEEE International Conference on Systems, Man, and Cybernetics, October 7-10, 2018, Miyazaki, Japan (IEEE), 2639–2644. doi:10.1109/smc.2018.00451
Jia, Q., Xing, X., and Li, G. (2007). “Formation Path Tracking Controller of Multiple Robot System by High Order Sliding Mode,” in 2007 IEEE International Conference on Automation and Logistics, August 18-21, 2007, Jinan, China (IEEE), 923–927. doi:10.1109/ical.2007.4338698
Khoo, S., Xie, L., and Man, Z. (2009). Robust Finite-Time Consensus Tracking Algorithm for Multirobot Systems. Ieee/asme Trans. Mechatron. 14, 219–228. doi:10.1109/tmech.2009.2014057
Khoo, S., Xie, L., Yu, Z., and Man, Z. (2008). “Finite-time Consensus Algorithm of Multi-Agent Networks,” in 2008 10th International Conference on Control, Automation, Robotics and Vision, October 17-20, 2008, Hanoi, Vietnam (IEEE), 916–920. doi:10.1109/icarcv.2008.4795640
Kuramoto, Y. (1975). “Self-entrainment of a Population of Coupled Non-linear Oscillators,” in International symposium on mathematical problems in theoretical physics (Berlin, Heidelberg: Springer), 420–422.
Levant, A. (1993). Sliding Order and Sliding Accuracy in Sliding Mode Control. Int. J. Control. 58, 1247–1263. doi:10.1080/00207179308923053
Liu, Z., and Guo, L. (2008). Connectivity and Synchronization of Vicsek Model. Sci. China Ser. F-inf. Sci. 51, 848–858. doi:10.1007/s11432-008-0077-2
Liu, Z., and Guo, L. (2009). Synchronization of Multi-Agent Systems without Connectivity Assumptions. Automatica 45, 2744–2753. doi:10.1016/j.automatica.2009.09.015
Ma, C.-Q., and Zhang, J.-F. (2010). Necessary and Sufficient Conditions for Consensusability of Linear Multi-Agent Systems. IEEE Trans. Automat. Contr. 55, 1263–1268. doi:10.1109/tac.2010.2042764
Moreno, J. A., and Osorio, M. (2008). “A Lyapunov Approach to Second-Order Sliding Mode Controllers and Observers,” in 2008 47th IEEE Conference on Decision and Control, December 9-11, 2008, Cancun, Mexico (IEEE), 2856–2861. doi:10.1109/cdc.2008.4739356
Olfati-Saber, R., Fax, J. A., and Murray, R. M. (2007). Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 95, 215–233. doi:10.1109/jproc.2006.887293
Olfati-Saber, R., and Murray, R. M. (2004). Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Automat. Contr. 49, 1520–1533. doi:10.1109/tac.2004.834113
Ren, W., and Beard, R. W. (2005). Consensus Seeking in Multiagent Systems under Dynamically Changing Interaction Topologies. IEEE Trans. Automat. Contr. 50, 655–661. doi:10.1109/tac.2005.846556
Ren, C. E., and Chen, C. L. P. (2015). Sliding Mode Leader‐following Consensus Controllers for Second‐order Non‐linear Multi‐agent Systems. IET Control. Theor. Appl. 9, 1544–1552. doi:10.1049/iet-cta.2014.0523
Ren, W., and Atkins, E. (2007). Distributed Multi-Vehicle Coordinated Controlvia Local Information Exchange. Int. J. Robust Nonlinear Control. 17, 1002–1033. doi:10.1002/rnc.1147
Ren, W. (2007). Distributed Attitude Alignment in Spacecraft Formation Flying. Int. J. Adapt. Control. Signal. Process. 21, 95–113. doi:10.1002/acs.916
Su, H., Chen, G., Wang, X., and Lin, Z. (2011). Adaptive Second-Order Consensus of Networked mobile Agents with Nonlinear Dynamics. Automatica 47, 368–375. doi:10.1016/j.automatica.2010.10.050
Tang, Y., Gao, H., Zou, W., and Kurths, J. (2012). Distributed Synchronization in Networks of Agent Systems with Nonlinearities and Random Switchings. IEEE Trans. Cybern 43, 358–370. doi:10.1109/TSMCB.2012.2207718
Utkin, V., Guldner, J., and Shi, J. (2009). Sliding Mode Control in Electro-Mechanical Systems. Boca Raton, FL: CRC Press.
Utkin, V. I. (1993). Sliding Mode Control Design Principles and Applications to Electric Drives. IEEE Trans. Ind. Electron. 40, 23–36. doi:10.1109/41.184818
Utkin, V. (1978). Methods for Constructing Discontinuity Planes in Multidimensional Variable Structure Systems. Automation and remote Control 39, 1466–1470.
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., and Shochet, O. (1995). Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 75, 1226–1229. doi:10.1103/physrevlett.75.1226
Xu, J., Xie, L., Li, T., and Lum, K. Y. (2013). Consensus of Multi‐agent Systems with General Linear Dynamics via Dynamic Output Feedback Control. IET Control. Theor. Appl. 7, 108–115. doi:10.1049/iet-cta.2012.0221
Xue, X., Wu, F., and Yuan, C. (2021). Robust Consensus for Linear Multi-Agent Systems with Structured Uncertainties. Int. J. Control. 94, 675–686. doi:10.1080/00207179.2019.1612096
Yu, S., and Long, X. (2015). Finite-time Consensus for Second-Order Multi-Agent Systems with Disturbances by Integral Sliding Mode. Automatica 54, 158–165. doi:10.1016/j.automatica.2015.02.001
Yu, W., Chen, G., Cao, M., and Kurths, J. (2009). Second-order Consensus for Multiagent Systems with Directed Topologies and Nonlinear Dynamics. IEEE Trans. Syst. Man. Cybern B Cybern 40, 881–891. doi:10.1109/TSMCB.2009.2031624
Yu, Z., Yu, S., Jiang, H., and Hu, C. (2021). Distributed Consensus for Multi-Agent Systems via Adaptive Sliding Mode Control. Int. J. Robust Nonlinear Control. 31, 7125–7151. doi:10.1002/rnc.5670
Zhang, J., Lyu, M., Shen, T., Liu, L., and Bo, Y. (2017). Sliding Mode Control for a Class of Nonlinear Multi-Agent System with Time Delay and Uncertainties. IEEE Trans. Ind. Electro. 65, 865–875. doi:10.1109/TIE.2017.2701777
Keywords: sliding mode, control, robust consensus, multi-agent systems, uncertain parameters
Citation: ZHAO N and ZHU J-d (2021) Robust Consensus Problem of Heterogeneous Uncertain Second-Order Multi-Agent Systems Based on Sliding Mode Control. Front. Control. Eng. 2:744027. doi: 10.3389/fcteg.2021.744027
Received: 19 July 2021; Accepted: 08 September 2021;
Published: 01 October 2021.
Edited by:
Ya Zhang, Southeast University, ChinaReviewed by:
Liang SUN, University of Science and Technology Beijing, ChinaDan Ma, Northeastern University, China
Copyright © 2021 ZHAO and ZHU. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian-dong ZHU, emh1amlhbmRvbmdAbmpudS5lZHUuY24=
 Ni ZHAO
Ni ZHAO Jian-dong ZHU2*
Jian-dong ZHU2*