- 1Laboratory of Informatics and Systems Engineering for Clinical Research, IRCCS Fondazione Salvatore Maugeri, Pavia, Italy
- 2Department of Electrical, Computer and Biomedical Engineering, University of Pavia, Pavia, Italy
- 3Molecular Cardiology Laboratories, IRCCS Fondazione Salvatore Maugeri, Pavia, Italy
- 4Department of Psychiatry, McLean Hospital, Harvard Medical School, Belmont, MA, USA
Over the last decade, high-throughput genotyping and sequencing technologies have contributed to major advancements in genetics research, as these technologies now facilitate affordable mapping of the entire genome for large sets of individuals. Given this, genome-wide association studies are proving to be powerful tools in identifying genetic variants that have the capacity to modify the probability of developing a disease or trait of interest. However, when the study’s goal is to evaluate the effect of the presence of genetic variants mapping to specific chromosomes regions on a specific phenotype, the candidate loci approach is still preferred. Regardless of which approach is taken, such a large data set calls for the establishment and development of appropriate analytical methods in order to translate such knowledge into biological or clinical findings. Standard univariate tests often fail to identify informative genetic variants, especially when dealing with complex traits, which are more likely to result from a combination of rare and common variants and non-genetic determinants. These limitations can partially be overcome by multivariate methods, which allow for the identification of informative combinations of genetic variants and non-genetic features. Furthermore, such methods can help to generate additive genetic scores and risk stratification algorithms that, once extensively validated in independent cohorts, could serve as useful tools to assist clinicians in decision-making. This review aims to provide readers with an overview of the main multivariate methods for genetic data analysis that could be applied to the analysis of cardiovascular traits.
Introduction
The interaction of several genetic and environmental factors modulates the clinical expression of common cardiovascular diseases (CVDs), such as coronary artery disease (CAD), cerebrovascular disease, peripheral arterial disease, and stroke. Poor diet, physical inactivity, smoking, and harmful use of alcohol have all been established as key risk factors that can affect the clinical expression of many CVDs (1). While predisposition to CVD as indicated by the presence of family history suggests that genetic factors play a role in the expression of the trait, the characteristics of inheritance often do not follow Mendelian patterns. For multifactorial diseases, this atypical pattern of inheritance impairs the elucidation of the genetic underpinnings. Indeed, multiple genetic factors with variable effects and effect size have to be identified to account for such a complex “polygenic” inheritance. On the other hand, the variable expressivity commonly found in monogenic cardiac diseases, even among subjects with the same genetic defect, represents a major limitation for the definition of genotype-based risk stratification algorithms (2).
Over the last decade, genome-wide association studies (GWASs) successfully identified more than 1,100 associations of genetic markers with cardiovascular traits, such as stroke, CAD, peripheral arterial disease, variability of the human electrocardiogram, and monogenic cardiac diseases (3). Although providing strong evidence of statistical association with these traits (p-value <1 × 10−8), single genetic variants identified by GWASs only explain a small proportion of the disease risk or phenotype variability (4–6). As an example, the recently identified CAD-associated variants reviewed in Ref. (4) induce each an average increase in terms of disease risk of ~18% [odds ratio (OR) = 1.18] (5). Further refining in genetic risk prediction and resuming multi-markers information in CVD will require alternative analytical strategies.
In the following sections, this review will address the main multivariate approaches to perform genetic variants selection from GWAS or candidate region studies, how the deriving findings could be modeled to define specific risk profiles and risk stratification algorithms and how to evaluate the prediction accuracy of the defined models.
Identification of Informative Genetic Variants
Identifying informative genetic markers among millions of candidates generated by microarrays or next generation sequencing (NGS) platforms has historically been a process of ranking variants according to their level of statistical association with a specific trait. This is first estimated by one-SNP-at-a-time testing approaches, and then a subset of these associated variants is selected based on a defined significance threshold (7). More recently, methods have emerged that are better suited for large cohorts of individuals deeply characterized by phenotypic measurements. Multivariate machine learning methods can be applied to identify informative subsets of genetic variants and non-genetic factors that jointly contribute to the overall phenotype expression (8). Annotating the identified markers could then be performed by accessing resources providing information on genomic variants previously associated with a trait of interest (3, 9, 10) and functional annotation tools (11–15). Once validated on independent cohorts of individuals, functional studies will allow researchers to translate evidence of statistical association and informative predictive models into biologically relevant findings (16).
Multivariate Methods for Common Genetic Variants Selection
Multivariate approaches of feature selection allow researchers to identify a subset or a combination of informative common genetic variants and non-genetic covariates that underlies the risk of developing a trait (17). These approaches offer a method that can overcome the limitations of the one-variant-at-a-time testing strategy characterizing univariate tests, which are incapable of capturing the multifactorial characteristics of many cardiovascular traits (e.g., additive effects of multiple variants, interactions between genetic and non-genetic factors) (18). In general, these approaches select informative variables not based on the strength of their statistical association with the trait, but rather on the basis of their capability to correctly predict the trait value in independent data.
A distinction has then to be made between multivariate methods for the analysis of binary traits (i.e., when the dependent variable indicates the presence or absence of a specific condition) and methods for quantitative traits analysis (i.e., when the dependent variable is characterized by a continuous distribution).
Binary Traits Analysis
The analysis of binary traits offers several alternatives that draw from both frequentist and Bayesian methods (Table 1). In order to identify informative sets of genetic and non-genetic variables expected to jointly affect a disease phenotype, stepwise logistic regression is one of the most consolidated approaches. The first step of this approach consists in testing simultaneously an initial set of SNPs in a logistic regression model as predictors of disease status which is represented by the binary-dependent variable. Then, different models are subsequently compared with the initial model to estimate whether a different set of predictors improved the fit, which is measured by goodness of fit metrics such as deviance or log-likelihood (19). Identifying the optimal model can be performed by a forward search strategy (the selection starts with the intercept of the regression, and then sequentially adds into the model the predictor that most improves the fit), a backward search strategy (it starts by including all variables, and sequentially deletes the predictor that has the lowest impact on the fit), or a combination of both (19). However, it is important to consider that this approach may prove computationally intensive when large sets of variables need to be analyzed, making the task of feature selection difficult.
The Least Absolute Shrinkage and Selection Operator (LASSO) (22) is a shrinkage method that represents a sound alternative to stepwise regression for the identification of informative genetic variants. The LASSO approach silences non-informative variables by setting their regression coefficient to 0 through a penalty parameter called lambda (λ). The optimal value to be assigned to λ can be learned by a resampling strategy performed on the data: the value guaranteeing the lowest average classification error on the test sets will be applied to the regression model. Vaarhorst and colleagues (34) used LASSO to identify predictors of coronary heart disease (CHD), starting from a set of candidate variants, whereas Hughes and colleagues (35) applied the algorithm to the identification of genetic variants to define a risk score for coronary risk prediction. The elastic net (25) is an extension of the LASSO that is robust to extreme correlations among predictors, which also provides a more efficient, effective system for handling the analysis of unbalanced datasets.
Bayesian methods, such as the binary outcome stochastic search (BOSS) (27) and bags of naive Bayes (BoNB) (28) algorithms, also provide alternative approaches. BOSS is a feature selection approach deriving from the method described in Ref. (36) based on a latent variable model that links the observed outcome to the underlying genetic variants mapping to candidate regions of interest. A Markov Chain Monte Carlo approach is used for model search and to evaluate the posterior probability of each predictor in determining the latent variable profile (27). A latent variable profile is defined as a stochastic vector of same size of the number of SNPs; the vector may assume 0/1 values, thus expressing the fact that a marker is considered (value equal to 1) or not (value equal to 0) as a predictor of the outcome. The model estimates the posterior probability of such latent variable; as a consequence, the most likely latent variable will determine the set of SNPs with the highest risk prediction potential for developing a disease. BoNB (28) is an algorithm for genetic biomarkers selection from the simultaneous analysis of genome-wide SNP data based on the naive Bayes (NB) (37) classification framework. The predictive value (marginal utility) of each genetic variant is assessed by a resampling strategy. By randomly shuffling the genotypes of an informative variant, an overall decrease in terms of classification accuracy will be observed, and if an uninformative variant is permuted, no substantial loss will be observed. This strategy, coupled with appropriate statistical tests, allows BoNB to identify informative sets of SNPs. These methods have been tested on real datasets on type 1 (28, 38) and type 2 diabetes (27), respectively.
Classification and regression trees (RTs) methods (29) fall under the category of decision tree learning. In these tree structures, leaves represent the predicted phenotypic outcome, whereas nodes and branches represent the set of genetic variants and clinical covariates that predict the phenotypic outcome. These methods recursively partition data into subsets according to the variables’ values: each partition corresponds with a “split” based on the set of variables being considered, defining a tree-like structure (19). Classification trees (CTs) are designed to analyze categorical traits and facilitate the identification of informative interactions between variables and stratifications in the data starting from a limited numbers of predictors.
Random forests (RFs) (30) are based on CTs, as they aggregate a large collection of de-correlated trees, and then average them (19). RFs generate a multivariate ranking of the analyzed variables according to their predictive importance with respect to the outcome. Even more, they can be easily applied to analyze unbalanced datasets, and they are able to account for correlation and informative interactions among features. Such characteristics make this approach particularly appealing for high-dimensional genomic data analysis (39). RFs have been applied to identify genetic variants influencing coronary artery calcification in hypertensive subjects (40), bicuspid aortic valve condition (41), and high-density lipoprotein (HDL) cholesterol level (42). Maenner and colleagues (43) applied RFs to identify SNPs involved in gene-by-smoking interactions related to the early-onset of CHD using the Framingham Heart Study data.
ABACUS is an Algorithm based on a BivAriate CUmulative Statistic, which allows identifying combinations of common and rare genetic variants associated with a disease by focusing on predefined SNPs-sets (e.g., belonging to specific pathways) (32). ABACUS calculates a statistic for each pair of SNPs within each SNPs set and generates an aggregated score measuring the cumulative evidence of association of the SNPs annotated in the SNP set. This method has been tested on GWAS on type 1 and type 2 diabetes (32).
Specific implementations of LASSO, elastic net, CTs, RFs, and stepwise Cox proportional hazard regression (44) have been also proposed for the identification of SNPs associated with time to event outcomes (Table 1).
Quantitative Traits Analysis
Many of the feature selection methods for binary traits derive from algorithms originally established for quantitative traits analyses (Table 1). Linear regression (45) coupled with stepwise feature selection is probably one of the most commonly applied approaches when dealing with the task of identifying informative predictors with respect to continuous traits starting from a limited set of variables.
The LASSO and the elastic net shrinkage algorithms for regression problems work similarly for classification. Warren and colleagues (46) used LASSO and HyperLASSO (24) to predict low-density lipoprotein (LDL) and HDL cholesterol, two lipid traits of clinical relevance. Bottolo and colleagues (33) published the results from the validation and implementation of a method called Graphical Unit Evolutionary Stochastic Search (GUESS), a Bayesian variable selection approach able to analyze single and multiple responses, searching for the best combinations of SNPs to predict the traits. The authors applied the method to study genetic regulation of lipid metabolism in the Gutenberg Health Study (GHS), confirming the association of previously identified loci for blood lipid phenotypes.
Though largely similar to CTs, RTs differ from CTs in that the dependent variable is continuous, and a regression model is fitted to each node to perform the task of prediction. Additionally, RFs for regression problems are also widely employed and implemented in specific analytical packages.
Multivariate Models for Decision Support
Demographic, clinical, and genetic risk factors identified by the previously described methods or selected based on prior knowledge can be combined in order to define specific predictive models, which could assist clinicians during the decision make steps of the clinical practice (47–49). Such models can be defined by making use of the above mentioned methods. For example, multilocus genetic risk profiles can be defined by weighting genetic variants by the corresponding regression coefficients (50, 51). Similarly, tree-based approaches or regression methods can be applied to define risk stratification algorithms combining genetic and non-genetic information (49, 51).
Multilocus Genetic Risk Profiles
The theory of multifactorial, polygenic liability relies on the combined effect of multiple common genetic variants, each explaining a small amount of phenotypic variance and possibly interacting with environmental factors, all contributing to the overall risk (52, 53). Polygenic risk score (PRS) approaches were introduced to examine the load of genetic risk associated with a given disease by simultaneously testing a broad set of common variants (54). Essentially, the PRS approach capitalizes on the identification of genetic risk variants derived from large, mega-, or meta-analyses for specific disorders and generates an index of genetic vulnerability associated with the disease (54). Affected subjects present higher values of the PRS than not affected subjects. The advantage of polygenic modeling is that the genetic vulnerability is represented by a larger set of gene-mapping variants contributing to the risk of the disease, rather than a single genetic variant. There are several different ways to implement polygenic modeling approaches (55). All methods rely on selecting variants on a training set using univariate or multivariate approaches or focusing on candidate loci identified by previous studies. The risk alleles of the identified sets of genetic variants are then used to generate a PRS either by summing the number of risk alleles (“un-weighted” approach) or by weighting the number of risk alleles by the effect size of the association deriving from regression models (“weighted” approach) (50). Either way, the PRS is tested for association in a replication sample via traditional regression-based statistics and standard metrics are used to estimate its predictive power (56).
Polygenic risk score usually explain 1–5% of the variation in complex traits, which is already an improvement compared with GWAS single genetic variants, which typically yield relatively small increment of risk with ORs <1.5-fold, with the exception of traits such as height, for which a GWAS identified a SNP explaining almost 5% of the phenotypic variance (53, 57). PRS have been applied to several CVD studies and are found to be a significant predictor of CAD (58, 59), incident cardiovascular (60), CHD (61), atrial fibrillation, and stroke (62). Furthermore, Pfeufer and colleagues (63) assessed the cumulative effect of SNPs modulating the QT interval in the general population. For a more comprehensive review of PRS findings in CVD, we encourage readers to consider the report by Abraham and Inouye (51).
Risk Stratification Algorithms
Risk stratification algorithms are designed to be intuitive tools that can assist clinicians in identifying patients at high risk of adverse events, thus informing decision-making by following a defined set of logical steps (64–66). These algorithms can be derived by the integration of genetic information (e.g., single SNPs, mutations on causative loci, PRSs) with known clinical and behavioral risk factors by appropriate multivariate methods. When defined by regression methods, they can be interrogated by nomograms, graphical tools that allow interpreting the risk of developing a certain trait based on an individual’s characteristics (67).
Priori et al. (47) proposed a risk stratification algorithm to identify long QT syndrome (LQTS) patients at high risk of adverse cardiac events (defined as occurrence of syncope, cardiac arrest, or sudden death before the age of 40 years and in absence of therapies). LQTS is a genetic disorder caused by mutations that affect ion-channel encoding genes or other genes that indirectly modulate the function of ion channels. The algorithm was based on the combination of information about the presence of genetic variants on one of the three main LQTS genes (KCNQ1, KCNH2, and SCN5A defining LQT1, LQT2, and LQT3), gender, and QT interval duration (≥500 or <500 ms), which are known independent risk predictors in LQTS. Three risk groups were identified based on the observed probability of an adverse cardiac event: low risk (probability <30%), intermediate risk (30–49%), and high risk (≥50%). Based on the published risk stratification algorithms for LQT1, LQT2, and LQT3 patients (47, 68), Tomás and colleagues (48) investigated whether common variants on NOS1AP locus can add additional insights for risk stratification in this group of patients. The authors demonstrated that the presence of the NOS1AP rs10494366 variant improved event risk stratification for previously identified LQT1, LQT2, and LQT3 patients. The presence of the GG or GT genotype of NOS1AP rs10494366 increased the risk of cardiac events compared with homozygotes for the T allele in all the subgroups of LQTS patients defined by different combinations of gender and genetic locus (Figure 1).
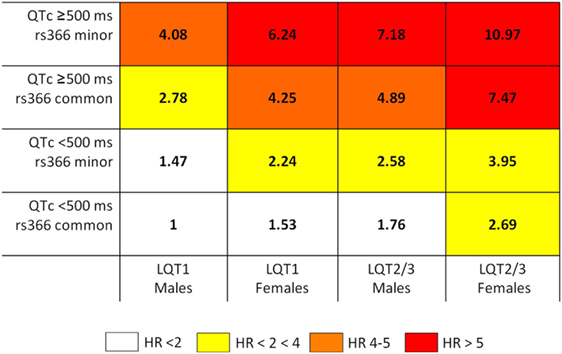
Figure 1. rs10494366 common variant on NOS1AP modulates risk of events in LQTS (48). The schema reports the combined hazard ratios (HRs) from Cox regression by risk categories. The risk stratification schema includes the common variant rs10494366 on NOS1AP gene and known risk predictors in LQTS, represented by: QTc ≥ 500 ms, gender, and LQTS subgroup. Each box shows the combined HR for patients sharing clinical and genetic characteristics. The reference category (HR = 1) is represented by individuals LQT1, males, QT < 500 ms and homozygote for the common allele of NOS1AP rs10494366. Reprinted from the manuscript by Tomás and colleagues (48) with permission from Elsevier.
Talmud et al. (69) evaluated whether the inclusion of information regarding the genotype of rs10757274 on 9p21.3 locus to the risk factors defining the Framingham risk score (FRS) allowed increasing the accuracy in identifying patients at risk of CHD in a prospective study. Results showed that, although rs10757274 did not add substantially to the usefulness of the FRS for predicting future events, it did improve reclassification of CHD risk, and thus may have clinical utility.
Ripatti et al. (58) tested 13 SNPs – associated with myocardial infarction or CAD by previous GWASs – in a case–control design including 3,829 CHD cases and 48,897 control participants and a prospective cohort design including 30,725 individuals free of CVD. In prospective cohort analyses, the weighted PRS defined using the set of selected SNPs was significantly associated with a first CHD event. Furthermore, when compared with the bottom quintile of the PRS distribution, individuals in the top quintile shared a 1.66-fold increased covariates-adjusted risk of CHD. When focusing on its risk prediction capability, the PRS did not improve the C index over clinical risk factors but increased slightly the integrated discrimination index (p-value <0.001). Similar results were obtained from the case–control analyses.
Model Assessment Strategies
Once multivariate sets of SNPs, PRSs or risk stratification algorithms are defined on an initial cohort (training set), their accuracy in predicting the condition of new examples must be assessed on independent populations (test set). In the absence of independent cohorts, it is possible to rely on resampling strategies like K-Fold Cross Validation (K-Fold CV) (19), holdout (70), and bootstrap (71). Several metrics are available to evaluate and compare the discriminative power of predictive models on the test set, based on the trait’s distribution (72, 73).
Conclusion
The goal of this review is to provide readers with an overview about the main multivariate methods that can be applied to the identification of informative genetic variants and to the definition of risk prediction tools in the context of CVDs. It is important to note that some methods described have been applied to intermediate phenotypes that could be considered precursors to their manifestation as cardiovascular traits, but these methods have not yet been applied to the analysis of cardiovascular traits. Their application to large CVD cohorts could lead to interesting findings.
Multivariate methods allow the identification of complex additive effects due to the presence of multiple genetic variants on specific loci or complex interactions among genetic and non-genetic risk factors able to modulate the probability of developing a specific disease or its severity.
Still, the task of identifying informative combinations of genetic variants by multivariate search strategies can be extremely computationally intensive due to the high number of models to be explored and, in many cases, to the impossibility of parallelizing the analyses. Missing values represent a common limitation to these approaches, although it could be partially solved by resorting to multivariate imputation methods. Furthermore, large sets of samples thoroughly characterized in terms of phenotype characteristics are needed in order to avoid overfitting issues and to increase the probability of defining models whose predictive performances can be confirmed in independent cohorts.
Author Contributions
AM and GG conceived the study and drafted the manuscript. RB and CN conceived the study and revised the manuscript critically for important intellectual content. All authors approved the final version of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank Ms. Cara E. Bigony (McLean Hospital) for editorial support. This work was supported by the grant RF-2011-02348444 from the Italian Ministry of Health.
References
2. Priori SG. Inherited arrhythmogenic diseases: the complexity beyond monogenic disorders. Circ Res (2004) 94:140–5. doi:10.1161/01.RES.0000115750.12807.7E
3. Burdett T, Hall PN, Hasting E, Hindorff LA, Junkins HA, Klemm AK, et al. The NHGRI-EBI Catalog of Published Genome-Wide Association Studies [Online]. (2016). Available from: www.ebi.ac.uk/gwas
4. Roberts R. Genetics of coronary artery disease. Circ Res (2014) 114:1890–903. doi:10.1161/CIRCRESAHA.114.302692
5. Bjorkegren JL, Kovacic JC, Dudley JT, Schadt EE. Genome-wide significant loci: how important are they? Systems genetics to understand heritability of coronary artery disease and other common complex disorders. J Am Coll Cardiol (2015) 65:830–45. doi:10.1016/j.jacc.2014.12.033
6. Nikpay M, Goel A, Won HH, Hall LM, Willenborg C, Kanoni S, et al. A comprehensive 1,000 genomes-based genome-wide association meta-analysis of coronary artery disease. Nat Genet (2015) 47:1121–30. doi:10.1038/ng.3396
7. Panagiotou OA, Ioannidis JP; Genome-Wide Significance Project. What should the genome-wide significance threshold be? Empirical replication of borderline genetic associations. Int J Epidemiol (2012) 41:273–86. doi:10.1093/ije/dyr178
8. Okser S, Pahikkala T, Airola A, Salakoski T, Ripatti S, Aittokallio T. Regularized machine learning in the genetic prediction of complex traits. PLoS Genet (2014) 10:e1004754. doi:10.1371/journal.pgen.1004754
9. Stenson PD, Mort M, Ball EV, Howells K, Phillips AD, Thomas NS, et al. The human gene mutation database: 2008 update. Genome Med (2009) 1:13. doi:10.1186/gm13
10. Landrum MJ, Lee JM, Riley GR, Jang W, Rubinstein WS, Church DM, et al. ClinVar: public archive of relationships among sequence variation and human phenotype. Nucleic Acids Res (2014) 42:D980–5. doi:10.1093/nar/gkt1113
11. Kumar P, Henikoff S, Ng PC. Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nat Protoc (2009) 4:1073–81. doi:10.1038/nprot.2009.86
12. Adzhubei IA, Schmidt S, Peshkin L, Ramensky VE, Gerasimova A, Bork P, et al. A method and server for predicting damaging missense mutations. Nat Methods (2010) 7:248–9. doi:10.1038/nmeth0410-248
13. Reva B, Antipin Y, Sander C. Predicting the functional impact of protein mutations: application to cancer genomics. Nucleic Acids Res (2011) 39:e118. doi:10.1093/nar/gkr407
14. Choi Y, Sims GE, Murphy S, Miller JR, Chan AP. Predicting the functional effect of amino acid substitutions and indels. PLoS One (2012) 7:e46688. doi:10.1371/journal.pone.0046688
15. Limongelli I, Marini S, Bellazzi R. PaPI: pseudo amino acid composition to score human protein-coding variants. BMC Bioinformatics (2015) 16:123. doi:10.1186/s12859-015-0554-8
16. Edwards SL, Beesley J, French JD, Dunning AM. Beyond GWASs: illuminating the dark road from association to function. Am J Hum Genet (2013) 93:779–97. doi:10.1016/j.ajhg.2013.10.012
17. Ritchie MD, Holzinger ER, Li R, Pendergrass SA, Kim D. Methods of integrating data to uncover genotype-phenotype interactions. Nat Rev Genet (2015) 16:85–97. doi:10.1038/nrg3868
18. Saeys Y, Inza I, Larranaga P. A review of feature selection techniques in bioinformatics. Bioinformatics (2007) 23:2507–17. doi:10.1093/bioinformatics/btm344
19. Hastie T, Tibshirani R, Friedman R. The Elements of Statistical Learning. Data Mining, Inference and Prediction. New York: Springer (2009).
20. Demsar J, Curk T, Erjavec A, Gorup C, Hocevar T, Milutinovic M, et al. Orange: data mining toolbox in Python. J Mach Learn Res (2013) 14:2349–53.
21. Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software: an update. SIGKDD Explor (2009) 11:10–8. doi:10.1145/1656274.1656278
22. Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc Series B Stat Methodol (1996) 58:267–8.
23. Chang CC, Chow CC, Tellier LC, Vattikuti S, Purcell SM, Lee JJ. Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience (2015) 4:7. doi:10.1186/s13742-015-0047-8
24. Hoggart CJ, Whittaker JC, De Iorio M, Balding DJ. Simultaneous analysis of all SNPs in genome-wide and re-sequencing association studies. PLoS Genet (2008) 4:e1000130. doi:10.1371/journal.pgen.1000130
25. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Series B Stat Methodol (2005) 67:301–20. doi:10.1111/j.1467-9868.2005.00503.x
26. Jain RK. Ridge regression and its application to medical data. Comput Biomed Res (1985) 18:363–8. doi:10.1016/0010-4809(85)90014-X
27. Russu A, Malovini A, Puca AA, Bellazzi R. Stochastic model search with binary outcomes for genome-wide association studies. J Am Med Inform Assoc (2012) 19:e13–20. doi:10.1136/amiajnl-2011-000741
28. Sambo F, Trifoglio E, Di Camillo B, Toffolo GM, Cobelli C. Bag of naive Bayes: biomarker selection and classification from genome-wide SNP data. BMC Bioinformatics (2012) 13(Suppl 14):S2. doi:10.1186/1471-2105-13-S14-S2
29. Breiman L, Friedman J, Olshen R, Stone C. Classification and Regression Trees. Belmont, CA: Wadsworth Publishing Company (1984).
31. Yang W, Charles Gu C. Random forest fishing: a novel approach to identifying organic group of risk factors in genome-wide association studies. Eur J Hum Genet (2014) 22:254–9. doi:10.1038/ejhg.2013.109
32. Di Camillo B, Sambo F, Toffolo G, Cobelli C. ABACUS: an entropy-based cumulative bivariate statistic robust to rare variants and different direction of genotype effect. Bioinformatics (2014) 30:384–91. doi:10.1093/bioinformatics/btt697
33. Bottolo L, Chadeau-Hyam M, Hastie DI, Zeller T, Liquet B, Newcombe P, et al. GUESS-ing polygenic associations with multiple phenotypes using a GPU-based evolutionary stochastic search algorithm. PLoS Genet (2013) 9:e1003657. doi:10.1371/journal.pgen.1003657
34. Vaarhorst AA, Lu Y, Heijmans BT, Dolle ME, Bohringer S, Putter H, et al. Literature-based genetic risk scores for coronary heart disease: the cardiovascular registry Maastricht (CAREMA) prospective cohort study. Circ Cardiovasc Genet (2012) 5:202–9. doi:10.1161/CIRCGENETICS.111.960708
35. Hughes MF, Saarela O, Stritzke J, Kee F, Silander K, Klopp N, et al. Genetic markers enhance coronary risk prediction in men: the MORGAM prospective cohorts. PLoS One (2012) 7:e40922. doi:10.1371/journal.pone.0040922
36. Bottolo L, Richardson S. Evolutionary stochastic search for Bayesian model exploration. Bayesian Anal (2010) 5:35. doi:10.1214/10-BA523
37. Russell S, Norvig P. Artificial Intelligence: A Modern Approach. 2nd ed. Upper Saddle River, NJ: Prentice Hall (2003).
38. Sambo F, Malovini A, Sandholm N, Stavarachi M, Forsblom C, Makinen VP, et al. Novel genetic susceptibility loci for diabetic end-stage renal disease identified through robust naive Bayes classification. Diabetologia (2014) 57:1611–22. doi:10.1007/s00125-014-3256-2
39. Chen X, Ishwaran H. Random forests for genomic data analysis. Genomics (2012) 99:323–9. doi:10.1016/j.ygeno.2012.04.003
40. Sun YV, Bielak LF, Peyser PA, Turner ST, Sheedy PF II, Boerwinkle E, et al. Application of machine learning algorithms to predict coronary artery calcification with a sibship-based design. Genet Epidemiol (2008) 32:350–60. doi:10.1002/gepi.20309
41. Wooten EC, Iyer LK, Montefusco MC, Hedgepeth AK, Payne DD, Kapur NK, et al. Application of gene network analysis techniques identifies AXIN1/PDIA2 and endoglin haplotypes associated with bicuspid aortic valve. PLoS One (2010) 5:e8830. doi:10.1371/journal.pone.0008830
42. Heidema AG, Feskens EJ, Doevendans PA, Ruven HJ, van Houwelingen HC, Mariman EC, et al. Analysis of multiple SNPs in genetic association studies: comparison of three multi-locus methods to prioritize and select SNPs. Genet Epidemiol (2007) 31:910–21. doi:10.1002/gepi.20251
43. Maenner MJ, Denlinger LC, Langton A, Meyers KJ, Engelman CD, Skinner HG. Detecting gene-by-smoking interactions in a genome-wide association study of early-onset coronary heart disease using random forests. BMC Proc (2009) 3(Suppl 7):S88. doi:10.1186/1753-6561-3-s7-s88
44. Cox DR. Regression models and life-tables. J R Stat Soc Series B Stat Methodol (1972) 34:187–220.
45. Hocking RR. The analysis and selection of variables in linear regression. Biometrics (1976) 32:1–49. doi:10.2307/2529336
46. Warren H, Casas JP, Hingorani A, Dudbridge F, Whittaker J. Genetic prediction of quantitative lipid traits: comparing shrinkage models to gene scores. Genet Epidemiol (2014) 38:72–83. doi:10.1002/gepi.21777
47. Priori SG, Schwartz PJ, Napolitano C, Bloise R, Ronchetti E, Grillo M, et al. Risk stratification in the long-QT syndrome. N Engl J Med (2003) 348:1866–74. doi:10.1056/NEJMoa022147
48. Tomás M, Napolitano C, De Giuli L, Bloise R, Subirana I, Malovini A, et al. Polymorphisms in the NOS1AP gene modulate QT interval duration and risk of arrhythmias in the long QT syndrome. J Am Coll Cardiol (2010) 55:2745–52. doi:10.1016/j.jacc.2009.12.065
49. Wasan PS, Uttamchandani M, Moochhala S, Yap VB, Yap PH. Application of statistics and machine learning for risk stratification of heritable cardiac arrhythmias. Expert Syst Appl (2013) 40(7):2476–86. doi:10.1016/j.eswa.2012.10.054
50. Sebastiani P, Solovieff N, Sun JX. Naive Bayesian classifier and genetic risk score for genetic risk prediction of a categorical trait: not so different after all! Front Genet (2012) 3:26. doi:10.3389/fgene.2012.00026
51. Abraham G, Inouye M. Genomic risk prediction of complex human disease and its clinical application. Curr Opin Genet Dev (2015) 33:10–6. doi:10.1016/j.gde.2015.06.005
52. Zondervan KT, Cardon LR. The complex interplay among factors that influence allelic association. Nat Rev Genet (2004) 5:89–100. doi:10.1038/nrg1270
53. Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, et al. Finding the missing heritability of complex diseases. Nature (2009) 461:747–53. doi:10.1038/nature08494
54. International Schizophrenia Consortium, Purcell SM, Wray NR, Stone JL, Visscher PM, O’Donovan MC, et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature (2009) 460:748–52. doi:10.1038/nature08185
55. Simonson MA, Wills AG, Keller MC, McQueen MB. Recent methods for polygenic analysis of genome-wide data implicate an important effect of common variants on cardiovascular disease risk. BMC Med Genet (2011) 12:146. doi:10.1186/1471-2350-12-146
56. Dudbridge F. Power and predictive accuracy of polygenic risk scores. PLoS Genet (2013) 9:e1003348. doi:10.1371/journal.pgen.1003348
57. Visscher PM. Sizing up human height variation. Nat Genet (2008) 40:489–90. doi:10.1038/ng0508-489
58. Ripatti S, Tikkanen E, Orho-Melander M, Havulinna AS, Silander K, Sharma A, et al. A multilocus genetic risk score for coronary heart disease: case-control and prospective cohort analyses. Lancet (2010) 376:1393–400. doi:10.1016/S0140-6736(10)61267-6
59. Tikkanen E, Havulinna AS, Palotie A, Salomaa V, Ripatti S. Genetic risk prediction and a 2-stage risk screening strategy for coronary heart disease. Arterioscler Thromb Vasc Biol (2013) 33:2261–6. doi:10.1161/ATVBAHA.112.301120
60. Havulinna AS, Kettunen J, Ukkola O, Osmond C, Eriksson JG, Kesaniemi YA, et al. A blood pressure genetic risk score is a significant predictor of incident cardiovascular events in 32,669 individuals. Hypertension (2013) 61:987–94. doi:10.1161/HYPERTENSIONAHA.111.00649
61. Ganna A, Magnusson PK, Pedersen NL, de Faire U, Reilly M, Arnlov J, et al. Multilocus genetic risk scores for coronary heart disease prediction. Arterioscler Thromb Vasc Biol (2013) 33:2267–72. doi:10.1161/ATVBAHA.113.301218
62. Tada H, Shiffman D, Smith JG, Sjogren M, Lubitz SA, Ellinor PT, et al. Twelve-single nucleotide polymorphism genetic risk score identifies individuals at increased risk for future atrial fibrillation and stroke. Stroke (2014) 45:2856–62. doi:10.1161/STROKEAHA.114.006072
63. Pfeufer A, Sanna S, Arking DE, Muller M, Gateva V, Fuchsberger C, et al. Common variants at ten loci modulate the QT interval duration in the QTSCD Study. Nat Genet (2009) 41:407–14. doi:10.1038/ng.362
64. Cousins MS, Shickle LM, Bander JA. An introduction to predictive modeling for disease management risk stratification. Dis Manage (2002) 5:157–67. doi:10.1089/109350702760301448
65. Thanassoulis G, Vasan RS. Genetic cardiovascular risk prediction: will we get there? Circulation (2010) 122:2323–34. doi:10.1161/CIRCULATIONAHA.109.909309
66. Hosein FS, Bobrovitz N, Berthelot S, Zygun D, Ghali WA, Stelfox HT. A systematic review of tools for predicting severe adverse events following patient discharge from intensive care units. Crit Care (2013) 17:R102. doi:10.1186/cc12747
67. Shaw LJ, Min JK, Hachamovitch R, Hendel RC, Borges-Neto S, Berman DS. Nomograms for estimating coronary artery disease prognosis with gated stress myocardial perfusion SPECT. J Nucl Cardiol (2012) 19:43–52. doi:10.1007/s12350-011-9468-7
68. European Heart Rhythm Association, Heart Rhythm Society, Zipes DP, Camm AJ, Borggrefe M, Buxton AE, et al. ACC/AHA/ESC 2006 guidelines for management of patients with ventricular arrhythmias and the prevention of sudden cardiac death: a report of the American College of Cardiology/American Heart Association Task Force and the European Society of Cardiology Committee for Practice Guidelines (writing committee to develop guidelines for management of patients with ventricular arrhythmias and the prevention of sudden cardiac death). J Am Coll Cardiol (2006) 48:e247–346. doi:10.1016/j.jacc.2006.07.010
69. Talmud PJ, Cooper JA, Palmen J, Lovering R, Drenos F, Hingorani AD, et al. Chromosome 9p21.3 coronary heart disease locus genotype and prospective risk of CHD in healthy middle-aged men. Clin Chem (2008) 54:467–74. doi:10.1373/clinchem.2007.095489
70. Schorfheide F, Wolpin KI. On the use of holdout samples for model selection. Am Econ Rev (2012) 102:477–81. doi:10.1257/aer.102.3.477
71. Efron B, Tibshirani RJ. An Introduction to the Bootstrap. New York & London: Taylor & Francis (1994).
72. Hyndman RJ, Koehler AB. Another look at measures of forecast accuracy. Int J Forecast (2006) 22:679–88. doi:10.1016/j.ijforecast.2006.03.001
Keywords: SNPs, multivariate methods, risk scores, risk stratification, cardiovascular diseases
Citation: Malovini A, Bellazzi R, Napolitano C and Guffanti G (2016) Multivariate Methods for Genetic Variants Selection and Risk Prediction in Cardiovascular Diseases. Front. Cardiovasc. Med. 3:17. doi: 10.3389/fcvm.2016.00017
Received: 12 March 2016; Accepted: 23 May 2016;
Published: 08 June 2016
Edited by:
Alexandre Francois Roy Stewart, University of Ottawa Heart Institute, CanadaReviewed by:
Yuqi Zhao, University of California Los Angeles, USANaif A. M. Almontashiri, Taibah University, Saudi Arabia
Copyright: © 2016 Malovini, Bellazzi, Napolitano and Guffanti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alberto Malovini, YWxiZXJ0by5tYWxvdmluaUBmc20uaXQ=
 Alberto Malovini
Alberto Malovini Riccardo Bellazzi
Riccardo Bellazzi Carlo Napolitano3
Carlo Napolitano3 Guia Guffanti
Guia Guffanti