Wiring the Past: A Network Science Perspective on the Challenge of Archeological Similarity Networks

1. Introduction

Starting from the 1960s, among the majority of active scientists it was becoming clear that “the ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe. [… Such a] hypothesis, breaks down when confronted with the twin difficulties of scale and complexity” (Anderson, 1972). The behavior of systems made up by many interacting elements—i.e., complex systems—is not to be understood in terms of a simple extrapolation of the properties of a few components. It is not possible to explain an organizational level only in terms of the lower ones. At each scale, entirely new properties appear, and the understanding of the emerging phenomena requires research which is as fundamental in its nature as any other. Therefore, it seems clear that, more than details about the nature of the components, what we need is a map of the interactions. Complex systems are in general suitably described through their networks of contacts, that is, in terms of nodes (representing the system’s components) and links (standing for their interactions), which allows to catch their essential features in a simple and general representation.

Coral reefs, brains, the airports, the World Wide Web, actors, and actresses that have been in a movie together have very little in common except for the fact that they all can be regarded as systems composed by a large number of interconnected elements. Nonetheless, there is a lot we can learn about each one of these things by mapping them onto a network and neglecting about the individual properties of their parts (Buchanan, 2003; Watts, 2004). Nowadays, it is indeed a common knowledge that scholars from different disciplines, regardless of the specificities of their research domains, can find in this approach a valuable ally when tackling complexity.

However, there are many difficulties that may arise. The mapping process itself is not a trivial step. Data do not come in network form by themselves. In principle, depending on what the question is, researchers would choose the most appropriate network representation. Anyhow, if those carrying out the study are network scientists (experts in the technique), they may not know enough about the details of the information embedded (or discarded) in the data. On the other hand, if they are the experts who collected the data, but do not know much about the technicalities of network science, their choice may be influenced by the need to “keep it simple.”

In this article, we deal with those issues inherent to the particular challenge that is building a network from archeological data, notoriously incomplete and fragmentary. In the first section, we expose a brief discussion on the peculiar situation of history and archeology among the fields to which network science has been applied. We argue that, generally speaking, human past studies are quite disconnected from the rest of interdisciplinary applications and that this prevents them from fully exploiting the potential of network science methods. Then, after an overall description of the issues at hand (Section 3), we review the literature about the most common type of archeological networks, i.e., networks of archeological contexts where the corresponding assemblages are used to infer past interactions (Section 4). More specifically, we address technical difficulties faced when constructing networks of archeological sites where links are established based on some kind of similarity that takes into account the material evidences found in those sites, hereafter Archeological Similarity Networks or ASN. We propose a basic characterization in formal terms of ASN as a well-defined class of networks with its own specific features. Our goal is to give some hints about how the interesting questions that archeological applications put on the table of networks scientists could be formalized in order to be properly addressed within the framework of interdisciplinary collaborations. At this aim, a computational experiment is devised as an illustrative example of how simple models can help the cause (Section 5).

Throughout the article, we devote special attention to the problem of quantifying the similarity between sites, especially in relation with the ubiquitous issues of data incompleteness and the reliability of the inferred interactions.

2. At the Periphery of Network Science

Ideally, network science advances through the combination of two complementary research approaches. The first one corresponds to when network scientists, looking at networks as abstract mathematical objects, identify a general question or problem and develop a method for addressing it. The second one is what researchers from any other field do when, trying to extract information from some data, find that the limitations of other existing methodologies prevent them from reaching their goal and come to the conclusion that adopting a network science approach may be the solution. At the same time, they generate new network-data, that is, refined information encoded in the form of nodes and links suitable to inspire the design of a new network tool or to be used as benchmark (Figure 1). In the first case, a “universal toolbox” (or theory) grows by abstracting from individual case studies. In the second one, the understanding of a particular case study (application) advances by applying the appropriate universal tool, while the theory building process is indirectly fed (new data).

FIGURE 1

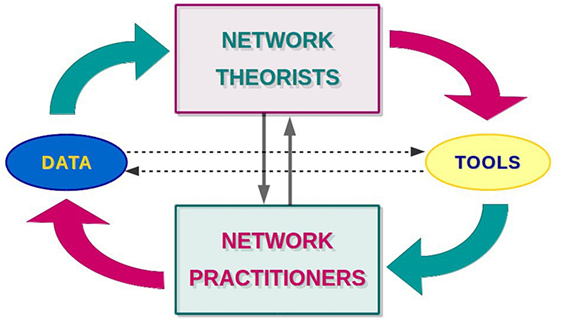
Figure 1. Network science. Ideally, network theorists devise analytical tools that network practitioners apply to their data, while network practitioners generate new data that theorists use for testing and inspiring new techniques. However, in the real world, things are more complicated. Not all the data enter in this cycle, data and tools undergo ad hoc filtering and adaptations, and theorists and practitioners are not always perfectly distinguishable roles.

Although this perfectly balanced way to progress may look meaningful and elegant, it is nothing more than a very rough simplification of how things actually work. There exist many factors that complicate the real scenario, affecting the different application fields in a very uneven way and, we would argue, pushing disciplines such as history or archeology to the periphery of applied network science.

The first factor is a semantic issue. It is not a trivial task to translate into the specific language of each discipline questions that are expressed in terms as general and abstract as those normally used in network science. Unfortunately, the complexity of the task increases somehow proportionally to the distance between the discrete, often binary, quantitative language of network science and the language in which raw information is expressed. Data from humanities are usually the hardest to translate into mathematical terms, and history and archeology are no exception.

Additionally, almost all the analytical techniques have been developed starting from available network data—that is, publicly accessible digital data—whose features have shaped the questions that network scientists considered worthy to be addressed. Therefore, if data of a new case study or research field are too different in nature from those studied till that moment, the appropriated technique may not have been invented yet.

Indeed, despite their generality, not all network representations are the same. In some case it is crucial to retain additional information beyond the list of existing connections. For instance, nodes may be entities located in a geographical space (spatial networks (Barthélemy, 2011)) and the relations under study may be spatial in nature. Then it is usually of fundamental importance to take into account the node coordinates in order to compute pair distances to be associated to the connection as costs. In some other cases, nodes represent objects that belong to different classes (e.g., affiliation networks (Borgatti and Halgin, 2011) of people taking part in social events or scholars coauthoring academic papers) and can only connect with elements of the other class (bipartite networks (Holme et al., 2003)). In these and many other analogous situations, data specificities cannot be disregarded and the definitions of network metrics need to be properly modified. Otherwise, tools developed to deal with data that do not have the same properties may lead to erroneous results.

The first time a new class of data is introduced, it is typically up to the researchers working on the case study to adapt the existing techniques to the novel features of their data. They may publish both their dataset and the adapted analytical tools, so that people with the same problem are able to apply the new method, perhaps improving it, while publishing new data of the same class. In this way, techniques evolve. Different scholars contribute to perfect them, testing each new version on a growing number of benchmark datasets, finally standardizing the variant—or variants—that the community recognizes as the most useful.¹

However, quite often networks practitioners prefer to design a way to preprocess their data in order to make existing analytic tools suitable to be applied, occasionally losing part of the relevant information. In this case, usually little to no attention is devoted to reporting the methodological details and complete raw data are rarely published. As a consequence, any new case study with similar data issues is like the first one and needs to be treated from scratch. Researchers facing similar difficulties benefit from the efforts of others only in terms of suggestions and inspirations, but no real technical innovation is triggered and most of network science potential gets wasted. This happens almost systematically in the case of data from archeological excavations. Indeed, among the networks used as benchmarks for testing new techniques, there are networks constructed from data as diverse as airports and flights, web pages connected by hyperlinks, physical contacts between proteins or data about social grooming behavior among primates and many more (Lancichinetti et al., 2008). None of them have been published in history or archeology journals, not even the one whose nodes are Florentine families of the fifteenth century (Padgett and Ansell, 1993) which was built by political scientists meddling with history. Although an in depth analysis of the reasons behind this tendency is beyond the scope of the present work, there are at least four elements that are worth mentioning:

• It can be partially blamed on the relative novelty of the application of formal network methods to the field. Even though it is beyond argument that the number of articles on network applications appeared on archeology journals has been increasing continuously during the last decade (Collar et al., 2015), the fact that a large majority of these were published quite recently, when the big hunt for benchmarks was almost over, may have had a negative impact on the diffusion of these network datasets.

• Moreover, it is not a common practice among researchers in humanities to publish datasets along with the results, in their articles or in repositories, and therefore such networks have very few chances to circulate.

• On the other hand, recent years have witnessed a substantial new movement in network research, with the focus shifting away from the analysis of the properties of individual nodes or edges within small systems to consideration of the statistical and dynamical properties of networks (Strogatz, 2001; Albert and Barabasi, 2002; Newman, 2003; Boccaletti et al., 2006; Costa et al., 2007). Such a change of interest pushed away the most common archeological research questions from the main trends in network science.

• Finally, the fourth element—probably the most important one—is the peculiar nature of archeological networks and their construction. As extensively discussed in Lemercier (2010), the resistance offered by raw historical or archeological data is so difficult to overcome that it is almost impossible for network scientists to build networks by their own. To build a network from raw archeological record is challenging because, in general, one has to face all the typical issues of the other classes of data at once. At a very general level, we would suggest that the origin of the difference lies in the way of collecting data. Normally, natural sciences and, to a less extent, social sciences do it by carrying out controllable and repeatable experiments, while this is not possible for historians and archeologists. Therefore, issues that researchers from other fields have to face more or less sporadically, archeologists and historians have to deal with all the time: heterogeneous sources, incompleteness, uncertainty, definition of reliable proxies for interactions that are never directly measurable, and so on.

Summarizing, archeologists started applying formal network methods quite recently and do not publish their dataset very often, hence their network data do not circulate as much as others. In any case, their raw data are intrinsically difficult to map onto networks and network scientists would not take the challenge to use them by themselves. On the contrary, data already converted into simple networks—i.e., containing no other information besides a list of links—do not retain any of the peculiarity of the original archeological data and have a somehow loose and not always transparent relationship with the empirical evidences they are derived from. Anyhow, fundamental research on network building from new typologies of data and network metrics redefinition is nowadays mostly devoted to prevent information waste when dealing with huge systems about whom we know almost everything.²

All these factors make archeological applications quite a separate branch within applied network science, isolated from the positive feedback loop described at the beginning of this section. No network technique inspired by typical issues faced by archeologists has been devised ever and no systematic characterization of such networks has been carried out up to now.

3. ASN: Networks Inferred from the Archeological Record

In most archeological networks, nodes are sites³ linked through common attributes, that is, any kind of archeological evidence. Similarities in specific traits of the material culture are understood as proxy of interactions, such as economic exchanges, cultural affinity, or social proximity. There exists a shared underlying general hypothesis: the more the contexts resemble each other, the stronger was their past interaction. Hence, it makes sense and it is useful to label such networks as Archeological Similarity Networks (ASN).

In order to outline the most common difficulties faced when building ASN, let us summarize here the basic ingredients for a proper network representation of a system:

1. A definition of such system that allows to identify its boundaries, separating what is within from what is outside.

2. A definition of the elemental parts that will constitute the nodes of the network.

3. A definition of what the connections are supposed to mean and a well-defined way to determine which ones do exist and, in some cases, how strong they are.

Depending on the circumstances, each one of these three ingredients may present different challenges. We start discussing some ambiguities in the concepts and definitions of borders and nodes that may represent a problem in network construction in general, and ASN in particular.

3.1. A Matter of Borders

The first ingredient may seem trivial, but it is not so infrequent that the system under consideration is indeed a part of a larger one with blurred borders. Such borders can be conceptual, spatial, or temporal, being the last two situations especially relevant for historical and archeological case studies.

Conceptually blurred borders are an ubiquitous issue: if we are interested in the behavior of a specific class of objects, should we exclude all the individuals who do not belong to this class? What happens with the interactions between the elements in our system and those outside of it?⁴

The typical issue related to spatial borders concerns the interactions with what is outside such borders. In a network where nodes represent settlements, the decision about where to draw the frontiers of the system can be crucial. Even if the system under study is a political entity with well-defined geographic limits, it can nonetheless be unwise to cut out everything that does not belong to that entity. Imagine that one is interested in knowing which settlements the most important ones according to some network analysis measure. Disregarding everything that is outside the borders will make the node representing an important city connecting two regions as peripheral as any small village close to a deserted area. In a network made up of many nodes, from thousands to millions, nodes at the border represent a very small fraction and this kind of issues are just unimportant nuisances. On the contrary, when dealing with small systems, issues related to spatial borders need to be carefully tackled.

Additionally, establishing limits at the temporal dimension also give rise to some challenging questions. The conceptualization of such issues has been addressed from a different perspective in Lemercier (2015). From a network science viewpoint, time-changing systems display a rich phenomenology. Nodes can be created and destroyed; sometimes one splits into two, sometimes two merge into one. Connections appear and disappear; links may increase or weaken their strength. It is difficult to capture meaningful information in a simplified manner. Imagine someone trying to take a picture of something that is moving. The photographer surely will choose a fast shutter speed. But the temporal resolution of archeological data is limited. It is like being in a dark place, unable to see subject clearly. The challenge is how to find the best trade-off between a blurred and a dark image, that is, to select the appropriate time window when trying to reconstruct an evolving network.⁵

3.2. The Choice of Building Blocks

The definition of the nodes may represent a real difficulty if there are more than two scales (local and global) not clearly separated or when the spatial resolution is not homogeneous enough. Archeological findings in some cases can be naturally grouped together depending on the context they belong to (buildings, military camps, villages, etc.), but they may also be scattered over areas where no other remains have been found. Is it better to discard such findings or should we aggregate them according to some criterion?

It is worth noting that not only spatial nodes face these dilemmas. In order to quantify the similarity between assemblages, a necessary previous step is the discretization of the archeological record into categories. When can we say that two sites share the same cultural trait? When are two artifacts similar enough to be considered an evidence of the same trait? If we are considering amphoric types or ceramic compositional groups, how are we supposed to deal with geographic variations or imitations? Basically, it is the issue of discretizing a nearly continuous spectrum of differences. Cluster analysis algorithms can be helpful to group or classify objects based on their individual properties. Alternatively, it is also possible to accept different hypotheses, defining for each of them a different set of nodes and, consequently, different networks. Hopefully, we will find properties that are shared by a large majority of such networks, thus providing information that can be regarded as reliable.

4. Quantifying Similarities to Infer Connections

Each one of the issues discussed in the previous section has been addressed by a number of authors applying network science techniques to archeology but also in many other contexts. Setting the limits of systems and their subparts is a necessary step to progress in almost any field of knowledge and it is increasingly common to perform such tasks by means of quantitative methods in order to minimize arbitrariness and subjectivity.

On the contrary, determining which connections do exist between the elements of the system under study is the most defining issue of formal network science applications. It is therefore to this last aspect that we will devote greater attention.

As already mentioned, in ASN links are established based on the presence of common traits in the material culture. The archeological record needs to be discretized into categorical attributes that can be ceramic compositional groups, architectonic elements or techniques, stamps on bricks or amphorae, or any other distinctive features. Then each context is characterized by the presence/absence of some of such categorical attributes and by their abundance. These networks are hence originally bipartite: as in affiliations networks, there are two classes of nodes, the archeological contexts and the categorical attributes. Contexts are connected only with attributes, i.e., attributes that are present in the corresponding assemblages, and vice versa, attributes are connected to the sites where they have been found. In principle, as for scholars collaborating in academic publications (Newman, 2001) or jazz musicians playing in the same band (Gleiser and Danon, 2003), one may put a link between two nodes of the same class if they are connected with the same node of the other class.

Nevertheless, ASN have a peculiar feature that makes them different from normal affiliation networks. Links in bipartite networks are usually binary: They exist or do not exist, an author is or is not in a certain article, a person participated or did not participated in a given social event. There is no value (weight, strength, or cost) associated to such connections.⁶ On the contrary, this is not the case for archeological sites. Categorical attributes, besides being either present or absent in a given assemblage, have frequencies that naturally determine the strength of the link. We can thus state that ASN are spatial networks derived as the one-mode version (projection) of weighted bipartite networks. Whether and how to retain information about the site locations and the relative abundances of categorical attributes when building an ASN is, in our opinion, the real “network science” issue at the core of applications in archeology.

When it comes to materialize resemblances among a set of entities into connectivity patterns, it is mainly the question one wants to address what determines which aspects and data are to be included, as well as their relative importance. Depending on the specific conditions of the research, such crucial task can be carried out either through qualitative reasoning, combining information from heterogeneous sources, or by applying some similarity metric. If the system under study is small and include only a reduced number of sites, qualitative arguments based on a deep knowledge of the domain is often a natural choice. For instance, Mizoguchi’s studies (Mizoguchi, 2009, 2013) establish links between ten regional entities whenever the author found archeologically recognizable similarities in pottery styles and mortuary traditions. Nodes are linked if one or more kinds of stylistic traits are common to both of them, without need for any formal classification of such data into categorical attributes. The resulting networks have unweighted links (binary network) and can be regarded as an unimodal projections of bipartite networks only in a very loose or metaphorical sense.

The work of Emma Blake somewhat resembles Mizoguchi’s. Blake also deals with a small system, in this case a set of eighteen settlements from pre-Roman west-central Italy (Blake, 2013). Interactions are inferred by means of the copresence of identical types of rare objects and imports, subject to a condition of geographic proximity. The author’s interest lies in direct interactions, thus excluding long-range connections that would require intermediate stops in a hypothetical travel. Instead of considering the connections as weighted with a traveling cost, Blake filters data according to a spatial criterion. Additionally, for reasons inherent to the case study, she discards common pottery eluding the necessity to deal with categories and frequencies of artifacts’ typologies. This approach allows to build a simple network to which simple analytic tools can be applied. Links are not weighted and nodes have no geographical coordinates, but the connectivity pattern embeds information about both relative node positions and the relevance of copresences thanks to the ad hoc filtering process. Filtering is an often necessary step for authors that make the choice of building a binary network. However, any criterion adopted for discarding some classes of data or long-range connections implies a degree of subjectivity and can be considered, to a certain extent, necessarily arbitrary.

An example of the opposite choice can be found in the articles by Shawn Graham (2006). Even though his network is not constructed using material culture to infer relations among sites, difficulties are analogous to those faced by other authors. Graham connects single pieces of evidence (bricks) as a function of shared attributes, namely, find spots, stamps and fabrics. The starting point is technically a two-mode network for each attribute, composed by a set of individual bricks on one hand, and the nominal values of the attributes on the other. It is explicitly argued that, unless the metrics are specifically designed for bipartite data, it is preferable to use a projection instead. Therefore, a projected network onto the set of bricks is made for each attribute and then the totality of connections is considered. No filter is applied and bricks sharing either finding place, stamp or fabric are connected. The resulting network is again a binary network suitable to be analyzed by means of simple metrics. However, unless the diversity of the nominal values of these attribute is comparable with the number of bricks, such a union of projections is necessarily, by construction, an extremely highly connected network. Network analytic tools, especially rankings, may become less reliable when the number of links of each node is close to the total number of nodes in the system. Basically, when the density of connection is very high, differences between nodes decrease to the point that any conclusion about which nodes are more “central” than others does not make sense anymore. In such situations, retaining information about link weights—e.g., counting whether a pair of nodes shares one, two, or three attributes—could help highlighting interactions of interest otherwise hidden behind too many of indistinguishable ties.

One of the first works in this direction is probably the article by Søren Sindbaek (2007). With the aim of shedding light to the communication and exchange networks in the Early Medieval periods, Sindbaek uses archeological sources to connect a quite large set of geographic locations (Sindbaek, 2007, 2013). In these affiliation networks based on material remains, edge weights are the number of shared artifact types. In addition, a threshold is applied, discarding those below three common attributes. Link weights play an important role in determining relative positions of the nodes when using visualization algorithms. Therefore the results deduced from visual inspections are more accurate than it would be in the unweighted case.⁷

Ties also carry a value equal to the number of distinct copresent forms of material culture in Fiona Coward’s articles (Coward, 2010, 2013). Coward states that an unweighted one-mode representation of the data would have lead to a fully connected network due to “the sheer quantity of different forms of material culture that formed part of this study” (Coward, 2010). Thus the author chooses “the use of valued relations” despite it being “potentially somewhat problematic in that many formal methods of social network analysis are defined primarily for binary or dichotomous relations.” She also discusses the possibility—embraced in by several scholars in less recent works—that connections are restricted to a limited number of their closest neighbors. Such an option is discarded because for the purposes of the article it was deemed important to maximize the data.

Similarly, Tom Brughmans’ work on Roman tablewares in eastern Mediterranean (Brughmans, 2010), followed by Brughmans and Poblome (2015), starts from a weighted bipartite network of sites and pottery forms, from which projections are made. In the same way as the two aforementioned authors, projected edges are also weighted by the number of co-occurrences. All these authors choose to build their ASN as weighted projections of two-mode networks whose weights are not included. In other words, they consider the number of different categorical attributes common to the two sites, but do not take into account the amount of samples, or the other attributes that are not present in both. With this approach, provided that the number of shared categories is the same, whether the archeological evidence they have in common represents a big or a small proportion of the totality of the corresponding assemblages does not make any difference.

Among similarity measures that tackle this issue, the Brainerd-Robinson similarity coefficient (Brainerd, 1951; Robinson, 1951) is surely the most frequently used. The application of this coefficient (hereafter referred to as BR) goes far beyond network building, being the measure adopted for comparing collections in a broad number of archeological studies. Unlike the well-known Pearson Correlation Coefficient, BR is specifically designed for compositional data (Cowgill, 1990), that is, data that can be expressed in terms of percentages, and only takes positive values. It is equal to 200 for identical collections and equal to 0 in the case of collections that have nothing in common.

Mark Golitko and colleagues (Golitko et al., 2012; Golitko and Feinman, 2015) employ BR coefficients to build a weighted ASN of assemblages according to the frequencies of different Mayan obsidian sources. Further, they reduce network density by applying a link weight cutoff, up to the critical value above which the network would become disconnected (more than just one connected component).

In the same manner, John Hart and William Engelbrecht in their study of the evolution of the northern Iroquoian ethnic landscape (Hart and Engelbrecht, 2012) calculate BR similarity coefficients over a hundred sites, by looking at decoration motifs on collars and wedges. The same approach is adopted in numerous works on the relations between US Southwest sites in late pre-Hispanic period. Topics as diverse as network evolution at different spatial scales (Mills et al., 2013), the brokerage role of sites and its impact on social capital (Peeples and Haas, 2013) or migrations and depopulation phenomena (Borck et al., 2015) are explored looking at the similarities among ceramic assemblages. Mills and colleagues (Mills et al., 2013) also evaluate the potential impact of ceramic sample size with bootstrapping techniques. That is, BR coefficients from the complete dataset are compared to the ones obtained in artificial scenarios with smaller samples, where data for each site is drawn (with replacement) from its original attribute assemblage. Despite the weight threshold applied for visualization purposes, the analytical process preserves weights and the calculation of centrality measures take raw similarity scores into account (Everett and Borgatti, 2005). After this step, the analysis is carried out both in weighted projections (raw BR coefficients) and binarized versions of it, applying a threshold and thus emphasizing strong ties over weak ones.

Finally, there is one example that considers similarity in a broader though detailed sense. In their study of the diffusion of fired bricks around Europe in the Hellenistic Period (Östborn and Gerding, 2015), Per Östborn and Henrik Gerding follow the approach presented in Östborn and Gerding (2014) for the configuration of the similarity network. Roughly, the strategy consists in allowing attributes of different nature to contribute to the comparison of sites, provided that each nature (e.g., numerical, categorical) goes with an adequate meaning of similarity. Under just one necessary condition (contemporaneity) they perform an extensive analysis of network properties as a function of a lower threshold on the number of common attributes.

The literature shows the wide spectrum of choices made by scholars given the specificities of each case study. All the reviewed works start—sometimes not explicitly—from two-mode networks that can be either unweighted or weighted. As pointed out in Brughmans (2013), there are not published archeological studies that deal with bipartite systems directly, and so far, the ubiquitous decision is still to project according to similarity criteria. Scholars have chosen between the use of simple projections (binary ties established with at least one shared attribute) and a handful of different ways of including weights.

Generally, not much attention is devoted to the precise implications of choosing one similarity measure over another. Articles focusing on the case study, sometimes lack of methodological details, while not many methodological articles are available so far. Exceptions are found in Östborn and Gerding (2014), where the authors propose a systematic method to derive similarities from a combination of different types of attributes; and in Peeples and Roberts (2013), where the crucial aspect of binarizing or not a weighted network is accurately addressed. In few cases, some general considerations of the kind do appear along the literature. For instance, in their work Matt Peeples and collaborators (Peeples et al., 2016) stress that different similarity measures can amplify certain effects derived from data aspects (e.g., chi-square distance emphasizes rare categories, while BR emphasize the common ones).

Evidently, there is not a universal answer, no measure is better than any other in absolute terms. Nevertheless, this decision is of great repercussion since it strongly conditions the subsequent network analysis and would be both useful and interesting to address it not only based on considerations inherent to the meaning embedded in each metric. In the next section, we try to outline how to take a step in this direction by means of a simple computational experiment.

5. Sketching a Reliability Test for Similarity Measures

The problem of how to choose the best way to quantify similarities is an extremely complex issue. We have seen how it has been addressed by authors in the framework of their individual case studies, taking into account the specific features of their data or the meaning of the connections. Here, we want to outline a complementary approach, that is, a quantitative methodology to compare the performance of similarity measures in the context of data scarcity.

Imagine that there are some evidences, some artifact assemblages that have been found in some archeological sites. We know that the samples are incomplete. Hence, when trying to reconstruct the interaction patterns between sites, it is crucial to choose a similarity measure that does not critically depend on the fluctuations in the relative proportions of categorical attributes due to the incompleteness of the archeological record. In other words, given the same historical facts, if we rewind history back to the moment when such events occurred and let everything afterward happen all over again many times, we obtain different outputs as the result of contingency in the excavation and conservation processes. Historical facts are the same, but evidences are not. A good similarity measure is a measure that is robust against the effects of chance, a measure that allows us to build a network that gives always the same result, regardless how many times we rewind history.

In the real world, we have only one set of evidences and there is no way to create other sets of data that are the result of the same events but a different conservation process. We can resample data, but we cannot separate between necessity and contingency. Random permutations consist in reassigning attributes to the sites at random, thus destroying any sort of correlation, while often conserving the size of the corresponding assemblages and the number of artifacts belonging to each category. Typically, permuted datasets are compared with the original empirical evidence in order to separate the unique features of latter from traits that it shares with the former (Hart and Engelbrecht, 2012; Coward, 2013; Peeples et al., 2016). The general idea is that such unique features can be regarded as the only true result of facts (necessity), unlike the spurious (contingent) characteristics also observed in the randomized data. However, there can be traits that are not present in the permuted datasets, but which are still the consequence of contingency (e.g., the location of samples from a very small category), or quantities that are kept fixed while randomizing that are just the product of accidents (e.g., the sizes of sites and assemblages).

In order to clarify this point, let us make a very simple example. Suppose we throw a coin many times but keep note of just three draws in the following sequence: head, head, and tail. Resampling means changing the order and getting all the possible sequences composed by two heads and one tail. Rewinding history means throwing the coin many times obtaining all the possible sequences of length three and the same number of heads and tails on average. In this case, the disparity in the proportion is the product of contingency while the underlying rule gives the same probability to get head or tail. The first case is a random permutation of data, while the second one is a proper Monte Carlo Simulation (MCS) where draws are generated from a probability distribution (in this case, just the same probability p = 0.5 for both outputs). In the case of MCS, features to be regarded as necessary are those shared by most of the simulated dataset (e.g., the presence of at least one head and one tail). A good similarity measure should be based on such features.

Obviously enough, in real situations, the probability distributions from which empirical data were drawn are unknown and we cannot perform MCS. But we can model them and use MCS to test the reliability of similarity measures. We can create very simple models and analyze the behavior of different metrics. In the next paragraphs, we present an example of how to do so. Without attempting to carry out an exhaustive study, we briefly introduce the toy model that we devised and provide some hints about how it could be used, focusing more on the concepts than the technical details. The basic hypothesis behind ASN can be restated as “differences in the similarities between assemblages matters.” The most important additional element is that space and geography do play a role. We do not need anything more to design an ideal scenario that can be used as a controlled setting for testing similarity measures.

The ancient—and never-existent—people of ARSITESTS lived in an extremely rough landscape characterized by high mountains, deep valleys and few passes. A huge canyon divided the region into two. Because of the very high costs of opening routes in their land, the ARSITESTS had only one road connecting all their villages and cities and crossing the canyon only once. Goods were exchanged along this road only and therefore most of the interactions between settlements took place with the closest neighbors according to the path of the route. They were produced and traded in quite localized areas of the region (let say, valleys) and just in rare occasions traveled a bit longer distances. Such ideal scenario can be easily translated into a formal model by representing the road stretched to a linear path as a segment on which goods (categorical attributes) are distributed according to a Gaussian distribution centered in the center of their production area. In this way, there will be great abundance of each attribute in the places where they were produced, something less in the surroundings, and just few samples in places separated by a greater distance (Figure 2).

FIGURE 2

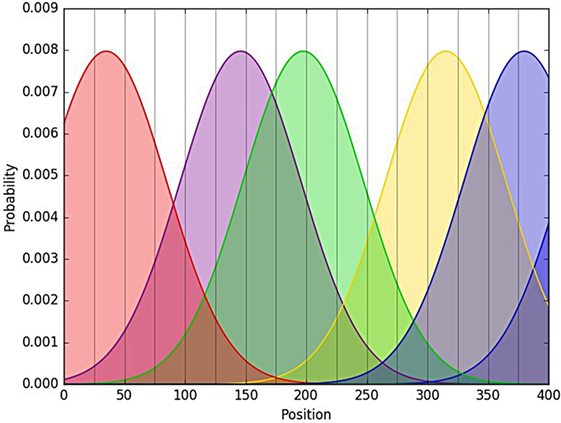
Figure 2. Categorical attributes on a stretched road. The horizontal axis represents ARSITESTS’ road, while each colored curve is the probability distribution function for a different categorical attribute. The higher the curve, the more probable for samples belonging to the corresponding category to be found in that position. Vertical lines stand for separations between bin-sites.

For the sake of mathematical simplicity, and keeping in mind that this experiment is for testing purpose only, the discretization of this linear unidimensional space is performed by dividing it into bins of the same width. Each bin corresponds to an archeological site in the region and hence a node in our ASN.

In the present example, we consider N_b = 40 bins and N_a = 40 categorical attributes. The centers of the Gaussian distribution are distributed along the segment except for a gap around the middle point corresponding to the canyon. The number of samples Q and any other parameter in the model are the same for each categorical attribute.

We expect the network built from such synthetic evidences to have a number of easily recognizable features: nodes should have few strong ties (adjacent bins) and a larger number of weak ones; sites located close to the two ends of the roads should appear as much more peripheral nodes than the others; two main clusters are expected to be clearly present grouping together nodes from each of the two sides of the canyon and sites located close to where the road crossed the river should be the bridge between such two groups.

As a first qualitative check, we consider that a good similarity measure is a measure that allows to construct a network that renders all these features with high accuracy. However, in order to compare different measures quantitatively, we need to devise some kind of test. Here, we introduce some general ideas through a simple application. It has to be understood as an illustrative example of how similar problems could be addressed and the results presented have no generality.

Network features as those described above are supposed to be reflected in network metrics measuring the importance (centrality) of the nodes. In particular, nodes located at the center of the two subregions are expected to be more central in terms of amount of strong links (Weighted Degree Centrality), while nodes close to the canyon are expected to have great importance because of their intermediation role (Betweenness Centrality). In this synthetic case study, the probability distribution for each attribute is known by construction. Hence, we can perform MCS generating as many datasets as we need by extracting exactly Q locations for each category of attributes from the corresponding Gaussian probability functions. Whenever the position of a sample falls into a bin, it is assigned to the assemblage of that site. All the synthetically generated datasets have the same number Q of attributes for each type but are not identical. Differences between them can be regarded as the results of contingency in the excavation and conservation processes, here simulated through random draws from Gaussian probability distributions. On the contrary, their similarities are due to the underlying dynamics of the actual historical process, that is, to the probability distribution themselves that make that bins that are close to each other have similar assemblages. The balance between differences and similarities, i.e., between noise and signal, depends on the number of samples Q: If we extract just few samples for each categorical attribute (small Q), each draw will be very different from the other (Figure 3); On the contrary, if we extract a very large number of samples (large Q), they will be almost identical (Figure 4).

FIGURE 3

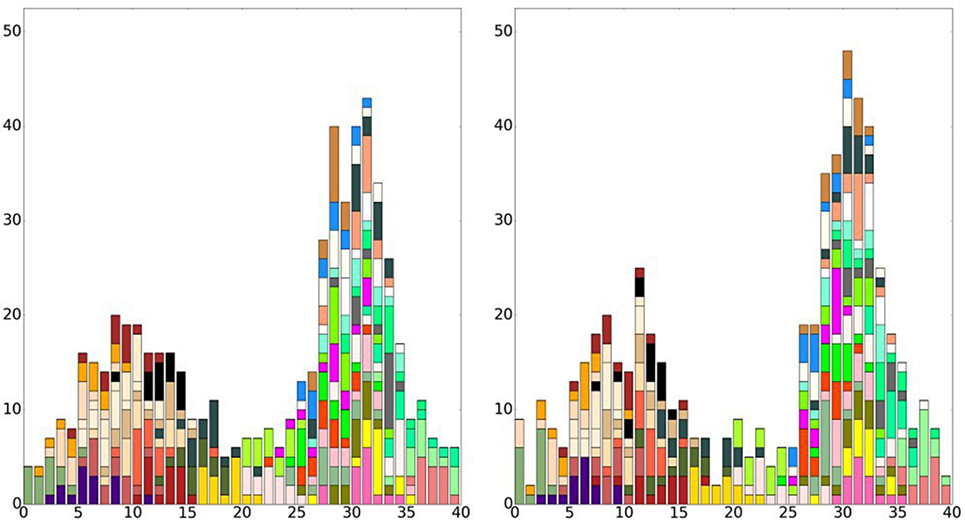
Figure 3. Examples of synthetic distributions of attributes for Q = 15. Each color represents a different categorical attribute. The two panels show two independent realizations of the MCS process. Differences are clear when the value of Q is low.

FIGURE 4

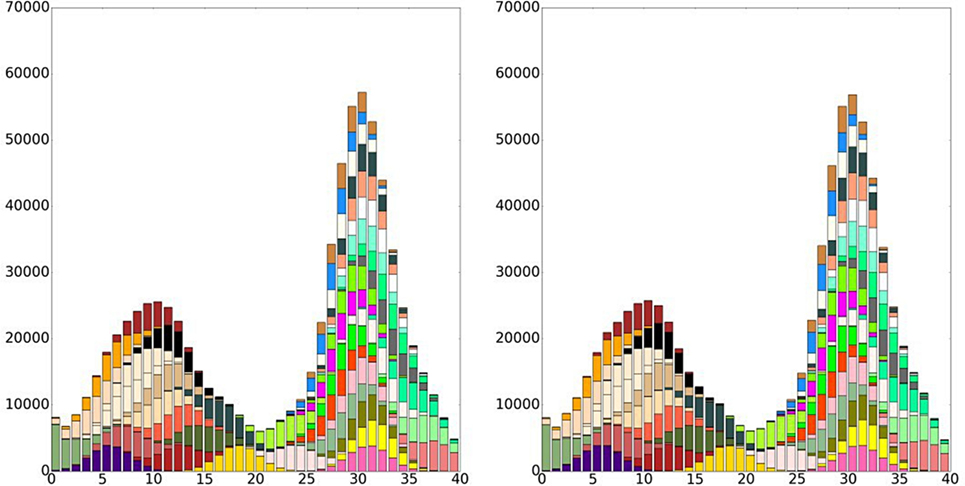
Figure 4. Examples of synthetic distributions of attributes for Q = 10000. When Q reaches high values, the distributions are hardly distinguishable.

The goal of the present test is to find out which similarity measure gives the most reliable result (network) in a certain range of value of the parameter Q.

For this example, let us consider two broadly used similarity measures: the Brainerd-Robinson Index (BR), very popular among archeologists, and the Jaccard Index (J) (Jaccard, 1901), broadly used in a variety of different contexts. For a fixed value of the number of samples Q, we generated n = 100 draws and built two networks for each one of them, one using J (J-network) and the other applying BR (BR-network). We are interested in knowing which set of networks displays less diversity. Therefore we computed the Weighted Degree Centrality and the Betweenness Centrality indexes for all the networks and measure the average correlation (Spearman Correlation Coefficient) between the sequences of values for each pair of networks of the same group, BR-networks with BR-networks and J-networks with J-networks. The higher is the average correlation, the more robust is the result, because a high correlation means that central nodes stay central and peripheral ones are always peripheral. Hence we can trust the results as independent on the accidents of the extraction process. In other words, if the average correlation is close to one, we can pick a single network, calculate the centrality of the nodes and rely on the obtained results considering that any other networks would have given the same output. On the contrary, if the average correlation is low, we have to assume that if a node is very central in a certain network, it is an accident, not a necessity and it could be peripheral in another one.

We repeated the procedure for several values of Q, ranging from Q = 15 to Q = 10,000. Results are shown in Figure 5: Although discussing them goes beyond of the scope of this work, we would like to stress that they are not trivial. Depending on the value of Q and on the considered centrality measure, the most reliable way to build a network varies significantly. In particular, it turns out that the BR index is not the most suitable measure if one is interested in studying which are the nodes that gather the most of the strongest connections (Weighted Degree Centrality), especially when data are scarce.

FIGURE 5

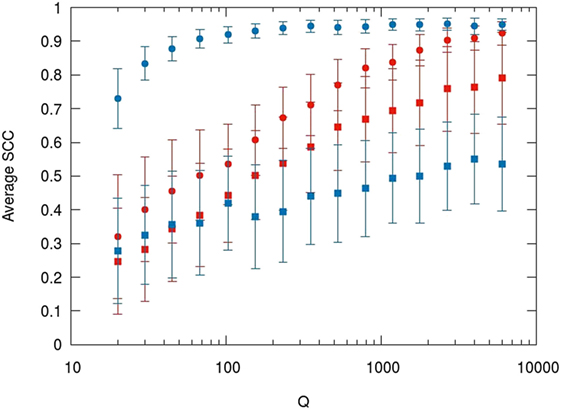
Figure 5. Average Spearman’s rank correlation coefficient of centrality measures as a function of Q. Colors represent the two similarity measures (red: BR; blue: J). Squares and circles represent Betweenness Centrality and Weighted Degree Centrality, respectively.

These conclusions are not general. Nevertheless, the potential of this kind of experiments deserve to be explored. Our model is simple and not realistic, still there are several parameters associated to real features of archeological case studies which we kept fixed and whose influence could be easily studied. Without introducing any further complication, we could explore the effect of varying the width of the Gaussian distributions that represent how localized artifact typologies are, or the number of sites and the number of different categorical attributes, or the number of samples for each category (data heterogeneity) that in our example is the same for all of them. Simple abstract models are a powerful way to test the available analytical tools before making a choice, not only about which similarity measure is the most suitable for building an ASN from a certain dataset, but also about which network metrics are the most reliable for describing the system under study.

6. Conclusion

There exists a production cycle through which network science advances that nourishes and is nourished by an increasingly broader variety of application fields.

New universal mechanisms and features common to systems that are very different in nature but formally similar are discovered. At the same time, new and old powerful analytic tools are adapted to every and each research question, while remaining suitable to be applied to broad classes of systems.

The key is not what data mean, but how data can be represented; not what a certain question states when expressed in natural language, but how it is mapped into formal, mathematical terms. The different may happen to be the same, and the alike may happen to have nothing to do.

In order for archeological applications to enter the productive cycle of network science, thus benefiting from the growth of the discipline, the difficulties faced by archeologists need to be translated into formal terms.

Computer generated data can help untangling different elements that usually coexist in real case studies, e.g., incompleteness and heterogeneity. Decomposing a problem into its fundamental parts tackling them one by one, is a strategy that has been proven fruitful throughout the history of science. At the same time, ideal scenarios allow us to explore the theoretic limits of techniques and tools. For instance, in our example in Section 5 (see Figure 5), we have seen how some network centrality measures (Betweenness Centrality) suffer not negligible fluctuations even when we simulate datasets that are so large that can be regarded as ideally complete. Is it a number of different categorical attributes equal to the number of sites not enough? Which is the perfect ratio? Are there metrics that are intrinsically unstable whose use should be avoided? These are just a few questions that can be posed and addressed through computer simulations in general and Monte Carlo methods in particular.

The range of problems susceptible to be addressed by means of a combination of mathematical and computational approaches as those used in network science is not limited to the topic touched in the present work. There are still general issues that do not have an answer. For instance, the amount of different categorical attributes—i.e., the number of nodes in one of the two classes in the bipartite network—strongly constraints the topology of the projection onto the other class of nodes. How many categories do we need in order to reproduce an arbitrary connectivity pattern?

Besides such abstract, theoretical discussions, inverse engineering can be a powerful ally for assessing the limits of what we can ask to real datasets: starting from a hypothetical set of network features, one may wonder which properties have to be possessed by the empirical evidences in order for that results to be obtained. It is in principle always possible to generate computer simulated assemblages that would give back a pattern of connections with the desired characteristics. This sort of experiments enable for compatibility tests on hypotheses expressed in terms of network measures that can be proven more or less statistically compatible with data.

There are also questions that have been answered in other scientific fields that—as far as we know—have not been addressed for ASN yet: Is it thresholding the best way to filter the noise or could we develop more tailored filtering methods? It can be argued that the real challenge is to remove redundancy and noise, not to get rid potentially informative weak ties.

The only possible framework for such kind of research to be developed in a healthy way is within interdisciplinary collaborations. Selecting the most relevant questions, translating them into formal terms, sorting the issues suitable to be addressed in the first place, are all tasks that require the simultaneous knowledge of the domain and the techniques. Awareness of the limits and potentialities of archeological data, mathematical language, and computational methods can be sometimes found in an individual research team. Nevertheless, if we want archeology to leave the periphery and enter the core of applied network science, its necessities have to be shared within the community of network science.

Author Contributions

LP and IM designed the work. LP, IM, and AD-G collected information and drafted the article.

Acknowledgement

We would like to thank Mario Morvan for his assistance on the processing of Figures 3 and 4.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

Funding for this work was provided by the European Research Council Advanced Grant EPNet (340828). AD-G acknowledges support from Ministerio de Economia y Competitividad of Spain Projects No. FIS2012-38266-C02-02 and No. FIS2015-71582-C2-2-P (MINECO/FEDER); and Generalitat de Catalunya Grant No. 2014SGR608.

Footnotes

1. ^The case of Local e Global efficiency measures on networks can be taken as a paradigmatic example (Latora and Marchiori, 2001; Vragović et al., 2005).
2. ^A paradigmatic example in this sense is the development of the multilayer framework. The basic idea is that there exists a richness in terms of diversity of connections that can be exploited by adopting a new, more detailed representation: “The way we have been dealing with this diversity of connections implies that all the aforementioned relations (personal, social, professional, etc.) are projected into a single layer, but indeed, not all processes can be simulated on such a simplified aggregated network of contacts.” Such framework is being developed for understanding “modern cyber, social and physical systems such as online social networks, transportation systems, metabolic and regulatory networks, etc.,” i.e., huge systems about which an almost unlimited amount of information is available (http://cosnet.bifi.es/network-theory/multiplex-networks/).
3. ^Although they can also be parts of a site (Mol and Mans, 2013) or groups of sites (Mizoguchi, 2009, 2013).
4. ^For a more in depth discussion of this topic within sociology, see Laumann et al. (1991).
5. ^We thank Sergi Lozano for this enlightening metaphor.
6. ^There are a few exceptions, such as recommendation networks (Zhou et al., 2007) and ecological (e.g., mutualistic) networks (Rezende et al., 2007).
7. ^Centrality measures are calculated but it remains unclear if weights are taken into account.

References

Albert, R., and Barabasi, A.L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics 74: 47–97. doi: 10.1088/1478-3967/1/3/006

CrossRef Full Text | Google Scholar

Anderson, P.W. (1972). More is different. Science 177:393–397. doi:10.1126/science.177.4047.393

CrossRef Full Text | Google Scholar

Barthélemy, M. (2011). Spatial networks. Physics Reports 499: 1–101. doi:10.1016/j.physrep.2010.11.002

CrossRef Full Text | Google Scholar

Blake, E. (2013). Social networks, path dependence, and the rise of ethnic groups in pre-Roman Italy. In Network Analysis in Archaeology: New Approaches to Regional Interaction. Edited by Carl Knappett, 203–221. Oxford: Oxford University Press.

Google Scholar

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D.-U. (2006). Complex networks: structure and dynamics. Physics Reports 424: 175–308. doi:10.1016/j.physrep.2005.10.009

CrossRef Full Text | Google Scholar

Borck, L., Mills, B.J., Peeples, M.A., and Clark, J.J. (2015). Are social networks survival networks? An example from the late pre-Hispanic US Southwest. Journal of Archaeological Method and Theory 22: 33–57. doi:10.1007/s10816-014-9236-5

CrossRef Full Text | Google Scholar

Borgatti, S.P., and Halgin, D.S. (2011). Analyzing affiliation networks. In The SAGE Handbook of Social Network Analysis. Edited by J. Scott and P. Carrington, 417–433. London: SAGE.

Google Scholar

Brainerd, G.W. (1951). The place of chronological ordering in archaeological analysis. American Antiquity 16: 301–13. doi:10.2307/276979

CrossRef Full Text | Google Scholar

Brughmans, T. (2010). Connecting the dots: towards archaeological network analysis. Oxford Journal of Archaeology 29: 277–303. doi:10.1111/j.1468-0092.2010.00349.x

CrossRef Full Text | Google Scholar

Brughmans, T. (2013). Thinking through networks: a review of formal network methods in archaeology. Journal of Archaeological Method and Theory 20: 623–62. doi:10.1007/s10816-012-9133-8

CrossRef Full Text | Google Scholar

Brughmans, T., and Poblome, J. (2015). Pots in space: an exploratory and geographical network analysis of Roman pottery distribution. In New Worlds Out of Old Texts: Developing Techniques for the Spatial Analysis of Ancient Narratives. Edited by E. Barker, S. Bouzarovski, C. Pelling, and L. Isaksen, 255–279. Oxford: Oxford University Press, Vol. 2000.

Google Scholar

Buchanan, M. (2003). Nexus: Small Worlds and the Groundbreaking Science of Networks. New York: W. W. Norton & Company, 56.

Google Scholar

Collar, A., Coward, F., Brughmans, T., and Mills, B.J. (2015). Networks in archaeology: phenomena, abstraction, representation. Journal of Archaeological Method and Theory 22: 1–32. doi:10.1007/s10816-014-9235-6

CrossRef Full Text | Google Scholar

Costa, L.F., Rodrigues, F.A., Travieso, G., and Villas Boas, P.R. (2007). Characterization of complex networks: a survey of measurements. Advances in Physics 56: 167–242. doi:10.1080/00018730601170527

CrossRef Full Text | Google Scholar

Coward, F. (2010). Small worlds, material culture and ancient near eastern social networks. In Social Brain, Distributed Mind. Edited by R. Dunbar, C. Gamble, and J. Gowlett, 448–479. Oxford: British Academy, Vol. 158.

Google Scholar

Coward, F. (2013). Grounding the net: social networks, material culture and geography in the epipalaeolithic and early neolithic of the near east (21-6.000 cal BCE). In Network Analysis in Archaeology: New Approaches to Regional Interaction. Edited by C. Knappett, 246–280. Oxford: Oxford University Press.

Google Scholar

Cowgill, G.L. (1990). Why Pearson’s r is not a good similarity coefficient for comparing collections. American Antiquity 55: 512–21. doi:10.2307/281281

CrossRef Full Text | Google Scholar

Everett, M.G., and Borgatti, S.P. (2005). Extending centrality. In Models and Methods in Social Network Analysis. Edited by P.J. Carrington, J. Scott, and S. Wasserman, 57–76. Cambridge: Cambridge University Press.

Google Scholar

Gleiser, P.M., and Danon, L. (2003). Community structure in jazz. Adv. Complex Syst. 6: 565. doi:10.1142/S0219525903001067

CrossRef Full Text | Google Scholar

Golitko, M., and Feinman, G.M. (2015). Procurement and distribution of pre-Hispanic Mesoamerican Obsidian 900 BCAD 1520: a social network analysis. Journal of Archaeological Method and Theory 22: 206–47. doi:10.1007/s10816-014-9211-1

CrossRef Full Text | Google Scholar

Golitko, M., Meierhoff, J., Feinman, G.M., and Williams, P.R. (2012). Complexities of collapse: the evidence of Maya obsidian as revealed by social network graphical analysis. Antiquity 86: 507–23. doi:10.1017/S0003598X00062906

CrossRef Full Text | Google Scholar

Graham, S. (2006). Networks, agent-based models and the Antonine Itineraries: implications for Roman archaeology. Journal of Mediterranean Archaeology 19: 45–64. doi:10.1558/jmea.2006.19.1.45

CrossRef Full Text | Google Scholar

Hart, J.P., and Engelbrecht, W. (2012). Northern Iroquoian ethnic evolution: a social network analysis. Journal of Archaeological Method and Theory 19: 322–49. doi:10.1007/s10816-011-9116-1

CrossRef Full Text | Google Scholar

Holme, P., Liljeros, F., Edling, C.R., and Kim, B.J. (2003). Network bipartivity. Physical Review E Covering Statistical Nonlinear Biological and Soft Matter Physics 68: 056107. doi:10.1103/PhysRevE.68.056107

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaccard, P. (1901). Distribution de la flore alpine dans le Bassin des Drouces et dans quelques regions voisines. Bulletin de la Société Vaudoise des Sciences Naturelles 37(140): 241–272.

Google Scholar

Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008). Benchmark graphs for testing community detection algorithms. Physical Review E Covering Statistical Nonlinear Biological and Soft Matter Physics 78: 046110. doi:10.1103/PhysRevE.78.046110

CrossRef Full Text | Google Scholar

Latora, V., and Marchiori, M. (2001). Efficient behavior of small-world networks. Physical Review Letters 87: 198701. doi:10.1103/PhysRevLett.87.198701

PubMed Abstract | CrossRef Full Text | Google Scholar

Laumann, E.O., Mardsen, P.V., and Prensky, D. (1991). The boundary specication problem in network analysis. In Research Methods in Social Network Analysis. Edited by L.C. Freeman, D.R. White, and A.K. Romney, 183–211. New Jersey: Transaction Publishers.

Google Scholar

Lemercier, C. (2010). Formal network methods in history: why and how? In Social Networks, Political Institutions, and Rural Societies, Edited by G. Fertig, 281–310. Turnhout: Brepols Publishers.

Google Scholar

Lemercier, C. (2015). Taking time seriously. How do we deal with change in historical networks? In Knoten und Kanten III. Soziale Netzwerkanalyse in Geschichts- und Politikforschung, Edited by M. Gamper, L. Reschke, and M. Düring, 183–211. Bielefeld: Transcript Verlag.

Google Scholar

Mills, B.J., Clark, J.J., Peeples, M.A., Haas, W.R., Roberts, J.M., Hill, J.B., et al. (2013). Transformation of social networks in the late pre-Hispanic US Southwest. Proceedings of the National Academy of Sciences of the United States of America 110: 5785–90. doi:10.1073/pnas.1219966110

PubMed Abstract | CrossRef Full Text | Google Scholar

Mizoguchi, K. (2009). Nodes and edges: a network approach to hierarchisation and state formation in Japan. Journal of Anthropological Archaeology 28: 14–26. doi:10.1016/j.jaa.2008.12.001

CrossRef Full Text | Google Scholar

Mizoguchi, K. (2013). The evolution of prestige good systems: an application of network analysis to the transformation of communication systems and their media. In Network Analysis in Archaeology: New Approaches to Regional Interaction. Edited by C. Knappett, 151–178. Oxford: Oxford University Press.

Google Scholar

Mol, A., and Mans, J. (2013). Old-boy networks in the indigenous Caribbean. In Network Analysis in Archaeology: New Approaches to Regional Interaction. Edited by C. Knappet, 306–332. Oxford: Oxford University Press.

Google Scholar

Newman, M. (2003). The structure and function of complex networks. SIAM Review 45: 167–256. doi:10.1137/S003614450342480

CrossRef Full Text | Google Scholar

Newman, M.E.J. (2001). The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. U.S.A. 98(2):404–409. doi:10.1073/pnas.98.2.404

CrossRef Full Text | Google Scholar

Östborn, P., and Gerding, H. (2014). Network analysis of archaeological data: a systematic approach. Journal of Archaeological Science 46: 75–88. doi:10.1016/j.jas.2014.03.015

CrossRef Full Text | Google Scholar

Östborn, P., and Gerding, H. (2015). The diffusion of fired bricks in Hellenistic Europe: a similarity network analysis. Journal of Archaeological Method and Theory 22: 306–44. doi:10.1007/s10816-014-9229-4

CrossRef Full Text | Google Scholar

Padgett, J.F., and Ansell, C.K. (1993). Robust action and the rise of the Medici, 1400-1434 on JSTOR. American Journal of Sociology 98: 1259–319. doi:10.1086/230190

CrossRef Full Text | Google Scholar

Peeples, M.A., and Haas, W.R. (2013). Brokerage and social capital in the Prehispanic U.S. Southwest. American Anthropologist 115: 232–47. doi:10.1111/aman.12006

CrossRef Full Text | Google Scholar

Peeples, M.A., Mills, B.J., Randall Haas, W., Clark, J.J., and Roberts, J.M. (2016). Analytical challenges for the application of social network analysis in archaeology. In The Connected Past: Challenges to Network Studies in Archaeology and History. Edited by T. Brughmans, A. Collar, and F. Coward, 59–84. Oxford: Oxford University Press.

Google Scholar

Peeples, M.A., and Roberts, J.M. (2013). To binarize or not to binarize: relational data and the construction of archaeological networks. Journal of Archaeological Science 40: 3001–10. doi:10.1016/j.jas.2013.03.014

CrossRef Full Text | Google Scholar

Rezende, E.L., Lavabre, J.E., Guimarães, P.R., Jordano, P., and Bascompte, J. (2007). Non-random coextinctions in phylogenetically structured mutualistic networks. Nature 448: 925–8. doi:10.1038/nature05956

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, W.S. (1951). A method for chronologically ordering archaeological deposits. American Antiquity 16: 293–301. doi:10.2307/276978

CrossRef Full Text | Google Scholar

Sindbaek, S.M. (2007). Networks and nodal points: the emergence of towns in early Viking Age Scandinavia. Antiquity 81: 119–32. doi:10.1017/S0003598X00094886

CrossRef Full Text | Google Scholar

Sindbaek, S.M. (2013). Broken links and black boxes: material affiliations and contextual network synthesis in the Viking World. In Network Analysis in Archaeology: New Approaches to Regional Interaction. Edited by C. Knappett, 71–94. Oxford: Oxford University Press.

Google Scholar

Strogatz, S.H. (2001). Exploring complex networks. Nature 410: 268–76. doi:10.1038/35065725

PubMed Abstract | CrossRef Full Text | Google Scholar

Vragović, I., Louis, E., and Díaz-Guilera, A. (2005). Efficiency of informational transfer in regular and complex networks. Physical Review E Covering Statistical Nonlinear Biological and Soft Matter Physics 71: 036122. doi:10.1103/PhysRevE.71.036122

PubMed Abstract | CrossRef Full Text | Google Scholar

Watts, D.J. (2004). Six Degrees: The Science of a Connected Age. New York: W. W. Norton & Company.

Google Scholar

Zhou, T., Ren, J., Medo, M., and Zhang, Y.-C. (2007). Bipartite network projection and personal recommendation. Physical Review E Covering Statistical Nonlinear Biological and Soft Matter Physics 76: 046115. doi:10.1103/PhysRevE.76.046115

PubMed Abstract | CrossRef Full Text | Google Scholar