Sorption and Desorption of the Model Aromatic Hydrocarbons Naphthalene and Benzene: Effects of Temperature and Soil Composition

Petroleum hydrocarbon (PHC) contamination is a global environmental issue. Understanding the key factors and mechanisms controlling the fate and mobility of PHCs in soils and aquifers is critical for environmental risk assessment, the development of remediation strategies, and policy decisions. This study focuses on the effects of soil composition and temperature on the sorption and desorption of two representative aromatic PHC compounds: naphthalene and benzene. The experiments were carried out using artificial sandy loam soil mixtures with temperatures ranging from 3 to 25°C. As expected, the sorption capacities of the soils were primarily controlled by the organic carbon content, while barely affected by the clay content. The sorption data for benzene and naphthalene followed linear to near-linear isotherms. Naphthalene sorption further increased with decreasing temperature, whereas temperature had little effect on benzene sorption. The latter was consistent with the very small magnitude of the sorption enthalpy of benzene. Under imposed dynamic temperature fluctuations, naphthalene sorption and desorption were shown to be reversible: model simulations demonstrated minimal kinetic limitation of the temperature-dependent soil-water partitioning. Our results imply that even in simple artificial soil systems, temperature variations can have complex, but predictable, effects on the soil-pore water partitioning of PHCs and, hence, on their mobility and bioavailability. Understanding the role of temperature is thus a prerequisite to unraveling the coupled abiotic and biotic processes that modulate the fate of PHCs in real-world soils.

Introduction

Although hydrocarbon extraction and storage are increasing all over the world, large and medium oil-spilling events have fortunately been decreasing since the 1970s (ITOPF, 2019). Nonetheless, spills continue to occur during extraction, transport, storage and refining of petroleum. These spills can have severe impacts on terrestrial, freshwater and marine ecosystems, because of the high toxicity of many petroleum hydrocarbons (PHCs) (Onwurah et al., 2007; Varjani, 2017).

In subsurface environments, the fate of PHCs and the associated contamination risks depend on the actual compounds, as well as their migration and degradation. For example, spilled PHCs can penetrate the soil profile due to gravity, sorb on and desorb from minerals and soil organic matter (OM), migrate with groundwater as a dissolved or free phase, be emitted to the atmosphere through volatilization, and transformed into other compounds through abiotic and biotic reactions. Thus, the fate of PHC contaminants is controlled by various environmental factors, including soil geochemistry and hydrology, climatic conditions, and the resident microbial community.

Soil composition exerts a key geochemical control on the sorption and desorption of PHC contaminants (Fine et al., 1997; Falciglia et al., 2011). For instance, OM is a dominant sorbent in soils and, therefore, sorbed PHC concentrations are routinely normalized to soil organic carbon (OC) contents and the sorption strength of the compounds expressed as their OC-water partition coefficients (K_OC) (Means et al., 1980; Grathwohl, 1990; Conte et al., 2001). While it is widely accepted that OM dominates sorption of aromatic compounds in soils, expandable clays (e.g., smectite) that have adequate interlayer space, high surface areas, and a relatively high abundance may be equally important sorbents for PHC contaminants (Sheng et al., 2001).

PHC contaminants can be degraded into smaller molecules by naturally occurring abiotic (e.g., photo-oxidation) and biotic reactions. These natural degradation processes are a more effective and preferable method for long-term PHC remediation than removal by mechanical and chemical interventions that are invasive to the soil ecosystem and tend to be expensive (Das and Chandran, 2011; Varjani, 2017). Biodegradation of PHCs may be limited by the supplies of electron acceptors (e.g., oxygen, sulfate, nitrate, oxidized organic compounds, etc.) and nutrients, which can be temporally and spatially constrained by the geochemical and hydro(geo)logical conditions at contaminated sites (Das and Chandran, 2011; Geng et al., 2015; Garg et al., 2017; Ngueleu et al., 2019). In natural soil environments, sorption–desorption processes may also be rate-controlling steps in PHC biodegradation (Al-Bashir et al., 1990; Mihelcic and Luthy, 1991; Guerin and Boyd, 1992). Therefore, a comprehensive understanding of the environmental variables controlling the sorption–desorption dynamics of PHCs is critical to predict their mobility and bioavailability in the subsurface.

Temperature is one of the master variables affecting the fate of PHCs in soils. To variable extents, all soil abiotic and biotic processes are dependent on temperature (Piatt et al., 1996; ten Hulscher and Cornelissen, 1996; Tremblay et al., 2005; Wang et al., 2011; Ngueleu et al., 2018). For instance, Ngueleu et al. (2018) measured higher sorption capacities of benzene and naphthalene to (semi-)arid coastal soils at 5°C than 35°C. However, how temperature affects the reversibility of PHC sorption and desorption is still debated (Wang et al., 2007). Some studies have observed hysteresis, that is, where sorption and desorption isotherms do not coincide. This hysteresis has been attributed to experimental error, changes in the chemical interactions during sorption and desorption due to physical processes such as the mechanical trapping of the sorbed PHC, and inelastic modification of the sorbent following sorption of the sorbate molecule(s) (Wang et al., 2007; Pignatello, 2012).

The present study builds on the hypothesis that the large seasonal variations in soil temperature in cold to cold-temperate regions, such as found in Canada, play a major role in the sorption and desorption dynamics of PHC contaminants and, thus, in their mobility and bioavailability. We therefore carried out sorption–desorption batch experiments at variable temperatures and with different soil compositions. Naphthalene and benzene were selected as representative PHC components. Soil composition was varied systematically by using artificial soil mixtures that cover the typical ranges of clay and OM contents of natural sandy loam soils. Sorption rates and isotherms were measured at fixed (i.e., static) temperatures. Because benzene sorption exhibited no discernable temperature dependence, naphthalene was further employed in experiments with a dynamic temperature regime to determine the reversibility of its sorption–desorption behavior. The dynamic temperature experiments directly address the hypothesis that soil temperature fluctuations may contribute to regulating PHC uptake from and release to soil pore waters.

Materials and Methods

Artificial Soil Mixtures

Four artificial soil mixtures, denoted AS-1, AS-2, AS-3, and AS-4 (Table 1), with different sandy loam textures were prepared by mixing quartz sand (OK-75, U.S. Silica), silt-sized quartz (Sil-Co-Sil^® 53, U.S. Silica), montmorillonite (Ceratosil^® WG, Süd-Chemie AG, Germany) and OM. For the quartz sand and silt-sized quartz, the ranges of particle size were 0.053 to 0.6 mm and less than 0.045 to 0.106 mm, respectively, based on the supplier’s product information. The montmorillonite comprised 8% sand-sized (>0.063 mm), 25% silt-sized (0.002–0.063 mm), and 67% clay-sized (<0.002 mm) material (Pronk et al., 2012). Fresh maple leaves were air-dried, ground, sieved (0.063–1 mm), and washed seven times with Milli-Q water, air-dried again and added as the source of soil OM. Because of their small particle sizes and abundant functional groups, the montmorillonite and OM were assumed to be the two soil components controlling PHC sorption/desorption. The montmorillonite and OM contents used were 5 and 15 weight % (wt%), and 1 and 5 wt%, respectively (Table 1). The artificial soil mixtures were analyzed for their organic and inorganic carbon contents on a CHNS Carlo Erba analyzer. The two AS-4 compositions listed in Table 1 are for two separately prepared soil mixtures used in the static and dynamic temperature experiments, respectively.

TABLE 1

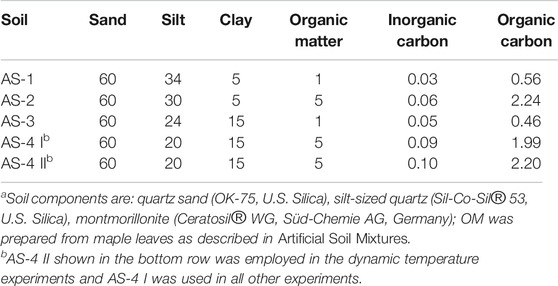
TABLE 1. Mineral and organic contents in weight % of the four artificial soils (AS).^a

Petroleum Hydrocarbon Stock and Experimental Solutions

Benzene (C₆H₆) and naphthalene (C₁₀H₈) were selected as representative PHC contaminants for the sorption and desorption experiments. Separate stock solutions of benzene and naphthalene (20 mg L⁻¹) were prepared by adding either benzene (≥99.9%, Sigma-Aldrich^®) or naphthalene (≥99%, Sigma-Aldrich^®) to Milli-Q water, which contained CaCl₂ (905.9 mg L⁻¹) as background electrolyte and HgCl₂ (271.5 mg L⁻¹) as biocide to prevent PHC biodegradation. Each stock solution was sealed in an amber bottle with a Teflon-faced septum and minimal headspace. To ensure complete dissolution, the benzene and naphthalene stock solutions were stirred with Teflon-coated magnetic bars for four to seven days. To prepare the experimental solutions, aliquots of the stock solutions were diluted with matrix solutions containing CaCl₂ (905.9 mg L⁻¹) and HgCl₂ (271.5 mg L⁻¹) and stirred for ∼15 min prior to starting the experiments. The concentrations of benzene and naphthalene in the stock and experimental solutions were determined by gas chromatography (GC, see Analytical Methods) before applied to the sorption and desorption experiments.

Sorption and Desorption Experiments

Time-Series Sorption Experiments

The extent of sorption and the time scale required to reach sorption equilibrium were determined in batch experiments with the four soil mixtures (AS-1 to 4) at different temperatures (Table 2). In an experiment, 15 g of a given AS was added in a 60 ml serum bottle to 53 ml diluted benzene or naphthalene solution (initial concentration C₀ = 2 mg L⁻¹). Averaged over all the experiments, the liquid-to-solid ratio was 3.51 ± 0.07 mL g⁻¹. The serum bottles were sealed with Teflon-faced septa and open-top unlined aluminum seals immediately following addition of the solution and AS mixture to the bottles. The headspace in the serum bottles was minimized to limit PHC volatilization. Control bottles were filled with 60 ml diluted benzene or naphthalene solution only. The experimental and control bottles were agitated on a rotary wheel at 10 revolutions per minute (rpm) in an environmental chamber (Percival Scientific CTH-118) with the temperature maintained at 25°C. Based on the results of the time-series sorption experiments at 25°C (see Time-Series Sorption Experiments), only AS-3 and AS-4 were used in the experiments at 10 and 3°C to assess the effect of temperature (Table 2). Each temperature was imposed for seven days, except the 25°C experiments with AS-3 and AS-4 in which temperature was maintained for four days, to allow sorption to reach equilibrium. At selected times, a set of triplicate experimental bottles plus corresponding duplicate control bottles were sacrificially sampled for GC analysis (see Analytical Methods).

TABLE 2

TABLE 2. Design of sorption and desorption experiments.

Dynamic Temperature Experiments

Based on the results of the separate sorption experiments conducted at the three temperatures (i.e., 25, 10, or 3°C, see Time-Series Sorption Experiments), the effects of a dynamic temperature regime were investigated to test the hypothesis that this would cause reversible PHC sorption and desorption. Based on the results of the separate sorption experiments (see Time-Series Sorption Experiments and Dynamic Temperature Experiments), the sorption and desorption experiments under dynamic temperature were only conducted with AS-4 and naphthalene (C₀ = 5 mg L⁻¹, liquid-to-solid ratio = 3.54 ± 0.07 mL g⁻¹). Temperature was first decreased in a stepwise fashion from 25 via 10 to 3°C, and then raised again from 3 through 10 to 25°C (Table 2). Each temperature was maintained for seven days. At selected times, a set of triplicate experimental bottles plus duplicate control bottles were sacrificially sampled for GC analysis (see Analytical Methods).

Sorption Isotherm Experiments

Aqueous-solid distributions of benzene and naphthalene were determined at the three different temperatures. Triplicate benzene or naphthalene solutions with initial concentrations of 1, 2, 5, 8, 11, and 13 mg L⁻¹ (see Supplementary Table S1 for GC determined concentrations of initial solutions) were mixed separately with the four AS at 25°C. Experiments at 10 and 3°C were conducted with AS-3 and AS-4 only (Table 2). The concentrations of benzene or naphthalene were identical in the experimental and control bottles, but the latter did not contain any AS. The isotherm experiments were run for 48 h, which was sufficient to reach sorption equilibrium according to the results of the time-series sorption experiments (see Time-Series Sorption Experiments and Dynamic Temperature Experiments).

Analytical Methods

At selected times during the time-series sorption and dynamic temperature experiments, or after equilibrium was reached in the sorption isotherm experiments, triplicate experimental bottles and corresponding duplicate control bottles were sacrificially sampled. Each bottle was centrifuged (1500 rpm, 10 min) at the same temperature at which they were being incubated during the experiments. Following centrifugation, 19 ml of supernatant was collected from each bottle with a glass syringe and a stainless-steel needle. A micro-extraction method was used to obtain the benzene or naphthalene concentration in the supernatant.

For the micro-extractions, 19 ml of solution (i.e., the stock solutions, initial experimental solutions, or supernatant samples obtained from the experiments) was mixed in 20 ml glass vials with 1 ml of dichloromethane extractant containing meta-fluorotoluene as an internal standard. The glass vials were sealed with Teflon-faced septa and open-top caps. They were shaken at 350 rpm for 20 min and then left to rest bottoms-up for ∼30 min until the organic phase fully settled. The organic phase was extracted using a gas-tight glass syringe and transferred to a screw-thread GC vial (VWR^®). The vials were loaded onto a GC sampler and analyzed for the benzene or naphthalene concentration on an Agilent 7890A GC instrument. Organic phase samples were injected at a port temperature of 275°C and passed through a DB5 capillary column. The concentrations of benzene and naphthalene were measured by a flame ionization detector (detection limit = 5 μg L⁻¹).

The fraction ($F_{sorb PHC}$, %) and concentration ($S$, mg kg⁻¹) of sorbed benzene or naphthalene onto a given AS were calculated using Eqs 1 and 2, respectively.

$F_{sorbPHC}=\frac{(C_0-C)}{C_0}\times 100\text{\%}(1)$

$S=\frac{V(C_0-C)}{m}(2)$

where $C_0$ (mg L⁻¹) is the initial concentration of the compound in the experimental solution, $C$ (mg L⁻¹) is the concentration measured in the aqueous phase of the sample collected during the experiment, $V$ (L) is the aqueous phase volume in the experimental bottle, and $m$ (kg) is the initial dry mass of the AS used.

Mathematical Modeling

The measured benzene and naphthalene concentrations in the sorption isotherm experiments were best fitted with linear and Freundlich isotherms:

$S_{eq}=K_d{C}_{eq}(3)$

$S_{eq}=K_{Fr}{C}_{eq}^{n_{Fr}}(4)$

where $S_{eq}$ (mg kg⁻¹) and $C_{eq}$ (mg L⁻¹) are the concentrations of sorbed and aqueous compound after equilibrium was reached, respectively; $K_d$ (L kg⁻¹) and $K_{Fr}$ (${\text{mg}}^{1-{\text{n}}_{\text{Fr}}}{\text{L}}^{{\text{n}}_{\text{Fr}}}{\text{kg}}^{-1}$) are the distribution coefficients for the linear and Freundlich models, respectively; and $n_{Fr}$ is the Freundlich exponent.

A two-site kinetic sorption model was applied to fit the dynamic temperature sorption data. The model assumes that sorption to a first pool of sites instantaneously equilibrates with the aqueous phase, while a second pool of sites accounts for the slow (kinetic) binding of the sorbate to the sorbent. The slow binding is assumed to follow first-order kinetics with respect to the sorbate occupancy of the kinetic sites (Šimůnek and van Genuchten, 2008; Maraqa and Khashan, 2014). Based on the linear isotherms observed during the sorption of naphthalene to AS-4 at 25, 10, and 3°C, the two-site kinetic sorption model was implemented using Eqs 5–8:

$S=S_1+S_2(5)$

$\frac{\partial S_1}{\partial t}=\frac{\partial }{\partial t}\left(f_{eq}{K}_{d}C\right)(6)$

$\frac{\partial S_2}{\partial t}=\lambda [\left(1-f_{eq}\right)K_{d}C-S_2](7)$

$\left(V+m{f}_{eq}{K}_d\right)\frac{\partial C}{\partial t}+m\frac{\partial S_2}{\partial t}=0(8)$

where $S_1$ (mg kg⁻¹) is the sorbed concentration bound to the equilibrium sites, $S_2$ (mg kg⁻¹) is the sorbed concentration bound to the kinetic sites, $t$ (s) is time, $f_{eq}$ (-) is the fraction of total sites that are in equilibrium with the aqueous phase (i.e., $f_{eq}$ = 1 means that all sites are equilibrium sites), and $\lambda$ (s⁻¹) is the first-order rate coefficient of kinetic sorption.

When fitting the dynamic temperature sorption data to the two-site kinetic model, the average mass of AS-4 (m = 15 g) and the average volume of naphthalene solution (V = 53 ml) in the experiments were imposed. Sorption isotherm and rate model parameters were obtained using the Melder-Mead simplex algorithm and fminsearchbnd function in MATLAB (Lagarias et al., 1998; Purchase, 2007; D’Errico, 2012). The fitting minimized the value of the root mean square error (RMSE) which was used as a quantitative measure of the goodness of fit.

The enthalpies of sorption, $\Delta H_s$, of the two hydrocarbon compounds were calculated using the integrated van’t Hoff equation and the distribution coefficients of the sorption isotherms (Wang et al., 2011; Ngueleu et al., 2018):

$\Delta H_s=\frac{\ln K_{T_1}-\ln K_{T_2}}{\frac{1}{T_2}-\frac{1}{T_1}}\times R(9)$

where $T_1$ (K) and $T_2$ (K) are absolute temperatures; $K_{T_1}$ and $K_{T_2}$ are the distribution coefficients of the isotherms at $T_1$ and $T_2$, respectively; and R is the gas constant [8.314 × 10⁻³ kJ (mol K)⁻¹].

Results

Time-Series Sorption Experiments

Sorption of Benzene and Naphthalene at 25°C

The time-series concentrations of benzene (Figure 1A) and naphthalene (Figure 1B) remaining in the aqueous phase as well as their sorbed concentrations (Figures 1C,D) are normalized to the initial dissolved concentration ($C_0$ = 2 mg L⁻¹). Most of the compound removal from solution occurred during the first 2 h, at which time the fractions of benzene sorbed ($F_{sorb benz}$) to AS-1, AS-2, AS-3 and AS-4 were 7%, 20%, 4% and 20%, respectively. The corresponding $F_{sorb naph}$ values after 2 h were 53%, 84%, 50%, and 84%. Thus, more naphthalene sorbed to the artificial soil mixtures than benzene, and AS-2 and AS-4 sorbed more of the PHCs than AS-1 and AS-3. Beyond 2 h, little further sorption was observed. For example, after 48 h the $F_{sorb benz}$ values were 6%, 18%, 6%, 20% for sorption to AS-1, AS-2, AS-3, and AS-4, respectively, and for $F_{sorb naph}$ the values were 54%, 84%, 52%, 85%, respectively.

FIGURE 1

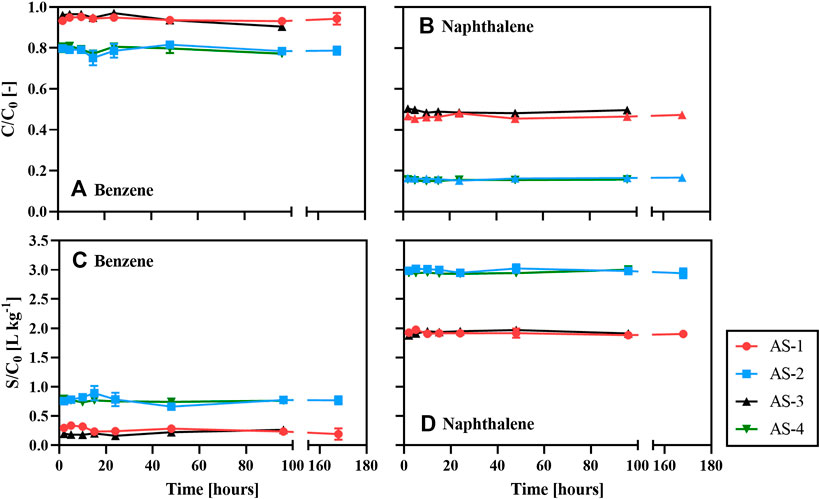
FIGURE 1. Normalized concentrations of aqueous benzene (A), aqueous naphthalene (B), sorbed benzene (C), and sorbed naphthalene (D) in the time-series sorption experiments with the four soil mixtures at 25°C.

Effects of Variable Organic Matter and Clay Contents

The relatively high sorption capacities of AS-2 and AS-4 can be attributed to their higher OM contents (5%), compared to those of AS-1 and AS-3 (1%, Table 1). This is consistent with the frequently reported dominant effect of soil OM on the sorption of benzene and naphthalene, especially at soil OC contents exceeding 0.1% (Karickhoff et al., 1979; Schwarzenbach and Westall, 1981; Redding et al., 2002). It is therefore common practice to normalize the fraction of sorbed hydrocarbon to the soil OC content ($F_{OC, sorb PHC}$, dimensionless) as follows:

$F_{OC, sorb PHC}=\frac{F_{sorb PHC}}{f_{OC}}(10)$

$$

where the values of $F_{sorbPHC}$ were those measured after 48 h of mixing, and $f_{OC}$ was the weight % of OC in the artificial soil mixture.

For benzene, the values of $F_{OC, sorb benz}$ were of comparable magnitudes for the four soil mixtures: 11.4 (AS-1), 8.2 (AS-2), 13.8 (AS-3), and 10.2 (AS-4). Thus, the high-OM mixtures yielded slightly lower $F_{OC, sorb benz}$ values. In contrast, for naphthalene much larger differences in $F_{OC, sorb naph}$ values were found between the high- and low-OM soil mixtures: 97.2 (AS-1), 37.4 (AS-2), 112.6 (AS-3), and 42.4 (AS-4).

Sorption of benzene and naphthalene to the artificial soil mixtures with the same OM content but different clay contents (i.e., AS-1 and AS-3, or AS-2 and AS-4) was undistinguishable (Figure 1). Hence, the montmorillonite content had no impact on the benzene and naphthalene sorption capacities. In contrast with our results, several previous studies (Sheng et al., 2001; Zhang et al., 2010; Yang et al., 2013; Martins et al., 2018) showed that clay minerals can be an important sorbent for organic contaminants. In our experiments, Ca²⁺ occupancy of the montmorillonite surface sites could have inhibited the sorption of benzene and naphthalene, possibly by shrinking the available sorption domains and/or changing the optimal interlayer spacing (Rogers et al., 1980; Sheng et al., 2001; Zhang et al., 2010). Because Ca²⁺ is a typical ion in natural soil solutions, we added it as the background electrolyte cation in our experiments (Pronk et al., 2012). This may have inadvertently suppressed the role of the clay mineral fraction.

Sorption of Benzene and Naphthalene at Different Temperatures

Because the OM content was the dominant factor controlling the sorption capacities of the AS mixtures, only AS-3 (1% OM) and AS-4 (5% OM) were selected to represent soils with low and high OC contents in the experiments where the temperature was the variable environmental factor. As described in Sorption and Desorption Experiments, sorption incubations were conducted at temperatures of 25, 10, and 3°C.

As with the prior sorption experiments that were performed at 25°C, most of the sorption occurred within the first 2 h at 10 and 3°C. Assuming that sorption equilibrium was assuredly reached after 48 h, the normalized concentrations of sorbed benzene and naphthalene to AS-3 were lower than those observed for AS-4 at all temperatures (Supplementary Figure S1), indicating that the OM content governed sorption capacities under the imposed experimental conditions. Benzene sorption was slightly less at 25°C than 3°C, in particular for AS-3. However, benzene sorption at 10°C was highest for AS-3 and lowest for AS-4. Thus, no clear temperature trend emerged for benzene sorption (Supplementary Figure S1A). By contrast, a systematic temperature dependence was observed for naphthalene: for sorption to both AS-3 and AS-4, the lowest, intermediate, and highest normalized sorbed concentrations were observed at 25, 10, and 3°C, respectively (Supplementary Figure S1B).

Dynamic Temperature Experiments

The sorption experiments conducted under static temperature revealed that the extent of sorption of naphthalene was not only much higher than for benzene, but also exhibited a consistent dependence on temperature. We therefore chose to use naphthalene and the high-OM soil AS-4 for the experiment where we imposed a dynamic temperature regime (Table 2).

Following the mixing of the dissolved naphthalene solution ($C_0$ = 5 mg L⁻¹) and AS-4 at 25°C, the concentration of aqueous naphthalene decreased by 85.2% (=$F_{sorb naph}$) within the first hour (Figure 2A). Between 24 and 48 h, the normalized concentration of sorbed naphthalene fluctuated somewhat until it reached 85.6% (=$F_{sorb naph}$) after 168 h. When the temperature was dropped from 25 to 10°C, sorbed naphthalene reached 87.9%, 88.9% and 88.7% after 0.5, 2, and 168 h after switching the temperature (or 336 h in cumulative time), respectively. With further decrease in the temperature to 3°C, $F_{sorb naph}$ values were 89.1%, 89.6%, and 88.9% after 0.5, 2, and 168 h after switching the temperature (or 504 h in cumulative time), respectively.

FIGURE 2

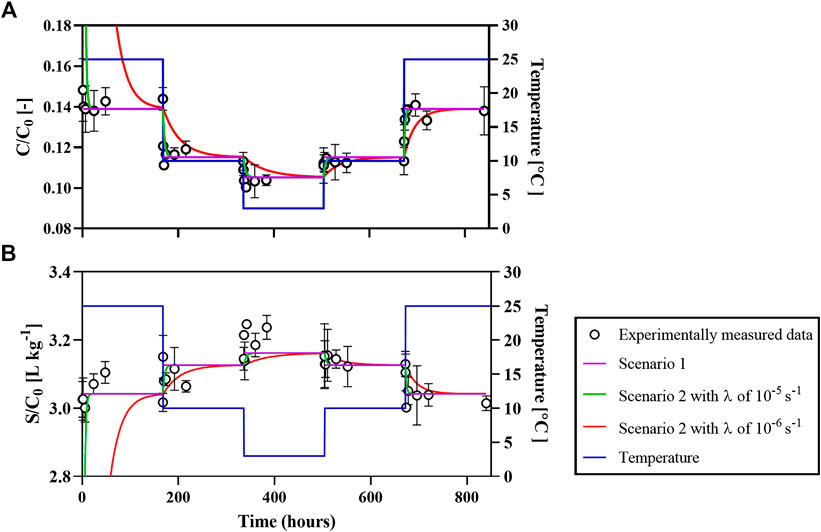
FIGURE 2. Normalized concentrations of aqueous naphthalene (A) and sorbed naphthalene (B) during incubation with AS-4 under dynamic temperature fluctuations (right Y axis). Experimentally measured data and model fits are plotted against the left Y axis. Scenario 1 assumes that AS-4 only carries equilibrium sorption sites (i.e., $f_{eq}$= 1), and scenario 2 only kinetic sites (i.e., $f_{eq}$= 0). The two simulations shown for scenario 2 are not the best fit to the model; they are included to show the expected behavior under kinetic limitation by imposing $\lambda$ values of 10⁻⁵ and 10⁻⁶ s⁻¹, respectively.

When the temperature was increased back from 3 to 10°C, naphthalene sorption decreased to 88.7% after 168 h (or 672 h in cumulative time). The further elevation of temperature from 10 to 25°C resulted in another drop of $F_{sorb naph}$ to 86.2% by the end of the experiment (or 840 hours in cumulative time). Whether during the stepwise decrease in temperature or the subsequent return to 25°C, the same $F_{sorb naph}$ values were observed at the same temperatures. (Note: the variations in $F_{sorb naph}$ at the three temperatures reflect slight variations in the soil and solution masses added to the experimental bottles.) Moreover, the sorption and desorption gradients (i.e., the changes in $F_{sorb naph}$ per °C) were the same between the temperature intervals of 25 to 10°C and 10 to 3°C, indicating a linear response of $F_{sorb naph}$ to changes in temperature.

At corresponding temperatures, somewhat higher fractions of sorbed naphthalene were observed in the dynamic temperature experiment compared to those in the time-series sorption experiments. The latter yielded values of 84.2%, 85.7%, and 88.5% at 25, 10, and 3°C, respectively. These differences are attributed to the slightly higher OC in the AS-4 batch used in the dynamic temperature experiment compared to all the other experiments with AS-4 (see Table 1).

Sorption Isotherms

The time-series sorption experiment showed that the sorption of benzene and naphthalene quickly reached equilibrium. Therefore, we derived the sorption isotherms from the data of the incubations of the different AS with benzene or naphthalene solutions measured after 48 h. For the range of hydrocarbon concentrations ($C_0$ = 1 to 13 mg L⁻¹) used in this study, the best fitting isotherm models were identified based on the smallest RMSE. For example, the Freundlich isotherm model yielded the best fit for benzene sorption to AS-1, AS-2, and AS-3 at 25°C, and to AS-3 at 10°C (Supplementary Table S2). However, when the Freundlich exponent $n_{Fr}$ approached 1 and the distribution coefficients $K_d$ and $K_{Fr}$ were comparable, the linear model was considered the better choice because of the smaller number of adjustable parameters. As a result, the data for naphthalene sorption to all four AS samples at all three temperatures, and the data for benzene sorption to AS-3 at 3°C and to AS-4 at 25, 10 and 3°C followed linear isotherms (Supplementary Table S2). Obviously, at sorbate concentrations higher than used here, these isotherms may potentially deviate from the linear model.

For benzene and naphthalene sorption at 25°C, the distribution coefficients $K_{Fr}$ (for the Freundlich isotherms) and $K_d$ (for the linear isotherms) were systematically lower for the low-OM soil mixtures (AS-1 and AS-3) and higher for the high-OM mixtures soil (AS-2 and AS-4). These results confirm the dominant control of the isotherms on the OM content also observed in the time-series incubations (Effects of Variable Organic Matter and Clay Contents). In addition, similar sorption isotherms were obtained for benzene at the different temperatures, regardless of the AS (Figure 3A). This is in line with the time-series sorption experiments that exhibited little temperature effect on benzene sorption. In contrast, naphthalene sorption isotherms were sensitive to the variable temperature. The naphthalene sorption isotherms to AS-3 and AS-4 generally generated the lowest $K_d$ values at 25°C and the highest values at 3°C, although the values were close at 10 and 3°C (Figure 3B; Supplementary Table S2).

FIGURE 3

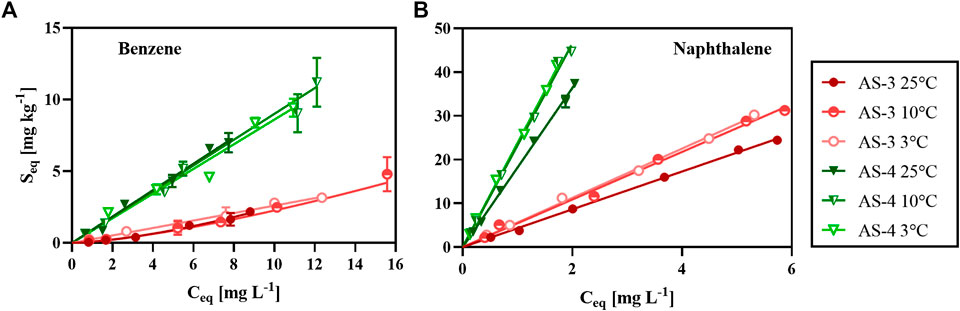
FIGURE 3. Sorption isotherms of benzene (A) and naphthalene (B) for AS-3 and AS-4 at 25, 10, and 3°C. Experimentally measured data for benzene with AS-3 at 25 and 10°C (solid and half-filled circles in A) were fitted to the Freundlich isotherm model (slightly curved lines in A) and all other data (circles and triangles in A and B) were fitted to the linear isotherm model (straight lines).

Discussion

Comparing Organic Carbon-Water Partition Coefficients

The organic carbon-water partition coefficients $K_{OC,L}$ (L kg⁻¹) and $K_{OC, Fr}$ (${\text{mg}}^{1-{\text{n}}_{\text{Fr}}}{\text{L}}^{{\text{n}}_{\text{Fr}}}{\text{kg}}^{-1}$) of naphthalene and benzene are calculated using equations:

$K_{OC,L}=\frac{K_d}{f_{OC}}(11)$

$K_{OC,Fr}=\frac{K_{Fr}}{f_{OC}}(12)$

Benzene exhibits a lower affinity to the AS than naphthalene: for benzene, $K_{OC,L}$ (43–46 L kg⁻¹) and $K_{OC,Fr}$ values (17–57 ${\text{mg}}^{1-{\text{n}}_{\text{Fr}}}{\text{L}}^{{\text{n}}_{\text{Fr}}}{\text{kg}}^{-1}$) are much lower than the $K_{OC,L}$ values for naphthalene (773–1,224 L kg⁻¹) under all the conditions imposed in this study. At 25°C, the $K_{OC}$ values of benzene vary to a greater extent between the AS with different OC contents than those of naphthalene: the relative standard deviations for benzene’s and naphthalene’s $K_{OC}$ values are 46% and 9.3%, respectively.

The large differences in partition coefficients between naphthalene and benzene likely reflect differences in sorption mechanisms. The higher $K_{OC}$ value for naphthalene sorption compared to benzene indicates a stronger affinity for binding to OM, probably due to the higher hydrophobicity of naphthalene. In addition, the $F_{OC, sorb naph}$ values for the low-OM AS (AS-1 and AS-3) are almost triple those of the high-OM AS (AS-2 and AS-4). We speculate that the correspondingly higher sorption densities per unit mass OC of AS-1 and AS-3 may reflect multi-layer sorption to the OM. That is, once naphthalene starts attaching to the OM, the next naphthalene molecules may sorb preferentially to the already attached naphthalene, a process also known as cooperative adsorption (Halsey, 1948; Schwarzenbach et al., 2002; Liu, 2015). In contrast, the differences in $F_{OC, sorb benz}$ values between the four AS are relatively small (Effects of Variable Organic Matter and Clay Contents), presumably indicating a lesser role of multi-layer sorption for benzene.

Temperature Sensitivity and Sorption Enthalpy

The partitioning coefficients derived from the sorption isotherm experiments at 3 and 25°C yield $\Delta H_s$ values (Eq. 9) for naphthalene with AS-3 and AS-4 of −8.2 and −8.4 kJ mol⁻¹, respectively. These negative and relatively small $\Delta H_s$ values imply that sorption to AS-3 and AS-4 is exothermic and that van der Waals forces are mainly responsible for the binding of naphthalene, which is consistent with it being a hydrophobic compound (ten Hulscher and Cornelissen, 1996; Wang et al., 2011). Because of the negative $\Delta H_s$ values, naphthalene sorption to the AS increases with decreasing temperature.

Benzene’s sorption enthalpy with AS-4 ($\Delta H_s$ = 2.1 kJ mol⁻¹) is positive with an absolute value that is four times smaller than the values for naphthalene. This implies weaker binding of benzene to AS-4 compared to naphthalene. In addition, benzene sorption should be slightly endothermic. The small absolute $\Delta H_s$ value is consistent with a lower temperature dependence of sorption for benzene than for naphthalene (Goring and Hamaker, 1972; ten Hulscher and Cornelissen, 1996). It is important to keep in mind that Eq. 9 computes $\Delta H_s$ values using conditional partition coefficients rather than true thermodynamic equilibrium constants. Therefore, the corresponding $\Delta H_s$ values are conditional enthalpies, valid for the particular soil and solution compositions under which they were obtained.

By extension, for PHC compounds other than naphthalene and benzene, reported sorption enthalpies with organic carbon sorbents could be used as a first indicator to predict how their sorption to soil OC may be affected by temperature. An important control on the magnitude of the sorption enthalpy is likely the compounds’ size expressed by the number of carbon atoms (Campbell and Sellers, 2013). Longer PHCs with more carbon atoms should be expected to have larger negative $\Delta H_s$ values and, therefore, higher sensitivities of their sorption/desorption behavior to changes in temperature. Thus, $\Delta H_s$ emerges as a key predictor in a broader modeling framework to predict the mobility and bioavailability of PHCs in subsurface environments under varying conditions, including variable temperature.

Reversible Naphthalene Sorption Under Dynamic Temperature Fluctuations

Visual inspection of Figure 2 shows that the temperature dependent naphthalene sorption and desorption reactions are fully reversible. Thermodynamically controlled reversible sorption of naphthalene to AS-4 is also readily evident from the results of the two-site sorption modeling (Mathematical Modeling) for the following three scenarios. In scenario 1, binding to AS-4 only occurs at equilibrium sorption sites (i.e., $f_{eq}$ = 1). Oppositely, scenario 2 assumes binding to kinetic sorption sites only (i.e., $f_{eq}$ = 0). Scenario 3 represents a combination of the previous two scenarios, with both equilibrium and kinetic sorption sites. The best model fitting parameters for the three scenarios are listed in Table 3.

TABLE 3

TABLE 3. The best fitting parameters of three scenarios using a two-site kinetic model for naphthalene sorption to AS-4 under the imposed dynamic temperature regime.

In scenario 1, naphthalene sorption to AS-4 reaches equilibrium instantaneously. Therefore, the concentration dynamics of sorbed naphthalene are only a function of the $K_d$ values at the three temperatures (Table 3). The model-fitted $K_d$ values in Table 3 are somewhat larger than those obtained from the sorption isotherm experiments (Supplementary Table S2). This likely reflects the higher $f_{OC}$ of the AS-4 used in the dynamic temperature experiments (2.20%) relative to the AS-4 used in the sorption isotherm experiments (1.99%) (see Supplementary Material S1 for further details). The simulation results of scenario 1 shown in Figure 2 show excellent agreement with the experimentally measured data points.

In scenario 2, the $K_d$ values are fixed at each of the three temperatures to the values obtained in scenario 1. Naphthalene sorption is then only a function of the rate coefficient $\lambda$. The best fit values of $\lambda$ are in the range 10⁻⁴ to 10⁻³ s⁻¹ (Table 3), indicating that the mass transfer of naphthalene from the aqueous phase to the sorption sites occurs on a time scale of 10² to 10³ s (=reciprocal of $\lambda$). In turn, this implies that most mass transfer after a temperature switch occurred before the first sampling point. In other words, the reaction kinetics are too fast to be captured by our observations. Because equilibrium is approached within minutes, the simulated naphthalene time series in scenario 2 are nearly identical to the simulation results of scenario 1 (data not shown). As shown in Figure 2, in order to observe a kinetic effect, $\lambda$ values would have to drop to 10⁻⁵ s⁻¹ or less. A value of 10⁻⁵ s⁻¹, which corresponds to a time scale of reaction of days, is compatible with previous studies on the sorption and desorption kinetics of naphthalene (Piatt et al., 1996; Ngueleu et al., 2018). When the value of $\lambda$ values is decreased further to 10⁻⁶ s⁻¹ in scenario 2 (Figure 2), kinetic lag times should become a dominant feature during each temperature segment and cause sorption/desorption hysteresis. Such features, however are not observed in our experimentally measured data.

The modeling results of scenario 3 are in line with the previous simulations. The best fits imply that most (97%) of sorption sites are equilibrium sites (Table 3). Since $f_{eq}$ is close to 1 and $S_2$ is very small, there are negligible differences in the simulated time-series aqueous and sorbed naphthalene concentrations when imposing $\lambda$ values between 10⁻² and 10⁻¹⁰ s⁻¹. In other words, the choice of a λ value in this range is arbitrary and meaningless. Ultimately, the reaction behavior predicted by scenario 3 is effectively identical to scenario 1.

In summary, sorption and desorption are reversible under the imposed dynamic temperature changes. The sorption enthalpy derived from the $K_d$ values in Table 3 ($\Delta H_s$ = −9.9 kJ mol⁻¹) confirm the relatively weak binding of naphthalene to AS-4, which in turn helps explain the prompt desorption during the temperature increases.

Implications

The dynamic temperature experiment in Figure 2 demonstrates in a very direct way the very fast and reversible sorption and desorption of naphthalene driven by changes in temperature: sequestration by the OM in AS-4 increases when temperature decreases and vice versa. Furthermore, the temperature sensitivity of the partitioning coefficients of benzene and naphthalene are related to their enthalpies of sorption. The latter are a function of both the molecular structure of the sorbate compound (e.g., the molecular length and aromaticity) and the nature of the binding sites of the soil matrix. In a similar fashion, the $K_{OC}$ (organic carbon-water partition coefficient) values for different PHC compounds can be related to compound-specific properties (e.g., molar volume, hexadecane-air partition coefficient) that have been experimentally determined for many organic compounds, as well as fitting parameters that account for variable soil OM properties (Nguyen et al., 2005; Endo et al., 2009; Endo and Goss, 2014). Thus, in principle, it should be possible to establish a thermodynamics-informed framework to predict the mobility of PHCs in soils that are exposed to fluctuating temperature regimes, for example during the fall and spring shoulder seasons. The development of such a framework takes on enhanced significance given the ongoing climate warming.

While our study focuses on the temperature effects on abiotic sorption and desorption, other soil reaction processes, including microbially-catalyzed reactions, are temperature-dependent. Microbial activity typically increases with increasing temperature until some optimum temperature is reached (Hobbs et al., 2013). Thus, for example, we would expect that rising soil temperatures in spring would have a dual impact on the bioavailability and degradation of compounds such as naphthalene: 1) desorption of the compound from the soil matrix into the aqueous, bioavailable pool, and 2) higher microbial biodegradation rates of the soluble compound, at least as long as the temperature remains below the temperature optimum. Several approaches exist to predict the effect of temperature on microbial biodegradation rates, such as macromolecular rate theory (MMRT) (Hobbs et al., 2013; Schipper et al., 2014), which accounts for the temperature optimum, or Arrhenius-type relationships (Dale et al., 2006), which do not estimate a temperature optimum. Note, however, that desorption of a PHC does not just increase its bioavailability but may also induce toxic effects to soil biota.

Natural soils are spatially heterogenous with pore spaces and small cavities of various sizes and geometries, which may affect the macroscopic sorption/desorption dynamics of PHCs. These effects are not addressed with the well-mixed artificial soils used in this study. In addition, we used single compounds (benzene and naphthalene) in the experiments to advance our fundamental understanding of the sorption and desorption reactions. However, PHC contamination in the field normally involves mixtures of compounds that may partition over soil, water and gas phases. Future work may therefore focus on testing the extent to which the knowledge of simple systems, such as the ones used here, can be extrapolated to more complex, real-world soil-PHC systems. Moreover, further insights on the mechanisms of PHC interactions with natural soils may require the use of advanced molecular analysis tools.

Conclusions

Under the imposed experimental conditions in this study, the extent of sorption of benzene was significantly lower than that of naphthalene, regardless of temperature and the soil mixture used. We attribute this to the higher $K_{OC}$, larger molecular size, and higher hydrophobicity of naphthalene. Using a unique artificial soil approach, we showed that the clay mineral used had a limited effect on the sorption of benzene and naphthalene, whereas higher organic matter concentrations enhanced the sorption capacities for both organic compounds. Thus, our results provide further evidence that the soil organic matter content, more so than the clay mineral content, is the dominant factor controlling benzene and naphthalene sorption. Temperature had little effect on benzene sorption, which was consistent with a very low absolute magnitude of the sorption enthalpy. We demonstrated the temperature sensitivity and reversibility of naphthalene sorption and desorption by imposing a dynamic temperature regime to an artificial soil-naphthalene suspension. Higher and lower fractions of sorbed naphthalene were observed under cooler and warmer conditions, respectively. That is, the partition coefficient of naphthalene increased with decreasing temperature.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Conflict of Interest

Author KS was employed by the company Imperial Oil. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Author contributions

BS and SN contributed equally to this study in laboratory experiments, data processing and writing the manuscript. SN, FR, PVC, CS, and GP designed the experiments. SN was responsible for the two-site model simulations. PVC and FR supervised the work and helped BS and SN interpret the data. All authors contributed to the preparation of the manuscript and have approved its final version.

Funding

Funding was provided by the Canada Excellence Research Chair (CERC) program, two Natural Sciences and Engineering Research Council Partnership Grants with Imperial Oil Resources Ltd. (Engage Grant to Rezanezhad: EGP-516205-17, Collaborative Research and Development Grant to Van Cappellen: CRDPJ: 533227-18), and Qatar National Research Fund (NPRP9-93-1-021).

Acknowledgments

The authors thank Marianne Vandergriendt, Shirley Chatten, Sierra Cranmer-Smith, and Lindsay Norwood for their assistance with laboratory experiments and analyses.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvc.2020.581103/full#supplementary-material

References

Al-Bashir, B., Cseh, T., Leduc, R., and Samson, R. (1990). Effect of soil/contaminant interactions on the biodegradation of naphthalene in flooded soil under denitrifying conditions. Appl. Microbiol. Biotechnol. 34, 414–419. doi:10.1007/BF00170071

CrossRef Full Text | pubmed | Google Scholar

Campbell, C. T., and Sellers, J. R. V. (2013). Enthalpies and entropies of adsorption on well-defined oxide surfaces: Experimental measurements. Chem. Rev. 113, 4106–4135. doi:10.1021/cr300329s

Google Scholar

Conte, P., Zena, A., Pilidis, G., and Piccolo, A. (2001). Increased retention of polycyclic aromatic hydrocarbons in soils induced by soil treatment with humic substances. Environ. Pollut. 112, 27–31. doi:10.1016/S0269-7491(00)00101-9

Google Scholar

D’Errico, J. (2012). Fminsearchbnd, fminsearchcon (bound constrained optimization using fminsearch). MATLAB Central File Exchange. Available at: http://www.mathworks.com/matlabcentral/fileexchange/8277-fminsearchbnd-fminsearchcon. (Accessed March 30, 2020).

Google Scholar

Dale, A. W., Regnier, P., and Van Cappellen, P. (2006). Bioenergetic controls on anaerobic oxidation of methane (AOM) in coastal marine sediments: a theoretical analysis. Am. J. Sci. 306, 246–294. doi:10.2475/ajs.306.4.246

CrossRef Full Text | Google Scholar

Das, N., and Chandran, P. (2011). Microbial degradation of petroleum hydrocarbon contaminants: an overview. Biotechnol. Res. Int. 2011, 1–13. doi:10.4061/2011/941810

CrossRef Full Text| Google Scholar

Endo, S., and Goss, K.-U. (2014). Applications of polyparameter linear free energy relationships in environmental chemistry. Environ. Sci. Technol. 48, 12477–12491. doi:10.1021/es503369t

CrossRef Full Text | Google Scholar

Endo, S., Grathwohl, P., Haderlein, S. B., and Schmidt, T. C. (2009). LFERs for soil organic carbon−water distribution coefficients (Koc) at environmentally relevant sorbate concentrations. Environ. Sci. Technol. 43, 3094–3100. doi:10.1021/es803157e

CrossRef Full Text | Google Scholar

Falciglia, P. P., Giustra, M. G., and Vagliasindi, F. G. A. (2011). Low-temperature thermal desorption of diesel polluted soil: influence of temperature and soil texture on contaminant removal kinetics. J. Hazard Mater. 185, 392–400. doi:10.1016/j.jhazmat.2010.09.046

CrossRef Full Text | pubmed | Google Scholar

Fine, P., Graber, E. R., and Yaron, B. (1997). Soil interactions with petroleum hydrocarbons: abiotic processes. Soil Technol. 10, 133–153. doi:10.1016/S0933-3630(96)00088-8

CrossRef Full Text | Google Scholar

Garg, S., Newell, C. J., Kulkarni, P. R., King, D. C., Adamson, D. T., Renno, M. I., et al. (2017). Overview of natural source zone depletion: processes, controlling factors, and composition change. Groundwater Monit R 37, 62–81. doi:10.1111/gwmr.12219

CrossRef Full Text | Google Scholar

Geng, X., Boufadel, M. C., Lee, K., Abrams, S., and Suidan, M. (2015). Biodegradation of subsurface oil in a tidally influenced sand beach: impact of hydraulics and interaction with pore water chemistry. Water Resour. Res. 51, 3193–3218. doi:10.1002/2014WR016870

CrossRef Full Text | Google Scholar

Goring, C. A. I., and Hamaker, J. W. (1972). Organic chemicals in the soil environment. New York, NY: Marcel Dekker, Inc.

Google Scholar

Grathwohl, P. (1990). Influence of organic matter from soils and sediments from various origins on the sorption of some chlorinated aliphatic hydrocarbons: implications on Koc correlations. Environ. Sci. Technol. 24, 1687–1693. doi:10.1021/es00081a010

CrossRef Full Text | Google Scholar

Guerin, W. F., and Boyd, S. A. (1992). Differential bioavailability of soil-sorbed naphthalene to two bacterial species. Appl. Environ. Microbiol. 58, 1142–1152. doi:10.1128/aem.58.4.1142-1152.1992

CrossRef Full Text | pubmed | Google Scholar

Halsey, G. (1948). Physical adsorption on non‐uniform surfaces. J. Chem. Phys. 16, 931–937. doi:10.1063/1.1746689

CrossRef Full Text | Google Scholar

Hobbs, J. K., Jiao, W., Easter, A. D., Parker, E. J., Schipper, L. A., and Arcus, V. L. (2013). Change in heat capacity for enzyme catalysis determines temperature dependence of enzyme catalyzed rates. ACS Chem. Biol. 8, 2388–2393. doi:10.1021/cb4005029

CrossRef Full Text | pubmed | Google Scholar

ITOPF (2019). Oil tanker spill statistics 2018. Available at: http://www.itopf.org/fileadmin/data/Documents/Company_Lit/Oil_Spill_Stats_2018.pdf (Accessed July 25, 2019).

Google Scholar

Karickhoff, S., Brown, D., and Scott, T. (1979). Sorption of hydrophobic pollutants on natural sediments. Water Res. 13, 241–248. doi:10.1016/0043-1354(79)90201-X

CrossRef Full Text | Google Scholar

Lagarias, J. C., Reeds, J. A., Wright, M. H., and Wright, P. E. (1998). Convergence properties of the nelder-mead simplex method in low dimensions. SIAM J. Optim. 9, 112–147. doi:10.1137/S1052623496303470

CrossRef Full Text | Google Scholar

Liu, S. (2015). Cooperative adsorption on solid surfaces. J. Colloid Interface Sci. 450, 224–238. doi:10.1016/j.jcis.2015.03.013

CrossRef Full Text | pubmed | Google Scholar

Maraqa, M. A., and Khashan, S. A. (2014). Modeling solute transport affected by heterogeneous sorption kinetics using single-rate nonequilibrium approaches. J. Contam. Hydrol. 157, 73–86. doi:10.1016/j.jconhyd.2013.11.005

CrossRef Full Text | Pubmed | Google Scholar

Martins, E. C., de Freitas Melo, V., Bohone, J. B., and Abate, G. (2018). Sorption and desorption of atrazine on soils: the effect of different soil fractions. Geoderma 322, 131–139. doi:10.1016/j.geoderma.2018.02.028

CrossRef Full Text | Google Scholar

Means, J. C., Wood, S. G., Hassett, J. J., and Banwart, W. L. (1980). Sorption of polynuclear aromatic hydrocarbons by sediments and soils. Environ. Sci. Technol. 14, 1524–1528. doi:10.1021/es60172a005

CrossRef Full Text | Google Scholar

Mihelcic, J. R., and Luthy, R. G. (1991). Sorption and microbial degradation of naphthalene in soil-water suspensions under denitrification conditions. Environ. Sci. Technol. 25, 169–177. doi:10.1021/es00013a020

CrossRef Full Text | Google Scholar

Ngueleu, S. K., Rezanezhad, F., Al-Raoush, R. I., and Van Cappellen, P. (2018). Sorption of benzene and naphthalene on (semi)-arid coastal soil as a function of salinity and temperature. J. Contam. Hydrol. 219, 61–71. doi:10.1016/j.jconhyd.2018.11.001

CrossRef Full Text | Pubmed | Google Scholar

Ngueleu, S. K., Al-Raoush, R. I., Shafieiyoun, S., Rezanezhad, F., and Van Cappellen, P. (2019). Biodegradation kinetics of benzene and naphthalene in the vadose and saturated zones of a (semi)-arid saline coastal soil environment. Geofluids 2019, 1–15. doi:10.1155/2019/8124716

CrossRef Full Text | Google Scholar

Nguyen, T. H., Goss, K.-U., and Ball, W. P. (2005). Polyparameter linear free energy relationships for estimating the equilibrium partition of organic compounds between water and the natural organic matter in soils and sediments. Environ. Sci. Technol. 39, 913–924. doi:10.1021/es048839s

CrossRef Full Text | Google Scholar

Onwurah, I. N. E., Ogugua, V. N., Onyike, N. B., Ochonogor, A. E., and Otitoju, O. F. (2007). Crude oil spills in the environment, effects and some innovative clean-up biotechnologies. Int. J. Environ. Res. 1, 307–320. doi:10.22059/IJER.2010.142

Google Scholar

Piatt, J. J., Backhus, D. A., Capel, P. D., and Eisenreich, S. J. (1996). Temperature-dependent sorption of naphthalene, phenanthrene, and pyrene to low organic carbon aquifer sediments. Environ. Sci. Technol. 30, 751–760. doi:10.1021/es9406288

CrossRef Full Text | Google Scholar

Pignatello, J. J. (2012). Dynamic interactions of natural organic matter and organic compounds. J. Soils Sediments 12, 1241–1256. doi:10.1007/s11368-012-0490-4

CrossRef Full Text | Google Scholar

Pronk, G. J., Heister, K., Ding, G. C., Smalla, K., and Kögel-Knabner, I. (2012). Development of biogeochemical interfaces in an artificial soil incubation experiment; aggregation and formation of organo-mineral associations. Geoderma 189–190, 585–594. doi:10.1016/j.geoderma.2012.05.020

CrossRef Full Text | Google Scholar

Purchase, K. (2007). Fminsearchbnd new (improved bounded fminsearch algorithm). MATLAB Central File Exchange. Available at: https://www.mathworks.com/matlabcentral/fileexchange/17804-fminsearchbnd-new (Accessed March 30, 2020).

Google Scholar

Redding, A. Z., Burns, S. E., Upson, R. T., and Anderson, E. F. (2002). Organoclay sorption of benzene as a function of total organic carbon content. J. Colloid Interface Sci. 250, 261–264. doi:10.1006/jcis.2001.8205

CrossRef Full Text | pubmed | Google Scholar

Rogers, R. D., McFarlane, J. C., and Cross, A. J. (1980). Adsorption and desorption of benzene in two soils and montmorillonite clay. Environ. Sci. Technol. 14, 457–460. doi:10.1021/es60164a005

CrossRef Full Text | Google Scholar

Schipper, L. A., Hobbs, J. K., Rutledge, S., and Arcus, V. L. (2014). Thermodynamic theory explains the temperature optima of soil microbial processes and high Q 10 values at low temperatures. Global Change Biol. 20, 3578–3586. doi:10.1111/gcb.12596

CrossRef Full Text | pubmed | Google Scholar

Schwarzenbach, R. P., Gschwend, P. M., and Imboden, D. M. (2002). Environmental organic chemistry. Hoboken, NJ, USA: John Wiley & Sons, Inc. doi:10.1002/0471649643

Google Scholar

Sheng, G., Johnston, C. T., Teppen, B. J., and Boyd, S. A. (2001). Potential contributions of smectite clays and organic matter to pesticide retention in soils. J. Agric. Food Chem. 49, 2899–2907. doi:10.1021/jf001485d

CrossRef Full Text | Pubmed | Google Scholar

Šimůnek, J., and van Genuchten, M. T. (2008). Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 7, 782–797. doi:10.2136/vzj2007.0074

Google Scholar

ten Hulscher, T. E. M., and Cornelissen, G. (1996). Effect of temperature on sorption equilibrium and sorption kinetics of organic micropollutants - a review. Chemosphere 32, 609–626. doi:10.1016/0045-6535(95)00345-2

CrossRef Full Text | Google Scholar

Tremblay, L., Kohl, S. D., Rice, J. A., and Gagné, J.-P. (2005). Effects of temperature, salinity, and dissolved humic substances on the sorption of polycyclic aromatic hydrocarbons to estuarine particles. Mar. Chem. 96, 21–34. doi:10.1016/j.marchem.2004.10.004

CrossRef Full Text | Google Scholar

Varjani, S. J. (2017). Microbial degradation of petroleum hydrocarbons. Bioresour. Technol. 223, 277–286. doi:10.1016/j.biortech.2016.10.037

CrossRef Full Text | Pubmed | Google Scholar

Wang, G., Kleineidam, S., and Grathwohl, P. (2007). Sorption/desorption reversibility of phenanthrene in soils and carbonaceous materials. Environ. Sci. Technol. 41, 1186–1193. doi:10.1021/es060805s

CrossRef Full Text | Google Scholar

Wang, L., Yang, Z., and Niu, J. (2011). Temperature-dependent sorption of polycyclic aromatic hydrocarbons on natural and treated sediments. Chemosphere 82, 895–900. doi:10.1016/j.chemosphere.2010.10.054

CrossRef Full Text | pubmed | Google Scholar

Yang, L., Jin, M., Tong, C., and Xie, S. (2013). Study of dynamic sorption and desorption of polycyclic aromatic hydrocarbons in silty-clay soil. J. Hazard Mater. 244–245, 77–85. doi:10.1016/j.jhazmat.2012.11.029

CrossRef Full Text | pubmed | Google Scholar

Zhang, W., Ding, Y., Boyd, S. A., Teppen, B. J., and Li, H. (2010). Sorption and desorption of carbamazepine from water by smectite clays. Chemosphere 81, 954–960. doi:10.1016/j.chemosphere.2010.07.053

CrossRef Full Text | pubmed | Google Scholar