- 1School for the Environment, University of Massachusetts Boston, Boston, MA, United States
- 2State Key Laboratory of Marine Environmental Science, College of Ocean and Earth Sciences, Xiamen University, Xiamen, China
- 3Department of Biology, The University of North Carolina at Greensboro, Greensboro, NC, United States
Commonly we see the diffuse attenuation coefficient of downwelling irradiance (Kd) expressed as a sum of the contributions of various constituents. We show here that, both theoretically and numerically, because Kd is an apparent optical property (AOP), this approach is not consistent with radiative transfer. We further advocate the application of models of Kd developed in past decades that are not only consistent with radiative transfer but also provide more accurate estimates, in particular for coastal turbid waters.
Background
Solar radiation is the energy source for the entire earth system. In aquatic environments, unlike terrestrial environments, solar radiation can penetrate to great depths to fuel photosynthesis and to heat up the upper layer (Zaneveld et al., 1981; Platt, 1986; Lewis et al., 1990). The propagation of solar radiation from surface to greater depths can be expressed as (Mobley, 1994)
Here Ed (W/m2/nm) is the downwelling irradiance, z (m) is the depth from the surface (0− for subsurface), Kd (m−1) is the attenuation coefficient of downwelling irradiance between surface and depth z, and λ (nm) for wavelength. Since the variation of Ed(0−) is independent of water properties (except extremely turbid waters where the enhanced upwelling flux will result in significant contributions to Ed(0−) due to internal reflection), it is then imperative to describe the variation of Kd for various aquatic environments when quantifying the impact of water constituents on the heat budget (Morel and Antoine, 1994; Ohlmann et al., 2000), the feedback of oceanic systems on climate changes (Rochford et al., 2001; Gnanadesikan and Anderson, 2009), as well as the vertical variation of primary production (Sathyendranath and Platt, 1995).
Historically, with an objective of easy modeling and efficient calculation for large scale applications, Kd is commonly expressed as (Smith and Baker, 1978; Morel, 1988; Morel and Maritorena, 2001),
with Kw the contribution of pure (sea)water, and Kbio the contributions of phytoplankton. In this expression, i.e., the so-called “Case-1” scheme (Morel and Prieur, 1977), the attenuation of pure (sea)water is considered as a background, while other constituents that are actively changing, such as phytoplankton and suspended mineral solids, are considered as added contributions. In addition, the contributions of colored dissolved organic matter (CDOM) and organic detritus are considered as co-varying with phytoplankton, and lumped into the Kbio term. So their contributions are not ignored or omitted as might be implied by the equation, although its application is limited to “Case-1” waters.
In order to explicitly evaluate and understand the impact of constituents such as CDOM and/or suspended mineral particles or particulate inorganic matter (PIM) on the propagation of solar radiation, Kd in many studies is expanded as a sum of more components, although there are subtle variations among these models (Smith and Baker, 1978; Baker and Smith, 1982; Gallegos et al., 1990; Devlin et al., 2009; Kim et al., 2015),
Here KCDOM and KPIM are the diffuse attenuation coefficients resulted from CDOM and PIM, respectively. In essence, these biogeo-optical models of Kd effectively treat Kd, an apparent optical property (AOP) (Preisendorfer, 1976), as an inherent optical property (IOP) (Preisendorfer, 1976), which is not consistent with the definitions and the nature of variations of Kd (Stavn, 1988). The attitude of treating Kd as an IOP might stem from that Kd of “Case 1” water, after correcting for the sun angle effect, can be considered as a “quasi” IOP (Gordon, 1989). However, it was never claimed that this would work in any other water types than “Case 1” water. Many subsequent studies have, for the most part, somehow ignored these limitations in applications.
Fundamentally Kd is sun-angle dependent (Stavn, 1988; Mobley, 1994) (also weakly dependent on atmospheric properties). So, considering the model of Morel and Maritorena (2001), it is specifically stated that the model and the empirical coefficients (Equation 3 in Morel and Maritorena, 2001) are valid just for low zenith sun angles. But this restriction has in fact largely been ignored by the research community, which leads to inconsistent applications and errors. For instance, if we use this model for early morning or late afternoon situations, because of the likely large sun angle, this can easily result in 30% or greater errors in estimating Kd (Morel et al., 2002; Lee et al., 2005b). In the following, we demonstrate the non-additive nature of Kd theoretically and numerically.
Theoretical Model of Kd
Based on radiative transfer, Kd is a function of IOPs (especially the absorption, a, and backscattering, bb, coefficients) as (Lee et al., 2005b),
Here μd (μu) is the average cosine and rd (ru) is the shape factor for the downwelling (upwelling) light field (Stavn and Weidemann, 1989), respectively. R is the irradiance reflectance (Gordon et al., 1975). Through numerical simulations via Hydrolight, it was found that the above expression could be simplified as (Lee et al., 2005b)
with m0−3 constants that are independent of wavelength and water properties. Note that these model parameters vary weakly with depth (Lee et al., 2005b) due to changes of light field structure, consistent with the change of μd with depth (Stavn, 1988; Berwald et al., 1995; McCormick, 1995). Also note that for large zenith angles, the forward scattering coefficient will also contribute to the diffuse attenuation coefficient through its contribution to μd, μu, rd and ru (Stavn and Weidemann, 1989). Mathematically, Equation (5) can be rewritten as,
Consequently, although a(λ) and bb(λ) are additive, a nature of IOPs, the interaction term between a(λ) and bb(λ) (the third term on the right side of Equation 6) is not additive, thus Kd cannot be additive—a general nature of AOPs. This characteristic is further highlighted in details below.
For simplicity, let's consider a medium has just two constituents: pure seawater and suspended inorganic mineral particles (PIM). For pure seawater alone, following Equation (6), there is
Here aw(λ) and bbw(λ) are the spectral absorption and backscattering coefficients of pure seawater.
For suspended inorganic mineral particles alone,
with aPIM and bbPIM being the absorption and backscattering coefficients of suspended mineral particles.
Therefore, a sum () of the two contributions to Kd following Equations (2) and (3) resulted in,
However, when the medium is composed of both pure seawater and suspended mineral particles, its Kd following radiative transfer (Equation 6) is
Clearly, as shown above, when there are more constituents, because the light field is determined by the bulk properties (Stavn, 1988; Stavn and Weidemann, 1989; Lee et al., 2005b), aw and aPIM will affect the contribution of both bbw and bbPIM to Kd. However, when Kd is treated as an additive property of Kw and KPIM, the effect of aw on the contribution of bbPIM and the effect of aPIM on the contribution of bbw are excluded.
Numerical Demonstration
To demonstrate the above point numerically, Figure 1 compares Kd spectra from Hydrolight (Mobley and Sundman, 2013) simulations with , where the two component spectra (Kw and KPIM) were also obtained from Hydrolight simulations using the same constituents as for Kd. Specifically, spectral (400–800 nm, 10 nm interval) Ed(z) were simulated with Hydrolight, and Kd between surface and z is calculated following
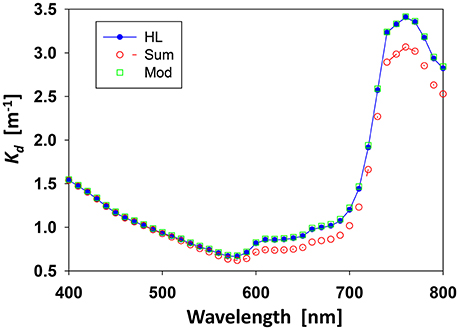
Figure 1. Comparison of Kd spectra between Hydrolight simulation (blue), sum of individual components (red), and that from semi-analytical model based on bulk IOPs (green). The range for Kd is between surface and 5 m.
For the derivation of Kw from Hydrolight, all other constituents were held to 0 except for the properties of pure seawater. Values of aw are a combination of Lee et al. (2015) and Pope and Fry (1997) while values of bbw are those of Morel (1974). For the derivation of KPIM from Hydrolight, PIM was set as 10 g/m3 and the default optical model parameters for suspended minerals included in Hydrolight were used to get the absorption and scattering coefficients of PIM. Note that this PIM concentration is just a low-medium value for turbid coastal waters (Babin et al., 2003; Doxaran et al., 2009). For this simulation, an idealized “transparent pure seawater” was used where very low values of aw (0.1 × 10−4 m−1) and bbw (0.5 × 10−5 m−1) were employed. With such a setup the contribution of this “transparent pure seawater” to the calculated Kd (Equation 11) is then negligible, and the resultant Kd from Hydrolight simulations can be considered as KPIM. The sun angle for all simulations for both Kw and KPIM was set as 30° from zenith along with a clear sky.
There are distinct differences in Kd (at least for this case) in the longer wavelengths (~10–15% for the 600–800 nm range), where aw makes significant contributions to the total a; and this contribution, when there are sediments, to Kd is not represented in the additive descriptions of Kd (the red curve). For the shorter wavelengths (<~500 nm), because most (>~98%) of the contributions to Kd comes from PIM, the sum of the two terms match the bulk results well. Certainly the impact of the non-additive nature of Kd depends on the values of both a and bb. For “Case-1” waters or waters where the scattering coefficients are relatively small, it might be applicable, without great errors, to treat Kd(λ) as an additive property. However, this will depend on the validity of the above-mentioned assumptions. While not based on any assumptions of “Case-1” conditions or dependencies, the modeled Kd spectrum following Equation 5 is in an excellent agreement with the Hydrolight Kd spectrum (~1% differences, see Figure 1), which highlights the much wider applicability of models based on radiative transfer. And, the robust performance of this model was also demonstrated in Zimmerman et al. (2015) for the quite turbid Chesapeake Bay waters.
Historically (Lorenzen, 1972; Smith and Baker, 1978; Woodruff et al., 1999; Gallegos, 2001; Devlin et al., 2008), there are also studies that treat the attenuation coefficient (K(PAR)) of the photosynthetic available radiation (PAR) as being additive of the contributions of individual constituents,
with Kx(PAR) for contributions except phytoplankton and pure (sea)water. Following the above logic and discussion regarding spectral Kd, we easily observe that this model is not consistent with radiative transfer either (Morel, 1988). In particular, it is ambiguous of the light spectra that should be used for the calculation of Kw(PAR) or Kbio(PAR). Further, because K(PAR) is the attenuation coefficient of solar radiation of a wide spectral range (400–700 nm, i.e., the PAR spectral range), while the spectral quality of Ed(z) changes significantly from surface to depths, which then causes K(PAR) to change greatly (as much as a factor of 4) from surface to depth (Lee et al., 2005a; Lee, 2009). Consequently, the applicability of such biogeo-optical models for K(PAR) is ambiguous at the very least.
Conclusions
Because the interaction term (the third term on the right side of Equation 6) of Kd(λ) (or K(PAR)) depends on the values of both a and bb, the contribution of this term to Kd is not always small or negligible. Also, this interaction term is not a linear function of a and bb. Therefore, for consistency with radiative transfer and for more accurate estimation, and also to incorporate advancements in ocean optics of recent decades, it is better to get bulk IOPs first from biogeochemical properties, and then to calculate Kd based on IOPs. In short, IOPs are additive, but AOPs are not.
Author Contributions
All authors contributed to the hypothesis and overall discussions regarding diffuse attenuation of solar radiation. ZL drafted the manuscript and both SS and RS commented and edited the manuscript before submission.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Funding support provided by the National Key Research and Development Program of China (2016YFC1400905, 2016YFC1400904, #2016YFA0601201, SS), the National Oceanic and Atmospheric Administration (NOAA) JPSS VIIRS Ocean Color Cal/Val Project (NA11OAR4320199, ZL), the National Aeronautic and Space Administration (NASA) Water and Energy Cycle, Ocean Biology and Biogeochemistry Programs (NNX14AK08G, NNX14AQ47A, ZL), and the University of Massachusetts Boston are greatly appreciated.
References
Babin, M., Morel, A., Fournier-Sicre, V., Fell, F., and Stramski, D. (2003). Light scattering properties of marine particles in coastal and open ocean waters as related to particle mass concentration. Limnol. Oceanogr. 48, 843–859. doi: 10.4319/lo.2003.48.2.0843
Baker, K. S., and Smith, R. C. (1982). Bio-optical classification and model of natural waters. 2. Limnol. Oceanogr. 27, 500–509. doi: 10.4319/lo.1982.27.3.0500
Berwald, J., Stramski, D., Mobley, C. D., and Kiefer, D. A. (1995). Influences of absorption and scattering on vertical changes in the average cosine of the underwater light field. Limnol. Oceanogr. 40, 1347–1357. doi: 10.4319/lo.1995.40.8.1347
Devlin, M. J., Barry, J., Mills, D. K., Gowen, R. J., Foden, J., and Tett, P. (2008). Relationships between suspended particulate material, light attenuation and Secchi depth in UK marine waters. Estuarine Coastal Shelf Sci. 79, 429–439. doi: 10.1016/j.ecss.2008.04.024
Devlin, M. J., Barry, J., Mills, D. K., Gowen, R. J., Foden, J., and Tett, P. (2009). Estimating the diffuse attenuation coefficient from optically active constituents in UK marine waters. Estuarine Coastal Shelf Sci. 82, 73–83. doi: 10.1016/j.ecss.2008.12.015
Doxaran, D., Ruddick, K., McKee, D., Gentili, B., Tailliez, D., Chami, M., et al. (2009). Spectral variations of light scattering by marine particles in coastal waters, from visible to near infrared. Limnol. Oceanogr. 54, 1257–1271. doi: 10.4319/lo.2009.54.4.1257
Gallegos, C., Correll, D., and Pierce, J. (1990). Modeling spectral diffuse attenuation, absorption, and scattering coefficients in a turbid estuary. Limnol. Oceanogr. 35, 1486–1502. doi: 10.4319/lo.1990.35.7.1486
Gallegos, C. L. (2001). Calculating optical water quality targets to restore and protect submersed aquatic vegetation: overcoming problems in partitioning the diffuse attenuation coefficient for photosynthetically active radiation. Estuaries 24, 381–397. doi: 10.2307/1353240
Gnanadesikan, A., and Anderson, W. G. (2009). Ocean water clarity and the ocean general circulation in a coupled climate model. J. Phys. Oceanogr. 39, 314–332. doi: 10.1175/2008JPO3935.1
Gordon, H. R. (1989). Can the Lambert-Beer law be applied to the diffuse attenuation coefficient of ocean water?. Limnol. Oceanogr. 34, 1389–1409. doi: 10.4319/lo.1989.34.8.1389
Gordon, H. R., Brown, O. B., and Jacobs, M. M. (1975). Computed relationship between the inherent and apparent optical properties of a flat homogeneous ocean. Appl. Optics 14, 417–427. doi: 10.1364/AO.14.000417
Kim, G. E. M., Pradal, A., and Gnanadesikan, A. (2015). Quantifying the biological impact of surface ocean light attenuation by colored detrital matter in an ESM using a new optical parameterization. Biogeosciences 12, 5119–5132. doi: 10.5194/bg-12-5119-2015
Lee, Z. P. (2009). KPAR: An optical property associated with ambiguous values. J. Lake Sci. 21, 159–164. doi: 10.18307/2009.0202
Lee, Z. P., Du, K., Arnone, R., Liew, S. C., and Penta, B. (2005a). Penetration of solar radiation in the upper ocean - A numerical model for oceanic and coastal waters. J. Geophys. Res. 110:C09019. doi: 10.1029/2004JC002780
Lee, Z. P., Du, K. P., and Arnone, R. (2005b). A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. 110:C0201. doi: 10.1029/2004JC002275
Lee, Z., Wei, J., Voss, K., Lewis, M., Bricaud, A., and Huot, Y. (2015). Hyperspectral absorption coefficient of “pure” seawater in the range of 350–550 nm inverted from remote sensing reflectance. Appl. Optics 54, 546–558. doi: 10.1364/AO.54.000546
Lewis, M. R., Carr, M., Feldman, G., Esaias, W., and McMclain, C. (1990). Influence of penetrating solar radiation on the heat budget of the equatorial pacific ocean. Nature 347, 543–545. doi: 10.1038/347543a0
Lorenzen, C. J. (1972). Extinction of light in the ocean by phytoplankton. J. Cons. Int. Explor. Mar. 34, 262–267.
McCormick, N. J. (1995). Mathematical models for the mean cosine of irradiance and the diffuse attenuation coefficient. Limnol. Oceanogr. 40, 1013–1018. doi: 10.4319/lo.1995.40.5.1013
Mobley, C. D. (1994). Light and Water: Radiative Transfer in Natural Waters. New York, NY: Academic Press.
Mobley, C. D., and Sundman, L. K. (2013). HydroLight 5.2 User's Guide. Bellevue, WA: Sequoia Scientific, Inc.
Morel, A. (1974). “Optical properties of pure water and pure sea water,” in Optical Aspects of Oceanography, eds N. G. Jerlov and E. S. Nielsen (New York, NY: Academic), 1–24.
Morel, A. (1988). Optical modeling of the upper ocean in relation to its biogenous matter content (Case I waters). J. Geophys. Res. 93, 10749–10768. doi: 10.1029/JC093iC09p10749
Morel, A., and Antoine, D. (1994). Heating rate within the upper ocean in relation to its bio-optical state. J. Phys. Oceanogr. 24, 1652–1665. doi: 10.1175/1520-0485(1994)024<1652:HRWTUO>2.0.CO;2
Morel, A., Antoine, D., and Gentili, B. (2002). Bidirectional reflectance of oceanic waters: accounting for Raman emission and varying particle scattering phase function. Appl. Optics 41, 6289–6306. doi: 10.1364/AO.41.006289
Morel, A., and Maritorena, S. (2001). Bio-optical properties of oceanic waters: a reappraisal. J. Geophys. Res. 106, 7163–7180. doi: 10.4319/lo.1977.22.4.0709
Morel, A., and Prieur, L. (1977). Analysis of variations in ocean color. Limnol. Oceanogr. 22, 709–722. doi: 10.1029/2000JC000319
Ohlmann, J. C., Siegel, D. A., and Mobley, C. D. (2000). Ocean radiant heating. Part I: Optical influences. J. Phys. Oceanogr. 30, 1833–1848. doi: 10.1175/1520-0485(2000)030<1833:ORHPIO>2.0.CO;2
Platt, T. (1986). Primary production of ocean water column as a function of surface light intensity: algorithms for remote sensing. Deep-Sea Res. 33, 149–163. doi: 10.1016/0198-0149(86)90115-9
Pope, R., and Fry, E. (1997). Absorption spectrum (380–700 nm) of pure waters: II. Integrating cavity measurements. Appl. Optics 36, 8710–8723. doi: 10.1364/AO.36.008710
Preisendorfer, R. W. (1976). Hydrologic optics vol. 1: introduction, National Technical Information Service. Office of Naval Research, Springfield.
Rochford, P. A., Kara, A. B., Wallcraft, A. J., and Arnone, R. A. (2001). Importance of solar subsurface heating in ocean general circulation models. J. Geophys. Res. 106, 30923–30938. doi: 10.1029/2000JC000355
Sathyendranath, S., and Platt, T. (1995). “Remote sensing of water-column primary production,” in Measurement Of Primary Production from the Molecular to the Global Scale, eds W. K. Li and W. Maestrini (Copenhagen: ICES Marine Science Symposia), 236–243.
Smith, R. C., and Baker, K. S. (1978). The bio-optical state of ocean waters and remote sensing. Limnol. Oceanogr. 23, 247–259. doi: 10.4319/lo.1978.23.2.0247
Stavn, R. (1988). Lambert-Beer law in ocean waters: optical properties of water and of dissolved/suspended materials, optical energy budgets. Appl. Optics 27, 222–231. doi: 10.1364/AO.27.000222
Stavn, R. H., and Weidemann, A. D. (1989). Shape factors, two-flow models, and the problem of irradiance inversion in estimating optical parameters. Limnol. Oceanogr. 34, 1426–1441. doi: 10.4319/lo.1989.34.8.1426
Woodruff, D. L., Stumpf, R. P., Scope, J. A., and Paerl, H. W. (1999). Remote estimation of water clarity in optically complex estuarine waters. Remote Sens. Environ. 68, 41–52. doi: 10.1016/S0034-4257(98)00108-4
Zaneveld, J. R. V., Kitchen, J. C., and Pak, H. (1981). The influence of optical water type on the heating rate of a constant depth mixed layer. J. Geophys. Res. 86, 6426–6428. doi: 10.1029/JC086iC07p06426
Keywords: solar radiation, apparent optical properties, inherent optical properties, diffuse attenuation coefficient, optical additivity
Citation: Lee Z, Shang S and Stavn R (2018) AOPs Are Not Additive: On the Biogeo-Optical Modeling of the Diffuse Attenuation Coefficient. Front. Mar. Sci. 5:8. doi: 10.3389/fmars.2018.00008
Received: 14 July 2017; Accepted: 11 January 2018;
Published: 30 January 2018.
Edited by:
Kevin Ross Turpie, University of Maryland, Baltimore County, United StatesReviewed by:
Emmanuel Devred, Fisheries and Oceans Canada, CanadaKnut Barthel, University of Bergen, Norway
Copyright © 2018 Lee, Shang and Stavn. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhongping Lee, emhvbmdwaW5nLmxlZUB1bWIuZWR1
 Zhongping Lee
Zhongping Lee Shaoling Shang2
Shaoling Shang2 Robert Stavn
Robert Stavn