- 1Department of Life Sciences, Eilat Campus, Ben-Gurion University of the Negev, Beer-Sheva, Israel
- 2The Interuniversity Institute for Marine Sciences of Eilat, Eilat, Israel
- 3Department of Ocean Sciences, Rosenstiel School of Marine and Atmospheric Science, University of Miami, Miami, FL, United States
- 4Institute of Earth Sciences, The Hebrew University, Jerusalem, Israel
- 5Department of Computer Science, Jerusalem Institute of Technology, Jerusalem, Israel
- 6Department of Life-Sciences, Ben-Gurion University of the Negev, Beer-Sheva, Israel
Schooling is very common in adult and juvenile fish, but has been rarely studied during the larval stage. Recent otolith micro-chemistry studies of coral reef fish have demonstrated that cohorts of larvae can move through similar paths and settle within a few meters one from another. However, little is known about the processes involved in the formation and maintenance of these cohorts. Here we use a biophysical modeling approach to examine whether local hydrodynamics, various individual behaviors, or larval schooling can explain cohesive patterns observed for Neopomacentrus miryae in the Gulf of Aqaba/Eilat (Red Sea), and whether schooling is feasible in terms of initial encounter probability and cohesiveness maintenance. We then examine the consequences of schooling behavior on larval settlement success and connectivity. Our results indicate that: (1) Schooling behavior is necessary for generating cohesive dispersal patterns, (2) Initial larval encounter of newly-hatched larvae is plausible, depending mainly on initial larval densities and patchiness, and (3) schooling behavior increases the rate of larval settlement while decreasing the percentage of realized connections. Together with mounting evidence of cohesive dispersal, this numerical study demonstrates that larval schooling throughout the pelagic phase is realistic, and has a significant effect on settlement success and connectivity patterns. Future research is needed to understand the mechanisms of fission-fusion dynamics of larval cohorts and their effect on dispersal. Our findings should be considered in future efforts of larval dispersal models, specifically in the context of marine connectivity and the planning of marine protected area networks.
Introduction
Adult and juvenile fish often swim in groups. Such schooling behavior can help reduce drag and conserve energy (Weihs, 1975), improve orientation (Codling et al., 2007), reduce the risk of predation (Shaw, 1978), and enhance the detection of food and mates (Shaw, 1978). On the other hand, schooling fish may suffer higher mortality and lower growth rates due to competition within the group (Hixon and Jones, 2005). The prevalence of schooling suggests that the overall balance would seem to be positive (Shaw, 1978).
The advantages of schooling may similarly benefit the pelagic larval phase that characterizes the life-cycle of most coral reef fishes (Leis, 2006). These larvae are thought to actively group, mainly during late larval stages, once their sensory and movement capacities have matured enough to support this behavior (Shaw, 1978; Arvedlund and Kavanagh, 2009). Specifically, larval schooling may be similar to adult fish schooling, where collective behavior emerges from simple “individual-fish” rules based on the location of the nearest neighbor/s (Couzin et al., 2002).
Little is known about the frequency of schooling behavior across species and its ontogenetic dynamics. Previous studies indicated that Aldrichetta forsteri and Gobiosoma boscifish larvae school at early stages when their size is ~5 mm and their fins are not fully developed yet (Breitburg, 1991; Kingsford and Tricklebank, 1991). However schooling was also reported at later larval and post-larval stages for different species (reviewed in Leis, 2006).
Mounting evidence, derived from the analysis of otolith micro-chemistry (Ben-Tzvi et al., 2012; Shima and Swearer, 2016) and genetic relatedness (Bernardi et al., 2012; Selwyn et al., 2016), suggests that cohorts of coastal marine fish may be sharing a substantial portion of their dispersal histories (by “cohort” we mean a group of larvae of same age). While it is tempting to relate these patterns to larval behavior, they may also result from aggregation by prevailing hydrological features and/or local cohesive Lagrangian structures (Siegel et al., 2008). The relative contribution of biological, physical, and bio-physical processes to the generation and maintenance of such cohesive dispersal pattern, i.e., shared dispersal paths among individuals within the same cohort, is largely unexplored.
This gap of knowledge is critical, given the demographic and ecological ramifications of the dispersive fate of marine larvae (Levin, 2006). Specifically, the dispersal outcome of schooling larvae is likely to differ from individual larvae as larval schools are characterized by faster swimming speeds, and higher precision of orientation (Irisson et al., 2015). Distinguishing between individual and schooling dispersal is important since dispersal and connectivity are central elements affecting population dynamics, and are often considered when designing marine protected areas networks (Cowen and Sponaugle, 2009). Additional importance of larval schooling lies in its potential effect on the ecology of pelagic ecosystems via planktonic predator-prey dynamics (McGurk, 1986; Frank et al., 1993; Bradbury et al., 2003), planktonic patchiness enhancement (Bradbury et al., 2003), species diversity (Hill, 1973).
In the current study we used a biophysical model of the Gulf of Aqaba (GoA) to test which aspect of larval behavior is necessary and sufficient to reproduce patterns of cohesive dispersal reported for Neopomacentrus miryae in the GoA (Ben-Tzvi et al., 2012). Briefly, Ben-Tzvi et al. (2012) have demonstrated that newly settled N. miryae cohorts shared a highly similar otolith micro-chemistry pattern within each cohort compared to between cohorts. In the current study, we tested whether different scenarios generate cohesive cohorts by examining passive drift, as well as by invoking larval behaviors such as simple random walk (SRW), auto-correlated directional swimming (CRW; Berenshtein et al., 2017), ontogenetic vertical migration (OVM; Paris and Cowen, 2004; Irisson et al., 2010; Huebert et al., 2011), biased correlated directional swimming (BCRW; Staaterman et al., 2012; Mouritsen et al., 2013), and schooling behavior (Irisson et al., 2015). We then examined the plausibility of larval encounter during the early pelagic phase; their capacity to overcome turbulent velocities and remain grouped; and finally, we quantified the relative changes in settlement-success and connectivity in schooling vs. non-schooling dispersal.
Methods
Study Site
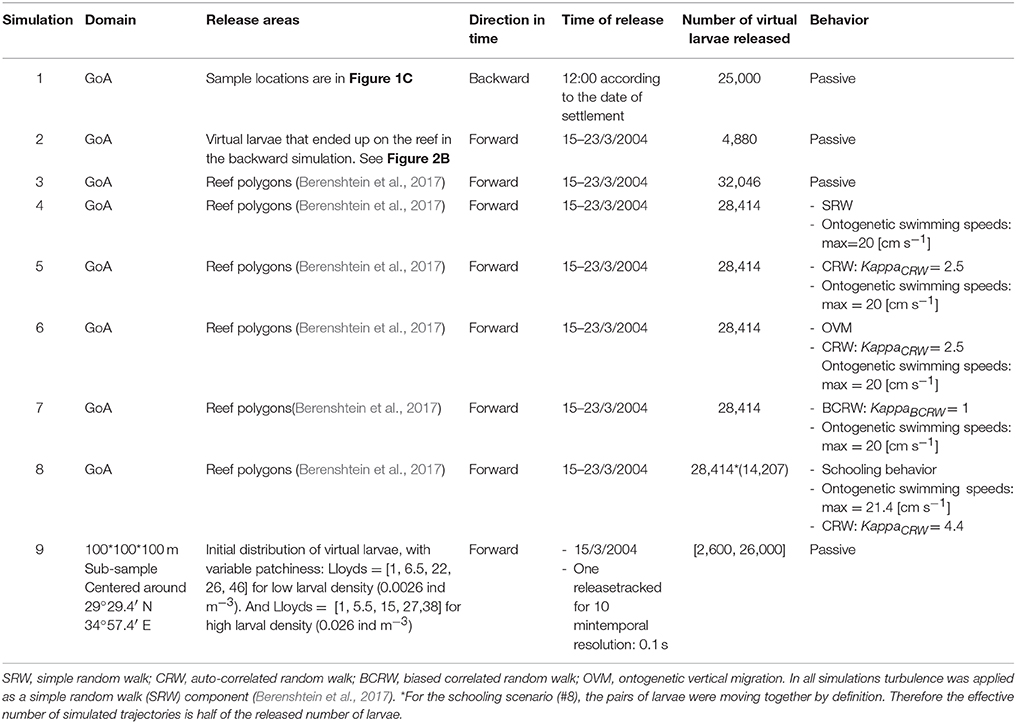
The Gulf of Aqaba is a semi-enclosed elongated extension of the Red Sea (Figure 1A), stretching across ~180 km (Figure 1B), with maximal width and depth of ~27 km and 1,850 m respectively. The GoA circulation is characterized by deep mixing during winter (Feb-March), and stratification during the rest of the year, with a strong density-driven exchange flow with the Red sea during April–August (Biton and Gildor, 2011). The GoA circulation is also dominated by a chain of several sub-meso-scale eddies along its main axis (Biton and Gildor, 2011).
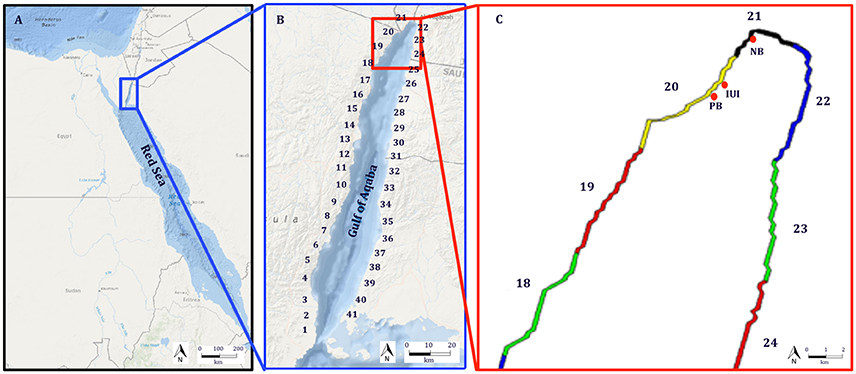
Figure 1. Study area: (A) The Red Sea, and (B) The Gulf of Aqaba (GoA). Numbers in (B) represents the 41 reef polygons which are used in the biophysical model. (C) Cohort recruitment sites in the northern GoA: Princess Beach (PB), Inter-University Institute (IUI), and the North Beach (NB).
Study Fish
Neopomacentrus miryae is endemic to the Red Sea and is highly abundant in the GoA. The ecology of this species was described by Fishelson et al. (1974) referring to it as Abudefduf azysron (Dor and Allen, 1974). Adult N. miryae are planktivorous, found in large stationary schools along vertical walls of forereefs, with males guarding and aerating demersal eggs. N. miryae spawning season spans between November-May, and larvae are found at depths of 0-100 m in the water column, with highest abundance at the top 25 m (Kimmerling et al., 2017).
Biophysical Model of the GoA
The biophysical model of the GoA (Berenshtein et al., 2017) was composed of 3 parts: First, the winds at 10 m above sea level were computed using an atmospheric model- Weather Research and Forecasting model (WRF; Skamarock et al., 2001), Next, wind data was used to force a 3D high resolution oceanographic model- Massachusetts Institute of Technology general circulation model (MITgcm; Marshall et al., 1997), Finally, an offline particle tracking algorithm (modified from Fredj et al., 2016) made use of the 3D circulation data combined with larval biological traits to compute larval trajectories. The resolution of the MITgcm data was of 1 h (temporal), 300 m (horizontal), and 32 depth layers most of which were concentrated in the upper 300 m (Biton and Gildor, 2011; Berenshtein et al., 2017). The temporal resolution of the particle tracking model was of 10 min (time-step length), with a spatial resolution of centimeters due to a continuous 3D grid, and spatial interpolation of larval positions. The detailed description of the model can be found in Berenshtein et al. (2017).
Backward and Forward-in-Time Passive Simulations
For our simulations we used 5 real recruitment events which occurred at 3 sites in the northwestern coast of the GoA: North Beach (NB), Inter-University Institute (IUI), and Princess Beach (PB) (Figure 1C; Ben-Tzvi et al., 2012). In Ben-Tzvi et al. (2012), newly-recruited fish were collected with hand-nets, and their age and day of recruitment was determined using otolith analysis. Newly-recruited fish that shared the same site, age and recruitment day were considered of the same cohort (Ben-Tzvi et al., 2012).
To examine whether the local hydrodynamics (advection and turbulence) could generate patterns of cohort cohesiveness similar to those observed in N. miryae (Ben-Tzvi et al., 2012), we performed backward and forward-in-time simulations using the dates and locations of the collected cohorts and their estimated PLDs (Figure 2C; Ben-Tzvi et al., 2012).

Figure 2. (A) Trajectories of passive virtual larvae released at the locations and times of settlement (n = 5,000 per site) and tracked backward in time for a duration of 28–29 days (Sim. #1, Table 1). Virtual larvae from (A) with final positions in the reef (n = 244) were multiplied (×20) and tracked forward in time for 28–29 days (B). Magenta asterisks in (A,B) represent particle release locations. (C) Pelagic Larval Durations (PLD) of the recruiting cohorts from April-March 2004, which were deducted from otolith analysis in Ben-Tzvi et al. (2012). Maps in (A,B) were generated using MATLAB R2014b (The MathWorks Inc., Natick, MA, USA), and are rotated views of the GoA (73° Clockwise).
The rational of this approach was that if currents were to generate a cohesive dispersal pattern, they would have to be sufficiently strong and persistent to overcome the system's stochasticity. Such pattern would result in similar trajectories in backward and forward-in-time simulations, connecting between the settlement sites, and the hatching locations on the reef.
In the backtracking simulation (Sim. #1, Table 1) 5,000 passive virtual larvae were released from each of the recruitment sites at their corresponding dates. In the forward simulation (Sim. #2, Table 1), 20 virtual larvae were released from each of the locations of virtual larvae which ended up on the reef in the backtracking simulation, releasing a total of 4,480 virtual larvae (Sim. #2, Table 1).
We then visually examined the simulated trajectories for indication of cohort-unique dispersal trajectories, imposed solely by local hydrodynamics.
Pairwise Distances and Probability of Adjacent Settlement
To determine if various larval behaviors can generate the observed cohesive dispersal pattern we released pairs of virtual larvae from the entire fringing reef of the GoA (41 reef polygons in Figure 1B) and tracked them forward in time (Sim. #3–8, Table 1). For each simulation, 1,000 pairs of larvae, characterized by identical hatching times and locations, were released daily at midnight across 9 release days (15th−23th of March 2004). Larval trajectories were computed in the biophysical model according to advection, turbulence, and larval behavior (Berenshtein et al., 2017). Mortality was not applied in the biophysical simulations.
To quantitatively assess the occurrence of cohesive dispersal we computed: (1) larval pairwise distances, i.e., the distance separating paired virtual larvae across the PLD, and (2) the probability of sampling 2 settled nearest neighbors, which hatched at the same location and time. While the former corresponds to the observed similarity in larval paths deducted from the trace-element of otolith rings, the latter corresponds to the similarity in the site of origin deducted from the trace-element of otolith cores (Ben-Tzvi et al., 2012).
Since very little is known about the behavior of N. miryae larvae, we chose to apply the commonly observed and modeled larval behaviors for other species within the Pomacentridae family (Leis and Carson-Ewart, 2003; Irisson et al., 2009, 2015; Mouritsen et al., 2013; Berenshtein et al., 2014). Behaviors, which include movement toward a common direction (e.g., OVM and BCRW), are expected to produce convergence of larval paths, which would be expressed in reduced pairwise distances compared to passive simulations. The following behavioral scenarios were implemented (Sim. #3–8, Table 1).
Simple Random Walk (SRW)
For this scenario, ontogenetic swimming speeds were applied according to Fisher (2005):
Age (t) and PLD are expressed in hours.
Hatching speeds were parameterized with () 2 cm s−1, reaching maximum swimming speeds () of 20 cm s−1, which are typical values for Pomacentridae (Leis and Carson-Ewart, 1997; Fisher, 2005). Here, the movement directions were drawn from a random distribution, therefore un-correlated and traditionally termed “Simple Random Walk” (SRW). Note, that in all the following behaviors, larval swimming speeds are modeled similarly (Equation 1), with the exception of the passive scenario, were larvae are immobile.
Auto-Correlated Directional Swimming (CRW)
Auto-correlated directional swimming for individual larvae was simulated as a CRW process, such that larval heading at a given time step is correlated to the previous one.
Where θi and θi−1 are the current and previous headings, and δθ is the turning angle, which is drawn from a von-Mises distribution.
Where I0 is a modified Bessel function of order 0, and Kappa is the concentration parameter of the von-Mises distribution (Codling et al., 2004; Staaterman et al., 2012; Berenshtein et al., 2017). Briefly, the von-Mises Kappa controls the modeled precision of orientation, such that high Kappa values would result in directional trajectories, compared to low Kappa values. For example, Kappa = 0, 2, and 4 will result in a total decay of directional correlation after 10, 100, and 240 min respectively (Berenshtein et al., 2017). Kappa values for individual larvae were estimated from the experimental data of Irisson et al. (2015) for the con-familial Chromis atripectoralis using maximum likelihood estimation for von-Misses distribution (R core team, 2013) for each headings sequence (i.e., each individual Drifting In-Situ Chamber experiment). Following this analysis Kappa was set to 2.5.
Ontogenetic Vertical Migration (OVM)
The occurrence of OVM was not documented for N. miryae but was demonstrated in other pomacentrids, with larvae shown to migrate deeper with age (Paris and Cowen, 2004; Irisson et al., 2009; Huebert et al., 2011). This behavior was implemented in our model (Sim. #6, Table 1), such that larvae at the age of 0-5 days post-hatch (DPH) maintained a depth range of 0-25 m, and larvae at the age of 6–27 DPH maintained a depth range of 25-100 m. This is achieved by a vertical movement speed of 2 cm s−1. Larvae older than 27 DPH were within their competence window, and settled to the reef upon encounter.
Biased-Correlated Directional Swimming (BCRW)
Biased-correlated directional swimming for individual larvae was simulated as a biased correlated random walk process (BCRW) such that larval headings are drawn from a von-Mises distribution centered around a pre-defined azimuth; we used 17°, which is the axial direction of the GoA (i.e., larvae that swim toward this direction will end up at the northern tip of the GoA). To date, there is no empirical information about a common swimming directions of larvae in the GoA (in contrast to other locations, e.g., Bottesch et al., 2016), but using the axial direction of the GoA makes biological sense since it minimizes the coastal encounters of the larvae, and therefore minimizes their risk of predation. Kappa values for BCRW individual larvae were estimated from the experimental data of Irisson et al. (2015) (see explanation in CRW section above) resulting in kappa = 1.
Schooling Behavior
For schooling behavior, we simulated the most simplified scenario in which pairs of larvae were moving together keeping the exact same positions and paths. Therefore, the effective number of virtual larvae released is half from that of the other strategies (Table 1). We have computed the Kappa parameter of the von-Mises distribution of turning angles from Irisson et al. (2015) data for the con-familial C. atripectoralis. Mean Kappa value for CRW computed from that data equaled to 4.4 (see explanation in CRW section above). The mean terminal swimming speed of schooling larvae was set to 21.4 cm s−1 which is 7% faster than the individual terminal swimming speed (Irisson et al., 2015).
Passive
In addition the behaviors mentioned above, we have included a passive scenario to provide a baseline for the effect of the various behaviors on the pairwise distances.
Encounter Probability Estimation
For schooling behavior to occur, larvae need to encounter one another. We therefore sought to examine the probability of larvae encountering each other in the pelagic environment soon after hatching (within 1 day).
To address this question, we used two approaches. The first is spatiotemporally explicit, using 3D currents and turbulence from our biophysical model. In the second approach, we use mathematical models modified from the classical planktonic predator-prey encounter rate and probability models (Gerritsen and Strickler, 1977; Kiørboe and MacKenzie, 1995).
Encounter Probability Using the 3D Spatiotemporally Explicit Model
The first approach raised several computational challenges. First, it required a high temporal resolution (<1 s), whereas the temporal resolution of our model is of 10 min. Second, it required realistic densities of larvae, which can be orders of magnitude higher than could be tracked in biophysical models across the entire GoA. Third, to compute all possible pairwise distances across time requires immense computational power.
We therefore created a sub-sample of 100 × 100 × 100 m (length × width × depth) of the GoA, centered around 29°29.4′ N 34°57.4′ E. In this space we followed either 2,600 or 26,000 passive virtual larvae, which correspond to the lower and mid-level values of measured densities of the con-familial Stegastes partitus larvae (<6 DPH, Paris and Cowen, 2004). The larvae, were released on the 15th of March 2004 at 12:00 p.m., and tracked for 10 min at a temporal resolution of 0.1 s. Initial positions of the passive larvae were generated at levels of patchiness [Lloyd's index of patchiness (L); (Lloyd, 1967)] that ranged from random distribution (L = 1) to moderately clumped (L = 40) distribution (Bradbury et al., 2003).
Random distributions were generated by selecting random XYZ coordinates within the cubic domain. Clumped distributions were generated using an iterative algorithm which produced the initial positions of virtual larvae around predefined number of centroids (Np1 = 20), randomly drawn from a uniform distribution within a pre-defined distance (Rp1 = 20 m) from a given patch centroid. For each iteration, to compute Lloyd's index of patchiness, 100 samples (7 × 7 × 7 m) were randomly placed in the domain. Then Npi and the Rpi were iteratively modified until reaching the desired range of patchiness. The sample's volume (343 m3) is within the range of typical ichthyoplankton samples (Kimmerling et al., 2017). Visualization examples of the spatial patterns are presented in Supplementary Figure S1.
We assumed a detection distance of 0.1 m, which corresponds to the visual acuity in fish larvae (Renee Lara, 2001). Encounter probability was computed as the proportion of larvae, out of the total number released, that came within 0.1 m of at least one other larvae throughout the 10 min simulation.
Encounter Probability Using the Classic Encounter Model
For the classic approach we used the encounter rate model from Kiørboe and MacKenzie (1995) between planktonic predator and prey. Here the encounter rate (Er) was a function of larval density (D; using 0.026 and 0.0026 ind m−3), detection distance (R; using 0.1 m), and swimming speed (v; using values of 0 and 0.02 m s−1; Fisher, 2005).
Turbulent velocity (w) was computed following Kiørboe and MacKenzie (1995), using turbulent dissipation rates (ε) of 10−7 and 10−4 m2 s−3 which represent the range of turbulent dissipation rates for the shelf and coastal zones (Kiorboe and Saiz, 1995).
Encounter probability was computed following Gerritsen and Strickler (1977), where encounters were assumed to be randomly occurring events (Poisson distribution). Therefore the probability encountering at least one larvae (PE) was formulated as a function of the time interval (t; using 10 min and 24 h).
The term e−Ert in Equation (6) represents the probability encountering 0 larvae.
Assessment of the Capacity of Newly Hatched Larvae to Overcome Turbulence and Remain Grouped
To assess the capacity of adjacent larvae to overcome horizontal turbulence and stay grouped, we computed turbulent velocity using Kiørboe and MacKenzie (1995) approach (Equation 5), and compared it to the combined velocity of two larvae swimming one toward the other.
Assessment of Grouping Tendency From Kimmerling et al. (2017) Data
The grouping tendency of N. miryae and Chromis viridis was assessed using the sampling data from Kimmerling et al. (2017). We focused on these two species as they were the species examined in Ben-Tzvi et al. (2012), with N. miryae demonstrating cohesive dispersal pattern, while C. viridis did not. The frequency and number of individuals occurring in the ichthyoplankton samples was recorded, and their Lloyds Index of Patchiness was computed.
Settlement Success and Connectivity Network Density
Settlement-success was computed as the percent of virtual larvae that have reached a reef polygon within their competence window (last 48 h of their PLD; Berenshtein et al., 2017). Network-density was computed as the percent of realized connections out of all possible connections between the different polygons in the GoA domain. Network-density considered only whether or not connections occurred, without considering the connections strength.
Settlement success and network density were computed per release event (N = 9; Sim #5 and #8, Table 1). Paired t-tests were used to examine the significance of differences in terms of settlement-success and network-density between schooling vs. individual CRW larvae. Shapiro-Wilk test was used to examine the normality of the paired differences. All simulations and statistical analyses were run on MATLAB R2014b (The MathWorks Inc., Natick, MA, USA) and R (R core team, 2013).
Results
Backward and Forward-in-Time Passive Simulations
Backtracking of passive virtual larvae from the sites and times of settlement by N. miryae (Figure 2A) resulted in a wide spread of trajectories around the northern two-thirds of the GoA; with a high degree of overlap between cohorts (Figure 2A). Similarly, forward-in-time trajectories, released from reef sources from the backtracking simulations, did not show any channeling patterns toward the observed settlement sites, but instead were widespread across most of the GoA area (Figure 2B). Both backward and forward in-time trajectories showed no evidence for prevailing currents that could generate cohort cohesion (Ben-Tzvi et al., 2012).
Pairwise Distances and Probability of Adjacent Settlement
The analysis of pairwise-distances indicated that all but the schooling scenarios resulted in a high degree of dispersion. Mean pairwise distances at the end of the PLD ranged between 13 and 38 km, for pairs of larvae that hatched at the same location and time (Figure 3). Behaviors which include movement toward similar horizontal or vertical directions among larvae (BCRW and OVM) resulted in path convergence in comparison to the passive scenario, while dispersive behaviors which lacked “common movement direction” (SRW and CRW) resulted in greater path divergence in comparison to the passive scenario. Yet, even for the most convergent scenario (BCRW), the pairwise distances were far from generating patterns of cohesive dispersal, i.e., cohort members that settled within a few meters one from another (Ben-Tzvi et al., 2012). By definition, pairwise-distances under the schooling behavior scenario equaled zero. All behaviors are characterized by a nearly linear increase of pairwise distances with slopes slightly decreasing toward the end of the PLD due to the bounded domain of the GoA. An exception is BCRW, which shows a considerably earlier and steeper decline in the pairwise distances due to convergence of larvae toward the northern tip of the GoA.
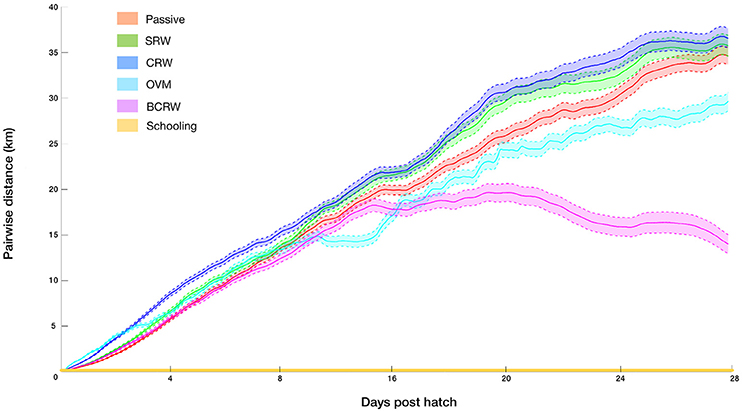
Figure 3. Distances between pairs of virtual larvae that hatched at the same locations and times throughout the pelagic larval duration (PLD) for the following strategies: passive, simple random walk (SRW), auto-correlated directional swimming (CRW), ontogenetic vertical migration (OVM), biased correlated random walk (BCRW), and schooling behavior (simulation #3–8, Table 1). Shaded areas indicate 99% confidence intervals (N = 32,046 and 28,414 for the passive and other strategies respectively).
Similarly, the probability of sampling a nearest neighbor pair which hatched at the same location and time for all but the “schooling behavior” strategy was extremely low (<0.00004). Naturally, in the schooling behavior scenario, as the larval pairs hatched, moved, and settled together, the probability for pairwise settlement is maximal.
Larval Encounter Probabilities
The probability of larval encounter per 10 min, from the 3D biophysical model, ranged between 0.0046 and 0.49 at low larval densities, and 0.046-0.78 at high larval densities, depending the degree of initial larval patchiness (Figure 4; for spatial distribution see Supplementary Figure S1).
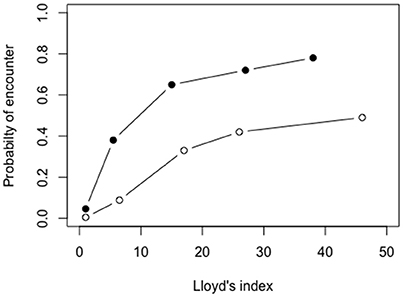
Figure 4. Encounter probabilities of passive larvae as a function of the patchiness of initial larval distribution, implementing high (0.026 ind m−3; full circles) and low (0.0026 ind m−3; empty circles) larval densities. Simulations were carried out in the 3D biophysical model within a sub-sample of 100 × 100 × 100 m (length × width × depth) in the Gulf of Aqaba centered around 29°29.4′ N 34°57.4′ E during the 15th of March 2004 at 12:00–12:10 p.m.
Encounter probabilities computed with the classic encounter model (Kiørboe and MacKenzie, 1995) ranged from 0.001 to 0.99 depending on larval density, time span, turbulent velocity, and swimming speeds (Table 2). Across 24 h, for high larval densities, the encounter probability of swimming larvae is 0.2 and 0.99 for low and high turbulent dissipation rates respectively (Table 2, Supplementary Figure S2). Increase in larval density, time span, turbulent velocity, and swimming speeds resulted in an increase in encounter probabilities.
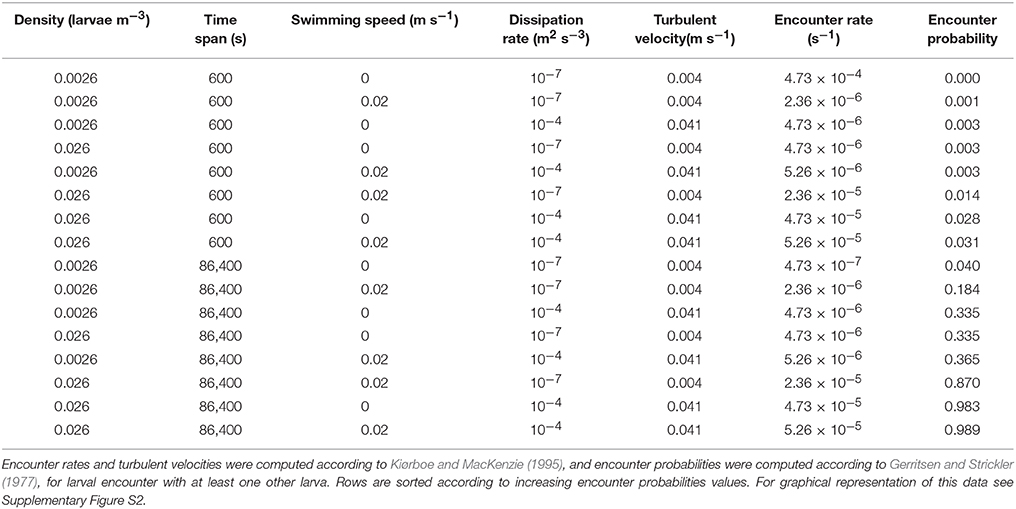
Table 2. Sensitivity analysis of larval encounter rates and probabilities as a function of larval density, time span, larval swimming speeds, and turbulent velocities.
Assessment of the Capacity of Newly Hatched Larvae to Overcome Turbulence and Remain Grouped
Computation of turbulent velocity (Equation 5) for dissipation rate of 10−4 m2 s−3 resulted in a turbulent velocity of w = 0.041 m s−1. Given maximal larval speeds during the first 24 h after hatching is 0.02–0.03 m s−1, larvae that swim toward each other would be able to overcome turbulent velocity and remain grouped. Dissipation rate of 10−4 m2 s−3 represents the upper limit of coastal and shelf dissipation rates, suggesting that such larvae, which can swim since hatching, will be able to overcome turbulent velocity and remain grouped at nearly all oceanic conditions, from early stages of their PLD.
Assessment of Grouping Tendency From Kimmerling et al. (2017) Data
For N. miryae, 90% of the samples contained two or more larvae, compared to only 29% in C. viridis. Lloyd's index of patchiness for N. miryae was 64 compared to 27 for C. viridis.
Settlement Success and Connectivity Network Density
Settlement success of schooling larvae was significantly higher than that of non-schooling larvae (pairwise t-test, t = 26.3, df = 8, p < 0.01, Figure 5). Connectivity network density in schooling larvae was significantly lower than that achieved in the non-schooling scenario (pairwise t-test, t = −35.2, df = 8, p < 0.01, Figure 5).
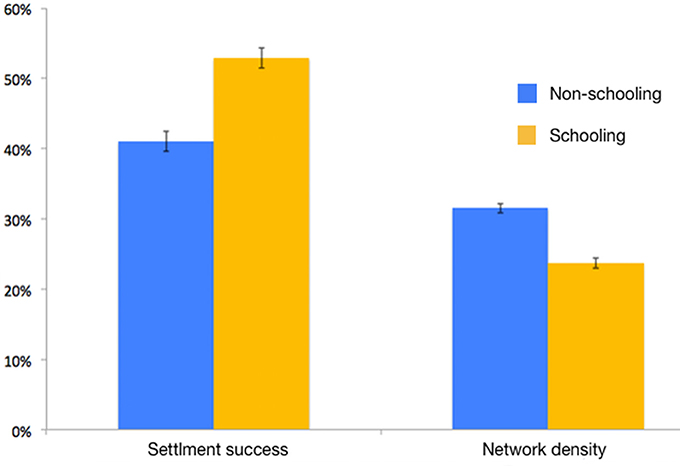
Figure 5. Settlement success and connectivity network density (i.e., the percentage of realized connections out of all possible connections) of individual and schooling larvae (Sim. #5 vs. #8 in Table 1).
Discussion
Of the simulation scenarios considered in the current study, patterns of cohesive dispersal could only be reproduced by schooling behavior (Figure 3). This would seem to suggest that newly hatched N. miryae may actively form long-lived schools.
To school, larvae must encounter one another, yet schooling does not seem to occur immediately after hatching for the following reasons: (1) There is no indication for synchronous hatching from Pomacenridae demersal eggs, (2) There is no genetic structure between larval cohorts (Ben-Tzvi et al., 2012), and (3) Larval swimming velocities at hatching are not necessarily sufficient to overcome turbulent velocity. Therefore, N. miryae encounter their conspecifics shortly—but not immediately—after hatching.
The larval encounter analyses computed in this study demonstrated feasible probabilities for pelagic larval encounter within 24 h (Table 2, Figure 4). However, both encounter computation methods encompass some limitations. The mathematical model assumes larval distributions are random rather than clumped. The latter has been documented for fish larvae (e.g., Bradbury et al., 2003, L>3; Frank et al., 1993, L>2), and for later-stage larvae of N. miryae in the GoA (Kimmerling et al., 2017, L = 64). The 3D—spatio-temporally explicit model is limited as well, since advection, and turbulence transport the larvae away from their initially confined cubic domain to waters which are empty of larvae. This alters the shape and the volume of the waters encompassing the larval patch, resulting in a modification of the effective densities across time. Despite these limitations, both methods indicate that larval encounter within the first 24 h post-hatching can be feasible.
Even when larvae encounter each other they still need to overcome turbulent velocity to keep together. The fact that larval swimming velocities soon after hatching were similar to the upper range of turbulent velocities (Dissipation rate of 10−4 m3 s−2; Table 2) suggests that fish larvae can maintain schooling in most oceanic conditions.
To keep together, larvae may utilize their vision and lateral line senses similarly to adult fish (Partridge and Pitcher, 1980), and their olfactory sense similarly to settlement stage larvae (Lecchini et al., 2014). They may also use their auditory sense, as fish larvae can produce sounds during the night (Staaterman et al., 2014).
The fact that larvae within cohorts stayed together through their PLD (Ben-Tzvi et al., 2012) suggests a high cohort fidelity and a lack of (or little) mixing with other cohorts or sporadic individuals (i.e., cohesive dispersal). This, in turn, suggests that N. miryae larvae would form scarce and clumped patches in the pelagic environment.
The spatial scale of cohesive dispersal is unknown due to the limited information about the spatial heterogeneity of trace-elements used in Ben-Tzvi et al. (2012). However, using the available information, we can make a simplistic assessment of the spatial extent of newly formed cohorts, which results in length scales of tens to hundreds of meters (Supplementary Data S1). At these small scales, convergent oceanographic features, which could potentially aggregate larvae but are too small to be resolved by the MITgcm model, could occur (e.g., Gildor et al., 2009). Yet, such features are rare and persistent across no more than a few days, and therefore cannot produce the observed cohesive pattern across the PLD (Ben-Tzvi et al., 2012).
Schooling behavior, along with other biological and physical factors (e.g., Fronts, pycnoclines, and heterogeneous distribution of larva predator and prey) can contribute to larval patchiness (e.g., McGurk, 1986; Frank et al., 1993). Ichthyoplankton samples from Kimmerling et al. (2017) suggest a stronger tendency of N. miryae to be found in groups compared to C. viridis, whose otolith analysis lacked any evidence for cohesive dispersal (Ben-Tzvi et al., 2012). Note however, that the larvae of these two species are characterized by different spatio-temporal dynamics which may also effect their tendency to be found in groups (Kimmerling et al., 2017). Naturally, Interplay between biological and physical factors can effect schooling dynamics, as more patchy populations have a higher probability of encounter, and therefore facilitate schooling.
Previous studies demonstrated that the extent of patchiness often follows a “U” shaped curve across ontogeny (for example in Capelin and Sandlance larvae/eggs; Bradbury et al., 2003). Initial high patchiness is attributed to the coherence of larvae/eggs patches from mass-spawning/hatching at specific areas; the following decrease is attributed mainly to advection and mortality; and the increase toward the end of the PLD is attributed to active larval behavior (Bradbury et al., 2003). While Frank et al. (1993) attributed that increase to the occurrence of prey (Sagitta elegans), schooling behavior may have also played a role in these dynamics.
In our current biophysical model, mortality was not applied. In other modeling efforts, mortality is mostly applied as a constant rate in time and space due to limited empirical information. Such application of mortality is not expected to effect the results and the conclusions of this study (e.g., Berenshtein et al., 2017).
Increased schooling capacity can affect fitness both positively and negatively. Positive effects include increased swimming speeds and orientation capacities (Irisson et al., 2015), which are manifested in increased settlement success (Figure 5; Berenshtein et al., 2017); while negative effects may include higher probability of predator encounter due to increased mobility (swimming velocity and directional persistence; Visser and Kiørboe, 2006), increased competition for food, and the reduction of variation in effective dispersal paths (i.e., connectivity; Figure 5).
The increased settlement success of schooling larvae is attributed to higher swimming speeds and a more precise orientation (Irisson et al., 2015), which lead to an increase in displacement associated with larval behavior (Berenshtein et al., 2017). This, in turn, allows the larvae to depart from entraining currents (e.g., sub-mesoscale eddies) and increases their probability of reaching the coast and settling (Berenshtein et al., 2017). The decrease in connectivity network density (Figure 5) is attributed to the reduction of the variation in dispersal trajectories. In other words, a population of larvae which disperses in pairs for example, can produce half of the dispersal paths generated by individually dispersing larvae.
These changes in settlement success and connectivity are important as these factors are central in population dynamics, affecting the biogeography and the genetic structure of populations in multiple marine species (Cowen and Sponaugle, 2009). Moreover, larval supply from external (non-local) sources is essential for sustaining populations, i.e., sites which receive larvae from multiple sources would be less susceptible for a population collapse compared to sites which are dependent on fewer sources (Cowen et al., 2006). As schooling in fish larvae might be very common (reviewed in Leis, 2006), in-situ and laboratory studies are needed to examine ontogenetic larval collective behavior, and specifically their fission-fusion dynamics across their PLD. This, in conjunction with ichthyoplankton analyses of species abundances throughout ontogeny, could set the basis for a realistic incorporation of schooling behavior in biophysical models.
In conclusion, this study supports the occurrence of schooling of N. miryae in the GoA across the PLD for realistic reconstruction of observed settlement patterns. In addition, our study demonstrates the effects of schooling behavior on larval settlement success and connectivity. The dynamics and characteristics of larval schooling should be further studied, and its application should be considered in larval dispersal models when managing fisheries and determining marine protected areas.
Author Contributions
IB, HG, YA, EF, and MK participated in data analysis, EF adjusted and run the atmospheric model, and helped with the particle tracking algorithm, HG and YA adjusted and run the oceanographic model, IB, CP, and MK participated in conceiving, designing, and drafting the study.
Funding
This study was supported by the United States-Israel Bi-national Science Foundation (BSF grant 2008/144 to MK 1210 and CP).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dr. Ofer Ben-Tzvi for providing details about the field sampling. We thank Dr. Robin Faillettaz for support with graphics. We thank the IUI staff and the Paris lab for their contribution in various aspects of this study. We greatly thank two reviewers who substantially improved the quality of our manuscript. This study was supported by the United States–Israel Bi-national Science Foundation (BSF grant 2008/144 to MK and CP).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2018.00254/full#supplementary-material
References
Arvedlund, M., and Kavanagh, K. (2009). The senses and environmental cues used by marine larvae of fish and decapod crustaceans to find tropical coastal ecosystems. Ecol. Connect. among Trop. Coast. Ecosyst. 135–184. doi: 10.1007/978-90-481-2406-0_5
Ben-Tzvi, O., Abelson, A., Gaines, S. D., Bernardi, G., Beldade, R., Sheehy, M. S., et al. (2012). Evidence for cohesive dispersal in the sea. PLoS ONE 7:e42672. doi: 10.1371/journal.pone.0042672
Berenshtein, I., Kiflawi, M., Shashar, N., Wieler, U., Agiv, H., and Paris, C. B. (2014). Polarized light sensitivity and orientation in coral reef fish post-larvae. PLoS ONE 9:e88468. doi: 10.1371/journal.pone.0088468
Berenshtein, I., Paris, C. B., Gildor, H., Fredj, E., Amitai, Y., Lapidot, O., et al. (2017). Auto-correlated directional swimming can enhance settlement success and connectivity in fish larvae. J. Theor. Biol. 439, 76–85. doi: 10.1016/j.jtbi.2017.11.009
Bernardi, G., Beldade, R., Holbrook, S. J., and Schmitt, R. J. (2012). Full-sibs in cohorts of newly settled coral reef fishes. PLoS ONE 7:e44953. doi: 10.1371/journal.pone.0044953
Biton, E., and Gildor, H. (2011). The general circulation of the Gulf of Aqaba (Gulf of Eilat) revisited: the interplay between the exchange flow through the Straits of Tiran and surface fluxes. J. Geophys. Res. 116:C08020. doi: 10.1029/2010JC006860
Bottesch, M., Gerlach, G., Halbach, M., Bally, A., Kingsford, M. J., and Mouritsen, H. (2016). A magnetic compass that might help coral reef fish larvae return to their natal reef. Curr. Biol. 26, R1266–R1267. doi: 10.1016/j.cub.2016.10.051
Bradbury, I. R., Snelgrove, P. V. R., and Pepin, P. (2003). Passive and active behavioural contributions to patchiness and spatial pattern during the early life history of marine fishes. Mar. Ecol. Prog. Ser. 257, 233–245. doi: 10.3354/meps257233
Breitburg, D. L. (1991). Settlement patterns and presettlement behavior of the naked goby, Gobiosoma bosci, a temperate oyster reef fish. Mar. Biol. 109, 213–221. doi: 10.1007/BF01319389
Codling, E. A., Hill, N. A., Pitchford, J. W., and Simpson, S. D. (2004). Random walk models for the movement and recruitment of reef fish larvae. Mar. Ecol. Prog. Ser. 279, 215–224. doi: 10.3354/meps279215
Codling, E. A., Pitchford, J. W., and Simpson, S. D. (2007). Group navigation and the “many-wrongs principle” in models of animal movement. Ecology 88, 1864–1870. doi: 10.1890/06-0854.1
Couzin, I. D., Krausew, J., Jamesz, R., Ruxtony, G. D., and Franksz, N. R. (2002). Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1–11. doi: 10.1006/jtbi.2002.3065
Cowen, R. K., and Sponaugle, S. (2009). Larval dispersal and marine population connectivity. Ann. Rev. Mar. Sci. 1, 443–466. doi: 10.1146/annurev.marine.010908.163757
Cowen, R. K., Paris, C. B., and Srinivasan, A. (2006). Scaling of connectivity in marine populations. Science 311, 522–527. doi: 10.1126/science.1122039
Dor, M., and Allen, G. R. (1974). Neopomacentrus miryae, a new species of pomacentrid fish from the Red Sea. Proc. Biol. Soc. Washingt. 90, 183–188.
Fishelson, L., Popper, D., and Avidor, A. (1974). Biosociology and ecology of pomacentrid fishes around the Sinai Peninsula (northern Red Sea). J. Fish Biol. 6, 119–133. doi: 10.1111/j.1095-8649.1974.tb04532.x
Fisher, R. (2005). Swimming speeds of larval coral reef fishes: impacts on self-recruitment and dispersal. Mar. Ecol. Prog. Ser. 285, 223–232. doi: 10.3354/meps285223
Frank, K. T., Carscadden, J. E., and Leggett, W. C. (1993). Causes of spatio-temporal variation in the patchiness of larval fish distributions: differential mortality or behaviour? Fish. Oceanogr. 2, 114–123. doi: 10.1111/j.1365-2419.1993.tb00129.x
Fredj, E., Carlson, D. F., Amitai, Y., Gozolchiani, A., and Gildor, H. (2016). The particle tracking and analysis toolbox (PaTATO) for Matlab. Limnol. Ocean. Methods 14, 586–599. doi: 10.1002/lom3.10114
Gerritsen, J., and Strickler, J. R. (1977). Encounter probabilities and community structure in zooplankton: a mathematical model. J. Fish. Res. Board Canada 34, 73–82. doi: 10.1139/f77-008
Gildor, H., Fredj, E., Steinbuck, J., and Monismith, S. (2009). Evidence for submesoscale barriers to horizontal mixing in the ocean from current measurements and aerial photographs. J. Phys. Oceanogr. 39, 1975–1983. doi: 10.1175/2009JPO4116.1
Hill, M. O. (1973). Diversity and Evenness: a unifying notation and its consequences. Ecology 54, 427–432. doi: 10.2307/1934352
Hixon, M. A., and Jones, G. P. (2005). Competition, predation, and density-dependent mortality in demersal marine fishes. Ecology 86, 2847–2859. doi: 10.1890/04-1455
Huebert, K. B., Cowen, R. K., and Sponaugle, S. (2011). Vertical migrations of reef fish larvae in the Straits of Florida and effects on larval transport. Limnol. Oceanogr. 56, 1653–1666. doi: 10.4319/lo.2011.56.5.1653
Irisson, J. O., Guigand, C., and Paris, C. B. (2009). Detection and quantification of marine larvae orientation in the pelagic environment. Limnol. Ocean. Methods 7, 664–672. doi: 10.4319/lom.2009.7.664
Irisson, J.-O., Paris, C. B., Guigand, C., and Planesa, S. (2010). Vertical distribution and ontogenetic “migration” in coral reef fish larvae. Limnol. Oceanogr. 55, 909–919. doi: 10.4319/lo.2010.55.2.0909
Irisson, J. O., Paris, C. B., Leis, J. M., and Yerman, M. N. (2015). With a little help from my friends: group orientation by larvae of a coral reef fish. PLoS ONE 10:e0144060. doi: 10.1371/journal.pone.0144060
Kimmerling, N., Zuqert, O., Amitai, G., Gurevich, T., Armoza-Zvuloni, R., Kolesnikov, I., et al. (2017). Quantitative species-level ecology of reef fish larvae via metabarcoding. Nat. Ecol. Evol. 2, 306–316. doi: 10.1038/s41559-017-0413-2
Kingsford, M. J., and Tricklebank, K. A. (1991). Ontogeny and behavior of Aldrichetta forsteri (Teleostei: Mugilidae). Copeia 1991, 9–16. doi: 10.2307/1446243
Kiørboe, T., and MacKenzie, B. (1995). Turbulence-enhanced prey encounter rates in larval fish: effects of spatial scale, larval behaviour and size. J. Plankton Res. 17, 2319–2331. doi: 10.1093/plankt/17.12.2319
Kiorboe, T., and Saiz, E. (1995). Planktivorous feeding in calm and turbulent environments, with emphasis on copepods. Mar. Ecol. Prog. Ser. 122, 135–146. doi: 10.3354/meps122135
Lecchini, D., Peyrusse, K., Lanyon, R. G., and Lecellier, G. (2014). Importance of visual cues of conspecifics and predators during the habitat selection of coral reef fish larvae. C. R. Biol. 337, 345–351. doi: 10.1016/j.crvi.2014.03.007
Leis, J. M. (2006). Are Larvae of demersal fishes plankton or nekton? Adv. Mar. Biol. 51, 57–141. doi: 10.1016/S0065-2881(06)51002-8
Leis, J. M., and Carson-Ewart, B. M. (1997). In situ swimming speeds of the late larvae of some coral reef fishes. Mar. Ecol. Prog. Ser. 159, 165–174. doi: 10.3354/meps159165
Leis, J. M., and Carson-Ewart, B. M. (2003). Orientation of pelagic larvae of coral-reef fishes in the ocean. Mar. Ecol. Prog. Ser. 252, 239–253. doi: 10.3354/meps252239
Levin, L. A. (2006). Recent progress in understanding larval dispersal: new directions and digressions. Integr. Comp. Biol. 46, 282–297. doi: 10.1093/icb/icj024
Marshall, J., Adcroft, A., Hill, C., Perelman, L., and Heisey, C. (1997). A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Ser. 102, 5753–5766. doi: 10.1029/96JC02775
McGurk, M. D. (1986). Natural mortality of marine pelagic fish eggs and larvae: role of spatial patchiness. Mar. Ecol. Prog. Ser. 34, 227–242. doi: 10.3354/meps034227
Mouritsen, H., Atema, J., Kingsford, M. J., and Gerlach, G. (2013). Sun compass orientation helps coral reef fish larvae return to their natal reef. PLoS ONE 8:e66039. doi: 10.1371/journal.pone.0066039
Paris, C. B., and Cowen, R. K. (2004). Direct evidence of a biophysical retention mechanism for coral reef fish larvae. Limnol. Oceanogr. 49, 1964–1979. doi: 10.4319/lo.2004.49.6.1964
Partridge, B. L., and Pitcher, T. J. (1980). The sensory basis of fish schools: relative roles of lateral line and vision. J. Comp. Physiol. 135, 315–325.
R core team (2013). R: The R Project for Statistical Computing. Available online at: https://www.r-project.org/
Renee Lara, M. (2001). Morphology of the eye and visual acuities in the settlement-intervals of some coral reef fishes (Labridae, Scaridae). Environ. Biol. Fishes 62, 365–378. doi: 10.1023/A:1012214229164
Selwyn, J. D., Hogan, J. D., Downey-Wall, A. M., Gurski, L. M., Portnoy, D. S., and Heath, D. D. (2016). Kin-aggregations explain chaotic genetic patchiness, a commonly observed genetic pattern, in a marine fish. PLoS ONE 11:e0153381. doi: 10.1371/journal.pone.0153381
Shaw, E. (1978). Schooling Fishes: the school, a truly egalitarian form of organization in which all members of the group are alike in influence, offers substantial benefits to its participants. Am. Sci. 66, 166–175.
Shima, J. S., and Swearer, S. E. (2016). Evidence and population consequences of shared larval dispersal histories in a marine fish. Ecology 97, 25–31. doi: 10.1890/14-2298.1
Siegel, D. A., Mitarai, S., Costello, C. J., Gaines, S. D., Kendall, B. E., Warner, R. R., et al. (2008). The stochastic nature of larval connectivity among nearshore marine populations. Proc. Natl. Acad. Sci. U.S.A. 105, 8974–8979. doi: 10.1073/pnas.0802544105
Skamarock, W. C., Klemp, J. B., and Dudhia, J. (2001). “Prototypes for the WRF (Weather Research and Forecasting) model,” in Preprints, 9th Conference on Mesoscale Processes, J11–J15, American Meteorological Society (Fort Lauderdale, FL).
Staaterman, E., Paris, C. B., and Helgers, J. (2012). Orientation behavior in fish larvae: a missing piece to Hjort's critical period hypothesis. J. Theor. Biol. 304, 188–196. doi: 10.1016/j.jtbi.2012.03.016
Staaterman, E., Paris, C. B., and Kough, A. S. (2014). First evidence of fish larvae producing sounds. Biol. Lett. 10:20140643. doi: 10.1098/rsbl.2014.0643
Visser, A. W., and Kiørboe, T. (2006). Plankton motility patterns and encounter rates. Oecologia 148, 538–546. doi: 10.1007/s00442-006-0385-4
Keywords: larval dispersal, schooling, cohorts, coral reef fish larvae, cohesive dispersal, settlement, connectivity, Gulf of Aqaba/Eilat
Citation: Berenshtein I, Paris CB, Gildor H, Fredj E, Amitai Y and Kiflawi M (2018) Biophysical Simulations Support Schooling Behavior of Fish Larvae Throughout Ontogeny. Front. Mar. Sci. 5:254. doi: 10.3389/fmars.2018.00254
Received: 23 December 2017; Accepted: 03 July 2018;
Published: 25 July 2018.
Edited by:
Alberto Basset, University of Salento, ItalyReviewed by:
Ulisses Miranda Azeiteiro, University of Aveiro, PortugalKevin Sorochan, Dalhousie University, Canada
Copyright © 2018 Berenshtein, Paris, Gildor, Fredj, Amitai and Kiflawi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Igal Berenshtein, aWJlcmVuc2h0ZWluQHJzbWFzLm1pYW1pLmVkdQ==
 Igal Berenshtein
Igal Berenshtein Claire B. Paris
Claire B. Paris Hezi Gildor
Hezi Gildor Erick Fredj
Erick Fredj Yael Amitai
Yael Amitai Moshe Kiflawi6,2
Moshe Kiflawi6,2