- 1School of Biological Sciences, Faculty of Sciences, The University of Adelaide, Adelaide, SA, Australia
- 2Environment Institute, Faculty of Sciences, The University of Adelaide, Adelaide, SA, Australia
- 3Department for Environment and Water, State Herbarium of South Australia, Adelaide, SA, Australia
Mangroves provide many ecosystem services including a considerable capacity to sequester and store large amounts of carbon, both in the sediment and in the above-ground biomass. Assessment of mangrove above-ground carbon stock relies on accurate measurement of tree biomass, which traditionally involves collecting direct measurements from trees and relating these to biomass using allometric relationships. We investigated the potential to predict tree biomass using measurements derived from unmanned aerial vehicle (UAV), or drone, imagery. This approach has the potential to dramatically reduce time-consuming fieldwork, providing greater spatial survey coverage and return for effort, and may enable data to be collected in otherwise hazardous or inaccessible areas. We imaged an Avicennia marina (grey mangrove) stand using an RGB camera mounted on a UAV. The imaged trees were subsequently felled, enabling physical measurements to be taken for traditional biomass estimation techniques, as well as direct measurements of biomass and tissue carbon content. UAV image-based tree height measurements were highly accurate (R2 = 0.98). However, the variables that could be measured from the UAV imagery (tree height and canopy area) were poor predictors of tree biomass. Using the physical measurement data, we identified that trunk diameter is a key predictor of A. marina biomass. Unfortunately, trunk diameter cannot be directly measured from the UAV imagery, but it can be predicted (with some error) using models that incorporate other UAV image-based measurements, such as tree height and canopy area. However, reliance on second-order estimates of trunk diameter leads to increased uncertainty in the subsequent predictions of A. marina biomass, compared to using physical measurements of trunk diameter taken directly from the trees. Our study demonstrates that there is potential to use UAV-based imagery to measure mangrove A. marina tree structural characteristics and biomass. Further refinement of the relationship between UAV image-based measurements and tree diameter is needed to reduce error in biomass predictions. UAV image-based estimates can be made far more quickly and over extensive areas when compared to traditional data collection techniques and, with improved accuracy through further model-calibration, have the potential to be a powerful tool for mangrove biomass and carbon storage estimation.
Introduction
Coastal vegetation is an important biological carbon sink, capable of sequestering greater amounts of carbon per unit area than terrestrial forests (Mcleod et al., 2011). The greatest proportion of carbon in coastal systems, commonly referred to as “blue carbon”, is stored below ground in the sediment, with a smaller proportion stored in the above-ground biomass (Nellemann and Corcoran, 2009). Among the three key blue carbon ecosystems (mangroves, seagrasses and saltmarshes), mangroves have the greatest above ground biomass and carbon storage, due to their larger, woody growth forms (Alongi, 2014).
The capacity for mangroves to sequester and store carbon is of global significance and has led to international initiatives and policy instruments, recognizing the value of mangroves for mitigating anthropogenic carbon emissions. These include the 2013 Coastal Wetlands Supplement to the Intergovernmental Panel on Climate Change (IPCC) Guidelines for National Greenhouse Gas Inventories (IPCC, 2014); the United Nations Framework Convention on Climate Change (UNFCCC) Reducing Emissions from Deforestation and Forest Degradation (REDD+) scheme; and a number of carbon financing mechanisms that include mangrove systems (Plan Vivo, 2013; Emmer et al., 2015; Wylie et al., 2016); although there are currently only a handful of projects that are actually trading carbon credits from mangroves. The use of “default values” for mangrove carbon sequestration and storage (usually based on global averages; IPCC, 2014) is permitted by these initiatives and instruments. However, these default values are considered inadequate to account for the spatial heterogeneity of carbon stored in above-ground mangrove biomass (Kelleway et al., 2016; Owers et al., 2016, 2018a), which is dependent on factors such as geographic setting, species composition and growth form (Hickey et al., 2018 and references therein). Consequently, carbon financing and accounting methods recommend and reward the use of accurate, site-based measurements of mangrove above- and below-ground carbon pools that capture variability and improve confidence in carbon stock estimates (Gibbs et al., 2007; Kauffman and Donato, 2012; Howard et al., 2014; IPCC, 2014). However, the mangrove above-ground carbon pool is generally poorly quantified (Owers et al., 2018b).
Direct measurement of mangrove biomass is traditionally done using established forest inventory techniques that involve the laborious collection of tree measurements (e.g., height, canopy/crown area, diameter at breast height) within designated plots, which are then used in allometric equations that relate these non-destructive tree measurements to tree above ground biomass (Kauffman and Donato, 2012; Picard et al., 2012). Biomass estimates for mangroves can subsequently be converted to estimates of above ground carbon using a standard multiplier of 0.45–0.50 (IPCC, 2014). Estimates of biomass and carbon per tree can be scaled-up to area estimates using averaged values and tree density metrics from the surveyed plots, on the assumption that these are representative of the wider mangrove area. Collecting in situ measurements from mangrove trees is time and resource demanding, as well as potentially hazardous, particularly in dense mangrove stands or remote sites with limited accessibility and the risk of contracting potentially fatal diseases transmitted by mosquitoes or encountering predatory animals (e.g., crocodiles). These impediments can lead to poor survey coverage and measurement errors when carrying out in situ surveys of mangroves. In areas where it is not safe, practical or affordable to collect physical measurements from mangroves, default carbon values (rather than site-based values) may be used to estimate site carbon stocks (IPCC, 2014). However, this introduces a large amount of uncertainty to the above-ground biomass and derived carbon estimates and results in lower carbon market prices (Gibbs et al., 2007; Kauffman and Donato, 2012; Howard et al., 2014).
Remote sensing techniques offer approaches for collecting data on mangrove distribution and structure (Hamilton et al., 2018) that avoid many of the challenges of traditional methods. Global and regional estimates of mangrove height, canopy area, succession, biomass and derived carbon stocks have been made by extracting structural information from various remotely sensed products. These approaches used data from Shuttle Radar Topography Mission (SRTM) (Rahman and Aslan, 2017); Synthetic Aperture Radar (SAR) systems (Lee et al., 2015); the Advanced Land Observing Satellite (ALOS) Panchromatic Remote-sensing Instrument for Stereo Mapping (PRISM) (Aslan et al., 2018); and combinations of the previously mentioned active (i.e., radar) and passive (e.g., Landsat) remotely sensed products (Aslan et al., 2016). These landscape-scale estimates of mangrove biomass and carbon stocks are extremely valuable and have a variety of applications (e.g., national carbon accounting and monitoring change at a broad scale) (Aslan et al., 2016). However, they generally lack the fine-scale spatial resolution required to inform accurate, site-based assessments of mangrove biomass and carbon stocks and are not intended to capture fine-scale heterogeneity (Owers et al., 2018a). Such resolution is achievable through well-designed, extensive, in situ surveys that are stratified in such a way that they capture heterogeneity across a site (for example associated with geomorphology, species composition and tidal inundation levels). However, as discussed above, there are often practical barriers to carrying out such surveys. Owers et al. (2018b) demonstrated the use of a terrestrial laser scanner for generating accurate and precise site-level estimates of biomass (and derived estimates of carbon) in mangroves. However, the impracticalities of this method, such as the size/weight and cost of the instrument, as well as the difficulty of collecting good data in dense canopy (Wilkes et al., 2017), mean it may be unsuitable for mapping mangrove biomass in the majority of cases.
There is a clear need for an easy-to-deploy, comparatively cheap method for collecting high spatial resolution data on mangrove structure at a local scale. Such a method could support the site-level assessment and monitoring of mangrove biomass for carbon accounting and crediting purposes, which is currently likely to be cost prohibitive to carbon crediting project proponents (Bell-James, 2016). The use of Unmanned Aerial Vehicles (UAVs) for ecological research and management has grown significantly in the last decade (Anderson and Gaston, 2013) including applications for collection of structural measurements from plants, predominantly driven by forestry (e.g., Panagoitidis et al., 2017) and agriculture (Bendig et al., 2015). These approaches are increasingly being applied to conservation and management, particularly in terrestrial forest ecosystems (Paneque-Gálvez et al., 2014; Messinger et al., 2016), but have not yet been widely applied for mapping coastal vegetation (although see Otero et al., 2018). UAVs have the potential to provide a relatively low-cost, low-risk and quick approach to surveying mangrove above-ground biomass compared to on-the-ground forest inventory methods (Otero et al., 2018). In addition, they can collect much higher spatial resolution data than most other remote sensing approaches (although see Owers et al., 2018b), with the ability to generate cm-resolution, three-dimensional canopy models over hundreds of hectares; making them the ideal tool for high resolution, site-based assessments of mangrove above-ground biomass and carbon stocks.
In this study, we aim to establish proof-of-concept for the accurate (i.e., as close as possible to the true value) measurement of Avicennia marina (grey mangrove) tree biomass using variables derived from UAV-imagery. Destructive sampling of the imaged trees generated data for calibration and validation of allometric relationships. This enabled us to (1) test the accuracy of UAV image-based tree measurements and biomass predictions from our new models based only on UAV-estimated variables; (2) assess how well previously published allometric equations approximate our South Australian A. marina tree biomass, based on variables estimated from the UAV imagery; and (3) compare the best estimates of biomass based on UAV-derived data to those based on traditional field-based forest inventory approaches.
Materials and Methods
The mangrove study area was at North Arm Creek, north of Adelaide, in South Australia (−34.825, 138.560; Figure 1). Avicennia marina is a predominantly tropical species and is at the edge of its range in South Australia. It is the only mangrove found in the state and is a protected species of native vegetation, which cannot be removed without permission according to the South Australian Native Vegetation Act 1991. Specific and limited areas of A. marina trees were planned for removal as part of a state road construction project (removal was permitted by the South Australian Native Vegetation Council, application number 2015/3111/292). We converted the vegetation clearance into an opportunity to gather destructive samples and were granted limited access to the site by the construction company. Our access constraints dictated our study area, survey and sampling approach, as well as constraining our sample size. The study methodology is outlined in Figure 2.
Figure 1. Map of survey and sampling location at North Arm Creek (indicated by green dot), north of Adelaide in South Australia (approximate site location: –34.8245, 138.5602).
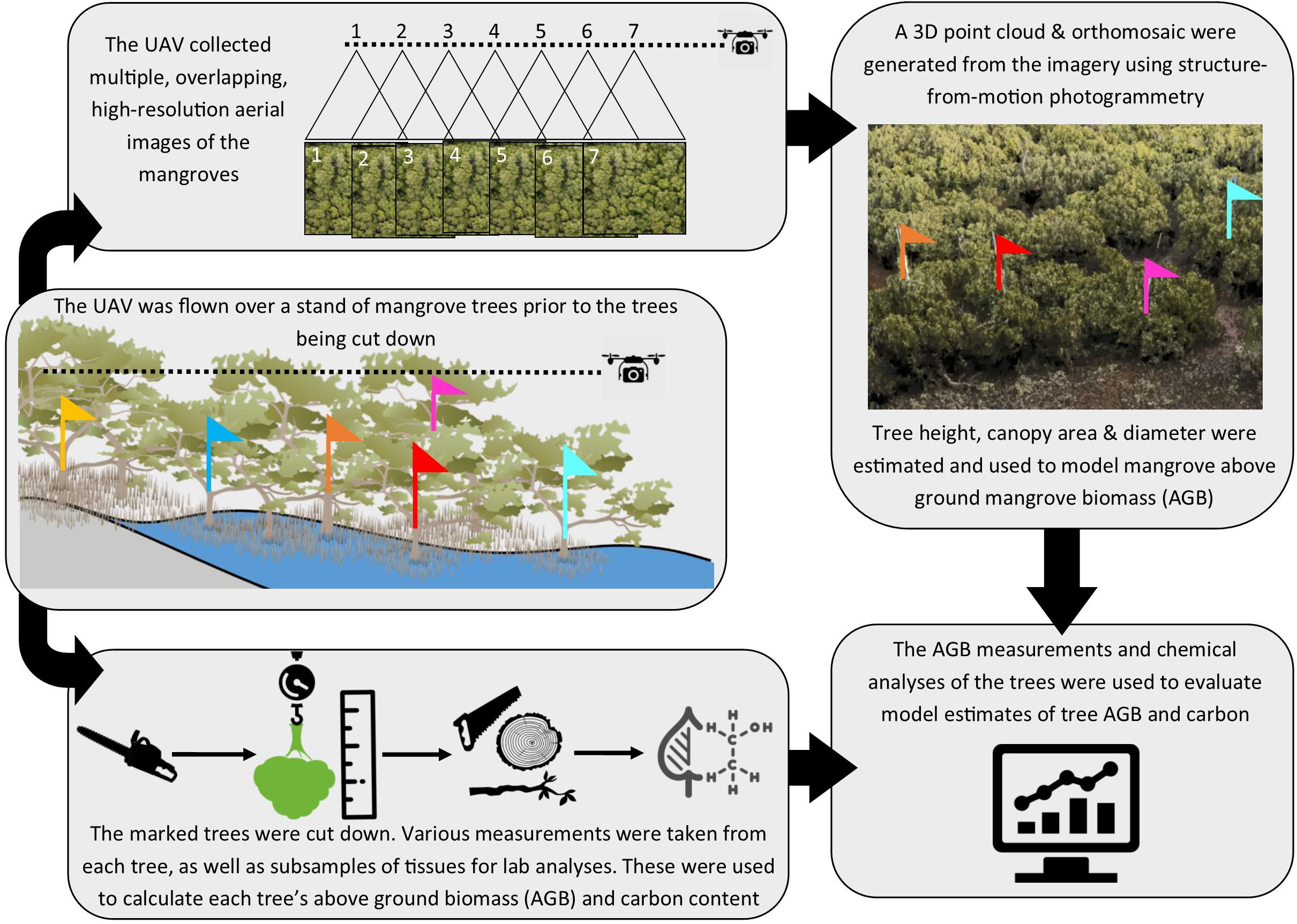
Figure 2. Schematic of workflow used in the study, which was initiated with tree marking prior to UAV flight, with subsequent harvesting of trees and analyses of tree samples and imagery.
UAV Data Collection and Processing
Prior to mangrove clearance, we marked 10 individual trees within the mangrove stand using lengths of plastic pipe tipped with uniquely colored flags. The pipes were strapped to the main trunk of each tree and were taller than the trees such that that the colored flags emerged above the tree canopy and were visible to the UAV flying overhead. The locations of the 10 trees that were imaged by the UAV and subsequently removed are shown in Supplementary Figure S1. They were sampled along a transect that ran approximately from north to south and was perpendicular to the nearby North Arm Creek.
A 20 megapixel Sony RX100iii camera was hard mounted onto a 3DR Iris + UAV to capture RGB images of the mangroves. An automated lawnmower type pattern was flown at 40 m above ground level with 80% overlap and side lap. These image-capture parameters were selected to yield a suitable point cloud to represent the complex canopy structure and enable measurement of canopy height. A georectified orthomosaic with a nominal spatial resolution of 1.5 cm was subsequently generated (Dittmann et al., 2017) with Pix4D Mapper Pro photogrammetry software. We manually digitized the canopies of the 10 individually marked trees from the orthomosaic. The digitized canopy extents were used to compute the canopy area (m2) of each tree. The maximum height (m) of each tree’s canopy was measured from the point cloud, determined as the difference between the highest point within each canopy and the height of the bare ground visible at the nearest gap in the canopy.
Forest Inventory Data Collection
After completing the UAV imaging, the marked trees (n = 10) were felled by cutting at ground level (therefore no below ground biomass was removed or provided). In addition to the 10 trees we had marked, we were also provided with an additional 10 trees that were unmarked. Because they were unmarked, these additional trees were not individually identifiable on the UAV imagery, but could still be used to establish allometric relationships for predicting the biomass of A. marina trees in South Australia. The subset of A. marina trees used in the UAV study (n = 10) were imaged and felled on 29th June 2017. The 10 additional trees that were harvested, but not imaged, were felled within 2-weeks of the UAV imaging. The exact positions of the un-imaged trees were not provided to us by the construction company that removed them; but they were collected from the same general area as the UAV imaged trees. Wet weights of all trees were measured on the same day as harvesting.
We took the following measurements from the felled trees (n = 20): total height, total wet weight, diameter at 30 cm (basal diameter; D30) and diameter at breast height (130 cm; DBH). Total tree diameter at 130 cm (DBH) and 30 cm (D30) was calculated for multi-stemmed trees using the square root of the sum of the squared diameter values from all stems in each tree. We were unable to directly measure the canopy area of the trees, as we did not have access to them prior to harvesting. After harvesting, we were unable to suspend the trees in such a way as to recreate the natural shape of the canopies.
Lab Analyses of Tree Biomass and Carbon
After taking measurements from the whole trees, we separated each tree into three compartments: trunk, branches and foliage (including leaves, fruits and inflorescences) (Kauffman and Donato, 2012). We took the total wet weight of each compartment of each tree and collected a minimum of three sub-samples for dry weight measurement and further lab analyses. The dry weight of each sub-sample was measured after oven-drying at 60°C until a constant weight was achieved. The total dry weight (i.e., biomass) of each compartment of each tree was calculated by multiplying the compartment’s wet weight by the average wet:dry weight ratio from all sub-samples.
We analyzed sub-samples of trunk, branch and foliage (99, 83, and 84 samples, respectively) for carbon content using a Nu Instruments isotope ratio mass spectrometer (IRMS). The majority of samples (foliage, small-medium branches and small-medium diameter trunk samples) were ground and homogenized directly in a steel ball mill to a fine grain size. For larger diameter branch and trunk samples, we collected material for analysis using cross-sectional transects with a micro-drill. This produced a fine powder which was homogenized manually before being analyzed. Using cross sectional transects ensured the material analyzed from the larger diameter branch and trunk samples was representative of the different types of wood and bark present. Ground samples were then analyzed in the IRMS (average weight of sample = 2.309 mg, range = 2.006 – 2.499 mg). After analysis, we generated estimates of tree compartment carbon content and total tree carbon content. This involved multiplying the biomass estimate for each compartment of each tree by the average proportion of carbon in each compartment (pooled across all trees), then summing the compartment carbon values for each tree (to get total tree carbon content).
Data Analyses
Data analyses were performed on a suite of measured and modeled metrics relevant to biomass. We had both physical (n = 20 trees) and UAV image-based (n = 10 trees) measurements of tree height, as well as UAV image-based measurements of canopy area. In addition, data from the UAV imagery was used to model DBH and D30 (see further details below), which could not be directly measured from the imagery. We also had the measured biomass and carbon content of each tree from destructive harvesting. This enabled us to compare a variety of approaches for modeling biomass and determine which was the most accurate for use on our South Australian A. marina trees.
For clarity throughout this manuscript, we have used different terms to distinguish “regression models” and “allometric equations”. We refer to regression models when we have built the models with our own data from the UAV imagery and used these to make predictions of parameters such as diameter metrics and tree biomass. This is an arbitrary distinction, but one that we feel makes our various analyses easier to distinguish, discuss and compare. We use the term allometric equations (which are essentially formulae derived from regression models) when we are referring to previously published relationships between tree measurements and biomass, or attempting to develop new relationships with our own data from destructive harvesting. The allometric equations are deterministic in that they contain fixed coefficients and constants and only require the user to input parameter values for the appropriate predictor variables (i.e., measurement values of tree height, diameter or canopy area).
Unmanned aerial vehicle image-based measures of tree height were assessed against field measured tree height using correlation analysis. A suite of linear regression models of DBH and D30 were built using different combinations of image-based measurements as predictor variables (tree height and canopy area) and the best of these was selected and used to generate predictions of DBH and D30 for each tree (calibrated and validated using our direct measurements of these variables from the felled trees). We then generated a further set of linear regression models of tree biomass as a function of single or multiple UAV image-based predictor variables (tree height, canopy area, DBH and D30). Note that we did not include second order (derived) variables (DBH and D30) in the same models as the UAV image-based variables they were derived from (height and/or canopy area).
All model variables were logged (using natural log unless stated otherwise) as is standard in allometric approaches. However, to assess model prediction ability, the predicted log (biomass) estimates from models were back-transformed to produce estimates in kg that could be compared to the measured biomass values. Back-transformation can lead to biased estimates, so we multiplied the estimates from the models by a correction factor to adjust for this. The correction factor was calculated using the method from Sprugel (1983): Exp (model root mean square error/2). Model evaluation statistics (R2 and AIC) are provided, as well as mean model prediction error based on the difference between observed (directly measured) tree biomass and model-prediction of biomass for each tree using leave-one-out cross validation. Analyses were carried out in the R Statistical Software (R Core Team, 2017).
We also generated a range of linear regression models that used the physically measured attributes of all 20 harvested trees as predictor variables for tree biomass. These models are expressed as allometric equations, based on their coefficients and intercepts, and were evaluated based on mean prediction error (see details above). In addition to these newly generated allometric relationships (based on our own destructive sampling data), we also tested the accuracy of 10 previously published allometric equations for estimating the biomass of A. marina trees. The published equations we used were taken from studies of A. marina trees from Western Australia (Clough et al., 1998), Northern Territory (Comley and McGuinness, 2005) and New South Wales (Owers et al., 2018a); none of these studies included trees from South Australia. We did not take physical measurements of canopy area from our sampled trees, but we did estimate canopy area for the trees that were imaged by the UAV; this prevents the application of any published allometric equations that include canopy area to the full dataset of 20 harvested trees. We used mean prediction error (difference in kg between observed and predicted tree biomass) to compare all the tested allometric equations (previously published and new) against each other and the models of biomass based only on image-based predictor variables.
Results
Direct Tree Measurements
Trees ranged from 2.1 – 6.7 m tall, weighing between 6.1 and 208.1 kg (Table 1). Raw tree measurement data for all felled trees (n = 20) and summary data for the subset of trees that were imaged by the UAV (n = 10) are provided in the Supplementary Data Worksheet and Supplementary Table S1. The average proportion biomass (dry weight as a proportion of total wet weight) for the tree compartments were 0.55 (std = 0.06, n = 104), 0.53 (std = 0.05, n = 94) and 0.37 (std = 0.02, n = 97) for trunk, branch and foliage, respectively. The elemental analysis found that all tree compartments contained similar total carbon percentages, with averages of 44.5% for trunk samples (std = 2.15, n = 99), 44.3% for branch samples (std = 2.05, n = 83) and 44.4% for foliage samples (std = 1.54, n = 84). The overall average carbon content, pooled across all tree compartments was 44.3% (std = 1.96, n = 287).
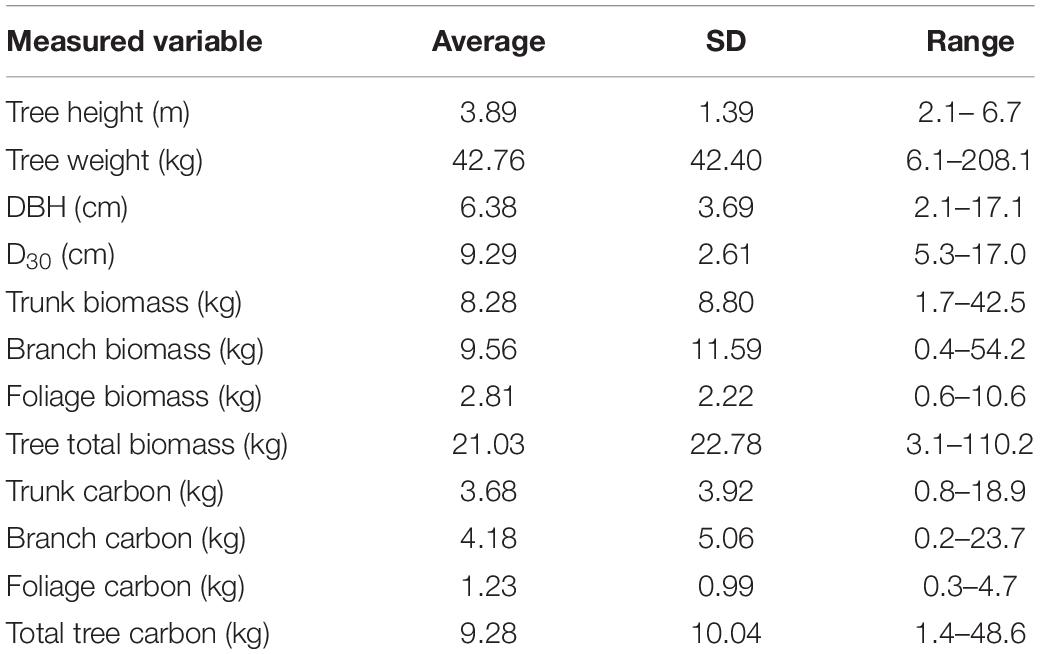
Table 1. Summary statistics for physical measurement data collected from the 20 harvested trees used in this study.
Estimation of Tree Structural Variables From UAV Canopy Height Model
The imagery captured with the UAV was processed to yield an orthomosaic (Figure 3A) suitable for measuring canopy area and a structure-from-motion point cloud suitable for measuring canopy height (Figure 3B). Estimates of canopy area, taken from the orthomosaic, ranged from 0.2 to 3.4 m2 (average = 1.2 m2, std = 0.8 m2). Directly measured tree height and UAV image based tree height measured from the point cloud had a strongly positive correlation (R2 = 0.98; Figure 4A).

Figure 3. (A) an orthomosaic and (B) a structure-from-motion point cloud of mangroves mapped using a 3DR Iris + UAV with a Sony RX100 20-megapixel camera mounted. Both images were generated from multiple overlapping photographs using Pix 4D Mapper Pro software.
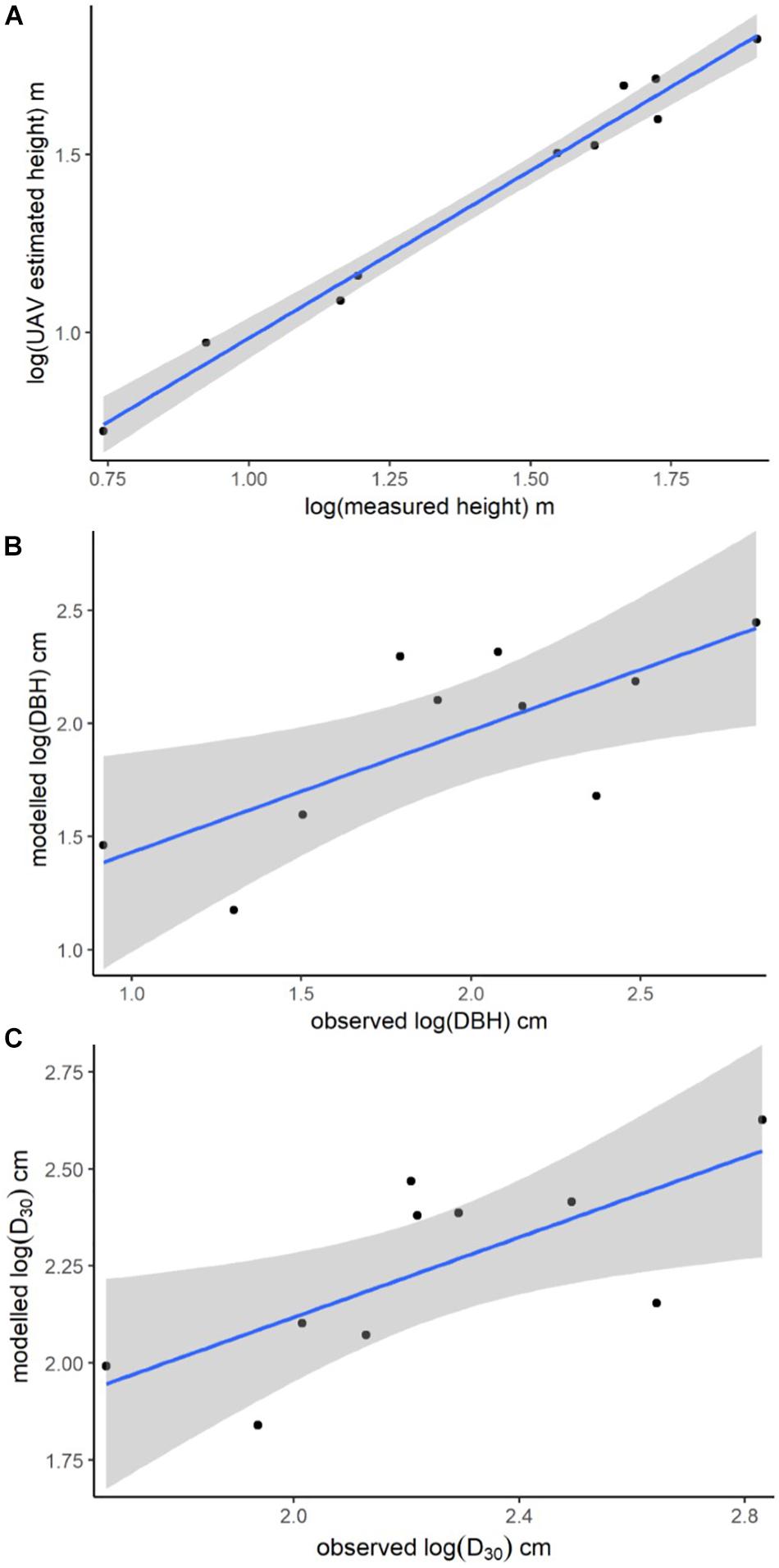
Figure 4. Plots of UAV image-based model-predictions against physically measured values. (A) Linear model showing the relationship between the logged measurements of tree height from the UAV image-based structure-from-motion point cloud and the logged measurements of tree height taken from the felled trees. Linear model predictions of (B) log (DBH) as a function of UAV image-based measurements of tree height plotted against the log of physical measurements of tree DBH; and (C) log (D30) as a function of UAV image-based measurements of tree height and canopy area plotted against the log of physically measured tree D30. Shading = 95% confidence intervals.
The full suite of models generated for predicting tree DBH and D30 from UAV-estimates of tree height and canopy area are provided in the (Supplementary Tables S2, S3), with only the best models described here. The best model of log (DBH) included the single predictor variable log (UAV image-based tree height), had an R2 of 0.54 and a mean prediction error of 0.21 log (cm) (Figure 4B). The best model for prediction of D30 included both UAV image-based tree height and canopy area as predictors, had an R2 of 0.52 and a mean prediction error of 0.08 log (cm) (Figure 4C).
Avicennia marina Tree Biomass Estimation Using Models and Published Allometric Equations
We tested a suite of new models and previously published allometric equations, but focus here only on those that performed the best in terms of prediction accuracy, assessed by cross validation and calculation of mean prediction error (details of all models and equations are provided in the Supplementary Tables S4–S6).
Direct Estimation of A. marina Tree Biomass Based on Models With UAV-Derived Predictor Variables
The best model of A. marina biomass predicted using just the UAV image-based variables (n = 10 trees) included only D30 as a predictor (Supplementary Table S4). Although it was the top-ranked of the candidate models we tested, it did not predict biomass very accurately; with a mean prediction error of 17.4 kg. This large average prediction error is predominantly due to the model’s under-prediction of the largest tree, which had an observed biomass of >110 kg, as well as slight over-prediction of smaller tree biomass values (see “UAV Model” box in Figure 5B).
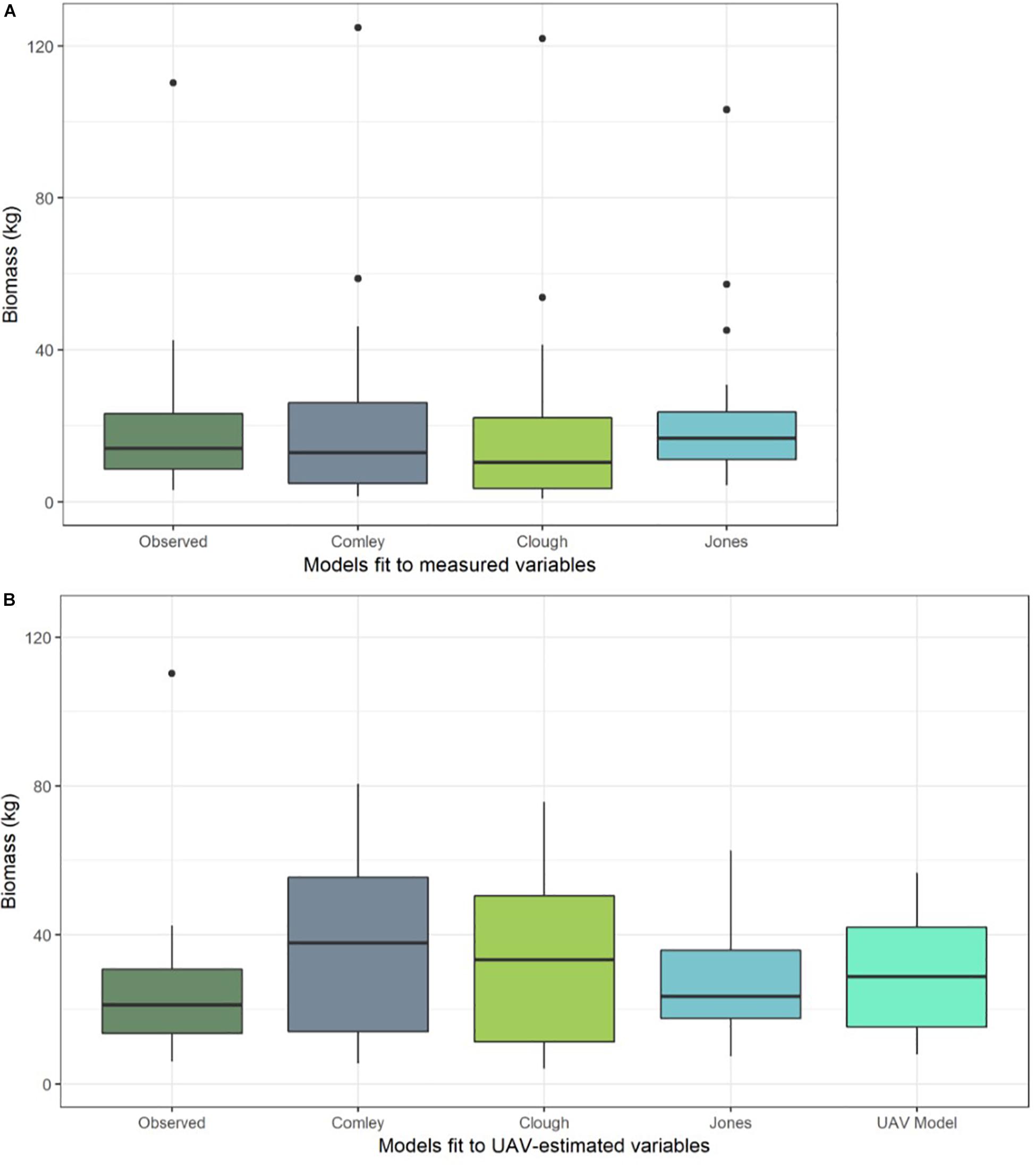
Figure 5. Boxplots of predicted biomass (kg) from a selection of the best performing allometric equations [Comley and McGuinness (2005); Owers et al. (2018a) and Jones – this study] when fit to (A) physically measured tree data from all harvested trees (n = 20) and (B) predictions from the same equations, but using UAV image-based measurements of variables to predict biomass (rather than physically measured variables). Predictions of tree biomass from the best model that was trained directly on the UAV image-based measurement data are also shown in (B) (“UAV Model”). Horizontal dark line shows the median biomass prediction, upper and lower box extents show the first and third quartiles respectively, whiskers extend to 1.5 times the interquartile range and black points indicate outliers.
Assessment of the Best Allometric Relationship for A. marina Tree Biomass From South Australian Trees
From the suite of new allometric equations we developed using the direct measurements from 20 felled trees, the best predictions of tree biomass were achieved with an equation that included both measured DBH and D30 as predictor variables (“Jones” in Table 2). This equation resulted in a mean prediction error of 4.33 kg when tested on the full dataset (n = 20 trees). A summary of all the new allometric equations we developed and tested using the direct tree measurement dataset (n = 20 trees) is provided in Supplementary Table S5.
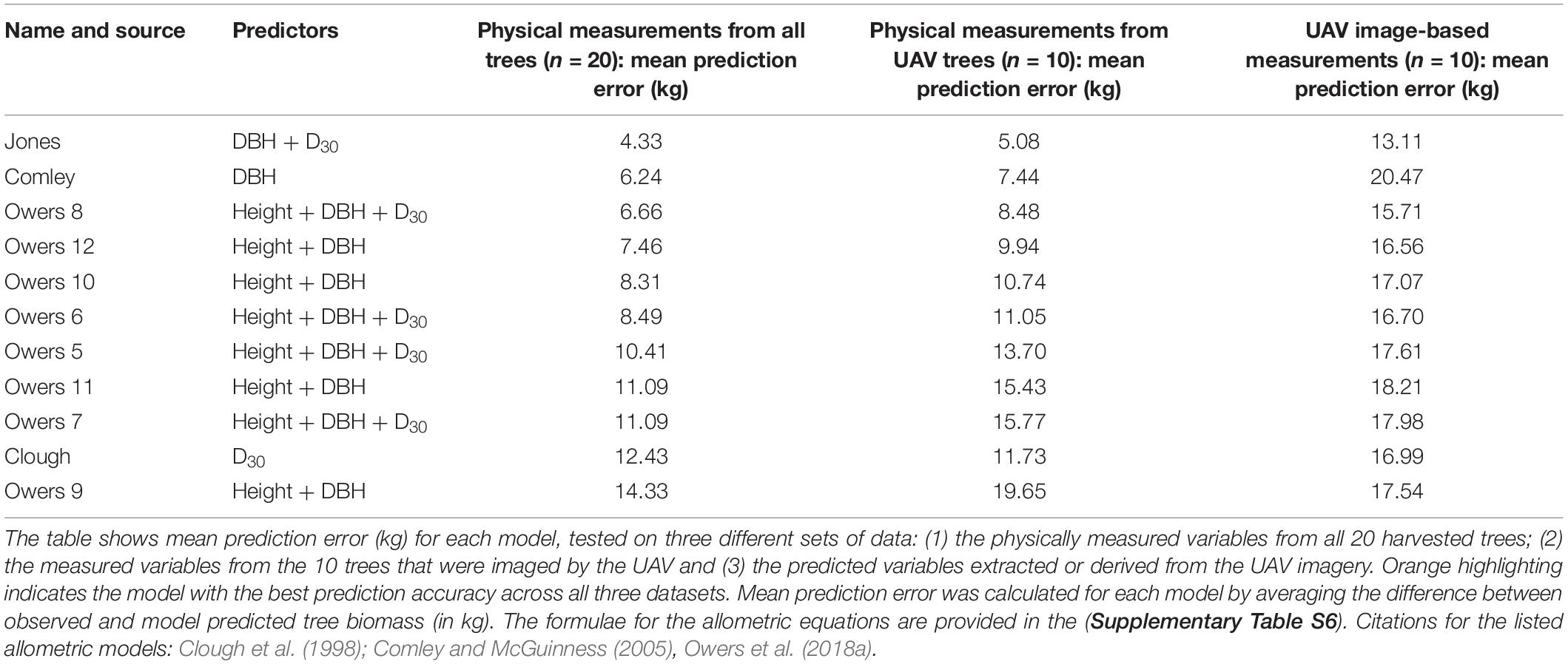
Table 2. A comparison of biomass prediction accuracy (based on both physical tree measurements and UAV image-based tree measurements) using previously published allometric equations and the best allometric relationship established from the trees in this study (“Jones”).
Of the 10 previously published allometric equations that we fit to the measured data from all harvested trees (n = 20), we found that those developed by Comley and McGuinness (2005) and Owers et al. (2018a); eqn. 8) achieved the lowest (i.e., best) prediction errors, being 6.24 and 6.66 kg, respectively. However, both these allometric equations predicted biomass less accurately than the best new allometric equation developed in this study from the tree measurement data collected in South Australia (Table 2 and Figure 5A). The top three allometric equations for predicting biomass consistently relied on diameter measurements (either DBH, D30 or both) as predictors with the Owers equation also including tree height (see Comley, Owers 8 and Jones; Table 2).
Comparison of Approaches: Predicting Biomass Using UAV-Derived Predictor Variables
When we used the allometric models to predict tree biomass based on UAV image-based measurements (n = 10 trees), as opposed to physical measurements taken from the trees, the prediction error generally increased (Table 2). This error is due to over-prediction of biomass for smaller trees combined with an inability to adequately predict the largest tree’s biomass (Figure 5B) and is likely the result of a smaller sample size. Although ranked second for biomass prediction accuracy when using physically measured variables (from the larger data set of 20 trees), we found that the Comley and McGuinness (2005) equation predicted tree biomass particularly poorly when using the UAV image-based measurements (mean prediction error = 20.47 kg; Table 2 and Figure 5B). Our own, newly developed allometric equation remained one of the best for biomass prediction when using UAV image-based measurements, albeit with considerable increases in prediction error compared to using the same equation with direct physical measurements of variables (Table 2; see “Jones” box in Figure 5).
Discussion
This study explored the potential for using imagery collected by UAVs to model the above-ground biomass of mangroves, specifically A. marina (grey mangrove) trees from South Australia. To that end, this study had two main parts. The first tested the ability of existing and new allometric equations to predict tree above-ground biomass, which was achieved through destructive sampling (n = 20 trees) and recording relevant biophysical data (tree structural measurements, biomass and carbon content) for use in allometric equations. The second part of the study was an assessment of the utility of UAV image-based measurements for estimating tree above-ground biomass, and a comparison of this approach to more traditional forest inventory and allometry-based methods. We acquired drone imagery to generate a three-dimensional model and orthomosaic, enabling measurement of tree height and canopy area, which were subsequently used to model DBH and D30. We then tested the potential for predicting above-ground biomass in two ways: (1) directly from the UAV image based measurements of tree structure (height, canopy area, DBH and D30) and (2) using UAV-image based measurements of tree structural characteristics in allometric equations.
Our new allometric equation for predicting above-ground biomass of A. marina performed better than the previously published equations we tested (when estimating from field measured data), achieving a mean prediction error of 4.33 kg (>1.6 kg better than the next-best model). This is perhaps unsurprising as the other equations were based on samples of the same species from regions of Australia in areas that are bio-climatically distinct from South Australia (Clough et al., 1998; Comley and McGuinness, 2005; Owers et al., 2018a). It is likely that the environmental conditions in South Australia, at the temperate edge of the range of this predominantly tropical species, will differ markedly from the other geographic areas where allometric relationships for the species have been developed.
We were able to measure tree height from the UAV image data with very high accuracy (height, R2 = 0.98), as well as model two other structural variables that are important for above-ground biomass estimation with reasonable accuracy [log (DBH) and log (D30); R2 = 0.54 and 0.52, respectively]. However, estimation of above-ground biomass from UAV image-based measurements or derived variables was relatively poor, with the best mean prediction error achieved in any of the models being 13.1 kg (Table 2). We expect that prediction errors would improve with a larger sample size.
Testing A. marina Allometric Equations on South Australian Trees
Avicennia marina is the only species of mangrove that grows in the hot and dry climate of South Australia, where it is reported to have a different growth form compared to other regions where the species is found (Clough, 1982). Kauffman and Donato (2012) stress the importance of using species-specific and regionally relevant allometric equations when assessing mangrove biomass for carbon reporting purposes. This recommendation is supported by the findings of Owers et al. (2018a) who identified spatial variability in both biomass and carbon storage in A. marina and other mangroves based on structure and growth form. As far as we are aware, there were previously no published allometric equations for A. marina based on trees sampled in South Australia. Therefore, we felt it important to test the appropriateness of a range of previously published allometric equations for A. marina on our South Australian trees, as well as attempting to develop new, more accurate, allometric equations for our study region. We note that Kauffman and Donato (2012) recommended that at least 15–20 trees should be used to develop an allometric model that is representative of a particular species and region, and Roxburgh et al. (2015) found that a minimum of 17 trees was required to fit an allometric equation with standard deviation within 5% of the mean observed tree biomass. The variation in measured tree structural variables (Table 1) indicates that although the sample design and sampling area were constrained, we managed to collect trees that represented a wide range of sizes, weights and growth forms; as opposed to only collecting trees with similar growth characteristics, which would limit the generalization of our results (Roxburgh et al., 2015).
The full dataset of 20 harvested trees enabled us to robustly test both previously published and new allometric relationships, to establish the most appropriate equation for South Australian A. marina. Unfortunately, we could not include four of the equations previously developed by Owers et al. (2018a) in our assessment, because these required measurements of canopy area, which we were not able to physically measure on all 20 trees. Canopy or crown area was shown to be an important predictor of tree biomass in Owers et al. (2018a) study on A. marina, which was undertaken in a different region of Australia as well as for other mangrove species (e.g., Fu and Wu, 2011; Yin and Wang, 2019) and other types of trees (e.g., Popescu et al., 2003). However, two other previous studies [by Clough et al. (1998) and Comley and McGuinness (2005)] did not use canopy area as a predictor variable in their allometric equations for A. marina biomass. In the models we developed for predicting biomass directly from UAV image-based tree measurements, canopy area was not a good predictor variable and was not selected in the best performing models (for further discussion see sections “Tree Structure Variables Estimated Using the UAV Imagery” and “Predictions of Tree Biomass Based on UAV Derived Variables”). The importance of canopy area as a predictor of biomass for this species is likely to be based on regional differences in growth form, which varies widely across the species’ range in Australia (Clough, 1982).
Of the previously published allometric equations for predicting A. marina biomass from tree measurements, Comley and McGuinness (2005) and equation 8 from Owers et al. (2018a) performed the best. However, we demonstrated that the new equation developed from our own data resulted in the lowest mean prediction error. All three of these equations relied on diameter measurements as predictors of biomass (with the Owers et al., 2018a equation also including tree height), but varied in their coefficient values (Table 2). This strong relationship between trunk diameter metrics and tree biomass is supported by previous studies on mangroves (e.g., Chave et al., 2005; Dharmawan and Siregar, 2008; Komiyama et al., 2008; Kauffman and Cole, 2010). The dependence on diameter measurements for accurate tree biomass predictions is likely to be strengthened in A. marina as it often grows in a multi-stemmed form (Clough et al., 1998), therefore a single height or canopy area estimate may not be representative of the total trunk and branch biomass associated with the tree’s multiple stems. The combined DBH and/or D30 measurements which we calculated, based on the sum of the squared diameter values from all stems, account for multiple stems in a single tree and are therefore likely to be a representative predictor of biomass in multi-stemmed trees.
Tree and Compartment Carbon Content
Our analyses of carbon content provided average values (∼ 44%) that are lower than the multiplier values commonly used for converting mangrove biomass to carbon when specific carbon concentrations are not available for a region, site or species (0.45–0.5) (Kauffman and Donato, 2012; IPCC, 2014). They are also slightly lower than recent estimates of carbon content for A. marina from New South Wales (Australia) reported by Owers et al. (2018a). The same study found differences in carbon content based on species and growth form, although these results were based on a smaller sample population (four individual A. marina trees, as opposed to our 20 trees), so may be expected to show greater variation. We analyzed over 230 samples from the different compartments of 20 trees and found no notable variation between tree compartments (trunk, branch, foliage) or between trees. We are confident that our results are representative of A. marina from the sampled region and recommend the use of these values when estimating above ground carbon storage for this species in South Australia.
Tree Structure Variables Estimated Using the UAV Imagery
The structure-from-motion point cloud that we generated from the UAV imagery provided very accurate estimates of tree height (R2 = 0.98). We also estimated canopy area from the orthomosaic, but could not assess the accuracy of these estimates because we were not able to take physical measurements of canopy area from the harvested trees prior to felling. Unfortunately, neither height nor canopy area were good predictors of tree biomass for our trees (Supplementary Tables S4, S5). This may be because many of the trees were multi-stemmed, with no apparent relationship between tree height or canopy area and the number of stems. This leads us to hypothesize that in the case of multi-stemmed trees, a single (maximum) height value or canopy area value may not be representative of the considerable woody biomass of the multiple stems beneath; resulting in these tree measurements being poor predictors of biomass.
Tree trunks are hidden beneath the canopy when looking down from above, therefore point clouds and orthomosaics derived from UAV imagery cannot resolve trunk structure, preventing direct estimates of tree diameter from the imagery. It may be possible, in some settings, to use ground-based or airborne LiDAR instruments to generate detailed point clouds of entire trees, including trunks and branches that are under the canopy (Owers et al., 2018b). However, the limitations of this approach include the expense of the instrument, its size and weight, and the need to be able to scan entire trees without obstruction, which is unlikely in dense forests with intermingled mangrove canopies. In lieu of direct estimates of diameter from the imagery, we built linear models to predict DBH and D30 based on tree height and canopy area variables extracted from the 3D structural information in the UAV imagery. There was some error associated with these model predictions, with model R2 values of 0.54 for the best model of DBH and 0.52 for the best model of D30. This error most likely impacted the accuracy of our biomass estimates from models and allometric equations which included diameter variables from UAV imagery as predictors of tree biomass.
Predictions of Tree Biomass Based on UAV Derived Variables
We found that using UAV image-based estimates of tree structural variables in allometric equations led to less accurate biomass estimates compared to when using forest inventory techniques to obtain physical measurements (Figure 5). In particular, the models and equations based on UAV image-based measurements were unable to predict the biomass of the largest tree, though it was predicted with reasonable accuracy by the allometric equations fit to physically measured tree data (Figure 5). The decreased accuracy of biomass estimates from equations and models fit to UAV image-based measurement data is likely due to the propagation of errors beginning from image measurements of canopy structure, which were then used to estimate structural variables (such as trunk diameter).
The considerable difference in the ability of the best allometric equations to accurately estimate tree biomass when using measured vs. UAV-image estimated variables (Figure 5 and Table 2) highlights the sensitivity of the allometric equations to measurement errors, and the need for any UAV imaged based measurement method to obtain accurate estimates of the key tree structural characteristics. The measurements taken from the UAV-based imagery were extremely accurate for tree height, but the model-predicted diameter estimates of diameter had significant error associated with them. This is problematic because the best allometric equations (evaluated using physical measurements from the trees) are those that rely on diameter measurements (DBH and D30). As discussed above in section: “Tree Structure Variables Estimated Using the UAV Imagery”, trunk diameter cannot be estimated directly from the UAV photogrammetric products (point cloud and orthomosaic). Although the models using UAV imagery currently achieve low predictive power for tree diameter (and subsequently the image-derived measurements are poor predictors of biomass), we propose that small sample size (n = 10) reduces our ability to constrain the relationship between canopy area, tree height and diameter metrics. Nonetheless, this preliminary assessment of the UAV approach to mangrove biomass prediction offers some promising initial results.
The relationship between tree height, canopy area and trunk diameter may be better constrained with additional data collected from trees using traditional field methods. Therefore, the models of DBH and D30 can be refined without the need for further destructive sampling of this protected species of native vegetation. If the predictive relationship between height, canopy area and diameter can be improved, it would result in lower prediction error for diameter metrics from UAV image-based estimates of height and canopy area. This in turn would lead to more robust estimates of A. marina biomass from methods using UAV imagery.
Due to the reliance on diameter measurements for accurate prediction of A. marina biomass in our study area (and thus a requirement for accurate derivation of diameter measurements from UAV imagery), the ultimate biomass prediction method may incorporate a hybrid approach of field- and image-based measures (Otero et al., 2018). Such an approach would involve the use of site-based measures of diameter that could be used to calibrate UAV image-based biomass prediction models over a broader area. Once developed, this method would allow for far greater survey coverage than is achievable with on-the-ground surveys, as well as avoiding many of the assumptions inherent in forest inventory approaches when upscaling from small survey sub-plots to larger areas. Collecting data from UAV imagery over an entire study area, rather than sub-plots within it, would also implicitly account for heterogeneity in factors affecting mangrove growth and productivity such as micro-topography, inundation regime, light availability and ecotones. The effect of these factors on tree biomass and growth could only be accounted for with a forest inventory approach if it was extremely well-designed, with stratified survey coverage that sampled across the variability within the site.
Conclusion
Our study demonstrates the potential for using imagery collected by a UAV to build three-dimensional models of mangrove tree structure and extract variables from these for estimation of above-ground biomass and carbon. The results show that although the UAV image-based height measurements are very accurate, image based estimates of tree above-ground biomass are not currently as accurate as field-based estimates and therefore do not currently provide the same power as on-the-ground measurements for predicting mangrove above-ground biomass. However, considering the unusual access to felled A. marina trees, a species protected under the South Australian Native Vegetation Act 1991, the samples presented a rare opportunity to gain this valuable insight. The exceptional circumstances that provided access to the study site and felled trees was the result of a strong partnership between industry, government and the research team.
Having identified that the critical predictors of biomass for South Australian A. marina are diameter metrics, it is now possible to move forward with refining our ability to predict these from UAV-based aerial imagery. UAV image-based estimates can be made far more quickly over extensive areas when compared to traditional forest inventory data collection techniques and, with improved accuracy through further model-calibration, have the potential to be a powerful tool for mangrove biomass estimation. The findings and recommendations from this study can support the ongoing development of novel, site-based methods for accurate and cost-effective quantification of mangrove above-ground biomass and carbon for blue carbon accounting and crediting purposes.
Data Availability Statement
The datasets used in this study are supplied in the Supplementary Material. The point cloud and orthomosaic generated from the UAV data are available to download from the Figshare online repository 10.25909/5df49f6dd1459.
Author Contributions
AJ, BG, RR, KC, and MW were involved in the planning of the study. AJ, RR, BG, and WG participated in the data collection, processing, sample analyses, and data analyses. AJ prepared the first draft of the manuscript and all figures. All authors were involved in editing the manuscript.
Funding
This research was funded by a grant from the Goyder Institute for Water Research (project reference: CA-16-04), with co-funding received from SA Water, the South Australian EPA, Edith Cowan University and the University of Adelaide’s Environment Institute.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was undertaken on the traditional lands of the Kaurna people. We acknowledge and respect their spiritual relationship with their country and acknowledge their cultural and heritage beliefs as the traditional land owners. We would like to thank Lendlease particularly Kate Brickhill and Chris Podger, as well as safety, engineering and construction staff who enabled our access to the Northern Connector work site where the mangroves for this study were removed. We would also like to thank staff at the South Australian Department of Environment and Water and Department of Planning, Transport and Infrastructure who facilitated our collaboration with the Lendlease. We acknowledge the South Australian Museum (particularly David Stemmer) who provided access to their Bolivar site for the delivery and measurement of trees. We would also like to thank Jackson Stockbridge, Matthew McMillan, and Sidney Heitmann who assisted in the processing of tree samples and data, as well as Dillon Campbell who provided support with UAV image processing. Thanks to David Summers and Jarrod Hodgson for providing comments on an earlier version of this work, and to the three reviewers of this manuscript for their useful and constructive comments. We would also like to thank Prof. Lian Pin Koh for support and advice around the UAV component of this work.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2019.00784/full#supplementary-material
References
Alongi, D. M. (2014). Carbon cycling and storage in mangrove forests. Ann. Rev. Mar. Sci. 6, 195–219. doi: 10.1146/annurev-marine-010213-135020
Anderson, K., and Gaston, K. J. (2013). Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 11:138–146. doi: 10.1890/120150
Aslan, A., Rahman, A. F., and Robeson, S. M. (2018). Investigating the use of Alos Prism data in detecting mangrove succession through canopy height estimation. Ecol. Indic. 87, 136–143. doi: 10.1016/j.ecolind.2017.12.008
Aslan, A., Rahman, A. F., Warren, M. W., and Robeson, S. M. (2016). Mapping spatial distribution and biomass of coastal wetland vegetation in Indonesian Papua by combining active and passive remotely sensed data. Remote Sens. Environ. 183, 65–81. doi: 10.1016/j.rse.2016.04.026
Bell-James, J. (2016). Developing a framework for blue carbon in Australia: legal and policy considerations. UNSWLJ 39:1583.
Bendig, J., Yu, K., Aasen, H., Bolten, A., Bennertz, S., Broscheit, J., et al. (2015). Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Observ. Geoinform. 39, 79–87. doi: 10.1016/j.jag.2015.02.012
Chave, J., Andalo, C., Brown, S., Cairns, M. A., Chambers, J. Q., Eamus, D., et al. (2005). Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145, 87–99. doi: 10.1007/s00442-005-0100-x
Clough, B. B. (1982). Mangrove Ecosystems in Australia: Structure, Function and Management. Canberra: Australian National University Press.
Clough, B. F., Dixon, P., and Dalhaus, O. (1998). Allometric relationships for estimating biomass in multi-stemmed mangrove trees. Aust. J. Bot. 45, 1023–1031.
Comley, B., and McGuinness, K. (2005). Above-and below-ground biomass, and allometry, of four common northern Australian mangroves. Aust. J. Bot. 53, 431–436.
Dharmawan, I., and Siregar, C. (2008). Soil carbon and carbon estimation of Avicennia marina (Forsk.). Vierh. Stand at Ciasem, Purwakarta. J. Penelit. Hutan dan Konservasi Alam 5, 317–328. doi: 10.20886/jphka.2008.5.4.317-328
Dittmann, S., Thiessen, E., and Hartung, E. (2017). Applicability of different non-invasive methods for tree mass estimation: a review. Forest Ecol. Manag. 398, 208–215. doi: 10.1016/j.foreco.2017.05.013
Emmer, I., von Unger, M., Needelman, B., Crooks, S., and Emmett-Mattox, S. (2015). Coastal blue carbon in practice; a manual for using the VCS methodology for tidal wetland and seagrass restoration. VM 0033:1. doi: 10.1201/9780429435362-1
Fu, W., and Wu, Y. (2011). Estimation of aboveground biomass of different mangrove trees based on canopy diameter and tree height. Proc. Environ. Sci. 10, 2189–2194. doi: 10.1016/j.proenv.2011.09.343
Gibbs, H. K., Brown, S., Niles, J. O., and Foley, J. A. (2007). Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environ. Res. Lett. 2:045023. doi: 10.1088/1748-9326/2/4/045023
Hamilton, S. E., Castellanos-Galindo, G. A., Millones-Mayer, M., and Chen, M. (2018). Remote Sensing of Mangrove Forests: Current Techniques and Existing Databases. Threats to Mangrove Forests: Hazards, Vulnerability, and Management, eds C. Makowski and C. W. Finkl, (Cham: Springer International Publishing), 497–520.
Hickey, S. M., Callow, N. J., Phinn, S., Lovelock, C. E., and Duarte, C. M. (2018). Spatial complexities in aboveground carbon stocks of a semi-arid mangrove community: a remote sensing height-biomass-carbon approach. Estuarine Coast. Shelf Sci. 200, 194–201. doi: 10.1016/j.ecss.2017.11.004
Howard, J., Hoyt, S., Isensee, K., Telszewski, M., and Pidgeon, E. (2014). Coastal Blue Carbon: Methods for assessing carbon stocks and emissions factors in mangroves, tidal salt marshes, and seagrasses. Arlington: International Union for Conservation of Nature.
IPCC (2014). 2013 Supplement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Switzerland: IPCC.
Kauffman, J. B., and Cole, T. G. (2010). Micronesian mangrove forest structure and tree responses to a severe typhoon. Wetlands 30, 1077–1084. doi: 10.1007/s13157-010-0114-y
Kauffman, J. B., and Donato, D. (2012). Protocols for the Measurement, Monitoring and Reporting of Structure, Biomass and Carbon Stocks in Mangrove Forests. Bogor: Center for International Forestry Research (CIFOR).
Kelleway, J. J., Saintilan, N., Macreadie, P. I., and Ralph, P. J. (2016). Sedimentary factors are key predictors of carbon storage in SE Australian saltmarshes. Ecosystems 19, 865–880. doi: 10.1007/s10021-016-9972-3
Komiyama, A., Ong, J. E., and Poungparn, S. (2008). Allometry, biomass, and productivity of mangrove forests: a review. Aquatic Bot. 89, 128–137. doi: 10.1016/j.aquabot.2007.12.006
Lee, S., Fatoyinbo, T., Lagomasino, D., Osmanoglu, B., Simard, M., Trettin, C., et al. (2015). “Large-scale mangrove canopy height map generation from TanDEM-X data by means of Pol-InSAR techniques,” in Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Italy
Mcleod, E., Chmura, G. L., Bouillon, S., Salm, R., Bjork, M., Duarte, C. M., et al. (2011). A blueprint for blue carbon: toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 9:552–560. doi: 10.1890/110004
Messinger, M., Asner, G. P., and Silman, M. (2016). Rapid assessments of amazon forest structure and biomass using small unmanned aerial systems. Remote Sens. 8:615. doi: 10.3390/rs8080615
Nellemann, C., and Corcoran, E. (2009). Blue Carbon: the Role of Healthy Oceans in Binding Carbon: a Rapid Response Assessment. Nairobi: UNEP/Earthprint.
Otero, V., Van De Kerchove, R., Satyanarayana, B., Martínez-Espinosa, C., Fisol, M. A. B., Ibrahim, M. R. B., et al. (2018). Managing mangrove forests from the sky: forest inventory using field data and Unmanned Aerial Vehicle (UAV) imagery in the Matang Mangrove Forest Reserve, peninsular Malaysia. Forest Ecol. Manag. 411, 35–45. doi: 10.1016/j.foreco.2017.12.049
Owers, C. J., Rogers, K., Mazumder, D., and Woodroffe, C. D. (2016). Spatial variation in carbon storage: a case study for currambene Creek, NSW, Australia. J. Coast. Res. 75(Suppl.1), 1297–1301. doi: 10.2112/si75-260.1
Owers, C. J., Rogers, K., and Woodroffe, C. D. (2018a). Spatial variation of above-ground carbon storage in temperate coastal wetlands. Estuarine Coast. Shelf Sci. 210, 55–67. doi: 10.1016/j.ecss.2018.06.002
Owers, C. J., Rogers, K., and Woodroffe, C. D. (2018b). Terrestrial laser scanning to quantify above-ground biomass of structurally complex coastal wetland vegetation. Estuarine Coast. Shelf Sci. 204, 164–176. doi: 10.1016/j.ecss.2018.02.027
Panagoitidis, D., Abdollahnejad, A., Surovı, P., and Chiteculo, V. (2017). Determining tree height and crown diameter from high-resolution UAV imagery AU - Panagiotidis, Dimitrios. Int. J. Remote Sens. 38, 2392–2410. doi: 10.1080/01431161.2016.1264028
Paneque-Gálvez, J., McCall, M. K., Napoletano, B. M., Wich, S. A., and Koh, L. P. (2014). Small drones for community-based forest monitoring: an assessment of their feasibility and potential in tropical areas. Forests 5:1481. doi: 10.3390/f5061481
Picard, N., Saint-André, L., and Henry, M. (2012). Manual for Building Tree Volume and Biomass Allometric Equations: From Field Measurement to Prediction. Italy: FAO.
Plan Vivo (2013). The Plan Vivo Standard for Community Payments for Ecosystem Services Programmes. Edinburgh: Plan Vivo. 35.
Popescu, S. C., Wynne, R. H., and Nelson, R. F. (2003). Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 29, 564–577. doi: 10.5589/m03-027
R Core Team (2017). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Rahman, A. F., and Aslan, A. (2017). The first global-scale 30 m resolution mangrove canopy height map using Shuttle Radar Topography Mission data. arXiv [preprint].
Roxburgh, S. H., Paul, K. I., Clifford, D., England, J. R., and Raison, R. J. (2015). Guidelines for constructing allometric models for the prediction of woody biomass: how many individuals to harvest? Ecosphere 6:art38. doi: 10.1890/es14-00251.1
Sprugel, D. G. (1983). Correcting for bias in log-transformed allometric equations. Ecology 64, 209–210. doi: 10.2307/1937343
Wilkes, P., Lau, A., Disney, M., Calders, K., Burt, A., and de Tanago, J. Gonzalez, et al. (2017). Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote Sens. Environ. 196, 140–153. doi: 10.1016/j.rse.2017.04.030
Wylie, L., Sutton-Grier, A. E., and Moore, A. (2016). Keys to successful blue carbon projects: lessons learned from global case studies. Mar. Policy 65(Suppl. C), 76–84. doi: 10.1016/j.marpol.2015.12.020
Keywords: blue carbon, allometry, unmanned aerial vehicle, photogrammetry, coastal wetlands
Citation: Jones AR, Raja Segaran R, Clarke KD, Waycott M, Goh WSH and Gillanders BM (2020) Estimating Mangrove Tree Biomass and Carbon Content: A Comparison of Forest Inventory Techniques and Drone Imagery. Front. Mar. Sci. 6:784. doi: 10.3389/fmars.2019.00784
Received: 19 August 2019; Accepted: 04 December 2019;
Published: 22 January 2020.
Edited by:
Benjamin Allen Lange, Norwegian Polar Institute, NorwayReviewed by:
Stuart E. Hamilton, Salisbury University, United StatesChristian Joshua Sanders, Southern Cross University, Australia
Severino Salmo, Ateneo de Manila University, Philippines
Copyright © 2020 Jones, Raja Segaran, Clarke, Waycott, Goh and Gillanders. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alice R. Jones, YWxpY2Uuam9uZXMwMUBhZGVsYWlkZS5lZHUuYXU=
 Alice R. Jones
Alice R. Jones Ramesh Raja Segaran
Ramesh Raja Segaran Kenneth D. Clarke1
Kenneth D. Clarke1 Michelle Waycott
Michelle Waycott