Accuracy of Empirical Satellite Algorithms for Mapping Phytoplankton Diagnostic Pigments in the Open Ocean: A Supervised Learning Perspective

Stock, Andy; Subramaniam, Ajit

doi:10.3389/fmars.2020.00599

ORIGINAL RESEARCH article

Front. Mar. Sci., 28 July 2020

Sec. Ocean Observation

Volume 7 - 2020 | https://doi.org/10.3389/fmars.2020.00599

Accuracy of Empirical Satellite Algorithms for Mapping Phytoplankton Diagnostic Pigments in the Open Ocean: A Supervised Learning Perspective

$\r\nAndy Stock*$ Andy Stock^* $Ajit Subramaniam\r\n$ Ajit Subramaniam

Lamont-Doherty Earth Observatory, The Earth Institute, Columbia University, Palisades, NY, United States

Monitoring phytoplankton community composition from space is an important challenge in ocean remote sensing. Researchers have proposed several algorithms for this purpose. However, the in situ data used to train and validate such algorithms at the global scale are often clustered along ship cruise tracks and in some well-studied locations, whereas many large marine regions have no in situ data at all. Furthermore, oceanographic variables are typically spatially auto-correlated. In this situation, the common practice of validating algorithms with randomly chosen held-out observations can underestimate errors. Based on a global database of in situ HPLC data, we applied supervised learning methods to train and test empirical algorithms predicting the relative concentrations of eight diagnostic pigments that serve as biomarkers for different phytoplankton types. For each pigment, we trained three types of satellite algorithms distinguished by their input data: abundance-based (using only chlorophyll-a as input), spectral (using remote sensing reflectance), and ecological algorithms (combining reflectance and environmental variables). The algorithms were implemented as statistical models (smoothing splines, polynomials, random forests, and boosted regression trees). To address clustering of data and spatial auto-correlation, we tested the algorithms by means of spatial block cross-validation. This provided a less confident picture of the potential for global mapping of diagnostic pigments and hence the associated phytoplankton types using existing satellite data than suggested by some previous research and a fivefold cross-validation conducted for comparison. Of the eight diagnostic pigments, only two (fucoxanthin and zeaxanthin) could be predicted in marine regions that the algorithms were not trained in with considerably lower errors than a constant null model. Thus, global-scale algorithms based on existing, multi-spectral satellite data and commonly available environmental variables can estimate relative diagnostic pigment concentrations and hence distinguish phytoplankton types in some broad classes, but are likely inaccurate for some classes and in some marine regions. Overall, the ecological algorithms had the lowest prediction errors, suggesting that environmental variables contain information about the global spatial distribution of phytoplankton groups that is not captured in multi-spectral remote sensing reflectance and satellite-derived Chl a concentrations. Weighting training observations inversely to the degree of spatial clustering improved predictions. Finally, our results suggest that more discussion of the best approaches for training and validating empirical satellite algorithms is needed if the in situ data are unevenly distributed in the study region and spatially clustered.

Introduction

Accounting for almost half of the world’s net primary production (Field et al., 1998), phytoplankton are the foundation of the marine food web and have a major climate-regulating function through the ocean’s biological pump: the oceans have stored about 1/3 of historic anthropogenic CO₂ emissions (Sabine et al., 2004; Gruber et al., 2019). The ecosystem services provided by phytoplankton depend in part on biomass, which has long been routinely monitored at the global scale by means of ocean color remote sensing from satellites (O’Reilly et al., 1998), but also on community composition. Phytoplankton communities, however, are substantially affected by climate change (Richardson and Schoeman, 2004; Doney et al., 2009; Hoegh-Guldberg and Bruno, 2010; Poloczanska et al., 2013). Because different types of phytoplankton play different ecological and biogeochemical roles, the development of algorithms that can map phytoplankton community composition from space is an important challenge in satellite monitoring of the oceans (Bracher et al., 2017).

Scientists have already proposed many algorithms for this purpose (Mouw et al., 2017). Early algorithms focused on the detection of single taxa, such as coccolithophores (Brown and Yoder, 1994), diatoms (Sathyendranath et al., 2004) and Trichodesmium (Subramaniam et al., 2001) that had singular optical properties that help distinguish them. Many recent algorithms instead distinguish between various phytoplankton functional types (PFTs; e.g., Alvain et al., 2008), phytoplankton size classes (PSCs; e.g., Brewin et al., 2010), or combine both classifications (e.g., Hirata et al., 2011). While the definition of PFTs differs between studies (IOCCG, 2014), they are usually broad taxonomic groups (like diatoms and prokaryotes) that are related to biogeochemical or ecological processes. Other algorithms estimate the concentrations of diagnostic pigments that serve as biomarkers for PFTs and PSCs (e.g., Pan et al., 2010; Bracher et al., 2015a; Moisan et al., 2017; Wang et al., 2018). Sometimes, pigment and PFT algorithms are combined. For example, Moisan et al. (2017) presented an algorithm for mapping diagnostic pigments, and then used the generated pigment maps as input for a PFT algorithm. The algorithms can be further classified based on the input data that they use (Mouw et al., 2017). For example, abundance-based algorithms (e.g., Brewin et al., 2010; Hirata et al., 2011) use only chlorophyll-a concentrations to predict the relative abundances of different phytoplankton types. Spectral algorithms instead use variations in the optical properties of different phytoplankton types to distinguish them. Some spectral algorithms directly link satellite-measured remote sensing reflectance or normalized water-leaving radiance to PFTs, PSCs or pigments (e.g., Alvain et al., 2005, 2008; Li et al., 2013; Ben Mustapha et al., 2014). Others estimate absorption or backscattering derived from satellite-measured radiance, which then allow the estimation of characteristics of the phytoplankton community (e.g., Ciotti and Bricaud, 2006; Bracher et al., 2009; Kostadinov et al., 2009, 2010, 2016; Mouw and Yoder, 2010; Devred et al., 2011; Bricaud et al., 2012; Sadeghi et al., 2012a, b; Roy et al., 2013). Ecological algorithms (e.g., Raitsos et al., 2008; Palacz et al., 2013; Hu et al., 2018a) combine spectral and environmental variables related to the mechanisms that affect the biogeography of different phytoplankton types, such as sea surface temperature (Rudorff and Kampel, 2012).

The existing algorithms have been validated against in situ data, but important questions about the accuracy of satellite algorithms for mapping phytoplankton community composition remain for at least four reasons. First, some algorithms have been validated using randomly selected hold-out observations not used to train the algorithm (e.g., Hirata et al., 2011). Yet many oceanographic in situ observations tend to be clustered along the tracks of research cruises or in specific study areas, while in many marine regions, there are no observations available at all. Because many oceanographic variables are spatially and temporally autocorrelated, the in situ observations may not be independent and thus potentially violate a key assumption of validation with randomly held-out observations. Some algorithms have been validated using independent data from a different source (e.g., Brewin et al., 2014b). However, which data count as truly independent for the validation of statistical models is a complicated question (Roberts et al., 2017; Gregr et al., 2019). In practice, validating algorithms with randomly selected held-out observations provides an estimate of their accuracy when making predictions in the proximity of available data, in the case of oceanographic data often along cruise tracks or inside observation clusters. Yet given the sparsity and clustering of in situ data at least at the global scale, it would be informative to also estimate global algorithms’ errors when extrapolating to marine regions where no in situ observations for statistical model training exist. This challenge is addressed in the research presented here, and is relevant to many satellite-derived ocean variables other than phytoplankton community composition. Second, the in situ data used to train and validate algorithms have uncertainties associated with them (Brewin et al., 2011). Most commonly, PFTs and PSCs are inferred from the concentrations of diagnostic pigments measured by means of high-performance liquid chromatography (HPLC), but the relationships between pigments and phytoplankton types are ambiguous (Nair et al., 2008). For example, while Uitz et al. (2006) estimated widely used coefficients for calculating size-fractionated chlorophyll in three PSCs based on diagnostic pigment measurements, these have been repeatedly modified for specific regions and biological conditions (Brewin et al., 2010; Devred et al., 2011; Hirata et al., 2011). Other methods to distinguish phytoplankton types from in situ samples exist, but all have limitations. Brewin et al. (2014b) compared size-fractionated chlorophyll concentrations estimated by size-fractionated filtration and by HPLC-based methods, finding reasonable agreement between these two approaches but also noted that they biased chlorophyll estimates for some size classes. Furthermore, pigment concentrations estimated by means of HPLC have errors themselves, and results can differ between laboratories (Latasa et al., 1996; Claustre et al., 2004). By now, HPLC measurements of phytoplankton pigments have, however, been extensively quality-tested and have proven useful for efficiently distinguishing some phytoplankton types and size classes (Van Heukelem and Hooker, 2011; Mouw et al., 2017; Kramer and Siegel, 2019; Lombard et al., 2019). Third, as described above, the different existing algorithms often have outputs that cannot be directly compared. Consequently, only one quantitative intercomparison of abundance-based, spectral and ecological algorithms has been published to date (Brewin et al., 2011). This study used mostly Atlantic and Mediterranean data, converted different algorithm outputs to size classes, and compared models that were trained at different geographical scales. Consequently, it provided a much-needed initial comparison, but complimentary additional analyses are required to obtain a reliable picture of different algorithms’ performance in different situations. Fourth, a comparison of microplankton phenology predicted by various satellite algorithms and climate models found considerable differences between these model outputs (Kostadinov et al., 2017). For these reasons, additional investigations of the accuracy of satellite algorithms for predicting different aspects of phytoplankton community composition are needed.

Here, we build on supervised learning methods adjusted for spatially auto-correlated data to partially address the first of these challenges, i.e., the lack of in situ observations in some marine regions, and their possible non-independence. First, to estimate errors when extrapolating to regions without in situ data and to account for possible non-independence of in situ observations, we use spatial block cross-validation (Roberts et al., 2017), in a hierarchical variant designed for model selection and tuning among many possibilities when data are spatially clustered (Stock et al., 2018a). We also report prediction errors estimated with fivefold cross-validation, ignoring the data’s spatial structure, for comparison. Second, we uphold the assumption that pigment concentrations measured by HPLC can serve as adequate biomarkers for PFTs and PSCs. However, because of the ambivalent relationships between diagnostic pigment concentrations and PSCs or PFTs, we do not undertake the transformation from pigments to different classes of phytoplankton. Instead, we follow other recent research and directly predict the spatial distribution of eight diagnostic pigments (Pan et al., 2010; Bracher et al., 2015a; Moisan et al., 2017; Wang et al., 2018). In contrast to previous pigment algorithms, we predict relative (% of total diagnostic pigment) and not absolute concentrations (mass per volume), because absolute pigment concentrations are positively correlated with Chl a (Kramer and Siegel, 2019) and hence partially reflect biomass. Third, given their different outputs, we do not test specific published algorithms. Instead, we train flexible statistical models that mimic existing algorithms based on their input data. We use smoothing splines and polynomials with only Chl a as predictor (also called features or independent variables) as abundance-based algorithms; random forests and boosted regression trees using multi-spectral remote sensing reflectances as spectral algorithms; and the same types of statistical models using additional satellite-measured environmental predictors, such as wind stress and sea surface temperature, as ecological algorithms. This approach does not reproduce and compare specific existing algorithms. Instead, it allows us to investigate how much, if at all, the additional data used by spectral and ecological algorithms contain relevant information for mapping the pigments’ global distribution and hence, aspects of phytoplankton community composition.

Based on this research design, we answer three questions: first, how well can empirical algorithms implemented as flexible statistical models and using existing, multi-spectral ocean color and related satellite data as input predict the relative concentrations of phytoplankton diagnostic pigments in regions without in situ data for model training? Second, how much (if at all) does the additional data used by spectral and ecological algorithms improve spatial predictions? Third, how different are estimates of the algorithms’ prediction errors calculated with spatial block cross-validation and cross-validation based on randomly splitting the data into training and validation sets?

Materials and Methods

Statistical Models and Predictors

To ensure exact documentation and reproducibility, our source code is available online¹. Figure 1 summarizes the inputs (predictors), outputs (responses), and types of statistical models that we used to predict the spatial distribution of phytoplankton diagnostic pigments. Table 1 summarizes the satellite data used as predictors in detail.

FIGURE 1

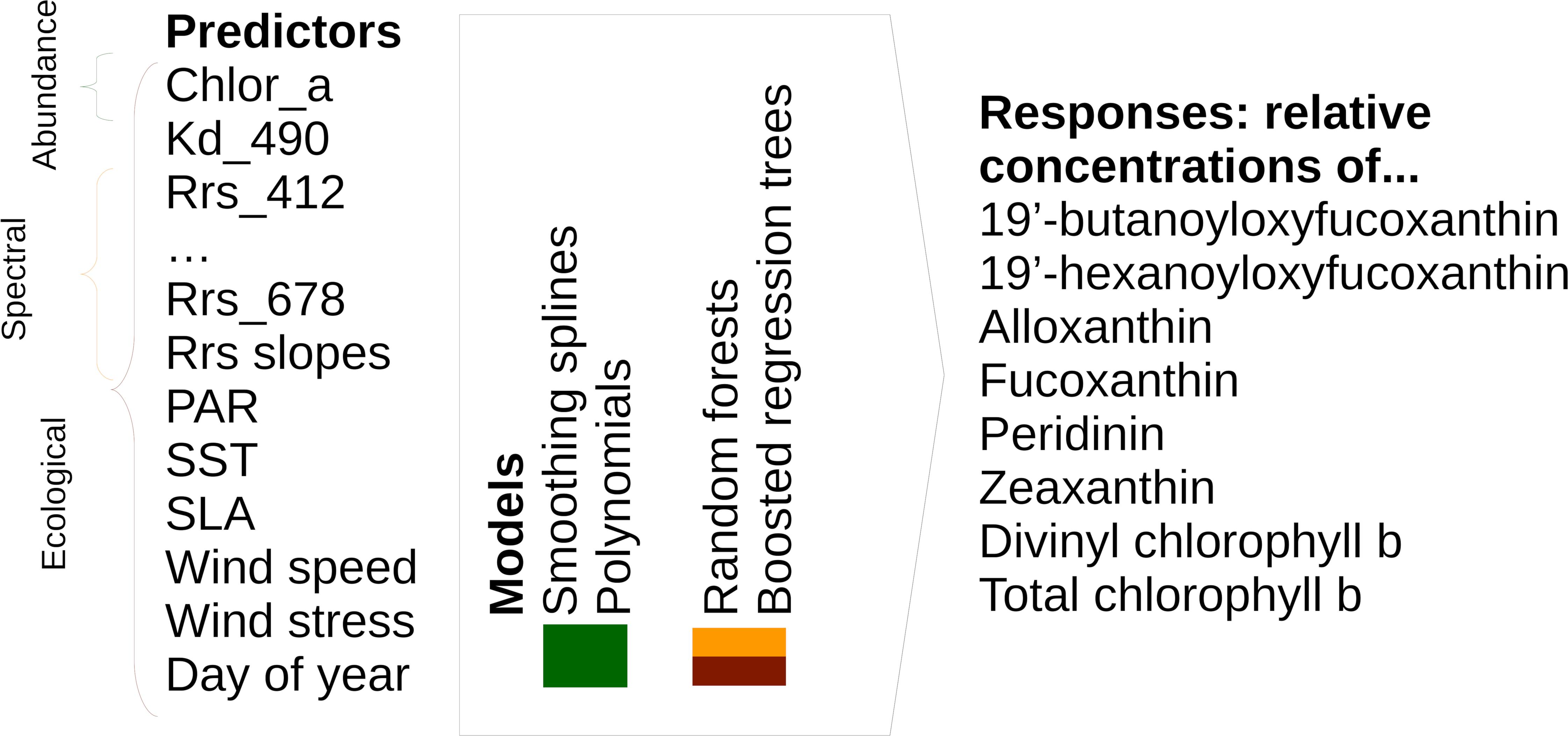
Figure 1. Overview of model types, including predictors and responses, included in this study. Please note that we tested spectral and ecological models using both raw Rrs and Rrs normalized as described in Section “Statistical Models and Predictors.”

TABLE 1

Table 1. Data sources for predictors.

Abundance-based algorithms use only chlorophyll-a as input. We modeled the relationships between each pigment’s relative concentration and chlorophyll-a by means of smoothing splines and polynomials. Spectral algorithms use remote sensing reflectances (Rrs) or normalized water-leaving radiances measured in different wavelength bands, as well as derived variables describing absorption and backscattering, to predict variables related to phytoplankton community composition. For our algorithms, we used Rrs at all bands from 412 to 678 nm from MODIS-Aqua. In addition, we tested models using Rrs normalized by dividing them by the mean for the associated chlorophyll-a concentration instead of raw Rrs, following Alvain et al. (2005). For this purpose, we re-calculated a look-up table (LUT) linking chlorophyll-a to Rrs based on the data in Table 1, but given the size of these global daily data, we built the look-up table only from every 15th day in 2003, 2008, 2013, and 2017. We calculated mean Rrs at each wavelength in chlorophyll-a bins that were 0.05 mg m^–3 wide, and used cubic splines between bin centers to interpolate the expected Rrs for the precise chlorophyll-a values (Supplementary Figure S1). Alvain et al. (2008, 2005) also used comparisons between neighboring bands as one of the factors for distinguishing PFTs. To allow easier representation of such criteria in our tree-based statistical models (see section “Spectral and Ecological Algorithms”), we also included reflectance slopes (difference of Rrs divided by difference in wavelength) as predictors. We again used two types of statistical models to learn the relationships between these spectral variables and diagnostic pigments: random forests (Breiman, 2001) and boosted regression trees (Friedman, 2001; Elith et al., 2008). These are flexible statistical models that can represent non-linear and interactive relationships between variables.

Ecological models use data describing environmental conditions in addition to chlorophyll a and spectral data. As for spectral models, we used random forests and boosted regression trees to model the relationships between predictors and pigment concentrations, and tested variations of the models including both raw and normalized Rrs. We chose the environmental predictors based on existing ecological algorithms (Raitsos et al., 2008; Hu et al., 2018a; see Table 1 for a full list of predictors). However, in contrast to these studies, we did not include latitude and longitude as predictors, as this resulted in overfitting to the spatial structure of the in situ data (e.g., sharp east–west or north–south boundaries separating cruises and clusters of in situ observations).

Diagnostic Pigments

We extracted HPLC data for 2003-2017 from the NASA SeaBASS archive (Werdell and Bailey, 2002). SeaBASS data are collected and processed by different contributors, but following consistent protocols, and have undergone rigorous quality checks (Werdell et al., 2003). Another large, harmonized collection of HPLC data is MAREDAT (Peloquin et al., 2013). Unfortunately, MAREDAT contains no data newer than 2008. While there are other relevant data sets, they have so far not been fully harmonized (Bracher et al., 2017), or were published after conclusion of this research (Kramer and Siegel, 2019). Thus, to maintain the best consistency between the in situ observations, we did not include any HPLC data from sources other than SeaBASS in this study. We extracted concentrations (mg m^–3) of the seven diagnostic pigments suggested by Vidussi et al. (2001) and Uitz et al. (2006): 19′-butanoyloxyfucoxanthin, 19′-hexanoyloxyfucoxanthin, alloxanthin, fucoxanthin, peridinin, zeaxanthin and total chlorophyll b. We then calculated the unweighted sum DP of the seven pigments’ concentrations (Vidussi et al., 2001). Furthermore, we extracted divinyl chlorophyll-b as a diagnostic pigment for prochlorococcus; while divinyl chlorophyll-a is commonly used for this purpose, data for this pigment were missing for too many sampling stations to be included. We calculated relative concentrations by dividing each pigment’s concentration by DP (Vidussi et al., 2001), because absolute concentrations can co-vary with biomass in addition to community composition, and because relative pigment concentrations are the foundation of deriving PSCs and PFTs from pigments (e.g., Hirata et al., 2011). We used the unweighted sum of pigment concentrations instead of a weighted sum, as, e.g., proposed by Uitz et al. (2006), to maintain a direct link to absolute pigment concentrations predicted by previous algorithms. In total, we extracted 29,232 observations for our study period. We removed observations from depths greater than 10 m (Brewin et al., 2010). If more than one observation existed in the upper 10 m of the water column for a given sampling station and day, we retained only the observation closest to the surface. We also removed observations that were made within 50 km of land based on global GSHHS intermediate-resolution shorelines (Wessel and Smith, 1996). The resulting data set contained 4,885 observations.

Match-Ups

Bailey and Werdell (2006) suggest strict match-up requirements for validation of satellite data: A 3 h time window and using the mean of pixels in a small spatial window (few km) around the in situ location. However, many past diagnostic pigment, PSC and PFT remote sensing studies have used less strict criteria to match in situ with satellite data, in order to obtain larger matched data sets. For example, some authors used a 24 h or same-calendar-day instead of the suggested 3 h window (Bracher et al., 2015a), or matched in situ observations to 8-day composites of satellite data (Raitsos et al., 2008; Li et al., 2013; Wang et al., 2018). Furthermore, while Bailey and Werdell (2006) suggest using a small window of pixels around each in situ observation at the sensor’s native resolution (about 1.1 km at nadir for MODIS), most diagnostic pigment, PSC and PFT remote sensing studies based on these instruments have used 3 pixel × 3 pixel windows at 4 or 9 km resolution (Alvain et al., 2005; Brewin et al., 2010; Ben Mustapha et al., 2014; Wang et al., 2018), resulting in easier data preparation, but a substantially larger spatial window.

Given the trade-off between tightly matching in situ and satellite observations and achieving a matched data set of sufficient size, as well as the ad hoc choice of match-up criteria in many previous diagnostic pigment, PFT and PSC mapping studies, we investigated spatiotemporal auto-correlation in our data as follows. We first created a global grid of points regularly spaced at 2,000 km intervals, and removed points that were within 300 km of land. Then, we extracted MODIS-Aqua Rrs for each day in 2017 in a 200 km by 200 km window centered around each point (Supplementary Figure S2), and normalized the remote sensing reflectances within each window to mean 0 and variance 1 (to make variograms comparable across windows). We calculated an experimental spatiotemporal variogram for each window and wavelength band (R package gstat; Pebesma, 2004; Gräler et al., 2016). If there were more than 12,000 pixels for a window and wavelength, we randomly sampled 12,000 observations in order to achieve acceptable computation times. We finally averaged the individual variograms for each wavelength to obtain a representation of the global average spatial auto-correlation across different distances (Supplementary Figure S3). While the full interpretation of the variograms is beyond the scope of this study and complicated by the fact that MODIS-Aqua observes different swaths on adjacent days, the geostatistical analysis suggested that remote sensing reflectances in the open oceans, on average, changed more over 1–2 days than over several 10 s of kilometers, in line with previous research suggesting that phytoplankton communities (and hence, in case-1 waters, remote sensing reflectances) can be relatively homogeneous at this spatial scale (Aiken et al., 2007). We thus created match-ups using a same-calendar-day temporal window, and using the median of a 3 × 3, 4 km-pixel spatial window. However, we discarded match-ups that had fewer than 3 valid pixels in the 3 × 3 window, or where one or more pixels in the window diverged from the median by more than 20%. We also discarded observations that had no data for one of the 8 diagnostic pigments, but retained observations where a pigment’s concentration was below the detection limit, setting them to 0 (Li et al., 2013). Lastly, we discarded observations that had either in situ or remotely sensed chlorophyll-a concentrations >3 mg m^–3 to make sure that our analysis was limited to open-ocean conditions (Alvain et al., 2005). Our final data set consisted of 446 matched in situ pigment and satellite observations (Figure 2).

FIGURE 2

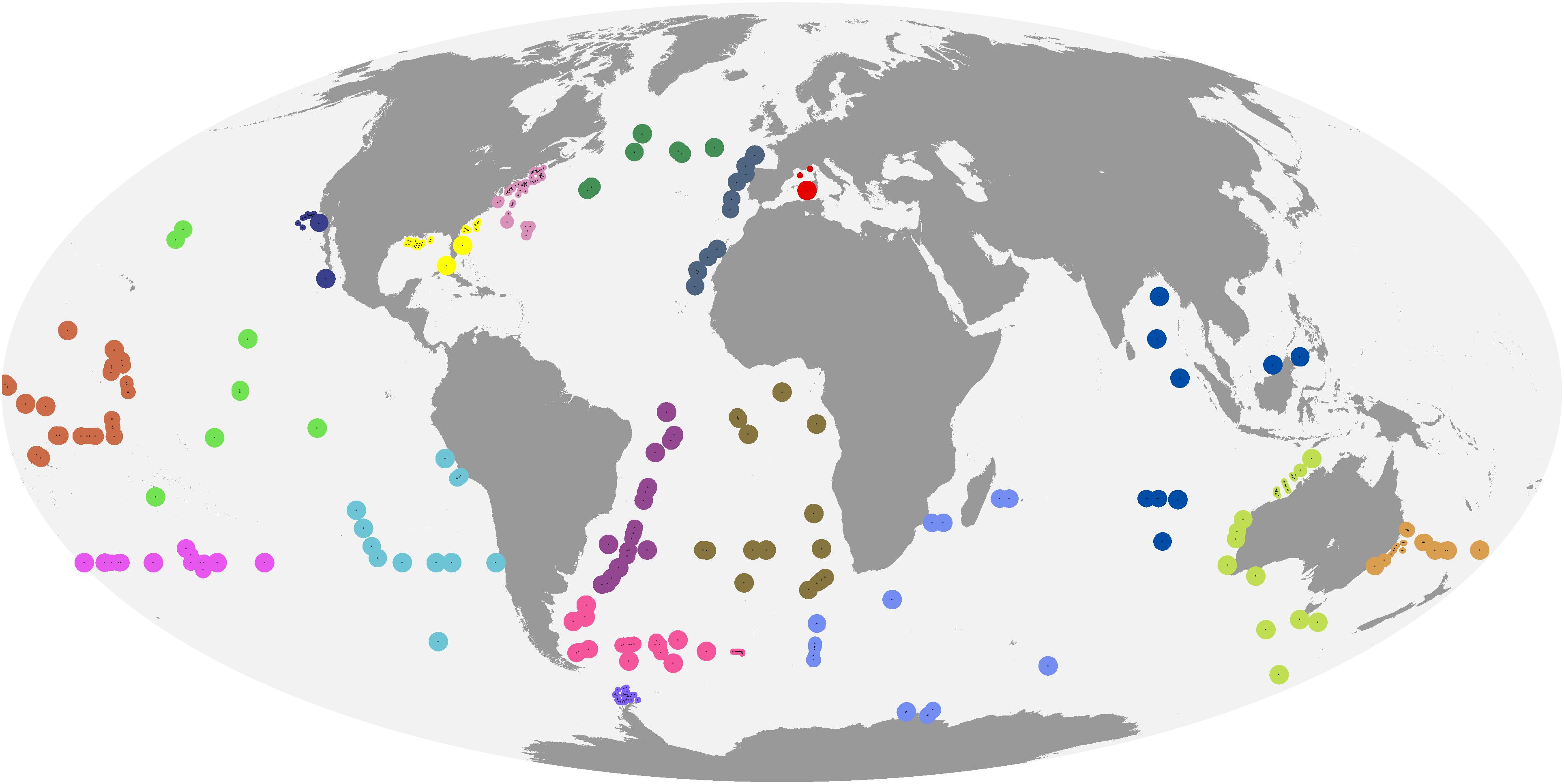
Figure 2. Matched in situ and satellite observations. Colors indicate cross-validation blocks, and the areas of the circles are proportional to spatial weights.

Observation Weights

Many in situ observations were clustered in space. Thus, models fitted to these data would in practice be optimized for performance in those locations with many close-by observations (Stock, 2015). We thus weighted the observations when training algorithms. There are several ways to calculate spatial observation weights. However, weights based on Voronoi polygons or Kriging assign too large weights to observations near the edges of clusters, and weights based on cell declustering are sensitive to the definition of a regular grid (Bel et al., 2009). If the data form many separate clusters and are arranged linearly (like in situ data collected along research cruise tracks), these problems can be especially pronounced (Stock et al., 2018a). We thus assigned spatial observation weights by means of the following approach, similar to cell declustering but based on local point densities in circles around each data point instead of non-overlapping grid cells. For each observation i, we counted the number n(i) of neighboring observations within a 200 km radius, excluding i itself. We then calculated the weight as w(i) = 1 − min[9,n(i)]/10. Thus, while w(i) = 1 for spatially isolated observations, w(i) was reduced by 0.1 for each observation within 200 km, down to a minimum of w(i) = 0.1 if nine or more observations were within 200 km of observation i. The 200 km threshold was chosen ad hoc based on the spatiotemporal variograms. While not showing a sharp sill and range (distance threshold where data become spatially un-correlated), the variograms suggested that ocean color observations separated by 200 km were considerably more different than observations in close proximity. We acknowledge that, for lack of more empirically or theoretically justified alternatives that would not have produced artifacts on our data, our weighting method is an ad hoc solution. We hence repeated the analyses with the common method of using equal weights for all observations in model training for comparison.

Model Training and Testing

We trained and tuned the models, and estimated their errors when extrapolating to new regions, by means of double spatial block cross-validation (Stock et al., 2018a). This approach nests two spatial block cross-validations (Roberts et al., 2017) inside each other. The inner cross-validation serves to select tuning parameters for a given algorithm, whereas the outer cross-validation provides an estimate of the trained and tuned algorithm’s performance in marine regions without in situ observations (as they have been completely withheld from all training and tuning steps).

There are many ways to identify cross-validation blocks, which should be informed by the study’s objective (e.g., interpolation vs. extrapolation) and characteristics of the data (Roberts et al., 2017). Because some marine regions had no matched in situ and satellite observations at all, we consider global satellite mapping of phytoplankton community composition an extrapolation problem (in the sense of extrapolation to regions not observed in situ, even if spatially surrounded by regions with in situ data), and accordingly chose large spatial blocks. In this way, our error estimates reflect the performance of the algorithms in regions for which no training data are available, and provide a measure of the degree to which the relationships learned by the algorithms where data exist hold up in other geographical areas. Furthermore, because the observations were unevenly distributed, automatic clustering approaches to identify blocks would have created unacceptable artifacts. For example, using marine bioregions (Longhurst, 2010) as spatial blocks would have resulted in situations where one or a few observations close to a large cluster fall just outside of the region boundary, get assigned to a separate block and gain inappropriately high influence on error estimates (Supplementary Figure S4). Furthermore, biogeographical boundaries in the oceans are dynamic (Reygondeau et al., 2013). We thus assigned observations to blocks manually, according to the considerations above (Figure 2). The individual blocks contained between 8 and 94 observations.

For comparison, we also calculated errors by means of a nested fivefold cross-validation (splitting the in situ data randomly into folds; Supplementary Figure S5), again using the inner cross-validation to tune models and the outer cross-validation to estimate their prediction errors. This error estimate corresponds to the mean of repeated validations using randomly assigned training (for model fitting), development (for tuning) and validation (for error estimation) sets.

Algorithms

Null Model

As baseline to compare the algorithms against, we defined a null model that does not use any predictors. Instead, the null model predicts the weighted (see section “Observation Weights”) mean of the observed pigment concentrations in the training data. The rationale for using such a baseline is that, while the acceptable level of error depends on an algorithms’ applications, an algorithm that is not substantially better (here tentatively defined as at least 30% lower cross-validated prediction error) than a constant calculated based on the in situ data alone will not be useful for most applications.

Abundance-Based Algorithms

Existing abundance-based algorithms differ in the ways in which they establish relationships between chlorophyll-a and PFTs, PSCs or diagnostic pigments. For example, Hirata et al. (2011) use five different equations with up to six parameters as predictive models for various PFTs. Brewin et al. (2010) used exponential equations based on Sathyendranath et al. (2001) as abundance-based PSC algorithms, yet no such general equations have been proposed for relating diagnostic pigments to Chl-a. We therefore implemented abundance-based algorithms by fitting two types of flexible statistical models to the chlorophyll-a and diagnostic pigment data. First, we fitted polynomials of degrees 1 (lines) to 15, and treated the degree of the polynomials as a tuning parameter (i.e., we tested a polynomial of each degree in the internal cross-validation, and chose the degree resulting in the lowest internal cross-validated mean squared error, for error estimation in the outer cross-validation). Second, because polynomials tend to make inaccurate predictions near the boundaries of the range of the training data, we also used smoothing splines, piece-wise continuous functions that can mimic any relationship between two variables. Similar to the degree of polynomials, the splines’ flexibility (given as effective degrees of freedom) was a tuning parameter.

Spectral and Ecological Algorithms

Also empirical spectral and ecological algorithms have been implemented using various functional forms, including rule-based classification (Alvain et al., 2005), principal components regression (Bracher et al., 2015a), and artificial neural networks (ANNs; e.g., Raitsos et al., 2008; Palacz et al., 2013; Ben Mustapha et al., 2014). ANNs are one of the most common statistical foundations of such algorithms, and have a long history of application in other domains of ocean remote sensing (Keiner, 1999). However, ANNs are prone to overfitting, and training them requires an initial random parametrization that may lead to substantially different fitted models. Remote sensing applications of machine learning methods have hence made increasing use of random forests (RFs), which are less sensitive to overfitting and require no choice of initial values (Belgiu and Drăguţ, 2016). Hu et al. (2018a) found that RFs outperformed ANNs in a PSC classification task. We hence implemented spectral and ecological algorithms using RFs (Breiman, 2001). To test if this choice of an underlying statistical model influences our results, we additionally trained boosted decision trees (BRTs) using the same input data (Friedman, 2001; Elith et al., 2008).

Both approaches are based on decision trees, a type of regression or classification model able to represent non-linear relationships and interactions between variables. However, such trees are prone to over-fitting, and thus rarely the best choice for predictive modeling. RFs overcome this problem by combining many trees as follows. Each tree is fitted to a bootstrap sample of the training data. Furthermore, at each split in the tree, only a subset of all predictors is considered, in order to make the trees less similar to one another. For a given set of predictor values, the RFs’ prediction is the mean of all individual trees’ predictions. We used RFs with 2,000 trees; the number of predictors considered at each split is a tuning parameter, again chosen based on the internal cross-validation MSE.

Also BRTs combine many individual decision trees, but in a different way. First, a single tree with only few splits (the interaction depth, a tuning parameter determining the level of interaction between predictors that the model can represent) is fitted to the data. Then, the tree’s predictions are multiplied by a small factor (the learning rate, a second tuning parameter). A new tree is fit to the residuals, and its predictions are again multiplied by the learning rate and added to the first tree’s prediction. This process is repeated for a fixed number of trees (the third tuning parameter), and in this way approximates the function to be learned in many small steps.

Final Model Choice, Training and Predictions

For each pigment, we trained the type of model that performed best in the double spatial block cross-validation on the full data set (Kuhn and Johnson, 2013). We then created global maps showing the mean relative concentration of each pigment in 2013–2017, but only for pigments whose error was a considerable improvement (as defined in section “Null Model”) over the null model according to the spatial block cross-validation. Because the in situ data used here contained no Arctic observations, we did not predict pigment concentrations beyond 66 degrees north.

Results

Algorithm Performance

For fucoxanthin and zeaxanthin, the best algorithms according to the spatial block cross-validation made substantially better predictions than the null model (54 and 42% lower MAE; Figure 3). For the other diagnostic pigments, the algorithms achieved smaller improvements over the null model: 16% for 19′-butanoyloxyfucoxanthin, 12% for 19′-hexanoyloxyfucoxanthin, 18% for divinyl chlorophyll b, 8% for total chlorophyll b, 6% for peridinin and no improvement at all for alloxanthin. The algorithms for these pigments failed to appropriately predict the variability of in situ observations (Figure 4). With the exception of alloxanthin and peridinin (the two pigments for which the algorithms performed worst), ecological algorithms had the lowest prediction errors. For example, abundance-based and spectral algorithms achieved only a 19% and, respectively, 22% reduction of the null model’s MAE for fucoxanthin compared to 54% for the ecological algorithm.

FIGURE 3

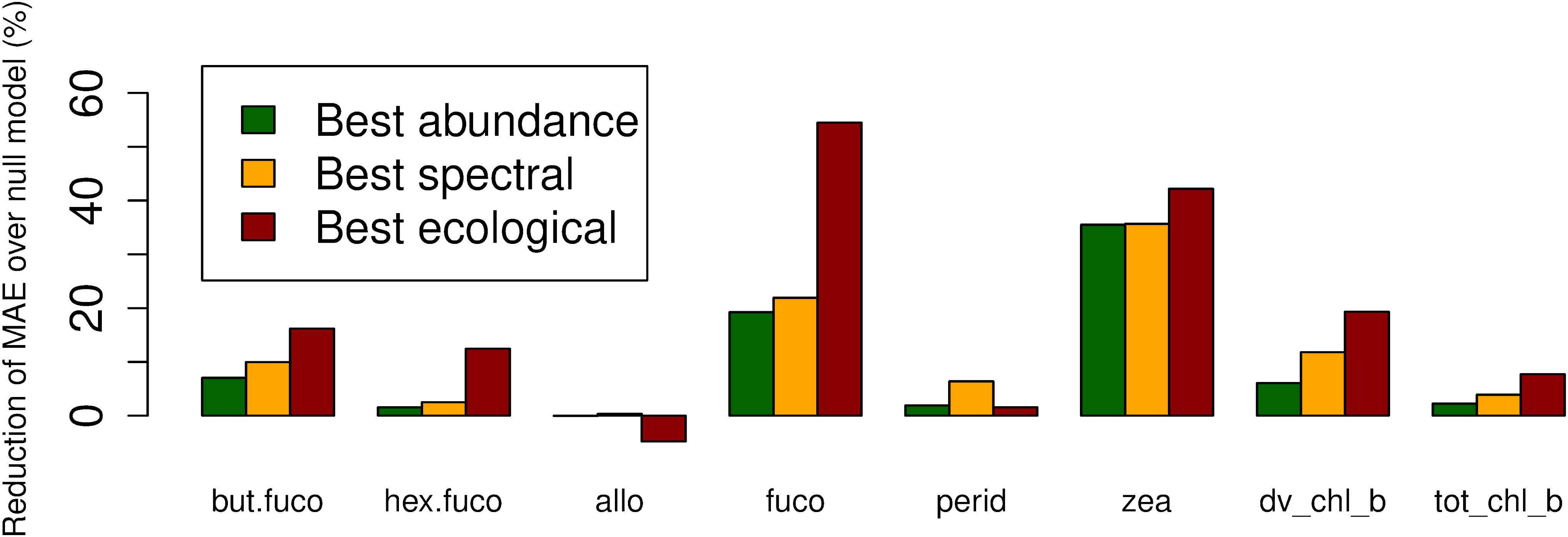
Figure 3. Reduction of mean absolute error (in comparison to a null model which always predicts the mean of the training data) of the best-performing abundance-based, spectral and ecological algorithms for each diagnostic pigment.

FIGURE 4

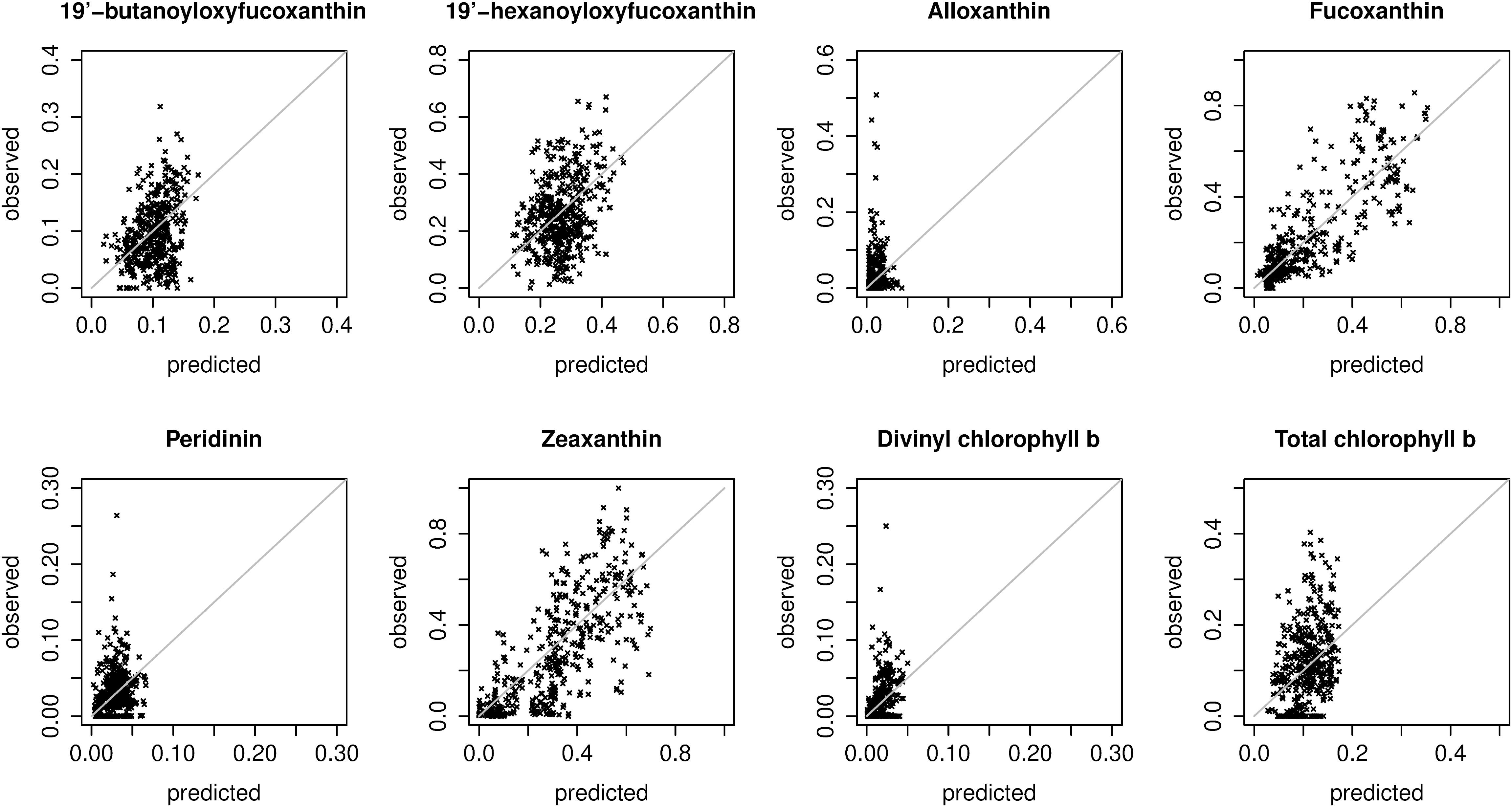
Figure 4. Scatter plots of predicted and observed relative pigment concentrations. Predictions were extracted from the spatial block cross-validation: for each in situ observation, the prediction was made with a model trained on all spatial blocks except the block containing the observation (i.e., the plots show extrapolation errors). The plots show predictions made with the best overall model for each pigment (Table 2). Note that the axis limits differ between plots.

We compared the best-performing abundance-based algorithms (smoothing splines with declustering weights) for fucoxanthin and zeaxanthin to functions linking total Chl a to the proportion of Chl a in diatoms and in prokaryotes fitted using a global data base by Hirata et al. (2011). Our learned relationships were very similar to Hirata et al.’s (2011) (Supplementary Figure S6), even though we predicted related variables and did not manually impose any functional form on the possible relationships between Chl a and the pigments.

Prediction errors estimated as RMSEs or as correlations between predicted and observed relative pigment concentrations told the same story as MAEs (Table 2). Differences between the two types of statistical models tested for each algorithm type (splines and polynomials for abundance-based algorithms, random forests and boosted regression trees for spectral and ecological algorithms) were small. However, splines often worked slightly better than polynomials. For some pigments, boosted regression trees worked slightly better than random forests, and for others, vice versa. The best-performing algorithms are highlighted in Table 2, and summarized in Table 3.

TABLE 2

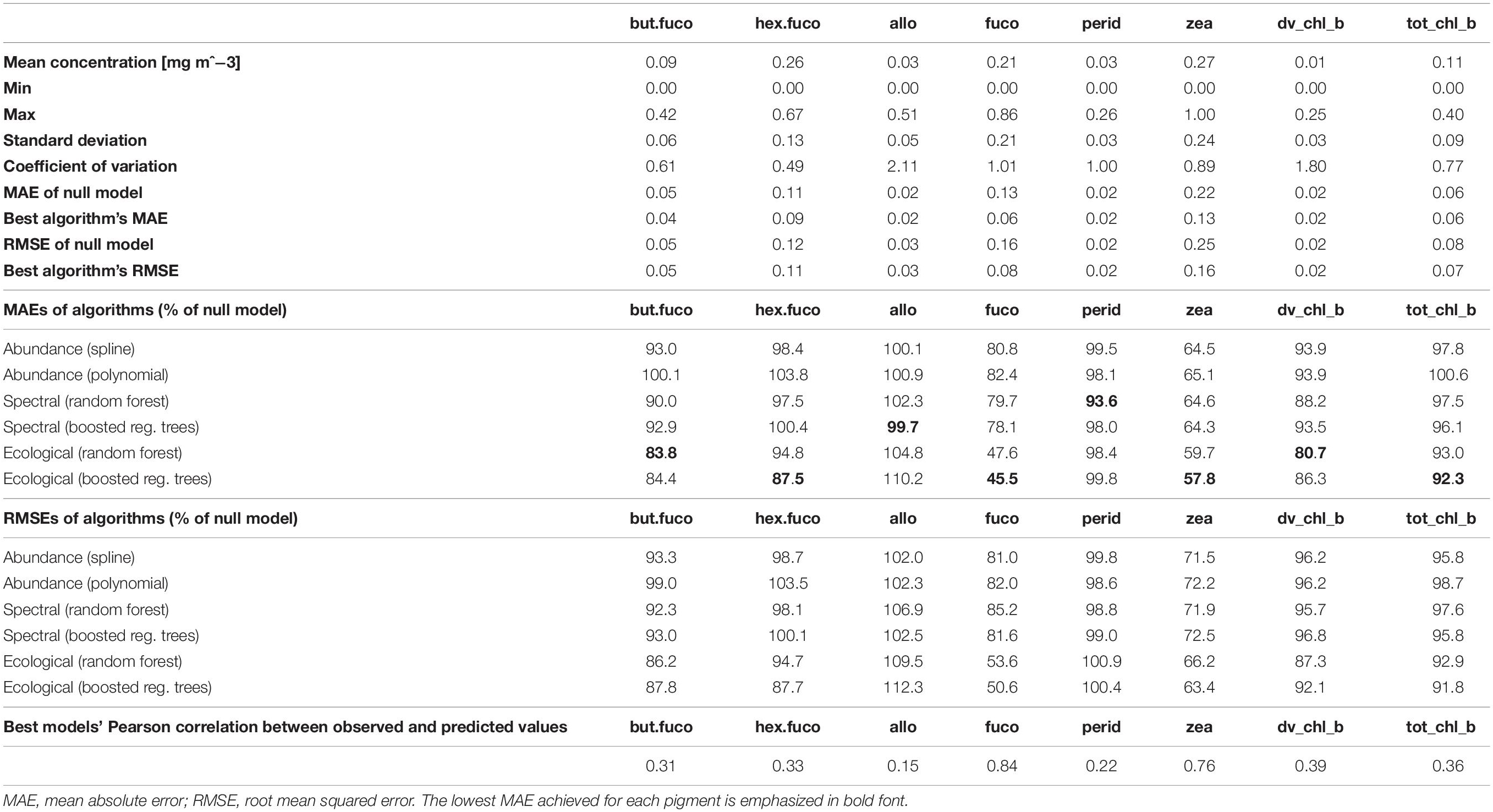
Table 2. Summary statistics of in situ data and prediction errors achieved by the different model types, estimated by means of spatial block cross-validation.

TABLE 3

Table 3. Tuning parameters of the best statistical models, obtained by training and tuning on the full match-up data set.

Normalizing remote sensing reflectances by their mean for the respective chlorophyll-a concentration, as in Alvain et al. (2005, 2008), slightly reduced prediction errors for some spectral and ecological algorithms (Supplementary Table S1), but we considered the improvement too small and inconsistent to justify the additional computational cost of normalization. However, our statistical models could learn interactions between raw reflectances and Chl a; empirical algorithms that cannot automatically include predictor interactions may benefit more from such normalization. Because our method to calculate declustering weights for model training was based on ad hoc considerations, we repeated the double spatial block cross-validation with equal weights for all observations. Using declustering weights led to lower prediction errors for 7 out of 8 diagnostic pigments, in some cases considerably lower (Supplementary Table S2). For example, for fucoxanthin, using declustering weights reduced the MAE of the best identified algorithm by 20% compared to the best MAE of algorithms trained using equal weights. Finally, we compared abundance-based algorithms using in situ and satellite-measured chlorophyll a as input. For most tested pigments and statistical model types, algorithms using in situ chlorophyll a had lower prediction errors than algorithms using satellite-measured chlorophyll a (Supplementary Table S3).

Estimates of variable importance can be derived from random forests based on the reduction of variance in the individual trees’ leafs if split on a predictor, and from boosted regression trees based on the reduction of MSE when a predictor is included. However, such estimates can be biased when predictors are correlated (Nicodemus et al., 2010). In our data, for example, remote sensing reflectances in adjacent wavelength bands were highly correlated (with coefficients >0.9). Given the resulting difficulty in interpretation, we do not report details of variable importance, but only note one general observation: SST was the most influential predictor for the five pigments with the largest reduction of MAE compared to the null model, and shared the first place with Slope_488_531 for total chlorophyll b (at least one of the reflectance slopes was among the 3 most important predictors for all pigments). The importance of SST as proxy for the global spatial distribution of diagnostic pigments is consistent with previous findings that SST is an important environmental predictor of the spatial distribution of phytoplankton types at broad spatial scales (Raitsos et al., 2008), and with a large body of research suggesting that SST has a strong influence on phytoplankton communities (Richardson and Schoeman, 2004). Some more recent abundance- and radiance-based algorithms have hence included SST in addition to chlorophyll-a and spectral variables (Pan et al., 2013; Ward, 2015). Of course, because of its latitudinal gradient and seasonal variability, this may not be an indicator of biological causation as much as an environmental correlation, i.e., part of the relationship between SST and phytoplankton community composition is likely a proxy for other broad-scale biogeographical factors. While we have argued that spatial block cross-validation provides a more relevant estimate of prediction errors when in situ data are spatially clustered and unevenly distributed over a study area, we also calculated errors by means of fivefold cross-validation for comparison (Table 4 and Supplementary Table S4). Like a single set of randomly withheld validation observations, this method assumes that training and testing observations are independent yet allows them to be in close spatial proximity to each other. The fivefold cross-validation suggested lower MAE estimates for all pigments except fucoxanthin. When expressed as percent of the null model MAE (calculated using the same cross-validation folds), the fivefold cross-validation suggested larger improvements over the null model for more pigments than spatial block cross-validation. Taken together, these results would suggest that, in contradiction to the spatial block cross-validation results, the global spatial distribution of at least three additional pigments could be predicted reasonably well by the best algorithms (19′-butanoyloxyfucoxanthin, 19′-hexanoyloxyfucoxanthin, divinyl chlorophyll b).

TABLE 4

Table 4. Comparison of the best algorithms’ mean absolute errors (MAEs) calculated with fivefold cross-validation and with spatial block cross-validation.

Spatial Distribution of Prediction Errors

The best diagnostic pigment algorithms extrapolated well to some marine regions but not to others: the accuracy of predicted relative pigment considerations varied considerably between spatial blocks (Figure 5). While some blocks had comparatively high MAEs for most pigments (e.g., the two blocks off the North American east coast), there were no blocks where predictions were always more accurate or inaccurate than elsewhere. For example, prediction errors in the Mediterranean Sea were relatively small for fucoxanthin, but relatively large for zeaxanthin. As another example, the southernmost block in this study had a three times larger MAE than the block with the next-largest error for alloxanthin, and also a relatively large error for some other pigments. However, this block also had one of the lowest MAEs for divinyl chlorophyll b: because of very low observed divinyl chlorophyll b concentrations, the algorithm - which underestimated higher concentrations found elsewhere according to Figure 4 – performed well in this block. In general, while there were no striking patterns of error that held for all pigments, there were moderate to strong positive relationships between the standard deviation of observed pigment concentrations within blocks and the blocks’ MAEs, except for zeaxanthin, where this relationship was weak.

FIGURE 5

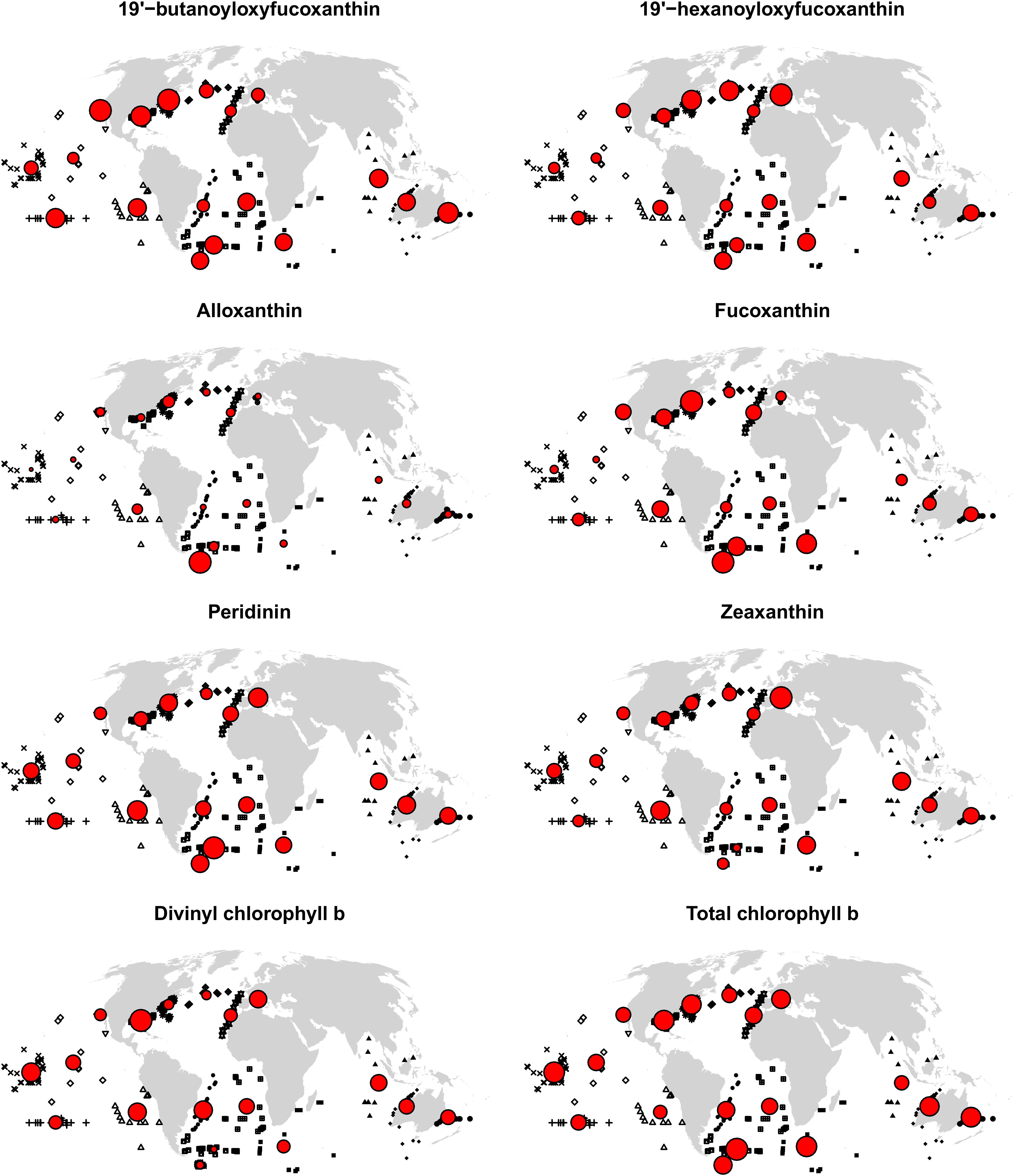
Figure 5. MAEs for each spatial cross-validation block. In situ observations are shown in black, with symbols indicating blocks (see also Figure 1). Circles are centered on block centroids, and circle areas are proportional to block MAEs (errors when extrapolating to the block with an algorithm trained on all other blocks), standardized such that the block with the largest MAE for the respective pigment is represented with a circle of the same size in the eight maps. Consequently, circle sizes cannot be compared between pigments; and many large circles in a map do not imply large MAEs in absolute terms, but little variability of MAEs between spatial blocks.

Diagnostic Pigment Maps

Given that, according to the spatial block cross-validation, only the algorithms for fucoxanthin and zeaxanthin were considerable improvements over simply using the global mean of in situ observations as prediction, we only report predicted spatial distributions for these two pigments (Figure 6). Fucoxanthin, a diagnostic pigment for diatoms, was the dominant pigment in the Southern Ocean and at temperate and higher northern latitudes, but less so in the north-eastern and northern central Atlantic. The global, sharp decrease of fucoxanthin at about 50–55 degrees south may be an artifact of the spatial structure of the in situ data, as it coincides with the locations of several in situ observations. At lower latitudes, fucoxanthin concentrations were very low, but contributing 10–15% to the total diagnostic pigment concentrations in equatorial upwelling zones, and up to about 25% in upwelling zones closer to the continents (fucoxanthin concentrations in upwelling zones increased further toward the coasts, but we do not show predictions within 200 km of land because the algorithms were only trained and tested for open-ocean conditions). Zeaxanthin, a diagnostic pigment for prokaryotes (e.g., cyanobacteria), had an almost opposite spatial distribution. It was the dominant pigment in much of the tropical and subtropical oceans, with lower concentrations in upwelling zones, where it, however, still accounted for more than 30% of the total diagnostic pigments in many places. At higher northern latitudes, predicted zeaxanthin concentrations were very low, whereas in the Southern Ocean, they ranged from almost none to about 30% of the total pigment. The only other published global-scale diagnostic pigment maps (Wang et al., 2018) predict broader classes of pigments (for example, photosynthetic carotenoids as sum of 19′-hexanoyloxyfucoxanthin, 19′-butanoyloxyfucoxanthin, fucoxanthin, and peridinin). Given that our algorithms for most of the individual pigments had rather large errors, making a direct comparison of those and our predicted spatial distributions is not feasible. However, at broad spatial scales, the predicted concentrations of fucoxanthin and zeaxanthin were consistent with previously published global spatial distributions of micro-and picoplankton generated with different algorithms (Brewin et al., 2010; Ward, 2015).

FIGURE 6

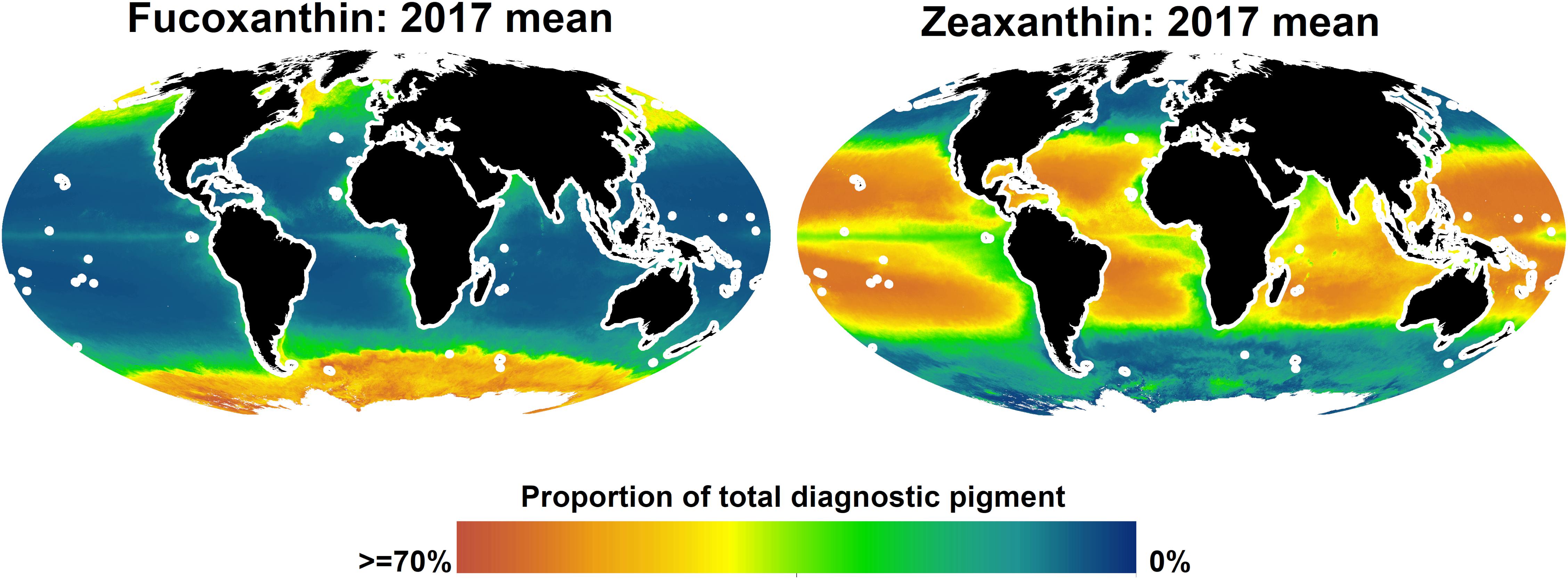
Figure 6. Predicted global distributions of fucoxanhin and zeaxanthin in 2017, as proportion of total diagnostic pigment. Predictions beyond 66 degrees north or within 200 km of land are not shown.

Discussion

Algorithm Errors

By means of spatial block cross-validation and fivefold cross-validation, we compared three types of algorithms implemented as flexible statistical models and distinguished by their input data, predicting relative concentrations of eight phytoplankton diagnostic pigments. However, compared to a null model simply predicting the mean of in situ measurements, the algorithms achieved considerably lower errors only for two pigments: fucoxanthin and zeaxanthin. For the other six pigments, the algorithms failed to represent the variability encountered in situ. Because of the biological and empirical links between diagnostic pigments and phytoplankton community composition, this result is not only relevant for direct remote sensing of diagnostic pigments, but also with regard to remote sensing of PFTs and PSCs. Hence, it may at first glance appear to contradict some previous research. For example, Pan et al. (2010) mapped various diagnostic pigments in northeastern US waters with reported accuracies of roughly 35%. Wang et al. (2018) report that the ratio of broad groups of diagnostic pigments to chlorophyll-a could be predicted well at the global scale. Similarly, authors predicting the spatial distributions of PFTs and PSCs – whose in situ concentrations are most commonly estimated based on HPLC measurements of diagnostic pigments (Mouw et al., 2017) – have reported high accuracy of their predictions. For example, Hirata et al. (2011) estimated the proportion of chlorophyll-a in six PFTs at the global scale with a mean error below 6%, and Raitsos et al. (2008) reported a classification accuracy >70% when distinguishing four PFTs in a large Atlantic study region.

There are, however, several explanations for these seemingly divergent results. First, our study is the first to explicitly estimate global diagnostic pigment algorithms’ errors when making predictions for geographical regions from which all in situ data were withheld. This is a harder test than hold-out validation sets consisting of randomly chosen observations or cross-validation with random assignment of observations to folds; yet we consider it more relevant for global mapping and mapping of large study areas where in situ observations are clustered in some locations, but absent from others. In other situations, randomly selected hold-out observations can be more appropriate. For example, Raitsos et al. (2008) focused on a part of the North Atlantic that was well-covered by in situ data, and the authors cautioned readers that extrapolation beyond that region should not be attempted. Second, we estimated the relative concentrations of the diagnostic pigments (i.e., which proportion of the total diagnostic pigment concentration was made up by each individual pigment, in order to decouple the pigment concentrations from variation driven by biomass). Some existing algorithms instead predict absolute concentrations, e.g., mass per volume as opposed to percent-of-total-pigment (Bracher et al., 2015a). In our data, absolute pigment concentrations were for most pigments more strongly correlated with both in situ and satellite-measured chlorophyll-a than relative concentrations; it is thus likely that absolute pigment concentrations can be predicted more accurately, including by abundance-based approaches. Third, data pre-processing can affect estimated prediction errors. For example, Hirata et al. (2011) report using a low-pass filter on diagnostic pigment concentrations sorted by chlorophyll-a concentration to improve the signal-to-noise ratio; removing part of the in situ variability of the response, while making broad-scale relationships easier to detect, would mean that errors calculated based on such filtered data may not capture an algorithms’ possible failure to reproduce the full variability encountered in situ. Fourth, many existing algorithms for satellite mapping of phytoplankton community composition predict only a small number of broad classes, e.g., broad groups encompassing multiple diagnostic pigments (Wang et al., 2018) or PSCs (micro-, nano-, and picoplankton). Fucoxanthin is a diagnostic pigment for microplankton, and zeaxanthin is a diagnostic pigment for picoplankton (Vidussi et al., 2001; Uitz et al., 2006). Indeed, Brewin et al. (2011) and Hu et al. (2018b) found that PSC algorithms made better predictions for micro- and picoplankton than for nanoplankton, consistent with our result that these two pigments can be mapped most accurately at the global scale. Yet because the size classes are mutually exclusive and collectively exhaustive, both pigments should be inversely related to the relative concentration of nanoplankton. It is thus likely that PSCs and some other broad classes can be better distinguished from space than individual diagnostic pigments or some more detailed PFTs derived from them. Finally, our results suggest that the relationships between satellite-measured predictors and diagnostic pigments measured in situ can be region-specific; regional-scale and locally optimized algorithms are thus likely to have lower prediction errors than our global ones. Finally, we used statistical models that are different from those used as foundation of previous algorithms, chosen based on established practices in spatial supervised learning as opposed to approaches that are traditionally more common in marine science. We tested two types of structurally different models for each kind of algorithm and found that they had similar errors. It is therefore unlikely that different underlying statistical models would produce very different results. Nevertheless, it is possible that minor improvements could be made when using the same data, but different statistical models. Taken together, the interpretation of our results must carefully consider differences between our and previously published algorithms, and between the prediction of relative pigment concentrations in this study and the prediction of absolute pigment concentrations, PSCs and PFTs in other research.

Advantages and Disadvantages of Supervised Learning Methods for Mapping Phytoplankton Community Composition

Mouw et al. (2017) provide a concise summary of the advantages and disadvantages of different types of PFT and PSC algorithms, but as their review focused on global-scale algorithms based only on ocean color and derived data, ecological algorithms were beyond its scope. Ecological algorithms have so far been implemented using supervised learning methods, e.g., as artificial neural networks (Raitsos et al., 2008; Palacz et al., 2013), polynomial regression (Pan et al., 2010), principal component regression (Bracher et al., 2015a) or here, using random forests and boosted regression trees. In this section, we briefly compile and expand the existing discussion of advantages and disadvantages of ecological algorithms and, generally, supervised learning approaches for remote sensing of phytoplankton community composition.

The main advantage of statistical models is their ability to extract complicated relationships between many variables from data, and to integrate spectral and environmental data (Brewin et al., 2011; IOCCG, 2014), which in our study reduced prediction errors. Thus, at least at the global scale and moderate spatial resolution, environmental data include information correlated with the spatial distribution of some phytoplankton types that is not captured by the included satellite-derived chlorophyll a and multi-spectral radiance data products. This gain in prediction accuracy by ecological algorithms is not very surprising, as environmental variables have been found to be correlated in time and space with PFTs and PSCs in other research (Brewin et al., 2012, 2017; Mouw et al., 2019).

Furthermore, statistical models are grounded in in situ data, and there are many hold-out techniques to estimate prediction errors. Consequently, algorithm validation is prima facie straightforward. However, as we have argued, and as demonstrated by the different results of the spatial block cross-validation and the fivefold cross-validation, the spatial and temporal auto-correlation and uneven spatial distribution of typical oceanographic in situ data mean that care must be taken to appropriately select observations for validation. Otherwise, one might obtain overoptimistic error estimates and select too flexible models (Roberts et al., 2017). Furthermore, it is essential to keep in mind that in situ diagnostic pigment concentrations (and derived variables such as PFTs and PSCs) used for training and validating statistical models have measurement errors themselves (Claustre et al., 2004; Brewin et al., 2014a).

Statistical models that are used as ecological algorithms to predict phytoplankton pigments, PFTs or PSCs only superficially integrate the vast existing body of knowledge on marine bio-optics and phytoplankton dynamics. Indeed, imposing a theoretically or empirically justified structure on a model (e.g., Brewin et al., 2017) can improve predictions by reducing the potential of the model to over-fit to noise instead of general relationships in the data, especially if the model must be trained on small data sets. We did not test such models in our analyses (instead selecting an appropriate level of flexibility for the models in the internal cross-validation). A related disadvantage is that statistical models can be difficult to interpret in terms of ocean biology and bio-optics (Brewin et al., 2011): in comparison to mechanistic models simulating phytoplankton dynamics (LeQuere et al., 2005), statistical models have strong limitations with regard to understanding ecological processes that give rise to the predicted spatial distributions of phytoplankton. Lastly, statistical modeling extracts relationships between variables from existing data, but not all relationships between the variables of interest will remain the same in a changing climate. In contrast to mechanistic models based on stable relationships between variables (e.g., the laws of physics), statistical models are therefore not suitable to make predictions in time beyond the immediate future (Kostadinov et al., 2017; Sathyendranath et al., 2017).

Consequences and Outlook for Satellite Mapping of Phytoplankton Community Composition

We tested various algorithms that differed both in the input data and the underlying statistical models. According to a spatial block cross-validation and compared to a null model, a constant function predicting the mean of in situ observations without incorporating any satellite data, the best algorithms achieved a considerably smaller average prediction error in regions they were not trained in for only two out of eight pigments. However, for the reasons described in Section “Algorithm Errors,” our analyses do not allow a comparison of specific existing algorithms. Instead, they support four general statements about diagnostic pigment, PFT and PSC algorithms. First, global-scale empirical algorithms using existing multi-spectral and satellite-derived environmental data as input will have large errors when predicting the relative concentrations of some diagnostic pigments (or derived phytoplankton classes) and in some marine regions. Second, errors calculated by holding out data from whole regions (spatial block cross-validation) and by randomly splitting the data into training and validation sets (fivefold cross-validation) were so different that they supported different conclusions about the accuracy of the algorithms. It is therefore crucial to carefully design and justify the methods used for validation of empirical satellite algorithms. Third, our ecological algorithms had lower prediction errors than our spectral or abundance-based algorithms, irrespectively of the statistical models that we used. This suggests that environmental variables like SST provide information that is not contained in remote sensing reflectance or chlorophyll-a concentrations, but useful for mapping the global spatial distribution of aspects of phytoplankton community composition (but see section “Advantages and Disadvantages of Supervised Learning Methods for Mapping Phytoplankton Community Composition”). We also found that using remote-sensing reflectances as predictors led to smaller improvements over predictions based only on Chl a, in line with other research finding weak relationships between spectral data and phytoplankton pigments at the global scale once the part of the signal that co-varies with Chl a concentrations is removed (Chase et al., 2017). Fourth, after testing various combinations of input data and different statistical models, we conclude that mapping the global spatial distribution of phytoplankton diagnostic pigments was primarily limited by the available data, not the statistical models used as empirical algorithms.

Satellite remote sensing of phytoplankton community composition is expected to improve in the near future, when data from new sources become available (e.g., as in situ data from autonomous vehicles carrying flow cytometers and other instruments), with ongoing efforts to harmonize plankton-related data from different sources, and when hyperspectral ocean color data from new satellite missions become available (Bracher et al., 2017; Mouw et al., 2017; Fossum et al., 2019; Lombard et al., 2019; Dierssen et al., 2020). Initial studies have suggested a strong potential of hyperspectral ocean color data to map phytoplankton community composition from space (Bracher et al., 2009; Sadeghi et al., 2012a, b; Wolanin et al., 2016; Losa et al., 2017). At the same time, we already have more than two decades of uninterrupted, global-coverage, multi-spectral ocean color data at comparatively high spatial and temporal resolutions. It is thus also important to understand how to best use the existing, large archives of satellite and in situ data for mapping phytoplankton communities.

A possible explanation for the large errors found in this study for most pigments when extrapolating to new regions is that empirical relationships between phytoplankton community composition and spectral and environmental variables may be region-specific. At present, most existing algorithms have been developed for the open ocean and do not perform well in coastal waters (Bracher et al., 2017; Mouw et al., 2017). Yet from an environmental-science point of view, monitoring phytoplankton communities in coastal ecosystems is important, because they are subject to many anthropogenic threats (Bracher et al., 2017; Stock et al., 2018b). Eutrophication, harmful algal blooms and water quality are important concerns in many coastal regions (Anderson et al., 2002; Howarth et al., 2002; Rabalais et al., 2002; Andersen et al., 2017). Experience with satellite mapping of other biological variables has shown that many coastal regions benefit from locally trained algorithms (e.g., Darecki and Stramski, 2004; Sá et al., 2015; Stock, 2015; Lewis et al., 2016), and relatively low prediction errors for regional-scale diagnostic pigment, PFT and PSC algorithms have been reported (Raitsos et al., 2008; Pan et al., 2010; Brewin et al., 2017). Furthermore, diagnostic pigment analyses can better distinguish phytoplankton types at regional than at the global scale (Kramer and Siegel, 2019). Taken together, our and previous results suggest that, at least with the data widely available at present, regional-scale efforts to map phytoplankton community composition can achieve higher prediction accuracies for more pigments or phytoplankton types than the global-scale algorithms presented here.

Ecological algorithms outperformed spectral and abundance-based algorithms in terms of prediction accuracy in regions they were not trained in for six out of eight diagnostic pigments. Given that large parts of the oceans have few in situ observations matched with valid ocean color data for algorithm development (or none at all), for projects primarily aiming to map the global spatial and temporal distributions of different pigments and the associated phytoplankton types as accurately as possible, including both spectral and environmental variables as predictors is recommended (after careful consideration of the disadvantages of such an approach; see section “Advantages and Disadvantages of Supervised Learning Methods for Mapping Phytoplankton Community Composition”). This result is in contradiction to previous research reporting that abundance, spectral and ecological algorithms can achieve similar accuracy (Brewin et al., 2011).

We found that using spatial declustering weights for algorithm training improved the algorithms’ prediction accuracy in most cases, yet our method to calculate weights was based on ad hoc considerations. Further investigation of the best methods to calculate declustering weights for training empirical satellite algorithms on auto-correlated and unevenly distributed data would hence be useful. Finally, the differences between errors estimated by means of fivefold cross-validation and spatial block cross-validation suggest that further research and discussion of the most appropriate ways to consider spatially auto-correlated or otherwise non-independent data in validation methods (Bracher et al., 2015b) is needed. We have argued that spatial block cross-validation was appropriate for our particular data set and application. Spatial block cross-validation can be used in any setting where a separation of data used for model training (calibration) and testing (validation) is needed, but other validation methods (e.g., defining blocks based on time) may be more appropriate in different settings. Future research developing empirical satellite algorithms should hence provide a strong justification for the choice of validation method.

Data Availability Statement

All datasets used in this study are publicly available from the sources listed in Table 1. Processed datasets generated for this study are available on request to the corresponding author.

Author Contributions

ASu initiated the research, guided the selection of data sources, and secured funding. ASt designed and conducted the statistical analyses, and wrote the first draft of the manuscript. Both authors contributed to the presentation and interpretation of results, edited and revised the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This work was supported in part by the Gulf of Mexico Research Initiative’s “Ecosystem Impacts of Oil and Gas Inputs to the Gulf” (ECOGIG) program. This is ECOGIG contribution #550. This work was also supported by NASA OBB grant NNX16AAJ08G and NSF OCE 1737128. ASt was supported by an Earth Institute Postdoctoral Fellowship at Columbia University.

Acknowledgments

We thank the participants of the Symposium on Oceanographic Data Analytics held November 27–30, 2018 in Trondheim (Norway) for feedback on early results from this research. This is LDEO contribution 8431.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.00599/full#supplementary-material

Footnotes

^ https://doi.org/10.6084/m9.figshare.11473446.v1

References

Aiken, J., Fishwick, J. R., Lavender, S., Barlow, R., Moore, G. F., Sessions, H., et al. (2007). Validation of MERIS reflectance and chlorophyll during the BENCAL cruise October 2002: preliminary validation of new demonstration products for phytoplankton functional types and photosynthetic parameters. Int. J. Remote Sens. 28, 497–516. doi: 10.1080/01431160600821036