- 1Cetacean Ecology and Acoustics Laboratory, The University of Queensland, Brisbane, QLD, Australia
- 2Marine Scotland, Edinburgh, United Kingdom
- 3DHI A/S, Hørsholm, Denmark
- 4Centre for Research into Ecological and Environmental Modeling, University of St Andrews, St Andrews, United Kingdom
The Population Consequences of Disturbance (PCoD) model is a conceptual framework used to assess the potential for population-level consequences following exposure of animals to a disturbance activity or stressor. This framework is a four-step process, progressing from changes in individual behavior and/or physiology, to changes in individual health, then vital rates, and finally to population-level effects. Despite its simplicity, there are few complete PCoD models available for any marine mammal species due to a lack of data available to parameterize many of the steps. Here, we present an application of the PCoD framework for migrating humpback whales exposed to a simulated commercial seismic survey scenario. We approached the framework in two ways; first, progressing sequentially forwards through the steps and basing our assessment on lactating females. This cohort was considered to be the most vulnerable in terms of energetic costs of disturbance, and most likely to influence any change in population growth due to future breeding success. Field measurements of behavioral responses of migrating humpback whales to seismic air guns from a previous study were used to parameterize an agent-based model (ABM). This ABM was used to estimate the probability of response, where a response was defined as a change in the migratory movement of female-calf pairs, and the duration of any resulting delay in migration. We then estimated the energetic consequences of any delay in migration for the lactating females and created population growth models with which to assess any population-level effects. The results of the forwards approach suggested a low potential for population consequences of seismic surveys on migrating humpbacks. Working backwards through the framework, we investigated “worst case” scenarios that could potentially lead to a population-level effect. Here, we started with increasing calf mortality and assumed that an exposure time greater than 48 h would increase mortality risk. We determined the most likely context in which this exposure would occur (resting area) and then tested this context within an ABM. This backwards approach illustrates how the PCoD model can be used to make management decisions regarding animal populations and exposure to anthropogenic stressors.
Introduction
Assessing the non-lethal effects of anthropogenic disturbance on marine mammal populations is a challenging goal, but one that is necessary for environmental decision makers and managers. While legislation in Europe (Council Directive 92/43/EEC, 1992) and the United States (Marine Mammal Protection Act, 1972) requires the assessment of population-level effects, management decisions are normally based on studies of individual behavioral responses. This is problematic because the relationship between individual behavioral responses to a disturbance and population-level effects is poorly understood.
The “population consequences of disturbance (PCoD)” model has been proposed as a framework with which to relate the response of individuals to a stressor to changes in their vital rates and health, and subsequently to changes in population dynamics (National Research Council, 2005; Harwood et al., 2016). This framework has been used in marine mammals to evaluate population-level impacts of disturbance-inducing activities. To date, no PCoD model has been fully parameterized with empirical data (Pirotta et al., 2018a) due to the fact they are data intensive and logistically challenging to complete. Therefore, most complete PCoD models include simulations, theoretical modeling, and expert opinion to move through the steps. For example, PCoD models have been developed to evaluate the effect of wind farm construction on the North Sea harbor porpoise (Phocoena phocoena) populations (e.g., King et al., 2015; Nabe-Nielsen et al., 2018). These models include a mix of empirical data, expert elicitation (King et al., 2015) and simulations of animals’ movements, energetics, and/or survival (New et al., 2014; Nabe-Nielsen et al., 2018). Other models have linked changes in foraging behavior in southern elephant seals (Mirounga leonina) to changes in the environment (New et al., 2014) and included simulations to complete the model. Similarly, full PCoD models assessing the effects of the Deepwater Horizon oil spill on bottlenose dolphin (Tursiops truncatus) populations (Schwacke et al., 2017) and the effects of oil and gas field developments on foraging gray whales (Eschrichtius robustus; Villegas-Amtmann et al., 2017) included theoretical modeling for certain parts.
Understanding the behavioral responsiveness of individuals to given stressors is the first, and most data-demanding, part of the PCoD framework. For marine mammal species, data have primarily come from studies on their response to naval sonar (Southall et al., 2016; Harris et al., 2018), wind turbines (Tougaard et al., 2009), seismic air guns used for oil and gas exploration (Dunlop et al., 2015), and vessel activities (Mikkelsen et al., 2019). The second part of the framework relates changes in an individual’s behavior and/or physiology to changes in health. Here, efforts have primarily focused on quantifying changes in the energy store of the individual due to a change in behavior (Schick et al., 2013; New et al., 2014). Most examples quantify the energetic impact of changes in foraging behavior (New et al., 2013; Nabe-Nielsen et al., 2014; Pirotta et al., 2014, 2015b, 2019; Villegas-Amtmann et al., 2015, 2017; Costa et al., 2016; McHuron et al., 2017). Impacts have usually been inferred from bioenergetic models, or from a scaled energy metric, rather than from any direct measure. To progress this into changes in vital rates, links must be made between energetics and the probability of offspring survival or female fecundity (Weinrich and Corbelli, 2009; New et al., 2014; Costa et al., 2016). For example, photographic assessments of the North Atlantic right whale (Eubalaena glacialis) and minke whale (Balaenoptera acutorostrata) have attempted to link individual health with survival, fertility (Schick et al., 2013; Rolland et al., 2016), and calf health (Christiansen et al., 2018).
The last part of the PCoD framework relates changes in the vital rates of individuals with changes in population dynamics. The most common approach has been to use a simple Leslie matrix to predict the growth of a population under different scenarios of anthropogenic disturbance (New et al., 2014; King et al., 2015; Schwacke et al., 2017). Other PCoD studies have developed more complex agent-based models (ABMs) that can simulate individuals within a population that are undertaking specific life functions (e.g., moving, feeding, accumulating energy, reproducing; New et al., 2013; Pirotta et al., 2014, 2015a; Villegas-Amtmann et al., 2015). These models are then used to predict how the population changes over time under different scenarios (Nabe-Nielsen et al., 2014; Villegas-Amtmann et al., 2017). ABMs have been successfully used to predict the population-level effect of a disturbance for pinnipeds (McHuron et al., 2017), and for Eastern North Pacific blue whales (Balaenoptera musculus; Pirotta et al., 2018b). However, ABMs are complex and require a lot of data on individual life histories within the population to be able to capture the variability in a real population.
The humpback whale is a capital breeder, meaning it uses stored energy for reproduction and survival. This enables it to undertake long migrations to breeding grounds that are spatially separated from its feeding grounds. As is typical of a K-selected species, humpback whales have delayed maturation and reach sexual maturity between 5 and 10 years of age (Clapham, 1992), with an expected life span in excess of 95 years (Chittleborough, 1965). Their annual life cycle comprises of periods of intense feeding in the polar areas (summer), followed by a migration to tropical and sub-tropical regions for breeding and birthing (winter). The gestational period ranges from 10 to 12 months (Chittleborough, 1958), and the lactation period ranges from 6 to 12 months (Chittleborough, 1965). Weaning occurs just before, during, or soon after the mother and calf’s first return migration from the feeding grounds to the breeding grounds (Clapham and Mayo, 1987; Baraff and Weinrich, 1993). Therefore, for reproductive females, the period following birth involves a high rate of energy flow to her calf, which coincides with fasting during the migration to the feeding grounds. These extreme energy demands (i.e., fasting while lactating) means only animals with a large body size to store such large amounts of energy can achieve this type of life cycle. A decline in the nutritional status of lactating females may reduce the likelihood of successive reproductive bouts (Lockyer, 1981; Craig et al., 2002) and reduce the rate of population growth. This would be especially detrimental in populations still recovering from whaling.
Many humpback whale populations migrate along coastlines, meaning they may be susceptible to coastal anthropogenic activities. Studies on the response of humpback whales to seismic survey “air gun” noise found migrating groups changed their movement behavior to avoid the noise source. Lactating females with their calf slowed their migration and some ceased to migrate until the source had passed by or ceased (Dunlop et al., 2015, 2016, 2017a,b, 2018). Naval sonar has been found to disrupt foraging in humpback whales (Sivle et al., 2016), with less evidence of a movement avoidance reaction but more-so if a calf was present (Wensveen et al., 2017). Given the wealth of data available for the eastern Australia humpback whale population (Noad et al., 2019) as well as their studied response to air guns, we used the PCoD framework to assess the likelihood of population-level consequences for this population of humpback whales migrating through a simulated commercial seismic survey scenario. As with these previous studies, our study presented here included some steps that incorporated modeled and/or simulated data as well as expert opinion. We did this as a series of analysis steps, with each using a mix of empirical and modeled data to produce outcomes for various scenarios. We first adopted a forwards approach to determine if observed individual behavioral responses to air gun signals were likely to lead to population-level consequences. We then used a backwards approach to determine if a “worse case” disturbance scenario could potentially have a detrimental effect on the population dynamics. Results can be used to make management decisions regarding humpback whales and seismic air gun exposure as well as direct future research to data-deficient steps within the PCoD framework. As the models are further developed, they may be used as a predictive tool to evaluate the consequences of human disturbance on large whale populations.
Materials and Methods
This study was based on the eastern Australian humpback whale population, a robust and fully-recovered (post-whaling) population that is still increasing at its likely maximum possible rate (Noad et al., 2019). Humpback whales were migrating southwards from their breeding grounds in the Great Barrier Reef, toward their feeding grounds in Antarctic waters along the eastern Queensland coastline of Australia (Figure 1). Both the forwards and backwards methodologies involved four discrete analysis steps which are summarized in Figures 2, 3. In the forwards approach (Figure 2), the first step utilized the results of a previous project (Dunlop et al., 2015, 2016, 2017a,b, 2018; Kavanagh et al., 2017) on the behavioral response of migrating humpback whales to seismic air guns (BRAHSS – see expanded description below). During the BRAHSS project, migrating whale groups were tracked for approximately 3 h while a seismic air gun or small air gun array was active for 1 h. These results were then used to parameterize an initial agent-based model (ABM) of migrating groups, which replicated observed baseline movement and responses to a 1 h air gun source as per the BRAHSS experiments. The BRAHSS project provided both raw input data for parameterization and consolidated movement data for model validation (see Supplementary Material for further details). The second step involved releasing parameterized agents (humpback whale groups including lactating females with their newborn calf) through a simulated full commercial seismic survey lasting for 10 days. Their response probability, and delay in migration time due to an increase in their transit time through the survey zone, were then quantified. The third step estimated the energetic consequences of the response (migratory delay), focusing on changes in lactating female energetics. Here, we used an energetic model of migrating, lactating, females to link changes in female migratory movement (i.e., a delay to the feeding grounds) with a change in female energy stores (i.e., a reduction in female body condition due to an increase in the proportion of blubber lost during migration). The fourth step estimated the population-level consequences of resultant changes, if any, on female fecundity. Here, we assumed a link between female body condition upon return to the feeding grounds and her likelihood of breeding the following year.
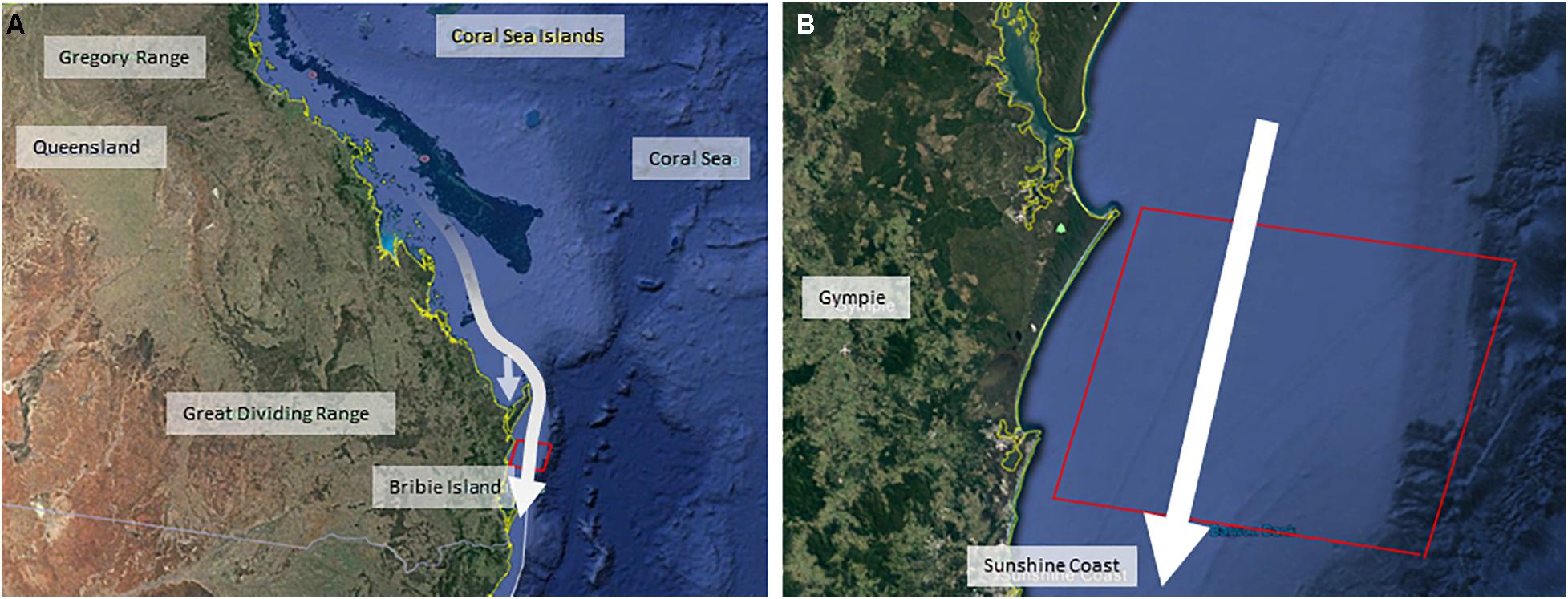
Figure 1. Maps illustrating the dimensions of the simulated commercial seismic survey, positioned off the Queensland coastline in Australia [with map (A) designating the eastern coastline of Queensland, and map (B) showing the simulated seismic air gun area off the Sunshine Coast, Queensland]. White arrows indicate the southwards direction of migration of the whale population from breeding grounds in the Great Barrier Reef through the commercial seismic survey zone (red box). The offshoot arrow in the Queensland map illustrates the use of the Hervey Bay resting area.
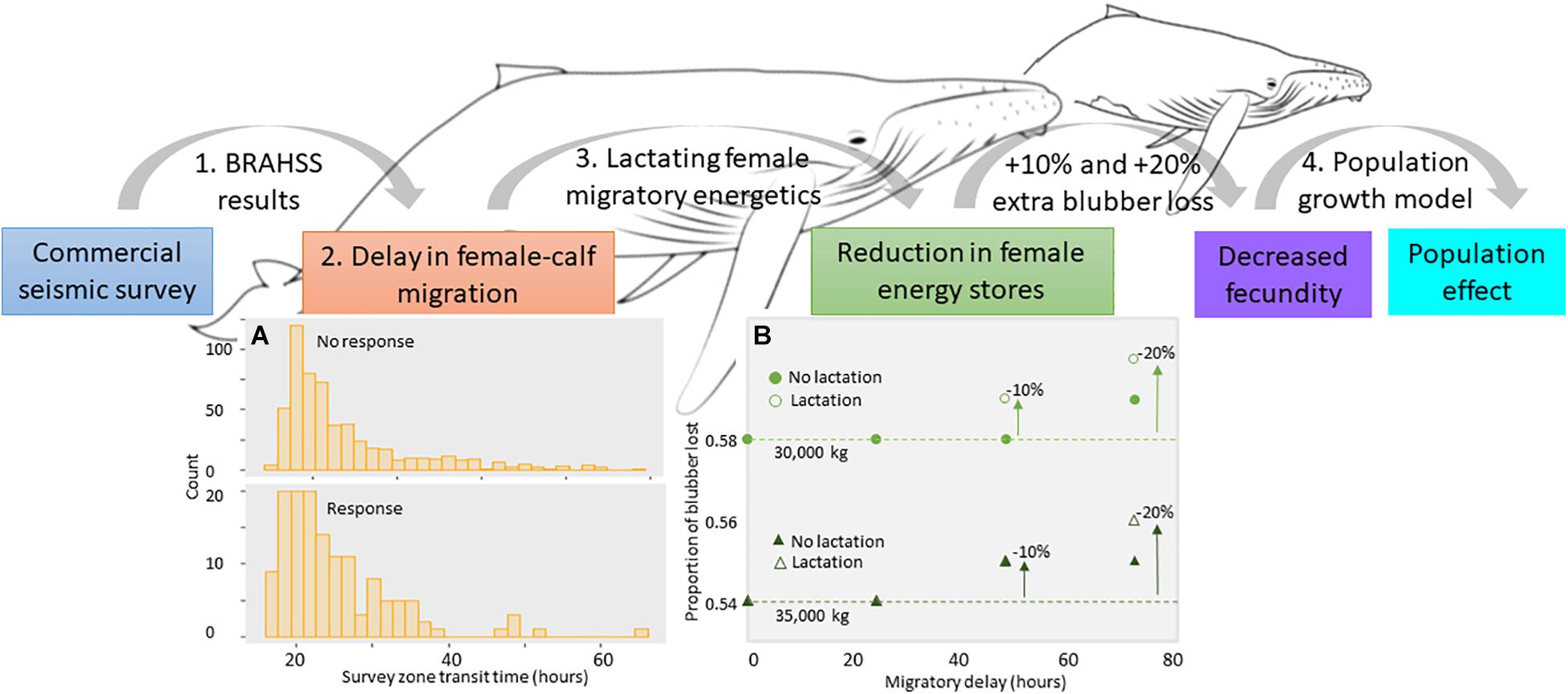
Figure 2. Overview of the forwards (top) PCoD approach. The model starts with the sound source (commercial seismic air gun sound), where the results of the BRAHSS experiments were used within an ABM, where parameterized agents migrated through a commercial seismic survey. The behavioral response was quantified as a delay in migration of humpback whale groups due to a change in the migratory movement (A). We concentrated on female-calf pairs (lactating females) and assumed a migratory delay would cause a deterioration in lactating female energy stores, quantified as an increase in the proportion of blubber lost over the whole migration (B). If severe, this would prevent them from becoming pregnant in the following breeding cycle, meaning a reduction in the population’s fecundity and growth rate. (A) Results of the ABM showing distribution of the number of hours that lactating female-calf pairs agents spent within the seismic survey zone for those that were primarily migrating. Distributions are separated into agents that responded and agents that didn’t respond to the seismic air gun array. (B) Results of the energetic model showing the change in the total proportion of blubber lost by a 30,000 and 35,000 kg female during its migration according to how many hours it was delayed within the seismic survey zone and whether or not the female continued to nurse while delayed. Dotted lines indicate no change. The 10 and 20% extra blubber loss thresholds are also indicated.
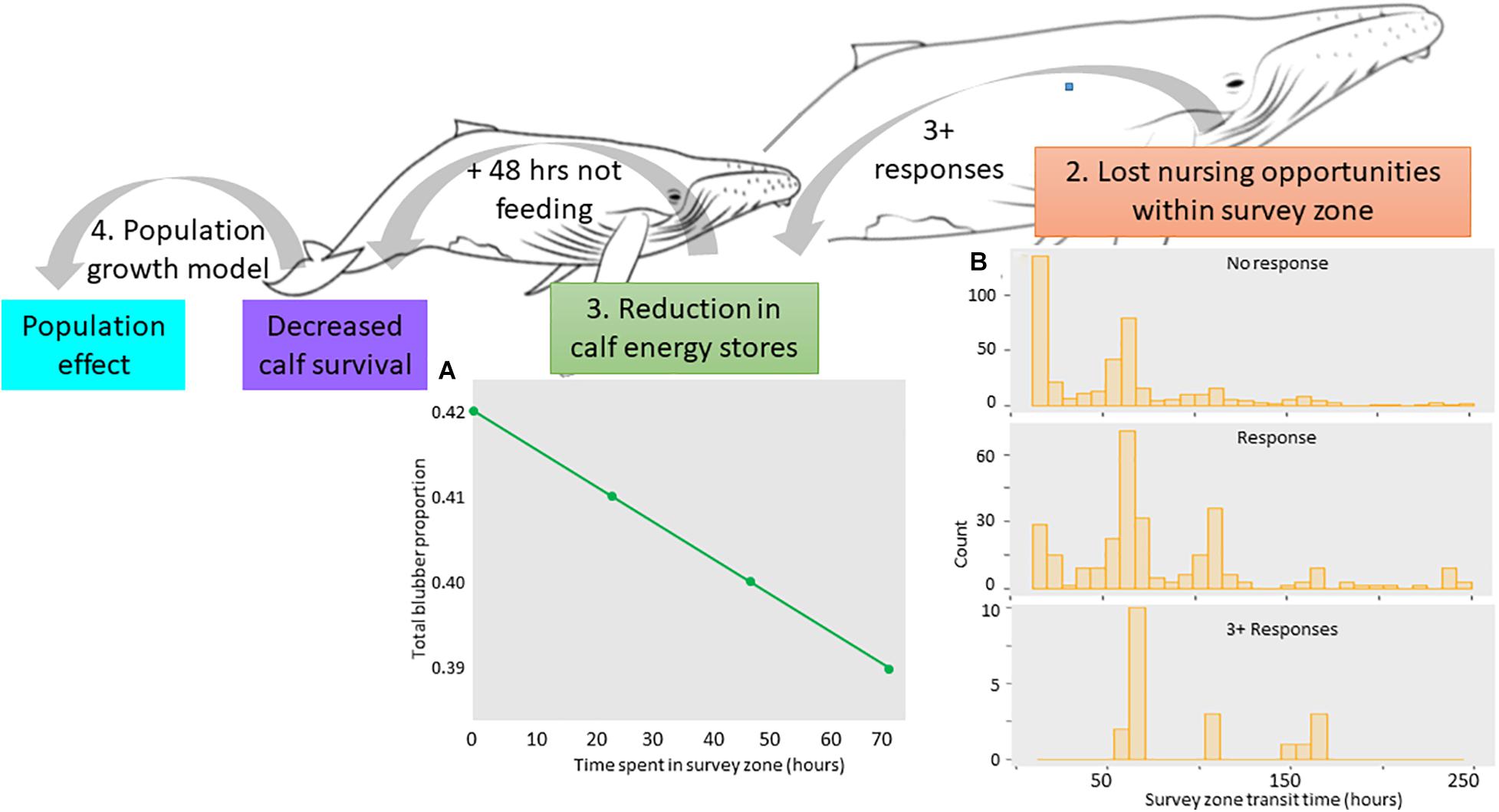
Figure 3. Overview backwards approach starting with the population effect of decreasing calf survival. Calf survival was assumed to reduce due to lack of feeding opportunities, where it was assumed 48 h of not feeding would reduce the calf’s energy stores (A), cause dehydration, and lead to calf mortality. To achieve this, we assumed the seismic survey took place in a resting/nursing area, where female-calf pairs spent more time within the survey zone. We assumed those that responded more three or more times [of which all spent longer than 48 h within the survey zone; (B)] would lose enough nursing opportunities to compromise the calf. (A) Results of the energetic model showing the change in the total proportion of blubber lost by a calf per delay day (measured as delay hours) assuming it was not feeding. (B) Results of the ABM showing distribution of the number of hours that lactating female-calf pairs agents spent within the seismic survey zone for those that were primarily resting. Distributions are separated into FC agents that didn’t respond, FC that responded, and FC agents responded three or more times to the seismic air gun array.
The backwards approach (Figure 3) started at the fourth step, which established a population-level effect according to changes in calf survival. We then used a calf energetic model to quantify the reduction in calf body condition as a result of not feeding for between 24 and 72 h (1–3 days). Next, we assumed, conservatively, a disturbance duration that could be detrimental to the calf. To determine the most likely scenario to achieve this disturbance duration, we followed Wilson et al.(2019; outlined in more detail in Supplementary Material). In brief, we estimated aggregate levels of disturbance by simulating individual exposure histories. We used these to predict the statistical distribution of disturbance durations experienced by different individuals in the population. Input parameters were; the probability that an individual will be disturbed on each day of the activity, the number of individuals expected to be in the affected area, and time spent within the survey zone (resident time). These parameters were manipulated until the mean disturbance time for an individual was that deemed to reduce the likelihood of the calf surviving. Finally, an ABM was run to test this scenario (second step), quantify the residence time of females-calf pairs within the survey zone, and determine if the time spent (and disturbance duration within the zone) could potentially affect enough female-calf pairs to cause a population-level consequence. Each step is outlined in more detail below.
Step 1: Behavioral Response of Migrating Humpback Whales to Seismic Air Guns
The data for step 1 resulted from a large and complex behavioral response experiment; BRAHSS (Behavioral Response of Australian Humpback whales to Seismic Survey; Dunlop et al., 2015, 2016, 2017a,b, 2018; Godwin et al., 2016; Williamson et al., 2016; Kavanagh et al., 2017). BRAHSS involved experimental trials with a single air gun, a small, clustered array, and a full commercial array where the exposure phase (air guns turned on) lasted for 1 h. Experiments were carried out on the eastern Australian humpback whales as the migrated southwards along the Sunshine Coast, Queensland, Australia (Figure 1). The observed behavioral response was a change in group movement, where groups changed their direction of travel and speed to avoid the air gun vessel. Female-calf pairs were observed to slow their migration speed and some were observed to cease migrating until the air guns ceased. The dose-response relationship, which included received level and source proximity (Dunlop et al., 2017b, 2018), was then used to parameterize the initial ABM. This ABM included 1 h of exposure to a seismic source (as per the BRAHSS experiments) and was validated as described in Supplementary Material. For further details on the BRAHSS experimental trials and results see Supplementary Material.
Step 2: Estimating the Migratory Delay in Humpback Whales Exposed to a Commercial Seismic Survey
For this step, the initial ABM was updated to simulate the movement of agents (groups of whales) traveling through a 10-day commercial seismic survey. The size of the simulated seismic survey area was 60 km north/south by 75 km west/east out to the continental shelf of the east coast of Australia and set up to resemble a 10-day seismic survey during the peak of migration in October (Figure 1). The array source level was set to 240 dB re 1 μPa2⋅s.
Empirical data from the BRAHSS project were used to parameterize 1028 agents. This number of agents represents a compromise between maximizing sample size and minimizing computation time. The start time and location of each agent was randomly allocated throughout the survey period, and to the north of the study area, out to 20 km offshore. Agents were designated either female-calf (FC) or other group composition (non-FC) due to the observed differences in the responses of these cohorts, with the probability of being an FC agent set to 0.66. Agents began in baseline mode 1 (M1), where agents were migrating southward, but then may have switched to baseline mode 2 (M2), where progression south was halted due to resting or socializing behavior. FC agents had a 0.33 probability of switching from M1 (migrating) to M2 (resting/milling), non-FC groups had a 0.2 probability of making the same switch. When the seismic air gun array was present, agents could exhibit a response depending on their proximity and received sound exposure level (SEL in dB re 1 μPa2⋅s). The transition of agents to a response mode was probabilistic, with the 0.5 probability of response set at 150 dB re 1 μPa2⋅s and the 1.0 probability of response at 200 dB re 1 μPa2⋅s (Supplementary Figure 1). However, proximity mediated the response to received level whereby a response could not be elicited if the separation distance between the agent and the source vessel exceeded 3.5 km, regardless of received level (matching what was found in the BRAHSS experiments, Dunlop et al., 2017a, 2018). The response mode reduced the southwards progress of the agent by decreasing its directional travel (see Supplementary Material for further details on agent movements).
The ABM output consisted of a time series of estimated agent parameters; time since agent was first released, position within the survey area, travel mode (M1 or M2), travel speed and course, whether or not a response was activated, and distance and received level of the air gun array. All were quantified every 5 min. ABM outputs were then summarized for each agent. These outputs were; total time taken to traverse the survey area, mean travel speed (which included periods of resting/socializing), whether or not the agent responded, total response time, and the number of times the agent responded. Overall, non-FC agents traveled at a mean speed of 5.7 km/h (1.58 m/s) and took 14.5 h to traverse the survey zone. FC agents traveled at a mean speed of 3.7 km/h (1.04 m/s) and took 22 h to traverse the zone.
The change in transit time through the survey area was used to estimate migratory delay. Relationships between transit time, whether or not the agent responded (yes or no), the amount of time the response lasted for, the number of times it responded, and group composition (FC or non-FC) were quantified using quasipoisson Generalized Linear Models (GLMs). Quasi models were used because the data were found to be over-dispersed. The response variable (time spent) was the number of hours agents spent traversing the survey zone with the following model fit to quantify differences in transit times across all FC and non-FC agents according to whether or not they responded:
Model 1: transit time ∼ group composition ∗ response activated.
Both “group composition (FC or non FC) and “response activated (yes or no) were two level factors. An interaction term between these variables (denoted by ∗) was included in the model. For agents that responded, we also reported the total response time and number of responses.
Step 3: The Energetics of Lactating Females
Migrating and lactating females were presumed to be the most vulnerable in terms of potential detrimental changes in migratory energetics. The energetics of this cohort were modeled by following the approach of Braithwaite et al. (2015), with some minor modifications. This provided energetic scenarios which could then be used to assess the energetic consequences of the ABM results in terms of modeling the extra loss of blubber due to a migratory delay caused by the seismic survey. Within the model, the total time taken to reach the feeding grounds was set at 81 days (estimated from the observed migration speed of 1.0 m/s from the BRAHSS project data) compared to 90 days used in Braithwaite et al. (2015). The starting weight for lactating females was set at either 30,000 kg (following Braithwaite et al., 2015), or 35,000 kg, to compare migratory energetics between females of different body conditions. The starting weight for a calf was set to 1,200 kg (following Braithwaite et al., 2015).
Energetic parameters (basal metabolic rate, cost of transport and lactation costs) were estimated for each successive 24 h period. First, we assumed that the response to a seismic survey would be a delay in migration (termed a “delay day” given that energetic parameters were quantified every 24 h) starting on day 16 of the southern migration. Day 1 was the start of the migration from breeding to feeding grounds and day 16 was the estimated travel time to reach the survey zone. One day of delay equated to an extra travel day to reach the feeding grounds. At this point in the migration, they would have traveled approximately 1,500 km at 1.0 m/s (following Braithwaite et al., 2015) before entering the seismic survey zone. On this day, as outlined in the energetic model (Supplementary Material), the weight of a female was estimated to be 29,488 kg (with a starting weight of 30,000 kg) or 34,452 kg (with a starting weight of 35,000 kg). The weight of a calf was estimated to be 1,648 kg, assuming a 28 kg/day growth rate (Braithwaite et al., 2015). The travel speed for a “delay day” was reduced to 0.7 m/s to match results from the BRAHSS project and which also matched how the ABM agents were parameterized. Taking a conservative approach, and following what was observed during the BRAHSS experiments, it was assumed that they made no progression south in terms of migratory distance covered during a “delay day” but continued to move at a reduced velocity. We assumed no lactation costs during a delay day, assuming a “worst case” scenario that disturbed females would not nurse. We also ran models including lactation costs, assuming the females would continue to nurse during each delay day. For the scenario assuming the calf would not nurse, the energetic costs to the calf (basal metabolic rate and cost of transport) were subtracted from the calf weight to give its weight loss per delay day. We assumed a constant lactation and calf growth rate following the “delay days” until the migratory distance was covered, including during the extra migration days required to return to the feeding grounds. The proportion of blubber lost for lactating females and their calf was then compared across delays of between 0 (no delay) to 3 days (i.e., up to 72 h).
Using these energetic model scenarios, the energetic cost to a lactating female was assessed for the estimated migratory delay from the ABM. We then assumed two thresholds at which a loss in body condition in the female would reduce her fecundity; greater than an additional 10% loss in blubber (compared to females that were not delayed), and greater than an additional 20% loss in blubber. The following step then created population models with which to assess any population-level effects.
Step 4: Fecundity and Population-Level Effects in the Humpback Whale Population
Much is known about the population dynamics of the eastern Australian humpback whale population from whaling data, current surveys, and age class studies. All three sources of information were combined to give a likely population age class structure for the year represented by the commercial air gun survey simulated in the ABM (2010). Different fecundities were then set, based on population growth simulations in combination with a Leslie matrix (see Supplementary Figure 3), for each breeding age class.
The starting year for the population growth model was 2009 (with 12,800 whales). The base model predicted the population growth over a 5-year period with no disturbance and therefore no change to the population growth rate. Next, the population model was re-run, this time assuming population-level effects of the seismic survey in 2010 (second year). Here, the effect was assumed to be a reduction in fecundity, with no effect on calf survival. In other words, we assumed females, due to the seismic survey, returned to the feeding grounds in a reduced body condition compared to normal and were less likely to breed the following year. Fecundity was progressively reduced and the 5-year population growth rates compared (Supplementary Figure 4a).
Backwards PCoD Model
The steps for the backwards model are summarized in Figure 2. For this model, it was assumed that reductions in population growth rate were due to increased calf mortality (step 4) due to reasons discussed within the results of the forwards model. We therefore started with scenarios of reduced population growth rate. The same set of population growth simulations referred to above were run with no changes in fecundity and a progressive reduction in calf survival (Supplementary Figure 4b). We then used the energetic model to estimate the loss in calf body condition (loss in blubber) per day of not feeding (step 3). Assuming at some point the calf would starve and not survive. However, we also assumed that 48 h of not feeding would cause the calf to be weak and dehydrated thus decreasing its likelihood of survival.
We then attempted to find a scenario that could cause lactating females with their calf to remain in the seismic survey zone, and be disturbed, for at least 48 h. ABMs are time consuming, complex and require a high amount of processing power. Therefore, we used a relatively simple approach to simulate individual exposure histories following computer code in Wilson et al. (2019)Supplementary Material. This code generated predicted distributions of the number of hours of disturbance experienced by animals within a cohort, under a range of different transit times and response probability scenarios. This meant we could run a range of scenarios without having to re-parameterize the ABM for every possible scenario.
For these simulations, the local population was set at 230 whales transiting the area per 24 h (based on population surveys at the time) and made up of seven different age classes/cohorts (Supplementary Material). Females that were lactating and pregnant were not separated from those that were lactating and not currently pregnant. A population of migrating whales, made up proportionally of different cohorts, were simulated over a 10.5 day seismic survey period (230 whales per day, 10.5 days, total population = 2,415 whales). Each cohort was allocated a range of transit times through the survey area and response probabilities. The time spent within the survey zone for each cohort was progressively increased from 22 h to 100 h and the response probability was set to 0.2 and then increased to 0.4. These parameters were then used to estimate an exposure history per individual, where each hour of transit time was allocated a 1 or 0 based on the response probability for that cohort. This exposure history was used as a simple way of estimating the number of hours of disturbance per individual where it was assumed that each disturbance event related to 1 h of disturbance. Individual exposure histories were combined to produce a summary of the distribution of predicted number of hours of disturbance within each cohort (Supplementary Figures 5, 6). This distribution was used to estimate the minimum, mean and maximum number of hours of disturbance per migrating cohort.
Using these results, the ABM was re-parameterized and run with one updated scenario (as determined by the analysis explained above; step 2). The same GLM models as outlined above were conducted to quantify the time spent by agents in the survey zone according to cohort (e.g., FC agent), whether or not the agent responded, and how many times the agent responded.
Results
Step 2: Estimating the Migratory Delay in Humpback Whales Exposed to a Commercial Seismic Survey
Of the 1028 agents simulated during the seismic survey, 695 were female-calf pairs (FC). Responses were activated in 185 agents, meaning the overall probability of response was 0.18.
Transit times ranged from 10 to 65 h, noting these transit times were dependent on agent type. A modeled non-FC agent spent less than 14 to 15 h in the survey zone and a modeled FC agent spent 23 to 25 h due to the increased time they spent resting (Model 1). Non-FC agents had a response probability of 0.13 (45 out of 333 agents responded) compared to a response probability of 0.2 (139 out of 695) in FC agents. This greater response probability in FC agents was likely due to the greater time taken to transit the survey zone. The distribution of transit times for FC agents showed that the majority of FC agents that didn’t respond spent less than 30 h in survey area (Figure 2A), whereas most FC agents that responded spent 20 to 40 h in the survey area (Figure 2A). Collectively, there was no evidence that the seismic survey caused a migratory delay of even one day in agents. However, there was a small shift toward longer transit times in FC agents that responded.
Non-FC agent transit times were generally under 24 h regardless of the total response time and number of times the agent responded. FC agent transit times were generally under 48 h, again regardless of the total response time and number of times the agent responded. Response activations per agent ranged from 0 to 2 and the response time (in those that responded) ranged from 5 to 220 min. For agents that responded once, total response time lasted between 5 and 190 min. For those responding twice, the response time lasted between 20 and 220 min.
Step 3: Energetic Consequences to the Lactating Female
For a lactating female with a start weight of 30,000 kg, travelling 7,000 km over 81 days, at 1.0 m/s, the proportion of blubber lost during her migration was 0.58. Blubber mass reduced from approximately 4,664 to 2,694 kg; a loss of 1,970 kg. A female at starting weight of 35,000 kg lost approximately 2,869 kg (proportion of 0.54). After a 3-day delay, the proportion of extra blubber utilized by females during the entire migration was 0.1, or 10%, in females of both starting weights (Figure 2B), increasing to a 2,740 kg loss in a 30,000 kg female and 2,923 kg in 35,000 kg females. This assumed a no lactation cost whilst being delayed within the seismic survey zone. If assuming the calf fed within the seismic zone, the proportion of blubber lost by 30,000 kg female delayed for 3 days was 0.6, and for a 35,000 kg female, 0.56 (i.e., an additional blubber loss of 0.2 or 20% during the migration for both females due to the added energetic cost of lactation; Figure 2B). The ABM found that the majority of FC agents that responded were delayed for less than one day, translating to a less than 10% extra blubber loss by a 30,000 kg and 35,000 kg female (Figure 2B). If assuming a female that lost an extra 10% in blubber upon return to the feeding grounds would not breed the following year, this would require a + 72 h delay in a 30,000 kg female assuming no lactation costs, and a + 48 h delay assuming lactation costs (Figure 2B). For a 35,000 kg female, this would require a + 48 h delay assuming both no lactation costs and lactation costs (Figure 2B). For females to lose an extra 20% in blubber, a delay of greater than 72 h would be required (if including lactation costs). Therefore, given the less than 24 h delay found in the ABM, there was no evidence from this study that a migratory delay in lactating females due to a commercial seismic survey would translate to significant energetic consequences in terms of extra loss of blubber during the migration.
Step 4: Changes in Fecundity, Calf Mortality, and Population-Level Effects
Since there was no evidence that the commercial seismic survey would cause even a 24 h delay in migration, and the reduction in body condition in lactating females was negligible, there was no evidence in this study to suggest the seismic survey would change female migratory energetics in such a way as to have an effect on annual breeder fecundity. For this reason, the last step (estimate of the population consequences due to a decrease in fecundity) was not implemented.
Backwards PCoD Model
Given the lack of evidence that female fecundity would significantly reduce whilst migrating through the survey zone, we concentrated on calf mortality as a potential population-level effect. According to the population growth model for this population (as outlined in Supplementary Material), a decrease in calf survival from 0.9 to 0.8 would reduce the population growth rate from 11.4 to 10.7%. The remainder of the analysis will determine if a “worst case” scenario could potentially achieve this population-level effect.
According to the energetic model for the calf (outlined in Supplementary Material), after 48 h of not feeding, a calf would lose approximately 8 kg in body weight based on its basal metabolic rate and cost of transport. In addition, the calf would not achieve the 28 kg per day weight gain of a calf that is feeding normally meaning, as time goes on, it would be at risk of being under-weight and therefore compromised. In terms of blubber loss, the calf’s blubber mass would reduce from 391 kg (proportion of 0.42 of its body mass) to 383 kg (body mass proportion of 0.40; Figure 3A). After 5 days of not feeding, the calf would have lost almost 20 kg in body weight with its blubber proportion reduced to 0.37. Though blubber loss may not be substantial, by this point the calf would likely be severely dehydrated, weak, and at increased risk from predation. We do not know how long a calf can survive without nursing and we do not know if the presence of a commercial seismic survey vessel would cause complete cessation of nursing. For the remainder of the analysis, however, we conservatively assumed that 48 h of not feeding would reduce the chance of the calf surviving the migration. It should be noted that this was deemed a “worst case” scenario only and, when empirical data become available to fill this knowledge gap, other scenarios can be investigated.
Exposure histories of 388 lactating individuals (out of a population of 2,415) found that the response probability would need to be 0.4 to achieve a mean of 40 h of disturbance for this cohort (Supplementary Figures 5b, 6). In this scenario, all individuals were disturbed for more than 24 h and 16 out of 388 (proportion of 0.04) were disturbed for more than 48 h. To achieve such an extended disturbance time required females to spend much longer in the survey zone. They would have had to migrate through a larger survey, multiple surveys, or switch their mode from primarily migrating to primarily resting/birthing.
Following these results, we focused on resting behavior in the subsequent ABM, (assuming females nursed whilst resting) by increasing the amount of time FC spent in M2. Under this scenario, modeled non FC agents spent 17 h traversing the area regardless of whether or not they responded (Model 1). FC agents that didn’t respond (n = 411) spent between 15 and 250 h transiting the area. This emulates a resting area along the migration route where some lactating females will continue to migrate, whereas others will stop and rest for up to 10 days. Of the 608 FC agents, 197 responded, meaning a response probability of 0.3. Modeled FC agents that didn’t respond spent 60 h in the survey area (Figure 3A), whereas those that did respond increased their transit time to 82 h; spending a further 22 h within the survey zone (Model 1). The distribution of transit times in these FC agents shifted from most spending between 15 and 70 h in the survey area (no response), to most spending between 50 and 120 h in the area (Figure 3B). However, for reasons outlined below, it is unlikely all of these FC agents would be at risk of losing the calf.
For FC agents that responded, response activations ranged from 1 to 6. For those responding only once, their total response time lasted between 5 and 155 min. It is difficult to see how, at this low response rate and response time, the calf would be at risk of not feeding the entire time it was within the survey zone. FC agents that responded three or more times (3% of the FC agents), had a total response time of 40 to 265 min and took between 55 and 167 h to transit the area (i.e., all more than 48 h). This equates to a higher risk of lost nursing opportunities, given the FC is unlikely to resume nursing directly after it ceased to respond to the seismic survey.
We cannot say if this would result in calf mortality. However, to illustrate how this risk can be used to estimate a population-level effect, we assumed lactating females that were in the area for more than 48 h, and subjected to more than three response activations, lost their calf. Incorporating this increase in calf mortality into the population growth model found that calf survival would decrease from 0.90 to 0.87 (an additional 3% assuming calf survival in an undisturbed population is 90%). Therefore, with our highly conservative “worst case” scenario, the extra calf mortality would only reduce the annual population increase from 11.4 to 11.2% equating to a small population-level effect. In addition, our final result is likely to be an over-estimate in that perhaps lactating females would require more than three response activations before ceasing to nurse, or, females would have to cease nursing for longer than 48 h for their calf to be severely compromised. Once knowledge gaps in female nursing behavior and calf survivability in the presence of seismic air guns become available, the framework presented here can be updated.
Discussion
The physiological constraints of migration mean that a marine migratory species, such as the humpback whale, are likely to be susceptible to human-induced changes in environmental conditions as they must travel through habitat with human presence (Lennox et al., 2016). Expanding human activities within the marine environment are of concern (Halpern et al., 2015), and therefore it is becoming increasingly important to produce a model framework with which to assess the consequences of these activities on marine species at the population level. Here, we developed a population consequences of disturbance model for a data-rich population of migrating humpback whales moving through a simulated seismic survey. We applied the framework in two ways; first to assess the potential for population-level consequences (forwards approach) given empirical data on behavioral responses to a commercial seismic survey. The forwards model suggested that running a commercial seismic survey though a robust population of migrating humpback whales would have a negligible effect on population growth. Second, we focused on calf mortality to determine if a “worst case scenario” level of disturbance could potentially lead to a detrimental effect on the population dynamics (backwards approach). Though this backwards approach was not based on empirical data, and therefore was subject to assumptions on female nursing behavior and calf health and survivability, it both identifies important data gaps and illustrates how scenarios can be applied. The forwards backwards model framework presented here can be easily updated once data gaps have been filled.
As is usual for PCoD models, the forwards model began with quantifying the behavioral response of individuals within the population (in this case humpback whale groups) exposed, temporarily, to an anthropogenic stressor (in this case various seismic air gun arrays). Results of field experiments found that groups, especially female-calf pairs, reduced their progress southwards (BRAHSS; Dunlop et al., 2015, 2016, 2017a,b, 2018) leading to a temporary migratory delay. To progress through the PCoD model, we assumed the survival and reproductive success of these females was linked to body condition during migration (Lockyer, 1986). Lactating females were assumed to be the most at risk to changes in fitness and body condition. Therefore, changes in their behavior were linked to changes in migratory energetics, and finally, population consequences as per other PCoD models (e.g., New et al., 2014; Villegas-Amtmann et al., 2015). According to the energetic model used in this study, lactating female-calf pairs returned to the feeding grounds with a less than 10% change in body condition after being “disturbed” or “delayed” for less than 24 h. Results of the ABM found no evidence of a delay of more than 24 h as they traversed through the seismic survey zone. In other words, because of the short migratory delay caused by the simulated seismic survey, we could not find evidence of significant (+ 10%) changes in body condition in lactating females and therefore assumed no evidence of any population-level changes due to changes in fecundity. Within the backwards approach analysis, we found that increasing the time lactating females spent within the survey zone would likely increase their probability of responding, the likelihood they would respond more than once, and their delay time. Within this model we concentrated on the relationship between calf mortality and disturbance within the survey area, assuming disturbed females would not nurse within the survey area. However, within this scenario we also found that FC agents that responded were delayed by approximately 22 h compared to those that did not respond, suggesting a negligible loss of extra blubber during the migration. Typical FC agent transit times shifted from most spending between 15 and 70 h in the survey area (no response), to most spending between 50 and 120 h in the area. At worst, this translates to an extra two days of migration. The energetic model found that only larger (35,000 kg) females delayed by 48 h would lose an extra 10% of blubber. However, these large females may not have the same relationship between body-condition and fecundity as smaller females. In summary, even in a resting area, a reduction in fecundity due to reduced female body condition is unlikely to be a contributing factor to population-level effects. As discussed later, the energetic model used here still requires empirical validation meaning we cannot fully discount an effect of a seismic survey on female body condition. However, for the remainder of this discussion we will assume a commercial seismic survey carried out on a robust population of southerly migrating humpback whales is unlike to reduce female fecundity.
The high costs of lactation in baleen whales (Lockyer, 1981) suggests that female humpback whales with insufficient energy reserves would produce smaller or poorer conditioned calves (Lockyer, 2007; Christiansen et al., 2014). Because of this, and the fact they are a long-lived species, female baleen whales are thought to prioritize their own body condition and survival above that of their offspring. For this reason, we concentrated on calf mortality rather than female fecundity. We ran a backwards PCoD model to determine if a “worst case” exposure regime would lead to population-level consequences via increased calf mortality. Here, we assumed the repercussion of the seismic survey was the reduced opportunity for nursing, given a decrease in resting behavior (and likely nursing) has been found in humpback whales in the presence of vessels (Morete et al., 2007; Sprogis et al., 2020). The maximal amount of milk a calf can receive is limited by the rate of delivery from the mother and the time available for feeding. Reduced nursing time means that the rate of milk delivery must increase to maintain ideal growth rates. This is only physiologically possible to a point, after which, calf growth will be compromised, and after that, calf survival. Assuming that maximal milk delivery rate is 70 kg day–1, Braithwaite et al. (2015), found that a reduction in feeding time of 7 days during migration would result in 20% less milk delivered to the calf. We found much shorter transit times within the survey area, even in an emulated resting area, meaning it is unlikely our scenario would significantly reduce the amount of milk delivered to the calf. However, we assumed, other effects, such as dehydration, would contribute to calf survivability. We therefore, conservatively, assumed that calf mortality would increase if females were disturbed and did not nurse for at least 48 h, noting that once this data gap is filled, the model presented here can be updated. Though this level of continuous disturbance would be unlikely in a migratory area where animals are passing through, it could be possible in a resting area where animals are stationary for a number of days. A dynamic state model assessing the effects of anthropogenic disturbance on blue whale (Balaenoptera musculus) female reproductive success concluded that intense, continuous disturbance (a seismic survey) in a feeding area would result in a deterioration in female condition, and an increase in calf abortions and starvation. However, these effects were only found to occur if females remained in the feeding area. If they moved, there was no detectable long-term effect (Pirotta et al., 2018b).
For this PCoD model, the first (behavioral response) and final (population dynamics) steps are well parameterized with empirical data. The step using entirely modeled data was step 3; the energetic model. Little is known about baleen whale energy dynamics during pregnancy and lactation (Oftedal, 1997; Williams et al., 2013; Christiansen et al., 2014) and, to date, the energetic model used here has not been validated. As highlighted throughout the study, we do not know what delay time it would take to reduce the body condition to a level at which the females won’t breed the following year. Rather, two threshold values were assumed; an extra blubber loss of greater than 10%, and 20%, upon return to the feeding grounds. We also do not know if, and for how long, during a disturbance event the calf would cease nursing, how long the calf would survive without nursing, or even the energetic consequences of missed feeding opportunities in a calf that does survive. In addition, our model doesn’t account for pregnancy costs on top of lactation costs, assuming that newly pregnant females would not have significant energetic costs from an early fetus. If the seismic survey was moved further south, and the fetus was more developed, perhaps this would translate to higher energetic costs of migration in these females, resulting in returning to the feeding grounds in poorer condition. This may not matter if the female’s reproductive cycle is two or three-yearly. However, there are females in the population with an annual cycle (Pallin et al., 2018) and these females are likely to be more susceptible to reduced fecundity if their body condition is compromised. There has been some advancement using drones to measure the body condition of whales (Christiansen et al., 2016) as well as the lipid content in their blubber (Kershaw et al., 2019). Using these techniques, future directions should therefore focus on validating the energetic model using empirical data on loss of body condition of females during migration, calf growth rates, and consequences of missed feeding opportunities in the calf. In addition, at the front end of the PCoD model, further information on the fine-scale responses of a female with a nursing calf to anthropogenic disturbance, in terms of lost feeding opportunities, would help determine if an increase in calf mortality is a conceivable effect.
Here, we have developed a PCoD model for humpback whales migrating through a commercial seismic survey. We used a forward approach to determine if such a survey would be likely to have population-level consequences, and a backwards approach to illustrate a potential scenario for small population-level consequences. Results suggest that animals staying within an area for an extended period of time, for example in breeding grounds or resting areas, are more likely to be vulnerable to negative effects than migrating individuals. Although this model was formulated for a robust population of whales where the perceived risk of a population-level effect in response to anthropogenic disturbance is relatively low, this model could be applied to other humpback whale populations that may be deemed less robust and more at risk. We have shown here that we can make predictions about humpback whales in other behavioral contexts (e.g., resting) from an ABM developed for migrating whales. In addition, results provide a framework with which to test for effects of anthropogenic noise sources in other populations that are more vulnerable to changes in fecundity and mortality. This means a vastly scaled-down BRS would be required to test these predictions and re-parameterize the ABM, ultimately reducing the need for high cost experiments.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The animal study was reviewed and approved by University of Queesland Animal Ethics Committee.
Author Contributions
RD conceived the study, analyzed the data, and led the writing of the manuscript. JB developed the original energetics model and provided advice to RD when modifying the model. LM developed the ABM model. CH aided in the utilization of the PCoD+ model for this study and made a substantial contribution to the writing of the manuscript. All co-authors reviewed and edited the final submission. All authors contributed to the article and approved the submitted version.
Funding
The authors declare that this study received funding from the Joint Industry Programme on E&P Sound and Marine Life (JIP), managed by the International Association of Oil & Gas Producers (IOGP). The principal contributing companies to the programme are BG group, BHP Billiton, Chevron, ConocoPhillips, Eni, ExxonMobil, IAGC, Santos, Statoil and Woodside, The United States Bureau of Ocean Energy Management (BOEM), Origin Energy, Beach Energy and AWE. The Australian Commonwealth Department of the Environment and the Redland City Council (RCC) for provided funding for the east coast Australian humpback whale population surveys. Funding for CH’s involvement was supported by U.S. Office of Naval Research grant N00014-16-1-2858: “PCoD+: Developing widely applicable models of the population consequences of disturbance”. Funders did not contribute to the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank DHI and the Joint Industry Program for supporting the development of the ABM. The University of Queensland kindly provided study leave support for RD to undertake the main data analysis for the study. She was hosted at the University of St Andrews, Centre for Research into Ecological and Environmental Modeling. We would also like to thank Michael Noad for providing survey data, Cormac Booth and John Harwood for providing advice and feedback on the PCoD approach, and Dana Cusano for helping with the ABM.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.624981/full#supplementary-material
References
Baraff, L., and Weinrich, M. T. (1993). Separation of humpback whale mothers and calves on a feeding ground in early autumn. Mar. Mamm. Sci. 9, 431–434. doi: 10.1111/j.1748-7692.1993.tb00476.x
Braithwaite, J. E., Meeuwig, J. J., and Hipsey, M. R. (2015). Optimal migration energetics of humpback whales and the implications of disturbance. Conserv. Physiol. 3:cov001. doi: 10.1093/conphys/cov001
Chittleborough, R. G. (1958). The breeding cycle of the female humpback whale, Megaptera nodosa (Bonnaterre). Aust. J. Mar. Freshw. Res. 9, 1–18. doi: 10.1071/MF9580001
Chittleborough, R. G. (1965). Dynamics of two populations of the humpback whale, Megaptera novaeangliae (Borowski). Mar. Freshw. Res. 16, 33–128. doi: 10.1071/MF9650033
Christiansen, F., Dujon, A. M., Sprogis, K. R., Arnould, J. P. Y., and Bejder, L. (2016). Noninvasive unmanned aerial vehicle provides estimates of the energetic cost of reproduction in humpback whales. Ecosphere 7:e01468. doi: 10.1002/ecs2.1468
Christiansen, F., Vikingsson, G. A., Rasmussen, M. H., and Lusseau, D. (2014). Female body condition affects foetal growth in a capital breeding mysticete. Funct. Ecol. 28, 579–588. doi: 10.1111/1365-2435.12200
Christiansen, F., Vivier, F., Charlton, C., Ward, R., Amerson, A., Burnell, S., et al. (2018). Maternal body size and condition determine calf growth rates in southern right whales. Mar. Ecol. Prog. Ser. 592, 267–281. doi: 10.3354/meps12522
Clapham, P. J. (1992). Age attainment of sexual maturity in humpback whales, Megaptera-novaeangliae. Can. J. Zool. Rev. Can. Zool. 70, 1470–1472. doi: 10.1139/z92-202
Clapham, P. J., and Mayo, C. A. (1987). The attainment of sexual maturity in female humpback whales. Mar. Mamm. Sci. 3, 279–283. doi: 10.1111/j.1748-7692.1987.tb00170.x
Costa, D. P., Schwarz, L., Robinson, P., Schick, R. S., Morris, P. A., Condit, R., et al. (2016). A bioenergetics approach to understanding the population consequences of disturbance: elephant seals as a model system. Adv. Exp. Med. Biol. 875, 161–169. doi: 10.1007/978-1-4939-2981-8_19
Council Directive 92/43/EEC, (1992). Council Directive 92/43/EEC of 21 May 1992 on the Conservation of Natural Habitats and of Wild Fauna and Flora. Brussels: European Economic Community.
Craig, A. S., Herman, L. M., and Pack, A. A. (2002). Male mate choice and male-male competition coexist in the humpback whale (Megaptera novaeangliae). Can. J. Zool. Rev. Can. Zool. 80, 745–755. doi: 10.1139/z02-050
Dunlop, R. A., Noad, M. J., McCauley, R. D., Kniest, E., Paton, D., and Cato, D. H. (2015). The behavioural response of humpback whales (Megaptera novaeangliae) to a 20 cubic inch air gun. Aquat. Mamm. 41, 412–433. doi: 10.1578/AM.41.4.2015.412
Dunlop, R. A., Noad, M. J., McCauley, R. D., Kniest, E., Slade, R., Paton, D., et al. (2016). Response of humpback whales (Megaptera novaeangliae) to ramp-up of a small experimental air gun array. Mar. Pollut. Bull. 103, 72–83. doi: 10.1016/j.marpolbul.2015.12.044
Dunlop, R. A., Noad, M. J., McCauley, R. D., Kniest, E., Slade, R., Paton, D., et al. (2017a). The behavioural response of migrating humpback whales to a full seismic airgun array. Proc. R. Soc. B Biol. Sci. 284:20171901. doi: 10.1098/rspb.2017.1901
Dunlop, R. A., Noad, M. J., McCauley, R. D., Kniest, E., Slade, R., Paton, D., et al. (2018). A behavioural dose-response model for migrating humpback whales and seismic air gun noise. Mar. Pollut. Bull. 133, 506–516. doi: 10.1016/j.marpolbul.2018.06.009
Dunlop, R. A., Noad, M. J., McCauley, R. D., Scott-Hayward, L., Kniest, E., Slade, R., et al. (2017b). Determining the behavioural dose-response relationship of marine mammals to air gun noise and source proximity. J. Exp. Biol. 220, 2878–2886. doi: 10.1242/jeb.160192
Godwin, E. M., Noad, M. J., Kniest, E., and Dunlop, R. A. (2016). Comparing multiple sampling platforms for measuring the behavior of humpback whales (Megaptera novaeangliae). Mar. Mamm. Sci. 32, 268–286. doi: 10.1111/mms.12262
Halpern, B. S., Frazier, M., Potapenko, J., Casey, K. S., Koenig, K., Longo, C., et al. (2015). Spatial and temporal changes in cumulative human impacts on the world’s ocean. Nat. Commun. 6:7615. doi: 10.1038/ncomms8615
Harris, C. M., Thomas, L., Falcone, E. A., Hildebrand, J., Houser, D., Kvadsheim, P. H., et al. (2018). Marine mammals and sonar: dose-response studies, the risk-disturbance hypothesis and the role of exposure context. J. Appl. Ecol. 55, 396–404. doi: 10.1111/1365-2664.12955
Harwood, J., King, S., Booth, C., Donovan, C., Schick, R. S., Thomas, L., et al. (2016). Understanding the population consequences of acoustic disturbance for marine mammals. Adv. Exp. Med. Biol. 875, 417–423. doi: 10.1007/978-1-4939-2981-8_49
Kavanagh, A. S., Noad, M. J., Blomberg, S. P., Goldizen, A. W., Kniest, E., Cato, D. H., et al. (2017). Factors driving the variability in diving and movement behavior of migrating humpback whales (Megaptera novaeangliae): implications for anthropogenic disturbance studies. Mar. Mamm. Sci. 33, 413–439. doi: 10.1111/mms.12375
Kershaw, J. L., Brownlow, A., Ramp, C. A., Miller, P. J. O., and Hall, A. J. (2019). Assessing cetacean body condition: is total lipid content in blubber biopsies a useful monitoring tool? Aquat. Conserv. Mar. Freshw. Ecosyst. 29, 271–282. doi: 10.1002/aqc.3105
King, S. L., Schick, R. S., Donovan, C., Booth, C. G., Burgman, M., Thomas, L., et al. (2015). An interim framework for assessing the population consequences of disturbance. Methods Ecol. Evol. 6, 1150–1158. doi: 10.1111/2041-210X.12411
Lennox, R. J., Chapman, J. M., Souliere, C. M., Tudorache, C., Wikelski, M., Metcalfe, J. D., et al. (2016). Conservation physiology of animal migration. Conserv. Physiol. 4:cov072. doi: 10.1093/conphys/cov072
Lockyer, C. (1981). Growth and energy budgets of large baleen whales from the Southern Hemisphere. Mamm. Sea 3, 379–487.
Lockyer, C. (1986). Body-fat condition in northeast Atlantic fin whales, Balaenoptera-physalus, and its relationship with reproduction and food resource. Can. J. Fish. Aquat. Sci. 43, 142–147. doi: 10.1139/f86-015
Lockyer, C. (2007). All creatures great and smaller: a study in cetacean life history energetics. J. Mar. Biol. Assoc. U. K. 87, 1035–1045. doi: 10.1017/S0025315407054720
Marine Mammal Protection Act, (1972). PUBLIC LAW 92-522-OCT. 21, 1972. Available online at: https://www.govinfo.gov/content/pkg/STATUTE-86/pdf/STATUTE-86-Pg1027.pdf. (accessed June 17, 2019).
McHuron, E. A., Costa, D. P., Schwarz, L., and Mangel, M. (2017). State-dependent behavioural theory for assessing the fitness consequences of anthropogenic disturbance on capital and income breeders. Methods Ecol. Evol. 8, 552–560. doi: 10.1111/2041-210X.12701
Mikkelsen, L., Johnson, M., Wisniewska, D. M., van Neer, A., Siebert, U., Madsen, P. T., et al. (2019). Long-term sound and movement recording tags to study natural behavior and reaction to ship noise of seals. Ecol. Evol. 9, 2588–2601. doi: 10.1002/ece3.4923
Morete, M. E., Bisi, T. L., and Rosso, S. (2007). Mother and calf humpback whale responses to vessels around the Abrolhos Archipelago, Bahia, Brazil. J. Cetecean Res. Manag. 9, 241–248.
Nabe-Nielsen, J., Sibly, R. M., Tougaard, J., Teilmann, J., and Sveegaard, S. (2014). Effects of noise and by-catch on a Danish harbour porpoise population. Ecol. Model. 272, 242–251. doi: 10.1016/j.ecolmodel.2013.09.025
Nabe-Nielsen, J., van Beest, F. M., Grimm, V., Sibly, R. M., Teilmann, J., and Thompson, P. M. (2018). Predicting the impacts of anthropogenic disturbances on marine populations. Conserv. Lett. 11:e12563. doi: 10.1111/conl.12563
National Research Council (2005). Marine Mammal Populations and Ocean Noise: Determining When Noise Causes Biologically Significant Effects. Washington, DC: National Academies Press.
New, L. F., Clark, J. S., Costa, D. P., Fleishman, E., Hindell, M. A., Klanjscek, T., et al. (2014). Using short-term measures of behaviour to estimate long-term fitness of southern elephant seals. Mar. Ecol. Prog. Ser. 496, 99–108. doi: 10.3354/meps10547
New, L. F., Harwood, J., Thomas, L., Donovan, C., Clark, J. S., Hastie, G., et al. (2013). Modelling the biological significance of behavioural change in coastal bottlenose dolphins in response to disturbance. Funct. Ecol. 27, 314–322. doi: 10.1111/1365-2435.12052
Noad, M. J., Kniest, E., and Dunlop, R. A. (2019). Boom to bust? Implications for the continued rapid growth of the eastern Australian humpback whale population despite recovery. Popul. Ecol. 61, 198–209. doi: 10.1002/1438-390X.1014
Oftedal, O. T. (1997). Lactation in whales and dolphins: evidence of divergence between baleen- and toothed-species. J. Mammary Gland Biol. Neoplasia 2, 205–230. doi: 10.1023/A:1026328203526
Pallin, L. J., Baker, C. S., Steel, D., Kellar, N. M., Robbins, J., Johnston, D. W., et al. (2018). High pregnancy rates in humpback whales (Megaptera novaeangliae) around the Western Antarctic Peninsula, evidence of a rapidly growing population. R. Soc. Open Sci. 5:180017. doi: 10.1098/rsos.180017
Pirotta, E., Booth, C. G., Costa, D. P., Fleishman, E., Kraus, S. D., Lusseau, D., et al. (2018a). Understanding the population consequences of disturbance. Ecol. Evol. 8, 9934–9946. doi: 10.1002/ece3.4458
Pirotta, E., Harwood, J., Thompson, P. M., New, L., Cheney, B., Arso, M., et al. (2015a). Predicting the effects of human developments on individual dolphins to understand potential long-term population consequences. Proc. R. Soc. B Biol. Sci. 282:20152109. doi: 10.1098/rspb.2015.2109
Pirotta, E., Mangel, M., Costa, D. P., Mate, B., Goldbogen, J. A., Palacios, D. M., et al. (2018b). A dynamic state model of migratory behavior and physiology to assess the consequences of environmental variation and anthropogenic disturbance on marine vertebrates. Am. Nat. 191, E40–E56. doi: 10.1086/695135
Pirotta, E., Merchant, N. D., Thompson, P. M., Barton, T. R., and Lusseau, D. (2015b). Quantifying the effect of boat disturbance on bottlenose dolphin foraging activity. Biol. Conserv. 181, 82–89. doi: 10.1016/j.biocon.2014.11.003
Pirotta, E., New, L., Harwood, J., and Lusseau, D. (2014). Activities, motivations and disturbance: an agent-based model of bottlenose dolphin behavioral dynamics and interactions with tourism in Doubtful Sound, New Zealand. Ecol. Model. 282, 44–58. doi: 10.1016/j.ecolmodel.2014.03.009
Pirotta, E., Schwarz, L. K., Costa, D. P., Robinson, P. W., and New, L. (2019). Modeling the functional link between movement, feeding activity, and condition in a marine predator. Behav. Ecol. 30, 434–445. doi: 10.1093/beheco/ary183
Rolland, R. M., Schick, R. S., Pettis, H. M., Knowlton, A. R., Hamilton, P. K., Clark, J. S., et al. (2016). Health of North Atlantic right whales Eubalaena glacialis over three decades: from individual health to demographic and population health trends. Mar. Ecol. Prog. Ser. 542, 265–282. doi: 10.3354/meps11547
Schick, R. S., Kraus, S. D., Rolland, R. M., Knowlton, A. R., Hamilton, P. K., Pettis, H. M., et al. (2013). Using hierarchical bayes to understand movement, health, and survival in the endangered North Atlantic right whale. PLoS One 8:e64166. doi: 10.1371/journal.pone.0064166
Schwacke, L. H., Thomas, L., Wells, R. S., McFee, W. E., Hohn, A. A., Mullin, K. D., et al. (2017). Quantifying injury to common bottlenose dolphins from the Deepwater Horizon oil spill using an age-, sex- and class-structured population model. Endanger. Species Res. 33, 265–279. doi: 10.3354/esr00777
Sivle, L. D., Wensveen, P. J., Kvadsheim, P. H., Lam, F.-P. A., Visser, F., Curé, C., et al. (2016). Naval sonar disrupts foraging in humpback whales. Mar. Ecol. Prog. Ser. 562, 211–220. doi: 10.3354/meps11969
Southall, B. L., Nowacek, D. P., Miller, P. J. O., and Tyack, P. L. (2016). Experimental field studies to measure behavioral responses of cetaceans to sonar. Endanger. Species Res. 31, 293–315. doi: 10.3354/esr00764
Sprogis, K. R., Videsen, S., and Madsen, P. T. (2020). Vessel noise levels drive behavioural responses of humpback whales with implications for whale-watching. eLife 9:e56760. doi: 10.7554/eLife.56760
Tougaard, J., Henriksen, O. D., and Miller, L. A. (2009). Underwater noise from three types of offshore wind turbines: estimation of impact zones for harbor porpoises and harbor seals. J. Acoust. Soc. Am. 125, 3766–3773. doi: 10.1121/1.3117444
Villegas-Amtmann, S., Schwarz, L. K., Gailey, G., Sychenko, O., and Costa, D. P. (2017). East or west: the energetic cost of being a gray whale and the consequence of losing energy to disturbance. Endanger. Species Res. 34, 167–183. doi: 10.3354/esr00843
Villegas-Amtmann, S., Schwarz, L. K., Sumich, J. L., and Costa, D. P. (2015). A bioenergetics model to evaluate demographic consequences of disturbance in marine mammals applied to gray whales. Ecosphere 6:183. doi: 10.1890/ES15-00146.1
Weinrich, M., and Corbelli, C. (2009). Does whale watching in Southern New England impact humpback whale (Megaptera novaeangliae) calf production or calf survival? Biol. Conserv. 142, 2931–2940. doi: 10.1016/j.biocon.2009.07.018
Wensveen, P. J., Kvadscheim, P. H., Lam, F.-P. A., von Benda-Beckmann, A. M., Sivle, L. D., Visser, F., et al. (2017). Lack of behavioural responses of humpback whales (Megaptera novaeangliae) indicate limited effectiveness of sonar mitigation. J. Exp. Biol. 220, 4150–4161. doi: 10.1242/jeb.161232
Williams, R., Vikingsson, G. A., Gislason, A., Lockyer, C., New, L., Thomas, L., et al. (2013). Evidence for density-dependent changes in body condition and pregnancy rate of North Atlantic fin whales over four decades of varying environmental conditions. ICES J. Mar. Sci. 70, 1273–1280. doi: 10.1093/icesjms/fst059
Williamson, M. J., Kavanagh, A. S., Noad, M. J., Kniest, E., and Dunlop, R. A. (2016). The effect of close approaches for tagging activities by small research vessels on the behavior of humpback whales (Megaptera novaeangliae). Mar. Mamm. Sci. 32, 1234–1253. doi: 10.1111/mms.12324
Keywords: agent-based modeling, anthropogenic activity, behavioral response, energetics, humpback whale, ocean noise, PCoD, seismic survey
Citation: Dunlop RA, Braithwaite J, Mortensen LO and Harris CM (2021) Assessing Population-Level Effects of Anthropogenic Disturbance on a Marine Mammal Population. Front. Mar. Sci. 8:624981. doi: 10.3389/fmars.2021.624981
Received: 03 November 2020; Accepted: 22 February 2021;
Published: 15 March 2021.
Edited by:
Elliott Hazen, University of California, Santa Cruz, United StatesReviewed by:
Fleur Visser, University of Amsterdam, NetherlandsElizabeth McHuron, University of Washington, United States
Copyright © 2021 Dunlop, Braithwaite, Mortensen and Harris. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rebecca A. Dunlop, ci5kdW5sb3BAdXEuZWR1LmF1
 Rebecca A. Dunlop
Rebecca A. Dunlop Janelle Braithwaite2
Janelle Braithwaite2 Lars O. Mortensen
Lars O. Mortensen Catriona M. Harris
Catriona M. Harris