Projected Shifts in 21st Century Sardine Distribution and Catch in the California Current

Introduction

In eastern boundary current upwelling regions, such as the California Current System (CCS), sardines and other small pelagic fish play a key role in the transfer of energy between planktonic organisms and higher trophic levels species, such as seabirds and marine mammals (Cury et al., 2000; Peck et al., 2021). Healthy sardine populations also account for a substantial fraction of the global fish catch (Fréon et al., 2005) and support important commercial fishing activities worldwide, yielding multimillion dollars ex-vessel revenues (i.e., revenues from landed catch) off the west coast of the United States alone (Pacific Fishery Management Council (PFMC), 2011). The ecological and economic significance of sardines in upwelling regions make them a prime candidate to explore how populations may respond to changing climate conditions (Cheung et al., 2015; Morley et al., 2018) and to identify potential drivers (e.g., warming and prey availability) and uncertainty sources (Frölicher et al., 2016) associated with shifts in distribution and abundance.

Environmental variability in the CCS occurs over a wide range of spatiotemporal scales and is seasonally driven by coastal upwelling of cool, nutrient rich waters in response to prevailing alongshore winds (Checkley and Barth, 2009). The combination of coastal and curl-driven upwelling produces elevated levels of new production along most of the west coast of the United States and contributes to shaping the habitats of planktonic organisms and forage fish (Rykaczewski and Checkley, 2008; Zwolinski et al., 2011; Fiechter et al., 2020). Physical, biogeochemical and ecosystem states in the CCS are further modulated by basin-scale variability associated with ocean-atmosphere couplings, such as the El Niño Southern Oscillation (Lynn and Bograd, 2002), Pacific Decadal Oscillation (Mantua et al., 1997) and North Pacific Gyre Oscillation (Di Lorenzo et al., 2008). These decadal changes in environmental conditions have been postulated as the main drivers of low-frequency variability of sardine and anchovy populations in the region (Chavez et al., 2003; Lindegren et al., 2013).

The combined effects of basin-scale forcing, regional processes, and local upwelling patterns on small pelagic fish habitat pose a significant challenge for predicting how sardine population dynamics will be affected by changing climate conditions in the CCS and in other eastern boundary current upwelling systems. Global projections from Earth System Models (ESMs) typically lack the necessary atmospheric and oceanic horizontal resolution to reproduce the full spectrum of processes associated with wind-driven coastal upwelling (Stock et al., 2011; Small et al., 2015). Higher-resolution regional models can resolve finer-scale physical and biogeochemical coastal dynamics but must be driven by realistic localized representations of future climate forcing. Dynamical downscaling of low-resolution (∼1° × 1°) ESM solutions has emerged as a valuable method for producing higher-resolution (∼0.1° × 0.1°) regional projections of environmental and ecosystem variability in eastern boundary current upwelling systems under anticipated future conditions (Echevin et al., 2012; Machu et al., 2015; Howard et al., 2020a; Pozo Buil et al., 2021).

The focus of this study is to extend the dynamical downscaling approach of Pozo Buil et al. (2021) to sardine population dynamics and catch in the CCS by integrating a full life-cycle individual-based model (IBM) for sardine and an agent-based model for its fishing fleet into the projections. By nature, the IBM allows for a mechanistic interpretation of environmental drivers regulating growth, reproduction, survival, and behavior of sardine (Fiechter et al., 2015; Rose et al., 2015), and it is thus well-suited to explore which and how underlying physical and biological processes will likely cause changes in sardine abundance and distribution over the course of the 21st century. While anthropogenic warming will undoubtedly play an important role (Cheung et al., 2015; Morley et al., 2018), the IBM projections can shed light on the relative extent to which future temperatures will affect sardine population dynamics through metabolism (growth, reproduction, and early life survival rates) and movement behavior (shift in thermal habitat). The IBM also offers insight into the possible influence on sardine of other bottom-up drivers, such as coastal upwelling intensity and prey availability, which may exhibit more subtle local and regional responses to climate change (Rykaczewski et al., 2015; Checkley et al., 2017) or whose trends have not yet emerged from natural variability (Brady et al., 2017). Since climate models have inherent physical and biogeochemical uncertainty (Frölicher et al., 2016), the robustness of sardine population and catch projections are assessed by downscaling three representative members of the CMIP5 ensemble (Bopp et al., 2013).

Materials and Methods

End-to-End Ecosystem Model

The numerical framework is an existing end-to-end ecosystem model that has already been successfully implemented to study historical sardine and anchovy population variability and their environmental drivers in the CCS (Fiechter et al., 2015; Rose et al., 2015; Politikos et al., 2018; Nishikawa et al., 2019) and in the Canary Current upwelling system (Sánchez-Garrido et al., 2018, 2021). The end-to-end model includes a regional ocean circulation component, a nutrient-phytoplankton-zooplankton (NPZ) component, a sardine population dynamics IBM component, and an agent-based fishing fleet component. Since detailed descriptions of the model can be found in Rose et al. (2015) and Fiechter et al. (2015), only an abbreviated overview of the different model components is provided here.

The ocean circulation model is an implementation of the Regional Ocean Modeling System (ROMS) (Shchepetkin and McWilliams, 2005; Haidvogel et al., 2008) for the broader California Current region (30°N to 48°N and 116°W to 134°W), with a horizontal grid resolution of 1/10° (ca. 10 km) and 42 non-uniform terrain-following vertical levels. The NPZ model is a customized version of the North Pacific Ecosystem Model for Understanding Regional Oceanography (NEMURO) (Kishi et al., 2007) specifically parameterized for the CCS (Fiechter et al., 2018, 2020). Physical transport of NPZ tracers is achieved by solving an advection-diffusion equation at every time step using archived daily velocities and mixing coefficients from ROMS. The IBM tracks sardine individuals on the ROMS grid in continuous (Lagrangian) space and over their full life cycle.

Scaling from individuals to the population level is done using a super-individual approach (Scheffer et al., 1995), where each super-individual in the IBM represents a larger number of individuals (called worth) with identical attributes (a super-individual can be envisioned as a school of identical fish). Super-individuals remain in the simulation until they either reach their oldest allowed age (10 years) or mortality sources reduce their worth to zero. All output from the IBM is scaled by the worths of super-individuals (for example, population abundance is the sum of the worths over all super-individuals, and mean length is a weighted average of the lengths of super-individuals with the weighting factors being their worths).

The IBM explicitly includes formulations for growth from bioenergetics and feeding on zooplankton prey (from NPZ component), reproduction, and natural and fishing mortality for the following life stages (as appropriate): eggs, yolk-sac larvae, feeding larvae, juveniles, non-mature adults, and mature adults. The development of eggs and yolk-sack larvae is determined uniquely by temperature; larvae transition to juveniles based on a weight threshold; juveniles become non-mature adults on January 1 of each model year; and adults reach maturity based on a length threshold. Since mature adults produce eggs which become the next spawning adults, recruitment is an emergent property in the model (as opposed to being imposed annually or defined a priori via a spawner-recruit relationship). Behavioral movement for juveniles and adults includes temperature and consumption cues using a kinesis approach that combines inertial and random displacements based on a proximity to optimal conditions (Humston et al., 2004; Watkins and Rose, 2013). When temperature and feeding conditions experienced by an individual are within a prescribed suitable range (defined here as within one standard deviation from the optimal value), the inertial component is weighted more heavily than the random component, thereby allowing the individual to maintain itself within a suitable thermal and foraging habitat by conserving its current heading and slowing down.

The fishing fleet model simulates daily fishing trips of boats out of 4 United States west coast ports (San Pedro, Monterey, Astoria and Westport). Choice of fishing locations and associated daily sardine catch are based on a simplified multinomial logit, agent-based approach where boats maximize their expected net revenue for each trip (e.g., Eales and Wilen, 1986). While the fleet model incorporates effort in the sense that no fishing occurs on a given day if a boat does not have access to fishing locations yielding a positive revenue, it does not account for specific fisheries management actions that have been imposed historically. For example, the simulations do not include the regulatory quotas imposed on the fishery during 1986–1991 following the sardine moratorium in California (Wolf, 1992) or the lack of a recent commercial fishery in the Pacific Northwest until 1999 (Emmett et al., 2005).

The version of the end-to-end model used here differs from its earlier implementation in several ways. (i) For computational efficiency, each component of the system is run in successive steps (i.e., offline coupling), starting with the physical circulation, then the NPZ component, and finally the fish and fleet components. When using archived daily fields, the offline approach yields a solution virtually identical to that of the fully coupled model, yet it allows for larger time steps for the NPZ (dt = 30 min) and fish and fleet (dt = 6 h) components compared to that of the physical and, hence fully coupled model (dt = 10 min); (ii) The fish IBM component includes only one coastal pelagic species, sardine, and no migratory predator. Earlier results from Rose et al. (2015) demonstrated that sardine and anchovy had small direct effects on each other in the simulations (i.e., dynamics were quasi-independent and therefore separable) and that predatory mortality was small compared to the other sources of mortality represented in the model; (iii) The diet for adult sardine has been adjusted to include higher feeding preferences on copepods and euphausiids. This modification yields a more realistic offshore extent of the sardine population (food is one of the movement cues) compared to that calculated in earlier implementations of the model where adult sardine favored microzooplankton. The new parameterization also leads to an emergent northward summer feeding migration (albeit of reduced amplitude and limited to older fish), thereby alleviating the need of a prescribed seasonal migration as in Rose et al. (2015) and Fiechter et al. (2015). (iv) The parameterization of the NPZ component was revisited to improve the representation of key phytoplankton and zooplankton functional groups in the CCS, especially euphausiids (Fiechter et al., 2018, 2020). Specific parameter values for the NPZ, sardine IBM, and fishing fleet models are provided as supplementary material and references for parameter sources are available in Rose et al. (2015).

Historical Simulation and Climate Projections

Four different numerical simulations of the end-to-end model were performed: a historical run for 1983–2010 and three downscaled climate projections for 1983–2100 based on the GFDL-ESM2M (Dunne et al., 2012), IPSL-CM5A-MR (Dufresne et al., 2013), and Hadley-GEM2-ES (Collins et al., 2011) earth system models under the Representative Concentration Pathway (RCP) 8.5 emission scenario. These models were selected for their inclusion of marine biogeochemical fields and to represent the spread of physical and biogeochemical futures in the CMIP5 ensemble: GFDL has a low rate of warming and increased primary production; Hadley has a high rate of warming and decreased primary production; and IPSL corresponds to a moderate scenario (Bopp et al., 2013; Pozo Buil et al., 2021). The primary purpose of the historical simulation was to generate a reference solution for the calibration and evaluation of the sardine IBM and fishing fleet model.

For the historical simulation, initial and open boundary conditions for physical variables are derived from the Simple Ocean Data Assimilation (SODA) reanalysis (Carton and Giese, 2008), and surface atmospheric fields are based on version 1 of the Cross-Calibrated Multi-Platform (CCMP1) winds (Atlas et al., 2011) and version 5 of the European Centre for Medium-Range Weather Forecasts (ERA5) reanalysis (Hersbach et al., 2020). Initial and boundary conditions for nitrate and silicic acid are derived from the World Ocean Atlas (WOA) (Conkright and Boyer, 2002), while other biogeochemical tracers are set to a small value (0.1 mmol N m^–3) for lack of better information. Total sardine population biomass is initialized so that the biomass contributed by mature (age-2 and older) adult individuals at the beginning of the simulation roughly matched the mean spawning stock biomass estimated for 1985–1999 (∼0.35 million metric tons) (Hill et al., 2010). Sardine super-individuals are randomly initialized within a subregion of the model between 30–35°N and within 100 km of the coast where surface temperatures and food availability on 1 January 1983 are within one standard deviation of their respective optimal values for kinesis.

For the downscaled projections, a “time-varying delta” method is used to generate open boundary and surface atmospheric forcing. For each ESM, time-varying deltas (representing monthly open boundary and surface atmospheric anomalies) are calculated relative to their respective 1980–2010 climatology and added to their corresponding climatology in the historical simulation (SODA and WOA for physical and biogeochemical open boundary conditions, and CCMP1 and ERA5 for surface atmospheric forcing) (Pozo Buil et al., 2021). The downscaled projections are generated for 1983–2100 using historical forcing for 1983–2005 and the RCP8.5 emission scenario for 2006–2100. The main advantage of using a time-varying delta method is that it corrects for inherent biases in the earth model solutions and produces continuous projections reflecting climate change effects in the CCS throughout the 21st century (as opposed to the more common “fixed delta” method that considers only a specific period of the future climate, e.g., 2070–2100). The initial location and biomass of sardine individuals for the projections is determined using the same approach as for the historical simulation.

Analysis

Evaluation of the end-to-end historical simulation includes sea surface temperatures and surface chlorophyll concentrations from the ROMS and NPZ models; sardine spawning stock biomass, age-class structure, recruitment, and egg distribution from the IBM; and regional annual catch from the fishing fleet model. Simulated sea surface temperatures and chlorophyll concentrations are respectively compared to NOAA’s OISST AVHRR dataset¹ and NASA’s SeaWiFS dataset.² Simulated sardine spawning stock biomass (age-2 and older individuals), age-class structure and recruitment are compared to stock assessment estimates from Table 10 in Hill et al. (2010); egg distribution patterns are evaluated against in situ observations of egg presence from Zwolinski et al. (2011); and simulated catch is compared to reported regional United States west coast landings from Table 1 in Hill et al. (2010). Recruitment is an emergent property in the IBM and represents the number of eggs that survive to enter the adult stage on January 1 of each year.

Analysis of the end-to-end model projections includes: (1) total annual adult sardine biomass from each downscaled solution and multi-model mean, as well as multi-model spread calculated as the standard deviation between the three projections and the multi-model mean, (2) spatial distributions of adult sardine abundance and egg production, (3) spatial maps of suitable thermal and feeding habitats, and (4) total annual catch in the southern (San Pedro), central (Monterey) and northern (Astoria and Westport) CCS. Since sardines in the model consume multiple prey types from the NPZ component, a functional response is applied to combine them into a single index (Rose et al., 2015). The functional response uses the prey biomasses, and after accounting for feeding preferences and efficiencies of sardine, generates the fraction of maximum possible consumption rate that would be achieved (hereafter referred to as “P”). The identification of thermal and feeding habitats is purposedly based on the parameters used in kinesis to weight inertial and random movement, so spatial changes in projected sardine distributions are directly relatable to future availability of suitable conditions in the CCS as perceived by individuals in the IBM. Suitable thermal and feeding habitats are thus defined as grid cell locations where temperature and P values are, respectively, within one standard deviation of their optimal value, (i.e., 11–16°C for temperature and greater than 0.75 for P). For these ranges, habitat quality is highest and inertial movement (indicative of good habitat) outweighs random behavior (indicative of poor habitat) in kinesis.

Total biomass is calculated by multiplying the body weight by the worth of a super-individual and summing over all super individuals representing mature adult sardines; worth is the number of actual fish represented by a super-individual and body weight is identical for all fish within a super-individual. Spawning stock biomass is further calculated by summing only over super-individuals representing age-2 and older mature adult sardines. Spatial distributions of abundance are calculated as yearly averages of instantaneous (every 5 days) summed adult worth in each grid cell, and egg production is determined by annually summing the number of eggs spawned (scaled up for the worths of spawners) in each grid cell. Adult abundance and egg production are subsequently mapped to a coarser 30 km resolution grid, which helps smooth out spatial variability in the model output not associated with coherent circulation features. Total annual catch is calculated by summing daily catch over all boats and all days of the year for each port. An unpaired, two-sample Student’s t-test is also performed on sardine abundances at each grid cell location to determine if the means of the distributions are statistically identical across the three downscaled solutions over the analysis period (2000–2100). The projections are considered statistically “robust” at a grid cell location if the pairwise (GFDL-Hadley, GFDL-IPSL, and Hadley-IPSL) t-tests support the hypothesis of identical means at the 95% confidence level.

Results

Model Evaluation

The evaluation of the ROMS and NPZ models focuses on sea surface temperatures and chlorophyll concentrations, as these two variables are intimately related to the presence of suitable thermal and feeding habitats for sardine individuals in the IBM. Despite a slight warm bias (∼0.5°C or less), simulated surface temperatures adequately reproduce observed spatial patterns and temporal variability, including the transition from a warmer to a colder regime in the northeast Pacific Ocean in 1999 associated with a phase change of the Pacific Decadal Oscillation (Peterson and Schwing, 2003) (Figure 1, upper panels). Simulated surface chlorophyll concentrations also demonstrate reasonable agreement with observed values in the spatial extent of the coastal upwelling zone and in their interannual variability and trend (Figure 1, lower panels).

FIGURE 1

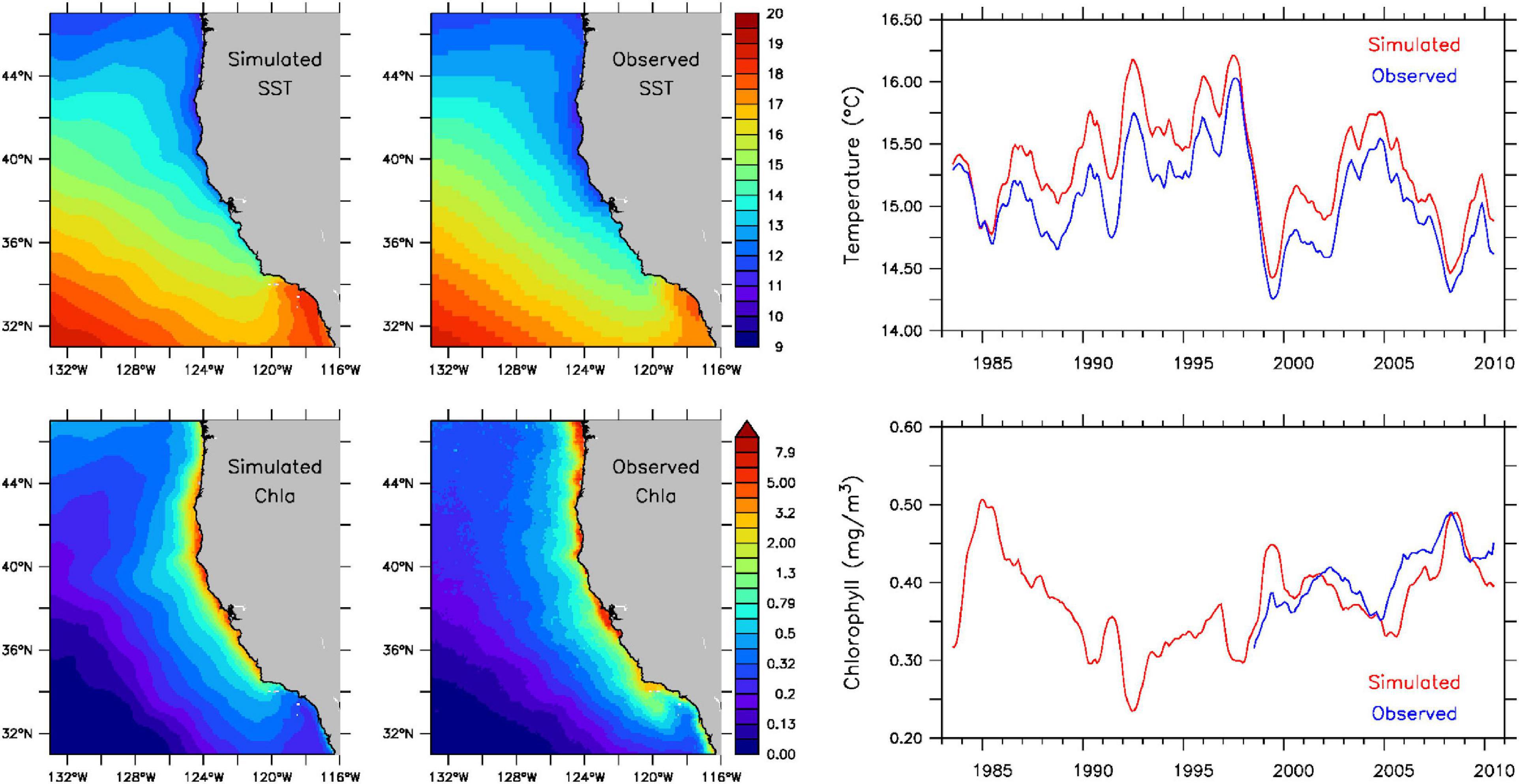
Figure 1. Historical surface temperatures (°C) (top) and chlorophyll concentrations (mg/m³) (bottom) from the ROMS and NPZ models for 1983–2010. Left panels: simulated and observed annual means. Right panel: monthly simulated (red) and observed (blue) spatial means. Observed temperatures are from NOAA’s OISST AVHRR dataset (https://www.ncdc.noaa.gov/oisst) and chlorophyll concentrations are from NASA’s SeaWiFS dataset (https://oceancolor.gsfc.nasa.gov/data/seawifs).

Historical sardine spawning stock biomass from the IBM exhibits low-frequency variability comparable to stock assessment estimates, with a rapid increase in biomass starting in the early 1990s, a period of peak biomass during the late 1990s and early 2000s, and a decline in the late 2000s (Figure 2, upper left panel). However, simulated values greatly underestimate the difference between high and low biomass periods. Over the 28 years, simulated values vary by a factor of about 1.5 times compared to an order of magnitude difference for observed biomass. This discrepancy is partly explained by lower average recruitment values (∼4,200 vs. ∼7,400 million individuals during 1990–2010) and smaller interannual variability. The model predicts a factor of 2–3 times between high and low recruitment years, whereas the factor is 5–10 times for recruitment reported in the stock assessment (Figure 2, lower left panel). However, the IBM reasonably replicates periods of high and low recruitment in the stock assessment, with correlation coefficients of 0.41 based on annual values and 0.71 based on 3-year running mean values. Furthermore, the IBM provides an acceptable representation of the observed age-class structure of the population, and adequately reproduces the observed latitudinal range (33–36°N) and offshore extent of sardine spawning based on in situ egg presence reported by Zwolinski et al. (2011) for 1998–2009 (Figure 2, right panels).

FIGURE 2

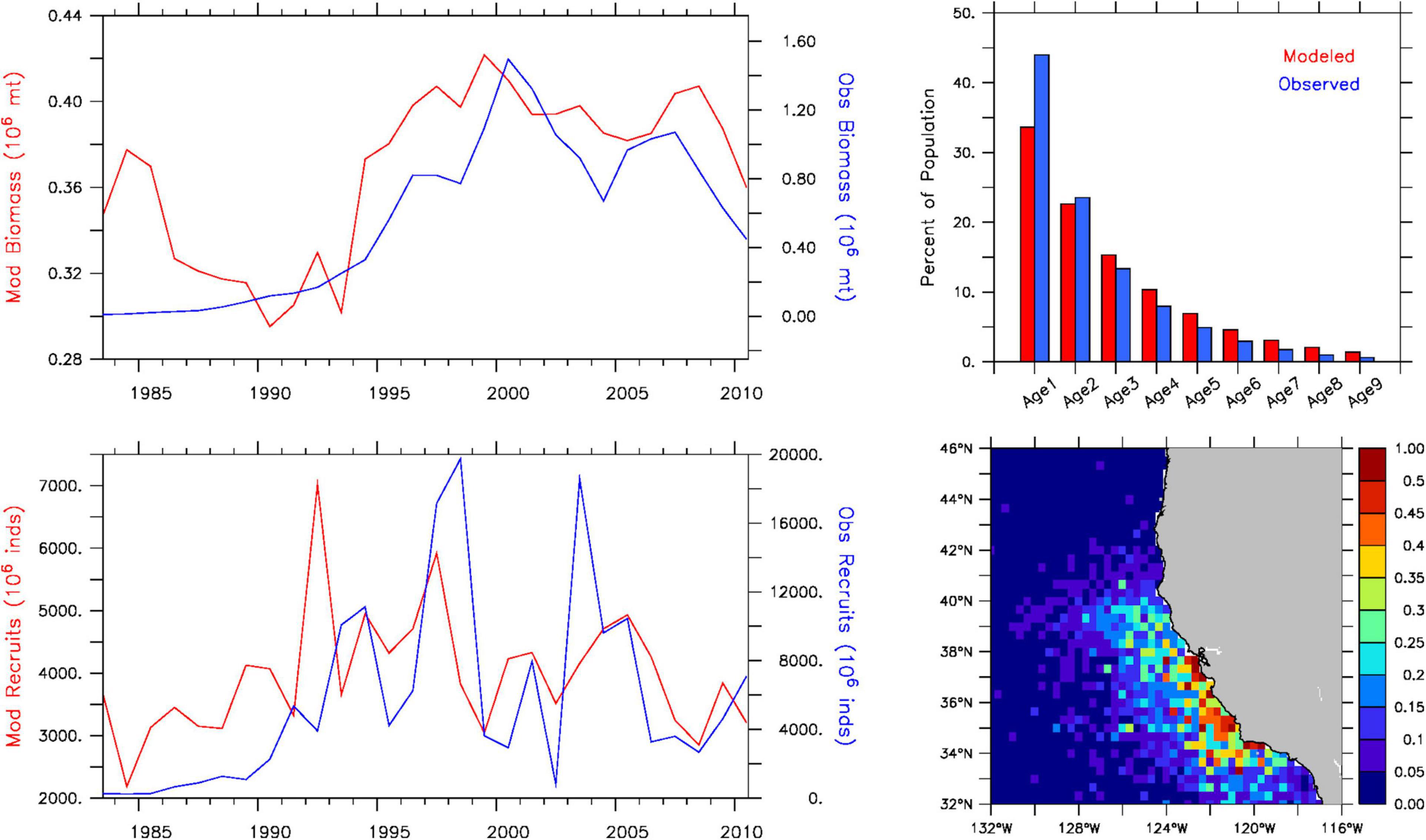
Figure 2. Historical sardine population dynamics from the IBM for 1983–2010. Top left: simulated (red) and observed (blue) spawning stock biomass (adults age-2 and older) (10³ metric tons). Top right: simulated (red) and observed (blue) age-class distribution (percent of population). Bottom left: simulated (red) and observed (blue) recruitment (millions of individuals). Bottom right: Annual mean simulated egg distribution (percent of total production contained in each grid cell). Observed values are from Hill et al. (2010) stock assessment estimates.

The cause for the order of magnitude discrepancy between the model and stock assessment during periods of higher and lower spawning stock biomass is difficult to pinpoint exactly, but prey availability and density-dependent mortality could both play a role. The quadratic natural mortality term in the NPZ component prevents large fluctuations in phytoplankton and zooplankton biomasses [as identified for simulated krill in Fiechter et al. (2020)], which could in turn have a stabilizing effect on recruitment via larval and juvenile growth, and on egg production via adult growth. Introducing density-dependent processes (either via mortality such as predation or crowding effects on prey availability and growth) would presumably improve the IBM’s ability to reproduce observed population-level patterns in spawning stock biomass. However, density-dependence was ultimately not included in the IBM to maximize simulated responses to variation in environmental variables and prey availability, thereby enabling more easily interpretable results in the projections. Including density-dependence would dampen responses and, given the uncertainty in how to formulate the density-dependence among processes and life stages (see Rose et al., 2001), would require extensive testing of alternative formulations of differing strength. An option for additional analyses would be to calibrate the density-dependence to match the historical spawner-recruit relationship (e.g., from stock assessment estimates), but it is not clear how this relationship may change under future conditions. Furthermore, since relative changes in simulated sardine abundance and distribution are comparable over an order of magnitude change in initial population biomass (Supplementary Figure 1), discrepancies in historical spawning stock biomass and recruitment should not fundamentally alter the qualitative spatial and temporal patterns identified in the IBM projections.

Comparing simulated catch to observed landings is obscured by the fact that the fleet model does not account for the sardine moratorium (1974–85) and subsequent period of limited fishing quotas (1986–1991) in California (Wolf, 1992) and for the lack of a recent commercial fishery in the Pacific Northwest until 1999 (Emmett et al., 2005). Excluding those periods and ramp-up phase of the fishery, simulated catch reasonably reproduces the magnitude and temporal variability of reported landings in the southern CCS during 2000–2010 and northern CCS during 2002–2010 (Supplementary Figure 2). However, the model exhibits significantly less similarity with landings in the central CCS, both in amplitude and year-to-year variation. The agreement between simulated catch and landings (at least for San Perdo, Astoria, and Westport) during the period of high sardine abundance suggests that, despite the factor 2–3 difference between simulated spawning stock biomass and stock assessment estimates, the model results are informative with careful interpretation and caveats.

Downscaled Projections

All three downscaled climate projections display substantial low-frequency variability in sardine biomass over the course of the 21st century, with a notable decrease in adult biomass during 2020–2040 and a rapid increase in adult biomass starting in the 2070s (Figure 3). However, the importance of the mid-century low biomass period and the magnitude of the end of the century increase differ markedly between the three projections. Based on the multi-model mean, sardine biomass decreases by about 40% between historical (2000–2020) and mid-century (2040–2060) values, with GFDL projecting a smaller decrease (∼15%) than the multi-model mean, and Hadley and IPSL projecting a larger decrease (up to 70% for IPSL). Comparatively, the change in sardine biomass during the second half of the century is more substantial, as evidenced by the 2.5–3 times increase in the multi-model mean between mid-century and end of the century values. Individual projections also exhibit greater spread, with GFDL and Hadley projecting a lower increase (closer to doubling), and IPSL projecting a much larger increase (∼7 times increase).

FIGURE 3

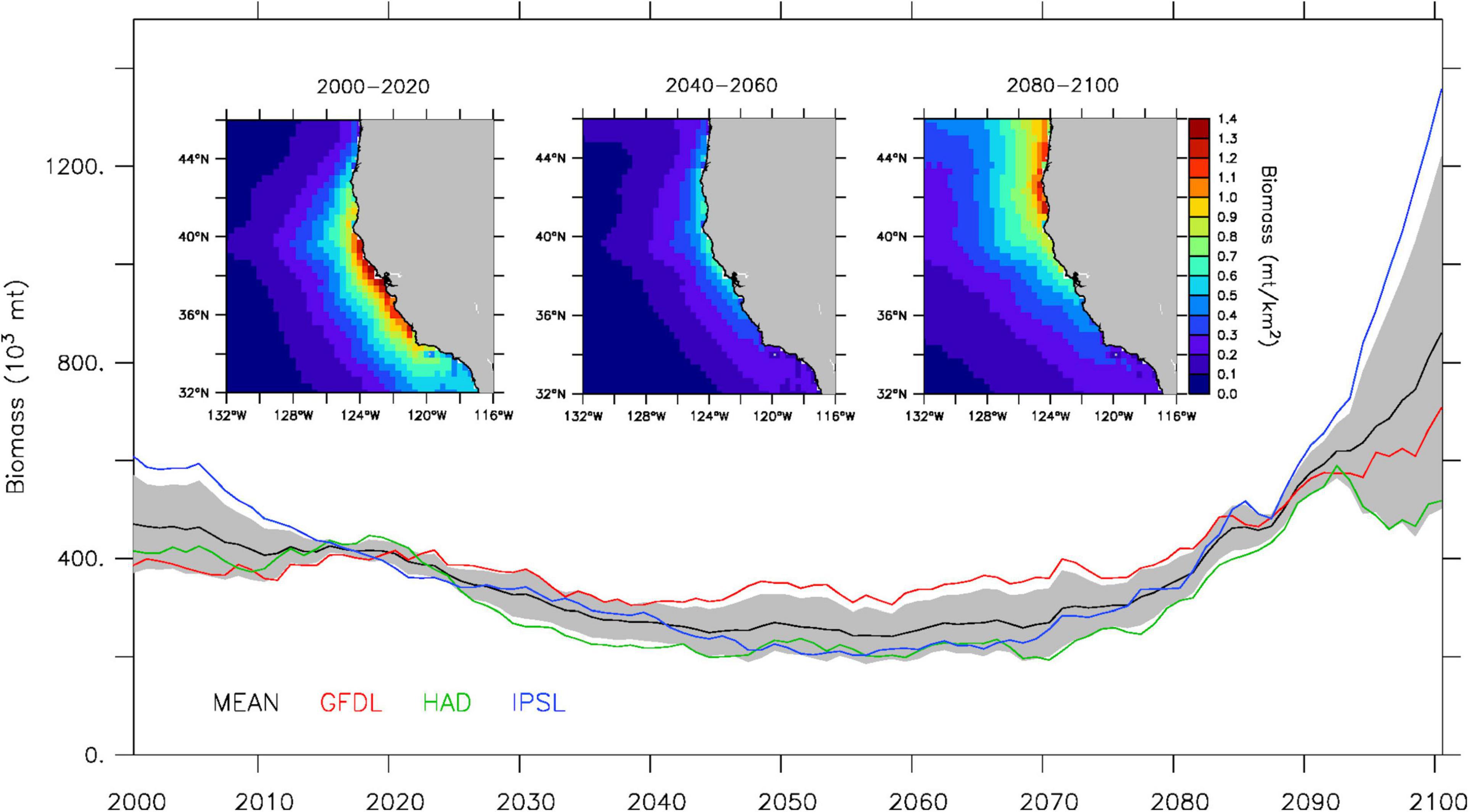
Figure 3. Projected sardine spawning stock biomass (10³ metric tons) for 2000–2100. The time series represent CCS-wide annual adult (age-2 and older) biomass from the ensemble mean (black) and individual GFDL (red), Hadley (green) and IPSL (blue) solutions (gray shading denotes ensemble spread). Insets represent the ensemble mean spatial biomass distribution (metric tons per km²) for 2000–2020 (left), 2040–2060 (center), and 2080–2100 (right).

The projected changes in total biomass are also accompanied by a regional redistribution of the sardine population over the course of the 21st century, as illustrated by the poleward shift in the multi-model mean between 2000–2020, 2040–2060, and 2080–2100 (Figure 3). While the poleward displacement of the sardine population is a common feature of all three downscaled projections, the timing and magnitude of the shift differ substantially between the GFDL, Hadley and IPSL solutions (Figure 4, upper panels). By mid-century, Hadley projects a region of peak abundance (∼37–46°N) on average 2° farther north than those in the GFDL and IPSL projections (∼35–44°N). In contrast, by the end of the century, Hadley and IPSL project that peak sardine abundance is limited to the northern CCS (north of 40°N), whereas GFDL suggests higher sardine abundance still occurs in the central CCS between 37–40°N. This poleward shift in sardine abundance over the course of the 21st century is accompanied by a similar displacement of peak egg production (i.e., primary spawning grounds) (Figure 4, lower panels).

FIGURE 4

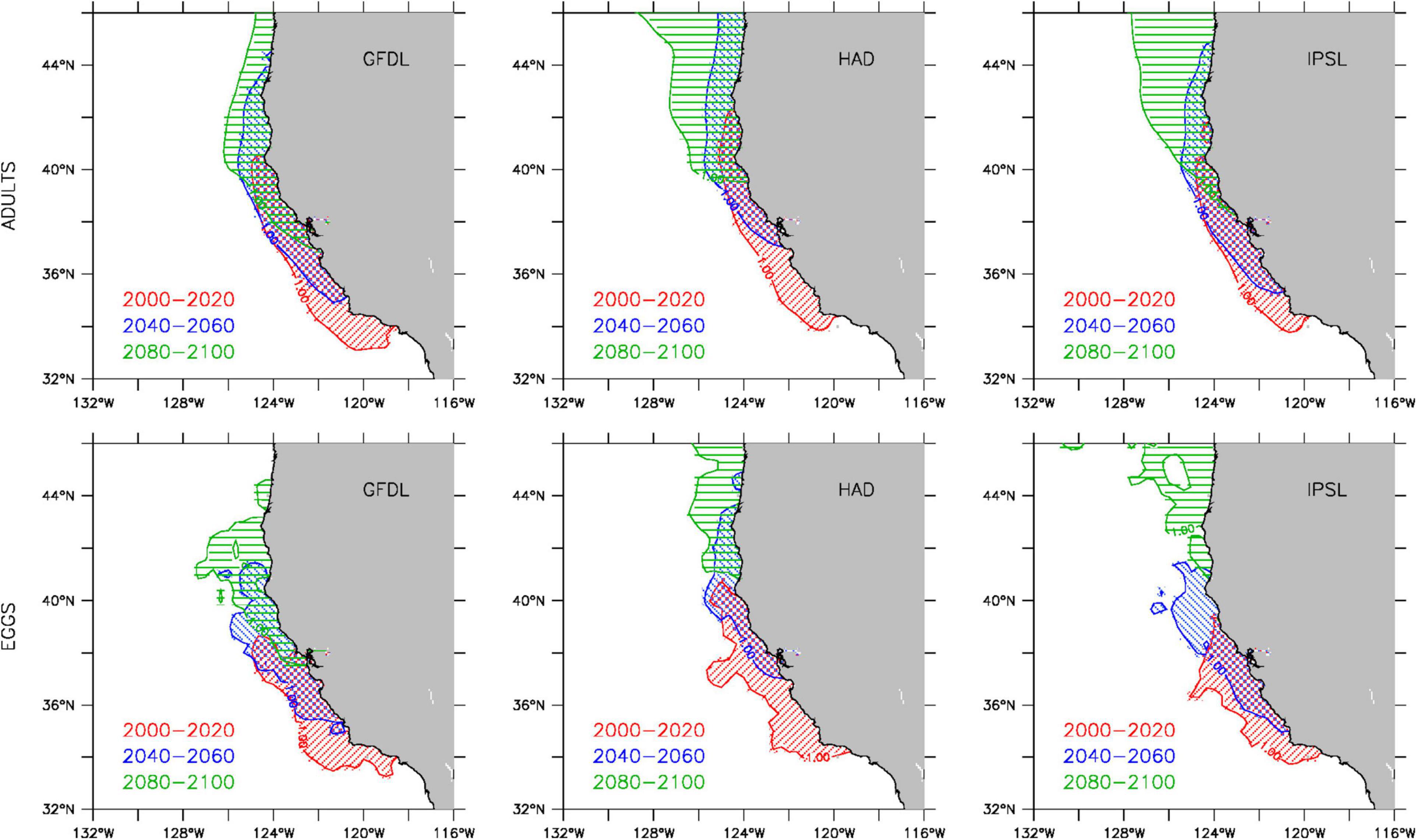
Figure 4. Projected spatial distributions of peak adult sardine abundance (top) and egg production (bottom) for 2000–2020 (red), 2040–2060 (blue), and 2080–2100 (green) from GFDL (left), Hadley (center), and IPSL (right) solutions. Regions of peak adult abundance and egg production are defined as locations where individual and egg counts are greater than one standard deviation above the mean (based on all locations where individuals and eggs were present).

The cues for behavioral movement in kinesis are used to identify whether temperature or food availability is the primary driver for the projected poleward shift of the sardine population (Figure 5). All three model solutions indicate that prey availability, and thus consumption, remain optimal throughout the 21st century in most coastal regions where sardines would normally be found. In contrast, simulated optimal temperatures for sardines become progressively limited in the southern and central CCS. By 2100, the GFDL projection (lowest rate of warming) retains a narrow coastal region of optimal temperature conditions in the central CCS (as far south as 34°N), while the Hadley projection (highest rate of warming) has virtually no suitable thermal habitat for sardines equatorward of 40°N. Hence, the poleward shift of the sardine population in the end-to-end model is primarily associated with a substantial reduction of thermal habitat in the southern and central CCS by the end of the century.

FIGURE 5

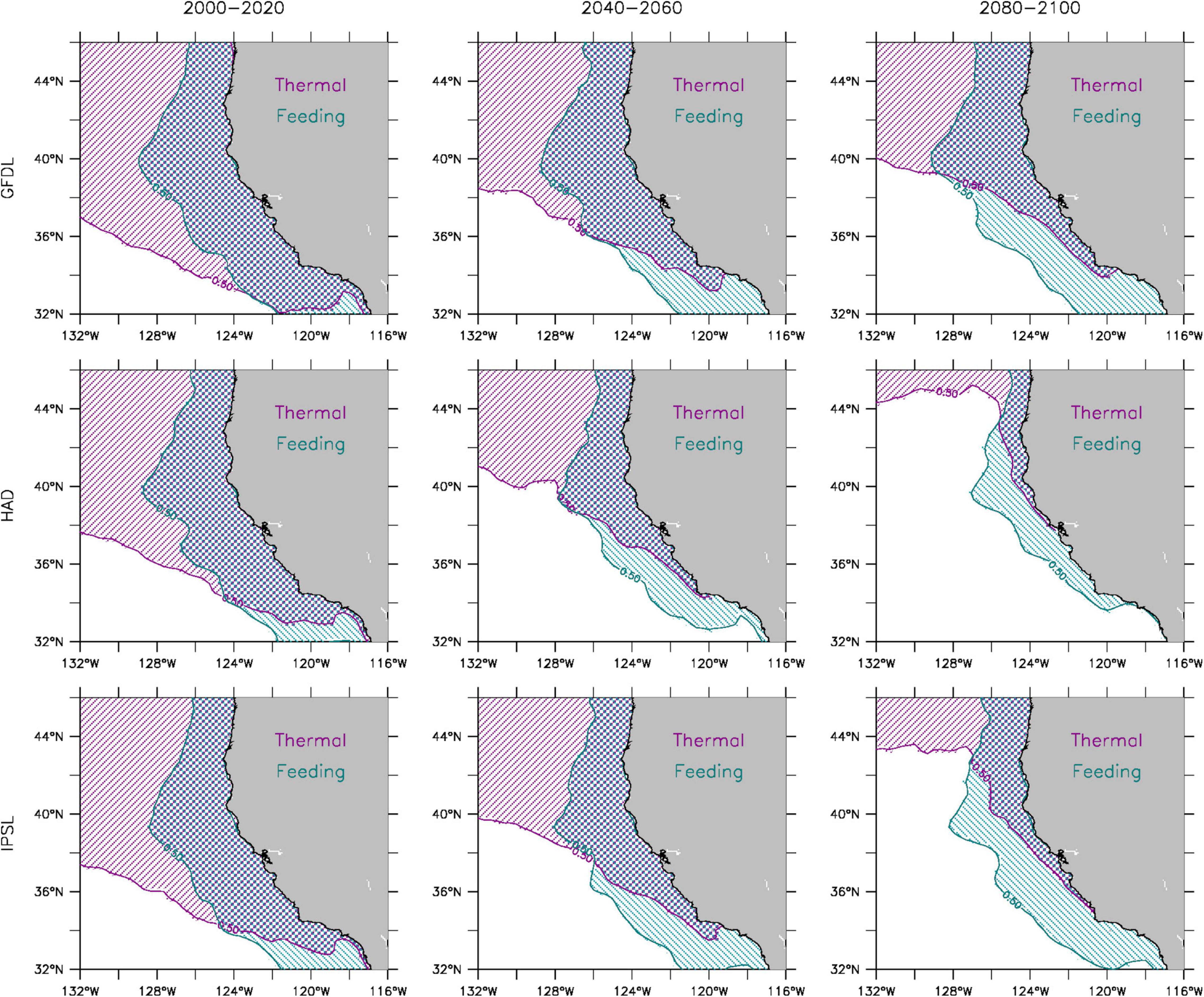
Figure 5. Feeding and thermal habitat suitability for adult sardines during 2000–2020 (left), 2040–2060 (center), and 2080–2100 (right) from GFDL (top), Hadley (middle), and IPSL (bottom) solutions. Shading denotes locations where temperature (magenta) and fraction of maximum consumption (P) (cyan) are within one standard deviation of their respective optimal values (as defined in kinesis for horizontal behavior) at least 50% of the time.

The progressive displacement of simulated peak sardine abundance from the southern to the northern CCS has clear implications for projected catch (Figure 6). All three model solutions indicate a substantial decrease of total catch in the southern and central CCS by the end of the century. The decrease is more pronounced and occurs more rapidly in the Hadley and IPSL projections, with catch in the southern and central CCS being 50–70% lower by mid-century (2040–2060) relative to historical conditions (2000–2020). Catch changes more gradually in the GFDL projection, with a decrease of ∼20% by mid-century (2040–2060) and another ∼10% by the end of the century (2080–2100) in both the southern and central CCS. In contrast, catch in the northern CCS consistently increases, reaching a factor of 2–3 times higher by the end of the century relative to historical values for all three projections. On aggregate across the entire CCS, simulated decadal variability in catch aligns closely with changes in total sardine population biomass, as evidence by a steady decrease during the first half of the 21st century, followed by a sharper increase starting around 2070. This pattern is least pronounced in the GFDL projection due to its reduced low-frequency sardine biomass variability (notably the mid-century minimum and end of the century maximum).

FIGURE 6

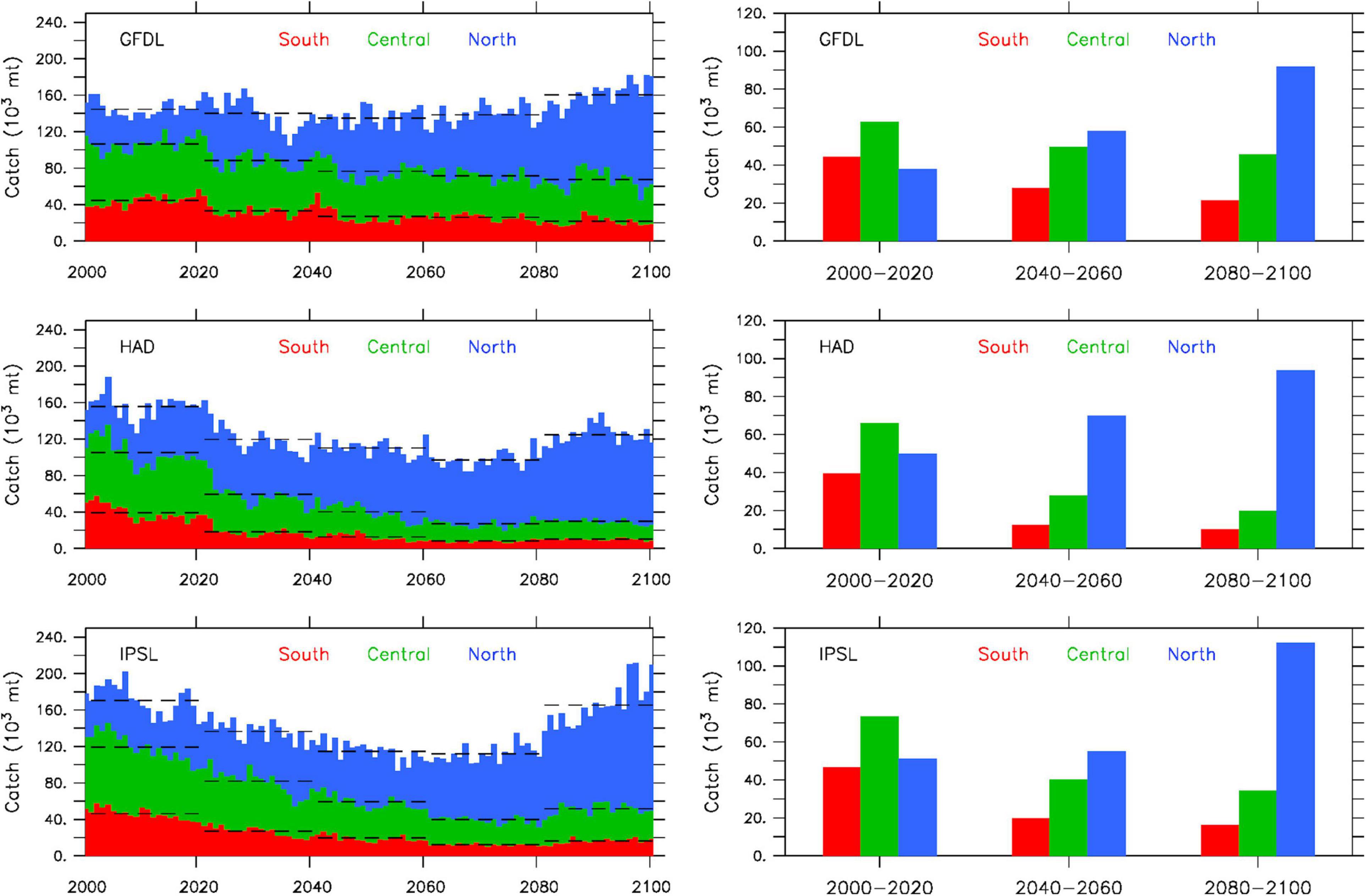
Figure 6. Projected sardine catch (10³ metric tons) for 2000–2100 in southern (red), central (green) and northern (blue) CCS from GFDL (top), Hadley (middle), and IPSL (bottom) solutions. Left: cumulative annual catch (bars) and 20-year averages (dashed lines). Right: 20-year average catch by region during 2000–2020, 2040–2060, 2080–2100. The three subregions correspond to catch originating from Long Beach (southern CCS), Monterey (central CCS) and Astoria + Westport (northern CCS).

Discussion

While the GFDL, Hadley, and IPSL projections each provide a plausible outcome for climate change impacts on sardine biomass and catch in the CCS, it is worth discussing their robustness by considering whether the three downscaled solutions describe statistically identical mean sardine populations. In general, mean abundances are statistically “robust” in the southern and central CCS, but not in the northern CCS where the downscaled solutions predict a large increase in sardine biomass late in the century (Supplementary Figure 3). The results also suggest that the mid-century decline in abundance is confined to the southern and central CCS and robustly predicted across the three projections. Furthermore, the spread of the multi-model ensemble over the entire domain is primarily determined by the model spread associated with “robust” locations in the southern and central CCS, until about 2090 when “non-robust” contributions from the northern CCS become an equally important source of uncertainty. The emergence of statistically different mean abundances underscores the need to understand not only physical and biological sources of uncertainty in the downscaled projections, but also how they may lead to diverging predictions of sardine population dynamics under future climate conditions in the CCS. For instance, the lack of robustness in the northern CCS could be associated with different representations of the latitudinal position and poleward displacement of the North Pacific Current bifurcation in the three ESM solutions (Supplementary Figure 4). It is therefore conceivable that the timing and magnitude of the simulated poleward shift of the sardine population in the IBM is influenced by both anthropogenic warming and basin-scale circulation patterns, with the latter having a stronger impact on the robustness of the projections.

The underlying physical, NPZ, and IBM models used here are obviously not perfect, and the downscaled solutions are only as valid as the assumptions made in the development and implementation of each component. Uncertainty in the physical response of the climate system to greenhouse gases occurs due the emissions scenario used for anthropogenic forcing, differences in the model physics (e.g., resolution, numerical methods, parameterizations), and internal variability (Hawkins and Sutton, 2009). Internal variability, caused by non-linear processes, can lead to substantially different evolutions of the climate system, even on long time scales (Deser et al., 2012a, 2020). Large ensembles of simulations using the same model and scenario but different initial conditions, indicate that natural variability could strongly influence regional trends, especially for dynamic variables such as sea level pressure and upwelling along the United States west coast (Deser et al., 2012b; Brady et al., 2017). While uncertainty in environmental variability is in part inherited from the earth system model solutions, some is generated locally, such as the lack of large amplitude fluctuations in phytoplankton and zooplankton biomass in the NPZ model.

Ignoring density-dependent processes in the sardine IBM represents another source of uncertainty for adequately reproducing the amplitude of historical and future fluctuations in sardine abundance in the CCS. While density-dependent mortality or crowding effects on food limitation may help improve the accuracy of future projections, such additions to the model would significantly increase uncertainty because of alternative ways to combine larval and juvenile processes to mimic the historical spawner-recruit relationship. Furthermore, the historical spawner-recruit relationship for forage species like sardine has its own uncertainties about how it affects population dynamics (Canales et al., 2020), and the sardine relationship for the CCS exhibits high variability, reflects past management actions, and will likely change under future conditions. The possibility of density-dependence in the adult stage must also be considered (Lorenzen, 2008; Andersen et al., 2017). The choice made here was to sacrifice some realism offered by including density-dependence to the benefit of generating clear responses to climate-induced environmental variation and avoiding over-constraining the model solution based on historical conditions (e.g., using density-dependent mortality to match observed spawner-recruit relationships). Hence, the model results should be considered as an exploratory interpretation about how climate change can propagate through the physics and lower trophic levels and affect sardine at the population level.

The degree of agreement between the IBM results and empirical data for the historical period was sufficient to support the analysis of the downscaled projections, as the IBM reproduces periods of relatively higher and lower sardine abundance and recruitment without density-dependent processes (Figure 2). A sensitivity study was also performed to confirm that the spatial and temporal patterns identified in the projections are mostly unaffected by initial sardine population biomass (Supplementary Figure 1). However, the model-data discrepancies in the historical comparisons of spawning stock biomass and recruitment are important to consider when interpreting the implications of the projections. The IBM results should be viewed in a relative sense as the magnitude of change (trend) is likely overestimated, while the amplitude of change (interannual variability) is presumably underestimated.

The projected decadal variability of the multi-model mean sardine population during the 21st century is to some extent consistent with known changes that have occurred during the 20th century between 1930 and 2010 (Schwartzlose et al., 1999), with a 10–20-year decline (1940–1950 vis-à-vis 2020–2040) followed by a low abundance period of ∼40 years (1950–1990 vis-à-vis 2040–2080) and a subsequent 10–20-year increase (1990–2010 vis-à-vis 2080–2100). In the projections, sardine biomass initially declines in response to a decrease in prey availability (i.e., zooplankton concentrations) affecting adult growth and reproductive output. This decline is eventually compensated, and outweighed toward the end of the century, by an increase in recruitment associated with enhanced early life survival (primarily eggs and yolk-sac larvae) caused by increasing near-surface ocean temperatures. Hence, the results underscore the fact that, while thermal tolerance primarily drives the spatial redistribution of sardines in the IBM, interannual and decadal variability in prey availability within a region of suitable habitat still contribute to temporal fluctuations in population abundance.

The overall poleward shift of the sardine population occurring in all three downscaled projections (albeit with different magnitudes and spatial details) is generally consistent with thermal displacements identified for marine heatwaves where intensities of 1–3°C resulted in 500–1,000 km poleward shifts of species distributions in the CCS (Jacox et al., 2020). This range of thermal heatwave intensities closely approximates the projected range of sea surface temperature warming in the CCS by GFDL (∼2°C), Hadley (∼4°C) and IPSL (∼3°C) for the end of the 21st century (Pozo Buil et al., 2021), which led to poleward population displacements in the sardine IBM of ∼500 km for GFDL (36 → 41°N) and ∼800 km for Hadley and IPSL (36 → 44°N) based on regions of peak abundance (Figure 4). The associated shift in sardine catch is also in agreement with the findings of Smith et al. (2021) derived from the same set of downscaled projections but using a different modeling framework based on a species distribution model for sardine and a more realistic fisheries model tuned to historical landings in the CCS. The results presented here suggest a 30–70% decrease in the southern and central CCS and a 50–70% increase in the northern CCS, which is comparable to the 20–50% decrease and up to 50% increase by 2080 projected by Smith et al. (2021). The agreement between the two studies is primarily due to catch being overwhelmingly affected by the projected poleward redistribution of the sardine population, a predominant feature emerging in both the IBM and species distribution model.

The exact magnitude of the thermal displacement sardines will experience in the CCS is dictated by the amount of warming that will occur during the 21st century and the results presented here for the Hadley model under the RCP8.5 scenario likely portray an upper bound. This shift could be dramatically reduced under mitigation scenarios (Morley et al., 2018) and fall closer to the GFDL solution which represents a relatively low rate of warming under RCP8.5 conditions. However, it should also be recognized that “optimal” thermal conditions are identified here based on fixed movement parameters from the IBM and, thus, do not account for phenotypic plasticity, which could reduce temperature constraints and expand habitat suitability. The geographical extent of suitable sardine habitat could also be further constrained by the expected decrease of oxygen levels in the CCS (Bograd et al., 2008; Rykaczewski et al., 2015). The mechanistic structure of the sardine IBM provides a valuable framework to determine the compounding effects that other stressors, such as hypoxia and hypercapnia, may have on metabolic rates and behavioral movement (McNeil and Sasse, 2016; Howard et al., 2020b). Such studies would not only yield a better understanding of the relative impacts of co-drivers associated with the redistribution of pelagic forage fish species in the California Current region under changing climate conditions, but also lead to more constrained estimates of uncertainty sources which, ultimately, determine the value of regional climate projections for marine ecosystem services to coastal communities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. The model output is deposited on Dryad at https://doi.org/10.7291/D1QQ3H.

Author Contributions

JF designed the numerical experiments, analyzed the model results, and wrote the manuscript. MP, MJ, and MA implemented the time-varying delta method and generated the physical downscaled solutions. KR assisted with the implementation of the IBM and fishing fleet models. All authors contributed to manuscript editing.

Funding

This work was supported by a grant from the National Atmospheric and Oceanic Administration (NOAA) CPO Coastal and Climate Applications (COCA) program and the NOAA Fisheries Office of Science and Technology (NA17OAR4310268).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.685241/full#supplementary-material

Footnotes

1. ^ https://www.ncdc.noaa.gov/oisst
2. ^ https://oceancolor.gsfc.nasa.gov/data/seawifs

References

Andersen, K. H., Jacobsen, N. S., Jansen, T., and Beyer, J. E. (2017). When in life does density dependence occur in fish populations?. Fish Fish. 18, 656–667. doi: 10.1111/faf.12195

CrossRef Full Text | Google Scholar

Atlas, R., Hoffman, R. N., Ardizzone, J., Leidner, S. M., Jusem, J. C., Smith, D. K., et al. (2011). A Cross-calibrated, Multiplatform Ocean Surface Wind Velocity Product for Meteorological and Oceanographic Applications. Bull. Am. Meteorol. Soc. 92, 157–174. doi: 10.1175/2010bams2946

CrossRef Full Text | Google Scholar

Bograd, S. J., Castro, C. G., Di Lorenzo, E., Palacios, D. M., Bailey, H., Gilly, W., et al. (2008). Oxygen declines and the shoaling of the hypoxic boundary in the California Current. Geophys. Res. Lett. 35:L12607. doi: 10.1029/2008GL034185

CrossRef Full Text | Google Scholar

Bopp, L., Resplandy, L., Orr, J. C., Doney, S. C., Dunne, J. P., Gehlen, M., et al. (2013). Multiple stressors of ocean ecosystems in the 21st century: projections with CMIP5 models. Biogeosciences 10, 6225–6245. doi: 10.5194/bg-10-6225-2013

CrossRef Full Text | Google Scholar

Brady, R. X., Alexander, M. A., Lovenduski, N. S., and Rykaczewski, R. R. (2017). Emergent anthropogenic trends in California Current upwelling. Geophys. Res. Lett. 44, 5044–5052. doi: 10.1002/2017gl072945

CrossRef Full Text | Google Scholar

Canales, T. M., Delius, G. W., and Law, R. (2020). Regulation of fish stocks without stock–recruitment relationships: the case of small pelagic fish. Fish Fish. 21, 857–871. doi: 10.1111/faf.12465

CrossRef Full Text | Google Scholar

Carton, J. A., and Giese, B. S. (2008). A Reanalysis of Ocean Climate Using Simple Ocean Data Assimilation (SODA). Mon. Weather Rev. 136, 2999–3017. doi: 10.1175/2007mwr1978

CrossRef Full Text | Google Scholar

Chavez, F. P., Ryan, J., Lluch-Cota, S. E., and Òiquen, M. (2003). From anchovies to sardines and back: multidecadal change in the Pacific Ocean. Science 299, 217–221. doi: 10.1126/science.1075880

PubMed Abstract | CrossRef Full Text | Google Scholar

Checkley, D. M. Jr., Asch, R. G., and Rykaczewski, R. R. (2017). Climate, anchovy, and sardine. Annu. Rev. Mar. Sci. 9, 469–493. doi: 10.1146/annurev-marine-122414-033819

PubMed Abstract | CrossRef Full Text | Google Scholar

Checkley, D. M., and Barth, J. A. (2009). Patterns and processes in the California Current System. Prog. Oceanogr. 83, 49–64. doi: 10.1016/j.pocean.2009.07.028

CrossRef Full Text | Google Scholar

Cheung, W. W. L., Brodeur, R. D., Okey, T. A., and Pauly, D. (2015). Projecting future changes in distributions of pelagic fish species of Northeast Pacific shelf seas. Prog. Oceanogr. 130, 19–31. doi: 10.1016/j.pocean.2014.09.003

CrossRef Full Text | Google Scholar

Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., et al. (2011). Development and evaluation of an Earth-System model – HadGEM2. Geosci. Model Dev. 4, 1051–1075. doi: 10.5194/gmd-4-1051-2011

CrossRef Full Text | Google Scholar

Conkright, M. E., and Boyer, T. P. (2002). World Ocean Atlas 2001: Objective Analyses, Data Statistics, and Figures, CD-ROM Documentation. Silver Spring, MD: National Oceanographic Data Center.

Google Scholar

Cury, P., Bakun, A., Crawford, R. J. M., Jarre-Teichmann, A., Quinones, R. A., Shannon, L. J., et al. (2000). Small pelagics in upwelling systems: patterns of interaction and structural changes in “wasp-waist” ecosystems. ICES J. Mar. Sci. 57, 603–618. doi: 10.1006/jmsc.2000.0712

CrossRef Full Text | Google Scholar

Deser, C., Knutti, R., Solomon, S., and Phillips, A. S. (2012a). Communication of the role of natural variability in future North American climate. Nat. Clim. Change 2, 775–779. doi: 10.1038/nclimate1562

CrossRef Full Text | Google Scholar

Deser, C., Phillips, A., Bourdette, V., and Teng, H. (2012b). Uncertainty in climate change projections: the role of internal variability. Clim. Dyn. 38, 527–546. doi: 10.1007/s00382-010-0977-x

CrossRef Full Text | Google Scholar

Deser, C., Lehner, F., Rodgers, K. B., Ault, T., Delworth, T. L., DiNezio, P. N., et al. (2020). Insights from earth system model initial-condition large ensembles and future prospects. Nat. Clim. Change 10, 277–286. doi: 10.1038/s41558-020-0731-2

CrossRef Full Text | Google Scholar

Di Lorenzo, E., Schneider, N., Cobb, K. M., Chhak, K., Franks, P. J. S., Miller, A. J., et al. (2008). North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 35:L08607. doi: 10.1029/2007GL032838

CrossRef Full Text | Google Scholar

Dufresne, J. L., Foujols, M. A., Denvil, S., Caubel, A., Marti, O., Aumont, O., et al. (2013). Climate change projections using the IPSL-CM5 Earth System Model: from CMIP3 to CMIP5. Clim. Dyn. 40, 2123–2165. doi: 10.1007/s00382-012-1636-1

CrossRef Full Text | Google Scholar

Dunne, J. P., John, J. G., Adcroft, A. J., Griffies, S. M., Hallberg, R. W., Shevliakova, E., et al. (2012). GFDL’s ESM2 Global Coupled Climate–Carbon Earth System Models. Part I: physical Formulation and Baseline Simulation Characteristics. J. Clim. 25, 6646–6665. doi: 10.1175/jcli-d-11-00560.1

CrossRef Full Text | Google Scholar

Eales, J., and Wilen, J. E. (1986). An examination of fishing location choice in the pink shrimp fishery. Mar. Resour. Econ. 4, 331–351. doi: 10.1086/mre.2.4.42628909

CrossRef Full Text | Google Scholar

Echevin, V., Goubanova, K., Belmadani, A., and Dewitte, B. (2012). Sensitivity of the Humboldt Current system to global warming: a downscaling experiment of the IPSL-CM4 model. Clim. Dyn. 38, 761–774. doi: 10.1007/s00382-011-1085-2

CrossRef Full Text | Google Scholar

Emmett, R. L., Brodeur, R. D., Miller, T. W., Pool, S. S., Bentley, P. J., Krutzikowsky, G. K., et al. (2005). Pacific sardine (Sardinops sagax) abundance, distribution, and ecological relationships in the Pacific Northwest. CalCOFI Rep. 46:122.

Google Scholar

Fiechter, J., Edwards, C. A., and Moore, A. M. (2018). Wind, Circulation, and Topographic Effects on Alongshore Phytoplankton Variability in the California Current. Geophys. Res. Lett. 45, 3238–3245. doi: 10.1002/2017gl076839

CrossRef Full Text | Google Scholar

Fiechter, J., Rose, K. A., Curchitser, E. N., and Hedstrom, K. (2015). The role of environmental controls in determining sardine and anchovy population cycles in the California Current: analysis of an end-to-end model. Prog. Oceanogr. 138, 381–398. doi: 10.1016/j.pocean.2014.11.013

CrossRef Full Text | Google Scholar

Fiechter, J., Santora, J. A., Chavez, F., Northcott, D., and Messié, M. (2020). Krill Hotspot Formation and Phenology in the California Current Ecosystem. Geophys. Res. Lett. 47:e2020GL088039. doi: 10.1029/2020gl088039

PubMed Abstract | CrossRef Full Text | Google Scholar

Fréon, P., Curry, P., Shannon, L., and Roy, C. (2005). Sustainable exploitation of small pelagic fish stocks challenged by environmental and ecosystem changes: a review. Bull. Mar. Sci. 76, 385–462.

Google Scholar

Frölicher, T. L., Rodgers, K. B., Stock, C. A., and Cheung, W. W. L. (2016). Sources of uncertainties in 21st century projections of potential ocean ecosystem stressors. Global Biogeochem. Cycles 30, 1224–1243. doi: 10.1002/2015gb005338

CrossRef Full Text | Google Scholar

Haidvogel, D. B., Arango, H., Budgell, W. P., Cornuelle, B. D., Curchitser, E., Di Lorenzo, E., et al. (2008). Ocean forecasting in terrain-following coordinates: formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 227, 3595–3624. doi: 10.1016/j.jcp.2007.06.016

CrossRef Full Text | Google Scholar

Hawkins, E., and Sutton, R. (2009). The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meterol. Soc. 90, 1095–1107. doi: 10.1175/2009bams2607.1

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hill, K. T., Lo, N. C. H., Macewicz, B. J., Crone, P. R., and Felix-Uraga, R. (2010). Assessment of the Pacific sardine resource in 2009 for U.S. management in 2010. NOAA-TM-NMFS-SWFSC-4452. California: NOAA Southwest Fisheries Science Center.

Google Scholar

Howard, E. M., Frenzel, H., Kessouri, F., Renault, L., Bianchi, D., McWilliams, J. C., et al. (2020a). Attributing Causes of Future Climate Change in the California Current System with Multimodel Downscaling. Global Biogeochem. Cycles 34:e2020GB006646. doi: 10.1029/2020gb006646

CrossRef Full Text | Google Scholar

Howard, E. M., Penn, J. L., Frenzel, H., Seibel, B. A., Bianchi, D., Renault, L., et al. (2020b). Climate-driven aerobic habitat loss in the California Current System. Sci. Adv. 6:eaay3188. doi: 10.1126/sciadv.aay3188

PubMed Abstract | CrossRef Full Text | Google Scholar

Humston, R., Olson, D. B., and Ault, J. S. (2004). Behavioral assumptions in models of fish movement and their influence on population dynamics. Trans. Am. Fish. Soc. 133, 1304–1328. doi: 10.1577/t03-040.1

CrossRef Full Text | Google Scholar

Jacox, M. G., Alexander, M. A., Bograd, S. J., and Scott, J. D. (2020). Thermal displacement by marine heatwaves. Nature 584, 82–86. doi: 10.1038/s41586-020-2534-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Kishi, M. J., Kashiwai, M., Ware, D. M., Megrey, B. A., Eslinger, D. L., Werner, F. E., et al. (2007). NEMURO - a lower trophic level model for the North Pacific marine ecosystem. Ecol. Modell. 202, 12–25. doi: 10.1016/j.ecolmodel.2006.08.021

CrossRef Full Text | Google Scholar

Lindegren, M., Checkley, D. M., Rouyer, T., MacCall, A. D., and Stenseth, N. C. (2013). Climate, fishing, and fluctuations of sardine and anchovy in the California Current. Proc. Natl. Acad. Sci. U. S. A.110, 13672–13677. doi: 10.1073/pnas.1305733110

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorenzen, K. (2008). Fish population regulation beyond “stock and recruitment”: the role of density-dependent growth in the recruited stock. Bull. Mar. Sci. 83, 181–196.

Google Scholar

Lynn, R. J., and Bograd, S. J. (2002). Dynamic evolution of the 1997-1999 El-Niño - La-Niña cycle in the southern California Current System. Prog. Oceanogr. 54, 59–75.

Google Scholar

Machu, E., Goubanova, K., Le, Vu, B., Gutknecht, E., and Garçon, V. (2015). Downscaling biogeochemistry in the Benguela eastern boundary current. Ocean Model. 90, 57–71. doi: 10.1016/j.ocemod.2015.01.003

CrossRef Full Text | Google Scholar

Mantua, N. J., Hare, S. R., Zhang, Y., Wallace, J. M., and Francis, R. C. (1997). A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 78, 1069–1079. doi: 10.1175/1520-0477(1997)078<1069:apicow>2.0.co;2

CrossRef Full Text | Google Scholar

McNeil, B., and Sasse, T. (2016). Future ocean hypercapnia driven by anthropogenic amplification of the natural CO₂ cycle. Nature 529, 383–386. doi: 10.1038/nature16156

PubMed Abstract | CrossRef Full Text | Google Scholar

Morley, J. W., Selden, R. L., Latour, R. J., Frölicher, T. L., Seagraves, R. J., and Pinsky, M. L. (2018). Projecting shifts in thermal habitat for 686 species on the North American continental shelf. PLoS One 13:e0196127. doi: 10.1371/journal.pone.0196127

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishikawa, H., Curchitser, E. N., Fiechter, J., Rose, K. A., and Hedstrom, K. (2019). Using a climate-to-fishery model to simulate the influence of the 1976–1977 regime shift on anchovy and sardine in the California Current System. Prog. Earth Planet. Sci. 6, 1–20.

Google Scholar

Pacific Fishery Management Council (PFMC) (2011). Status of the Pacific Coast Coastal Pelagic Species Fishery and Recommended Acceptable Biological Catches. Stock Assessment and Fishery Evaluation - 2011. Portland: Pacific Fishery Management Council.

Google Scholar

Peck, M. A., Alheit, J., Bertrand, A. I, Catalán, A., Garrido, S., Moyano, M., et al. (2021). Small pelagic fish in the new millennium: a bottom-up view of global research effort. Prog. Oceanogr. 191:102494. doi: 10.1016/j.pocean.2020.102494

CrossRef Full Text | Google Scholar

Peterson, W. T., and Schwing, F. B. (2003). A new climate regime in northeast pacific ecosystems. Geophys. Res. Lett. 30:1896. doi: 10.1029/2003GL017528

CrossRef Full Text | Google Scholar

Politikos, D. V., Curchitser, E. N., Rose, K. A., Checkley, D. M. Jr., and Fiechter, J. (2018). Climate variability and sardine recruitment in the California Current: a mechanistic analysis of an ecosystem model. Fish. Oceanogr. 27, 602–622. doi: 10.1111/fog.12381

CrossRef Full Text | Google Scholar

Pozo Buil, M., Jacox, M., Fiechter, J., Alexander, M. A., Bograd, S. J., Curchister, E. N., et al. (2021). A dynamically downscaled ensemble of future projections for the California Current System. Front. Mar. Sci. 8:612874. doi: 10.3389/fmars.2021.612874

CrossRef Full Text | Google Scholar

Rose, K. A., Cowan, J. H. Jr., Winemiller, K. O., Myers, R. A., and Hilborn, R. (2001). Compensatory density dependence in fish populations: importance, controversy, understanding and prognosis. Fish Fish. 2, 293–327. doi: 10.1046/j.1467-2960.2001.00056.x

CrossRef Full Text | Google Scholar

Rose, K. A., Fiechter, J., Curchitser, E. N., Hedstrom, K., Bernal, M., Creekmore, S., et al. (2015). Demonstration of a fully-coupled end-to-end model for small pelagic fish using sardine and anchovy in the California Current. Prog. Oceanogr. 138, 348–380.

Google Scholar

Rykaczewski, R. R., and Checkley, D. M. Jr. (2008). Influence of ocean winds on the pelagic ecosystem in upwelling regions. Proc. Natl. Acad. Sci. U. S. A. 105, 1965–1970. doi: 10.1073/pnas.0711777105

PubMed Abstract | CrossRef Full Text | Google Scholar

Rykaczewski, R. R., Dunne, J. P., Sydeman, W. J., García-Reyes, M., Black, B. A., and Bograd, S. J. (2015). Poleward displacement of coastal upwelling-favorable winds in the ocean’s eastern boundary currents through the 21st century. Geophys. Res. Lett. 42, 6424–6431. doi: 10.1002/2015gl064694

CrossRef Full Text | Google Scholar

Sánchez-Garrido, J. C., Werner, F. E., Fiechter, J., Ramos, A., Curchitser, E., Rose, K. A., et al. (2018). Decadal-scale variability of sardine and anchovy simulated with an end-to-end coupled model of the Canary Current ecosystem. Prog. Oceanogr. 171, 212–230. doi: 10.1016/j.pocean.2018.12.009

CrossRef Full Text | Google Scholar

Sánchez-Garrido, J. C., Fiechter, J., Rose, K. A., Werner, F. E., and Curchitser, E. N. (2021). Dynamics of anchovy and sardine populations in the Canary Current off NW Africa: responses to environmental and climate forcing in a climate-to-fish ecosystem model. Fish. Oceanogr. 30, 232–252. doi: 10.1111/fog.12516

CrossRef Full Text | Google Scholar

Scheffer, M., Baveco, J. M., DeAngelis, D. L., Rose, K. A., and van Nes, E. H. (1995). Super-individuals a simple solution for modelling large populations on an individual basis. Ecol. Model. 80, 161–170. doi: 10.1016/0304-3800(94)00055-m

CrossRef Full Text | Google Scholar

Schwartzlose, R. A., Alheit, J., Bakun, A., Baumgartne, T. R., Cloete, R., Crawford, R. J. M., et al. (1999). Worldwide large-scale fluctuations of sardine and anchovy populations. Afr. J. Mar. Sci. 21, 289–347. doi: 10.2989/025776199784125962

PubMed Abstract | CrossRef Full Text | Google Scholar

Shchepetkin, A. F., and McWilliams, J. C. (2005). The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002

CrossRef Full Text | Google Scholar

Small, R. J., Curchitser, E., Hedstrom, K., Kauffman, B., and Large, W. G. (2015). The Benguela Upwelling System: quantifying the Sensitivity to Resolution and Coastal Wind Representation in a Global Climate Model^∗. J. Clim. 28, 9409–9432. doi: 10.1175/jcli-d-15-0192.1

CrossRef Full Text | Google Scholar

Smith, J. A., Muhling, B., Sweeney, J., Tommasi, D., Pozo Buil, M., Fiechter, J., et al. (2021). The potential impact of a shifting Pacific sardine distribution on US West Coast landings. Fish. Oceanogr. 30, 437–454. doi: 10.1111/fog.12529

CrossRef Full Text | Google Scholar

Stock, C. A., Alexander, M. A., Bond, N. A., Brander, K. M., Cheung, W. W. L., Curchitser, E. N., et al. (2011). On the use of IPCC class models to assess the impact of climate on Living Marine Resources. Prog. Oceanogr. 88, 1–27. doi: 10.1016/j.pocean.2010.09.001

CrossRef Full Text | Google Scholar

Watkins, K. S., and Rose, K. A. (2013). Evaluating the performance of individual-based animal movement models in novel environments. Ecol. Model. 250, 214–234. doi: 10.1016/j.ecolmodel.2012.11.011

CrossRef Full Text | Google Scholar

Wolf, P. A. (1992). Recovery of the Pacific sardine and the California sardine fishery. CalCOFI Rep. 33, 76–86.

Google Scholar

Zwolinski, J. P., Emmett, R. L., and Demer, D. A. (2011). Predicting habitat to optimize sampling of Pacific sardine (Sardinops sagax). ICES J. Mar. Sci. 68, 867–879. doi: 10.1093/icesjms/fsr038

CrossRef Full Text | Google Scholar