Multidecadal Sea Level Variability in the Baltic Sea and Its Impact on Acceleration Estimations

Introduction

Sea level rise as a result of climate change is one of the significant environmental threats which requires a deep understanding not only globally but also on regional scales. This will lead to having more realistic future scenarios and, thus, helping decision-makers in planning a safer future for coastal regions (Dangendorf et al., 2014; Frederikse et al., 2016; Prandi et al., 2021). Although, because of the crustal land uplift, a substantial part of the Baltic Sea coast is safe from future sea level rise, understanding the mechanism of sea level variability in the region is important since several reliable sea level measurements stretching back to the 18th century are located in this region. To be able to use these measurements in global-scale analyses, the geophysical and climate-related processes need to be understood to separate the global effects from regional drivers. This is the reason that there have been numerous studies addressing these variations in the Baltic Sea (Hünicke and Zorita, 2008; Hünicke et al., 2015).

The Baltic Sea is a semi-enclosed basin, under the constant impact of external and internal forcings (Hünicke et al., 2017). Water discharge of the surrounding catchments, precipitation, and water inflow/outflow from the North Sea are the external variability factors. On the other hand, air pressure, wind, and density variations account for the internal forcing. Freshwater input acts as internal and external forcings as it changes both the volume and salinity of the water in the basin. The classification of contributors to external and internal forcings are according to Samuelsson and Stigebrandt (1996) that shows the external forces are responsible for 50–80% of sea level variations in the Baltic Sea for periods longer than 1 month, from 1977 to 1987. In the other two complementary studies (Kauker and Meier, 2003; Meier and Kauker, 2003), half of decadal sea salinity variation in the basin are attributed to freshwater inflow in the twentieth century. Additionally, sea level pressure (SLP) is found as a substantial factor on this time scale. Most recently, Gräwe et al. (2019) conducted thorough analyses on decomposing the role of different drivers in Baltic Sea level rise for the period 1950–2015 using different reanalyzes and in situ measurements. They found that 75% of the sea level rise in the basin is due to the water inflow from the North Sea.

High energy North Atlantic climate has a substantial influence on sea level variability of the Baltic Sea and consequently, it has been subject to different studies. In this respect, North Atlantic Oscillation (NAO) is a major driving force for the Baltic Sea on seasonal to decadal time scales (Andersson, 2002; Yan et al., 2004; Hünicke and Zorita, 2006; Hünicke et al., 2015). Gräwe et al. (2019) reasoned that NAO impacts the Baltic Sea by weakening or strengthening westerlies. This, in turn, leads to variations in inflow/outflow rate from/to the North Sea. Even though this is in line with the findings of Dangendorf et al. (2014) for the North Sea, they expressed a paucity of a thorough investigation on this topic. Other studies tie NAO to sea level variability in the Baltic Sea by thermal expansion due to temperature increase (Hünicke and Zorita, 2006; Dangendorf et al., 2012) or freshwater input by rising the river discharge to the basin and also direct contribution because of higher precipitation (Hünicke and Zorita, 2006, 2008; Lehmann et al., 2011).

Karabil et al. (2017) investigated the decadal variability of the Baltic Sea by analyzing a wide range of climate data (i.e., SLP, air temperature, precipitation, and climate indices) and concluded that the response of sea level to these factors is not homogeneous in the basin where they weaken toward the southern coasts. Pajak and Blaszczak-Bak (2019) reflected the asymmetry in terms of linear change using altimetry data between 1993 and 2017. Similar asymmetric variabilities were found by Barbosa (2008) on a centennial time scale. Karabil et al. (2018) introduced a new climate index to the basin, which represents the atmospheric circulation better than NAO. Passaro et al. (2015) found that the main driver for the annual cycle of sea level variations around the Baltic coasts is wind stress. They also found that steric parameters influence the inner basin variabilities. Passaro et al. (2021) investigated contemporary sea level variations, local drivers, and spatial patterns in the Baltic Sea. They optimized the satellite altimetry measurements for the basin to minimize the impact of rugged coastlines and sea ice cover in wintertime. They also found that wind is a major driver for the gradient of the sea level rise in the altimetry era.

Pajak and Kowalczyk (2019) used tide gauges along the Polish coast and satellite altimetry data to analyze the seasonal variations and reported a substantial agreement between these two datasets in this respect. In another study on the seasonal scale, Hünicke and Zorita (2008) investigated the annual signal changes in the basin and reported centennial variations in this signal. They speculated that precipitation drives these low-frequency variations. Xu et al. (2015) reported a fall in the correlation between the wintertime NAO and sea level variation in the last decade at the time of the study using altimetry data. Hünicke and Zorita (2008) showed that precipitation and temperature variations contribute to sea level changes in the Baltic Sea seasonally, but they are not as substantial as SLP.

The Baltic Sea basin is heterogeneously subject to postglacial rebound resulting from the last glacial age. The range of crustal uplift ranges from −1 to +12 mm/year in the basin although this range changes slightly in different models. This crustal movement requires accurate modeling to enable the use of sea levels recorded in the basin in a geocentric system. In addition to global glacial isostatic adjustment (GIA) models (e.g., Steffen and Wu, 2011; Roy and Peltier, 2018), the Nordic Commission of Geodesy (NKG) has released a semi-empirical land uplift model in which a GIA model is combined with geodetic observations (Vestøl et al., 2019). Madsen et al. (2019) used this model to reconstruct sea level for the Baltic Sea, and they found an average of 1.3 ± 0.3 mm/year sea level rise in the basin for the twentienth century. Richter et al. (2012) estimated a similar trend for the same period but used GNSS observations to correct the land uplift signal. GNSS-derived land uplift might not be enough to completely explain the GIA effect since it does not take the gravitational attraction of the accumulated mass on sea level into account (Tamisiea and Mitrovica, 2011). In the Baltic Sea, however, the ratio of sea level rise to uplift (because of geoid change) is negligible, 1–20. Thus, this ratio does not affect the agreement between the two aforementioned studies. Gräwe et al. (2019) concluded a 2.08 ± 0.49 mm/year rise for the period of 1950–2015.

There were also attempts to determine a possible acceleration in the sea level rise of the basin but their outcome are irreconcilable. Woodworth (1990) estimated decelerations for the majority of tide gauges located on the Baltic coasts using varying lengths of tide gauges from 1870 to 1981 [See Table 1(a) of the study for further information]. Donner et al. (2012) reported that there are decadal-scale accelerations and decelerations, using tide gauge data of varying lengths (1849–2006) but did not draw any solid conclusion. Stramska and Chudziak (2013) estimated the acceleration in the altimetry era and concluded that there is no statistically significant acceleration in the basin. Spada et al. (2014), on the other hand, reported a secular acceleration in the Baltic Sea and related it to isostatic adjustment. Hünicke and Zorita (2016) carried out a thorough investigation of the acceleration determination in the basin using multiple tide gauges and methods from 1900–2012. They found that although all-station-average-record yielded “almost statistically significant” acceleration, the individual estimations were statistically insignificant but positive for most of the tide gauges.

All aforementioned studies provide valuable information about the Baltic Sea level variability and the role of contributors on these variations in different periods. The analyses of all these studies were conducted on seasonal to decadal time scales. In contrast, the main focus of this study is the multidecadal variability of the Baltic Sea using tide gauge data and altimetry data. Since the length of the datasets may not lead to a reliable outcome when spectral methods are used, most of the analyses are carried out by comparing linear trends fitted to the multidecadal periods. As such, we first use three decades of altimetry data to evaluate the consistency between VLM-corrected tide gauge records and VLM-free satellite data by comparing sea level trends. The role of NAO on sea level rise and variation on the multidecadal time scale is also investigated. Furthermore, we analyze the multidecadal sea level variations in the tide gauge data and show that the global warming hiatus can be seen in the basin between the 1950s and 1970s. The link between this hiatus and sea level acceleration estimation is discussed in the last section of the study.

Data

Five datasets are used in this study, and they are briefly explained in this section.

Altimetry

Altimetry data are acquired from Radar Altimetry Database System (RADS; Scharroo et al., 2013) with standard geophysical and range corrections applied on them, except for wet tropospheric correction. The dataset is comprised of collinear measurements of Topex/Poseidon, Jason-1, Jason-2, and Jason-3 missions spanning the period from 1993 to 2020. The collinear data are clustered according to the equator pass time of the satellite for each pass and, thus, provide ready-to-use sea level anomaly (SLA) time series. The onboard radiometer correction for wet tropospheric correction is replaced by the model correction provided by European Centre for Medium-range Weather Forecasts (Xu et al., 2015). The poor performance of the radiometer is due to the large footprint of the instrument and hence land contamination (Brown, 2010). Although this replacement increases the number of altimetry measurements, it does not improve the number of time series which are long enough to use in the analyses. Time series with at least 75% of valid measurements are involved in the analyses; out of 1,286 time series in the basin, only 311 fulfill this condition (Figure 1). In addition to being relatively shallow, the basin has several islands and narrow subbasins which increase the land contamination on the backscattered waveforms of altimetry (Deng and Featherstone, 2006).

FIGURE 1

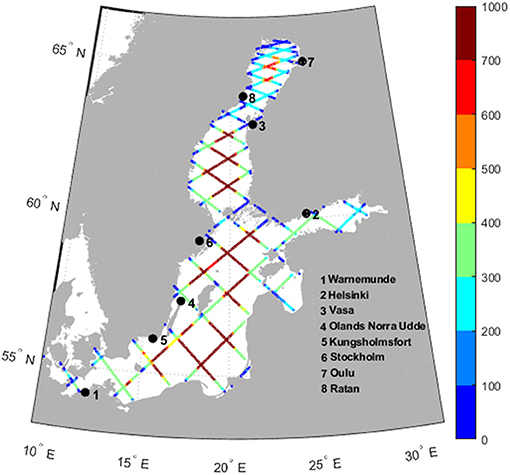
Figure 1. The collinear data of Topex/Poseidon and follow-on missions for the Baltic Sea. The color bar reflects the number of valid measurements in each of the bins. Only one-third of the bins are suitable to be used in trend analyses when they are constrained to have at least 75% of measurements (700–1000 on the color bar). The locations of the tide gauge stations are also marked on the map.

The main reason for the absence of any valid time series above 63° in latitude is the presence of sea ice in wintertime (Omstedt et al., 2004). This is flagged in the surface class of each measurement by RADS and these measurements are discarded from the dataset. Kudryavtseva and Soomere (2016, 2017) reported that in RADS datasets the surface flag of an altimetry measurement is set to sea ice when the ice concentration is 50% and showed that this threshold is suitable for the Baltic Sea. The same studies also recommended discarding measurements with proximities of closer than 0.2° to the nearest coast. The dataset used in this study follows this condition as measurements closer than 20 km to the nearest coast are excluded.

Radar Altimetry Database System uses Dynamic Atmospheric Correction (DAC) as an alternative to Inverted Barometer (IB) correction because it represents the atmospheric impact better than IB, which is a statistic model (Scharroo et al., 2016). To compare the altimetry measurements to the tide gauge records, this correction is only added back to the SLA data when the role of IB on trend estimation is analyzed in Altimetry Era section. The altimetry data in this study are also corrected for the geoid change of the GIA effect (further information about the GIA effect on geoid is provided in Land Uplift Model Section).

Tide Gauge

Monthly tide gauge records are provided by Permanent Service for Mean Sea Level (PSMSL; Holgate et al., 2012). One of the objectives of this study is detecting low-frequency variations in the Baltic Sea, which are generally of low amplitudes. Detection of these signals requires a certain level of accuracy in the observed data. For this reason, only datasets of the twentieth century are included in the dataset. Moreover, tide gauges with long gaps (longer than 2 years) are excluded. These criteria narrow down the number of tide gauges to eight (Figure 1 and Supplementary Table 1). Tidal modeling is not applied on the tide gauges records as these variations are almost negligible due to (1) the effect of the Danish Straits (Gräwe et al., 2019) and (2) the basin size, which is not considerably big to develop substantial tidal effects.

Land Uplift Model

To transform the relative sea level measurements to a geocentric system, an uplift model is required for the Baltic Sea because of the substantial rebound due to the last deglaciation. Following previous studies (Gräwe et al., 2019; Madsen et al., 2019), the uplift model developed by NKG is adopted to apply the crustal uplift correction. This model is released in two versions, NKG2016LU_abs and NKG2016LU_lev (Vestøl et al., 2019). For the latter version, the geoid variations due to GIA is not considered. However, the difference between the two models does not exceed 10% which is slightly higher than the previous studies estimated the geoid to land variation rate to be 5% (Tamisiea and Mitrovica, 2011). Tide gauge measurements are not deployed in developing this model (c.f., Hill et al., 2010) so that it can be used to correct the tide gauge measurements as an independent model. The model geographically extends from 0° to 50° in longitude and 49°-75° in latitude. The maximum uplift in the region is 9.6 mm/year, close to the Ratan tide gauge station. GIA renders uplift on all the tide gauges used in this study except for Warnemünde, which is located on the bulge and experiences a slight depression. The uncertainty of the estimated uplift varies along with the geographic extent of the model depending on the availability of geodetic measurements. However, along the Baltic coasts, it ranges from 0.2 to 0.3 mm/year (Vestøl et al., 2019). This study uses the NKG2016LU_abs version to correct the vertical land motion at the tide gauge locations.

Sea Level Pressure

Sea level pressure is one of the main drivers of sea level in the Baltic Sea and it is governed by NAO, particularly during wintertime. For SLP, the results of twentieth-century Reanalysis Project Version 3 (Compo et al., 2011; Giese et al., 2016; Slivinski et al., 2019), provided by the National Oceanic and Atmospheric Administration, is used. The dataset covers the whole twentieth century but extends only until 2016. Therefore, the dataset is augmented with reanalysis data of the National Centers for Environmental Prediction and the National Center for Atmospheric Research (Kalnay et al., 1996) to cover the gap between 2016 and 2020. To estimate the inverted barometric effect of SLP, the following equation is used (Ponte, 2006; Piecuch et al., 2016):

$\begin{array}{ll}{\eta }_{ib}=\frac{p_a-{\overline{p}}_a}{\rho g}& (1)\end{array}$

where p_a is the SLP in tide gauge location, ${\overline{p}}_a$ is mean global SLP over oceans, ρ = 1029 kg/m³ reference ocean water density, and g = 9.81 m/s² is the gravitational acceleration. Mean global SLP is estimated by masking the land in the models. It should be noted that this equation is based on the fact that the sea surface follows the variations in SLP. This is not completely valid for the Baltic Sea due to the impact of the Danish Straits which confines the water exchange with the North Sea. Hence, the SLP and the SLA are not synchronized. On the other hand, due to the gradient in the water density, the sea level in the north of the basin stands 30–35 cm higher than that of the Danish Straits. Nevertheless, this does not affect the SLA variations (Ekman and Mäkinen, 1996).

North Atlantic Oscillation

North Atlantic Oscillation is provided by the Climate Data Guide initiative, which is a project led by the University Corporation for Atmospheric Research and National Corporation for Atmospheric Research (Schneider et al., 2013). NAO is an atmospheric pattern that influences the sea level variation in the basin by intensifying the westerlies when it is positive and, thus, causes higher water inflow from the North Sea (Hurrell and Deser, 2009). NAO is estimated in two forms, station-based and principal component-based, and covers the period of 1899–2020. The latter form is used in this study as it is less prone to measurement noise than the former one and it represents the spatial pattern better.

Results

Sea level rise is analyzed in different multidecadal periods. It starts with the altimetry era and comparing the sea level rise estimated by satellite altimetry and tide gauge data. The impact of NAO on sea level rise on multidecadal periods is investigated. Multidecadal sea level variations since the beginning of the twentieth century and how they influence the sea level acceleration estimations are also scrutinized.

Altimetry Era

Satellite altimetry enabled the estimation of the absolute sea level rise since 1993 in nearly global coverage. This technique is more valuable in regions with substantial crustal motions such as the Baltic Sea. To this end, the sea level trend in the basin is estimated by a regression model and a proper noise model (Figure 2).

$\begin{array}{ll}\begin{array}{}\eta (t)=a_0+a_{1}t+{\displaystyle \sum _{i=1}^2[b_i\sin ({\omega }_{i}t)+c_i\cos ({\omega }_{i}t)}]+\epsilon \end{array}& (2)\end{array}$

where η is dynamic sea level, a, b, and c are coefficients to be estimated, t is time, ω_i is the frequency corresponding to annual and semiannual signals, and ε is the noise model. The noise model is autoregressive fractionally integrated with order one, which is also denoted as ARFIMA (1, d, 0) in which d and 0 show fractional memory parameter and order of moving average, respectively. To decide on a proper noise model, five noise models are tested and scored according to the Akaike information criterion (AIC) and Bayesian information criterion (BIC). ARFIMA (1, d, 0) was identified as the most suitable noise model for the majority of the time series. Details about the noise model analyses can be found in Supplementary Materials.

FIGURE 2

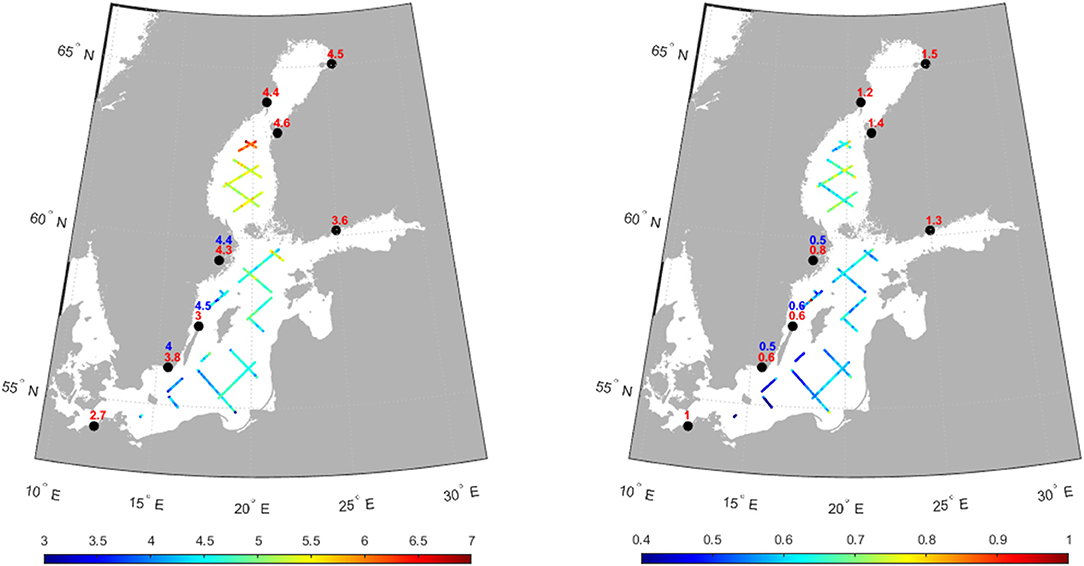
Figure 2. Left panel: the sea level trend map (mm/year) estimate by Equation (2) and right panel: corresponding uncertainty map. The values in red are estimated by tide gauge data (from 1993–2020) and the blue ones are those estimated by altimetry data within a 2° × 2° box of the respective tide gauge stations. The agreement between altimetry and tide gauge is significantly high except for one of the stations located on an island.

Sea level trend for the same period is also estimated in the tide gauges after applying the IB and land uplift corrections. The mean sea level rise in the region estimated by altimetry and tide gauge data are 4.8 ± 0.7 and 3.8 ± 1 mm/year, respectively. The difference between the mean trends can be attributed to the heterogeneous distribution of both datasets throughout the area and the underestimation of the uplift in all or some of the stations. There is a north-south pattern in the estimated trend in which the rise in the Gulf of Bothnia is 1.5 times larger than in southern coasts (the Baltic Proper). The uncertainty map (Figure 2, right panel) also follows the north-south pattern. The estimated sea level rise in the altimetry era in the Baltic Sea, 4.8 mm/year, is 1.5 times higher than that of estimated in global scale, ~3.2 ± 0.3 mm/year (Ablain et al., 2019; Cazenave et al., 2019).

One of the geodetic applications of satellite altimetry observations is the estimation of crustal land uplift by comparing them to tide gauges (e.g., Nerem and Mitchum, 2002; Kuo et al., 2004, 2008). The results of the tide gauges are compared with the altimetry wherever there are altimetry measurements inside the 2° × 2° box around the station. This narrows down the number of tide gauges to three. Considering the error budgets of observations and land uplift model, the agreement between the trends estimated by altimetry and tide gauges are comparatively high in two of these stations, Stockholm and Kungsholmsfort. Passaro et al. (2021) reached the same results for the trend difference between altimetry and tide gauge although a greater set of tide gauge and altimetry pairs was deployed. However, the estimated trend in Ölands Norra Udde station is not in line with the results of the other two stations with a 1.5 mm/year discrepancy. This does not necessarily mean that the uplift model is inaccurate as the sea level variations in island stations can be different from those on the mainland due to hydrodynamic effects.

To investigate the effect of SLP on the sea level rise in the altimetry era, the trend map in Figure 2 is reestimated by adding DAC to the altimetry observations (results are not shown). Although the variability of DAC and IB corrections is not exactly coherent in terms of the correlation coefficient, their contributions to the estimated trend are analogous. Removing these corrections does not change the overall outcome; however, an approximately constant fall of −0.2 mm/year can be seen in both altimetry and tide gauge results. The effect of SLP, therefore, is <10% and it slightly decreases the sea level rise in the region in the altimetry era.

NAO Related Sea Level Variation and Rise

North Atlantic Oscillation (NAO) is a climate mode that impacts the sea level variability in the North Atlantic by having imprints in buoyancy flux and surface wind stress with interannual to decadal variability (Curry and Mccartney, 2001). It has been clearly shown in previous studies (Andersson, 2002; Yan et al., 2004; Hünicke and Zorita, 2006; Hünicke et al., 2015; Xu et al., 2015; Karabil et al., 2017) that NAO is one of the governing factors in sea level variability of the Baltic Sea on seasonal to decadal periods. However, the role of NAO on multidecadal sea level variability and how it affects the sea level rise estimations on this time scale has yet to be studied.

The long-term records of tide gauges in the Baltic Sea offer an opportunity of investigating the long-term coherence between the sea level variation and NAO. Figure 3 shows the wavelet coherence (Grinsted et al., 2004) of the tide gauges and NAO. The effect of NAO can also be analyzed spatially by partitioning the basin into three subregions of north, middle, and south represented by Ratan, Stockholm, and Warnemünde, respectively. As it has been reported, NAO has a substantial impact on sea level variation of the basin not only in the altimetry era but also throughout the twentieth century in interannual and decadal scales. Additionally, this impact is stronger in the north and it fades out toward the south. The main question left, however, is the effect that NAO has on sea-level rise estimation in the Baltic Sea.

FIGURE 3

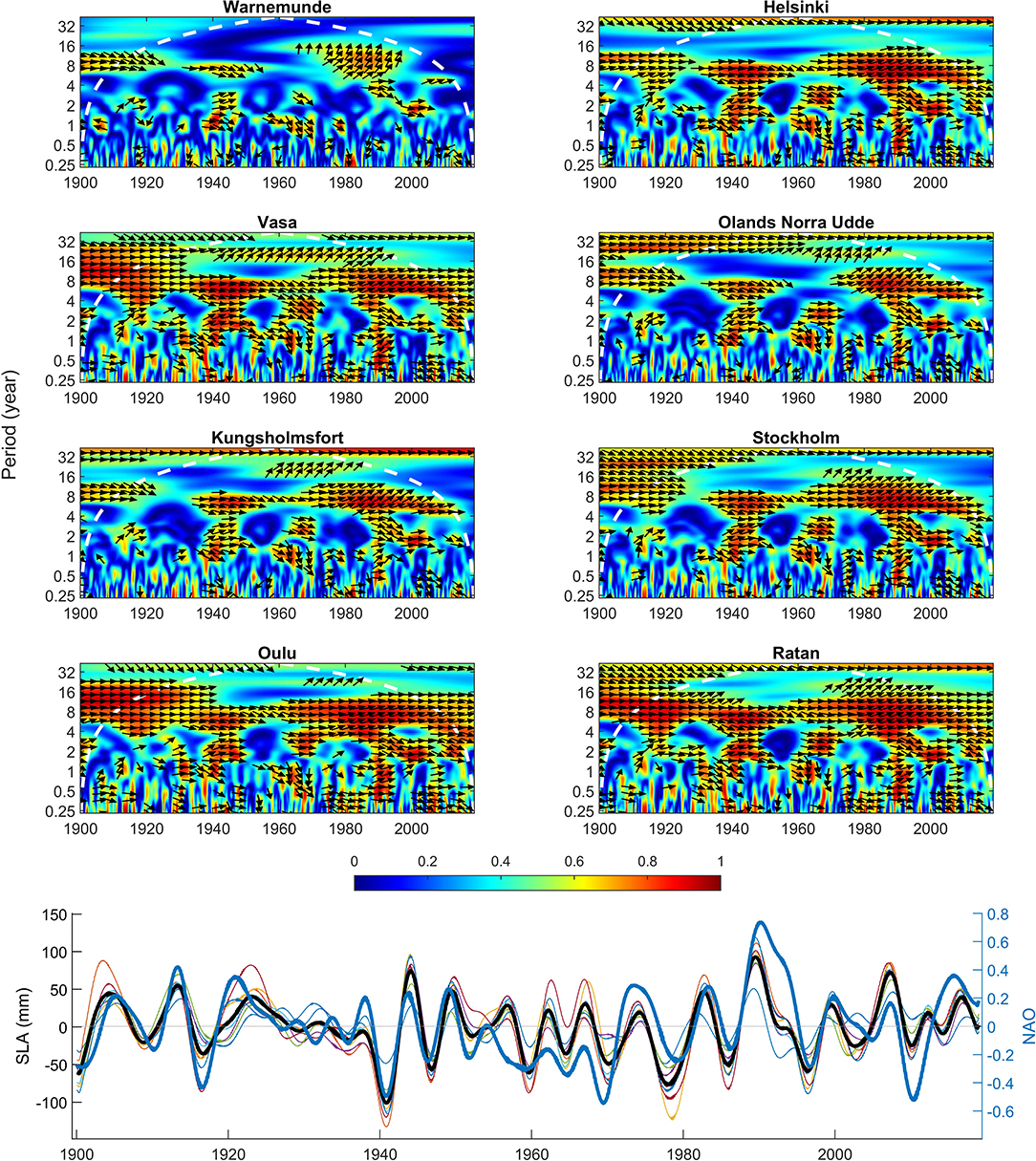
Figure 3. The wavelet coherency between North Atlantic Oscillation (NAO) and tide gauges (top four rows). The arrows represent the phase of the coherence as such to the right represents in phase and the left represents the opposite phase. NAO has a significant role in sea level variations of the Baltic Sea on seasonal to decadal time scales. The bottom panel shows the time series for the sea level anomaly (SLA) and NAO after removing periods shorter than 4 years. In the bottom panel, the thinner curves are for the individual tide gauge time series and the black curve is the mean of them. NAO is represented by thick blue line. The impact of NAO on the interannual to decadal time scale is not constant and it shows a higher correlation for some periods, for instance in the 1940s.

One of the most frequent methods to model internal variability is to augment the linear regression model with climate indices which govern the climate of the study region (Zhang and Church, 2012; White et al., 2014; Frankcombe et al., 2015). In the case of this study, this method can be formulated as

$\begin{array}{ll}\begin{array}{}\eta (t)=a_0+a_{1}t+{\displaystyle \sum _{i=1}^2[b_i\sin ({\omega }_{i}t)+c_i\cos ({\omega }_{i}t)}]+a_{3}NA{O}_t+\epsilon \end{array}& (3)\end{array}$

The effect of NAO on sea level variation of the Baltic Sea is not consistent in time, and it shows strong variations on seasonal to multidecadal time scales. Karabil et al. (2018) estimated correlations between two long-term tide gauges (Warnemünde and Stockholm) and NAO separately for winter and summer in 21-year gliding segments. They showed that correlation for different seasons and stations can range from −0.4 to 0.8. Additionally, the varying coherencies between NAO and the SLA time series (Figure 3) demonstrate that the influence of NAO depends not only on the period but also on the time scale. Due to the time variability of NAO impact, Equation (3) does not eliminate the NAO-related variations. To clarify this, another analysis is carried out. For periods longer than 16 years, the results of wavelet coherence are not reliable considering the cone of influence.

To see a clear picture of the variations in decadal and multidecadal scales, a low-pass bandwidth filter is applied on both SLA and NAO time series. Continuous wavelet transform is used to filter out signals with periods shorter than 4 years. This threshold is set according to visual analyses of the spectrograms which show that signals with periods shorter than this threshold are mostly nonstationary. The filtering is applied on the SLA of each tide gauge and then they are averaged to represent the basin-wide sea level variation (Figure 3, bottom panel). The main remark is the time variable impact of NAO on sea level variability of the basin. This leads to complexity in modeling its footprint on sea level rise estimations. For instance, the NAO influence on the mean SLA of the basin is more pronounced in the 1940s while it comparatively becomes less effective in the 1950s. A similar conclusion can be extended to sea level variations in the altimetry era in the middle and southern subregions by analyzing the coherence in the Stockholm and Kungsholmsfort stations.

Additionally, the impact of NAO is not identical for different seasons of the year. This causes that the fitting process in Equation (3) depends on the smoothing applied to both the SLA and NAO time series. This has been quantified by the coefficient of determination, which is a measure to quantify the fitting performance of a functional model. It is defined as 1−(SS_res/SS_tot) where SS_res represent the sum of the square of residuals and SS_tot shows the variance of the data (the SLA). For instance, the coefficient of determination for basin-average sea level trend accounts for only 0.29, while when a 13 months smoothing is applied and seasonal terms are removed from the equation, the coefficient of determination rises to 0.45. Low-pass filtering of time series, in turn, may lead to manipulations in the temporal correlation of the observations in time series, hence underestimation of uncertainty. Therefore, there is a trade-off between smoothing and uncertainty estimations.

Despite all these obstacles in modeling NAO-related variations of sea level, the silver lining is the quasi-periodic nature of these variations with seasonal to decadal components. These types of variations have generally insignificant contributions to trend estimation after three or more cycles (Karimi and Deng, 2020). Additionally, according to the coherence figures, the NAO signal can be considered stationary in the altimetry era for the northern subregion (Vasa, Ratan, and Oulu stations) where the coherence is above 0.5 and in phase. Thus, a multivariate regression model can provide some insights into the role of NAO in SLA trend estimations. Figure 4 shows the difference in trend estimation using Equations (2) and (3). The maximum contribution of NAO to SLA trend is less than 0.4 mm/year. Therefore, the internal variability imposed by NAO accounts for a maximum of ~10% of sea-level rise in the basin in the altimetry era.

FIGURE 4

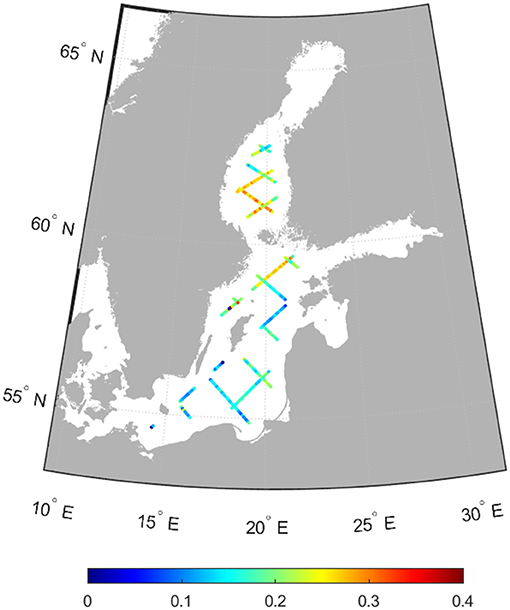
Figure 4. Contribution of NAO to sea level rise (mm/year) of the basin in the altimetry points. The trend map is the result of subtracting the rates estimated by Equation (2) from those of Equation (3). NAO has the highest impact on sea level rise of the Gulf of Bothnia where it reaches 0.4 mm/year. Comparing to the overall magnitude of the sea level trend, however, this figure is not substantial.

Multidecadal Sea Level Variations and Acceleration Estimations

The Baltic Sea is one of the best-monitored basins where the sea level has been recorded almost regularly since the beginning of the twentieth century or even earlier. This provides the possibility of analyzing low-frequency variations and investigate their occurrences and periodicities. We assume that the land uplift model completely removes the GIA effect and that the basin is not subject to any nonlinear solid earth signal which might leave an imprint on sea level variation of the twentieth century. By analyzing the multidecadal variations, we try to reconcile the contradicting acceleration results presented in the early 1990s and most recently.

The tide gauge records are low passed filtered using the same approach in the previous section but with a wider bandwidth which removes all decadal or shorter periods (Figure 5). The sea level rise in the basin can be divided into three phases where the breakpoints are 1945 and 1978. These breakpoints are chosen according to the results of spectral analyses in Figure 3. After a substantial fluctuation between 1940 and 1950, the low-frequency signal of the SLA follows a downward trend until it reaches another low in 1978, despite some dips and peaks in the interim. A linear regression model is also fitted to the monthly records of each phase to show the general tendency of the sea level rise in these phases. Moving the breakpoints a few years changes the estimated trends but the overall outcome for the three phases does not change. The estimated trends imply a multidecadal variation in almost all tide gauges. These findings can be linked to the results of other studies on a global scale. Dangendorf et al. (2019) and Frederikse et al. (2020) reported that the rate of global sea level rise experiences a pronounced drop in the period of 1950s−1970s. Frederikse et al. (2020) reported that this is a consequence of lower mass contribution to sea level rise with respect to before and after this period.

FIGURE 5

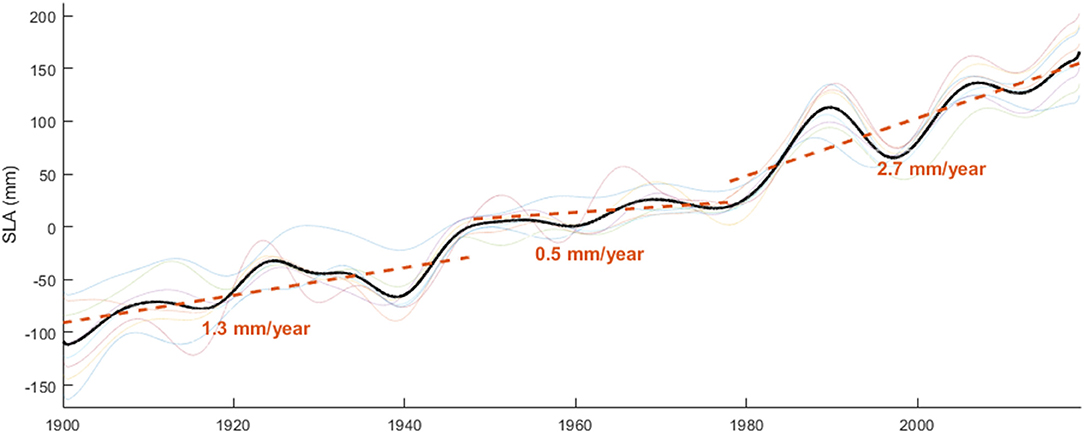
Figure 5. Sea level variation in the tide gauge stations after applying a low-pass filter to remove the decadal or shorter variations. The transparent curves demonstrate the variation of individual tide gauges and the black curve is the mean for all stations. The orange dashed lines represent the trend fitted to the monthly mean of the tide gauges (not the filtered). The global hiatus in sea level rise (the 1950–1970s) is evident in the sea level rise of the basin.

The presence of such multidecadal variations can be a substantial obstacle to estimate the sea level acceleration in the basin (Calafat and Chambers, 2013). Depending on the length of the dataset used for acceleration analyses, the outcome can be negative, positive, or insignificant when the range and magnitude of acceleration estimated for sea-level on a global scale is considered, ~0.01–~0.025 mm/year² (Church and White, 2006; Calafat and Chambers, 2013). Overlooking the physical processes with multidecadal periods can make the mathematical modeling results sensitive to the length of the dataset and the period in which it is applied on. In the case of this study, if the dataset is confined, for instance, to the period of 1944–2020, the acceleration estimations will yield considerable figures comparing with any other period (as shown in Supplementary Table 2). These interpretations, however, are apart from the statistical significance of the estimated accelerations when a proper noise model is deployed.

The results of the previous studies on the sea level acceleration of the Baltic Sea can be interpreted by these multidecadal variations. For instance, Woodworth (1990) estimated negative accelerations for most of the tide gauges in the Baltic Sea. Considering the slowdown period between the 1950s and 1970s, this is an expected outcome if one used the data until 1990. In another comprehensive study, Hünicke and Zorita (2016) found that most of the accelerations estimated for the individual tide gauges were statistically insignificant in all three methods used in the study. The first method in their study is a regression model with a quadratic term that represents the acceleration/deceleration, similar to Woodworth (1990). The results of this method resemble those presented in Supplementary Table 2 although more tide gauges are used, including those of this study. When this model is used to estimate the acceleration, it is very critical to include the low-frequency variations in the regression model. Otherwise, the estimated acceleration might be statistically insignificant due to the misfit raised from these variations.

In a case study on the Australian coasts, Agha Karimi (2021) reported how multidecadal variations can manipulate the magnitude of the estimated acceleration and its uncertainty when a quadratic term is used to represent the acceleration. Thus, if an additional term representing this low-frequency signal is added to the functional model of the acceleration estimation, a statistically significant figure may be estimated for individual tide gauges. Additionally, attributing a single figure for the rate of sea level rise for the whole period of analyses might be misleading as we are not aware of the exact point at which acceleration starts and also if it is subject to any change over the time series. The other two methods used by Hünicke and Zorita (2016) are based on a gliding linear trend (11-year segment) and fitting linear trend to the annual increment of the SLA. The latter suffers the same problem as the regression model with the quadratic term. The gliding linear trend, on the other hand, needs to have a longer segment length to filter out the impact of decadal and multidecadal signals. Due to the masking effect of multidecadal variations, Hünicke and Zorita (2016) could not reach a reliable figure for the acceleration of the Baltic Sea level.

Visser et al. (2015) listed 30 different methods to analyze the sea level trend and acceleration and reported that there is not a perfect approach to quantify these parameters. They showed that every method has shortcomings and recommended using a combination of methods to draw a solid conclusion. However, this combination should be complementary in a way that the deployed methods cover the shortcomings of others. In the case of this study, the wavelet transform lacks uncertainty measures. However, it gives a general tendency of the SLA variation in the basin which helps in forming up the phases and breakpoints. To overcome the uncertainty measure, we use the linear trend fitted to each tide gauge in three different periods covering two or three of the phases (Table 1). Considering the length of each period (at least 70 years), it can be assumed that the internal variability has only a trivial effect on the estimated trends. The hiatus is also intentionally involved in all three periods to account for its effect. All of the tide gauges show higher rates of rise in the period of 1944–2020 indicating that the sea level rise in the basin is accelerated over the last 120 years. If the rates from the altimetry era are taken into account, the acceleration is even more pronounced. Therefore, when this hiatus is considered, the sea level rise in the Baltic Sea is accelerating according to the trends fitted to the different multidecadal periods (Table 1). It should be noted that the tide gauge locations are confined to the northern and eastern coasts of the Baltic Sea and this conclusion may not be extended to Latvian and Polish coasts due to some local drivers.

TABLE 1

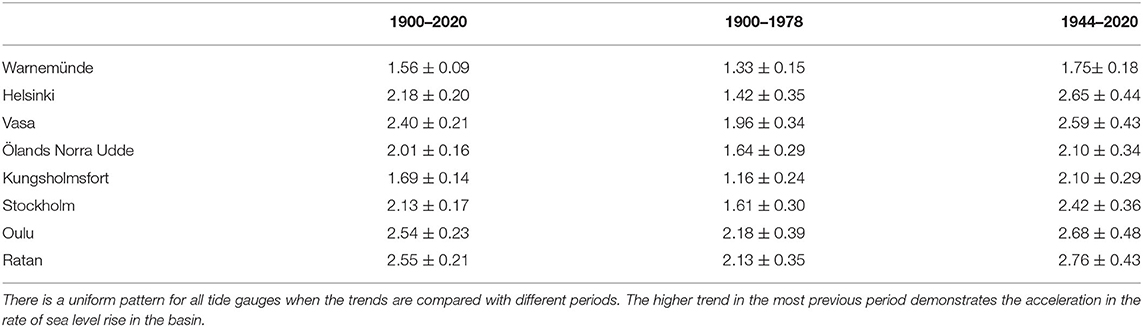
Table 1. Rate of sea level rise (mm/year) for three different periods each of which embraces the warming hiatus (1944–1978).

Conclusion

Multidecadal variations of the Baltic Sea level are analyzed using tide gauge data and altimetry measurements. Due to the paucity of reliable datasets with multicentennial length, multidecadal variations are investigated by fitting a linear regression model to multidecadal periods of the datasets and interpretation of low-passed time series. As an independent source of data, satellite altimetry is used to validate the uplift model of NKG in two tide gauge stations by comparing the linear trends. NAO influences the sea level variations in the basin on seasonal to decadal time scales. It is shown that this impact is not substantial on the multidecadal scale by fitting a multivariate linear regression model which accounts for the NAO variations and also applying bandwidth filtering.

Previous studies could not detect any statistically significant sea level acceleration in the Baltic Sea level. It is demonstrated that the presence of multidecadal variations can lead to this outcome. As such, the global warming hiatus, in the 1950–1970s, causes a slowdown in the rate of sea level rise in the basin which prevents quantitative determination of the acceleration. To overcome this, the mechanism (or sea level contributor) which leads to this slowdown needs to be identified, modeled, and added to the functional model of the acceleration estimations. Despite the lack of this information, we tried to reveal the acceleration in the basin by comparing the sea level trend in periods double of this hiatus (6–7 decades) since other methods such as gliding segment with decadal length are also sensitive to multidecadal variations. The results used in this study imply the sea level acceleration in all eight tide gauges.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

AA carried out conception, design, and analyses. AA, MB, and MH contributed to manuscript writing, revision, read, and approved the submitted version. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are appreciative to Dr. Sönke Dangendorf for his insightful comments about the work when they started this study. The authors thank the Climate Data Guide initiative, Radar Altimetry Database System (RADS), NOAA, Permanent Service for Mean Sea Level (PSMSL), NCEP, and NCAR for providing high-quality datasets which made this study possible.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.702512/full#supplementary-material

References

Ablain, M., Meyssignac, B., Zawadzki, L., Jugier, R., Ribes, A., Spada, G., et al. (2019). Uncertainty in satellite estimates of global mean sea-level changes, trend and acceleration. Earth Syst. Sci. Data 11, 1189–1202. doi: 10.5194/essd-11-1189-2019

CrossRef Full Text | Google Scholar

Agha Karimi, A. (2021). Internal variability role on estimating sea level acceleration in Fremantle tide gauge station. Front. Earth Sci. 9:474. doi: 10.3389/feart.2021.664947

CrossRef Full Text | Google Scholar

Andersson, H. C. (2002). Influence of long-term regional and large-scale atmospheric circulation on the Baltic sea level. Tellus A: Dyn. Meteorol. Oceanogr. 54, 76–88. doi: 10.3402/tellusa.v54i1.12125

CrossRef Full Text | Google Scholar

Barbosa, S. M. (2008). Quantile trends in Baltic sea level. Geophys. Res. Lett. 35:L22704. doi: 10.1029/2008GL035182

CrossRef Full Text | Google Scholar

Brown, S. (2010). A novel near-land radiometer wet path-delay retrieval algorithm: application to the Jason-2/OSTM advanced microwave radiometer. IEEE Trans. Geosci. Remote Sens. 48, 1986–1992. doi: 10.1109/TGRS.2009.2037220

CrossRef Full Text | Google Scholar

Calafat, F. M., and Chambers, D. P. (2013). Quantifying recent acceleration in sea level unrelated to internal climate variability. Geophys. Res. Lett. 40, 3661–3666. doi: 10.1002/grl.50731

CrossRef Full Text | Google Scholar

Cazenave, A., Hamlington, B., Horwath, M., Barletta, V. R., Benveniste, J., Chambers, D., et al. (2019). Observational requirements for long-term monitoring of the global mean sea level and its components over the altimetry era. Front. Mar. Sci. 6:582. doi: 10.3389/fmars.2019.00582

CrossRef Full Text | Google Scholar

Church, J. A., and White, N. J. (2006). A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 33, 6981–6992. doi: 10.1029/2005GL024826

CrossRef Full Text | Google Scholar

Compo, G. P., Whitaker, J. S., Sardeshmukh, P. D., Matsui, N., Allan, R. J., Yin, X., et al. (2011). The twentieth century reanalysis project. Q. J. R. Meteorol. Soc. 137, 1–28. doi: 10.1002/qj.776

CrossRef Full Text | Google Scholar

Curry, R. G., and Mccartney, M. S. (2001). Ocean gyre circulation changes associated with the north atlantic oscillation. J. Phys. Oceanogr. 31, 3374–3400. doi: 10.1175/1520-0485(2001)031&lt;3374:OGCCAW&gt;2.0.CO;2

CrossRef Full Text | Google Scholar

Dangendorf, S., Calafat, F. M., Arns, A., Wahl, T., Haigh, I. D., and Jensen, J. (2014). Mean sea level variability in the North Sea: processes and implications. J. Geophys. Res. Oceans 119, 6820–6841. doi: 10.1002/2014JC009901

CrossRef Full Text | Google Scholar

Dangendorf, S., Hay, C., Calafat, F. M., Marcos, M., Piecuch, C. G., Berk, K., et al. (2019). Persistent acceleration in global sea-level rise since the 1960s. Nat. Clim. Chang. 9, 705–710. doi: 10.1038/s41558-019-0531-8

CrossRef Full Text | Google Scholar

Dangendorf, S., Wahl, T., Hein, H., Jensen, J., Mai, S., and Mudersbach, C. (2012). Mean sea level variability and influence of the north atlantic oscillation on long-term trends in the german bight. Water 4, 170–195. doi: 10.3390/w4010170

CrossRef Full Text | Google Scholar

Deng, X., and Featherstone, W. E. (2006). A coastal retracking system for satellite radar altimeter waveforms: application to ERS-2 around Australia. J. Geophys. Res. Oceans 111:C06012. doi: 10.1029/2005JC003039

CrossRef Full Text | Google Scholar

Donner, R. V., Ehrcke, R., Barbosa, S. M., Wagner, J., Donges, J. F., and Kurths, J. (2012). Spatial patterns of linear and nonparametric long-term trends in Baltic sea-level variability. Nonlin. Processes Geophys. 19, 95–111. doi: 10.5194/npg-19-95-2012

CrossRef Full Text | Google Scholar

Ekman, M., and Mäkinen, J. (1996). Mean sea surface topography in the Baltic Sea and its transition area to the North Sea: a geodetic solution and comparisons with oceanographic models. J. Geophys. Res. Oceans 101, 11993–11999. doi: 10.1029/96JC00318

CrossRef Full Text | Google Scholar

Frankcombe, L. M., Mcgregor, S., and England, M. H. (2015). Robustness of the modes of Indo-Pacific sea level variability. Clim. Dyn. 45, 1281–1298. doi: 10.1007/s00382-014-2377-0

CrossRef Full Text | Google Scholar

Frederikse, T., Landerer, F., Caron, L., Adhikari, S., Parkes, D., Humphrey, V. W., et al. (2020). The causes of sea-level rise since 1900. Nature 584, 393–397. doi: 10.1038/s41586-020-2591-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Frederikse, T., Riva, R., Kleinherenbrink, M., Wada, Y., Van Den Broeke, M., and Marzeion, B. (2016). Closing the sea level budget on a regional scale: trends and variability on the Northwestern European continental shelf. Geophys. Res. Lett. 43, 864–872. doi: 10.1002/2016GL070750

PubMed Abstract | CrossRef Full Text | Google Scholar

Giese, B. S., Seidel, H. F., Compo, G. P., and Sardeshmukh, P. D. (2016). An ensemble of ocean reanalyses for 1815–2013 with sparse observational input. J. Geophys. Res. Oceans 121, 6891–6910. doi: 10.1002/2016JC012079

CrossRef Full Text | Google Scholar

Gräwe, U., Klingbeil, K., Kelln, J., and Dangendorf, S. (2019). Decomposing mean sea level rise in a semi-enclosed basin, the Baltic Sea. J. Clim. 32, 3089–3108. doi: 10.1175/JCLI-D-18-0174.1

CrossRef Full Text | Google Scholar

Grinsted, A., Moore, J. C., and Jevrejeva, S. (2004). Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin. Processes Geophys. 11, 561–566. doi: 10.5194/npg-11-561-2004

CrossRef Full Text | Google Scholar

Hill, E. M., Davis, J. L., Tamisiea, M. E., and Lidberg, M. (2010). Combination of geodetic observations and models for glacial isostatic adjustment fields in Fennoscandia. J. Geophys. Res. Solid Earth 115:B07403. doi: 10.1029/2009JB006967

CrossRef Full Text | Google Scholar

Holgate, S. J., Matthews, A., Woodworth, P. L., Rickards, L. J., Tamisiea, M. E., Bradshaw, E., et al. (2012). New data systems and products at the permanent service for mean sea level. J. Coastal Res. 29, 493–504. doi: 10.2112/JCOASTRES-D-12-00175.1

CrossRef Full Text | Google Scholar

Hünicke, B., and Zorita, E. (2006). Influence of temperature and precipitation on decadal Baltic Sea level variations in the 20th century. Tellus A: Dyn. Meteorol. Oceanogr. 58, 141–153. doi: 10.1111/j.1600-0870.2006.00157.x

CrossRef Full Text | Google Scholar

Hünicke, B., and Zorita, E. (2008). Trends in the amplitude of Baltic Sea level annual cycle. Tellus A: Dyn. Meteorol. Oceanogr. 60, 154–164. doi: 10.1111/j.1600-0870.2007.00277.x

CrossRef Full Text | Google Scholar

Hünicke, B., and Zorita, E. (2016). Statistical analysis of the acceleration of Baltic mean sea-level rise, 1900–2012. Front. Mar. Sci. 3:125. doi: 10.3389/fmars.2016.00125

CrossRef Full Text | Google Scholar

Hünicke, B., Zorita, E., Soomere, T., Madsen, K. S., Johansson, M., and Suursaar, Ü. (2015). “Recent change—sea level and wind waves,” in Second Assessment of Climate Change for the Baltic Sea Basin, ed. The BACC II Author Team, (Cham: Springer International Publishing), 155–185. doi: 10.1007/978-3-319-16006-1_9

CrossRef Full Text | Google Scholar

Hünicke, B., Zorita, E., and Von Storch, H. (2017). “The Challenge of Baltic Sea Level Change,” in Coastline Changes of the Baltic Sea from South to East: Past and Future Projection, eds J. Harff, K. Furmańczyk, and H. Von Storch (Cham: Springer International Publishing), 37–54. doi: 10.1007/978-3-319-49894-2_3

CrossRef Full Text | Google Scholar

Hurrell, J. W., and Deser, C. (2009). North Atlantic climate variability: the role of the North Atlantic Oscillation. J. Mar. Syst. 78, 28–41. doi: 10.1016/j.jmarsys.2008.11.026

CrossRef Full Text | Google Scholar

Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., et al. (1996). The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–472. doi: 10.1175/1520-0477(1996)077&lt;0437:TNYRP&gt;2.0.CO;2

CrossRef Full Text | Google Scholar

Karabil, S., Zorita, E., and Hünicke, B. (2017). Mechanisms of variability in decadal sea-level trends in the Baltic Sea over the 20th century. Earth Syst. Dynam. 8, 1031–1046. doi: 10.5194/esd-8-1031-2017

CrossRef Full Text | Google Scholar

Karabil, S., Zorita, E., and Hünicke, B. (2018). Contribution of atmospheric circulation to recent off-shore sea-level variations in the Baltic Sea and the North Sea. Earth Syst. Dyn. 9, 69–90. doi: 10.5194/esd-9-69-2018

CrossRef Full Text | Google Scholar

Karimi, A. A., and Deng, X. (2020). Estimating sea level rise around Australia using a new approach to account for low frequency climate signals. Adv. Space Res. 65, 2324–2338. doi: 10.1016/j.asr.2020.02.002

CrossRef Full Text | Google Scholar

Kauker, F., and Meier, H. E. M. (2003). Modeling decadal variability of the Baltic Sea: 1. Reconstructing atmospheric surface data for the period 1902–1998. J. Geophys. Res. Oceans 108:3267. doi: 10.1029/2003JC001797

CrossRef Full Text | Google Scholar

Kudryavtseva, N., and Soomere, T. (2017). Satellite altimetry reveals spatial patterns of variations in the Baltic Sea wave climate. Earth Syst. Dynam. 8, 697–706. doi: 10.5194/esd-8-697-2017

CrossRef Full Text | Google Scholar

Kudryavtseva, N. A., and Soomere, T. (2016). Validation of the multimission altimeter data for the Baltic Sea region. Est. J. Earth Sci. 65, 161–175. doi: 10.3176/earth.2016.13

CrossRef Full Text | Google Scholar

Kuo, C.-Y., Shum, C., Braun, A., Cheng, K.-C., and Yi, Y. (2008). Vertical motion determined using satellite altimetry and tide gauges. Terr. Atmos. Ocean. Sci. 19, 1–2. doi: 10.3319/TAO.2008.19.1-2.21(SA)

CrossRef Full Text | Google Scholar

Kuo, C. Y., Shum, C. K., Braun, A., and Mitrovica, J. X. (2004). Vertical crustal motion determined by satellite altimetry and tide gauge data in Fennoscandia. Geophys. Res. Lett. 31:L01608. doi: 10.1029/2003GL019106

CrossRef Full Text | Google Scholar

Lehmann, A., Getzlaff, K., and Harla,ß, J. (2011). Detailed assessment of climate variability in the Baltic Sea area for the period 1958 to 2009. Clim. Res. 46, 185–196. doi: 10.3354/cr00876

CrossRef Full Text | Google Scholar

Madsen, K. S., Høyer, J. L., Suursaar, Ü., She, J., and Knudsen, P. (2019). Sea level trends and variability of the Baltic Sea from 2D statistical reconstruction and altimetry. Front. Earth Sci. 7:243. doi: 10.3389/feart.2019.00243

CrossRef Full Text | Google Scholar

Meier, H. E. M., and Kauker, F. (2003). Modeling decadal variability of the Baltic Sea: 2. Role of freshwater inflow and large-scale atmospheric circulation for salinity. J. Geophys. Res. Oceans 108:3368. doi: 10.1029/2003JC001799

CrossRef Full Text | Google Scholar

Nerem, R. S., and Mitchum, G. T. (2002). Estimates of vertical crustal motion derived from differences of TOPEX/POSEIDON and tide gauge sea level measurements. Geophys. Res. Lett. 29, 40–44. doi: 10.1029/2002GL015037

CrossRef Full Text | Google Scholar

Omstedt, A., Pettersen, C., Rodhe, J., and Winsor, P. (2004). Baltic Sea climate: 200 yr of data on air temperature, sea level variation, ice cover, and atmospheric circulation. Clim. Res. 25, 205–216. doi: 10.3354/cr025205

CrossRef Full Text | Google Scholar

Pajak, K., and Blaszczak-Bak, W. (2019). Baltic sea level changes from satellite altimetry data based on the OptD method. Acta Geodyn. Geomater. 16, 235–244. doi: 10.13168/AGG.2019.0019

CrossRef Full Text | Google Scholar

Pajak, K., and Kowalczyk, K. (2019). A comparison of seasonal variations of sea level in the southern Baltic Sea from altimetry and tide gauge data. Adv. Space Res. 63, 1768–1780. doi: 10.1016/j.asr.2018.11.022

CrossRef Full Text | Google Scholar

Passaro, M., Cipollini, P., and Benveniste, J. (2015). Annual sea level variability of the coastal ocean: the Baltic Sea-North Sea transition zone. J. Geophys. Res. Oceans 120, 3061–3078. doi: 10.1002/2014JC010510

CrossRef Full Text | Google Scholar

Passaro, M., Müller, F. L., Oelsmann, J., Rautiainen, L., Dettmering, D., Hart-Davis, M. G., et al. (2021). Absolute Baltic Sea level trends in the satellite altimetry era: a revisit. Front. Mar. Sci. 8:647607. doi: 10.3389/fmars.2021.647607

CrossRef Full Text | Google Scholar

Piecuch, C. G., Thompson, P. R., and Donohue, K. A. (2016). Air pressure effects on sea level changes during the twentieth century. J. Geophys. Res. Oceans 121, 7917–7930. doi: 10.1002/2016JC012131

PubMed Abstract | CrossRef Full Text | Google Scholar

Ponte, R. M. (2006). Low-frequency sea level variability and the inverted barometer effect. J. Atmos. Ocean. Technol. 23, 619–629. doi: 10.1175/JTECH1864.1

CrossRef Full Text | Google Scholar

Prandi, P., Meyssignac, B., Ablain, M., Spada, G., Ribes, A., and Benveniste, J. (2021). Local sea level trends, accelerations and uncertainties over 1993–2019. Sci. Data 8, 1–8. doi: 10.1038/s41597-020-00786-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Richter, A., Groh, A., and Dietrich, R. (2012). Geodetic observation of sea-level change and crustal deformation in the Baltic Sea region. Phys. Chem. Earth Parts A/B/C 53–54, 43–53. doi: 10.1016/j.pce.2011.04.011

CrossRef Full Text | Google Scholar

Roy, K., and Peltier, W. R. (2018). Relative sea level in the Western Mediterranean basin: a regional test of the ICE-7G_NA (VM7) model and a constraint on late Holocene Antarctic deglaciation. Quat. Sci. Rev. 183, 76–87. doi: 10.1016/j.quascirev.2017.12.021

CrossRef Full Text | Google Scholar

Samuelsson, M., and Stigebrandt, A. (1996). Main characteristics of the long-term sea level variability in the Baltic sea. Tellus A 48, 672–683. doi: 10.3402/tellusa.v48i5.12165

CrossRef Full Text | Google Scholar

Scharroo, R., Leuliette, E., Lillibridge, J., Byrne, D., Naeije, M., and Mitchum, G. (2013). “RADS: Consistent multi-mission products,” in 20 Years of Progress in Radar Altimatry.

Google Scholar

Scharroo, R., Leuliette, E., Naeije, M., Martin-Puig, C., and Pires, N. (2016). “RADS Version 4: an efficient way to analyse the multi-mission altimeter database,” in Proceedings of the ESA Living Planet Symposium: ESA Special Publication SP-740, 13.

Google Scholar

Schneider, D. P., Deser, C., Fasullo, J., and Trenberth, K. E. (2013). Climate data guide spurs discovery and understanding. Eos Trans. Am. Geophys. Union 94, 121–122. doi: 10.1002/2013EO130001

CrossRef Full Text | Google Scholar

Slivinski, L. C., Compo, G. P., Whitaker, J. S., Sardeshmukh, P. D., Giese, B. S., Mccoll, C., et al. (2019). Towards a more reliable historical reanalysis: improvements for version 3 of the Twentieth Century Reanalysis system. Q. J. R. Meteorol. Soc. 145, 2876–2908. doi: 10.1002/qj.3598

CrossRef Full Text | Google Scholar

Spada, G., Olivieri, M., and Galassi, G. (2014). Anomalous secular sea-level acceleration in the Baltic Sea caused by isostatic adjustment. Ann. Geophys. 57:0432. doi: 10.4401/ag-6548

CrossRef Full Text | Google Scholar

Steffen, H., and Wu, P. (2011). Glacial isostatic adjustment in Fennoscandia—a review of data and modeling. J. Geodyn. 52, 169–204. doi: 10.1016/j.jog.2011.03.002

CrossRef Full Text | Google Scholar

Stramska, M., and Chudziak, N. (2013). Recent multiyear trends in the Baltic Sea level. Oceanologia 55, 319–337. doi: 10.5697/oc.55-2.319

CrossRef Full Text | Google Scholar

Tamisiea, M. E., and Mitrovica, J. X. (2011). The moving boundaries of sea level change: understanding the origins of geographic variability. Oceanography 24, 24–39. doi: 10.5670/oceanog.2011.25

CrossRef Full Text | Google Scholar

Vestøl, O., Ågren, J., Steffen, H., Kierulf, H., and Tarasov, L. (2019). NKG2016LU: a new land uplift model for Fennoscandia and the Baltic Region. J. Geodesy 93, 1759–1779. doi: 10.1007/s00190-019-01280-8

CrossRef Full Text | Google Scholar

Visser, H., Dangendorf, S., and Petersen, A. C. (2015). A review of trend models applied to sea level data with reference to the “acceleration–deceleration debate”. J. Geophys. Res. Oceans 120, 3873–3895. doi: 10.1002/2015JC010716

CrossRef Full Text | Google Scholar

White, N. J., Haigh, I. D., Church, J. A., Koen, T., Watson, C. S., Pritchard, T. R., et al. (2014). Australian sea levels—trends, regional variability and influencing factors. Earth-Sci. Rev. 136, 155–174. doi: 10.1016/j.earscirev.2014.05.011

CrossRef Full Text | Google Scholar

Woodworth, P. L. (1990). A search for accelerations in records of European mean sea level. Int. J. Clim. 10, 129–143. doi: 10.1002/joc.3370100203

CrossRef Full Text | Google Scholar

Xu, Q., Cheng, Y., Plag, H.-P., and Zhang, B. (2015). Investigation of sea level variability in the Baltic Sea from tide gauge, satellite altimeter data, and model reanalysis. Int. J. Remote Sens. 36, 2548–2568. doi: 10.1080/01431161.2015.1043405

CrossRef Full Text | Google Scholar

Yan, Z., Tsimplis, M. N., and Woolf, D. (2004). Analysis of the relationship between the North Atlantic oscillation and sea-level changes in northwest Europe. Int. J. Climatol. 24, 743–758. doi: 10.1002/joc.1035

CrossRef Full Text | Google Scholar

Zhang, X., and Church, J. A. (2012). Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 39:L21701. doi: 10.1029/2012GL053240

CrossRef Full Text | Google Scholar