Estimating Deep-Sea Fish Population Density From the Odour Extension Area: A Theoretical Basis and Comparison With the Conventional Methods

Accurately estimating the population density of deep-sea fish with a baited camera system has long been a significant challenge. Although several theoretical models have been developed using the first arrival time of an individual fish or time-varying fish abundance at the bait, none of the models allows for the spatio-temporal variability of the odour plume area extending from the bait. This study shows theoretically that the population density can be formulated as the inverse of the sample mean of the odour plume area extended until it reaches a first fish under the condition that fish at rest have a random dispersion. Each area estimate is governed by the homogeneous Poisson process and, hence, its probability density follows an exponential distribution. A large uncertainty can occur for each area estimate (sample), but the uncertainty decreases as the number of samples used to derive the sample mean increases by the law of large numbers. Numerical experiments conducted in the study indicate that the proposed method for inferring population density is also potentially applicable to cases in which the fish have a uniform or large-scale clumped dispersion. The experiments also show that the conventional method based on first arrival time fails to estimate the population density for any of the dispersion cases. This study also indicates that the reliability of the most popular inference method for estimating population density from the time-profile of fish abundance at the bait site was found to depend on the extension of the odour plume area and the dispersion pattern.

1 Introduction

The accurate estimation of population density is necessary for a precise understanding of the population dynamics of constituent species, the level of diversity, and the underlying ecosystem, all of which vary in response to surrounding environmental changes. Estimating the abundance of higher predators as well as endangered, low fecundity, and commercial species in the deep sea is especially crucial to sustaining the vulnerable deep-sea ecosystem (Norse et al., 2012; Watson and Morato, 2013; Clark et al., 2016; Nielsen et al., 2016; Fujiwara et al., 2021a). Various methods have been used to estimate population density, mainly targeting living creatures on land and in rivers. These methods include quadrat, removal, and mark-recapture approaches (e.g., Molles, 2015). Similarly, various approaches have been used for estimating fish in the ocean, including underwater visual census (e.g., Caldwell et al., 2016) and trawl sampling (Fitzpatrick et al., 2012; Johnson et al., 2013). However, the former method is infeasible in the deep sea and the latter carries the risk of damaging the ecosystem around the sea floor (Bailey et al., 2007).

A baited camera system, consisting of a lander equipped with bait and a camera, is seen as a promising means to conduct an efficient census of fish populations leading to a further evaluation of fish diversity or community composition (e.g., Cappo et al., 2003; Jamieson, 2016). Multiple efforts have been made to develop a method for estimating population density from two general perspectives. One approach is to use an empirical relation between population density and the “time of first arrival” (TOFA), that is, the elapsed time between the landing of the baited camera system and the arrival of the first fish at the bait (Priede and Merrett, 1996). Because it uses a simple empirical formula, the TOFA method has been widely applied for inferences regarding population density (Yau et al., 2001; Premke et al., 2006; Linley et al., 2017; Devine et al., 2018). However, recent studies have cast doubt on the method’s reliability, citing the large uncertainty inherent in the method (Farnsworth et al., 2007) and its inconsistency with independent underwater census results (Stoner et al., 2008; Yeh and Drazen, 2011; Schobernd et al., 2014; Harbour et al., 2020).

A second approach is to infer the population density from the abundance of fish attracted to the bait. Attempts have been made to explain the time profile of fish abundance, in a curve fitting sense, by assuming a decay of the odour plume (Priede et al., 1990), diffusive odour (Sainte-Marie and Hargrave, 1987) and/or foraging behaviour (Bailey and Priede, 2002). Fish abundance at the bait has recently been shown to be related to absolute population density in a theoretical study based on random foraging behaviour (Fransworth et al., 2007). A major metric in this approach is the maximum number of fish appearing within a single frame during the sampling period, which is often called MaxN (e.g., Cappo et al., 2003; Cappo et al., 2004; Cappo et al., 2006). This metric has been shown to correlate with independent observational data obtained from trawling or from an underwater visual census (Willis and Babcock, 2000; Willis et al., 2000; Stoner et al., 2008; Leitner et al., 2021). The approach has been improved, both theoretically and technically, toward wider applicability (Whitmarsh et al., 2018; Follana-Berná et al., 2019; Follana-Berná et al., 2020).

Meanwhile, Fujiwara et al. (2021b) proposed an alternative method for inferring population density, applying it to the Pacific sleeper shark Somniosus pacificus living in the deep Suruga Bay in the southern coastal area of Japan. With this method, population density is defined by the inverse of the area of the odour advected by the bottom current during the time before the arrival of the first fish, where the odour area is given by an ensemble average across field experiments conducted at different times and places. In this study, the proposed method will be referred to as ODORA (odour diffusion oriented abundance), suggesting an odorant which gives off a smell. The ODORA method uses the first arrival time to identify the time at which the odour area reaches the first fish. However, this method differs from the TOFA approach in that the population density is not directly parameterized by the first arrival time itself. Also, unlike the MaxN approach, the ODORA method counts only one fish arriving at the bait. Although this approach holds promise, no theoretical basis for it has been established, and hence its reliability and relevance to other methods are unknown.

In seeking to provide a sound theoretical basis for the ODORA method, this study develops useful underlying statistics for the method and indicates the limits of the method’s applicability. A distinctive feature of this method is its consideration of the spatio-temporal variability of the plume area. The importance of the plume area in the inference of population density has been discussed by Heagney et al. (2007) and Taylor et al. (2013) in the context of the MaxN approach; however, their plume area is assumed to be the triangular area as a function of the mean current velocity and elapsed time. In this study, we explore a more general relationship between the area of odour and population density by providing the theoretical basis of the ODORA method. Furthermore, the study examines the influence of the dispersion pattern of the fish on the estimation of population density. Previous studies in this field have often assumed random dispersion to provide a rigorous theoretical model for the inference of population density (Farnsworth et al., 2007; Dunlop et al., 2015; Follana-Berná et al., 2019; Follana-Berná et al., 2020). However, given that living creatures can have other dispersion patterns, such as uniform or clumped dispersion (e.g., Molles, 2015), a different assumption regarding the dispersion pattern may produce a different estimate of the population density.

In this study, we explore the influence of the odour plume area and dispersion pattern on the inference of population density but largely ignore the swimming properties of the fish. Although fish behaviour may be an important factor in population density estimation (Bailey and Priede, 2002; Cappo et al., 2003; Farnsworth et al., 2007; Dunlop et al., 2015), there is significant uncertainty in foraging patterns and the speed at which a fish swims toward the bait, which largely depend on body size, species, and competition (Moore and Howarth, 1996; Johansson and Leonardsson, 1998; Plaut, 2001; Krause et al., 2005). Nevertheless, a discussion of the response of the temporal evolution of fish abundance at the bait to changes in swimming speed in an idealized configuration is considered here as a possible means for further improving the method.

2 Theoretical Treatment for the Method

We begin with a brief review of the ODORA method in order to identify the primary question to be addressed (Section 2.1). We then develop the underlying statistics for this method (Section 2.2), which leads to statistics for the practical applicability of the method (Section 2.3). The symbols which may be important to understand the following argument are collated in Table 1.

TABLE 1

Table 1 Symbols and their descriptions in the theoretical treatment of the ODORA method.

2.1 The ODORA Method

In the ODORA method, the odour plume area includes all the locations reached by the odour advected from the bait. This area is referred to as the “searched area” and is analogous to the area revealed by shining a search light to find a target object. The area at the time the searched area reaches the first fish is referred to as the “minimum searched area”. The experiment is supposed to be conducted until one fish appears at the bait site. Using s_i to represent the minimum searched area in the i-th experiment (Figure 1A), the estimation of the population density, ρ̃, can be formulated as

$$\tilde{\rho }=\frac{k}{{\sum }_{i=1}^k{s}_i}.(1)$$

FIGURE 1

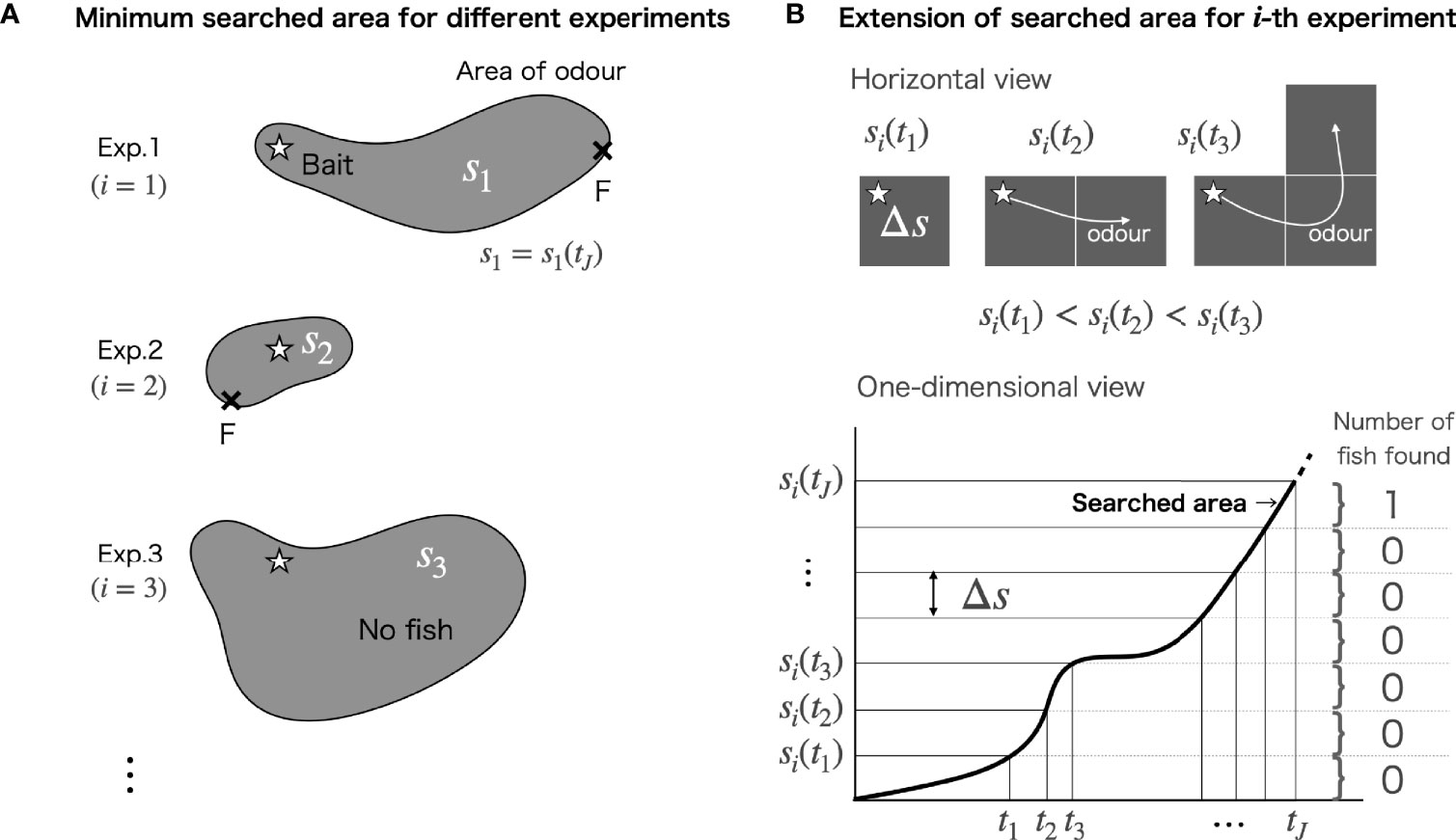
Figure 1 (A) Sketch of the experiment to produce the minimum searched area. The cross symbol with “F” denotes the position of the fish that searched first. (B) Schematic illustration of the extension rule of the searched area in horizontal (upper) and one-dimensional views (lower). The grey squares denote the searched area. The stars in panels (A, B) denote the location of the baited camera.

In practical application, we would consider that the numerator of (1) can be smaller than k, allowing for the case in which no fish appear in one or more out of the k experiments (Fujiwara et al., 2021b). However, for a rigorous argument, we here consider the case of (1). The equation can be written as

$$\tilde{\rho }=\frac{1}{\overline{s}},(2)$$

where

$$\overline{s}\equiv \frac{1}{k}\sum _{i=1}^k{s}_i(3)$$

is the sample mean for the minimum searched area.

We now introduce the “true” population density, ρ, which we define as the number of fish divided by the area of the supposed domain. The question here is whether (2) represents the true population density. For the ODORA method to be applicable, the following relation must hold

$$\frac{1}{\overline{s}}=\rho or \overline{s}=\frac{1}{\rho }(4)$$

Here, ρ^-1 is referred to as the equivalent area, defined as the area occupied by one fish, on average. In the following, we develop the underlying statistics for the ODORA method and explore the question of whether the sample mean of the minimum searched area (Eq. 3) can be used to determine the equivalent area.

2.2 Underlying Statistics

In general, the dispersion (distribution) patterns of living creatures, including plants, can be divided into three categories: random dispersion, uniform dispersion, and clumped dispersion (e.g., Molles, 2015). It seems clear that differences in dispersion pattern can significantly influence estimates of population density (e.g., Morisita, 1967). However, when seeking to estimate population density for a particular species, we are often uncertain of the species’ dispersion pattern. As a consequence, it is common to assume randomness in the fish distribution in theoretical models seeking to interpret the abundance of fish at a bait site (Farnsworth et al., 2007; Dunlop et al., 2015; Follana-Berná et al., 2019; Follana-Berná et al., 2020). Accordingly, we will here assume random dispersion in our theoretical argument, reserving for a later time in the discussion a description of the effects of other dispersion patterns (Section 3). We will also assume that the fish are anchored at their respective positions (no swimming or drifting) because of the uncertainty of fish behaviour.

Based on these conditions, we begin by articulating the area extension rule in the ODORA method. The following mathematical treatment is visualized in Figure 1B. Let s_i(t_j) be the searched area at a discretized elapsed time t_j for the i-th experiment. In the duration until the searched area reaches the first fish at the time t_j, the extension of the searched area in time satisfies the following relation,

$$s_i\left(t_1\right)<s_i\left(t_2\right)<s_i\left(t_3\right)<\cdots <s_i\left(t_J\right),(5)$$

where t₁<t₂< ··· <t_J. Note that s_i(t_j) gives the minimum searched area. All of the time-dependent areas include the location of the bait. Defining the minimum searched area and the area element as s≡s_i(t_j) and $\Delta s\equiv s/J$, respectively (Figure 1B), the area extension (Eq. 5) can be formulated as $s_i\left(t_{j+1}\right)=s_i\left(t_j\right)+\Delta s{(}^{\forall }j\le J)$. Note that this area extension rule is independent of the spatial form of the searched area, meaning that the rule can be applied for the area extension of an odour plume driven by any flow field.

Assuming the random dispersion of fish, which is the dispersion pattern treated here, means that our framework is based on a homogeneous Poisson process (e.g., Feller, 2008). In this process, the expected value of fish counts within an area s is given by ρs for a given population density, and hence the probability that a fish appears within an area element (Δs) can be expressed as p=ρs/J. Using this, the probability that no fish appears in an infinite number of j elements can be calculated by. lim_{J →∞} (1-ρs/J)^J=e ^-ρs. The complement of this probability, i.e., 1-e^-ρs, gives the probability that the first fish appears when the searched area reaches a value of s. Its derivative with respect to s leads to the corresponding probability density function in the form

$$f\left(s\right)=\rho e^{-\rho s}.(6)$$

This is the exponential distribution that will be used to provide the underlying statistics governing the ODORA method (Figure 2A). As is well-known in the statistics of the exponential distribution, the expected value of s, here denoted by E[s], can be calculated as

$$E[s]\equiv {\displaystyle {\int }_0^{\infty }sf(s)ds=}\frac{1}{\rho },(7)$$

FIGURE 2

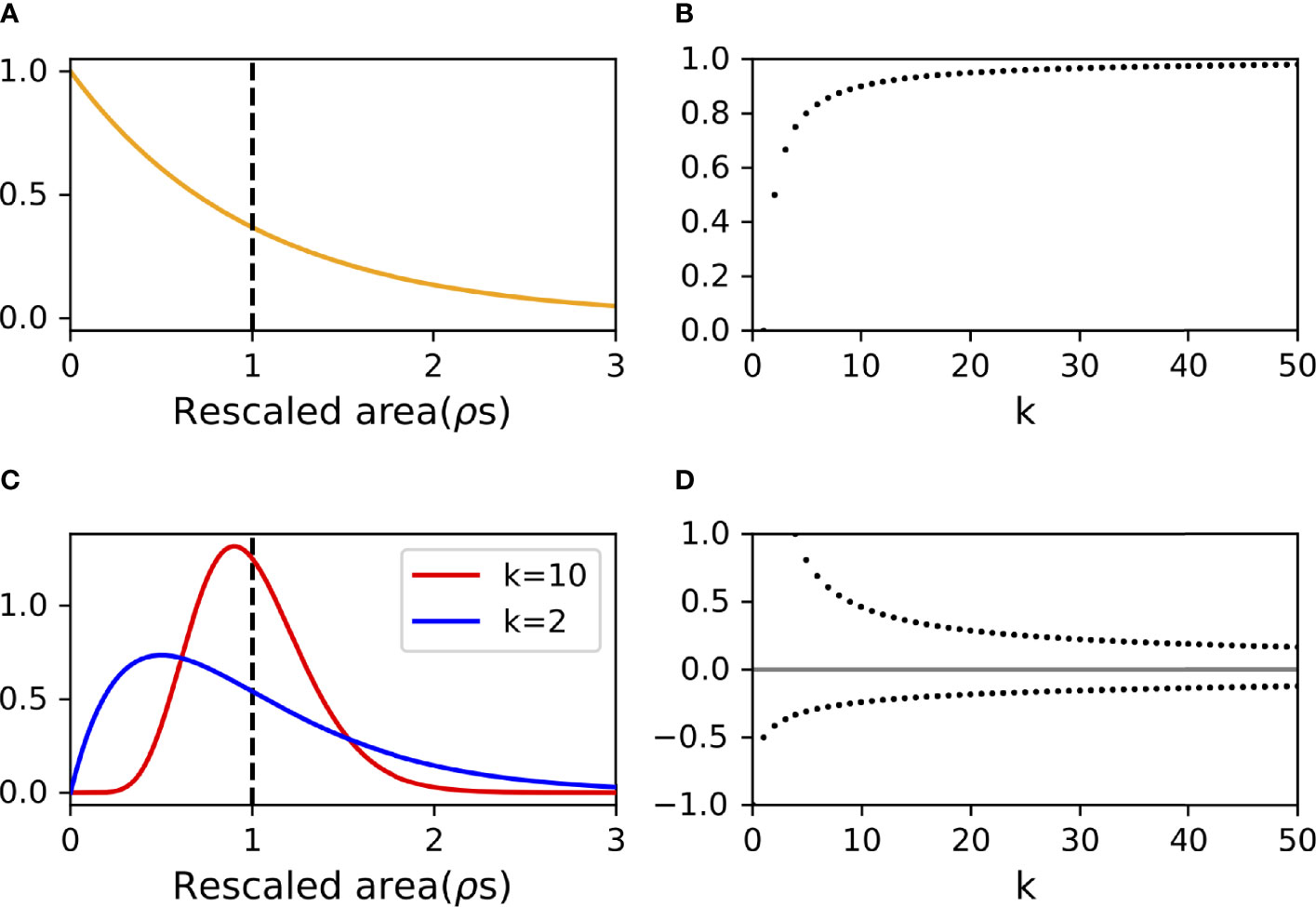
Figure 2 Probability distribution functions governing the minimum searched area (A) (Eq. 6) and its sample mean (C) (Eq. 9) assuming random fish dispersion. Note that the “Rescaled area” (nondimensional units) in (A) and (C) is the minimum searched area rescaled by the equivalent area ρ⁻¹. The dashed vertical lines indicate the point at which the minimum searched area equals the equivalent area. Panels (B, D) plot the bias in the mode population density from the actual value ($\rho {\overline{s}}^{\ast }$ in Eq. 13) and the uncertainty in the estimation of the population density (δ±/ρ in Eq. 12), respectively. Note that the upper bound of the uncertainty exceeds unity for k < 4 in panel (D) (See Eq. 12).

which is consistent with the equivalent-area (the inverse of the population density). This indicates that the ODORA method is able to derive the population density, in theory, based on the homogeneous Poisson process associated with the random dispersion pattern of the individuals.

Importantly, the expected value has uncertainty due to the variance, here denoted V[s]. With the variance, the population density would be formulated as $1/\left(E\left[s\right]\pm \sqrt{V\left[s\right]}\right)$. Because our distribution gives V[s]=1/ρ², the population density diverges to infinity. This suggests that no sample of the minimum searched area can yield an estimate of the population density with non-zero certainty. This problem has been pointed out by Farnsworth et al. (2007), although they discuss a first arrival time linked with the time-increase area under a framework governed by the homogeneous Poisson process, similar to ours. We should note that the variance here is applied for each minimum searched area obtained in each experiment. As asserted by the law of large numbers, the infinite uncertainty can be resolved by taking a sample mean of the minimum searched area.

In a field survey, only the arrival time, in general, is obtained from a time recorder equipped on a baited camera. Thus, the time t_J needs to be inferred from the relation,

$$\tau =t_J+t_f,(8)$$

Where τ and t_f’ are the arrival time of a fish and the time the fish took to arrive at the bait site from its original position, respectively. However, the inclusion of t_f does not influence the conclusion that the ODORA method obeys the exponential distribution because that relation merely shifts the time. For practical use, we can account for t_f as needed. We leave the method of identifying t_f to Fujiwara et al., (2021b).

2.3 Statistics for the Sample Mean

As explained in Section 2.1, the population density is estimated from the sample mean, $\overline{s}$, of the minimum searched areas obtained from k experiments (Eq. 3). Since the sample mean is determined from samples, s, that are independent of one another and follow the exponential distribution (Section 2.2), the probability density function that governs the sample mean is given by modifying the Erlang distribution (Figure 2C), a special case of the Gamma distribution (e.g., Feller, 2008) (see Supplementary Note 1),

$$Ga\left(\overline{s};k\right)=\frac{{\rho }^k}{(k-1)!}{k}^k{\overline{s}}^{k-1}{e}^{-k\rho \overline{s}}.(9)$$

The mean and variance of $\overline{s}$ are identified as

$$E[\overline{s}]=\frac{1}{\rho },(10)$$

$$V[\overline{s}]=\frac{1}{{\rho }^{2}k},(11)$$

respectively. Taking k=1 leads again to the exponential distribution (c.f., Eq. 6). The expected value is identical to the equivalent-area, independent of k, while the variance decreases with increasing k. This means that the sample mean from a larger number of experiments asymptotes to the equivalent-area with a smaller uncertainty, conforming to the law of large numbers.

The uncertainty in the population density can be quantified by

$${\delta }_{\pm }\equiv \left|\frac{1}{E[\overline{s}]}-\frac{1}{E[\overline{s}]\mp \sqrt{V[\overline{s}]}}\right|=\rho \frac{1}{\sqrt{k}\mp 1},(12)$$

with which an estimated population density can be expressed in the interval form, ρ-δ_-<ρ<ρ+δ₊. These intervals are asymmetric about ρ: the magnitude of the lower bound term (δ_-) is smaller than the magnitude of the upper bound term (δ₊) (See also Figure 2D). The uncertainty is infinite for k=1, as discussed in Section 2.2, but decreases with increasing k; the ratio, δ₊/ρ, becomes lower than unity for k≥4.

For a finite k, the expected value, E[$\overline{s}$], is always larger than the mode, which is the value most likely to appear (Figure 2C). Because the sample mean obtained from the experiments would likely be near the modal value, it may underestimate the equivalent-area. This leads to an overestimation of the population density, which can be quantified by

$$\rho =\frac{k-1}{k}\frac{1}{{\overline{s}}^{*}},(13)$$

where ${\overline{s}}^{*}$denotes the modal value of the sample mean, $\overline{s}$. The difference between the expected value of the population density (ρ) and that identified by the mode $(1/{\overline{s}}^{*})$ is negligible for a large k (Figure 2B). This formula is null for k=1, since this case leads to the probability density function being an exponential distribution, which has no extremum.

Eqs 12 and 13 would be useful to evaluate the reliability of the estimation of the population density in a field survey using the baited camera system, which obtains only a few samples in many cases. For example, consider the case that we compare two population densities, say ρ_U and ρ_L (ρ_U>ρ_L), estimated in different times or places under the same number of experiments. In this case, the condition for the difference of the population densities to be meaningful is given by ${\rho }_U/{\rho }_L>\left[1+1/\left(\sqrt{k}-1\right)\right]/\left[1-1/\left(\sqrt{k}+1\right)\right]$ from (12). Taking an example of k=4 (small number of experiments), if ρ_U/ρ_L>3, the difference between the two population densities is significant. Also, Eq. 13 would help correcting the estimated population density. For k=4, for example, it is inferred from (13) that the actual population density is likely to be 3/4 times smaller than the sample mean $(\sim 1/{\overline{s}}^{\ast }$). Note that those facts are applicable for k>1.

3 Performance: Influence of Dispersion Pattern

We conducted numerical experiments for the estimation of population density using the ODORA method under the random, clumped, and uniform dispersion patterns. The experiment was carried out in the square domain of size 1 km², where the “true” population density was fixed at 30 ind./km² a priori. The odour is advected from the bait by the background bottom current velocity field uniform in the experimental domain, where the current velocity is represented by the observed data collected in Fujiwara et al. (2021b) (Figure 3). The resultant time evolution of the searched area is shown in Figure 4 (left panels). By the definition, the minimum searched area is determined as the area at the time the odour reaches a fish; this area corresponds to s_i(t_j) in Section 2.2. The experiment was conducted 10,000 times, with different fish positions.

FIGURE 3

Figure 3 Time series of bottom current velocity observed by the baited camera system in Fujiwara et al. (2021b).

FIGURE 4

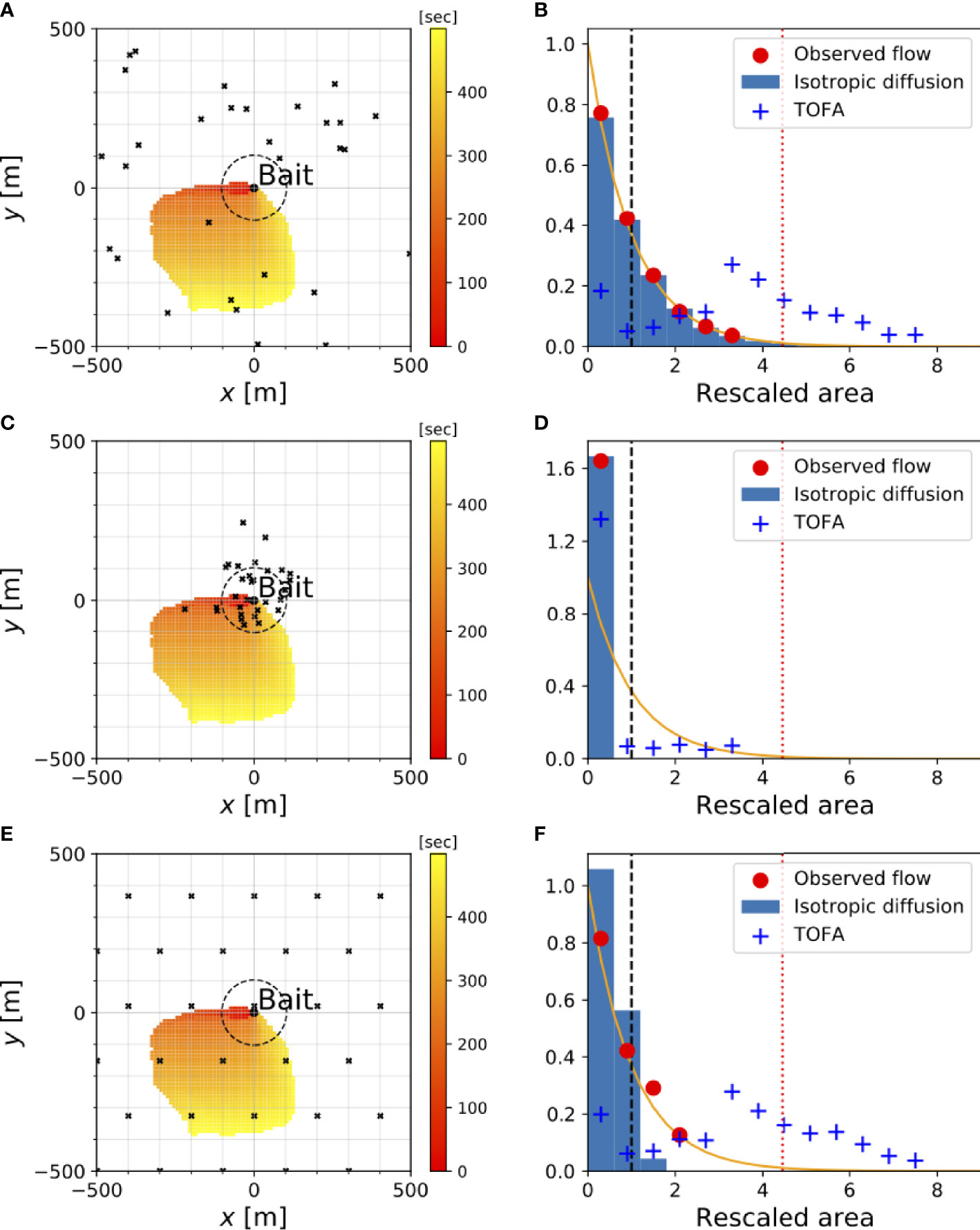
Figure 4 Histogram of the area (B, D, F) estimated by the ODORA (observed flow and isotropic diffusion cases) and TOFA methods in idealized numerical simulations for different dispersion patterns (A, C, E) (top:random; middle:clumped; bottom:uniform). An example of fish positions for each dispersion pattern in the x-y square domain is shown by the black x’s; those for the uniform dispersion case denote the average over the experiments. Color shade shows the searched area obtained from the observed flow at each elapsed time. For the histogram, the lateral axis is the estimated area rescaled by ρ⁻¹ (nondimensional units) and the vertical axis is its occurrence frequency normalized so that its integral over the entire range of the rescaled area is unity. The dotted red line in the histogram is the maximum searched area for the case of the observed flow. The dashed black circles (A, C, E) and dashed vertical lines (B, D, F) denote the equivalent-area.

We conducted the same experiment for isotropic diffusion rather than using the observed current velocity as a reference. In this case, the odour extends from the bait with horizontal diffusivity, D, and hence the odour area that reaches the fish at the nearest point is given by Dt_a, where t_a is the elapsed time from the onset of the diffusion. This area can be expressed as $\pi r_a^2$, where r_a is the distance of the fish from the bait, since the isotropic diffusion extends circularly. Thus, we identify the minimum searched area as $\pi r_a^2$ without solving the diffusion equation numerically.

The dispersion patterns were produced in the following manner: The random dispersion was created by a random number generator following the uniform occurrence probability over the entire experimental domain. The clumped dispersion was determined by a horizontal Gaussian distribution in the form, (N/2πσ²) exp (-∣x_m-μ∣²/2σ²), where μ and σ² are the mean position and the variance, respectively. The fish position, x_m(m=1,2,...,N) was determined randomly. N is the number of fish in the experimental domain (30 ind.). The uniform dispersion was represented by closed-packing in which the fish are located at a uniform distance from each other; each fish position is changeable randomly (with uniform probability) within the circular area inside the half-distance between the fish. The clumped and uniform dispersions defined above assume, respectively, a species having a specific habitat and a species in which each individual fish wanders in its territory. An example of each dispersion pattern is shown by the dots in the left panels of Figure 4.

We begin by briefly considering the results in the random dispersion case in order to assess the accuracy of the experiment. These results show that the minimum searched area closely follows the exponential distribution, as expected (Figure 4B). The mean value of the minimum searched area across the experiments is close to, but somewhat underestimates, the equivalent area (Table 2). This underestimation is due to the maximum limit on the observed searched area (s_max), as this limitation leads to

$$E[s]={\displaystyle {\int }_0^{s_{\max }}sf(s)ds=}\frac{1}{\rho }\left(1-e^{-\rho s_{\text{max}}}\right)<\frac{1}{\rho }.(14)$$

TABLE 2

Table 2 Expected value of estimated area rescaled by the equivalent area ρ^-1 (nondimensional units).

The error is represented by e^−ρs_max, which increases for smaller ρ or s_max. This suggests the need for a longer observation period in the ODORA method in order to estimate the population density with a greater accuracy. The isotropic diffusion case leads to a mean value of the minimum searched area closer to the equivalent area, but there is still a slight difference between the estimate and the equivalent area (Table 2). This difference is an artifact associated with searching for a fish in a circular area despite the fact that the random dispersion is defined in a square domain; the minimum searched area for the isotropic diffusion deviates from the exponential distribution when the circular area approaches the experimental domain.

For the clumped dispersion case, the accuracy of the estimation of population density largely depends on the centre (mean) and scale (variance) of the horizontal fish distribution. For the case when the fish are clumped around the bait (μ=(0m,0m) and σ=100 m), the histogram of the minimum searched area from the observed velocity data decreases with increasing value of the area faster than the exponential distribution (Figure 4D), which leads to an overestimation of the population density. This deviation from the exponential distribution, however, can be mitigated by increasing the horizontal scale of the fish distribution (Supplementary Figure S1B). This is due to the fact that a clumped dispersion similar to a Gaussian distribution is nearly equivalent to a random dispersion near the centre, where the occurrence probability of fish is nearly uniform among the various points. In contrast, when the centre of the clumped dispersion is located at some distance from the bait, the histogram of the minimum searched area deviates substantially from an exponential distribution (Supplementary Figure S1D), which leads to a poor estimation of the population density (Supplementary Table S1). Moreover, in this histogram, the isotropic diffusion and observed flow cases show much different profiles from each other, suggesting that the estimation of the population density is sensitive to the velocity field in the clumped dispersion case.

The results for the uniform dispersion case are similar to those for the random dispersion case (Figure 4F). However, there is a somewhat greater tendency to overestimate the population density. This is because the distance between any two fish is, on average, shorter than the radius of the equivalent area. In addition, the histograms of the minimum searched area are different for the observed velocity and isotropic diffusion cases, suggesting that the population density estimate largely depends on how the odour is advected.

In general, there is no way of knowing the dispersion pattern of a particular species of fish whose biological properties are not well known prior to a field experiment. The results above, however, show a clear difference between the clumped dispersion case and the others. In the case of clumped dispersion leading to an incorrect estimate, the minimum searched area for each experiment is likely to appear around a particular value (Figure 4D and Supplementary Figure S1D). The presence or absence of this feature in the experiments may provide an indication of the reliability of the estimated population density.

4 Discussion

4.1 Comparison With TOFA Method

The TOFA method (Priede and Merrett, 1996) is one of the principal inference methods for estimating fish population density. It assumes that a fish occupies a regular hexagonal area having a “radius” of a (length between the center and each apex) and that a fish approaches the bait linearly with a constant velocity, V_f, after detecting the odour plume advected by the current velocity, V_W, from the bait. Since the area of this hexagon is given by ca², where $c=3\sqrt{3}/2$, the population density is identified as 1/ca². Thus, to obtain the population density, the task is simply to estimate the radius a. Under the above assumptions, with the use of the relation to the arrival time, τ=a/V_W+a/V_f, the radius can be estimated by a=[V_f V_W/(V_f+V_W)]τ. Note that this relation to the arrival time corresponds to (8).

We can assess the performance of the TOFA method in estimating the population density in the sense of the expectation value. Because in this method there can be two ways to define the expectation of the hexagonal area, i.e., $c\overline{a^2}orc{\overline{a}}^2$, where the overbar denotes the sample mean across the experiments, we examine both cases. Here, to keep the consistency with the numerical experiment conducted in Section 3, swimming speed is ignored (V_f≫V_W) immediate arrival of a fish at the bait site (this corresponds to t_f→0 in (8)). This allows us to show the radius of the hexagon as simply a=V_Wτ. The background velocity, V_W, is given by the time average (vector mean) of the observed velocity in Fujiwara et al. (2021b), which was used in the previous section. For internal consistency, τ is given by the elapsed time when the minimum searched area derived from the observed velocity reaches the first fish (see section 3). Figure 5A provides an example showing the minimum searched area that reaches a fish (labelled by “F”) at τ=170 sec after the onset, along with the corresponding hexagonal area. The area estimation using the TOFA method was conducted in a numerical experiment with the same configuration as that in Section 3.

FIGURE 5

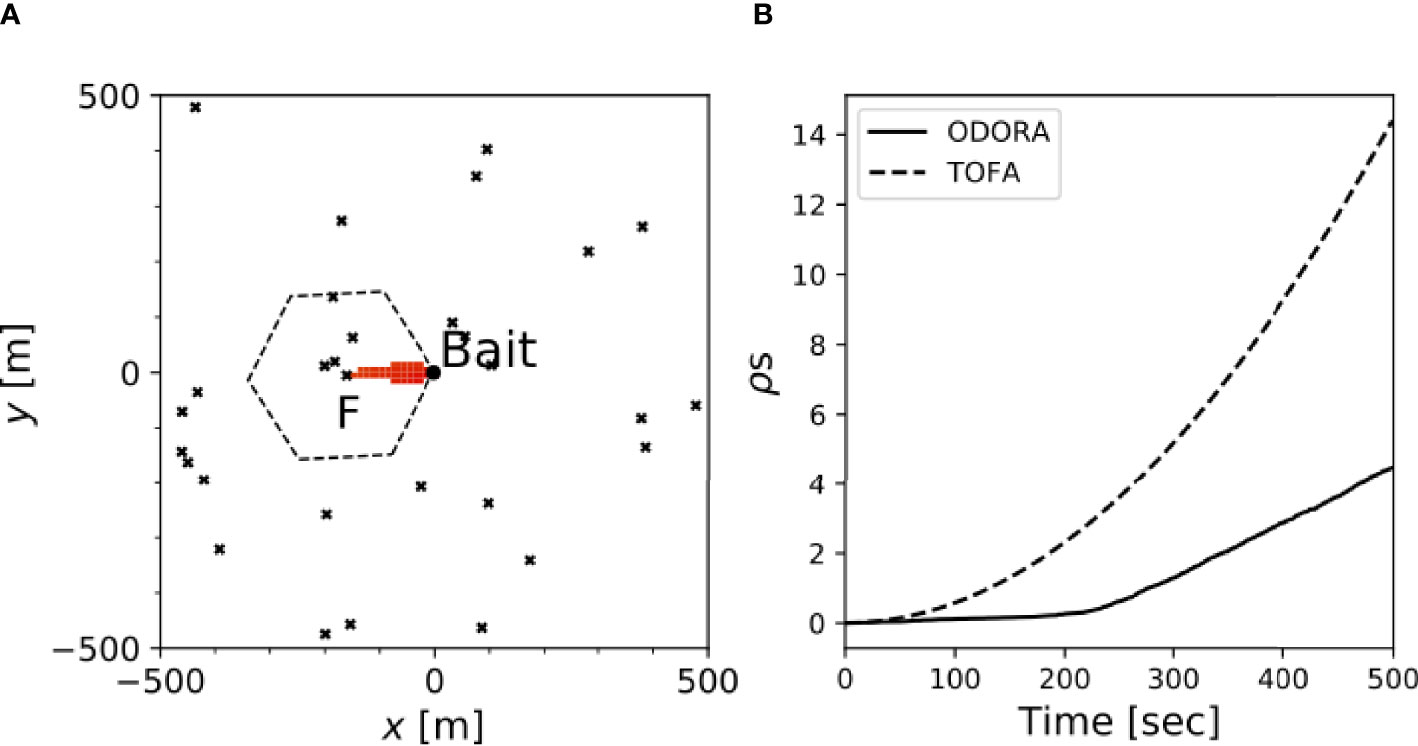
Figure 5 (A) Difference in the area enclosing the first fish, labeled F, between ODORA (in red) and TOFA methods (dashed hexagon). The fish positions in this panel show an example of the random dispersion pattern; (B) Time evolution of the area increment for each method.

The histograms of the estimated hexagonal area are plotted in Figure 4 (blue crosses in the right panels). For the random and uniform dispersion patterns, the area estimated by the TOFA method tends to have a large value, which leads to the mean value $(c\overline{a^2})$ being approximately four times larger than the equivalent area (Table 2). This overestimation is attributed to the fact that the hexagonal area is determined in proportion to the constant velocity, V_W, and hence it can increase quadratically in time irrespective of the actual time increase of the odour plume area (Figure 5B). This problem cannot be solved even if we define V_W as the velocity for each time rather than using the average (not shown). Estimation with $c{\overline{a}}^2$ instead of $c\overline{a^2}$ can mitigate the overestimation since ${\overline{a}}^2\le \overline{a^2}$ in general; however, the value is approximately three times larger than the equivalent area. These results indicate that the TOFA method can underestimate the population density in any case.

In addition to the substantial uncertainty inherent to the TOFA method (Farnsworth et al., 2007), its theoretical inconsistency may also be problematic. For any area estimation to function in the random dispersion case, which is governed by the homogeneous Poisson process, the predicted area must satisfy the condition that only one fish is located within it. Our numerical experiment, however, shows that the TOFA method includes more than one fish to occupy the hexagonal area (Figure 5A). This also violates a postulate of the method stating that only one fish occupies a hexagonal area. This problem is not attributable to the assumption of a hexagon, but rather results from the assumption that the area occupied by a fish is parameterized by a constant velocity.

4.2 Relevance to Measuring Fish Abundance at the Bait Site

Attempts have been made to infer population density from the data of fish assemblage at a bait site (see Section 1). Common to all the methods proposed so far, this approach supposes that fish originally dispersed within an area gather at the bait. This may allow us to generally formulate the temporal evolution of fish abundance at the bait, n(τ), as

$\begin{array}{ll}n\left(\tau \right)={\displaystyle {\int }_{A\left(t\left(\tau \right)\right)}f\left(\mathit{\text{x}}\right)d^{2}x}& (15)\end{array}$

where f(x) is population density that can vary in a horizontal place, x, and A(t(τ)) is the time-dependent area covering the original positions of fish that finally arrive at the bait. In general, it is required that t≤τ, since a fish arriving at the bait at τ must begin to move toward the bait at a time prior to the arrival. For simplicity, Eq. 15 does not include the process that the fish leavethe bait, and this implies that the fish count reaches the maximum when all the fish arrive at the bait site.

For the random dispersion case (homogeneous Poisson process), the population density is constant, as in f(x)=ρ, and hence Eq. 15 becomes

$$n(\tau )=\rho A(t(\tau )).(16)$$

This A(t(τ)) conceptually includes the “swept area” described by Farnsworth et al. (2007), which is defined as the geometric area determined by a straight-stretching plume and the original positions of the fish approaching the plume to forage for the bait. In the ODORA method, A(t(τ)) can be regarded as the searched area, s(t). In particular, if any fish arrives at the bait immediately after detecting the odour, then t= τ and hence the fish abundance at the bait would increase in proportion to the time evolution of the searched area, such as in Figure 5B (solid line). This suggests that the odour plume area can influence the inference of the population density from the time profile of fish abundance at the bait. Additionally, taking n(τ)=1 for a time τ=τ₀ (first arrival time) and taking an ensemble average leads to$\rho =1/\overline{s}({\tau }_0),$ which is equivalent to the formula for estimating the population density (see Eq. 4). Thus, the ODORA method is essentially identical to the inference method for estimating the population density from the fish assemblage at the bait.

Previous studies suggest the need for standardizing MaxN by the plume area (Heagney et al., 2007; Taylor et al., 2013). Such a standardization can be interpreted as an evaluation of the population density since Eq. 16 leads to ρ=n(τ_max)/A(t(τ_max)), where τ_max is the time for which n(τ) takes a maximum value. However, in these previous studies, the plume area was defined as the triangular area parameterized by a constant velocity and the elapsed time in the form, $0.165·$(V_Wτ)². As described in Section 4.1, this type of parameterization is essentially identical to the area definition used in the TOFA method and does not satisfy the conditions of a homogeneous Poisson process.

Models based on different assumptions have attempted to explain temporal changes in fish abundance at a bait site, adopting a single dispersion pattern (Sainte-Marie and Hargrave, 1987; Priede et al., 1990; Bailey and Priede, 2002; Farnsworth et al., 2007). Here, we examine the sensitivity of the time profile of fish abundance at the bait site to the dispersion pattern in the idealized uniform configuration, where the odour plume area is extended by an isotropic diffusion and a fish detecting the odour approaches the bait linearly with a constant swimming speed. These assumptions are the same as those adopted in Sainte-Marie and Hargrave (1987).

Isotropic diffusion causes the circular area extension of the odour in time, which is formulated by Dt = πr². Consider a fish located at distance r from the bait. This distance can be expressed as $r=\sqrt{\left(Dt/\pi \right)}$. This leads to an elapsed time for the fish to arrive at the bait after detecting the odour in the form $\sqrt{Dt/\pi }/$V_f, where V_f is the constant swimming speed. Thus, the arrival time of the fish after the onset of the odour diffusion can be written as

$$\tau =t+\beta \sqrt{t},(17)$$

where $\beta \equiv \sqrt{D/\pi }/V_f$ Converting from t to τ leads to

$$t\left(\tau \right)=\frac{1}{2}\left[(2\tau +{\beta }^2)-\sqrt{{\beta }^2({\beta }^2+4\tau )}\right],(18)$$

which gives the elapsed time for the area extension measured by the arrival time. In the following, we examine the theoretical time profile of fish abundance based on (15) and (18) for different dispersion patterns and compare them with the numerical experiments. The configuration of the numerical experiments is the same as that in section 3, except that the experiments are conducted 200 times, which is sufficient to identify an average time profile.

For the random dispersion case, we simply need to replace A(t(τ)) with Dt(τ) in (16), i.e.,

$$n(\tau )=\rho Dt(\tau )(19)$$

This time profile depends on the value of V_f due to the relation in (18). For a sufficiently large V_f to satisfy β²≪t, Eq. 19 reduces to n(τ)=ρDτ, i.e., the fish abundance shows a linear increase in time (Figure 6A). In contrast, for extremely small V_f (extremely large β), Eq. 19 asymptotes to n(τ)∝τ². Thus, for an appropriate finite value of V_f, the fish abundance approximately follows τ^α, the exponent of which ranges from 1 to 2 (Figure 6B). This does not contradict the time profile proportional to τ^3/2 found by Farnsworth et al. (2007) in the abundance data of Coryphaenoides armatus (King, 2006). It is important that such multiple shapes in the time profile dependent on the fish swimming speed are allowed by the two-dimensional spread of the odour plume. For example, a one-dimensional stretching of the plume driven by a constant current velocity (V_W), as was often supposed in previous studies, leads to only a linear profile in the fish abundance, since the second term of (17) is given by V_Wt/V_f in this case. Note that the deviation of the numerical result from the theory at a longer elapsed time is an artifact produced for the same reason noted in Section 3.

FIGURE 6

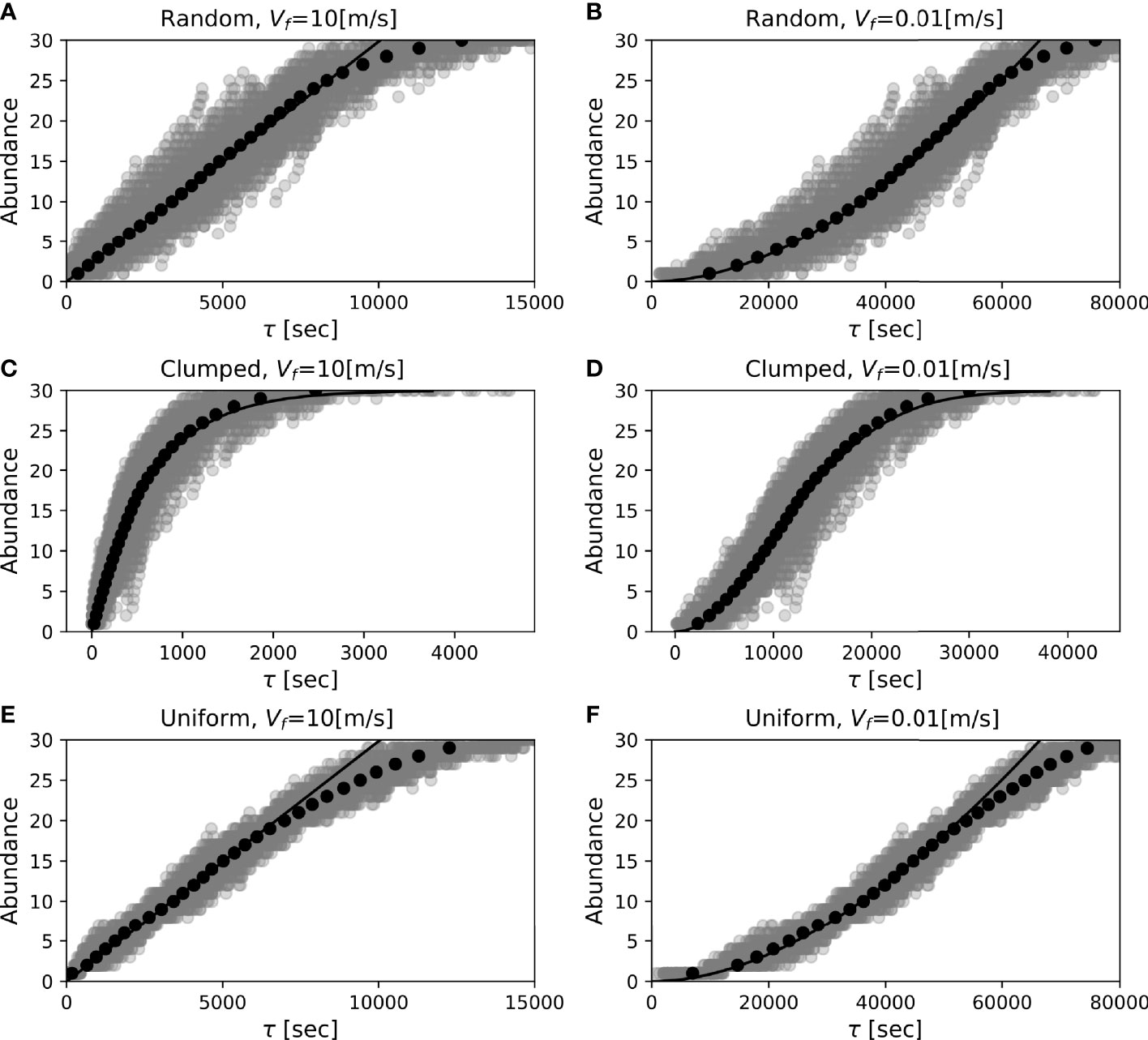
Figure 6 Time profiles of theoretical (black curve) and simulated (dots) fish abundance at bait for different swimming speeds (left: V_f=10 ms^-1, right: V_f=0.01 ms^-1) and different dispersion patterns (top:random; middle:clumped; bottom:uniform). The simulation is conducted under the same configuration as in the isotropic diffusion case in Figure 4, except that 200 experiments are conducted. The average of the arrivals for the individuals over the experiments is shown in black dots. The diffusion coefficient is set to 100 m²s^-1 in reference to the order of isopycnal eddy diffusivity (Tulloch et al., 2014).

The time profile of fish abundance that results when the clumped dispersion pattern is considered is different from that in the random dispersion case. Here, we consider the Gaussian population density discussed in Section 3. In the case where fish are clumped around the bait (μ=(0,0)), the integral of (15) gives

$$n(\tau )=N\left[1-\exp \left(-\frac{Dt(\tau )}{2\pi {\sigma }^2}\right)\right].(20)$$

This function shows different profiles due to the dependence of t(τ) on the swimming velocity (Figures 6C, D). In particular, when t(τ)=τ, Eq. 20 is formally identical to the model proposed by Priede et al. (1990) in fitting the curve to the observed data, although they explain it by the odour plume damping to the downstream. In the small value limit in t (short duration from the onset of the odour diffusion), Eq. 20 asymptotes to n(t)≃(N/2πσ²)Dt(τ), whose form is similar to the random dispersion case, (19), although the population density differs from the actual density (N/πσ²≠ρ). As we saw in Section 3, this indicates that the dispersion pattern around the centre of the clumped dispersion can be regarded as equivalent to random dispersion.

The uniform dispersion pattern again leads to (19) (Figures 6E, F). This is because the integral (15) in this case can be calculated as (m_x/L_x) (m_y/L_y)πr², where m_x and m_y are the fish counts within the intervals L_x and L_y for each direction of a square domain, respectively, and we see the equivalence that (m_x/L_y)(m_y/L_y)=ρ. However, the accuracy of the theoretical curve is reduced for smaller numbers of fish within a diffusion area, as the time reaching a certain abundance tends to be slightly shorter than the theoretical expectation. This is consistent with the underestimation tendency of the equivalent area by the ODORA method for the uniform dispersion case.

In the above discussion, we produced time profiles of fish abundance that were similar to those shown in previous studies. We are not using these results to claim the reliability of our theoretical configuration but rather to point out that the time profile of fish abundance changes with the combination of the horizontal extension properties of the odour plume and the dispersion pattern. These factors may need to be included in the model for inferring population density, along with fish behaviour.

Based on this result, a possible recommendation for a survey using the baited camera system would be to examine to what degree the time profile of fish assemblage at the bait site can be explained by that of the odour extension area. This would be helpful information to further consideration of another factor such as the fish behaviour or dispersion pattern. To this end, a current profiler needs to be equipped on the baited camera system and/or deployed in a wide area around the bait site to obtain current data utilized for the numerical simulation of the area extension of the odour plume as was done in the present study.

Further verification or improvement of the ODORA method would be necessary toward developing a sophisticated inference method for the population density. For example, we should consider the influence of the type of bait on the population density inference. The use of different bait types can lead to a different dispersal properties of the odour such as persistence time or area (Whitelaw et al., 1991; Sheaves, 1995), which consequently can cause differences in the number of individuals and/or species composition around the bait site (Whitelaw et al., 1991; Broadhurst and Hazin, 2001; Saila et al., 2002; Lowry et al., 2006; Heagney et al., 2007; Dorman et al., 2012). Also, for a comprehensive understanding of the deep-sea ecology, the inference method of the population density should be improved to be widely applicable for various species including benthic organisms. Although surveys regarding the populations of fish and other organisms have been conducted under a uniform methodological framework (e.g., Dunlop, 2013), we may still have insufficient knowledge on how the behavioural characteristics and odour sensitivity of each organism can yield a difference in the entire process throughout detecting the odour and approaching the bait site. Further analysis would be needed to clarify them, through applying the ODORA method to various species in field experiments.

5 Conclusions

This study presents statistics for ODORA, a method used to estimate fish population density on the basis of the area extension of the odour plume from a bait site. It was shown that this method conforms to the statistical framework of a homogeneous Poisson process when the positions of the fish are randomly dispersed, and, in theory, can estimate the actual population density with an uncertainty that decreases as the number of experiments increases.

The sensitivity of this method to different dispersion patterns was also examined. It was found that the method is applicable to the uniform dispersion case with somewhat lower accuracy, and that the method leads to highly variable results for the clumped dispersion case, depending on the horizontal scale and location of the original assemblage of fish. Notably, the TOFA method was shown to fail to effectively estimate the actual population density for any dispersion case. This lesser applicability results from an internal inconsistency in the theory that deviates from the assumptions of a homogeneous Poisson process due to the parameterization of the area occupied by a single fish using only a constant current velocity.

The ODORA method is identical to other methods for inferring population density using the abundance of fish attracted to a bait site, such as MaxN, except for the sole focus on the first fish arriving at the bait. Although methods based on fish assemblage at a bait site that incorporate fish behaviour such as foraging have been developed, we point out the need to consider the area of the odour plume and the dispersion pattern, which can substantially influence the modelled time profile of fish abundance at the bait.

The “odour plume area” assumed in the original ODORA method may not accurately represent the actual odour plume area, as it is advected by a horizontally uniform velocity and is defined as the total area of the locations that the odour reaches once. However, this method would be applicable even when the present definition of the odour plume area is replaced by the actual plume area, since the actual odour plume area always increases to satisfy the extension rule (Eq. 5). Further applications of the ODORA method would be possible by incorporating a simulation of odour advection using realistic ocean circulation data such as that created by assimilation techniques.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

KA, YF, ST: conceptualization. KA: formulation, analysis and experimental design. All authors involved in data interpretation and preparation of the manuscript.

Funding

This study was supported in part by JSPS KAKENHI to YF (Grant number JP16H04611) and the Environment Research and Technology Development Fund (JPMEERF20S20700) of the Environmental Restoration and Conservation Agency of Japan.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.854958/full#supplementary-material

Supplementary Data Sheet 1 | The observed velocity data used for this study (Independent CSV file).

References

Bailey D. M., Priede I. G. (2002). Predicting Fish Behaviour in Response to Abyssal Food Falls. Mar. Biol. 141, 831–840. doi: 10.1007/s00227-002-0891-9

CrossRef Full Text | Google Scholar

Bailey D. M., Wagner H.-J., Jamieson A. J., Ross M. F., Priede I. G. (2007). A Taste of the Deep-Sea: The Roles of Gustatory and Tactile Searching Behaviour in the Grenadier Fish Coryphaenoides Armatus. Deep. Sea. Res. Part I 54, 99–108. doi: 10.1016/j.dsr.2006.10.005

CrossRef Full Text | Google Scholar

Broadhurst M. K., Hazin F. H. (2001). Influences of Type and Orientation of Bait on Catches of Swordfish (Xiphias Gladius) and Other Species in an Artisanal Sub-Surface Longline Fishery Off Northeastern Brazil. Fish. Res. 53, 169–179. doi: 10.1016/S0165-7836(00)00297-6

CrossRef Full Text | Google Scholar

Caldwell Z. R., Zgliczynski B. J., Williams G. J., Sandin S. A. (2016). Reef Fish Survey Techniques: Assessing the Potential for Standardizing Methodologies. PloS One 11, e0153066. doi: 10.1371/journal.pone.0153066

PubMed Abstract | CrossRef Full Text | Google Scholar

Cappo M., Harvey E., Malcolm H., Speare P. (2003). Potential of Video Techniques to Monitor Diversity, Abundance and Size of Fish in Studies of Marine Protected Areas. Aquat. Protect. Areas-what. works. Best how. do. we. know. 1, 455–464.

Google Scholar

Cappo M., Harvey E., Shortis M. (2006). “Counting and Measuring Fish With Baited Video Techniques-An Overview,” in Australian Society for Fish Biology Workshop Proceedings (Australian Society for Fish Biology Tasmania), vol. vol. 1. , 101–114.

Google Scholar

Cappo M., Speare P., De'ath G. (2004). Comparison of Baited Remote Underwater Video Stations (BRUVS) and Prawn (Shrimp) Trawls for Assessments of Fish Biodiversity in Inter-Reefal Areas of the Great Barrier Reef Marine Park. J. Exp. Mar. Biol. Ecol. 302, 123–152. doi: 10.1016/j.jembe.2003.10.006

CrossRef Full Text | Google Scholar

Clark M. R., Althaus F., Schlacher T. A., Williams A., Bowden D. A., Rowden A. A. (2016). The Impacts of Deep-Sea Fisheries on Benthic Communities: A Review. ICES J. Mar. Sci. 73, i51–i69. doi: 10.1093/icesjms/fsv123

CrossRef Full Text | Google Scholar

Devine B. M., Wheeland L. J., Fisher J. A. (2018). First Estimates of Greenland Shark (Somniosus Microcephalus) Local Abundances in Arctic Waters. Sci. Rep. 8, 1–10. doi: 10.1038/s41598-017-19115-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Dorman S. R., Harvey E. S., Newman S. J. (2012). Bait Effects in Sampling Coral Reef Fish Assemblages With Stereo-BRUVs. PloS One 7, e41538. doi: 10.1371/journal.pone.0041538

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunlop K. M. (2013). Baited Underwater Camera Studies of the Biodiversity and Abundance of Animals in the Temperate, Tropical and Antarctic Marine Environment (Glasgow: Phd thesis, University of Glasgow).

Google Scholar

Dunlop K., Ruxton G., Scott E., Bailey D. (2015). Absolute Abundance Estimates From Shallow Water Baited Underwater Camera Surveys; a Stochastic Modelling Approach Tested Against Field Data. J. Exp. Mar. Biol. Ecol. 472, 126–. doi: 10.1016/j.jembe.2015.07.010

CrossRef Full Text | Google Scholar

Farnsworth K., Thygesen U. H., Ditlevsen S., King N. (2007). How to Estimate Scavenger Fish Abundance Using Baited Camera Data. Mar. Ecol. Prog. Ser. 350, 223–234. doi: 10.3354/meps07190

CrossRef Full Text | Google Scholar

Feller W. (2008). An Introduction to Probability Theory and its Applications Vol. vol 2 (John Wiley & Sons).

Google Scholar

Fitzpatrick B. M., Harvey E. S., Heyward A. J., Twiggs E. J., Colquhoun J. (2012). Habitat Specialization in Tropical Continental Shelf Demersal Fish Assemblages. PloS One 7, e39634. doi: 10.1371/journal.pone.0039634

PubMed Abstract | CrossRef Full Text | Google Scholar

Follana-Berná G., Palmer M., Campos-Candela A., Arechavala-Lopez P., Diaz-Gil C., Alós J., et al. (2019). Estimating the Density of Resident Coastal Fish Using Underwater Cameras: Accounting for Individual Detectability. Mar. Ecol. Prog. Ser. 615, 177–188. doi: 10.3354/meps12926

CrossRef Full Text | Google Scholar

Follana-Berná G., Palmer M., Lekanda-Guarrotxena A., Grau A., Arechavala-Lopez P. (2020). Fish Density Estimation Using Unbaited Cameras: Accounting for Environmental-Dependent Detectability. J. Exp. Mar. Biol. 527, 151376. doi: 10.1016/j.jembe.2020.151376

CrossRef Full Text | Google Scholar

Fujiwara Y., Kawato M., Poulsen J. Y., Ida H., Chikaraishi Y., Ohkouchi N., et al. (2021a). Discovery of a Colossal Slickhead (Alepocephaliformes: Alepocephalidae): An Active-Swimming Top Predator in the Deep Waters of Suruga Bay, Japan. Sci. Rep. 11, 1–16. doi: 10.1038/s41598-020-80203-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujiwara Y., Matsumoto Y., Sato T., Kawato M., Tsuchida S. (2021b). First Record of Swimming Speed of the Pacific Sleeper Shark Somniosus Pacificus Using a Baited Camera Array. J. Mar. Biolog. Assoc. U.K. 101, 1–8. doi: 10.1017/S0025315421000321

CrossRef Full Text | Google Scholar

Harbour R. P., Leitner A. B., Ruehlemann C., Vink A., Sweetman A. K. (2020). Benthic and Demersal Scavenger Biodiversity in the Eastern End of the Clarion-Clipperton Zone–an Area Marked for Polymetallic Nodule Mining. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.00458

CrossRef Full Text | Google Scholar

Heagney E. C., Lynch T. P., Babcock R. C., Suthers I. M. (2007). Pelagic Fish Assemblages Assessed Using Mid-Water Baited Video: Standardising Fish Counts Using Bait Plume Size. Mar. Ecol. Prog. Ser. 350, 255–266. doi: 10.3354/meps07193

CrossRef Full Text | Google Scholar

Jamieson A. J. (2016). “Landers: Baited Cameras and Traps,” in Biological Sampling in the Deep Sea, vol. vol. 1. (Oxford: Wiley Online Library).

Google Scholar

Johansson F., Leonardsson K. (1998). Swimming Speeds and Activity Levels of Consumers at Various Resource and Consumer Densities Under Predation Risk. Can. J. Zool. 76, 76–82. doi: 10.1139/z97-165

CrossRef Full Text | Google Scholar

Johnson A. F., Jenkins S. R., Hiddink J. G., Hinz H. (2013). Linking Temperate Demersal Fish Species to Habitat: Scales, Patterns and Future Directions. Fish 14, 256–280. doi: 10.1111/j.1467-2979.2012.00466.x

CrossRef Full Text | Google Scholar

King N. J. (2006). “Deep-Sea Demersal Ichthyofauna of Contrasting Localities,” in Mid-Atlantic Ridge, Nazare Canyon (North Atlantic Ocean) and Crozet Plateau (Southern Indian Ocean), With Special References to the Abyssal Grenadier, Coryphaenoides (Nematonurus) Armatus (Hecto) (United Kingdom: University of Aberdeen).

Google Scholar

Krause J., Ward A. J., Jackson A., Ruxton G., James R., Currie S. (2005). The Influence of Differential Swimming Speeds on Composition of Multi-Species Fish Shoals. J. Fish. Biol. 67, 866–872. doi: 10.1111/j.0022-1112.2005.00768.x

CrossRef Full Text | Google Scholar

Leitner A. B., Durden J. M., Smith C. R., Klingberg E. D., Drazen J. C. (2021). Synaphobranchid Eel Swarms on Abyssal Seamounts: Largest Aggregation of Fishes Ever Observed at Abyssal Depths. Deep. Sea. Res. Part Iss., 167. doi: 10.1016/j.dsr.2020.103423

CrossRef Full Text | Google Scholar

Linley T., Lavaleye M., Maiorano P., Bergman M., Capezzuto F., Cousins N., et al. (2017). Effects of Cold-Water Corals on Fish Diversity and Density (European Continental Margin: Arctic, Ne Atlantic and Mediterranean Sea): Data From Three Baited Lander Systems. Deep. Sea. Res. Part II 145, 8–21. doi: 10.1016/j.dsr2.2015.12.003

CrossRef Full Text | Google Scholar

Lowry M., Steffe A., Williams D. (2006). Relationships Between Bait Collections, Bait Type and Catch: A Comparison of the Nsw Trailer-Boat and Gamefish-Tournament Fisheries. Fish. Res. 78, 266–275. doi: 10.1016/j.fishres.2005.11.014

CrossRef Full Text | Google Scholar

Molles M. (2015). “Ecology,” in Concepts and Applications (New York: McGraw-Hill Education).

Google Scholar

Moore P., Howarth J. (1996). Foraging by Marine Scavengers: Effects of Relatedness, Bait Damage and Hunger. J. Sea. Res. 36, 267–273. doi: 10.1016/S1385-1101(96)90795-9

CrossRef Full Text | Google Scholar

Morisita M. (1957). A New Method for the Estimation of Density by the Spacing Method Applicable to Non-Randomly Distributed Populations. Physiol. Ecol. 7:134–44. (In Japanese; available as Forest Searvice translation no. 11116, USDA Forest Service, Washington, DC.).

Google Scholar

Nielsen J., Hedeholm R. B., Heinemeier J., Bushnell P. G., Christiansen J. S., Olsen J., et al. (2016). Eye Lens Radiocarbon Reveals Centuries of Longevity in the Greenland Shark (Somniosus Microcephalus). Science 353, 702–704. doi: 10.1126/science.aaf1703

PubMed Abstract | CrossRef Full Text | Google Scholar

Norse E. A., Brooke S., Cheung W. W., Clark M. R., Ekeland I., Froese R., et al. (2012). Sustainability of Deep-Sea Fisheries. Mar. Policy 36, 307–320. doi: 10.1016/j.marpol.2011.06.008

CrossRef Full Text | Google Scholar

Plaut I. (2001). Critical Swimming Speed: Its Ecological Relevance. Comp. Biochem. Physiol. Part A, 41–50, 131. doi: 10.1016/s1095-6433(01)00462-7

CrossRef Full Text | Google Scholar

Premke K., Klages M., Arntz W. (2006). Aggregations of Arctic Deep-Sea Scavengers at Large Food Falls: Temporal Distribution, Consumption Rates and Population Structure. Mar. Ecol. Prog. Ser. 325, 121–135. doi: 10.3354/meps325121

CrossRef Full Text | Google Scholar

Priede I. G., Merrett N. (1996). Estimation of Abundance of Abyssal Demersal Fishes; a Comparison of Data From Trawls and Baited Cameras. J. Fish. Biol. 49, 207–216. doi: 10.1111/j.1095-8649.1996.tb06077.x

CrossRef Full Text | Google Scholar

Priede I. G., Smith K. L. Jr., Armstrong J. D. (1990). Foraging Behavior of Abyssal Grenadier Fish: Inferences From Acoustic Tagging and Tracking in the North Pacific Ocean. Deep. Sea. Res. Part A 37, 81–101. doi: 10.1016/0198-0149(90)90030-Y

CrossRef Full Text | Google Scholar

Saila S. B., Nixon S. W., Oviatt C. A. (2002). Does Lobster Trap Bait Influence the Maine Inshore Trap Fishery? N Am. J. Fish. Manag. 22, 602–605. doi: 10.1577/1548-8675(2002)022<0602:DLTBIT>2.0.CO;2

CrossRef Full Text | Google Scholar

Sainte-Marie B., Hargrave B. (1987). Estimation of Scavenger Abundance and Distance of Attraction to Bait. Mar. Biol. 94, 431–443. doi: 10.1007/BF00428250

CrossRef Full Text | Google Scholar

Schobernd Z. H., Bacheler N. M., Conn P. B. (2014). Examining the Utility of Alternative Video Monitoring Metrics for Indexing Reef Fish Abundance. Can. J. Fish. Aqua. Sci. 71, 464–471. doi: 10.1139/cjfas-2013-0086

CrossRef Full Text | Google Scholar

Sheaves M. J. (1995). Effect of Design Modifications and Soak Time Variations on Antillean-Z Fish Trap Performance in a Tropical Estuary. Bull. Mar. Sci. 56, 475–489.

Google Scholar

Stoner A., Laurel B., Hurst T. (2008). Using a Baited Camera to Assess Relative Abundance of Juvenile Pacific Cod: Field and Laboratory Trials. J. Exp. Mar. Biol. Ecol. 354, 202–211. doi: 10.1016/j.jembe.2007.11.008

CrossRef Full Text | Google Scholar

Taylor M. D., Baker J., Suthers I. M. (2013). Tidal Currents, Sampling Effort and Baited Remote Underwater Video (Bruv) Surveys: Are We Drawing the Right Conclusions? Fish. Res. 140, 96–104. doi: 10.1016/j.fishres.2012.12.013

CrossRef Full Text | Google Scholar

Tulloch R., Ferrari R., Jahn O., Klocker A., LaCasce J., Ledwell J. R., et al. (2014). Direct Estimate of Lateral Eddy Diffusivity Upstream of Drake Passage. J. Phys. Oceanogr. 44, 2593–2616. doi: 10.1175/JPO-D-13-0120.1

CrossRef Full Text | Google Scholar

Watson R. A., Morato T. (2013). Fishing Down the Deep: Accounting for Within-Species Changes in Depth of Fishing. Fish. Res. 140, 63–65. doi: 10.1016/j.fishres.2012.12.004

CrossRef Full Text | Google Scholar

Whitelaw A., Sainsbury K., Dews G., Campbell R. (1991). Catching Characteristics of Four Fish-Trap Types on the North West Shelf of Australia. Mar. Freshw. Res. 42, 369–382. doi: 10.1071/MF9910369

CrossRef Full Text | Google Scholar

Whitmarsh S. K., Huveneers C., Fairweather P. G. (2018). What are We Missing? Advantages of More Than One Viewpoint to Estimate Fish Assemblages Using Baited Video. R. Soc Open Sci. 5, 171993. doi: 10.1098/rsos.171993

PubMed Abstract | CrossRef Full Text | Google Scholar

Willis T. J., Babcock R. C. (2000). A Baited Underwater Video System for the Determination of Relative Density of Carnivorous Reef Fish. Mar. Freshw. Res. 51, 755–763. doi: 10.1071/MF00010

CrossRef Full Text | Google Scholar

Willis T. J., Millar R. B., Babcock R. C. (2000). Detection of Spatial Variability in Relative Density of Fishes: Comparison of Visual Census, Angling, and Baited Underwater Video. Mar. Ecol. Prog. Ser. 198, 249–260. doi: 10.3354/meps198249

CrossRef Full Text | Google Scholar

Yau C., Collins M., Bagley P. M., Everson I., Nolan C., Priede I. G. (2001). Estimating the Abundance of Patagonian Toothfish Dissostichus Eleginoides Using Baited Cameras: A Preliminary Study. Fish. Res. 51, 403–412. doi: 10.1016/S0165-7836(01)00264-8

CrossRef Full Text | Google Scholar

Yeh J., Drazen J. C. (2011). Baited-Camera Observations of Deep-Sea Megafaunal Scavenger Ecology on the California Slope. Mar. Ecol. Prog. Ser. 424, 145–156. doi: 10.3354/meps08972

CrossRef Full Text | Google Scholar