Assessment of the variation of failure probability of upgraded rubble-mound breakwaters due to climate change

The effects of climate change on coastal areas are expected to significantly influence the risk for port operations. In the present work, a novel methodology for the quantitative assessment of the performances of upgraded rubble-mound breakwaters under a changing climate is proposed. For each considered upgrading option, the failure probability related to a certain limit state is calculated through the implementation of Monte Carlo (MC) simulations, using the factor of change (FoC) method to include the projected future climate. Three indexes are defined for the immediate and intuitive interpretation of the results: i) the ratio between the calculated and the maximum acceptable failure probability during lifetime (r); ii) the rate of the growth of the failure probability during lifetime (s); iii) the coefficient of variation of the failure probability due to both the intrinsic uncertainty of the MC simulation and the variability of future climate (v). The methodology was applied to the case study of the Catania harbor breakwater, considering the failure of different upgrading solutions due to the collapse of the outer armor layer and to excessive mean overtopping discharge. The results revealed the acceptability of the structural and hydraulic performances of all the tested configurations, under both present and future climate. Moreover, a high climate-related variability of the future failure probability was found. The usefulness of the proposed indexes for designer and decision-makers was also demonstrated. In particular, r gives direct information about the acceptability of the structure performances, enabling the immediate comparison between different configurations and climate scenarios. The index s is fundamental to calculate the appropriate times to implement repair interventions during the structure lifetime. Finally, v allows the identification of those situations which requires the design of highly flexible maintenance plans, able to adapt to a very variable climate avoiding excessive costs.

1 Introduction

Climate change is affecting worldwide coastal areas, generally enhancing erosion and flooding phenomena, which threat the existence of marine ecosystems as well as the development of economic activities linked to seaside tourism or port trade (Foti et al., 2020). The hydraulic performances of coastal and harbor defense structures are directly influenced by the effects of global warming, and in particular by mean sea level rise (Church et al., 2013; Galassi and Spada, 2014), increase of extreme storm surge height and frequency of occurrence (Lowe and Gregory, 2005; Vousdoukas et al., 2016), inter-annual variability of wave characteristics (Hemer et al., 2013; Camus et al., 2017; Morim et al., 2019), and reduction of extreme sea levels return period (Vousdoukas et al., 2018). Future increased wave run-up heights and overtopping rates are expected (Chini and Stansby, 2012; Isobe, 2013; Arns et al., 2017), with consequent alteration of port operability (Sanchez-Arcilla et al., 2016; Camus et al., 2019; Izaguirre et al., 2021). The risk of climate change in port operations and breakwater integrity is even more high when harbor breakwaters are aging and deteriorated. Indeed, structural degradation may reduce the safety and serviceability of structures (Li et al., 2015). Therefore, the design of upgrading solutions for existing harbor breakwaters in the face of climate change represents a challenge (Burcharth et al., 2014; Hughes, 2014), because of the intrinsic uncertainty of climate projections (Morim et al., 2018), and the impossibility to apply the assumption of stationary forcing (Chini and Stansby, 2012; Davies et al., 2017) typical of the traditional deterministic or semi-probabilistic design (i.e. level 0 and level I) methodologies.

Reliability-based design methods, which use the failure probability as a measure of the performance of the structure, should be employed for the assessment of the response of existing and upgraded breakwaters under a changing climate. Indeed, probabilistic approaches enable the inclusion of the uncertainty of the design variables, namely external forcing, coefficients of empirical design formulas, parameters describing geometry and material of the structure, in a more or less sophisticated way (Burcharth, 1987; Burcharth, 1993). Moreover, the concept of return period typical of traditional level 0 and I design methods, e.g. the ones proposed by Tomasicchio et al. (1996) and Burcharth and Sørensen (1999), is overcome. Even if the theoretical basis of the probabilistic design of harbor breakwaters date back to second half of the twentieth century (CIAD project group, 1985; van der Meer, 1988b; Burcharth, 1993), only recently it has been included in national codes and guidelines (US Army Corps of Engineers, 2002; Ports and Harbours Bureau et al., 2009; ROM 1.0-09, 2010). Several studies have been conducted for the definition of methodologies for the assessment of the failure probability of vertical or rubble-mound breakwaters, usually based on level III calculation methods, such as the Monte Carlo (MC) simulation technique (Castillo et al., 2004; Kim and Suh, 2010; Maciñeira et al., 2017; Lara et al., 2019).

However, there are few investigations which consider the influence of the effects of global warming on the structure response. Takagi et al. (2011) presented a methodology to evaluate the potential failure risk due to the sliding of vertical breakwaters in a future storm event using a MC simulation. Future wave climate was generated by imposing a 10% increase of the future wind speed of tropical cyclones in the Asia-Pacific Region, to be used as input of the spectral wave model SWAN. Also Suh et al. (2012) and Kim and Suh (2014) investigated the influence of future mean sea level and wave climate on the time-dependent risk of caisson sliding during the service life of the breakwater, using existing projection data-set as input of the MC simulations. Uncertainties in design variables (i.e. design wave height, horizontal and vertical wave force, friction coefficient) were modeled by the calculation of the corresponding mean and standard deviation as a function of their characteristic value, bias and coefficient of variation, which have been deduced from existing literature. Moreover, severe storm waves comparable with the design waves were assumed to occur approximately once a year, and to be composed by 1000 waves. Galiatsatou et al. (2018) proposed a reliability-based approach coupled with economic optimization techniques for the assessment of the performances and of the costs of differently upgraded rubble-mound breakwaters. Future climate conditions were defined based on state of art estimations of the 100-year extreme significant wave height and mean sea level rise increase, neglecting variations of storm surge height. The probability of port downtime was calculated using both level II and level III methods, with reference to the ultimate limit state (ULS) due to armor layer instability, excessive overtopping or toe scouring, and the serviceability limit state (SLS) due to wave transmission or wave diffraction.

The actual state of art of the probabilistic assessment of the performances of rubble-mound structures under the effects of climate change presents two main gaps. First, the expected future sea level and wave climate are included in a rough way. Indeed, projected mean sea level rise and variations of the significant wave height are used to adjust the present wave climate conditions, ignoring possible modifications of storm surge height, and with a simplified estimation of the frequency of occurrence and duration of extreme wave storms. The second research gap refers to the lack of indexes to quantitatively compare present and future performances of different configurations of the structure. In this context, the present work proposes a probabilistic methodology for the quantitative assessment of the influence of the effects of climate change on the response of upgraded rubble-mound harbor breakwaters, with reference to ULS or SLS due to independent failure modes. The factor of change method (Kilsby et al., 2007; Fatichi et al., 2011; Peres and Cancelliere, 2018) is employed to include the effects of climate change on wave climate, and the MC technique is used to estimate the failure probability of the structure. Easy-to-calculate indexes are defined to allow the comparison between the present and future responses of the tested configurations. In this way, the results of the application of the proposed methodology can guide both the design of upgrading solutions and maintenance plans for existing breakwaters and the related decision-making processes, minimizing the risk of over or under-design and providing useful inputs for the cost-benefit analysis.

The paper is organized as follows. Section 2 describes the proposed probabilistic methodology and presents the data used for its application to the emblematic case study of the Catania harbor breakwater (Italy) under present, RCP4.5 and RCP8.5 climate scenarios. The obtained results on marine climate and failure probability are compared and discussed in section 3. Finally, section 4 summarizes the main conclusions of the work and suggests possible future developments.

2 Methods and materials

2.1 Characterization of local extreme wave climate

The probabilistic assessment of the performances of upgraded rubble-mound breakwaters requires the statistical characterization of local extreme wave climate, considering both present and future scenarios. To this aim, time series of wave climate descriptors are needed, which can be derived from buoy measurements or reanalysis models for the present climate, and from climate projection models for the future scenarios. In particular, the following wave climate variables are here considered: i) significant wave height; ii) mean wave period; iii) sea storm duration. Moreover, the storm surge phenomenon is studied, focusing on its correlation with extreme significant wave height.

For the present climate, the directional extreme value analysis of the offshore significant wave height (H_s0) is performed, by applying the peak over threshold (POT) method to detect the extreme events and evaluate the mean number of storms per year (λ). In the present work, peaks with H_s0 higher than 1.50 m are considered, assuming a minimum temporal distance equal to 12 hours between independent events (Boccotti, 2004). The adaptation of extreme value distributions (e.g. Generalized Extreme Value, Weibull, Generalized Pareto) to the obtained samples of extreme events is performed through the method of moments estimation (MME). Such a method allows the calculation of the scale, shape and location parameters of the selected probability distribution functions by replacing the theoretical mean, standard deviation, skewness and kurtosis for the specified distribution by the corresponding sample moments. The scale parameter (α_sc) provides indications about the scale on the horizontal axis of the probability density function (PDF) plot. The shape parameter (κ_sh) affects the general shape of the PDF. Finally, the location parameter (ζ_lc) gives information about where the probability distribution is centered in the horizontal axis of the PDF plot. The best fitting distribution is identified through the visual comparison between the sample data and the PDF, as well as through the Kolmogorov-Smirnov goodness-of-fit test, which determines whether a sample comes from a specific distribution.

The effects of climate change on extreme wave climate are introduced by modifying the scale, shape and location parameters of the distribution fitted to the present directional extreme H_s0, based on factors of change (FoC) derived from the comparison of the projected future scenarios and the baseline climate provided by the same projection model (Kilsby et al., 2007; Fatichi et al., 2011; Peres and Cancelliere, 2018). The FoC method consists in the evaluation of the difference between statistics (e.g. mean, standard deviation, skewness, kurtosis) of a climate variable computed for the future scenario and for the present control period provided by the projection model, by applying the following formula:

$\begin{array}{ll}FoC=\frac{M_{m,f}}{M_{m,c}}& (1)\end{array}$

where M_m,f and M_m,c are the generic statistical moments evaluated for the modeled future and control periods, respectively. Once the FoC is calculated, the future value of the considered statistical moment (M_f) is evaluated by multiplication to the observed moment in the control period (M_obs,c):

$\begin{array}{ll}{M}_f=FoC\times M_{obs,c}& (2)\end{array}$

The FoC method is here applied considering the samples of extreme H_s0 derived from the application of the POT method, with threshold equal to 1.50 m and minimum distance between independent events equal to 12 hours, to the time series of the observed control period, the modeled control period and the future period. The future period is divided into sub-periods, using a yearly moving time window covering the same number of years of the control period. For each future sub-period, the MME method is employed to estimate α_sc, κ_sh and ζ_lc of the extreme value distributions of H_s0 which take into account the effects of climate change, using as input data mean, standard deviation, skewness and kurtosis of extreme H_s0 calculated through equations 1 and 2.

The statistical characterization of mean wave period, sea storm duration and storm surge height is performed by modeling their correlation to H_s0. When dealing with coastal structure design, both copula functions (Muhaisen et al., 2010; Mercelis et al., 2014; Salvadori et al., 2015; Malliouri et al., 2021; Radfar et al., 2022) and site-specific empirical relationships (Takagi et al., 2011; Suh et al., 2013; Mercelis et al., 2014; Maciñeira et al., 2017; Tabarestani et al., 2020) are widely employed to model the correlation between dependent climate variables. In the present work, the definition of empirical relationships between H_s0 and the offshore mean wave period (T_m0), the sea storm duration (d_s) and the storm surge height (h_ss) is proposed, because of their greater ease of use. The site-specific coefficients of such empirical relationships, whose mathematical form is considered not to change in time, are calculated through the application of the least squares method to both the measured (or reanalysis) and projected data-sets, thus obtaining different values for present and future climate scenarios. The latter are analyzed using the same yearly moving time window defined for the application of the FoC method.

Once the offshore wave climate has been characterized, the wave propagation towards the breakwater needs to be performed. Wave propagation is usually simulated by means of numerical models, which take into account shoaling, refraction and breaking processes.

2.2 Calculation of the failure probability during lifetime

Once the most suitable upgrading concepts for the considered rubble-mound breakwater have been identified (Burcharth et al., 2014) and designed applying traditional (i.e. level 0 or II) methods, their performances during lifetime can be assessed in terms of failure probability, and then compared to the design requirements. The useful life of harbor breakwaters is long enough to experience the effects of climate change (Hallegatte, 2009), because its minimum length ranges between 25 and 50 years, depending on the economic repercussions due to partial or total loss of functionality (Tomasicchio et al., 1996; ROM 1.0-09 (2010)). Therefore, future scenarios accounting for the effects of climate change must be considered for the probabilistic calculations.

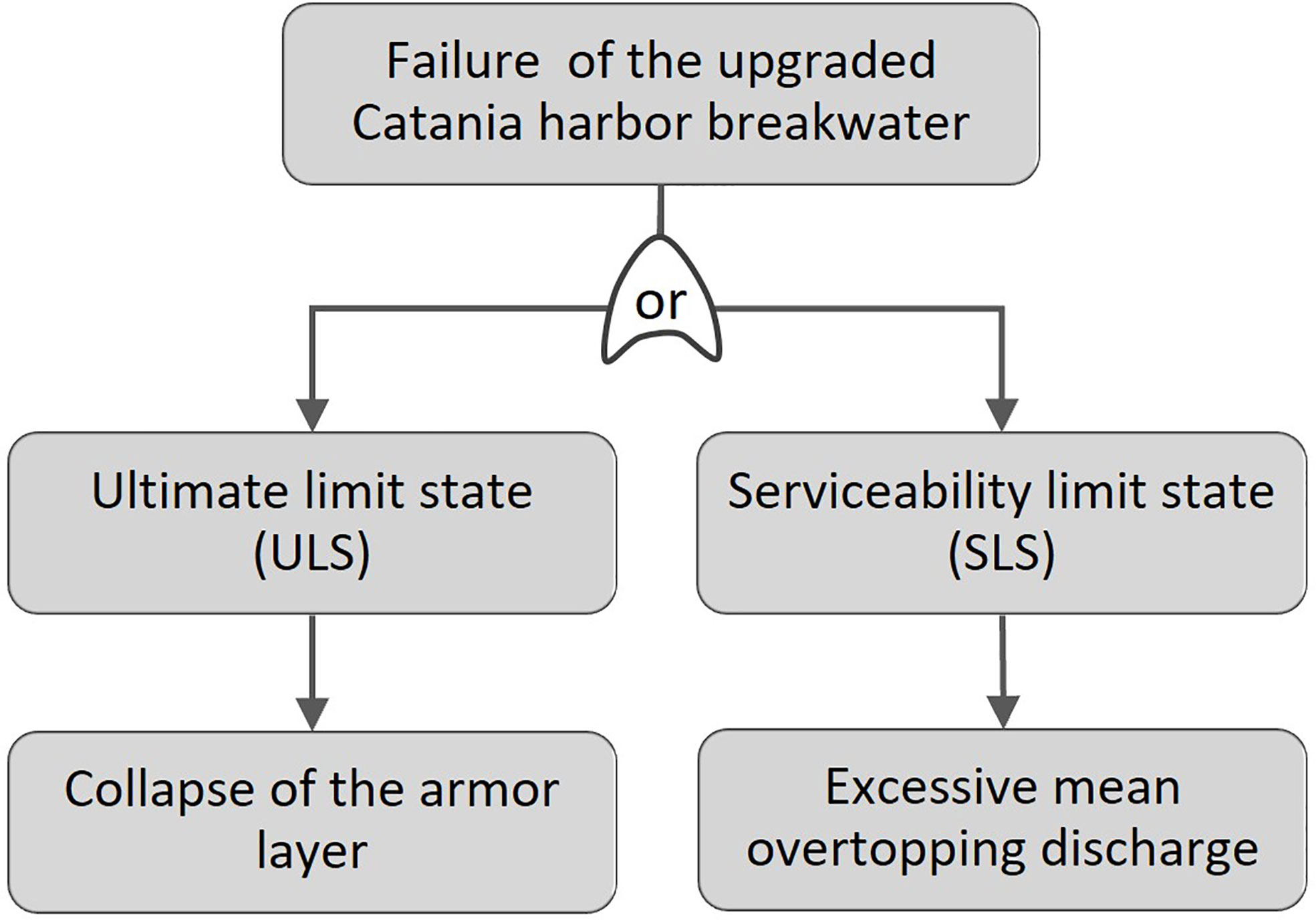
Here, a methodology for the assessment of the failure probability of upgraded harbor rubble-mound breakwaters during lifetime under the effects of climate change is proposed. First, a failure tree is defined. Then, the main failure modes referred to ULS or SLS are selected, assuming that they are related according to a series system. The series system, which implies that the failure of the structure occurs if at least one of the considered failure modes takes place, is typically employed for coastal structures (US Army Corps of Engineers, 2002). The governing equation of the selected failure mode (e.g. stability of the armor layer, mean overtopping discharge, toe berm stability, etc) is derived from state of art or site-specific experimental or numerical equations, and re-written as a reliability function (US Army Corps of Engineers, 2002; Jonkman et al., 2015):

$\begin{array}{ll}Z=R-S& (3)\end{array}$

where R is the resistance of the structure to the external solicitations S, being both R and S stochastic variables. R is usually linked to the geometry of the structure and to the characteristics of the component materials, whereas S sually contains the water density and the hydrodynamic parameters. If Z<0 (i.e. R<S), the selected limit state is overcome by the structure and the failure occurs. When the failure probability (i.e. P_f = P(Z<0)) is greater or smaller than the acceptance limit, the structure is under-designed or over-designed, and needs to be modified to improve its performances or reduce the construction costs, respectively. The modified structure is the new object of the probabilistic calculations, and the optimization process goes on in an iterative way until the design requirements are reached (Kim and Suh, 2006; Malliouri et al., 2021).

Figure 1 summarizes the proposed procedure to be applied for the calculation of the probability that the structure reaches a certain limit state, described by a reliability function Z. A level III method is employed, which is based on the implementation of probabilistic simulations through the MC technique. Such a method overcomes the concept of design return period, which is typical of level 0 or level I design approaches, and uses the whole probability distributions of the variables involved in the design process, also modeling their reciprocal correlations. According to the indications of ROM 1.0-09 (2010), each realization of the MC simulation is a life cycle of the structure, which consists of a known number of meteorological years. For a certain climate scenario, during each meteorological year, a certain number of sea storms is randomly generated from the probability distribution functions of the wave climate parameters for the considered site, which have been previously defined following the procedure described in section 2.1. Such sea storms may cause or not the achievement of the considered limit state. Therefore, the failure probability during lifetime is defined as the probability that the structure reaches at least once the considered limit state during its life cycle. The failure probability during a t-years life cycle and its standard deviation are calculated as follows (Lara et al., 2019):

$\begin{array}{ll}{P}_{f,t}=P_f(0,t)=\frac{N_f(0,t)}{N_r}& (4)\end{array}$

$\begin{array}{ll}{\sigma }_{P_{f,t}}={\sigma }_{P_f}(o,t)=\sqrt{\frac{P_f(0,t)\times \left(1-P_f(0,t)\right)}{N_r}}& (5)\end{array}$

FIGURE 1

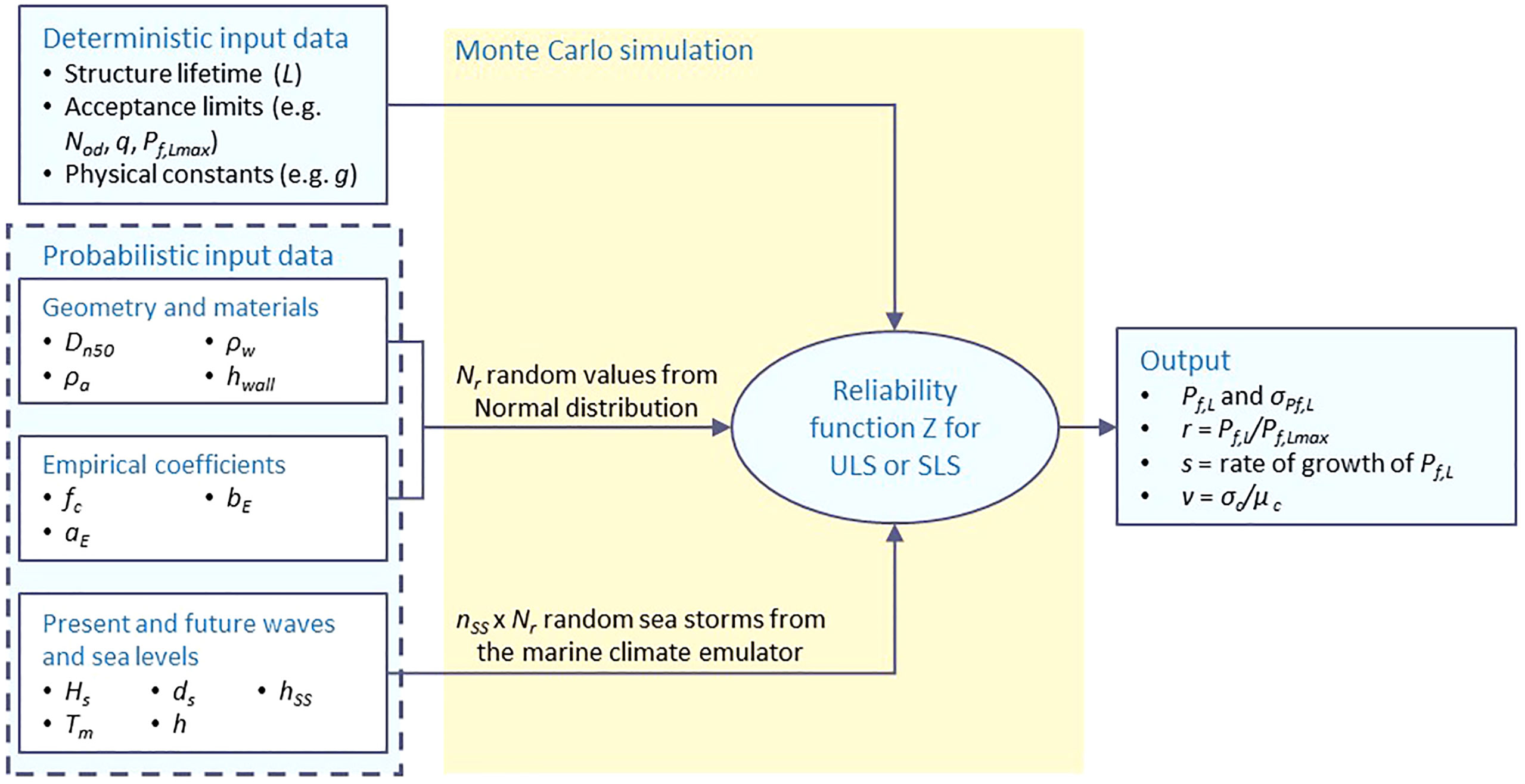
Figure 1 Block diagram of the proposed methodology for assessment of the failure probability of upgraded harbor rubble-mound breakwaters.

Where N_f(0, t) is the number of t-years life cycles with at least one failure (i.e. Z<0) and N_r is the total number of simulated life cycles (i.e. realizations of the MC simulation). The given definition of P_f,t implies that the following relationship is valid:

$\begin{array}{ll}{P}_{f,t}=P_f(0,t)={\displaystyle \sum _{i=1}^t{P}_f(i-1,t)}& (6)\end{array}$

The length of the structure life cycle t is set equal to the structure lifetime (L) suggested by codes and guidelines which include the use of level III design methods, e.g. ROM 1.0-09 (2010). Therefore, in the following the failure probability P_f,L is considered. The maximum acceptable failure probability during lifetime (P_f,Lmax), whose value depends on the design requirements, is also fixed according to the above mentioned codes and guidelines. The most appropriate number of realizations of the MC simulation is selected through a preliminary analysis of the stabilization process of P_f,L and of its coefficient of variation (CV=σ_Pf,L/P_f,L ) by varying N_r. The aim of such an analysis is the identification of the value of N_r able to provide a compromise between accuracy of the simulation results and calculation times. In the present work, a maximum acceptable CV equal to 0.35 is considered. It should be noted that the required number of realizations to obtain a certain CV increases for lower P_f,L.

The N_r life cycles are randomly simulated using as input data the probability distributions of the involved stochastic variables, which are: i) descriptors of the structure geometry and materials (e.g. density of water and of blocks, slope of the armor layer, height of the wave wall); ii) empirical coefficients of the reliability function; iii) descriptors of sea level and wave climate. The first two groups of variables are described using normal distributions, whose mean and standard deviation are deduced from existing literature or available data-sets (van der Meer, 1988b; Burcharth, 1992; Lara et al., 2019). The corresponding random values are generated for each simulated life cycle, under the hypothesis of no changes of the structure composition, geometry and behavior during lifetime, and imposing truncation limits to the normal distributions to avoid unrealistic values. Instead, the random generation of sea levels and sea storms occurring during the structure useful life is performed by a marine climate emulator, whose detailed description is presented in section 2.3. The number of sea storms (n_ss) to generate for each life cycle is evaluated as follows:

$\begin{array}{ll}{n}_{ss}=L\times \lambda & (7)\end{array}$

where λ is the mean annual frequency of sea storms derived from the POT analysis of the H_s0 time series corresponding to the selected climate scenario (see section 2.1). Therefore, for each simulation a total of n_ss × N_r different sea storms are simulated. Finally, physical constants (e.g. g) and limits values of parameters used to quantify the structure performances (e.g. limit damage conditions or mean overtopping discharges) are considered as deterministic variables.

In order to enable the immediate and quantitative comparison between the failure probabilities during lifetime calculated for different structure configurations under both present and future climate, easy-to-calculate indexes are here proposed. The first index (r), which is defined to quantify the safety level ensured by the structure, is calculated according to the following formula:

$\begin{array}{ll}r=\frac{P_{f,L}}{P_{f,Lmax}}& (8)\end{array}$

If r is greater than one, the failure probability is not acceptable, otherwise the performances of the structure are sufficient to satisfy the design requirements. Besides the value of P_f,L, also the rate of the growth of the failure probability during lifetime provides useful information about the performances of the structure and indications to plan possible structural interventions. Such a rate can be calculated as the slope s of the linear regression model which describes the variation of P_f,t from the null value of the year zero to the final value corresponding to the year L (see equation 6). If the effects of possible maintenance interventions are not included, s is always greater than or equal to zero, meaning that P_f,t can only increase or remain constant during the period between the years zero and L. Finally, since the time series of climate data under a certain scenario are elaborated using a yearly-moving time window of fixed length (see section 2.1), the enhancement of the MC outputs uncertainty due to the variability of the input climate among the defined sub-periods can be quantified using the following coefficient of variation:

$\begin{array}{ll}v=\frac{{\sigma }_c}{{\mu }_c}& (9)\end{array}$

where σ_c and μ_c are the standard deviation and the mean of P_f,L calculated with reference to the above-mentioned sub-periods of the considered future scenario. If the coefficient of variation is greater than or equal to one, P_f,L shows high variability as the future time window changes.

2.3 Marine climate emulator

A marine climate emulator has been designed to generate random sea storms and sea levels, also considering the effects of climate change, to be used for the performance of the MC simulations described in section 2.2. The required input data are the extreme value distributions of H_s0 and the site-specific empirical relationships between H_s0 and T_m0, d_s and h_ss, which are defined for the present and future scenarios following the procedure described in section 2.1. The mean water depth at the breakwater site (h) is assumed independent from the other climate descriptors and normally distributed, with standard deviation calculated according to the following formula (Castillo et al., 2006):

$\begin{array}{ll}\sigma =\frac{(h+h_{at})-(h-h_{at})}{4}& (10)\end{array}$

where h_at is the astronomical tide characteristic of the studied site.

For each climate scenario, and for each defined sub-period, a random offshore sea storm is generated according to the following procedure:

1. an initial random H_s0 is drawn from the central fit of the extreme value distribution of offshore significant wave height;

2. a final random H_s0 is drawn from the normal distribution having mean equal to H_s0 previously generated from the central fit, and standard deviation corresponding to the width of the 95% confidence bounds (CB) of the extreme value distribution of the offshore significant wave height;

3. an initial random value of each H_s0-dependent variable (i.e. T_m0, d_s and h_ss) is generated form the central fit of the corresponding site-specific empirical relationships, using as input the last drawn H_s0;

4. a final random value of each H_s0-dependent variable is generated form the normal distribution having mean equal to the value previously generated from the central fit of the site-specific empirical law and standard deviation corresponding to the width of its 95% CB.

The above described procedure is repeated n_ss × N_r times, in order to obtain the required number of offshore sea storms for the performance of the MC simulation (see section 2.2).

The offshore wave conditions need to be propagated towards the coast. As stated in section 2.1, wave propagation is usually simulated by means of numerical models. However, the numerical propagation of each randomly generated wave condition towards the breakwater site would significantly increase the calculation time required for the performance of MC simulations. Therefore, the possibility to define more or less complex site-specific formulations calibrated on a data-set made up of measured or reanalysis extreme offshore wave conditions and corresponding numerically propagated ones should be considered, in order to avoid the performance of a numerical simulation for each sea storm to generate. Such site-specific formulations include the propagation processes simulated with the numerical model in a simplified manner, thus taking into account both shoaling and refraction, as well as wave breaking. Wave breaking is further checked at the breakwater site using the breaking criteria for the identification of depth limited or steepness limited waves. The application of such criteria requires the knowledge of the water depth at the breakwater site for each simulated sea storm, which is calculated as the sum between the corresponding h_ss and a random value of h drawn from its normal distribution.

2.4 Case study

2.4.1 The Catania harbor breakwater

The Catania harbor breakwater was selected for the application of the proposed methodology for the quantitative assessment of the performances of upgraded rubble-mound breakwaters under a changing climate. The Port of Catania, which is located on the Eastcoast of Sicily, is one of the Italian commercial ports of national interest, thanks to its barycentric position with respect to the Suez Channel, the Strait of Gibraltar, the European ports and the North-African ports (see Figure 2A). The “Levante” breakwater represents the main protection of the harbor basin from the offshore waves (see Figure 2B). The wave rose and the plot of extreme H_s0 against mean wave direction showed in Figure 2C indicate that the most energetic sea states come from the angular sector centered in the 90°N direction. The Catania harbor breakwater was born in the XVIII century as a composite structure, and then converted into the present 2.25 km long rubble-mound breakwater (Franco, 1994; Oumeraci, 1994; Takahashi, 2002). The actual armor layer appears severely damaged, and its mean sea side slope significantly reduced, because of the off-shore slip of the 62 t cubic concrete blocks. The deteriorated structure, which lost the original geometrical and structural homogeneity, may not be able to withstand the increasingly frequent extreme marine events and properly limit the consequent overtopping discharges. Such a condition would correspond to limitations to the harbor activities, which must be overcome to ensure the satisfaction of the actual and projected future demand of port services. Therefore, the local Port Authority decided to perform a restoration and upgrading intervention.

FIGURE 2

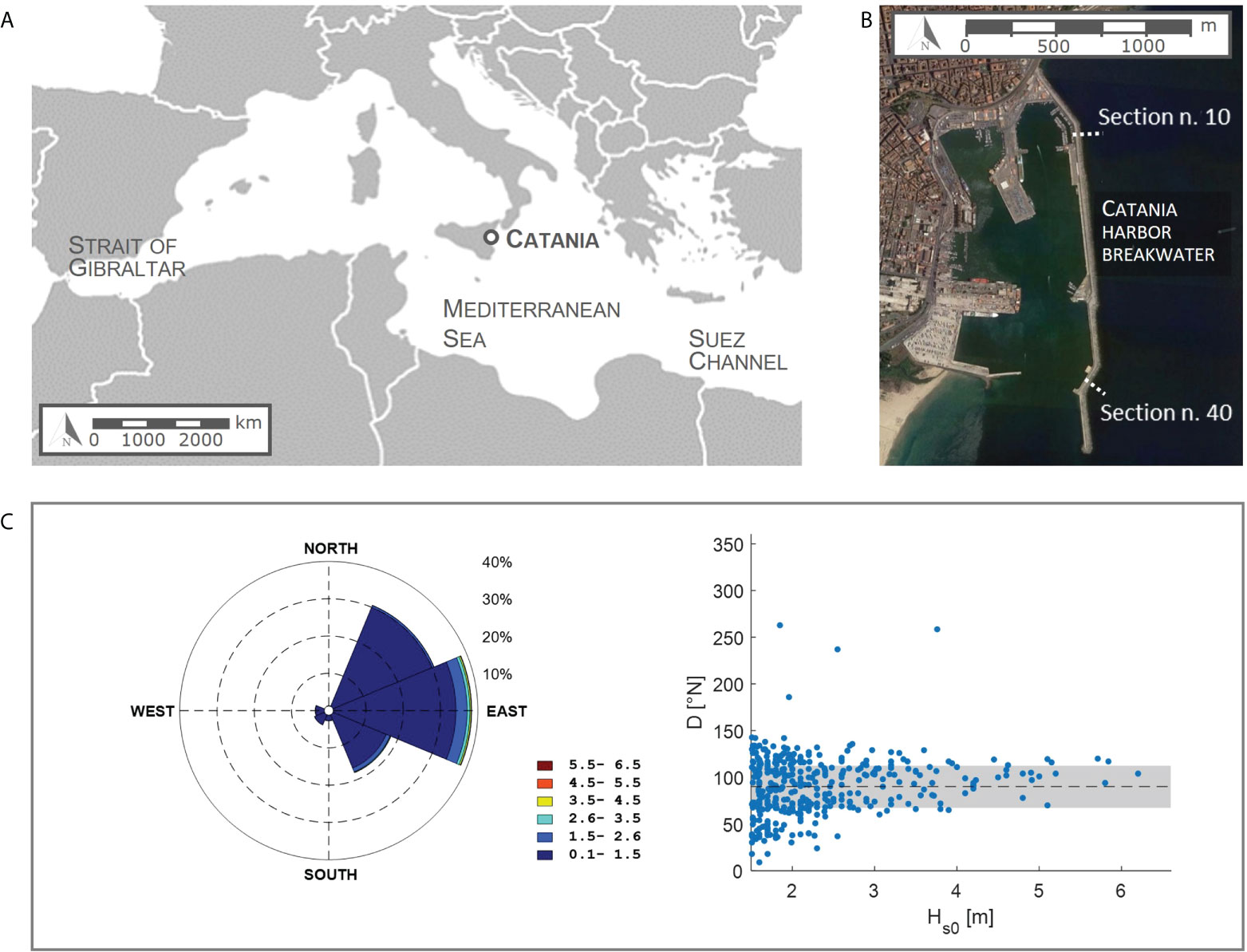
Figure 2 (A) Location of Catania. (B) Layout of the port of Catania, and indication of the outer breakwater representative cross-sections (satellite view from Google Earth 2020). (C) Wave rose and plot of the offshore significant wave heights greater than 1.50 m against mean wave direction (the shaded area represents the 45°-wide sector centered in the 90°N direction).

Following the suggestions of Burcharth et al. (2014), upgrading solutions which consist in the heightening of the existing wave wall and/or the addition of extra armor blocks were considered. The extra armor units can be placed according to a regular design slope or following the irregularities of the existing structure through the construction of a single or double layer, with a toe berm to ensure their stability. In particular, the following six configurations have been verified through the performance of physical and numerical tests (Stagnitti et al., 2020; Stagnitti et al., 2022):

1. configuration E, which is the existing structure whose wave wall height is +8.50 m above mean sea level (see Figure 3A);

2. configuration EM, which consists in the simple heightening of the wave wall up to +9.50 m above mean sea level (see Figure 3B);

3. configuration AS, which consists in the armor layer restoration with 30 t Antifer according to the design slope of 1:2 (see Figure 3C);

4. configuration AD, which consists in the addition of a double layer of 30 t Antifer smaller than the existing ones, following the irregularities of the present armor layer (see Figure 3D);

5. configuration CM, which involves the addition of a single layer of 62 t cubes equal to the existing ones, following the irregularities of the present armor layer (see Figure 3E);

6. configuration CS, which consists in the raising of the wave wall up to +9.50 m above mean sea level and the addition of a single layer of 62 t cubes equal to the existing ones according to the design slope of 1:2, after the regularization of the present armor layer (see Figure 3F).

FIGURE 3

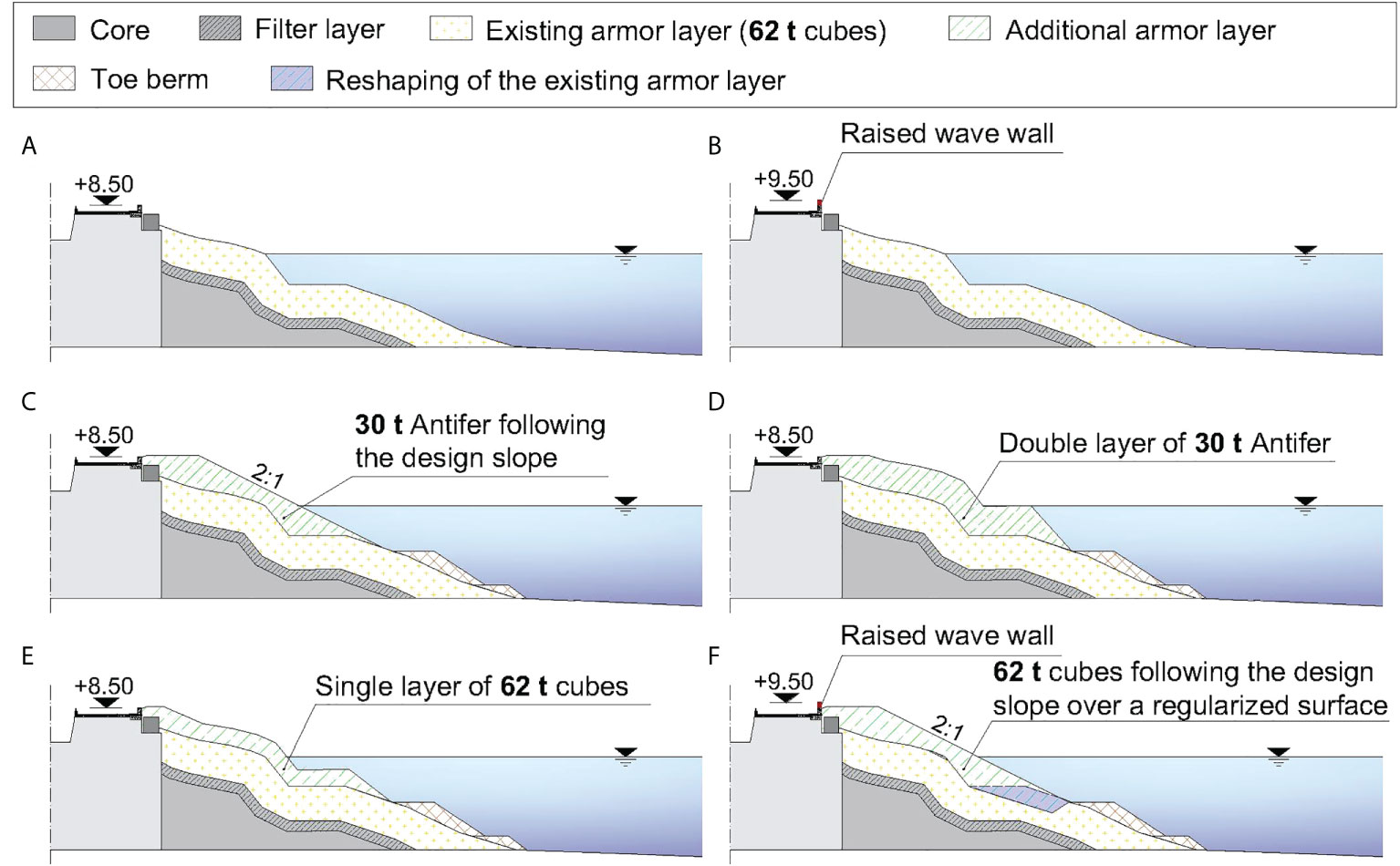
Figure 3 Configurations of the Catania harbor breakwater: (A) existing structure; (B) existing structure with heightened wave wall; (C) upgraded structure with additional 30 t Antifer units placed according to a 2:1 slope; (D) upgraded structure with additional double layer of 30 t Antifer units; (E) upgraded structure with one additional layer of 62 t cubes; (F) upgraded structure with additional 62 t cubes placed according to a 2:1 slope over the reshaped existing armor layer, and with heightened wave wall.

It should be noted that the non-homogeneity of the existing armor layer has strong consequences on the design of the quarry stone berm to be constructed at the toe of the additional blocks. Indeed, if the toe berm is designed with a constant shape for the whole breakwater, without including the reshaping of the existing armor layer, at some cross-section the additional blocks may not be directly in contact with the internal slope of the berm.

2.4.2 Composite modelling

The definition of the reliability functions to be used for the assessment of the failure probability of existing and upgraded breakwaters requires the identification of formulas for the description of damage dynamics and overtopping phenomenon valid for the considered structures. Because of the non-conventional nature of the existing and upgraded Catania harbor breakwater, the response of the existing and upgraded structure to increasing wave load was assessed through the combination of experimental and numerical results on damage dynamics and overtopping phenomena, i.e. by performing the composite or hybrid modeling (Oumeraci, 1999; Guanche et al., 2015; Di Lauro et al., 2019; Kamphuis, 2020). In this way, the performances of existing design formulas in representing damage progression and overtopping phenomenon were assessed, and new site-specific relationships were defined. In particular, the experimental results were employed to investigate damage dynamics of the outer armor layer and acquire data for the calibration of the numerical model, whose outputs were used for the analysis of the overtopping phenomenon.

The experimental campaign was carried out at the Hydraulic Laboratory of the University of Catania (Stagnitti et al., 2020; Stagnitti et al., 2022). A total of 192 two-dimensional physical model tests were performed at 1:70 scale inside a flume 18.00 m long, 1.20 m high and 2.40 m wide, built within a tank equipped with a flap-type wavemaker for the generation of random waves using JONSWAP spectra. The six configurations described in section 2.4.1 were studied considering two representative cross-sections of the breakwater, namely sections no. 10 and no. 40 (see Figure 2B), in order to assess how the lack of uniformity along the existing armor layer may influence the design of upgrading solutions. Configurations AS, AD and CM at section no. 10 are characterized by the lack of direct contact between the additional armor blocks and the toe berm (e.g. Figures 3C–E), contrary to configuration CS at section no. 10 and AS, AD, CM and CS at section no. 40 (e.g. Figure 3F). For each tested configuration, five different sea states of 4500 waves, divided into three equal intervals, were generated. The reproduced waves were perpendicular to the structure, since the most energetic sea storms reaching the Catania harbor breakwater come from 90°N (see Figure 2C). The first four sea states correspond to wave conditions having return period equal to 5, 10, 50 and 100 years, respectively. Instead, the fifth sea state is characterized by significant wave height equal to 120% of the 100-years return period one. Experimental data regarding wave characteristics, reflection phenomenon, damage dynamics and mean overtopping discharge were acquired. In particular, the incident and reflected wave motion was measured through the four-gauge method of Faraci et al. (2015). Damage progression of the outer armor layer was investigated through the analysis of the traditional damage parameter N_od and of novel descriptors of the armor surface roughness. Finally, a specially designed measuring system was employed for the acquisition of the overtopping volumes. o mean sea level) in the range 0.88÷2.13 and Iribarren number in the range 2.15÷2.76.

The stability of the upgrading solutions with additional armor layer (i.e. configurations AS, AD, CM and CS) was examined in depth. To the authors’ knowledge, no damage progression formulas exist for rubble-mound structures with more than two layers of cube-shaped units placed according a slope of 1:2. Therefore, the experimental N_od measured at the end of each sea state were compared to the traditional formula of van der Meer (1988a), hereinafter vdM formula, which is valid for double layers of cubes laid on a slope of 1:1.5 with a notional permeability equal to 0.4:

$\begin{array}{ll}\frac{H_s}{\Delta D_{n50}}=f_c\times \left(6.7\frac{N_{od}^{0.4}}{N_w^{0.3}}+1\right)\times {\left(\frac{2\pi H_s}{g{T}_m^2}\right)}^{-0.1}& (11)\end{array}$

where N_w is the number of incident waves, Δ = ρa/ρw − 1 and D_n50 are respectively the relative density and the median nominal diameter of the armor blocks, H_sis the incident significant wave height, T_m is the mean wave period, g is the gravity acceleration and f_c is an empirical coefficient equal to 1.00 with a standard deviation (σ) equal to 0.10. As expected, the vdM formula does not provide a good approximation of the experimental damage, since the tested structures differ from the traditional structure type for which the vdM formula was calibrated, in terms of geometry, layering and porosity. In particular, the vdM formula overestimates the measured N_od, which is accordance with the fact that the tested sections are characterized by a slope flatter than 1:1.5. The adaptation of the vdM formula to the experimental data was performed through the calibration of the empirical coefficient f_c, using the least squares method. The physical model results reveal the existence of two different responses of the structure in the case of direct or not direct contact between the additional armor units and the toe berm, hereinafter indicated as SS and NSS configurations. For this reason, two different f_c were calculated, distinguishing between SS and NSS configurations. Figures 4A, B shows the experimental N_od as a function of the stability parameter Hs/ΔD_n50, together with the fitted equation 11 and its 95% CB. As reported in Table 1, the experimental f_c is equal to 1.72 (σ = 0.29) and 1.35 (σ= 0.20) for SS and NSS configurations, respectively.

FIGURE 4

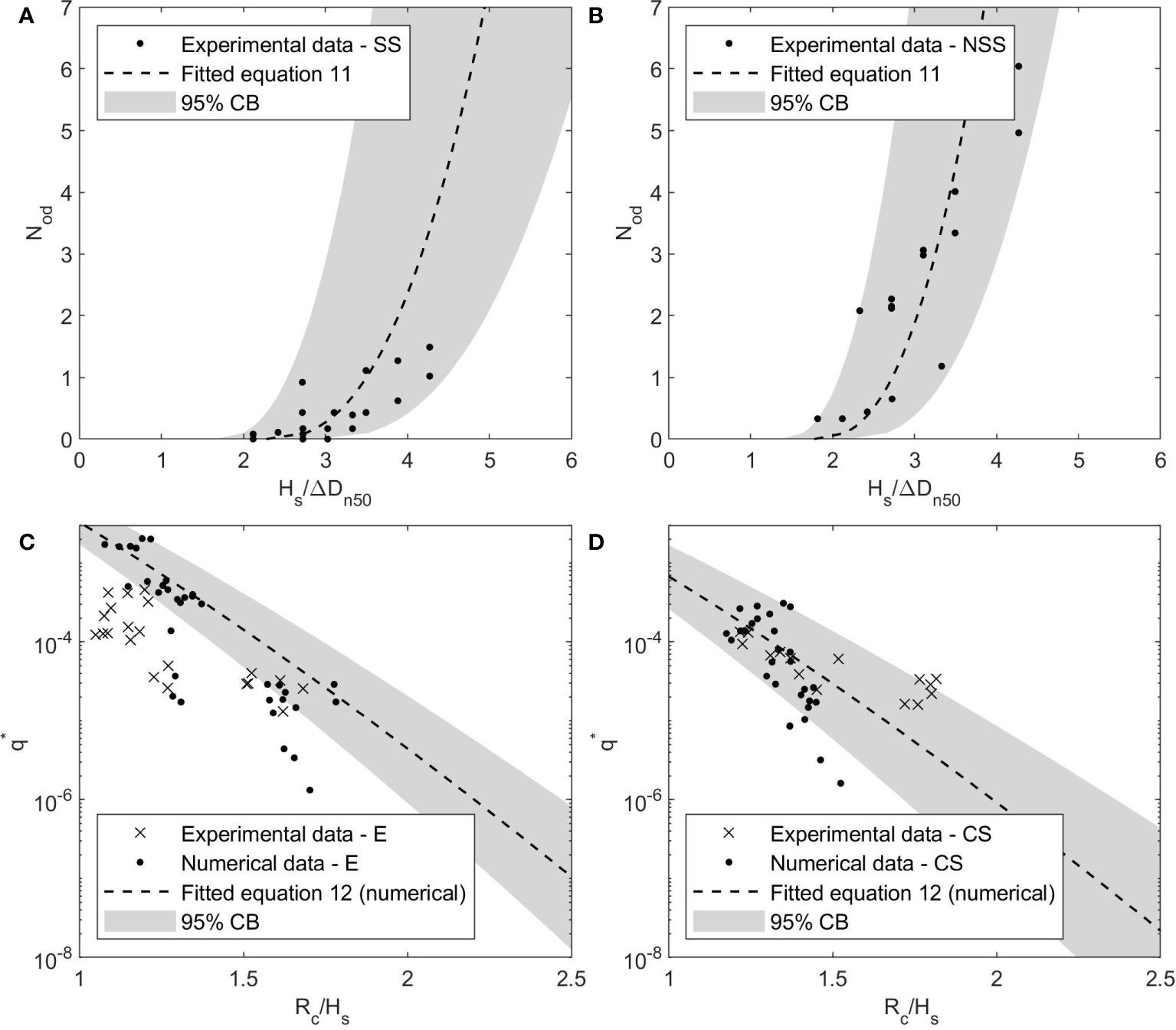
Figure 4 Site-specific experimental formulas for the variation of the damage parameter N_od as a function of the stability number for: (A) SS configurations; (B) NSS configurations. Comparison between experimental and numerical data and site-specific numerical formulas for the variation of the non-dimensional mean overtopping discharge as a function of the non-dimensional structure free-board: (C) configuration E; (D) configuration CS "q*" is the name of the plotted variable.

TABLE 1

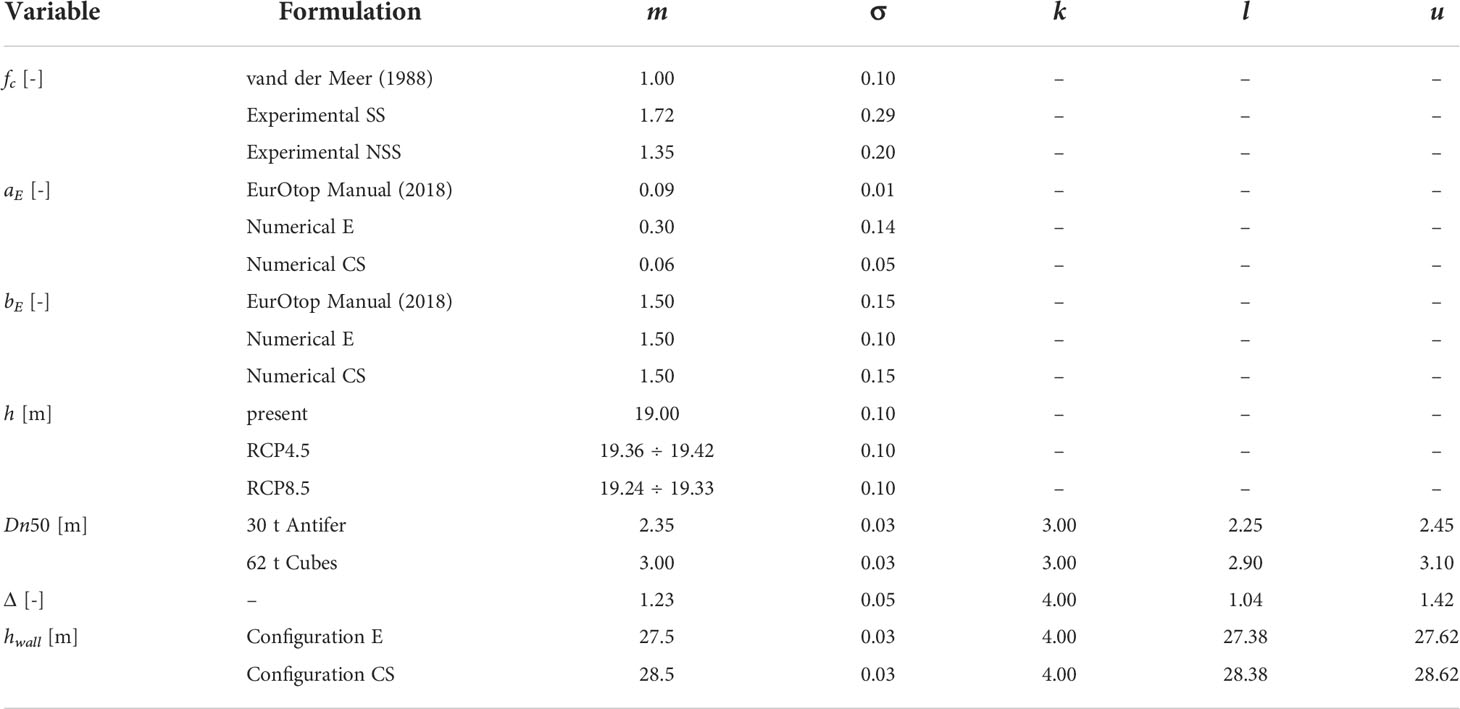
Table 1 Mean (m) and standard deviation (σ) of the normally distributed variables used to perform the Monte Carlo simulations, and parameter k for the calculation of the lower (l) and upper (u) limits of the truncated distributions (f_c coefficient of the ULS reliability function, a_E and b_E coefficients of the SLS reliability function, h mean water depth, D_n50 mean nominal diameter, Δ relative density, h_wall height of the wave wall measured with respect to the toe of the structure).

The experimental results on overtopping and reflection phenomena were employed for the calibration of the numerical model of the Catania harbor breakwater, which allowed the construction of larger data-set for the investigation of the overtopping phenomenon. The extensively validated IH2VOF numerical model (Lara et al., 2008; Guanche et al., 2009; Di Lauro et al., 2019), was employed, which is able to solve the 2D Volume-Averaged Reynolds averaged Navier–Stokes (VARANS) equations (Lara et al., 2011). Section n. 40 of the Catania harbor breakwater was studied (see Figure 2B), considering configurations E and CS, which according to the experimental results are the less and most performing solutions, respectively. The 2D simulations were performed inside a numerical flume 4.50 m wide and 0.65 m high, meshed using a uniform grid with Δx equal to 0.020 m and Δy equal to 0.010 m. The porosity parameters characteristic of each layer of the structure, namely α, β, c_A and n Lara et al., 2011), were calibrated on the basis of the state of art suggestions and the experimental reflection coefficient and mean overtopping discharge. In particular, according to Lara et al. (2008), for all the porous media α and c_A were set equal to 200 and 0.34, respectively. Instead, n and β have been calibrated against experimental results, thus obtaining: i) n=0.32 and β=1.20 for the core; ii) n=0.35 and β=2.00 for the filter layer; iii) n=0.30 and β=1.50 for the existing armor layer; iv) n=0.25 and β=5.00 for the additional armor layer; v) n=0.35 and β=3.00 for berm at the toe of the additional armor layer. The hydraulic response of the two considered configurations was investigated by simulating five sea states of 1500 waves, each of which was repeated six times in order to take into account the effect of wave sequence on overtopping phenomena. Therefore, a total of 60 numerical simulations were performed. The good correspondence between the experimental and numerical results is showed in Figures 4C, D, where the non-dimensional mean overtopping discharge q^* is expressed as a function of the non-dimensional structure free-board R_c/H_s, being R_c the maximum value between the crest level and the wave wall height referred to mean sea level.

The numerical q^* was compared to the prediction of the traditional formula proposed by (EurOtop, 2018), hereinafter EurOtop formula:

$\begin{array}{ll}{q}^{*}=\frac{q}{\sqrt{g{H}_s^3}}=a_E\times exp\left[-{\left(b_E\times \frac{R_c}{H_s{\gamma }_f}\right)}^{1.3}\right]& (12)\end{array}$

where γ_f is the roughness factor (equal to 0.47 for double layer of artificial cubes), and a_E and b_E are empirical parameters equal to 0.09 (σ = 0.0135) and 1.50 (σ = 0.1500), respectively. Despite the predictions of the EurOtop formula are quite good, two site-specific formulas were fitted to the numerical data acquired for configurations E and CS at section no. 40, using the least squares method. Figures 4C, D shows equation 12 adapted to the numerical data and the 95% CB of the fitting. As reported in Table 1, the experimental a_E and b_E are equal to 0.30 (σ = 0.14) and 1.50 (σ = 0.01) for configuration E, and to 0.06 (σ = 0.05) and 1.50 (σ = 0.15) for configuration CS. It should be noted that the site-specific a_E and b_E are quite similar to the EurOtop ones. However, the fitted empirical coefficients improve the performances of equation 12 in reproducing q^* higher than 10^-3 for configuration E, and q^* lower than 5×10^-5 for configuration CS.

2.4.3 Climate data

The evaluation of the performances of the upgraded Catania harbor breakwater requires wave climate and sea level data for the studied site, to be used as input for the MC simulations. As regards the present climate, the freely available measured wave data of the Italian National Sea Wave Measurement Network (RON) were employed (Piscopia et al., 2004), which consists of time series of offshore significant wave height (H_s0), peak wave period (T_p0), mean wave period (T_m0) and mean wave direction (D) for the period 1989-2014. From 1989 to 2001 the wave measurements were taken every three hours, whereas from 2002 to 2014 the acquisition interval was thirty minutes. The present mean sea level was deduced from the design data provided by the local Port Authority, and it is equal to 16.50 m and 19.00 m for sections n. 10 and 40, respectively. The second value was selected as the mean of the normal distribution of h, whose standard deviation was calculated through equation 10, assuming that h_at is equal to 0.20 m (see Table 1). The storm surge was introduced using the ERA5 reanalysis data (Hersbach et al., 2019), which are available for the period 1989-2017, with a time step of 10 minutes.

For the future climate, the ocean surface wave projections and the water level change time series for the European coast provided by the Copernicus Climate Change Service were employed (Caires and Yan, 2020; Yan et al., 2020). Such data were generated by the ECMWF’s Wave Model (SAW) and the Deltares Global Tide and Surge Model (GTSM) version 3.0, respectively, forced by surface wind from a member of the EURO-CORDEX climate model ensemble (i.e. the HIRHAM5 regional climate model downscaled from the global climate model EC-EARTH). The wave data-set is made of hourly time series of H_s0, T_p0, T_m0D and wave spectral directional width for the European coastline along the 20 m bathymetric contour with 30 km spatial resolution. The sea level data-set consists of time series of mean sea level, storm surge residual, tidal elevation and total water level, with a time step of 10 minutes. The wave and sea level time series are available for the following climate scenarios: i) the baseline climate (HIST), which refers to the period 1976-2005; ii) the future climate RCP4.5, which corresponds to an optimistic emission scenario where emissions start declining beyond 2040; iii) the future climate RCP8.5, where emissions continue to rise throughout the century (i.e. business-as-usual scenario). It should be noted that the future wave data refers to the period 2041-2100 for both RCP4.5 and RCP8.5. On the contrary, the future water level time series covers the years 2071-2100 for RCP4.5, and the years 2041-2070 for RCP8.5. For this reason, in the present work only the periods 2071-2100 under RCP4.5 scenario and 2041-2070 under RCP8.5 scenario were considered. For the future scenarios, the mean of the normal distribution of present h was corrected by adding the projected mean sea level rise (SLR), which according to the employed data-set ranges between 0.36 ÷ 0.42 m and 0.24 ÷ 0.33 m for RCP4.5 and RCP8.5, respectively (see Table 1).

The statistical characterization of the extreme local wave climate was performed according to the procedure described in section 2.1. As discussed in section 2.4.1, under the present climate the most energetic sea storms come from the 90°N direction (see Figure 2C). Therefore, extreme events, whose rounded frequency of occurrence (λ) is equal to 13 events/year, were considered to come from such direction. Moreover, only the years 1989-2005 of the measured time series of H_s0 were used for the analysis of present extreme wave climate, in order to ensure a statistically significant comparison with the baseline HIST scenario. The visual comparison between different extreme value PDF and the sample of extreme H_s0, and the results of the Kolmogorov-Smirnov test with statistical significance level equal to 5% revealed that the best fitting distribution for present extreme H_s0 is the Weibull distribution with a_sc=1.14, κ_sh=1.30 and ζ_lc=1.56. According to the climate projection model, no significant variations of extreme wave direction are expected for the future scenarios. Therefore, the effects of climate change on the present Weibull distribution have been introduced by modifying its a_sc, κ_sh and ζ_lc, using the FoC method. The FoC method has been applied using a 17-years moving window for the analysis of the future time series, in order to analyze sub-periods having the same length of the considered present period. In this way, 14 sub-periods have been obtained for each future scenario. The ranges of the calculated a_sc, κ_sh and ζ_lc are summarized in Figure 5A. Depending on the considered sub-period, λ ranges between 12÷13 events/year and 13÷14 events/year under RCP4.5 and RCP8.5, respectively (see Figure 5B). Figure 6 shows the plots of some of the fitted Weibull distributions in terms of H_s0 expressed as a function of the return period (T_r), which refer to the present climate and the sub-periods 2084-2100 under RCP4.5 scenario and 2053-2069 under RCP8.5 scenario.

FIGURE 5

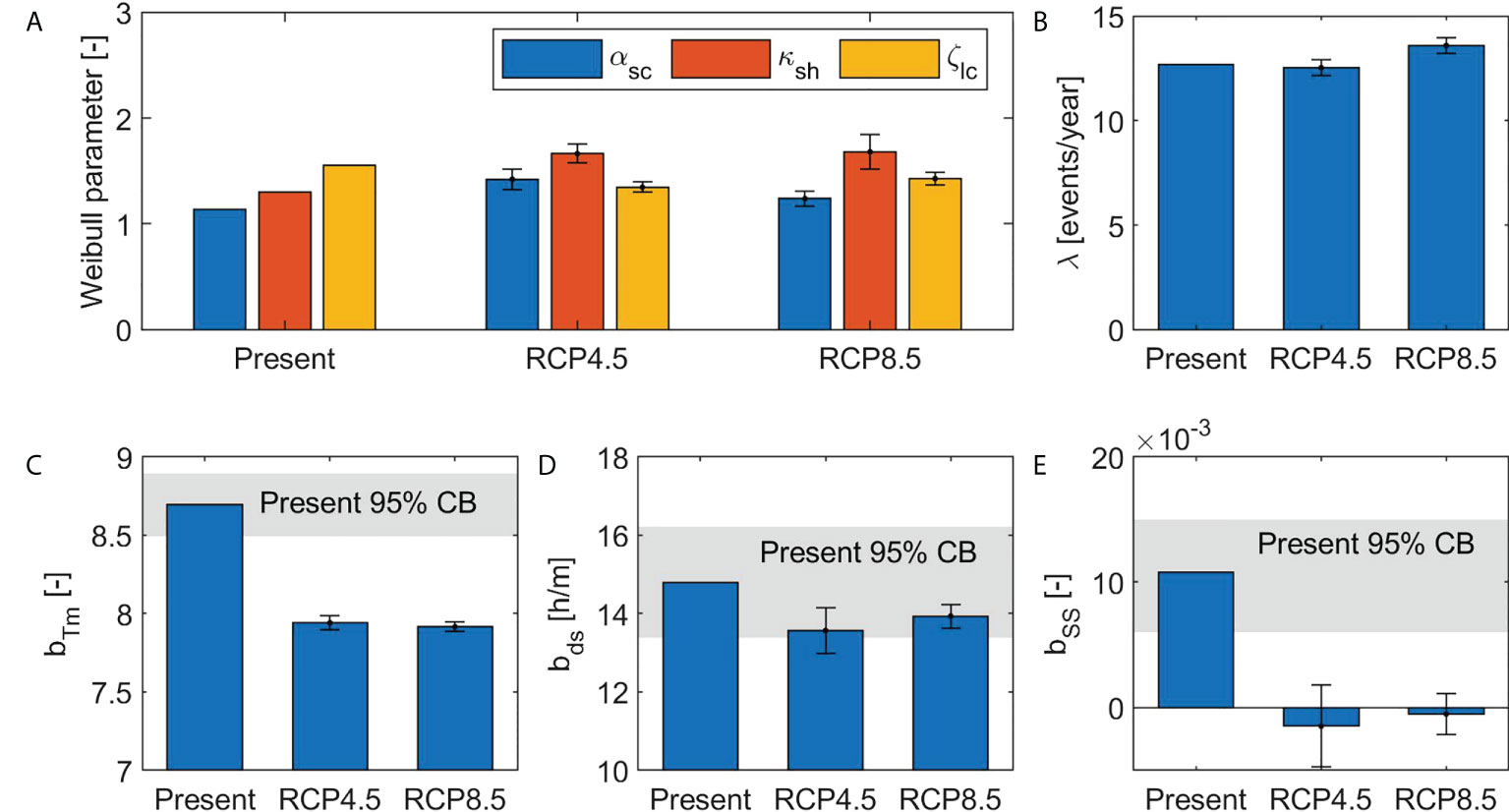
Figure 5 Characterization of the local extreme wave climate under present and future scenarios: (A) scale (a_sc), shape (κ_sh) and location (ζ_lc) parameters of the Weibull distribution of extreme H_s0; (B) mean number of sea storms per year; (C) coefficient of the site-specific empirical relationship between significant wave height and mean wave period; (D) coefficient of the site-specific empirical relationship between significant wave height and sea storm duration; (E) coefficient of the site-specific empirical parameter of the relationship between significant wave height and storm surge height. The mean (bar value) and standard deviation (vertical error bars) were calculated with reference to the 14 future sub-periods of each future scenario.

FIGURE 6

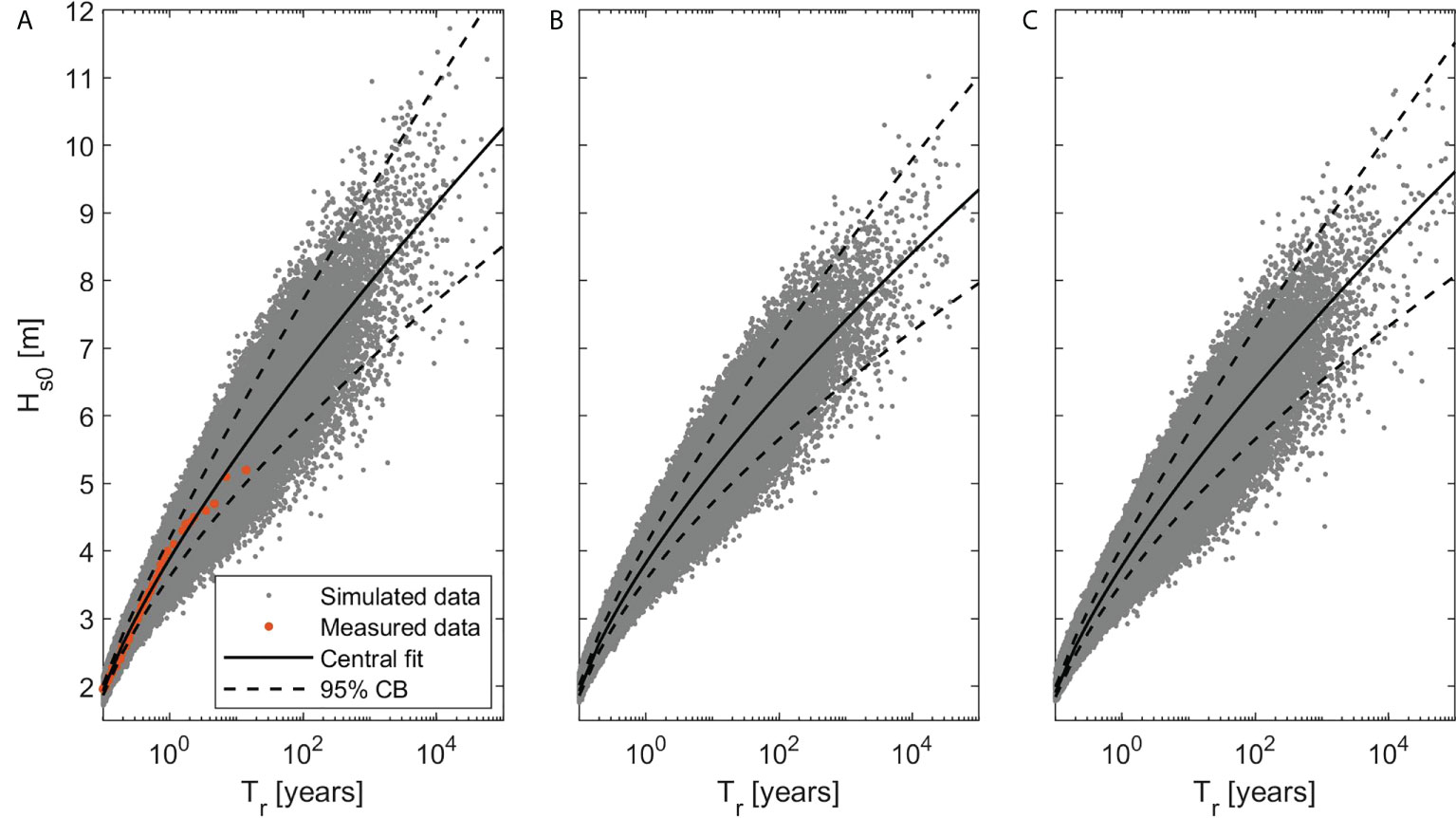
Figure 6 Central fit and 95% confidence bounds of the Weibull distribution of extreme offshore significant wave height for the site of Catania: (A) present (1989-2005); (B) sub-period 2084-2100 under RCP4.5 scenario; (C) sub-period 2053-2069 under RCP8.5 scenario.

The correlations between extreme H_s0 and T_m0, d_s and h_ss were modeled through the definition of site-specific empirical formulas, whose coefficients were calculated considering the present and the future scenarios (see section 2.1). The offshore mean wave period was calculated by adapting the formula proposed by Boccotti (2004):

$\begin{array}{ll}{T}_{m0}=b_{Tm}\pi \sqrt{\frac{H_{s0}}{4g}}& (13)\end{array}$

where b_Tm is the empirical non-dimensional coefficient evaluated through the least squares method, and H_s0 and T_m0 are measured in m and s, respectively. The estimate of the wave storms duration (measured in hours) was performed using the following linear relationship, which is similar to the one proposed by Laface and Arena (2016) for the equivalent exponential storm model:

$\begin{array}{ll}{d}_s=b_{ds}{H}_{s0}& (14)\end{array}$

where b_ds (hours/m) is an empirical coefficient dependent on the site characteristics, evaluated through the least squares method. Finally, the storm surge height (h_ss, measured in meters) was using the following linear relationship, which is similar to the one proposed by Salmun et al. (2011):

$\begin{array}{ll}{h}_{SS}=b_{SS}{H}_{s0}& (15)\end{array}$

where b_ss is an empirical non-dimensional coefficient depending on the site characteristics, evaluated through the least squares method. Figures 5C–E shows the ranges of the fitted site-specific empirical coefficients.

According to the procedure for the generation of random sea storms described in section 2.3, the definition of a site-specific formulation for wave propagation towards the breakwater site is required. A previously generated data-set of deep-water and corresponding shallow water wave conditions was available for the studied site. In particular, the offshore significant wave height and mean wave period time series for the years 2006-2019 provided by Korres et al. (2019) were propagated towards the the breakwater site using the spectral wave model SWAN (Booij et al., 1999). The analysis of the correlation between extreme H_s0 and corresponding propagated H_s revealed that the following linear relationship provides a quite reliable description of the propagation process for the site of interest:

$\begin{array}{ll}{H}_s=c_{Hs}{H}_{s0}& (16)\end{array}$

where c_Hs is the empirical coefficient estimated through the application of the least squares method, which is equal to 0.70, with lower and upper 95% CB equal to 0.69 and 0.72, respectively. The coefficient of determination of the fitted formula is R² = 0.87. As regards the mean wave period, it was found that T_m at the breakwater site can be assumed equal to T_m0, with R² of the fitted regression model equal to 0.98. The above-described simplified formulation for wave propagation is justified by the very mild slope of the bathymetry of the site of interest, and also by the quite high depth at the toe of the structure (i.e. between 16.50 and 19.00 m under MSL, with 100-year return period dispersion parameter k_dh between 0.50 and 0.60). Under the hypothesis of no modification of the local bathymetry, the site-specific wave propagation relationships were employed for both present and future scenarios. The breaking conditions were checked at the breakwater site through the application of criteria proposed by Kamphuis (1991) and Goda (2009).

More details about the extreme value distributions of H_s0 and the fitted site-specific empirical relationships between climate variables are provided in the Supplementary Material.

2.4.4 Monte Carlo simulations

The simplified fault tree represented in Figure 7 was considered. For ULS, the collapse of the armor layer was analyzed, considering the case of addition of an extra armor layer over the existing one (i.e. configurations AS, AD, CM and CS). Instead, for SLS, the excessive mean overtopping discharge was studied for the existing structure (i.e. configuration E) and the solution with both raise of the wave wall and addition of extra armor unit (i.e. configuration CS). The proposed methodology for the calculation of the failure probability (see section 2.2) was applied to section n. 40 of the Catania harbor breakwater, which is the most exposed one to the wave motion (see Figure 2B).

FIGURE 7

Figure 7 Fault tree for the upgraded Catania harbor breakwater.

For each considered limit state, MC simulations were performed to assess the failure probability during lifetime, considering the present climate (1989-2005) and the future scenarios RCP4.5 (2071-2100) and RCP8.5 (2041-2070). Both the state of art formulas and the ones adapted to the experimental and numerical data were considered (see section 2.4.2), in order to compare the results and assess the effect of using specific design formulations. For the ULS, the following reliability function was derived by writing equation 11 in accordance with the format of equation 3:

$\begin{array}{ll}{Z}_1=f_c\times \left(6.7\frac{N_{od}^{0.4}}{N_w^{0.3}}+1\right)\times \text{Δ}{D}_{n50}-H_s\times {\left(\frac{2\pi H_s}{g{T}_m^2}\right)}^{0.1}& (17)\end{array}$

where the number of incident waves N_w is calculated as the ratio between the sea storm duration expressed in seconds and the mean wave period, i.e. (3600 d_s)/T_m. The coefficient f_c, D_n50 and Δ are assumed to follow a normal distribution (van der Meer, 1988b; Burcharth, 1992), whose mean (m) and standard deviation (σ) are reported in Table 1. The normal distributions of D_n50 and Δ ere truncated, in order to avoid the unrealistic values during the random generation process. Therefore, such distributions were characterized also through the parameter kwhich allows the calculation of the lower (l) and upper (u) truncation limits:

$\begin{array}{ll}\begin{array}{l}l=m-k\sigma \\ u=m+k\sigma \end{array}& (18)\end{array}$

The damage parameter N_od as set equal to 2.00, which is the damage limit correspondent to the collapse of the outer armor layer (CIRIA et al., 2007). For the SLS, the following reliability function was derived by writing equation 12 in accordance with the format of equation 3:

$\begin{array}{ll}{Z}_2=q-\sqrt{g{H}_s^3}\times a_E\times exp\left[-{\left(b_E\times \frac{R_c}{H_s{\gamma }_f}\right)}^{1.3}\right]& (19)\end{array}$

where R_c = h_wall – (h+h_ss). The parameter h_wall which is the height of the wave wall measured with respect to the toe of the structure, follows a normal distribution (Lara et al., 2019) that was truncated to avoid the random generation of unrealistic values. The coefficients a_E and b_E are assumed normally distributed. Table 1 reports the characteristics of the above mentioned normal distributions. The limit q was set equal to 5×10³ m³/s m, which is the the acceptable mean overtopping discharge to ensure safety for larger yachts (EurOtop, 2018).

According the indications of ROM 1.0-09 (2010), the structure useful life was set equal to 50 years, and P_f,Lmax for both ULS and SLS was assumed equal to 10^-1. The number of generated life cycles (N_r) for each MC simulation, which was defined through the analysis of the convergence of P_f,L was 2.25×10⁴, and the obtained CV were in the range 0.02÷0.35 (see Supplementary Material for more details). Since the rounded λ is equal to 13 events/year for the present climate (see section 2.4.3), according to equation 7, 650 random sea storms were generated for each of the 50 simulated life cycles under present climate, thus obtaining a total of 1.46×10⁷ sea storms. As regards the future sub-periods, λ ranges between 12÷14 events/year (see section 2.4.3), and hence 600÷700 random H_s0 were generated for each of the 50 simulated life cycles. Therefore, for each future sub-period a total of 1.35÷1.58×10⁷ sea storms were generated. For instance, Figure 6 shows the point clouds of the simulated H_s0 as a function of the return period, considering the present climate and two representative future sub-periods under RCP4.5 and RCP8.5 scenarios, together with the corresponding Weibull distributions used for the random generation.

3 Results and discussion

3.1 Marine climate

The extreme wave climate and sea levels characteristic of the site of Catania under present and future climate (see section 2.4.3) were analyzed and compared, in order to acquire preliminary information useful for the interpretation of the final outcomes obtained through the application of the proposed methodology for the quantitative assessment of the performances of upgraded rubble-mound breakwaters under a changing climate.

As regards the extreme significant wave height, Figure 5A shows that the Weibull distributions of extreme H_s0 calculated for the future sub-periods are characterized by higher a_sc and κ_sh than the present ones, but lower ζ_lc. As a consequence, future extreme H_s0 lower than the present ones are expected for the site of interest, in agreement with the findings of both global (Hemer et al., 2013; Camus et al., 2017; IPCC, 2019; Morim et al., 2019) and regional (Lionello et al., 2008) existing studies. Instead, the frequency of occurrence of extreme events is not expected to suffer significant modifications in the future. Indeed, the data reported in Figure 5B shows that the maximum variations of λ are equal to ± 1 event/year.

The expected future decrease of extreme H_s0 involves that also T_m0, d_s and h_ss are likely to decrease under the RCP4.5 and RCP8.5 scenarios. Indeed, according to equations 13-15, such variables are directly correlated to H_s0. Moreover, as showed in Figure 5C, the empirical coefficient of the site-specific relationship between H_s0 and T_m0, namely b_Tm, assumes values slightly lower than the present one, by 0.09 times on average, thus increasing the reduction of the future T_m0 due to the expected lower H_s0. Figure 5E reveals also that the future values of coefficient of the site-specific relationship between H_s0 and h_ss, namely b_ss, are lower then the present one, by 1.09 times on average. Therefore, future h_ss is expected to be lower than the present one not only because of the decrease of H_s0, but also because of the lower projected b_ss. As regards the coefficient of the site-specific relationship between H_s0 and d_s, namely b_ds, no significant differences between present and future were found. Indeed, the future values vary within the 95% CB if the present estimate of b_ds (see Figure 5D).

Besides the variations of extreme wave climate, also mean sea level rise, which for the site of Catania is expected to reach values up to 0.42 m (see section 2.4.3), significantly affects the hydraulic performances of rubble-mound breakwaters, especially in the presence of depth-limited wave conditions. For the present case study, the failure probability due to the collapse of the outer armor layer (ULS) is influenced only by the projected reduction of extreme sea storm energy (see equation 17), whereas the failure probability due to excessive mean overtopping discharge depends on the combined effect of the expected less energetic wave climate and increased mean sea level (see equation 19).

3.2 Collapase of the outer armor layer (ULS)

The acceptability of the stability performances of the additional armor layer of the upgraded Catania harbor breakwater during lifetime is evaluated using the index r (see equation 8). Figure 8A shows the calculated r for each upgrading solution, considering both the traditional and site-specific reliability functions (i.e. vdM, SS and NSS). The displayed results refer to the present climate and to the sub-period with the highest P_f,L of each future scenario, namely 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5. The standard deviation of r, calculated by dividing σ_Pf,L by P_f,Lmax, is represented by the vertical error bars and ranges between 0.001÷0.025, being directly proportional to P_f,L(see equation 5) and r.

FIGURE 8

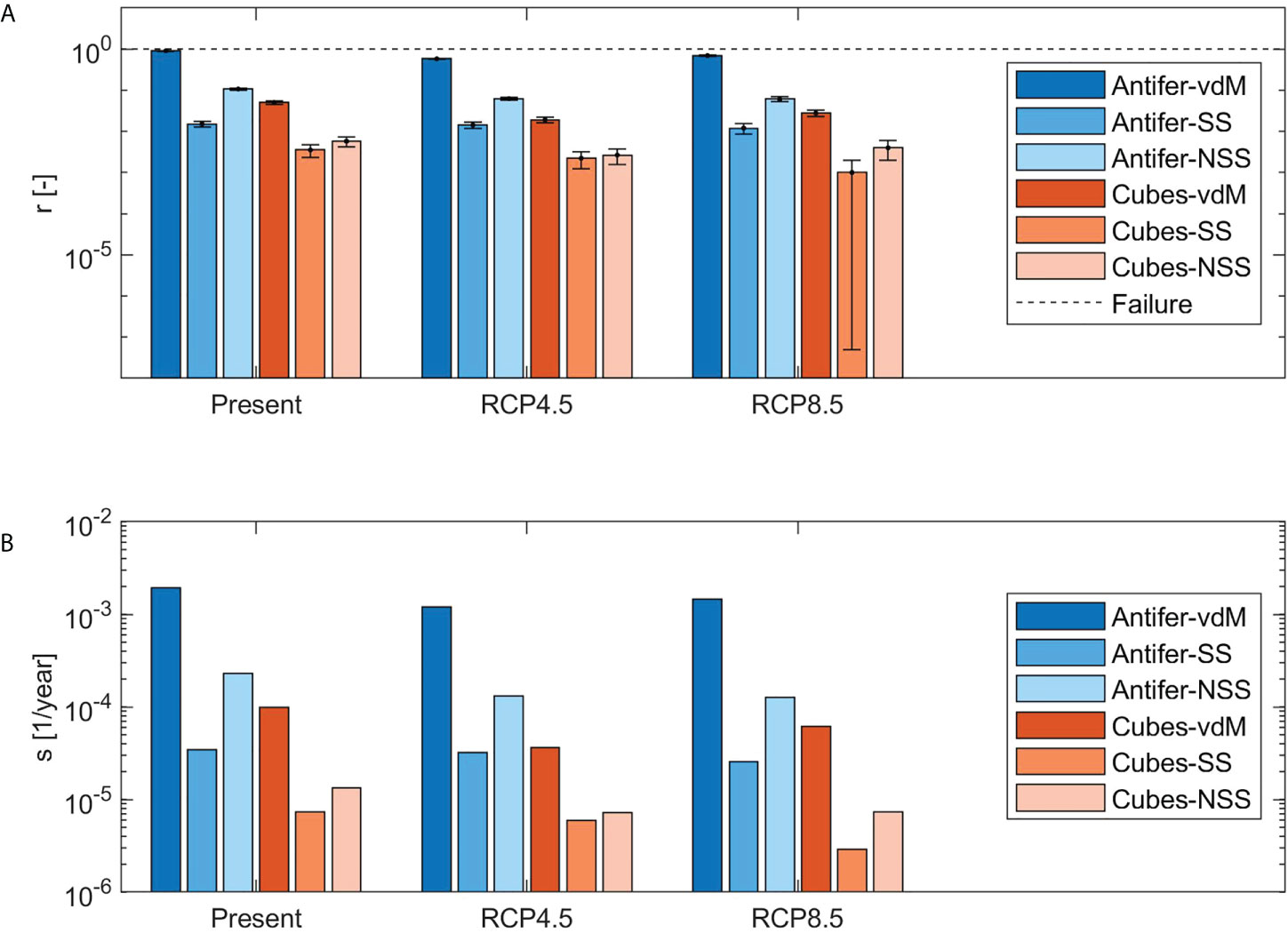
Figure 8 Indexes of the failure probability during lifetime due to the collapse of the outer armor layer, calculated for the present period (1989-2005) and the future sub-periods characterized by the highest P_f,L, i.e. 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5: (A) ratio between P_f,L and the acceptance limit (the vertical error bars represent the MC standard deviation); (B) rate of the growth of the failure probability during lifetime.

The index r calculated with the traditional and site-specific reliability functions is always smaller than one, which means that despite of the weight of the additional armor units (i.e. 62 t cubes or 30 t Antifer), all the upgraded configurations satisfy the design requirements, under both present and future climate. The results reveal that the future r is in general lower than the present one, for both the considered scenarios. In particular, the lowest values of r were found for the end of century under RCP4.5 scenario. Figure 9A shows that the percentage difference between future and present r (i.e. 100 (r_fut-r_pres)/r_pres) ranges between -72% and -6%. The quantitative comparison between present and future r demonstrates that all the considered upgrading options, which ensure acceptable performances under the present climate, are adequate also in the presence of the effects of climate change. Therefore, the cost-benefit analysis for the choice of the optimal solution will not be affected by the expected impacts of global warming on the considered structure. Such findings are consistent with the outcomes presented in section 3.1, and in particular with the fact that for the future lower. H_s are expected for the site of Catania. Indeed, the analysis of Z₁, expressed as a function of the only H_s by using equations 13-14, revealed that its first-order derivative with respect to H_s is always negative, thus implying that to lower values of H_s correspond higher Z_1. Anyway, the differences between present and future r are quite contained, and the order of magnitude of r does not change.

FIGURE 9

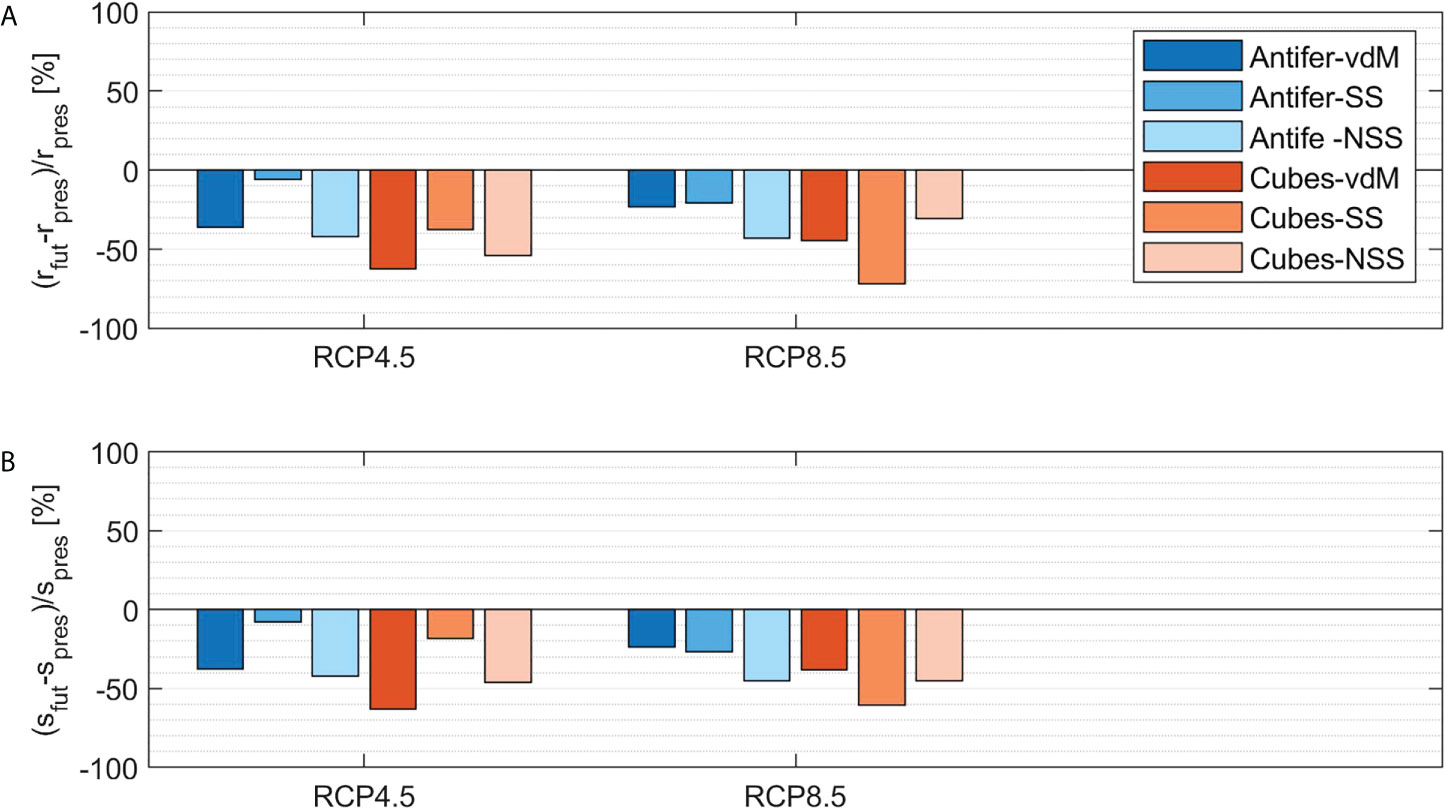
Figure 9 Comparison between the indexes of the failure probability due to the collapse of the outer armor layer, calculated for the present period (1989-2005) and the future sub-periods characterized by the highest P_f,L, i.e. 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5: (A) ratio between P_f,Land the acceptance limit; (B) rate of the growth of the failure probability during lifetime.

Figure 8A also shows that the values of evaluated for the upgrading solutions which consist in the addition of 30 t Antifer blocks, are higher than the ones calculated for the upgrading options which consist in the addition of 62 t cubic units, by 16 ÷ 24 times on average times when using the vdM formula, and by 3 ÷ 11 and 14 ÷ 22 for the SS and NSS formulas, respectively. Therefore, as expected, the doubling of the weight of the extra armor blocks involves a significant reduction of the probability of collapse of the outer armor layer. The use of the traditional or site-specific reliability functions produces substantial differences between the resulting r. Indeed, the vdM formula is far more conservative, giving r greater than the ones calculated with the SS and NSS formulations, by 34 and 8 times on average, respectively. Such a result indicates that the use of the traditional vdM formula would lead to a solution with a larger safety margin. Reasonably, r calculated for the case of additional armor blocks in direct contact with the toe berm (i.e. SS) is always smaller than the one evaluated in the case of absence of such direct contact (i.e. NSS), by a factor of 62% on average.

The rate of the growth of the failure probability during lifetime is displayed in Figure 8B, with reference to the present climate and the future sub-periods 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5. The index s behaves similarly to r. Indeed, as showed in Figure 9B, the future s values are always lower than the corresponding present ones, and the percentage difference between future and present s (i.e.100 (s_fut-r_pres)/r_pres) ranges between -63% and -8%. Figure 8B also shows that the upgrading solutions with additional 30 t Antifer units are characterized by higher s than the ones calculated for the solutions with extra 62 t cubes, by a factor of 19÷32, 4÷8 and 16÷17 when using the vdM, SS and NSS formulas, respectively. Moreover, the application of the vdM formula gives s greater by 49 and 9 times on average than the SS and NSS formulations, respectively. The best performances of the the additional armor layer in direct contact with the toe berm are confirmed. Indeed, s calculated with the SS formulation is on average 61% lower than s calculated with the NSS equation. The assessment of s of various upgrading options under different climate scenarios is fundamental for the design of maintenance plan able to ensure sufficient stability of the structure during lifetime. Indeed, if limit values of P_f,L are fixed and s is known, the appropriate times to implement repair interventions can be calculated.

The variability of P_f,L due to the use of a moving time window for the analysis of the future periods (i.e. 2071-2100 under RCP4.5 scenario and 2041-2070 under RCP8.5 scenario) is quantified by the coefficient of variation v (see equation 9). Figure 10 reveals that for both future scenarios, the highest values of v correspond to configurations characterized by the lowest r, namely the upgrading solutions with additional armor layer made up by 62 t cubes. Such a result is in accordance with the fact that in such cases v is most affected by the uncertainty of the MC simulations, which corresponds to higher σ_Pf,L, and hence greater CV. When considering the end of the century under RCP4.5 scenario, v assumes values between 0.38 and 0.88, thus indicating a low variability condition. Instead, the values of v calculated for the mid of the century under RCP8.5 range between 0.84 and 2.27, being always greater than the corresponding values for the end of the century under RCP4.5 scenario. When v is higher than one, which indicates the high variability of P_f,L, special attention should be paid to the flexibility of maintenance interventions during the planning processes. Indeed, design strategies that are reversible and flexible must be selected to keep the cost of being wrong about future climate change as low as possible (Hallegatte, 2009).

FIGURE 10

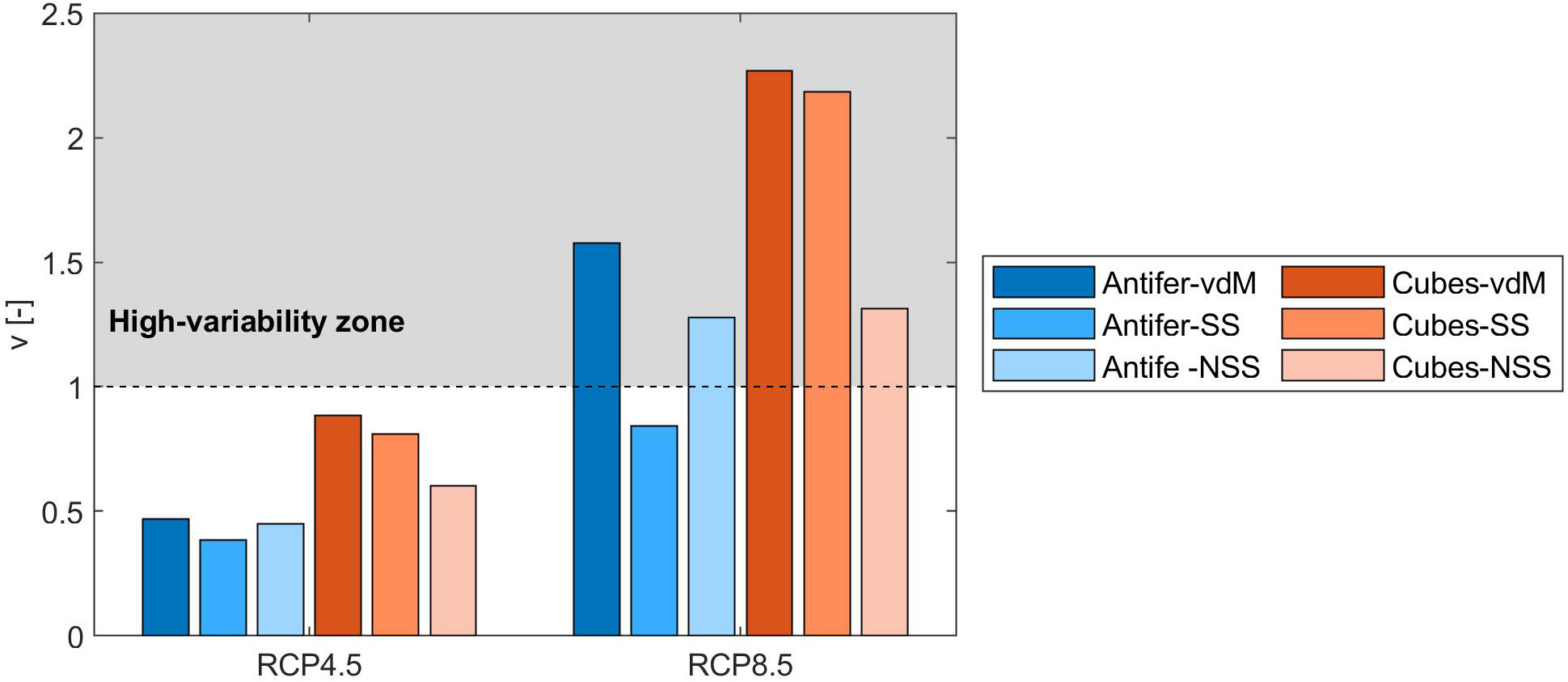
Figure 10 Coefficient of variation of the failure probability during lifetime due to the collapse of the outer armor layer, calculated with reference to the fourteen sub-periods of RCP4.5 and RCP8.5 future scenarios.

3.3 Excessive mean overtopping discharge (SLS)

The acceptability of the hydraulic performances of the existing and upgraded Catania harbor breakwater was also assessed, considering the SLS due to excessive mean overtopping discharge. Figure 11A shows the index r (see equation 8), which was calculated for the existing structure (i.e. configuration E) and for the upgrading solution with additional 62 t cubes over the regularized armor layer and further raised wave wall (i.e. configuration CS), considering both the traditional and site-specific formulas (i.e. EurOtop and empirical-numerical formulas). As for the failure probability due to the collapse of the outer armor layer (see section 5.2), the displayed values of r refer to the present climate and to the sub-period with the highest P_f,L of each future scenario, namely 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5. The standard deviation of r derived from σ_Pf,L (see equation 5), which is indicated by the vertical error bars, varies in the range 0.004÷0.019.

FIGURE 11

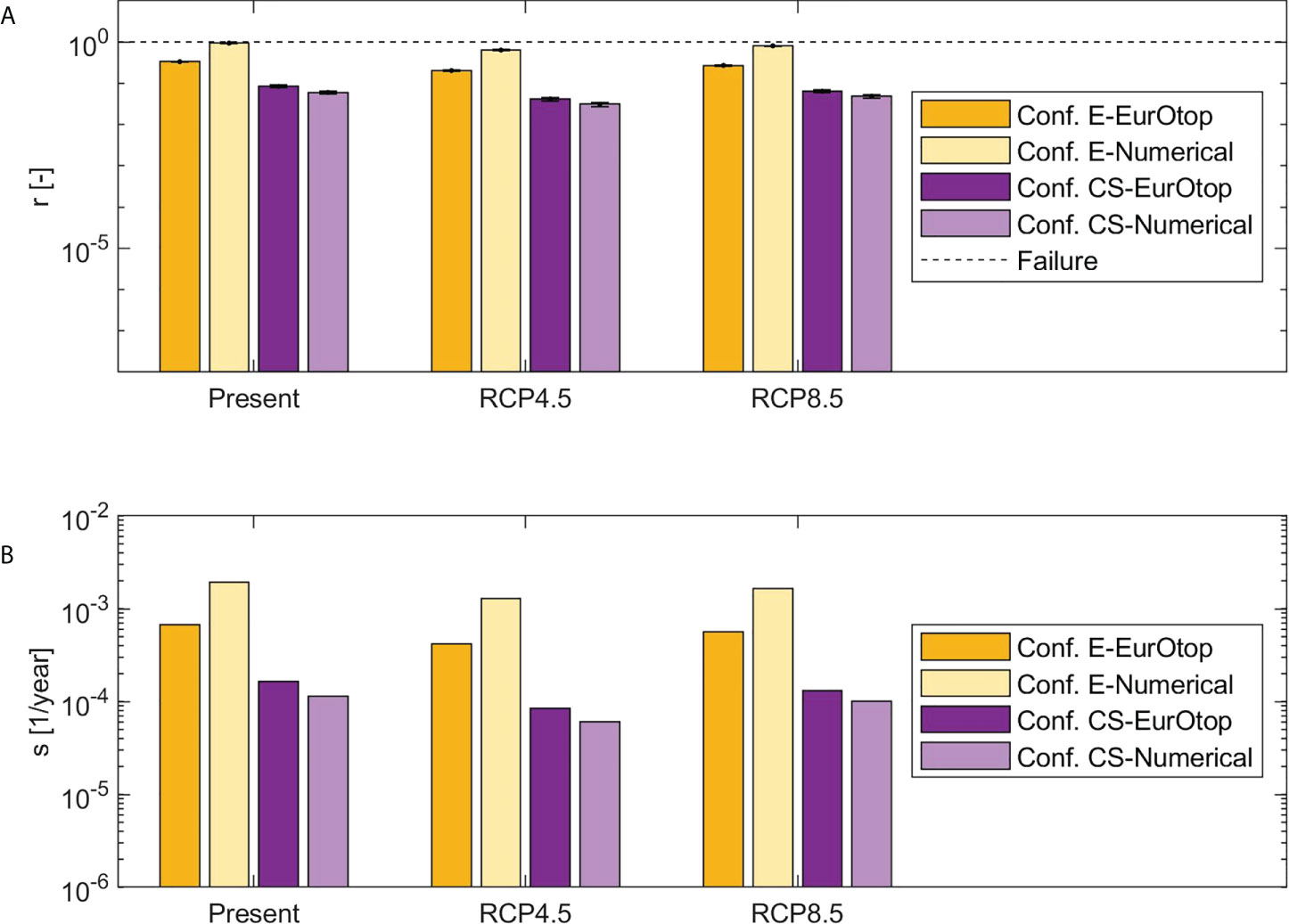
Figure 11 Indexes of the failure probability during lifetime due to excessive wave overtopping, calculated for the present period (1989-2005) and the future sub-periods characterized by the highest P_f,L,i.e. 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5: (A) ratio between P_f,Land the acceptance limit (the vertical error bars represent the MC standard deviation); (B) rate of the growth of the failure probability during lifetime.

The calculated r is always smaller than one, despite of the considered structure configuration (i.e. E or CS) and reliability function, under both present and future climate. Therefore, since the SLS is never reached and the design requirements are always satisfied, the upgrade could be not necessary when considering only the response of the breakwater in terms of mean overtopping discharge. However, configuration E ensures r very close to failure threshold, being r in the range 0.20÷0.94 depending on the employed formulation. The upgrading solution CS produces the reduction of r by about 0.77 and 0.94 times, employing the traditional and site-specific reliability function, respectively. As expected, the addition of extra units over the existing armor layer and the heightening of the wave wall involve a significant reduction of the probability of occurrence of excessive mean overtopping rates. The comparison between the obtained results for the present, RCP4.5 and RCP8.5 scenarios displayed in Figure 11A reveals that the future r is in general lower than the present one. As showed in Figure 12A, the percentage difference between future and present r ranges between -50% and -14%, with the highest reduction of r corresponding to the end of the century under RCP4.5 scenario. Therefore, both the existing and upgraded structure provide sufficient performances in the presence of the effects of climate change.

FIGURE 12

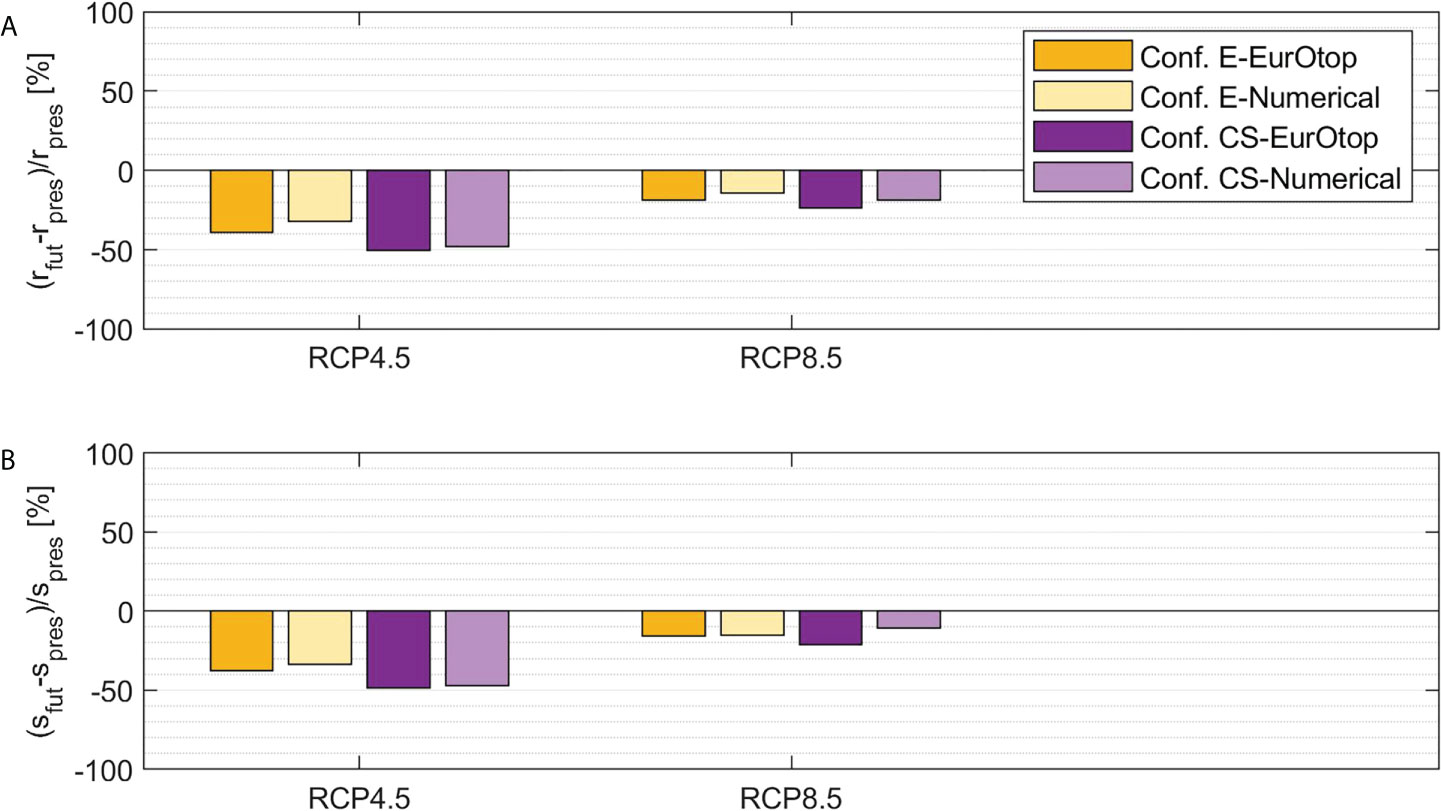
Figure 12 Comparison between the indexes of the failure probability due to excessive wave overtopping, calculated for the present period (1989-2005) and the future sub-periods characterized by the highest P_f,L, i.e. 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5: (A) ratio between P_f,L and the acceptance limit; (B) rate of the growth of the failure probability during lifetime.

Such an outcome is consistent with the fact that lower H_s and h_ss are expected for the site of Catania (see section 3.1), but it may appear in contrast with the projected SLR without a thorough analysis of the influence of each climate variable of equation 19. Figure 13 shows the comparison between ∂Z₂/∂H_s and ∂Z₂/∂H_c, evaluated for a set of possible H_s and R_c. ∂Z₂/∂H_s is negative, and its absolute value is higher than the positive ∂Z₂/∂H_c, for each considered couple H_s-R_c. Therefore, the increase of Z₂ due to decreasing H_s occurs at a greater rate than the decrease of Z₂ due to decreasing R_c, and vice versa. In order to make clear such a finding, in Figure 13 the case of H_s equal to 6.00 m and R_c equal to 8.50 m above mean sea level is highlighted. Following the above explanation, the fact that future r is lower than the present one is reasonable. Indeed, the reliability function Z₂ suffers most the effect of slightly lower H_s than the influence of higher R_c caused by SLR. Anyway, the differences between present and future probability of failure are modest. Indeed, the order of magnitude of r does not change.

FIGURE 13

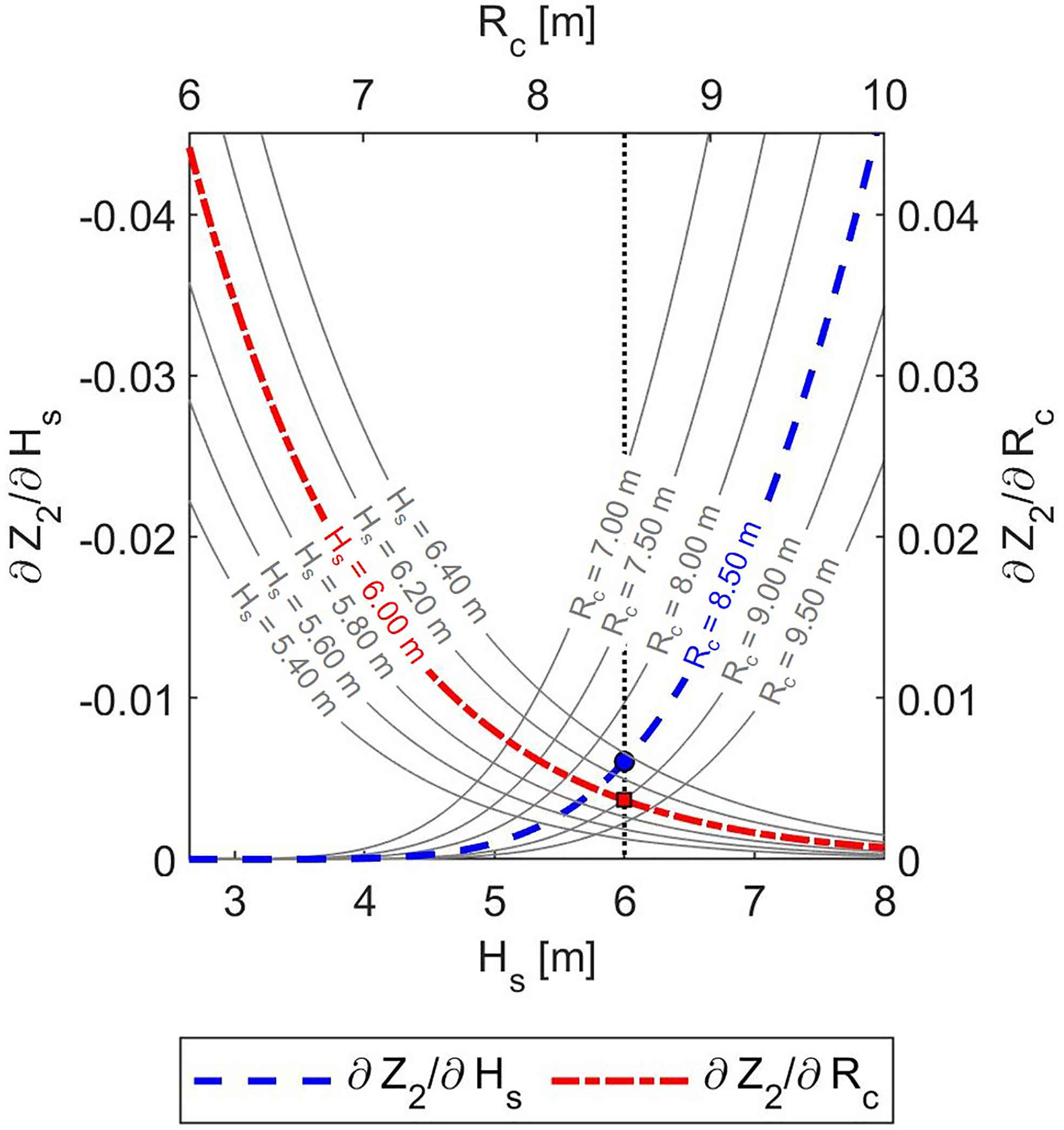
Figure 13 Comparison between the first-order partial derivatives of the reliability function Z₂ for excessive wave overtopping discharge, evaluated considering a_E and b_E suggested by (EurOtop, 2018) and a set of H_s and R_c. The circle and the square indicate the first-order partial derivatives of Z₂ in the case of H_s = 6.00 m and R_c = 8.50 m.

The use of the EurOtop formula or of its adaptation to the numerical data produces differences between the resulting r. Indeed, the empirical-numerical formula is more conservative for configuration E, giving r greater by about 0.66 times than the traditional one. On the contrary, the empirical-numerical formula is less conservative for configuration CS, giving smaller r by about 0.36 times than the traditional one. Hence, in the latter case the lack of specific formulation does not imply the design of a not sufficiently performing structure. However, the differences between r evaluated through the traditional and adapted formula for mean overtopping discharge are modest with respect to the discrepancies observed for the armor layer stability, by two orders of magnitude (see section 3.2).

Figure 11B shows the growth of the failure probability during the structure lifetime, calculated for the present climate and the future sub-periods 2084-2100 under RCP4.5 and 2053-2069 under RCP8.5. As already observed for the ULS related to the collapse of the outer armor layer, the index s behaves similarly to r. Indeed, as showed in Figure 12B, the percentage difference between future and present s ranges between -49% and -11%. Configuration CS is characterized by lower s than the ones calculated for configuration E, on average by a factor of 0.77 and 0.94 when using the traditional and site-specific reliability function, respectively. Furthermore, for configuration E the empirical-numerical formula provides s higher than the EurOtop one, by about 0.66 times. On the contrary, for configuration CS the site-specific formula gives s lower than the traditional one, by about 0.39 times. The knowledge of s corresponding to the considered upgrading options under different climate scenarios allows the definition of maintenance plan able to ensure adequate hydraulic performances during the whole structure lifetime.

As for the ULS due to the collapase of the outer armor layer, the variability of future P_f,L during the periods 2071-2100 under RCP4.5 scenario and 2041-2070 under RCP8.5 scenario is quantified using the coefficient of variation v (see equation 9). In accordance with the findings discussed in section 3.2, Figure 14 shows that for both future scenarios the highest values of v correspond to the upgraded configuration CS, which is characterized by the lowest r. The values of coefficient of variation calculated for the mid of the century under RCP8.5 scenario are greater than the corresponding values for the end of the century under RCP4.5 scenario. In particular, v of RCP4.5 scenario assumes values in the range 0.57÷1.00. Therefore, P_f,L is characterized by low variability for all the tested cases under RCP4.5 scenario. On the contrary, v of RCP8.5 scenario ranges between 2.03 and 2.36, thus indicating the high variability of P_f,L, and hence the necessity to design reversible and flexible maintenance plan to ensure the best compromise between performances and costs.

FIGURE 14

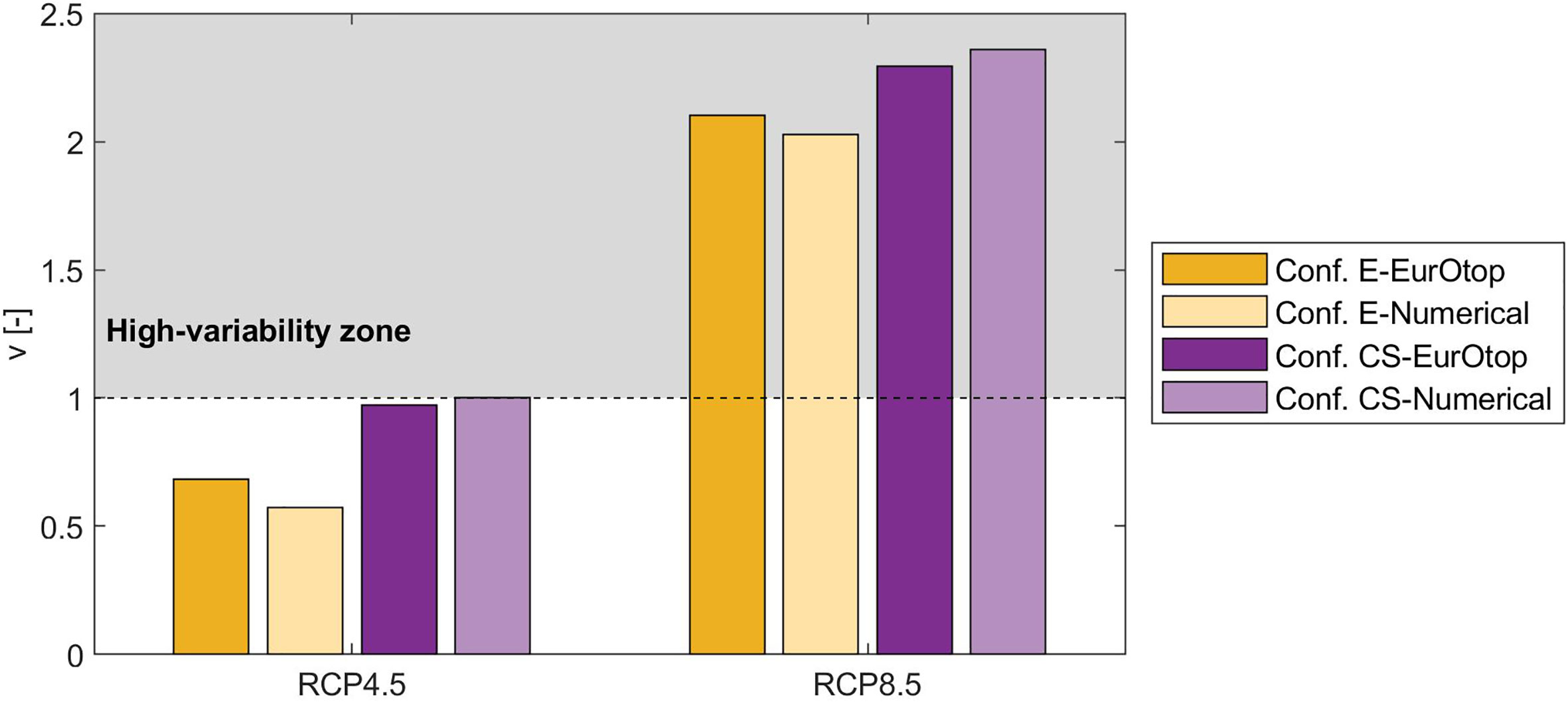
Figure 14 Coefficient of variation of the failure probability during lifetime due to excessive wave overtopping, calculated with reference to the fourteen sub-periods of RCP4.5 and RCP8.5 future scenarios.

4 Conclusion

The effects of climate change on coastal areas produce the increase of risk for port integrity, thus implying the need for upgrade exiting harbor breakwater. In this context, the present work proposes a methodology for the assessment of the impact of climate change on the performances of upgraded rubble-mound structures, based on the calculation of the failure probability during lifetime due to independent failure modes. The limits of existing design methodologies are overcome, which are mainly linked to the rough inclusion of expected future climate variations and to the lack of quantitative indexes for the comparison between the results.

The probability that the structure reaches a certain ULS or SLS during the lifetime is calculated through the MC simulation technique. After simulating a certain number of structure random life cycles, the failure probability during lifetime is defined as the ratio between the number of life cycles with at least one failure and the total number of realizations of the MC simulation. The failure occurs when the reliability function describing the failure mode assumes negative values. Such a function is derived from traditional or site-specific empirical relationships between hydrodynamic, geometry and material variables, which are all described by probability density functions derived from state of art or from adaptation to the available data. The probability distribution of extreme significant wave height identified through the POT method is calculated using the MME adaptation method, whose combination with the FoC method allows the inclusion of the effects of projected climate change (Kilsby et al., 2007; Fatichi et al., 2011; Peres and Cancelliere, 2018). Moreover, the correlations between wave climate descriptors are modeled by site-specific empirical relationships, calibrated for both the present and future scenarios. Once the failure probabilities have been assessed, the following three index are calculated to enable the quantitative comparison between present and future climate scenarios, and also between different configurations of the structure: i) r is the ratio between the calculated and the maximum acceptable failure probability during lifetime, which assumes values greater (smaller) than one if the failure occurs (does not occur); ii) s, whose unit of measure is 1/year, represents the rate of the growth of the failure probability along the lifetime; iii) v is a measure of the dispersion of the obtained failure probabilities due to the combination of the uncertainty due to MC convergence and the variability of future climate.

The proposed methodology was applied considering the failure probability due to the collapse of the outer armor layer (ULS) or to excessive mean overtopping discharge (SLS) during lifetime of different upgraded configurations of the Catania harbor breakwater (Italy). The index r calculated with the traditional and site-specific reliability functions under present climate is always smaller than one, thus indicating acceptable structural and hydraulic performances for all the tested configurations. In accordance with the climate projections for the site of interest (Caires and Yan, 2020; Yan et al., 2020), lower r and s were calculated for both ULS and SLS under RCP4.5 and RCP8.5 scenarios, although their order of magnitude does not change. The variation of P_f,L due to future climate variability was quantitatively assessed through the index v, which assumes values equal or greater than one for highly dispersed data. The maximum values of v were found under RCP8.5 scenarios, for those configurations characterized by the lowest failure probabilities.

The obtained results demonstrate that the proposed methodology is able to give useful quantitative information to optimize both design and decision-making processes of upgrading solutions for harbor breakwater under the effects of climate change. Indeed, the index r is measure of the adequacy of upgrading options to withstand future external forcing. Moreover, the knowledge of s for different climate scenarios gives useful information for the design of maintenance plan based on the calculation of the appropriate times to implement repair interventions during the structure lifetime. Finally, the outcomes of the analysis of the index v allow the identification of the upgrading options whose P_f,L presents high variability under the considered future scenarios. In such cases, highly flexible maintenance plan should be designed, in order to reach an optimal compromise between structure performances and costs. Future research should focus on the inclusion of the structural modifications of the breakwater due to deterioration processes and/or maintenance interventions, which clearly influence the growth of the failure probability during lifetime.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JL, RM and EF contributed to conception and design of the study. MS organized the database, performed the probabilistic analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work has been funded by: the project VARIO, financed by the program PIACERI of the University of Catania; the project REST COAST, financed by Horizon 2020 European Union Funding for Research and Innovation (H2020-Green DEAL REST-COAST, proposal number 101037097); the project ISYPORT in the framework of PNR 2015-2020 (code no. PON ARS01-01202).

Acknowledgments

The Authors would like to thank the Port Authority of Eastern Sicily for supporting the work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.986993/full#supplementary-material

References

Arns A., Dangendorf S., Jensen J., Talke S., Bender J., Pattiaratchi C. (2017). Sea-Level rise induced amplification of coastal protection design heights. Sci. Rep. 7, 40171. doi: 10.1038/srep40171

PubMed Abstract | CrossRef Full Text | Google Scholar

Boccotti P. (2004). Idraulica marittima (Turin, Italy: UTET Università).

Google Scholar

Booij N. R. R. C., Ris R. C., Holthuijsen L. H. (1999). A third-generation wave model for coastal regions: 1. model description and validation. J. geophysical research: Oceans 104, 7649–7666.

Google Scholar

Burcharth H. F. (1987). The lessons from recent breakwater failures. in developments in breakwater design (Vancouver: World Federation of Engineering Organizations Technical Congress). doi: 10.1029/98JC02622

CrossRef Full Text | Google Scholar

Burcharth H. F. (1992). “Introduction of partial coefficients in the design of rubble mound breakwaters,” in Coastal structures and breakwaters (London, England: Thomas Telford), 543–566.

Google Scholar

Burcharth H. F. (1993). “Reliability evaluation and probabilistic design of coastal structures,” in International seminar on hydro-technical engineering for future development of ports and harbors (Un’yushō Kōwan Gijutsu Kenkyūjo).

Google Scholar

Burcharth H. F., Andersen T. L., Lara J. L. (2014). Upgrade of coastal defence structures against increased loadings caused by climate change: A first methodological approach. Coast. Eng. 87, 112–121. doi: 10.1016/j.coastaleng.2013.12.006

CrossRef Full Text | Google Scholar

Burcharth H. F., Sørensen J. D. (1999). “Design of vertical wall caisson breakwaters using partial safety factors,” in Coastal Engineering: Proceedings of the 26th Conference on Coastal Engineering, (Reston, VA, US: American Society of Civil Engineers). 2138–2151.

Google Scholar

Caires S., Yan K. (2020). Ocean surface wave time series for the European coast from 1976 to 2100 derived from climate projections, (for [extracted period], [experiment], etc ). Copernicus Climate Change Service (C3S) Climate Data Store (CDS). doi: 10.24381/cds.572bf382

CrossRef Full Text | Google Scholar

Camus P., Losada I., Izaguirre C., Espejo A., Menéndez M., Pérez J. (2017). Statistical wave climate projections for coastal impact assessments. Earth’s Future 5, 918–933. doi: 10.1002/2017EF000609

CrossRef Full Text | Google Scholar

Camus P., Tomás A., Díaz-Hernández G., Rodríguez B., Izaguirre C., Losada I. (2019). Probabilistic assessment of port operation downtimes under climate change. Coast. Eng. 147, 12–24. doi: 10.1016/j.coastaleng.2019.01.007

CrossRef Full Text | Google Scholar

Castillo E., Losada M. A., Mínguez R., Castillo C., Baquerizo A. (2004). Optimal engineering design method that combines safety factors and failure probabilities: Application to rubble-mound breakwaters. J. waterway port coastal ocean Eng. 130, 77–88. doi: 10.1061/(ASCE)0733-950X(2004)130:2(77)

CrossRef Full Text | Google Scholar

Castillo C., Mínguez R., Castillo E., Losada M. A. (2006). An optimal engineering design method with failure rate constraints and sensitivity analysis. Application to composite breakwaters. Coast. Eng. 53, 1–25. doi: 10.1016/j.coastaleng.2005.09.016

CrossRef Full Text | Google Scholar

Chini N., Stansby P. (2012). Extreme values of coastal wave overtopping accounting for climate change and sea level rise. Coast. Eng. 65, 27–37. doi: 10.1016/j.coastaleng.2012.02.009

CrossRef Full Text | Google Scholar

Church J. A., Clark P. U., Cazenave A., Gregory J. M., Jevrejeva S., Levermann A., et al. (2013). “Sea Level change,” in Tech. rep (Cambridge, England: PM Cambridge University Press).

Google Scholar

CIAD project group (1985). “Final report CIAD project group. breakwaters. computer aided evaluation of the reliability of a breakwater design,” in Tech. rep (Zoetermeer, the Netherlands: CIAD Association).

Google Scholar

CIRIA, CUR, CETMEF (2007). The rock manual: the use of rock in hydraulic engineering. 2nd edition Vol. c683 (London, England:C683, CIRIA).

Google Scholar

Davies G., Callaghan D. P., Gravois U., Jiang W., Hanslow D., Nichol S., et al. (2017). Improved treatment of non-stationary conditions and uncertainties in probabilistic models of storm wave climate. Coast. Eng. 127, 1–19. doi: 10.1016/j.coastaleng.2017.06.005

CrossRef Full Text | Google Scholar

Di Lauro E., Lara J. L., Maza M., Losada I. J., Contestabile P., Vicinanza D. (2019). Stability analysis of a non-conventional breakwater for wave energy conversion. Coast. Eng. 145, 36–52. doi: 10.1016/j.coastaleng.2018.12.008

CrossRef Full Text | Google Scholar

EurOtop. (2018). Manual on wave overtopping of sea defences and related structures. An overtopping manual largely based on European research, but for worldwide application. Van der Meer J. W., Allsop N. W. H., Bruce T., De Rouck J., Kortenhaus A., Pullen T., et al. www.overtopping-manual.com.

Google Scholar

Faraci C., Scandura P., Foti E. (2015). Reflection of sea waves by combined caissons. J. Waterway Port Coastal Ocean Eng. 141, 04014036. doi: 10.1061/(ASCE)WW.1943-5460.0000275

CrossRef Full Text | Google Scholar

Fatichi S., Ivanov V. Y., Caporali E. (2011). Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 34, 448–467. doi: 10.1016/j.advwatres.2010.12.013

CrossRef Full Text | Google Scholar

Foti E., Musumeci R. E., Stagnitti M. (2020). Coastal defence techniques and climate change: A review. Rendiconti Lincei. Sci. Fisiche e Naturali 31, 123–138. doi: 10.1007/s12210-020-00877-y

CrossRef Full Text | Google Scholar

Franco L. (1994). Vertical breakwaters: the italian experience. Coast. Eng. 22, 31–55. doi: 10.1016/0378-3839(94)90047-7

CrossRef Full Text | Google Scholar

Galassi G., Spada G. (2014). Sea-Level rise in the mediterranean sea by 2050: Roles of terrestrial ice melt, steric effects and glacial isostatic adjustment. Global Planetary Change 123, 55–66. doi: 10.1016/j.gloplacha.2014.10.007

CrossRef Full Text | Google Scholar

Galiatsatou P., Makris C., Prinos P. (2018). Optimized reliability based upgrading of rubble mound breakwaters in a changing climate. J. Mar. Sci. Eng. 6, 92. doi: 10.3390/jmse6030092

CrossRef Full Text | Google Scholar

Goda Y. (2009). A performance test of nearshore wave height prediction with clash datasets. Coast. Eng. 56, 220–229. doi: 10.1016/j.coastaleng.2008.07.003

CrossRef Full Text | Google Scholar

Guanche R., Iturrioz A., Losada I. J. (2015). Hybrid modeling of pore pressure damping in rubble mound breakwaters. Coast. Eng. 99, 82–95. doi: 10.1016/j.coastaleng.2015.02.001

CrossRef Full Text | Google Scholar

Guanche R., Losada I. J., Lara J. L. (2009). Numerical analysis of wave loads for coastal structure stability. Coast. Eng. 56, 543–558. doi: 10.1016/j.coastaleng.2008.11.003

CrossRef Full Text | Google Scholar

Hallegatte S. (2009). Strategies to adapt to an uncertain climate change. Global Environ. Change 19, 240–247. doi: 10.1016/j.gloenvcha.2008.12.003

CrossRef Full Text | Google Scholar

Hemer M. A., Fan Y., Mori N., Semedo A., Wang X. L. (2013). Projected changes in wave climate from a multi-model ensemble. Nat. Climate Change 3, 471–476. doi: 10.1038/nclimate1791

CrossRef Full Text | Google Scholar

Hersbach H., Bell B., Berrisford P., Horányi A., Sabater J. M., Nicolas J., et al. (2019). Global reanalysis: goodbye era-interim, hello era5. ECMWF Newsl 159, 17–24. doi: 10.21957/vf291hehd7

CrossRef Full Text | Google Scholar

Hughes S. A. (2014). Coastal engineering challenges in a changing world. J. Appl. Water Eng. Res. 2, 72–80. doi: 10.1080/23249676.2014.977360

CrossRef Full Text | Google Scholar

IPCC (2019). IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. Pörtner H.-O., Roberts D.C., Masson-Delmotte V., Zhai P., Tignor M., Poloczanska E., et al. (eds.)

Google Scholar

Isobe M. (2013). Impact of global warming on coastal structures in shallow water. Ocean Eng. 71, 51–57. doi: 10.1016/j.oceaneng.2012.12.032

CrossRef Full Text | Google Scholar

Izaguirre C., Losada I., Camus P., Vigh J., Stenek V. (2021). Climate change risk to global port operations. Nat. Climate Change 11, 14–20. doi: 10.1038/s41558-020-00937-z

CrossRef Full Text | Google Scholar

Jonkman S. N., Steenbergen R. D. J. M., Morales-Nápoles O., Vrouwenvelder A. C. W. M., Vrijling J. K. (2015). Probabilistic design: risk and reliability analysis in civil engineering. (Netherlands: TU Delft, Department Hydraulic Engineering).

Google Scholar

Kamphuis J. (1991). Incipient wave breaking. Coast. Eng. 15, 185–203. doi: 10.1016/0378-3839(91)90002-X

CrossRef Full Text | Google Scholar

Kamphuis J. W. (2020). Introduction to coastal engineering and management Vol. 48 (Singapore: World Scientific).

Google Scholar

Kilsby C. G., Jones P. D., Burton A., Ford A. C., Fowler H. J., Harpham C., et al. (2007). A daily weather generator for use in climate change studies. Environ. Model. Software 22, 1705–1719. doi: 10.1016/j.envsoft.2007.02.005

CrossRef Full Text | Google Scholar

Kim S.-W., Suh K.-D. (2006). Application of reliability design methods to donghae harbor breakwater. Coast. Eng. J. 48, 31–57. doi: 10.1142/S0578563406001325

CrossRef Full Text | Google Scholar

Kim S.-W., Suh K.-D. (2010). Reliability analysis of breakwater armor blocks: Case study in korea. Coast. Eng. J. 52, 331–350. doi: 10.1142/S0578563410002208

CrossRef Full Text | Google Scholar

Kim S.-W., Suh K.-D. (2014). Determining the stability of vertical breakwaters against sliding based on individual sliding distances during a storm. Coast. Eng. 94, 90–101. doi: 10.1016/j.coastaleng.2014.09.001

CrossRef Full Text | Google Scholar

Korres G., Ravdas M., Zacharioudaki A. (2019). Mediterranean Sea waves hindcast (cmems med-waves) set (Lecce, Italy: Copernicus Monitoring Environment Marine Service (CMEMS). doi: 10.25423/CMCC/MEDSEA_HINDCAST_WAV_006_012

CrossRef Full Text | Google Scholar

Laface V., Arena F. (2016). A new equivalent exponential storm model for long-term statistics of ocean waves. Coast. Eng. 116, 133–151. doi: 10.1016/j.coastaleng.2016.06.011

CrossRef Full Text | Google Scholar

Lara J. L., Losada I. J., Guanche R. (2008). Wave interaction with low-mound breakwaters using a rans model. Ocean Eng. 35, 1388–1400. doi: 10.1016/j.oceaneng.2008.05.006

CrossRef Full Text | Google Scholar

Lara J. L., Losada I. J., Maza M., Guanche R. (2011). Breaking solitary wave evolution over a porous underwater step. Coast. Eng. 58, 837–850. doi: 10.1016/j.coastaleng.2011.05.008

CrossRef Full Text | Google Scholar

Lara J. L., Lucio D., Tomas A., Di Paolo B., Losada I. J. (2019). High-resolution time-dependent probabilistic assessment of the hydraulic performance for historic coastal structures: Application to luarca breakwater. Philos. Trans. R. Soc. A 377, 20190016. doi: 10.1098/rsta.2019.0016

CrossRef Full Text | Google Scholar

Lionello P., Cogo S., Galati M. B., Sanna A. (2008). The mediterranean surface wave climate inferred from future scenario simulations. Global Planetary Change 63, 152–162. doi: 10.1016/j.gloplacha.2008.03.004

CrossRef Full Text | Google Scholar

Li Q., Wang C., Ellingwood B. R. (2015). Time-dependent reliability of aging structures in the presence of non-stationary loads and degradation. Struct. Saf. 52, 132–141. doi: 10.1016/j.strusafe.2014.10.003

CrossRef Full Text | Google Scholar

Lowe J., Gregory J. (2005). The effects of climate change on storm surges around the united kingdom. Philos. Trans. R. Soc. A: Mathematical Phys. Eng. Sci. 363, 1313–1328. doi: 10.1098/rsta.2005.1570

CrossRef Full Text | Google Scholar

Maciñeira E., Peña E., Bajo V., Sande J., Noya F. (2017). “Probabilistic design of a secondary breakwater in the new harbour basin of the port of la coruña,” in Coastal structures and solutions to coastal disasters 2015: Resilient coastal communities (Reston, VA, US: American Society of Civil Engineers), 482–490.

Google Scholar

Malliouri D. I., Memos C. D., Soukissian T. H., Tsoukala V. K. (2021). Assessing failure probability of coastal structures based on probabilistic representation of sea conditions at the structures’ location. Appl. Math. Model. 89, 710–730. doi: 10.1016/j.apm.2020.08.001

CrossRef Full Text | Google Scholar

Mercelis P., Dufour M., Alvarez Gebelin A., Gruwez V., Doorme S., Sas M., et al. (2014). “Generation of multivariate wave conditions as input for a probabilistic level iii breakwater design,” in International Conference on Offshore Mechanics and Arctic Engineering, (New York, US: American Society of Mechanical Engineers) Vol. 45431. V04BT02A022.

Google Scholar

Morim J., Hemer M., Cartwright N., Strauss D., Andutta F. (2018). On the concordance of 21st century wind-wave climate projections. Global planetary Change 167, 160–171. doi: 10.1016/j.gloplacha.2018.05.005

CrossRef Full Text | Google Scholar

Morim J., Hemer M., Wang X. L., Cartwright N., Trenham C., Semedo A., et al. (2019). Robustness and uncertainties in global multivariate wind-wave climate projections. Nat. Climate Change 9, 711–718. doi: 10.1038/s41558-019-0542-5

CrossRef Full Text | Google Scholar

Muhaisen O. S., Elramlawee N. J., García P. A. (2010). Copula-evt-based simulation for optimal rubble-mound breakwater design. Civil Eng. Environ. Syst. 27, 315–328. doi: 10.1080/10286600903134246

CrossRef Full Text | Google Scholar

Oumeraci H. (1994). Review and analysis of vertical breakwater failures - lessons learned. Coast. Eng. 22, 3–29. doi: 10.1016/0378-3839(94)90046-9

CrossRef Full Text | Google Scholar

Oumeraci H. (1999). “Strengths and limitations of physical modelling in coastal engineering–synergy effect with numerical modelling and field measurement,” in Proceedings of HYDRALAB-workshop(Hannover, Germany), 7–38.

Google Scholar

Peres D. J., Cancelliere A. (2018). Modeling impacts of climate change on return period of landslide triggering. J. Hydrology 567, 420–434. doi: 10.1016/j.jhydrol.2018.10.036

CrossRef Full Text | Google Scholar

Piscopia R., Inghilesi R., Corsini S., Franco L. (2004). Italian Wave Atlas (Italy, US Lib: University of Roma TRE). Congr.G1989.21.C7, pp. 134.

Google Scholar

Ports and Harbours Bureau, Ministry of Land, Infrastructure, Transport and Tourism, Port and Airport Research Institute, N (2009). Technical standards and commentaries on port and harbour facilities in Japan (Tokyo, Japan: The Overseas Coastal Area and Development Institute of Japan).

Google Scholar

ROM 1.0-09 (2010). Recommendations for the project design and construction of breakwaters (Part 1: Calculation and Project Factors. Climate Agents). Spain: Puertos del Estado.

Google Scholar

Radfar S., Shafieefar M., Akbari H. (2022). Impact of copula model selection on reliability-based design optimization of a rubble mound breakwater. Ocean Eng. 260, 112023. doi: 10.1016/j.oceaneng.2022.112023

CrossRef Full Text | Google Scholar

Salmun H., Molod A., Wisniewska K., Buonaiuto F. S. (2011). Statistical prediction of the storm surge associated with cool-weather storms at the battery, new york. J. Appl. meteorology climatology 50, 273–282. doi: 10.1175/2010JAMC2459.1

CrossRef Full Text | Google Scholar

Salvadori G., Durante F., Tomasicchio G., D’Alessandro F. (2015). Practical guidelines for the multivariate assessment of the structural risk in coastal and off-shore engineering. Coast. Eng. 95, 77–83. doi: 10.1016/j.coastaleng.2014.09.007

CrossRef Full Text | Google Scholar

Sanchez-Arcilla A., Sierra J. P., Brown S., Casas-Prat M., Nicholls R. J., Lionello P., et al. (2016). A review of potential physical impacts on harbours in the mediterranean sea under climate change. Regional Environ. Change 16, 2471–2484. doi: 10.1007/s10113-016-0972-9

CrossRef Full Text | Google Scholar

Stagnitti M., Iuppa C., Musumeci R. E., Foti E. (2020). Catania harbor breakwater: Physical modelling of the upgraded structure. Coast. Eng. Proc. 36, 2–2. doi: 10.9753/icce.v36v.papers.2

CrossRef Full Text | Google Scholar

Stagnitti M., Musumeci R. E., Foti E. (2022). Surface roughness measurement for the assessment of damage dynamics of existing and upgraded cube-armored breakwaters. Coast. Eng.

Google Scholar

Suh K.-D., Kim S.-W., Kim S., Cheon S. (2013). Effects of climate change on stability of caisson breakwaters in different water depths. Ocean Eng. 71, 103–112. doi: 10.1016/j.oceaneng.2013.02.017

CrossRef Full Text | Google Scholar

Suh K.-D., Kim S.-W., Mori N., Mase H. (2012).Effect of climate change on performance-based design of caisson breakwaters. J. Waterway Port Coastal Ocean Eng. 138, 215–225. doi: 10.1061/(ASCE)WW.1943-5460.0000126

CrossRef Full Text | Google Scholar

Tabarestani M. K., Feizi A., Bali M. (2020). Reliability-based design and sensitivity analysis of rock armors for rubble-mound breakwater. J. Braz. Soc. Mechanical Sci. Eng. 42, 1–13. doi: 10.1007/s40430-020-2207-8

CrossRef Full Text | Google Scholar

Takagi H., Kashihara H., Esteban M., Shibayama T. (2011). Assessment of future stability of breakwaters under climate change. Coast. Eng. J. 53, 21–39. doi: 10.1142/S0578563411002264

CrossRef Full Text | Google Scholar

Takahashi S. (2002). Design of vertical breakwaters. PHRI reference document no. 34. (Japan: Port and Airport Research Institute).

Google Scholar

Tomasicchio U., Adamo F., Benassai E., Boccotti P., Colombo P., Lamberti A., et al. (1996). Istruzioni tecniche per la progettazione delle dighe marittime (Italy: Ministero dei Lavori Pubblici).

Google Scholar

US Army Corps of Engineers (2002). Coastal engineering manual (Vicksburg, Mississippi, US: US Army Engineering Research and Development Center).

Google Scholar

van der Meer J. W. (1988a). “Stability of cubes, tetrapods and accropode,” in Breakwaters ’88 (London, England: Thomas Telford American Society of Civil Engineers), 59–68.

Google Scholar

van der Meer J. W. (1988b). Deterministic and probabilistic design of breakwater armor layers. J. waterway port coastal ocean Eng. 114, 66–80. doi: 10.1061/(ASCE)0733-950X(1988)114:1(66)

CrossRef Full Text | Google Scholar

Vousdoukas M. I., Mentaschi L., Voukouvalas E., Verlaan M., Jevrejeva S., Jackson L. P., et al. (2018). Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 9, 1–12. doi: 10.1038/s41467-018-04692-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Vousdoukas M. I., Voukouvalas E., Annunziato A., Giardino A., Feyen L. (2016). Projections of extreme storm surge levels along europe. Climate Dynamics 47, 3171–3190. doi: 10.1007/s00382-016-3019-5

CrossRef Full Text | Google Scholar

Yan K., Muis S., Irazoqui Apecechea M., Verlaan M. (2020). Water level change time series for the European coast from 1977 to 2100 derived from climate projections, (for [extracted period], [experiment], etc ). Copernicus Climate Change Service (C3S) Climate Data Store (CDS). doi: 10.24381/cds.8c59054f

CrossRef Full Text | Google Scholar