Biogenic silica cycling in the Skagerrak

Dissolved silicate (H₄SiO₄) is essential for the formation of the opaline skeletal structures of diatoms and other siliceous plankton. A fraction of particulate biogenic silica (bSi) formed in surface waters sinks to the seabed, where it either dissolves and returns to the water column or is permanently buried. Global silica budgets are still poorly constrained since data on benthic bSi cycling are lacking, especially on continental margins. This study describes benthic bSi cycling in the Skagerrak, a sedimentary depocenter for particles from the North Sea. Biogenic silica burial fluxes, benthic H₄SiO₄ fluxes to the water column and bSi burial efficiencies are reported for nine stations by evaluating data from in-situ benthic landers and sediment cores with a diagenetic reaction-transport model. The model simulates bSi contents and H₄SiO₄ concentrations at all sites using a novel power law to describe bSi dissolution kinetics with a small number of adjustable parameters. Our results show that, on average, 1100 mmol m^-2 yr^-1 of bSi rains down to the Skagerrak basin seafloor, of which 50% is released back to overlying waters, with the remainder being buried. Biogenic silica cycling in the Skagerrak is generally consistent with previously reported global trends, showing higher Si fluxes and burial efficiencies than deep-sea sites and similar values compared to other continental margins. A significant finding of this work is a molar bSi-to-organic carbon burial ratio of 0.22 in Skagerrak sediments, which is distinctively lower compared to other continental margins. We suggest that the continuous dissolution of bSi in suspended sediments transported over long distances from the North Sea leads to the apparent decoupling between bSi and organic carbon in Skagerrak sediments.

1 Introduction

Global marine biogeochemical cycling of dissolved silicate (H₄SiO₄) and biogenic silica (bSi) is mainly controlled by riverine inputs and by outputs by burial at the seafloor (Wollast, 1974; DeMaster, 1981; Nelson et al., 1995; Tréguer et al., 1995; Ragueneau et al., 2000; DeMaster, 2002; Tréguer and de la Rocha, 2013; Rahman et al., 2017; DeMaster, 2019). Silicon (Si) is an essential nutrient in the ocean for a number of siliceous organisms such as diatoms, silicoflagellates, siliceous sponges and radiolaria (DeMaster, 2002). The bSi and carbon (C) cycles are coupled via biomineralization in the surface ocean and subsequent dissolution of detritus in the water column and burial in sediments. The tightness of this coupling is thus important for the sequestration of atmospheric CO₂ (Dugdale et al., 1995; Ragueneau et al., 2006; Tréguer and de la Rocha, 2013; Tréguer et al., 2018; Tréguer et al., 2021).

The global ocean is undersaturated with respect to bSi (Hurd, 1973; Nelson et al., 1995; Ragueneau et al., 2000; Tréguer and de la Rocha, 2013). Biogenic siliceous material dissolves as it sinks through the water column and only a fraction of the bSi exported from the surface ocean reaches the seafloor (Nelson and Gordon, 1982; Wollast and Mackenzie, 1981; Nelson et al., 1991; Nelson et al., 1995; Tréguer et al., 1995). Upon sedimentation, bSi is subject to further dissolution, although the regenerated dissolved H₄SiO₄ can reprecipitate into authigenic minerals (Mackenzie et al., 1981; Mackenzie and Kump, 1995; Michalopoulos and Aller, 1995; Loucaides et al., 2010; Ehlert et al., 2016) or adsorb to mineral surfaces (Huang, 1975; Sigg and Stumm, 1981; Swedlund, 1999; Davis et al., 2001; Davis et al., 2002). The competition between these processes determines the proportion of bSi that is reintroduced to the water column as a benthic flux of H₄SiO₄ and the proportion that is permanently buried. Tréguer and de la Rocha (2013) underlined the importance of the benthic bSi cycle by showing that most of the marine bSi dissolves at the sediment-water interface rather than during the sinking of silica particles.

Based on molar bSi:C ratios and particulate organic carbon (POC) burial rates, DeMaster (2002) updated global estimates of bSi burial on continental margins and demonstrated that the contribution of these regions to the global Si budget is more important than previously thought. Since then, more studies have focused on the margins, e.g. in the North Atlantic (Schlüter and Sauter, 2000; Schmidt et al., 2001; Oehler et al., 2015b). Yet, current global Si budgets still lack sufficient data, especially with regard to benthic fluxes and burial efficiencies, to accurately constrain bSi burial and dissolution on continental margins.

To our knowledge, no comprehensive study on bSi cycling has been published for the Skagerrak; a continental margin representing the largest depocenter for sediments transported from the North Sea (Eisma and Kalf, 1987; Van Weering et al., 1987; Van Weering et al., 1993). Here, we present a dataset on bSi cycling for the Skagerrak and quantify benthic fluxes of H₄SiO₄, bSi rain rates to the seafloor, burial fluxes and burial efficiencies using a combination of geochemical observations and modelling. We propose a novel model for bSi cycling in Skagerrak sediments with potential broader applicability. We compare our results with other regions to highlight bSi cycling in the Skagerrak in a global context.

2 Study area

The Skagerrak strait is located between Denmark, Norway and Sweden and links the North Sea and the Kattegat with maximum water depths of approximately 700 m (Figure 1). Surface waters in the Skagerrak circulate anticlockwise. Water from the North Sea enters the Skagerrak through the Jutland Current from the south, which, together with the Baltic Current, results in the outflowing Norwegian Coastal Current leaving the Skagerrak to the north (Van Weering et al., 1987; Otto et al., 1990). Annual total sediment deposition in the Skagerrak is 46 · 10⁶ tons yr^-1 (De Haas and Van Weering, 1997). Sediment composition varies between sand (<40% clay), mainly along the Danish coast, and fine-grained silt and clay sediments in the deeper parts (Stevens et al., 1996). Substantial animal burrows are present in the upper 10 - 20 cm in the fine-grained areas (Canfield et al., 1993a; Kristensen et al., 2018). Skagerrak sediments are characterized by a large lateral input of mostly lithogenic material from the North Sea (Van Weering et al., 1993; De Haas and Van Weering, 1997). Nutrient supply from external waters and local rivers support an annual primary productivity of 130 g C_org m^-2 yr^-1 (Beckmann and Liebezeit, 1988). Both siliceous (diatoms) and carbonaceous (haptophytes) frustule-building phytoplankton are present in the Skagerrak, with diatoms being dominant during the early bloom in February-March and a second bloom in May-June (Gran‐Stadniczeñko et al., 2019).

FIGURE 1

Figure 1 Study area and sampling sites of MUCs and BIGOs within the Skagerrak. Black arrows indicate the surface water circulation.

3 Materials and methods

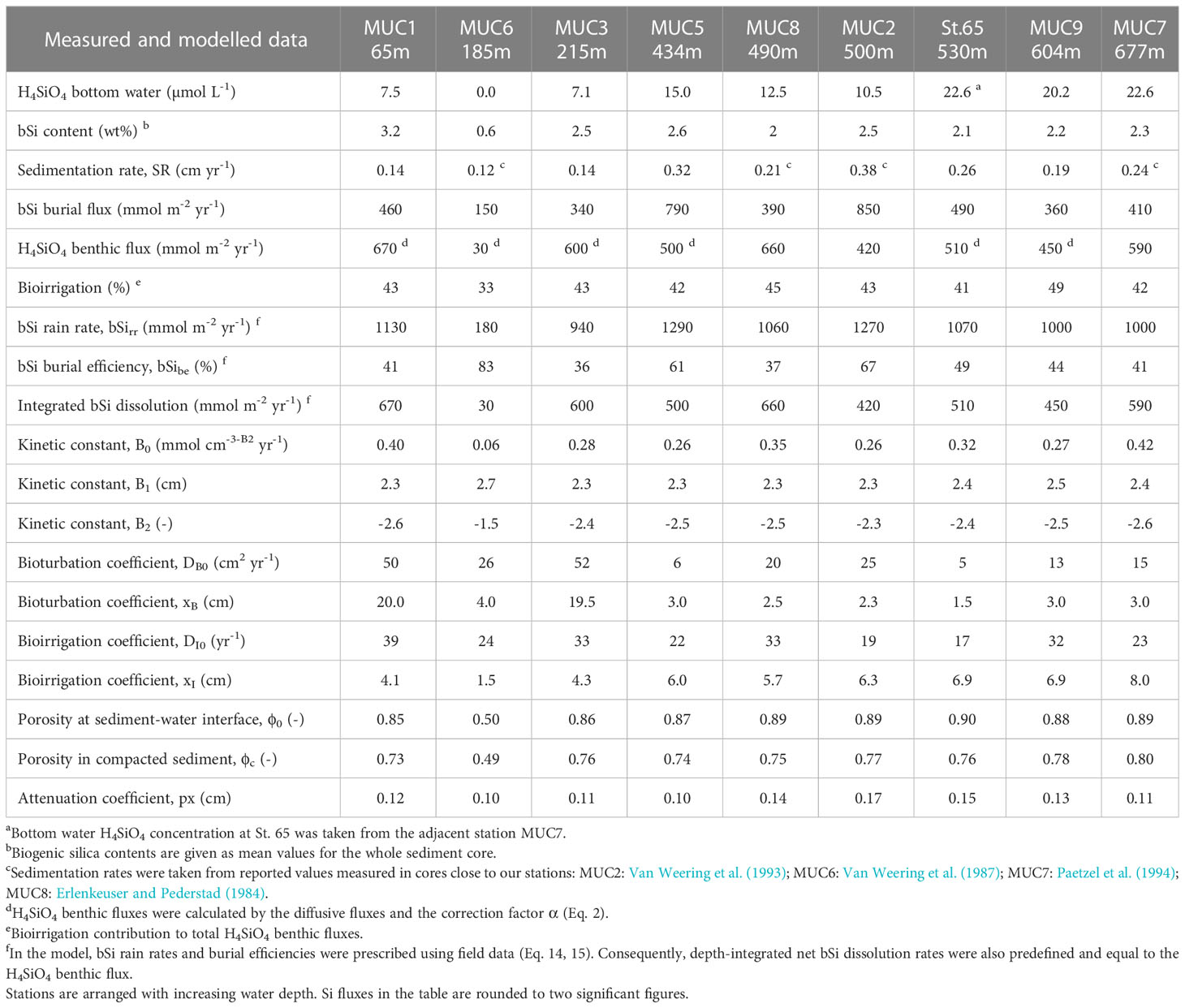
Data are presented from nine stations (65 to 677 m water depth) visited over two sampling campaigns, AL557 and AL561, with R/V Alkor in June and August 2021, respectively (Schmidt, 2021, Thomas et al., 2022). Only data from St. 65 are from June 2021 (Figure 1; Table 1). At each station, a short sediment core was recovered (<50cm) using a multiple-corer (MUC). Sediments at these sites were dominated by fine-grained material except MUC6, which was taken from a more sandy area (Table 1). At three stations during AL561, autonomous benthic landers (Biogeochemical Observatories, BIGO) were deployed to determine benthic H₄SiO₄ fluxes.

TABLE 1

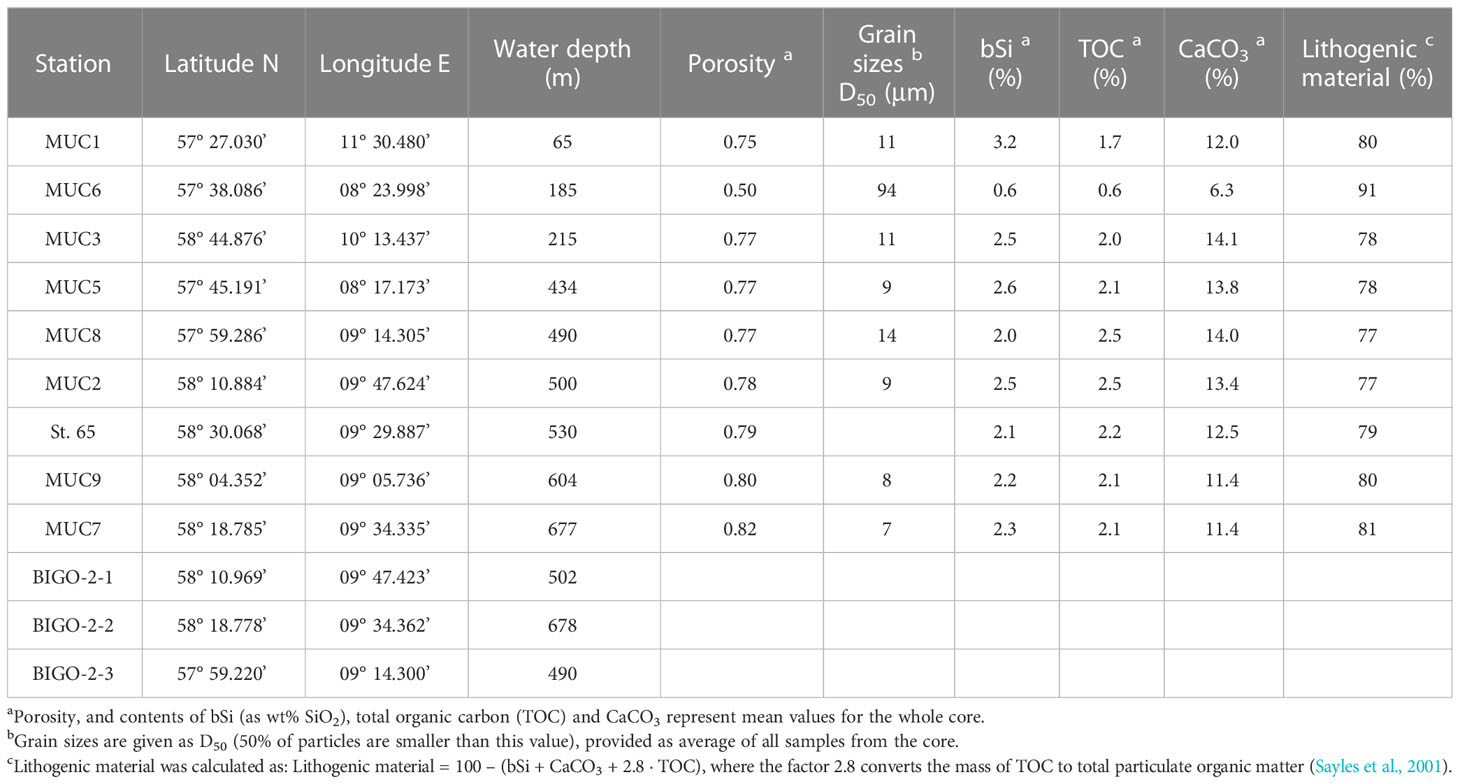
Table 1 Summary of sampling sites and general information on multicorer (MUC) and biogeochemical observatory (BIGO) stations.

3.1 Sampling

Sediment samples for porosity and solid phase analyses from the MUC were taken every centimetre and subsequently stored refrigerated at 4°C. An additional core from each station was subsampled at the same resolution for ²¹⁰Pb radionuclide and grain size analyses. From a third core, sediment for porewater analysis was sampled in an argon-filled glove bag in a refrigerated laboratory adjusted to bottom water temperatures (ca. 7°C). The samples were centrifuged at 4000 rpm at 8°C for 20 min to separate porewater from the solid phase. Subsequently, the supernatant water was filtered through a 0.2 µm cellulose-acetate syringe filter inside the glove bag. Porewater from St. 65 (AL557) was sampled with syringes and rhizones (0.15 µm pore size).

3.2 In-situ flux measurements

For the measurement of total solute fluxes, the GEOMAR BIGO type lander (Biogeochemical Observatory) was deployed as described in detail by (Sommer et al. (2009). BIGO-2 contained two circular flux chambers (internal diameter 28.8 cm area 651.4 cm²). A TV-guided launching system allowed smooth placement of the observatory on the sea floor. Approximately 2 hours (BIGO-2-1) or 4 hours (BIGO-2-2 & -3) after the observatories were placed on the seabed, the chambers were slowly driven into the sediment (~30 cm h^-1). During this initial period, where the bottom of the chambers was not closed by the sediment, the water inside the flux chamber was periodically replaced with ambient bottom water. The water body inside the chamber was replaced once more with ambient bottom water after the chamber had been driven into the sediment to flush out solutes that might have been released from the sediment during chamber insertion. To determine fluxes of H₄SiO_4, eight sequential water samples were removed with glass syringes (volume ~ 47 ml) using syringe water samplers. The syringes were connected to the chamber using 1 m long Vygon tubes with a dead volume of 5.2 ml. Prior to deployment, these tubes were filled with distilled water.

3.3 Analytical methods

Porewater H₄SiO₄ analysis was done onboard immediately after filtering using standard methods (Grasshoff et al., 1999) with a Hitachi U-2001 spectrophotometer. The analytical precision of the analysis was better than 2 μmol L^-1. The porewater samples from St. 65 (AL557) were stored frozen until they were analyzed for H₄SiO₄ six months after sampling with a TECAN infinite 200 plate reader at 810 nm according to the method by Ringuet et al. (2011). Porewater sub-samples for total dissolved iron (Fe), potassium (K) and lithium (Li) were acidified with 10 μL of suprapure concentrated HNO₃ per mL of sample and stored refrigerated at 4°C in the dark for later analyses at GEOMAR by inductively coupled plasma optical emission spectroscopy (ICP-OES, Varian ICP 720-ES). A seawater standard (IAPSO) was used for quality control. The analytical accuracy was better than 2%.

Porosity was determined from the loss of water after freeze-drying. Biogenic silica contents were analyzed on freeze-dried and homogenized sediment by a wet-leaching procedure based on the method of Müller and Schneider (1993) using 1 M NaOH as the leaching solution. An internal sediment standard was used for quality control and the analytical accuracy was better than 7%. The presented bSi contents are given as wt% SiO₂. This method may underestimate bSi content if particles are coated with metal oxides that protect bSi from dissolution or if bSi is incorporated into authigenic clay minerals (Michalopoulos and Aller, 2004; Rahman et al., 2017). Biogenic silica may also be overestimated if coexisting non-biogenic compounds are extracted by the alkaline leach (DeMaster, 1991; Kamatani and Oku, 2000). In particular, for sediments with high contents of lithogenic silica, alkaline leaching of lithogenic silica can interfere with the measured bSi content (Ragueneau and Tréguer, 1994; Zhu et al., 2023). Total carbon (TC) and total organic carbon (TOC) were analyzed on freeze-dried and homogenized sediment using a EuroEA 3000 element analyzer. For TOC analysis, sediments were first decarbonized with 0.25 N HCl on a hotplate at ~70°C. Total inorganic carbon (TIC) was calculated by subtracting TOC from TC. TIC values are reported as weight percent CaCO₃ assuming that all TIC occurs as calcium carbonate. The analytical accuracy was better than 5% for TOC and TC based on repeated analyses of certified reference material BSTD1 (soil standard).

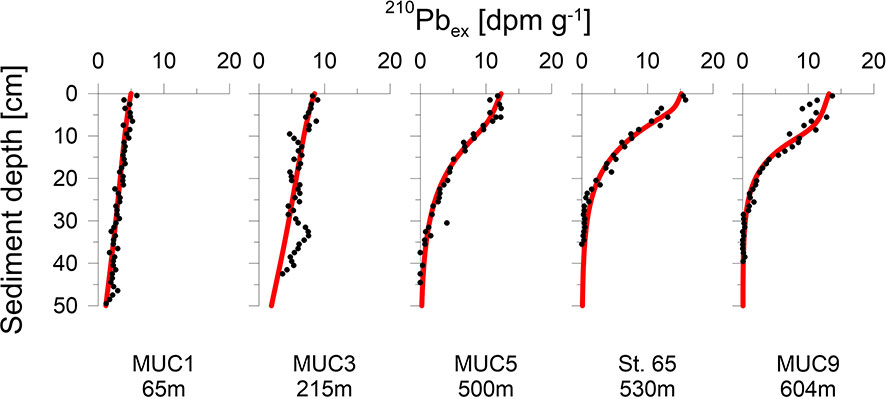
Analysis of ²¹⁰Pb was carried out at stations MUC1, MUC3, MUC5, MUC9 and St.65. Freeze-dried and homogenized sediment was embedded into containers sealed with a two-component epoxy resin. Samples were left standing for two weeks to ensure steady state equilibration between ²²⁶Ra and ²¹⁴Bi. Activities of total ²¹⁰Pb were measured via its peak intensity at 46.5 keV by gamma spectrometry on n-type planar or coaxial Canberra Ge-detectors at GEOMAR (MUC5), Göttingen (St.65) and IAF Dresden (MUC1, MUC3, MUC9). Total ²¹⁰Pb activities were corrected for the natural background decay of ²²⁶Ra at 295 keV in marine sediments to obtain excess ²¹⁰Pb (²¹⁰Pb_ex) values.

3.4 Grain size determination

Bulk grain size distributions were determined for each station except St. 65. Samples were treated with 10% - 30% hydrogen peroxide and 60% acetic acid to dissolve organic and carbonate compounds. Subsequently, samples were dispersed in water using tetra-sodium diphosphate decahydrate. Grain size distributions were determined at the CEN, University of Hamburg, with a laser-diffraction particle-sizer (Sympatec HELOS/KF Magic; range 0.5/18 to 3500 μm). Accuracy of measurements and absence of a long-term instrumental drift was ensured by regular analysis of an in-house standard (standard deviation for mean grain size and D₅₀ over the analysis period was < 1.1 µm). Statistical evaluation of the grain size distribution was based on the graphical method (Folk and Ward, 1957), calculated using GRADISTAT software (Blott and Pye, 2001).

3.5 Steady-state calculations

Biogenic silica burial fluxes (bSi_bur) were calculated as follows:

$\begin{array}{ll}{\text{bSi}}_{\text{bur}}=\text{ ds }(1-\text{ϕ})\text{ SR bSi }& (1)\end{array}$

Where ds is the density of dry solids, ϕ is the mean porosity of the whole sediment core, bSi is the mean bSi content of each sediment core in wt% SiO₂ and SR is the sediment accumulation or sedimentation rate in compacted sediments. Mean bSi contents were used due to scattering of bSi and an absence of clear trends with sediment depth. SR was either determined from ²¹⁰Pb_ex data (Eq. 7) or taken from literature values close to the station (Table 2).

TABLE 2

Table 2 Measured and modelled results for bSi cycling.

At BIGO stations, benthic fluxes of H₄SiO₄ (J_Si) were calculated from least-square linear regression fits of concentration versus time plots of the data obtained by benthic chamber in-situ measurements and the height of overlying water in the benthic chamber (Dale et al., 2021). The H₄SiO₄ benthic fluxes represent the mean flux of both benthic chambers at each station. At non-BIGO stations, porewater gradients of H₄SiO₄ were used to calculate H₄SiO₄ benthic fluxes by applying Fick’s First Law. This approach only considers diffusive transport and does not account for additional non-local transport by bioirrigation, in contrast to in-situ BIGO measurements that provide the total flux. The enhancement of solute transport by bioturbation and bioirrigation was obtained by calculating a correction factor, α (Ståhl et al., 2004). The factor (mean α = 2.2) was calculated as the ratio between benthic fluxes determined from in-situ measurements and porewater gradients at the three BIGO stations. The correction factor was then applied to the diffusive flux at non-BIGO stations to obtain total H₄SiO₄ benthic fluxes:

$\begin{array}{ll}{\text{J}}_{\text{Si}}=-\text{ ϕ}{\text{ D}}_{\text{sed}}\frac{\text{d}[\text{C}]}{\text{dx}}\text{ α }& (2)\end{array}$

Where J_Si is the H₄SiO₄ benthic flux, ϕ is porosity, d[C]/dx is the concentration gradient between porewater (taken at 0.5cm) and bottom water (taken from overlying water of the MUCs), and D_sed is the molecular diffusion coefficient of H₄SiO₄ corrected for tortuosity (0.58 · 10^-5 cm² s^-1) and bottom water temperatures (7°C) taken from Rebreanu et al. (2008). H₄SiO₄ fluxes were always directed out of the sediment. In this study, they are reported as positive numbers.

Rain rates of bSi (bSi_rr) were then calculated as the sum of bSi burial fluxes and H₄SiO₄ benthic fluxes:

$\begin{array}{ll}{\text{bSi}}_{\text{rr}}={\text{bSi}}_{\text{bur}}+{\text{ J}}_{\text{Si}}& (3)\end{array}$

The percent bSi burial efficiency (bSi_be) was then calculated as follows:

$\begin{array}{ll}{\text{bSi}}_{\text{be}}=\frac{{\text{bSi}}_{\text{bur}}}{{\text{bSi}}_{\text{rr}}}100\text{\% }& (4)\end{array}$

3.6 Model description

To simulate bSi turnover, we used a steady-state numerical transport-reaction model for dissolved H₄SiO₄ and particulate bSi and ²¹⁰Pb_ex. The following one-dimensional partial differential equations (Berner, 1980) were applied to solve for the concentration profiles of H₄SiO₄ and bSi:

$\begin{array}{ll}\text{ds }(1-\text{ϕ})\frac{\text{δbSi}}{\text{δt}}=\frac{\text{δ}}{\text{δx}}\left(\text{ds }(1-\text{ϕ}){\text{ D}}_{\text{B}}\frac{\text{δBSi}}{\text{δx}}-\text{ ds }(1-\text{ϕ})\text{ us BSi}\right)-\text{ds }(1-\text{ϕ})\text{ RbSi }& (5)\end{array}$

$\begin{array}{ll}\text{ϕ }\frac{{\text{δH}}_4{\text{SiO}}_4}{\text{δt}}=\frac{\text{δ}}{\text{δx}}\left(\text{ϕ}{\text{ D}}_{\text{s}}\frac{{\text{δH}}_4{\text{SiO}}_4}{\text{δx}}-\text{ϕ}{\text{ upw H}}_4{\text{SiO}}_4\right)+\text{ϕ}{\text{ D}}_{\text{I}}(\text{BW}-{\text{H}}_4{\text{SiO}}_4)+\text{ϕ RbSi }& (6)\end{array}$

where x is sediment depth, t is time, ds is the density of dry solids (= 2.5 g cm^-3), ϕ is porosity, D_s is the tortuosity-corrected molecular diffusion coefficient, D_B is the bioturbation coefficient, D_I is the bioirrigation coefficient, BW denotes the concentration of H₄SiO₄ in ambient bottom water, us and upw are burial velocities for solids and porewater, respectively, and RbSi is the rate of bSi dissolution.

The following equation was used to simulate particle-bound ²¹⁰Pb_ex and derive burial velocities and bioturbation rates:

$\begin{array}{ll}\text{ds }(1-\text{ϕ})\frac{{\text{δ Pb}}_{\text{ex}}}{\text{δt}}=\frac{\text{δ}}{\text{δx}}(\text{ds }(1-\text{ϕ}){\text{ D}}_{\text{B}}\frac{{\text{δ Pb}}_{\text{ex}}}{\text{δx}}-\text{ ds }(1-\text{ϕ}){\text{ us Pb}}_{\text{ex}})-\text{ds }(1-\text{ϕ}){\text{ λ Pb}}_{\text{ex}}& (7)\end{array}$

where Pb_ex is the excess activity of ²¹⁰Pb in sediments and λ is the ²¹⁰Pb decay constant (0.031 yr^-1).

Sediment compaction was considered in the model by fitting the following function to the porosity data at each station:

$\begin{array}{ll}\text{ϕ}={\text{ϕ}}_{\text{c}}+{({\text{ϕ}}_0-{\text{ϕ}}_{\text{c}})}^{(-\frac{\text{x}}{\text{px}})}& (8)\end{array}$

where ϕ₀ is the porosity at the sediment surface, ϕ_c is the porosity in compacted sediment and px is the attenuation coefficient. Burial velocities of solids and solutes were then described as:

$\begin{array}{ll}\text{us}=\frac{\text{SR }(1-{\text{ϕ}}_{\text{c}})}{(1-\text{ϕ})}& (9)\end{array}$

$\begin{array}{ll}\text{upw}=\frac{\text{SR }{\text{ϕ}}_{\text{c}}}{\text{ϕ}}& (10)\end{array}$

The distribution of ²¹⁰Pb_ex in surface sediments was used to constrain bioturbation rates:

$\begin{array}{ll}{\text{D}}_{\text{B}}={\text{D}}_{\text{B}0}\exp (-\frac{{\text{x}}^2}{2{\text{x}}_{\text{B}}^2})& (11)\end{array}$

where D_B0 is the bioturbation coefficient at the sediment-water interface and x_B controls the bioturbation mixing depth.

Flushing of animal burrows by bioirrigation was mathematically described as:

$\begin{array}{ll}{\text{D}}_{\text{I}}={\text{D}}_{\text{I}0}\exp (-\frac{{\text{x}}^2}{2{\text{ x}}_{\text{I}}^2})& (12)\end{array}$

where D_I0 is the bioirrigation coefficient at the sediment-water interface and x_I controls the bioirrigation depth. Bioirrigation rates were constrained from porewater H₄SiO₄ concentrations.

Most models that simulate bSi dissolution use a rate that decreases rapidly with sediment depth to simulate porewater H₄SiO₄ concentrations (e.g. McManus et al., 1995; Rabouille et al., 1997; Khalil et al., 2007). Three different explanations have been put forward to explain the decrease in bSi dissolution; (i) saturation control by high porewater H₄SiO₄ levels (McManus et al., 1995; Rabouille et al., 1997), (ii) different phases of bSi undergoing dissolution, each with its own reactivity (Boudreau, 1990, Archer et al., 1993, McManus et al., 1995), and (iii) retardance of dissolution due to progressive coating of particle surfaces by Al-containing minerals (Kamatani et al., 1988; McManus et al., 1995). Since the underlying mechanisms are unknown in Skagerrak sediments, we made no attempt to resolve the different factors controlling the rate decline with depth. Instead, we applied an empirical power law model to simulate the combined effect of these processes, which implicitly includes dissolution, reprecipitation and adsorption, and which we refer to as the depth-dependent net bSi dissolution rate (RbSi). Thus, true bSi dissolution rates may be higher if large amounts of H₄SiO₄ are removed from porewaters by adsorption or reprecipitation.

Based on previous modelling work (Middelburg, 1989; Boudreau and Ruddick, 1991; Boudreau et al., 2008), Stolpovsky et al. (2015) proposed a depth-dependent power function to simulate POC degradation in bioturbated sediments:

$\begin{array}{ll}\text{RPOC}={\text{B}}_0{(\text{x}+{\text{B}}_1)}^{{\text{B}}_2}& (13)\end{array}$

where RPOC is the rate of POC degradation with sediment depth (mmol cm^-3 yr^-1) and B₀ (mmol cm^-3-B2 yr^-1), B₁ (cm) and B₂ (dimensionless) are parameters defining the decrease in POC degradation rate. Given that the rates of both bSi dissolution and POC degradation decrease with sediment depth, we assumed that the power law from Stolpovsky et al. (2015) is applicable to describe bSi dissolution kinetics:

$\begin{array}{ll}\text{RbSi}={\text{B}}_0{(\text{x}+{\text{B}}_1)}^{{\text{B}}_2}& (14)\end{array}$

where RbSi is the depth-dependent net rate of bSi dissolution (mmol cm^-3 yr^-1). The values of B₀, B₁ and B₂ for bSi dissolution are expected to be different to those for POC degradation that were constrained from a global database of benthic oxygen and nitrate fluxes (Stolpovsky et al., 2015). Following Stolpovsky et al. (2015), we assume that the rain rate of bSi to the seafloor provides an upper limit of the total amount of bSi available for dissolution and that its burial efficiency describes the limit of bSi preservation. Consequently, bSi rain rates and burial efficiencies are model input parameters. If bSi_rr and bSi_be are known, the value of one of the parameters B₀, B₁ or B₂ can be determined from the other two, i.e. for B₀:

$\begin{array}{ll}{\text{B}}_0=\frac{((1+{\text{B}}_2)(-100+{\text{bSi}}_{\text{be}}){\text{ bSi}}_{\text{rr}})}{(100({\text{B}}_2^{1+\text{B}2}-{\text{B}}_1{({\text{B}}_1+\text{L})}^{{\text{B}}_2}-\text{L }{({\text{B}}_1+\text{L})}^{{\text{B}}_2}))}& (15)\end{array}$

where L is the depth at which bSi no longer dissolves. Since the depth profiles of bSi and H₄SiO₄ indicate that bSi dissolution stops near the bottom of the sediment core, we assumed L to be 50 cm.

Two adjustable parameters, B₁ and B₂, are required to simulate net bSi dissolution. These were constrained from the measured bSi and H₄SiO₄ data. In total, 10 parameters (B₁, B₂, SR, ϕ₀, ϕ_c, px, D_I0, x_I, D_B0, x_B) were adjusted to fit the porosity, ²¹⁰Pb_ex, H₄SiO₄ and bSi data. The parameters SR, D_B0 and x_B were evaluated by a Monte Carlo procedure (2000 runs) after Dale et al. (2021). For each model run, the parameters were randomly varied from 0.05 to 4 cm yr^-1 for SR, 1 to 30 cm² yr^-1 for D_B0 and 1 to 3 cm for x_B. These ranges were chosen based on literature values and visual identification of the bioturbation layer in the ²¹⁰Pb_ex data. At stations MUC1 and MUC3, no clear bioturbation layer was observed. Here, ranges of D_B0 and x_B for the Monte Carlo runs were extended to 1 - 150 cm² yr^-1 and 1 - 30 cm, respectively.

Upper boundary conditions were set as constant concentrations for H₄SiO₄ and constant particulate fluxes to the seafloor for bSi. For ²¹⁰Pb_ex, a constant rate of supply was set at the upper boundary from the measured integrated ²¹⁰Pb_ex activity in the sediment and the decay constant λ:

$\begin{array}{ll}{\text{FPb}}_{\text{ex}}=\text{λ ds }(1-{\text{ϕ}}_0)\underset{0}{\overset{\infty }{\int }}{\text{Pb}}_{\text{ex}}\text{ dx }& (16)\end{array}$

where FPb_ex is the flux of ²¹⁰Pb_ex to the seafloor. At the lower boundary at 50 cm, a zero gradient condition was imposed for all model variables.

Model input data for each station are summarized in Table 2. The model was run to steady-state using the partial differential equation solver implemented in Mathematica 12.2. Mass conservation > 99% was achieved in all model runs. Mean deviations between the model and measured H₄SiO₄, bSi and ²¹⁰Pb_ex data, expressed as root mean square errors, were 27 μmol L^-1, 0.4 wt% and 0.6 dpm g^-1, respectively.

4 Results

4.1 ²¹⁰Pb_ex activities, sedimentation rates and mixing

At stations MUC5, MUC9 and St.65, ²¹⁰Pb_ex activities decreased exponentially below the upper centimetres where ²¹⁰Pb_ex activities tended to be more constant (Figure 2). In contrast, stations MUC1 and MUC3 showed an almost linear ²¹⁰Pb_ex decrease throughout the whole core. Sedimentation rates determined by the model ranged from 0.14 to 0.32 cm yr^-1 (Table 2) and varied with water depth, but no clear trend was observed.

FIGURE 2

Figure 2 Measured data (symbols) and model simulations (curves) of ²¹⁰Pb_ex.

Sediment mixing by bioturbation was limited to the upper 5 - 10 cm at most sites (Figure 3C, Eq. 11) with bioturbation coefficients (D_B0) and mixing coefficients (x_B) of 5 - 26 cm² yr^-1 and 1.5 - 4.0 cm, respectively (Table 2). In contrast, bioturbation was predicted to proceed throughout the whole sediment core at stations MUC1 and MUC3. At these sites, extreme DB₀ and x_B values in the range of 50 cm² yr^-1 and 20 cm, respectively, were required to simulate the measured ²¹⁰Pb_ex data. Bioirrigation was most intense in the upper layers and extended up to 5 - 20 cm depth, with deeper bioirrigation observed with increasing water depth (Figure 3C).

FIGURE 3

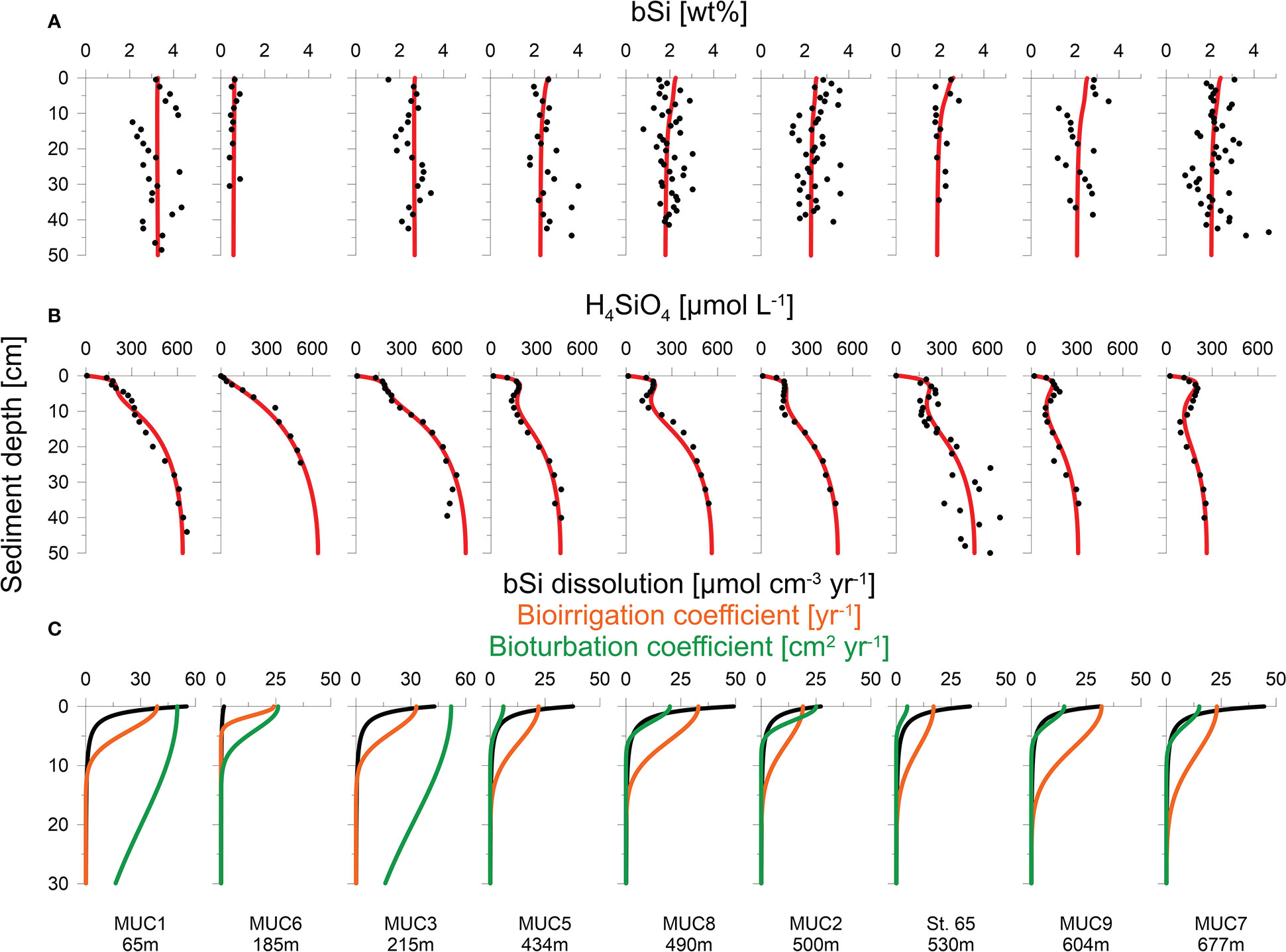
Figure 3 Measured data (symbols) and model simulations (curves) of (A) H₄SiO₄ concentration, (B) bSi content and (C) net bSi dissolution rates (black), bioirrigation coefficient (orange) and bioturbation (green). Note different depth scale in (C).

4.2 Dissolved and solid phase geochemistry

Sediments were generally fine-grained with mean D₅₀ values ranging from 7 to 14 μm (Table 1). MUC6 contained a higher proportion of sand with a D₅₀ of 94 μm. Solid phase bSi contents varied between 1 and 5 wt%, except for the sandy station MUC6, where lower values of 0.4 - 0.9 wt% were observed (Figure 3A). Biogenic silica showed no clear trend with sediment depth. CaCO₃ varied from ca. 6 – 13% and lithogenic material from 77 - 91% (Table 1).

H₄SiO₄ concentrations in the Skagerrak generally increased with sediment depth up to asymptotic concentrations of 300 - 660 μmol L^-1 (Figure 3B). Although asymptotic values were not reached at every station, the data indicate that the maximum asymptotic concentrations decreased with water depth. Furthermore, concentration plateaus, or local minima, were observed between 2 - 15 cm and were most pronounced at the deeper stations (>400 m). Total dissolved Fe concentrations were below the detection limit in the upper 5 - 10 cm, followed by an increase up to a maximum concentration of 40 - 135 μmol L^-1 (Figure 4A). Thereafter, dissolved Fe concentrations tended to decrease. The zone of increasing dissolved Fe concentrations coincided with the concentration plateaus of H₄SiO₄ at the deeper sites. Dissolved K and Li concentrations showed near-constant concentrations with sediment depth, ranging between 10 and 12 mmol L^-1 and 24 and 36 μmol L^-1, respectively, across the different sites (Figure 4B).

FIGURE 4

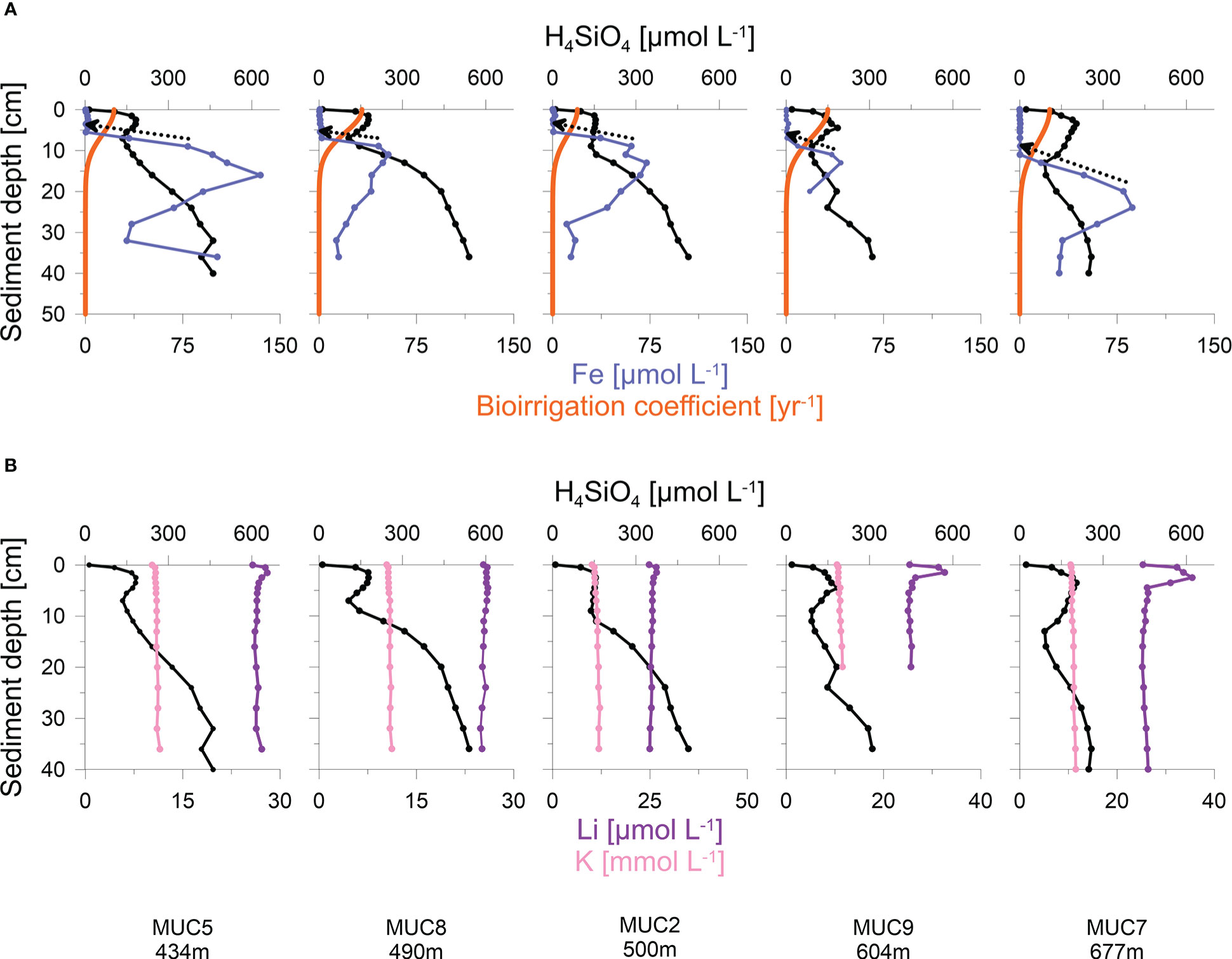
Figure 4 (A) Porewater concentrations of H₄SiO₄, total dissolved Fe and model simulations of bioirrigation (orange curves). Dashed arrows indicate the gradient used to calculate diffusive Fe fluxes; and (B) Porewater concentrations of H₄SiO₄, K and Li at deep-water stations with distinct H₄SiO₄-minima. Note different scales in Li and K concentrations.

4.3 Si fluxes and burial efficiencies

Burial fluxes varied between 150 and 850 mmol m^-2 yr^-1. (Table 2). H₄SiO₄ fluxes at the three BIGO stations ranged between 420 and 660 mmol m^-2 yr^-1, which is similar to reported in-situ flux measurements of 360 - 609 mmol m^-2 yr^-1 in the Skagerrak basin between 411 - 682 m water depth (Hall et al., 1996). Benthic fluxes at stations that were calculated based on porewater gradients and the correction factor α for non-diffusive transport (Eq. 2) were between 450 - 670 mmol m^-2 yr^-1, except for the sandy station MUC6 that showed a lower rate of 30 mmol m^-2 yr^-1. Bioirrigation accounted for 33 - 49% of the total benthic H₄SiO₄ flux. Biogenic silica rain rates varied between 180 and 1290 mmol m^-2 yr^-1 with burial efficiencies of 36 - 83%. Fluxes and burial efficiencies varied between the different stations, but no clear trend was observed with water depth (Figure 5).

FIGURE 5

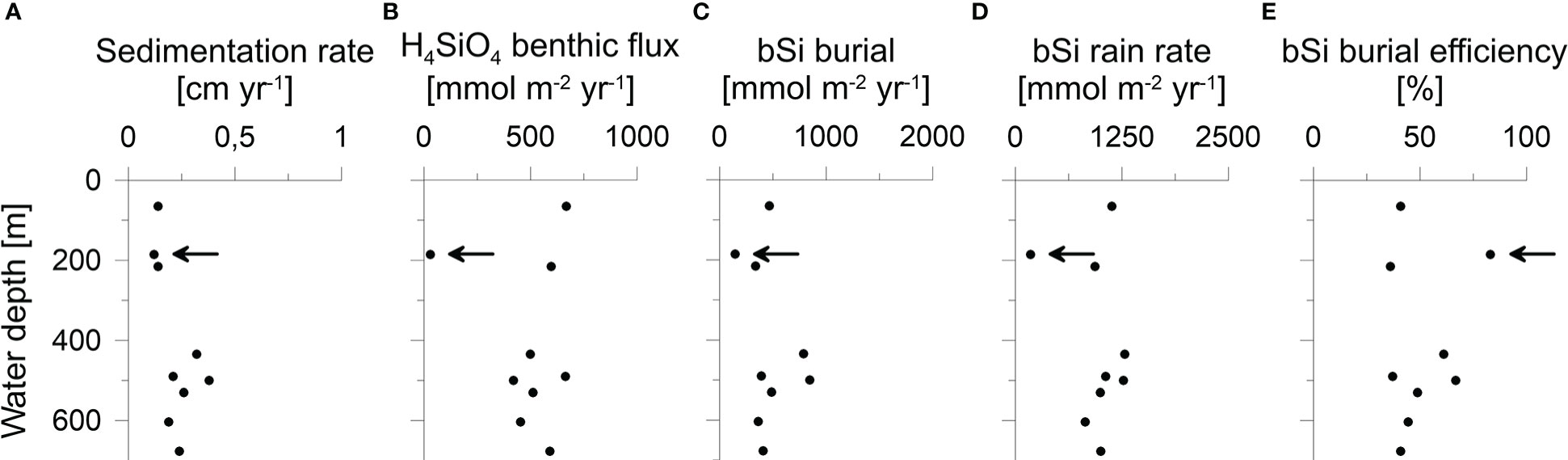
Figure 5 (A) Sedimentation rate, (B) H₄SiO₄ benthic flux, (C) bSi burial flux, (D) bSi rain rate and (E) burial efficiency plotted against water depth. Data at 185 m water depths correspond to the sandy station MUC6 (indicated by the arrow).

4.4 Modelled bSi dissolution

The model predicted that most of the net bSi dissolution takes place within the top sediment layer (Figure 3C). The adjustable parameters B₁ and B₂ that describe bSi dissolution varied between 2.3 and 2.5 cm, and -2.3 and -2.6 (dimensionless), respectively, excluding sandy station MUC6 (Table 2). At this station, B₁ and B₂ were 2.7 and -1.5, respectively. There were no clear trends in B₀, B₁ and B₂ across different sites.

5 Discussion

5.1 Biogenic silica cycling

The major fluxes of bSi in Skagerrak sediments are investigated in this study through numerical interpretation of the geochemical data. In our approach, the down-core decrease in net bSi dissolution, bioirrigation and bioturbation can be quantified with our novel kinetic bSi dissolution model with reasonable confidence. The two adjustable parameters needed to describe bSi dissolution, B₁ and B₂, show consistent values across the stations with fine-grained material, demonstrating the potential to apply the model elsewhere in comparable environments. Our kinetic description of bSi dissolution represents an alternative to previous approaches. It is especially applicable for regions where bSi dissolution rates and underlying mechanisms that control dissolution rates are unknown but where data for bSi rain rate and burial are available.

Biogenic silica burial fluxes were calculated based on ²¹⁰Pb derived sedimentation rates that are in the range of reported values from nearby locations (Erlenkeuser and Pederstad, 1984; Van Weering et al., 1993; Deng et al., 2020). A mean bSi burial efficiency of 50% in fine-grained sediments in the Skagerrak basin indicates that about half of the annual bSi raining onto the seafloor, on average ca. 1100 mmol m^-2 yr^-1, is buried in the sediment. The other half dissolves and is subsequently returned to the water column. This calculation excludes the sandy station MUC6 and shallow stations MUC1 and MUC3, where non-exponential ²¹⁰Pb_ex profiles indicate substantial sediment mixing and more uncertainty in calculated bSi rain rates. The unusually intense and deep mixing rates required to simulate the data at MUC1 and MUC3 compared to other sites could be attributed to bottom trawling, which is frequent in the MUC1 region at water depths<200 m (Sköld et al., 2018). Piles of sediment alongside furrows created by dragging trawl doors through the sediment can reach 1 to 2 dm in height (Bradshaw et al., 2021) and it may be that sediment cores taken at stations MUC1 and MUC3 penetrated such sediment piles during sampling. We find this explanation more convincing than deep bioturbation since no visual evidence of macrofauna was observed below ca. 10 cm depth during the slicing of the sediment cores. Furthermore, if the bioturbation parameters were set to values similar to those predicted for the undisturbed sites, sedimentation rates of 1 to 2 cm yr^-1 would be required to fit the ²¹⁰Pb_ex data (results not shown); a magnitude that seems unlikely for the Skagerrak. For a seafloor surface area of the Skagerrak basin below 200 m of about 10700 km², and assuming a mean bSi burial flux of 550 mmol m^-2 yr^-1, we calculated a mean annual bSi burial flux of 6 · 10⁹ mol yr^-1.

Ongoing dissolution of bSi leads to the accumulation of H₄SiO₄ in porewaters and drives H₄SiO₄ fluxes to the bottom water. Scanning electron micrographs have revealed evidence of chemical erosion of bSi in Skagerrak sediments (Meyenburg and Liebezeit, 1993). According to our model, the bulk of net bSi dissolution occurs in the upper 5 centimetres (Figure 3C). A steep down-core decline in the dissolution rate is mirrored by the steep increase in H₄SiO₄ concentrations below the sediment-water interface. This is not evident in the bSi profiles that show high variability, possibly due to interannual changes in bulk sediment supply and/or bSi rain rate. Our bSi contents are lower than ca. 6 wt% measured in a single sediment sample from the top 50 cm at 325 m water depth in the Skagerrak (Bohrmann, 1986). Meyenburg and Liebezeit (1993) and Fengler et al. (1994) reported 0.1 - 0.6 wt% bSi at water depths of 80 and 183 m, which is similar to the sandy station MUC6, although the sediment type in their data was not reported.

No obvious trends between Si fluxes and individual environmental factors were observed at our stations, despite sizeable differences in water depth. Aside from H₄SiO₄ concentration and temperature in the water column, water depth typically controls the amount of bSi that reaches the seafloor (Nelson et al., 1995; Ragueneau et al., 2000; Tréguer and de la Rocha, 2013), with lower fluxes expected at deeper stations. However, apart from the sandy station MUC6, our data reveal relatively little variability in Si fluxes across stations (Figure 5; Table 2). Additional input of bSi to the deeper sites from the North Sea may partly explain this observation (see section 5.3). We observed a higher bSi burial efficiency at MUC6 where the sediment was coarser, which could point toward an additional control by grain size (Table 1; Figure 5E). Similar trends of burial efficiency and grain size were reported in sediments of the Helgoland mud area (Oehler et al., 2015b); a sedimentary depocenter in the southern North Sea.

To frame bSi cycling in the Skagerrak in a global context, we compared our bulk fluxes to sites compiled by Dale et al. (2021), most of which are from the deep-sea (>3000 m water depth). In general, the Skagerrak bSi burial data aligns well with the global trend (Figure 6) and extends the existing database towards continental margin sites of higher burial efficiencies and burial fluxes. The Skagerrak data is in the range of other continental margins, such as the Peru shelf (Froelich et al., 1988), the Helgoland mud area (Oehler et al., 2015b) and the Guaymas Basin (Geilert et al., 2020). Variations in bSi cycling among continental margins likely stem from a combination of different regional settings, i.e. water depth, surface productivity, sedimentation rates and sediment composition.

FIGURE 6

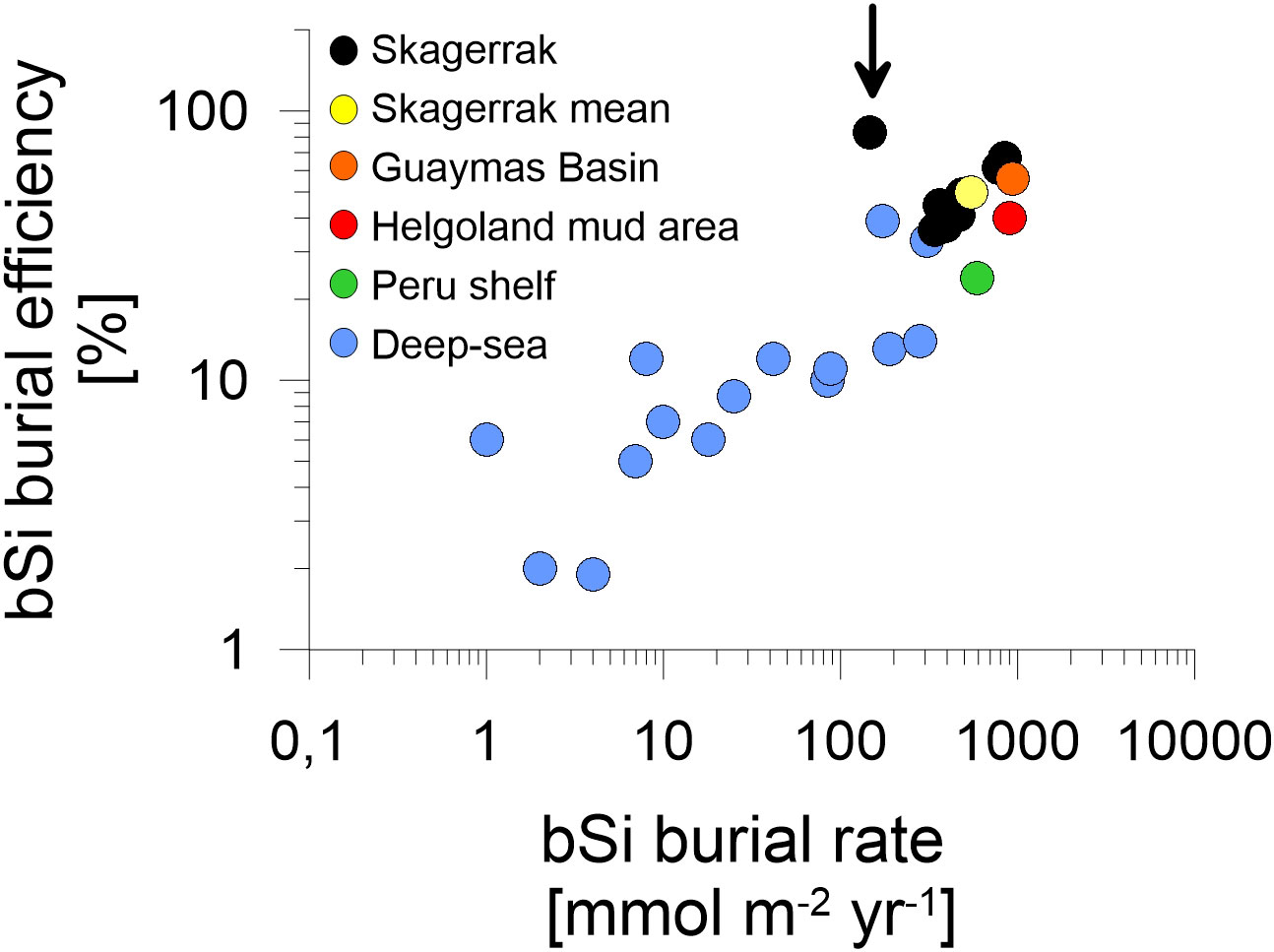
Figure 6 Log-log plot of regional mean bSi data adapted from the compiled dataset presented by Dale et al. (2021). Biogenic silica burial rates are plotted against bSi burial efficiencies. Individual Skagerrak stations (black) and a Skagerrak mean value of stations > 400 m water depth (yellow) are compared to deep-sea regions at >3000 m water depth (blue), the Peru shelf (green) by Froelich et al. (1988), the Helgoland mud area (red) by Oehler et al. (2015b) and the Guaymas Basin (orange) by Geilert et al. (2020). Data indicated by the arrow corresponds to sandy station MUC6.

5.2 Controls on H₄SiO₄ porewater concentrations

The rapid downcore increase in H₄SiO₄ to a constant asymptotic concentration observed in the Skagerrak is typical for fine-grained marine sediments (Hurd, 1973; Schink et al., 1974; McManus et al., 1995; Rabouille et al., 1997; Khalil et al., 2007; Oehler et al., 2015b; Ehlert et al., 2016). The tendency for a decrease in the maximum concentration with increasing water depth has been attributed to the proportion of lithogenic material present in the sediment, whereby the release of dissolved aluminium from clay minerals and subsequent adsorption or incorporation into the particulate silica phase lowers bSi solubility (Van Beusekom et al., 1997; Van Cappellen and Qiu, 1997; Dixit et al., 2001; Dixit and Van Cappellen, 2003). At our sites, lithogenic material changed only slightly with water depth (Table 1). Consequently, inhibition of bSi dissolution by aluminium may not be a major control on H₄SiO₄ distributions in our sediment cores, although this conclusion would be strengthened with data on dissolved aluminium concentrations.

Especially at the deeper stations (>400 m), H₄SiO₄ porewater profiles were characterized by decreases or local minima of H₄SiO₄ concentrations between 2 - 15 cm (Figure 3B). The model predicts that the H₄SiO₄ minima are caused by more intense removal of H₄SiO₄ in discrete sediment layers by bioirrigation versus H₄SiO₄ added by bSi dissolution. It further predicts more intense bioirrigation at the deeper stations where the minima are more pronounced (Figure 3C). This is supported by reports that deep-water Skagerrak sediments are preferably colonized by deeply penetrating deposit feeders, whereas suspension and interface feeders are more abundant at shallower depths (Rosenberg et al., 1996; Dauwe et al., 1998). However, our results differ from Kristensen et al. (2018), who observed decreasing bioirrigation intensity with water depth. In addition, our modelled bioirrigation extends deeper than the zone where dissolved Fe is below the detection limit (Figure 4A). Given that bioirrigation enhances the transport of oxidants into the sediment, and that dissolved Fe is rapidly oxidized, this may indicate that our model overestimates the depth of bioirrigation. Hence, it might be possible that the H₄SiO₄ minima observed at deeper sites are not caused by deep-reaching bioirrigation. Instead, high rates of H₄SiO₄ removal by adsorption or precipitation might lower H₄SiO₄ concentrations in distinct sediment layers.

High sedimentary manganese and iron oxide contents have been reported for the Skagerrak, especially in deep waters (Canfield et al., 1993a; Thamdrup et al., 1994). Experimental studies have demonstrated that H₄SiO₄ can adsorb to iron oxides (Huang, 1975; Sigg and Stumm, 1981; Swedlund, 1999; Davis et al., 2001; Davis et al., 2002), suggesting that this process is a potential sink for H₄SiO₄ in Skagerrak sediments. Since the depths of local H₄SiO₄ minima and dissolved iron removal coincide (Figure 4A), this sink may be relevant for the formation of observed H₄SiO₄ minima. In order to estimate the significance of this process, potential H₄SiO₄ adsorption fluxes were calculated from the diffusive flux of Fe and then compared to H₄SiO₄ removal by bioirrigation integrated over the depth interval centred on the H₄SiO₄ minima, typically spanning 5 cm (Figure 4A). Under the assumption that all dissolved Fe is consumed by iron oxide formation, the diffusive flux of Fe (Eq. 2) was calculated at the depth where Fe increases. With a diffusion coefficient (D_sed) of 121 cm² yr^-1 (Schulz and Zabel, 2006), dissolved Fe removal fluxes of 6 - 14 mmol m^-2 yr^-1 were calculated for the stations shown in Figure 4. Given mean H₄SiO₄ concentrations at the depth of H₄SiO₄ minima of ca. 150 μmol L^-1 and assuming a pH value of 8, a molar Si/Fe sorption density on iron oxides of 0.2 is expected (Davis et al., 2002). Multiplying the Fe flux by the molar Si/Fe ratio yields potential H₄SiO₄ adsorption fluxes of 1 - 3 mmol m^-2 yr^-1. This corresponds to only 2 - 6% of bioirrigation fluxes integrated over the depth of H₄SiO₄ minima. It illustrates that H₄SiO₄ adsorption to iron oxides may be a feasible but probably not a dominant pathway of local H₄SiO₄ removal in Skagerrak sediments.

During authigenic clay formation, H₄SiO₄ is consumed in the presence of dissolved cations (e.g. K and Li) and weathered clay minerals, a process referred to as reverse weathering (Mackenzie et al., 1981; Mackenzie and Kump, 1995; Loucaides et al., 2010; Ehlert et al., 2016). Reverse weathering occurs in anoxic marine sediments rich in biogenic opal and metal hydroxides (Michalopoulos and Aller, 1995; Michalopoulos et al., 2000) but has not been investigated in the Skagerrak. Previous studies have demonstrated reverse weathering to be a dominant process altering H₄SiO₄ porewater profiles on continental margins (Michalopoulos and Aller, 1995; Michalopoulos and Aller, 2004; Wallmann et al., 2008; Ehlert et al., 2016; Spiegel et al., 2021). Furthermore, the competition between bSi dissolution and reprecipitation during reverse weathering can create features similar to the H₄SiO₄ minima in our dataset (Spiegel et al., 2021). Since dissolved cations are consumed during reverse weathering, we compared the porewater distribution of H₄SiO₄ to dissolved K and Li concentrations (Figure 4B). The concentration profiles of K and Li are near-constant with sediment depth and, thus, do not show obvious indications for reverse weathering, i.e. uptake in the same horizon as H₄SiO₄ minima. However, we note that the effect of reverse weathering on dissolved cation concentrations, especially for K (~10 mM), might be too low relative to bulk porewater concentrations to result in distinct porewater signatures.

Since our model describes a continuous decline in net bSi dissolution with sediment depth, we are currently unable to resolve processes that operate in narrow depth intervals where the H₄SiO₄ porewater plateaus are observed. Hence, explicitly describing adsorption, precipitation and aluminium inhibition could lead to a better fit to the data and consequently to a more detailed description of the benthic bSi cycle in the Skagerrak. A model that includes these additional sinks may also be able to reproduce the data using shallower penetration depths of bioirrigation that are more consistent with those that have been previously reported by Kristensen et al. (2018). Further empirical data on these processes in Skagerrak sediments and elsewhere would benefit future bSi model descriptions. Since their parameterization is uncertain on the basis of our dataset and yet to be investigated in the Skagerrak, we reiterate that our simple model currently only provides net bSi dissolution rates.

5.3 Effect of lateral sediment supply on bSi/TOC ratios

DeMaster (2002) calculated global bSi burial on continental margins of 1.8 - 2.8 · 10¹² mol yr^-1 based on organic carbon burial and a mean molar bSi/TOC burial ratio of 0.6. However, DeMaster (2002) and subsequent budgets (Tréguer and de la Rocha, 2013; DeMaster, 2019) excluded continental margins dominated by high lithogenic loads, such as the Skagerrak, in their calculations. Rahman et al. (2016) and Rahman et al. (2017) reported bSi burial fluxes based on ³²Si isotopes in tropical and subtropical deltaic regions dominated by significant lithogenic inputs. Their results, when incorporated into more recent global Si budgets, point toward a greater significance of margins in total bSi burial (Tréguer et al., 2021). Since we have no ³²Si data, we compared our findings to previous approaches utilizing sedimentary bSi/TOC molar ratios. Based on our field data (Table 1), we calculated a mean bSi/TOC molar ratio of 0.22 in Skagerrak sediments, which is distinctively lower than the mean ratio of 0.6 applied by DeMaster (2002). Other continental margin settings with high lithogenic inputs and where bSi was determined by the same method (Müller and Schneider, 1993) showed molar ratios of 1.0 for the Guaymas basin (Geilert et al., 2020), 0.52 for the Helgoland mud area (Oehler et al., 2015a; Oehler et al., 2015b) and 0.55 for the Amazon shelf (Spiegel et al., 2021). Dale et al. (2021) reported much lower ratios of 0.14 for the Peruvian oxygen minimum zone, which was attributed to a lack of bioturbation and enhanced bSi dissolution in undersaturated surface sediment layers. Tréguer et al. (2021) reported ratios between 2.4 and 11 in tropical and subtropical deltaic systems. The wide range in molar bSi/TOC ratios, presumably related to the differing diagenetic regimes, emphasizes the need to further study continental margins to better constrain global bSi burial.

Low bSi/TOC ratios in the Skagerrak may be confounded by the long transit time of sediments on the order of several months from the central North Sea and 1 - 2 years from the southern North Sea to the Skagerrak (Hainbucher et al., 1987; Dahlgaard et al., 1995; Salomon et al., 1995). Since seawater is undersaturated with respect to bSi, we hypothesize repeated resuspension and deposition during particle transport leads to more extensive bSi dissolution relative to POC. This may set the Skagerrak apart from most other continental margins with regard to the coupling between bSi and TOC. Similar regions need to be investigated in order to determine whether the Skagerrak is a unique environment with regards to bSi cycling or is emblematic of continental margins exhibiting protracted transport pathways.

6 Conclusions

In this study, we present bSi cycling in Skagerrak sediments based on geochemical data and modelling. Approximately 1100 mmol m^-2 yr^-1 of bSi annually rains onto the seafloor at the sites investigated, of which half dissolves in sediments and is reintroduced into the water column and half is permanently buried. Biogenic silica cycling shows some spatial variability across stations, which can probably be explained by differences in water depth, sedimentation rate and sediment grain size. At deep-water sites, we observed distinct minima or plateaus in the porewater profiles of H₄SiO₄ that are likely caused by deep-reaching bioirrigation rather than H₄SiO₄ removal by adsorption to iron oxide minerals. The contribution of reverse weathering to these minima remains uncertain. Biogenic silica cycling in the Skagerrak generally aligns with the global trends and shows comparable burial fluxes and burial efficiencies to other margins. However, Skagerrak sediments are characterized by distinctively lower molar bSi/TOC ratios compared to most other continental margins, which we suggest is due to decoupling between bSi and organic carbon during the long travel time of suspended matter transported from the North Sea. It is currently unclear whether Si cycling in the Skagerrak behaves similarly to other depocenters where sediment is first transported over large distances before it finally accumulates on the seafloor. The model presented here simulates bSi cycling and quantifies net bSi dissolution, bioirrigation and bioturbation in Skagerrak sediments with few adjustable parameters but does not yet fully resolve the mechanisms behind H₄SiO₄ release and removal that operate in distinct and narrow depth intervals. Further work on the parameterization of bSi adsorption, reprecipitation and inhibition of bSi dissolution by aluminium would improve the predicted bSi kinetics. Our results contribute to the global dataset on bSi cycling and demonstrate the importance of continuing investigations in different regions, especially on continental margins, to better understand regional variability in bSi cycling and to constrain global Si budgets.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

TS processed most of the samples in the laboratory and wrote the manuscript. TS, KW and AD developed the numerical model used in the study and contributed with discussions. NL helped with cruise planning, sample preparation in the laboratory and contributed with discussions. MS coordinated the research cruise Al561 and contributed with discussions. SS coordinated the biogeochemical observatory (BIGO) deployments and helped with evaluating the BIGO data. HK helped with the ²¹⁰Pb analyses and contributed with discussions. AP provided the porewater data for station 65. SL provided the grain-size data and helped with the interpretation. All authors contributed to the paper by drafting, reading, finalizing, and approving the text. All authors contributed to the article and approved the submitted version.

Funding

Funding for this study was provided by the Federal Ministry of Education and Research, Germany, via the APOC project (03F0874B) – “Anthropogenic impacts on particulate organic carbon cycling in the North Sea”. AP was funded by the Federal Ministry of Education and Research, Germany, via the CARBOSTORE project (03F0875A) – "Carbon Storage in German Coastal Seas.

Acknowledgments

We wish to thank the captain and crew of RV Alkor for supporting our research at sea, as well as our colleagues Regina Surberg, Bettina Domeyer, Anke Bleyer, Matthias Türk, Asmus Petersen and Christoph Böttner for their help onboard during the cruise and in the GEOMAR laboratories. We thank Andreas Neumann from the Helmholtz-Zentrum Hereon (Geesthacht, Germany) for providing sediment samples from RV Alkor cruise Al557. We would also like to acknowledge Bernd Kopka and Marvin Blaue from the Laboratory for Radioisotopes at the University of Göttingen and Christian Kunze and Robert Arndt from the IAF Dresden for the ²¹⁰Pb analyses.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2023.1141448/full#supplementary-material

References

Archer D., Lyle M., Rodgers K., Froelich P. (1993). What Controls Opal Preservation in Tropical Deep-Sea Sediments? Paleoceanography 8, 7–21. doi: 10.1029/92PA02803

CrossRef Full Text | Google Scholar

Beckmann M., Liebezeit G. (1988). Organic carbon in the north Sea in May/June 1986: Distribution and controlling factors. Mitt. Geol.-Palaontol. Inst. Univ. Hamburg 65, 99–116.

Google Scholar

Berner R. A. (1980). Early diagenesis: A theoretical approach, Princeton series in geochemistry (Princeton, N.J: Princeton University Press).

Google Scholar

Blott S. J., Pye K. (2001). GRADISTAT: A grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landf. 26, 1237–1248. doi: 10.1002/esp.261

CrossRef Full Text | Google Scholar

Bohrmann G. (1986). Accumulation of biogenie silica and opal dissolution in upper quaternary skagerrak sediments. Geo-Mar. Lett. 6, 165–172. doi: 10.1007/BF02238088

CrossRef Full Text | Google Scholar

Boudreau B. P. (1990). Asymptotic forms and solutions of the model for silica-opal diagenesis in bioturbated sediments. J. Geophys. Res. 95, 7367. doi: 10.1029/JC095iC05p07367

CrossRef Full Text | Google Scholar

Boudreau B. P., Arnosti C., Jørgensen B. B., Canfield D. E. (2008). Comment on “Physical model for the decay and preservation of marine organic carbon.” Science 319, 1616–1616. doi: 10.1126/science.1148589

CrossRef Full Text | Google Scholar

Boudreau B. P., Ruddick B. R. (1991). On a reactive continuum representation of organic matter diagenesis. Am. J. Sci. 291, 507–538. doi: 10.2475/ajs.291.5.507

CrossRef Full Text | Google Scholar

Bradshaw C., Jakobsson M., Brüchert V., Bonaglia S., Mörth C.-M., Muchowski J., et al. (2021). Physical disturbance by bottom trawling suspends particulate matter and alters biogeochemical processes on and near the seafloor. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.683331

CrossRef Full Text | Google Scholar

Canfield D. E., Jørgensen B. B., Fossing H., Glud R., Gundersen J., Ramsing N. B., et al. (1993a). Pathways of organic carbon oxidation in three continental margin sediments. Mar. Geol. 113, 27–40. doi: 10.1016/0025-3227(93)90147-N

PubMed Abstract | CrossRef Full Text | Google Scholar

Canfield D. E., Thamdrup B., Hansen J. W. (1993b). The anaerobic degradation of organic matter in Danish coastal sediments: Iron reduction, manganese reduction, and sulfate reduction. Geochim. Cosmochim. Acta 57, 3867–3883. doi: 10.1016/0016-7037(93)90340-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Dahlgaard H., Herrmann J., Salomon J. C. (1995). A tracer study of the transport of coastal water from the English channel through the German bight to the kattegat. J. Mar. Syst. 6, 415–425. doi: 10.1016/0924-7963(95)00017-J

CrossRef Full Text | Google Scholar

Dale A. W., Paul K. M., Clemens D., Scholz F., Schroller-Lomnitz U., Wallmann K., et al. (2021). Recycling and burial of biogenic silica in an open margin oxygen minimum zone. Glob. Biogeochem. Cycles 35, e2020GB006583. doi: 10.1029/2020GB006583

CrossRef Full Text | Google Scholar

Dauwe B., Herman P., Heip C. (1998). Community structure and bioturbation potential of macrofauna at four north Sea stations with contrasting food supply. Mar. Ecol. Prog. Ser. 173, 67–83. doi: 10.3354/meps173067

CrossRef Full Text | Google Scholar

Davis C. C., Chen H.-W., Edwards M. (2002). Modeling silica sorption to iron hydroxide. Environ. Sci. Technol. 36, 582–587. doi: 10.1021/es010996t

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis C. C., Knocke W. R., Edwards M. (2001). Implications of aqueous silica sorption to iron hydroxide: Mobilization of iron colloids and interference with sorption of arsenate and humic substances. Environ. Sci. Technol. 35, 3158–3162. doi: 10.1021/es0018421

PubMed Abstract | CrossRef Full Text | Google Scholar

De Haas H., Van Weering T. C. E. (1997). Recent sediment accumulation, organic carbon burial and transport in the northeastern north Sea. Mar. Geol. 136, 173–187. doi: 10.1016/S0025-3227(96)00072-2

CrossRef Full Text | Google Scholar

DeMaster D. J. (1981). The supply and accumulation of silica in the marine environment. Geochim. Cosmochim. Acta 45, 1715–1732. doi: 10.1016/0016-7037(81)90006-5

CrossRef Full Text | Google Scholar

DeMaster D. J. (1991). “Measuring biogenic silica in marine sediments and suspended matter,” in Geophysical monograph series. Eds. Hurd D. C., Spencer D. W. (Washington, D. C.: American Geophysical Union), 363–367. doi: 10.1029/GM063p0363

CrossRef Full Text | Google Scholar

DeMaster D. J. (2002). The accumulation and cycling of biogenic silica in the southern ocean: Revisiting the marine silica budget. Deep Sea Res. Part II Top. Stud. Oceanogr. 49, 3155–3167. doi: 10.1016/S0967-0645(02)00076-0

CrossRef Full Text | Google Scholar

DeMaster D. J. (2019). “The global marine silica budget: Sources and sinks,” in Encyclopedia of ocean sciences, vol. 3 . Eds. Cochran K., Bokuniewicz H., Yager P. (Elsevier Academic Press), 473–483. doi: 10.1016/B978-0-12-409548-9.10799-7

CrossRef Full Text | Google Scholar

Deng L., Bölsterli D., Kristensen E., Meile C., Su C.-C., Bernasconi S. M., et al. (2020). Macrofaunal control of microbial community structure in continental margin sediments. Proc. Natl. Acad. Sci. 117, 15911–15922. doi: 10.1073/pnas.1917494117

CrossRef Full Text | Google Scholar

Dixit S., Van Cappellen P. (2003). Predicting benthic fluxes of silicic acid from deep-sea sediments. J. Geophys. Res. 108, 3334. doi: 10.1029/2002JC001309

CrossRef Full Text | Google Scholar

Dixit S., Van Cappellen P., van Bennekom A. J. (2001). Processes controlling solubility of biogenic silica and pore water build-up of silicic acid in marine sediments. Mar. Chem. 73, 333–352. doi: 10.1016/S0304-4203(00)00118-3

CrossRef Full Text | Google Scholar

Dugdale R. C., Wilkerson F. P., Minas H. J. (1995). The role of a silicate pump in driving new production. Deep Sea Res. Part Oceanogr. Res. Pap. 42, 697–719. doi: 10.1016/0967-0637(95)00015-X

CrossRef Full Text | Google Scholar

Ehlert C., Doering K., Wallmann K., Scholz F., Sommer S., Grasse P., et al. (2016). Stable silicon isotope signatures of marine pore waters – biogenic opal dissolution versus authigenic clay mineral formation. Geochim. Cosmochim. Acta 191, 102–117. doi: 10.1016/j.gca.2016.07.022

CrossRef Full Text | Google Scholar

Eisma D., Kalf J. (1987). Dispersal, concentration and deposition of suspended matter in the north Sea. J. Geol. Soc 144, 161–178. doi: 10.1144/gsjgs.144.1.0161

CrossRef Full Text | Google Scholar

Erlenkeuser H., Pederstad K. (1984). Recent sediment accumulation in skagerrak as depicted by 210pb-dating. Nor. Geol. Tidsskr. 64, 135–152.

Google Scholar

Fengler G., Grossman D., Kersten M., Liebezeit G. (1994). Trace metals in humic acids from recent skagerrak sediments. Mar. pollut. Bull. 28, 143–147. doi: 10.1016/0025-326X(94)90389-1

CrossRef Full Text | Google Scholar

Folk R. L., Ward W. C. (1957). Brazos river bar [Texas]; a study in the significance of grain size parameters. J. Sediment. Res. 27, 3–26. doi: 10.1306/74D70646-2B21-11D7-8648000102C1865D

CrossRef Full Text | Google Scholar

Froelich P. N., Arthur M. A., Burnett W. C., Deakin M., Hensley V., Jahnke R., et al. (1988). Early diagenesis of organic matter in Peru continental margin sediments: Phosphorite precipitation. Mar. Geol. 80, 309–343. doi: 10.1016/0025-3227(88)90095-3

CrossRef Full Text | Google Scholar

Geilert S., Grasse P., Doering K., Wallmann K., Ehlert C., Scholz F., et al. (2020). Impact of ambient conditions on the Si isotope fractionation in marine pore fluids during early diagenesis. Biogeosciences 17, 1745–1763. doi: 10.5194/bg-17-1745-2020

CrossRef Full Text | Google Scholar

Gran-Stadniczeñko S., Egge E., Hostyeva V., Logares R., Eikrem W., Edvardsen B. (2019). Protist diversity and seasonal dynamics in skagerrak plankton communities as revealed by metabarcoding and microscopy. J. Eukaryot. Microbiol. 66, 494–513. doi: 10.1111/jeu.12700

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen H.P., Koroleff F. (1999). Determination of nutrients. In Methods of seawater analysis. 1st ed. Grasshoff K., Kremling K., Ehrhardt M. eds. doi: 10.1002/9783527613984.ch10

CrossRef Full Text | Google Scholar

Hainbucher D., Pohlmann T., Backhaus J. (1987). Transport of conservative passive tracers in the north Sea: First results of a circulation and transport model. Cont. Shelf Res. 7, 1161–1179. doi: 10.1016/0278-4343(87)90083-5

CrossRef Full Text | Google Scholar

Hall P. O. J., Hulth S., Hulthe G., Landén A., Tengberg A. (1996). Benthic nutrient fluxes on a basin-wide scale in the skagerrak (North-Eastern north Sea). J. Sea Res. 35, 123–137. doi: 10.1016/S1385-1101(96)90741-8

CrossRef Full Text | Google Scholar

Huang C. P. (1975). The removal of aqueous silica from dilute aqueous solution. Earth Planet. Sci. Lett. 27, 265–274. doi: 10.1016/0012-821X(75)90038-2

CrossRef Full Text | Google Scholar

Hurd D. C. (1973). Interactions of biogenic opal, sediment and seawater in the central equatorial pacific. Geochim. Cosmochim. Acta 37, 2257–2282. doi: 10.1016/0016-7037(73)90103-8

CrossRef Full Text | Google Scholar

Kamatani A., Ejiri N., Treguer P. (1988). The dissolution kinetics of diatom ooze from the Antarctic area. Deep Sea Res. Part Oceanogr. Res. Pap. 35, 1195–1203. doi: 10.1016/0198-0149(88)90010-6

CrossRef Full Text | Google Scholar

Kamatani A., Oku O. (2000). Measuring biogenic silica in marine sediments. Mar. Chem. 68, 219–229. doi: 10.1016/S0304-4203(99)00079-1

CrossRef Full Text | Google Scholar

Khalil K., Rabouille C., Gallinari M., Soetaert K., DeMaster D. J., Ragueneau O. (2007). Constraining biogenic silica dissolution in marine sediments: A comparison between diagenetic models and experimental dissolution rates. Mar. Chem. 106, 223–238. doi: 10.1016/j.marchem.2006.12.004

CrossRef Full Text | Google Scholar

Kristensen E., Røy H., Debrabant K., Valdemarsen T. (2018). Carbon oxidation and bioirrigation in sediments along a skagerrak-Kattegat-Belt Sea depth transect. Mar. Ecol. Prog. Ser. 604, 33–50. doi: 10.3354/meps12734

CrossRef Full Text | Google Scholar

Loucaides S., Michalopoulos P., Presti M., Koning E., Behrends T., Van Cappellen P. (2010). Seawater-mediated interactions between diatomaceous silica and terrigenous sediments: Results from long-term incubation experiments. Chem. Geol. 270, 68–79. doi: 10.1016/j.chemgeo.2009.11.006

CrossRef Full Text | Google Scholar

Mackenzie F. T., Kump L. R. (1995). Reverse weathering, clay mineral formation, and oceanic element cycles. Science 270, 586–586. doi: 10.1126/science.270.5236.586

CrossRef Full Text | Google Scholar

Mackenzie F. T., Ristvet B. L., Thorstenson C. D., Lerman A., Leeper R. H. (1981). “Reverse weathering and chemical mass balance in a coastal environment,” In Martin J. M., Burton J. D., Eisma D. eds. River inputs from ocean systems (UNEP-UNESCO, Switzerland), 152–187.

Google Scholar

McManus J., Hammond D. E., Berelson W. M., Kilgore T. E., Demaster D. J., Ragueneau O. G., et al. (1995). Early diagenesis of biogenic opal: Dissolution rates, kinetics, and paleoceanographic implications. Deep Sea Res. Part II Top. Stud. Oceanogr. 42, 871–903. doi: 10.1016/0967-0645(95)00035-O

CrossRef Full Text | Google Scholar

Meyenburg G., Liebezeit G. (1993). Mineralogy and geochemistry of a core from the Skagerrak/Kattegat boundary. Mar. Geol. 111, 337–344. doi: 10.1016/0025-3227(93)90139-M

CrossRef Full Text | Google Scholar

Michalopoulos P., Aller R. C. (1995). Rapid clay mineral formation in Amazon delta sediments: Reverse weathering and oceanic elemental cycles. Sci. New Ser. 270, 614–617. doi: 10.1126/science.270.5236.614

CrossRef Full Text | Google Scholar

Michalopoulos P., Aller R. C. (2004). Early diagenesis of biogenic silica in the Amazon delta: Alteration, authigenic clay formation, and storage. Geochim. Cosmochim. Acta 68, 1061–1085. doi: 10.1016/j.gca.2003.07.018

CrossRef Full Text | Google Scholar

Michalopoulos P., Aller R. C., Reeder R. J. (2000). Conversion of diatoms to clays during early diagenesis in tropical, continental shelf muds. Geology 28, 1095. doi: 10.1130/0091-7613(2000)28<1095:CODTCD>2.0.CO;2

CrossRef Full Text | Google Scholar

Middelburg J. J. (1989). A simple rate model for organic matter decomposition in marine sediments. Geochim. Cosmochim. Acta 53, 1577–1581. doi: 10.1016/0016-7037(89)90239-1

CrossRef Full Text | Google Scholar

Müller P. J., Schneider R. (1993). An automated leaching method for the determination of opal in sediments and particulate matter. Deep Sea Res. Part Oceanogr. Res. Pap. 40, 425–444. doi: 10.1016/0967-0637(93)90140-X

CrossRef Full Text | Google Scholar

Nelson D. M., Ahern J. A., Herlihy L. J. (1991). Cycling of biogenic silica within the upper water column of the Ross Sea. Mar. Chem. 35, 461–476. doi: 10.1016/S0304-4203(09)90037-8

CrossRef Full Text | Google Scholar

Nelson D. M., Gordon L. I. (1982). Production and pelagic dissolution of biogenic silica in the southern ocean. Geochim. Cosmochim. Acta 46, 491–501. doi: 10.1016/0016-7037(82)90153-3

CrossRef Full Text | Google Scholar

Nelson D. M., Tréguer P., Brzezinski M. A., Leynaert A., Quéguiner B. (1995). Production and dissolution of biogenic silica in the ocean: Revised global estimates, comparison with regional data and relationship to biogenic sedimentation. Glob. Biogeochem. Cycles 9, 359–372. doi: 10.1029/95GB01070

CrossRef Full Text | Google Scholar

Oehler T., Martinez R., Schückel U., Winter C., Kröncke I., Schlüter M. (2015a). Seasonal and spatial variations of benthic oxygen and nitrogen fluxes in the helgoland mud area (southern north Sea). Cont. Shelf Res. 106, 118–129. doi: 10.1016/j.csr.2015.06.009

CrossRef Full Text | Google Scholar

Oehler T., Schlüter M., Schückel U. (2015b). Seasonal dynamics of the biogenic silica cycle in surface sediments of the helgoland mud area (southern north Sea). Cont. Shelf Res. 107, 103–114. doi: 10.1016/j.csr.2015.07.016

CrossRef Full Text | Google Scholar

Otto L., Zimmerman J. T. F., Furnes G. K., Mork M., Saetre R., Becker G. (1990). Review of the physical oceanography of the north Sea. Neth. J. Sea Res. 26, 161–238. doi: 10.1016/0077-7579(90)90091-T

CrossRef Full Text | Google Scholar

Paetzel M., Schrader H., Bjerkli K. (1994). Do decreased trace metal concentrations in surficial skagerrak sediments over the last 15–30 years indicate decreased pollution? Environ. pollut. 84, 213–226. doi: 10.1016/0269-7491(94)90132-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabouille C., Gaillard J.-F., Tréguer P., Vincendeau M.-A. (1997). Biogenic silica recycling in surficial sediments across the polar front of the southern ocean (Indian sector). Deep Sea Res. Part II Top. Stud. Oceanogr. 44, 1151–1176. doi: 10.1016/S0967-0645(96)00108-7

CrossRef Full Text | Google Scholar

Ragueneau O., Schultes S., Bidle K., Claquin P., Moriceau B. (2006). Si And c interactions in the world ocean: Importance of ecological processes and implications for the role of diatoms in the biological pump: Si AND c INTERACTIONS IN THE OCEAN. Glob. Biogeochem. Cycles 20, GB4S02. doi: 10.1029/2006GB002688

CrossRef Full Text | Google Scholar

Ragueneau O., Tréguer P. (1994). Determination of biogenic silica in coastal waters: Applicability and limits of the alkaline digestion method. Mar. Chem. 45, 43–51. doi: 10.1016/0304-4203(94)90090-6

CrossRef Full Text | Google Scholar

Ragueneau O., Tréguer P., Leynaert A., Anderson R. F., Brzezinski M. A., DeMaster D. J., et al. (2000). A review of the Si cycle in the modern ocean: Recent progress and missing gaps in the application of biogenic opal as a paleoproductivity proxy. Glob. Planet. Change 26, 317–365. doi: 10.1016/S0921-8181(00)00052-7

CrossRef Full Text | Google Scholar

Rahman S., Aller R. C., Cochran J. K. (2016). Cosmogenic ³² Si as a tracer of biogenic silica burial and diagenesis: Major deltaic sinks in the silica cycle. Geophys. Res. Lett. 43, 7124–7132. doi: 10.1002/2016GL069929

CrossRef Full Text | Google Scholar

Rahman S., Aller R. C., Cochran J. K. (2017). The missing silica sink: Revisiting the marine sedimentary Si cycle using cosmogenic ³² Si: The missing sedimentary silica sink. Glob. Biogeochem. Cycles 31, 1559–1578. doi: 10.1002/2017GB005746

CrossRef Full Text | Google Scholar

Rebreanu L., Vanderborght J.-P., Chou L. (2008). The diffusion coefficient of dissolved silica revisited. Mar. Chem. 112, 230–233. doi: 10.1016/j.marchem.2008.08.004

CrossRef Full Text | Google Scholar

Ringuet S., Sassano L., Johnson Z. I. (2011). A suite of microplate reader-based colorimetric methods to quantify ammonium, nitrate, orthophosphate and silicate concentrations for aquatic nutrient monitoring. J. Env. Monit 13, 370–376. doi: 10.1039/C0EM00290A

CrossRef Full Text | Google Scholar

Rosenberg R., Hellman B., Lundberg A. (1996). Benthic macrofaunal community structure in the Norwegian trench, deep skagerrak. J. Sea Res. 35, 181–188. doi: 10.1016/S1385-1101(96)90745-5

CrossRef Full Text | Google Scholar

Salomon J. C., Breton M., Guegueniat P. (1995). A 2D long term advection–dispersion model for the channel and southern north Sea part b: Transit time and transfer function from cap de la Hague. J. Mar. Syst. 6, 515–527. doi: 10.1016/0924-7963(95)00021-G

CrossRef Full Text | Google Scholar

Sayles F. L., Martin W. R., Chase Z., Anderson R. F. (2001). Benthic remineralization and burial of biogenic SiO2, CaCO3, organic carbon, and detrital material in the southern ocean along a transect at 170° West. Deep Sea Res. Part II Top. Stud. Oceanogr. 48, 4323–4383. doi: 10.1016/S0967-0645(01)00091-1

CrossRef Full Text | Google Scholar

Schink D. R., Fanning K. A., Pilson M. E. Q. (1974). Dissolved silica in the upper pore waters of the Atlantic ocean floor. J. Geophys. Res. 79, 2243–2250. doi: 10.1029/JC079i015p02243

CrossRef Full Text | Google Scholar

Schlüter M., Sauter E. (2000). Biogenic silica cycle in surface sediments of the Greenland Sea. J. Mar. Syst. 23, 333–342. doi: 10.1016/S0924-7963(99)00070-6

CrossRef Full Text | Google Scholar

Schmidt M., Sommer S., Böttner C., Dale A. W., Lenz N., Spiegel T., et al (2021). Dynamics and variability of POC burial in depocenters of the North Sea (Skagerrak), Cruise No. AL561, 2.08.2021 – 13.08.2021, Kiel – Kiel, APOC, Alkor-Berichte, AL561 (Kiel, Germany: GEOMAR Helmholtz Centre for Ocean Research Kiel), 34 pp. doi: 10.3289/CR_AL561

CrossRef Full Text | Google Scholar

Schmidt M., Botz R., Rickert D., Bohrmann G., Hall S. R., Mann S. (2001). Oxygen isotopes of marine diatoms and relations to opal-a maturation. Geochim. Cosmochim. Acta 65, 201–211. doi: 10.1016/S0016-7037(00)00534-2

CrossRef Full Text | Google Scholar

Schulz H. D., Zabel M. (2006). Marine geochemistry (Berlin/Heidelberg: Springer-Verlag). doi: 10.1007/3-540-32144-6

CrossRef Full Text | Google Scholar

Sigg L., Stumm W. (1981). The interaction of anions and weak acids with the hydrous goethite (α-FeOOH) surface. Colloids Surf. 2, 101–117. doi: 10.1016/0166-6622(81)80001-7

CrossRef Full Text | Google Scholar

Sköld M., Göransson P., Jonsson P., Bastardie F., Blomqvist M., Agrenius S., et al. (2018). Effects of chronic bottom trawling on soft-seafloor macrofauna in the kattegat. Mar. Ecol. Prog. Ser. 586, 41–55. doi: 10.3354/meps12434

CrossRef Full Text | Google Scholar

Sommer S., Linke P., Pfannkuche O., Schleicher T., Schneider v. D D., Reitz A., et al. (2009). Seabed methane emissions and the habitat of frenulate tubeworms on the captain arutyunov mud volcano (Gulf of cadiz). Mar. Ecol. Prog. Ser. 382, 69–86. doi: 10.3354/meps07956

CrossRef Full Text | Google Scholar

Spiegel T., Vosteen P., Wallmann K., Paul S. A. L., Gledhill M., Scholz F. (2021). Updated estimates of sedimentary potassium sequestration and phosphorus release on the Amazon shelf. Chem. Geol. 560, 120017. doi: 10.1016/j.chemgeo.2020.120017

CrossRef Full Text | Google Scholar

Ståhl H., Tengberg A., Brunnegård J., Bjørnbom E., Forbes T. L., Josefson A. B., et al. (2004). Factors influencing organic carbon recycling and burial in skagerrak sediments. J. Mar. Res. 62, 867–907. doi: 10.1357/0022240042880873

CrossRef Full Text | Google Scholar

Stevens R. L., Bengtsson H., Lepland A. (1996). Textural provinces and transport interpretations with fine-grained sediments in the skagerrak. J. Sea Res. 35, 99–110. doi: 10.1016/S1385-1101(96)90739-X

CrossRef Full Text | Google Scholar

Stolpovsky K., Dale A. W., Wallmann K. (2015). Toward a parameterization of global-scale organic carbon mineralization kinetics in surface marine sediments: Benthic carbon mineralization. Glob. Biogeochem. Cycles 29, 812–829. doi: 10.1002/2015GB005087

CrossRef Full Text | Google Scholar

Swedlund P. (1999). Adsorption and polymerisation of silicic acid on ferrihydrite, and its effect on arsenic adsorption. Water Res. 33, 3413–3422. doi: 10.1016/S0043-1354(99)00055-X

CrossRef Full Text | Google Scholar

Thamdrup B., Fossing H., Jørgensen B. B. (1994). Manganese, iron and sulfur cycling in a coastal marine sediment, Aarhus bay, Denmark. Geochim. Cosmochim. Acta 58, 5115–5129. doi: 10.1016/0016-7037(94)90298-4

CrossRef Full Text | Google Scholar

Thomas H., Freund W., Mears C., Meckel E., Minutolo F., Nantke C., et al. (2022). ALKOR scientific cruise report. the ocean's alkalinity - connecting geological and metabolic processes and time-scales: mechanisms and magnitude of metabolic alkalinity generation in the north Sea cruise no. AL557 Vol. 22 (Kiel, Germany: GEOMAR Helmholtz-Zentrum für Ozeanforschung Kiel).

Google Scholar

Tréguer P., Bowler C., Moriceau B., Dutkiewicz S., Gehlen M., Aumont O., et al. (2018). Influence of diatom diversity on the ocean biological carbon pump. Nat. Geosci. 11, 27–37. doi: 10.1038/s41561-017-0028-x

CrossRef Full Text | Google Scholar

Tréguer P. J., de la Rocha C. L. (2013). The world ocean silica cycle. Annu. Rev. Mar. Sci. 5, 477–501. doi: 10.1146/annurev-marine-121211-172346

CrossRef Full Text | Google Scholar

Tréguer P., Nelson D. M., Van Bennekom A. J., DeMaster D. J., Leynaert A., Quéguiner B. (1995). The silica balance in the world ocean: A reestimate. Science 268, 375–379. doi: 10.1126/science.268.5209.375

PubMed Abstract | CrossRef Full Text | Google Scholar

Tréguer P. J., Sutton J. N., Brzezinski M., Charette M. A., Devries T., Dutkiewicz S., et al. (2021). Reviews and syntheses: The biogeochemical cycle of silicon in the modern ocean. Biogeosciences 18, 1269–1289. doi: 10.5194/bg-18-1269-2021

CrossRef Full Text | Google Scholar

Van Beusekom J. E. E., Van Bennekom A. J., Tréguer P., Morvan J. (1997). Aluminium and silicic acid in water and sediments of the enderby and crozet basins. Deep Sea Res. Part II Top. Stud. Oceanogr. 44, 987–1003. doi: 10.1016/S0967-0645(96)00105-1

CrossRef Full Text | Google Scholar

Van Weering T. C. E., Berger G. W., Kalf J. (1987). Recent sediment accumulation in the skagerrak, northeastern north Sea. Neth. J. Sea Res. 21, 177–189. doi: 10.1016/0077-7579(87)90011-1

CrossRef Full Text | Google Scholar

Van Weering T. C. E., Berger G. W., Okkels E. (1993). Sediment transport, resuspension and accumulation rates in the northeastern skagerrak. Mar. Geol. 111, 269–285. doi: 10.1016/0025-3227(93)90135-I

CrossRef Full Text | Google Scholar

Wallmann K., Aloisi G., Haeckel M., Tishchenko P., Pavlova G., Greinert J., et al. (2008). Silicate weathering in anoxic marine sediments. Geochim. Cosmochim. Acta 72, 2895–2918. doi: 10.1016/j.gca.2008.03.026

CrossRef Full Text | Google Scholar

Wollast R. (1974). “The silica problem,” in The Sea, vol. 5 . Ed. Goldberg E. D. (New York: Wiley-Interscience), 365–381.

Google Scholar

Wollast R., Mackenzie F. T. (1983). “The global cycle of silica,” in Silicon geochemistry and biogeochemistry. Ed. Aston S. R. (San Diego, Calif: Academic), 39–76.

Google Scholar

Zhu D., Sutton J. N., Leynaert A., Tréguer P. J., Schoelynck J., Gallinari M., et al. (2023). Revisiting the biogenic silica burial flux determinations: A case study for the East China seas. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1058730

CrossRef Full Text | Google Scholar