Selective 1H-14N Distance Measurements by 14N Overtone Solid-State NMR Spectroscopy at Fast MAS

Introduction

H-N distance is of importance for deeper insights into the structures and dynamics of chemical and biological systems due to the ubiquity of both proton and nitrogen. Such distance can be obtained by solid-state nuclear magnetic resonance (ssNMR) through the determination of H-N dipolar coupling, which is inversely proportional to the cube of the H-N distance. There are a few reasons why ssNMR has advantages for the H-N measurement over traditional diffraction techniques. First, ssNMR spectroscopy is applicable to various systems no matter their states, i.e., lacking long-range order or even being a disorder, which are intractable by diffraction techniques. Second, it enables the precise location of the H-atom positions, which is poorly determined by X-ray diffraction (XRD) or electron diffraction (Guzmán-Afonso et al., 2019).

Despite such advantages, the H-N distance measurement by NMR has difficulties due to some unfavorable nuclear characteristics of these two elements. For nitrogen, it has two stable and NMR active isotopes, ¹⁵N and ¹⁴N. The former is preferred in ssNMR because it is a spin-1/2 nucleus; thus, it is easy to manipulate and to obtains high resolution. Many methods have been designed to measure ¹H-¹⁵N distances (Hohwy et al., 2000; Zhao et al., 2001; Schnell and Saalwächter, 2002; Fu, 2003; Chevelkov et al., 2009; Hou et al., 2011; Schanda et al., 2011; Paluch et al., 2013; Hou et al., 2014; Nishiyama et al., 2016). Nevertheless, the main drawback of ¹⁵N isotope is its insensitivity owing to the low natural abundance (0.4%). It makes the measurements lengthy for sufficient signal-to-noise ratio (S/N); otherwise, 1) the isotopic labeling is needed, which is not always simple and cost-effective or 2) dynamic nuclear polarization experiments are required (Zhao et al., 2018). However, the ¹H-¹⁵N experiments on that work only allowed the determination of the shortest ¹H-¹⁵N distance due to the dipolar truncation effect. On the other hand, ¹⁴N isotope benefits from the high natural abundance (99.6%), but it suffers from the severe quadrupolar broadening and complicated spin dynamics because ¹⁴N is an integer quadrupolar nucleus (spin I = 1). For protons, the intense ¹H–¹H homonuclear dipolar couplings in the solid state cause ¹H line broadening and shorten the ¹H coherence time. Consequently, these unfavorable characteristics of both N isotopes and H nucleus make H-N distance measurement by NMR challenging.

The development of fast magic-angle spinning (MAS, ν_R ≥ 60 kHz) with proton detection has made ¹⁴N NMR spectroscopy a routinely used method, overcoming the difficulty associated with quadrupolar interaction (Cavadini et al., 2006; Gan et al., 2007; Cavadini, 2010; Nishiyama et al., 2011; Brown, 2014; Pandey and Nishiyama, 2015; Shen et al., 2015; Pandey et al., 2016; Carnevale et al., 2017; Hung et al., 2019; Jarvis et al., 2019; Rankin et al., 2019; Wijesekara et al., 2020). Furthermore, under fast MAS conditions, the strong ¹H–¹H dipolar network is largely suppressed (Nishiyama, 2016). These two advantages potentially facilitate the ¹H-¹⁴N distance measurement. Recently, our group have introduced a combination of phase-modulated (PM) pulse (Nimerovsky et al., 2014; Makrinich et al., 2017; Makrinich et al., 2018), SR4²₁ recoupling (Brinkmann and Kentgens, 2006), and rotational-echo saturation-pulse double-resonance (RESPDOR) (Gan, 2006; Chen et al., 2010a; Chen et al., 2010b; Lu et al., 2011) (PM-S-RESPDOR) that can extract multiple ¹H-¹⁴N distances with high accuracy at fast MAS of 70 kHz (Duong et al., 2019). Such success mainly comes from the robustness that universal fraction curves can be obtained for the distance measurement under the saturation by the PM pulse for a wide range of ¹⁴N quadrupolar coupling constant (C_Q) and ¹H-¹⁴N dipolar coupling. This broadband characteristics of PM pulse is useful when we work on systems containing a single ¹⁴N site, as shown in the previous study. However, complications may arise for systems where multiple ¹⁴N sites are present, as shown below.

For example, a 5-spin system, as shown in Figure 1, consists of two N and three H atoms. We assume that the ¹⁴N and ¹H NMR peaks are well resolved for simplicity. The first difficulty associated with this system is the ambiguity of ¹H-¹⁴N distance measurement. For instance, we can determine the distance of H3-N by PM-S-RESPDOR sequence but cannot know whether such distance is between H3 and N1 or H3 and N2. The second difficulty relates to the complex spin dynamics of H2 nucleus, which is close to both N1 and N2 nuclei. As PM pulse is broadband, it completely saturates both ¹⁴N1 and ¹⁴N2 nuclei; thus, the PM-S-RESPDOR sequence will give the H2-N fraction curve experiencing the combined effects of H2-N1 and H2-N2 pairs. The H2-N distance from the fraction curve would be shorter than those extracted from H2-N1 or H2-N2 pair; or in other words, no reliable distance is yielded. A solution to overcome this cumulative contribution is to selectively saturate each N nucleus, which can be achieved in the manner of Delays Alternating with Nutation for Tailored Excitation (DANTE) (Vitzthum et al., 2011; Vitzthum et al., 2012; Lu et al., 2013; Pourpoint et al., 2014). This approach can be our future work.

FIGURE 1

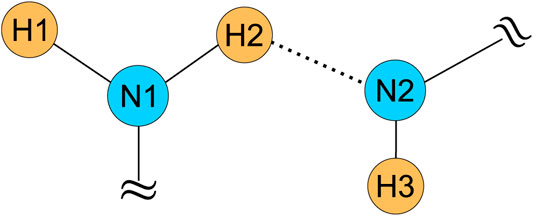
FIGURE 1. The 5-spin system with two N and three H atoms complicating the ¹H-¹⁴N distance measurements by PM-S-RESPDOR.

An alternative approach is the ¹⁴N overtone (OT) NMR spectroscopy, where the forbidden transitions |Δm| = 2 are weakly allowed (m is the energy level) (Bloom and LeGros, 1986; Tycko and Opella, 1987; Jayanthi and Ramanathan, 2011; O’Dell and Ratcliffe, 2011; Nishiyama et al., 2013; O’Dell and Brinkmann, 2013; O’Dell et al., 2013; Haies et al., 2015a; Haies et al., 2015b; Shen et al., 2017; Concistré et al., 2018; Gan et al., 2018; Pandey and Nishiyama, 2018). Because it is twice the fundamental frequency, ¹⁴N OT frequency is more available to commercial MAS probes since many probes are not designed to tune to ¹⁴N Larmor frequency. Importantly, the ¹⁴N overtone excitation can achieve band-selective observation of ¹⁴N (Pandey and Nishiyama, 2018). The narrow bandwidth results from the slow effective ¹⁴N OT nutation, which is proportional to C_Q/ν₀, where ν₀ is the ¹⁴N Larmor frequency. Besides the selectivity, ¹⁴N OT spectra are free from the first-order quadrupolar interaction because of the symmetric transitions, m = −1 ↔ m = +1. Therefore, ¹⁴N OT NMR is much narrower than the single-quantum ¹⁴N spectra and robust to the misadjustment of the magic angle. Moreover, since the transitions are only between two energy levels involved in OT (m = ±1), the spin dynamics of ¹⁴N OT behaves similarly to that of spin-1/2. Hence, for a ¹H-¹⁴N OT system, the working conditions under RESPDOR can also be described by rotational-echo double-resonance (REDOR) (Gullion and Schaefer, 1989; Gullion, 2007) depending on whether the population transfer is saturation (RESPDOR) or inversion (REDOR) (Nimerovsky et al., 2017). Since the ideal saturation or inversion by continuous-wave (CW) is impractical, the working condition is an intermediate between REDOR and RESPDOR regimes. In this work, we combine ¹⁴N OT and REDOR sequence (¹H-¹⁴N OT-REDOR) to explore its feasibility for distance measurements. This sequence is firstly demonstrated using two model biological compounds of L-tyrosine.HCl (Tyr) and N-acetyl-L-alanine (AcAla) and then applied to a more complex dipeptide system of L-alanyl-L-alanine (AlaAla) that involves two inequivalent nitrogen sites in a single molecule.

Pulse Sequence and the Universal Expression

Figure 2 depicts the ¹H-¹⁴N OT-REDOR sequence. It is identical to the conventional S-REDOR sequence (Chen et al., 2010b), where SR4²₁ recoupling (lasting for τ_mix) is used to recover the ¹H-¹⁴N dipolar coupling and CW (lasting for τ_CW) is used to saturate/invert the ¹⁴N OT populations between the two energy levels. We note that since SR4²₁ is not γ-encoded, the interval between the two SR4 blocks should be rotor-synchronized to avoid the spatial modulation of the recoupled ¹H-¹⁴N dipolar couplings. For distance measurement, we measure two signals, S₀ and S’, acquired without and with CW pulse, respectively, for obtaining the fraction curve ΔS/S₀ = (S₀–S′)/S₀ as a function of τ_mix.

FIGURE 2

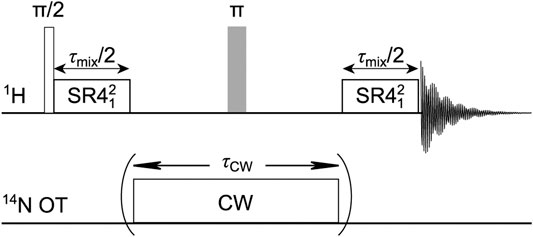
FIGURE 2. ¹H-¹⁴N OT-REDOR sequence. On ¹H channel, SR4²₁ recoupling is used to reintroduce the ¹H-¹⁴N dipolar couplings. On ¹⁴N OT channel, CW pulse is used to perturb ¹⁴N OT populations. For the fraction curve, two sets of data (S₀ and S′) are acquired by employing OT-REDOR sequence without and with CW pulse (within the two brackets), respectively.

The fraction curve excludes the signal attenuation from T₂ relaxation, making it dependent solely on the dipolar coupling constant as for the case of REDOR with complete inversion. However, for ¹⁴N OT, complete inversion is difficult to achieve. Subsequently, the distance is extracted by fitting the fraction curve to either the numerically exact or universal curves. For the numerically exact curve, the simulation is extremely difficult as it must work in the laboratory frame without high-field approximation, leading to time-consuming calculations (O’Dell and Brinkmann, 2013). Even if this condition is met, various parameters must be known; for instance, the ¹⁴N C_Q and the ¹⁴N OT effective nutation fields, which are not straightforwardly determined. For the universal curve, it has shown to be an almost identical match to the numerically exact ¹H-¹⁴N PM-S-RESPDOR curve, allowing simple distance extractions (Duong et al., 2019). In addition, the condition and knowledge required by the numerically exact ¹H-¹⁴N OT-REDOR curve above are not necessary for the universal curve. Indeed, semiquantitative evaluation for ¹⁴N OT transitions only requires the fitting parameter f and the ¹H-¹⁴N dipolar coupling (shown below). Thus, for objective fitting, we use the universal curve approach, which is derived by following the original work of Gan or later analysis of Chen and coworkers (Gan, 2006; Chen et al., 2010a). The derivation starts with fundamental ¹⁴N transitions for verification and then applies to ¹⁴N OT.

A general expression for any spin and type of experiment is

$\frac{\Delta S}{S_0}=1-{\displaystyle \sum }_{i,j}{P}_i{W}_{ij}REDOR\left(\left|\Delta m\right|\right),(1)$

where P_i = 1/(2I + 1) is the population of spin state m = i under high-temperature approximation, W_ij is the population transfer probability from m = i to m = j spin state, and REDOR(|Δm|) presents the normalized dipolar-dephased signal intensity for classical REDOR. The general expression helps to derive the universal curves mentioned in Figure 3. It is worth noting that the natural abundance of a specific isotope should also be considered in Eq. (1). However, the natural abundance of ¹⁴N isotope is 99.6%, very close to 100%; hence, we can safely neglect it.

FIGURE 3

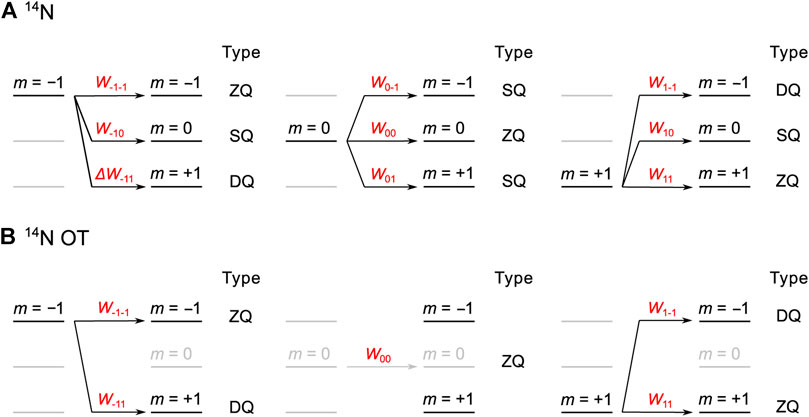
FIGURE 3. The population transfers and their probabilities (W_ij) for ZQ (Δm = 0), SQ (|Δm| = 1), and DQ (|Δm| = 2) transitions of (A)¹⁴N and (B)¹⁴N OT to derive the universal curves.

For ¹⁴N (I = 1) spin, under the Zeeman interaction with the external magnetic field, there are three energy levels of m = 0 and ±1. We assume the population for each level is 1/3. The population transfers among the energy levels are categorized into zero- (ZQ or Δm = 0), single- (SQ or |Δm| = 1), and double-quantum (DQ or |Δm| = 2) transitions, which determine the RESPDOR effect. Both energy levels m = +1 and m = −1 are involved in all three ZQ, SQ, and DQ transitions, as shown in Figure 3A. Under the ideal saturation of ¹⁴N spin, W_±1j for these transfers are equal; hence, each transition has W_±1j of 1/3. On the other hand, the energy level m = 0 is only involved in ZQ and SQ transitions, but there are two SQ transitions of (m = 0 → m = −1) and (m = 0 → m = +1). Hence, for m = 0, W_0j of ZQ, SQ, and DQ transitions are 1/3, 2/3, and 0/3, respectively. Taken together, under the complete saturation of ¹⁴N spin, ΣP_iW_ij for ZQ, SQ, and DQ transitions for m = (−1, 0, 1) are 1/3·3/3, 1/3·4/3, and 1/3·2/3, respectively (see Figure 3A). Replacing these P_i and W_ij in Eq. (1), the universal expression for ¹⁴N is given by

$\begin{array}{l}\frac{\Delta S}{S_0}=1-\frac{3}{9}-\frac{4}{9}.REDOR\left(\left|\Delta m\right|=1\right)-\frac{2}{9}.REDOR\left(\left|\Delta m\right|=2\right) \\ =\frac{2}{3}-\frac{\pi \sqrt{2}}{9}{J}_{1/4}\left(\frac{\pi }{4}\left(b_{1H-14N}/2\pi \right){\tau }_{mix}\right)J_{-1/4}\left(\frac{\pi }{4}\left(b_{1H-14N}/2\pi \right){\tau }_{mix}\right)\\ -\frac{\pi \sqrt{2}}{18}{J}_{1/4}\left(\frac{2\pi }{4}\left(b_{1H-14N}/2\pi \right){\tau }_{mix}\right)J_{-1/4}\left(\frac{2\pi }{4}\left(b_{1H-14N}/2\pi \right){\tau }_{mix}\right),\end{array}(2)$

where J_±1/4 denotes the ±1/4-order Bessel functions of the first kind and b_1H–14N/(2π) is the ¹H-¹⁴N dipolar coupling constant while τ_mix is the total mixing time of SR4²₁ recoupling sequence. Eq. (2) is identical to the universal curve for ¹H-¹⁴N RESPDOR in the literature (Gan, 2006; Chen et al., 2010b), verifying our analysis.

Next, we consider the case of ¹⁴N OT. Again, three energy levels are present with the population P_i of 1/3 for each level. The energy level m = 0 is not involved in OT transitions; thus, it is blurred in Figure 3B. P_i of m = 0 remains at ZQ transition, meaning that W_0j is 1 for j = 0 and 0 for j ≠ 0. Conversely, both energy levels m = ±1 are involved in the saturation/inversion of ZQ and DQ transitions. However, owing to the slow and orientation-dependent effective nutation of ¹⁴N OT, the complete saturation/inversion is difficult. Considering this incompletion, we assume that the DQ W_±1j for m = ±1 are f with 0 ≤ f ≤ 1, in which f = 0.5 corresponds to complete saturation while f = 1.0 corresponds to complete inversion. Although we mentioned that the working condition for ¹H-¹⁴N OT-REDOR is between REDOR and RESPDOR regimes in the Introduction section, this does not mean that f should be between 0.5 and 1.0. Indeed, if the complete saturation is not achieved, parameter f could be smaller than 0.5. With the introduction of f, W_±1j for ZQ and DQ transitions are 1–f and f, respectively. Combining P_i of each transition for each level and under incomplete saturation/inversion of ¹⁴N OT, Figure 3B shows that ΣP_iW_ij for ZQ, SQ, and DQ transitions are 1/3·(1 + 2(1–f)), 0, and 1/3·2f, respectively. The universal expression for REDOR/RESPDOR on ¹⁴N OT is given by

$\begin{array}{l}\frac{\Delta S}{S_0}=1-\left(1-\frac{2f}{3}\right)-\frac{2f}{3}.REDOR\left(\left|\Delta m\right|=2\right) \\ =\frac{2f}{3}\left[1-REDOR\left(\left|\Delta m\right|=2\right)\right]\\ =\frac{2f}{3}\left[1-\frac{\pi \sqrt{2}}{4}{J}_{1/4}\left(\frac{2\pi }{4}\left(b_{1H-14N}/2\pi \right){\tau }_{mix}\right)J_{\mathrm{-}1/4}\left(\frac{2\pi }{4}\left(b_{1H-14N}/2\pi \right){\tau }_{mix}\right)\right].\end{array}(3)$

From Eq. (3), the coefficient for REDOR (|Δm| = 2) is proportional to f, affecting the slope of the fraction curve. However, since f uniformly affects the other elements in the equation, the universal curves derived from Eq. (3) would reach the maximum at the same τ_mix no matter f value. It is worth noting that the introduction of f makes the fitting among universal curves and experimental fraction curve better, but it makes the extracted b_1H–14N inaccurate. Particularly, when the fraction curve has not reached the maximum ΔS/S₀, universal curves generated by different combinations of f and b_1H–14N can reproduce the very similar fraction curve, thus giving ambiguous results. To avoid this situation, our fitting strategy consists of two steps. The first is to determine f, which is possible only when the fraction curve of the shortest H-N distance must show the maximum. Under this condition, the fitting parameter f is determined as the ratio of the experimental and theoretical maxima ΔS/S₀ (2/3 = 0.67). That precisely known f leads to the unambiguous determination of b_1H–14N. For longer H-N distance, the REDOR curve may possibly not show the maximum while the oscillation is damped, making the fitting difficult. Under this situation, accurate distance determinations are still possible by the second step. It is to use this observed f from the first step for measuring longer ¹H-¹⁴N distances of the same ¹⁴N site. This strategy is a disadvantage of OT-REDOR compared to PM-S-RESPDOR. The latter does not require the prior knowledge of the fitting parameter f owing to the complete saturation of all ¹⁴N crystallites by the PM pulse, thus enabling the reliable fitting even when the maximum is not observed.

It is of practical use to clarify the differences between the universal expressions for ¹H-¹⁴N RESPDOR and ¹H-¹⁴N OT-REDOR. This can be done by comparing the universal curves resulting from Eqs. 2, 3 under the same b_1H–14N. Figure 4 compares the three universal curves, one from Eq. (2) and two from Eq. (3) with f = 0.5 (complete saturation) and f = 1.0 (complete inversion). These two f values are chosen because they correspond to ideal RESPDOR (f = 0.5) and REDOR (f = 1.0) conditions and our working condition is an intermediate between these two, as mentioned in the Introduction. The two curves from Eq. (3) are identical except for the intensity (a factor of 2), which is in agreement with the discussion above (see Figure 4). A notable difference between the universal curves of ¹H-¹⁴N OT and that of ¹H-¹⁴N is that the dephasing rate of the former curves is about two times faster than that of the latter (0.77 ms compared to 1.60 ms, respectively). This is because, for ¹H-¹⁴N OT, the REDOR effect is determined by the DQ transitions, whereas, for ¹H-¹⁴N, the RESPDOR effect is determined by both the SQ and DQ transitions. Such a faster dephasing rate associated with the multiple quantum transitions has been known in the literature (Pruski et al., 1999). This potentially allows ¹H-¹⁴N OT-REDOR to probe long ¹H-¹⁴N distance better than ¹H-¹⁴N RESPDOR as it is less affected by the poor sensitivity and uncertainty of ΔS/S₀ at long τ_mix.

FIGURE 4

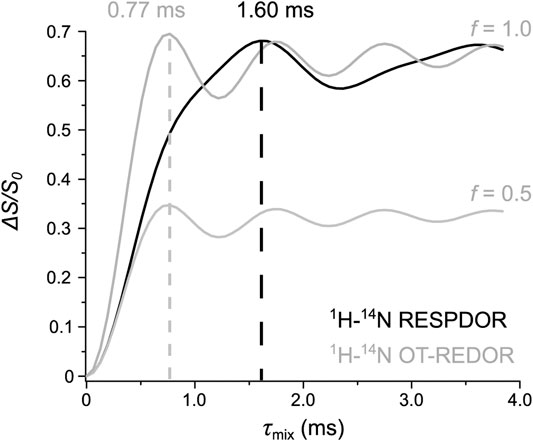
FIGURE 4. Comparison between the universal curves of ¹H-¹⁴N RESPDOR (black) and ¹H-¹⁴N OT-REDOR (grey) with f = 0.5 (complete saturation) and 1.0 (complete inversion) derived from Eqs 2,3, respectively, under the same ¹H-¹⁴N dipolar coupling of 2.0 kHz. The optimum τ_mix of both curves are shown and highlighted by the dashed lines.

Results and Discussions

In this section, we firstly explore the feasibility of ¹H-¹⁴N OT-REDOR on two model biological compounds of Tyr and AcAla. These two compounds only consist of a single ¹⁴N site and were well characterized by ¹H-¹⁴N PM-S-RESPDOR in the previous study. Upon the feasibility test, we apply this technique to a more complex dipeptide system of AlaAla where two inequivalent ¹⁴N sites are present.

L-Tyrosine.HCl

In order to obtain an efficient ¹H-¹⁴N OT-REDOR fraction curve, experimental optimizations are required. Such optimizations require the knowledge of ¹⁴N OT resonance frequency as it significantly affects the sensitivity of OT experiments due to the narrow bandwidth. In this current work, the ¹⁴N OT frequency is indirectly determined by the two-dimensional (2D) ¹H-{¹⁴N OT} D- or T-HMQC (sequences in Supplementary Figures S1A,B respectively) at the second OT spinning sideband (n = -2 SSB) for the highest S/N. Such n value depends on the sense of rotation with respect to the magnetic field (Gan et al., 2018). For our configuration, the magnetic field is toward the top of the magnet and the spinning rotation is clockwise looking from the top. Taking benefits of optimum S/N, all the remaining experiments were also performed at the second ¹⁴N OT SSB (n = −2). Figure 5 clearly indicates the ¹⁴N OT frequency and its correlations to both proton sites of NH₃ and CH by the D-HMQC experiment. The smaller correlation of N to CH under τ_mix of 0.51 ms is explained due to the longer ¹H-¹⁴N distance compared to the directly bonded H-N distance of the NH₃ group. This 2D spectrum is in agreement with the ¹H-{¹⁴N} D-HMQC spectrum in the previous study (Duong et al., 2019).

FIGURE 5

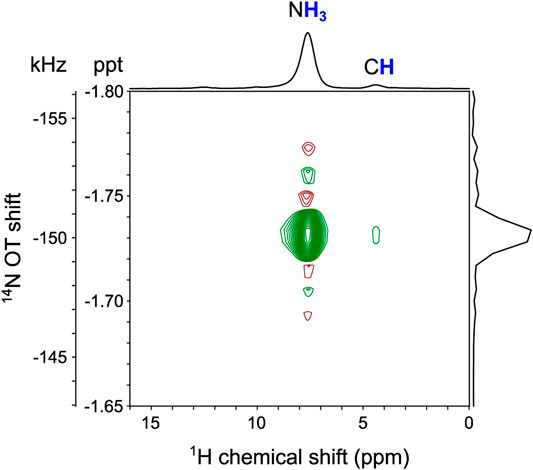
FIGURE 5. The 2D ¹H-{¹⁴N OT} D-HMQC experiment of Tyr at the magnetic field (B₀) of 14.1 T and ν_R of 62.5 kHz. The experiment was performed at the second ¹⁴N OT SSB (n = -2) for the highest S/N. Further details are given in the Experiments section.

After the ¹⁴N OT frequency has been determined, the next parameter for optimization is τ_CW so that as many as possible ¹⁴N crystallites can be saturated/inverted. The ¹⁴N OT rf-field was 120 kHz, the highest technically possible value. It was calibrated by the use of the Bloch–Siegert shift of the proton approach (Hung et al., 2020). However, it is noted that the ¹⁴N OT nutation frequency is scaled on C_Q, the magnetic field, the powder distribution, making it much weaker than ¹⁴N OT rf-field. Figure 6 shows the signal fraction ΔS/S₀ of NH₃ and CH at a fixed τ_mix of 1.15 ms (or 18 loops of SR4²₁ recoupling blocks) under varying τ_CW values.

FIGURE 6

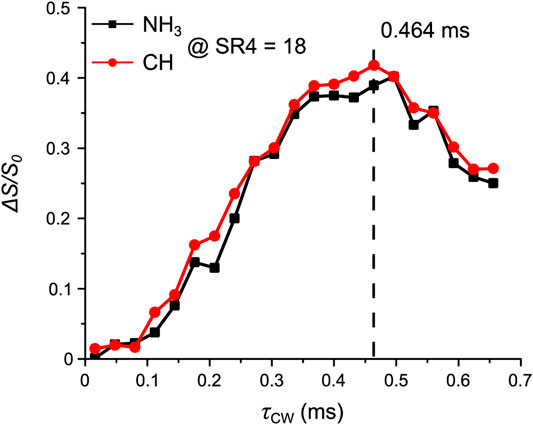
FIGURE 6. Tyr: the signal fraction ΔS/S₀ of NH₃ (black squares) and CH (red circles) as a function of τ_CW. Experiments were performed at τ_mix of 1.15 ms. The optimum τ_CW is shown and highlighted by the dashed line. Further experimental details are given in the Experiments section.

Once the parameters were optimized, we performed the ¹H-¹⁴N OT-REDOR experiment on Tyr. Figure 7A shows the one-dimensional (1D) ¹H spin echo (S₀), the dephased (S′), and the difference (S₀–S’) spectra, in which the former two were extracted from the ¹H-¹⁴N OT-REDOR experiment with τ_mix of 0.51 ms, whereas the latter is calculated from the former two. The NH₃ and CH sites are evidently assigned in Figure 7A and are located in the molecular structure of Tyr (Figure 7B). The experimental fraction curves (black circles) of NH₃ and CH are shown in Figures 7C,D, respectively. There are two important points to mention for the fraction curve of NH₃ in Figure 7C. First, the oscillation is observed and the maximum ΔS/S₀ is reached at τ_mix of 0.6 ms. In our previous study, the ¹H-¹⁴N PM-S-RESPDOR fraction curve shows the maximum at τ_mix of ∼1.4 ms (Duong et al., 2019), which is about two times slower than that of ¹H-¹⁴N OT-REDOR fraction curve. This result is in qualitative agreement with the analysis in Pulse Sequence and the Universal Expression and Figure 4. Second, the fraction curve in Figure 7C shows the experimental maximum ΔS/S₀ of 0.55, smaller than the theoretical maximum of 0.67 by the universal curve in Eq. (3) for complete inversion. Thus, the fitting parameter f of 0.55/0.67∼0.82 is required for the reliable fittings. In addition, the value of 0.82 is close to f = 1 in the case of complete inversion, revealing the dominance of the inversion process under the application of ¹⁴N OT CW pulse. Once f is determined, the only unknown remaining parameter is b_1H–14N. Moreover, according to the fitting strategy in Pulse Sequence and the Universal Expression, this fitting parameter f can also be used in Figure 7D. This is because f only depends on ¹⁴N C_Q, τ_CW, and ¹⁴N OT nutation frequency (which are the same as fraction curves in Figures 7C,D are from the single experiment) and thus should remain the same for other ¹H-¹⁴N pairs from the same ¹⁴N site. The ¹H-¹⁴N dipolar couplings, thus distances, can be extracted by fitting the scaled universal curves (red solid lines) to the experimental fraction curves (black circles) presented in Figures 7C,D. Although the fraction curve in Figure 7C shows the oscillation up to τ_mix of ∼1.8 ms, the fitting by the universal curves is only up to τ_mix of ∼1.0 ms, owing to the poor agreement between the experimental and universal curves for NH₃ at τ_mix > 1.0 ms (Supplementary Figure S2A). The deviation is mainly caused by the fact that each crystallite experiences different ¹⁴N OT saturation/inversion extent depending on its relative orientation between quadrupolar tensor to the rotor-fixed frame, whereas, for the universal approach, the behaviors of the entire crystallites are considered uniform. The root-mean-square deviation (RMSD) in Figures 7C,D was calculated for the best fit of ¹H-¹⁴N dipolar couplings. It is noted that, for NH₃ (Figure 7C), a scaling factor P₂(cos(θ)) (θ, the angle between H-N and C-N, is 109.5°) is used for the dynamic average of the N-H dipolar coupling due to the threefold rotation. The ¹H-¹⁴N distances by OT-REDOR are shown in Table 1 along with those by PM-S-RESPDOR and neutron diffraction (ND). The distances are in good agreement with each other, which demonstrates the feasibility of OT-REDOR for obtaining accurate ¹H-¹⁴N distances. It is worth noting that the longer distances by ssNMR than those from neutron result from the different vibrational averages of the internuclear distances of the two techniques (Ishii et al., 1997).

FIGURE 7

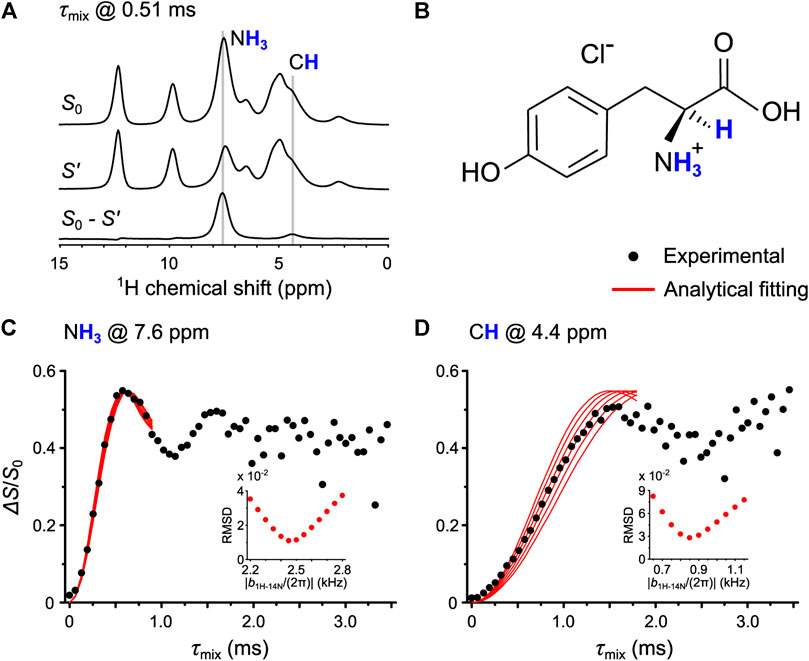
FIGURE 7. (A) The 1D ¹H spin echo (S₀), the dephased (S′), and the difference (S₀–S′) spectra of Tyr. The former two were extracted from ¹H-¹⁴N OT-REDOR with τ_mix of 0.51 ms, whereas the latter is calculated from the former two. (B) The molecular structure of Tyr where NH₃ and CH are presented. (C,D) The fitting of experimental ¹H-¹⁴N OT-REDOR fraction curves (black circles) by the universal curves (red lines) for NH₃ at 7.6 ppm in (C) and CH at 4.4 ppm in (D). The fitting parameter f for universal curves is 0.82. The RMSD analyses (inset) were calculated for the best fitting ¹H-¹⁴N dipolar couplings.

TABLE 1

TABLE 1. ¹H-¹⁴N distances measured by OT-REDOR, PM-S-RESPDOR, and ND on Tyr.

N-Acetyl-L-alanine

To further demonstrate the feasibility of OT-REDOR for a system with a larger ¹⁴N C_Q, we apply it to AcAla. A similar experimental procedure as described for Tyr was applied, including the 1) determination of ¹⁴N OT resonance frequency, 2) optimization of τ_CW, and 3) implementation of OT-REDOR. These experiments were all performed at the second ¹⁴N OT SSB for the highest S/N. For step 1, the ¹H-{¹⁴N OT} T-HMQC was performed (Supplementary Figure S3). Again, for the efficient OT-REDOR fraction curve, τ_CW must be optimized. For step 2, such optimization for NH (black squares) at τ_mix of 0.19 ms (or three loops of SR4²₁ recoupling blocks) and CH (red circles) at τ_mix of 0.96 ms (or 15 loops of SR4²₁ recoupling blocks) under identical τ_CW range is shown in Figure 8. The reason for different τ_mix is due to the large difference between ¹H-¹⁴N distances for these proton sites. The optimum τ_CW of 0.192 ms for ¹⁴NH in AcAla is shorter than τ_CW of 0.464 ms for ¹⁴NH₃ in Tyr. This result is expected since the ¹⁴N site of NH has a larger quadrupolar interaction, thus resulting in a larger ¹⁴N OT nutation field and shorter pulse length for efficient saturation/inversion.

FIGURE 8

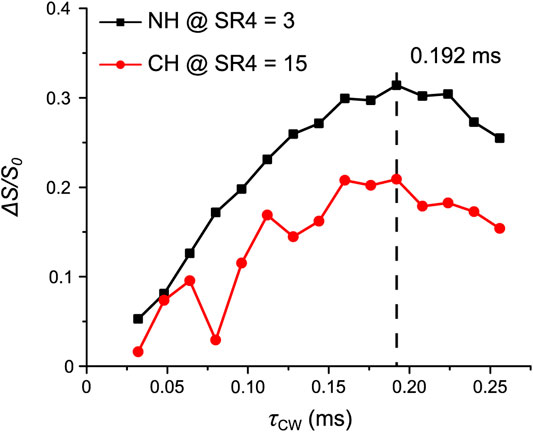
FIGURE 8. AcAla: the signal fraction ΔS/S₀ of NH (black squares) at τ_mix of 0.19 ms and CH (red circles) at τ_mix of 0.96 ms as a function of τ_CW. The optimum τ_CW is shown and highlighted by the dashed line. Further experimental details are given in the Experiments section.

For step 3, these parameters were used for the OT-REDOR experiment on AcAla. Figure 9A shows the one-dimensional (1D) ¹H spin echo (S₀), the dephased (S′), and the difference (S₀–S′) spectra. The former two were extracted from the ¹H-¹⁴N OT-REDOR experiment with τ_mix of 0.26 ms, whereas the latter results from the difference of the former two. For readability, the intensity of the difference spectrum is triple, showing the NH and CH sites which experience the REDOR effect. These two sites are also located in the molecular structure of AcAla (Figure 9B). Figures 9C,D show the fittings between the universal curves (red lines) and the experimental fraction curves (black circles) for NH and CH, respectively. For reliable fittings, the fitting parameter f must be known. From Figure 9C, the experimental maximum ΔS/S₀ intensity of 0.33 results in f of 0.33/0.67 = 0.50. While Tyr shows the dominance of inversion (f = 0.82), AcAla experiences the saturation of overall magnetization (f = 0.50). The difference may arise from the large frequency linewidth (up to 8.6 kHz in Supplementary Figure S3) of ¹⁴N OT spectrum of NH of AcAla relative to the weak ¹⁴N OT nutation frequency. Since both fraction curves in Figures 9C,D were obtained from the single experiment where ¹⁴N C_Q, τ_CW, and ¹⁴N OT nutation frequency are the same, the identical f value can be used in Figure 9D. The extracted ¹H-¹⁴N distances are summarized in Table 2 along with those from PM-S-RESPDOR and XRD. The distances are in agreement with each other. We note that the deviation between the distance of N–H by XRD and those by OT-REDOR and PM-S-RESPDOR is due to the poor capability of XRD to locate H position, resulting from the limited scattering power of hydrogen and the vibrational effect mentioned in L-Tyrosine.HCl. In short, the applicability of OT-REDOR on Tyr and AcAla for obtaining accurate ¹H-¹⁴N distances has been validated.

FIGURE 9

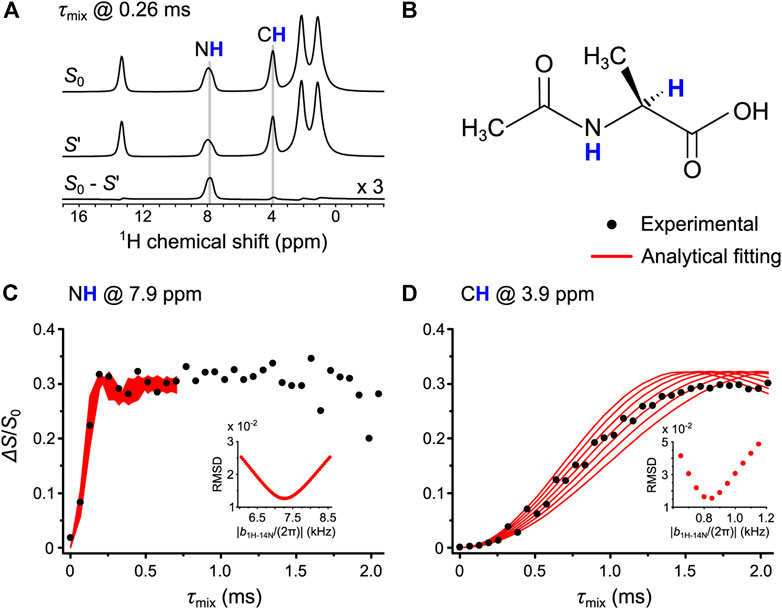
FIGURE 9. (A) The 1D ¹H spin echo (S₀), the dephased (S′), and the difference (S₀–S′) spectra of AcAla. These spectra result from the ¹H-¹⁴N OT-REDOR experiment with τ_mix of 0.26 ms. For readability, the intensity of the difference spectrum is triple. (B) The molecular structure of AcAla where NH and CH are located. (C,D) The fitting of experimental ¹H-¹⁴N OT-REDOR fraction curves (black circles) by the universal curves (red lines) for NH at 7.9 ppm in (C) and CH at 3.9 ppm in (D). The fitting parameter f for universal curves is 0.50. The RMSD analyses (inset) were calculated for the best fitting ¹H-¹⁴N dipolar couplings.

TABLE 2

TABLE 2. ¹H-¹⁴N distances measured by OT-REDOR, PM-S-RESPDOR, and XRD on AcAla.

L-Alanyl-L-alanine

In the previous section, OT-REDOR experiments have been successfully applied to Tyr and AcAla, both containing a single ¹⁴N site. As the main usage of OT-REDOR is for systems where multiple ¹⁴N sites are present, here, we apply this sequence to AlaAla. Besides the 1D ¹H spin echo (S₀) at the top, Figure 10A also shows the two difference (S₀–S’) spectra where 1) NH₃ and 2) NH sites are saturated/inverted during ¹H-¹⁴N OT-REDOR experiments with τ_mix of 0.51 ms and 0.19 ms, respectively. The NH, NH₃, CH(1), and CH(2) sites are unambiguously assigned (Figure 10A) and located in the molecular structure of AlaAla (Figure 10B). This compound consists of two ¹⁴N sites of NH₃ and NH; hence, it is similar to the combination of ¹⁴N sites of Tyr and AcAla.

FIGURE 10

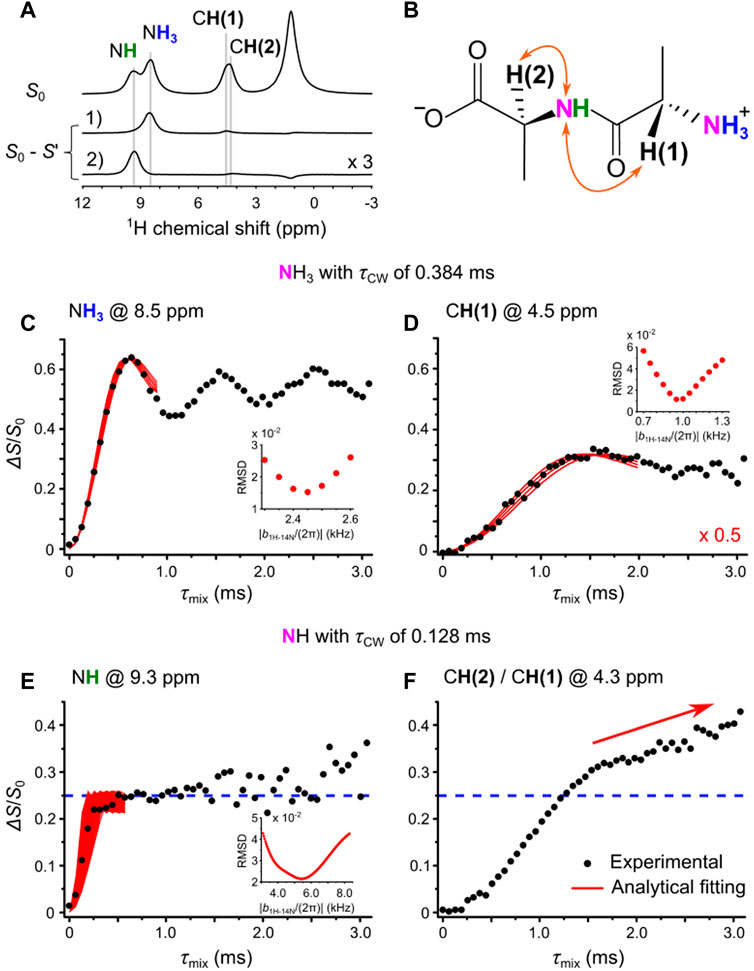
FIGURE 10. (A) The 1D ¹H spin echo and the two difference spectra where 1) NH₃ and 2) NH sites are saturated/inverted during ¹H-¹⁴N OT-REDOR experiments with τ_mix of 0.51 ms and 0.19 ms, respectively. For readability, the intensity of spectrum 2) is triple. (B) The NH, NH₃, CH(1), and CH(2) sites, assigned in (A), are located in the molecular structure of AlaAla. (C–F) The fitting of experimental ¹H-¹⁴N OT-REDOR fraction curves (black circles) by the universal curves (red lines) for NH₃ at 8.5 ppm in (C) and CH(1) at 4.5 ppm in (D) when ¹⁴NH₃ OT was saturated/inverted by CW pulse with τ_CW of 0.384 ms and NH at 9.3 ppm in (E) when ¹⁴NH OT was saturated/inverted by CW pulse with τ_CW of 0.128 ms. The fitting parameter f for universal curves is (C,D) 0.94 and (E) 0.37. For (D), the universal curves are halved, highlighted by a factor of 0.5 in red. For (E), the maximum signal fraction ΔS/S₀ of 0.25 for NH is presented by the horizontal dash line. For (F), the signal fraction ΔS/S₀ of CH(2)/CH(1) at 4.3 ppm with ¹⁴NH OT irradiation is over this line and is still increasing with τ_mix (highlighted by the arrow). The RMSD analyses (inset) were calculated for the best fitting ¹H-¹⁴N dipolar couplings. The two arrows show the proximity of both CH(2)/CH(1) to ¹⁴NH site.

Similar experimental procedures were applied. D-HMQC experiments were performed again at the second ¹⁴N OT SSB (n = -2) for the highest S/N to determine ¹⁴N OT frequencies (Supplementary Figures S4A,B). Then, τ_CW for ¹⁴NH₃ and ¹⁴NH of AlaAla were optimized, which were 0.384 and 0.128 ms, respectively (Supplementary Figures S4C,D). These optimized values, similar to those of Tyr and AcAla, were used to obtain ¹H-¹⁴N OT-REDOR fraction curves.

We discuss first the case where ¹⁴NH₃ is saturated/inverted by CW pulse with τ_CW of 0.384 ms. The experimental fraction curves of NH₃ and CH(1) (black circles) are shown in Figures 10C,D, respectively. For NH₃, the experimental curve shows the oscillation and the maximum ΔS/S₀ is 0.63 (see Figure 10C). Thus, the fitting parameter f of 0.63/0.67∼0.94 for universal curves is required for reliable fittings. This indicates that an almost complete inversion of ¹⁴N OT is achieved (f = 1), similar to the case of NH₃ of Tyr. Another similarity to Tyr is that significant deviation is observed, especially at long τ_mix for the full-scale fitting between the fraction curve of Figure 10C and the universal curves (see Supplementary Figure S2B). For CH(1), the fraction curve reaches the plateau ΔS/S₀ of 0.35 at τ_mix of 1.50 ms (Supplementary Figure S5). The reason for the lower signal fraction ΔS/S₀ is the overlapping of ¹H signals of CH(1) and CH(2) sites, in which only CH(1) is close to ¹⁴NH₃. For a good match with the experimental fraction curve, we need to halve the universal curves in Figure 10D. The reason for using a factor of 0.5 is explained in the Supplementary Eq. S3. Without scaling, the obtained ¹H-¹⁴N distance by NMR is in poor agreement with that reported from XRD (see Supplementary Figure S5). The fitting of the scaled universal curves to the ¹H-¹⁴N OT-REDOR fraction curves gives the ¹H-¹⁴N distances of 1.05 ± 0.03 Å for NH₃ (after a modulation factor of P₂(cos(θ)) as described in L-Tyrosine.HCl and Pulse Sequence and the Universal Expression and 2.09 ± 0.05 Å for CH(1) (after halving the universal curves). Both measured distances are in good agreement with those reported from XRD (see Table 3).

TABLE 3

TABLE 3. ¹H-¹⁴N distances measured by OT-REDOR and XRD on AlaAla.

We then consider the case where ¹⁴NH is saturated/inverted by CW pulse with τ_CW of 0.128 ms. The fraction curves of NH and CH(2)/CH(1) (black circles) are shown in Figures 10E,F, respectively. For NH in Figure 10E, the experimental curve shows the plateau ΔS/S₀ of 0.25 at τ_mix of 0.50 ms and then large fluctuations of ΔS/S₀ at τ_mix larger than 1.50 ms. The origin of such fluctuations may be due to t₁ noise from spinning frequency fluctuation (Nishiyama et al., 2020). As the maximum ΔS/S₀ is smaller than the theoretical maximum of 0.67 of the universal curve, a fitting parameter f of 0.25/0.67∼0.37 is required. Based on the fittings of the universal curves (red solid lines) to the ¹H-¹⁴N OT-REDOR fraction curve, the ¹H-¹⁴N distance is measured to be 1.19 ± 0.20 Å. This value is in excellent agreement with ¹H-¹⁵N distance by inverse cross-polarization with variable contact (CPVC) (Nishiyama et al., 2016) (Supplementary Figure S6) and in close agreement with the distance of 0.96 Å by XRD (see Table 3). An advantage of ¹H-¹⁴N OT-REDOR compared to ¹H-¹⁵N inverse CPVC is that multiple H-N distances can be simultaneously determined by the former, whereas only directly bonded distance is determined by the latter due to the dipolar truncation effect. Indeed, ¹H-¹⁵N inverse CPVC only provides the distance of directly bonded H-N for the NH site (see Supplementary Figure S6). For CH(2)/CH(1) fraction curve, its fraction signal ΔS/S₀ is larger than 0.25 and continues to grow at long τ_mix (see Figure 10F). Although this curve is the combination of two curves because there are two CH groups that are close to ¹⁴NH site and their ¹H chemical shifts are overlapped, ΔS/S₀ is larger than 0.25 may result from the intermolecular couplings. Because of this complexity, we did not fit this with the universal curves.

In conclusion, for AlaAla, the ¹H-¹⁴N OT-REDOR experiment can be used for the accurate measurement of ¹H-¹⁴N distances for the bonded H–N distances of each nitrogen. However, extracting distances for nonbonded H-N pairs is still difficult, especially when the chemical shifts of these ¹H sites are overlapped, as shown in Figure 10F. Such problem will be solved by the multidimensional NMR experiments, for example, with an addition of the ¹³C dimension.

Conclusion

In summary, we have presented the feasibility of ¹H-¹⁴N OT-REDOR with proton detection at fast MAS to extract ¹H-¹⁴N distances for Tyr, AcAla, and AlaAla. Owing to the selective characteristics of ¹⁴N OT spectroscopy, this sequence is useful for systems with multiple ¹⁴N sites. Other advantages of ¹⁴N OT are the availability of commercial MAS probes, the robustness of misadjustment of the magic angle, and the fast dephasing rate. The final advantage is that it allows probing longer ¹H-¹⁴N distances better than ¹H-¹⁴N RESPDOR experiment. For efficient ¹H-¹⁴N OT-REDOR fraction curve, the ¹⁴N OT resonance frequency, in this work, must be determined with D- or T-HMQC experiments and the CW pulse length must be optimized. For reliable ¹H-¹⁴N distances, the fitting parameter f is a prerequisite; otherwise, distances cannot be accurately determined. The knowledge of f value also enables the evaluation of saturation/inversion degree of ¹⁴N OT by the CW pulse. For Tyr and AcAla compounds, the extracted distances from OT-REDOR are in good agreement with PM-S-RESPDOR and the diffraction techniques. For AlaAla, the extracted ¹H-¹⁴N distances from directly bonded N–H well agree with those reported from XRD and ¹H-¹⁵N inverse CPVC. However, this is not the case for nonbonded N–H pairs since distance deviations from those reported by XRD are observed. The reason for such deviation is the overlapping of ¹H signals. This issue can be overcome by performing multidimensional NMR experiments. In conclusion, we believe that the ¹H-¹⁴N OT-REDOR has the potential of selectively measuring ¹H-¹⁴N distances on systems containing multiple ¹⁴N sites, giving deep insights into structural studies of biological, chemical, and pharmaceutical compounds. It is worth noting that ¹⁴N selective saturation can also be achieved in the manner of DANTE. It is promising to perform ¹H-¹⁴N DANTE-RESPDOR experiments in future studies.

Experiments

L-tyrosine.HCl (Tyr), N-acetyl-L-alanine (AcAla), and L-alanyl-L-alanine were purchased from Sigma-Aldrich and used as received. The samples were separately packed into 1.0 mm zirconia rotors and then inserted into 1 mm ¹H/X double-resonance probe. The rotors were spun at a MAS frequency of 62.5 kHz, except for ¹H-¹⁵N inverse CPVC at 70 kHz.

All NMR experiments were recorded at a room temperature of 25 °C on JNM-ECZ600R (JEOL RESONANCE Inc.) at 14.1 T solid-state NMR spectrometers. The ¹H and ¹⁴N OT Larmor frequencies are 600.0 and 86.8 MHz, respectively. For the highest S/N, the ¹⁴N OT frequency was set at the second SSB (n = −2). The ¹⁴N and ¹⁴N OT shifts are referenced to CH₃NO₂, whose ¹⁴N and ¹⁴N OT shifts are equal to 0 ppm or 0 kHz. The ¹H rf-field was 328 kHz for π/2 and π pulses and 140 kHz for the SR4²₁ recoupling sequence. The ¹⁴N OT rf-field was 120 kHz.

For Tyr, the 2D ¹H-{¹⁴N} D-HMQC spectrum in Figure 5 was recorded using the sequence shown in Supplementary Figure S1A with 8 scans, 32 t₁ points, and rotor-synchronized t₁ increment of 16.0 µs. τ_p, τ_mix, and recycling delay (RD) were 200 µs, 512 µs, and 4 s, respectively. The experimental time was about 0.6 h. The States-TPPI method was employed for quadrature detection along the indirect dimension. For Figure 6, τ_CW was optimized within the range from 16 µs to 656 µs with a step of 32 µs; the ¹⁴N OT frequency was −1.73 ppt (parts per thousand), the τ_mix was fixed at 1152 µs, the number of scans (NS) was 18, and RD was 5.0 s. The experimental time was 1.1 h. For Figure 7, the ¹H-¹⁴N OT-REDOR was performed at τ_CW of 464 µs, ¹⁴N OT frequency of −1.73 ppt, NS of 72, RD of 6.5 s, and τ_mix from 0 to 3456 µs with a step of 64 µs. The experimental time was 14.3 h.

For AcAla, the τ_CW optimization in Figure 8 was implemented within the range from 32 µs to 256 µs with a step of 16 µs; the ¹⁴N OT frequency was −1.267 ppt, NS was 18 and RD was 10.0 s, and τ_mix was fixed at 192 µs for NH at 7.9 ppm and 960 µs for CH at 3.9 ppm. The experimental times for both experiments were 1.5 h. For Figure 9, the ¹H-¹⁴N OT-REDOR was performed at τ_CW of 192 µs, ¹⁴N OT frequency of −1.267 ppt, NS of 108, RD of 10 s, and τ_mix from 0 to 2048 µs with a step of 64 µs. The experimental time was 19.8 h.

For AlaAla, the ¹H-¹⁴N OT-REDOR experiments in Figure 10 were performed at NS of 144, RD of 2.5 s, τ_mix from 0 to 3072 µs with a step of 64 µs, and τ_CW, ¹⁴N OT frequencies were of 384 µs, −1.72 ppt and 128 µs, −1.26 ppt for ¹⁴NH₃ and ¹⁴NH, respectively. The experimental times for both experiments were 9.8 h.

NMR data are available upon request.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

ND was responsible for methodology, NMR measurements, and analysis; ZG was responsible for conceptualization, and methodology; YN was responsible for conceptualization, methodology, and supervision. All authors were responsible for writing the manuscript.

Funding

This work was supported by JSPS KAKENHI Grant Number 20K05483 to YN. ZG acknowledges the support from the US National Science Foundation through NSF/DMR-1644779 and the National High Magnetic Field Laboratory at Florida.

Conflict of Interest

YN is employed by JEOL RESONANCE Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors YN.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2021.645347/full#supplementary-material.

References

Bloom, M., and LeGros, M. A. (1986). Direct detection of two-quantum coherence. Can. J. Phys. 64, 1522–1528. doi:10.1139/p86-271

CrossRef Full Text | Google Scholar

Brinkmann, A, and Kentgens, A. P. (2006). Proton-selective 17O-1H distance measurements in fast magic-angle-spinning solid-state NMR spectroscopy for the determination of hydrogen bond lengths. J. Am. Chem. Soc. 128, 14758–14759. doi:10.1021/ja065415k

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, S. P. (2014). Nitrogen-proton correlation experiments of organic solids at natural isotopic abundance. eMagRes. 3, 243–254. doi:10.1002/9780470034590.emrstm1323

CrossRef Full Text | Google Scholar

Carnevale, D., Ji, X., and Bodenhausen, G. (2017). Double cross polarization for the indirect detection of nitrogen-14 nuclei in magic angle spinning NMR spectroscopy. J. Chem. Phys. 147, 184201. doi:10.1063/1.5000689

PubMed Abstract | CrossRef Full Text | Google Scholar

Cavadini, S. (2010). Indirect detection of nitrogen-14 in solid-state NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 56, 46–77. doi:10.1016/j.pnmrs.2009.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Cavadini, S., Antonijevic, S., Lupulescu, A., and Bodenhausen, G. (2006). Indirect detection of nitrogen-14 in solids via protons by nuclear magnetic resonance spectroscopy. J. Magn. Reson. 182, 168–172. doi:10.1016/j.jmr.2006.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Lu, X., Wang, Q., Lafon, O., Trébosc, J., Deng, F., et al. (2010a). Distance measurement between a spin-1/2 and a half-integer quadrupolar nuclei by solid-state NMR using exact analytical expressions. J. Magn. Reson. 206, 269–273. doi:10.1016/j.jmr.2010.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Wang, Q., Hu, B., Lafon, O., Trébosc, J., Deng, F., et al. (2010b). Measurement of hetero-nuclear distances using a symmetry-based pulse sequence in solid-state NMR. Phys. Chem. Chem. Phys. 12, 9395–9405. doi:10.1039/b926546e

PubMed Abstract | CrossRef Full Text | Google Scholar

Chevelkov, V., Fink, U., and Reif, B. (2009). Accurate determination of order parameters from 1H,15N dipolar couplings in MAS solid-state NMR experiments. J. Am. Chem. Soc. 131, 14018–14022. doi:10.1021/ja902649u

PubMed Abstract | CrossRef Full Text | Google Scholar

Concistré, M., Kuprov, I., Haies, I. M., Williams, P. T. F., and Carravetta, M. (2018). ¹⁴N overtone NMR under MAS: signal enhancement using cross-polarization methods. J. Magn. Reson. 298, 1–5. doi:10.1016/j.jmr.2018.10.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Duong, N. T., Rossi, F., Makrinich, M., Goldbourt, A., Chierotti, M. R., Gobetto, R., et al. (2019). Accurate 1H-14N distance measurements by phase-modulated RESPDOR at ultra-fast MAS. J. Magn. Reson. 308, 106559. doi:10.1016/j.jmr.2019.07.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, R. (2003). Measurement of 15N-1H bond lengths by rotational-echo double-resonance NMR spectroscopy. Chem. Phys. Lett. 376, 62–67. doi:10.1016/S0009-2614(03)00951-5

CrossRef Full Text | Google Scholar

Gan, Z. (2006). Measuring multiple carbon-nitrogen distances in natural abundant solids using R-RESPDOR NMR. Chem Commun (Camb). 7, 4712–4714. doi:10.1039/b611447d

CrossRef Full Text | Google Scholar

Gan, Z., Amoureux, J. P., and Trébosc, J. (2007). Proton-detected ¹⁴N MAS NMR using homonuclear decoupled rotary resonance. Chem. Phys. Lett. 435, 163–169. doi:10.1016/j.cplett.2006.12.066

CrossRef Full Text | Google Scholar

Gan, Z., Hung, I., Nishiyama, Y., Amoureux, J. P., Lafon, O., Nagashima, H., et al. (2018). 14N overtone nuclear magnetic resonance of rotating solids. J. Chem. Phys. 149, 064201. doi:10.1063/1.5044653

PubMed Abstract | CrossRef Full Text | Google Scholar

Gullion, T. (2007). Rotational-Echo, Double-Resonance NMR. MRI. 1, 713–718. doi:10.1007/1-4020-3910-7_89

CrossRef Full Text | Google Scholar

Gullion, T., and Schaefer, J. (1989). Rotational-echo double-resonance NMR. J. Magn. Reson. Imaging. 81, 196–200. doi:10.1016/0022-2364(89)90280-1

CrossRef Full Text | Google Scholar

Guzmán-Afonso, C., Hong, Y. L., Colaux, H., Iijima, H., Saitow, A., Fukumura, T., et al. (2019). Understanding hydrogen-bonding structures of molecular crystals via electron and NMR nanocrystallography. Nat. Commun. 10, 3537. doi:10.1038/s41467-019-11469-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Haies, IM, Jarvis, JA, Bentley, H, Heinmaa, I, Kuprov, I, Williamson, PT, et al. (2015a). (14)N overtone NMR under MAS: signal enhancement using symmetry-based sequences and novel simulation strategies. Phys. Chem. Chem. Phys. 17, 6577–87. doi:10.1039/C4CP03994G

PubMed Abstract | CrossRef Full Text | Google Scholar

Haies, I. M., Jarvis, J. A., Brown, L. J., Kuprov, I., Williamson, P. T., and Carravetta, M. (2015b). (14)N overtone transition in double rotation solid-state NMR. Phys. Chem. Chem. Phys. 17, 23748–23753. doi:10.1039/C5CP03266K

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohwy, M., Jaroniec, C. P., Reif, B., Rienstra, C. M., and Griffin, R. G. (2000). Local structure and relaxation in solid-state NMR: accurate measurement of amide N−H bond lengths and H−N−H bond angles. J. Am. Chem. Soc. 122, 3218–3219. doi:10.1021/ja9913737

CrossRef Full Text | Google Scholar

Hou, G., Byeon, I. J. L., Ahn, J., Gronenborn, A. M., and Polenova, T. (2011). ¹H-¹³C/¹H-¹⁵N heteronuclear dipolar recoupling by R-symmetry sequences under fast magic angle spinning for dynamics analysis of biological and organic solids. J. Am. Chem. Soc. 133, 18646–18655. doi:10.1021/ja203771a

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, G., Lu, X., Vega, A. J., and Polenova, T. (2014). Accurate measurement of heteronuclear dipolar couplings by phase-alternating R-symmetry (PARS) sequences in magic angle spinning NMR spectroscopy. J. Chem. Phys. 141, 104202. doi:10.1063/1.4894226

PubMed Abstract | CrossRef Full Text | Google Scholar

Hung, I., Gor’kov, P., and Gan, Z. (2019). Efficient and sideband-free ¹H-detected ¹⁴N magic-angle spinning NMR. J. Chem. Phys. 151, 154202. doi:10.1063/1.5126599

PubMed Abstract | CrossRef Full Text | Google Scholar

Hung, I., Gor'kov, P., and Gan, Z. (2020). Using the heteronuclear Bloch-Siegert shift of protons for B1 calibration of insensitive nuclei not present in the sample. J. Magn. Reson. 310, 106636. doi:10.1016/j.jmr.2019.106636

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishii, Y., Terao, T., and Hayashi, S. (1997). Theory and simulation of vibrational effects on structural measurements by solid-state nuclear magnetic resonance. J. Chem. Phys. 107, 2760–2774. doi:10.1063/1.474633

CrossRef Full Text | Google Scholar

Jarvis, J. A., Concistre, M., Haies, I. M., Bounds, R. W., Kuprov, I., Carravetta, M., et al. (2019). Quantitative analysis of 14N quadrupolar coupling using 1H detected 14N solid-state NMR. Phys. Chem. Chem. Phys. 21, 5941–5949. doi:10.1039/c8cp06276e

PubMed Abstract | CrossRef Full Text | Google Scholar

Jayanthi, S., and Ramanathan, K. V. (2011). Excitation and correlation of ¹⁴N overtone transitions and measurement of heteronuclear dipolar coupling using DAPT. Chem. Phys. Lett. 502, 121–125. doi:doi:10.1016/j.cplett.2010.12.007

CrossRef Full Text | Google Scholar

Lu, X., Lafon, O., Trébosc, J., and Amoureux, J. P. (2011). Detailed analysis of the S-RESPDOR solid-state NMR method for inter-nuclear distance measurement between spin-1/2 and quadrupolar nuclei. J. Magn. Reson. 215, 34–49. doi:10.1016/j.jmr.2011.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, X., Trébosc, J., Lafon, O., Carnevale, D., Ulzega, S., Bodenhausen, G., et al. (2013). Broadband excitation in solid-state NMR using interleaved DANTE pulse trains with N pulses per rotor period. J. Magn. Reson. 236, 105–116. doi:10.1016/j.jmr.2013.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Makrinich, M., Gupta, R., Polenova, T., and Goldbourt, A (2017). Saturation capability of short phase modulated pulses facilitates the measurement of longitudinal relaxation times of quadrupolar nuclei. Solid State Nucl. Magn. Reson. 84, 196–203. doi:10.1016/j.ssnmr.2017.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Makrinich, M., Nimerovsky, E., and Goldbourt, A. (2018). Pushing the limit of NMR-based distance measurements – retrieving dipolar couplings to spins with extensively large quadrupolar frequencies. Solid State Nucl. Magn. Reson. 92, 19–24. doi:10.1016/j.ssnmr.2018.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Nimerovsky, E., Gupta, R., Yehl, J., Li, M., Polenova, T., and Goldbourt, A. (2014). Phase-modulated LA-REDOR: A robust, accurate and efficient solid-state NMR technique for distance measurements between a spin-1/2 and a quadrupole spin. J. Magn. Reson. 244, 107–113. doi:10.1016/j.jmr.2014.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Nimerovsky, E, Makrinich, M, and Goldbourt, A (2017). Analysis of large-anisotropy-spin recoupling pulses for distance measurement under magic-angle spinning NMR shows the superiority and robustness of a phase modulated saturation pulse. J. Chem. Phys. 146, 124202. doi:10.1063/1.4978472

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyama, Y. (2016). Fast magic-angle sample spinning solid-state NMR at 60-100kHz for natural abundance samples. Solid State Nucl. Magn. Reson. 78, 24–36. doi:10.1016/j.ssnmr.2016.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyama, Y., Agarwal, V., and Zhang, R. (2020). t₁-Noise Suppression by γ-Free Recoupling Sequences in Solid-State NMR for Structural Characterization of Fully Protonated Molecules at Fast MAS. J. Phys. Chem. C. 128, 26332–26343. doi:10.1021/acs.jpcc.0c08828

CrossRef Full Text | Google Scholar

Nishiyama, Y, Endo, Y, Nemoto, T, Utsumi, H, Yamauchi, K, Hioka, K, et al. (2011). Very fast magic angle spinning (1)H-(14)N 2D solid-state NMR: sub-micro-liter sample data collection in a few minutes. J. Magn. Reson. 208, 44–48. doi:10.1016/j.jmr.2010.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyama, Y., Malon, M., Gan, Z., Endo, Y., and Nemoto, T. (2013). Proton-nitrogen-14 overtone two-dimensional correlation NMR spectroscopy of solid-sample at very fast magic angle sample spinning. J. Magn. Reson. 230, 160–164. doi:10.1016/j.jmr.2013.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyama, Y., Malon, M., Potrzebowski, M. J., Paluch, P., and Amoureux, J. P. (2016). Accurate NMR determination of C-H or N-H distances for unlabeled molecules. Solid State Nucl. Magn. Reson. 73, 15–21. doi:10.1016/j.ssnmr.2015.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Dell, L. A., and Brinkmann, A. (2013). ¹⁴N overtone NMR spectra under magic angle spinning: Experiments and numerically exact simulations. J. Chem. Phys. 138, 064201. doi:10.1063/1.4775592

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Dell, L. A., He, R., and Pandohee, J. (2013). Identifying H–N proximities in solid-state NMR using ¹⁴N overtone irradiation under fast MAS. CrystEngComm. 15, 8657–8667. doi:10.1039/c3ce40967h

CrossRef Full Text | Google Scholar

O’Dell, L. A., and Ratcliffe, C. I. (2011). ¹⁴N magic angle spinning overtone NMR spectra. J. Chem. Phys. 514, 168–173. doi:10.1016/j.cplett.2011.08.030

CrossRef Full Text | Google Scholar

Paluch, P., Pawlak, T., Amoureux, J. P., and Potrzebowski, M. J. (2013). Simple and accurate determination of X-H distances under ultra-fast MAS NMR. J. Magn. Reson. 233, 56–63. doi:10.1016/j.jmr.2013.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandey, M. K., Amoureux, J. P., Asakura, T., and Nishiyama, Y. (2016). Sensitivity enhanced (14)N/(14)N correlations to probe inter-beta-sheet interactions using fast magic angle spinning solid-state NMR in biological solids. Phys. Chem. Chem. Phys. 18, 22583–22589. doi:10.1039/c6cp03848d

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandey, M. K., and Nishiyama, Y. (2015). Proton-detected 3D ¹⁴N/¹⁴N/¹H isotropic shift correlation experiment mediated through ¹H-¹H RFDR mixing on a natural abundant sample under ultrafast MAS. J. Magn. Reson. 258, 96–101. doi:10.1016/j.jmr.2015.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandey, M. K., and Nishiyama, Y. (2018). A one-dimensional solid-state NMR approach for 14NH/14NH overtone correlation through 1H/1H mixing under fast MAS. Phys. Chem. Chem. Phys. 20, 25849–25853. doi:10.1039/c8cp05000g

PubMed Abstract | CrossRef Full Text | Google Scholar

Pourpoint, F., Trébosc, J., Bonhomme, C., Durupthy, O., Steunou, N., Lafon, O., et al. (2014). Quantitative analysis of the proximities of OH ligands and vanadium sites in a polyoxovanadate cluster using frequency-selective ¹H-⁵¹V solid-state NMR spectroscopy. J. Phys. Chem. C. 118, 18580–18588. doi:10.1021/jp505194q

CrossRef Full Text | Google Scholar

Pruski, M., Bailly, A., Lang, D. P., Amoureux, J. P., and Fernandez, C. (1999). Studies of heteronuclear dipolar interactions between spin-1/2 and quadrupolar nuclei by using REDOR during multiple quantum evolution. Chem. Phys. Lett. 307, 35–40. doi:10.1016/S0009-2614(99)00490-X

CrossRef Full Text | Google Scholar

Rankin, A. G. M., Trébosc, J., Paluch, P., Lafon, O., and Amoureux, J. P. (2019). Evaluation of excitation schemes for indirect detection of 14N via solid-state HMQC NMR experiments. J Magn Reson. 303, 28–41. doi:10.1016/j.jmr.2019.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Schanda, P., Meier, B. H., and Ernst, M. (2011). Accurate measurement of one-bond H-X heteronuclear dipolar couplings in MAS solid-state NMR. J. Magn. Reson. 210, 246–259. doi:10.1016/j.jmr.2011.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnell, I., and Saalwächter, K. (2002). (15)N-(1)H bond length determination in natural abundance by inverse detection in fast-MAS solid-state NMR spectroscopy. J. Am. Chem. Soc. 124, 10938–10939. doi:10.1021/ja026657x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, M., Chen, Q., and Hu, B. (2017). Composite pulses in directly and indirectly detected 14N MAS overtone spectroscopy. Solid State Nucl. Magn. Reson. 84, 132–136. doi:10.1016/j.ssnmr.2017.01.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, M., Trébosc, J., O'Dell, L. A., Lafon, O., Pourpoint, F., Hu, B., et al. (2015). Comparison of various NMR methods for the indirect detection of nitrogen-14 nuclei via protons in solids. J. Magn. Reson. 258, 86–95. doi:10.1016/j.jmr.2015.06.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Tycko, R., and Opella, S. J. (1987). Overtone NMR spectroscopy. J. Chem. Phys. 86, 1761. doi:10.1063/1.452176

CrossRef Full Text | Google Scholar

Vitzthum, V., Caporini, M. A., Ulzega, S., and Bodenhausen, G. (2011). Broadband excitation and indirect detection of nitrogen-14 in rotating solids using Delays Alternating with Nutation (DANTE). J. Magn. Reson. 212, 234–239. doi:10.1016/j.jmr.2011.06.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitzthum, V., Caporini, M. A., Ulzega, S., Trébosc, J., Lafon, O., Amoureux, J. P., et al. (2012). Uniform broadband excitation of crystallites in rotating solids using interleaved sequences of delays alternating with nutation. J. Magn. Reson. 223, 228–236. doi:10.1016/j.jmr.2012.05.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Wijesekara, A. V., Venkatesh, A., Lampkin, B. J., VanVeller, B., Lubach, J. W., Nagapudi, K., et al. (2020). Fast acquisition of proton‐detected HETCOR solid‐state NMR spectra of quadrupolar nuclei and rapid measurement of NH bond lengths by frequency selective HMQC and RESPDOR pulse sequences. Chemist. 26, 7881–7888. doi:10.1002/chem.202000390

CrossRef Full Text | Google Scholar

Zhao, L., Hanrahan, M. P., Chakravarty, P., Dipasquale, A. G., Sirois, L. E., Nagapudi, K., et al. (2018). Characterization of pharmaceutical cocrystals and salts by dynamic nuclear polarization-enhanced solid-state NMR spectroscopy. Cryst. Growth Des. 18, 2588–2601. doi:10.1021/acs.cgd.8b00203

CrossRef Full Text | Google Scholar

Zhao, X., Sudmeier, J. L., Bachovchin, W. W., and Levitt, M. H. (2001). Measurement of NH bond lengths by fast magic-angle spinning solid-state NMR spectroscopy: A new method for the quantification of hydrogen bonds. J. Am. Chem. Soc. 123, 11097–11098. doi:10.1021/ja016328p

PubMed Abstract | CrossRef Full Text | Google Scholar