Coarse-Grained Modeling and Molecular Dynamics Simulations of Ca2+-Calmodulin

Calmodulin (CaM) is a calcium-binding protein that transduces signals to downstream proteins through target binding upon calcium binding in a time-dependent manner. Understanding the target binding process that tunes CaM’s affinity for the calcium ions (Ca²⁺), or vice versa, may provide insight into how Ca²⁺-CaM selects its target binding proteins. However, modeling of Ca²⁺-CaM in molecular simulations is challenging because of the gross structural changes in its central linker regions while the two lobes are relatively rigid due to tight binding of the Ca²⁺ to the calcium-binding loops where the loop forms a pentagonal bipyramidal coordination geometry with Ca²⁺. This feature that underlies the reciprocal relation between Ca²⁺ binding and target binding of CaM, however, has yet to be considered in the structural modeling. Here, we presented a coarse-grained model based on the Associative memory, Water mediated, Structure, and Energy Model (AWSEM) protein force field, to investigate the salient features of CaM. Particularly, we optimized the force field of CaM and that of Ca²⁺ ions by using its coordination chemistry in the calcium-binding loops to match with experimental observations. We presented a “community model” of CaM that is capable of sampling various conformations of CaM, incorporating various calcium-binding states, and carrying the memory of binding with various targets, which sets the foundation of the reciprocal relation of target binding and Ca²⁺ binding in future studies.

Introduction

Calmodulin (CaM) is a calcium-binding protein that is present in all eukaryotic cells (Berchtold and Villalobo, 2014; Villalobo et al., 2018; Chin and Means, 2000). CaM is composed of two globular domains separated by a central linker. The two domains (N- and C-domains) are constituted of two calcium-binding helix-loop-helix motifs each, namely, EF-hand motifs (Chattopadhyaya et al., 1992; Fernandes and Oliveira-Brett, 2017). Upon sufficient increase in Ca²⁺ concentration, Ca²⁺-free CaM transitions to the Ca²⁺-loaded CaM (Figure 1), exposing the hydrophobic target-binding surfaces of CaM to the solvent (Figure 2) (Barton et al., 2002; Vetter and Leclerc, 2003; Park et al., 2008; Gromiha and Gromiha, 2010; Wu et al., 2012; Fernandes and Oliveira-Brett, 2017). This transition is accompanied by large conformational changes mutually induced by the conformational changes in the CaM-binding target (CaMBT) peptides (Wang et al., 2013; Liu et al., 2017a; Archer et al., 2019; Bekker et al., 2020). The most unique feature of CaM is its reciprocal relation between Ca²⁺ binding and target binding (Meador et al., 1993; Weinstein and Mehler, 1994; Wall et al., 1997; Wriggers et al., 1998; Chin and Means, 2000; Hoeflich and Ikura, 2002; Westerlund and Delemotte, 2018), where the conformational changes in the CaM/CaMBT compound further tune CaM’s affinity for the Ca²⁺ ions (Hoffman et al., 2014; Zhang et al., 2017). The important feature that the net charges of Ca²⁺ ions vary with the conformations of a calcium-binding loop (Zhang et al., 2021), however, has not been accurately captured in molecular dynamics simulations on calcium-binding proteins.

FIGURE 1

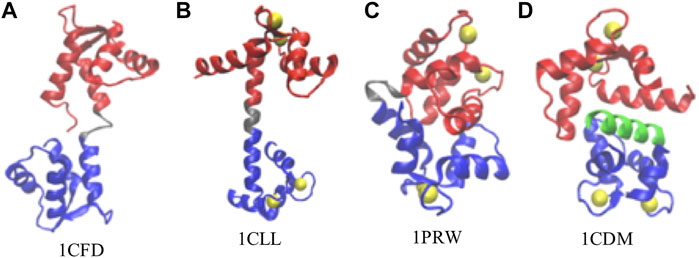
FIGURE 1. Representative conformations of calmodulin (CaM). (A) Ca²⁺-free CaM, or apoCaM (PDB ID: 1CFD); (B) Ca²⁺-bound CaM, or holoCaM, in the extended conformation (PDB ID: 1CLL); (C) holoCaM in the collapsed conformation without a target peptide (PDB ID: 1PRW); (D) holoCaM with a target peptide (PDB ID 1CDM). We visualized the structures using the Visual Molecular Dynamics (VMD) program (Humphrey et al., 1996). Ca²⁺ ions are shown in yellow spheres, the N-terminal and C-terminal domains of CaM are shown in red and blue, respectively, the central linker is shown in grey, and the target peptide is in green.

FIGURE 2

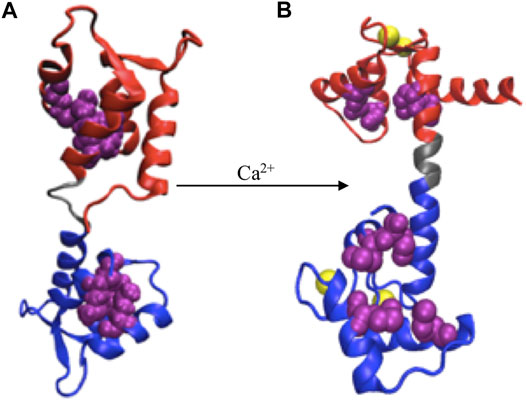
FIGURE 2. Ca²⁺ induced conformational change. (A) apoCaM, (B) holoCaM. Ca²⁺ ions are shown in yellow spheres, the N-terminal and C-terminal domains of CaM are shown in red and blue, respectively, and the central linker is shown grey. Upon conformational change, the four methionine residues (shown as beads in purple), initially buried inside the EF-hands, are exposed to the solvent.

The 148-amino acid CaM is an evolutionarily conserved protein across all vertebrates (Davis and Thorner, 1989; Tripathi et al., 2015a), while it is capable of binding more than 300 variations of CaMBTs (Yamniuk and Vogel, 2004). Such structural variability permits its regulation upon the stimulation of calcium ions processes (Clapham, 2007; Carafoli, 2002; Bootman, 2012) in a wide range of biological activities (Chin and Means, 2000; Hoeflich and Ikura, 2002) including cellular motility, neurogenesis, memory formation, muscle contraction, and neuronal transmission (Bootman, 2012; Marambaud et al., 2009; Berridge, 2006). A large and growing body of literature has investigated the structures and dynamics of CaM upon calcium binding (Wriggers et al., 1998; Mehler et al., 1991; Her et al., 2018; Anthis et al., 2011). The crystal structure of the Ca²⁺-CaM shows a dumbbell-like structure with a central α-helical linker (Figure 1B). However, in solution, the central linker demonstrates higher flexibility (Wriggers et al., 1998; Her et al., 2018; Anthis et al., 2011; Ikura et al., 1992; Chou et al., 2001), which enables the two globular domains of CaM to orient independently from each other (Wriggers et al., 1998; Shepherd and Vogel, 2004; Qin and Squier, 2001). Moreover, this flexibility of the central linker could justify the compact structure of the Ca²⁺-CaM (Figure 1D) upon target binding (Barton et al., 2002; Shepherd and Vogel, 2004). Additionally, Ca²⁺-CaM has been shown to crystallize in the collapsed conformation in the absence of the target (Figure 1C), indeed providing more evidence of the backbone plasticity of the Ca²⁺-CaM (Fallon and Quiocho, 2003) and domain-domain interactions. The structural distribution between the collapsed and extended conformations is roughly 1:9 (Anthis et al., 2011).

A myriad of computational approaches, ranging from all-atom to coarse-grained (Weinstein and Mehler, 1994; Spoel et al., 1996; Wriggers et al., 1998; Vigil et al., 2001; Yang et al., 2001; Barton et al., 2002; Komeiji et al., 2002; Yang et al., 2004; Zuckerman, 2004; Monticelli et al., 2008; Nandigrami and Portman, 2016; Liu et al., 2017b; Gong and Sun, 2017; Robustelli et al., 2018; Delfino et al., 2019; Sun and Kekenes-Huskey, 2021), have been employed to model the structural dynamics of CaM. However, these models have yet to capture the reciprocal relation between Ca²⁺ binding and target binding. The modeling of CaM is often limited for a specific purpose to either bind the target or the calcium ions. As such, CaM is treated as a folded protein (Shepherd and Vogel, 2004; Yang et al., 2004; Zuckerman, 2004) or a folded protein with intrinsically disordered regions (Robustelli et al., 2018), where, in most cases, Ca²⁺ effects are ignored for simplicity (Spoel et al., 1996; Yang et al., 2001; Shepherd and Vogel, 2004; Robustelli et al., 2018). When Ca²⁺ is considered, it is treated as a particle with fixed charges as in an aqueous solution (Monticelli et al., 2008; Gong and Sun, 2017). When Ca²⁺ ions are implicitly included, their charges are often distributed to all the negatively charged residues present in the EF-hand motifs (Nandigrami and Portman, 2016) without any consideration of the coordination geometry of the Ca²⁺ ion, which is influenced by the conformation of a calcium-binding loop (Zhang et al., 2021). Our group has recently proposed a coarse-grained model to study the dynamics of CaM that accounts for both considerations (Wang et al., 2013; Zhang et al., 2017), but it is yet to reproduce the reciprocal relationship between calcium binding and target binding as both require intensive data-driven efforts.

One of the main challenges for developing an appropriate force field involving Ca²⁺ is that CaM is a structurally flexible protein about its central linker while the binding of Ca²⁺ to the two domains of CaM increases the rigidity of the local domains. A compromise between rigidity and softness has to be considered in order for CaM to accurately select, bind, and activate its binding targets. We, therefore, turned to the coarse-grained approach that adopts the Associative memory, Water mediated, Structure, and Energy Model (AWSEM) force field (Wang et al., 2011; Zhang et al., 2017) to fulfill these requirements. The next challenge is to properly include the Ca²⁺ ions in the force field of a coarse-grained model since this would allow us to understand the reciprocal relationship between calcium binding to CaM and binding of a target (Wang et al., 2013; Tripathi et al., 2015b). Although in separate studies, there have been development in AWSEM force fields on structurally flexible proteins (Wu et al., 2018) or on di-valent ions (Tsai et al., 2016), both features, however, have yet to be combined for modeling CaM. Particularly, the coordination chemistry of Ca²⁺ ions and the structural flexibility allowing CaM to flex according to its binding targets and surrounding environment is important in modeling the adaptive behavior of CaM (Wang et al., 2013; Liu et al., 2017a; Archer et al., 2019; Bekker et al., 2020). By taking into account the coordination chemistry of the Ca²⁺ ions as well as the flexible nature of the central linker of CaM, our proposed model for Ca²⁺-CaM elucidates the many-body effects of calcium binding on the geometrical shape of the calcium-binding loop and allows large conformational changes for binding various targets.

Materials and Methods

Coarse-Grained Modeling Using the AWSEM Force Field

We used the AWSEM force field (Davtyan et al., 2012; Tsai et al., 2016) to build the model of Ca²⁺-CaM. AWSEM is a transferable coarse-grained protein model, which uses three beads ($C_{\alpha }$, $C_{\beta }$, and O atom from the peptide bond) to represent each amino acid residue (except for glycine, which lacks $C_{\beta }$). The positions of all the rest of the other atoms along the backbone are deduced by assuming an ideal geometry of the system. The total energy function used in AWSEM is given in Eq. 1,

$V=V_{BB}+V_{PMF}+V_{DH}+V_{FM}(1)$

which is composed of two main terms: the physics-based terms, $V_{BB}+V_{PMF}+V_{DH}$, and the knowledge-based term, $V_{FM}$.

(a) The backbone term, $V_{BB}$, from Eq. 1, maintains the backbone geometry of protein. Its expression is given in Eq. 2,

$V_{BB}=V_{con}+V_{chain}+V_{\chi }+V_{rama}+V_{excl}.(2)$

$V_{con}$ and $V_{chain}$ represent the connectivity and chain terms, respectively. The former links neighboring residues, while the latter maintains ideal bond angles around the $C_{\alpha }$ atoms of each residue. The chirality potential, $V_{\chi }$, which is applied to all residues except for glycine, maintains the local residue chirality. $V_{rama}$ represents the Ramachandran potential, which biases the protein chain conformation toward the allowed Ramachandran regions. The excluded volume potential, $V_{excl}$, is used to avoid chain collapse and unphysical entanglements.

(b) The many-body potential of mean force $V_{PMF}$, from Eq. 1, takes into account the nature of the interacting residues, and its expression is given in Eq. 3:

$V_{\text{PMF}}=V_{\text{contact}}+V_{\text{burial}}+V_{\text{HB}}(3)$

The contact term $V_{\text{contact}}$ represents the pairwise additive and the many-body terms that consider interactions between residues far apart in sequence. The burial term $V_{\text{burial}}$ accounts for a particular residue’s type propensity. The hydrogen bond term $V_{\text{HB}}$ is composed of three other terms given in Eq. 4:

$V_{HB}=V_{\beta }+V_{P-AP}+V_{helical},(4)$

where $V_{\beta }$ and $V_{P-AP}$ are for the hydrogen bonding interactions in β-sheet conformations. The former stabilizes already formed β hydrogen bonds, while the latter allows a protein to undergo parallel and anti-parallel β-sheet conformations before the stabilization of the hydrogen bond. The helical term $V_{helical}$ ensures the formation of α-helices.

(c) The electrostatic interactions in solution with implicit solvent are described by the Debye–Hückel term (Tsai et al., 2016) $V_{DH}$ from Eq. 1. The expression is given in Eq. 5:

$V_{DH}=K_{Elec}{\displaystyle \sum }_{i<j}\frac{q_i{q}_j}{{\epsilon }_r{r}_{ij}}\text{exp}\left(-\frac{r_{ij}}{l_D}\right),(5)$

where $q_i$ and $q_j$ represent the charges of beads $i$ and $j$; $r_{ij}$ is the distance between the two beads; $K_{Elec}={\left(4\pi {\epsilon }_0\right)}^{-1}=332.24 kcalmo{l}^{-1}{e}^{-2}\mathit{Å}$; ${\epsilon }_r$ represents the dielectric constant of the media; and $l_D$ is the Debye–Hückel screening length, which is given by $l_D=\sqrt{\raisebox{1ex}{${\epsilon }_r{\epsilon }_0{k}_{B}T$}\!\left/ \!\raisebox{-1ex}{$2e^{2}I$}\right.}$. $k_B$ is the Boltzmann constant, $T$ is the temperature, $e$ represents the elementary electric charge, and $I$ is the ionic strength of the implicit solvent.

(d) $V_{FM}$ from Eq. 1, is a bioinformatic fragment memory potential that structurally biases short fragments of the protein chain, typically composed of 3–9 residues at a time, towards conformations that are based on “memory” structures. As listed in Table 1, the memory structures selected from the Protein Data Bank (PDB) were used to speed up the conformational search of the native states. Its expression is given in Eq. 6:

$V_{FM}=-{\lambda }_{FM}{\displaystyle \sum }_{m=1}^{60}.{\displaystyle \sum }_{n=1}^3{W}_n^m{\displaystyle \sum }_{i,j\mathrm{\ni }3\le |i-j|\le 9}{\gamma }_{ij}exp\left[-\frac{{\left(r_{ij}-r_{ij}^m\right)}^2}{2{\sigma }_{ij}^2}\right],(6)$

where the outer sum is over the aligned memory (from $m=1 to 60$), the sum in the middle with a variable $n$ is over the three segments of CaM ($n=1$ is N-domain, $n=2$ is central linker, and $n=3$ is C-domain), and the inner sum is over all possible pairs of $C_{\alpha }$ and $C_{\beta }$ atoms within the memory fragments that are separated by two or more residues; $|i-j|\le 9$ gives the maximum sequence separation of interacting residues, which is either the length of the memory or the maximum cutoff, whichever is shorter. $r_{ij}$ and $r_{ij}^m$ represent the instantaneous distance and the corresponding distance in the memory fragment between the atoms $i$ and $j$; ${\gamma }_{ij}$ is the residue type dependence interaction strength; ${\sigma }_{ij}$ represents the sequence separation dependent width. Its expression is given by ${\sigma }_{ij}=|i-j{|}^{0.15}$.

TABLE 1

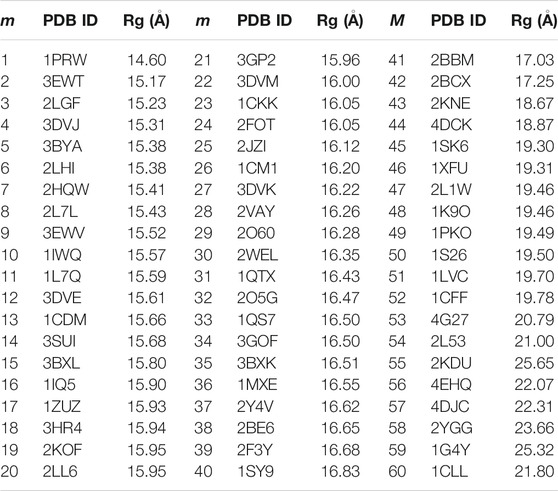
TABLE 1. The PDB IDs of the 60 non-redundant CaM memory structures for the AWSEM model and the Rg of the CaM. In the case of CaM complexes, only the coordinates of CaM were used for memory. m is the index for the memories.

We used 60 non-redundant structures of CaM taken from our prior study (Tripathi et al., 2015c) (Table 1), either free or in complex with the target peptides, to build the memory fragments for the coarse-grained model of CaM. We used the 60 sequence homologs of Ca²⁺-CaM since we are interested in studying the dynamics and the folding properties of CaM. We divided each memory into three segments: N-domain of CaM, from residue 5 to residue 76; the flexible central linker, from residue 77 through residue 81; and C-domain of CaM, from residue 82 to residue 147 (as illustrated in Figure 1). The weight of each segment is controlled by a memory weight parameter $W_n^m$ and a global parameter ${\lambda }_{FM}$ (Eq. 6). Because the central linker has its own memories of large variations in the structures, essentially it was modeled with more structural flexibility than the two globular domains of CaM.

We summarized CaM models using various values of ${\lambda }_{FM}$ and $W_n^m$ parameters in Table 2 for our molecular simulations. All other parameters for AWSEM were set by default as defined in the original ASWEM study (Davtyan et al., 2012; Tsai et al., 2016). The parameters of the default setting are also provided in the Supplemental Information (SI 1).

TABLE 2

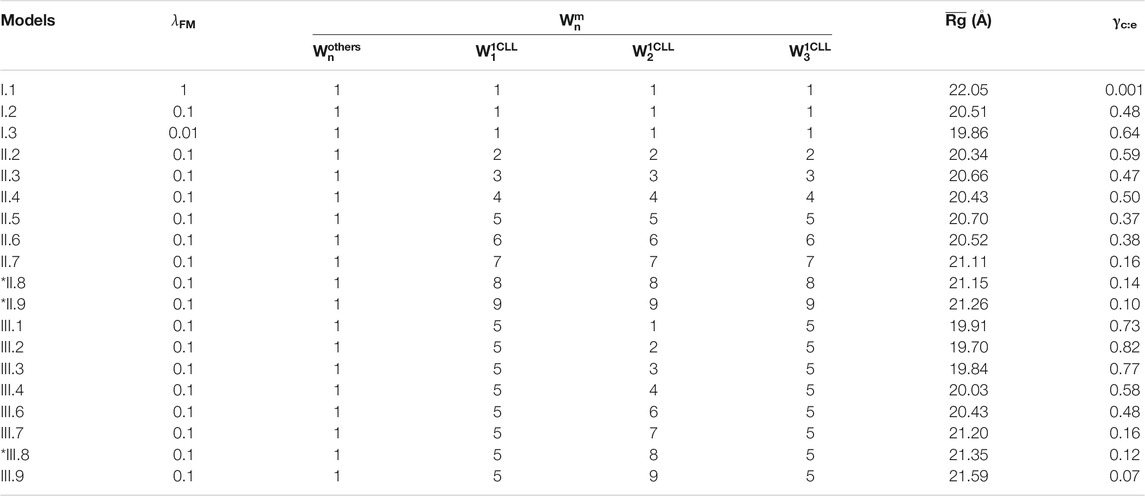
TABLE 2. Summary of Ca²⁺-CaM models with different values of the global and local memory weight and the average Rg ($\overline{\mathbf{Rg}}$) and the ratio between the collapsed and extended states (γ_c:e) from the umbrella sampling simulations. The models that best reproduce experimental results from our simulations are marked with *. The experimental measured Rg = 20.0 ∼ 22.5 Å and γ_c:e ∼ 0.11.

Modeling Ca²⁺ Ions in ASWEM Force Field

Calcium-binding proteins in most cases contain the EF-hand calcium-binding motif which is formed by the pentagonal bipyramidal geometry (Figure 3; Supplementary Figure S1 in the SI) (Drake et al., 1997; Yang et al., 2002). The literature on modeling those proteins, in general, does not clearly explain how Ca²⁺-binding effects are considered during the simulations. We developed an implicit Ca²⁺ model that evenly splits the Ca²⁺ charges to a selection of residues. Partial charges on the sidechain beads of the negatively charged residues that coordinate Ca²⁺ collectively in the Ca²⁺ binding loops (Figure 3) were adjusted to reflect the Ca²⁺- binding effect (Table 3). To note, charges on those acidic residues which do not coordinate (Ca²⁺) remain intact (−1 e). This simple approach incorporates the coordination geometry of the Ca²⁺ and allows us to improve the modeling of many-body effects in the local Ca²⁺ binding loops which furthermore controls the open/close state of the helix-loop-helix EF-hand and the global conformation of calmodulin.

FIGURE 3

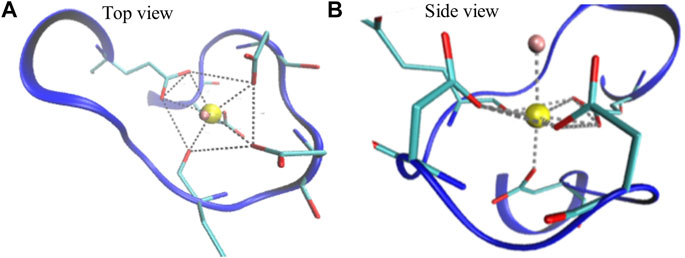
FIGURE 3. Illustration of a Ca²⁺ binding loop at the fourth EF-hand of CaM (PDB ID: 1CLL). The pentagonal bipyramidal geometry of the Ca²⁺ coordination is represented with the dotted lines in the top view (A) and side view (B). The red sticks linked with the dotted lines represent oxygen atoms that participate in coordination. The water molecule, shown in pink, completes the spherical coordination through hydrogen bonding.

TABLE 3

TABLE 3. The adjusted partial charges of the negatively charged residues participated in calcium coordination in the four calcium-binding loops of CaM. The amino acid sequences of the calcium-binding loops are provided as a reference. The subscript indices stand for the positions of the starting/ending residues in the CaM sequence. Underscored residues are the selected amino acids with negative charges as shown in the third column. We adjusted the partial charges on the sidechain beads of those residues based on the bipyramidal pentagonal coordination geometry of the calcium ion.

In this study, we compared the abovementioned approach (approach III) with two other calcium models:

I. Splitting the Ca²⁺ charges evenly to the neighboring negatively charged residues (Tsai et al., 2016).

II. Splitting the Ca²⁺ charges evenly to the residues that participate with the calcium coordination and the radius of gyration of the sidechain beads are constrained by a stiff harmonic potential with a force constant of 30 kcal/mol/Ų.

III. The same with approach II except that the harmonic constraint is removed.

Comparing to approach I of Ca²⁺ in AWSEM (Tsai et al., 2016), in approach III calcium charges were split according to the coordination chemistry of calcium; comparing to approach II, in approach III more degrees of freedom to the Ca²⁺ coordination residues allow sampling of more different conformations of CaM.

Simulation Details

We performed the coarse-grained simulations with the open-source MD package LAMMPS, in which AWSEM code was implemented (Davtyan et al., 2012). We used the periodic boundary conditions on the cubic box of 400 Å on each side so that even unfolded CaM can fit in the box. Initial velocities were chosen randomly from a Boltzmann distribution with the average squared velocity equal to 3 ${\text{k}}_B$T/m, where ${\text{k}}_B$ is the Boltzmann constant, m is the mass, and the temperature is T. We also used the cutoff distance of 3.5 Å and κ (inverse of the Debye length) = 0.0127 Å⁻¹ in the electrostatic term.

Simulated annealing: firstly, we denatured the protein at 450 K using the initial structure built from the crystal structure (PDB ID: 1CLL) (Chattopadhyaya et al., 1992); then, we performed simulated annealing on Ca²⁺-CaM by cooling down the system to a low temperature (280 K) for 2,000,000 time steps for each value of ${\lambda }_{FM}$ (models I.1–3 in Table 2).

Production simulation: we employed the umbrella sampling (US) method (Roux, 1995) to evaluate the thermodynamic properties of Ca²⁺-CaM using different memory parameters. We conducted the production simulations in canonical ensemble (NVT) at the constant temperature of 300 K. Radius of gyration (Rg) of Ca²⁺-CaM was used as the reaction coordinate, which was restrained by a harmonic potential $E_{Restr}^i=\frac{1}{2}\text{k}{\left({\text{Rg}}^{\text{i}}-{\text{Rg}}_0^{\text{i}}\right)}^2$ with a force constant k = 50 kcal/Ų. The equilibrium positions of the harmonic potential ${\text{Rg}}_0$ range from 13.00 Å to 26.00 Å with a bin size of 0.25 Å, making up a total of 53 windows (i = 0, 1, 2, …, 52). The setup of the force constant and the equilibrium positions of the windows is justified by the fluctuations of Rg around the corresponding equilibrium positions as well as the overlap in the Rg distribution between neighboring windows, which are provided in Supplementary Figures S4–S5, respectively, in the SI. For each window, 2,000,000 time-steps of constrained molecular simulations were conducted using different initial conditions. To generate the initial structures at each window for the US simulations, molecular dynamics simulations were carried out for the Ca²⁺-CaM from the crystal structure of CaM (PDB ID: 1CLL, in the coarse-grained model) at a temperature T = 300 K. Structures with Rg closest to ${\text{Rg}}_0^{\text{i}}$ were selected as the initial configurations. A set of 5 US simulations were carried out at each window with the same initial configuration and different random initial velocities. The integration time step is 2 fs. It is important to note that with the smoothed CG potential, the realistic time represented by a time step is longer than 2 fs. Coordinates and Rg were recorded every 1,000 time steps for analyses, making up 10, 000 frames of data for analysis at each window. We analyzed the data using a multi-state Bennett acceptance ratio (MBAR) estimator with the pymbar program (Shirts and Chodera, 2008).

Data Analysis

We described the conformational changes of the Ca²⁺-CaM during the simulations by calculating the radius of gyration ($\text{R}\text{g}$) and the pairwise comparison (${\text{Q}}_w$) from the crystal structure (PDB ID: 1CLL).

Radius of Gyration ($\mathbf{R}\mathbf{g}$)

Rg describes the compactness of the protein, and its definition is given in Eq. 7:

$\text{R}\text{g}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\text{m}}_i\Delta r_i^2}{{{\displaystyle \sum }}_{i=1}^N{\text{m}}_i}}.(7)$

In the case of PDB structures, ${\text{m}}_i$ is the mass of the $i^{th}$ atom and $\Delta {\text{r}}_i$ is the distance between the $i^{th}$ atom and the center of mass of the system. In the case of coarse-grained structures, only the C_α beads are used, ${\text{m}}_i$ is the mass of the C_α bead of the $i^{th}$ residue, and $\Delta {\text{r}}_i$ is the distance between the C_α bead of the $i^{th}$ residue and the center of mass of the system.

Pairwise Comparison

$Q_w$ measures the degree of similarity of conformations from the trajectories with respect to the native structure through the pairwise comparison. In other words, it compares the pairwise distances of $C_{\alpha }$ atoms (beads) among the residues in each instantaneous structure to counterpart in the native structure. This value is normalized to 1, with a higher value corresponding to the greater similarity to the native structure. In this case, $Q_w$ is the extended crystal structure of Ca²⁺-CaM (PDB ID: 1CLL), $Q_w$ = 1. The expression of the order parameter $Q_w$ is given in Eq. 8:

$Q_w=\frac{2}{\left(N-2\right)\left(N-3\right)}{\displaystyle \sum }_{|j-i|\ge 2}exp\left[-\frac{{\left(r_{ij}-r_{ij}^m\right)}^2}{2{\sigma }_{ij}^2}\right],(8)$

where $N$ is the total number of residues, $r_{ij}$ represents the instantaneous distance between $C_{\alpha }$ atoms (beads) of residues i and j, $r_{ij}^m$ is the same distance in the reference structure (PDB ID: 1CLL), and ${\sigma }_{ij}$ is obtained from the following relation ${\sigma }_{ij}={\left(1+|i-j|\right)}^{0.15}$.

Definition of Collapsed and Extended Conformations of CaM

In our analyses, we used the parameter Rg to define a collapsed or extended conformation. The Rg cutoff was set according to the potential of mean force (PMF) and distribution of Rg in our simulations (Figures 4–8). A collapsed conformation is defined if Rg < 18.5Å; otherwise, an extended conformation is defined.

FIGURE 4

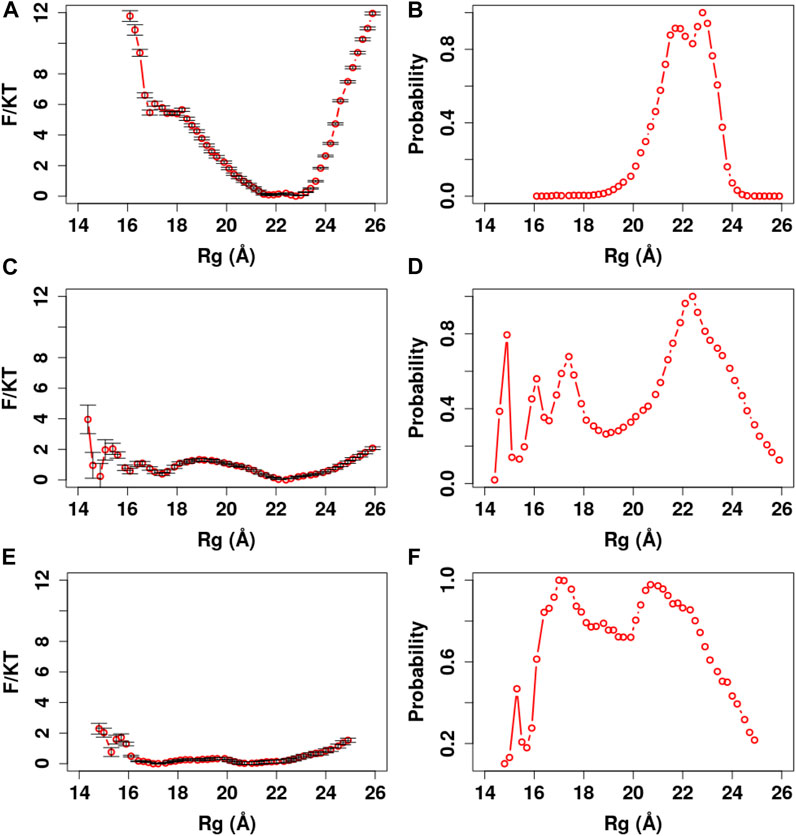
FIGURE 4. PMF and Rg distribution of the Ca²⁺-CaM models using the global memory weight of different order of magnitudes. The memory weight parameters of the Ca²⁺-CaM models are listed in Table 2 (model I; ${\lambda }_{FM}$ = 1, 0.1, 0.01, and $W_n^{\text{m}}$ = 1). (A, C, E) The reweighted free energy profile as a function of Rg from US simulations with ${\lambda }_{FM}$ = 1, 0.1, 0.01, respectively. (B, D, F) The probability distribution as a function of Rg. The standard errors in the PMF are provided.

FIGURE 5

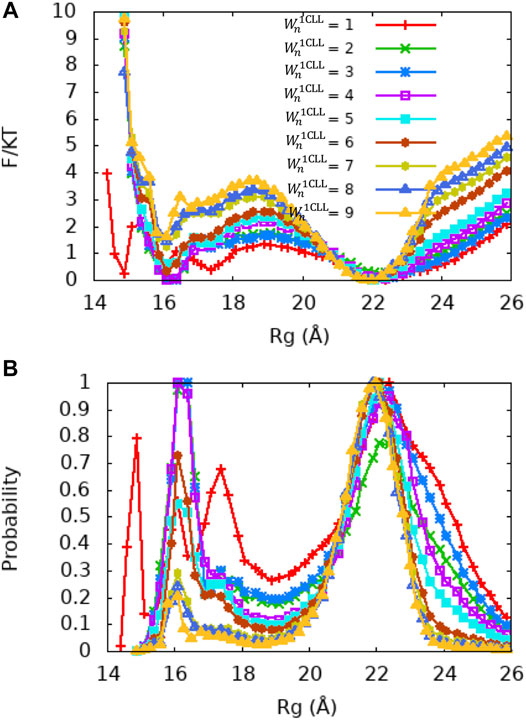
FIGURE 5. PMF and Rg distribution of the Ca²⁺-CaM models for different values of the local memory weight $W_n^{1\text{CLL}}$ (n = 1, 2, 3). The memory weight parameters of the Ca²⁺-CaM models are listed in Table 2 (model II; ${\text{λ}}_{FM}=0.1$, $W_n^{\text{others}}$ = 1, and $W_n^{1\text{CLL}}=1-9$). (A) The reweighted free energy profile as a function of Rg from US simulations (B) and the probability distribution as a function of Rg. The standard errors are too small to show and are provided in Figures S6 in the SI.

FIGURE 6

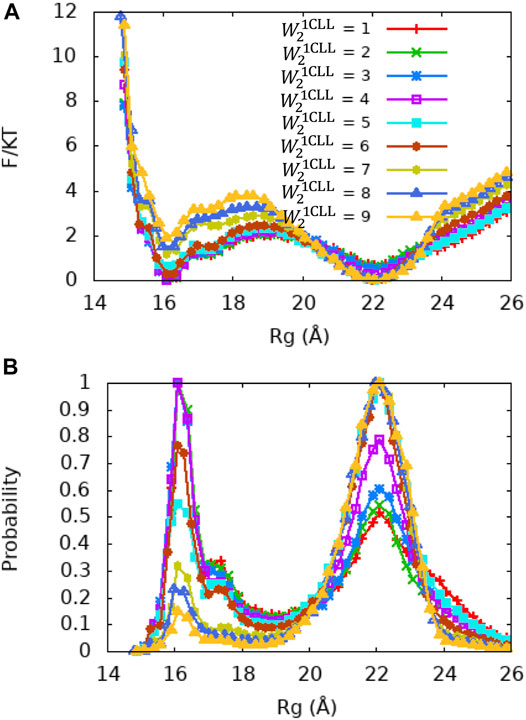
FIGURE 6. PMF and Rg distribution of the Ca²⁺-CaM models for different values of the local memory weight $W_n^{1\text{CLL}}$ (n = 2) for the central linker of CaM. The memory weight parameters of the Ca²⁺-CaM models are listed in Table 2 model III; ${\text{λ}}_{FM}=0.1$, $W_n^{\text{others}}$ = 1, $W_{\mathrm{1,3}}^{1\text{CLL}}=5$, $W_2^{1\text{CLL}}=1-9$. (A) The reweighted free energy profile as a function of Rg from US simulations (B) and the probability distribution as a function of Rg. The standard errors in the PMF are provided in Figure S7 in the SI.

FIGURE 7

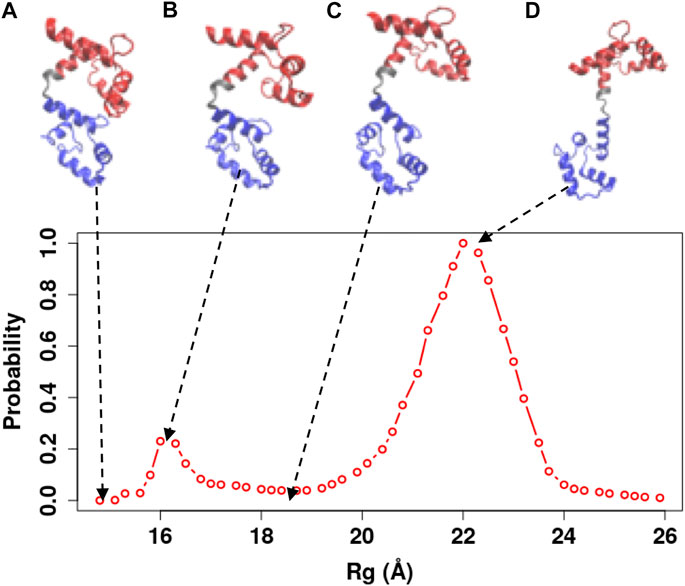
FIGURE 7. Representative snapshots of the Ca²⁺-CaM model obtained from our simulations. The model that best reproduces experimental measurements was used (${\text{λ}}_{FM}=0.1$, $W_n^{\text{others}}$ = 1, $W_{\mathrm{1,3}}^{1\text{CLL}}=5$, and $W_2^{1\text{CLL}}=8$). (A) The completely collapsed conformation of the Ca²⁺-CaM; (B) the collapsed conformation; (C) the intermediate conformation; and (D) the extended conformation. These structures are represented along the probability distribution of Rg.

FIGURE 8

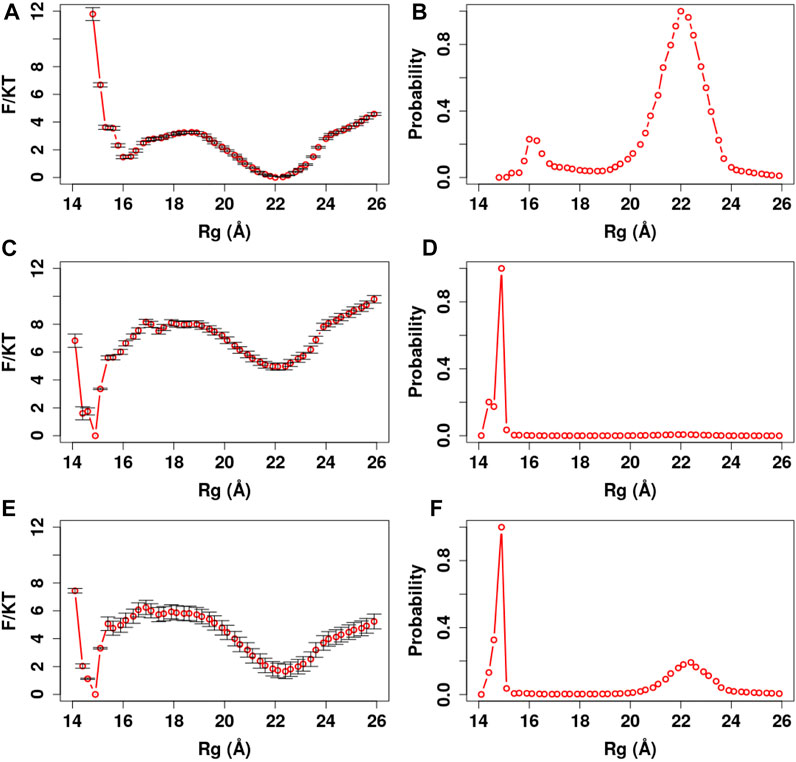
FIGURE 8. PMF and Rg distribution of the Ca²⁺-CaM for different Ca²⁺ models. The optimized memory parameters for the Ca²⁺-CaM model were used (${\text{λ}}_{FM}=0.1$, $W_n^{\text{others}}$ = 1, $W_{\mathrm{1,3}}^{1\text{CLL}}=5$, and $W_2^{1\text{CLL}}=8$). The three charge models are described in the Method section. (A) The reweighted free energy profile as a function of Rg from the US simulations (B) and the probability distribution as a function of Rg. The standard errors in the PMF are provided.

Results and Discussion

The goal is to create a computational model for CaM accommodating its several key functions including divalent ion binding, conformational dynamics, and target recognition. In order to achieve this, we adopted a pool of 60 CaM or CaM complex structures from our previous study (Tripathi et al., 2015c) representing full-length CaM without mutations and its complex with 24 unique target proteins/peptides. As stated in the Materials and Methods Simulation Details, our approach is to tune the two scaling parameters ${\lambda }_{FM}$ and $W_n^m$ to adjust the global and each segment of the multiple memories, respectively, relative to other terms in the total energy function. After optimizing the memory parameters, three models of calcium are compared to describe the divalent ion binding.

Each of the 60 memories has a specific conformation of calmodulin which could be helpful in target recognition and target selection; therefore, clustering the 60 memories may leave out important conformations that accommodate recognition of a specific target protein. Potentially, there could be as many as 181 fragment memory parameters to be determined in the most complicated scenario. However, in the general practice of AWSEM modeling, a search in the available determined structures in the database according to the match in the desired amino acid sequence is conducted to generate a library of memory structures. Therefore, to avoid excessive tuning of the parameters, the individual memory weight W_n^m is kept as a constant default value. Because the unbound extended form of the Ca²⁺/CaM (PDB code: 1CLL) was found to be most dominant experimentally, we adjusted its local memory weight parameter correspondingly, while keeping others the default $W_n^{others}=1$. The actual parameters we tuned eventually reduce to ${\lambda }_{FM}$ and $W_n^{1CLL}(n=1, 2, 3$ to represent N-domain, central linker, and C-domain of the protein).

Parameterization of our CG model was guided by the existing following experimental measures: $\text{R}\text{g}$ of Ca²⁺-CaM spans from 20.0 to 22.5 Å measured by small angle X-ray scattering (SAXS) experiments (Seaton et al., 1985; Heidorn and Trewhella, 1988; Kataoka et al., 1991); in addition, the population of CaM’s collapsed conformation is about 10% measured by nuclear magnetic resonance (NMR) experiments (Anthis et al., 2011) (i.e., the ratio between the population of the collapsed conformation and that of the extended population is ${\gamma }_{c:e}\sim 0.11$).

The Global Parameter Weight Controls the Energy Barrier Between Extended and the Collapsed States of Ca²⁺-CaM

Firstly, we determined the magnitude of the fragment memory interaction by investigating its effect on the folding properties of Ca²⁺-CaM. We carried out simulated annealing using the unfolded structure of the Ca²⁺-CaM ($Q_w\sim 0.2$ as shown in Supplementary Figure S2 in the SI) with three orders of magnitudes of the global scaling parameter ${\lambda }_{FM}$ = 1, 0.1, 0.01. At ${\lambda }_{FM}=1$, the system transitions abruptly from the unfolded to the folded state (Supplementary Figures S3A, S3B) in the SI; at ${\lambda }_{FM}=0.1$, smooth transitions of Ca²⁺-CaM from the unfolded to the folded structure were observed with $Q_w$ reaching a maximum value of 0.67 (Supplementary Figures S3C, S3D) in the SI; at ${\lambda }_{FM}=0.01$, the maximum value of $Q_w$ was less than 0.55 and the total energy of the system did not stabilize on a long timescale (Supplementary Figures S3E, S3F) in the SI.

In addition, we carried out US simulations to evaluate thermodynamic properties of Ca²⁺-CaM with the global scaling parameter in three orders of magnitudes ${\lambda }_{FM}$ = 1, 0.1, and 0.01, while keeping the local memory scaling parameters $W_n^m$ = 1. The PMF and the probability distribution as a function of $\text{R}\text{g}$ were computed using the MBAR estimator (Figure 4) and the average Rg ($\overline{\text{Rg}}$) and the ratio between the population of collapsed conformation and that of the extended conformation (γ_c:e) were evaluated from the PMF. For ${\lambda }_{FM}=1$, Ca²⁺-CaM mostly samples the extended conformations (with Rg ∼ 21.5 to 22.5 Å) and the free energy barrier between the extended and collapsed conformations is quite large (∼6 k_BT); therefore, the system lacks the capacity of shifting between multiple conformations. For ${\lambda }_{FM}=0.1$, there are four minima in the PMF of Ca²⁺-CaM with Rg ranging from 15 to 22 Å (Figure 4), and the free energy barrier between the collapsed states and the extended state is ∼ k_BT; the $\overline{\text{Rg}}$ of Ca²⁺-CaM is within the experimental range ($\overline{\text{Rg}}$= 20.51 Å); however, γ_c:e (∼ 0.48) is much higher than the experimental one (∼ 0.11) (Anthis et al., 2011). It is worthwhile to note that the minimum at Rg ∼ 15 Å resembles a completely collapsed structure as found in our previous study (Homouz et al., 2009). For ${\lambda }_{FM}=0.01$, there are noticeably two minima located at Rg ∼ 17 Å and Rg ∼ 20.5 Å, sampling a somewhat collapsed conformation and a less extended conformation (comparing with ${\lambda }_{FM}$ = 1, 0.1) respectively with free energy barrier < k_BT. $\overline{\text{Rg}}$ = 19.86 Å, below the experimentally measured Rg range (Seaton et al., 1985; Heidorn and Trewhella, 1988; Kataoka et al., 1991) and γ_c:e (∼ 0.64) is much higher than the experimental value (Anthis et al., 2011).

In summary, the global memory parameter ${\lambda }_{FM}$ is effective for controlling the sampling of the collapsed and extended conformations of CaM as well as reproducing the averaged Rg. A large value of the scaling parameter ${\lambda }_{FM}$ might tend to limit the malleability of Ca²⁺-CaM in favor of the extended conformation (initial configuration of the simulations). Decreasing ${\lambda }_{FM}$ leads to an increase in γ_c:e and a decrease in $\overline{\text{Rg}}$. This is because decreasing the weight of the memory potential favors the hydrophobic interactions among residues of the two domains of Ca²⁺-CaM and reduces the free energy barrier between the two major conformations of Ca²⁺-CaM (extended and collapsed forms); consequently, the system becomes more flexible and can shift easily between the extended and collapsed conformations.

Single Memory Optimization Captures the Dynamics of Ca²⁺-CaM

Although the global fragment memory weight of ${\lambda }_{FM}=0.1$ resulted in a system that can sample the major two conformations of the Ca²⁺-CaM and $\overline{\text{Rg}}$ is within the experimental range (Seaton et al., 1985; Heidorn and Trewhella, 1988; Kataoka et al., 1991), the ratio between the collapsed and the extended populations γ_c:e did not match the experimentally measured value (Anthis et al., 2011). Therefore, finer tuning of the local memory parameters W_n^m is required for reproducing γ_c:e in the abovementioned NMR experiment (Anthis et al., 2011).

Since the crystal structure of Ca²⁺-CaM (PDB ID: 1CLL) demonstrates a value of Rg that is closest to the experimentally measured values and does not bind a target, we first examined whether variation in single memory weight of this structure ($W_n^{1\text{CLL}}$) could give rise to the conformational changes of the Ca²⁺-CaM. We performed a series of molecular simulations using US with $W_n^{1\text{CLL}}$ = 1, 2, … , 9 and maintaining ${\lambda }_{FM}=0.1$ and $W_n^{\text{others}}=1$ (Table 2 Model II). From the PMF profiles and the probability distributions shown in Figure 5, we show that the Ca²⁺-CaM samples both the extended and collapsed conformations in all the models we explored. In general, with the increase of $W_n^{1\text{CLL}}$, stability of the collapsed state decreases and the barrier between the extended and collapsed states increases, hence an increase in $\overline{\text{Rg}}$ and decrease in γ_c:e. Specifically, without tuning any other local memory weights, $W_n^{1\text{CLL}}=8,9$, and $\overline{\text{Rg}}$and γ_c:e match with experimental values (Seaton et al., 1985; Heidorn and Trewhella, 1988; Kataoka et al., 1991; Anthis et al., 2011) quite well (Table 2).

Central Linker of the Ca²⁺-CaM Determines the Conformational Change of Ca²⁺-CaM

Although the X-ray crystallography experiment shows that the central linker that connects the two domains of Ca²⁺-CaM has a helical structure, numerous studies including NMR have shown its high flexibility in solution. To explore the relationship between the flexible linker and the dynamics of Ca²⁺-CaM in more detail, we carried out a series of US molecular simulations with the memory weight of the central linker of the Ca²⁺-CaM, $W_2^{1\text{CLL}}=\mathrm{1,2},\dots ,9$ while keeping ${\lambda }_{FM}=0.1$ and $W_n^{\text{others}}$ = 1, and $W_n^{1\text{CLL}}$(n = 1,3) = 5 (Table 2 Model III). As shown in the PMF profiles (Figure 6), $W_2^{1\text{CLL}}$ shows a similar effect on the thermodynamic properties of the Ca²⁺-CaM; with the increase of $W_2^{1\text{CLL}}$, stability of the collapsed state decreases and the barrier between the extended and collapsed states increases, hence an increase in $\overline{\text{Rg}}$ and decrease in γ_c:e (Table 2). This is likely because the two globular domains of CaM consist of stable secondary structures (mostly α-helices) and the involving fragments are fully represented and heavily weighted by $W_n^{\text{others}}$ (n = 1, 3) in other 59 memories, whereas the central linker connecting the two domains of CaM is modeled as an intrinsically disordered peptide; hence, the stability of the Ca²⁺-CaM is more sensitive to the parameter $W_2^{1\text{CLL}}$ corresponding to the central linker of CaM. Therefore, tuning $W_n^{1\text{CLL}}$ for the whole CaM is mostly equivalent to tuning $W_2^{1\text{CLL}}$ for the central linker. This can also be seen in the three highlighted models in Table 2, which reproduce the experimentally measure Rg and γ_c:e well (Seaton et al., 1985; Heidorn and Trewhella, 1988; Kataoka et al., 1991; Anthis et al., 2011).

In order to illustrate the conformational changes of Ca²⁺-CaM in solution, we selected representative snapshots from the simulations using the Ca²⁺-CaM model with ${\lambda }_{FM}=0.1$, $W_n^{\text{others}}$ = 1, $W_{\mathrm{1,3}}^{1\text{CLL}}$ = 5, and $W_2^{1\text{CLL}}=8$, as highlighted in Table 2. The unstructured central linker of the extended structure (Figure 7D) unwraps and bends to allow the two domains of the Ca²⁺-CaM to interact with each other, as shown in Figure 7A–C). Figure 7A represents a completely collapsed structure similar to the compact structure (PDB ID: 1PRW) or in CaM-target complexes, however, the chance for Ca²⁺-CaM to sample this structure is low. Figure 7B represents a collapsed structure. Figure 7C represents a structure in the transition state between the collapsed and extended states.

Coordination Geometry Is Necessary for Representing Divalent Ions in Coarse-Grained Models

Although it can be tempting to use the available intrinsically disordered protein (IDP) force fields such as AWSEM-IDP (Wu et al., 2018) (due to the disordered nature of the central linker) to study the dynamics of Ca²⁺-CaM, the heterogeneity of CaM needs to be considered. The high rigidity of the two domains upon calcium-binding limits the use of IDP force fields, thus making the computational investigation of CaM even more complex.

We further manifest the importance of coordination chemistry by comparing the three approaches to modeling Ca²⁺ as described in Method Modeling Ca²⁺Ions in ASWEM Force Field in Figure 8. With approach I, the Ca²⁺ charges were evenly distributed to all the negatively charged residues (Tsai et al., 2016) and Ca²⁺-CaM presents an equal probability of sampling the completely collapsed conformation and the extended conformation (γ_c:e = 1.01). $\overline{\text{Rg}}$∼ 18.64 Å is well below the experimental values (Seaton et al., 1985; Heidorn and Trewhella, 1988; Kataoka et al., 1991). With approach II by applying constraints on the Ca²⁺ loops, Ca²⁺-CaM samples favorably the completely collapsed conformation with Rg ∼ 15 Å (γ_c:e = 22.87). Consequently, the binding selectivity of Ca²⁺-CaM could be impeded due to the lack of the flexibility of calcium-binding loop in the system. Being confined in this completely collapsed conformation, Ca²⁺-CaM lacks the capacity of recognizing, binding, and activating the targets. With approach III (w/coordination chemistry), Ca²⁺-CaM samples both extended and collapsed conformations while preferring the former.

Force field development for Ca²⁺ ion is mostly limited to the aqueous solution rather than in protein-bound environments (Probst et al., 1985). One of the main challenges in computer simulations of macromolecules remains the development of force fields with the appropriate implementation of the metal ion (Gifford et al., 2007; Duarte et al., 2014; Li and Merz, 2017; Liao et al., 2017; Fracchia et al., 2018; Huang and MacKerell, 2018). Due to the high sensibility of the molecules upon bivalent metal ion binding, taking the Ca²⁺-induced conformational changes in CaM as an example, a lack of appropriate approach to model its effects on the molecules could impede the capability of the target molecule to transduce its signals, thus, leading to the inactivation and/or malfunction of the signaling pathways (Gaertner et al., 2004; Wang et al., 2011).

Most calcium-binding proteins such as CaM contain the EF-hand (helix-loop-helix) structural domain as the calcium-binding motif (Lepšík and Field, 2007; Capozzi et al., 2006). In this motif, the calcium ion is coordinated in a pentagonal bipyramidal configuration (Figure 3). The canonical positions 1, 3, 5, 7, 9, and 12 represent the positions of the residues involved in calcium coordination (Clapham, 2007; Gifford et al., 2007). Table 3 shows simple and efficient ways to consider the effect of the Ca²⁺ ions in the force field, where we distributed its charges to the negatively charged residues present in the pentagonal bipyramidal configuration. In contrast to other approaches where the harmonic constraint is applied to the calcium coordinated residues in the loop, or the charges are distributed to all the negatively charged residues in the system, our approach (III) not only considers the heterogeneity of CaM but also takes into account the coordination chemistry of calcium by giving the coordinated residues the freedom to participate to the different conformations of the system, which are relevant to the target selectivity of Ca²⁺-CaM.

The Distribution of Ca²⁺-CaM Conformations Is Beyond the Extended and the Collapsed Structures

Ca²⁺-CaM undergoes substantial conformational changes upon binding to a target, in most cases, the Ca²⁺-CaM develops a collapsed form that wraps around the target peptide with the two domains coming in proximity (Meador et al., 1993; Westerlund and Delemotte, 2018; Tidow and Nissen, 2013). For various CaMBT molecules, CaM undergoes structural rearrangement to different degrees during the complex formation. Thus, the collapsed conformation of the intact Ca²⁺-CaM (e.g., Figure 7) assembles a vast variety of structures including a structure that resembles the compact conformation of a specific Ca²⁺-CaM/target complex (Figure 1D). This was also observed by X-ray crystallography (Fallon and Quiocho, 2003) and NMR studies (Anthis et al., 2011). This collapsed structure of the Ca²⁺-CaM (Figure 7A) confirms the earlier experiments that show multiple conformations of the Ca²⁺-CaM in solution, as well as the interaction between opposing domains of CaM (Johnson, 2006; Anthis et al., 2011; Her et al., 2018).

Previous studies have shown that the high flexibility of the linker in solution allows the two domains to independently undergo multiple conformations (Malmendal et al., 1999; Chou et al., 2001; Barton et al., 2002; Hoeflich and Ikura, 2002; Komeiji et al., 2002; Park et al., 2008; Wu et al., 2012). Structural differences can be inferred from crystallography, but the dynamical insights are pivotal to understand Ca²⁺-CaM interactions with the targets. Experimental and computational studies including NMR spectroscopy, X-ray crystallography, small-angle X-ray scattering, and molecular dynamics simulations unveil important details of the dynamics of Ca²⁺-CaM and paint a clear portrait of its conformational motions at the origin of the binding selectivity. The available structures of Ca²⁺-CaM show that it crystallizes into two major conformations: extended (Chattopadhyaya et al., 1992) and collapsed (Fallon and Quiocho, 2003), while in solution, Ca²⁺-CaM adopts multiple conformations (Project et al., 2006; Park et al., 2008; Wu et al., 2012; McCarthy et al., 2015; Fernandes and Oliveira-Brett, 2017; Jing et al., 2017; Her et al., 2018; Villalobo et al., 2018; Shimoyama, 2019). The conformational changes of CaM upon Ca²⁺ binding have been under intensive investigation (Weinstein and Mehler, 1994; Gilli et al., 1998; Project et al., 2006; Park et al., 2008; Wu et al., 2012). The goal of such studies is to understand the molecular mechanism that leads to the Ca²⁺-CaM target binding selectivity. How Ca²⁺-CaM interacts with its CaMBTs is of major interest. This presented community model of CaM allows transitions between a rich set of states beyond the two major extended or the collapsed conformations and are applicable for various Ca²⁺ bound conditions; this further could improve the interpretation of how target binding may tune CaM’s affinity for Ca²⁺ ions (Gaertner et al., 2004; Zhang et al., 2017).

Conclusion

Here, we developed a “community model” of CaM that samples various conformations of CaM, incorporates various calcium-binding states, and carries the memory of binding with various targets. The model would be useful for studying the reciprocal relationship interplay between target binding and calcium binding through CaM’s conformational changes as the next step. We demonstrated a workflow of the development of the AWSEM model for CaM guided by physical knowledge and experimental data. Should new structures of CaM (or CaM/CaMBT complex) structures become available, the model can be easily expanded by including these structures in the memory library.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

MC conceived and designed the research. JN performed the simulations and prepared the figures. MC, JN, PZ, JE, WL, and KK performed data analysis and wrote the article. PW provided critical advice. All authors contributed to the manuscript, read, and approve the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Drs. Neal M. Waxham, Piotr Cieplak, and Qian Wang for stimulating discussions. The work was supported by a grant from the National Institutes of Health (2R01GM097553). MSC and PGW are grateful for the funding support from the National Science Foundation (PHY2019745). PGW is grateful for the support from the D. R. Bullard-Welch Chair at Rice University, Grant C-0016. The authors acknowledge the computing resources from the computing clusters uHPC and Sabine at the University of Houston.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2021.661322/full#supplementary-material

References

Anthis, N. J., Doucleff, M., and Clore, G. M. (2011). Transient, Sparsely Populated Compact States of Apo and Calcium-Loaded Calmodulin Probed by Paramagnetic Relaxation Enhancement: Interplay of Conformational Selection and Induced Fit. J. Am. Chem. Soc. 133 (46), 18966–18974. doi:10.1021/ja2082813

PubMed Abstract | CrossRef Full Text | Google Scholar

Archer, C. R., Enslow, B. T., Taylor, A. B., De la Rosa, V., Bhattacharya, A., and Shapiro, M. S. (2019). A Mutually Induced Conformational Fit Underlies Ca2+-Directed Interactions between Calmodulin and the Proximal C Terminus of KCNQ4 K+ Channels. J. Biol. Chem. 294 (15), 6094–6112. doi:10.1074/jbc.ra118.006857

PubMed Abstract | CrossRef Full Text | Google Scholar

Barton, N. P., Verma, C. S., and Caves, L. S. D. (2002). Inherent Flexibility of Calmodulin Domains: A Normal-Mode Analysis Study. J. Phys. Chem. B 106 (42), 11036–11040. doi:10.1021/jp026692q

CrossRef Full Text | Google Scholar

Bekker, G. J., Fukuda, I., Higo, J., and Kamiya, N. (2020). Mutual Population-Shift Driven Antibody-Peptide Binding Elucidated by Molecular Dynamics Simulations. Sci. Rep. 10 (1), 1406. doi:10.1038/s41598-020-58320-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Berchtold, M. W., and Villalobo, A. (2014). The many Faces of Calmodulin in Cell Proliferation, Programmed Cell Death, Autophagy, and Cancer. Biochim. Biophys. Acta (Bba) - Mol. Cel Res. 1843 (2), 398–435. doi:10.1016/j.bbamcr.2013.10.021

CrossRef Full Text | Google Scholar

Berridge, M. J. (2006). Calcium Microdomains: Organization and Function. Cell Calcium 40 (5), 405–412. doi:10.1016/j.ceca.2006.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bootman, M. D. (2012). Calcium Signaling. Cold Spring Harbor Perspect. Biol. 4 (7). doi:10.1101/cshperspect.a011171

PubMed Abstract | CrossRef Full Text | Google Scholar

Capozzi, F., Casadei, F., and Luchinat, C. (2006). EF-hand Protein Dynamics and Evolution of Calcium Signal Transduction: an NMR View. J. Biol. Inorg. Chem. 11 (8), 949–962. doi:10.1007/s00775-006-0163-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Carafoli, E. (2002). Calcium Signaling: A Tale for All Seasons. Proc. Natl. Acad. Sci. 99 (3), 1115–1122. doi:10.1073/pnas.032427999

CrossRef Full Text | Google Scholar

Chattopadhyaya, R., Meador, W. E., Means, A. R., and Quiocho, F. A. (1992). Calmodulin Structure Refined at 1.7 Å Resolution. J. Mol. Biol. 228 (4), 1177–1192. doi:10.1016/0022-2836(92)90324-d

PubMed Abstract | CrossRef Full Text | Google Scholar

Chin, D., and Means, A. R. (2000). Calmodulin: a Prototypical Calcium Sensor. Trends Cel Biol. 10 (8), 322–328. doi:10.1016/s0962-8924(00)01800-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Chou, J. J., Li, S., Klee, C. B., and Bax, A. (2001). Solution Structure of Ca(2+)-Calmodulin Reveals Flexible Hand-like Properties of its Domains. Nat. Struct. Biol. 8 (11), 990–997. doi:10.1038/nsb1101-990

PubMed Abstract | CrossRef Full Text | Google Scholar

Clapham, D. E. (2007). Calcium Signaling. Cell 131 (6), 1047–1058. doi:10.1016/j.cell.2007.11.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis, T. N., and Thorner, J. (1989). Vertebrate and Yeast Calmodulin, Despite Significant Sequence Divergence, Are Functionally Interchangeable. Proc. Natl. Acad. Sci. 86 (20), 7909–7913. doi:10.1073/pnas.86.20.7909

PubMed Abstract | CrossRef Full Text | Google Scholar

Davtyan, A., Schafer, N. P., Zheng, W., Clementi, C., Wolynes, P. G., and Papoian, G. A. (2012). AWSEM-MD: Protein Structure Prediction Using Coarse-Grained Physical Potentials and Bioinformatically Based Local Structure Biasing. J. Phys. Chem. B 116 (29), 8494–8503. doi:10.1021/jp212541y

PubMed Abstract | CrossRef Full Text | Google Scholar

Delfino, F., Porozov, Y., Stepanov, E., Tamazian, G., and Tozzini, V. (2019). Structural Transition States Explored with Minimalist Coarse Grained Models: Applications to Calmodulin. Front. Mol. Biosciences 6 (104). doi:10.3389/fmolb.2019.00104

PubMed Abstract | CrossRef Full Text | Google Scholar

Drake, S. K., Zimmer, M. A., Kundrot, C., and Falke, J. J. (1997). Molecular Tuning of an EF-hand-like Calcium Binding Loop. J. Gen. Physiol. 110 (2), 173–184. doi:10.1085/jgp.110.2.173

PubMed Abstract | CrossRef Full Text | Google Scholar

Duarte, F., Bauer, P., Barrozo, A., Amrein, B. A., Purg, M., Åqvist, J., et al. (2014). Force Field Independent Metal Parameters Using a Nonbonded Dummy Model. J. Phys. Chem. B 118 (16), 4351–4362. doi:10.1021/jp501737x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fallon, J. L., and Quiocho, F. A. (2003). A Closed Compact Structure of Native Ca2+-Calmodulin. Structure 11 (10), 1303–1307. doi:10.1016/j.str.2003.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandes, I. P. G., and Oliveira-Brett, A. M. (2017). Calcium-induced Calmodulin Conformational Change. Electrochemical Evaluation. Bioelectrochemistry 113, 69–78. doi:10.1016/j.bioelechem.2016.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Fracchia, F., Del Frate, G., Mancini, G., Rocchia, W., and Barone, V. (2018). Force Field Parametrization of Metal Ions from Statistical Learning Techniques. J. Chem. Theor. Comput. 14 (1), 255–273. doi:10.1021/acs.jctc.7b00779

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaertner, T. R., Putkey, J. A., and Waxham, M. N. (2004). RC3/Neurogranin and Ca2+/calmodulin-dependent Protein Kinase II Produce Opposing Effects on the Affinity of Calmodulin for Calcium. J. Biol. Chem. 279 (38), 39374–39382. doi:10.1074/jbc.m405352200

PubMed Abstract | CrossRef Full Text | Google Scholar

Gifford, J. L., Gifford, M. P., and Walsh, H. J. (2007). Structures and Metal-Ion-Binding Properties of the Ca2+-Binding helix-loop-helix EF-Hand Motifs. Biochem. J. 405 (2), 199–221. doi:10.1042/BJ20070255

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilli, R., Lafitte, D., Lopez, C., Kilhoffer, M.-C., Makarov, A., Briand, C., et al. (1998). Thermodynamic Analysis of Calcium and Magnesium Binding to Calmodulin. Biochemistry 37 (16), 5450–5456. doi:10.1021/bi972083a

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, Z., and Sun, H. (2017). A Coarse-Grained Force Field Parameterized for MgCl2 and CaCl2 Aqueous Solutions. J. Chem. Inf. Model. 57 (7), 1599–1608. doi:10.1021/acs.jcim.7b00206

PubMed Abstract | CrossRef Full Text | Google Scholar

Gromiha, M. M. (2010). “Chapter 6 - Protein Stability,” in Protein Bioinformatics. Editor M. M. Gromiha (Singapore: Academic Press).

Google Scholar

Heidorn, D. B., and Trewhella, J. (1988). Comparison of the crystal and Solution Structures of Calmodulin and Troponin C. Biochemistry 27 (3), 909–915. doi:10.1021/bi00403a011

PubMed Abstract | CrossRef Full Text | Google Scholar

Her, C., Thompson, A. R., Karim, C. B., and Thomas, D. D. (2018). Structural Dynamics of Calmodulin-Ryanodine Receptor Interactions: Electron Paramagnetic Resonance Using Stereospecific Spin Labels. Scientific Rep. 8 (1), 10681. doi:10.1038/s41598-018-29064-8

CrossRef Full Text | Google Scholar

Hoeflich, K. P., and Ikura, M. (2002). Calmodulin in Action. Cell 108 (6), 739–742. doi:10.1016/s0092-8674(02)00682-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, L., Chandrasekar, A., Wang, X., Putkey, J. A., and Waxham, M. N. (2014). Neurogranin Alters the Structure and Calcium Binding Properties of Calmodulin. J. Biol. Chem. 289 (21), 14644–14655. doi:10.1074/jbc.m114.560656

PubMed Abstract | CrossRef Full Text | Google Scholar

Homouz, D., Sanabria, H., Waxham, M. N., and Cheung, M. S. (2009). Modulation of Calmodulin Plasticity by the Effect of Macromolecular Crowding. J. Mol. Biol. 391 (5), 933–943. doi:10.1016/j.jmb.2009.06.073

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, J., and MacKerell, A. D. (2018). Force Field Development and Simulations of Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol. 48, 40–48. doi:10.1016/j.sbi.2017.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: Visual Molecular Dynamics. J. Mol. Graphics 14 (1), 33–38. doi:10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ikura, M., Clore, G., Gronenborn, A., Zhu, G., Klee, C., and Bax, A. (1992). Solution Structure of a Calmodulin-Target Peptide Complex by Multidimensional NMR. Science 256 (5057), 632–638. doi:10.1126/science.1585175

PubMed Abstract | CrossRef Full Text | Google Scholar

Jing, Z., Qi, R., Liu, C., and Ren, P. (2017). Study of Interactions between Metal Ions and Protein Model Compounds by Energy Decomposition Analyses and the AMOEBA Force Field. J. Chem. Phys. 147 (16), 161733. doi:10.1063/1.4985921

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, C. K. (2006). Calmodulin, Conformational States, and Calcium Signaling. A Single-Molecule Perspective. Biochemistry 45 (48), 14233–14246. doi:10.1021/bi061058e

PubMed Abstract | CrossRef Full Text | Google Scholar

Kataoka, M., Head, J. F., Vorherr, T., Krebs, J., and Carafoli, E. (1991). Small-angle X-ray Scattering Study of Calmodulin Bound to Two Peptides Corresponding to Parts of the Calmodulin-Binding Domain of the Plasma Membrane Calcium Pump. Biochemistry 30 (25), 6247–6251. doi:10.1021/bi00239a024

PubMed Abstract | CrossRef Full Text | Google Scholar

Komeiji, Y., Ueno, Y., and Uebayasi, M. (2002). Molecular Dynamics Simulations Revealed Ca2+ -dependent Conformational Change of Calmodulin. FEBS Lett. 521 (1), 133–139. doi:10.1016/s0014-5793(02)02853-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Lepšík, M., and Field, M. J. (2007). Binding of Calcium and Other Metal Ions to the EF-Hand Loops of Calmodulin Studied by Quantum Chemical Calculations and Molecular Dynamics Simulations. The J. Phys. Chem. B 111 (33), 10012–10022.

Google Scholar

Li, P., and Merz, K. M. (2017). Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 117 (3), 1564–1686. doi:10.1021/acs.chemrev.6b00440

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, Q., Pabis, A., Strodel, B., and Kamerlin, S. C. L. (2017). Extending the Nonbonded Cationic Dummy Model to Account for Ion-Induced Dipole Interactions. J. Phys. Chem. Lett. 8 (21), 5408–5414. doi:10.1021/acs.jpclett.7b02358

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, F., Chu, X., Lu, H. P., and Wang, J. (2017). Molecular Mechanism of Multispecific Recognition of Calmodulin through Conformational Changes. Proc. Natl. Acad. Sci. U S A. 114, E3927. doi:10.1073/pnas.1615949114

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, F., Chu, X., Lu, H. P., and Wang, J. (2017). Molecular Mechanism of Multispecific Recognition of Calmodulin through Conformational Changes. Proc. Natl. Acad. Sci. USA 114 (20), E3927–E3934. doi:10.1073/pnas.1615949114

PubMed Abstract | CrossRef Full Text | Google Scholar

Malmendal, A., Evenäs, J., Forsén, S., and Akke, M. (1999). Structural Dynamics in the C-Terminal Domain of Calmodulin at Low Calcium Levels 1 1Edited by P. E. Wright. J. Mol. Biol. 293 (4), 883–899. doi:10.1006/jmbi.1999.3188

PubMed Abstract | CrossRef Full Text | Google Scholar

Marambaud, P., Dreses-Werringloer, U., and Vingtdeux, V. (2009). Calcium Signaling in Neurodegeneration. Mol. Neurodegeneration 4 (1), 20. doi:10.1186/1750-1326-4-20

CrossRef Full Text | Google Scholar

McCarthy, M. R., Thompson, A. R., Nitu, F., Moen, R. J., Olenek, M. J., Klein, J. C., et al. (2015). Impact of Methionine Oxidation on Calmodulin Structural Dynamics. Biochem. Biophysical Res. Commun. 456 (2), 567–572. doi:10.1016/j.bbrc.2014.11.091

PubMed Abstract | CrossRef Full Text | Google Scholar

Meador, W., Means, A., and Quiocho, F. (1993). Modulation of Calmodulin Plasticity in Molecular Recognition on the Basis of X-ray Structures. Science 262 (5140), 1718–1721. doi:10.1126/science.8259515

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehler, E. L., Pascual-Ahuir, J.-L., and Weinstein, H. (1991). Structural Dynamics of Calmodulin and Troponin C. Protein Eng. Des. Sel 4 (6), 625–637. doi:10.1093/protein/4.6.625

PubMed Abstract | CrossRef Full Text | Google Scholar

Monticelli, L., Kandasamy, S. K., Periole, X., Larson, R. G., Tieleman, D. P., and Marrink, S.-J. (2008). The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theor. Comput. 4 (5), 819–834. doi:10.1021/ct700324x

PubMed Abstract | CrossRef Full Text | Google Scholar

Nandigrami, P., and Portman, J. J. (2016). Coarse-grained Molecular Simulations of Allosteric Cooperativity. J. Chem. Phys. 144 (10), 105101. doi:10.1063/1.4943043

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, H. Y., Kim, S. A., Korlach, J., Rhoades, E., Kwok, L. W., Zipfel, W. R., et al. (2008). Conformational Changes of Calmodulin upon Ca2+ Binding Studied with a Microfluidic Mixer. Proc. Natl. Acad. Sci. 105 (2), 542–547. doi:10.1073/pnas.0710810105

CrossRef Full Text | Google Scholar

Probst, M. M., Radnai, T., Heinzinger, K., Bopp, P., and Rode, B. M. (1985). Molecular Dynamics and X-ray Investigation of an Aqueous Calcium Chloride Solution. J. Phys. Chem. 89 (5), 753–759. doi:10.1021/j100251a007

CrossRef Full Text | Google Scholar

Project, E., Friedman, R., Nachliel, E., and Gutman, M. (2006). A Molecular Dynamics Study of the Effect of Ca2+ Removal on Calmodulin Structure. Biophysical J. 90 (11), 3842–3850. doi:10.1529/biophysj.105.077792

CrossRef Full Text | Google Scholar

Qin, Z., and Squier, T. C. (2001). Calcium-Dependent Stabilization of the Central Sequence between Met76 and Ser81 in Vertebrate Calmodulin. Biophysical J. 81 (5), 2908–2918. doi:10.1016/s0006-3495(01)75931-0

CrossRef Full Text | Google Scholar

Robustelli, P., Piana, S., and Shaw, D. E. (2018). Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. USA 115 (21), E4758–E4766. doi:10.1073/pnas.1800690115

PubMed Abstract | CrossRef Full Text | Google Scholar

Roux, B. (1995). The Calculation of the Potential of Mean Force Using Computer-Simulations. Comput. Phys. Commun. 91 (1-3), 275–282. doi:10.1016/0010-4655(95)00053-i

CrossRef Full Text | Google Scholar

Seaton, B. A., Head, J. F., Engelman, D. M., and Richards, F. M. (1985). Calcium-induced Increase in the Radius of Gyration and Maximum Dimension of Calmodulin Measured by Small-Angle X-ray Scattering. Biochemistry 24 (24), 6740–6743. doi:10.1021/bi00345a002

PubMed Abstract | CrossRef Full Text | Google Scholar

Shepherd, C. M., and Vogel, H. J. (2004). A Molecular Dynamics Study of Ca2+-Calmodulin: Evidence of Interdomain Coupling and Structural Collapse on the Nanosecond Timescale. Biophysical J. 87 (2), 780–791. doi:10.1529/biophysj.103.033266

CrossRef Full Text | Google Scholar

Shimoyama, H. (2019). A Structural Comparison of 'real' and 'model' Calmodulin Clarified Allosteric Interactions Regulating Domain Motion. J. Biomol. Struct. Dyn. 37 (6), 1567–1581. doi:10.1080/07391102.2018.1462730

PubMed Abstract | CrossRef Full Text | Google Scholar

Shirts, M. R., and Chodera, J. D. (2008). Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 129 (12), 124105. doi:10.1063/1.2978177

PubMed Abstract | CrossRef Full Text | Google Scholar

Spoel, D. V. D., Groot, B. L. D., Hayward, S., Berendsen, H. J. C., and Vogel, H. J. (1996). Bending of the Calmodulin central helix: a Theoretical Study. Protein Sci. 5 (10), 2044–2053. doi:10.1002/pro.5560051011

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, B., and Kekenes-Huskey, P. M. (2021). Assessing the Role of Calmodulin's Linker Flexibility in Target Binding. Int. J. Mol. Sci. 22 (9). doi:10.3390/ijms22094990

PubMed Abstract | CrossRef Full Text | Google Scholar

Tidow, H., and Nissen, P. (2013). Structural Diversity of Calmodulin Binding to its Target Sites. Febs j 280 (21), 5551–5565. doi:10.1111/febs.12296

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripathi, S., Wang, Q., Zhang, P., Hoffman, L., Waxham, M. N., and Cheung, M. S. (2015). Conformational Frustration in Calmodulin-Target Recognition. J. Mol. Recognit. 28 (2), 74–86. doi:10.1002/jmr.2413

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripathi, S., Waxham, M. N., Cheung, M. S., and Liu, Y. (2015). Lessons in Protein Design from Combined Evolution and Conformational Dynamics. Sci. Rep. 5, 14259. doi:10.1038/srep14259

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripathi, S., Waxham, M. N., Cheung, M. S., and Liu, Y. (2015). Lessons in Protein Design from Combined Evolution and Conformational Dynamics. Scientific Rep. 5 (1), 14259. doi:10.1038/srep14259

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, M.-Y., Zheng, W., Balamurugan, D., Schafer, N. P., Kim, B. L., Cheung, M. S., et al. (2016). Electrostatics, Structure Prediction, and the Energy Landscapes for Protein Folding and Binding. Protein Sci. 25 (1), 255–269. doi:10.1002/pro.2751

PubMed Abstract | CrossRef Full Text | Google Scholar

Vetter, S. W., and Leclerc, E. (2003). Novel Aspects of Calmodulin Target Recognition and Activation. Eur. J. Biochem. 270 (3), 404–414. doi:10.1046/j.1432-1033.2003.03414.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vigil, D., Gallagher, S. C., Trewhella, J., and García, A. E. (2001). Functional Dynamics of the Hydrophobic Cleft in the N-Domain of Calmodulin. Biophysical J. 80 (5), 2082–2092. doi:10.1016/s0006-3495(01)76182-6

CrossRef Full Text | Google Scholar

Villalobo, A., Ishida, H., Vogel, H. J., and Berchtold, M. W. (2018). Calmodulin as a Protein Linker and a Regulator of Adaptor/scaffold Proteins. Biochim. Biophys. Acta (Bba) - Mol. Cel Res. 1865 (3), 507–521. doi:10.1016/j.bbamcr.2017.12.004

CrossRef Full Text | Google Scholar

Wall, M. E., Clarage, J. B., and Phillips, G. N. (1997). Motions of Calmodulin Characterized Using Both Bragg and Diffuse X-ray Scattering. Structure 5 (12), 1599–1612. doi:10.1016/s0969-2126(97)00308-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., Liang, K.-C., Czader, A., Waxham, M. N., and Cheung, M. S. (2011). The Effect of Macromolecular Crowding, Ionic Strength and Calcium Binding on Calmodulin Dynamics. PLOS Comput. Biol. 7 (7), e1002114. doi:10.1371/journal.pcbi.1002114

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., Zhang, P., Hoffman, L., Tripathi, S., Homouz, D., Liu, Y., et al. (2013). Protein Recognition and Selection through Conformational and Mutually Induced Fit. Proc. Natl. Acad. Sci. 110 (51), 20545–20550. doi:10.1073/pnas.1312788110

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinstein, H., and Mehler, E. L. (1994). Ca2+-Binding and Structural Dynamics in the Functions of Calmodulin. Annu. Rev. Physiol. 56, 213–236. doi:10.1146/annurev.ph.56.030194.001241

PubMed Abstract | CrossRef Full Text | Google Scholar

Westerlund, A. M., and Delemotte, L. (2018). Effect of Ca2+ on the Promiscuous Target-Protein Binding of Calmodulin. Plos Comput. Biol. 14 (4), e1006072. doi:10.1371/journal.pcbi.1006072

PubMed Abstract | CrossRef Full Text | Google Scholar

Wriggers, W., Mehler, E., Pitici, F., Weinstein, H., and Schulten, K. (1998). Structure and Dynamics of Calmodulin in Solution. Biophysical J. 74 (4), 1622–1639. doi:10.1016/s0006-3495(98)77876-2

CrossRef Full Text | Google Scholar

Wu, G., Gao, Z., Dong, A., and Yu, S. (2012). Calcium-induced Changes in Calmodulin Structural Dynamics and Thermodynamics. Int. J. Biol. Macromolecules 50 (4), 1011–1017. doi:10.1016/j.ijbiomac.2012.02.017

CrossRef Full Text | Google Scholar

Wu, H., Wolynes, P. G., and Papoian, G. A. (2018). AWSEM-IDP: A Coarse-Grained Force Field for Intrinsically Disordered Proteins. J. Phys. Chem. B 122 (49), 11115–11125. doi:10.1021/acs.jpcb.8b05791

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamniuk, A. P., and Vogel, H. J. (2004). Calmodulin's Flexibility Allows for Promiscuity in its Interactions with Target Proteins and Peptides. Mb 27 (1), 33–58. doi:10.1385/mb:27:1:33

CrossRef Full Text | Google Scholar

Yang, C., Jas, G. S., and Kuczera, K. (2001). Structure and Dynamics of Calcium-Activated Calmodulin in Solution. J. Biomol. Struct. Dyn. 19 (2), 247–271. doi:10.1080/07391102.2001.10506736

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Jas, G. S., and Kuczera, K. (2004). Structure, Dynamics and Interaction with Kinase Targets: Computer Simulations of Calmodulin. Biochim. Biophys. Acta (Bba) - Proteins Proteomics 1697 (1), 289–300. doi:10.1016/j.bbapap.2003.11.032

CrossRef Full Text | Google Scholar

Yang, W., Lee, H.-W., Hellinga, H., and Yang, J. J. (2002). Structural Analysis, Identification, and Design of Calcium-Binding Sites in Proteins. Proteins 47 (3), 344–356. doi:10.1002/prot.10093

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Han, J., Cieplak, P., and Cheung, M. S. (2021). Determining the Atomic Charge of Calcium Ion Requires the Information of its Coordination Geometry in an EF-Hand Motif. J. Chem. Phys. 154 (12), 124104. doi:10.1063/5.0037517

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Tripathi, S., Trinh, H., and Cheung, M. S. (2017). Opposing Intermolecular Tuning of Ca2+ Affinity for Calmodulin by Neurogranin and CaMKII Peptides. Biophysical J. 112 (6), 1105–1119. doi:10.1016/j.bpj.2017.01.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuckerman, D. M. (2004). Simulation of an Ensemble of Conformational Transitions in a United-Residue Model of Calmodulin. J. Phys. Chem. B 108 (16), 5127–5137. doi:10.1021/jp0370730

CrossRef Full Text | Google Scholar