Distinct binding strategies of plasma proteins on gold surfaces: flexibility versus stability in the protein corona formation

When in contact with biological matrices, gold nanoparticles (AuNPs) become coated with a protein corona, which governs their biological identity and mediates interactions with cells and tissues. This study explores the adsorption behavior and conformational dynamics of two key plasma proteins, human serum albumin (HSA) and transferrin (TRF), on AuNP surfaces using Brownian Dynamics (BD) and atomistic Molecular Dynamics (MD) simulations. The results reveal multiple binding mechanisms for HSA and TRF on Au (111) surfaces. HSA exhibits significant reorientations during binding, initiated by negatively charged residues and stabilized by hydrophilic amino acids, with its structural rigidity requiring multiple reversible anchoring attempts before achieving more energetically favorable interactions. In contrast, TRF demonstrates rapid and stable binding due to its intrinsic local flexibility, retaining docked orientations with minimal reorientation. While both proteins utilize electrostatic interactions to approach the surface, TRF’s disordered structure enables swift adaptation, whereas HSA’s rigidity supports strong interactions upon relaxation. These findings highlight contrasting binding strategies, with TRF prioritizing speed and flexibility, and HSA exploiting domain rearrangements for sustained stability. Importantly, the results obtained at the all-atom level of resolution are critical for the development of coarse-grained and mesoscale models. The approach in classifying protein orientation enhances our understanding of the protein corona’s shape and morphology and could advance its effective representation in lower-resolution models. The insights gained from these simulations enable us to analyze the different adsorption behavior of TRF and HSA, providing a deeper understanding of how their structural properties influence protein corona formation.

1 Introduction

Gold nanoparticles (AuNPs) are widely recognized for their diverse applications in biomedicine (Dykman and Khlebtsov, 2012; Pyne et al., 2020), including drug delivery (Erik et al., 2012; Matus and Hakkinen, 2024), diagnostics (Ray et al., 2022), and therapeutic interventions (Bloise et al., 2022; Neupane et al., 2018). When introduced into a biological environment, such as blood plasma, AuNPs quickly become coated with a complex layer of biomolecules, predominantly proteins, forming what is known as the protein/biomolecule corona (Bewersdor et al., 2020; Wang et al., 2013; Tenzer et al., 2011; Monopoli et al., 2012). This corona not only determines the biological identity of nanoparticles, but also governs their interactions with cells, their biodistribution, and their immune responses (Trinh et al., 2022; Monopoli et al., 2012). The protein corona is typically categorized into two layers: the hard corona, consisting of proteins tightly adsorbed onto the nanoparticle surface with long residence times, and the soft corona, characterized by loosely associated proteins in dynamic equilibrium with the surrounding solution (Zhang et al., 2020; Lee, 2023; Baimanov et al., 2019; Mohammad-Beigi et al., 2020; Wang et al., 2013). Despite extensive experimental and computational approaches (Lynch et al., 2009; Nel et al., 2009; Feng Ding et al., 2013), the molecular mechanisms underlying protein adsorption and corona formation remain poorly understood. Computational methods including fully atomistic classical molecular dynamics (Brancolini et al., 2019a) and coarse-grained methods (Brancolini et al., 2019b; Brancolini and Tozzini, 2019; Brancolini et al., 2019a; Vilaseca et al., 2013; Shao and Hall, 2016; Power et al., 2019; Vilanova et al., 2016; 2025), have proven particularly valuable in elucidating protein-nanoparticle interactions at atomic and molecular scales. However, significant gaps in knowledge persist regarding how the intrinsic structural properties of proteins influence their adsorption dynamics, conformational changes, and binding stability on nanoparticle surfaces. Among the proteins present in human plasma, Human Serum Albumin (HSA) and Transferrin (TRF) are of particular interest due to their abundance (Schenk et al., 2008) and distinct structural properties and roles in biological systems. HSA, a globular and highly soluble protein stabilized by numerous disulfide bridges, function as a transports molecule for various substances (Theodore Peters, 1996). In contrast, TRF, a glycoprotein specialized in iron transport (Gomme et al., 2005), is known for its structural flexibility and specific binding affinity to gold nanoparticle surfaces (Gkouvatsos et al., 2012). These distinct characteristics make HSA and TRF ideal candidates for studying how protein structure influences adsorption mechanisms. Previous studies (Dai et al., 2023), have revealed intriguing insights into protein-AuNP interactions. For example, experiments with HSA on various NP shapes (spheres, rods, and flowers) showed that adsorption often leads to conformational changes, such as a reduction in $\alpha$-helical content, with these effects being strongly influenced by NP morphology. Similarly, TRF interactions with gold nanostructures have been shown to enhance membrane affinity and lipid perturbation, driven by slight protein unfolding (Mcdonagh et al., 2015). These findings underscore the importance of understanding how structural dynamics and flexibility impact protein-NP interactions, particularly for biomedical applications. In this work, the Au (111) face, considered the most stable and commonly observed in gold NPs, was assumed to approximate a large, flat crystalline surface when the NP’s exposed area exceeded the protein’s diameter. Here, we focus on the distinct adsorption dynamics of HSA and TRF on gold surfaces, aiming to elucidate how their structural properties govern their respective binding mechanisms. Using a combination of atomistic Molecular Dynamics and Brownian Dynamics simulations we explore the conformational changes, binding kinetics, and adsorption energetics of these proteins when interacting with a Au surface. The study reveals a critical trade off between the speed and flexibility that characterizes the binding mechanism for TRF versus the stability and energy optimization observed for the adsorption process of HSA. The insights gained from these simulations enable us to analyze how the adsorption dynamics affects protein conformational changes, including unfolding, domain reorientation, and flattening, which are critical for determining the density and stability of the protein corona. These insights also have broader implications for the development of coarse-grained models, enabling computationally efficient simulations while retaining key structural features of protein-NP systems.

2 Materials and methods

2.1 Computational details: preparation of atomic coordinates

The atomic coordinates of both proteins were derived from their full amino acid sequences to include previously missing residues from experimental models, ensuring a complete structural representation. The 585-aminoacidic structure of HSA (UniProt: P02768) was obtained from the AlphaFold Protein Structure Database (Varadi et al., 2024) (ID: AF-F6KPG5-F1-v4), yielding a model with an average per-residue measure of local confidence pLDDT score of 94.25. This model was subsequently aligned to a chosen experimental crystal structure to verify that incorporating the previously missing loops and flexible regions did not cause significant deviations from the experimentally determined ordered domains. The alignment was performed on the crystal structure (PDB ID: 1AO6) using TM-align (Zhang and Skolnick, 2005), achieving a TM-score of 0.979, indicating close structural similarity. For TRF (UniProt: P02787), the 679-residue structure was modelled using Alphafold3 (Ronneberger et al., 2021), resulting in a pTM score of 0.91. Although the AlphaFold-predicted structure does not include iron, structural comparisons with iron-bound (3QYT) and apo forms (7Q1L) of transferrin confirm that the overall protein fold is preserved, with a TM-score of 0.983 and 0.9995, respectively, justifying its use in adsorption studies. The PDB2PQR software (Dolinsky et al., 2004) has been used with the PROPKA method (Olsson et al., 2011) to assign titration states of the protein side chains at physiological pH (7.4), resulting in total charges of −13 for HSA and −3 for TRF. Partial atomic charges were assigned to the protein atoms based on the OPLS force field (Robertson et al., 2015).

2.2 Brownian dynamics docking

Rigid-body Brownian Dynamics (BD) simulations were conducted to perform docking using the SDA software (version 7) (Martinez et al., 2015). The ProMetCS (Kokh et al., 2010) continuum solvent model was applied to account for protein-metal surface interactions. Two primary components of the total interaction energy $U_{\mathit{tot}}$ were considered in the ProMetCS model: electrostatic interaction energy which arises from metal polarization, and non-polar interaction energy. The electrostatic interaction energy $U_{el}$, includes Coulombic interactions as well as electrostatic desolvation effects for both the protein and the metal. Meanwhile, the non-polar interaction energy $U_{np}$, encompasses Lennard-Jones (LJ) forces, which account for van der Waals interactions and weak chemical forces, along with non-polar desolvation effects. Results are reported in Table Supplementary Figure S1 ESI. Given that the structures were treated as rigid bodies, the individual energy and potential components were stored in three-dimensional grids centered on the protein and surface structures.

A neutral Au (111) surface, with a surface area of 20 × 20 ${\text{nm}}^2$ and three atomic layers, was constructed for the simulations. Electrostatic potential grids were calculated using the APBS software (Jurrus et al., 2018) with an ionic strength of 150 mM and ionic radius of 1.5 A, a solvent dielectric constant of 78.0 (Supplementary Figure S1 ESI) and a temperature of 300 K. The effective charges for each protein were computed using the Effective Charges for Macromolecules (ECM) method (Gabdoulline and Wade, 1996) implemented in SDA. Three energy grids were calculated for each system: two Lennard-Jones (LJ) energy grids and one electrostatic desolvation grid, using the make_edhdlj_grid tool. A total of 5,000 BD trajectories were simulated for 2 ns each with a time step of 2 ps. At the start of each simulation, the protein’s center of mass was placed 7 nm away from the Au (111) surface in a random orientation in order to leave a space greater than 2 nm between the protein and the surface, where the protein-surface interaction energy is negligible. For details on the parameters of the Protein-Metal FF, we refer to the paper (Kokh et al., 2010). The dynamics were run in a simulation box of 18 × 18 × 20 ${\text{nm}}^2$, with the surface atoms kept fixed throughout the simulation. During the BD simulations, the protein’s coordinates were recorded at each time step based on the most favorable docked positions, determined by the lowest interaction energies. A total of 2000 docked positions were recorded. If the coordinates at a given time step had a root-mean-square deviation (RMSD) of less than 2 Å from a previously recorded complex, they were considered part of the same complex. For both, HSA and TRF, translational and rotational diffusion coefficients in pure solvent were calculated using the software HYDROPRO (García De La Torre et al., 2000) and used in the BD simulations. From the docking results, the 2,000 most energetically favorable configurations were grouped into representative clusters using a single-linkage hierarchical agglomerative clustering algorithm.

2.3 Protein-Au (111) molecular dynamics simulations

Flexible refinement of the representative docking structures was conducted through Molecular Dynamics (MD) simulations in explicit solvent using the GROMACS software package (Bekker et al., 1993). For structural refinement, the two most populated clusters from each protein docking were selected. The same protein structures and protonation states used in the BD simulations served as the starting point for the MD simulations. A cubic simulation box was constructed, containing the protein, spce water molecules, and the Au surface. Periodic boundary conditions were applied. The Au (111) surface was modelled as a crystalline slab with dimensions of $15\times 15$ ${\text{nm}}^2$, consisting of four atomic layers along the z-axis (perpendicular to the surface). The slab remained rigid during the simulations. To avoid interactions between periodic images, the box size in the z-direction was adjusted to maintain at least 3 nm of space between the proteins and the box edge. The proteins were positioned 1.2 nm above the surface, retaining their docked orientations. This distance was chosen based on previous studies (Brancolini et al., 2012) showing that starting the proteins in direct contact with the surface (or closer distances) can lead to kinetic trapping and minimal conformational relaxation on the nanosecond timescale. At this distance, the interactions between the protein and the surface were dominated by long-range electrostatic forces, handled by the Particle-Mesh Ewald (PME) method, as cut-off distances used for non-bonding interactions were set to 1.10 nm. For the gold surface, the GolP force field (Wright et al., 2013), a modification of the OPLS force field (Robertson et al., 2015), was employed in the simulations. Gold atoms in the surface and bulk were kept frozen, though dipole charges on the gold atoms were allowed to move (Iori and Corni, 2008). The structures were energy minimized for 2000 steps using the steepest descent method. All bonds were constrained using the LINCS algorithm (Hess et al., 1997). After, the system was equilibrated at constant volume and temperature ensemble of 300 K using a Nose-Hoover thermostat (Nose, 1984; Hoover, 1985). No NPT equilibration was performed to the presence of the rigid metal surface. For each protein-gold conformation, five independent 500 ns simulations were performed (denoted as d1, d2, d3, d4, and d5), each initiated with different random velocities. To compare the conformational changes of the proteins in the presence of the gold surface with those in solution, an additional 500 ns simulation of the protein in pure water was conducted using the same procedure. Trajectory analysis focused on properties such as density, temperature, potential energy, and other macroscopic parameters, which were examined using GROMACS tools.

3 Results and discussion

3.1 Docking of HSA and TRF onto gold

BD simulations were used to generate trajectories of protein diffusion and identify the binding orientations (referred to as “encounter complexes”) of HSA and TRF on the Au (111) surface. To reliably determine the most frequently occurring binding orientations, a single-linkage hierarchical clustering algorithm was applied to protein-surface encounter complexes based on their spatial orientation (Martinez et al., 2015). Structures were clustered using a 3 $\mathring{\mathrm{A}}$ cutoff of C$\alpha$ atoms, after optimal superposition of the surface. Each cluster was represented by the structure closest to all other members and ranked by the interaction energy of this representative. This method enables the identification of structurally similar encounter complexes and extraction of representative binding modes from large ensembles. The robustness and precision of this approach have been validated in previous studies (Kokh et al., 2010; Penna et al., 2014; Ozboyaci et al., 2016).

After clustering analysis, the two most populated complexes formed between each protein and the Au surface were selected for further analysis. For the HSA-gold complexes, these two structures represented 97.6% of all observed complexes. Similarly, the two most prevalent TRF-gold complexes accounted for 89.7% of the total observed complexes. These most common protein-surface complex structures are depicted in Figure 1.

Figure 1

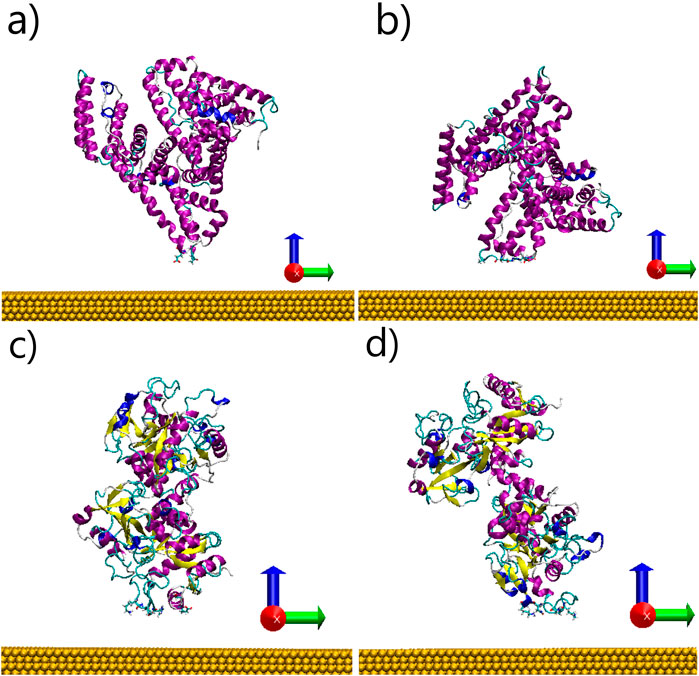
Figure 1. Encounter complexes of Human Serum Albumin (a, b) and Transferrin (c, d) on neutral gold obtained by BD simulation. The structures of representative complexes for the two most populated clusters are shown. The protein backbone is shown in cartoon representation while the residues contacting the gold surface are shown in licorice representation.

Supplementary Table S1 reports the interaction energies and contact residues of the two most populated orientations for both HSA and TRF proteins.

3.1.1 HSA clusters

Clustering analysis of HSA encounter complexes revealed two genuinely distinct binding orientations. The most populated cluster, Cluster A, is accounting for 59.2$\%$ of the obtained complexes while the most energetically favorable cluster, Cluster B is accounting only for 38.4$\%$ of the total complexes. Results are reported in Supplementary Table S1. In Cluster A the protein makes direct contact with the gold surface mainly with three charged residues and the electrostatic interactions ($U_{el}=-136.3$ kJ/mol), contribute significantly to the total interaction energy in this orientation ($U_{\mathit{tot}}=-176.6$ kJ/mol). This indicates that binding is allowed by the charged residues to form up to three favorable contacts that anchor the protein to the surface and compensate for the relatively small contact area. In contrast, although Cluster B is more energetically favorable ($U_{\mathit{tot}}=-229.3$ kJ/mol), it appears significantly less accessible during BD simulations compared to Cluster A. HSA protein in this case interact with the gold through large number of residues, forming favorable Lennard-Jones interactions and contributing to $U_{np}$. This non polar interaction component ($-242.9$ kJ/mol), along with non-polar desolvation term, results as the dominant contribution to the binding. Notably, residue HIS128 is able to engage the surface with its imidazole ring parallel maximizing the interaction with gold. These findings highlight the balance between electrostatic and non-polar interactions in determining the preferred binding orientation of HSA on gold surfaces.

3.1.2 TRF clusters

Cluster A represents the most populated and energetically favorable cluster. In this cluster, both the non-polar and electrostatic interactions contribute favorably to the total binding energy ($U_{\mathit{tot}}=-238.6$ kJ/mol). For the non-polar term, HIS14 and HIS289 give a notable contribute, where HIS14 approaches the surface with their imidazole rings parallel, maximizing the interaction with the gold. On the electrostatic term, the favorable contribution is primarily due to the contact between the charged side chains of residues ASP24, LYS280, and GLU281. The presence of ARG23 provides another important favorable contact, with its guanidinium group approaching the gold surface in a perpendicular orientation. The $\sim 130$ kJ/mol energy difference from Cluster B is primarily due to Cluster A’s stronger electrostatic interactions. In contrast, Cluster B relies mainly on non-polar interactions, optimizing binding through multiple lower-affinity contacts.

3.2 Molecular dynamics of docked complexes

To elucidate the binding mechanism of HSA and TRF proteins binding to an Au (111) surface, we performed 20 MD simulations for each protein, starting with docking-derived orientations. These included two initial configurations per protein, each simulated five times with a different random velocity generator seeds (d1-d5), and all runs lasting 500 ns. For each protein, we simulated two different orientations relative to the gold surface. The initial placements of the protein from docking-derived structures were positioned 1.2 nm away from the surface ensuring interactions via long-range electrostatic forces at the start of the simulations. Major changes in global orientation were observed for the HSA complexes, while the TRF complexes demonstrated good stability, maintaining the original docked orientation during binding. Figure 2 presents the average Coulomb and Lennard-Jones components of the protein-Au (111) interaction, as reported for both the simulated HSA and TRF complexes. On the metal surface water molecules form two layers (Supplementary Figure S2 ESI) that drive the diffusion of the protein towards it. During the anchoring phase, the protein first makes contact with the second water layer bound to the surface. Prior to the induced fit, the anchored protein gradually rearranges its structure to directly bind the relevant groups to the solid surface, displacing the water layer immediately adjacent to it. Penna et al. define this process as “Lockdown phase” (Penna et al., 2014). The simulations have consistently shown various anchoring and lockdown events, even within the same complexes (Supplementary Figure S3 ESI). Notably, the HSA Complexes have exhibited instances of reversible anchoring, as the protein comes adrift sometime after anchoring in the gold slab, especially when this phase sees involved hydrophobic amino acids. In general, we observed negatively charged residues driving the anchoring initiation event for HSA protein such as GLU60-311 and ASP129-365-562, whether for TRF the residues driving the anchoring are equally distributed between polar (THR165, SER435-437, ASN553-555-557), negatively charged (GLU281) and positively charged (LYS280-552-557), as can be depicted by Supplementary Figure S3. The lockdown phase seems highly enhanced by hydrophilic amino acids such as histidines, polar and charged groups. We hypothesize that the success rate of these events is directly influenced by the protein’s local flexibility, which allows key residues to reach out and engage effectively. The following sections will present and discuss these findings in detail. First, we provide an overview of the structural changes the proteins undergo before, during, and after binding, highlighting their connection to the observed anchoring and lockdown mechanisms. Next, we analyze the binding mechanism for each simulated complex and replica, identifying the specific residues responsible for anchoring and lockdown events. Finally, we conduct an in-depth examination of the protein’s overall shape and orientation post-binding, discussing the further implications for coarse-grained and meso-scale models.

Figure 2

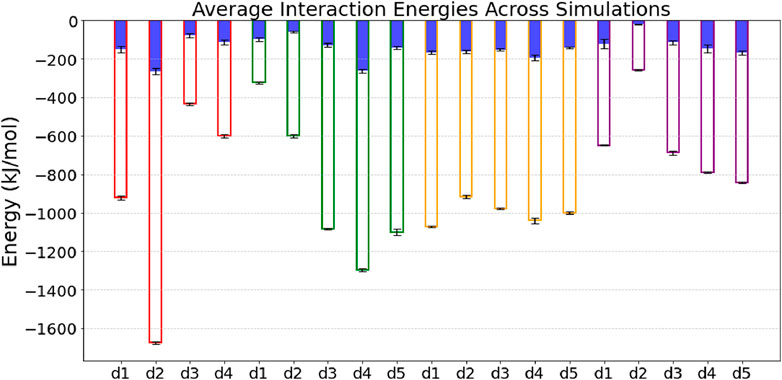
Figure 2. Average Coulomb and Lennard-Jones components of the protein-Au (111) interaction, reported for all proteins and complexes. HSA Complex A (Coul = blue, LJ = red), HSA Complex B (Coul = blue, LJ = green), TRF Complex A (Coul = blue, LJ = yellow), TRF Complex B (Coul = blue, LJ = purple). Energies are taken from the last 50 ns of the five (four for HSA-A) independent MD runs for each complex.

3.2.1 Structural changes of protein after binding

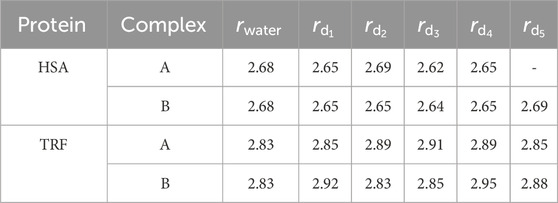
To elucidate whether and how the binding of HSA and TRF to the Au (111) surface may influence the structural stability and induce internal rearrangements in the protein structure, we calculated the radius of gyration, which provides a preliminary measure of the change in protein shape upon binding. For HSA and TRF in pure water, we obtain a gyration radius of 2.68 and 2.83 nm, respectively. As shown in Table 1, binding does not significantly alter the overall size of the proteins. Moreover, we calculated the percentage of disorder, which provides a quantitative measure of how protein adsorption affects the overall disorder in its secondary structure. This serves as an indicator of local flexibility and conformational changes upon binding. We observed a notable increase (up to 15$\%$) in the disordered secondary structure is observed upon binding (Supplementary Figures S4-S7 ESI). For HSA, the largest increase in disordered structure arises from the most energetically favorable simulations within specific complexes (e.g., A-d2, B-d3, B-d4). Interestingly, the temporal dynamics of structural disorder reveal significant differences between HSA and TRF. For TRF, a slight increase in its already disordered secondary structure primarily occurs during the diffusion phase, supporting the conformational selection model, wherein conformational changes precede binding. This preliminary adaptation enables TRF to immediately expose the hydrophilic residues, swiftly anchoring to the surface and establishing a fast, stable lockdown with a final orientation that aligns with its docked state. In contrast, HSA has demonstrated distinct binding mechanism. Structural disorder in HSA increases continuously before, during, and after binding to the gold surface, persisting for up to 200 ns—a significantly longer timescale compared to TRF. HSA’s inherently more ordered secondary structure requires more time for extensive internal rearrangements to achieve irreversible anchoring and lockdown. As a result, HSA often experiences reversible anchoring during initial contact through hydrophobic residues, struggling to retain its initial configuration. Multiple attempts are required for HSA to achieve a stable orientation, as we will discuss in details in the coming section. During the early stages of the binding process, structural fluctuations can be observed while the protein is diffusing towards the surface (Supplementary Figures S8-S11 ESI). For HSA, these fluctuations are more pronounced in the C-terminal domain, while in TRF, they are concentrated within the amino acid range of 420–580. As the number of surface contacts increases during binding, these fluctuations gradually decrease across all the simulations, reflecting stabilization of the protein-surface complex.

Table 1

Table 1. Gyration radii from MD simulations, expressed in nm.

3.2.2 Binding mechanism of HSA - a complexes

After three anchoring attempts towards the surface, all mediated by ALA364 and ASP365, simulation d5 resulted in HSA diffusing away from the surface and binding to the top of the simulation box, so we will not discuss this simulation further. In simulation d1, HSA first attempts to anchor onto the surface at around 10 ns, with ALA364 and ASP365 interacting with the water molecules in the second layer, but no residues managing to penetrate the first water layer adjacent to the surface. This interaction led to a temporary diffusion of the protein away from the surface, similarly as observed in d5, but after undergoing a rotation exposing the C-terminal domain IIIB to the surface, a second anchoring attempt was observed through LEU585, and the protein is finally locked-down through residues GLU542, GLN543 and LYS545. After induced fit, the total number of aminoacids in close contact $(<7\mathring{A})$ with the surface is 54, with the majority being aliphatic $(\sim 33\%)$, negatively charged $(\sim 20\%)$ and positively charged $(\sim 19\%)$ aminoacids. Notably, four aromatic residues (PHE395-551-554 and TYR401), three cysteines (558-559-567), MET548 and the carboxylate of the C-terminal residue LEU585 play a relevant role in stabilizing the binding. In simulations d2, d3 and d4 the docked orientation is partially retained, with residues LYS313, ALA364 and ASP365 commonly found in the binding across all simulations. However, the total binding energy is extremely different, particularly between simulation d2 and the other two. In d2, the anchoring is driven mainly by electrostatic interactions with GLU311 and ASP365, and the lockdown process is strongly enhanced first by LYS372 and immediately after by HIS367. The protein fully tilts towards the domain IIIA first and IIIB after, allowing the co-adsorption of a large number of residues (up to 82), while maintaining a steady binding with the IIB domain due to the strong interaction with HIS367. The key reason for the great energy difference between d2 and simulations d3 and d4 is found in the relaxation of the the C-terminal domain towards the surface. Simulation d3 anchors the surface with the a similar mechanism as d2, favoring electrostatic interactions with GLU311 and ASP365 and locking down the binding with GLU311 first and HIS367 after. However, in the final part of the simulation, d3 shows the protein interacting solely through domain IIB, leading to a significantly lower number of contacts (22 residues). In d4 the protein attempts to anchor the surface in three distinct moments: at 20 ns, through the already seen ALA364 and ASP365, that again led to reversible anchoring, at 60 ns, through GLU368, and finally at 150 ns, with the anchoring driven by ALA363 first, and multiple charged residues immediately after (LYS313, ASP314, LYS317, GLU321). The protein is locked down by direct interaction of the surface with ALA363 and HIS367, and tilts in the opposite direction, allowing the N-terminal domain IA to interact in one point through residues GLN93 and GLU94. In the final binding a total of 32 amino-acids interact with the gold surface. Simulation d4 presents a “bridge” type of conformation that will be discussed later in this paper, where the $\alpha$-helix of domain IIA does not relax on the surface together with the two contact points. Figure 3 presents the contact count for each residue upon HSA binding to gold over the four simulated replica. The more populated binding sites span from residue 299 to 399 and from residue 539 to 585.

Figure 3

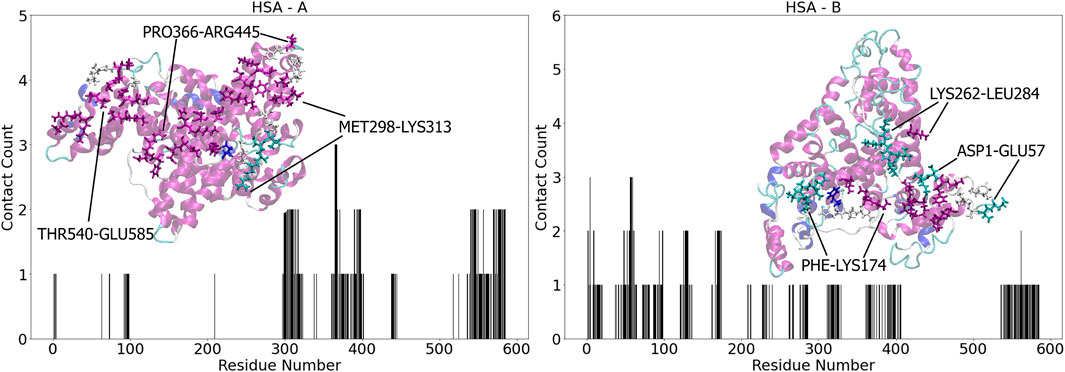
Figure 3. Contact number for HSA - A (left) and HSA - B (right) residues upon binding with Au (111), respectively. The contact count represents the cumulative occurrences across multiple simulations, accounting for repeated contacts of the same residue. Insets: graphical representations of the most populated binding sites for each complex in licorice, colored accordingly to the protein secondary structure.

3.2.3 Binding mechanism of HSA - b complexes

The simulations for Complex B reveal that only d1 and d5 retain the docking conformation after molecular dynamics. In d1, THR124 and ASP129 immediately anchor the protein, followed by the locked down phase through HIS128 and GLN170. A total of 19 residues in domain IB keep the protein attached to the gold surface, with PHE127 and the CYS124-CYS169 disulfide bond stabilizing the binding. No relaxation of other domains towards the surface is observed in this simulation, resulting in the lowest binding energy for the HSA complexes (Figure 2). In contrast, after a first, weak anchoring attempt through ALA172, d2 sees the protein diffusing away from the surface and undergoing a rotation that favors anchoring to the N-terminal domain IA, specifically through SER58 and GLU60. After, the same two residues enhance the lockdown towards the surface, and in the final stages key interactions come from the parallel guanidinium groups of ARG81 and ARG98, the CYS75-CYS91 disulfide bond, the carboxamide of ASN61, and the perpendicular orientation of PHE50’s aromatic ring. HIS3 also highly stabilizes the binding here. Simulation d3 shows residue GLN94 anchoring the surface and locking down the contact together with PRO96, with an additional relaxation of domain IIB towards the surface, that leads to a much favorable interaction energy (Figure 2). Here, three aromatic residues (PHE228, TYR263, PHE326), two histidines (3 and 367), the CYS316-CYS361 disulfide bond, and the carboxamide groups of ASN61 and GLN94 lying parallel to the surface strengthen the binding. In simulation d4, the protein first attempts to anchor the surface with ASP121, but it immediately undergoes a rotation towards domain IIIA and the C-terminal domain IIIB, with ASP562 anchoring the surface and immediately locking down the structure. In the final stage of the simulation we find contact residues in common with Complex A, simulation d2. The $\sim 300$ kJ/mol difference in binding energy appears to stem from the ability of residue HIS367 to interact with gold, that in simulation A-d4 does not seem to be able to approach the surface in the critical stages of the binding process. Across all simulations of Complex A and Complex B, the most favorable binding energies occur when the protein binds the surface near domains IIIA and IIIB, underscoring the importance of these regions. In simulation d5, the protein interacts first with the second layer of water molecules with THR125 and ASP129, and locking it down with ALA172 first and GLN170 after. The final binding is observed mainly through domains IA, IB, and IIA, resulting in a total of 58 favorable contacts. The binding is primarily stabilized by the N-terminal residue ASP1, the aromatic residues PHE11 and PHE127, HIS128, and a large number (14) of negatively charged residues, whose carboxylated groups are oriented parallel to the surface plane.

3.2.4 Binding mechanism of TRF - a complexes

Differently from the HSA complexes, the five independent simulations of both TRF Complex A and B all retained the docking-derived conformation. From visual inspection, four of the simulations (d1, d2, d4, and d5) maintained a conformation perpendicular to the surface throughout the trajectory, while d3 adopted a bridge-like conformation lying horizontally to the surface plane. The protein initially anchors to the surface through HIS14; however, this interaction with the second water layer appears too weak to stabilize the protein and facilitate the conformational rearrangements necessary for the lockdown phase within relevant timescales. The protein then diffuses away from the surface. Approximately 30 nanoseconds later, the protein effectively re-anchors through favorable electrostatic interactions with residues LYS280 and GLU281, followed by a relaxation of the C-lobe. The binding is locked down in two points through favorable interactions with residues SER28 and LYS280, and it is further strengthen by HIS25, HIS273 and PHE479, with the rings lying parallel to the surface. The majority of other contact residues are polar and aliphatic in nature. Simulation d1 anchors the gold slab with residue GLU281 as well, but locks down the binding through HIS14 and PRO288. This results in a tilting of the protein towards the lobe that is located oppositely to the C-terminal one, resulting in a global conformation different from the one in d3, although with some common contact residues, as can be depicted also from Figure 4. Simulations d2 and d4 both anchors the gold slab with a similar mechanism through GLU281 and lock down the protein with residues HIS14 and HIS289. In the final binding mode we observe a significant large number (up to 26) of polar amino acids involved. Finally, simulation d5 sees the anchoring phase mainly driven by THR165 and the following lock down involving residues GLU13, LYS41 and HISD289. The simulations all yielded very similar interaction energies with the gold surface, both for the Lennard-Jones and Coulomb interactions (Figure 2). 5$\%$ of the residues were commonly found in the binding site across all five replicas, and 25$\%$ were shared between replicas d1, d2, d4, and d5. While the global orientation from the initial docking was partially retained across the replicas, the individual induced fit mechanisms and final orientations differed. This appears to depend heavily on the specific residues involved in the early anchoring and locking-down processes of the binding mechanism.

Figure 4

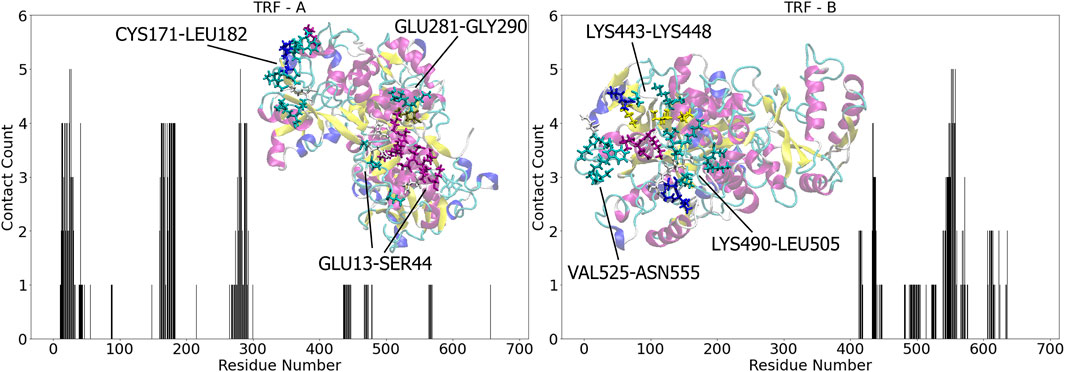
Figure 4. Contact number for TRF - A (left) and TRF - B (right) residues upon binding with Au (111), respectively. The contact count represents the cumulative occurrences across multiple simulations, accounting for repeated contacts of the same residue. Insets: graphical representations of the most populated binding sites for each complex in licorice, colored accordingly to the protein secondary structure.

3.2.5 Binding mechanism of TRF - b complexes

The interaction energies between TRF Complex B and gold after MD simulations are in good agreement with the results obtained from docking, ranking this complex as less energetically favorable than Complex A. The reason for the energy difference between Complex A and B is found in the capability of the protein to interact with the surface via two distinct lobes. In Complex B the protein interacts only through the C-terminal lobe. Figure 4 shows that a significant number of the same contact residues remain constant across all replicas, indicating that the docked orientation is consistently maintained throughout the simulations. However, after the induced fit, two dominant global conformations emerge: a skewed orientation and a fully perpendicular one. All the simulations steadily interact with the gold slab through ASN553, ASN555, ASP558 and LYS557. Simulation d2 leads to the least favorable binding energy, as the protein maintains a conformation fully perpendicular to the surface, interacting through a very small number of residues, mainly polar and negatively charged. This kind of conformation is obtained with both the anchoring and the lockdown phase are driven by SER435 and SER437. Noteworthy is the interaction via ARG568 in the final binding, whose guanidinium group lies parallel to the surface. ASN553, ASN555 and LYS557 drive the anchoring of both simulations d1 and d5, but different residues (LYS557 and SER435-ASN553) involved in the lockdown phase led to different induced fit mechanisms. In simulation d1, an additional interaction region is seen spanning residues 567-672. Conversely, in simulation d5, the interaction with the sulfur of MET499 causes a large number of residues 447-526 to relax towards the surface, resulting in the most favorable interaction for this type of complex. As we will observe in the coming section, both mechanisms result in a skewed protein conformation. In simulations d3 and d4, the protein was found anchoring the surface with LYS552, ASN553 and ASN555 and locking it down with the same residues, with the addition of LYS557. This mechanism led to a favorable interaction with two additional regions of the protein: 414-419 and 607-637. Key contacts in these intervals are given by HIS606 and ARG623.

3.2.6 Shape and orientation of protein after binding

In this section, we propose an approach to quantify and classify the overall shape and orientation of a protein after binding with a flat surface. Traditional metrics like RMSD, while useful for assessing overall structural deviation, are insufficient for classifying shape and orientation, as they do not capture directional changes or anisotropic deformation along individual spatial axes, nor do they provide information about the protein’s orientation relative to the surface. In the proposed approach, we initially assumed to model the proteins as ellipsoids, and we determine the length of their semi-axes by calculating the principal moments of inertia. In practice, at each time frame of the trajectory, we obtain the protein’s principal moments of inertia and the corresponding normalized principal axes directly using the GROMACS tool gmx principal (v. 2024.2) (Bekker et al., 1993; Abraham et al., 2015). This tool performs the diagonalization of the inertia tensor, directly providing its eigenvalues and eigenvectors at each time. We assign $I_a$ as the moment of the minor principal axis, $I_b$ for the middle axis and $I_c$ for the major axis. From the principal moments of inertia la $I_a\le I_b\le I_c$ the semi-axes of an ellipsoid can be computed, assuming a uniform mass distribution m. The semi-major axis a is given by Equation 1, as

$a=\sqrt{\frac{5}{2}\cdot \frac{I_b+I_c-I_a}{m}},(1)$

$b=\sqrt{\frac{5}{2}\cdot \frac{I_a+I_c-I_b}{m}},(2)$

the intermediate semi-axis b is given by Equation 2

$c=\sqrt{\frac{5}{2}\cdot \frac{I_a+I_b-I_c}{m}},(3)$

and the semi-minor axis c is given by Equation 3.

Each protein shape is then classified as ellipsoid, spheroid or spherical by computing the relative differences between all pairs of the semi-axes. If all semi-axes are within 10% of each other, the shape of the protein is considered to be spherical. If two of the semi-axes are within 10% of each other while the third one differs, the shape of the protein is classified as a spheroid. In this case, the shape can be either oblate or prolate, depending on whether the dissimilar semi-axis is smaller or larger compared to the other similar two. Finally, if none of the semi-axes fall within 10% of similarity, the shape of the protein is identified as an ellipsoid. After this preliminary classification, we further quantify the eccentricity of these protein minimal models. Normally, eccentricity is calculated for a 2D ellipse using its two semi-axes (major and minor). However, since we are classifying 3D objects, we define two eccentricities: major $(e_1)$ and minor $(e_2)$. These are described by Equation 4, 5,

$e_1=\sqrt{1-\frac{c^2}{a^2}},(4)$

$e_2=\sqrt{1-\frac{b^2}{a^2}},(5)$

where $a$, $b$ and $c$ are the largest, middle and smallest semi-axes, respectively, as defined above. Following the shape classification, we evaluated the orientation of the principal axes of inertia with respect to the Au surface. We define the $xy$ plane as the plane of the gold surface and evaluate which of the three plane formed by the principal axes is parallel to the surface, if any. In this way, we gain insight into the orientation in which the minimal model adsorbs onto the surface, i.e., whether it adopts a major side-on, minor side-on, tip-on or tilted orientation (see Supplementary Figure S12 for a graphical representation of the different cases). These orientations are defined on the basis of approximating the protein as an ellipsoid. Specifically we define an orientation to be major side-on if the plane formed by the semi-axes $a$ and $b$ are mostly parallel to the Au surface. The plane formed by a pair of principal axes is considered to be mostly parallel to the surface if the angle between this plane and the $xy$ plane (Au surface) is less than 15°. Minor side-on orientations correspond to the case when the plane formed by the semi-axes $a$ and $c$ are mostly parallel to the Au surface, while tip-on correspond to the case where the plane formed by the semi-axes $b$ and $c$ is mostly parallel to the Au surface. An orientation is considered to be tilted when none of the planes formed by any pair of principal axes can be considered mostly parallel to the Au surface. For tilted conformations, we then define a secondary classification based on which plane formed by a pair of principal axes forms an angle with the $xy$ plane $15°<\epsilon <45°$. For an ellipsoid, if this plane corresponds to the $ab$ plane, the conformation is classified as tilted major side-on. If the plane is formed by the $a$ and $c$ semi-axes, the structure is identified as tilted minor side-on. If the plane is the one formed by $b$ and $c$, the protein is considered tilted tip-on. For spheroidal objects, the primary conformation classification simplifies to three cases; side-on, tip-on and tilted because the minor and major side-on orientations are indistinguishable, as two of the semi-axes are of similar length. Note that for spherical objects, all conformations defined above are indistinguishable from each other, because the symmetry of the shape renders any orientation relative to the surface equivalent. For a graphical representation of the possible orientations, see Supplementary Figure S12 ESI.

The simulations in pure water show that HSA presents a spheroid shape, specifically oblate, with semi-axes $a=4.11\pm 0.03$ nm, $b=3.91\pm 0.04$ nm, $c=2.47\pm 0.02$ nm, and eccentricities $e_1=0.80\pm 0.01$ and $e_2=0.31\pm 0.01$. All values are obtained by averaging over the last 100 ns of the simulation. On the other hand, TRF exhibits an ellipsoid shape, with semi-axes $a=4.93\pm 0.05$ nm, $b=3.47\pm 0.03$ nm, $c=2.47\pm 0.03$ nm, and eccentricities $e_1=0.87\pm 0.01$ and $e_2=0.71\pm 0.01$. A graphical representation of the proteins’ minimal models in pure water is shown in Figures 5–a for HSA and Figure 6a for TRF. The eccentricities of the adsorbed complexes on the surface of Au (111) are presented in Table 2, together with their orientation classification. The final orientations are illustrated in Figures 5–bc for HSA and Figures 6b,c for TRF. The reported orientations correspond to the most populated ones (that is, the orientations in which the protein spends the most time) in the last 100 ns of the simulation, during which the protein is assumed to be steadily adsorbed to the surface. Our analysis suggests that both proteins retain their individual shapes, an oblate spheroid for HSA and an ellipsoid for TRF, even after adsorption on the gold surface (Supplementary Figure S13 ESI). However, after relaxation on the surface, we can observe a change in the $e_2$ values, particularly for HSA (Supplementary Figure S13 ESI). Since $e_2$ represents the eccentricity between the middle and major axes, a change in this value implies that the aspect ratio of the spherical side is modified upon interaction with the surface. Indeed, in Section 3.2.1 we have observed partial structural rearrangements in HSA’s RMSF and secondary structure upon binding. Here, it appears that these structural rearrangements also lead to variations in the second eccentricity $e_2$, allowing the protein to adapt to the interaction with the surface while maintaining its overall shape. For both HSA and TRF, the preferred final binding orientations are generally tip-on, as summarized in Table 2.

Figure 5

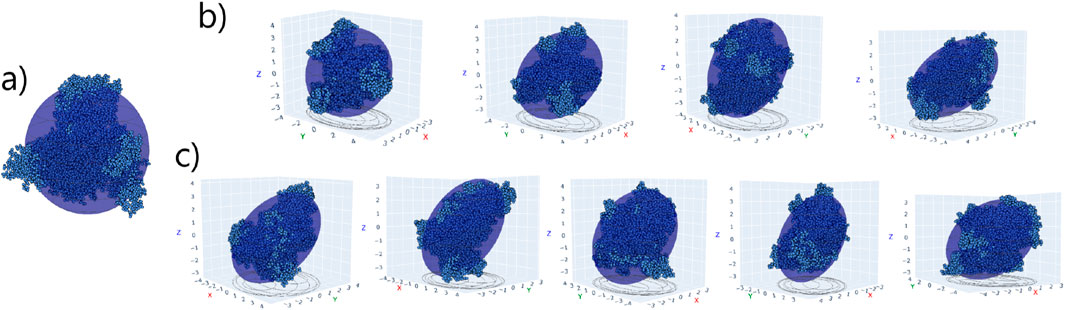
Figure 5. (a) HSA structure overlapped with equivalent spheroid in pure water. (b,c) HSA - A (d1-d4) and HSA - B (d1-d5) complexes, respectively, in their final binding orientations on the Au (111) surface (not shown). The xy plane corresponds to the Au surface.

Figure 6

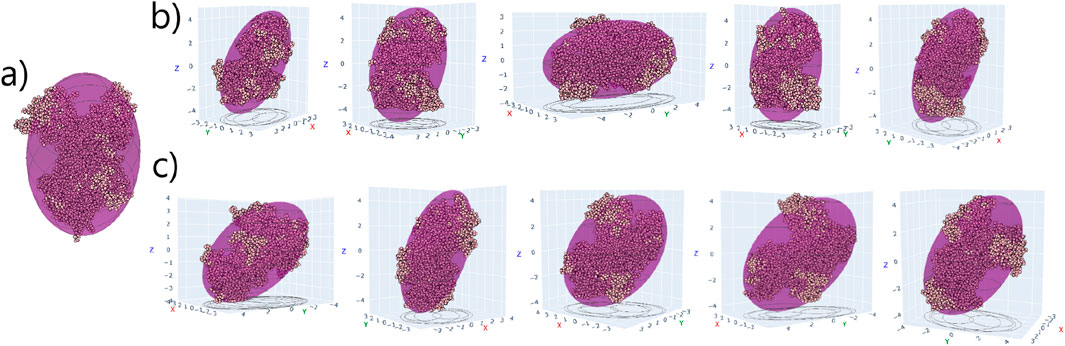
Figure 6. (a) TRF structure overlapped with equivalent ellipsoid in pure water. (b,c) TRF - A (d1-d5) and TRF - B (d1-d5) complexes, respectively, in their final binding orientations on the Au (111) surface (not shown). The xy plane corresponds to the Au surface.

Table 2

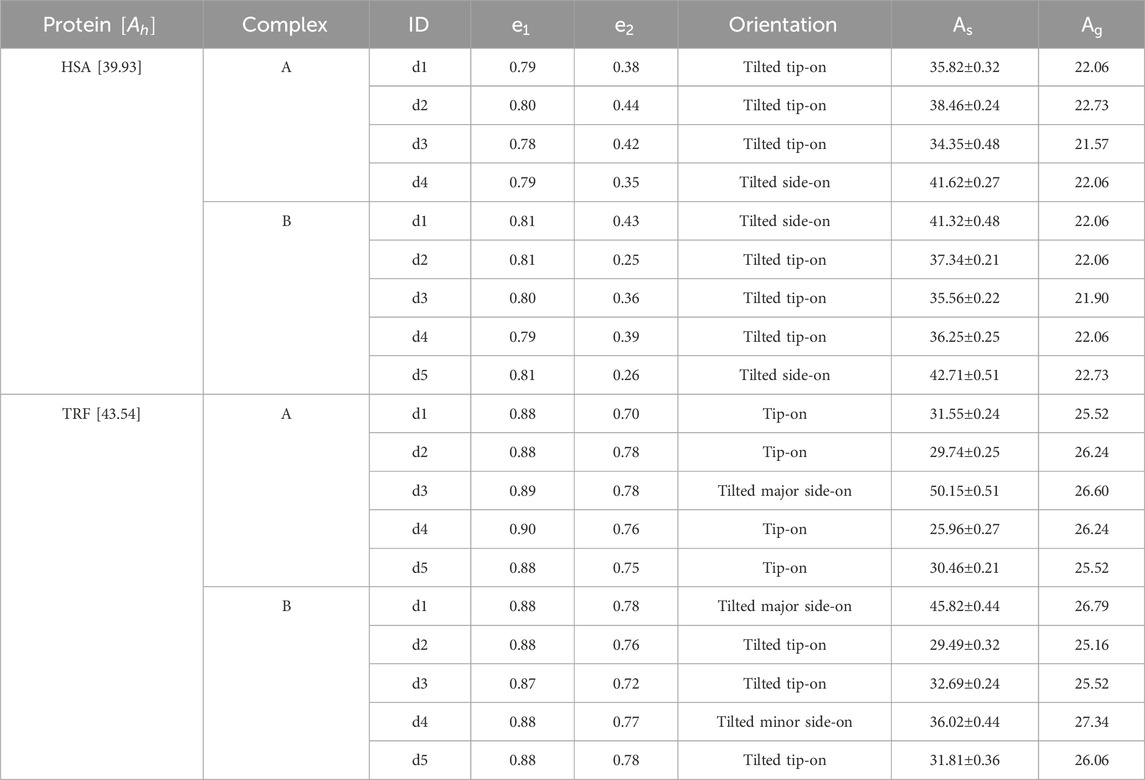
Table 2. Orientation analysis of proteins after adsorption on Au (111). Next to each protein name, the value in brackets $[A_h]$ (in ${\text{nm}}^2$) represents the contact area between a sphere of radius equal to the protein’s hydrodynamic size and the Au surface. $e_1$ and $e_2$ are the major and minor eccentricity, respectively. $A_s$: The contact area between the minimal shape (spheroid or ellipsoid) in its specific orientation and the surface, measured in ${\text{nm}}^2$. This value is measured over the last 100 ns of the simulations, taking into account variations in the orientation and in the semi-axes length. $A_g$: the contact area between the equivalent sphere of size of the gyration radius (see Table 1) in ${\text{nm}}^2$.

We then computed the surface area occupied by the proposed minimal models - e.g., the projected binding area - in their specific orientations, and compared it to the area obtained when representing the protein as a sphere of equivalent hydrodynamic or gyration size, as shown in Table 2. The hydrodynamic radius was determined using HYDROPRO (García De La Torre et al., 2000) on the protein structure in pure water, while the gyration radius used is as in Table 1. For these, the projected binding area corresponds to $A=\pi r^2$, with $r$ either hydrodynamic or gyration radius. For the ellipsoid and spheroid, the projected binding area was calculated as follows. The equivalent ellipsoid/spheroid was generated with its specified semi-axes lengths and rotated according to the orientation of its principal axes of inertia. A total of 10,000 points were used to plot the surface of the minimal shape. The surface points of the ellipsoid/spheroid were then flattened onto the XY plane by removing the Z component. To estimate the projected binding area, we computed the convex hull of these points, forming the smallest convex polygon that encloses all of them. The area of this polygon, obtained using the 2D ConvexHull function from SciPy (Virtanen et al., 2020), corresponds to the projected area of the ellipsoid. This method can be used to calculate the projected binding area when the minimal shape is tilted, even by a very small angle. When the shape is perfectly parallel to the surface, the projected area simplifies to the area of the projected 2D ellipse or sphere, depending on the shape and side facing the surface. In the limit case of tip-on orientations, the occupied surface area is about 30 ${\text{nm}}^2$ for HSA and 27 ${\text{nm}}^2$ for TRF, while in major side-on orientations it can reach up to 50 ${\text{nm}}^2$ for HSA and 54 ${\text{nm}}^2$ for TRF. This highlights how different orientations of anisotropic protein shapes can lead to a wide range of occupied surface areas, significantly impacting the packing density of multiple proteins on the surface. It also underscores the limitations of representing proteins as simple spheres based on equivalent hydrodynamic or gyration radii, as such approximations fail to capture different organizations. As shown in Table 2, representing the protein as a hydrodynamic or gyration sphere often leads to an inaccurate estimation of the projected binding area, which can be either significantly smaller or larger than the actual value. More complex protein shapes, like those studied here, can exhibit a wide range of projected areas that vary significantly with orientation. An accurate estimation of the projected binding area has important implications for dynamic and kinetic models of protein adsorption on surfaces. It directly influences surface coverage calculations, affecting the estimated protein density and the availability of binding sites for further adsorption events. For instance, on a flat 10,000 ${\text{nm}}^2$ surface, the estimated number of TRF molecules that can adsorb varies significantly depending on the chosen model. As an example, we consider TRF complex A, replica d3. Using the hydrodynamic radius, $\sim 230$ molecules can fit, while the radius of gyration allows for $\sim 376$. However, by employing a more refined model—such as the one proposed here, which accounts for the observed tilted major side-on orientation—the estimated number of adsorbed molecules is reduced to approximately $\sim 199$ molecules. For this reason, it is essential to account for more complex molecular shapes and orientations in adsorption models.

We must warn that the orientation classification presented so far is based solely on the planes formed between the semi-axes and their orientation relative to the $xy$ plane, not on the specific direction of the individual semi-axes. In other words, even if the protein initially adopts a tip-on orientation, it may undergo orientational readjustments by rotating around a particular semi-axis, eventually returning to a tip-on orientation, but on the completely opposite side. A dynamic orientation analysis has important implications in the adsorption process. Short-lived or unstable orientations may indicate that the protein is still undergoing significant adjustments to better adapt to the surface. To analyze how the orientation evolves over time, we computed the azimuthal and elevation angles of a unit vector aligned with one of the principal axes of inertia at each frame of the trajectory. Specifically, we chose as reference the axis that in the classified orientation is the most orthogonal to the $xy$ plane, as in Figures 7–a. The aligned vector can be characterized by two angles, the azimuthal $\alpha \in [-\mathrm{180,180}]$ and the elevation $\epsilon \in [-\mathrm{90,90}]$, which track its rotation about the $z$-axis and its inclination relative to the $xy$-plane, respectively. A schematic representation of the derivation of $\alpha$ and $\epsilon$ is shown in Figure 7, together with the evolution of these two angles over the time for selected complexes.

Figure 7

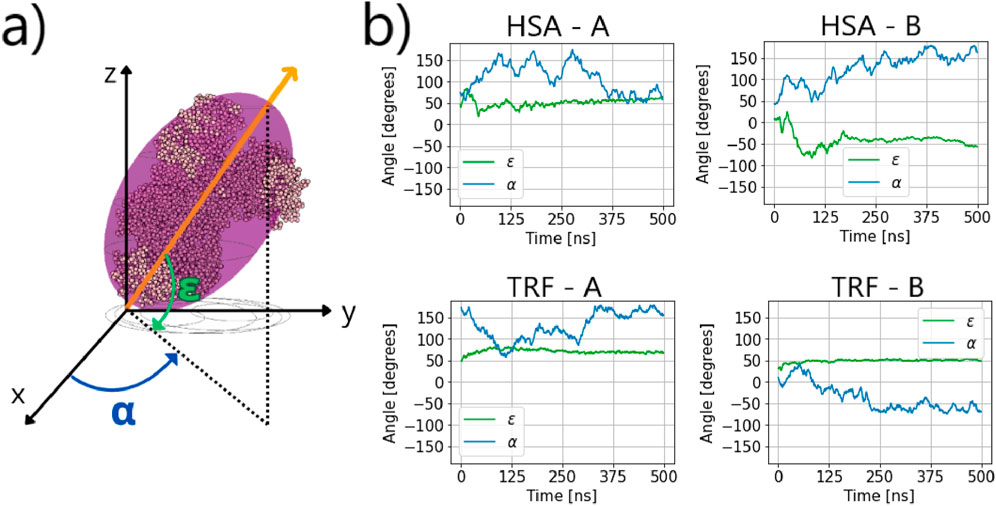
Figure 7. (a) TRF structure overlapped with equivalent ellipsoid and definition of dynamic orientation. Any protein is described by a position vector that corresponds to one of the principal axes of inertia (the most orthogonal to the $xy$-plane). The orientation of this vector is characterized by two polar angles, azimuthal $(\alpha )$ around the $z$-axis and elevation $(\epsilon )$ with the $xy$-plane. (b) Spherical angles $\alpha$ (blue) and $\epsilon$ (green) of four case studies, one for each complex investigated.

Our data show small fluctuations in the angle $\epsilon$ for TRF complexes, which align with the mechanisms described in Section 3.2.4, Section 3.2.5. TRF does not undergo significant re-orientational adjustments, either before or after binding to the Au surface. In contrast, HSA complexes exhibit a substantial number of replicas with major re-orientations, as indicated by greater fluctuations of $\epsilon$. These re-orientations predominantly occur before and during the binding to the surface, as response to the multiple reversible anchoring attempts discussed in Section 3.2.2, Section 3.2.3. Once the protein successfully binds, no major rotational changes are observed at this angle. Furthermore, we observe that the rate of re-orientations depends on the residues involved in the anchoring and lock-down mechanisms and the protein’s inherent dynamic flexibility. Our long-timescale simulations suggest that once lock-down begins, rotational motion in $\epsilon$ reaches a relatively steady state or, at the very least, occurs in a more gradual fashion. In contrast, rotation around the $z$-axis remains unrestricted even after binding, as evidenced by persistent large fluctuations in the angle $\alpha$ across all complexes. The plots with the time evolution of $\alpha$ and $\epsilon$ for all the replicas simulated in this study are available in Supplementary Figure S14 ESI. These results suggests that while the protein achieves a stable interaction with the surface, it retains rotational freedom around this axis, potentially leading to slow structural adjustments to optimize binding. The fact that the azimuthal angle remains completely free to fluctuate even after binding has significant implications for the protein’s ability to achieve optimal interaction with the surface. The binding to Au (111) does not impose strong energetic constraints on in-plane rotations around the z-axis perpendicular to the surface. However, it is important to note that, at least within the limited number of systems and replicas investigated in this study, larger variations in the energy landscape (Figure 2) appear to be more strongly associated with fluctuations in the elevation angle and azimuthal angle, rather than in the azimuthal one alone. This is expected, since changes in the elevation angle correspond to the binding of different regions (and consequently different residues) of the protein to the surface, as discussed in the binding mechanisms Sections 3.2.2-3.2.5. In contrast, variations in the azimuthal angle, while influencing orientation, do not lead to changes in the contact points. Instead, they could be linked to the observed structural rearrangements of the protein still relaxing and adapting to the surface. In some cases, global re-orientations took place also in later stages of the simulations, when the protein is steadily attached to the surface. An example of this is observed in HSA B, replicas d1 and d3, and TRF B- d1, where variations in the $\epsilon$ of the principal axes of inertia take place even within the final 100 ns of the simulations (Supplementary Figure S15 ESI) despite the protein being steadily anchored to the surface. In the two HSA B replicas, it is interesting to observe that the orientation shifts from a tilted side-on to a tilted tip-on one. This transition occurs as a result of the adsorption of new residues in the late stages of the simulation. We observe d1 binding to the surface some additional residues in the C-terminal domain, while d3 adsorbs several residues in the 228–367. In both cases, this additional adsorption causes the opposite side of the protein to lift, in a sort of lever-like mechanism. In d1 we observe the 237-370 domain lifting and, perhaps unsurprisingly, in d3 it is the C-terminal domain that raises. Despite adsorbing completely opposite domains, both systems exhibit a remarkably balanced counteracting movement on either side. This highlights the strong connection between these two regions, which align along the longer semi-axes of the protein, as well as the inherent tendency of HSA to maintain its overall globular shape. In TRF B d1, we observe the additional adsorption of residues in the 434–438 range. This causes the major semi-axis to tilt towards the surface, from a tip-on to a major side-on orientation, bringing the 100–210 domain closer to it, though without establishing direct binding.

4 Discussion, conclusion, and perspectives

The binding mechanism and orientation of proteins on surfaces have important implications for their biological outcome, influencing functionality, potential toxicity, and interactions with membranes. This is particularly relevant in nanomaterials, where nanoparticles are rapidly coated by a protein corona upon contact with biological fluids. In this study, we systematically examined the dynamics of two relevant plasma proteins, HSA and TRF, on neutral gold surfaces using BD simulations in a continuum solvent and MD simulations with explicit solvent. Our findings indicate that the adsorption process of large plasma proteins follows a three-step mechanism: i) directed diffusion of the protein from the bulk solution toward the water/solid interface; ii) initial anchoring to dense interfacial water layers via interactions with hydrophilic amino acids; iii) lockdown phase, driven by interactions between strongly interacting amino acids and the Au (111) surface. We observe that interfacial water is responsible for the biased diffusion of the protein towards the surface, but also determines the outcome of the second phase, leading to reversible anchoring and re-orientation if dominated by hydrophobic amino acids.

In addition to that, we observe a direct correlation between immediate or reversible anchoring and protein’s local flexibility. Orientational rearrangements are analyzed in detail and discussed in relation to the binding mechanism and structural properties. The inherent local flexibility of TRF facilitates rapid adjustments, allowing swift and stable anchoring. In contrast, HSA’s rigidity hinders efficient initial contact, leading to reversibility or misaligned anchoring and major re-orientation. However, once anchored, HSA achieves superior interaction energies, as its slower relaxation process and the rotational freedom around the axis orthogonal to the surface allow the structure to effectively adjust to the surface. Our results suggest a trade-off between speed and flexibility in TRF’s binding mechanism versus stability and energy optimization in HSA. Such insights enhance our understanding of protein-surface interactions, particularly how intrinsic structural properties influence the formation, organization, and stability of protein coronas.

The adsorption of proteins onto nanomaterials can induce structural changes that alter their overall shape (Sheibani et al., 2021; Picco et al., 2021; Cao et al., 2021; Musicò et al., 2025). To better understand the global shape of the protein corona, it is important to be able to clearly determine the proteins’ shape and their orientation over the surface. For this reason, we propose a systematic method for classifying the shape and orientation of the protein relative to the surface after binding. Our observations indicate a predominant tip-on orientation for both HSA and TRF, with their overall shape that can be approximated to spheroidal and ellipsoidal models, respectively. Interestingly, side-on orientations, which one might expect to be more energetically favorable due to their larger contact area with the surface, do not always correspond to the most stable complexes. We attribute this to two main factors: ii) the time length and number of replicas simulated may not be sufficient to observe proteins fully relaxing on the surface. Over longer timescales or larger sampling, it is possible that the proteins under analysis adopt a more stable side-on orientation, maximizing their contact with the surface; ii) limitations in the minimal models. We must emphasize that these models should be used solely to classify the final shape and orientation of the protein on the surface. Although they may capture key geometric trends, they do not account for critical features such as protein flexibility in the contact area, internal structural fluctuations, and, most importantly, uneven mass distribution. Despite these limitations, our approach to classifying protein shape and orientation remains a valuable tool for understanding the overall organization of proteins adsorbed on surfaces at larger time and length scales. In fact, we observe differences in the projected binding area between representing the proteins as ellipsoids and representing them as single spheres of equivalent hydrodynamic size. This distinction has important implications in the context of kinetic and dynamic models of protein adsorption on both flat surfaces and nanoparticles (Dell’Orco et al., 2010; Vilaseca et al., 2013; Vilanova et al., 2016; Power et al., 2019; Vilanova et al., 2025). Recent models account for the fact that once a protein occupies a specific projected binding area on the surface, that space becomes unavailable for additional protein binding, assuming the projected area can be accurately determined (Rouse and Lobaskin, 2021). The orientation a protein adopts on a surface directly impacts both the available binding area for other proteins in solution and the overall surface concentration of adsorbed proteins. Different orientations can lead to significant variations in packing density, particularly for proteins with highly anisotropic shapes, where variations in orientation can result in drastically different surface coverage and organization (Vilaseca et al., 2013). Additionally, the parametrization of coarse-grained models greatly benefits from accurate shape, orientation, and contact surface data, as these models aim to capture the key aspects of adsorption affinity from full-atomistic simulations while reducing computational costs Brancolini and Tozzini (2019).

From a dynamic point of view, we observed significant re-orientations in HSA complexes, whereas TRF complexes exhibited minimal or no re-orientations. Our analysis reveals a direct correlation between these re-orientations and the anchoring mechanism, leading us to hypothesize that both phenomena are influenced by the intrinsic local flexibility of the protein. These findings align with previous studies on small proteins and peptides, where rigid proteins undergo domain-domain reorientation and require longer times for adsorption (Penna et al., 2014; Hoefling et al., 2011; Norde, 2008; Agashe et al., 2005), and with the notion that protein orientational motions occur much faster than conformational changes (Agashe et al., 2005). Our results extend this concept to larger proteins interacting with gold surfaces, emphasizing how domain reorientation can significantly influence the composition and properties of the protein corona.

In summary, our results reveal distinct binding strategies: TRF exploits its inherent structural flexibility for rapid and stable anchoring, while HSA’s rigidity poses initial challenges but enables strong, energetically favorable interactions upon relaxation. This trade-off between speed and flexibility in the binding of TRF versus stability and energy optimization in HSA enhances our understanding of protein-surface interactions, particularly how intrinsic structural properties influence the formation and stability of protein coronas. These findings offer valuable insights into the mechanisms underlying protein adsorption on gold surfaces, which have broad implications for nanobiotechnology and biomaterials design. The distinct dynamics observed for HSA and TRF underscore the importance of tailoring surface functionalization to accommodate specific protein properties. Importantly, the results obtained at the all-atom level of resolution are critical for the development of coarse-grained and mesoscale models. The approach in classifying protein orientation enhances our understanding of the protein corona’s shape and morphology and could advance its effective representation in lower-resolution models. The insights gained from these simulations enable us to analyze the different adsorption behavior of TRF and HSA, providing a deeper understanding of how their structural properties influence protein corona formation.

Future research could focus on exploring how variations in surface chemistry, charge, or topography influence the adsorption dynamics of rigid and flexible proteins. Additionally, extending these studies to multi-protein systems would provide a deeper understanding of protein corona formation and shape in macromolecular crowding conditions, and its implications for applications such as biosensors, drug delivery systems, and nanomedicine. Future work should focus on investigating conformational changes induced by protein adsorption, as these alterations can expose new binding sites, influencing protein-protein interactions and aggregation. Understanding these structural rearrangements is crucial for predicting nanoparticle corona formation and assessing how they affect protein’s biological function, stability, and interactions with other biomolecules. The insights gained from our analysis can inform the design of coarse-grained models that incorporate the geometrical features of interacting beads, thereby improving the representation of protein-nanoparticle systems while significantly reducing computational cost. By bridging multiscale molecular dynamics simulations with experimental techniques, we can refine our understanding of protein-surface interactions, enabling the design of more effective and biocompatible nanomaterials.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

BC: Formal Analysis, Investigation, Methodology, Visualization, Writing – original draft, Writing – review and editing. HL: Conceptualization, Formal Analysis, Supervision, Writing – review and editing. GB: Conceptualization, Funding acquisition, Resources, Supervision, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by funding from the Italian Ministry of University and Research (MUR) under the PRIN2020 program (project code: 2020LW7XWH). The total project funding amounted to €861,000, with €210,000 allocated to the CNR NANO Operational Unit. The funding was formalized under Protocol No. 0001370 dated 29/04/2022. The Coordinator for the University of Parma was Prof. Roberto Perris and the Principal Investigator for the CNR NANO unit was Giorgia Brancolini, serving as the Unit Leader. Other Italian partners involved in the project include the University of Ferrara (UniFe), and the University of Padua (UniPD). BC’s PhD project was funded through a stipend provided by Research Ireland (Grant No. GOIPG/2023/5034) and the Technological University of Dublin (First Time Supervisor Award). The funder had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgments

GB acknowledges the funding by PRIN 2020 (Grant Nr. 2020LW7XWH). GB. and BC. acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources on Marconi100 and support. GB. acknowledges Oak Ridge National Laboratory by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy is acknowledged for the supercomputing project CNMS2020-B- 00433. GB. acknowledges Facilities of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, are also acknowledged. BC and HL acknowledge the Irish Research Council under grant number GOIPG/2023/5034. BC and HL acknowledge the TU Dublin First Time Supervisor Award.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnano.2025.1603727/full#supplementary-material

References

Abraham, M. J., Murtola, T., Schulz, R., Páll, S., Smith, J. C., Hess, B., et al. (2015). GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1-2, 19–25. doi:10.1016/j.softx.2015.06.001

CrossRef Full Text | Google Scholar

Agashe, M., Raut, V., Stuart, S. J., and Latour, R. A. (2005). Molecular simulation to characterize the adsorption behavior of a fibrinogen γ -chain fragment. Langmuir 9, 1103–1117. doi:10.1021/la0478346

CrossRef Full Text | Google Scholar

Baimanov, D., Cai, R., and Chen, C. (2019). Understanding the chemical nature of nanoparticle protein interactions. Bioconjugate Chem. 30, 1923–1937. doi:10.1021/acs.bioconjchem.9b00348

PubMed Abstract | CrossRef Full Text | Google Scholar

Bekker, H., Berendsen, H. J. C., and Van Der Spoel, D. (1993). Gromacs: a parallel computer for molecular dynamics simulations. Phys. Comput. 92, 252–256.

Google Scholar

Bewersdor, T., Glitscher, E. A., Bergueiro, J., Eravci, M., Miceli, E., Haase, A., et al. (2020). The influence of shape and charge on protein corona composition in common gold nanostructures. Mater. Sci. Eng. C 117, 111270. doi:10.1016/j.msec.2020.111270

CrossRef Full Text | Google Scholar

Bloise, N., Strada, S., Dacarro, G., and Visai, L. (2022). Gold nanoparticles contact with cancer cell: a brief update. Inernational J. Mol. Sci. 23, 7683. doi:10.3390/ijms23147683

PubMed Abstract | CrossRef Full Text | Google Scholar

Brancolini, G., Bellucci, L., Maschio, M. C., Felice, R. D., and Corni, S. (2019a). The interaction of peptides and proteins with nanostructures surfaces: a challenge for nanoscience. Curr. Opin. Colloid Interface Sci. 41, 86–94. doi:10.1016/j.cocis.2018.12.003

CrossRef Full Text | Google Scholar

Brancolini, G., Kokh, D. B., Calzolai, L., Wade, R. C., and Corni, S. (2012). Docking of ubiquitin to gold nanoparticles. ACS Nano 6, 9863–9878. doi:10.1021/nn303444b

PubMed Abstract | CrossRef Full Text | Google Scholar

Brancolini, G., Lopez, H., Corni, S., and Tozzini, V. (2019b). Low-resolution models for the interaction dynamics of coated gold nanoparticles with β2-microglobulin. Int. J. Mol. Sci. 20, 3866. doi:10.3390/ijms20163866

PubMed Abstract | CrossRef Full Text | Google Scholar

Brancolini, G., and Tozzini, V. (2019). Multiscale modeling of proteins interaction with functionalized nanoparticles. Curr. Opin. Colloid Interface Sci. 41, 66–73. doi:10.1016/j.cocis.2018.12.001

CrossRef Full Text | Google Scholar

Cao, C., Zhang, L., Kent, B., Wong, S., Garvey, C. J., and Stenzel, M. H. (2021). The protein corona leads to deformation of spherical micelles. Angew. Chem. Int. Ed. 60, 10342–10349. doi:10.1002/anie.202101129

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, J., Chen, C., Yin, M., Li, H., Li, W., Zhang, Z., et al. (2023). Interactions between gold nanoparticles with different morphologies and human serum albumin. Front. Chem. 11, 1273388–15. doi:10.3389/fchem.2023.1273388

PubMed Abstract | CrossRef Full Text | Google Scholar

Dell’Orco, D., Lundqvist, M., Oslakovic, C., Cedervall, T., and Linse, S. (2010). Modeling the time evolution of the nanoparticle-protein corona in a body fluid. PLOS One 5, e10949–8. doi:10.1371/journal.pone.0010949

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolinsky, T. J., Nielsen, J. E., Mccammon, J. A., and Baker, N. A. (2004). PDB2PQR: an automated pipeline for the setup of Poisson – Boltzmann electrostatics calculations. Nucleic Acids Res. 32, 665–667. doi:10.1093/nar/gkh381

PubMed Abstract | CrossRef Full Text | Google Scholar

Dykman, L., and Khlebtsov, N. (2012). Gold nanoparticles in biomedical applications: recent advances and perspectives. Chem. Soc. Rev. 41, 2256–2282. doi:10.1039/c1cs15166e

PubMed Abstract | CrossRef Full Text | Google Scholar

Erik, C., Dreaden, X. H., Alaaldin, M. A., and El-Sayed, M. A. (2012). The golden age: gold nanoparticles for biomedicine. Chem. Soc. Rev. 41, 2740–2779. doi:10.1039/c1cs15237h

CrossRef Full Text | Google Scholar

Feng Ding, R. C., Slaven, R., Ke, P. C., Chen, P., Geitner, N. K., Brown, J. M., et al. (2013). Direct observation of a single nanoparticle–ubiquitin corona formation. Nanoscale 5, 9162–9169. doi:10.1039/c3nr02147e

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabdoulline, R. R., and Wade, R. C. (1996). Effective charges for Macromolecules in solvent. J. Phys. Chem. 100, 3868–3878. doi:10.1021/jp953109f

CrossRef Full Text | Google Scholar

García De La Torre, J., Huertas, M. L., and Carrasco, B. (2000). Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophysical J. 78, 719–730. doi:10.1016/S0006-3495(00)76630-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Gkouvatsos, K., Papanikolaou, G., and Pantopoulos, K. (2012). Regulation of iron transport and the role of transferrin. Biochimica Biophysica Acta - General Subj. 1820, 188–202. doi:10.1016/j.bbagen.2011.10.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomme, P. T., Mccann, K. B., and Bertolini, J. (2005). Transferrin: structure, function and potential therapeutic actions. Drug Discov. Today 10, 267–273. doi:10.1016/S1359-6446(04)03333-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hess, B., Bekker, H., Berendsen, H. J. C., and Fraaije, J. G. E. M. (1997). LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18, 1463–1472. doi:10.1002/(SICI)1096-987X(199709)18:12⟨1463::AID-JCC4⟩3.0.CO;2-H

CrossRef Full Text | Google Scholar

Hoefling, M., Monti, S., Corni, S., and Gottschalk, K. E. (2011). Interaction of β -sheet folds with a gold surface. PLOS One 6, e20925. doi:10.1371/journal.pone.0020925

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical dynamics: equilibrium phase-space distributions canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1965–1967. doi:10.1103/PhysRevA.31.1695

CrossRef Full Text | Google Scholar

Iori, F., and Corni, S. (2008). Including image charge effects in the molecular dynamics simulations of molecules on metal surfaces. J. Comput. Chem. 29, 1656–1666. doi:10.1002/jcc.20928

PubMed Abstract | CrossRef Full Text | Google Scholar

Jurrus, E., Engel, D., Star, K., Monson, K., Brandi, J., Felberg, L. E., et al. (2018). Improvements to the APBS biomolecular solvation software suite. Protein Sci. 27, 112–128. doi:10.1002/pro.3280

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokh, D. B., Corni, S., Winn, P. J., Hoefling, M., Gottschalk, K. E., and Wade, R. C. (2010). ProMetCS: an atomistic force field for modeling protein-metal surface interactions in a continuum aqueous solvent. J. Chem. Theory Comput. 6, 1753–1768. doi:10.1021/ct100086j

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H. (2023). Differences in protein distribution, conformation, and dynamics in hard and soft coronas: dependence on protein and particle electrostatics. Phys. Chem. Chem. Phys. 25, 7496–7507. doi:10.1039/d2cp05936c

PubMed Abstract | CrossRef Full Text | Google Scholar

Lynch, I., Salvati, A., and Dawson, K. A. (2009). What does the cell see? Nat. Nanotechnol. 4, 546–547. doi:10.1038/nnano.2009.248

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinez, M., Bruce, N. J., Romanowska, J., Kokh, D. B., Ozboyaci, M., Yu, X., et al. (2015). SDA 7: a modular and parallel implementation of the simulation of diffusional association software. J. Comput. Chem. 36, 1631–1645. doi:10.1002/jcc.23971

PubMed Abstract | CrossRef Full Text | Google Scholar

Matus, M. F., and Hakkinen, H. (2024). Rational design of targeted gold nanoclusters with high affinity to integrin αvβ3 for combination cancer therapy. Bioconjugate Chem. 35, 1481–1490. doi:10.1021/acs.bioconjchem.4c00248

PubMed Abstract | CrossRef Full Text | Google Scholar

Mcdonagh, B. H., Volden, S., Lystvet, S. M., Singh, G., Ese, M.-h. G., Ryan, J. A., et al. (2015). Self-assembly and characterization of transferrin–gold nanoconstructs and their interaction with bio-interfaces. Nanoscale 7, 8062–8070. doi:10.1039/c5nr01284h

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammad-Beigi, H., Hayashi, Y., Zeuthen, C. M., Eskandari, H., Scavenius, C., Juul-Madsen, K., et al. (2020). Mapping and identification of soft corona proteins at nanoparticles and their impact on cellular association. Nat. Commun. 11, 4535. doi:10.1038/s41467-020-18237-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Monopoli, M. P., Åberg, C., Salvati, A., and Dawson, K. A. (2012). Biomolecular coronas provide the biological identity of nanosized materials. Nat. Nanotechnol. 7, 779–786. doi:10.1038/nnano.2012.207

PubMed Abstract | CrossRef Full Text | Google Scholar

Musicò, A., Zendrini, A., Reyes, S. G., Mangolini, V., Paolini, L., Romano, M., et al. (2025). Extracellular vesicles of different cellular origin feature distinct biomolecular corona dynamics. Nanoscale Horizons 10, 104–112. doi:10.1039/d4nh00320a

PubMed Abstract | CrossRef Full Text | Google Scholar

Nel, A. E., Mädler, L., Velegol, D., Xia, T., Hoek, E. M., Somasundaran, P., et al. (2009). Understanding biophysicochemical interactions at the nano-bio interface. Nat. Mater. 8, 543–557. doi:10.1038/nmat2442

PubMed Abstract | CrossRef Full Text | Google Scholar

Neupane, S., Pan, Y., Li, H., Patnode, K., Farmakes, J., Liu, G., et al. (2018). Engineering protein gold nanoparticle/nanorod complexation via surface modification for protein immobilization and potential therapeutic applications. ACS Appl. Nano Mater. 1, 4053–4063. doi:10.1021/acsanm.8b00839

CrossRef Full Text | Google Scholar

Norde, W. (2008). My voyage of discovery to proteins in flatland …and beyond. beyond. Colloids Surfaces B Biointerfaces 61, 1–9. doi:10.1016/j.colsurfb.2007.09.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Nose, S. (1984). A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52, 255–268. doi:10.1080/00268978400101201

CrossRef Full Text | Google Scholar

Olsson, M. H. M., Søndergaard, C. R., Rostkowski, M., and Jensen, J. H. (2011). PROPKA3: consistent treatment of internal and surface residues in empirical pKa predictions. J. Chem. Theory Comput. 7, 525–537. doi:10.1021/ct100578z

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozboyaci, M., Kokh, D. B., and Wade, R. C. (2016). Three steps to gold: mechanism of protein adsorption revealed by Brownian and molecular dynamics simulations. Phys. Chem. Chem. Phys. 18, 10191–10200. doi:10.1039/c6cp00201c

PubMed Abstract | CrossRef Full Text | Google Scholar

Penna, M. J., Mijajlovic, M., and Biggs, M. J. (2014). Molecular-level understanding of protein adsorption at the interface between water and a strongly interacting uncharged solid surface. J. Am. Chem. Soc. 136, 5323–5331. doi:10.1021/ja411796e

PubMed Abstract | CrossRef Full Text | Google Scholar

Picco, A. S., Capeletti, L. B., Cardoso, M. B., and Bettini, J. (2021). Inside the protein corona: from binding parameters to unstained hard and soft coronas visualization. Nano Lett. 21, 8250–8257. doi:10.1021/acs.nanolett.1c02416

CrossRef Full Text | Google Scholar

Power, D., Rouse, I., Poggio, S., Brandt, E., Lopez, H., Lyubartsev, A., et al. (2019). A multiscale model of protein adsorption on a nanoparticle surface. Model. Simul. Mater. Sci. Eng. 27, 084003. doi:10.1088/1361-651X/ab3b6e

CrossRef Full Text | Google Scholar

Pyne, A., Nandi, S., Ghosh, M., Roy, T., Dhara, S., and Sarkar, N. (2020). Denaturant-mediated modulation of the formation and drug encapsulation responses of gold nanoparticles. Langmuir 36, 7634–7647. doi:10.1021/acs.langmuir.0c01293

PubMed Abstract | CrossRef Full Text | Google Scholar

Ray, M., Brancolini, G., Luther, D. C., Jiang, Z., Cao-milán, R., Cuadros, A. M., et al. (2022). High affinity protein surface binding through co-engineering of nanoparticles and proteins. Nanoscale 14, 2411–2418. doi:10.1039/d1nr07497k

PubMed Abstract | CrossRef Full Text | Google Scholar

Robertson, M. J., Tirado-rives, J., and Jorgensen, W. L. (2015). Improved peptide and protein torsional energetics with the OPLS-AA force field. J. Chem. Theory Comput. 11, 3499–3509. doi:10.1021/acs.jctc.5b00356

PubMed Abstract | CrossRef Full Text | Google Scholar

Ronneberger, O., Tunyasuvunakool, K., Bates, R., Žídek, A., Ballard, A. J., Cowie, A., et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589. doi:10.1038/s41586-021-03819-2

CrossRef Full Text | Google Scholar

Rouse, I., and Lobaskin, V. (2021). A hard-sphere model of protein corona formation on spherical and cylindrical nanoparticles. Biophysical J. 120, 4457–4471. doi:10.1016/j.bpj.2021.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Schenk, S., Schoenhals, G. J., Souza, G. D., and Mann, M. (2008). A high confidence, manually validated human blood plasma protein reference set. BMC Med. Genomics 1, 41. doi:10.1186/1755-8794-1-41

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao, Q., and Hall, C. K. (2016). Protein adsorption on nanoparticles: model development using computer simulation. J. Phys. Condens. Matter 28, 414019. doi:10.1088/0953-8984/28/41/414019

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheibani, S., Basu, K., Farnudi, A., Ashkarran, A., Ichikawa, M., Presley, J. F., et al. (2021). Nanoscale characterization of the biomolecular corona by cryo-electron microscopy, cryo-electron tomography, and image simulation. Nat. Commun. 12, 573. doi:10.1038/s41467-020-20884-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Tenzer, S., Docter, D., Rosfa, S., Wlodarski, A., Rekik, A., Knauer, S. K., et al. (2011). Nanoparticle size is a critical physicochemical determinant of the human blood plasma corona: a comprehensive quantitative proteomic analysis. ACS Nano 5, 7155–7167. doi:10.1021/nn201950e

PubMed Abstract | CrossRef Full Text | Google Scholar

Theodore Peters, J. (1996). All about albumin: biochemistry, genetics, and medical applications. San Diego, CA: Academic Press.

Google Scholar

Trinh, D. N., Gardner, R. A., Franciosi, A. N., Mccarthy, C., Keane, M. P., Soliman, M. G., et al. (2022). Nanoparticle biomolecular corona-based enrichment of plasma glycoproteins for N-glycan profiling and application in biomarker discovery. ACS Nano 16, 5463–5475. doi:10.1021/acsnano.1c09564

PubMed Abstract | CrossRef Full Text | Google Scholar

Varadi, M., Bertoni, D., Magana, P., Paramval, U., Pidruchna, I., Radhakrishnan, M., et al. (2024). AlphaFold Protein Structure Database in 2024: providing structure coverage for over 214 million protein sequences. Nucleic Acid Res. 52, 368–375. doi:10.1093/nar/gkad1011

PubMed Abstract | CrossRef Full Text | Google Scholar

Vilanova, O., Martinez-serra, A., Monopoli, M. P., and Franzese, G. (2025). Characterizing the hard and soft nanoparticle-protein corona with multilayer adsorption. Front. Nanotechnol. 6, 1–16. doi:10.3389/fnano.2024.1531039

CrossRef Full Text | Google Scholar

Vilanova, O., Mittag, J. J., Kelly, P. M., Milani, S., Dawson, K. A., Rädler, J. O., et al. (2016). Understanding the kinetics of protein-nanoparticle corona formation. ACS Nano 10, 10842–10850. doi:10.1021/acsnano.6b04858

PubMed Abstract | CrossRef Full Text | Google Scholar

Vilaseca, P., Dawson, A., and Franzese, G. (2013). Understanding and modulating the competitive surface-adsorption of proteins through coarse-grained molecular dynamics simulations. Soft Matter 9, 6978–6985. doi:10.1039/c3sm50220a

CrossRef Full Text | Google Scholar

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., et al. (2020). Scipy 1.0: fundamental algorithms for scientific computing in python. Nat. Methods 17, 261–272. doi:10.1038/s41592-019-0686-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Li, J., Pan, J., Jiang, X., Ji, Y., Li, Y., et al. (2013). Revealing the binding structure of the protein corona on gold nanorods using synchrotron radiation-based techniques: understanding the reduced damage in cell membranes. J. Am. Chem. Soc. 135, 17359–17368. doi:10.1021/ja406924v

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, L. B., Rodger, P. M., Corni, S., and Walsh, T. R. (2013). GolP-CHARMM: first-principles based force fields for the interaction of proteins with Au(111) and Au(100). J. Chem. Theory Comput. 9, 1616–1630. doi:10.1021/ct301018m

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., and Skolnick, J. (2005). TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 33, 2302–2309. doi:10.1093/nar/gki524

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Wu, J. L. Y., Lazarovits, J., and Chan, W. C. W. (2020). An analysis of the binding function and structural organization of the protein corona. J. Am. Chem. Soc. 142, 8827–8836. doi:10.1021/jacs.0c01853

PubMed Abstract | CrossRef Full Text | Google Scholar