- 1 Biosystems Group, School of Computing, University of Leeds, Leeds, UK
- 2 Leeds Institute of Molecular Medicine, University of Leeds, Leeds, UK
- 3 Division of Biomedical Engineering, School of Engineering, University of Glasgow, Glasgow, UK
- 4 Institute of Integrative and Comparative Biology, University of Leeds, Leeds, UK
- 5 Institute of Membrane and Systems Biology, University of Leeds, Leeds, UK
A commentary on
Shared strategies for behavioral switching: understanding how locomotor patterns are turned on and off
by Mesce, K. A., and Pierce-Shimomura, J. T. (2010). Front. Behav. Neurosci. 4:49. doi: 10.3389/fnbeh.2010.00049
In their perspectives article, Mesce and Pierce-Shimomura (2010) make a case for the existence of two locomotion gaits in C. elegans, and for the ability of this nematode worm to choose between them. Here, we offer a counter-perspective, namely, that the variety of observed behaviors are more appropriately described as a single gait.
In what follows we focus on pure forward locomotion, which is generally believed to be controlled by a dedicated circuit, distinct from the circuits that control backward locomotion and head motor behavior. With regard to our question of gaits, we are not aware of any evidence that links head swings with the generation of propulsive (forward/backward) locomotion, so these will not be considered here.
Are Swimming and Crawling Characterized by Qualitatively Different Patterns of Body Bending?
In C. elegans, forward locomotion, whether “swimming” (in liquids) or “crawling” (in or on gels) involves smooth propagation of undulations from head to tail. We argue that while such propagations can vary in kinematic parameters such as frequency, wavelength, and amplitude, these variations are continuous and there is no evidence for more than a single fundamental behavior1. If, as Mesce and Pierce-Shimomura (2010) argue, “bends propagate at uniform velocity for crawling, but “whip” to the back of the body after characteristic pauses when the whole-body of the worm is bent into a C-shaped posture during swimming,” then these characteristic pauses would be evident in plots of bending angle over time: the longer the pauses in extreme maximally bent positions, the squarer the bending wave would appear. In fact, in Pierce-Shimomura et al.’s own data, bending plots over time show proportionately little time spent in the extreme positions (Pierce-Shimomura et al., 2008; Vidal-Gadea et al., 2009). Our own data for worms in liquid buffer solution confirm this (Figure 1C). More generally, Figure 1D clearly shows the equivalence of temporal patterns of dorso-ventral bending for “swimming,” “crawling,” and intermediate behaviors, upon normalization by amplitude and undulation period.
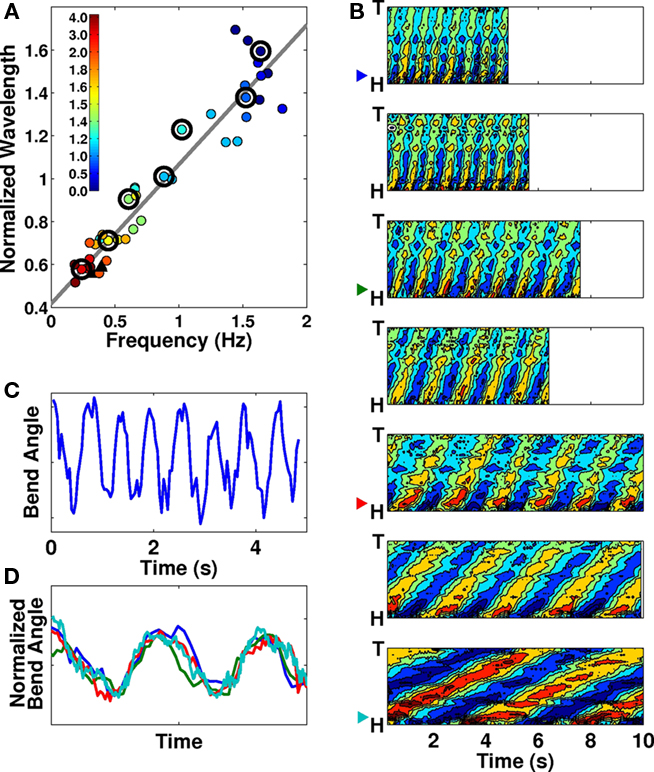
Figure 1. (A) Frequency–wavelength relation across a range of gelatin concentrations (filled circles) and agar surfaces (black triangles). Colors represent gelatin concentrations (%) as indicated. The best linear fit to the data is superimposed. Adapted from Figure 1B in Berri et al. (2009). Large black circles indicate which contour plots are shown in (B). (B) Seven contour plots of bending angle (represented by color, with dark red corresponding to extreme dorsal bending and dark blue to extreme ventral bending) over time (horizontal) and along the body (vertical), selected to show the range of observed forward locomotion behaviors, from “swimming” in liquid buffer solution (top) to “crawling” in relatively stiff gelatin (bottom; see methods in Berri et al., 2009 for additional details). Note the linear propagation along the entire body without changes in wave speed. (C) Trace of bending angle versus time for a point near the head of a worm in buffer solution [same data as top plot in (B)]. Note that the worm does not dwell in the maximally bent positions (peaks and troughs of the curve). (D) Bending angle traces as in (C), taken from the 1st, 3rd, 5th, and 7th panels of (B; see color-coded arrow heads) and normalized by undulation period and amplitude. Note the similarity of the waveforms.
Furthermore, if, as claimed, swimming worms “whip” their bodies and propagate bends at non-uniform velocity, this would be evidenced by non-linear stripes in the contour plots for swimming worms (Figure 1B of Pierce-Shimomura et al., 2008). Our own data (Figures 1A,B, reproduced with permission from Berri et al., 2009) similarly show uniform bend propagation for worms exhibiting a range of behaviors (corresponding to a range of physical conditions). Whether looking at the spacing between the stripes (the period of undulation), the inclination of the stripes (the speed of bend propagation) or the amount of overlap (the wavelength along the body), we find only a gradual change between consecutive plots. Finally, we note that bending along the body directly maps muscle activation. Calcium imaging of muscle activity during locomotion of unrestrained worms in water and on agar (Pierce-Shimomura et al., 2008) indicates a clear one-to-one relationship between muscle activity and bending. This strong match holds in both environments and does not break down for fast undulations (during swimming). Therefore, it is reasonable to expect that the same one-to-one relationship should hold in intermediate environments (up to a fixed phase lag which of course differs in different conditions). Another way of putting it is that body curvature is an equally appropriate (and easier to obtain) metric. In summary, the data strongly suggest that the entire transition from “swimming” to “crawling” corresponds to modulation of a single gait. Indeed, we find no evidence of a qualitative distinction between the undulation patterns.
Are Swimming and Crawling Characterized by Different Frequencies of Undulation?
Mesce and Pierce-Shimomura (2010) state that C. elegans worms “crawl with a persistent S-shaped posture on a dry substrate with ∼1 Hz high-amplitude bends, and swim in liquid with ∼2 Hz lower amplitude bends.” Indeed, the existence of two locomotion frequencies might be grounds to define two distinct gaits. However, it is important to point out the current consensus that the worm modulates its frequency of undulations as a function of the resistivity (viscosity or visco-elasticity) of the physical environment. This was demonstrated in Berri et al. (2009) for gelatin solutions (not methylcellulose as described in Mesce and Pierce-Shimomura, 2010). Similar results were independently reproduced for high molecular weight dextran (Fang-Yen et al., 2010). In fact, while this is not mentioned in Mesce and Pierce-Shimomura (2010), Pierce-Shimomura et al. similarly report a nearly threefold modulation of the bending frequency (0.6–1.5 Hz) in what they dub “swim-like” behavior (Vidal-Gadea et al., 2009), while frequencies of 0.2–0.4 Hz are dubbed “crawl-like,” despite the fact that the peak of the power spectrum for “crawling” appears to fall at about 0.8 Hz (Vidal-Gadea et al., 2009). It is therefore clear that C. elegans locomotion cannot be characterized by discrete sets of kinematic parameters, but rather by a broad and continuous range of such parameters.
Can Worms Switch Spontaneously between the Discrete Gaits of Swimming and Crawling?
Transitions between two undulation frequencies in a single environment, if spontaneous, could support the existence of two gaits. However, we note that any observed transitions (in the wild type) were only reported for certain high concentrations (2.25 and 2.75%) of methylcellulose (Vidal-Gadea et al., 2009), for which “crawling” and “swimming” (if they are indeed distinct behaviors) are characterized by quite similar frequencies. Specifically the transitions are quantified by a difference of 0.2 Hz or less in the undulation frequency. This frequency difference is comparable in value to the variability in frequency (1.2–1.5 Hz) for locomotion in 0.5% methylcellulose (Vidal-Gadea et al., 2009), all of which is dubbed swimming. The small magnitude of the transitions may raise questions, not only about the validity of the classification, but even about the selective advantage worms might gain by such “decisions.”
That said, it is clear from the bending plots in Vidal-Gadea et al. (2009) that some small frequency transitions were observed by Pierce-Shimomura et al. But are these transitions really spontaneous and internally selected? Here we provide an alternative interpretation, motivated in part by our own, possibly related observations. One technical difficulty in working with many polymer solutions (e.g., agar, gelatin, methylcellulose) is obtaining homogeneous environments with different concentrations of the colloidal particles. Indeed, in characterizing a transition as a function of the environment, any observation of a change of behavior must be explicitly controlled against possible changes in the worm’s local, microscopic environment before such differences can be attributed to an internal decision. We therefore needed an objective metric to quantify the local stiffness (or visco-elasticity) of our medium. Using image analysis, and treating the worm as a deformable body governed by Newton’s equations of motion (applied to low Reynolds’ numbers), we numerically estimated the ratio of drag coefficients for each short extract of recorded locomotion. Indeed, plotting the data against this physical metric, the smooth and continuous transition in Figures 1D–F of Berri et al. (2009) is immediately obtained. In the absence of such an objective characterization of the microscopic physical environment, it is impossible to have confidence in any statement about behavioral transitions being “spontaneous” and driven by “decision” rather than by some possible response of worms to local changes in the physical environment. In Vidal-Gadea et al. (2009), we might ask whether, e.g., the sudden (small) change in frequency observed for worms in 2–3% methylcellulose could be due to the worm moving into or out of contact with the more rigid agar surface underneath.
Does the Existence of a Swim-Defective Mutant Imply Multiple Gaits?
Mesce and Pierce-Shimomura argue that the identification of “swim-defective” mutants supports the existence of a distinct swimming gait, but we note that the three examples given by Pierce-Shimomura et al. (2008) exhibit some locomotion defect on agar as well. That aside, and even in the extreme case of a mutant with a clear phenotype in liquid and none on agar, it is important to ask whether this discrepancy between water and agar may be explained by the change in the physical environment. If so, then such data on its own would by no means be inconsistent with the single gait hypothesis. Indeed, Fang-Yen et al. (2010) have shown that “swimming” and “crawling” differ greatly in the relative significance of internal versus environmental forces (i.e., mechanical load). Thus, the selective manifestation of these “swim-defective” mutations could simply be due to the dominance of body forces in liquid, with strong external forces masking the locomotion defect on agar. Therefore, for swim-defective mutant data to support a two gait hypothesis, either (i) the importance of the physics in generating/masking the phenotype in different environments would have to be ruled out (e.g., by showing the phenotype is independent of the ratio of external to internal forces), or (ii) a neural mechanism/circuit underlying the selective manifestation of uncoordination would need to be identified.
In conclusion, we argue that, in the absence of compelling evidence of a qualitative difference in the pattern of undulations or wave propagation (or in the underlying neural control circuitry), the conclusion that C. elegans can choose to switch between swimming and crawling, while interesting and possibly appealing, remains a conjecture. What is certain is that C. elegans is able to modulate its locomotion over an impressively broad range of wavelengths and frequencies. Understanding the mechanism behind this modulation is an exciting question that promises to shed important light on the organization and function of this and other nervous systems and their coupling to the physics of body and environment.
Footnote
- ^Specifically, these three quantitative metrics capture the temporal and spatial properties of the body undulation to a good degree of accuracy (although additional metrics could always be added to capture the complex, non-sinusoidal features of the waveform).
References
Berri, S., Boyle, J. H., Tassieri, M., Hope, I. A., and Cohen, N. (2009). Forward locomotion of the nematode C. elegans is achieved through modulation of a single gait. HFSP J. 3, 186–193.
Fang-Yen, C., Wyart, M., Xie, J., Kawai, R., Kodger, T., Chen, S., Wen, Q., and Samuel, A. D. T. (2010). Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc. Natl. Acad. Sci. U.S.A. 107, 20323–20328.
Mesce, K. A., and Pierce-Shimomura, J. T. (2010). Shared strategies for behavioral switching: understanding how locomotor patterns are turned on and off. Front. Behav. Neurosci. 4:49. doi: 10.3389/fnbeh.2010.00049
Pierce-Shimomura, J. T., Chen, B. L., Mun, J. J., Ho, R., Sarkis, R., and McIntire, S. L. (2008). Genetic analysis of crawling and swimming locomotory patterns in C. elegans. Proc. Natl. Acad. Sci. U.S.A. 105, 20982–20987.
Vidal-Gadea, A., Topper, S., Young, L., and Pierce-Shimomura, J. T. (2009). Neural Mechanisms for Switching Locomotory Patterns in C. elegans. Neuroscience 366:17. Calabrese Ronald: Faculty of 1000 Biology, 11 November, 2009. Conference 2009 October 16–21. Available at: http://f1000biology.com/article/id/1182956/evaluation
Citation: Boyle JH, Berri S, Tassieri M, Hope IA and Cohen N (2011) Gait modulation in C. elegans: It’s not a choice, it’s a reflex! Front. Behav. Neurosci. 5:10. doi: 10.3389/fnbeh.2011.00010
Received: 16 November 2010;
Accepted: 22 February 2011;
Published online: 07 March 2011.
Copyright: © 2011 Boyle, Berri, Tassieri, Hope and Cohen. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence:bi5jb2hlbkBsZWVkcy5hYy51aw==

 Stefano Berri2
Stefano Berri2
