- 1Center for Nonlinear Science, University of North Texas, Denton, TX, United States
- 2GIOYA HEI, E305, The Hub Workspace, San Gwann, Malta
- 3Center for Mind/Brain Science, University of Trento, Rovereto, Italy
1. Introduction
Several theoretical models have been proposed to account for brain and behavioral asymmetry (e.g., Ghirlanda and Vallortigara, 2004; Vallortigara, 2006; Abrams and Panaggio, 2012; Rogers and Vallortigara, 2015; reviews in Ocklenburg and Güntürkün, 2018; Vallortigara and Rogers, 2020).
An interesting approach is based on competition and cooperation in phenotypically asymmetric individuals. Ghirlanda et al. (2009) suggested that population-level lateralization can arise as an evolutionarily stable strategy and that left- and right- lateralized individuals in unequal numbers can be evolutionary stable based solely on the balance between competitive and cooperative interactions. Cooperative activities would favor individuals with the same lateralization (by coordinating physical activities, efficiently using the same tools, etc.). Competitive activities would favor individuals different from the majority who would be able to surprise opponents, adopting behaviors to which opponents are less accustomed (e.g., human left-handers that may hold an advantage in fighting or, in more recent times, in certain sporting activities, review in Frasnelli and Vallortigara, 2018).
More specifically, the model by Ghirlanda et al. (2009) introduces a fitness function, f(x) = a(x) + cs(x), where a(x) accounts for antagonistic interaction (say a competition function) and s(x) for synergistic interaction (say a cooperation function); c is the control parameter tuning the relative strength between a(x) and s(x). The variable x is given by the ratio between L and R. The model shows, in an almost fully analytical way, that under proper conditions, there exists an unequal number of equilibrium of left-and right-lateralized individuals.
2. A different perspective
The model can be described from a different perspective, by a more numerical approach, which is both probabilistic and evolutionary. It can be viewed as a sort of very simple “in silico” simulation of individual lives. The algorithm is reported below.
• Let us take a population (e.g., 10,000 individuals) where each individual can assume one of two possible states, say “L” or “R.” As initial conditions, we can assign state R or L in a totally random way, in any random ratio.
• For each generation (i.e., iteration), each individual has the probability of having a progeny proportional to his/her fitness level (we employ the same fitness function suggested in Ghirlanda et al., 2009). The progeny (if any) will have the same state (L or R) as his parent.
• At each generation, the population would expect to increase because it consists of parents with their possible progeny, but some individuals die in a proportion such that the total number of individuals remains the same (in our example, 10,000 individuals). The distribution of deaths is assumed to be uniform across the population (e.g., if the number of R-individuals is 3 times greater than L-, then when an individual would die, the probability that they are an R- is three times greater than L-).
The algorithm, implemented using R Core Team (2021), leads to the same outcome as in Ghirlanda et al. (2009) who chose the parameter values (Ka = 5, Ks = 1), so that a(x) decreases more rapidly than s(x) increases, so in the fitness function competition varies more quickly than cooperation. Using these parameters in our model, we observe that after some iterations, the system moves to an equilibrium in the same way, as follows: for c <0.68, we have 50% L and 50% R, meaning that function a(x) dominates (competition); for 0.68 <c <1.57, we have an “unequal number” equilibrium between 50 and 100%, so both a(x) and s(x) are relevant (a mixture of competition and cooperation); for c > 1.57, we have 100% L (or 100% R) meaning that Functions (x) dominates (cooperation).
The simulation confirms the behavior of the previous model in a detailed way and, in particular, it shows that whatever the initial proportion between L and R, it will converge to the predefined equilibrium imposed by the “c” parameter. We could describe it as a game: putting a group of individuals (large enough) on a desert island, whatever the L/R initial ratio, it will always evolve to the ratio defined by “c,” the relative strength between competition and cooperation (refer to Figure 1).
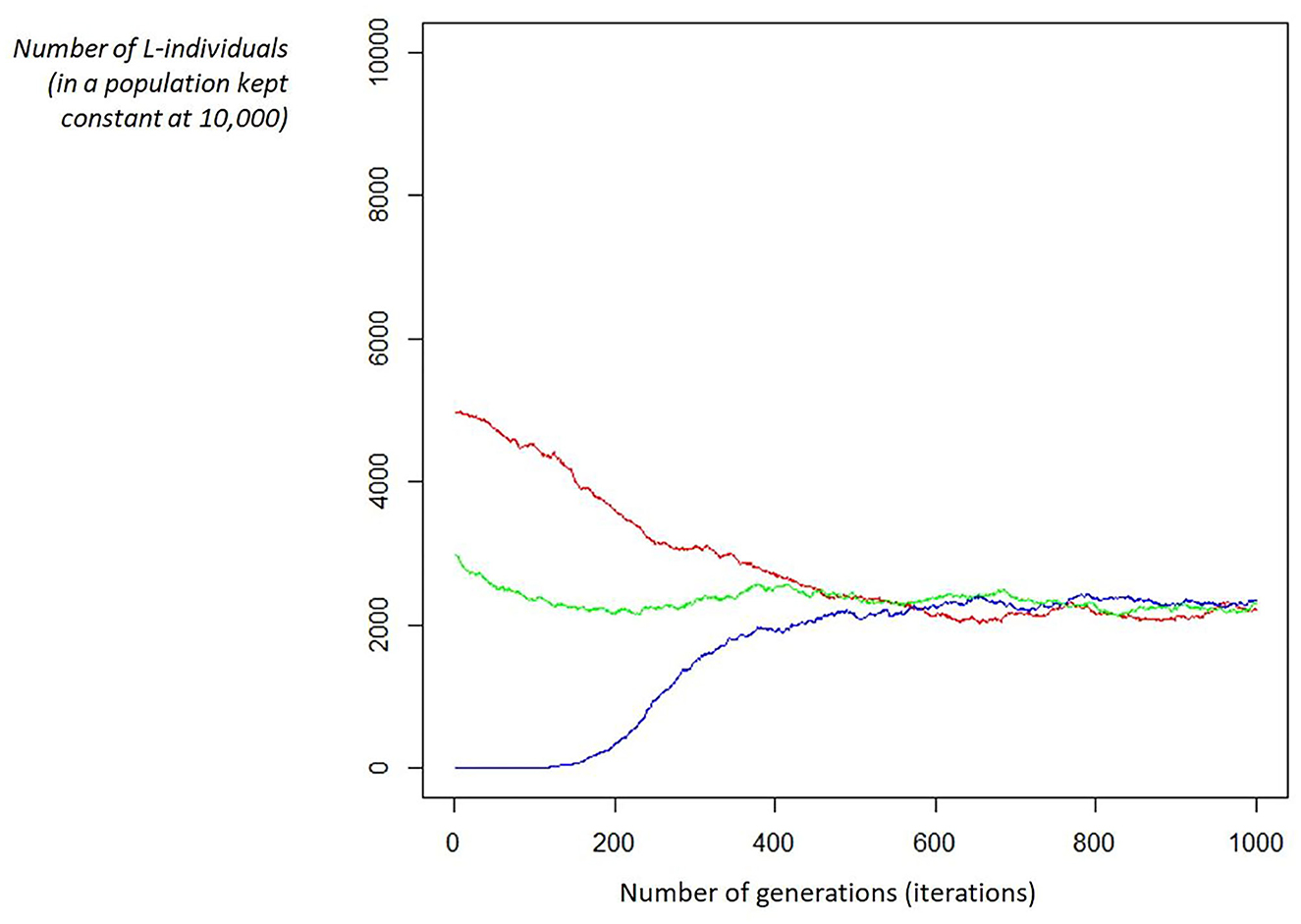
Figure 1. Examples of convergence. Given the fitness function parameters (e.g., c = 0.9, Ka = 5, Ks = 1) and a fixed population (e.g., 10,000 individuals), the ratio between L/R individuals will converge to the same proportion (ruled by the “c” parameter): in this case, c = 0.9 leads to a proportion of 22% of L-individual, whatever the starting ratio (in the figure, 3 starting ratios are shown: red is L = 50.00%, blue is L = 0.05%, and green is L = 30.00%).
3. Discussion
The simulation does not provide in itself any novel outcome, but it describes the dynamics from a different point of view, suggesting new possible interpretations and developments. In particular, it can suggest considering the issue of a single individual perspective.
Once all of the parameters are fixed (e.g., c = 0.9, Ka = 5, Ks = 1), an individual fitness can be evaluated according to the L/R ratio of the full population, i.e., a single individual fitness function f(x) has only one input variable x, which is the proportion of L and R on the whole population. Now, in a real-life condition, how can the single individual asymmetry be related to the total ratio of L and R, in a numerical sense? Of course, the individual does not have a direct measure of how many left- or right-lateraled individuals are there in the population, but they should obey the fitness rule anyway, and therefore, they should have some form of the estimate of the L and R ratio. How can an individual undergo such an indirect estimate?
Well, we can think of an individual who, in their life, has to deal with a subset of the full population. This subset would be made of the actual individuals they can cooperate or compete with, a kind of neighborhood, which is their actual behavioral environment. It is likely that such an environment, apart from small oscillations, will have quite a similar R-L proportion value as the whole population. Thus, the individual would interact with a portion of the L- and R- population only, which can determine their fitness in line with the other portions of the population. It is in the interaction with others (L or R) with whom an individual exhibits cooperation and competition, and according to the proportion of them they have to deal with, that their fitness would achieve a proper value.
However, this view is only partially convincing. Let us suppose an individual is right-handed (or for other non-human species that it exhibits some lateral bias in the use of eyes, ears, tails whatever, e.g., Vallortigara and Versace, 2017): interacting with many right-handed individuals would lead to cooperating more, according to the number of right-handed individuals they would interact with. Some issues seem still open, e.g., will an individual meet a large enough number of others, so that the L/R proportion will be in line with the whole population?
Now, let us suppose that it is not the direct interaction with others as single individuals but the outcome of being in a biased existing world as a group that would matter. For example, suppose that R is the majority: this would have the effect of having more available, say, tools for manipulation for right-handed individuals. We can imagine this as an environmental change made by R individuals, which is made to be more suitable for R individuals.
In such a view, we can think that the described sport superiority (confrontation) of the left-handed in some disciplines (review in Rogers et al., 2013) can not be (or not only) because of a direct effect on individuals' confrontations but as the outcome of an environmental change: if, say, a famous athlete wins again and again, they will attract many sponsorships and this would impact their fitness. The number of wins is not important, nor the number of one-to-one confrontations, but rather the environmental effect.
We could conceive that the information related to minority and majority, to L/R ratio, could come from actions on the environment by asymmetrical individuals which, in turn, would affect the R and L single individual fitness. In this view, the individual fitness function could be not linked to the “x” ratio because of the frequency of L and R direct interactions or direct mechanisms (such as quorum sensing) but because of experiencing environmental changes affecting the ratio between L and R.
We speculate that this kind of dynamic could be an instance of stigmergy, a term introduced by Grassé to describe a form of indirect communication mediated by modification of the environment that he observed in some species of termites (Theraulaz and Bonabeau, 1999) and since widely suggested to be a pillar of optimization tasks performed by ant colonies and other social insects (Dorigo et al., 2000; Theraulaz, 2014). In this perspective, the L and R equilibrium could express a kind of intelligence (in a mathematical meaning of the term) known as “swarm intelligence.” The view here is that a single L or R individual is just passively and unknowingly undergoing the mechanics of fitness, and there is not a leader in the game imposing an R and L ratio, or a fixed ratio genetically predetermined.
What seems to emerge instead is that the system self-organizes in an intelligent way because it moves autonomously toward an optimal equilibrium—so it is intelligent only when operating as a group.
It could be conjectured as a self-organizing complex system. The individual (in the L/R evaluation) does not know what the equilibrium is. The population as a whole would lead them to a better equilibrium if each individual could communicate with any other in an indirect way through the environmental change in a social way, as a form of stigmergy. It could perhaps be conjectured that whether stigmergy is communicated in a social way, behavioral population, asymmetries are more likely to appear in social species.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by funding from the European Research Council under the European Union's Horizon 2020 research and innovation program (Grant Agreement 833504 SPANUMBRA) and from the grant by the Progetti di Ricerca di Rilevante Interesse Nazionale [PRIN 2017 ERC-SH4-A (2017PSRHPZ)] to GV.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abrams, D. M., and Panaggio, M. J. (2012). A model balancing cooperation and competition can explain our right-handed world and the dominance of left-handed athletes. J. R. Soc. Interface 9, 2718–2722. doi: 10.1098/rsif.2012.0211
Dorigo, M., Bonabeau, E., and Theraulaz, G. (2000). Ant algorithms and stigmergy. Fut. Gen. Comput. Syst. 16, 851–871. doi: 10.1016/S0167-739X(00)00042-X
Frasnelli, E., and Vallortigara, G. (2018). Individual-level and population-level lateralization: two sides of the same coin. Symmetry 10, 739. doi: 10.3390/sym,10120739
Ghirlanda, S., Frasnelli, E., and Vallortigara, G. (2009). Intraspecific competition and coordination in the evolution of lateralization. Phil. Trans. R. Soc. B36, 4861–4866. doi: 10.1098/rstb.2008.0227
Ghirlanda, S., and Vallortigara, G. (2004). The evolution of brain lateralization: a game theoretical analysis of population structure. Proc. R. Soc. B 271, 853–857. doi: 10.1098/rspb.2003.2669
R Core Team. (2021). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online at: https://www.R-project.org/ (accessed February 13, 2022).
Rogers, L. J., and Vallortigara, G. (2015). When and why did brains break symmetry? Symmetry 7, 2181–2194. doi: 10.3390/sym7042181
Rogers, L. J., Vallortigara, G., and Andrew, R. J. (2013). Divided Brains. The Biology and Behaviour of Brain Asymmetries. New York, NY: Cambridge University Press. doi: 10.1017/CBO9780511793899
Theraulaz, G. (2014). Embracing the creativity of stigmergy in social insects. Archit. Design 84, 54–59. doi: 10.1002/ad.1808
Theraulaz, G., and Bonabeau, E. (1999). A brief history of stigmergy. Artif. Life 5, 97–116. doi: 10.1162/106454699568700
Vallortigara, G. (2006). The evolutionary psychology of left and right: costs and benefits of lateralization. Dev. Psychobiol. 48, 418–427. doi: 10.1002/dev.20166
Vallortigara, G., and Rogers, L. J. (2020). A function for the bicameral mind. Cortex 124, 274–285. doi: 10.1016/j.cortex.2019.11.018
Vallortigara, G., and Versace, E. (2017). “Laterality at the neural, cognitive, and behavioral levels,” in “APA Handbook of Comparative Psychology: Vol. 1. Basic Concepts, Methods, Neural Substrate, and Behavior, ed J. Call (Washington, DC: American Psychological Association), 557–577. doi: 10.1037/0000011-027
Keywords: lateralization, brain asymmetry, stigmergy, swarm intelligence, evolutionary models, self-organizing systems, complexity
Citation: Tonello L and Vallortigara G (2023) Evolutionary models of lateralization: Steps toward stigmergy? Front. Behav. Neurosci. 17:1121335. doi: 10.3389/fnbeh.2023.1121335
Received: 11 December 2022; Accepted: 11 January 2023;
Published: 02 February 2023.
Edited by:
Luca Tommasi, University of Studies G. d'Annunzio Chieti and Pescara, ItalyReviewed by:
Julian Packheiser, Ruhr University Bochum, GermanyCopyright © 2023 Tonello and Vallortigara. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lucio Tonello,  bHVjaW8udG9uZWxsb0BneS5lZHUubXQ=
bHVjaW8udG9uZWxsb0BneS5lZHUubXQ=
†ORCID: Lucio Tonello orcid.org/0000-0002-4848-3182
Giorgio Vallortigara orcid.org/0000-0001-8192-9062
 Lucio Tonello
Lucio Tonello Giorgio Vallortigara
Giorgio Vallortigara