Synchronization of Non-linear Oscillators for Neurobiologically Inspired Control on a Bionic Parallel Waist of Legged Robot

Introduction

Legged robot technique has made remarkable progress in the past few decades, and produced a series of very famous achievements: StarlETH (Hutter et al., 2012), ANYmal (Hutter et al., 2016; Hwangbo et al., 2019), HyQ series (Semini et al., 2011, 2016), MIT Cheetah series (Seok et al., 2013; Wensing et al., 2017), Boston Dynamics Spotmini series¹. Great contribution has been made in the aspects of leg structure (Ananthanarayanan et al., 2012), leg control (Barasuol et al., 2013), limb coordination (Gehring et al., 2016), compliance control (Eich et al., 2009), balance control (Raibert and Tello, 1986), adaptive control (Manoonpong et al., 2013), and so on (Schwendner et al., 2014; Gehring et al., 2016), which continuously improve the flexibility, stability, coordination and intelligence of robots in related fields.

No robot has been able to act as flexibly and as animal-like as cat or a dog until today. The control strategy is not the only reason for this, as there are many differences between the structure of natural creatures and robots. Inspired by biologists (Galis et al., 2014), along with demand for high-flexibility and high-speed robots, many scholars have carried out in-depth research on the bionic torso (Albiez et al., 2006). The bionic torso structure can be divided into two types: torso with active joint (Khoramshahi et al., 2013; Satoh and Fujimoto, 2018) and with passive joint (Takuma et al., 2010; Haynes et al., 2012). An additional active joint on a torso can effectively improve the motion range and dexterity of a robot. Most passive joints use elastic elements to collect energy during movement and to improve compliance. However, the function of a biological torso for load capacity, movement, coordination and other aspects is obviously much more than these. Therefore, this paper builds a bionic parallel waist to replace the original rigid torso for the advantages of strong carrying capacity and high control accuracy of the parallel structure. Actually, the parallel robot has been widely used in the industry fields (Dallej et al., 2006; Cong et al., 2011; He et al., 2015). Its structure (Villarreal-Cervantes et al., 2010), kinematics (Plitea et al., 2013), dynamics (Staicu, 2009), control (Liu et al., 2018b), and so on have all been studied before. Although the parallel structure has been directly applied to legged robot, showing better performance than serial structure (Kuehn et al., 2017), no bionical method is used on the parallel structure. This paper investigates the CPG-based network for neurobiologically inspired control of the bionic parallel waistf and discusses the related issues.

At present, CPG models have been applied in various robots (Donati et al., 2016; Santos et al., 2016; Liu et al., 2018a), and can be divided into two categories (Wu et al., 2009): neuron-based models and oscillatior-based models. Neuron-based models mainly include the Matsuoka neuron oscillator model (Matsuoka, 1985, 1987), the Kimura model (Kimura et al., 2001, 2002; Fukuoka et al., 2003), cellular neural network (CNNs) (Arena and Fortuna, 2000; Arena et al., 2001), and recurrent neural network (Rao and Kamat, 1995; Senda and Tanaka, 2000). The biological significance of the models is relatively clear. The oscillator-based models include the Kuramoto oscillator (Acebron et al., 2005), the Hopf harmonic oscillator (Righetti and Ijspeert, 2006; Righetti, 2008), the Van der Pol oscillator (Van der Pol and Van der Mark, 1928; Dutra et al., 2003), and more. These oscillator-based models can periodically generate non-linear oscillation signals and are widely used as CPG oscillation units since they contain a fewer number of parameters and have sophisticated background implementation theories. All of these above can be used for robot control and the networks with oscillators will not differ too much within the same robot, with respect to the architecture and coupling topology, which are related to the physical structure and control frame. In terms of waveforms that determine what trajectories will actually be performed by each joint during a cycle, the oscillator must be selected cautiously. In some robots with simple structure, waveform has a relatively small effect on the movement of single joint and whole body. Therefore, for the parallel platform in this paper, the spatial mechanism with six degrees of freedom is related to six coupling limbs. The movement of each limb directly affects the smoothness and stability of overall system, so we have to focus on the transition smoothness, transformation quickness, and velocity/acceleration impact of the oscillator.

Synchronization means an exact match of the scaled amplitude with a desired phase difference (Chung and Dorothy, 2010). Different phase lead or lag has already been performed in the oscillators with the same frequency to manipulate different locomotion of various robots (Ijspeert, 2008). There are two points that need to be figured out. One is the stability of the synchronization. The stable theory of the coupled oscillator system can help to determine the exact parameters, and they are the constraints that make the system converge at final moment (Buchli and Ijspeert, 2004; Kopell et al., 2006). This consideration has been fully discussed both in architectural symmetries and diffusion-like couplings (Buono and Golubitsky, 2001; Ashwin, 2003; Ramezani et al., 2017). Another point is that the transition process needs to be clear and controllable, since it concerns the trajectory of every movement of the limbs and joints. An unreasonable transition between two perfect stable states will also lead to an unexpected locomotion. In fact, in the premise of synchronization stability, the transition process in both joint space and Cartesian space should be taken into serious consideration. In this paper, the transition state of coupled non-linear oscillators is analyzed in detail to guarantee the rational locomotion in every single moment.

In our previous work, we have researched on legged robot about trajectory planning (Zhu and Guo, 2016; Zhu et al., 2018a), deviation correction (Zhu et al., 2016, 2017), force control (Zhu et al., 2015; Zhu and Jin, 2016), energy optimization (Jin et al., 2013; Zhu et al., 2014), and locomotion diversity (Zhu et al., 2018b), aiming to achieve excellent coordination and flexibility of legged robot. The bionic parallel waist is supposed to be a good choice for the issue from both a biological and a robotic point of view. At present, the majority of parallel robots utilize the model control theory (Jin et al., 2014). Each angle of joint with the strong coupling and structure constraints needs to be calculated, since all joint actuators are involved in the locomotion of parallel robots at the same time. All trajectories (position, velocity, acceleration, and torque) have to be designed for accurate control and high speed. Although these methods can be used in the bionic robot, we are more inclined to the bionic control method, for it is hard to design every possible movement in the solution space in advance. Thus, synchronization of σ-Hopf oscillators for the bionic parallel waist of a legged robot is proposed to realize neurobiologically inspired control. The paper is organized as follows. Materials and Method introduces the bionic parallel robot system and the method. In Analysis of Synchronization, synchronization of σ-Hopf oscillators is analyzed. Neurobiologically Inspired Control and Results illustrates CPG-Based locomotion control and results. The performances and findings are discussed and concluded in Simulation.

Materials and Methods

For the coordinated locomotion of a legged robot, a bionic parallel waist is developed for the method proposed in this paper. We will introduce the system of the parallel waist and synchronization method of coupled σ-Hopf oscillators in the following part: sections Platform and System, σ-Hopf Harmonic Oscillator, Network, and Synchronization of σ-Hopf Oscillators.

Platform and System

In mammals, the waist (both bone and muscle) plays an extraordinary role in movement (Grondin and Potvin, 2009), and researchers found that robots with waists performed better than those with a rigid body (Coros et al., 2011). The parallel platform in this paper is used as the waist of the four-legged robot to obtain better coordination ability. Its structure is shown in Figure 1A. The moving platform at the waist connects the front legs, while the rear legs are linked to the stationary platform. The whole parallel platform is supposed to be the robot torso and can achieve shift, rotation, and synthesis movements. Six identical limbs connecting the moving platform to the stationary platform are the actuating mechanism of the waist. There are two spherical joints between coupler links, and one rotation joint for the connection of an input rod and the motor. So, the moving platform can move with 6 spatial degrees of freedom effectively under the actuation of 6 brushless DC motors. The magnet encoders are mounted next to the input rods and are connected by gears. They are shown in Figure 1B. Force sensors are mounted on the long linkages and used for the payload calculation. All information obtained through encoders and force sensors are sent to the controller for locomotion generation.

FIGURE 1

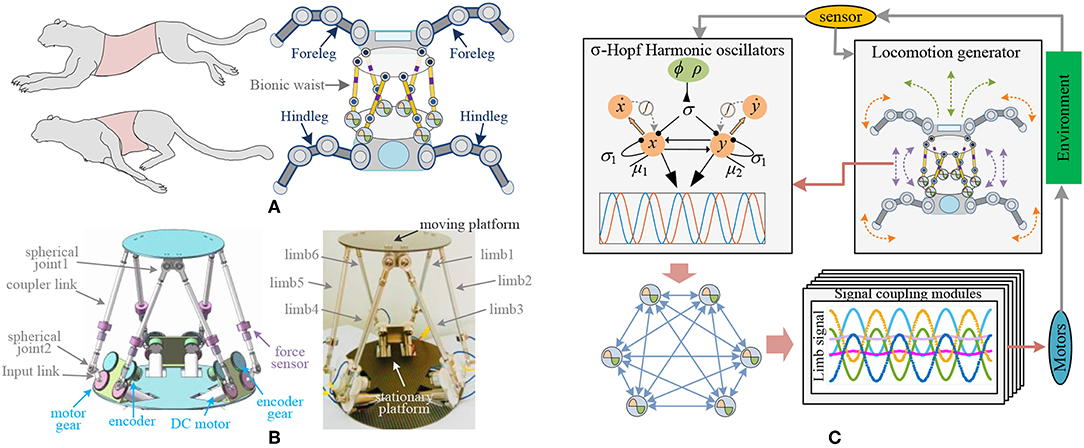
Figure 1. Architecture of bio-inspired legged robot with parallel waist. (A) Mechanical structure of bio-inspired robot. (B) Mechanical structure of bionic waist. (C) Framework of robot system, including locomotion generator of the robot, σ-Hopf oscillators, synchronous network, and coupling signal modules.

Most existing legged robots without waist structures adjust the action of the rigid torso by controlling the leg movement (Cao and Poulakakis, 2016; Zhang et al., 2016). Some others enhance the movement ability by active or passive joints. But the presented parallel waist has far more flexibility and larger load capacity, which can easily assist the robot to achieve pitching, stretching, and torsion of the torso. Therefore, the robot equipped with a bionic waist needs to carry out overall behavior planning including torso and legs, so as to generate motion rhythm and control parameters for the waist. With the bionic control method, these parameters will be used to adjust the CPG oscillator and synchronous network, and then generate the control signal for the motor driver, which is shown in Figure 1C.

σ-Hopf Harmonic Oscillator

The important role of CPG in bionic control is self-evident and the details have been investigated in the field of biology (Macintosh et al., 1993; Jorgensen et al., 2003), neuroscience (Grillner et al., 2007; Jean-Xavier and Perreault, 2018), and robotics (Wang et al., 2012). Especially in the application of multi-degree-of-freedom or multi-joint robots, it is particularly prominent due to the coupling and synchronization ability of CPG signals, which can form a signal transmission network similar to natural creature. However, no matter how complex the network is or what change post-processing makes, the controllability of the original signal generated by CPG affects the control performance of robots directly. Then we must control CPG signal at every single moment. That is to say, if CPG is regarded as a simple control wave, we should not only pay attention to its frequency and amplitude, but also control its offset, the speed of ascending, and descending (shape of the signal). They are not problems in the model control (Jin et al., 2014), since all of the required control variables can be “designed out.” CPG waveform in the bionic control is subject to the control of oscillation and coupling property, and cannot be changed easily (Zhu et al., 2018b). In the present paper, the σ-Hopf oscillator is proposed [σ is one special parameter to distinguish it from the orignal Hopf oscillator (Drazin, 2008)] for two reasons. One is the Stability. The symmetric limit circle prevents the classical problem of instability due to switching between two stable systems and the stability of coupled Hopf oscillators has also been previously discussed (Pham and Slotine, 2005; Kato and Kamimura, 2008). The other reason is the consideration for excellent locomotion diversity and smoothness by changing amplitude, frequency, phase, and waveform, which has been fully investigated in our published paper (Zhu et al., 2018b). Its features and characteristics will be introduced in the following. The form of synchronous coupling of σ-Hopf is

$\begin{array}{ll}\stackrel{\bullet }{\upsilon }=\left[\begin{array}{c}ẋ\\ ẏ\end{array}\right]=\left[\begin{array}{c}{\sigma }_1(x-a)-\sigma (y-b)\\ {\sigma }_1(y-b)+\sigma (x-a)\end{array}\right]+\text{g}(t)+\text{u}(t)& (1)\end{array}$

where,

$\begin{array}{ll}\{\begin{array}{c}\sigma =\pi /(\rho ·(e^{-\lambda y}+1)·\phi )+\pi /((1-\rho )·(e^{\lambda y}+1)·\phi )\\ {\sigma }_1=-\alpha ({(x-a)}^2+{(y-b)}^2-\mu )\hfill \end{array}& (2)\end{array}$

Equivalently,

$\begin{array}{ll}\stackrel{\bullet }{\upsilon }=\text{f}(\upsilon ,\alpha ,\mu ,\sigma (\rho ,\lambda ,t))+\text{g}(t)+\text{u}(t)& (3)\end{array}$

where x and y are the state variables; a, b is the center of the limit cycle; μ is amplitude of the oscillations. The bifurcation parameter α can switch from −1 to 1 such that this would change the stable limit cycle dynamics to the dynamics with a globally stable equilibrium point (Strogatz, 2015). In the σ(ρ, λ, t), λ is strength and φ is the period factor; 0 < ρ <1 denotes the duty factor and determines the transformation speed between the ascending and descending phases. In (2), the parameters φ and ρ are uncorrelated. That means that the movement period will not be influenced by a change in the duty factor. g(t) is coupling input, for a single oscillator g(t) = 0. u(t) = –sign(y)u is the external input to control the oscillation signal by the external sensing information (i.e., contact detection in the legged robot; Righetti, 2008; Aoi et al., 2013). The coverage coefficient and frequency were always coupled together and cannot be controlled independently. Therefore, we decoupled it and induced the duty factor ρ so that the frequency and shape of the waveform can be controlled independently (Zhu et al., 2018b). The presence of σ(t) here is different from the original Hopf oscillator and plays an important role in changing the oscillation waveform. We will later see that they can be useful for different patterns of locomotion. In the next section, we present how to construct a stable synchronization of σ-Hopf oscillators for the purpose of diverse locomotion pattern modulation.

Network

Synchronization permits different actuators to oscillate with a prescribed phase lead or lag to regulate different movement patterns. On the basis of the joint number, structure connection and behavioral characteristics of different robots [legged robot (Kalouche et al., 2015; Bjelonic et al., 2016; Owaki and Ishiguro, 2017), snake robot (Wang et al., 2016), swimming robot (Stefanini et al., 2006), and flying robot (Corke et al., 2003; Ramezani et al., 2017)], the behavior control networks are also different. The type of oscillator (Wang et al., 2018) and phase difference (Aoi et al., 2011) formation method are also important factors. The specific network architecture is shown in Figure 2. The parallel waist platform adopts the same control frame as the leg of the robot, and each limb is driven by an oscillator. The full coupled two-way ring architecture is constructed, since it has better transition performance than one-way ring architecture (Chung and Dorothy, 2010). For the coupled σ-Hopf oscillators in this paper, (3) can be rewritten with a diffusive coupling with the phase-rotated neighbor

$\begin{array}{l}\stackrel{\bullet }{{\upsilon }_i}=\text{f}({\upsilon }_i,{\mu }_i,{\sigma }_i({\rho }_i,\lambda ,t))\\ -k(t){\displaystyle \sum _{j\in {𝔑}_i}^{n_i}}({\upsilon }_i-\frac{{\mu }_i}{{\mu }_j}\text{R}(\Delta {\Phi }_{ij}){\upsilon }_j)+\text{u}(t)& (4)\end{array}$

$\begin{array}{ll}\text{R}(\Delta \Phi )=\left[cos(\Delta \Phi )-sin(\Delta \Phi );sin(\Delta \Phi )cos(\Delta \Phi )\right]& (5)\end{array}$

in which, the positive scalar k(t) denotes the coupling gain and can be time-varying for different locomotion. R(ΔΦ)${SO}$(2) is a 2-D rotational transformation of the phase difference ΔΦ_ij between the ith and jth oscillators. The desired phase offset ΔΦ_ij guides υ_i to synchronize with υ_j. N_i denotes the set that contains only the local neighbors of the ith σ-Hopf oscillator, and n_i is the number of the neighbors. Both N_i and n_idepend on the coupled σ-Hopf oscillators and network architecture. Since the coordination motion pattern of the bionic waist is determined by the relative phase between the oscillators, the phase offset matrix ΔΦ_ij is the key in the network. Generally, ΔΦ_ij = Φ_i – Φ_j (i, j = 1,…,6, 0 ≤ ΔΦ_ij ≤ 2π), ΔΦ_ij = –ΔΦ_ji, ΔΦ_ij = ΔΦ_ik + ΔΦ_kj and ΔΦ_ii = 0 (i, j = 1,…,6). So, the locomotion of the waist is determined by [ΔΦ₁₂, ΔΦ₂₃, ΔΦ₃₄, ΔΦ₄₅, ΔΦ₅₆, ΔΦ₆₁], which can be written as [Δ₁₂, Δ₂₃, Δ₃₄, Δ₄₅, Δ₅₆, Δ₆₁] for simplification. The full coupled network with ΔΦ is shown in Figure 2.

FIGURE 2

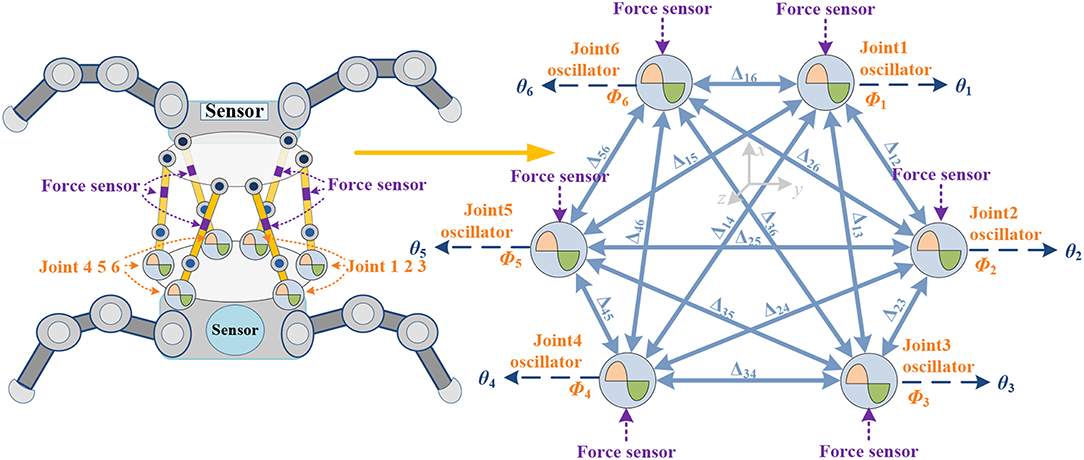
Figure 2. Two-way ring architecture network. Every limb composes of 2 links, 2 spherical hinges, 1 actuator, and 1 force sensor. Φ_i is denoted as oscillation phase of ith joint, θ_i is the control signal of ith joint. Geometric structure is shown in Appendix (Supplementary Material).

Theoretically, a 6RSS parallel platform can realize the independent and coupled locomotion of three translational and three rotational motions in the Cartesian coordinate system (Ahmet and Koksal, 2014) In this paper, four main torso movements of the mammals (Rossignol, 2004) are discussed: Stretching and flexing along Z axial (motion pattern A), lateral movement along X axial (motion pattern B), pitch around Y axial (motion pattern C), and torsion around Z axial (motion pattern D). According to the symmetry of motion and the established coordinate system shown in Appendix (Supplementary Material), the oscillators always operate synchronously. From a lateral perspective, all mentioned actions are symmetrical along the X axial except rotation movement around the Z axial. The joint 1–6, 2–5, and 3–4 have the opposite turning direction to guarantee the symmetric loading, so Δ₁₆ = Δ₂₅ = Δ₃₄ = 180° (for the rotation around the Z axial, Δ₁₆ = Δ₂₅ = Δ₃₄ = 0°). The oscillator amplitude is also symmetric along the X axial. Vertically, in the motion pattern A, oscillators on the same side along the X axial keep same pace, then Δ₁₂ = Δ₂₃ = 0°and Δ₆₅ = Δ₅₄ = 0°; in motion pattern B, there are Δ₁₂ = Δ₆₅ = 0° and Δ₂₃ = Δ₅₄ = 180°according to the asymmetric structure along the Y axial; in motion pattern C, there are Δ₁₆ = Δ₂₅ = Δ₃₄ = 180°, Δ₁₂ = Δ₆₅ = 180° and Δ₂₃ = Δ₅₄ = 0°, since the actuator 1 and 6 are located in the positive half of X axial and joint 2 (or 3) and 5 (or 4) are located in the negative half; in motion pattern D, all actuators have the same rotational direction, so Δ₁₆ = Δ₂₅ = Δ₃₄ = 0°, Δ₁₂ = Δ₆₅ = 180°, Δ₂₃ = Δ₅₄ = −180° and Δ₁₃ = Δ₆₄ = 0°. Other independent or coupled locomotions can be obtained by similar analysis, even if they never occur in vertebrates. Additionally, the range of movements are associated with the amplitude control signals. We will illustrate these relationships in Neurobiologically Inspired Control and Results.

Synchronization of σ-Hopf Oscillators

The neurobiological approach to an engineered bionic waist is to produce the analytical model of oscillators that matches the real need of bioinspired legged robot. It will benefit the coordinated locomotion between the waist and leg joints, but the limit-cycle dynamics, synchronization of the coupled oscillator and feedback signals integration have to be taken into consideration (Ijspeert, 2008; Seo et al., 2010). Thus, we have proposed (1) with period parameter ϕ, amplitude μ, coupled input g(t), and feedback input u(t). This is the base for the bionic waist to perform agile maneuvering in decoupled, symmetric or unsymmetric locomotion in Cartesian space. For the synchronization of a network, we rewrite the coupled Hopf oscillators with the related concern:

$\begin{array}{ll}\stackrel{\bullet }{{\upsilon }_i}=\text{f}({\upsilon }_i,{\mu }_i,{\sigma }_i({\rho }_i))-k(t){\displaystyle \sum _{j\in {𝔑}_i}^{n_i}}({\upsilon }_i-\frac{{\mu }_i}{{\mu }_j}\text{R}(\Delta {\Phi }_{ij}){\upsilon }_j).& (6)\end{array}$

If the external sensing input u(t) is taken as some initial state of the oscillator, its value will not affect the stability. If σ equals to a constant or ρ = 0.5, ascending and descending will equal to each other, it will be the standard Hopf oscillator, and its stability with a diffusive coupling has been proved (Pham and Slotine, 2005). When ρ≠0.5, the σ-Hopf oscillation waveform is asymmetrical. Although the total time in one period is still unchanged, it presents different frequencies (π/(ρ·(e^−λy+1)·φ) for ascending and π/((1-ρ)·(e^λy+1)·ϕ) for descending), and leads to asymmetrical oscillation signals. Thus, to demonstrate the synchronization of the modified oscillators, $\left\{\stackrel{\bullet }{\bar{\upsilon }}\right\}$ is denoted for the symmetric oscillators (with ρ = 0.5). According the stable theory of phase synchronization, we construct (6) into

$\begin{array}{ll}\left\{\stackrel{\bullet }{\bar{\upsilon }}\right\}=\text{f}(\left\{\bar{\upsilon }\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{\bar{\upsilon }\right\}& (7)\end{array}$

where ρ ∈ ℝⁿ, and different ρ makes synchronization of oscillators with different wave shape possible. Specially, if ρ = 0.5, the shape of waveform will equal to the original waveform. The matrix G is a Laplacian matrix with phase shifts R(ΔΦ_ij). Considering instantaneous deformation, $\left\{{\bar{\upsilon }}_0\right\}$ is denoted for the original oscillators signal without synchronization, $\left\{\bar{\upsilon }\right\}$ is for the original oscillators signal with synchronization, and$\left\{\Delta {\bar{\upsilon }}_s\right\}$ is the change between them. So

$\begin{array}{ll}\bar{\upsilon }={\bar{\upsilon }}_0+\Delta {\bar{\upsilon }}_s(\text{G}({\bar{\upsilon }}_0))& (8)\end{array}$

For simplicity, $\Delta {\bar{\upsilon }}_s(\text{G}({\bar{\upsilon }}_0))$is written as$\Delta {\bar{\upsilon }}_s$,

$\begin{array}{l}\left\{\stackrel{\bullet }{\bar{\upsilon }}\right\}=\text{f}(\left\{\bar{\upsilon }\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{\bar{\upsilon }\right\}=\text{f}(\left\{{\bar{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})\\ +\text{f}(\left\{\Delta {\bar{\upsilon }}_s\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}-k(t)\text{G}\left\{\Delta {\bar{\upsilon }}_s\right\}\hfill \\ =\text{f}(\left\{{\bar{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})+{G}\left\{\text{G}({\bar{\upsilon }}_0),k(t)\right\}& (9)\end{array}$

$\begin{array}{l}{G}\left\{\text{G}({\bar{\upsilon }}_0),k(t)\right\}=\text{f}(\left\{\Delta {\bar{\upsilon }}_s\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}\\ -k(t)\text{G}\left\{\Delta {\bar{\upsilon }}_s\right\}.\hfill & (10)\end{array}$

When finally it gets stable, {υ} → {υ₀}. Then,

$\begin{array}{l}\left\{\stackrel{\bullet }{\bar{\upsilon }}\right\}=\text{f}(\left\{{\bar{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})+{G}\left\{{\bar{\upsilon }}_0,k(t)\right\}\end{array}$

$\begin{array}{rr}\{\begin{array}{c}\hfill \left\{\Delta {\overline{\upsilon }}_s\right\}=0\\ f(\{\Delta {\overline{\upsilon }}_0\},\mu ,{\sigma }^{\rho =0.5})=0\hfill \\ \hfill G\{G({\overline{\upsilon }}_0),k(t)\}=0\end{array}& (11)\end{array}$

So

$\begin{array}{ll}G\{G({\overline{\upsilon }}_0),k(t)\}\{{}_{=0,steadystate}^{\ne 0,transitionstate}& (12)\end{array}$

It shows that the signals of oscillators with synchronization in the transition state are different from that of original oscillators, but they will turn back to their original form after the convergence.

The modified signals of oscillators (with ρ≠0.5) without synchronization is denoted as $\left\{{\widehat{\upsilon }}_0\right\}$ and {Δυ₀}is the deviation between $\left\{{\bar{\upsilon }}_0\right\}$ and $\left\{{\widehat{\upsilon }}_0\right\}$. According to (8), for modified signal with synchronization

$\begin{array}{rr}{\widehat{\upsilon }}_0={\bar{\upsilon }}_0+\Delta {\widehat{\upsilon }}_0& (13)\end{array}$

$\begin{array}{ll}\widehat{\upsilon }={\widehat{\upsilon }}_0+\Delta {\widehat{\upsilon }}_s({\widehat{\upsilon }}_0)={\widehat{\upsilon }}_0+\Delta {\widehat{\upsilon }}_s({\bar{\upsilon }}_0,\Delta {\widehat{\upsilon }}_0).& (14)\end{array}$

$\Delta {\widehat{\upsilon }}_s({\bar{\upsilon }}_0,\Delta {\widehat{\upsilon }}_0)$ is written as $\Delta {\widehat{\upsilon }}_s$. For $\left\{\stackrel{\bullet }{\widehat{\upsilon }}\right\}$, we have

$\begin{array}{ll}\left\{\stackrel{\bullet }{\widehat{\upsilon }}\right\}=\left\{{\stackrel{\bullet }{\bar{\upsilon }}}_0\right\}+\left\{\Delta {\stackrel{\bullet }{\widehat{\upsilon }}}_0\right\}+\left\{\Delta {\stackrel{\bullet }{\widehat{\upsilon }}}_s\right\}=\left\{{\stackrel{\bullet }{\widehat{\upsilon }}}_0\right\}+\left\{\Delta {\stackrel{\bullet }{\widehat{\upsilon }}}_s\right\}& (15)\end{array}$

$\begin{array}{ll}\left\{{\stackrel{\bullet }{\bar{\upsilon }}}_0\right\}=\text{f}(\left\{{\bar{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}& (16)\end{array}$

$\begin{array}{ll}\left\{\Delta {\stackrel{\bullet }{\widehat{\upsilon }}}_0\right\}=\text{f}(\left\{\Delta {\widehat{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_0\right\}& (17)\end{array}$

$\begin{array}{ll}\left\{\Delta {\stackrel{\bullet }{\widehat{\upsilon }}}_s\right\}=\text{f}(\left\{\Delta {\widehat{\upsilon }}_s\right\},\mu ,{\sigma }^{\rho \ne 0.5})-k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_s\right\}& (18)\end{array}$

$\begin{array}{l}\left\{{\stackrel{\bullet }{\widehat{\upsilon }}}_0\right\}=\text{f}(\left\{{\bar{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}\\ +\text{f}(\left\{\Delta {\widehat{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})-k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_0\right\}& (19)\end{array}$

$\begin{array}{l}\left\{\stackrel{\bullet }{\widehat{\upsilon }}\right\}=\text{f}(\left\{{\bar{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})+\text{f}(\left\{\Delta {\widehat{\upsilon }}_0\right\},\mu ,{\sigma }^{\rho =0.5})\\ +{G}\text{'}\left\{{\bar{\upsilon }}_0,\Delta {\widehat{\upsilon }}_0,k(t)\right\}& (20)\end{array}$

$\begin{array}{l}{G}\text{'}\left\{{\bar{\upsilon }}_0,\Delta {\widehat{\upsilon }}_0,k(t)\right\}=\text{f}(\left\{\Delta {\widehat{\upsilon }}_s\right\},\mu ,{\sigma }^{\rho \ne 0.5})-k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}\\ -k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_0\right\}-k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_s\right\}.& (21)\end{array}$

Remark:

1. If $\Delta {\widehat{\upsilon }}_0$ ≠0 and k(t) ≠ 0, the process will be signal synchronization of modified Hopf oscillators. For any fixed parameters, the deformation $\Delta {\widehat{\upsilon }}_0$ of ${\widehat{\upsilon }}_0$ and ${\bar{\upsilon }}_0$ will be a constant, so $\text{G}\left\{\Delta {\widehat{\upsilon }}_0\right\}$ ≠ 0. The related $\Delta {\widehat{\upsilon }}_s({\bar{\upsilon }}_0,\Delta {\widehat{\upsilon }}_0)$ will be determined by $k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}+k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_0\right\}$ and the amplitude is also fixed, so ${G}\text{'}$ is not equal to 0. Under the influence of ${G}\text{'}$, modified oscillators signal with synchronization will be different from original signal (ρ = 0.5), and the deformation depends on the specific parameters ρ and k. Also, for any parameter k(t) satisfying the stability condition (Pham and Slotine, 2005), ${\widehat{\upsilon }}_0$ will have a corresponding stable state.

2. If $\Delta {\widehat{\upsilon }}_0$ = 0, k(t) ≠ 0, thus ${\widehat{\upsilon }}_0={\bar{\upsilon }}_0$ and $\left\{\stackrel{\bullet }{\widehat{\upsilon }}\right\}=\left\{{\stackrel{\bullet }{\bar{\upsilon }}}_0\right\}$, it means they are original oscillators signal with synchronization, $k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}+k(t)\text{G}\left\{\Delta {\widehat{\upsilon }}_0\right\}$ will 0, then $\Delta {\widehat{\upsilon }}_s({\bar{\upsilon }}_0,\Delta {\widehat{\upsilon }}_0)=0$, ${G}\text{'}$ is equal to ${G}$, and suitable k(t) will make it global stable.

3. Usually, in the synchronization, the convergence strength k(t) ≠0. But if k(t) is approaching 0 gradually and the time is long enough for stabilization with a certain value of it, things will be different. We assume that k_n+1 < k_n for ∀ n, Then, every part of ${G}\text{'}$ in (21) can be constructed in stable amplitude formⁿ

$\begin{array}{ll}{{H}}_{{G}}^n={{H}}_{\text{f}}^n-{{H}}_G^n-{{H}}_0^n-{{H}}_s^n,& (22)\end{array}$

$\begin{array}{ll}{{H}}_{\text{f}}^n\propto ({{H}}_0^n,{{H}}_s^n)and{{H}}_G^n=0.& (23)\end{array}$

Then,

$\begin{array}{ll}k\to 0\Rightarrow {{H}}_0^{},{{H}}_s^{}\to 0\Rightarrow {{H}}_{\text{f}}^{}\to 0\Rightarrow {{H}}_{{G}}^n.& (24)\end{array}$

So every change of k will have a new ${{H}}_G^n$ and it will never equal to 0 before stable. It seems very hard to let ${{H}}_G^n\to 0$, since it is hard to know how long it needs to get stable. But if the small deformation of waveform is acceptable, large convergence rate will be achieved. Thus, there is a trade off between convergence rate and final deformation, and the details will be discussed as follows.

Analysis of Synchronization

Through the transition state analysis of the synchronization process, k(t) is the only parameter which can be adjusted, which determines the convergence rate and the steady state of the oscillator synchronization. For the original symmetric hopf oscillator, k(t) can be large to meet the requirement of rapid convergence, while for σ-hopf oscillator, whose waveform can be asymmetric, the process will be different and specific analysis is required.

1. When ρ = 0.5, there is $\Delta {\widehat{\upsilon }}_0$ = 0. k(t) is convergence strength and ${G}\left\{\text{G}({\bar{\upsilon }}_0),k(t)\right\}$ converges to zero. The different value of k(t), initial points and phase factors will cause different convergence rates. The convergence process of ${G}\left\{\text{G}({\bar{\upsilon }}_0),k(t)\right\}$is shown in Figure 3. Generally speaking, on the premise of global stable, the larger k(t) leads to faster convergence rate, as well as motion pattern transformation. If the initial point is designed close to the limit cycle with the concern of synchronization, it also contributes to the fast convergence rate. The phase factors reflect the synchronization relation of the oscillators and determine the phase difference at steady state.

2. When ρ ≠ 0.5, there is $\Delta {\widehat{\upsilon }}_0$ ≠ 0. Through the separate adjustment of k, ρ and phase factors, $\text{G}\left\{{\bar{\upsilon }}_0\right\}$ whose trend is consistent with ${G}\text{'}\left\{\text{G}({\bar{\upsilon }}_0),k(t)\right\}$, is analyzed. The different process of approaching to a steady state is shown in Figure 4. As in the previous analysis, $k(t)\text{G}\left\{{\bar{\upsilon }}_0\right\}$ does not equal 0 in a steady state and it also stabilizes to a non-circular asymmetrical limit cycle, which brings about an asymmetrical oscillation waveform as analyzed by (21). For a certain motion pattern with fixed coupling parameter, only the effects of the k and ρ on the oscillator need to be analyzed. For example, in motion pattern B, the oscillators on the left and right side along the X axial are symmetrical, so taking the oscillator 1 as a representative. The convergence rate, asymmetry rate (the difference between the positive and negative areas, 0 means no difference), period change and duty ratio (the ratio of ascending part in one period cycle, 0.5 represents the symmetry waveform) of the steady-state waveforms with different k and ρ are shown in Figure 5. The convergence rate is mainly determined by k. The convergence is very slow in k <1 with almost no distortion, fast in k = 1–5 with a little distortion and extremely fast in k > 5 with large distortion and period change. After k = 10, convergence rate should have been <1 s (steady state is judged by checking the change of peak values in adjacent period). Besides, there are two findings: (1) large ρ value brings about large distortion, as shown in Figures 4B, 5B. (2) In the raise of k value, the waveform tends to be symmetrical (asymmetry rate tends to 0 and the duty ratio tends to 0.5) with period shrinking. That means the entire waveform is changed to be “small” and “smooth,” which is much different from expected, as shown in Figures 4A, 5C,D.

FIGURE 3

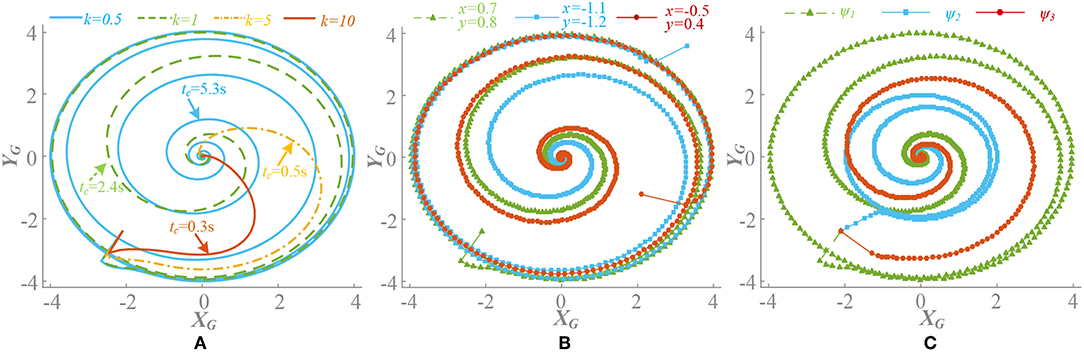
Figure 3. Convergence process of ${G}\left\{G({\bar{\upsilon }}_0),k(t)\right\}$with influence of different parameter (ρ = 0.5). Signal of limb 1 is selected. (A) Different value of k(t), phase factors ψ_i = Φ_i/2π, ψ = [0, 0.5, 0.5, 0, 0, 0.5], initial point is (0.7, 0.8). Different k(t) leads a different convergence rate. (B) Different initial points (x₀, y₀), k(t) = 1, ψ = [0, 0.5, 0.5, 0, 0, 0.5]. Initial point has little influence on convergence rate, but is important to synchronization process. (C) Different phase factors ψ₁ = [0, 0.5, 0.5, 0, 0, 0.5], ψ₂ = [0, 0.5, 0, 0.5, 0, 0.5], ψ₃ = [0.2, 0.4, 0.6, 0.1, 0.9, 0.7]. k(t) = 1, initial point is (0.7, 0.8). A different phase factor means a different synchronization process.

FIGURE 4

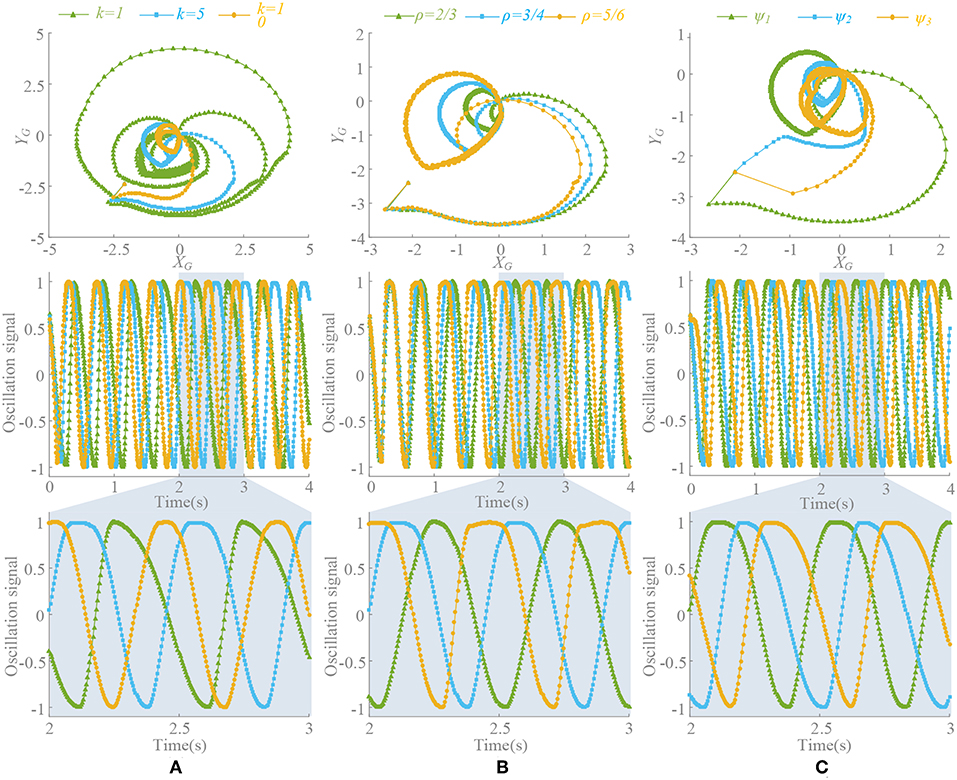
Figure 4. Influence of different parameters with ρ≠0.5. Signal of limb 1 is selected. (A) Different value of k(t), phase factors ψ_i = Φ_i/2π, ψ = [0, 0.5, 0.5, 0, 0, 0.5], ρ = 3/4 and initial point (0.7, 0.8). Different k(t) leads a different limit circle scale of $G\left\{{\bar{\upsilon }}_0\right\}$ and the deformation is directly related to $k(t)G\left\{{\bar{\upsilon }}_0\right\}$. (B) Different ρ = [2/3, 3/4, 5/6], initial point (0.7, 0.8), and k(t) = 5. Large ρ leads to large deformation. (C) Different phase factors ψ₁ = [0, 0.5, 0.5, 0, 0, 0.5], ψ₂ = [0, 0.5, 0, 0.5, 0, 0.5], ψ₃ = [0.2, 0.4, 0.6, 0.1, 0.9, 0.7], k(t) = 5, initial point (0.7, 0.8), and ρ = 3/4. Different motion pattern has different limit circle of $G\left\{{\bar{\upsilon }}_0\right\}$.

FIGURE 5

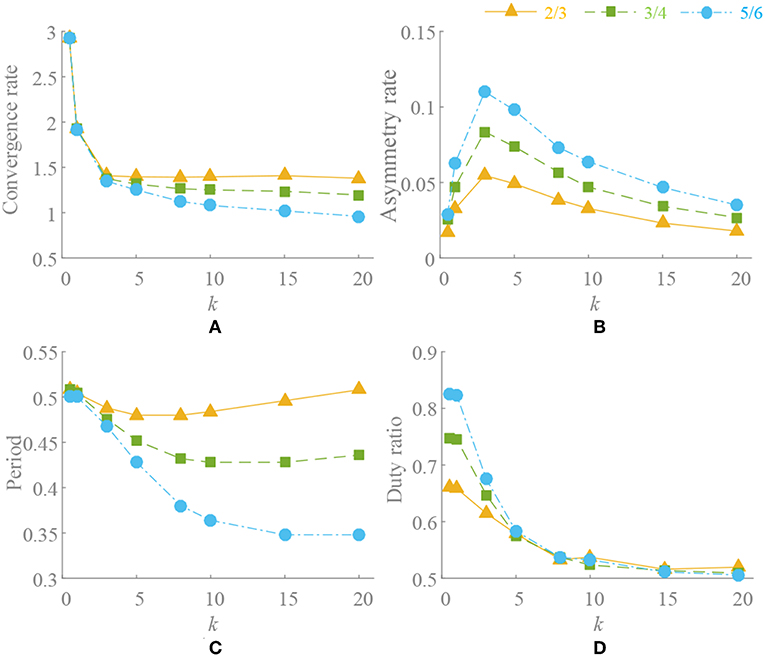
Figure 5. Convergence and deformation of waveform. Oscillation period is set to T = 0.5s. k = [0.5, 1, 3, 5, 8, 10, 15, 20], ρ = [2/3, 3/4, 5/6]. (A) Convergence rate. (B) Asymmetry rate. (C) Period change. (D) Duty ratio.

Since the value of k(t) determines the convergence rate and the magnitude of the distortion, a function k_e(t) is proposed:

$\begin{array}{ll}{k}_e(t)=\kappa e^{-\eta ·(t-t_0)}& (25)\end{array}$

in which, η is the descend factor and related to time. κ is the initial strength. t₀ is the begin moment. A little time will be taken for large convergence strength and long for a small value. So, the convergence process is mainly determined by the state of k_e(t) > = 1, then the effective time T_effective of convergence can be solved by

$\begin{array}{ll}{e}^{-\eta ·(t-t_0)}\ge 1/\kappa & (26)\end{array}$

$\begin{array}{ll}{T}_{effective}=(t-t_0)\ge ln(\kappa )/\eta .& (27)\end{array}$

Therefore, in the steady state, when k(t) = 0, the distortion vanishes and the period recovers to normal. The problem of oscillation deformation caused by the asymmetry factor is solved. However, the adjustment capability of synchronization is not available at this moment. If the phase difference is inaccurate as required before k(t) = 0, it cannot be adjusted any more. Therefore, choosing the right parameters to ensure fast and stable convergence is important. It can be seen from the Figure 6 that κ and η are approximately linearly correlated. According to the finds above, when κ is too large, deformation must not be ignored. Then κ and η are better taking values within [1, 10]. In this paper, κ = η = 5 and the convergence time is 0.32 s. Finally, the σ-Hopf oscillators with synchronization used in the system is

$\begin{array}{l}{\stackrel{\bullet }{\upsilon }}_i=\text{f}({\upsilon }_i,{\mu }_i,{\sigma }_i({\rho }_i,\lambda ,t))-\kappa e^{-\eta ·(t-t_0)}.\\ {\displaystyle \sum _{j\in {𝔑}_i}^{n_i}}({\upsilon }_i-\frac{{\mu }_i}{{\mu }_j}\text{R}(\Delta {\Phi }_{ij}){\upsilon }_j)+\text{u}(t)& (28)\end{array}$

in which, the positive scalar κ denotes the coupling gain and can be time-varying for different locomotion, η denotes the descend factor, and t₀ is the start point.

FIGURE 6

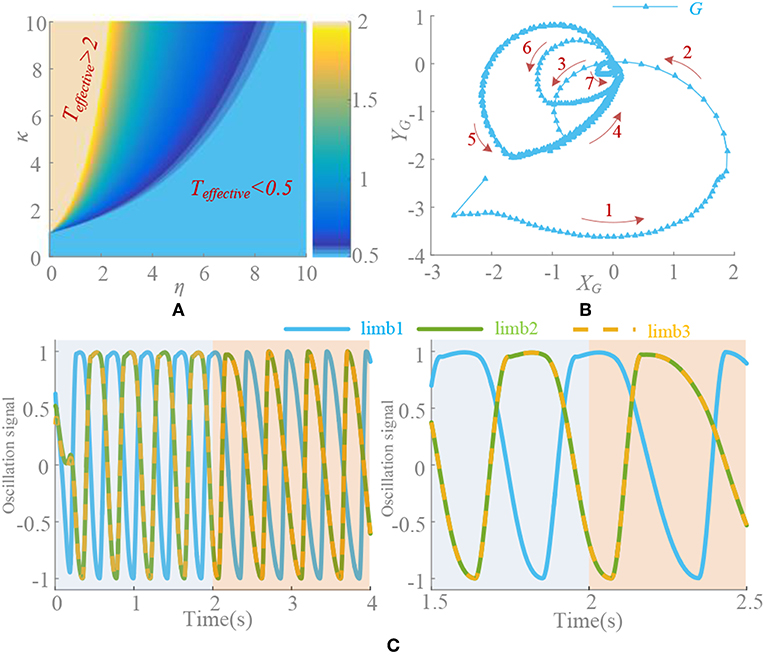
Figure 6. (A) Effective time surface of k_e(t). T_effective>2s and T_effective <0.5s is marked. T = 0.5s. (B) Convergence process. Red arrow is the direction of limit circle. (C) Deformation elimination. k(t) = 5 in 0–2 s and changes to k_e(t) at 2 s (t₀ = 2 s). ρ = 5/6, κ = η = 5, t₀ = 2 s, ψ = [0, 0.5, 0.5, 0, 0, 0.5] and signal of limb 1, 2, and 3 are selected.

Neurobiologically Inspired Control and Results

The forward and inverse kinematics of parallel robots is a cumbersome task, and there are a lot of related researches (Merlet and Pmerlet, 2006; Li and Wen, 2011; Huang et al., 2013). So, the presented CPG signal processing and network construction is used for parallel bionic waists in this section. It can effectively avoid complex solving processes and achieve coordinated bionic behavior. But the formation and construction of coupling bionic behavior of such parallel structures is still unknown. The waist is mainly composed of lumbar bones and muscles. It helps the torso to achieve multi-directional bending and axial torsion and transmits (spinal) nerve signals and loads of legs (Hashemirad et al., 2009; Galis et al., 2014). The proposed parallel waist can achieve identical functions, which provide a structural basis for the control strategy. In this paper, four main movements: stretch, lateral shift, pitch and torsion (motion pattern A, B, C, and D) are discussed. In order to prove the effectiveness of the method, the range deviation, motion transformation characteristics, and position error of the waist will be analyzed from the amplitude, phase, and deformation of the oscillation signal, respectively.

Amplitude and Frequency

According to the bionic waist structure and coupling network established in Materials and Method, the phase relationship of the six oscillation signals is shown in Figure 7A. These signals will be directly used to drive the limbs of the platform. Due to the problem of multiple solutions in the inverse kinematics of parallel robots (Ahmet and Koksal, 2014), repeat movements occur in the full rotation range of the actuator. That is to say, the different configurations of actuator can result in the same position of the moving platform, so the appropriate range of joint rotation must be selected, which satisfies both the maximum movement space and the requirement of smooth locomotion. Compared to the series structure, it is not so simple to achieve independent movement in the parallel bionic waist, since the movement of a single actuator will cause multiple degrees of freedom of the moving platform. Learning from the forward and inverse kinematics of the parallel robot and the structural characteristics of the bionic waist (see Appendix in Supplementary Material), the amplitude and offsets of the oscillation signal are tuned. The control waveform shown in Figure 7B is a result of the amplitude and phase adjustment for the range and direction of the locomotion.

FIGURE 7

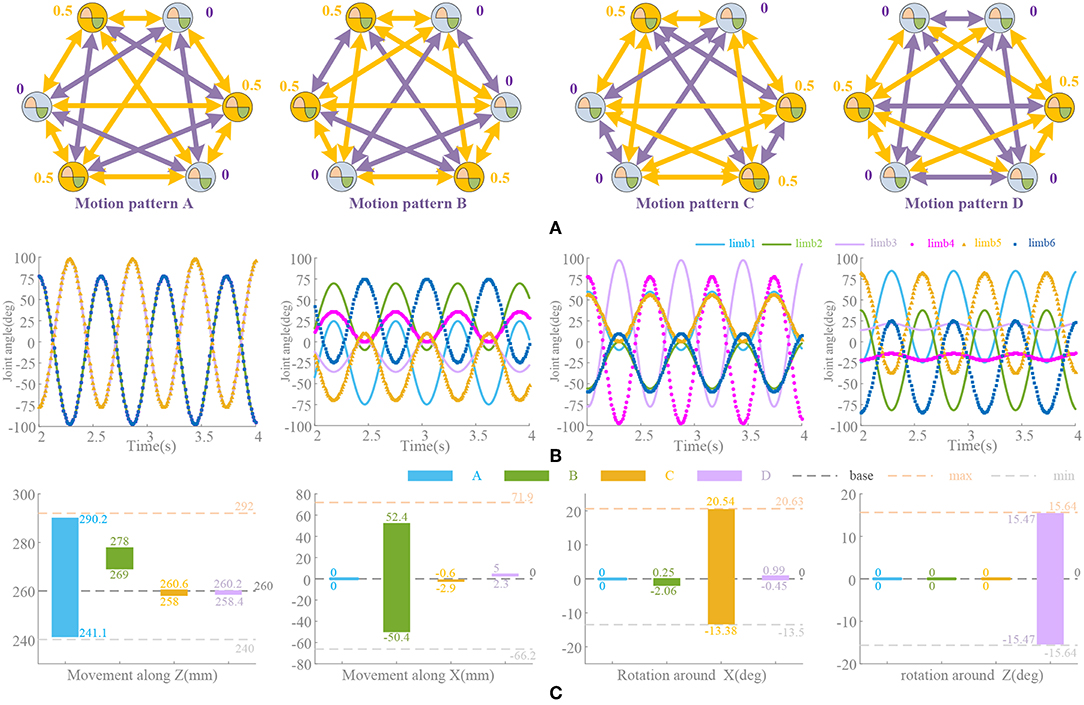
Figure 7. Different motion patterns in different directions. (A) Network configuration. Coupling factors are set according to Materials and Method. Yellow arrows link oscillators with 180° phase difference. Phase factors (ψ_i = Φ_i/2π) is marked. Purple arrows mean no phase difference. (B) Amplitude and offset of oscillation signals. (C) Deviations between neurobiologically inspired control and kinematics solution [the forward and inverse kinematics formula and structure parameters are shown in Appendix (Supplementary Material)]. Movement along and around axial Y is not taken into consideration for the symmetry of structure and movement.

In order to verify the effectiveness of the motion synthesis, the limit range of movement under CPG based control is compared with that obtained by kinematics solution. The deviations of the main motions are shown in Figure 7C. Among them, the actuator range is referenced to the maximum motion position and distributed according to the oscillator waveform (approximate linear distribution). However, the actual parallel platform motion is decomposed into a rotation of 6 actuators with strong non-linear coupling property, which depends on the complexity of motion synthesis, so there are movements in other directions besides the main control directions, i.e., almost every motion pattern will cause movements along axial Z. If the pre-processing module or network is used for non-linear mapping and planning, this phenomenon can be improved and more complicated locomotion can be realized, but in this paper the limbs are directly driven by the oscillation signals at present.

With regard to frequency, most of the motions in quadruped mammals are in low frequencies, and even high-speed running will not carry out in too high frequency. The frequency transition problem has been discussed in detail (Nachstedt et al., 2017). Since the parallel waist frequency does not change too much and has no abrupt change, it will not cause waveform deformation and position deviation. Of course, in order to improve the adaptability, optimization and adaptive methods can be used for frequency adjustment, and there are many methods (Righetti et al., 2006; Nachstedt et al., 2017).

Phase

According to the foregoing illustration, the phase differences in the four typical motions have been determined by the structure and the motion state. In nature, such states in mammals are very easy to transform, i.e., the stretching (motion pattern A) of the torso is easy to transform into a lateral shifting motion (motion pattern B) or a pitching motion (motion pattern C). While the motion pattern D is relatively independent. Generally, it is necessary to return to the initial state before performing other locomotion. According to the symmetric distribution of the actuators (Δ₁₆ = Δ₂₅ = Δ₃₄ = 180°), the motion patterns A, B, and C can be simplified to consider the phase difference of the single-sided actuator 1–2–3. According to Figure 8, three changes are conducted: A → C, C → B, and A → B. A → C and C → B can be supposed as similar locomotion, since only one group of oscillators needs to change phase, indicating that most of the actuators have similar movements in the two motion patterns. Therefore, the transformation should be very smooth. But A → B needs to change two sets of oscillators which cannot be a similar motion. If a transformation like A → B is unavoidable, it is best to change through similar motion, such as A → C → B through a bending motion or A → AB → B through a coupling transition. It is recommended to change state between adjacent motion patterns. Otherwise, it will cause large deviation and even malfunction. In the transformation, the oscillation amplitude should be adjusted at the same time, since it is related to both the changing process and result.

FIGURE 8

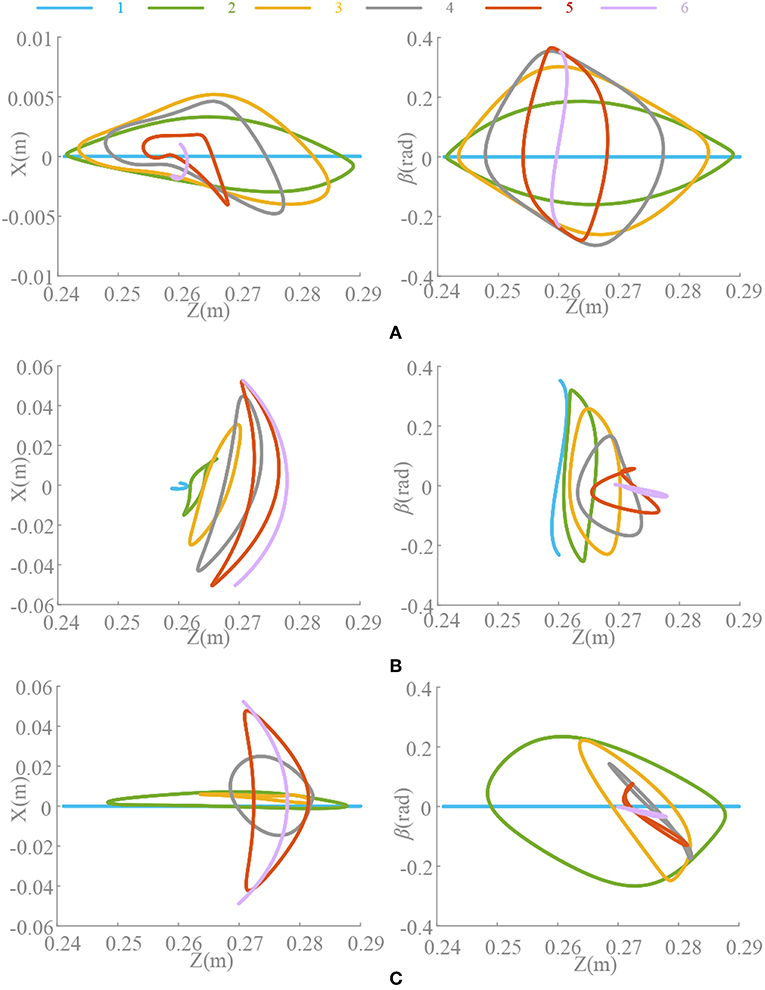
Figure 8. Transformation of different motion patterns. β is the pitch angle round Y. (A) Motion pattern A → motion pattern C. (B) Motion pattern C → motion pattern B. (C) Motion pattern A → motion pattern B. All transformation is conducted in 5 steps. Both phase and amplitude changes linearly.

CPG-based locomotion control with phase difference adjustment enables fast transformation between motion patterns and formation of several coupling motions. Without a doubt, most of the mammalian movements are a synthesis of simple movements, i.e., the running process is the synthesis of motion pattern A and motion pattern C. In addition, it is worth mentioning that the motion pattern of the parallel waist is not only determined by the phase difference of the oscillator, but also by the amplitude.

Duty Factor ρ

The significance of introducing σ is to make an asymmetrical duty cycle in oscillation, so that the locomotion is more controllable and coordinated, such as the leg swinging of walking robot (Xiong et al., 2017), the wings flapping of flying robot (Briod et al., 2014), and the fin swaying of underwater robots (Wang et al., 2019). But the asymmetry oscillation always brings about deformation of the waveform as well as the period changes, which has been discussed in Materials and Method and Analysis of Synchronization. And we noticed that selection of ρ is also influenced by the phase difference, i.e., in the Z-direction motion, the difference between the oscillator 1 and the oscillator 2 is 180°. Therefore, in order to maintain the consistent action, if the ρ of the oscillator 1 is 3/4, the ρ of the oscillator 2 should be 1/4. Thus, the locomotion coordination can be ensured. So, if the motion transformation is performed, the value of ρ must also be changed correspondingly. A fixed ρ value may not satisfy the phase difference requirement. The coupling motion of motion pattern A and C is analyzed in Figure 9. In the transformation from motion pattern A to C (Δ₁₃ = 0 → Δ₁₃ = 0.5), ρ should do the same change.

FIGURE 9

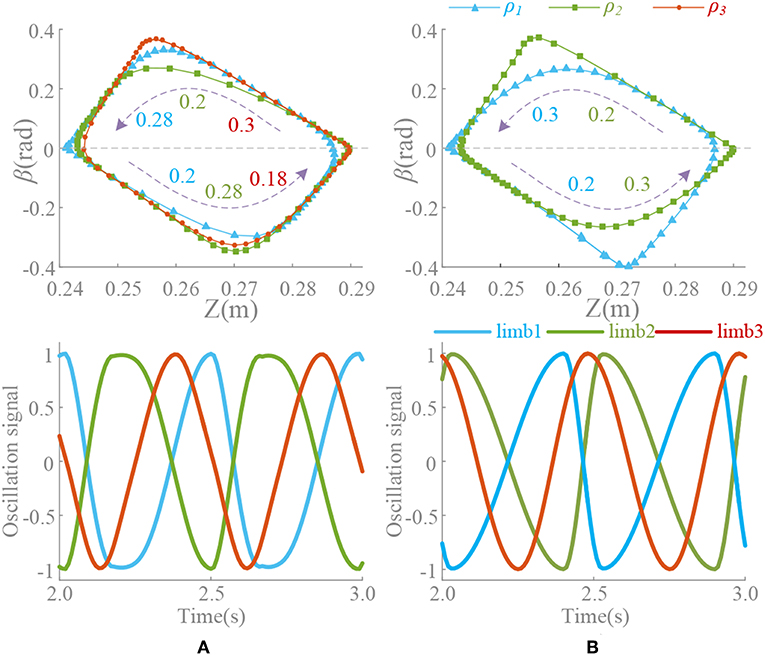
Figure 9. Position trajectory and waveform of coupling motion. T = 0.5 s, ψ = [0, 0.5, 0.2, 0.3, 0, 0.5], ρ₁ = [3/4, 1/4, 0.55, 0.45, 3/4, 1/4], ρ₂ = [1/4, 3/4, 0.45, 0.55, 1/4, 3/4], ρ₃ = [3/4, 1/4, 3/4, 1/4, 3/4, 1/4]. Forward duration (below zero line) and back duration (above zero line) are influenced by ρ^limb3, which is corresponding to limb 3 and Δ₁₃. β is the pitch angle round Y. (A) Constant coupling strength, k(t) = 5. (B) Proposed coupling strength k(t) = k_e(t).

During the above motion, the existence ${G}\text{'}\left\{\text{G}({\bar{\upsilon }}_0),k(t)\right\}$ in the (21) leads an unexpected change on period of oscillation signal in the steady state. Unsuitable ρ will make it worse. ρ^limb3 keeping unchange (ρ^limb3 = 3/4) through the transformation (Δ₁₃ = 0.2) leads an unpredictable forward-back duration ratio shown in Figure 9A. This effect cannot be eliminated if k is non-zero, which reduces the control ability of ρ to the waveform. Moreover, the effect or the change is actually difficult to detect or predict. The method of this paper can control the waveforms of each oscillator as well as the ρ and phase difference, so that some special motion points even can control effectively shown in Figure 9B. The value of ρ should be adjusted timely according to the phase difference to make the transformation more coordinated and less impact. Furthermore, precise control and smooth motion are to be further improved by optimizing control and learning, evolution and other methods.

Simulation

To investigate the effects of neurobiologically inspired control method on bionic parallel waist, we conducted co-simulation by MATLAB/ADAMS. The parameters of the parallel platform are shown in the Appendix (Supplementary Material). The control frame is presented in Platform and System and shown in Figure 1C. With the bionic control method, control signals for the motor driver are generated by the oscillators and synchronous network. Specifically, we set 3 transition states for magnitude (S_M), phase (S_P), and coupling strength (S_C) to evaluate the performance of the method. Oscillation signals, joint angles, and moving platform locomotion trajectories including movements and rotations are shown in Figure 10. Before 2.5 s, the platform performs in motion pattern A, so there are only movements along Z axial. The magnitudes are regulated by linear transformation in 0.5 s and they make the moving distance change from 0.25–0.28 mm to 0.241–0.292 mm. To perform a bending movement (rotation around Y axial), ψ is gradually set from [0, 0.5, 0, 0.5, 0, 0.5] to [0, 0.5, 0.2, 0.7, 0, 0.5] in 0.5 s from the moment at 2.5 s to regulate the phases of limb 3 and 4. This leads the moving platform to rotate around Y axial and slight movements along X axial. In the coupling strength transition at 4.5 s, coupling strength k(t) = 5 turns to k(t) = k_e(t) and signals become stable in 0.32 s according to the effective time surface of k_e(t). The duty factor is set constant as ρ = [1/4, 3/4, 1/4, 3/4, 1/4, 3/4] and the distortion begin to diminish at 3.5 s when k(t) = k_e(t). Influence on the movements and rotations of this factor also can be seen in Figure 9.

FIGURE 10

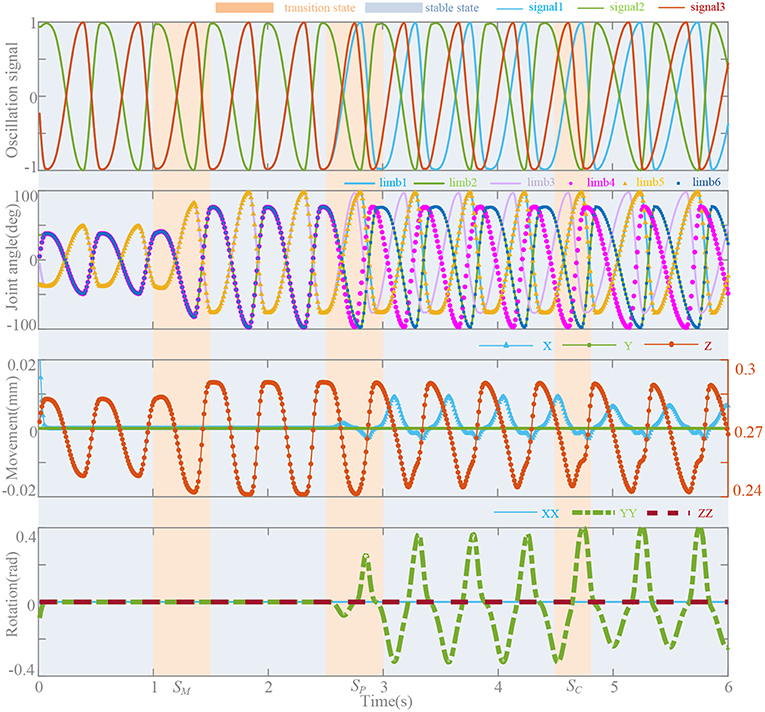
Figure 10. Oscillation signals, joint angles, and locomotion trajectories. T = 0.5 s, k(t) = 5, ψ = [0, 0.5, 0, 0.5, 0, 0.5], and ρ = [1/4, 3/4, 1/4, 3/4, 1/4, 3/4]. Magnitude transition (S_M): movement Z (0.25, 0.28 mm) → (0.241, 0.292 mm). Phase transition (S_P): ψ → [0, 0.5, 0.2, 0.7, 0, 0.5]. Coupling strength transition (S_C), k(t) = 5 → k(t) = k_e(t).

Conclusion

A synchronous bionic control strategy based on σ-Hopf for a bionic parallel waist is proposed. To identify and evaluate waveform distortion of asymmetry σ-Hopf oscillation in synchronization, the transition state is analyzed. The variable coupling strength is raised to eliminate distortion and ensure effective and stable synchronization simultaneously. On this basis, the bionic control network for the parallel waist is constructed to realize the typical behavior. The effects of amplitude, frequency, phase, and duty factor on the behavioral deviation, motion pattern transformation, and forward-back duration adjustment are discussed. The main contributions of this paper are:

1. σ-Hopf oscillator has a symmetrical circular limit cycle and the waveform is regular and stable. Different from other oscillators, its frequency, amplitude, and duty ratio can be adjusted independently, which contribute to the control of different moving speeds, motion range, and forward-back duration. These advantages can enhance behavioral diversity and agility of bionic robot, which is of great significance for bionic control.

2. The waveform characteristics of σ-Hopf oscillator makes the synchronization process more complicated than symmetric oscillator. Our analysis and methods show a way to eliminate the deformation and ensure the fast convergence. Thus, without changing the characteristics of σ-Hopf oscillator, synchronization process is achieved and can be used for the coordinated behavior and coupled locomotion of the multi-joint bionic robot.

3. The σ-Hopf oscillator based neurobiologically inspired control is put forward to enhance the controllability for the bionic waist, which has really strong coupling characteristics. Not only the initial and final state of motion, but also the intermediate state and instantaneous state can be controlled precisely. This will benefit the transition and transformation of the locomotion and makes the coupling motion more flexible.

In this paper we provide a waveform-controllable oscillator and an undistorted synchronization method for the bionic robot, i.e., legged robot, flying robot, and swimming robot, etc. In the future, we will build the entire motion control network of the quadruped robot with bionic waist for coordinated motion. As the network architecture becomes more complex, the proposed method will make more sense for the controllable locomotion and synchronization process.

Data Availability

All datasets generated for this study are included in the manuscript and/or the Supplementary Files.

Author Contributions

YZ designed the method. YZ, SZ, DG, and QL designed and performed the simulations. YZ and SZ analyzed the data and wrote the paper.

Funding

This research was funded by the National Natural Science Foundation of China (No. 51605039), the Thirteenth 5-Year Plan Equipment Pre-research Field Fund (No. 61403120407), the China Postdoctoral Science Foundation (No. 2018T111005 and 2016M592728), Fundamental Research Funds for the Central Universities, CHD (No. 300102259308, 300102258203, and 300102259401).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnbot.2019.00059/full#supplementary-material

Footnotes

1. ^https://www.bostondynamics.com/robots.

References

Acebron, J., Bonilla, L. L., Pérez-Vicente, C. J., Ritort, F., and Spigler, R. (2005). The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185. doi: 10.1103/RevModPhys.77.137

CrossRef Full Text | Google Scholar

Ahmet, D., and Koksal, E. (2014). Modeling and trajectory tracking control of 6-DOF RSS type parallel manipulator. Robotica 32, 643–657. doi: 10.1017/S0263574713000908

CrossRef Full Text | Google Scholar

Albiez, J., Luksch, T., Dilmann, R., and Berns, K. (2006). “A behaviour network concept for controlling walking machines,” in Adaptive Motion of Animals and Machines, eds H. Kimura, K. Tsuchiya, A. Ishiguro, and H. Witte (Tokyo: Springer), 237–244. doi: 10.1007/4-431-31381-8_21

CrossRef Full Text | Google Scholar

Ananthanarayanan, A., Azadi, M., and Kim, S. (2012). Towards a bio-inspired leg design for high-speed running. Bioinspir Biomim. 7:046005. doi: 10.1088/1748-3182/7/4/046005

PubMed Abstract | CrossRef Full Text | Google Scholar

Aoi, S., Katayama, D., Fujiki, S., Tomita, N., Funato, T., Yamashita, T., et al. (2013). A stability-based mechanism for hysteresis in the walk-trot transition in quadruped locomotion. J. R. Soc. Interface 10:20120908. doi: 10.1098/rsif.2012.0908

PubMed Abstract | CrossRef Full Text | Google Scholar

Aoi, S., Yamashita, T., and Tsuchiya, K. (2011). Hysteresis in the gait transition of a quadruped investigated using simple body. Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys. 83(6 Pt 1):061909. doi: 10.1103/PhysRevE.83.061909

PubMed Abstract | CrossRef Full Text | Google Scholar

Arena, P., and Fortuna, L. (2000). Collective behavior in cellular neural networks to model the central pattern generator. Int. J. Syst. Sci. 31, 827–841. doi: 10.1080/002077200406561

CrossRef Full Text | Google Scholar

Arena, P., Fortuna, L., Frasca, M., and Marchese, C. (2001). “Multi-template approach,” in IEEE International Symposium on Circuits and Systems (Sydney, NSW: IEEE), 37–40. doi: 10.1109/ISCAS.2001.921240

CrossRef Full Text | Google Scholar

Ashwin, P. (2003). The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space (Progress in Mathematics), Vol. 35. Basel: Bulletin of the London Mathematical Society, 430–431.

Google Scholar

Barasuol, V., Buchli, J., Semini, C., Frigerio, M., Pieri, E. R. D., and Caldwell, D. G. (2013). “A reactive controller framework for quadrupedal locomotion on challenging terrain,” in Proceedings of IEEE International Conference on Robotics and Automation (Karlsruhe: ICRA), 2554–2561. doi: 10.1109/ICRA.2013.6630926

CrossRef Full Text | Google Scholar

Bjelonic, M., Kottege, N., and Beckerle, N. P. (2016). “Proprioceptive control of an over-actuated hexapod robot in unstructured terrain,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (Daejeon: IEEE). doi: 10.1109/IROS.2016.7759321

CrossRef Full Text | Google Scholar

Briod, A., Kornatowski, P., Zufferey, J., and Floreano, D. (2014). A Collision-resilient Flying Robot. J. Field Robot. 31, 496–509. doi: 10.1002/rob.21495

CrossRef Full Text | Google Scholar

Buchli, J., and Ijspeert, A. J. (2004). “Distributed central pattern generator model for robotics application based on phase sensitivity analysis biologically inspired approaches to advanced information technology,” in First International Workshop (Lausanne). doi: 10.1007/978-3-540-27835-1_25

CrossRef Full Text | Google Scholar

Buono, P. L., and Golubitsky, M. (2001). Models of central pattern generators forquadruped locomotion. I. Primary gaits. J. Math. Biol. 42, 291–326. doi: 10.1007/s002850000058

CrossRef Full Text | Google Scholar

Cao, Q., and Poulakakis, I. (2016). Quadrupedal running with a flexible torso: control and speed transitions with sums-of-squares verification. Art. Life Robot. 21, 384–392. doi: 10.1007/s10015-016-0330-5

CrossRef Full Text | Google Scholar

Chung, S. J., and Dorothy, M. (2010). Neurobiologically inspired control of engineered flapping flight. J. Guidance Control Dyn. 33, 440–453. doi: 10.2514/1.45311

CrossRef Full Text | Google Scholar

Cong, M., Liu, D., Du, Y., Wen, H., and Wu, Y. (2011). Application of triune parallel serial robot system for full mission tank training. Ind. Robot. 38, 533–544. doi: 10.1108/01439911111154108

CrossRef Full Text | Google Scholar

Corke, P. I., Peterson, R. A., and Rus, D. (2003). “Networked robots: flying robot navigation using a sensor net,” in Robotics Research. The Eleventh International Symposium (Siena: ISRR). doi: 10.1007/11008941_25

CrossRef Full Text | Google Scholar

Coros, S., Karpathy, A., Jones, B., Reveret, L., and Panne, M. (2011). Locomotion skills for simulated quadrupeds. ACM T GRAPHIC. 30, 1–12. doi: 10.1145/2010324.1964954.

CrossRef Full Text | Google Scholar

Dallej, T., Andreff, N., Mezouar, Y., and Martinet, P. (2006). “3D pose visual servoing relieves parallel robot control from joint sensing,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (Beijing), 4291–4297. doi: 10.1109/IROS.2006.281959

CrossRef Full Text | Google Scholar

Donati, E., Indiveri, G., and Stefanini, C. (2016). “A novel spiking CPG-based implementation system to control a lamprey robot,” in IEEE International Conference on Biomedical Robotics and Biomechatronics (Singapore), 1364. doi: 10.1109/BIOROB.2016.7523822

CrossRef Full Text | Google Scholar

Drazin, P. G. (2008). Nonlinear Systems (Cambridge Texts in Applied Mathematics). Cambridge: Cambridge Univ. Press.

Google Scholar

Dutra, M. S., De Pina Filho, A. C., and Romano, V. F. (2003). Modeling of a bipedal locomotor using coupled nonlinear oscillators of Van der Pol. Biol. Cybern. 88, 286–292. doi: 10.1007/s00422-002-0380-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Eich, M., Grimminger, F., and Kirchner, F. (2009). Adaptive compliance control of a multi-legged stair-climbing robot based on proprioceptive data. Industr. Robot 36, 331–339. doi: 10.1108/01439910910957084

CrossRef Full Text | Google Scholar

Fukuoka, Y.H, Kimura, A. H., and Cohen (2003). Adaptive dynamic walking of a quadruped robot on irregular terrain based on biological concepts. Int. J. Robot. Res. 22, 187–202. doi: 10.1177/0278364903022003004

CrossRef Full Text | Google Scholar

Galis, F., Carrier, D. R., Van Alphen, J., Mije, S. V. D., Van Dooren, T. J. M., Metz, J., et al. (2014). Fast running restricts evolutionary change of the vertebral column in mammals. Process Natl Acad Sci U.S.A. 111, 11401–11406. doi: 10.1073/pnas.1401392111

PubMed Abstract | CrossRef Full Text | Google Scholar

Gehring, C., Coros, S., Hutler, M., Bellicoso, D., Huter, M., Bellicoso, D., et al. (2016). Practice makes perfect: an optimization-based approach to controlling agile motions for a quadruped robot. IEEE Robot. Autom. Mag. 23, 34–43. doi: 10.1109/MRA.2015.2505910

CrossRef Full Text | Google Scholar

Grillner, S., Wallén, P., Saitoh, K., Kozlov, A., and Robeertson, B. (2007). Neural bases of goal-directed locomotion in vertebrates—an overview. Brain Res. Rev. 57, 2–12. doi: 10.1016/j.brainresrev.2007.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Grondin, D. E., and Potvin, J. R. (2009). Effects of trunk muscle fatigue and load timing on spinal responses during sudden hand loading. J. Electromyogr. Kinesiol. 19, e237–45. doi: 10.1016/j.jelekin.2008.05.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Hashemirad, F., Talebian, S., Hatef, B., and Kahlaee, A. H. (2009). The relationship between flexibility and EMG activity pattern of the erector spinae muscles during trunk flexion–extension. J. Electromyogr. Kinesiol. 19, 746–753. doi: 10.1016/j.jelekin.2008.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Haynes, G. C., Pusey, J., Knopf, R., Johnson, A. M., and Koditschek, D. (2012). “Laboratory on legs: an architecture for adjustable morphology with legged robots,” in SPIE Defense, Security, and Sensing (Baltimore, MD: International Society for Optics and Photonics), 786–796. doi: 10.1117/12.920678

CrossRef Full Text | Google Scholar

He, B., Zhang, P., and Hou, S. (2015). Accuracy analysis of a spherical 3-DOF parallel underactuated robot wrist. Int. J. Adv. Manuf. Tech. 79, 395–404. doi: 10.1007/s00170-015-6837-4

CrossRef Full Text | Google Scholar

Huang, J., Chen, Y., and Zhong, Z. (2013). Udwadia-kalaba approach for parallel manipulator dynamics. J. Dyn. Syst. Measur. Control. 135:061003. doi: 10.1115/1.4024600

CrossRef Full Text | Google Scholar

Hutter, M., Gehring, C., Bloesch, M., Hoepflinger, M., Remy, C. D., and Siegwart, R. (2012). “Starleth a compliant quadrupedal robot for fast, efficient, and versatile locomotion,” in International Conference on Climbing & Walking Robot-Clawar (Baltimore, MD:), 1–8. doi: 10.1108/01439911311309942

CrossRef Full Text | Google Scholar

Hutter, M., Gehring, C., Jud, D., Lauber, A., Bellicoso, D., Tsounis, V., et al. (2016). “ANYmal - a highly mobile and dynamic quadrupedal robot,” in IEEE/RSJ International Conference on Intelligent Robots & Systems (Daejeon), 483–490. doi: 10.1109/IROS.2016.7758092

CrossRef Full Text | Google Scholar

Hwangbo, J., Lee, J., Dosovitskiy, A., Bellicoso, D., Tsounis, V., Koltun, V., et al. (2019). Learning agile and dynamic motor skills for legged robots. Sci. Robot. 4:eaau5872. doi: 10.1126/scirobotics.aau5872

CrossRef Full Text | Google Scholar

Ijspeert, A. J. (2008). Central pattern generators for locomotion control in animals and robots: a review. Neural Netw. 21, 642–653. doi: 10.1016/j.neunet.2008.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Jean-Xavier, C., and Perreault, M. C. (2018). Influence of brain stem on axial and hindlimb spinal locomotor rhythm generating circuits of the neonatal mouse. Front. Neurosci. 12:53. doi: 10.3389/fnins.2018.00053

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, B., Chen, C., and Li, W. (2013). Power consumption optimization for a hexapod walking robot. Intell. Robot. Syst. 71, 195–209. doi: 10.1007/s10846-012-9771-9

CrossRef Full Text | Google Scholar

Jin, Y., Chanal, H., and Paccot, F. (2014). “Robotics and automation,” in Handbook of Manufacturing Engineering and Technology, Parallel Robot, ed A. Nee (London: Springer).

Google Scholar

Jorgensen, M. J., Marras, W. S., and Gupta, P. (2003). Cross-sectional area of the lumbar back muscles as a function of torso flexion. Clin. Biomech. 18, 280–286. doi: 10.1016/s0268-0033(03)00027-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalouche, S., Rollinson, D., and Choset, H. (2015). “Modularity for maximum mobility and manipulation: control of a reconfigurable legged robot with series-elastic actuators,” in IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR) (West Lafayette, IN: IEEE). doi: 10.1109/SSRR.2015.7442943

CrossRef Full Text | Google Scholar

Kato, N., and Kamimura, S. (2008). Bio-mechanisms of Swimming and Flying Fluid Dynamics, Biomimetic Robots, and Sports Science. Berlin: Springer.

Google Scholar

Khoramshahi, M., Spröwitz, A., Tuleu, A., Ahmadabadi, M. N., and Ljspeert, A. J. (2013). “Benefits of an active spine supported bounding locomotion with a small compliant quadruped robot,” in IEEE International Conference on Robotics and Automation (Karlsruhe), 3329–3334. doi: 10.1109/ICRA.2013.6631041

CrossRef Full Text | Google Scholar

Kimura, A., Fukuoka, Y., Konaga, K., Hada, Y., and Takase, K. (2001). “Adaptive dynamic walking of a quadruped robot on irregular terrain using a neural system model,” in Proceedings of IEEE/Rsj International Conference on Intelligent Robots and Systems, Vol. 4 (Maui, HI: IEEE), 2312–2317. doi: 10.1007/3-540-36460-9_10

CrossRef Full Text | Google Scholar

Kimura, H. Y., Fukuoka, Y., Hada, and Takase, K. (2002). “Three-dimensional adaptive dynamic walking of a quadruped-rolling motion feedback to CPGs controlling pitching motion,” in Proceeding of 2002 IEEE International Conference of Robotics and Automation (Washington, DC), 2228–2233. doi: 10.1109/ROBOT.2002.1013563

CrossRef Full Text | Google Scholar

Kopell, N., Ermentrout, G. B., and Williams, T. L. (2006). On chains of oscillators forced at one end: SIAM journal on applied mathematics. Soc. Industr. Appl. Math. 51, 1397–1417. doi: 10.2307/2101972

CrossRef Full Text | Google Scholar

Kuehn, D., Schilling, M., Stark, T., Zenzes, M., and Kirchner, F. (2017). System design and testing of the hominid robot charlie. J. Field Robot. 34, 666–703. doi: 10.1002/rob.21662

CrossRef Full Text | Google Scholar

Li, K., and Wen, R. (2011). “Active vibration isolation of 6-RSS parallel mechanism using integrated force feedback controllor,” in Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation (Shangshai), 314–317. doi: 10.1109/ICMTMA.2011.80

CrossRef Full Text | Google Scholar

Liu, C., Li, X., Zhang, C., and Chen, Q. (2018a). Multi-layered CPG for adaptive walking of quadruped robots. J. Bionic. Eng. 15, 341–355. doi: 10.1007/s42235-018-0026-8

CrossRef Full Text | Google Scholar

Liu, X., Han, G., Xie, F., Meng, Q., and Zhang, S. (2018b). A novel parameter optimization method for the driving system of high-speed parallel robots. ASME. J. Mech. Robot. 10:041010. doi: 10.1115/1.4040028

CrossRef Full Text | Google Scholar

Macintosh, J. E., Bogduk, N., and Pearcy, M. J. (1993). The effects of flexion on the geometry and actions of the lumbar erector spinae. SPINE 18, 884–893. doi: 10.1097/00007632-199306000-00013

PubMed Abstract | CrossRef Full Text | Google Scholar

Manoonpong, P., Parlitz, U., and Wörgötter, F. (2013). Neural control and adaptive neural forward models for insect-like, energy-efficient, and adaptable locomotion of walking machines. Front. Neural Circ. 7:12. doi: 10.3389/fncir.2013.00012

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsuoka, K. (1985). Sustained oscillations generated by mutually inhibiting neurons with adaptation. Biol. Cybern. 52, 367–376. doi: 10.1007/BF00449593

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsuoka, K. (1987). Mechanism of frequency and pattern control in the neural rhythm generators. Biol. Cybern. 56, 345–353.

Google Scholar

Merlet, J., and Pmerlet, J. P. (2006). Parallel Robots (Solid Mechanics and Its Applications), 2nd Edn. Berlin: Springer. doi: 10.1115/1.2900773

CrossRef Full Text | Google Scholar

Nachstedt, T., Tetzlaff, C., and Manoonpong, P. (2017). Fast dynamical coupling enhances frequency adaptation of oscillators for robotic locomotion control. Front. Neurorobot.11:14. doi: 10.3389/fnbot.2017.00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Owaki, D., and Ishiguro, A. (2017). A quadruped robot exhibiting spontaneous gait transitions from walking to trotting to galloping. Sci. Rep. 7:277. doi: 10.1038/s41598-017-00348-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Pham, Q. C., and Slotine, J. J. (2005). Stable concurrent synchronization in dynamic system networks. Neural Netw. 20, 62–77. doi: 10.1016/j.neunet.2006.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Plitea, N., Lese, D., Pisla, D., and Vaida, C. (2013). Structural design and kinematics of a new parallel reconfigurable robot. Robot. Com. Int. Manuf. 29, 219–235. doi: 10.1016/j.rcim.2012.06.001

CrossRef Full Text | Google Scholar

Raibert, M. H., and Tello, E. R. (1986). Legged robots that balance. IEEE. 1, 89–89. doi: 10.1109/MEX.1986.4307016

CrossRef Full Text | Google Scholar

Ramezani, A., Chung, S. J., and Hutchinson, S. (2017). A biomimetic robotic platform to study flight specializations of bats. Sci. Robot. 2:aal2505. doi: 10.1126/scirobotics.aal2505

CrossRef Full Text | Google Scholar

Rao, D. H., and Kamat, H. V. (1995). “Artificial neural networks for the emulation of human locomotion patterns,” in Conference of the Biomedical Engineering Society of India, in Proceedings of the First Regional Conference IEEE, Vol. 2, (New Delhi), 80–81. doi: 10.1109/RCEMBS.1995.532167

CrossRef Full Text | Google Scholar

Righetti, L. (2008). “Pattern generators with sensory feedback for the control of quadruped locomotion,” in IEEE International Conference on Robotics and Automation (Pasadena, CA: IEEE, 819–824. doi: 10.1109/ROBOT.2008.4543306

CrossRef Full Text | Google Scholar

Righetti, L., Buchli, J., and Ijspeert, A. J. (2006). Dynamic hebbian learning in adaptive frequency oscillators. Phys. D Nonlinear Phenomena. 216, 269–281. doi: 10.1016/j.physd.2006.02.009

CrossRef Full Text | Google Scholar

Righetti, L., and Ijspeert, A. J. (2006). Design Methodologies for Central Pattern Generators: An Application to Crawling Humanoids. Philadelphia, PA: Robotics: Science and Systems Ii, August, University of Pennsylvania, DBLP.

Google Scholar

Rossignol, S. (2004). Adaptive mechanisms of spinal locomotion in cats. Integr. Comp. Biol. 44, 71–79. doi: 10.1093/icb/44.1.71

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, C. P., Alves, N., and Moreno, J. C. (2016). Biped locomotion control through a biomimetic CPG-based controller. J. Intell. Robot. Syst. 85, 1–24. doi: 10.1007/s10846-016-0407-3

CrossRef Full Text | Google Scholar

Satoh, S., and Fujimoto, K. (2018). Gait generation for a biped robot with knees and torso via trajectory learning and state-transition estimation. Artif Life Robot. 23, 489–497. doi: 10.1007/s10015-018-0476-4

CrossRef Full Text | Google Scholar

Schwendner, J., Joyeux, S., and Kirchner, F. (2014). Using embodied data for localization and mapping. J. Field Robot. 31, 263–295. doi: 10.1002/rob.21489

CrossRef Full Text | Google Scholar

Semini, C., Barasuol, V., Goldsmith, J., Frigerio, M., Focchi, M., Gao, Y., et al. (2016). Design of the hydraulically actuated, torque-controlled quadruped robot HyQ2Max. IEEE/ASME Trans. Mech. 99, 635–646. doi: 10.1109/TMECH.2016.2616284

CrossRef Full Text | Google Scholar

Semini, C., Tsagarakis, N. G., Guglielmino, E., Focchi, M., Cannella, F., and Caldwell, D. G. (2011). Design of HyQ - a hydraulically and electrically actuated quadruped robot. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 225, 831–849. doi: 10.1177/0959651811402275

CrossRef Full Text | Google Scholar

Senda, K., and Tanaka, T. (2000). On Nonlinear Dynamic that Generates Rhythmic Motion with Specific Accuracy. Montreal, QC: Animals and Machines (AMAM), 8–12.

Google Scholar

Seo, K., Chung, S. J., and Slotine, J. J. E. (2010). CPG-based control of a turtle-like underwater vehicle. Auton. Robot. 28, 247–269. doi: 10.1007/s10514-009-9169-0

CrossRef Full Text | Google Scholar

Seok, S., Wang, A., Chuah, M. Y., Otten, D., Lang, J., and Kim, S. (2013). “Design principles for highly efficient quadrupeds and implementation on the MIT Cheetah robot,” in IEEE International Conference on Robotics & Automation (Karlsruhe), 3307–3312. doi: 10.1109/ICRA.2013.6631038

CrossRef Full Text | Google Scholar

Staicu, S. (2009). Inverse dynamics of the 3-PRR planar parallel robot. Robot. Autonom. Syst. 57, 556–563. doi: 10.1016/j.robot.2008.09.005

CrossRef Full Text | Google Scholar

Stefanini, C., Orlandi, G., Menciassi, A., Ravier, Y., Spina, G. L., Grillner, S., et al. (2006). “A mechanism for biomimetic actuation in lamprey-like robots,” in IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics (Pisa). doi: 10.1109/BIOROB.2006.1639151

CrossRef Full Text | Google Scholar

Strogatz, S. H. (2015). Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Comput. Phys. 8, 532. doi: 10.1063/1.4823332

CrossRef Full Text | Google Scholar

Takuma, T., Ikeda, M., and Masuda, T. (2010). “Facilitating multi-modal locomotion in a quadruped robot utilizing passive oscillation of the spine structure,” in International Conference on Intelligent Robots and Systems (Taipei: IEEE), 4940–4945. doi: 10.1109/IROS.2010.5649134

CrossRef Full Text | Google Scholar

Van der Pol, B., and Van der Mark, J. (1928). The heartbeat considered as a relaxation oscillation, and an electrical model of the heart. Philos. Mag. 6, 763–775. doi: 10.1080/14786441108564652

CrossRef Full Text | Google Scholar

Villarreal-Cervantes, M. G., Cruz-Villar, C. A., Alvarez-Gallegos, J., and Flores, E. A. P. (2010). Differential evolution techniques for the structure-control design of a five-bar parallel robot. Eng. Optimiz. 42, 535–565. doi: 10.1080/03052150903325557

CrossRef Full Text | Google Scholar

Wang, R., Wang, S., Wang, Y., Tan, M., and Yu, J. (2019). A paradigm for path following control of a ribbon-fin propelled biomimetic underwater vehicle. IEEE Tran. Syst. Man Cybernet. Syst. 49, 482–493. doi: 10.1109/TSMC.2017.2705340

CrossRef Full Text | Google Scholar

Wang, X., Li, M., Wang, P., Guo, W., and Sun, L. (2012). Bio-inspired controller for a robot cheetah with a neural mechanism controlling leg muscles. J. Bionic. Eng. 9, 282–293. doi: 10.1016/S1672-6529(11)60120-0

CrossRef Full Text | Google Scholar

Wang, Y., Xue, X., and Chen, B. (2018). Matsuoka's CPG with desired rhythmic signals for adaptive walking of humanoid robots. IEEE Trans. Cybernet. 48, 1–14. doi: 10.1109/TCYB.2018.2870145

CrossRef Full Text | Google Scholar

Wang, Z., Gao, Q., and Zhao, H. (2016). CPG-inspired locomotion control for a snake robot basing on nonlinear oscillators. J. Intell. Robot. Syst. 85, 1–19. doi: 10.1007/s10846-016-0373-9

CrossRef Full Text | Google Scholar

Wensing, P., Kim, S., and Slotine, J. J. E. (2017). Linear matrix inequalities for physically consistent inertial parameter identification: a statistical perspective on the mass distribution. IEEE Robot. Autom. Lett. 3, 60–67. doi: 10.1109/LRA.2017.2729659

CrossRef Full Text | Google Scholar

Wu, Q. D., Liu, C. J., Zhang, J. Q., and Chen, Q. (2009). Survey of locomotion control of legged robots inspired by biological concept. Sci. China Ser. F Inform. Sci. 52, 1715–1792. doi: 10.1007/s11432-.009-0169-7

CrossRef Full Text | Google Scholar

Xiong, X., Worgotter, F., and Manoonpong, P. (2017). Adaptive and energy efficient walking in a hexapod robot under neuromechanical control and sensorimotor learning. IEEE Trans. Cybernet. 46, 2521–2534. doi: 10.1109/TCYB.2015.2479237

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, G., Rong, X., Chai, H., Li, Y., and Li, B. (2016). Torso motion control and toe trajectory generation of a trotting quadruped robot based on virtual model control. Adv. Robot. 30, 284–297. doi: 10.1080/01691864.2015.1113889

CrossRef Full Text | Google Scholar

Zhu, Y., Chen, L., Liu, Q., Qin, R., and Jin, B. (2018a). Omnidirectional jump of a legged robot based on the behavior mechanism of a jumping spider. Appl. Sci. 8:51. doi: 10.3390/app8010051

CrossRef Full Text | Google Scholar

Zhu, Y., and Guo, T. (2016). Galloping trajectory generation of a legged transport robot based on energy consumption optimization. J. Robot. 2016, 1–9. doi: 10.1155/2016/9645730

CrossRef Full Text | Google Scholar

Zhu, Y., Guo, T., Liu, Q., Zhu, Q., Zhao, X., and Jin, B. (2017). Turning and radius deviation correction for a hexapod walking robot based on an ant-inspired sensory strategy. Sensors 17:2710. doi: 10.3390/s17122710

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., and Jin, B. (2016). Compliance control of a legged robot based on improved adaptive control: method and experiments. Int. J. Robot. Autom. 31, 366–373. doi: 10.2316/Journal.206.2016.5.206-4536

CrossRef Full Text | Google Scholar

Zhu, Y., Jin, B., and Li, W. (2015). Leg compliance control of a hexapod robot based on improved adaptive control in different environments. J. Cent. South Univ. 22, 904–913. doi: 10.1007/s11771-015-2600-0

CrossRef Full Text | Google Scholar

Zhu, Y., Jin, B., Li, W., and Li, S. (2014). Optimal design of hexapod walking robot leg structure based on energy consumption and workspace. Trans. Can. Soc. Mech. Eng. 38, 305–317. doi: 10.1139/tcsme-2014-0022

CrossRef Full Text | Google Scholar

Zhu, Y., Jin, B., Wu, Y., Guo, T., and Zhao, X. (2016). Trajectory correction and locomotion analysis of a hexapod walking robot with semi-round rigid feet. Sensors 16:E1392. doi: 10.3390/s16091392

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., Wu, Y., Liu, Q., Guo, T., Qin, R., and Hui, J. (2018b). A backward control based on σ-Hopf oscillator with decoupled parameters for smooth locomotion of bio-inspired legged robot. Robot. Auton. Syst. 106, 165–178. doi: 10.1016/j.robot.2018.05.009

CrossRef Full Text | Google Scholar