Entropy, Uncertainty, and the Depth of Implicit Knowledge on Musical Creativity: Computational Study of Improvisation in Melody and Rhythm

Recent neurophysiological and computational studies have proposed the hypothesis that our brain automatically codes the nth-order transitional probabilities (TPs) embedded in sequential phenomena such as music and language (i.e., local statistics in nth-order level), grasps the entropy of the TP distribution (i.e., global statistics), and predicts the future state based on the internalized nth-order statistical model. This mechanism is called statistical learning (SL). SL is also believed to contribute to the creativity involved in musical improvisation. The present study examines the interactions among local statistics, global statistics, and different levels of orders (mutual information) in musical improvisation interact. Interactions among local statistics, global statistics, and hierarchy were detected in higher-order SL models of pitches, but not lower-order SL models of pitches or SL models of rhythms. These results suggest that the information-theoretical phenomena of local and global statistics in each order may be reflected in improvisational music. The present study proposes novel methodology to evaluate musical creativity associated with SL based on information theory.

Introduction

Statistical Learning in the Brain: Local and Global Statistics

The notion of statistical learning (SL) (Saffran et al., 1996), which includes both informatics and neurophysiology (Harrison et al., 2006; Pearce and Wiggins, 2012), involves the hypothesis that our brain automatically codes the nth-order transitional probabilities (TPs) embedded in sequential phenomena such as music and language (i.e., local statistics in nth-order levels) (Daikoku et al., 2016, 2017b,c; Daikoku and Yumoto, 2017), grasps the entropy/uncertainty of the TP distribution (i.e., global statistics) (Hasson, 2017), predicts the future state based on the internalized nth-order statistical model (Daikoku et al., 2014; Yumoto and Daikoku, 2016), and continually updates the model to adapt to the variable external environment (Daikoku et al., 2012, 2017d). The concept of brain nth-order SL is underpinned by information theory (Shannon, 1951) involving n-gram or Markov models. TP (local statistics) and entropy (global statistics) are used to estimate the statistical structure of environmental information. The nth-order Markov model is a mathematical system based on the conditional probability of sequence in which the probability of the forthcoming state is statistically defined by the most recent n state (i.e., nth-order TP). A recent neurophysiological study suggested that sequences with higher entropy are learned based on higher-order TP whereas those with lower entropy are learned based on lower-order TP (Daikoku et al., 2017a). Another study suggested that certain regions or networks perform specific computations of global statistics (i.e., entropy) that are independent of local statistics (i.e., TP) (Hasson, 2017). Few studies, however, have investigated how perceptive systems of local and global statistics interact. It is important to examine the entire process of brain SL in both computational and neurophysiological areas (Daikoku, 2018b).

Statistical Learning and Information Theory

Local Statistics: Nth-Order Transitional Probability

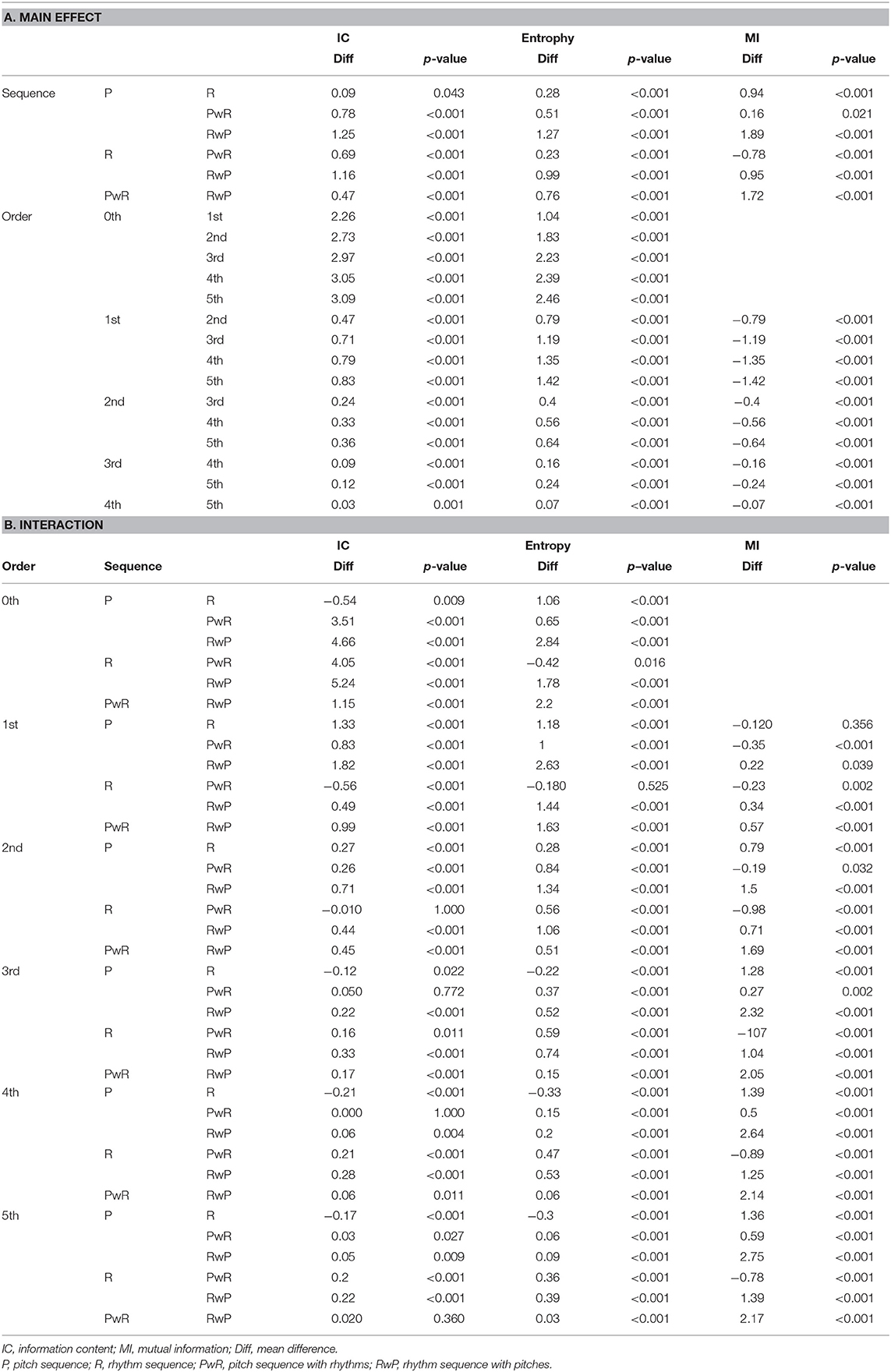
Research suggests that there are two types of coding systems involved in brain SL (see Figure 1): nth-order TPs (local statistics at various order levels) (Daikoku et al., 2017a; Daikoku, 2018a) and uncertainty/entropy (global statistics) (Hasson, 2017). The TP is the conditional probability of an event B, given that the most recent event A has occurred—this is written as P(B|A). The nth-order TP distributions sampled from sequential information such as music and language can be expressed by nth-order Markov models (Markov, 1971). The nth-order Markov model is based on the conditional probability of an event e_n+1, given the preceding n events based on Bayes' theorem [P(e_n+1|e_n)]. From a psychological viewpoint, the formula can be interpreted as positing that the brain predicts a subsequent event e_n+1 based on the preceding events e_n in a sequence. In other words, learners expect the event with the highest TP based on the latest n states, and are likely to be surprised by an event with lower TP. Furthermore, TPs are often translated as information contents [ICs, -log₂1/P(e_n+1|e_n)], which can be regarded as degrees of surprising and predictable (Pearce and Wiggins, 2006). A lower IC (i.e., higher TPs) means higher predictability and smaller surprise whereas a higher IC (i.e., lower TPs) means lower predictability and larger surprise. In the end, a tone with lower IC may be one that a composer is more likely to predict and choose as the next tone compared to tones with higher IC. IC can be used in computational studies of music to discuss the psychological phenomena involved in prediction and SL.

FIGURE 1

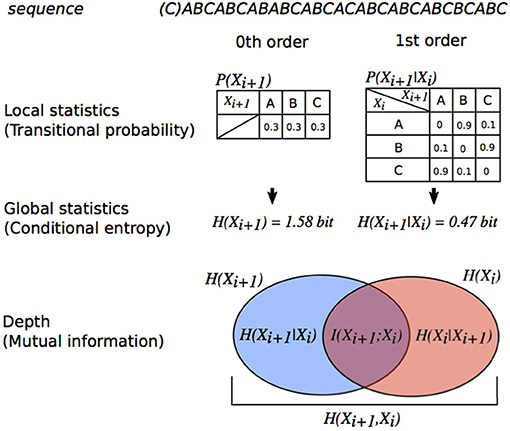
Figure 1. Relationship between order of transitional probabilities, entropy, conditional entropy, and MI illustrated using a Venn diagram. The degree of dependence on X_i for X_i+1 is measured by MI (MI (I(X;Y)) = entropy (H(X_i+1)] – conditional entropy [H(X_i+1|X_i))). The MI of sequences in this figure is more than 0. Thus, each event X_i+1 in the sequence is dependent on a preceding event X_i.

Global Statistics: Entropy and Uncertainty

Entropy (i.e., global statistics, Figure 1) is also used to understand the general predictability of a sequence (Manzara et al., 1992; Reis, 1999; Cox, 2010). It is calculated from probability distribution, interpreted as uncertainty (Friston, 2010), and used to evaluate the neurophysiological effects of global SL (Harrison et al., 2006) as well as decision making (Summerfield and de Lange, 2014), anxiety (Hirsh et al., 2012), and curiosity (Loewenstein, 1994). A previous study reported that the neural systems of global SL were partially independent of those of local SL (Hasson, 2017). Furthermore, reorganization of learned local statistics requires more time than the acquisition of new local statistics, even if the new and previously acquired information sets have equivalent entropy levels (Daikoku et al., 2017d). Some articles, however, suggest that the global statistics of sequence modulate local SL (Daikoku et al., 2017a). Furthermore, uncertainty of auditory and visual statistics is coded by modality-general, as well as modality-specific, neural systems (Strange et al., 2005; Nastase et al., 2014). This suggests that the neural basis that codes global statistics, as well as local statistics, is a domain-general system. Although domain-general and domain-specific learning system in the brain are under debate (Hauser et al., 2002; Jackendoff and Lerdahl, 2006), there seems to be neural and psychological interactions in perceptions between local and global statistics.

Depth: Mutual Information

Mutual information (MI) and pointwise MI (PMI) are measures of the mutual dependence between two variables. PMI refers to each event in sequence (local dependence), and MI refers to the average of all events in the sequence (global dependence). In the framework of SL based on TPs [P(e_n+1|e_n)], MI explains how an event e_n+1 is dependent on the preceding event e_n. Thus, MI is key to understanding the order of SL. For example, a typical oddball sequence consisting of a frequent stimulus with high probability of appearance and a deviant stimulus with low probability of appearance has weak dependence between two adjacent events (e_n, e_n+1) and shows low MI, because event e_n+1 appears independently of the preceding events e_n. In contrast, an SL sequence based on TPs, but not probabilities of appearance, has strong dependence on the two adjacent events and shows larger MI. For example, a typical SL paradigm that consists of the concatenation of pseudo-words with three stimuli has large MI until second-order Markov or tri-gram models [i.e., P(C|AB)] whereas it has low MI from third-order Markov or four-gram models [i.e., P(D|ABC)]. Thus, MI is sometimes used to evaluate levels of SL in both neurophysiological (Harrison et al., 2006) and computational studies (Pearce et al., 2010). In sum, the three types of information-theoretical evaluations of SL models (i.e., IC, entropy, and MI) can be explained in terms of psychological aspects. (1) IC reflects local statistics. A tone with lower IC (i.e., higher TPs) may be one that a composer is more likely to predict and choose as the next tone compared to tones with higher IC. (2) Entropy reflects global statistics and is interpreted as the uncertainty of whole sequences. (3) MI reflects the levels of orders in statistics and is interpreted as the dependence of preceding sequential events in SL. Using them, the present study investigated how local statistics, global statistics, and the levels of the orders in musical improvisation interact.

Musical Improvisation

Implicit statistical knowledge is considered to contribute to the creativity involved in musical composition and musical improvisation (Pearce and Wiggins, 2012; Norgaard, 2014; Wiggins, 2018). Additionally, it is widely accepted that implicit knowledge causes a sense of intuition, spontaneous behavior, skill acquisition based on procedural learning, and creativity, and is also closely tied to musical expression, such as composition, playing, and intuitive creativity. Particularly, in musical improvisation, musicians are forced to express intuitive creativity and immediately play their own music based on long-term training associated with procedural and implicit learning (Clark and Squire, 1998; Ullman, 2001; Paradis, 2004; De Jong, 2005; Ellis, 2009; Müller et al., 2016). Thus, compared to other types of musical composition in which a composer deliberates and refines a composition scheme for a long time based on musical theory, the performance of musical improvisation is intimately bound to implicit knowledge because of the necessity of intuitive decision making (Berry and Dienes, 1993; Reber, 1993; Perkovic and Orquin, 2017) and auditory-motor planning based on procedural knowledge (Pearce et al., 2010; Norgaard, 2014). This suggests that the stochastic distribution calculated from musical improvisation may represent the musicians' implicit knowledge and creativity in music that has been developed via implicit learning. Few studies have investigated the relationship between musical improvisation and implicit statistical knowledge. The present study, using real-world improvisational music, first proposed a computational model of musical creativity in improvisation based on TP distribution, and examined how local statistics, global statistics, and hierarchy in music interact.

Methods

Extraction of Spectral and Temporal Information

General Methodologies

The three musicians of William John Evans (Autumn Leaves from Portrait in Jazz, 1959; Israel from Explorations, February 1961; I Love You Porgy from Waltz for Debby, June 1961; Stella by Starlight from Conversations with Myself, 1963; Who Can I Turn To? from Bill Evans at Town Hall, 1966; Someday My Prince Will Come from the Montreux Jazz Festival, 1968; A Time for Love from Alone, 1969), Herbert Jeffrey Hancock (Cantaloupe Island from Empyrean Isles, 1964; Maiden Voyage from Flood, 1975; Someday My Prince Will Come from The Piano, 1978; Dolphin Dance from Herbie Hancock Trio '81, 1981; Thieves in the Temple from The New Standard, 1996; Cottontail from Gershwin's World, 1998; The Sorcerer from Directions in Music, 2001), and McCoy Tyner (Man from Tanganyika from Tender Moments, 1967; Folks from Echoes of a Friend, 1972; You Stepped Out of a Dream from Fly with the Wind, 1976; For Tomorrow from Inner Voice; 1977; The Habana Sun from The Legend of the Hour, 1981; Autumn Leaves from Revelations, 1988; Just in Time from Dimensions, 1984) were used in the present study. The highest pitches with length were extracted based on the following definitions: the highest pitches that can be played at a given point in time, pitches with slurs that can be counted as one, and grace notes were excluded. In addition, the rests that were related to highest-pitch sequences were also extracted. This spectral and temporal information were divided into four types of sequences: [1] a pitch sequence without length and rest information (i.e., pitch sequence without temporal information); [2] a temporal sequence without pitch information (i.e., temporal sequence without pitches); [3] a pitch sequence with length and rest information (i.e., pitch sequence with temporal information); and [4] a temporal sequence with pitch information (i.e., temporal sequence with pitches).

Pitch Sequence Without Temporal Information

For each type of pitch sequence, all of the intervals were numbered so that an increase or decrease in a semitone was 1 and −1 based on the first pitch, respectively. Representative examples were shown in Figure 2. This revealed the relative pitch-interval patterns but not the absolute pitch patterns. This procedure was used to eliminate the effects of the change in key on transitional patterns. Interpretation of the key change depends on the musician, and it is difficult to define in an objective manner. Thus, the results in the present study may represent a variation in the statistics associated with relative pitch rather than absolute pitch.

FIGURE 2

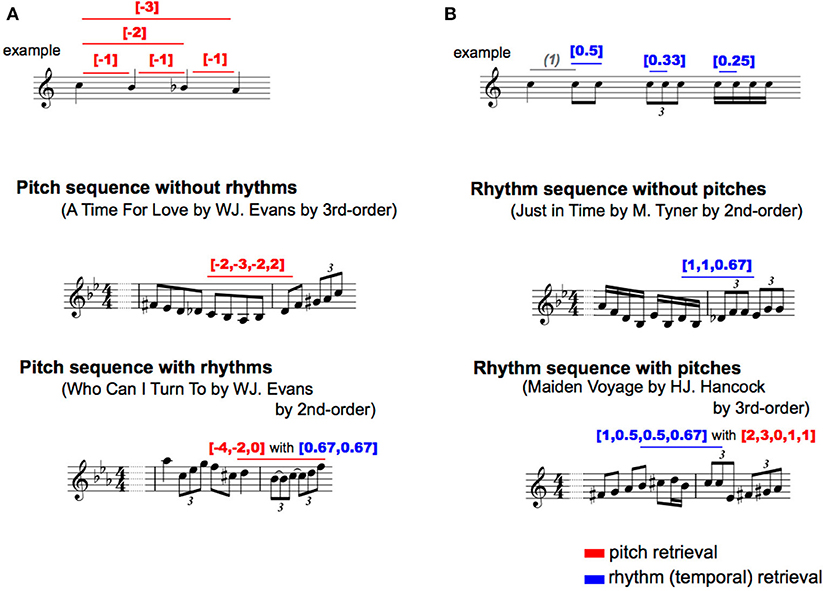
Figure 2. Representative phrases of each type of transition pattern. Red: pitch transition, Blue: rhythm (temporal) transition. (A) Pitch; (B) Rhythm.

Temporal Sequence Without Pitches

The onset times of each note were used for analyses. Although, note onsets ignore the length of notes and rests, this methodology can capture the most essential rhythmic features of the music (Povel, 1984; Norgaard, 2014). To extract a temporal interval between adjacent notes, all onset times were subtracted from the onset of the preceding note. Then, for each type of temporal sequence, the second to last temporal interval was divided by the first temporal interval. Representative examples are shown in Figure 2. This revealed relative rhythm patterns but not absolute rhythm patterns; it is independent of the tempo of each piece of music.

Pitch Sequence With Temporal Information

The two methodologies of pitch and temporal sequences were combined. For each type of sequence, all of the intervals were numbered so that an increase or decrease in a semitone was 1 and −1 based on the first pitch, respectively. Additionally, for each type of pitch sequence, all onset times were subtracted from the onset of the preceding note, and the second to last temporal intervals were divided by the first temporal interval. The representative examples were shown in Figure 2. On the other hand, a temporal interval of first-order model was calculated as a ratio to the crotchet (i.e., quarter note), because only a temporal interval is included for each sequence and the note length cannot be calculated as a relative temporal interval. Thus, the patterns of pitch sequence (p) with temporal information (t) were represented as [p] with [t].

Temporal Sequence With Pitches

The methodologies of sequence extraction were the same as those of the pitch sequence with rhythm (see Figure 2), whereas the TPs of the rhythm, but not pitch, sequences were calculated as a statistic based on multi-order Markov chains. The probability of a forthcoming temporal interval with pitch was statistically defined by the last temporal interval with pitch to six successive temporal interval with pitch (i.e., first- to six-order Markov chains). Thus, the relative pattern of temporal sequence (r) with pitches (p) were represented as [t] with [p].

Modeling and Analysis

The TPs of the sequential patterns were calculated based on 0th−5th-order Markov chains. The nth-order Markov chain is the conditional probability of an event e_n+1, given the preceding n events based on Bayes' theorem:

$\begin{array}{cc}\begin{array}{r}P(e_{n+1}|e_n)=\frac{P(e_{n+1}\cap e_n)}{P(e_n)}\end{array}& (1)\end{array}$

The ICs (I[e_n+1|e_n]) and conditional entropy [H(B|A)] in the nth-order TP distribution (hereafter, Markov entropy) were calculated using TPs in the framework of information theory.

$\begin{array}{cc}\begin{array}{rcl}I(e_{n+1}|e_n)& =& {log}_2\frac{1}{P(e_{n+1}|e_n)}(bit)\end{array}& (2)\end{array}$

$\begin{array}{cc}\begin{array}{rcl}H(B|A)& =& {-\sum }_i{\displaystyle \sum _j}P(ai)P(bj|ai){log}_{2}P(bj|ai)(bit)\end{array}& (3)\end{array}$

where P(bj|ai) is a conditional probability of sequence “ai bj.” Then, MI [I(X;Y)] were calculated in 1st-, 2nd-, and 3rd-order Markov models. MI is an information theoretic measure of dependency between two variables (Cover and Thomas, 1991). The MI of two discrete variables X and Y can be defined as

$\begin{array}{cc}\begin{array}{r}I(X;Y)={\sum }_{y\in Y}{\sum }_{x\in X}p(x,y)log(\frac{p(x,y)}{p(x)p(y)})(bit)\end{array}& (4)\end{array}$

where p(x,y) is the joint probability function of X and Y, and p(x) and p(y) are the marginal probability distribution functions of X and Y, respectively. From entropy values, the MI can also be expressed as

$\begin{array}{cc}\begin{array}{lll}I(X;Y)& =& {\sum }_{x,y}p(x,y)log(\frac{p(x,y)}{p(x)p(y)})\\ & =& {\sum }_{x,y}p(x,y)log(\frac{p(x,y)}{p(x)})-{\sum }_{x,y}p(x,y)logp(y)\\ & =& {\sum }_{x,y}p(x)p(y|x)logp(y|x)-{\sum }_{x,y}logp(y)p(x,y)\\ & =& {\sum }_{x}p(x)({\sum }_{y}p(y|x)logp(y|x))\\ & & -{\sum }_{y}logp(y)({\sum }_{x}p(x,y))\\ & =& -{\sum }_{x}p(x)H(Y|X=x)-{\sum }_{y}p(y)logp(y)\\ & =& -H(Y|X)+H(Y)\\ & =& H(Y)-H(Y|X)(bit)\end{array}& (5)\end{array}$

where H(X) and H(Y) are the marginal entropies, H(X|Y) and H(Y|X) are the conditional entropies, and H(X,Y) is the joint entropy of X and Y (Figure 1). Based on psychological and information-theoretical concepts, the Equation (5) can be regarded that the amount of entropy (uncertainty) remaining about Y after X is known. That is, the MI is corresponding to reduction in entropy (uncertainty). Then, the transitional patterns with 1st−20th highest TPs in all musicians, which show higher predictabilities in each musician, were used as local statistics of familiar phrases. The applied familiar phrases and the TPs were shown in Supplementary material. The TPs of familiar phrases were averaged. Repeated-measure analysis of variances (ANOVAs) with factors of order and type of sequence were conducted in each IC, entropy, and MI. Furthermore, the global statistics and MI in each order were compared with local statistics of familiar phrases by Pearson's correlation analysis. Statistical significance levels were set at p = 0.05 for all analyses.

Results

Local vs. Global Statistics

The means of IC, conditional entropy, and mutual information were shown in Figure 3. The means of IC, conditional entropy, and mutual information were shown in Figure 3. The main sequence effect were significant [IC: F_{(2.39, 47.89)} = 1010.07, p < 0.001, partial η² = 0.98; Entropy: F_{(1.20, 23.92)} = 828.82, p < 0.001, partial η² = 0.98; MI: F_{(2.00, 39.91)} = 225.54, p < 0.001, partial η² = 0.92] (Table 1). The main order effect were significant [IC: F_{(2.05, 40.93)} = 2909.59, p < 0.001, partial η² = .99; Entropy: F_{(1.55, 31.03)} = 2166.02, p < 0.001, partial η² = 0.99; MI: F_{(1.68, 33.59)} = 2468.35, p < 0.001, partial η² = 0.99] (Table 1). The order-sequence interactions were significant [IC: F_{(3.39, 67.76)} = 592.24, p < 0.001, partial η² = 0.97; Entropy: F_{(2.25, 44.94)} = 282.95, p < 0.001, partial η² = 0.93; MI: F_{(1.82, 36.45)} = 351.48, p < 0.001, partial η² = 0.95)] (Table 1).

FIGURE 3

Figure 3. The means of information content (IC), Conditional entropy, and mutual information (MI). Error bars represent standard errors of the means. P, pitch sequence; R, rhythm sequence; PwR, pitch sequence with rhythms; RwP, rhythm sequence with pitches.

TABLE 1

Table 1. ANOVA results.

Local vs. Global Statistics

All of the results in correlation analysis are shown in Figure 4. In pitch sequence without temporal information, 1st−5th-order models showed that the conditional entropies of the TP distributions were moderately (0.4 ≦ |r| < 0.7) related to the ICs of TPs of familiar phrases (1st: r = 0.65, p = 0.001; 2nd: r = 0.66, p = 0.001; 3rd: r = 0.63, p = 0.002; 4th: r = 0.66, p = 0.001; 5th: r = 0.69, p = 0.001). In pitch sequence with temporal information, 1st-, 4th, and 5th-order models showed that the conditional entropies of the TP distributions were moderately (0.4 ≦ |r| < 0.7) related to the ICs of TPs of familiar phrases (1st: r = 0.58, p = 0.006; 4th: r = 0.49, p = 0.023; 5th: r = 0.43, p = 0.049), and 2nd- and 3rd-order models showed that the conditional entropies of the TP distributions were strongly (0.7 ≦ |r| < 1.0) related to the ICs of TPs of familiar phrases (2nd: r = 0.73, p < 0.001; 3rd: r = 0.82, p < 0.001). In temporal sequence with pitches, 0th−5th-order models showed that the conditional entropies of the TP distributions were moderately (0.4 ≦ |r| < 0.7) related to the ICs of TPs of familiar phrases (0th: r = 0.68, p = 0.001; 1st: r = 0.61, p = 0.004; 2nd: r = 0.72, p < 0.001; 3rd: r = 0.45, p = 0.043; 4th: r = 0.45, p = 0.004; 5th: r = 0.47, p = 0.003).

FIGURE 4

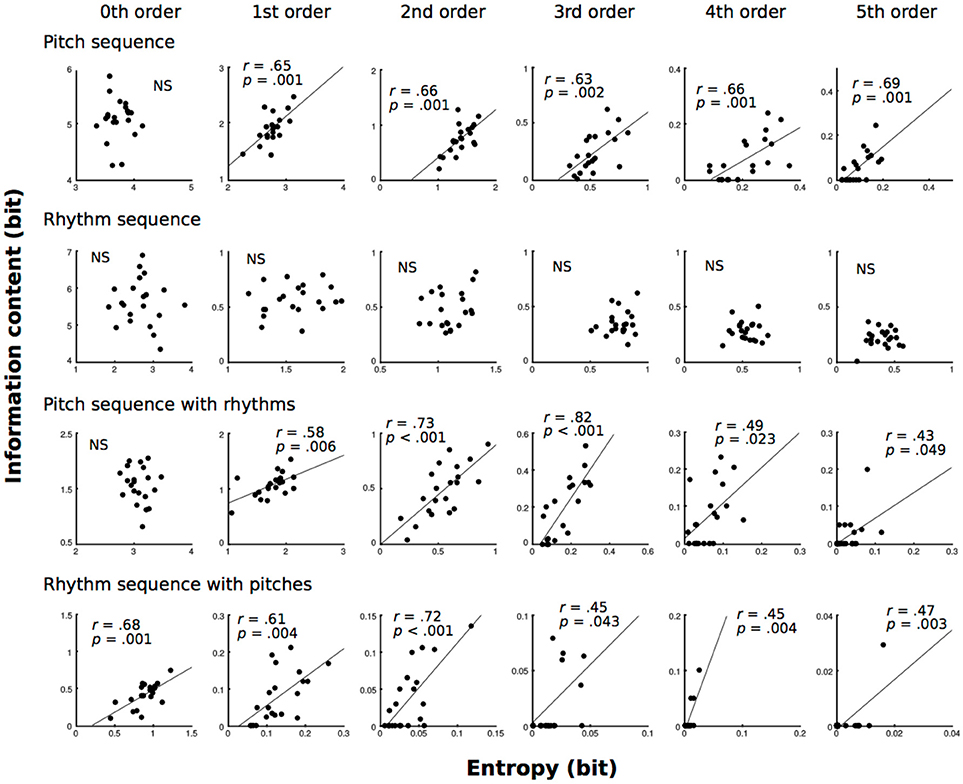
Figure 4. The correlation analysis between conditional entropy (global statistics) and ICs of familiar phrases (local statistics) based on zeroth- to fifth-order Markov models of pitch and temporal (rhythm) sequences.

Local Statistics vs. Hierarchy

All of the results are shown in Figure 5. In pitch sequence without temporal information, 3rd−5th-order models showed that the MI of the TP distributions were moderately (0.4 ≦ |r| < 0.7) related to the ICs of TPs of familiar phrases (3rd: r = 0.45, p = 0.043; 4th: r = 0.45, p = 0.043; 5th: r = 0.47, p = 0.03). In pitch sequence with temporal information, 2nd- and 3rd-order models showed that the MI of the TP distributions were moderately (0.4 ≦ |r| < 0.7) related to the ICs of TPs of familiar phrases (2nd: r = 0.44, p = 0.046; 3rd: r = 0.49, p = 0.025).

FIGURE 5

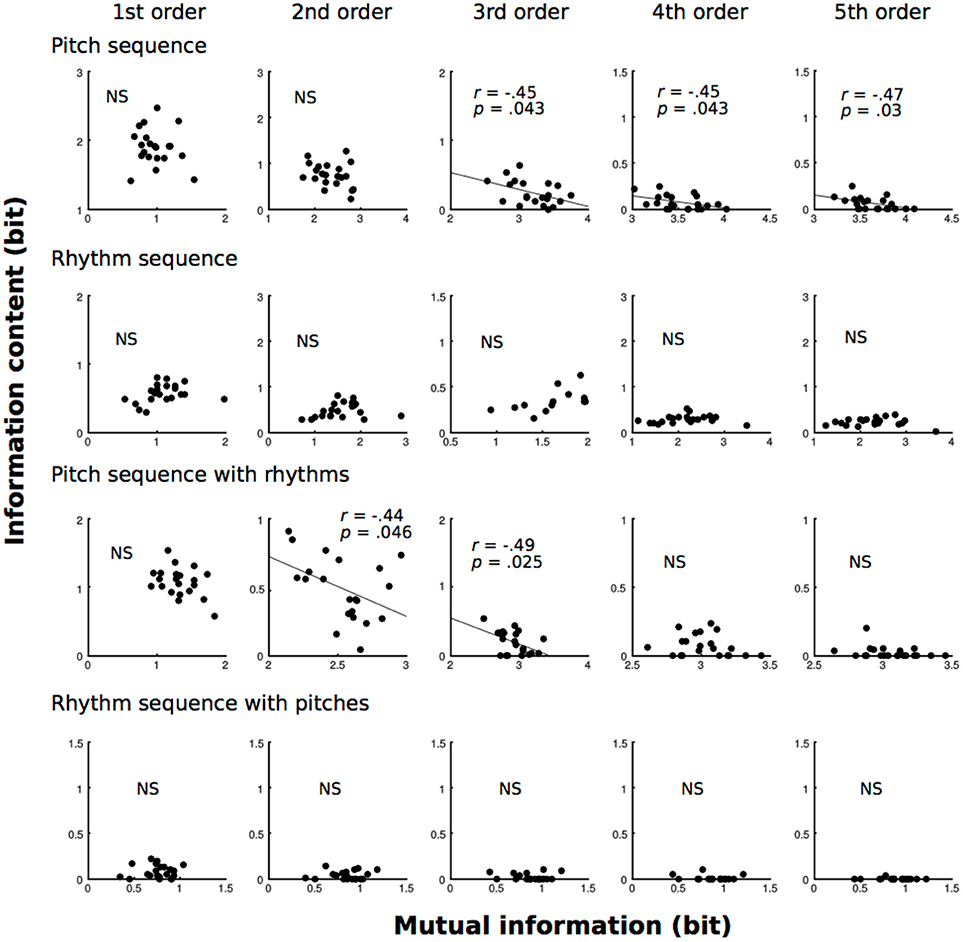
Figure 5. The correlation analysis between MI and ICs of familiar phrases (local statistics) based on zeroth- to fifth-order Markov models of pitch and temporal (rhythm) sequences.

Discussion

Psychological Notions of Information Theory

The present study investigated how local statistics (TP and IC), global statistics (conditional entropy), and levels of orders (MI) in musical improvisation interact. The TP, IC, conditional entropy, and MI can be calculated based on Markov models, which are also applied to psychological and neurophysiological studies on SL (Harrison et al., 2006; Furl et al., 2011; Daikoku, 2018b). Based on psychological and neurophysiological studies on SL (Harrison et al., 2006; Pearce et al., 2010; de Zubicaray et al., 2013; Daikoku et al., 2015; Monroy et al., 2017), these three pieces of information can be translated to psychological indices: a tone with lower IC (i.e., higher TPs) may be one that a composer is more likely to predict and choose as the next tone compared to tones with higher IC whereas entropy and MI are interpreted as the global predictability of the sequences and the levels of order for the prediction, respectively. Previous studies also suggest that musical creativity in part depends on SL (Pearce, 2005; Pearce et al., 2010; Omigie et al., 2012, 2013; Pearce and Wiggins, 2012; Hansen and Pearce, 2014; Norgaard, 2014), and that musical training and experience is associated with the cognitive model of probabilistic structure in the music involved in SL (Pearce, 2005; Pearce and Wiggins, 2006; Pearce et al., 2010; Omigie et al., 2012, 2013; Pearce and Wiggins, 2012; Hansen and Pearce, 2014; Norgaard, 2014). The present study, using improvisational music by three musicians, examined how local and global statistics embedded in music interact, and discussed them from the interdisciplinary viewpoint of SL.

Local vs. Global Statistics

In pitch sequence with and without temporal information, higher-order (1st−5th order) models detected positive correlations between global (conditional entropy) and local statistics (IC) in musical improvisation whereas no significance was detected in a lower-order (0th order) model. To understand the local statistics of familiar phrases, the present study used only the transitional patterns that showed the 1st−20th highest TPs for all musicians, which can be interpreted as higher predictabilities for each musician. Thus, the results suggest that, when the TPs of familiar phrases are decreased, the conditional entropy (uncertainty) of the entire TP distribution is increased. This finding is mathematically and psychologically reasonable. When improvisers are attempting to use various types of phrases, the variability of sequential patterns is increasing. In the end, the ICs (degree of surprise) of familiar phrases are positively correlated with the conditional entropy (uncertainty) of the entire sequential distribution. It is of note that this correlation could not be detected in a lower-order (0th order) model, and that no correlation was detected in a temporal sequence without pitches. This suggests that the interaction between local and global statistics may be stronger in the SL of spectral sequence compared to that of temporal sequence. Furthermore, these correlations may be detectable in higher-order models. This may suggest that higher-order SL can connect with grasping entropy. In sum, skills of musical improvisation and intuition may strongly depend on SL of pitch compared with that of rhythm. In addition, this phenomenon on intuition may occur in higher-, but not lower-order levels in SL. The higher-order SL model of pitches may be important to grasp the entire process of hierarchical SL in musical improvisation.

Local Statistics vs. Hierarchy

In pitch sequences without temporal information, higher-order (3rd−5th order) models showed negative correlations between dependence of previous events (MI) and local statistics (IC), and no significance was detected in lower-order (0th−2nd order) models. This finding is also mathematically and psychologically reasonable. When players strongly depend on previous sequential information to improvise music, they tend to use familiar phrases because familiar phrases with higher TPs P(X_i+1|X_i) tend to have strong dependence on previous sequential information (X_i). In the end, the ICs (degree of surprise) of familiar phrases are decreased when improvisers depend on previous sequential information that can be detected as larger MIs. Interestingly, this correlation could not be detected in a lower-order model (0th order), and no correlation was detected in the temporal sequence without pitches. As shown in the correlation between local and global statistics, the interaction between local statistics and levels of orders may be stronger in the SL of spectral sequence compared to that of temporal sequence. Furthermore, these correlations may be detectable in higher-order models. In contrast, fourth- and fifth-order models of pitch sequence with temporal information did not show correlations. Thus, rhythms may modulate the levels of orders in the SL of pitches in improvisational music (Daikoku, 2018c). This hypothesis may be supported in the models of temporal sequence with pitches. No correlation was detected in temporal sequence (Daikoku et al., 2018) with pitches. Future study is needed to investigate how rhythms affect improvisational music, and how the SL of rhythms interact with those of pitches. It is of note that the present study did not directly investigate the improviser's statistical knowledge of music, as only the statistics of music were analyzed. However, the transition probabilities shape only a small part of their respective styles. Future study should investigate the SL of music from many improvisers using interdisciplinary approaches of neurophysiology and informatics in parallel. The methodologies in this study are missing important information that constructs music such as beat, stresses, and ornamental note, which inspire the rhythm and intonation. Furthermore, the present study only analyzed three improvisers. To discuss universal phenomena in SL associated with improvisation, future study will be needed to examine a body of pieces of music.

Conclusion

The present study investigated how local statistics (TP and IC), global statistics (entropy), and levels of orders (MI) in musical improvisation interact. Generally, the interactions among local statistics and global statistics were detected in higher-order SL models of pitches, but not lower-order SL models of spectral sequence or SL models of temporal sequence. The results of the present study suggested that information-theoretical phenomena of local and global statistics in each hierarchy can be reflected in improvisational music. These results support a novel methodology to evaluate musical creativity associated with SL based on information theory.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by Grant-in-Aid for Grant for Groundbreaking Young Researchers of Suntory foundation, and Nakayama Foundation for Human Science. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncom.2018.00097/full#supplementary-material

References

Berry, D. C., and Dienes, Z. (1993). Implicit Learning: Theoretical and Empirical Issues. Hove: Lawrence Erlbaum.

Google Scholar

Clark, R. E., and Squire, L. R. (1998). Classical conditioning and brain systems: the role of awareness. Science 280, 77–81. doi: 10.1126/science.280.5360.77

PubMed Abstract | CrossRef Full Text | Google Scholar

Cover, T. M., and Thomas, J. A. (1991). Elements of Information Theory. New York, NY: Wiley.

Google Scholar

Cox, G. (2010). “On the relationship between entropy and meaning in music: an exploration with recurrent neural networks,” in Proceedings of the Cognitive Science Society, Vol. 32 (Portland, OR).

Google Scholar

Daikoku, T. (2018a). Time-course variation of statistics embedded inmusic: corpus study on implicit learning and knowledge. PLoS ONE 13:e0196493. doi: 10.1371/journal.pone.0196493

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T. (2018b). Neurophysiological markers of statistical learning in music and language: hierarchy, entropy and uncertainty. Brain Sci. 8:114. doi: 10.3390/brainsci8060114

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T. (2018c). Musical Creativity and Depth of Implicit Knowledge: Spectral and Temporal Individualities in Improvisation. Front. Comput. Neurosci. 12:89. doi: 10.3389/fncom.2018.00089

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., Ogura, H., and Watanabe, M. (2012). The variation of hemodynamics relative to listening to consonance or dissonance during chord progression. Neurol. Res. 34, 557–563. doi: 10.1179/1743132812Y.0000000047

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., Okano, T., and Yumoto, M. (2017a). “Relative difficulty of auditory statistical learning based on tone transition diversity modulates chunk length in the learning strategy,” in Proceedings of the Biomagnetic (Sendai), 22–24.

Google Scholar

Daikoku, T., Takahashi, Y., Futagami, H., Tarumoto, N., and Yasuda, H. (2017b). Physical fitness modulates incidental but not intentional statistical learning of simultaneous auditory sequences during concurrent physical exercise. Neurol. Res. 39, 107–116. doi: 10.1080/01616412.2016.1273571

CrossRef Full Text | Google Scholar

Daikoku, T., Takahashi, Y., Tarumoto, N., and Yasuda, H. (2018). Motor Reproduction of Time Interval Depends on Internal Temporal Cues in the Brain: Sensorimotor Imagery in Rhythm. Front. Psychol. 9:1873. doi: 10.3389/fpsyg.2018.01873

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., Takahashi, Y., Tarumoto, N., and Yasuda, H. (2017c). Auditory statistical learning during concurrent physical exercise and the tolerance for pitch, tempo, and rhythm changes. Motor Control 5, 1–24. doi: 10.1123/mc.2017-0006

CrossRef Full Text | Google Scholar

Daikoku, T., Yatomi, Y., and Yumoto, M. (2015). Statistical learning of music- and language-like sequences and tolerance for spectral shifts. Neurobiol. Learn. Mem. 118, 8–19. doi: 10.1016/j.nlm.2014.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., Yatomi, Y., and Yumoto, M. (2016). Pitch-class distribution modulates the statistical learning of atonal chord sequences. Brain Cogn. 108, 1–10. doi: 10.1016/j.bandc.2016.06.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., Yatomi, Y., and Yumoto, M. (2017d). Statistical learning of an auditory sequence and reorganization of acquired knowledge: a time course of word segmentation and ordering. Neuropsychologia 95, 1–10. doi: 10.1016/j.neuropsychologia.2016.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., Yatomi, Y., and Yumoto, M. (2014). Implicit and explicit statistical learning of tone sequences across spectral shifts. Neuropsychologia 63, 194–204. doi: 10.1016/j.neuropsychologia.2014.08.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Daikoku, T., and Yumoto, M. (2017). Single, but not dual, attention facilitates statistical learning of two concurrent auditory sequences. Sci. Rep. 7:10108. doi: 10.1038/s41598-017-10476-x

PubMed Abstract | CrossRef Full Text | Google Scholar

De Jong, N. (2005). Learning Second Language Grammar by Listening. Ph.D. thesis, Netherlands Graduate School of Linguistics.

de Zubicaray, G., Arciuli, J., and McMahon, K. (2013). Putting an “end” to themotor cortex representations of action words. J. Cogn. Neurosci. 25, 1957–1974. doi: 10.1162/jocn_a_00437

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellis, R. (2009). “Implicit and explicit learning, knowledge and instruction,” in Implicit and explicit Knowledge in Second Language Learning, Testing and Teaching, eds R. Ellis, S. Loewen, C. Elder, R. Erlam, J. Philip, and H. Reinders (Bristol: Multilingual Matters), 3–25.

Google Scholar

Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138. doi: 10.1038/nrn2787

PubMed Abstract | CrossRef Full Text | Google Scholar

Furl, N., Kumar, S., Alter, K., et al. (2011). Neural prediction of higher-order auditory sequence statistics. NeuroImage 54, 2267–2277. doi: 10.1016/j.neuroimage.2010.10.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, N. C., and Pearce, M. (2014). Predictive uncertainty in auditory sequence processing. Front. Psychol. 5:1052. doi: 10.3389/fpsyg.2014.01052

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison, L. M., Duggins, A., and Friston, K. J. (2006). Encoding uncertainty in the hippocampus. Neural Netw. 19, 535–546. doi: 10.1016/j.neunet.2005.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasson, U. (2017). The neurobiology of uncertainty: Implications for statistical learning. Philos. Trans. R. Soc. Lond. B Biol. Sci. 372:1711. doi: 10.1098/rstb.2016.0048

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauser, M. D., Chomsky, N., and Fitch, W. T. (2002). The faculty of language: what is it, who has it, and how did it evolve? Science 298, 1569–1579. doi: 10.1126/science.298.5598.1569

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirsh, J. B., Mar, R. A., and Peterson, J. B. (2012). Psychological entropy: a framework for understanding uncertainty-related anxiety. Psychol. Rev. 119, 304–320. doi: 10.1037/a0026767

CrossRef Full Text | Google Scholar

Jackendoff, R., and Lerdahl, F. (2006). The capacity for music: What is it, and what's special about it? Cognition 100, 33–72. doi: 10.1016/j.cognition.2005.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Loewenstein, G. (1994). The psychology of curiosity: a review and reinterpretation. Psychol. Bull. 116, 75–98.

Google Scholar

Manzara, L. C., Witten, I. H., and James, M. (1992). On the entropy of music: an experiment with Bach chorale melodies. Leonardo 2, 81–88. doi: 10.2307/1513213

CrossRef Full Text | Google Scholar

Markov, A. A. (1971). Extension of the Limit Theorems of Probability Theory to a Sum of Variables Connected in a Chain. Markov chain, Vol. 1. John Wiley and Sons (Reprinted in Appendix B of: R. Howard D. Dynamic Probabilistic Systems).

Google Scholar

Monroy, C. D., Gerson, S. A., Domínguez-Martínez, E., Kaduk, K., Hunnius, S., and Reid, V. (2017). Sensitivity to structure in action sequences: an infant event-related potential study. Neuropsychologia. doi: 10.1016/j.neuropsychologia.2017.05.007. [Epub ahead of print].

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, N. C., Genzel, L., Konrad, B. N., Pawlowski, M., Neville, D., Fernández, G., et al. (2016). Motor skills enhance procedural memory formation and protect against age-related decline. PLoS ONE 11:e0157770. doi: 10.1371/journal.pone.0157770

PubMed Abstract | CrossRef Full Text | Google Scholar

Nastase, S., Iacovella, V., and Hasson, U. (2014). Uncertainty in visual and auditory series is coded by modality-general and modality-specific neural systems. Hum. Brain Mapp. 35, 1111–1128. doi: 10.1002/hbm.22238

PubMed Abstract | CrossRef Full Text | Google Scholar

Norgaard, M. (2014). How jazz musicians improvise: the central role of auditory and motor patterns. Music Percept. 31, 271–287. doi: 10.1525/mp.2014.31.3.271

CrossRef Full Text | Google Scholar

Omigie, D., Pearce, M., and Stewart, L. (2012). Tracking of pitch probabilities in congenital amusia. Neuropsychologia 50, 1483–1493. doi: 10.1016/j.neuropsychologia.2012.02.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Omigie, D., Pearce, M., Williamson, V., and Stewart, L. (2013). Electrophysiological correlates of melodic processing in congenital amusia. Neuropsychologia 51, 1749–1762. doi: 10.1016/j.neuropsychologia.2013.05.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Paradis, M. (2004). A Neurolinguistic Theory of Bilingualism. Amsterdam: John Benjamins.

Google Scholar

Pearce, M. (2005). The Construction and Evaluation of Statistical Models of Melodic Structure in Music Perception and Composition. PhD thesis, School of Informatics, City University, London.

Pearce, M., and Wiggins, G. A. (2006). Expectation in melody: the influence of context and learning. Music Percep. 23, 377–405. doi: 10.1525/mp.2006.23.5.377

CrossRef Full Text | Google Scholar

Pearce, M. T., Ruiz, M. H., Kapasi, S., Wiggins, G. A., and Bhattacharya, J. (2010). Unsupervised statistical learning underpins computational, behavioural and neural manifestations of musical expectation. NeuroImage 50, 302–313. doi: 10.1016/j.neuroimage.2009.12.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Pearce, M. T., and Wiggins, G. A. (2012). Auditory expectation: the information dynamics of music perception and cognition. Topics Cogn. Sci. 4, 625–652. doi: 10.1111/j.1756-8765.2012.01214.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Perkovic, S., and Orquin, J. L. (2017). Implicit statistical learning in real-world environments leads to ecologically rational decision making. Psychol. Sci. 29, 34–44. doi: 10.1177/0956797617733831

PubMed Abstract | CrossRef Full Text | Google Scholar

Povel, D. (1984). A theoretical framework for rhythm perception. Psychol. Res. 45, 315–337. doi: 10.1007/BF00309709

PubMed Abstract | CrossRef Full Text | Google Scholar

Reber, A. S. (1993). Implicit Learning and Tacit Knowledge. An Essay on the Cognitive Unconscious. New York, NY: Oxford University Press x.

Google Scholar

Reis, B. Y. (1999). Simulating Music Learning With Autonomous Listening Agents: Entropy, Ambiguity And Context. Unpublished doctoral dissertation, Computer Laboratory, University of Cambridge.

Google Scholar

Saffran, J. R., Aslin, R. N., and Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science 274, 1926–1928. doi: 10.1126/science.274.5294.1926

PubMed Abstract | CrossRef Full Text | Google Scholar

Shannon, C. E. (1951). Prediction and entropy of printed english. Bell Syst. Tech. J. 30, 50–64. doi: 10.1002/j.1538-7305.1951.tb01366.x

CrossRef Full Text | Google Scholar

Strange, B. A., Duggins, A., Penny, W., Dolan, R. J., and Friston, K. J. (2005). Information theory, novelty and hippocampal responses: Unpredicted or unpredictable? Neural Netw. 18, 225–230. doi: 10.1016/j.neunet.2004.12.004

CrossRef Full Text | Google Scholar

Summerfield, C., and de Lange, F. P. (2014). Expectation in perceptual decision making: neural and computational mechanisms. Nat. Rev. Neurosci. 15, 745–756. doi: 10.1038/nrn3838

PubMed Abstract | CrossRef Full Text | Google Scholar

Ullman, M. T. (2001). The declarative/procedural model of lexicon and grammar. J. Psychol. Res. 30, 37–69. doi: 10.1023/A:1005204207369

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiggins, G. A. (2018). Creativity, information, and consciousness: the information dynamics of thinking. Phys. Life Rev. [Epub ahead of print]. doi: 10.1016/j.plrev.2018.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Yumoto, M., and Daikoku, T. (2016). “IV Auditory system. 5 basic function,” in Clinical Applications of Magnetoencephalography, eds S. Tobimatsu and R. Kakigi (Tokyo: Springer), 97–112.

Google Scholar