- 1Department of Neurology, University of South Alabama, Mobile, AL, USA
- 2Division of System Neurophysiology, National Institute for Physiological Sciences, Okazaki, Japan
- 3Department of Speech Pathology and Audiology, University of South Alabama, Mobile, AL, USA
- 4Department of Neurosurgery, University of South Alabama, Mobile, AL, USA
Over the last 30 years, the functions (and dysfunctions) of the sensory-motor circuitry have been mostly conceptualized using linear modelizations which have resulted in two main models: the “rate hypothesis” and the “oscillatory hypothesis.” In these two models, the basal ganglia data stream is envisaged as a random temporal combination of independent simple patterns issued from its probability distribution of interval interspikes or its spectrum of frequencies respectively. More recently, non-linear analyses have been introduced in the modelization of motor circuitry activities, and they have provided evidences that complex temporal organizations exist in basal ganglia neuronal activities. Regarding movement disorders, these complex temporal organizations in the basal ganglia data stream differ between conditions (i.e., parkinsonism, dyskinesia, healthy control) and are responsive to treatments (i.e., l-DOPA, deep brain stimulation). A body of evidence has reported that basal ganglia neuronal entropy (a marker for complexity/irregularity in time series) is higher in hypokinetic state. In line with these findings, an entropy-based model has been recently formulated to introduce basal ganglia entropy as a marker for the alteration of motor processing and a factor of motor inhibition. Importantly, non-linear features have also been identified as a marker of condition and/or treatment effects in brain global signals (EEG), muscular activities (EMG), or kinetic of motor symptoms (tremor, gait) of patients with movement disorders. It is therefore warranted that the non-linear dynamics of motor circuitry will contribute to a better understanding of the neuronal dysfunctions underlying the spectrum of parkinsonian motor symptoms including tremor, rigidity, and hypokinesia.
Introduction
Regarding conditions associated with movement disorders, identification of neuronal correlates to motor symptoms is an important step in characterizing pathological conditions and developing new therapeutics aimed to “correct” or to “normalize” network activity and motoric skills (1, 2). Over the last 30 years, the functions (and dysfunctions) of the sensory-motor circuitry have been mainly conceptualized by linear modelization, which has resulted in two main hypotheses on the occurrence of hypokinesia (i.e., parkinsonism) and hyperkinesia (i.e., dyskinesia). The first hypothesis (e.g., “rate hypothesis”) is based on the circuitry organization of the cortico-basal ganglia-thalamo-cortical loop and its sequential arrangement of excitatory and inhibitory pathways (3, 4). This model postulates that hypokinesia is associated with an imbalanced activity between excitatory and inhibitory drives, in favor of excitation in the output basal ganglia nuclei (e.g., GPi/SNr). The second hypothesis (e.g., “oscillatory hypothesis”) is based on oscillatory activities identified in both single unit and network (i.e., local field potentials, LFPs) activities (5–8). Evidences have linked increased beta band (10–30 Hz) activity to hypokinetic conditions (9–11). In animal models for parkinsonism, the rate and oscillatory hypotheses have generally predicted the effects of anti-parkinsonian treatments on neural activities (i.e., reduced firing rate in GPi/SNr and oscillatory activities in beta band) (4, 12–14), but clinical studies comparing basal ganglia data streams between neurological conditions have reported conflicting data (15–25). In addition to these common models, and based on computational approach, Terman’s group introduced the notion of “connectivity strength” between basal ganglia nuclei as a factor affecting rhythmic firing generation and suggested causal relationship to parkinsonian tremor (26).
The linear analyses used to define basal ganglia activities either in the rate or oscillatory models measure the resultant linear combinations of independent patterns in the data stream. Analyses in the time and frequency domains envisage the interspike interval (ISI) series by the summation of probability distributions for different durations of ISIs (i.e., firing rate, its range or standard deviation) or several frequencies (power spectrum) respectively. These analyses have also been successfully used to characterize the kinetics of movement disorders as well as the EMG in patients with movement disorders and network activities (10, 11).
However, other studies have shown that the irregularity in the neuronal firing activity (27–34), LFPs/EEG (35–38), EMG (39, 40), or kinetics of movement (41, 42) is not random in nature but exhibits a complex temporal organization. In the last decade there has been a growing body of evidence that suggests that linear analyses for basal ganglia circuitry does not fully describe the dynamic nature of these signals, thus justifying the use of non-linear analyses to complement their characterizations (2, 43–47).
In the following sections, we review the findings regarding the non-linear dynamics of physiological functions in Parkinsonism. Finally, we discuss the new challenges and avenues offered by the introduction of these tools to characterize the functions of motor circuitries.
Non-Linear Systems and Common Tools for Their Investigation Related to Movement Disorders
The term non-linear systems refer to organized systems that generate output activities that are not directly proportional to its input. Non-linear systems exhibit complex dynamics which cannot be fully described by a linear combination of the individual activities of their constituent parts. While, linear analyses mostly focus on central tendencies to describe the status of a system (i.e., mean rate of firing activity, mean power spectrum over period of time), non-linear analyses offer some insights in the organization (if any) of the variability of status of a system by quantifying the persistence of certain patterns or “shift” in the irregularity (or “apparent randomness”) of the time series. Because it isn’t possible to point out a single cause for the complex behaviors in non-linear systems, some analyses may have to account for more than one type of non-linearity and several analytical tools may be required to characterize the behaviors of the system. The fast expansion of the number of non-linear tools makes their systematic review beyond the scope of this article. In the next paragraph, we limit our introduction to non-linear analyses to those most commonly used in the field of motor circuitry activities which is the approximate entropy (ApEn).
As highlighted by Pincus (48), irregularity in a time series results in high standard deviation and unpredictability. While variants of standard deviation appropriately quantify the deviation from centrality (i.e., variability in magnitude), other tools are required to grade the extent of unpredictability (also referred as irregularity or complexity). Irregularity in time series can be graded by exact regularity statistics such as entropy measures. However, their implementations require large set of data free from noise. In real world conditions, and in vivo experimentation, these two conditions cannot be respected since recordings are limited to relatively short period of time, and noise originating from the monitoring systems can contaminate the data. Approximate entropy (ApEn) is an approximation of the Kolmogorov–Sinai entropy that was developed by Pincus to provide a tool to grade regularity in short noisy data set. The calculation of ApEn is model-independent; in system biology, this can reduce biases resulting from the assumption on the organization of the data set. ApEn [and its variants SampEn (49)] is a discriminatory tool to distinguish data sets on the basis of regularity. In Pincus’ ApEn, the algorithm uses three parameters to compute the approximation of entropy: (i) the length of the data set (i.e., number of spike intervals), (ii) the embedding dimension (m), and (iii) the vector comparison length (r). The choice of input parameters has been discussed by Pincus and Goldberger (50) and needs to be in a meaningful range. The authors concluded that, for m = 2, values of r from 0.1 to 0.25 SD, where SD is the standard deviation of the signal, produce good statistical validity of ApEn and SampEn. Because ApEn value is also dependent on the length of the time series (N), the three input parameters must be constant between pairs of compared data sets. A very important property of ApEn is the relative consistency which states that if dataset A is more regular than dataset B for one choice of parameters (m, r, N), then it should also exhibit this for all other choices of parameters (49). Finally, by normalizing the vector comparison to the SD of each time series ensuring that ApEn remains unchanged under uniform process magnification (49). In other words, and related to neurophysiological signals, the irregularity of neuronal entropy is decorrelated from the firing rate and the LFP entropy is decorrelated from the amplitude of the signal. Other relatively common tools to investigate the non-linear features in the motor circuitry include the correlation dimension and sample entropy. These values are closely related to the approximate entropy by their algorithms and are reviewed in details elsewhere (51).
Non-Linear Dynamic of Movement Kinematics and EMG in Parkinsonism
The parkinsonian tremor is a cardinal symptom of the condition which exhibits a modal frequency between 4 and 6 Hz, whereas the postural tremor is between 5 and 12 Hz (52–55). The time-dependent organization of parkinsonian tremor was reported to be more regular (lower approximate entropy, ApEn) in Parkinson’s Disease (PD) patients compared to those with the physiological tremor monitored in the healthy control group (41, 56). Importantly, both STN deep brain stimulation (DBS) and medication reduce tremor regularity (increase entropy) but fail to normalize it to healthy control values (57, 58). Specific to the effects of DBS, tremor entropy decreases with the voltage increase (59). In addition to the tremor, gait kinematics were found less regular in PD patients (higher entropy) than in healthy controls (60–64). As previously observed for the tremor, levodopa partially normalized the regularity of the temporal organization of gait patterns (65).
Differences in EMGs characteristics between PD patients and healthy persons include an increased tonic background activity (66), increased synchronization in 8–12 Hz, decreased amplitude in the 20–25 Hz (56, 67), and an alternating pattern of EMG bursts during voluntary movement (68). In the non-linear domain, both EMG and acceleration signals exhibit lower complexity (lower entropy) in PD patients than in healthy subjects (56). The complexity of the PD tremor was found to be further reduced by anti-parkinsonian treatments including DBS (57, 69).
The identification of non-linear features in the kinetics of some disorders and their related EMG activities has therefore raised the question of whether there could be central changes in non-linear features of sensory-motor circuitry activities.
Non-Linear Dynamic in Network and Neuronal Datastream in Parkinsonism
Stam et al. (70, 71) identified non-linear features in EEGs recorded from Parkinsonian patients. Later, entropy (or complexity) of EEGs was reported to be increased in PD patients comparatively to healthy controls (72). This finding was confirmed by Han et al. who further indicated that PD is associated with an increased complexity of the EEG’s rhythm (73).
Non-linear temporal organization has also been identified in the interval interspikes series (ISIs) recorded from basal ganglia neurons in the awake normal primate and in Parkinsonian patients (47). These analyses have established that the non-linear temporal organization of ISIs in the time series results in the replication of complex patterns that cannot be statistically explained by random trials from the probability distribution of the ISIs (2, 47). In other words, the non-linear temporal organization of basal ganglia ISIs is less irregular than what its probability distribution would suggest if ISIs were randomly sorted. Yet, the clinical relevance of these neuronal non-linear features to movement disorders is not clear. A retrospective analyses of a database of PD and dystonia neurons with temporal organizations [as defined in Ref. (2)], Sanghera et al. (74) found a lower neuronal entropy in the GPi of dystonia patients comparatively to PD patients. The evidence that changes in non-linear features may account for the effects of treatments for movement disorders was initially established by Dorval and colleagues (43). This study in the Parkinsonian primate reported a change in non-linear features in GPi neuronal data stream following DBS of the STN, a treatment effective both for Parkinson Disease and dystonia (75). We have confirmed this finding in Parkinsonian patients by establishing that the dopaminergic agonist apomorphine, administered during DBS operative procedure, decreases neuronal entropy in the STN (46). This finding has also helped establish a first link between neurotransmission (especially dopaminergic) and neuronal entropy.
Taken together, the available data on non-linear dysfunctions of sensory-motor circuit have suggested that the hypokinetic condition is associated to higher entropy at least in the GPi and STN. Recently, the basal ganglia neuronal entropy was introduced as a putative interfering factor in the current model for the selection and the inhibition of motor program. The entropy-based model for basal ganglia dysfunctions in movement disorders envisage neuronal entropy under Shannon–Brillouin interpretation (76) as a measure of disorder, unpredictability and reduced motor information. Under this hypothesis high neuronal entropy in the STN and GPi neuronal data stream is interpreted as a network condition generating a large number different pattern possibilities leading to a signal with limited order or “organization” and reduced information. In regard to the concept of selection and inhibition of motor program along the basal ganglia circuitry (77), the entropy-hypothesis introduces complexity of neuronal data stream as a factor which enhances the inhibition of motor program by decreasing its informative nature (see Figure 1). In the parkinsonian state, the “entropy hypothesis” predicts that high STN and GPi neuronal entropies would decrease information in the data stream and motor program selection resulting in hypokinesia. There is currently no clinical or experimental data available to directly relate the changes in BG neuronal entropy to circuitry alterations resulting in the parkinsonian states. In theory, the entropy hypothesis suggests that high GPi neuronal entropy underlies an inadequate compression [or reduction of the dimensionality (78)] of up-stream population activity into the output neurons of the BG circuitry (78). This could be the consequence of the striatal dopaminergic depletion (46) and/or some circuitry reorganizations such as increased interconnections between elements of the motor circuitry (79). Experimental research in animal models for movement disorders is warranted to explore these avenues.
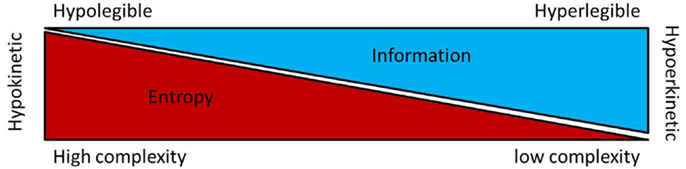
Figure 1. This figure shows a putative relationship between entropy, information and kinesia regarding the motoric functions of the basal ganglia. In the so called “Entropy hypothesis,” increase entropy (or irregularity) in the firing rate of STN and/or GPi neurons result in loss of information [Shannon–Brillouin’s interpretation of entropy (76)] and decreased kinesia [for details, see Ref. (80)].
Discussion
Investigation of non-linear dynamics associated to parkinsonism is still in its infancy but available data shows that both conditions and treatments affect the complex temporal organizations found in motoric kinetics, EMG, global signals, and basal ganglia neuronal activities.
Today, the drawing of a non-linear functional model related to the anatomo-pathology of the parkinsonian basal ganglia is not reachable yet. Though it is remarkable that both global signals (EEG) and single unit activities show entropy increases in parkinsonism, the lack of well-controlled comparisons between pathological and normal states of motor-related territories remains an issue in interpreting these data in regard to the effects of the conditions per se on movement disorders. In addition, the lack of data on the relationships between neuronal entropy and global signal entropy, as well as on the inter-nuclei entropy relationships (2, 47, 81) continue to be major obstacles to linking the alteration of non-linear basal ganglia dynamic to the histological changes of the circuitry associated to the PD condition. A systemic evaluation of the main neurotransmitters on the non-linear dynamic of basal ganglia neurons is necessary to draw a non-linear functional-anatomical model of the motor circuitry both in the normal and the pathological conditions. Single unit recordings combined with LFPs in an animal model for movement disorders (82, 83), and in patients (84), will certainly help to progress in this research direction.
The use of non-linear domain analyses to describe the changes in motor-related dynamics is warranted to provide new qualitative and quantitative information regarding the nature of the alterations in sensory-motor processing associated to the parkinsonian condition. Entropy is a general and commonly used parameter in this new field. The fact that this feature can be followed from the neuronal activity up to the kinetics of movement (via the EEG and EMG) offers an interesting opportunity to investigate the motor information downstream from the central level up to the effectors under a single framework but without warranting a causal relationship. Arguably, this may be less directly accessible within the framework of the rate or oscillatory hypotheses. However, the aim of entropy-related algorithms (i.e., ApEn/SampEn) is not to identify the complex patterns in the time series. Additional non-linear analytical tools need to be integrated in order to better identify non-linear hallmarks in the neuronal and global signals. The identification of such patterns could become relevant in future algorithms for closed-loop devices aimed to deliver on-demand anti-parkinsonian treatments (85). An additional research orientation would be to investigate whether the delivery of non-linear complex patterns could improve the benefit of DBS.
Conclusion
The use of non-linear domain analyses to describe the neuronal and network activities inside the basal ganglia may provide new qualitative and quantitative information relative to the nature of the sensory-motor processing, as well as its distortion in pathological conditions. It is expected that the inclusion of key non-linear features into silicone-based models of the basal ganglia could better reproduce the complexity and non-stationarity of signals recorded in normal and pathological conditions. In translational research, non-linear analytical tools may provide new strategies to improve the efficiency of brain-interfaces and other closed-loop systems aimed to control therapeutic delivery in movement disorders.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Dr. Olivier Darbin is supported by the Department of Neurology at the University of South Alabama College of Medicine (Mobile, AL, USA) and by the Division of System Neurophysiology, National Institute for Physiological Sciences, Okazaki, Aichi, Japan. The authors would like to thank Dr. D. E. Salter for the editing of the manuscript.
References
1. Mackinnon CD, Rothwell JC. Unraveling the mysteries of motor cortical function in Parkinson disease. Neurology (2013) 80:1726–7. doi: 10.1212/WNL.0b013e3182918d4b
2. Darbin O, Soares J, Wichmann T. Nonlinear analysis of discharge patterns in monkey basal ganglia. Brain Res (2006) 1118:84–93. doi:10.1016/j.brainres.2006.08.027
3. Gerfen CR. The neostriatal mosaic: multiple levels of compartmental organization in the basal ganglia. Annu Rev Neurosci (1992) 15:285–320. doi:10.1146/annurev.ne.15.030192.001441
4. Nambu A. A new dynamic model of the cortico-basal ganglia loop. Prog Brain Res (2004) 143:461–6. doi:10.1016/S0079-6123(03)43043-4
5. Eusebio A, Brown P. Oscillatory activity in the basal ganglia. Parkinsonism Relat Disord (2007) 13(Suppl 3):S434–6. doi:10.1016/S1353-8020(08)70044-0
6. Montgomery EB Jr. Basal ganglia physiology and pathophysiology: a re- appraisal. Parkinsonism Relat Disord (2007) 13:455–65. doi:10.1016/j.parkreldis.2007.07.020
7. Stein E, Bar-Gad I. Beta oscillations in the cortico-basal ganglia loop during parkinsonism. Exp Neurol (2012) 245:52–9. doi:10.1016/j.expneurol.2012.07.023
8. Weinberger M, Dostrovsky JO. A basis for the pathological oscillations in basal ganglia: the crucial role of dopamine. Neuroreport (2011) 22:151–6. doi:10.1097/WNR.0b013e328342ba50
9. Weinberger M, Hutchison WD, Dostrovsky JO. Pathological subthalamic nucleus oscillations in PD: can they be the cause of bradykinesia and akinesia? Exp Neurol (2009) 219:58–61. doi:10.1016/j.expneurol.2009.05.014
10. Eusebio A, Brown P. Synchronisation in the beta frequency-band – the bad boy of parkinsonism or an innocent bystander? Exp Neurol (2009) 217:1–3. doi:10.1016/j.expneurol.2009.02.003
11. Gatev P, Darbin O, Wichmann T. Oscillations in the basal ganglia under normal conditions and in movement disorders. Mov Disord (2006) 21:1566–77. doi:10.1002/mds.21033
12. Galvan A, Wichmann T. Pathophysiology of parkinsonism. Clin Neurophysiol (2008) 119:1459–74. doi:10.1016/j.clinph.2008.03.017
13. Obeso JA, Marin C, Rodriguez-Oroz C, Blesa J, Benitez-Temino B, Mena-Segovia J, et al. The basal ganglia in Parkinson’s disease: current concepts and unexplained observations. Ann Neurol (2008) 64(Suppl 2):S30–46. doi:10.1002/ana.21481
14. Tang JK, Moro E, Mahant N, Hutchison WD, Lang AE, Lozano AM, et al. Neuronal firing rates and patterns in the globus pallidus internus of patients with cervical dystonia differ from those with Parkinson’s disease. J Neurophysiol (2007) 98:720–9. doi:10.1152/jn.01107.2006
15. Schrock LE, Ostrem JL, Turner RS, Shimamoto SA, Starr PA. The subthalamic nucleus in primary dystonia: single-unit discharge characteristics. J Neurophysiol (2009) 102:3740–52. doi:10.1152/jn.00544.2009
16. Lenz FA, Suarez JI, Metman LV, Reich SG, Karp BI, Hallett M, et al. Pallidal activity during dystonia: somatosensory reorganisation and changes with severity. J Neurol Neurosurg Psychiatry (1998) 65:767–70. doi:10.1136/jnnp.65.5.767
17. Merello M, Cerquetti D, Cammarota A, Tenca E, Artes C, Antico J, et al. Neuronal globus pallidus activity in patients with generalised dystonia. Mov Disord (2004) 19:548–54. doi:10.1002/mds.10700
18. Sanghera MK, Grossman RG, Kalhorn CG, Hamilton WJ, Ondo WG, Jankovic J. Basal ganglia neuronal discharge in primary and secondary dystonia in patients undergoing pallidotomy. Neurosurgery (2003) 52:1358–70. doi:10.1227/01.NEU.0000064805.91249.F5
19. Starr PA, Rau GM, Davis V, Marks WJ Jr, Ostrem JL, Simmons D, et al. Spontaneous pallidal neuronal activity in human dystonia: comparison with Parkinson’s disease and normal macaque. J Neurophysiol (2005) 93:3165–76. doi:10.1152/jn.00971.2004
20. Lee JI, Verhagen Metman L, Ohara S, Dougherty PM, Kim JH, Lenz FA. Internal pallidal neuronal activity during mild drug-related dyskinesias in Parkinson’s disease: decreased firing rates and altered firing patterns. J Neurophysiol (2007) 97:2627–41. doi:10.1152/jn.00443.2006
21. Walker HC, Watts RL, Schrandt CJ, Huang H, Guthrie SL, Guthrie BL, et al. Activation of subthalamic neurons by contralateral subthalamic deep brain stimulation in Parkinson disease. J Neurophysiol (2011) 105:1112–21. doi:10.1152/jn.00266.2010
22. Tang JK, Moro E, Lozano AM, Lang AE, Hutchison WD, Mahant N, et al. Firing rates of pallidal neurons are similar in Huntington’s and Parkinson’s disease patients. Exp Brain Res (2005) 166:230–6. doi:10.1007/s00221-005-2359-x
23. Stefani A, Bassi A, Mazzone P, Pierantozzi M, Gattoni G, Altibrandi MG, et al. Subdyskinetic apomorphine responses in globus pallidus and subthalamus of parkinsonian patients: lack of clear evidence for the ‘indirect pathway’. Clin Neurophysiol (2002) 113:91–100. doi:10.1016/S1388-2457(01)00683-6
24. Levy R, Dostrovsky JO, Lang AE, Sime E, Hutchison WD, Lozano AM. Effects of apomorphine on subthalamic nucleus and globus pallidus internus neurons in patients with Parkinson’s disease. J Neurophysiol (2001) 86:249–60.
25. Montgomery EB Jr. Subthalamic nucleus neuronal activity in Parkinson’s disease and epilepsy subjects. Parkinsonism Relat Disord (2008) 14:120–5. doi:10.1016/j.parkreldis.2007.06.014
26. Terman D, Rubin JE, Yew AC, Wilson CJ. Activity patterns in a model for the subthalamopallidal network of the basal ganglia. J Neurosci (2002) 22:2963–76.
27. Korn H, Faure P. Is there chaos in the brain? II. Experimental evidence and related models. C R Biol (2003) 326:787–840. doi:10.1016/j.crvi.2003.09.011
28. Mpitsos GJ, Burton RM Jr, Creech HC, Soinila SO. Evidence for chaos in spike trains of neurons that generate rhythmic motor patterns. Brain Res Bull (1988) 21:529–38. doi:10.1016/0361-9230(88)90169-4
29. Mendez MA, Zuluaga P, Hornero R, Gomez C, Escudero J, Rodriguez-Palancas A, et al. Complexity analysis of spontaneous brain activity: effects of depression and antidepressant treatment. J Psychopharmacol (2011) 26(5):636–43. doi:10.1177/0269881111408966
30. Friedman A, Deri I, Friedman Y, Dremencov E, Goutkin S, Kravchinsky E, et al. Decoding of dopaminergic mesolimbic activity and depressive behavior. J Mol Neurosci (2007) 32:72–9. doi:10.1007/s12031-007-0016-5
32. London M, Hausser M. Dendritic computation. Annu Rev Neurosci (2005) 28:503–32. doi:10.1146/annurev.neuro.28.061604.135703
33. Usakli AB. Modeling of movement-related potentials using a fractal approach. J Comput Neurosci (2010) 28:595–603. doi:10.1007/s10827-010-0242-7
34. Kozma R, Bressler S, Perlovsky L, Venayagamoorthy GK. Advances in neural networks research: an introduction. Neural Netw (2009) 22:489–90. doi:10.1016/j.neunet.2009.07.008
35. Battaglia D, Hansel D. Synchronous chaos and broad band gamma rhythm in a minimal multi-layer model of primary visual cortex. PLoS Comput Biol (2011) 7:e1002176. doi:10.1371/journal.pcbi.1002176
36. Elger CE, Widman G, Andrzejak R, Arnhold J, David P, Lehnertz K. Nonlinear EEG analysis and its potential role in epileptology. Epilepsia (2000) 41(Suppl 3):S34–8. doi:10.1111/j.1528-1157.2000.tb01532.x
37. Manyakov NV, Van Hulle MM. Synchronization in monkey visual cortex analyzed with an information-theoretic measure. Chaos (2008) 18:037130. doi:10.1063/1.2949928
38. McKenna TM, McMullen TA, Shlesinger MF. The brain as a dynamic physical system. Neuroscience (1994) 60:587–605. doi:10.1016/0306-4522(94)90489-8
39. Arjunan SP, Kumar DK. Fractal based modelling and analysis of electromyography (EMG) to identify subtle actions. Conf Proc IEEE Eng Med Biol Soc (2007) 2007:1961–4.
40. Zhang X, Zhou P. Sample entropy analysis of surface EMG for improved muscle activity onset detection against spurious background spikes. J Electromyogr Kinesiol (2012) 22:901–7. doi:10.1016/j.jelekin.2012.06.005
41. Meigal AY, Rissanen SM, Tarvainen MP, Georgiadis SD, Karjalainen PA, Airaksinen O, et al. Linear and nonlinear tremor acceleration characteristics in patients with Parkinson’s disease. Physiol Meas (2012) 33:395–412. doi:10.1088/0967-3334/33/3/395
42. Miller DJ, Stergiou N, Kurz MJ. An improved surrogate method for detecting the presence of chaos in gait. J Biomech (2006) 39:2873–6. doi:10.1016/j.jbiomech.2005.10.019
43. Dorval AD, Russo GS, Hashimoto T, Xu W, Grill WM, Vitek JL. Deep brain stimulation reduces neuronal entropy in the MPTP-primate model of Parkinson’s disease. J Neurophysiol (2008) 26(5):636–43. doi:10.1152/jn.90763.2008
44. Li W, Jia D, Wang JL, Liang Q, Jian Z, Wang XL, et al. Deterministic dynamics in neuronal discharge from pallidotomy targets. J Int Med Res (2008) 36:979–85. doi:10.1177/147323000803600514
45. Rodriguez M, Pereda E, Gonzalez J, Abdala P, Obeso JA. Neuronal activity in the substantia nigra in the anaesthetized rat has fractal characteristics. Evidence for firing-code patterns in the basal ganglia. Exp Brain Res (2003) 151:167–72. doi:10.1007/s00221-003-1442-4
46. Lafreniere-Roula M, Darbin O, Hutchison WD, Wichmann T, Lozano AM, Dostrovsky JO. Apomorphine reduces subthalamic neuronal entropy in parkinsonian patients. Exp Neurol (2010) 225:455–8. doi:10.1016/j.expneurol.2010.07.016
47. Lim J, Sanghera MK, Darbin O, Stewart RM, Jankovic J, Simpson R. Nonlinear temporal organization of neuronal discharge in the basal ganglia of Parkinson’s disease patients. Exp Neurol (2010) 224(2):542–4. doi:10.1016/j.expneurol.2010.05.021
48. Pincus S, Kalman RE. Irregularity, volatility, risk, and financial market time series. Proc Natl Acad Sci U S A (2004) 101:13709–14. doi:10.1073/pnas.0405168101
49. Richman JS, Moorman JR. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol (2000) 278:H2039–49.
50. Pincus SM, Goldberger AL. Physiological time-series analysis: what does regularity quantify? Am J Physiol (1994) 266:H1643–56.
51. Zurek S, Guzik P, Pawlak S, Kosmider M, Piskorski J. On the relation between correlation dimension, approximate and sample entropy parameters, and a fast algorithm for their calculation. Physica A (2012) 391:6601–10. doi:10.1016/j.physa.2012.07.003
54. Deuschl G, Bain P, Brin M. Consensus statement of the movement disorder society on tremor. Ad hoc scientific committee. Mov Disord (1998) 13(Suppl 3):2–23. doi:10.1002/mds.870131303
55. Brown P. Oscillatory nature of human basal ganglia activity: relationship to the pathophysiology of Parkinson’s disease. Mov Disord (2003) 18:357–63. doi:10.1002/mds.10358
56. Vaillancourt DE, Newell KM. The dynamics of resting and postural tremor in Parkinson’s disease. Clin Neurophysiol (2000) 111:2046–56. doi:10.1016/S1388-2457(00)00467-3
57. Sturman MM, Vaillancourt DE, Metman LV, Bakay RA, Corcos DM. Effects of subthalamic nucleus stimulation and medication on resting and postural tremor in Parkinson’s disease. Brain (2004) 127:2131–43. doi:10.1093/brain/awh237
58. Kovacs N, Balas I, Illes Z, Kellenyi L, Doczi TP, Czopf J, et al. Uniform qualitative electrophysiological changes in postoperative rest tremor. Mov Disord (2006) 21:318–24. doi:10.1002/mds.20712
59. Sadeghirazlighi M, Jafari AH, Firoozabadi SM, Shahidi GA. Study of chaotic behavior of tremor of some Parkinsonians under deep brain stimulation. Australas Phys Eng Sci Med (2012) 35:25–30. doi:10.1007/s13246-011-0111-3
60. Bartsch R, Plotnik M, Kantelhardt JW, Havlin S, Giladi N, Hausdorff JM. Fluctuation and synchronization of gait intervals and gait force profiles distinguish stages of Parkinson’s disease. Physica A (2007) 383:455–65. doi:10.1016/j.physa.2007.04.120
61. Hausdorff JM. Gait dynamics in Parkinson’s disease: common and distinct behavior among stride length, gait variability, and fractal-like scaling. Chaos (2009) 19:026113. doi:10.1063/1.3147408
62. Hausdorff JM, Lertratanakul A, Cudkowicz ME, Peterson AL, Kaliton D, Goldberger AL. Dynamic markers of altered gait rhythm in amyotrophic lateral sclerosis. J Appl Physiol (2000) 88:2045–53.
63. Kurz MJ, Stergiou N. Hip actuations can be used to control bifurcations and chaos in a passive dynamic walking model. J Biomech Eng (2007) 129:216–22. doi:10.1115/1.2486008
64. Pothakos K, Kurz MJ, Lau YS. Restorative effect of endurance exercise on behavioral deficits in the chronic mouse model of Parkinson’s disease with severe neurodegeneration. BMC Neurosci (2009) 10:6. doi:10.1186/1471-2202-10-6
65. Kurz MJ, Hou JG. Levodopa influences the regularity of the ankle joint kinematics in individuals with Parkinson’s disease. J Comput Neurosci (2010) 28:131–6. doi:10.1007/s10827-009-0192-0
66. Robichaud JA, Pfann KD, Comella CL, Brandabur M, Corcos DM. Greater impairment of extension movements as compared to flexion movements in Parkinson’s disease. Exp Brain Res (2004) 156:240–54. doi:10.1007/s00221-003-1782-0
67. Vaillancourt DE, Slifkin AB, Newell KM. Regularity of force tremor in Parkinson’s disease. Clin Neurophysiol (2001) 112:1594–603. doi:10.1016/S1388-2457(01)00593-4
68. Rissanen S, Kankaanpaa M, Tarvainen MP, Nuutinen J, Tarkka IM, Airaksinen O, et al. Analysis of surface EMG signal morphology in Parkinson’s disease. Physiol Meas (2007) 28:1507–21.
69. Sturman MM, Vaillancourt DE, Metman LV, Sierens DK, Bakay RA, Corcos DM. Deep brain stimulation and medication for parkinsonian tremor during secondary tasks. Mov Disord (2007) 22:1157–63. doi:10.1002/mds.21518
70. Jelles B, Achtereekte HA, Slaets JP, Stam CJ. Specific patterns of cortical dysfunction in dementia and Parkinson’s disease demonstrated by the acceleration spectrum entropy of the EEG. Clin Electroencephalogr (1995) 26:188–92.
71. Stam CJ, Jelles B, Achtereekte HA, Rombouts SA, Slaets JP, Keunen RW. Investigation of EEG non-linearity in dementia and Parkinson’s disease. Electroencephalogr Clin Neurophysiol (1995) 95:309–17. doi:10.1016/0013-4694(95)00147-Q
72. Pezard L, Jech R, Ruzicka E. Investigation of non-linear properties of multichannel EEG in the early stages of Parkinson’s disease. Clin Neurophysiol (2001) 112:38–45. doi:10.1016/S1388-2457(00)00512-5
73. Han C-X, Wang J, Yi G-S, Che Y-Q. Investigation of EEG abnormalities in the early stage of Parkinson’s disease. Cogn Neurodyn (2013) 7:1–9.
74. Sanghera ODMK, Alam M, Krauss JK, Friehs G, Jankovic J, Simpson RK, et al. Entropy measurements in pallidal neurons in dystonia and Parkinson’s disease. Mov Disord (2012) 27(Suppl 1):S1–639.
75. Ostrem JL, Racine CA, Glass GA, Grace JK, Volz MM, Heath SL, et al. Subthalamic nucleus deep brain stimulation in primary cervical dystonia. Neurology (2011) 76:870–8. doi:10.1212/WNL.0b013e31820f2e4f
76. Longo G, Miquel PA, Sonnenschein C, Soto AM. Is information a proper observable for biological organization? Prog Biophys Mol Biol (2012) 109(3):108–14. doi:10.1016/j.pbiomolbio.2012.06.004
77. Nambu A. A new approach to understand the pathophysiology of Parkinson’s disease. J Neurol (2005) 252(Suppl 4):IV1–4.
78. Bar-Gad I, Morris G, Bergman H. Information processing, dimensionality reduction and reinforcement learning in the basal ganglia. Prog Neurobiol (2003) 71:439–73. doi:10.1016/j.pneurobio.2003.12.001
79. Villalba RM, Smith Y. Differential structural plasticity of corticostriatal and thalamostriatal axo-spinous synapses in MPTP-treated Parkinsonian monkeys. J Comp Neurol (2011) 519:989–1005. doi:10.1002/cne.22563
80. Darbin O, Dees D, Martino A, Adams E, Naritoku D. An entropy-based model for basal ganglia dysfunctions in movement disorders. Biomed Res Int (2013) 2013:5. doi:10.1155/2013/742671
81. Gilmour TP, Lagoa C, Jenkins WK, Rao AN, Berk MA, Venkiteswaran K, et al. Transfer entropy between cortical and basal ganglia electrophysiology. Signal Processing in Medicine and Biology Symposium (SPMB), 2012 IEEE. New York, NY: IEEE (2012). p. 1–5.
82. Darbin O, Newton L, Wichmann T. A new probe to monitor the effects of drugs on local field potentials. J Neurosci Methods (2006) 155:291–5. doi:10.1016/j.jneumeth.2006.01.010
83. Darbin O, Wichmann T. Effects of striatal GABA A-receptor blockade on striatal and cortical activity in monkeys. J Neurophysiol (2008) 99:1294–305. doi:10.1152/jn.01191.2007
84. Priori A, Giannicola G, Rosa M, Marceglia S, Servello D, Sassi M, et al. Deep brain electrophysiological recordings provide clues to the pathophysiology of Tourette syndrome. Neurosci Biobehav Rev (2013) 37(6):1063–8. doi:10.1016/j.neubiorev.2013.01.011
Keywords: entropy, EMG, EEG, single unit, movement disorders
Citation: Darbin O, Adams E, Martino A, Naritoku L, Dees D and Naritoku D (2013) Non-linear dynamics in parkinsonism. Front. Neurol. 4:211. doi: 10.3389/fneur.2013.00211
Received: 30 June 2013; Accepted: 12 December 2013;
Published online: 25 December 2013.
Edited by:
Alberto Albanese, Università Cattolica del Sacro Cuore, ItalyReviewed by:
William Hutchison, University Health Network, CanadaMaria Stamelou, University of Athens, Greece
Copyright: © 2013 Darbin, Adams, Martino, Naritoku, Dees and Naritoku. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Olivier Darbin, Department of Neurology, University of South Alabama, 307 University Blvd., Mobile, AL 36688, USA e-mail:b2RhcmJpbkB1c291dGhhbC5lZHU=
 Olivier Darbin
Olivier Darbin Elizabeth Adams3
Elizabeth Adams3 Daniel Dees
Daniel Dees