The solubility of oxygen in water and saline solutions

Oxygen is one of the key reaction partners for many redox reactions also in the context of nuclear waste disposal. Its solubility influences radionuclides’ behavior, corrosion processes and even microbial activity. Therefore, a reliable calculation of the solubility of molecular oxygen in aqueous solutions is relevant for any safety assessment. Available geochemical speciation and reactive transport programs handle these data very differently. In some codes, the hypothetical equilibrium between dissolved oxygen and water is used to balance redox reactions. Equilibrium constants are given in “temperature grids” for up to 573.15 K. In other cases, temperature functions for the solubility of gaseous oxygen in water are given, without any reference to a valid temperature range. These settings become even more complicated when used in the context of modeling equilibria in high-saline solutions applying the Pitzer formalism. This raised the question about the experimental foundation of equilibrium constants given in such data files and their validity for the solubility of molecular oxygen in saline solutions. For this article, a thorough literature review was conducted with respect to the solubility of molecular oxygen in pure water and saline solutions. From these primary experimental O₂ solubility data a temperature-dependent Henry’s law function as well as temperature-dependent binary and ternary Pitzer ion-interaction coefficients were derived. An internally consistent set of thermodynamic data for dissolved oxygen is presented, along with statements about its validity in terms of temperature and, as far as Pitzer interaction coefficients are concerned, of solution composition. This self-consistent activity-fugacity model containing thermodynamic data, Henry’s law temperature equation, and Pitzer interaction coefficients is capable of providing a more accurate description of redox transformations, allowing a reduction of conservatism in safety assessment calculations, not only in the context of a nuclear repository. The model reproduces well the reliable experimental data available, and is capable to predict the oxygen solubility in complex solution media. The temperature functions used to describe Henry’s constant and the Pitzer interaction coefficients are consistent with the implementation in commonly used geochemical computational programs, allowing direct use without further modification.

1 Introduction

Redox reactions are important for the description of geochemical reactions in general (e.g., pyrite oxidation) and of solubility limitations of radioactive contaminants in particular. In a final deep geological repository (DGR) for radioactive waste, attainment of anoxic conditions is very likely in the post-closure phase of operation. In the event of any post-closure access of an aqueous solution to the waste, and assuming anoxic conditions, many radionuclides are immobile to a large extent through the formation of poorly soluble (hydro-)oxides in their reduced tetravalent form [e.g., TcO₂(am), U(OH)₄(am), Np(OH)₄(am), PuO₂(am/cr), etc.] (Grenthe et al., 2020). However, under strongly reducing conditions even their trivalent forms e.g., Pu(OH)₃(am/cr) might exist, showing a higher solubility and thus mobility than the tetravalent actinides (Grenthe et al., 2020). This holds also for higher redox states (penta-, hexa- or heptavalent), which are more soluble in water. Concerning all of these redox-triggered transformations, exact knowledge of the redox potential (E_H/pe) is essential, which in turn depends on the correct description of dissolved oxygen. For an assessment of the maximum likely mobilization of radionuclides from the near field of a DGR under the prerequisite of intrusion of water, the mass of available dissolved oxygen (being present, e.g., by diffusional transport or freshwater intrusion) is one key factor for the retardation of radionuclides in aqueous solution.

In geochemical speciation codes such as PHREEQC (Parkhurst and Appelo, 2013), Geochemist’s Workbench (Bethke, 2022), or EQ3/6 (Wolery, 1992), redox reactions of any kind are linked for computational reasons to the hypothetical half-cell reaction

$2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\rightleftharpoons {\mathrm{O}}_2\left(\mathrm{g}\right)+4{\mathrm{H}}^{+}+4{\mathrm{e}}^{-}(1)$

Or, alternatively, to another form involving dissolved oxygen:

$2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\rightleftharpoons {\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)+4{\mathrm{H}}^{+}+4{\mathrm{e}}^{-}(2)$

Adding the reaction

$4{\mathrm{H}}^{+}+4{\mathrm{e}}^{-}\rightleftharpoons 2{\mathrm{H}}_2\left(\mathrm{g}\right)(3)$

for which, by definition, ${\log }_{10}K\left(3\right)=0$ the half-cell reactions become

$2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\rightleftharpoons {\mathrm{O}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\left(\mathrm{g}\right)(4)$

$2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\rightleftharpoons {\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)+2{\mathrm{H}}_2\left(\mathrm{g}\right)(5)$

Reactions (Eq. 4) and (Eq. 5) are sometimes referred to as “logK-E_H-reaction.” In data files for the above-mentioned codes, equilibrium constants for these reactions are either given as functions of temperature or as “temperature grids,” where pre-calculated values at defined temperatures (usually 0, 25, 60, 100, 150, 200, 250, and 300°C) are displayed. Unfortunately, this is usually done without any references to literature or a hint to the validity limits at all. The situation becomes even more obscure if the reaction (Eq. 5) containing O₂(aq) is used as half-cell reaction, because this reaction must in fact be considered as addition of reaction (Eq. 4) and

${\mathrm{O}}_2\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right).(6)$

This poses the question about the experimental foundations for the calculation of the solubility of molecular oxygen in water at temperatures up to 573.15 K. If applied in calculations for high-saline solutions the question arises concerning the impact of ionic strength in general or the presence of specific electrolytes on the solubility of molecular oxygen in particular. In such cases, the Pitzer ion-interaction approach provides a tool for calculating the activity coefficient in concentrated salt solutions (Pitzer, 1991). For this purpose, coefficients for a virial equation are used for binary and ternary interactions between ions as well as uncharged species in aqueous solution, reflecting the deviation from the behavior in pure water. In some data files, e.g., the “Yucca Mountain Pitzer file” (Mariner, 2004) delivered with the EQ3/6 code, Pitzer coefficients for O₂(aq) are included, some valid at 298.15 K only, others are given with a temperature function of unknown validity range. Compilations of data from different sources may cause inconsistencies, which, especially when using the interaction coefficients, may have a significant negative impact on the results of the models obtained.

Facing the task of extending a thermodynamic database based on traceable experimental data, simple adoption of precalculated equilibrium constants in temperature grids from parameter files in geochemical codes is not appropriate, particularly since they are provided in many databases without reference to the source of the primary data. Consequently, these data had to be comprehensibly and consistently recalculated from experimental data for the solubility of oxygen at various temperatures in both pure water and salt solutions and from standard formation data.

For this purpose, solubility data of O₂ in pure water as well as in a wide variety of electrolyte solutions were critically evaluated and combined with well-established thermodynamic data for liquid water H₂O(l), H₂(g), and O₂(g) to create an internally consistent set of equilibrium constants for reactions (Eqs 4–6). With respect to O₂(g) solubility data, the focus was on the system of oceanic salts (including carbonates), which are relevant as potential host rocks implying solutions of high ionic strengths. The alkali ((di-)hydrogen) phosphates were included for inorganic phosphate ions that can form in nuclear waste repositories when phosphate glasses or lanthanide phosphate monazites (LnPO₄), as waste forms of highly active waste streams, undergo dissolution processes in contact with water. The acids of the anions contained in the system were included in the data set to represent the case of acid-forming oxidation of minerals (acid mine drainage). Hydroxides were included to allow calculation for alkaline solutions from cement pore waters.

2 Theory and methods

Henry’s law constant (K_O2(aq)) using the partial pressure of O₂ in the gas phase describes the equilibrium condition for dissolution reaction of O₂ in water (Eq. 6) with γ_O2(aq) being the O₂ activity coefficient, m_O2(aq) the molal O₂ concentration in solution and f_O2(aq) the O₂ fugacity in the gas phase.

$K_{O_2\left(aq\right)}=\frac{\left[{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}{\left[{\mathrm{O}}_2\left(\mathrm{g}\right)\right]}=\frac{{\gamma }_{O_2\left(aq\right)}\bullet m_{O_2\left(aq\right)}}{f_{O_2\left(g\right)}}(7)$

Geochemical codes treat the temperature dependence of equilibrium constants as polynomial functions with several temperature-dependent terms (Eq. 8) or mathematically equivalent transformations thereof.

${\log }_{10}K\left(T\right)=A_1+A_{2}T+\frac{A_3}{T}+A_4\ln T+\frac{A_5}{T^2}+A_6{T}^2(8)$

The Pitzer formalism is widely used to account for the deviation from ideality of aqueous solutions of high ionic strength. It has proven capable of calculating solubilities in saturated solutions in the system of oceanic salts: Na⁺, K⁺, Mg²⁺, Ca²⁺ – Cl⁻, SO₄²⁻, HCO₃⁻ – CO₂(g) – H₂O(l). The probably most cited paper in this respect is the one by Harvie, Møller and Weare (Harvie et al., 1984), whose results are often referred to as “HMW-database.” The usability of their database was demonstrated for a huge amount of application cases. One example especially relevant for nuclear waste disposal is by Herbert, who successfully modeled dissolution and precipitation processes in complex, saturated salt solutions in German rock salt formations (Herbert et al., 2000). Later, the HMW-database was extended to higher temperatures (Christov and Møller, 2004). Its popularity, as well as that of the Pitzer formalism in general, was promoted by the fact that it got implemented in various geochemical codes, such as PHREEQC, EQ3/6, Geochemist’s Workbench, but also in CHEMAPP (Eriksson and Spencer, 1995; Eriksson et al., 1997), GEMS (Wagner et al., 2012; Kulik et al., 2013), or recently TOUGHREACT (Zhang et al., 2006). In parallel, the HMW-database was further developed and extended in response to the necessities of national programs for the disposal of radioactive waste in salt rock formations with the potential to contain high-saline solutions, e.g., the Yucca Mountain project (United States) (Mariner, 2004), the Waste Isolation Pilot Plant project (United States) (Domski and Nielsen, 2019), or the Oceanic Salt System from Voigt (2020) (Voigt, 2020a; Voigt, 2020b) with the alkali phosphate data from Scharge et al. (2013), Scharge et al. (2015) and the carbonate data from Harvie et al. (1984) as compiled in the THEREDA project in Germany (Moog et al., 2015; THEREDA, 2023). The Pitzer formalism was also applied to marine chemistry. Millero and co-workers over many years worked on a database specifically suited for seawater, e.g., (Pierrot and Millero, 2017). Recently, the Scientific Committee on Ocean Research of the International Council for Science (SCOR) created working group 145 to establish a reference seawater chemical speciation model, which is based on the Pitzer model (Turner et al., 2016).

The Pitzer formalism extends the Debye-Hückel equation with a virial expansion to account for binary and ternary ionic-strength-dependent specific interactions between ions of likewise and opposite charge (Pitzer, 1991). Explicit formulations for binary and ternary solutions of cations and anions are given by Scharge et al. (2012). In the present work, non-ideal interactions between a neutral component O₂(aq) and cations or anions are investigated. More specifically, the focus is set on binary λ-interactions (between a neutral and a charged solute) and ternary ζ-interactions (one uncharged and two oppositely charged solutes), η-interactions (one uncharged and two similar charged solutes) and µ-interactions (two different uncharged and one charged solutes). The activity coefficient for a neutral species according to Pitzer (Pitzer, 1991) is:

$\begin{array}{ll}\hfill \ln {\gamma }_N& =2\left({\displaystyle \sum _c}{m}_c{\lambda }_{Nc}+{\displaystyle \sum _a}{m}_a{\lambda }_{Na}+{\displaystyle \sum _n}{m}_n{\lambda }_{Nn}\right)+{\displaystyle \sum _c}{\displaystyle \sum _a}{m}_c{m}_a{\zeta }_{Nca}+{\displaystyle \sum _c}{\displaystyle \sum _{c^{\prime }}}{m}_c{m}_{c^{\prime }}{\eta }_{Nc{c}^{\prime }}\hfill \\ \hfill & +{\displaystyle \sum _a}{\displaystyle \sum _{a^{\prime }}}{m}_a{m}_{a^{\prime }}{\eta }_{Na{a}^{\prime }}+{\displaystyle \sum _c}{\displaystyle \sum _n}{m}_c{m}_n{\mu }_{Nnc}+{\displaystyle \sum _a}{\displaystyle \sum _n}{m}_a{m}_n{\mu }_{Nna}\hfill \end{array}(9)$

Note, that in Eq. 9 η_Ncc’, η_Naa’, µ_Nn’c and µ_Nn’a refer to interactions between a neutral solute and to two different non-neutral solutes with likewise charge. These interactions are mathematically identical to a ternary ζ-interaction. It is perhaps for this reason, that sometimes they are not properly distinguished in data files and instead referred to as ζ- or even ψ-interactions altogether.

A few publications are available in the literature providing Pitzer interaction coefficients for molecular oxygen in electrolyte solutions. Namely, the works of Clegg and Brimblecombe (1990), Millero et al. (2002a), Millero et al. (2002b), Millero et al. (2003), Millero and Huang (2003), Geng and Duan (2010), and Zheng and Mao (2019) are worth mentioning here. However, combining these data sets with the only existing Pitzer data set valid for higher temperatures and including the whole Oceanic Salt System (THEREDA) leads to inconsistencies. Such inconsistent databases will produce incorrect modeling results. This is demonstrated in Figure 1 by recalculating experimental data of O₂ solubility in NaCl solution from literature (Millero et al., 2002a; Millero et al., 2002b; Millero et al., 2003). This does not mean that the various available Pitzer datasets for oxygen are of poor quality. However, it illustrates the importance of consistent data sets.

FIGURE 1

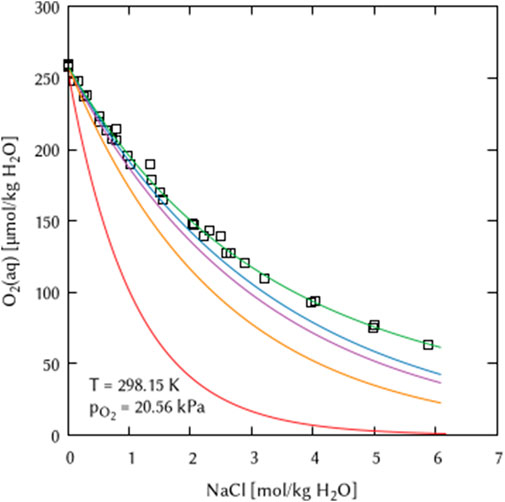
FIGURE 1. Effect of combining inconsistent Pitzer datasets on the example of O₂ solubility in NaCl solution. □ Experimental data from Millero et al. (2002a), Millero et al. (2002b), Millero et al. (2003), lines: Calculation using the THEREDA Pitzer dataset (Moog et al., 2015; Voigt, 2020a; Voigt, 2020b; THEREDA, 2023) in combination with: blue) Millero et al. (2003), purple) Clegg and Brimblecombe (1990), orange) Geng and Duan (2010), red) Zheng and Mao (2019), green) this work.

2.1 Data treatment

This work focusses on primary experimental results. Respective literature on the solubility of molecular oxygen in pure water as well as in electrolyte solutions was collected, critically assessed, and used to recalibrate the temperature-dependent Henry’s law constant as well as the Pitzer interaction coefficients.

In many publications, the O₂ solubility data are given in figures only. In these cases, the data were re-digitized using the software package “Engauge Digitizer” from Mitchell et al. (2020). The uncertainty resulting from this digitization step depends on the quality of the graphics, but in most cases can be neglected compared to the experimental uncertainty.

Experimentally obtained O₂ solubility data are published using various different formats and units. Here, all datasets were recalculated to a micromolal scale (µmoles O₂ per kg of water) as a function of salt concentration in molal scale (moles salt per kg of water). If the concentration data were available in a volume-related concentration unit, e.g., molar (moles per liter solution), they were converted using the density functions according to Söhnel and Novotný (1985). All solubility data on molecular oxygen in both, pure water and electrolyte solutions are provided in the supporting information.

2.2 Parameter optimization

All parameters for temperature dependency equations—for Henry’s law temperature equation as well as for the Pitzer interaction coefficients—were determined using the geochemical speciation software PHREEQC (batch version 3.7) (Parkhurst and Appelo, 2013) coupled with the parameter estimation software UCODE_2014 (Poeter et al., 2014) that uses a minimization of sum of squared residuals approach.

To determine the numerical values for the parameters of the temperature dependent Henry’s law Eq. 8, data for the oxygen solubility in pure water were collected from the literature. These solubility datasets were used to fit the simplified temperature function equation using parameters A₁, A₃, and A₄ only. The common geochemical codes (e.g., ChemApp, Geochemist’s Workbench, PHREEQC, ToughReact) use six temperature parameters (Eq. 8 or mathematically equivalent transformations thereof) for the temperature-dependent description of reaction constants. Since a complete set of these temperature parameters must be specified in the code-specific parameter files, the other parameters (A₂, A₅ and A₆) are set to zero. Older codes like EQ3/6 use a temperature-dependend grif of up to eight logK values; these can be easily calculated from the parameterized equation.

Most geochemical programs treat the Pitzer coefficients and their temperature parameter in a different way. There, polythermal equations use terms where the temperature is given relative to a reference temperature (mostly T = 298.15 K, sometimes referred to as “25°-centered”), see Eq. 10 or mathematically equivalent transformations thereof.

$P=X_0+X_1\left(\frac{1}{T}-\frac{1}{T_r}\right)+X_2\ln \left(\frac{T}{T_r}\right)+X_3\left(T-T_r\right)+X_4\left(T^2-{T_r}^2\right)+X_5\left(\frac{1}{T^2}-\frac{1}{{T_r}^2}\right)(10)$

P is a Pitzer coefficient (here λ, ζ or η), T is the temperature in Kelvin, and T_r is the reference temperature (298.15 K) and ln the natural logarithm.

It was numerically impossible to fit all necessary temperature function parameters for all relevant Pitzer coefficients simultaneously. Therefore, a step-by-step approach was chosen: By definition, the coefficient λ(O₂-Cl⁻) and therefore all temperature parameters for (X₀–X₅) were set to 0. First, the Pitzer coefficients at T = 298.15 K were fitted using the experimental O₂ solubility data for the chemical subsystem H⁺, Na⁺, K⁺ - Cl⁻, OH⁻ - H₂O(l) only. The resulting values of the coefficients were then used in the successive fitting of the chemical subsystems H⁺, Na⁺, K⁺ - SO₄²⁻ - H₂O(l), Na⁺, K⁺ - CO₃²⁻ - H₂O(l) and H⁺, Na⁺, K⁺ - PO₄³⁻ - H₂O(l). All obtained interaction coefficients were then used as boundary conditions to fit interaction coefficients within the chemical subsystems of the Earth alkaline chlorides and Earth alkaline sulfates, respectively: Mg²⁺, Ca²⁺ - Cl⁻, OH⁻ - H₂O(l) as well as Mg²⁺ - SO₄²⁻, OH⁻ - H₂O(l). Finally, the interaction coefficients η(Cl⁻-SO₄²⁻) and η(Na⁺-Mg²⁺) for ternary salt solutions (NaCl + Na₂SO₄, NaCl + MgCl₂) were fitted.

During the parameter determination, first all possible combinations of binary (λ) and ternary (ζ/η/µ) Pitzer coefficients should be determined. It became apparent that not all such coefficients were needed to describe the system, or that some combinations of binary and ternary coefficients were strongly cross-correlated. By reducing the number of adjustable coefficients, it was possible to create a data set that was sufficient to describe the system while using a minimum number of coefficients.

The coefficient for the ternary interaction ζ(O₂-Na⁺-OH⁻) is not needed for the description of the system at 298.15 K. However, for the polythermal description of the system, this interaction cannot be neglected. Therefore, the coefficient was set to zero at 298.15 K.

The values of the Pitzer coefficients at T = 298.15 K correspond to the X₀ parameters in Eq. 10. Thus, in the following steps, the Pitzer coefficients valid at T = 298.15 K were used as boundary parameters for the fits of the temperature dependency parameters X₁ to X₅. It was found that only the first two parameters (X₁ and X₂) had to be adjusted to fully describe the temperature dependency of the O₂(aq) Pitzer coefficients. Thus, all other parameters (X₃, X₄ and X₅) are set to zero.

A simultaneous fit of the temperature equations parameters including all chemical systems was not possible. Therefore, temperature parameters for the systems of solutions of binary electrolytes were iteratively fitted individually and sequentially until none of the parameters changed. Figure 2 shows the fitting scheme for the generation of the Pitzer interaction coefficients temperature parameters. Thus, a consistent set of parameterized temperature equations of the Pitzer interaction coefficients could be deduced.

FIGURE 2

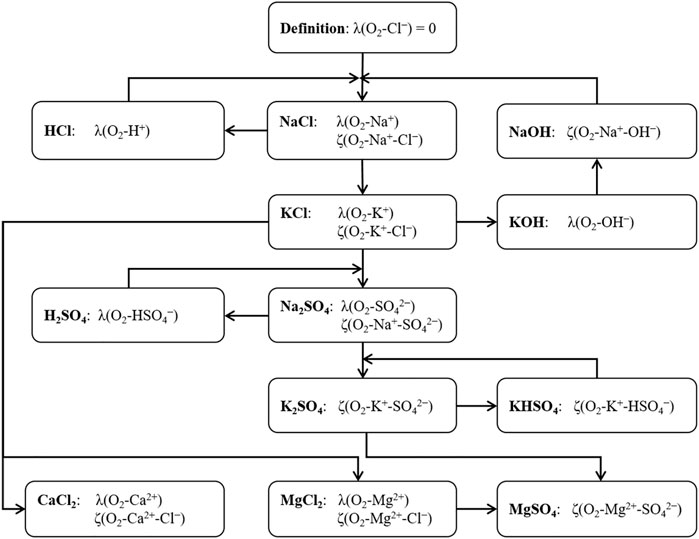
FIGURE 2. Fitting scheme for the generation of the Pitzer interaction coefficients temperature parameters.

The coefficient for the ternary interaction ζ(O₂-K⁺-HSO₄⁻) could not be retrieved at 298.15 K as there are no experimental data for this temperature. The only O₂ solubility data available for the alkali hydrosulfate (NaHSO₄ and KHSO₄) system were acquired at 310.2 K (Lang and Zander, 1986). The experimental data of the chemical system O₂-Na₂SO₄-H₂O could be described without a ternary interaction coefficient. For the description of the experimental data of the chemical system O₂-K₂SO₄-H₂O, however, a ternary interaction coefficient ζ(O₂-K⁺-HSO₄⁻) had to be introduced. To do so, the value for the ζ(O₂-K⁺-HSO₄⁻) coefficient was determined only in the context of the fits of the temperature parameters but had to be used as temperature independent one, since only experimental measured values for a single temperature are available. Verifying calculations including this coefficient in the fits of the 298.15 K data (X₀ parameter) showed that this coefficient has no influence on the previously determined systems—namely, O₂-K₂SO₄-H₂O.

For the chemical systems for which no O₂ solubility data are available at temperatures different from T = 298.15 K (carbonate system, phosphate system, ternary salt mixtures) no temperature parameters of the Pitzer coefficients could be obtained. Consequently, these Pitzer coefficients are valid at T = 298.15 K only and not included in Figure 2.

3 Data assessment

3.1 Literature review and data selection

The aim of this work was to create a thermodynamic data set to calculate the oxygen solubility in pure water as well as in solutions containing ions ubiquitous in nature: Na⁺, K⁺, Mg²⁺, Ca²⁺, Cl⁻, HSO₄⁻/SO₄²⁻, HCO₃⁻/CO₃²⁻, H₂PO₄⁻/HPO₄²⁻/PO₄³⁻.

IUPAC published two reviews by Battino et al. (1981) and Clever et al. (2014) on available solubility data of molecular oxygen in pure water as part of the Solubility Data Series. This data collection was used here as a basis to create a temperature function for the solubility of O₂. From these reviews, only solubility data within the temperature range from 273.15 up to 373.15 K with an oxygen partial pressure of 101.325 kPa were used. Solubility data at temperatures above 373.15 K were omitted as they are not the focus of the intended future usage of this data set. Moreover, due to the large scattering of the experimental data, using them significantly impaired the quality of the fitting results of the Henry’s law constant’s temperature equation at lower temperatures—specifically below 298.15 K.

For the O₂ solubility in salt solutions, the number of publications containing experimental data is quite limited. A critical data evaluation was performed using the following criteria:

• Completeness of experimental conditions given,

• For datasets of electrolyte solutions: Agreement of the O₂ solubility in the peripheral system (pure water at the given temperature) with accepted experimental values of the review workers of IUPAC or the calculated values from the temperature function of this work,

• Consistency in the order of magnitude and progression of the O₂ solubility decrease with increasing salt concentration between datasets from different sources,

• Total gas pressure up to 101.325 kPa (1 atm): experimental datasets derived at higher pressures were discarded,

• Temperature range: References with experimental O₂ solubility were ranked higher when they 1) provide data at T = 298.15 K and 2) provide data over a broader temperature range. This was done in order to create a data set with the highest possible applicability while maintaining consistency with the interaction coefficients valid at T = 298.15 K that were created in the first fitting step.

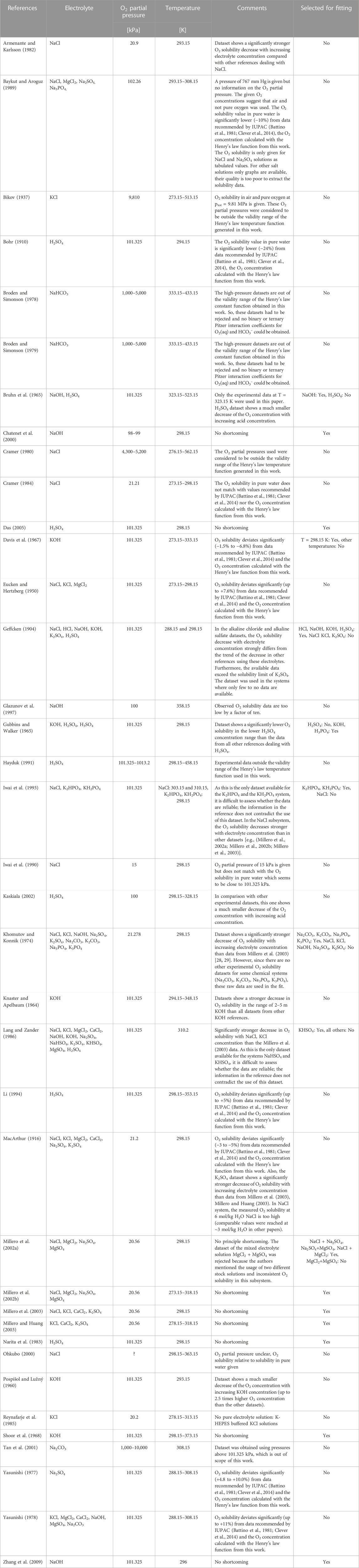
The literature review and data assessment on O₂ solubility in salt solutions is given in Table 1.

TABLE 1

TABLE 1. Literature review and data assessment on O₂ solubility in salt solutions.

4 Modelling results and discussion

4.1 Solubility of oxygen in pure water

The obtained temperature parameters for the logK_H,cp of the O₂ solubility in pure water are given in Table 2. The resulting temperature dependency equation describes the oxygen solubility in pure water very well (see Figure 3) while using only three of the six possible temperature terms.

TABLE 2

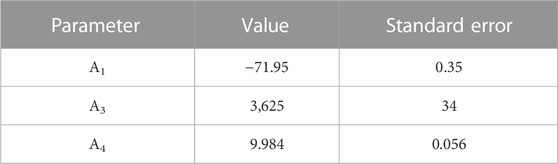
TABLE 2. Temperature parameters of the logarithmic Henry’s law constant (logK_H,cp) for the O₂ solubility in pure water, Eq. 8.

FIGURE 3

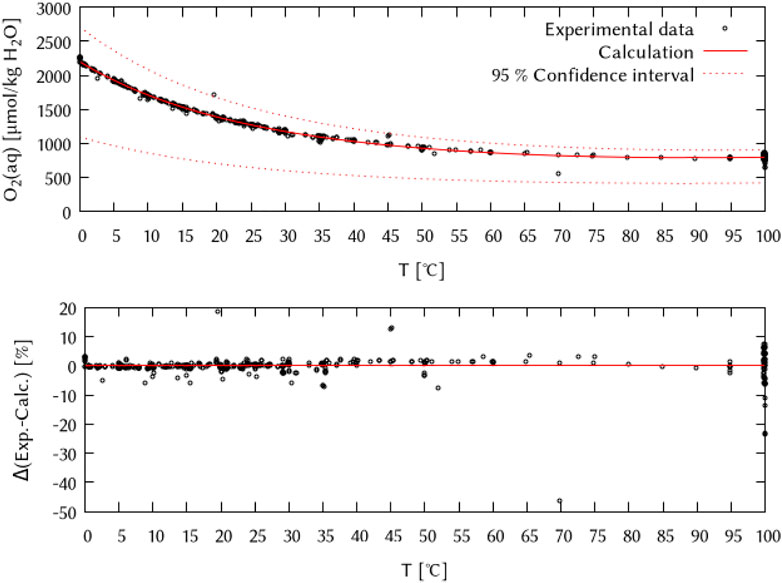
FIGURE 3. Temperature dependency of the logarithmic Henry’s law constant of the O₂ solubility in pure water (expressed in µmol/kg H₂O∙101.325 kPa). Points: experimental data from literature references given by IUPAC (Battino et al., 1981; Clever et al., 2014), solid line: calculation (this work), dashed line: 95% confidence interval.

Comparing the value at T = 298.15 K calculated with the obtained temperature function of Henry’s constant with values found in other thermodynamic databases shows very good agreement, see Table 3.

TABLE 3

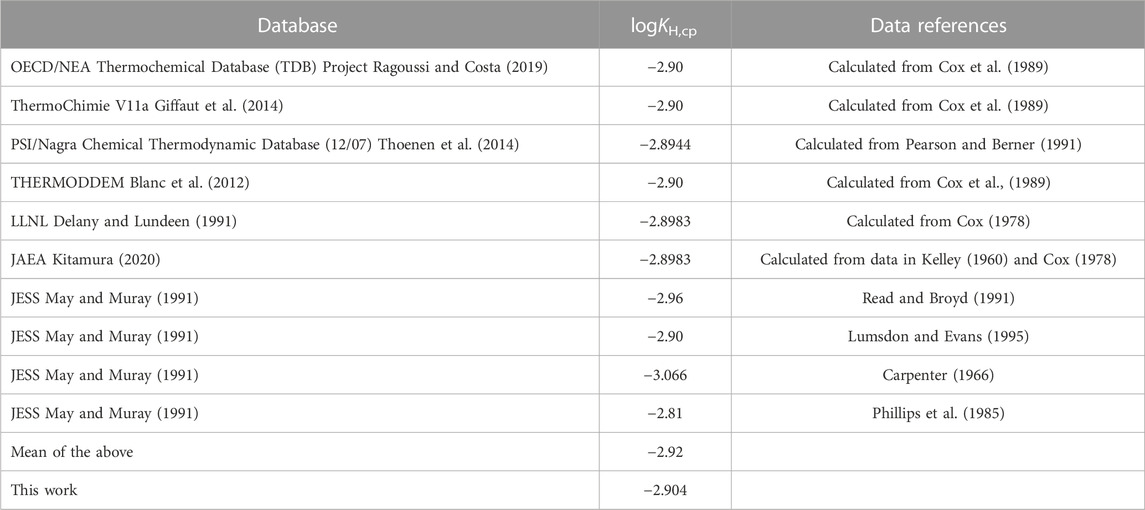
TABLE 3. Comparison of the logarithmic Henry’s law constant (logK_H,cp) for the O₂ solubility in pure water at T = 298.15 K used in different thermodynamic database projects and other sources.

4.2 Thermodynamic data for O₂(aq)

To create an internally consistent set of equilibrium constants for reactions (Eqs 4, 5) it is necessary to select thermodynamic data for H₂O(l), O₂(g) and H₂(g). The temperature function for the standard molar Gibbs enthalpy of formation is calculated with

${∆}_{\mathrm{f}}{G}_m^0\left(T\right)={∆}_{\mathrm{f}}{G}_{i,T=T_0}^0-S_m^0\left({T-T}_0\right)+{\displaystyle \underset{T_0}{\overset{T}{\int }}}{C}_{p,m}^0\left(T\right)\mathrm{d}T-T{\displaystyle \underset{T_0}{\overset{T}{\int }}}\frac{C_{p,m}^0\left(T\right)}{T}\mathrm{d}T(11)$

Within the frame of this chapter, we adopt the following general temperature function as extension of Eq. 8:

$f\left(T\right)=A_1+A_{2}T+\frac{A_3}{T}+A_4\ln T+\frac{A_5}{T^2}+A_6{T}^2+A_7{T}^3+A_{8}T\ln T(12)$

Application of this temperature function for $C_{p,m}^0\left(T\right)$, integration and rearrangement of Eq. 12 yields a general expression for the standard Gibbs energy of formation:

${∆}_{\mathrm{f}}{G}_m^0\left(T\right)=B_1+B_{2}T+\frac{B_3}{T}+B_4\ln T+\frac{B_5}{T^2}+B_6{T}^2+B_7{T}^3+B_{8}T\ln T(13)$

with

$B_1={∆}_{\mathrm{f}}{G}_{i,T=T_0}^0+S_m^0{T}_0-A_1{T}_0-\frac{A_2}{2}{T}_0^2-\frac{A_6}{3}{T}_0^3-A_3\left(\ln T_0-1\right)+\frac{A_5}{T_0}(14)$

$B_2=-S_{i,T=T_0}^0+A_1\left(1+\ln T_0\right)+A_2{T}_0+\frac{A_6}{2}{T}_0^2-\frac{A_3}{T_0}-\frac{A_5}{2T_0^2}(15)$

$B_3=-\frac{A_5}{2}(16)$

$B_4=A_3(17)$

$B_5=0(18)$

$B_6=-\frac{A_2}{2}(19)$

$B_7=-\frac{A_6}{6}(20)$

$B_8=-A_1(21)$

For the corresonding temperature function for O₂(aq) the compiled solubility data for oxygen in pure water (Table 2) were used. The equilibrium constant for reaction (Eq. 6) can be expressed as [index numbers of coefficients refer to the general function (Eq. 12)]

${\Delta }_{\mathrm{r}}{G}^0\left(T\right)\left(6\right)=-\mathrm{R}T\ln \left(10\right){\log }_{10}K\left(T\right)\left(6\right)=A_1+A_{2}T+A_{8}T\ln T(22)$

Using the corresponding parameters for O₂(g) the temperature function for the standard molar Gibbs enthalpy of formation is then calculated with

${∆}_{\mathrm{f}}{G}_{O_2\left(\mathrm{a}\mathrm{q}\right)}^0\left(T\right)={\Delta }_{\mathrm{r}}{G}^0\left(T\right)\left(6\right)+{∆}_{\mathrm{f}}{G}_{O_2\left(\mathrm{g}\right)}^0\left(T\right)(23)$

For the next step, we use the following relations, where all temperature parameters $A_i$ refer to the temperature function for ${\Delta }_{\mathrm{r}}{G}^0\left(T\right)\left(6\right)$ in the form of the general function (Eq. 12). For this specific case only $A_1,A_2,\mathrm{a}\mathrm{n}\mathrm{d}{A}_8$ are unlike zero.

${∆}_{\mathrm{r}}{H}^0\left(T\right)\left(6\right)=-T^2\frac{\partial }{\partial T}{\left(\frac{{\Delta }_{\mathrm{r}}{G}^0\left(T\right)\left(5\right)}{T}\right)}_p=A_1+\frac{2A_3}{T}-A_4\left(1-\ln T\right)+\frac{3A_5}{T^2}-A_6{T}^2-2A_7{T}^3-A_{8}T(24)$

${∆}_{\mathrm{r}}S\left(T\right)\left(6\right)=-\frac{\partial }{\partial T}{\left({\Delta }_{\mathrm{r}}{G}^0\left(T\right)\left(6\right)\right)}_p=-A_2+\frac{A_3}{T^2}-\frac{A_4}{T}+\frac{2A_5}{T^3}-2A_{6}T-3A_7{T}^2-A_8\left(1+\ln T\right)(25)$

${{\Delta }_{\mathrm{r}}C}_p^0\left(T\right)\left(6\right)=\frac{\partial }{\partial T}{\left({∆}_{\mathrm{r}}{H}^0\left(T\right)\left(6\right)\right)}_p=-\frac{{2A}_3}{T^2}+\frac{A_4}{T}-\frac{6A_5}{T^3}-2A_{6}T-6A_7{T}^2-A_8(26)$

One notes that the $T^{-3}$-term in Eq. 26 is not present in the standard T-function, Eq. 12. However, it is unequal to zero only if there is a $T^{-2}$-term in $\log K\left(T\right)$. This happens to be not the case in our proposal for $\log K\left(T\right)\left(6\right)$.

After evaluation for $T=T_0$ standard molar enthalpy of formation, standard entropy, and standard partial molal heat capacity of O₂(aq) is calculated using the relations:

${∆}_{\mathrm{f}}{H}_{O_2\left(\mathrm{a}\mathrm{q}\right),T=T_0}^0={∆}_{\mathrm{r}}{H}_{T=T_0}^0\left(6\right)(27)$

$S_{O_2\left(\mathrm{a}\mathrm{q}\right),T=T_0}^0={∆}_{\mathrm{r}}{S}_{T=T_0}^0\left(6\right)+S_{O_2\left(\mathrm{g}\right),T=T_0}^0(28)$

$C_{p,O_2\left(\mathrm{a}\mathrm{q}\right)}^0\left(T\right)={{\Delta }_{\mathrm{r}}C}_p^0\left(T\right)\left(6\right)+C_{p,O_2\left(\mathrm{g}\right)}^0\left(T\right)(29)$

with ${∆}_{\mathrm{f}}{H}_{{\mathrm{O}}_2\left(\mathrm{g}\right),T=T_0}^0=0$.

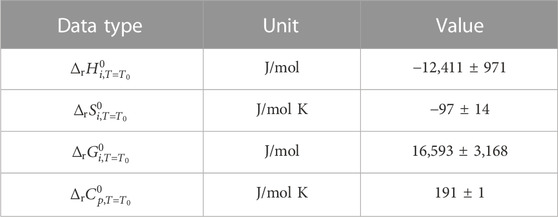
Selected and calculated thermodynamic data are summarized in Tables 4–6. Standard formation data were adopted from Cox et al. (1989); heat capacities between 280 and 500 K were adopted from Chase (1998). For liquid water ${∆}_{\mathrm{f}}{H}_{H_2\mathrm{O}\left(\mathrm{l}\right),T=T_0}^0$ and $S_{H_2\mathrm{O}\left(\mathrm{l}\right),T=T_0}^0$ are identical in both sources. Applying the temperature function for $C_{p,{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)}^0\left(T\right)$ as indicated in Table 5, a value of $C_{p,{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right),T=T_0}^0$ = 75.418 J/mol∙K could be obtained, which is in good agreement with $C_{p,{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right),T=T_0}^0$ = 75.351 ± 0.080 J/mol∙K from Cox et al. (1989) and Chase (1998). For gaseous oxygen Cox et al. (1989) lists $S_{O_2\left(\mathrm{g}\right),T=T_0}^0$ = 205.152 ± 0.005 J/mol·K which covers $S_{O_2\left(\mathrm{g}\right),T=T_0}^0$ = 205.147 J/mol·K given by Chase (1998). For gaseous oxygen, a value of $C_{p,{\mathrm{O}}_2\left(\mathrm{g}\right),T=T_0}^0$ = 29.376 J/K mol could be obtained, which exactly matches the value given by Chase (1998) and is in close agreement with $C_{p,{\mathrm{O}}_2\left(\mathrm{g}\right),T=T_0}^0$ = 29.378 ± 0.003 J/mol·K given in (Cox et al., 1989). For gaseous hydrogen Cox et al. (1989) and Chase (1998) list identical values for $S_{H_2\left(\mathrm{g}\right),T=T_0}^0$ and $C_{p,{\mathrm{H}}_2\left(\mathrm{g}\right),T=T_0}^0$.

TABLE 4

TABLE 4. Standard reaction data for O₂(aq).

TABLE 5

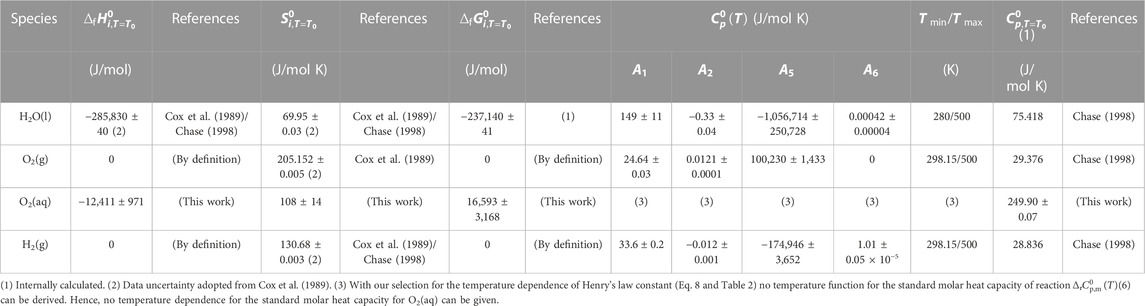
TABLE 5. Standard formation data for H₂O(l), O₂(g), H₂(g), and O₂(aq). Temperature parameters for ${\mathit{C}}_{\mathit{p}}^{\mathit{0}}\left(\mathit{T}\right)$ with regard to the general function (Eq. 12) were fitted to values from Chase (1998).

TABLE 6

TABLE 6. Temperature parameters for logK(T) for E_H reaction (Eqs 4, 5) according to Eq. 8.

Uncertainties for standard formation data for O₂(g), H₂(g), and H₂O(l) were adopted from Cox et al. (1989). Uncertainties for standard reaction and standard formation data for O₂(aq) were calculated from the error of the temperature parameters for reaction (Eq. 6) in Table 2.

The obtained values are in good agreement with ${∆}_{\mathrm{f}}{H}_{O_2\left(\mathrm{a}\mathrm{q}\right),T=T_0}^0$ = −12,134 J/mol and $S_{O_2\left(\mathrm{a}\mathrm{q}\right),T=T_0}^0$ = 109 J/mol·K as given by Shock et al. (1989). A significant difference remains for the standard partial molal heat capacity for O₂(aq) at 298.15 K which is given in the same source as $C_{p,T=T_0}^0=234$ J/mol·K. A reason for this is probably that Shock et al. in their work evaluated experimental data by Benson et al. (1979) and Stephan et al. (1956) only. Finally, with

${∆}_{\mathrm{r}}{G}_m^0\left(T\right)={\displaystyle \sum _i}{\upsilon }_i{∆}_{\mathrm{f}}{G}_i^0\left(T\right)(30)$

${∆}_{\mathrm{r}}{G}_m^0\left(T\right)=-\mathrm{R}T\ln \left(10\right){\log }_{10}K\left(T\right)(31)$

it was possible to calculate the temperature functions for $\log K\left(T\right)$ for reaction (Eqs 4, 5) by rearrangement of Eq. 31 and summation of corresponding temperature parameters for ${∆}_{\mathrm{f}}{G}_i^0\left(T\right)$. Table 6 summarizes the results.

The valid range of temperature for reaction (Eq. 4) [formation of O₂(g)] is determined by the available heat capacity data for H₂O(l). For reaction (Eq. 5) [formation of O₂(aq)] it is limited by the availability of solubility data. Note, that for the latter reaction the given validity range is valid for low saline solutions only. In saline solutions where Pitzer coefficients are applied and the geochemical code works with a half-cell reaction involving O₂(aq), the valid temperature range can be lower and depends on the particular system, see Section 4.5.

Using the temperature parameters in Table 6 the so-called “temperature grid” for “logK for E_H-reaction” for codes like EQ3/6 was re-calculated. The results are given in Table 7. The range of temperature for which our parameters should be used is in fact narrower than is suggested in some data files for EQ3/6 or Geochemist’s Workbench.

TABLE 7

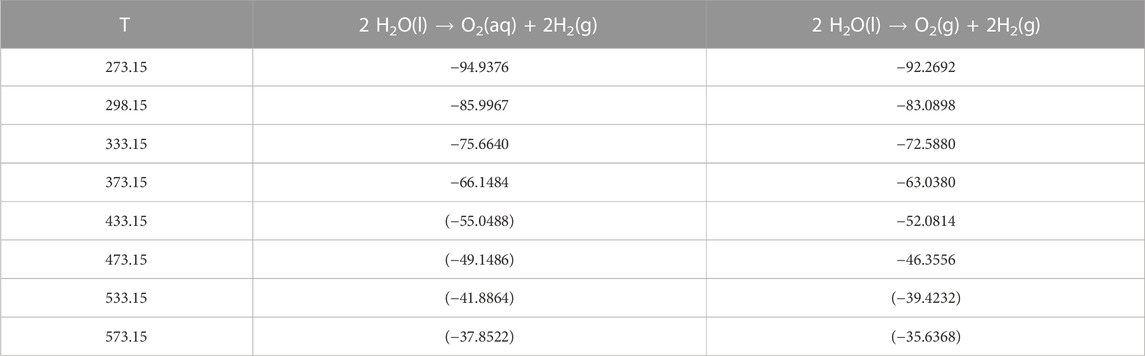
TABLE 7. Calculated equilibrium constants for E_H reactions (Eqs 4, 5) as a function of temperature. Values in brackets are beyond the recommended range of validity.

Not surprisingly, equilibrium constants given in Table 7 are similar to those currently available in data files for geochemical codes. The values given in this work, however, can be traced back to published standard formation and solubility data.

4.3 Solubility of oxygen in electrolyte solutions at T = 298.15 K

4.3.1 The system Na⁺, K⁺, H⁺/Cl⁻, OH⁻ - H₂O(l)

All binary mixtures of the chemical systems Na⁺, K⁺, H⁺/Cl⁻, OH⁻ - H₂O(l) were fitted simultaneously to obtain the Pitzer coefficients. As an initial coefficient λ(O₂(aq)-Cl⁻) was set to zero. Binary interaction coefficients (λ) for all cations and anions in the system could be obtained. During parameter reduction, it was found that only the ternary interaction coefficients ζ(O₂(aq)-Na⁺-Cl⁻) and ζ(O₂(aq)-K⁺-Cl⁻) are necessary to describe the system (Figure 4). Later fits of the temperature dependence parameters showed that a ternary ζ(O₂(aq)-Na⁺-OH⁻) coefficient becomes necessary at higher temperatures. At T = 298.15 K this coefficient was set to 0.

FIGURE 4

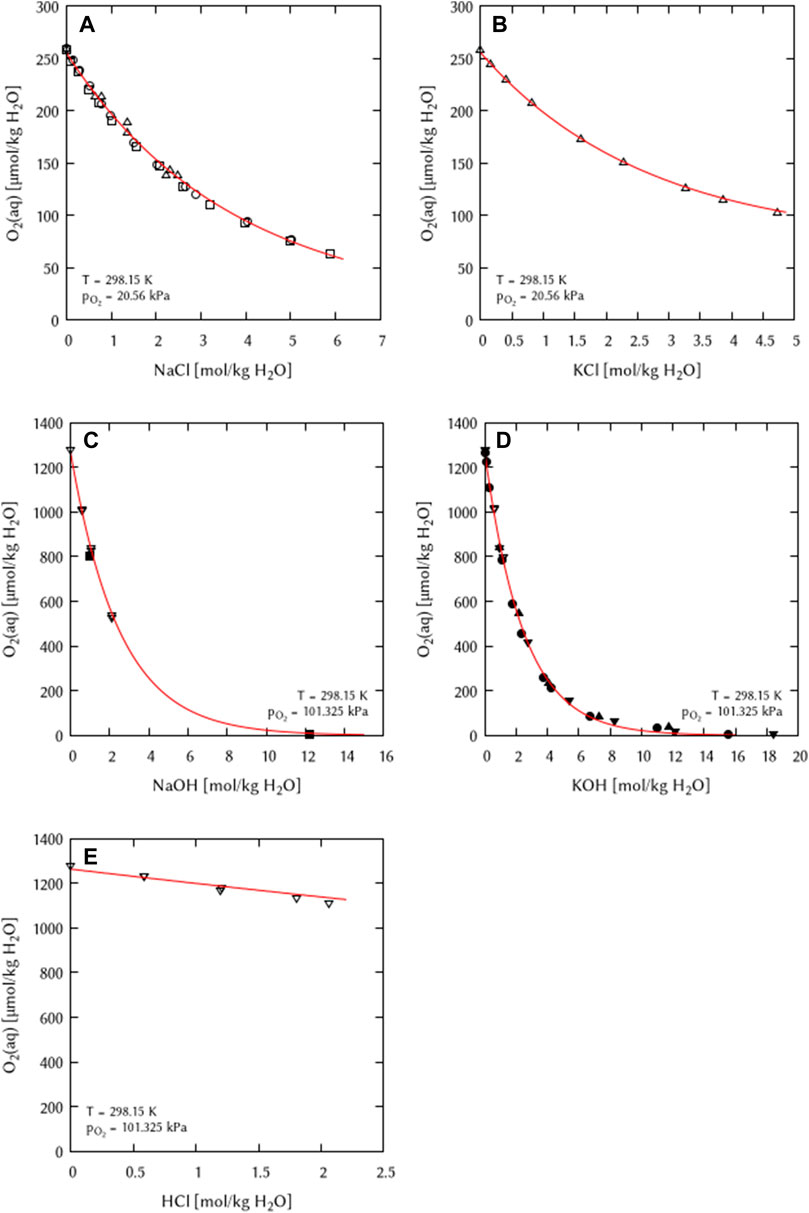
FIGURE 4. Modelling of the O₂ solubility in binary solutions of (A) NaCl, (B) KCl, (C) NaOH, (D) KOH, and (E) HCl as a function of the electrolyte concentration at T = 298.15 K (Points: Experimental data from: □ Millero et al. (2002a), ○ Millero et al. (2002b), ▵ Millero et al. (2003), ▿ Geffcken (1904), ■ Chatenet et al. (2000), ● Davis et al. (1967), ▴ Gubbins and Walker (1965), ▾ Shoor et al. (1968), Lines: this work).

4.3.2 The system Na⁺, K⁺, H⁺/HSO₄⁻, SO₄²⁻ - H₂O(l)

The obtained binary interaction coefficients (λ) were used as initial values for the simultaneous fitting of the binary mixtures of the system Na⁺, K⁺, H⁺/HSO₄⁻, SO₄²⁻ - H₂O(l). The full set of binary [λ(O₂(aq)-HSO₄⁻) and λ(O₂(aq)-SO₄²⁻)] and ternary interaction coefficients [ζ(O₂(aq)-Na⁺- SO₄²⁻) and ζ(O₂(aq)-K⁺- SO₄²⁻)] was found do be necessary for a full description of the system (Figure 5).

FIGURE 5

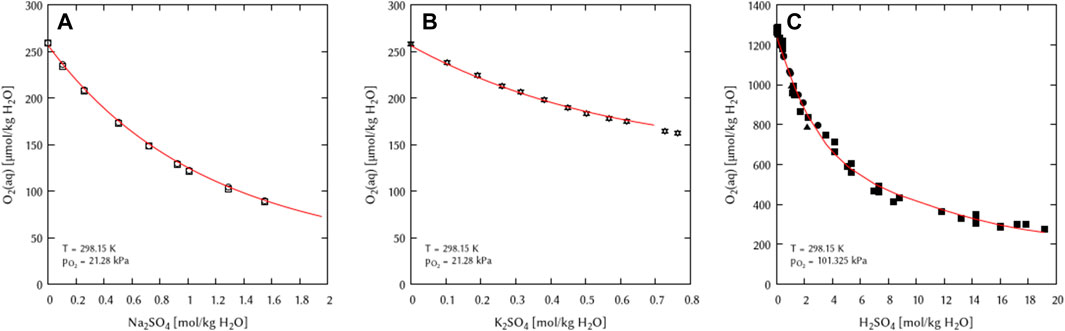
FIGURE 5. Modelling of the O₂ solubility in binary solutions of (A) Na₂SO₄, (B) K₂SO₄, and (C) H₂SO₄ as a function of the electrolyte concentration at T = 298.15 K (Points: Experimental data from: □ Millero et al. (2002a), ○ Millero et al. (2002b), ▵ Millero et al. (2003), ▿ Millero and Huang (2003), ■ Das (2005), ● Geffcken (1904), ▴ Narita et al. (1983), Lines: this work).

For the solubility of oxygen in NaHSO₄ or KHSO₄ solutions, there are no data at T = 298.15 K available in literature. Thus, the ζ(O₂(aq)-K⁺-HSO₄⁻) value was not fitted from data at 298.15 K but from the only available data at 310.2 K from Lang and Zander (1986). The value was derived from a fitting using the polythermal data set (see Section 4.4). Since no temperature dependency could be retrieved, the ζ(O₂(aq)-K⁺-HSO₄⁻) value was set temperature independent. Therefore, the obtained value must be set to the 298.15 K term (A₀) in Eq. 10. The implementation of the ζ(O₂(aq)-K⁺-HSO₄⁻) coefficient had no influence of the fitting of the ζ(O₂(aq)-K⁺-SO₄⁻) coefficient, which was counterchecked. No value had to be fitted for ζ(O₂(aq)-Na⁺-HSO₄⁻) in NaHSO₄ solutions because the dataset derived in this work was already sufficient to describe the oxygen solubility in this solution without another ternary interaction coefficient (see Section 4.4.2).

4.3.3 The system Na⁺, K⁺/CO₃²⁻ - H₂O(l)

The previously obtained binary interaction coefficients (λ) were used as boundary conditions for the simultaneously fitting of the binary mixtures of the system Na⁺,K⁺/CO₃²⁻ - H₂O(l). A binary [λ(O₂-CO₃²⁻)] as well as two ternary interaction coefficients [ζ(O₂(aq)-Na⁺-CO₃²⁻) and ζ(O₂(aq)-K⁺-CO₃²⁻)] are required to describe the two systems (Figure 6).

FIGURE 6

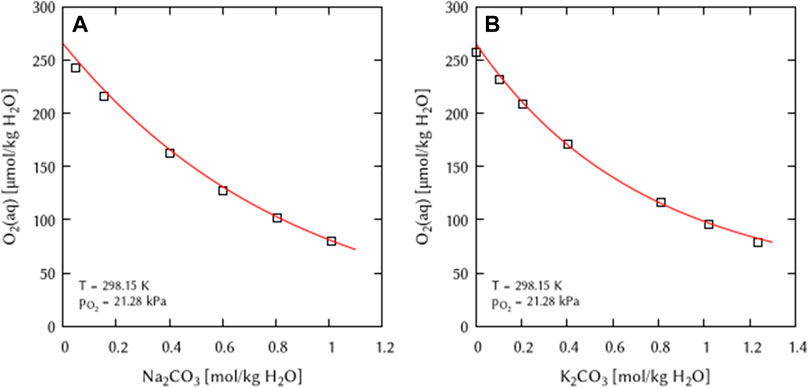
FIGURE 6. Modelling of the O₂ solubility in binary solutions of (A) Na₂CO₃, and (B) K₂CO₃ as a function of the electrolyte concentration at T = 298.15 K (Points: Experimental data from □ Khomutov and Konnik (1974), Lines: this work).

4.3.4 The system Na⁺, K⁺, H⁺/H₃PO₄, H₂PO₄⁻, HPO₄²⁻, PO₄³⁻ - H₂O(l)

The O₂ solubility in solutions of Na₃PO₄, K₃PO₄, K₂HPO₄, KH₂PO₄, and H₃PO₄ were fitted simultaneously to obtain the interaction coefficients. For the System O₂-K₃PO₄ it was found that no ternary interaction coefficient ζ(O₂(aq)-K⁺-PO₄³⁻) is necessary to describe the experimental data while a ζ(O₂(aq)-Na⁺-PO₄³⁻) was required for the System O₂-Na₃PO₄. Also for the acidic potassium phosphate solutions (KH₂PO₄ and K₂HPO₄) as well as for phosphoric acid solutions, ternary interaction coefficients were found to be indispensable to fully describe these systems (Figure 7). No experimental O₂ solubility data were available for the acidic sodium phosphate solutions (NaH₂PO₄ and Na₂HPO₄). Therefore, it cannot be specified whether or not ternary interaction coefficients are necessary in these subsystems.

FIGURE 7

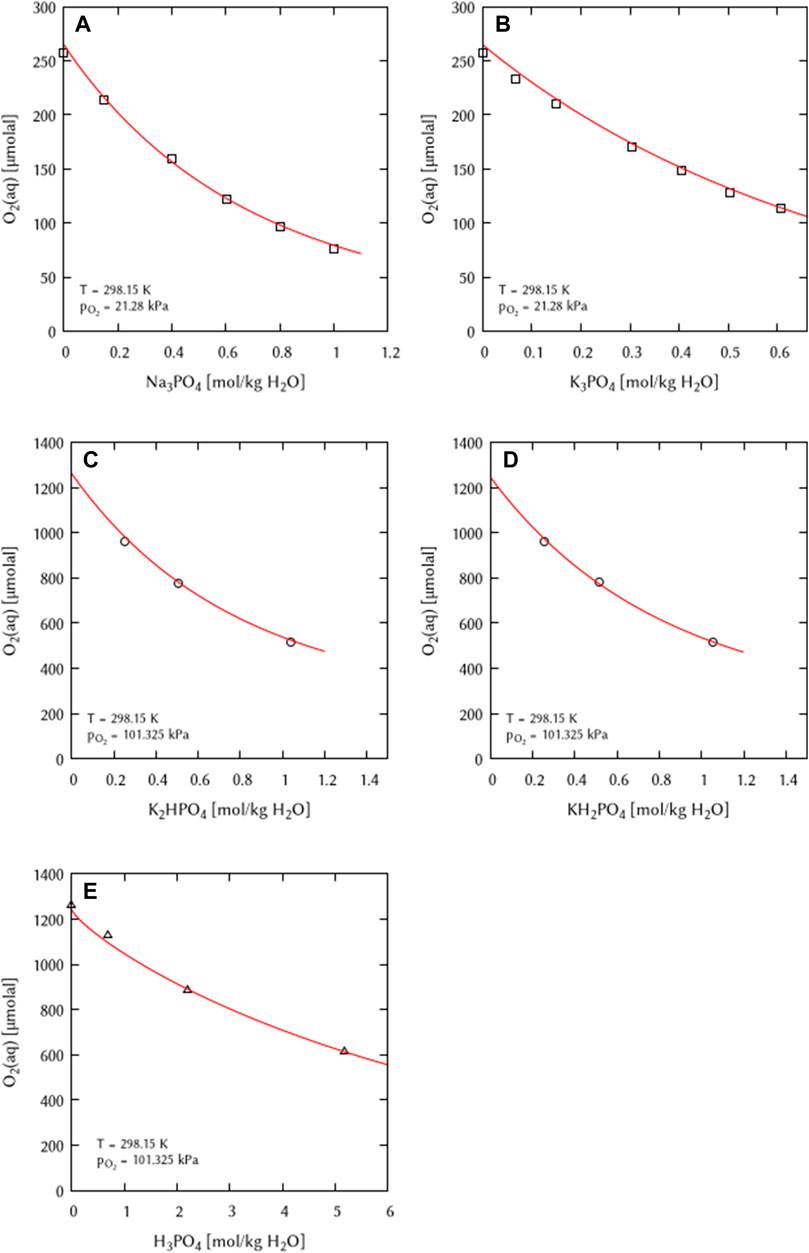
FIGURE 7. Modelling of the O₂ solubility in binary solutions of (A) Na₃PO₄, (B) K₃PO₄, (C) K₂HPO₄, (D) KH₂PO₄, and (E) H₃PO₄ as a function of electrolyte concentration at T = 298.15 K (Points: Experimental data from □ Khomutov and Konnik (1974), ○ Iwai et al. (1993), ▵ Gubbins and Walker (1965), Lines: this work).

4.3.5 Earth alkaline salt solutions (CaCl₂, MgCl₂, MgSO₄)

Using the previously determined Pitzer coefficients as boundary conditions, the interaction coefficients for Earth alkaline salts and mixtures of salt solutions were deduced. For all three systems, a binary as well as a ternary interaction coefficient was necessary for a complete description (Figure 8).

FIGURE 8

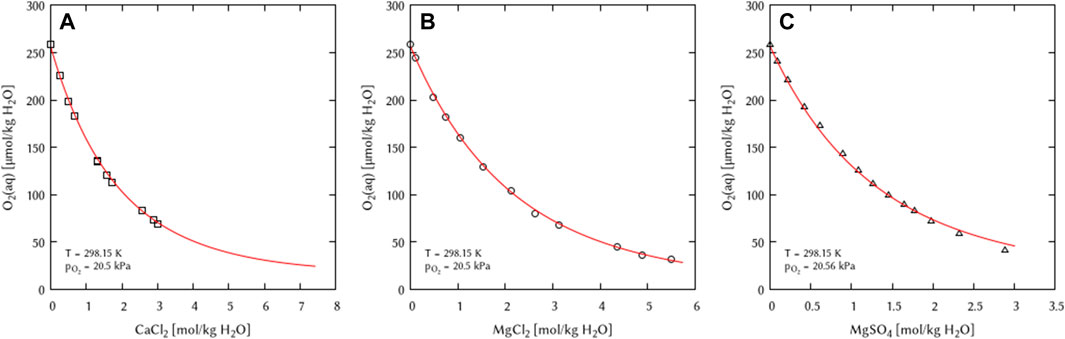
FIGURE 8. Modelling of the O₂ solubility in binary solutions of (A) CaCl₂, (B) MgCl₂, and (C) MgSO₄ as a function of electrolyte concentration at T = 298.15 K (Points: Experimental data from □ Millero et al. (2003), ○ Millero et al. (2002a), ▵ Millero et al. (2002b) Lines: this work).

4.3.6 Interaction coefficients for ternary salt solutions

The O₂ solubility data in ternary solutions of NaCl + MgCl₂ and NaCl + Na₂SO₄ was used to deduce the coefficients η(O₂(aq)-Na⁺-Mg²⁺) and η(O₂(aq)-Cl⁻-SO₄²⁻). The O₂ solubility data in the ternary solution of Na₂SO₄ + MgSO₄ was not used in the fitting procedure but to verify the obtained η coefficient (Figure 9). The obtained calculation results are in good agreement with the experimental data. The O₂ solubility data in the ternary solution of MgCl₂ + MgSO₄ was also not used in the fitting, the authors claimed the usage of two different stock solutions within the experiment (Millero et al., 2002a). Only one data point matches with the calculation suggesting that—in agreement with the primary source—this point belonged to one charge of stock solutions while the other points belong to the experiments with other stock solutions.

FIGURE 9

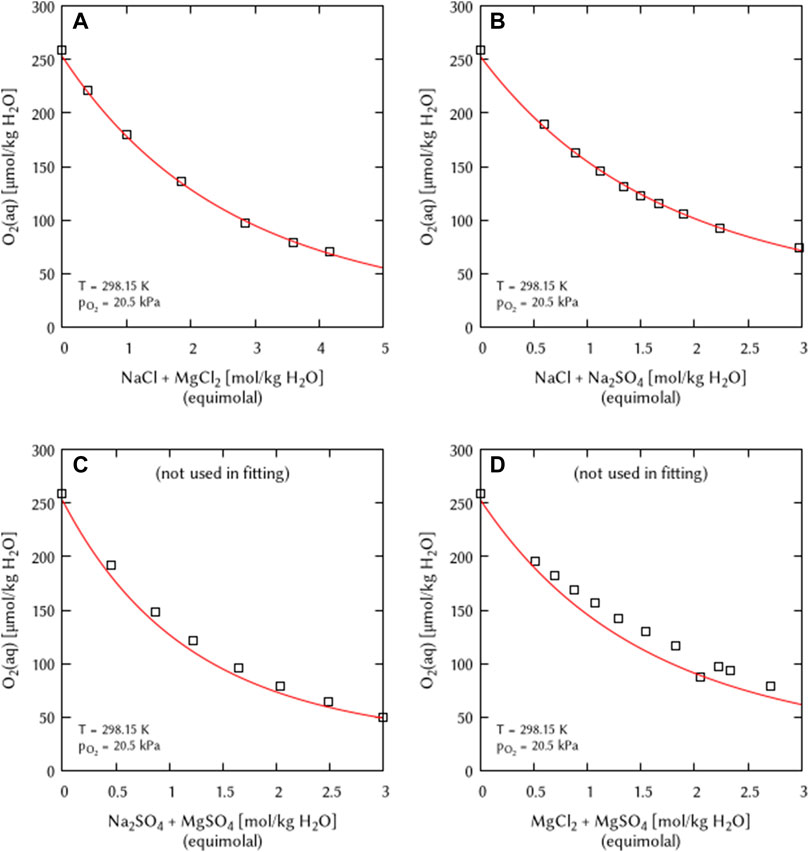
FIGURE 9. Modelling of the O₂ solubility in equimolal solutions of (A) NaCl + MgCl₂, (B) NaCl + Na₂SO₄, (C) Na₂SO₄+MgSO₄, and (D) MgCl₂ + MgSO₄ as a function of electrolyte concentration at T = 298.15 K (Points: Experimental data from □ Millero et al. (2002a), Lines: this work).

Millero et al. (2002a) also experimentally studied O₂ solubility in the quaternary-reciprocal systems Na⁺, Mg²⁺/Cl⁻, SO₄²⁻ - H₂O were given. Interaction coefficients for these kind of systems could not be deduced because the Pitzer ion-interaction approach is limited to coefficients for ternary interactions while in this case a coefficient would be necessary for an interaction between four different species (O₂-c-a-a’/O₂-c-c’-a) in solution.

The obtained Pitzer interaction coefficients—ion-neutral species pairs, λ and ion-neutral species triplets, ζ and η—are given in Table 8.

TABLE 8

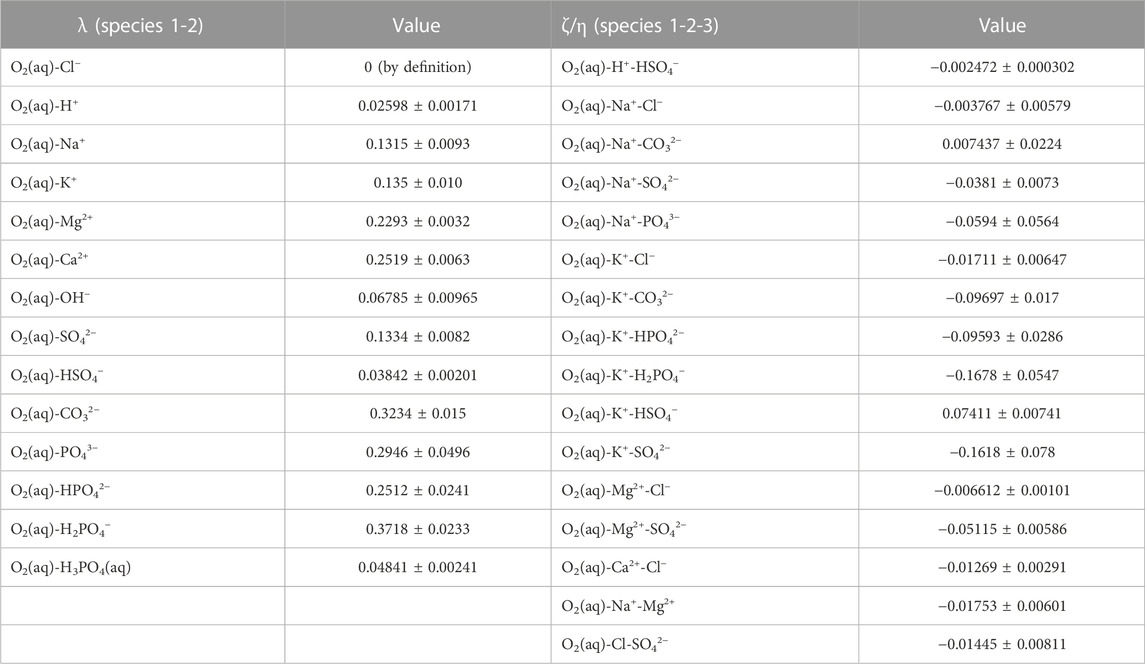
TABLE 8. Binary and ternary ion-neutral species interaction coefficients (λ, ζ, η) for the solubility of O₂ in salt solutions at T = 298.15 K. The uncertainty information refers to one standard deviation.

4.4 Temperature dependency of O₂ solubility in salt solutions

For the polythermal description of O₂ solubility in electrolyte solutions, the Pitzer interaction coefficients valid for 298.15 K were used as a boundary condition for fitting of the temperature parameters for Eq. 10 on top of them. These parameter fittings were run individually for each electrolyte and then iterated until no changes were observed anymore.

4.4.1 The system Na⁺, K⁺, H⁺/Cl⁻, OH⁻ - H₂O(l)

The binary systems of the alkali metal chlorides, alkali metal hydroxides and hydrochloric acid allowed to determine the temperature dependency for two binary interaction coefficients: λ(O₂(aq)-Na⁺), λ(O₂(aq)-K⁺), and λ(O₂(aq)-H⁺) as well as for two ternary coefficients ζ(O₂(aq)-Na⁺-Cl⁻) and ζ(O₂(aq)-K⁺-Cl⁻) (see Figures 10, 11). For each coefficient, the temperature dependency can be described using only two of the six parameters of Eq. 10, which are the $X_1\left(1/T-1/T_r\right)$ and the $X_2\ln \left(T/T_r\right)$ terms.

FIGURE 10

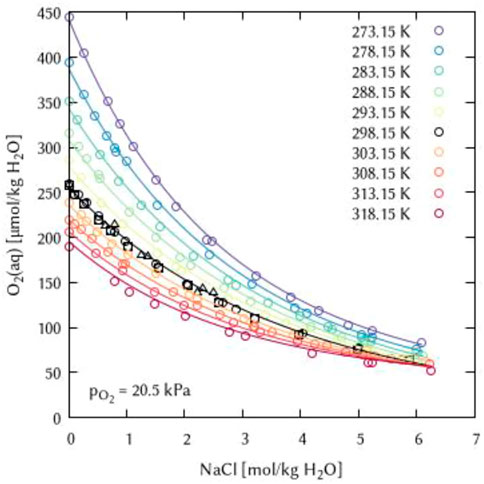
FIGURE 10. Modelling of the O₂ solubility in sodium chloride solution as a function of temperature and NaCl concentration. (Points: Experimental data from □ Millero et al. (2002a), ○ Millero et al. (2002b), ▵ Millero et al. (2003), Lines: this work).

FIGURE 11

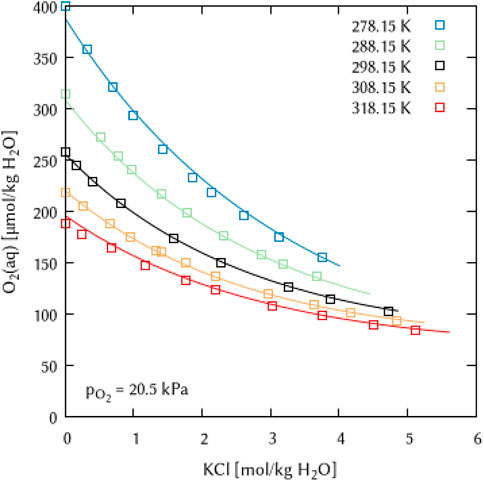
FIGURE 11. Modelling of the O₂ solubility in potassium chloride solution as a function of temperature and KCl concentration. (Points: Experimental data from □ Millero et al. (2003), Lines: this work).

For the ternary coefficient ζ(O₂(aq)-Na⁺-OH⁻) with a value of 0 at T = 298.15 K, only the first parameter of the temperature dependency equation was found to be necessary to adequately describe the experimental points available (Figure 12).

FIGURE 12

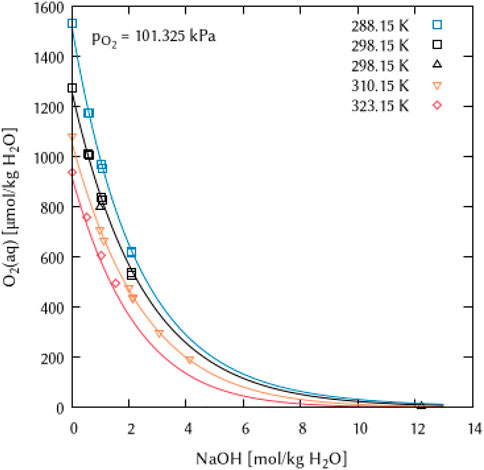
FIGURE 12. Modelling of the O₂ solubility in sodium hydroxide solution as a function of temperature and NaOH concentration. (Points: Experimental data from □ Geffcken (1904), ▵ Chatenet et al. (2000), ▿ Lang and Zander (1986) and ⬦ Bruhn et al. (1965), Lines: this work).

Even though the few available experimental points on O₂ solubility at higher KOH concentrations and raised temperatures (T = 353.15–373.15 K) are not well reproduced in terms of the expected trend of temperature dependence (Figure 13), the introduction of another ternary coefficient ζ(O₂(aq)-K⁺-OH⁻) or temperature dependence parameters thereof did not lead to any improvement. Furthermore, it can be assumed that the deviation of the calculation from the expected trend (lowering the O₂ solubility with increasing temperature) in this concentration and temperature range is lower than the experimental uncertainty to be expected.

FIGURE 13

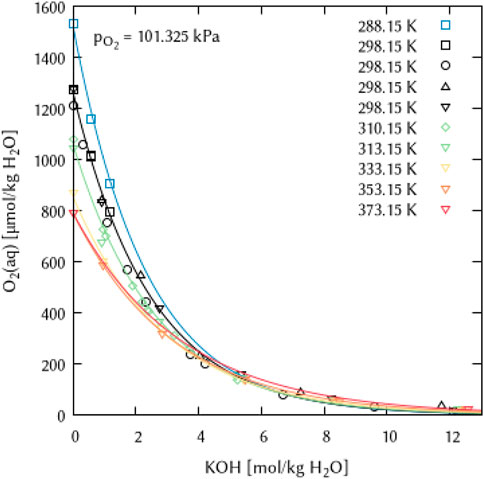
FIGURE 13. Modelling of the O₂ solubility in potassium hydroxide solution as a function of temperature and KOH concentration. (Points: Experimental data from □ Geffcken (1904), ○ Davis et al. (1967), ▵ Gubbins and Walker (1965), ▿ Shoor et al. (1968) and ⬦ Lang and Zander (1986), Lines: this work).

For solutions of hydrochloric acid, even in the polythermal system, no ternary interaction coefficient and thus no temperature parameters were necessary to describe the very few points on O₂ solubility as a function of temperature and electrolyte concentration (Figure 14).

FIGURE 14

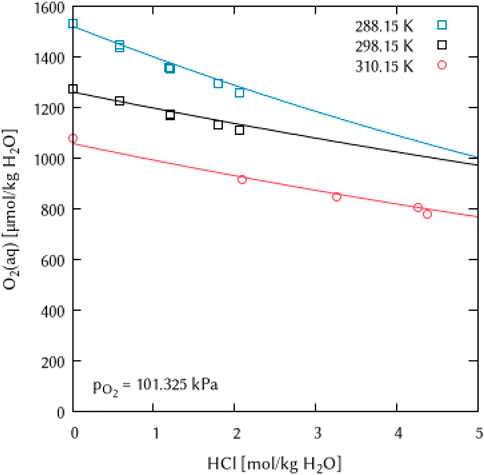
FIGURE 14. Modelling of the O₂ solubility in hydrochloric acid solution as a function of temperature and HCl concentration. (Points: Experimental data from □ Geffcken (1904) and ○ Lang and Zander (1986), Lines: this work).

4.4.2 The system Na⁺, K⁺, H⁺/HSO₄⁻, SO₄²⁻ - H₂O(l)

In the systems of alkali metal sulfate and sulfuric acid solutions, it was possible to obtain parameters describing the temperature dependence of the Pitzer interaction coefficients. Again, the fitting of a maximum of two terms was sufficient to describe the available data points for the Na₂SO₄ and H₂SO₄ systems (Figures 15, 16).

FIGURE 15

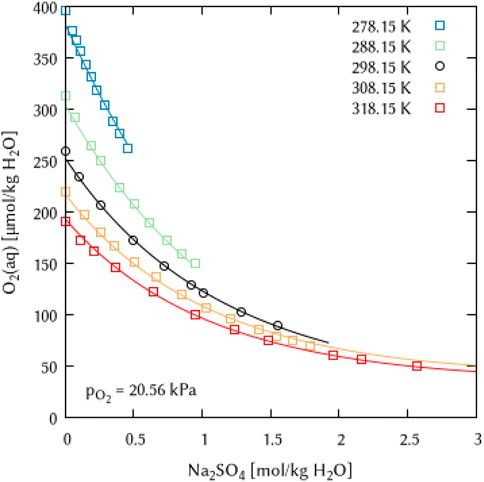
FIGURE 15. Modelling of the O₂ solubility in sodium sulfate solution as a function of temperature and Na₂SO₄ concentration. (Points: Experimental data from ○ Millero et al. (2002a) and □ Millero et al. (2002b), Lines: this work).

FIGURE 16

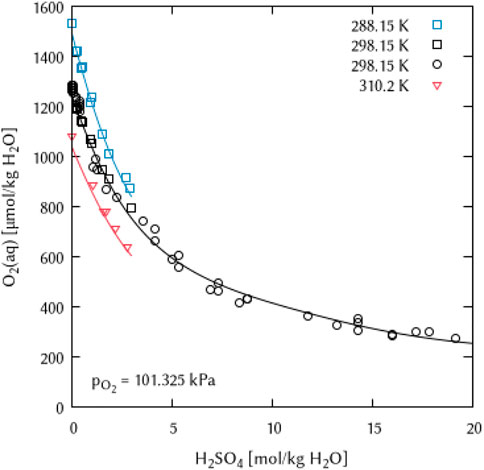
FIGURE 16. Modelling of the O₂ solubility in sulfuric acid solution as a function of temperature and H₂SO₄ concentration. (Points: Experimental data from □ Geffcken (1904), ○ Das (2005) and ▿ Lang and Zander (1986), Lines: this work).

In the K₂SO₄ solutions, O₂ solubility is poorly described at both very low (278.15 K) and very high (318.15 K) temperatures, yielding too high values with increasing electrolyte concentration (Figure 17) in both cases. Since the temperature dependence equation of the Pitzer interaction coefficients in the geochemical codes centers around the value of 298.15 K (see Eq. 10), these effects cannot be compensated, as a fit improvement in the temperature range above 298.15 K causes a corresponding deterioration below 298.15 K and vice versa.

FIGURE 17

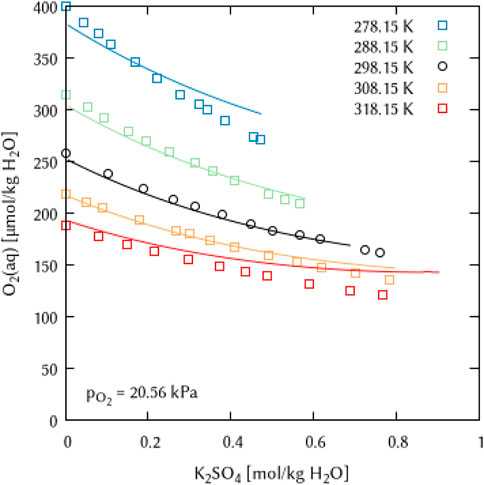
FIGURE 17. Modelling of the O₂ solubility in potassium sulfate solution as a function of temperature and K₂SO₄ concentration. (Points: Experimental data from ○ Millero et al. (2003) and □ Millero and Huang (2003), Lines: this work).

The systems Na⁺/HSO₄⁻ - H₂O(l) and K⁺/HSO₄⁻ - H₂O(l) could not be used for the estimation of the ternary interaction coefficients ζ(O₂(aq)-Na⁺-HSO₄⁻) or ζ(O₂(aq)-K⁺-HSO₄⁻) because of the lack of O₂ solubility data at 298.15 K. The only available experimental datasets are at 310.2 K generated by Lang and Zander (1986). Thus, it is not possible to obtain a ζ coefficient at 298.15 K that is necessary for the fitting with the temperature dependency equation used in this study. The systems Na⁺/HSO₄⁻ - H₂O(l) and K⁺/HSO₄⁻ - H₂O(l) were modelled using the obtained dataset. Results indicate that no ternary interaction coefficient ζ(O₂(aq)-Na⁺-HSO₄⁻) is necessary to describe the O₂ solubility data in the system Na⁺/HSO₄⁻ - H₂O(l) (see Figure 18).

FIGURE 18

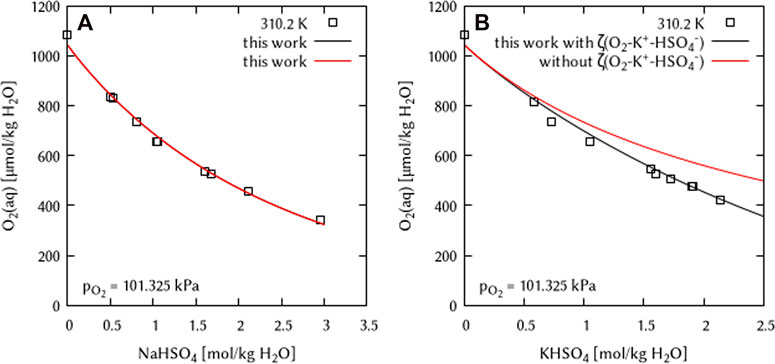
FIGURE 18. Modelling of the O₂ solubility in binary solutions of (A) NaHSO₄, and (B) KHSO₄ as a function of electrolyte concentration at 310.2 K using the Pitzer coefficient set of this work. [Points: Experimental data from □ Lang and Zander (1986), Lines: this work].

Modelling results for the chemical system K⁺/HSO₄⁻ - H₂O(l) without an ternary interaction coefficient show a discrepancy between the experimental results from Lang and Zander (1986) and the modelling. Thus, a ternary interaction coefficient ζ(O₂(aq)-K⁺-HSO₄⁻) was fitted at T = 310.2 K. Due to the lack of solubility data at other temperatures, no parameters for the temperature function could be derived. Therefore, this ternary coefficient was assumed to be temperature independent.

4.4.3 Earth alkaline salt solutions (CaCl₂, MgCl₂, MgSO₄)

The binary systems of the alkaline Earth metal salts CaCl₂, MgCl₂ and MgSO₄ were used to derive the temperature dependency parameters for the binary interaction coefficients λ(O₂(aq)-Ca²⁺) and λ(O₂(aq)-Mg²⁺) as well as for the ternary coefficients ζ(O₂(aq)-Ca²⁺-Cl⁻), ζ(O₂(aq)-Mg²⁺-Cl⁻) and ζ(O₂(aq)-Mg²⁺-SO₄²⁻), see Figures 19–21. For the magnesium salt solutions, the temperature dependency of the interaction coefficients requires two parameters [$X_1\left(1/T-1/T_r\right)$ and $X_2\ln \left(T/T_r\right)$] while for the calcium chloride solution, the $X_1\left(1/T-1/T_r\right)$ temperature parameter alone was sufficient for the complete description of the system.

FIGURE 19

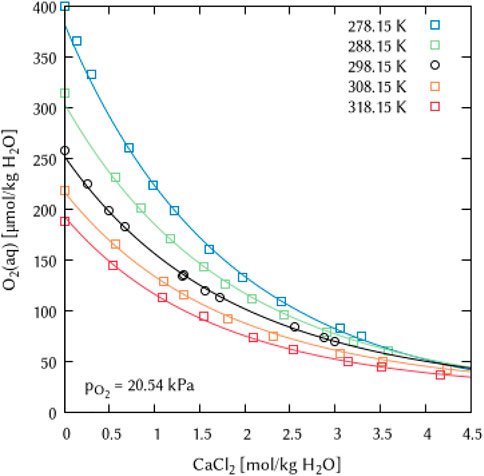
FIGURE 19. Modelling of the O₂ solubility in calcium chloride solution as a function of temperature and CaCl₂ concentration. [Points: Experimental data from ○ Millero et al. (2003) and □ Millero and Huang (2003), Lines: this work].

FIGURE 20

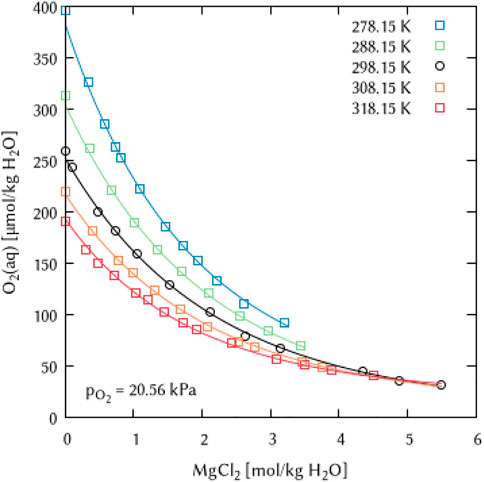
FIGURE 20. Modelling of the O₂ solubility in magnesium chloride solution as a function of temperature and MgCl₂ concentration. [Points: Experimental data from ○ Millero et al. (2002a) and □ Millero et al. (2002b), Lines: this work].

FIGURE 21

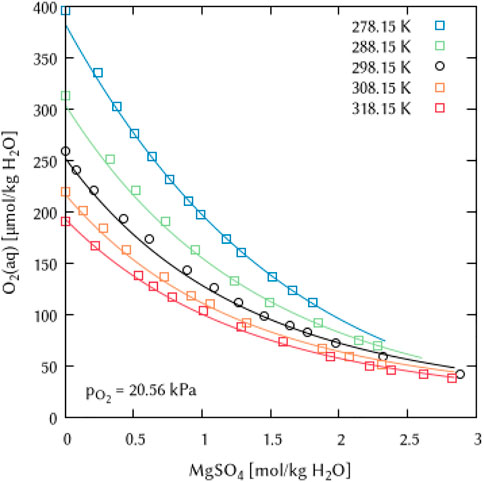
FIGURE 21. Modelling of the O₂ solubility in magnesium sulfate solution as a function of temperature and MgSO₄ concentration. [Points: Experimental data from ○ Millero et al. (2002a) and □ Millero et al. (2002b), Lines: this work].

The full list of obtained temperature parameters for the polythermal Pitzer interaction coefficients is given in Table 9.

TABLE 9

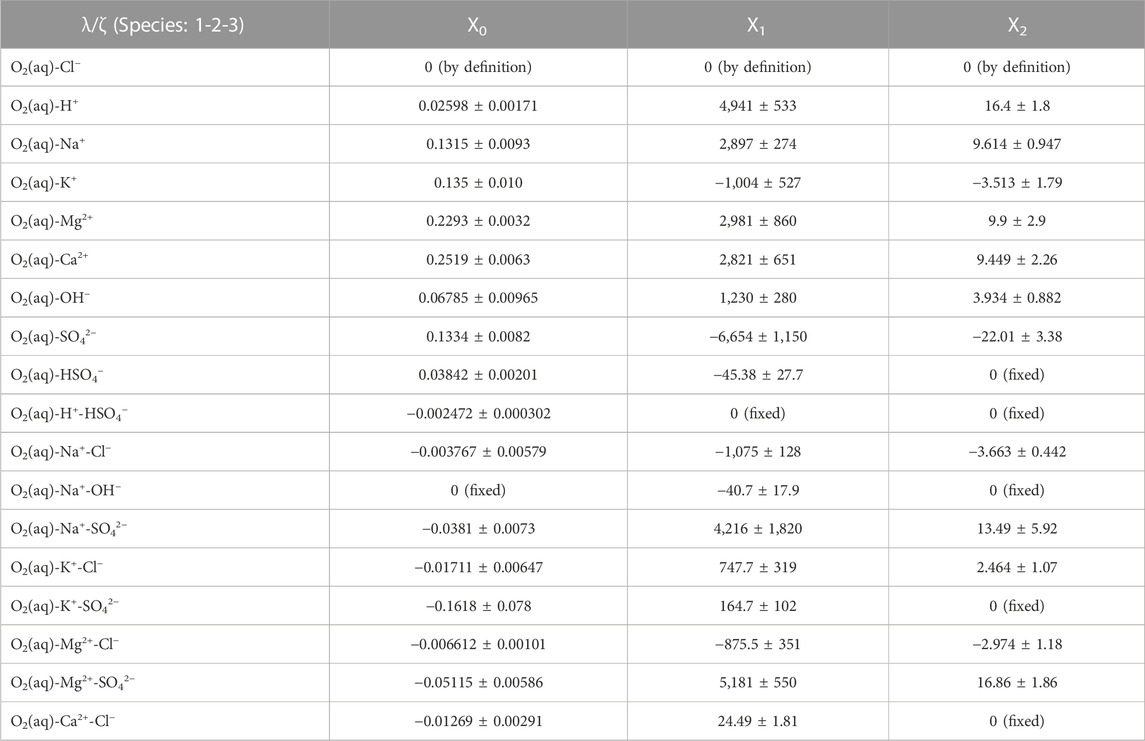
TABLE 9. Parameters for the temperature dependency function of the binary and ternary interaction coefficients (λ, ζ). The uncertainty information refers to one standard deviation.

For the carbonate, the phosphate, and ternary systems in the oceanic salt system, no temperature dependency parameters of the interaction coefficients could be deduced so far due to the very limited data available. Therefore, for polythermal datasets, the temperature function parameters X₁–X₅ for the Pitzer interaction coefficients are set to zero.

4.5 Validity ranges

The conservative validity range for this dataset is given as follows:

• Temperature: T = 273–318 K,

• Ionic strength: I ≤ 5 mol/kg H₂O,

• O₂ partial pressure: p(O₂) ≤ 101.325 kPa.

This generalized specification is not valid for all chemical subsystems. The validity ranges of temperature and ionic strength of the individual background electrolyte are given in Table 10 according to the experimental data sets used for the parameter fitting.

TABLE 10

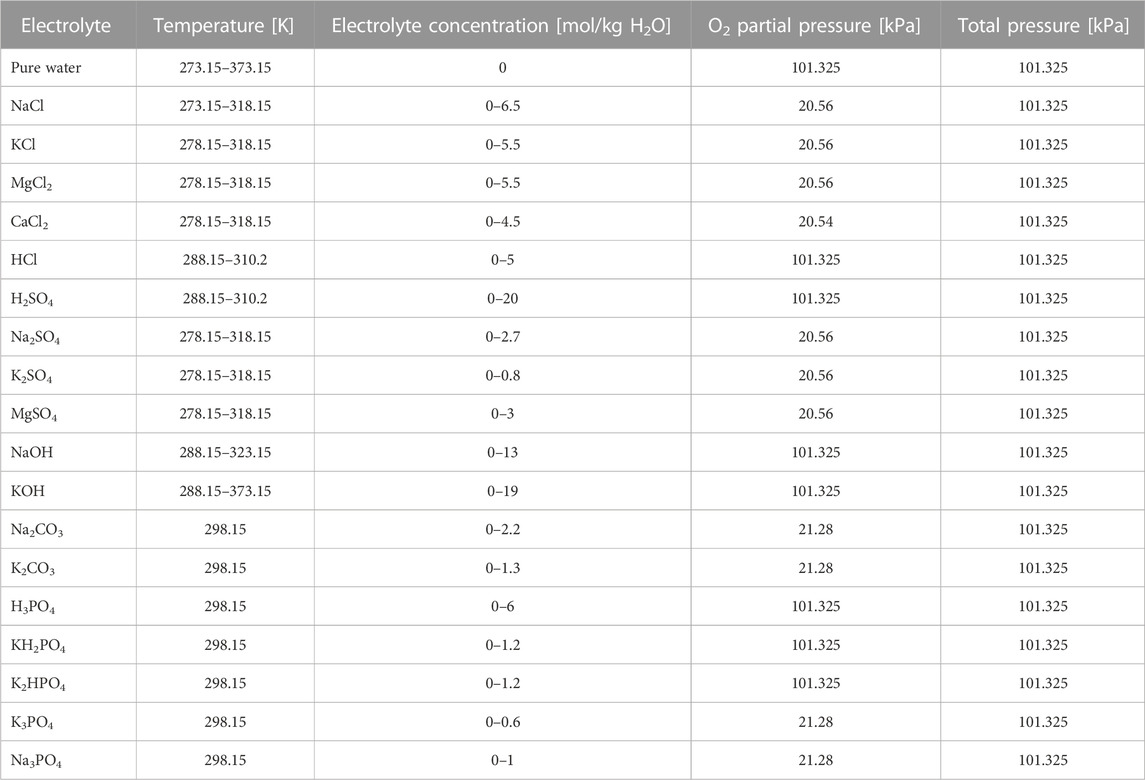
TABLE 10. Validity ranges (T, I, p) according to the experimental conditions used for the parameter fitting.

4.6 Known deficiencies

4.6.1 Missing interactions coefficient for binary solutions

For the O₂ solubility in binary solutions of bicarbonates only one experimental dataset (O₂ in NaHCO₃ solutions with T = 323–423 K and p = 1–5 MPa) is available in literature (Broden and Simonson, 1978) and (Broden and Simonson, 1979). It was not possible to extrapolate to 298.15 K and 101.325 kPa using the temperature and pressure dependency functions given in the articles or other extrapolation methods. Therefore, neither this binary interaction coefficient λ(O₂(aq)-HCO₃⁻) nor its temperature function parameters could be deduced so far.

4.6.2 Missing interaction coefficients for ternary solutions

There are no O₂ solubility data for other ternary mixtures of salt solutions published in literature beside the work of Millero et al. (2002a) (system Na⁺, Mg²⁺/Cl⁻, SO₄²⁻ - H₂O(l) at 298.15 K). Therefore only the interaction coefficients ζ(O₂(aq)-Na⁺-Mg²⁺) and ζ(O₂(aq)-Cl⁻-SO₄²⁻) for these ternary systems could be deduced. Here, especially the ternary interaction coefficients with hydroxide [ζ(O₂(aq)-OH⁻-Cl⁻) and ζ(O₂(aq)-OH⁻-SO₄²⁻)] would be of interest, since the O₂ solubility decreases significantly more in alkaline solutions than in neutral or acidic electrolyte solutions. For all other ternary (or higher) mixtures, no interaction coefficients could be obtained. The same applies to the temperature dependence of the O₂ interaction parameters in ternary electrolyte solutions.

Ternary interactions coefficients for systems with alkaline Earth ions (Mg²⁺, Ca²⁺) and bivalent or trivalent anions (CO₃²⁻, SO₄²⁻, PO₄³⁻)—except ζ(O₂(aq)-Mg²⁺-SO₄²⁻)—are assumed to be unnecessary because of the low solubility of the formed solid phases, e.g., calcite, dolomite, gypsum or apatite. The contributions of these ions in such solutions are sufficiently covered by the binary interaction coefficients.

5 Conclusion

In this paper, a set of thermodynamic formation data for dissolved oxygen O₂(aq) consistent with standard formation data for O₂(g), H₂(g), H₂O(l), and a temperature-dependent Henry’s law constant is presented. In combination with binary and ternary Pitzer coefficients they allow the calculation of oxygen solubility in concentrated salt solutions of the system Na⁺, K⁺, H⁺, Ca²⁺, Mg²⁺/Cl⁻, SO₄²⁻, CO₃²⁻, PO₄³⁻, OH⁻ - H₂O(l), including also the associated acids and bases. By combining a very large number of experimental papers, which have been subjected to critical evaluation, the data set is based on a wide range of data, which in turn ensures robustness.

Contrary to values for the so-called logK-E_H-grid circulating among geochemical modelers, values given herein can be traced back to experimental solubility data and standard formation data. Moreover, their validity in terms of temperature and solution composition is clearly stated.

The use of the dataset allows a more accurate description of the redox state of saline solutions. This does not only improve the description of the solubility of redox-sensitive radionuclides, but is also applicable to a variety of other processes—from material corrosion to microbial activity. The presented dataset allows modeling with a broader application range than the data compilations previously available in the literature, both in terms of the number of chemical subsystems and the temperature range. With a more precise description of redox conditions, it is possible to further reduce conservatism in safety assessment calculations, not only in the context of a nuclear repository.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FB: conceptualization, methodology, data analysis, software, fitting (Henry’s law constant and Pitzer ion-interaction coefficients), writing; HM: methodology and data review (thermodynamics), writing; VB: review and editing, supervision, funding acquisition.

Funding

This work was funded by BGE—the federal company for radioactive waste disposal, with the contract number 45181017.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2023.1158109/full#supplementary-material

References

Armenante, P. M., and Karlsson, H. T. (1982). Salting-out parameters for organic acids. J. Chem. Eng. Data 27, 155–156. doi:10.1021/je00028a016

CrossRef Full Text | Google Scholar

Battino, R., Cargill, R. W., Chen, C. T. A., Clever, H. L., Roth, J. A., Cramer, A. L., et al. (1981). IUPAC solubility data Series vol. 7: Oxygen and ozone. Oxford: Pergamon Press, 533.

Google Scholar

Baykut, S., and Aroguz, A. Z. (1989). The effect of different electrolytes on the solubility of gases in water. Chim. Acta Turc. 17, 365–375.

Google Scholar

Benson, B. B., Krause, D., and Peterson, M. A. (1979). The solubility and isotopic fractionation of gases in dilute aqueous solution. I. Oxygen. J. Solut. Chem. 8, 655–690. doi:10.1007/BF01033696

CrossRef Full Text | Google Scholar

Bethke, C. M. (2022). Geochemical and biogeochemical reaction modeling. 3rd Edition. Cambridge: Cambridge University Press. ISBN-13: 978-1-108-79086-4.

Google Scholar

Bikov, M. M. (1937). The solubility of gases in solutions of salts under pressure at high temperature. Tr. Voronezhsk. Gos. Univ. 9, 29–57.

Google Scholar

Blanc, P., Lassin, A., Piantone, P., Azaroual, M., Jacquemet, N., Fabbri, A., et al. (2012). Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 27 (10), 2107–2116. doi:10.1016/j.apgeochem.2012.06.002

CrossRef Full Text | Google Scholar

Bohr, C. (1910). Über die Löslichkeit von Gasen in konzentrierter Schwefelsäure und in Mischungen von Schwefelsäure und Wasser. Z. Phys. Chem. 71, 47–50. doi:10.1515/zpch-1910-7104

CrossRef Full Text | Google Scholar

Broden, A., and Simonson, R. (1978). Solubility of oxygen Part 1. Solubility of oxygen in water at temperatures ≤150°C and pressures ≤5MPa. Sven. Papperstidn. 81, 541–544.

Google Scholar

Broden, A., and Simonson, R. (1979). Solubility of oxygen Part 2. Solubility of oxygen in sodium hydrogen carbonate and sodium hydroxide solutions at temperatures ≤150°C and pressures ≤5MPa. Sven. Papperstidn. 82, 487–491.

Google Scholar

Bruhn, G., Gerlach, J., and Pawlek, F. (1965). Untersuchungen über die Löslichkeit von Salzen und Gasen in Wasser und wässrigen Lösungen bei Temperaturen oberhalb von 100 °C (Studies on the solubility of salts and gases in water and aqueous solutions at temperatures above 100 °C). Z. Anorg. Allg. Chem. 337 (1-2), 68–79. doi:10.1002/zaac.19653370111

CrossRef Full Text | Google Scholar

Carpenter, J. H. (1966). New measurements of oxygen solubility in pure and natural Water. Limnol. Ocean. 11, 264–277. doi:10.4319/lo.1966.11.2.0264

CrossRef Full Text | Google Scholar

M. W. Chase (Editor) (1998). “Journal of physical and chemical reference data, monograph No. 9, NIST-JANAF thermochemical Tables,” Published by the American chemical society and the American institutes of physics for the national Institute of standards and technology. Fourth Edition (Gaithersburg, Maryland: National Institute of Standards and Technology), 20899.

Google Scholar

Chatenet, M., Aurousseau, M., and Durand, R. (2000). Electrochemical measurement of the oxygen diffusivity and solubility in concentrated alkaline media on rotating ring-disk and disk electrodes—Application to industrial chlorine-soda electrolyte. Electrochim. Acta 45, 2823–2827. doi:10.1016/S0013-4686(00)00325-X

CrossRef Full Text | Google Scholar

Christov, C., and Møller, N. (2004). A chemical equilibrium model of solution behavior and solubility in the H-Na-K-Ca-OH-Cl-HSO₄-SO₄-H₂O system to high concentration and temperature. Geochim. Cosmochim. Acta 68 (18), 3717–3739. doi:10.1016/j.gca.2004.03.006

CrossRef Full Text | Google Scholar

Clegg, S., and Brimblecombe, P. (1990). The solubility and activity coefficient of oxygen in salt solutions and brines. Geochim. Cosmochim. Acta 54, 3315–3328. doi:10.1016/0016-7037(90)90287-U

CrossRef Full Text | Google Scholar

Clever, H. L., Battino, R., Miyamoto, H., Yampolski, Y., and Young, C. L. (2014). IUPAC-NIST solubility data Series. 103. Oxygen and ozone in water, aqueous solutions, and organic liquids (supplement to solubility data Series volume 7). J. Phys. Chem. Ref. Data 43, 033102-1–033102-209. doi:10.1063/1.4883876

CrossRef Full Text | Google Scholar

Cox, J. D. (1978). CODATA recommended key values for thermodynamics, 1977 Report of the CODATA Task Group on key values for thermodynamics, 1977. J. Chem. Thermodyn. 10 (10), 903–906. doi:10.1016/0021-9614(78)90050-2

CrossRef Full Text | Google Scholar

Cox, J. D., Wagman, D. D., and Medvedev, V. A. (1989). CODATA key values for thermodynamics. New York: Hemisphere Publishing Corp.

Google Scholar

Cramer, S. D. (1984). Oxygen solubility in brines. Ind. Eng. Chem. Process. Des. Dev. 23 (3), 618–620. doi:10.1021/i200026a035

CrossRef Full Text | Google Scholar

Cramer, S. D. (1980). The solubility of oxygen in brines from 0 to 300 °C. Ind. Eng. Chem. Process. Des. Dev. 19 (2), 300–305. doi:10.1021/i260074a018

CrossRef Full Text | Google Scholar

Das, T. N. (2005). Saturation concentration of dissolved O₂ in highly acidic aqueous solutions of H₂SO₄. Ind. Eng. Chem. Res. 44, 1660–1664. doi:10.1021/ie049539m

CrossRef Full Text | Google Scholar

Davis, R. E., Horvath, G. L., and Tobias, C. W. (1967). The solubility and diffusion coefficient of oxygen in potassium hydroxide solutions. Electrochim. Acta 12, 287–297. doi:10.1016/0013-4686(67)80007-0

CrossRef Full Text | Google Scholar

Delany, J. M., and Lundeen, S. R. (1991). The LLNL thermochemical data base - revised data and file format for the EQ3/6 package (No. UCID-21658). Livermore, CA, United States: Lawrence Livermore National Lab (LLNL.

Google Scholar

Domski, P., and Nielsen, S. R. (2019). WASTE ISOLATION PILOT PLANT AP-183 Revision 1 analysis plan to update the WIPP geochemical thermodynamic database (DATA0. FM1) to Data0. FM4 for CRA-2019.

Google Scholar

Eriksson, G., Hack, K., and Petersen, S. (1997). Chemapp—A programmable thermodynamic calculation interface. Werkst. Woche 96, 47–51.

Google Scholar

Eriksson, G., and Spencer, P. (1995). “A general thermodynamic software interface,” in Proceedings 2nd colloquium on process simulation (Otaniemi: Helsinki University of Technology), 113. (Report TKK-V-B104).

Google Scholar

Eucken, A., and Hertzberg, G. (1950). Aussalzeffekt und Ionenhydratation. Z. Phys. Chem. 195, 1–23. doi:10.1515/zpch-1950-19502

CrossRef Full Text | Google Scholar

Geffcken, G. (1904). Beiträge zur Kenntnis der Löslichkeitsbeeinflussung. Z. Phys. Chem. 49, 257–302. doi:10.1515/zpch-1904-4925

CrossRef Full Text | Google Scholar

Geng, M., and Duan, Z. (2010). Prediction of oxygen solubility in pure water and brines up to high temperatures and pressures. Geochim. Cosmochim. Acta 74, 5631–5640. doi:10.1016/j.gca.2010.06.034

CrossRef Full Text | Google Scholar

Giffaut, E., Grivé, M., Blanc, P., Vieillard, P., Colàs, E., Gailhanou, H., et al. (2014). Andra thermodynamic database for performance assessment: ThermoChimie. Appl. Geochem. 49, 225–236. doi:10.1016/j.apgeochem.2014.05.007

CrossRef Full Text | Google Scholar

Glazunov, A. I., Kryazhev, A. M., and Musinsky, S. V. (1997). Растворимость кислорода в растворах гидроокиси натрия (Oxygen solubility in sodium hydroxide solutions). Celljuloza, Bum. karton 7-8, 17–19.

Google Scholar

Grenthe, I., Gaona, X., Plyasunov, A. V., Rao, L., Runde, W. H., Grambow, B., et al. (2020). Second update on the chemical thermodynamics of uranium, neptunium, plutonium, americium and technetium. Boulogne-Billancourt, France: OECD Nuclear Energy Agency, Data Bank, 1572.

Google Scholar

Gubbins, K. E., and Walker, R. D. (1965). The solubility and diffusivity of oxygen in electrolytic solutions. J. Electrochem. Soc. 112, 469–471. doi:10.1149/1.2423575

CrossRef Full Text | Google Scholar

Harvie, C. E., Møller, N., and Weare, J. H. (1984). The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-H-Cl-SO₄-OH-HCO₃-CO₃-CO₂-H₂O system to high ionic strengths at 25°C. Geochim. Cosmochim. Acta 48 (4), 723–751. doi:10.1016/0016-7037(84)90098-X

CrossRef Full Text | Google Scholar

Hayduk, W. (1991). Final Report concerning the solubility of oxygen in sulfuric acid-zinc pressure leaching solutions. Ottawa, Canada: University of Ottawa, Chemical Engineering, 40.

Google Scholar

Herbert, H. J. (2000). “Zur Geochemie und geochemischen Modellierung hochsalinarer Lösungen,” in Hannover Bundesanstalt für Geowissenschaften und Rohstoffe (BGR). Editors J. Geologisches, and R. D. Sonderhefte (Stuttgart, Germany: Schweizerbart Science Publishers). ISBN 978-3-510-95845-0.

Google Scholar

Iwai, Y., Eya, H., Itoh, Y., Arai, Y., and Takeuchi, K. (1993). Measurement and correlation of solubilities of oxygen in aqueous solutions containing salts and sucrose. Fluid Phase Equilib. 83, 271–278. doi:10.1016/0378-3812(93)87030-5

CrossRef Full Text | Google Scholar

Iwai, Y., Kohashi, K., Eya, H., Honda, K., and Arai, Y. (1990). Measurement and correlation of oxygen solubilities in aqueous solutions containing salts and sugar. Kagaku Kogaku Ronbun 16, 1247–1251. doi:10.1252/kakoronbunshu.16.1247

CrossRef Full Text | Google Scholar

Kaskiala, T. (2002). Determination of oxygen solubility in aqueous sulphuric acid media. Min. Eng. 15, 853–857. doi:10.1016/S0892-6875(02)00089-4

CrossRef Full Text | Google Scholar

Kelley, K. K. (1960). High-temperature heat-content, heat-capacity, and entropy data for the elements and inorganic compounds. U. S. Bureau Mines Bull. 584, 232.

Google Scholar

Khomutov, N. E., and Konnik, E. I. (1974). Solubility of oxygen in aqueous electrolyte solutions. Russ. J. Phys. Chem. 48, 21–362. or Zh. Fiz. Khim, 48, (1974), 620–37.

Google Scholar

Kitamura, A. (2020). JAEA-TDB-RN in 2020: Update of JAEA’s thermodynamic database for solubility and speciation of radionuclides for performance assessment of geological disposal of high-level and TRU wastes. JAEA-Data/Code, 2020–020. doi:10.11484/jaea-data-code-2020-020

CrossRef Full Text | Google Scholar

Knaster, M. B., and Apelbaum, L. A. (1964). Растворимость водорода и кислорода в концентрированных растворах едкого кали (Solubility of hydrogen and oxygen in concentrated solutions of potassium hydroxide). Zh. Fiz. Khim. 38 (1), 223–225.

Google Scholar

Kulik, D. A., Wanger, T., Dmytrieva, S. V., Kosakowski, G., Hingerl, F. F., Chudneno, K. V., et al. (2013). GEM-selektor geochemical modeling package: Revised algorithm and GEMS3K numerical kernel for coupled simulation codes. Comput. Geosci. 17 (1), 1–24. doi:10.1007/s10596-012-9310-6

CrossRef Full Text | Google Scholar

Lang, W., and Zander, R. (1986). Salting-out of oxygen from aqueous electrolyte solutions: Prediction and measurement. Ind. Eng. Chem. Fundam. 25, 775–782. doi:10.1021/i100024a050

CrossRef Full Text | Google Scholar

Li, H. (1994). The solubilities of oxygen in sulphuric acid solutions containing copper and/or nickel sulphates at atmospheric and high pressure. Master thesis (Ottawa, Canada: University of Ottawa), 110.

Lumsdon, D. G., and Evans, L. J. (1995). “Predicting chemical speciation and computer simulation,” in Chemical speciation in the environment (Berlin, Germany: Springer), 86–134.

Google Scholar

MacArthur, D. G. (1916). Solubility of oxygen in salt solutions and the hydrates of these salts. J. Phys. Chem. 20, 495–502. doi:10.1021/j150168a003

CrossRef Full Text | Google Scholar

Mariner, P. (2004). In-drift precipitates/salts model. No. ANL-EBS-MD-000045, REV 02. Las Vegas, Nevada, USA: Yucca Mountain Project.

Google Scholar

May, P. M., and Muray, K. (1991). Jess, a joint expert speciation system—II. The thermodynamic database. Talanta 38 (12), 1419–1426. doi:10.1016/0039-9140(91)80290-G

PubMed Abstract | CrossRef Full Text | Google Scholar

Millero, F. J., Huang, F., and Graham, T. B. (2003). Solubility of oxygen in some 1-1, 2-1, 1-2, and 2-2 electrolytes as a function of concentration at 25°C. J. Solut. Chem. 32, 473–487. doi:10.1023/A:1025301314462

CrossRef Full Text | Google Scholar

Millero, F. J., Huang, F., and Laferiere, A. L. (2002). Solubility of oxygen in the major sea salts as a function of concentration and temperature. Mar. Chem. 78, 217–230. doi:10.1016/S0304-4203(02)00034-8

CrossRef Full Text | Google Scholar

Millero, F. J., Huang, F., and Laferiere, A. L. (2002). The solubility of oxygen in the major sea salts and their mixtures at 25°C. Geochim. Cosmochim. Acta 66, 2349–2359. doi:10.1016/S0016-7037(02)00838-4

CrossRef Full Text | Google Scholar

Millero, F. J., and Huang, F. (2003). Solubility of oxygen in aqueous solutions of KCl, K₂SO₄, and CaCl₂ as a function of concentration and temperature. J. Chem. Eng. Data 48, 1050–1054. doi:10.1021/je034031w

CrossRef Full Text | Google Scholar

Mitchell, M., Muftakhidinov, B., Winchen, T., van Schaik, B., Wilms, A., Kylesower, , et al. (2020). Engauge digitizer software. Available at: http://markummitchell.github.io/engauge-digitizer (Accessed February 19, 2020). doi:10.5281/zenodo.3558440

CrossRef Full Text | Google Scholar

Moog, H. C., Bok, F., Marquardt, C. M., and Brendler, V. (2015). Disposal of nuclear waste in host rock formations featuring high-saline solutions - implementation of a thermodynamic reference database (THEREDA). Appl. Geochem. 55, 72–84. doi:10.1016/j.apgeochem.2014.12.016

CrossRef Full Text | Google Scholar

Narita, E., Lawson, F., and Han, K. H. (1983). Solubility of oxygen in aqueous electrolyte solutions. Hydrometallurgy 10, 21–37. doi:10.1016/0304-386X(83)90074-9

CrossRef Full Text | Google Scholar

Ohkubo, M. (2000). 製塩工程における高濃度電解質水溶液の溶存酸素濃度測定 (Measurement of solubility of oxygen in electrolyte solution used in salt manufacturing process). Bull. Soc. Sea Water Sci. Jpn. 54 (2), 111–116. doi:10.11457/swsj1965.54.111

CrossRef Full Text | Google Scholar

Parkhurst, D. L., and Appelo, C. A. J. (2013). Description of input and examples for PHREEQC version 3—a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. U.S. Geological Survey, Book 6, Chapter 43, Section A of Techniques and Methods, 497.

Google Scholar

Pearson, F. J., and Berner, U. R. (1991). Nagra thermochemical data base I. Code data, 80. Nagra, Technical Report 91–17.

Google Scholar

Phillips, S. L., Phillips, C. A., and Skeen, J. (1985). Hydrolysis, formation and ionization constants at 25° C, and at high temperature-high ionic strength. Berkeley, CA, USA: Lawrence Berkeley Laboratory, 411. Lawrence Berkeley Laboratory Report No. LBL-14996.

Google Scholar

Pierrot, D., and Millero, F. J. (2017). The speciation of metals in natural waters. Aquat. Geochem. 23, 1–20. doi:10.1007/s10498-016-9292-4

CrossRef Full Text | Google Scholar

Pitzer, K. S. (1991). “Ion interaction approach: Theory and data correlation,” in Activity coefficients in electrolyte solutions. Editor K. S. Pitzer (Boca Raton, Florida: CRC Press), 75–153.

Google Scholar

Poeter, E. P., Hill, M. C., Lu, D., Tiedeman, C. R., and Mehl, S. (2014). UCODE_2014, with new capabilities to define parameters unique to predictions, calculate weights using simulated values, estimate parameters with SVD, evaluate uncertainty with MCMC, and More. Report Number: GWMI 2014-02. Indianapolis, Indiana, USA: Integrated Groundwater Modeling Center, 189.

Google Scholar

Pospíšol, J., and Lužný, Z. (1960). Absorptionskoeffizienten des Sauerstoffes in Lösungen von Kaliumhydroxyd. Collect. Czech. Chem. Commun. 25, 589–592. doi:10.1135/cccc19600589

CrossRef Full Text | Google Scholar

Ragoussi, M. E., and Costa, D. (2019). Fundamentals of the NEA Thermochemical Database and its influence over national nuclear programs on the performance assessment of deep geological repositories. J. Environ. Radioact. 196, 225–231. doi:10.1016/j.jenvrad.2017.02.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Read, D., and Broyd, T. W. (1991). Recent progress in testing chemical equilibrium models: The CHEMVAL project. Radiochim. Acta 52 (2), 453–456. doi:10.1524/ract.1991.5253.2.453

CrossRef Full Text | Google Scholar

Reynafarje, B., Costa, L. E., and Lehninger, A. L. (1985). O₂ solubility in aqueous media determined by a kinetic method. Anal. Biochem. 145, 406–418. doi:10.1016/0003-2697(85)90381-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Scharge, T., Muñoz, A. G., and Moog, H. C. (2012). Activity coefficients of fission products in highly salinary solutions of Na⁺, K⁺, Mg²⁺, Ca²⁺, Cl^-, and SO₄^2-: Cs⁺. J. Chem. Eng. Data 57 (6), 1637–1647. doi:10.1021/je200970v

CrossRef Full Text | Google Scholar

Scharge, T., Munoz, A. G., and Moog, H. C. (2015). Thermodynamic modeling of high salinary phosphate solutions. II. Ternary and higher systems. J. Chem. Thermodyn. 80, 172–183. doi:10.1016/j.jct.2013.12.017

CrossRef Full Text | Google Scholar

Scharge, T., Munoz, A. G., and Moog, H. C. (2013). Thermodynamic modelling of high salinary phosphate solutions. I. Binary systems. J. Chem. Thermodyn. 64, 249–256. doi:10.1016/j.jct.2013.05.013

CrossRef Full Text | Google Scholar

Shock, E. L., Helgeson, H. C., and und Sverjensky, D. A. (1989). Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Standard partial molal properties of inorganic neutral species. Geochim. Cosmochim. Acta 53, 2157–2183. doi:10.1016/0016-7037(89)90341-4

CrossRef Full Text | Google Scholar

Shoor, S. K., Walker, R. D., and Gubbins, K. E. (1968). Salting out of nonpolar gases in aqueous potassium hydroxide solutions. J. Phys. Chem. 73 (2), 312–317. doi:10.1021/j100722a006

CrossRef Full Text | Google Scholar

Söhnel, O., and Novotný, P. (1985). Densities of aqueous solutions of inorganic substances. Amsterdam, Netherlands: Elsevier Publishing Company, 336.

Google Scholar

Stephan, E. F., Hatfield, N. S., Peoples, R. S., and Pray, H. A. H. (1956). The solubility of gases in water and in aqueous uranyl salt solutions at elevated temperatures and pressures. Columbus, Ohio: Battelle Memorial Institute. Battelle Memorial Institute Report, BMI-1067.

Google Scholar

Tan, Z. Q., Gao, G. H., Yu, Y. X., and Gu, G. (2001). Solubility of oxygen in aqueous sodium carbonate solution at pressures up to 10 MPa. Fluid Phase Equilibria 180, 375–382. doi:10.1016/S0378-3812(01)00371-5

CrossRef Full Text | Google Scholar

THEREDA (2023). THEREDA – thermodynamic reference database. Available at: https://www.thereda.de/.

Google Scholar

Thoenen, T., Hummel, W., Berner, U. R., and Curti, E. (2014). The PSI/nagra chemical thermodynamic database 12/07. PSI Report No. 14-04. ISSN 1019-0643.

Google Scholar

Turner, D. R., Achterberg, E. P., Chen, C.-T. A., Clegg, S. L., Hatje, V., Maldonado, M. T., et al. (2016). Toward a quality-controlled and accessible pitzer model for seawater and related systems. Front. Mari. Sci. 3, 1–12. doi:10.3389/fmars.2016.00139

CrossRef Full Text | Google Scholar

Voigt, W. (2020). Hexary system of oceanic salts – polythermal pitzer dataset (numerical supplement). THEREDA J. 1 (1), 1–9. URN: urn:nbn:de:bsz:105-qucosa2-782361.

Google Scholar

Voigt, W. (2020). Temperature extension of NaCl Pitzer coefficients and ∆_RG°(NaCl). THEREDA J. 1 (2), 1–6. URN: urn:nbn:de:bsz:105-qucosa2-782374.

Google Scholar

Wagner, T., Kulik, D. A., Hingerl, F. F., and Dmytrieva, S. V. (2012). GEM-selektor geochemical modeling package: TSolMod library and data interface for multicomponent phase models. Can. Mineral. 50 (5), 1173–1195. doi:10.3749/canmin.50.5.1173

CrossRef Full Text | Google Scholar

Wolery, T. (1992). EQ3/6, A software package for the geochemical modelling of aqueous systems. UCRL MA 110662 Part I. Livermore, CA, USA: Lawrence Livermore National Laboratory.

Google Scholar

Yasunishi, A. (1977). Solubilities of sparingly soluble gases in aqueous sodium sulfate and sulfite solutions. J. Chem. Eng. Jpn. 10 (2), 89–94. doi:10.1252/jcej.10.89

CrossRef Full Text | Google Scholar

Yasunishi, A. (1978). Solubility of oxygen in aqueous electrolyte solutions. Kagaku Kogaku Rombunshu 4, 185–189. doi:10.1252/kakoronbunshu.4.185

CrossRef Full Text | Google Scholar

Zhang, C., Fan, F.-R., and Bard, A. J. (2009). Electrochemistry of oxygen in concentrated NaOH solutions: Solubility, diffusion coefficients, and superoxide formation. J. Am. Chem. Soc. 131, 177–181. doi:10.1021/ja8064254

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, G., Spycher, N., Sonnenthal, E., and Steefel, C. I. (2006). Implementation of a Pitzer activity model into TOUGHREACT for modeling concentrated solutions. TOUGH Symposium 2006, Technical Program and Abstracts, Berkley, May 15–17.

Google Scholar

Zheng, J., and Mao, S. (2019). A thermodynamic model for the solubility of N₂, O₂ and Ar in pure water and aqueous electrolyte solutions and its applications. Appl. Geochem. 107, 58–79. doi:10.1016/j.apgeochem.2019.05.012

CrossRef Full Text | Google Scholar