Novel evidence of team reasoning in spatially-framed experimental bargaining games

Introduction: Team reasoning and bounded best-response models have been used to explain coordination success and failure in games with focal points. Most attempts at discriminating between them have used games framed as matching problems in which players choose between alternative payoff distributions. But evidence suggests that coordination failures are less dramatic in games framed as bargaining problems in which players separately claim parts of a valuable surplus. We contrast team reasoning and bounded best-response models using a variant of an established experimental paradigm in which tacit bargaining games are given a spatial frame.

Methods: Participants (N = 100) took part in 24 one-shot spatially-framed bargaining games in which the total surplus was divided into two, four or eight valuable discs scattered on a grid where each player was located in a specific position. Twelve games had spatial cues suggesting a Least Unequal Efficient (LUE) surplus allocation in which each player claimed the discs closest to them, and 12 games had no such cues. Each player's payoff was the total value of the discs claimed by them but not by the other player. In this setup, bounded best-response models predict players would follow the dominant strategy of claiming all discs, while team reasoning predicts each player should claim one of the LUE shares.

Results: Across all games, the proportion of players claiming all discs ranged from 35 to 63%, exceeding 50% in just 4 games. In line with team reasoning, most non-dominant claims were LUE shares and players were significantly more likely to claim near than far discs.

Discussion: Exploiting spatial framing and leveraging payoff dominance, our experiment provides novel evidence for team reasoning in tacit bargaining. We also find some evidence that players favored by spatial cues sometimes do not accept that advantage. We discuss possible explanations for these patterns.

1 Introduction

It has been known for more than 60 years that ordinary people can often solve coordination problems more successfully than would be possible for the ideally rational agents of standard game theory, and that achieving this success involves using cues contained in the way games are framed—cues that the supposedly rational agents of the theory would treat as irrelevant (Schelling, 1960). However, many questions about when and how these cues are recognized and used remain unresolved. Two fundamentally different modes of non-standard game-theoretic reasoning have been proposed as explanations—bounded best-response reasoning, which grounds players' beliefs on propositions about the behavior of strategically naïve agents, and team reasoning, in which each player tries to play their part in the strategy profile that would be best for the players collectively.¹ Most attempts at discriminating between these modes of reasoning have used paradigms that are not intuitive representations of bargaining problems. To extend such attempts to games explicitly framed as bargaining problems, we present an experiment based on a variant of the bargaining table design that we used in a parallel experiment, reported in Isoni et al. (2013). Although the design change is very minor, it has radical implications, allowing us to make distinctions between team reasoning and bounded best-response reasoning that would not be possible in Isoni et al.'s design.²

1.1 Labeling effects in matching games

In non-cooperative game theory, the formal description of a game is a structure comprising a set of players, a set of strategies for each player, (in some games) a set of probabilistic “moves of nature”, and a payoff distribution (i.e., a utility or material payoff for each player for each combination of strategy profiles and moves of nature). The players are assumed to have common knowledge of the whole structure, incomplete information being represented by moves of nature. Game theory provides “solution concepts” that derive propositions about players' strategy choices and beliefs solely from the data contained in the formal description. A game may also have labels for individual players and/or strategies, and the players may have common knowledge of this labeling. Crucially, however, labels provide no information about the components of the formal description and are therefore not used by solution concepts. Thus, standard game theory implies that, if the formal structure of a game is held constant, there are no labeling effects: players' behavior and beliefs are independent of how that game is labeled.

From Schelling (1960) onwards, this hypothesis has been tested in many different matching games. In a two-player matching game, each player has the same number of strategies, each identified by the same arbitrary set of labels (e.g., “Heads” and “Tails”) for both players. If both players choose the same label, each gets a positive payoff; otherwise, both get zero. In a 2 × 2 Pure Coordination game, both pure-strategy equilibrium payoff distributions are (x, x) for some x > 0. In a Battle of the Sexes game, these distributions are (x, y) and (y, x) for some x > y > 0.

In contrast to standard game theory, Schelling (1960) presents intuitive arguments and informal experimental evidence in support of the hypothesis that players use “prominent” labels as cues for concerting their strategies in matching games, thus identifying one of the equilibria of the game as a focal point. A label is prominent (or, synonymously, salient) by virtue of properties that are commonly recognized as differentiating it from the other labels. For example, in a Pure Coordination game in which the strategy labels were “Heads” and “Tails”, 36 of Schelling's 42 participants chose “Heads”. Incentivized experiments have confirmed Schelling's hypothesis as applied to one-shot Pure Coordination games. Ordinary human players have shown a remarkable ability to find salient labeling cues even in the most unlikely settings (Mehta et al., 1994; Bardsley et al., 2010; Hargreaves Heap et al., 2017).

Schelling argues that his hypothesis extends to tacit bargaining games (such as Battle of the Sexes) in which players have conflicting preferences between two or more Nash equilibria, provided the conflict of interest is small relative to the potential efficiency gains. In such a game, the salient equilibrium “quite arbitrarily condemns one of the players to a smaller gain than the other for reasons that may seem purely accidental or incidental”. Nevertheless, “we have to suppose that a rational player can discipline himself to accept the lesser share if the clue points that way” (Schelling, 1960, p. 286). Schelling presents tacit bargaining not only as a model of real-world coordination problems in which communication is not possible or not permissible (e.g., between enemies in war or colluding firms in a cartel), but also of the final stage of explicit bargaining processes, after opportunities for communication have been exhausted (e.g., Isoni et al., 2014).

However, an experiment reported by Crawford et al. (2008) raised doubt about the applicability of Schelling's hypothesis to games with conflicts of interest. Crawford et al. studied matching games with a Battle of the Sexes structure in which each player (labeled “P1” or “P2”) selected one of two payoff distributions, presented in the form “P1 receives $a and P2 receives $b” and “P1 receives $b and P2 receives $a”. These payoffs were implemented if and only if both players chose the same distribution. Some games were unlabeled (i.e., that presentation was the only labeling). In other games, the payoff distributions were labeled “X” and “Y”. As a control, some labeled games were Pure Coordination games (i.e., with a = b). In the control games, the labels induced coordination on “X”, demonstrating the salience of that label. But when there was a conflict of interest, even if very small, this labeling had almost no tendency to increase efficiency relative to the corresponding unlabeled game. Crawford et al. also found that the players' failure to coordinate was not always the result of each player choosing the strategy associated with their preferred equilibrium: when the conflict of interest was relatively small, the opposite tendency was observed. This “after you” effect has often been interpreted as suggesting that the main obstacle to coordination in Battle of the Sexes is strategic uncertainty (i.e., uncertainty about the strategic choice of the coplayer) rather than naïve self-interest. However, in the absence of labeling cues that make one surplus division salient, such a tendency could also be a sign that the individual is willing to sacrifice their own self-interest for the good of the team.

1.2 The bargaining table paradigm

Isoni et al.'s (2013) experiment investigated whether Crawford et al.'s results extended to games that were set up as bargaining problems. Crawford et al.'s experiment, like previous investigations of Pure Coordination games, used the matching game paradigm. In this paradigm, each player is shown the same set of options and is given the objective of choosing the same option as their coplayer. An option is presented as a payoff distribution (to be implemented if both players chose that option), with a label (e.g., “X” or “Y” in Crawford et al.'s experiment) or without one. This paradigm represents a tacit bargaining problem as modeled in game theory (i.e., as a problem of equilibrium selection), but without any cues suggestive of real-world bargaining.

Drawing on Mehta et al.'s (1994) “squares and circles” Pure Coordination games, in which players aimed at coordinating by choosing the same assignment of circles to squares based on their respective positions on a rectangular grid, Isoni et al.'s experiment introduced a new way of presenting coordination problems—the bargaining table paradigm. Two players face a bargaining scenario represented on a “table”, seen by both players, consisting of a grid of squares. Each player has a “base” in one of the squares (to the left side of the table for one player, to the right for the other). “Discs” are located in some of the other squares. Each disc has a stated (positive) money value (in UK pounds), known to both players. Two of the scenarios used by Isoni et al. are reproduced in Figure 1.³

Figure 1

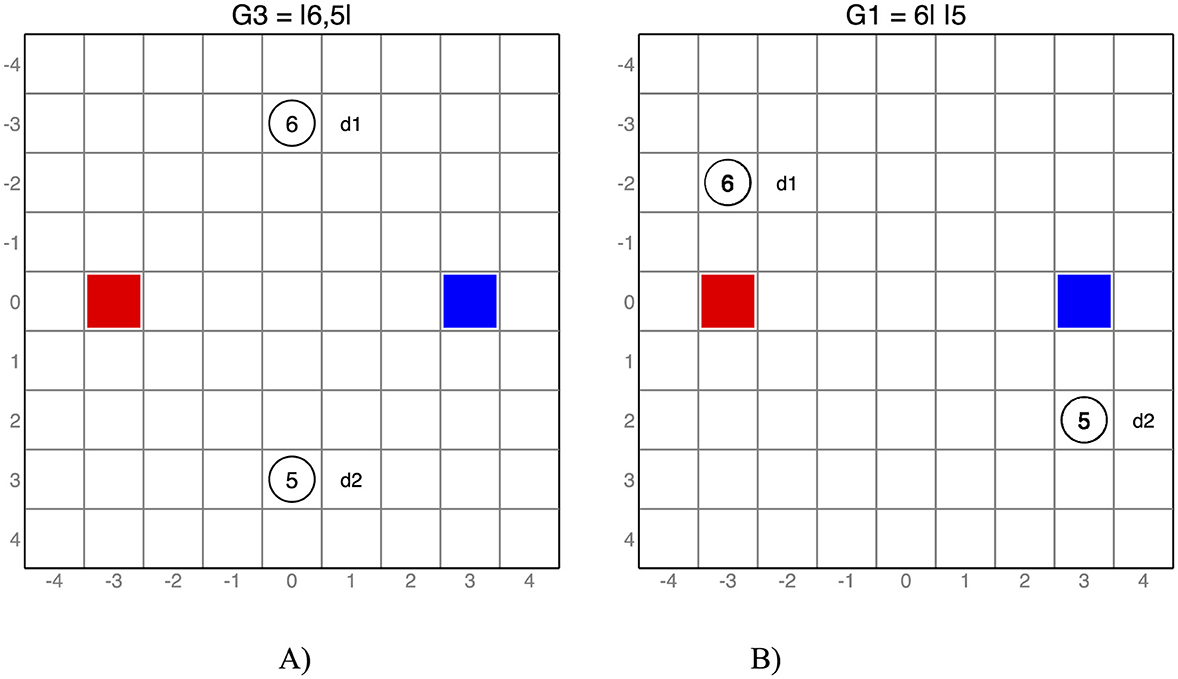
Figure 1. Examples of neutral and spatial-cue equality-incompatible scenarios. (A) A neutral scenario. (B) A spatial-cue scenario.

Simultaneously, each player chooses which discs to “claim”. The scenario is turned into a bargaining game by means of a payoff rule linking claims to payoffs. Isoni et al. used a single-agreement payoff rule according to which, if any disc is claimed by both players, both players' payoffs are zero; otherwise, the payoff for each player is the sum of the values of their claims. The game is described as an “opportunity to agree on a division of the discs”; non-overlapping claims (i.e., no disc claimed by both players) are referred to as “agreement”, overlapping claims (i.e., at least one disc claimed by both players) as “no agreement”. In some scenarios, like the spatial-cue scenario on the right in Figure 1, the spatial layout of the discs is such that the closeness rule—the rule that requires each player to claims those discs (or, as a tiebreaker, the “blocks” of contiguous discs) that are closer to their own base—induces an efficient outcome in which both players have positive (but not necessarily equal) payoffs.⁴ In such cases, the closeness rule is a potentially salient but theoretically payoff-irrelevant cue for coordination. As a control, this cue can be switched off by using layouts in which all discs are equidistant from the two bases, like the neutral scenario on the left in Figure 1. Thus, the bargaining table paradigm allows for a manipulation of the spatial framing of theoretically identical games.

If, like in the examples in Figure 1, there are exactly two discs, the formal description of the bargaining table game reduces to that of a Pure Coordination game (if the discs have equal value) or Battle of the Sexes game (otherwise) after iterated elimination of the weakly dominated strategies “Claim no discs” and “Claim both discs”. However, the bargaining table representation has very different connotations from the matching game representation of those games. It uses words (“claims” and “agreement”) that are likely to prime mental associations with real-world bargaining. Unlike arbitrary labels like “X” and “Y” appended to already well-defined options, the spatial cues are integrated into the activity of making claims. To achieve coordination, players have to claim different discs, rather than matching on the same label. Thus, each player's attention is directed to their own potential payoffs, rather than to the alternative payoff distributions. Notice that the only labeling properties that can aid coordination are relationships between specific players and specific discs. Such relationships may prime mental associations with concepts of ownership.

By using more than two discs, the bargaining table paradigm can also represent significant possibilities of real-life bargaining that have no equivalents in Pure Coordination or Battle of the Sexes games. For example, consider a table with three discs (d₁, d₂, and d₃) of equal value. The outcome in which one player claims only d₁ and the other claims only d₂ is not a Nash equilibrium, but it is rationalizable [as defined by Bernheim (1984) and Pearce (1984)]. Intuitively, reasonable actions by cautious players in a one-shot game can result in outcomes that leave some discs unclaimed.

In Isoni et al.'s (2013) experiment, each participant played 24 different bargaining table scenarios presented without feedback on players' claims. Full descriptions of these scenarios are reported in Section 2.3.

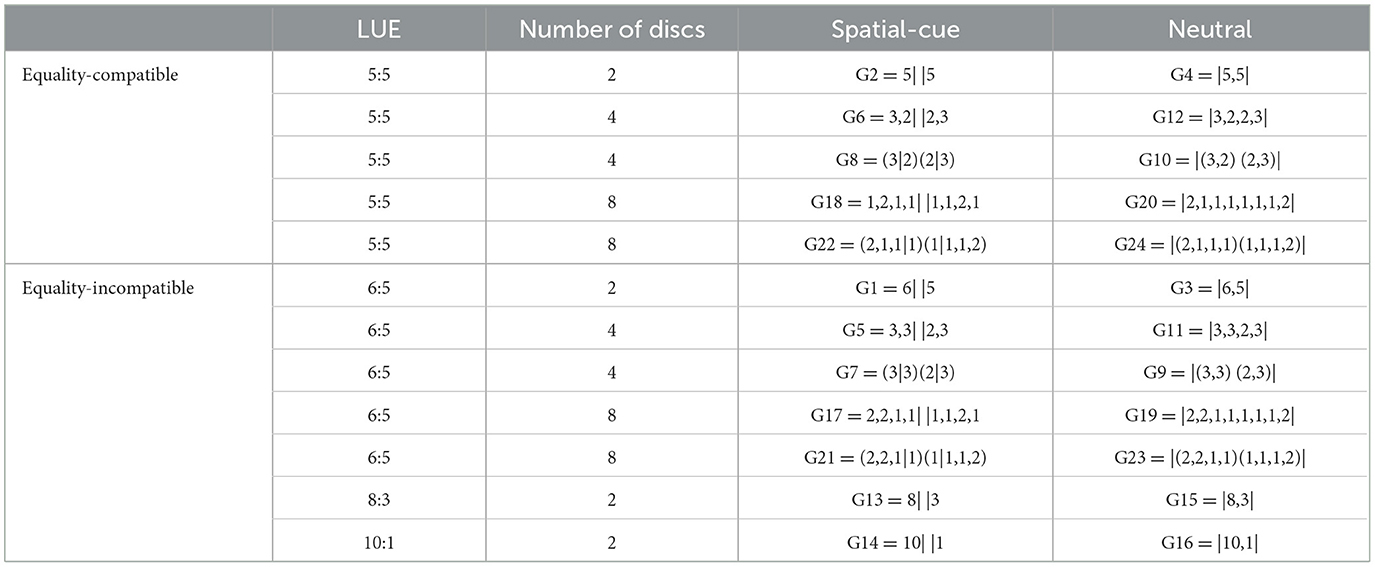
Twenty of these scenarios fitted into a 2 × 2 factorial design, which we now describe. The first factor was the applicability or inapplicability of the closeness rule. Ten of these factorial scenarios were spatial-cue scenarios in which there were at least two strategy profiles that induced a least unequal efficient (LUE) payoff distribution (i.e., a distribution in which payoff inequality is minimized subject to the constraint that each disc is claimed by exactly one player). In each such scenario, the closeness rule selected a unique LUE solution. Each spatial-cue scenario had a corresponding neutral scenario with exactly the same discs, relocated to be equidistant from the two bases. This factor allowed controlled tests of the effect of spatial cues.⁵

The second factor was the compatibility of efficiency and equality. Equality has been found to be a salient cue irrespective of its effects on payoffs (e.g., Mehta et al., 1994). In relation to payoffs, both equality and efficiency may be the source of focal points [see overview in Isoni et al., 2022]. The experiment was designed to include pairs of spatial-cue and neutral scenarios with equal LUE distributions (i.e., allowing the surplus to be shared equally between the two players—henceforth, equality-compatible scenarios), and pairs with unequal LUE distributions (i.e., not allowing the surplus to be divided equally—henceforth equality-incompatible scenarios). In each of 10 equality-compatible scenarios (analogous with Pure Coordination games), the LUE distribution gave £5 to each player. Each of these scenarios had a corresponding equality-incompatible scenario (analogous with a Battle of the Sexes game) which differed only by the addition of £1 to the value of one of the discs; in these scenarios, the LUE distribution gave £5 to one player and £6 to the other. This factor allowed controlled tests of whether payoff asymmetries and/or conflicts of interest reduce the effectiveness of spatial cues.⁶

Viewed in relation to Crawford et al.'s experiment, the main findings were as follows. In all spatial-cue scenarios, there was a strong tendency for players' claims to favor discs on their own side of the table. It was particularly common for players to claim all the discs on their side, as implied by the closeness rule. These tendencies consistently produced more efficient outcomes in spatial-cue scenarios than in the corresponding neutral scenarios. However, these tendencies were markedly less strong in equality-incompatible scenarios than in corresponding equality-compatible ones. These findings have been replicated in a more recent experiment (Isoni et al., 2020). Overall, the evidence supports Schelling's hypothesis that bargaining behavior is influenced by labeling cues, but the effect is weaker than would be suggested by simple extrapolation from Pure Coordination games.

1.3 Discriminating between modes of reasoning

The effects of labeling and other payoff-irrelevant cues in coordination and bargaining problems have been explained using two alternative approaches. Some theories, which following Faillo et al. (2017) we will refer to as theories of bounded best-response reasoning (Stahl and Wilson, 1994; Nagel, 1995; Costa-Gomes et al., 2001; Camerer et al., 2004; Crawford et al., 2008) cut off the infinite regress of best-response reasoning (i.e., looking for a player's best response to a coplayer who makes a best response to a coplayer of theirs who makes a best response…) by postulating either the actual existence of naïve “level 0” players or beliefs about their existence. If level 0 players are assumed to use salient labels as tie breakers when naïve thoughts about payoffs provide no guidance, higher-level players' choices of saliently labeled strategies can sometimes be explained as boundedly rational. Interestingly, however, Schelling (1960, p. 94) explicitly rejected this kind of explanation, preferring an approach that has since been formalized as team reasoning (Sugden, 1993, 2015; Bacharach, 2006).⁷ The essential idea is that players look for a strategy profile that stands out for them collectively as a means of coordination, using their common knowledge of the connotations of different labels.

Discriminating between these two modes of reasoning experimentally is difficult, because an immediate and unreflective perception that a label stands out is often evidence that it will also stand out for other people, and hence that it will be effective as a means of coordination. One way of separating the two modes is to use unlabeled matching games in which each player has three strategies (s₁, s₂, and s₃) and in which both players' payoffs are positive if they choose the same strategy and zero otherwise. For example, suppose the payoff distributions induced by these strategies are (10, 10), (10, 10), and (9, 9), respectively. If players use bounded best-response reasoning and if level 0 players naïvely choose s₁ or s₂, players at all higher levels will do the same but will often fail to coordinate. In contrast, sophisticated team-reasoning players may recognize the difficulty of coordinating on either s₁ or s₂ and see that s₃, despite its Pareto inefficiency, stands out as a means of coordination. Variants of this design have been used by Crawford et al. (2008), Bardsley et al. (2010), and Faillo et al. (2017). The evidence generated suggests that most individuals are capable of using both modes of reasoning in matching games, and that which is more likely to be used is sensitive to details of the games.

As noted earlier, in some versions of the matching game paradigm, conflicts of interest have been found to nullify the beneficial effects of labeling on coordination. However, in the bargaining table paradigm, the effects of spatial cues, although attenuated by conflicts of interest, have been found to persist. It is therefore important to identify the separate effects of the two modes of reasoning in bargaining problems. Because the three-strategy method described in the previous paragraph has no analog in the bargaining table paradigm (for example, it is not possible to specify the number and values of the discs on a bargaining table such that (10, 10) and (9, 9) are the only rationalizable outcomes), an entirely different method is needed.

1.4 The bargaining table paradigm with the multi-agreement payoff rule

To sharpen the contrast between bounded best-response reasoning and team reasoning in a bargaining table setup, the experiment we report in this paper introduced a variant of the payoff rule used by Isoni et al. (2013), and applied it to exactly the same bargaining table scenarios as in that experiment. The procedure by which players made claims on discs was unchanged. However, there was a small but highly consequential modification to the payoff rule used to determine players' payoffs based on their claims. In calculating payoffs, each disc was considered separately, effectively being the subject of a separate agreement. The payoff rule was: if a disc had been claimed by only one player, that player received the value of that disc, even if other discs had been claimed by both players. If neither player had claimed it, or if both had done so, the value of that disc was lost to both of them. Thus, according to this multi-agreement payoff rule, each player's payoff is the value of their own claims minus the value of discs that are claimed by both players.

As we explain below, this small modification results in sharply divergent predictions for different modes of reasoning. It also expands the usefulness of the bargaining table paradigm as a model of real-world bargaining. The single-agreement payoff rule is a useful representation of cases in which bargaining requires a single take-it-or-leave-it agreement. The multi-agreement payoff rule can model more complex situations in which agreement may happen on some of the issues at stake, but not on others (e.g., tariff negotiators may agree on tariff changes on particular goods while failing to agree on others; nations may agree on some borders but leave others disputed).

Viewed in the perspective of conventional game theory, this multi-agreement game is trivial. For each player, it is a weakly dominant strategy to claim all the discs. If a player views the game in the perspective of best-response reasoning, they will ask themself: “What is it best for me to do, given what I expect the other player to do?” The answer is immediate and intuitive: whatever your beliefs about your coplayer's claims, claiming all the discs is always a best response; and if you believe your coplayer will claim any given disc with probability strictly < 1, your best response must include claiming that disc.

In a model of bounded best-response reasoning, level 0 players might naturally be assumed to claim all the discs (naïvely ignoring the strategic nature of their situation). Given that assumption, if higher-level players choose weakly dominating strategies conditional on their beliefs, players at all levels will claim all the discs. But whatever level 0 players are assumed to do, and whether or not their behavior is affected by spatial cues, players at all higher levels will still claim all the discs.⁸ If a player claims all the discs, it is reasonable to interpret their decision as evidence of bounded or fully rational best-response reasoning.

However, a player who views the game in the perspective of team reasoning will ask themself “What is it best for us to do?” The answer to this question is clearly not that “each of us should claim all the discs, with the result that we will both be sure to get nothing”. A more plausible answer is that “we should try to find a way of ensuring that each disc is claimed by one and only one of us, and that the total value of the discs is shared as equally as possible between us”.

In some models of team reasoning, “What is it best for us to do?” is interpreted as a question about how to maximize the collective welfare of the players (e.g., Bacharach, 2006). In other models, it is interpreted as a question about what the members of the group would agree to do, if they were able to communicate and make binding agreements (e.g., Misyak and Chater, 2014; Sugden, 2015). On either interpretation, a strategy profile that has a uniquely salient label and produces an LUE payoff distribution has an obvious appeal as “best for us”. In Isoni et al.'s (2013) experiment, and thereby also in our multi-agreement variant, the closeness rule identified such a profile in every spatial-cue game.

We now consider the implications of team reasoning for neutral multi-agreement games. We assume that the players of neutral games do not recognize any cues, spatial or otherwise, that distinguish between the players. (For example, there may be common recognition of the distinction between higher and lower rows of the table or between discs with different values, but not that a specific player has a special relationship with particular rows or disc values.) Since the players' positions are identical, any (pure or mixed) strategy recommended by team reasoning to one player must also be recommended to the other. We therefore restrict attention to team strategies that are chosen by both players.

First, consider any equality-compatible scenario. The rule that each player claims some set of discs whose value sums to half the total on the table has obvious intuitive appeal as a team strategy. It also has a theoretical justification, which extends to equality-incompatible scenarios.

We define an LUE partition of the set of discs on the table as any partition {S₁, S₂} such that, if one player claims set S₁ and the other claims set S₂, the payoff distribution is LUE. Let v denote the absolute difference between the players' payoffs in this distribution. Consider the following team strategy. Independently, each player picks some LUE partition. (It doesn't matter which partition this is, or whether the players pick the same or different partitions.) Each player then picks one of the sets in their partition at random and claims the discs in that set. This strategy has two significant “best for us” features. First, each disc is claimed by each player with independent probability 1/2, maximizing the probability that that disc will be claimed by exactly one player.⁹ In other words, ex ante efficiency is maximized, given the neutral framing of the scenario. Second, the difference between the players' ex post payoffs is certain to be equal to the difference between the values of their claims. (As noted earlier, each player's payoff is the value of their own claims minus the value of discs that are claimed by both players.) Thus, in an equality-compatible scenario, there is certain to be ex post payoff equality. In an equality-incompatible scenario, the absolute difference between the players' payoffs is no greater than v, the LUE inequality.

This design allows us to discriminate between modes of reasoning by looking at the total value of each player's claims, with maximal claims (£10 in equality-compatible games and £11 in equality-incompatible games) indicating bounded best-response strategies and LUE claims (£5 in the 10 equality-compatible games, £5 or £6 in the 10 factorial equality-incompatible games¹⁰) indicating team reasoning strategies. The spatial framing manipulation that promotes the closeness rule in spatial-cue scenarios allows us to examine whether, in those scenarios, claims concentrate on discs located on each player's own side of the table, and whether that results in more efficient bargaining outcomes than in neutral scenarios and in expected payoff differences between the two players.

2 Materials and methods

This experiment was conducted contemporaneously with, and using the same subject pool as, the experiment reported in Isoni et al. (2013). No participant took part in both experiments. The procedures of the two experiments are very similar, the main difference being in the payoff rule, as explained earlier. The research was approved by the ethics committee of the School of Economics of the University of East Anglia.

2.1 Participants

We recruited 100 participants from the general population of the University of East Anglia in six experimental sessions (two with 18 participants and 4 with 16 participants). Each session lasted between 60 and 80 min. The average payment was £7.21 (min £5, max £15), including a £5 show-up fee.

2.2 Procedures

Upon arrival at the lab, each participant sat at a computer in a separate cubicle. The experimental instructions appeared on screen and were read aloud by an experimenter, with participants able to ask questions at any time. The full text of the instructions is reproduced in the Supplementary material.

Each participant was told they had been matched with another anonymous participant for the duration of the experiment. They took part in 24 spatially-framed, two-player, one-shot tacit bargaining games based on the scenarios described in detail in Section 2.3. The order in which the scenarios were presented was randomized independently for each participant. No feedback of any kind was provided between scenarios. At the end of the experiment, each pair of participants was paid according to their decisions in one of the 24 games, selected at random. The corresponding “real scenario” was brought back on their screens with an indication of both players' claims and the corresponding payoffs. Earnings were paid in cash at the end of the experimental session.

2.3 The scenarios

The scenarios used in the experiment were presented as the examples in Figure 1.

The bargaining problem is given a spatial representation via a 9 × 9 grid—the bargaining table. The two players are represented by the red and blue bases located in the two sides of the table, in cells (−2, 0) and (2, 0), respectively (where the first entry is the column coordinate and the second the row coordinate). The positions and the colors of the two bases were the same in all scenarios faced by each pair of participants. However, whether the left base was red or blue was varied between sessions. Each participant was allocated to the same base for all the scenarios, so half of the participants played as Left players and half as Right players. This allocation was disclosed at the end of the instructions, before the first scenario.

The objective of the game was to agree on a division of an available surplus, represented by the valuable discs scattered over the bargaining table. The rules of the game were described as follows:

“You and the other person have the opportunity to agree on who gets each disc.

You and the other person separately record which discs you propose to take. We will say that you are claiming those discs. You can claim as many (or as few) discs as you want. For each disc, these claims determine whether there is an agreement or not.

There is an agreement about a disc if it has not been claimed by both you and the other person. In this case, if that disc is yours according to the agreement, you get the disc and earn its money value.

But if any disc has been claimed by both you and the other person, there is no agreement about that disc. In this case, no one gets it and so no one earns its money value.”

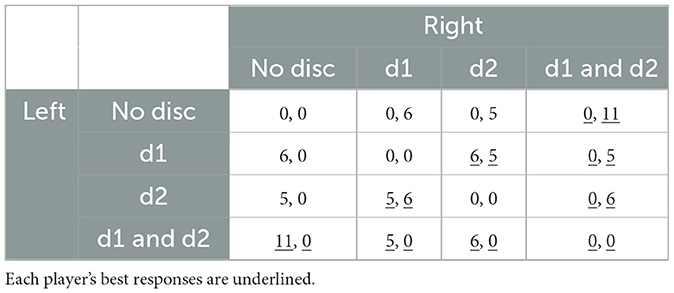
Given these multi-agreement payoff rules, the game resulting from both scenarios shown in Figure 1 can be described by the 4 × 4 payoff matrix shown in Table 1, where the first number in each cell represents the Left player's payoff and the second number represents the Right player's. Each player's best responses are underlined.

Table 1

Table 1. The payoff matrix of G1 = 6| |5 and G3 = |6, 5|.

The game has nine pure-strategy Nash equilibria. For each player, claiming both discs is a weakly dominant strategy. As explained, according to bounded best-response reasoning, each player would choose to claim both discs, and the outcome of the game would be that both players would get a payoff of zero. According to team reasoning, each player would claim just one of the discs, aiming for one of the 6:5 LUE allocations.

The two scenarios in Figure 1 differ with respect to the spatial framing. The scenario in panel A is a neutral scenario: both discs are in the middle column of the bargaining table, and hence are equidistant from the two players' bases. The scenario in panel B, on the other hand, is a spatial-cue scenario: one disc is on the left side of the table, closer to the left base, the other is on the right side, closer to the right base. We will use the compact notation G1 = 6| |5 and G3 = |6, 5|, where the two vertical lines denote the middle column of the table, to represent the spatial framing of these scenarios.

The premise of our experiment, supported by evidence based on a variant of this design (Isoni et al., 2013, 2020), is that team reasoners would use the closeness rule and identify the LUE division of the discs in which each player claims the disc(s) on their side of the table as the “obvious” solution of the coordination problem posed by the scenario. By including matched pairs of scenarios like G1 and G3, we can test whether this spatial framing has systematic effects on the outcome of tacit bargaining.

The 24 scenarios used in the experiment comprised eight scenarios with just two discs (G1–G4, G13–G16), eight with four discs (G5–G12), and eight with eight discs (G17–G24).

Table 2 shows all the scenarios using a compact notation similar to Isoni et al.'s (2013), in which vertical bars delimit the middle column of the bargaining table, round brackets enclose blocks of contiguous discs and discs are listed from left to right and from top to bottom. The table adopts the 2 (equality-compatible vs. equality-incompatible) × 2 (spatial-cue vs. neutral) classification introduced earlier and includes the four equality-incompatible scenarios with LUE 8:3 and 10:1. So, for each spatial-cue scenario, there is a corresponding neutral scenario with the same number of discs, disc values and disc block structure. For example, G21 = (2,2,1|1)(1|1,1,2) is an eight-disc spatial-cue scenario with two blocks of four discs each. The first block has three discs on the left-hand side and one in the middle column, the second has one in the middle column and three on the right-hand side. The corresponding neutral scenario is G23 = |(2,2,1,1)(1,1,1,2)|, in which the two blocks of four discs are stacked vertically in the nine cells of the middle column with just one gap in the middle. Supplementary Figure S1 shows sample displays for all 24 scenarios.

Table 2

Table 2. The scenarios used in the experiment.

In addition to the counterbalancing of the base colors, each scenario was presented in two further variations, obtained by changing the sign of both coordinates. This transposition amounts to flipping each disc's position relative to the (bottom-left/top-right) diagonal of the table and has the effect of changing each disc position from left to right and from top to bottom. For equality-incompatible scenarios, this also changes which side of the table (left or right, top or bottom) contains a larger share of the surplus. For example, in relation to G1 = 6| |5, this means that some participants saw the £6 disc in cell (−3, −2) as in Figure 1, and other participants saw that disc in cell (3, 2). For that scenario, the transposition resulted in a straight swap of the two discs' positions.¹¹

3 Results

We will start by looking at the distribution of claims by value (Section 3.1). We will then turn to the spatial distribution of claims (Section 3.2). The effect of claims on the efficiency of bargaining outcomes will be examined in Section 3.3. Section 3.4 will look at differences in expected payoffs between players induced by the spatial framing. Section 3.5 will conclude by examining individual-level heterogeneity.

3.1 The distribution of claims by value

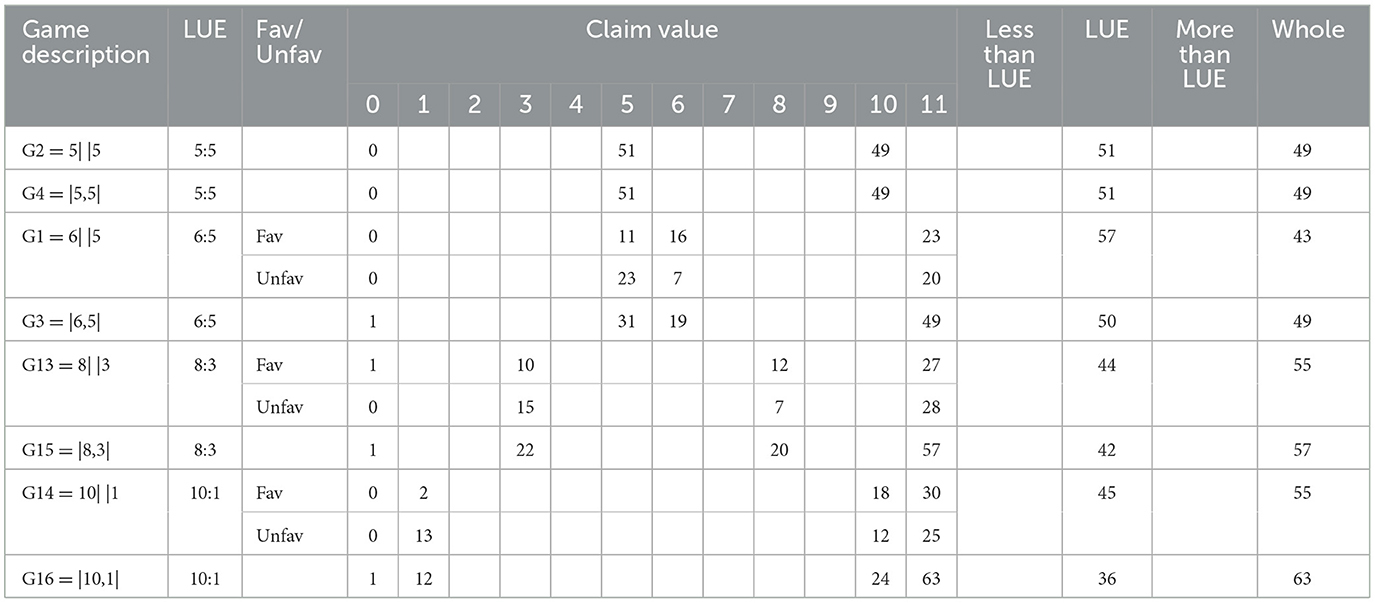
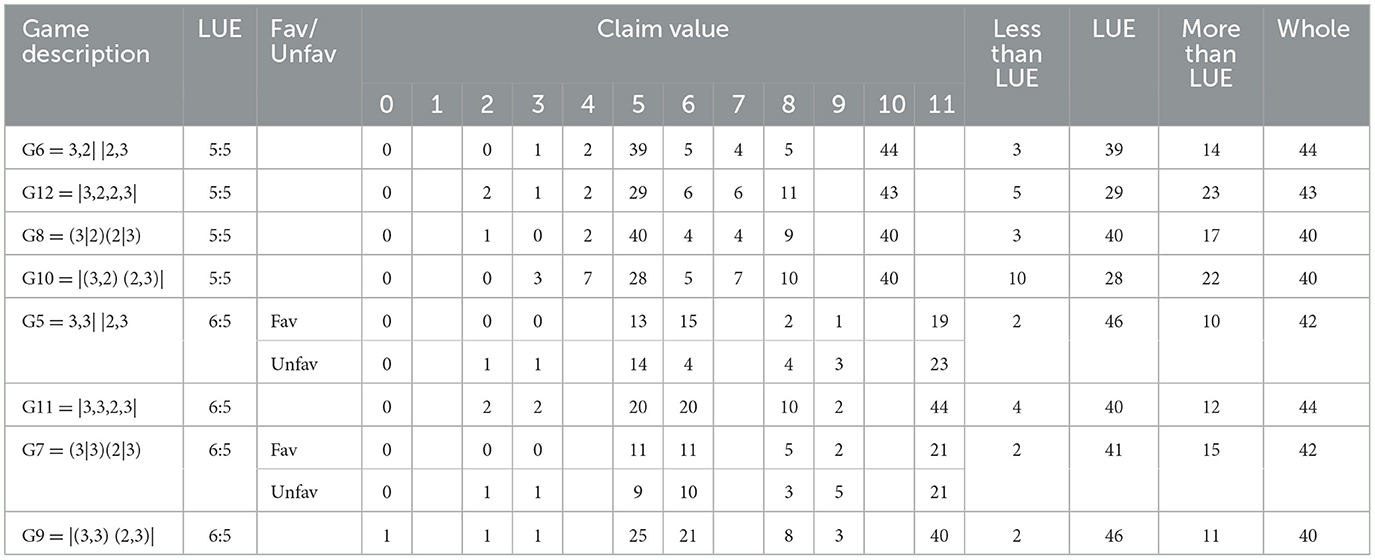
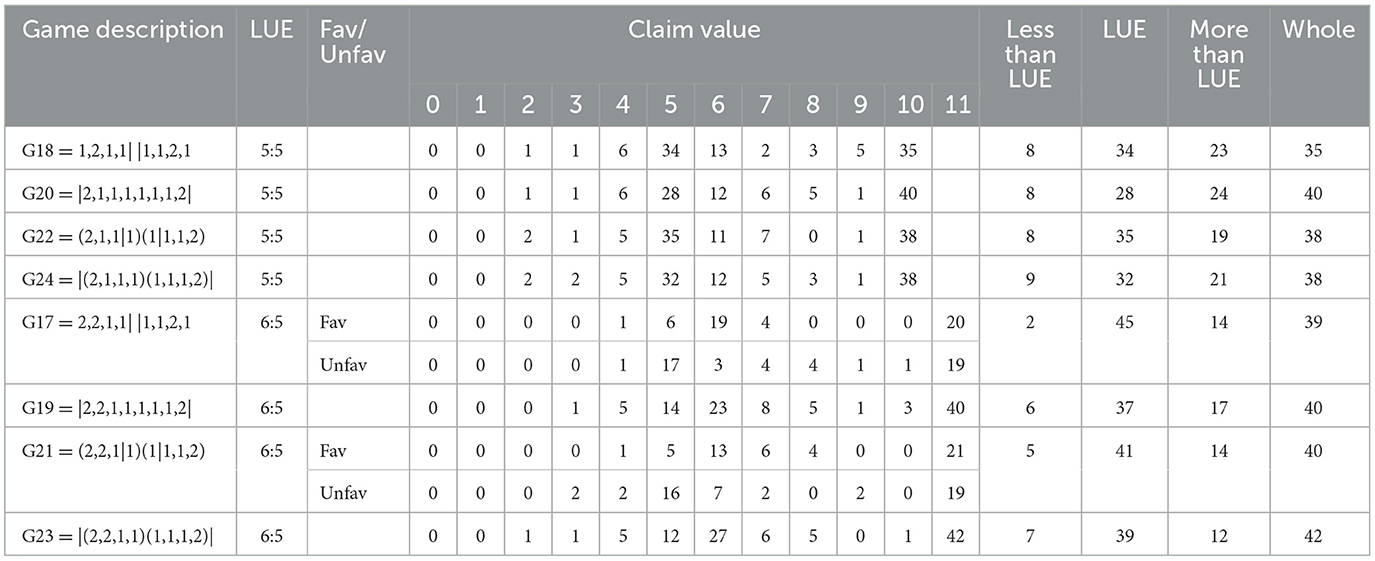
Tables 3–5 present summaries of the total values claimed by participants in scenarios with 2, 4, and 8 discs respectively. For each scenario, the table reports the LUE split (in the x:y format, where x is the higher LUE share if x≠y), the frequency of participants who claim each possible total allowed by the values of the discs in the scenario, the number of participants who claimed each of (i) at least one disc but less than the lower LUE share, (ii) one of the LUE shares, (iii) more than the higher LUE share but less than the whole surplus, and (iv) all discs (whole claims). For equality-incompatible spatial-cue scenarios, in which the closeness rule implies that one player (the favored player) should claim the higher of the two LUE shares and the other (the unfavored player) should claim the lower LUE share, the claims distributions are presented separately for the two players.

Table 3

Table 3. Distribution of claims by value in 2-disc games.

Table 4

Table 4. Distribution of claims by value in 4-disc games.

Table 5

Table 5. Distribution of claims by value in 8-disc games.

The three tables reveal the following regularities.

First, participants understand dominance. Across all scenarios, there are only 5 instances (4 in 2-disc scenarios and 1 in a 4-disc scenario) in which participants do not claim any disc. There is no scenario in which this happens more than once.

Second, while claiming all discs is a weakly dominant strategy, in all scenarios there is a sizeable proportion of participants who leave discs unclaimed. The percentage of whole claims ranges from a minimum of 35% (in G18 = 1,2,1,1| |1,1,2,1) to a maximum of 63% (in G16 = |10,1|). The percentage is higher in 2-disc scenarios (between 43 and 63%), where it increases with the difference between the two LUE shares, and lower in 4- (between 40 and 44%) and 8-disc scenarios (between 35 and 42%).

Third, LUE claims are extremely common. In 2-disc scenarios, where positive claim values can only result from LUE claims or whole claims, the total number of LUE claims is often greater than the number of whole claims. This happens for the least unequal LUEs (5:5 and 6:5). For larger payoff differences (LUE 8:3 or 10:1), whole claims are more common. Overall, LUE claims prevail in 9 scenarios, whole claims in 15.

Fourth, in 2-disc equality-incompatible scenarios, there is a mild tendency in the direction of the “after you” effect: in neutral scenarios with LUE 6:5 and 8:3, the majority of LUE claims are on the lower LUE share; in spatial-cue scenarios with LUE 6:5 and 8:3, there are more favored players claiming the lower LUE share than unfavored players claiming the higher LUE share; both patterns are reversed in scenarios with LUE 10:1. Because each LUE share can be obtained via multiple disc combinations, similar tendencies are much harder to detect in 4- and 8-disc scenarios, where they are only visible in G5 = 3,3| |2,3.

Fifth, in 4- and 8-disc scenarios, significant proportions of participants (between 12 and 32%) make claims that are neither LUE claims nor whole claims. The great majority of such claims (76% across all relevant scenarios) are greater than the higher LUE share.

3.2 The spatial distribution of claims

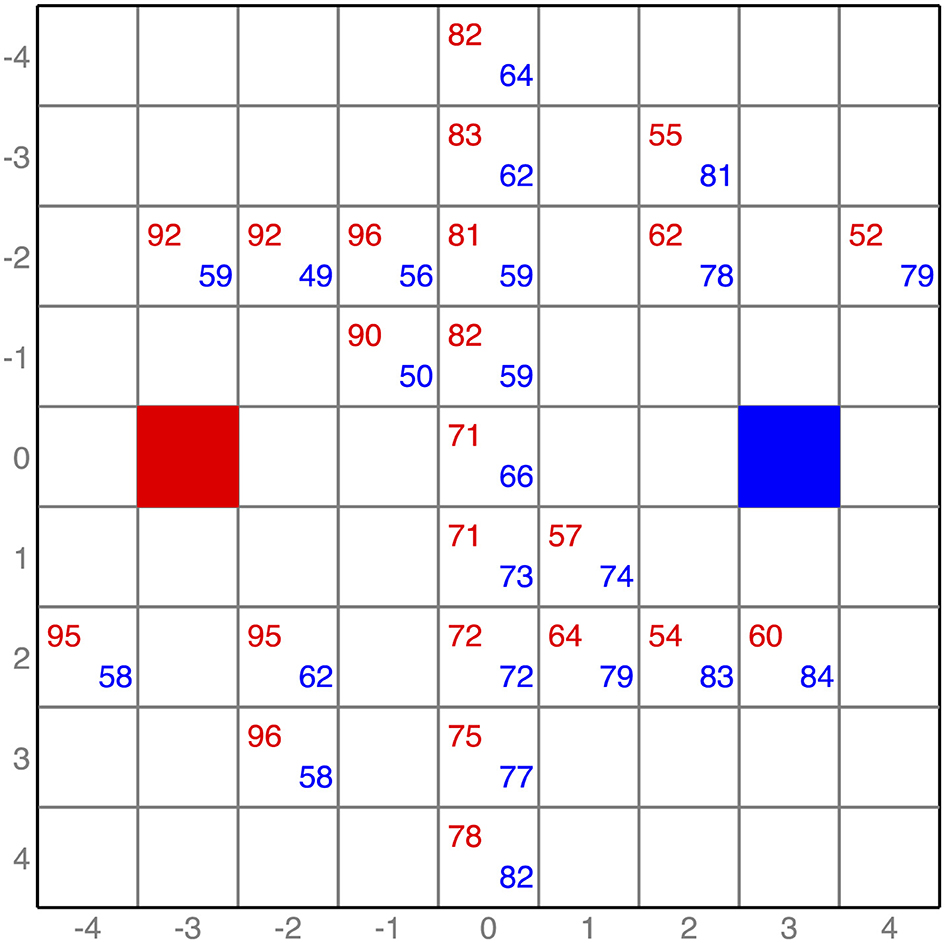
Figure 2 provides a summary of the spatial distribution of claims pooling across the 24 scenarios. For each of the cells of the bargaining table in which there was a disc, the figure reports the percentage of Left players (in red) and the percentage of Right players (in blue) who claimed a disc located in that cell. This aggregation is legitimate because the transposition of disc positions along the diagonal neutralizes any effects on claims driven by differences in disc values. Supplementary Tables S1, S2 report detailed information for individual spatial-cue and neutral scenarios.

Figure 2

Figure 2. The spatial distribution of claims.

Because of the high incidence of whole claims highlighted earlier, in all occupied cells both percentages are above 50%. Ignoring the middle column, a clear pattern emerges. In all the left-hand side cells of the table, the percentage of claims made by Left players exceeds the percentage of claims made by the Right player. The opposite is true for the right-hand side cells, where discs were claimed more frequently by Right than Left players. This pattern, necessarily driven by the 12 spatial-cue scenarios, is consistent with the application of the closeness rule.¹²

We conduct a statistical test of this spatial pattern as follows. For each player, we compute two variables: the proportion of claims they made on discs located on their side of the table averaged across all 12 spatial-cue scenarios, and the proportion of claims they made on discs located on the other side of the table, also averaged across all 12 spatial-cue scenarios. Across all scenarios, discs located on players' own side of the table represented 55.5% of their claims, while discs located on the other side of the table represented just 32.4%.¹³ We use the Wilcoxon singed-rank test to test the null hypothesis that the distribution of these two variables is the same. The null hypothesis is decisively rejected (p < 0.001).

3.3 The efficiency of bargaining outcomes

We will use the term efficiency to refer to the fraction of the available surplus obtained by the two players in the form of payoffs resulting from their claims. Because the multi-agreement payoff rule makes it a weakly dominant strategy for both players to claim all discs and this will result in both players obtaining a payoff of zero, bargaining outcomes can be expected to be highly inefficient if players adopt bounded best-response reasoning. To the contrary, team reasoning is expected to increase efficiency, especially in spatial-cue scenarios, in which the closeness rule picks out a specific LUE partition.

To study bargaining outcomes, we derive an empirical measure of efficiency comparable between scenarios. For this purpose, it is not very meaningful to use the participants' actual payoffs. In our experiment, like in many incentive-compatible coordination game experiments without communication, participants played many games without feedback, and were paid according to their decisions in just one. So, bargaining outcomes are technically defined only for the games used to determine players' payoffs. Computing payoffs in other games using the same player pairings, or other random pairings, is feasible but rather arbitrary and noisy. To circumvent these issues, we follow standard practice by basing our calculation of efficiency on a measure of expected payoffs. In each scenario, each participant could potentially be matched with all other participants who took the role of the other player (Left or Right) in that scenario and faced that scenario with an identical display in terms of disc values, disc positions and base colors. A player's expected payoff is the average of the payoffs they would have obtained from their claims when matched, in turn, with all these other potential coplayers. For each game, efficiency is computed as the sum of the average expected payoffs of Left and Right players divided by the total value of the discs on the table. So, it ranges from 0 (when in each possible pairing of participants, no disc is claimed by just one player) to 1 (when in each possible pairing of participants, all discs are claimed by just one player).

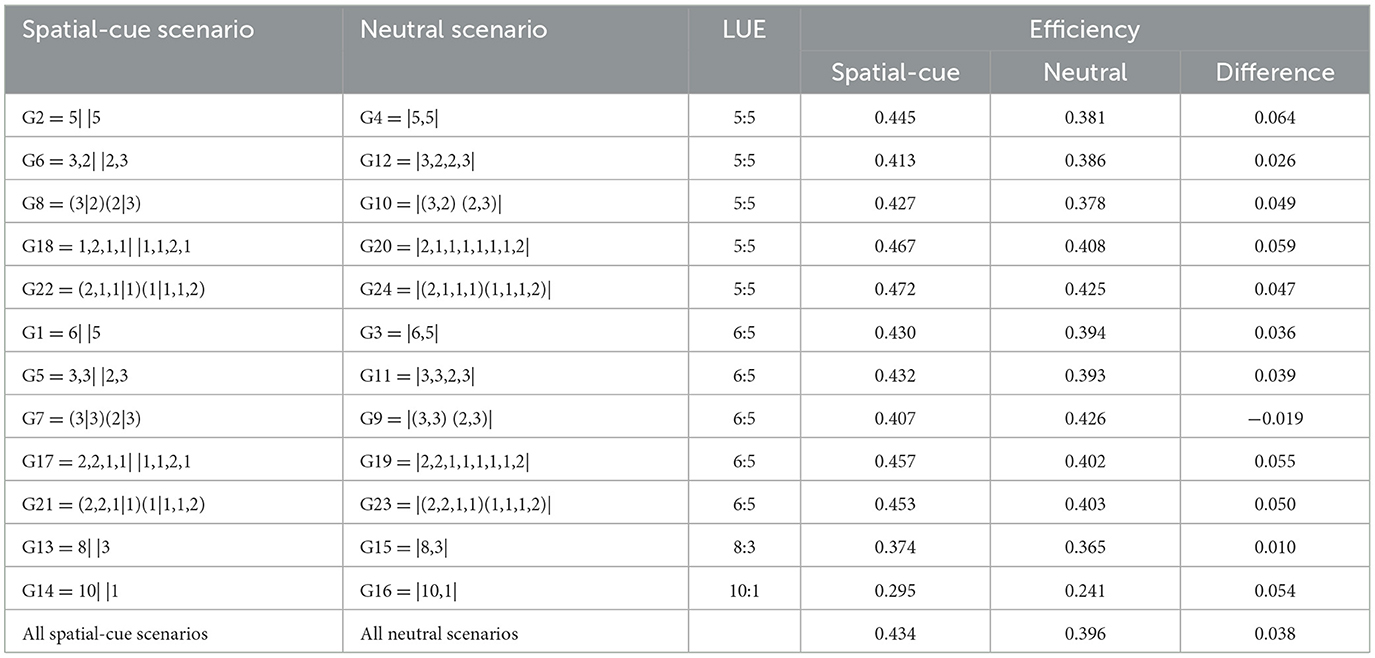
Table 6 reports efficiency statistics for matched pairs of spatial-cue and neutral scenarios. The last column shows the difference in efficiency arising from the spatial framing.

Table 6

Table 6. Efficiency in matched pairs of spatial-cue and neutral scenarios.

Not surprisingly given the large proportion of participants making whole claims, efficiency levels are generally low, ranging from 0.241 in G16 = |10,1| (an equality-incompatible neutral scenario with very unequal LUE) to 0.472 in G22 = (2,1,1|1)(1|1,1,2) (an equality-compatible spatial-cue scenario). Averaging by LUE value, efficiency is 0.420 in 5:5 and 6:5 scenarios, 0.370 in 8:3 and 0.268 in 10:1 scenarios, replicating the negative relationship between efficiency and LUE inequality reported by Isoni et al. (2013) for single-agreement bargaining table games.

The efficiency statistics in Table 6 allow us to examine the effects of spatial framing on coordination success. For 11 out of the 12 scenario pairs, the efficiency difference between the spatial-cue and the corresponding neutral scenario is positive, indicating that the application of the closeness rule visible in the spatial distribution of claims resulted in a general increase in efficiency.¹⁴ Averaging across all scenario pairs, efficiency is 0.434 in spatial-cue scenarios and 0.396 in neutral scenarios, with an average difference of 0.038, corresponding to an expected payoff difference of about £0.20.

We conduct statistical tests of these differences in efficiency using an adaptation of the bootstrap method employed by Isoni et al. (2019; 2020). We derive distributions of efficiency values for all scenarios by repeatedly resampling with replacement from the original data and creating 1,000 replicas of the original experiment. This produces distributions of efficiency levels for all scenarios, which can be used to compare efficiency in individual spatial-cue scenarios with their neutral counterparts by computing differences in efficiency and checking whether a null difference is included in the resulting two-sided 99 (respectively, 95) percent confidence intervals. To conduct an aggregate test, we look at the distribution of the difference between the mean efficiency in all 12 spatial-cue scenarios and the mean efficiency in all 12 neutral scenarios. The resulting boostrapped differences in efficiency and the relevant percentiles are reported in Supplementary Table S4.

Although the efficiency differences are not significant for individual scenarios, the clear general trend evident in Table 6 is reflected in the aggregate test. Averaging over all spatial-cue scenarios and over all neutral scenarios, 99% of the simulated experiments result in an efficiency difference of at least 0.010. The seemingly small differences in efficiency are the result of the effect that whole claims have in reducing expected payoffs and therefore efficiency levels.

3.4 Expected payoff differences in equality-incompatible spatial-cue scenarios

In all our spatial-cue scenarios, the closeness rule identifies one of the LUE partitions as the salient solution to the bargaining problem. In equality-incompatible scenarios, this means that one of the players (the favored player) should claim a larger share of the surplus. General adherence to this principle would entail that expected payoffs (as defined in the previous section) should be higher for favored than unfavored players. We now look at these differences.

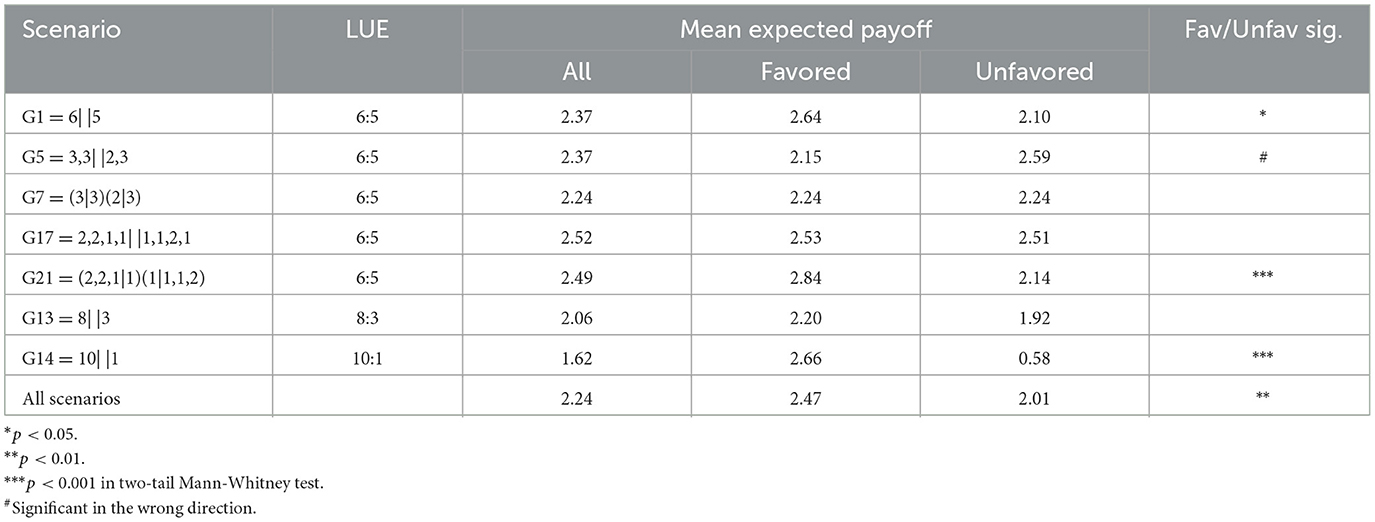
Table 7 reports summaries of mean expected payoffs for favored and unfavored players in the seven equality-incompatible spatial-cue scenarios.

Table 7

Table 7. Expected payoffs in equality-incompatible spatial-cue scenarios.

In five out of seven scenarios, the favored players' expected payoff is higher than the unfavored players'. In one scenario (G7 = (3|3)(2|3)) they are identical, and in one (G5 = 3,3| |2,3) the difference goes in the opposite direction. In three SCENARIOS, the effect is statistically significant (p < 0.05 in G1 = 6| |5, and p < 0.001 in G21 = (2,2,1|1)(1|1,1,2) and G14 = 10| |1). In G5 = 3,3| |2,3, the effect is significant in the opposite direction (p < 0.05). Averaging over the seven scenarios, favored players have an expected payoffs of £2.47, unfavored players of £2.01. This difference is statistically significant in a Mann-Whitney test (p < 0.01).

3.5 Individual-level heterogeneity

As discussed in Section 3.1, Tables 3–5 show that the vast majority of all claims in most scenarios were either whole claims, as implied by (bounded) best-response reasoning, or LUE claims, as implied by team reasoning. In 4- and 8-disc scenarios, a sizeable minority of participants made claims that totaled between the higher LUE share and the whole surplus.

Previous work suggests that individual players of coordination and tacit bargaining games are capable of both best-response and team reasoning and often use a different mode of reasoning in different games in the same experiment (e.g., Crawford et al., 2008; Faillo et al., 2017; Isoni et al., 2019). We now present some individual-level analysis to investigate such heterogeneity in our experiment.

We compute the proportion of whole claims and the proportion of LUE claims each participant made over the 24 scenarios. Excluding the possibility of making no claims, whole claims and LUE claims were the only possibility in 2-disc games. So, the sum of these proportions could range between 1/3 and 1.

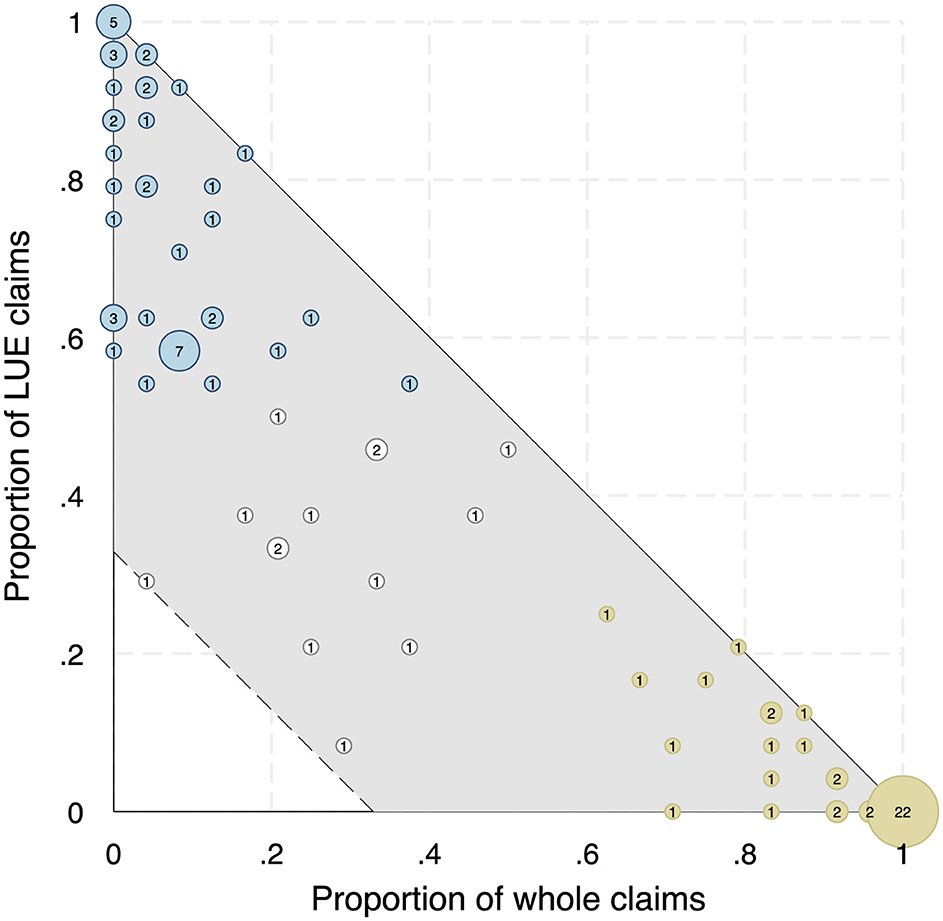
The bubble plot reported in Figure 3 summarizes the heterogeneity in participants' claims by plotting, for each combination of proportion of whole claims (horizontal axis) and proportion of LUE claims (vertical axis), the frequency of that combination in the sample. The shaded area represents the range of possible combinations. The size of the bubbles reflects the corresponding frequency, also shown in the graph.

Figure 3

Figure 3. Whole and LUE claims at the individual level.

The bubbles are color-coded to reflect each participant's most frequent strategy. Khaki bubbles show the 41 participants who behaved mostly as rational players by making whole claims in more than half of the scenarios. Twenty-eight of these participants (68%), found on the horizontal axis, never made LUE claims. Blue bubbles show the 45 participants who behaved mostly as team reasoners by making LUE claims in more than half of the scenarios. Eighteen of these participants (40%), found on the vertical axis, never made whole claims. White bubbles indicate participants who made neither whole nor LUE claims in more than half of the games. Only 1 participant never made whole or LUE claims.¹⁵

Only 27 participants (22 plus 5) out of 100 used the same strategy in all scenarios. This is in line with evidence suggesting participants are capable of more than one form of reasoning. However, the frequencies on the hypothenuse (including the two vertices) add up to just 33 participants (one third of the sample). These are participants who exclusively made claims consistent with (bounded) best-response or team reasoning. The remaining 67 participants used some other strategy in at least one of the scenarios. From Tables 3–5 we know that most of these participants claimed more than the higher LUE share but less than the whole surplus.

4 Discussion

The individual-level analysis in Section 3.5 suggests that most participants can be classified as members of one of two approximately equal-sized groups. One group had a strong tendency to make whole claims. Since making whole claims is a weakly dominant strategy, explaining this pattern of behavior is unproblematic. It is consistent both with standard theories of fully rational choice and with theories of bounded best-response reasoning, such as cognitive hierarchy theory (Camerer et al., 2004) and level-k theory (Stahl and Wilson, 1994; Nagel, 1995). Viewed in the perspective of conventional game theory, the only puzzle is why whole claims were not more common.

The defining characteristic of the second group is a strong tendency to make LUE claims. This tendency appears in all types of scenarios—whether equality-compatible or equality-incompatible, with or without spatial cues, or with two, four or eight discs. Making an LUE claim is clearly contrary to a player's self-interest (unless the player is completely certain that every disc not included in that claim will be claimed by their coplayer). However, the idea that the “best for us” solution to a bargaining problem is some LUE partition of the available surplus is very intuitive. Having recognized this, players who use team reasoning may still face the problem of coordinating on the same LUE partition, but if each player's claim is LUE, ex post inequality is certain to be equal to the difference between the values of the two LUE shares. If the two shares have equal value (as in equality-compatible games) or are only slightly different (as in all the equality-incompatible games except G13, G14, G15, and G16), this gives a “best for us” reason for each player to make an LUE claim. Thus, a general tendency to make LUE claims is an indicator of team reasoning.

A second property of the LUE-claiming group is a tendency for players to claim discs on their side of the table more frequently than discs on the other side in spatial-cue scenarios. In all spatial-cue scenarios, a player who follows the closeness rule (i.e., claims exactly the set of discs on their side) makes a specific LUE claim when at least one other LUE claim (i.e., the set of discs on the other side) is possible. In equality-compatible spatial-cue scenarios, this rule, if followed by both players, induces an efficient and equal distribution of the surplus. In equality-incompatible spatial-cue scenarios, the same rule induces an LUE partition of the surplus in which unfavored players experience disadvantageous inequality. The spatial layout of discs in a scenario is a payoff-irrelevant feature, analogous with strategy labels in matching games. If players perceive closeness as a particularly salient property, there is a “best for us” reason for each player to follow the closeness rule, even if that requires them to claim the smaller share in an LUE partition (“disciplining themselves” in Schelling's phrase). Using payoff-irrelevant cues to achieve coordination is another indicator of team reasoning. In the experiment, 64% of LUE claims by favored players were for the larger share of the surplus and 68% of LUE claims by unfavored players were for the smaller share. In 4- and 8-disc scenarios, favored players who made LUE claims rarely claimed an LUE share by claiming the discs that the closeness rule assigned to the unfavored player, and vice versa for unfavored players (see Supplementary Table S5).

It would be wrong to treat the remaining 36% of LUE claims by favored players or the remaining 32% of LUE claims by unfavored players as evidence against team reasoning. In an equality-incompatible spatial-cue scenario, a team-reasoning player can be expected to focus on the importance for us (i.e., the two players considered together) of reaching agreement on some LUE partition of the surplus. Each can see that such an agreement is possible only if one of us accepts the smaller share. The spatial cue of closeness, like a salient label in a Pure Coordination matching game, can be perceived as pointing to a particular solution for the players as a team. But, just as in such games, players may have different perceptions of salience or believe that their coplayers' perceptions are different from their own. LUE claims that do not follow the closeness rule may be evidence of differences in salience perception among team-reasoning players.

Another case where LUE claims do not follow the closeness rule is represented by the mild “after you” effect in 2-disc scenarios we alluded to in Section 3.1. The effect is barely visible in G1 = 6| |5, where 11 favored players go against the spatial cue and claim £5 and 7 unfavored player do so by claiming £6, and in G13 = 8| |3, where the corresponding numbers claiming £3 and £8 are 10 and 7, respectively. It is much more marked in G3 = |6,5|, where 31 players claim £5 and 19 claim £6. This could be part of a general predisposition by team reasoners to put their personal interest after that of the team, which in the presence of uncertainty about what the other team member would do (which is likely to be greater in neutral scenarios than in spatial-cue scenarios) manifests itself in a tendency to claim the lower LUE share.

But before inferring that the LUE-claiming group of players were acting on team reasoning, we should consider other possible explanations of the frequency of LUE claims in general and of the particular frequency of the claims implied by the closeness rule. Up to now, our definition of “best response” has implicitly assumed that each player's objective is to maximize the expected value of their material (i.e., monetary) payoff. But what if players have preferences for equality?

Inequality aversion may provide an explanation for claims that are higher than LUE but not whole. Suppose a player had dispersed beliefs about the value of their co-player's claims represented by some probability distribution. If they made claims equal to the median of that distribution, they would experience some disutility from disadvantageous inequality (“envy”) with respect to higher co-player's claims and some disutility of advantageous inequality (“guilt”) with respect to lower co-player's claims. If envy and guilt were equally impactful, claiming the median of the co-player's claims would minimize the expected disutility of inequality (claiming less than the median would increase envy more than it would decrease guilt, and vice versa for claiming more than the median). However, because envy is typically more impactful than guilt, the claim value that would minimize the expected disutility of inequality would be higher than the median of the co-player's claims. Additionally, making higher claims would result in a higher expected material payoff. So, claiming less than the whole surplus but more than the LUE share in equality-compatible scenarios, or more than the higher LUE share in equality-incompatible scenarios, may be seen as a form of bounded best-response reasoning by inequality averse players.

However, inequality aversion is not a satisfactory explanation of the prevalence of LUE claims, especially with respect to the lower LUE share. In the Supplementary material, we apply the inequality aversion model first proposed by Fehr and Schmidt (1999) to the multi-agreement bargaining table games used in our experiment.¹⁶ We show that, for an inequality averse player who believes their co-player will claim a specific set of disc with a total value equal to the lower LUE share, it is a best response to claim the remaining discs making up the higher LUE share. However, if an inequality averse player believes the set of discs claimed by their co-player to be equal to the higher LUE share, claiming the remaining discs making up the lower LUE share is not always a best response. This is because the multi-agreement payoff rule allows a player to reduce inequality at no material cost to themselves, and because disadvantageous inequality causes more disutility than advantageous inequality. This is most obvious when LUE is 8:3 or 10:1, because by claiming the more valuable disc in addition to the less valuable disc, a player can turn a large disadvantageous inequality into a smaller advantageous inequality, with no change in their material payoff.

This conclusion highlights an important difference between individual best-response reasoning and team reasoning. Inequality aversion is an “I”-attitude—the attitude of an individual (P1) to their position relative to that of another person (P2). P2 features in P1's reasoning only as a means to, or as a constraint on, the satisfaction of P1's preferences. The multi-agreement payoff rule allows bargaining-like situations in which, given reasonable beliefs about P2, P1 can choose whether to accept disadvantageous inequality or eliminate it by reducing P2's payoff at no material cost to themself. Inequality aversion can make the latter option preferable.

In contrast, team reasoning expresses a “we”-attitude—an attitude that a person holds as a member of a two-person group. In a two-person interaction in which mutual benefit can be achieved only if one person takes a smaller share of the surplus than the other, a team-reasoning individual may knowingly accept the smaller share if a payoff-irrelevant cue makes that division salient. In explaining why people accept the discipline of focal points, Schelling (1960, p. 65–66, 70, 112, 300) repeatedly uses rhetorical questions of the form “If not this, what?” In the bargaining problems we have studied, the equivalent question is: “If not me, who?”

Data availability statement

The raw data supporting the conclusions of this article can be found at: https://osf.io/68qtu/.

Ethics statement

The studies involving humans were approved by School of Economics Research Ethics Committee of the University of East Anglia. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

AI: Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing, Data curation, Software. AP: Conceptualization, Investigation, Methodology, Writing – review & editing, Funding acquisition, Resources. RS: Conceptualization, Funding acquisition, Investigation, Methodology, Resources, Formal analysis, Project administration, Writing – original draft, Writing – review & editing. KT: Conceptualization, Investigation, Methodology, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the Economic and Social Research Council of the UK (Award No. RES-000-22-3322) and by the Leverhulme Trust (Award F/00 204/AV).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frbhe.2025.1569272/full#supplementary-material

Footnotes

1. ^A strategy profile is a list of strategies, one for each player. Payoff profiles are defined similarly.

2. ^For this reason, direct comparisons between the two designs are not particularly informative in relation to our research questions.

3. ^In Figure 1, discs are labeled d1 and d2, and rows and columns are numbered −4 to 4. These labels were not shown to participants, but will be useful later on. Similarly, each scenario is given a label (like G3 = |6, 5| and G1 = 6| |5 in Figure 1), not seen by participants, that we will use in the description of our design and the presentation of our results.

4. ^No scenario had blocks of contiguous discs that spanned the two halves of the bargaining table.

5. ^The other four scenarios explored the effects of increasing the inequality of the LUE distribution (defined below) in 2-disc games. Two of these scenarios were spatial-cue scenarios and two were the corresponding neutral scenarios.

6. ^In comparison with Pure Coordination, Battle of the Sexes introduces both conflict of interest (i.e., the players have opposite preferences between the pure-strategy equilibrium) and payoff inequality (i.e., the players have unequal payoffs in both equilibria). By using a third game, Isoni et al. (2020) find that the coordination-inhibiting effects of Battle of the Sexes are mainly driven by conflict of interest.

7. ^Misyak and Chater's (2014) concept of “virtual bargaining” broadly fits with team reasoning but has not been used to explain behavior in coordination games.

8. ^Many theories of bounded best-response reasoning assume that level 0 players exist only in the minds of higher-level players (e.g., Crawford et al., 2008, p. 1447).

9. ^If each player claims a disc with probability p, the probability that there is an agreement on that disc is p(1 – p), which is maximized at p = 1/2.

10. ^In the remaining four equality-incompatible scenarios, LUE was either £8–£3 or £10–£1.

11. ^The diagonal transposition was applied between sessions, resulting in 52 and 48 participants respectively facing each of the two variations.

12. ^Figure 2 also reveals a slight tendency for Left players to make more claims than Right players, especially on discs located in the middle column.

13. ^The reason why these two percentages do not add up to 100% is that the definition of the two variables excludes the two discs located in the middle column in scenarios with blocks of contiguous discs G7 = (3|3)(2|3), G8 = (3|2)(2|3), G21 = (2,2,1|1)(1|1,1,2) and G22 = (2,1,1|1)(1|1,1,2). Supplementary Table S3 reports a breakdown of these statistics by scenario, and by Left/Right player.

14. ^For example, in each of G2 = 5| |5 and G4 = |5,5|, 51 participants made claims worth £5 and 49 participants made claims worth £10. Efficiency is 0.445 in G2 and 0.381 in G4. Because efficiency differences can only arise when both players claim £5 (if both claim £10, total payoff is £0; if one claims £10 and the other £5, total payoff is £5), these figures imply that in G2 those claiming £5 had a 0.75 probability of coordinating (equivalent to 85% claiming the close disc), while those doing so in G4 had a 0.5 probability of coordinating (equivalent to them choosing a disc at random).

15. ^Supplementary Figure S2 reports the same analysis for the 12 spatial-cue scenarios. The distributions are very similar.

16. ^A similar model was proposed by Bolton and Ockenfels (2000).

References

Bacharach, M. (2006). Beyond Individual Choice: Teams and Frames in Game Theory. Princeton, NJ: Princeton University Press.

Google Scholar

Bardsley, N., Mehta, J., Starmer, C., and Sugden, R. (2010). Explaining focal points: cognitive hierarchy theory versus team reasoning. Econ. J. 20, 40–79. doi: 10.1111/j.1468-0297.2009.02304.x

PubMed Abstract | Crossref Full Text | Google Scholar

Bernheim, B. D. (1984). Rationalizable strategic behavior. Econometrica 52, 1007–1028. doi: 10.2307/1911196

Crossref Full Text | Google Scholar

Bolton, G., and Ockenfels, A. (2000). ERC: a theory of equity, reciprocity, and competition. Am. Econ. Rev. 90, 166–193. doi: 10.1257/aer.90.1.166

Crossref Full Text | Google Scholar

Camerer, C. F., Ho, T. H., and Chong, J. K. (2004). A cognitive hierarchy model of games. Quart. J. Econ. 119, 861–898. doi: 10.1162/0033553041502225

Crossref Full Text | Google Scholar

Costa-Gomes, M., Crawford, V. P., and Broseta, B. (2001). Cognition and behavior in normal-form games: an experimental study. Econometrica 69, 1193–1235. doi: 10.1111/1468-0262.00239

Crossref Full Text | Google Scholar

Crawford, V. P., Gneezy, U., and Rottenstreich, Y. (2008). The power of focal points is limited: even minute payoff asymmetry may yield large coordination failures. Am. Econ. Rev. 98, 1443–1458. doi: 10.1257/aer.98.4.1443

Crossref Full Text | Google Scholar

Faillo, M., Smerilli, A., and Sugden, R. (2017). Bounded best-response and collective-optimality reasoning in coordination games. J. Econ. Behav. Org. 140, 317–335. doi: 10.1016/j.jebo.2017.05.015

Crossref Full Text | Google Scholar

Fehr, E., and Schmidt, K. (1999). A theory of fairness, competition and cooperation. Quart. J. Econ. 114, 817–868. doi: 10.1162/003355399556151

Crossref Full Text | Google Scholar

Hargreaves Heap, S. P., Rojo Arjona, D., and Sugden, R. (2017). Coordination when there are restricted and unrestricted options. Theory Decis. 83, 107–129. doi: 10.1007/s11238-017-9589-9

Crossref Full Text | Google Scholar

Isoni, A., Poulsen, A., Sugden, R., and Tsutsui, K. (2013). Focal points in tacit bargaining problems: experimental evidence. Eur. Econ. Rev. 59, 167–188. doi: 10.1016/j.euroecorev.2012.12.005

Crossref Full Text | Google Scholar

Isoni, A., Poulsen, A., Sugden, R., and Tsutsui, K. (2014). Efficiency, equality and labelling: an experimental investigation of focal points in explicit bargaining. Am. Econ. Rev. 104, 3256–3287. doi: 10.1257/aer.104.10.3256

Crossref Full Text | Google Scholar

Isoni, A., Poulsen, A., Sugden, R., and Tsutsui, K. (2019). Focal points and payoff information in tacit bargaining. Games Econ. Behav. 114, 193–214. doi: 10.1016/j.geb.2019.01.008

Crossref Full Text | Google Scholar

Isoni, A., Sugden, R., and Zheng, J. (2020). The Pizza Night game: efficiency, conflict and inequality in tacit bargaining games with focal points. Eur. Econ. Rev. 127:103428. doi: 10.1016/j.euroecorev.2020.103428

Crossref Full Text | Google Scholar

Isoni, A., Sugden, R., and Zheng, J. (2022). “Focal points in experimental bargaining games,” in Bargaining: Current Research and Future Directions, eds. E. Karagozoglu and K. B. Hyndman (London: Palgrave Macmillan).

Google Scholar

Mehta, J., Starmer, C., and Sugden, R. (1994). The nature of salience: an experimental investigation of pure coordination games. Am. Econ. Rev. 84, 658–673.

Google Scholar

Misyak, J., and Chater, N. (2014). Virtual bargaining: a theory of social decision-making. Philos. Trans. R. Soc. B 369:20130487. doi: 10.1098/rstb.2013.0487

PubMed Abstract | Crossref Full Text | Google Scholar

Nagel, R. (1995). Unraveling in guessing games: an experimental study. Am. Econ. Rev. 85, 1313–1326.

Google Scholar

Pearce, D. C. (1984). Rationalizable strategic behavior and the problem of perfection. Econometrica 52, 1029–1050. doi: 10.2307/1911197

Crossref Full Text | Google Scholar

Schelling, T. C. (1960). The Strategy of Conflict. Cambridge, MA: Harvard University Press.

Google Scholar

Stahl, D. O., and Wilson, P. W. (1994). Experimental evidence on players' models of other players. J. Econ. Behav. Org. 25, 309–327. doi: 10.1016/0167-2681(94)90103-1

Crossref Full Text | Google Scholar

Sugden, R. (1993). Thinking as a team: towards an explanation of non-selfish behavior. Soc. Philos. Pol. 10, 69–89. doi: 10.1017/S0265052500004027

Crossref Full Text | Google Scholar

Sugden, R. (2015). Team reasoning and intentional cooperation for mutual benefit. J. Soc. Ontol. 1, 143–166. doi: 10.1515/jso-2014-0006

Crossref Full Text | Google Scholar