Nanotribology of viruses reveals their adhesion strength and modality of motion on surfaces

Virus adsorption at solid-water interfaces is an ubiquitous phenomenon in the lifecycle of waterborne viruses, both in natural environments and in engineered systems. Airborne aqueous microdroplets containing viruses readily attach to solid surfaces. Inside the droplet, viruses may adhere to the solid-liquid interface. Investigating virus adsorption at solid-water interfaces could lead to new ways to suppress virus infectivity. To further improve our understanding of virus adsorption, we studied the friction dynamics of icosahedral viruses adsorbed to solid surfaces. Using the lateral torsion of cantilevers in atomic force microscopy to move individual capsids in a liquid environment, we found that the virions tend to roll rather than slide on the surface. In contrast, rigid, ligand-stabilized gold nanoparticles are more likely to combine rolling with sliding under the same conditions. The experiments indicate that the force required to drag the viruses on the surface is four times less than that of AuNPs, while the lateral force work needed to induce virus movement was $\sim 10^4$ kT, ten times less than that of the rigid gold nanoparticles. These results go beyond the paradigm that adhesion of nanoparticles is mainly governed by geometrical factors, such as size and area of contact, highlighting the need to amend modeling approaches to account for mechanically-compliant tribological response of biologically derived nanoparticles.

Introduction

Infections arising from surface-borne viral pathogens cost an estimated 94 million dollars in treatment and cause half a million deaths in the US annually (Wolcott et al., 2010). The recent SARS-CoV-2 pandemic raised key issues about the adhesion of virus particles to solid surfaces and increased interest in prophylactic approaches to curb virus spreading. In this context, the interaction of biological particles such as viruses with surfaces plays a central role in bio-hazard mitigation.

The majority of viruses encapsulate their genome inside proteinaceous shells held together by weak non-covalent bonds. At adsorption on a surface, depending on the strength of the adhesive interactions, such soft, mechanically compatible particles partially deform to increase the contact area with the surface with respect to rigid particles (Rimai et al., 1994; Zeng et al., 2017). There are indications that such malleability may play a role in a nanoparticle’s ability to infiltrate cells and/or cross-cellular synapses (Sun et al., 2015). Specifically, adhesive interactions bend the plasma membrane around the particle. In turn, a malleable particle will respond by shape distortion, a phenomenon that has been suggested to modulate the kinetics of cellular uptake (Yuan et al., 2010).

A physical mechanistic picture of adhesion (and friction) of soft, biologically derived nanoparticles on surfaces, such as viruses and exosomes, is still lacking. There are conceptually straightforward, yet important, questions that remain unanswered. For instance, after landing on a cell’s surface, how much of the virus diffusion on the surface is by rolling vs. sliding until they find an entry point? The answer to this question could inform future kinetic models of receptor mediated endocytosis and the interpretation of single particle tracking experiments in virus entry. Another problem is the stability or metastability of the virus adsorbed on a surface. Its understanding could potentially lead to new antiviral surface chemistries and better separation methods in the preparation of vaccines. However, while adhesion of solid nanoparticles at the air/substrate interface has been studied at microscopic scales, (Eppler et al., 2000; Cooper et al., 2001; Rao et al., 2007; Carrillo and Dobrynin, 2012; Oras et al., 2018), the dynamic response of mechanically compliant biological particles to adhesion in a physiological environment has been far less explored (García-Arribas et al., 2024). To address this gap, here we have turned to an atomic force microscopy (AFM) lateral force manipulation approach, which we applied to the study of two model viruses adsorbed on dissimilar surfaces.

When two solids are near contact, attractive intermolecular forces cause the bodies to stick together at contact points (Kinloch, 1980; Álvarez-Asencio, 2014). The force required to overcome these attractive interactions is termed the adhesion force. Adhesion depends on interfacial properties, including, but not limited to, roughness, contact time, deformation, specific interactions, impurities, presence of water, and ambient conditions (Kinloch, 1980; Marshall et al., 2010). All of these interactions are also involved in the resistance to sliding motion between two bodies (called friction).

Adhesion and friction (or lubrication) are some of the most familiar, studied, and technologically important macroscopic phenomena. However, how they emerge from microscopic interactions has been a puzzle until recently (Bhushan, 1995). In recent decades, advances in instrumentation, particularly the development of AFM, have extended the study of adhesion interactions to nanoscopic systems, (Bhushan, 1998; Carpick and Salmeron, 1997; De Pablo et al., 1999), through direct observation of the role of local properties such as physical defects and strain, and the interrogation of single nanoparticles (Minor and Dehm, 2019). These innovations led to an improved molecular-level understanding of adhesion and friction and the development of finer-grained mathematical models (Meng et al., 2020).

In surface-adsorbed particles for which constitutive interactions are similar in magnitude to adhesion interactions, the equilibrium shape of an adsorbed particle is the result of balancing elastic and adhesive interactions (Piersanti et al., 2022). The outcome of this energetic tug of war is, generally speaking, the concern of contact mechanics (Johnson et al., 1971; N Israelachvili, 2011). The small shape changes of an adsorbed virus particle with respect to its nominal shape in a homogeneous environment measured by cryo-electron microscopy or X-ray crystallography can be reliably observed in situ by topographic AFM mapping (Zeng et al., 2017).

In recent decades, AFM has been shown to be particularly suitable for interrogating the physical properties of viruses (Mateu, 2012; Roos et al., 2010) and virus-derived particles (Wu et al., 2024). In particular, AFM makes it possible to analyze individual particles in liquid with subnanometer resolution, providing three-dimensional topographic data with real-time capabilities, and facilitating the application of controlled forces (Baclayon et al., 2010). Through the lateral torsion of an AFM cantilever of known geometry and elastic moduli, quantitative forces can be applied to laterally manipulate nanoscopic objects on a solid surface (Schwarz et al., 1996; Falvo et al., 1997) or to collect tribological data (Tocha et al., 2006; Morel et al., 2005). For example, the energy required to remove surface-adsorbed functionalized carbon nanorods has been estimated by this method (Moya et al., 2022). Moreover, early demonstrations of lateral force manipulations of biomolecular material under ambient conditions included severing surface-adsorbed DNA strands (Guthold et al., 1999) and stretching of tobacco mosaic virus filaments across a solid substrate (Falvo et al., 1997). The large aspect ratio of these filamentous molecules benefited from a reduced number of degrees of freedom compared to that of other shapes, which facilitated the interpretation of the AFM torsional data. However, it was not clear until now whether the same approach could be translated to the problem of adsorbed spherical, mechanically compliant nanoparticles in a liquid.

AFM lateral manipulation of rigid spherical particles was demonstrated in air, including silica nanoparticles, (Heim et al., 1999), polystyrene microspheres, (Verma, 2015), and gold nanoparticles (Mougin et al., 2008). Mathematical models of the interaction between an idealized AFM probe and rigid micro and nanospheres have been developed, (Tafazzoli and Sitti, 2004; Sümer and Sitti, 2008), most of which are applicable to particles orders of magnitude larger than the most common virus capsids. It is likely that at submicroscopic scales such models would reach their validity limit. In addition, they apply only to rigid particles in an inert gas atmosphere. Their accuracy becomes questionable when the dynamics of surface-adsorbed virus particles are described because of particle compliance and strain under friction and adhesion, and because of the solvent (aqueous solution).

Unlike most similar studies on rigid microparticles, the experiments described here were carried out in an aqueous solution, an environment that drastically alters adhesion. This unexplored setting has practical relevance for virus and extracellular vesicle interactions with surfaces, and could be extended to biological interfaces (Sharma et al., 2018; Bhella, 2015; Gerba and Laskin, 1984). Thus, this work seeks to provide benchmark results for exploring friction at the nanoscale in an aqueous solution. Specifically, we implement the lateral force manipulation method to carry out the study of static and dynamic aspects of the surface adhesion of two icosahedral virus species, the brome mosaic virus (BMV) and the murine polyoma virus (MPyV), and, for comparison with a solid nanoparticle standard, of Au nanoparticles (NP) adsorbed from liquid onto two different, nearly atomically flat substrates, polar mica and nonpolar, highly-oriented pyrolithic graphite (HOPG). The purpose of comparing viruses with Au NPs was to highlight the contrast between the dynamics of a rigid spherical particle under shear and that of viruses.

Experimental

Sample preparation

BMV capsids were prepared according to the agroinfiltration method described in ref. (Gopinath et al., 2005). Yeast–derived MPyV particles were prepared according to the method described in ref. (Simon et al., 2014).

Au NPs with diameter 80 nm were synthesized by the polyol method introduced in 1989 by Fiévet et al. (2018), supplemented by an etching step (Lee et al., 2013). This approach results in nearly perfect spherical particles a few tens of nanometers in diameter and an overall reduced size heterogeneity compared to other colloidal methods; see supporting information (SI) document, Supplementary Figure S2. After purification, NPs are dissolved in pure water and have the surface coated with a thin layer of poly (dimethyldiallylammonium chloride) (PDADMAC) – a hydrophilic, positively charged polymer. Note that since this method yields good results only for particles above $\sim 30$ nm diameter, a different synthetic approach is needed for smaller particles.

Au NPs with an average diameter of 24 nm were synthesized according to seed mediated growth in the presence of cetyltrimethylamonium bromide (CTAB) (Jana et al., 2001) - hydrophobic surfactant with polar groups. The average particle diameter, size distribution, ligand thickness and dispersion in solution were verified by imaging on a JEOL 1010 TEM and DLS (Supplementary Figure S2 in SI).

We note that the difference in the surface ligand chemistry between the 80 nm Au NPs coated with PDADMAC and the 24 nm particles coated with CTAB leads to a very tenuous adhesive bond on HOPG of the 24 nm Au NPs, which highlights the importance of the surface ligand chemistry, even in buffer solutions.

BMV samples were prepared for AFM analysis similar to ref. (Zeng et al., 2017) by first freshly cleaving a $1\times 1$ cm piece of the atomically flat substrate. The substrates were either HOPG or mica. Then, 40 $\mu$L of a 0.05 mg/mL purified virus solution at $\sim 10^{11}$/${\text{cm}}^3$ particles in SAMA buffer (50 mM NaOAc, 8 mM Mg${(\mathrm{O}\mathrm{A}\mathrm{c})}_{\mathrm{2}}$, pH 4.5) was deposited onto the substrate and incubated for 30 min at room temperature. Following incubation, the samples were placed in the AFM liquid cell for imaging and manipulation. The samples, unlike in the study of bacteria or biomolecules that exhibit strong surface adhesion, were not rinsed because the low concentration of virus particles present in solution at equilibrium does not impede AFM function, and because rinsing will perturb the adsorbed/free equilibrium.

MPyV samples were prepared by first freshly cleaving a 1 cm × 1 cm piece of the substrate, then incubating 40 $\mu$L of a solution of 0.05 mg/mL capsid in MPyV storage buffer – 50 mM Tris (Tris (hydroxymethyl)aminomethane) at pH 7.4, 200 mM NaCl, 5% glycerol, for 30 min. The MPyV storage buffer was then blotted and replaced with pH 4.5 SAMA buffer before placing the sample in the AFM liquid cell for imaging and manipulation.

For samples in which BMV and MPyV were co-adhered for direct comparison, the substrate was first freshly cleaved, then MPyV was incubated for 30 min as described above, then the sample was dried and 40 $\mu$ L of BMV solution was immediately added and incubated for 30 min.

Determination of cantilever spring constant

Experiments were performed and data collected using an Asylum Cypher S atomic force microscope running proprietary IgorPro-based (Wavemetrics, Inc.) software from Aylum Research (Oxford Instruments, Ltd.). The AFM probe was an oxidatively-sharpened BioLever-mini™ BL-AC40TS silicon/silicon nitride cantilever. The cantilever had a nominal size of 38 × 16 × 0.2 $\mu$m, a 7 $\mu$m tetrahedral probe with tip radius of 8 nm, and nominal resonant frequency of 25 kHz. All data were collected in dynamic mode in solution. The actual spring constant of each cantilever $(K_n)$ was determined using the Sader method (Sader et al., 1999). Typically, the normal spring constant was found to be $\sim 0.09\pm 0.03$ N/m, in agreement with the manufacturer’s specifications.

The lateral spring constant $(K_l)$ was determined using a standard method (Moya et al., 2022) based on geometric conversion (Colchero, 1993) as shown in Equation 1.

$K_n/K_l\approx {\left(h/l\right)}^2/2(1)$

where h and l are the height of the probe and the length of the cantilever, respectively. It should be noted that formula 1 provides a quick but rough estimate of the lateral force constant. This approximate method has previously been used with satisfactory results (Moya et al., 2022; Green et al., 2004; Bilas et al., 2004; Zambudio et al., 2021) We note that there are different approaches, which would be preferable when higher precision is desired (Ogletree et al., 1996; Munz, 2010)

The sensitivity of the photodiode to lateral torsion of the cantilever was calibrated by scanning the 100 nm height step of a commercially available milled grid. The abrupt increases in lateral force as the probe crossed the step was recorded. The slopes of lateral deflection vs. horizontal distance were used to calibrate lateral force sensitivity and convert the measured lateral signal voltage to torsional displacement and then, using the lateral spring constant, into lateral force (see SI, Supplementary Figure S6 for an example).

Lateral force manipulation

To perform the manipulations, a topographic image was first collected of the particles adhered to a substrate. Then a particle which exhibited nominal physical features was isolated from nearby particles and selected as the object of investigation. Using the “MicroAngelo” tool in the AFM software, a typical probe path approximately 200 nm in length was prescribed which passed through the center of the capsid of interest normal to the length of the cantilever. A pre-scan along this path was performed in tapping mode during which a topographic profile was collected. From these data, a new probe path was created that passed through the capsid, with the tip starting at a small controllable distance below the particle height and above the surface of the substrate. A manipulation was then performed in dynamic mode with the amplitude feedback loop turned off. As the probe followed this path, the amplitude, normal deflection, and torsional deflection were collected as a function of the probe position. Following manipulation, a new topographic image was collected. Comparison of the first and second topographic images provided the data required to quantify changes in capsid position and/or structure.

In some lateral manipulation experiments, to facilitate direct comparison, BMV and MPyV particles were co-adhered alongside one another on the same substrate to create a heterogeneous particle sample. This practice ensured identical environments and probing for both species.

Data processing

Topographical data was processed using WSxM 5.0 Develop 10.2 (Horcas et al., 2007). For each manipulation, the topographic image generated by the z-piezo readout was investigated prior to and following the manipulation. Both files were first cleaned using the multi-flatten filter tool with the “line” subtraction type and substrate area parameter set at 60–80%. The corrected images were then aligned using the align images tool. The topography of the manipulated particle was taken along the axis of motion and the traces were overlayed to determine the distance of particle displacement. All other data processing was performed with OriginPro 2023. The pre-scan topography, deflection, and amplitude were plotted vs. path length without any processing. The lateral force was determined by converting the photodiode signal into the torsion distance at the tip, as seen in SI, Supplementary Figure S6, and then multiplying this distance by the lateral spring constant. The normal force could also be determined by multiplying the deflection by the normal spring constant. The lateral force trace vs. distance was integrated using the “integration” gadget of OriginPro to determine the lateral force work.

Results and discussion

The first step in an AFM lateral force manipulation experiment is the identification of adsorbed particles in dynamic (AC) mode. Figure 1a shows an example of a spread of MPyV particles on mica, in solution. The geometric building blocks that give the capsid its knobby aspect are called capsomers.

Figure 1

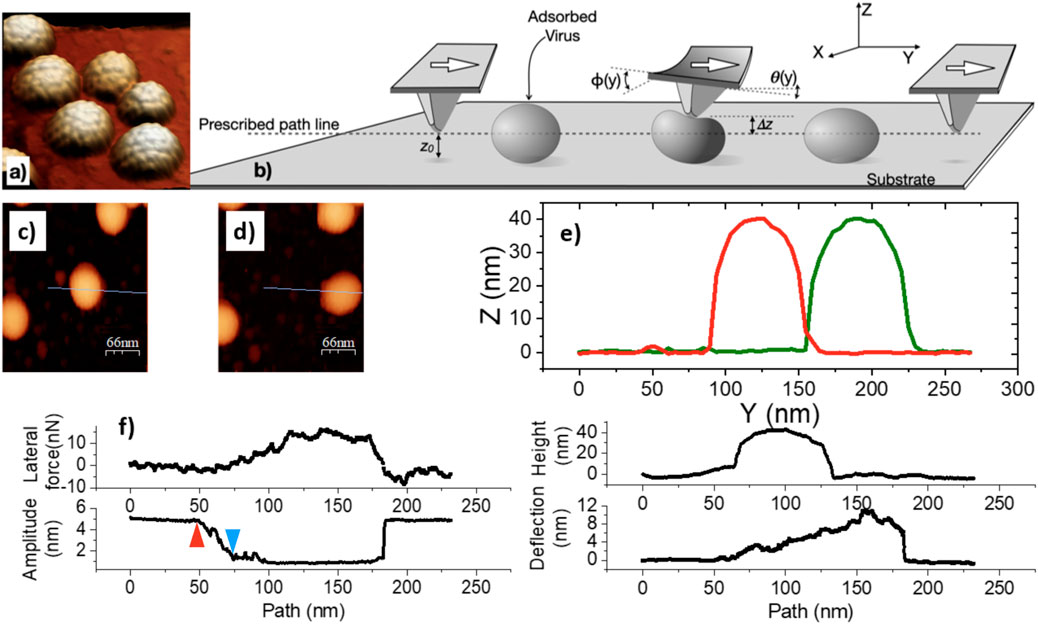
Figure 1. Principles of lateral force manipulation, illustrated with typical data for MPyV particles, adsorbed on HOPG, in buffer. (a) AFM topography of a group of MPyV capsids. (b) Cartoon of the lateral force manipulation experiment. $\varphi$ is the torsion angle, while $\theta$ is the deflection angle. $\mathrm{\Delta }z$ is the linear deflection associated with $\theta$. $z_0$ is the tip position above the surface, on the prescribed path parallel to the substrate. (c,d) Images before and after manipulation of a virus particle by the tip moving along the blue line. (The slightly elongated aspect of viruses in (c) is a thermal drift artifact.) (e) Topographic plot profiles of the particle before (green) and after (red) manipulation. (f) Lateral force, oscillation amplitude, topography, and deflection profiles for a particle undergoing displacement. The red marker is where contact between tip and virus occurs and amplitude starts dropping. The blue marker points to the moment where the amplitude is suppressed–possible where the break between static and dynamic friction occurs.

Members of the polyoma family are distinct from other icosahedral virus structures obeying the Caspar-Klug quasi-equivalent geometry (Caspar and Klug, 1962) by having all capsomers internally organized as pentameric oligomers of the protein VP1 (Supplementary Figure S1). In contrast, the BMV capsid has a T = 3 canonical Caspar-Klug structure (Caspar and Klug, 1962) formed of capsomers that are internally organized as hexameric or pentameric oligomers of the same coat protein (Supplementary Figure S1).

After imaging and particle selection, a linear path for tip motion was defined (dashed line, Figure 1b) which crossed the adsorbed particle of choice. The paths run perpendicular to the longest axis of the cantilever, through the center of the particle (blue line in Figures 1c,d) At the start, the tip was placed at a small vertical distance ($z_0\sim$4 nm in this case) from the sample surface, Figure 1b. The feedback loop for the probe actuator that drives the motion normal to the substrate was disabled during the tip motion along the manipulation path. Tip velocities were typically adjusted to $\sim 100$ nm/s; slower values gave raise to artifacts from thermal drift, higher values frequently dislodge and desorb the particle. From pre-scan and post-scan topographical images (Figures 1c,d) changes in particle position and height can be evaluated (Figure 1e).

Throughout the lateral manipulation experiment, the tip oscillates vertically ($\sim 5$ nm) at resonance. Changes in the amplitude of tip oscillation inform on the nature of the contact between the sample and the tip (Figure 1f, bottom left). Specifically, when the AFM tip is in full contact with the particle, the oscillation amplitude is reduced to zero and we expect it to have little influence on manipulation. In fact, the oscillation amplitude accounts for just $\sim 10\%$ of the smallest virus (BMV) size. In this case, this amplitude would apply a maximum force of $F=300$ pN to the virions, inducing a deformation of $F/k_v=1.5$ nm, where $k_v$ is the stiffness of BMV (Hernando-Pérez et al., 2016). This deformation represents only $\sim 5\%$ of the size of the virus. However, if the particle and tip are not in close contact, this amplitude reduction is only partial. Thus, the tip amplitude is a qualitative descriptor of the tip-particle contact tightness and, indirectly, an indicator of possible particle deviation from the prescribed path (like when the particle spins away from the probe). Parameters recorded simultaneously along the path included the oscillation amplitude, the deflection of the cantilever, and the torsion angles (Figure 1f). Together, this set of variables provides a set of clues about the nature of motion, as discussed below.

To examine a specific example as a preview, let us consider the data obtained from a MPyV particle in liquid on HOPG (Figure 1). First of all, we found that the particle can be pushed along without dissociating it from the surface into the liquid. This is important to note because it was not obvious before these experiments that the particles would not detach from the surface once they started to move. Particle release sometimes occurs depending on the buffer, substrate, and mechanical experimental parameters, but it is possible to tune those conditions to make dissociation a less likely event. Second, the height of the MPyV particle did not change after manipulation, suggesting that the process generally leaves the particles intact. Third, the distance moved from the initial location is limited to about half of the virus perimeter. After covering that distance, the probe loses contact with the virus particle in the cantilever, regaining the initial torsion and deflection values.

After the deflection and torsion angles $\varphi$ and $\theta$ (Figure 1b) were converted to nm and nN values, respectively (Figure 1f) (see the Methods section), we found that the maximum cantilever deflection (12 nm) can be used to estimate virus deformation. According to Figure 1f (bottom right), the maximum deflection of the cantilever reaches $d=12nm$. Knowing both the cantilever $k_c$ and virus spring $k_v$ constants (Hernando-Pérez et al., 2016) the maximum vertical deformation $\mathrm{\Delta }z=F/k_v=(k_{c}d)/k_v=6nm$, which accounts for a strain of $13\%$. This value is just below the critical strain found in some icosahedra protein viruses, (Llauró et al., 2016; Ortega-Esteban et al., 2020), although far below the $80\%$ shown by the lemon-shaped sMV1 virus (Cantero et al., 2023). Since the probe deflection takes positive values throughout probe/particle contact, we deduce that the tip climbs on the particle during manipulation. However, if MPyV behaved like a rigid particle, the estimated deflection would have been $\approx R(1+\cos \alpha )-z_0$ where $z_0\approx 5$ nm is the vertical offset from the surface, $R\approx 23$ nm and $\alpha \approx$ 0.1 rad. The expected deflection if MPyV were rigid and the tip climbed on top would be $\approx$ 38 nm, that is, about 3 times the observed value. Since probe deflection was only 30% of the particle height we infer that the tip did not climb all the way over the particle and descended on the other side, in which case we have to assume that the particle was sliding in front of the tip, or the tip did climb but the particle deformed under the tip with a force of $\sim 0.08\mathrm{N}/\mathrm{m}\times 12\mathrm{n}\mathrm{m}=1$ nN. The first hypothesis falls short in explaining the path length characteristics, as we shall see in more detail later. If the virus particle is compressed and the deformation is detectable, do we see something different when rigid particles are investigated under the same conditions? A representative data set for the manipulation of an Au nanoparticle (NP) displaced by lateral force manipulation is presented in Figure 2.

Figure 2

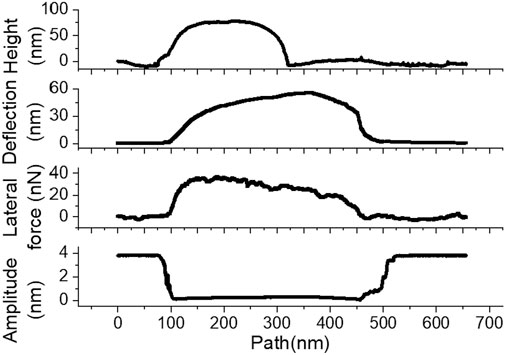
Figure 2. Representative pre-scan profile, deflection, lateral force, and amplitude data from an $80\pm 5$ nm Au NP on HOPG, subjected to lateral force manipulation.

Indeed, in this case, the maximum deflection reaches $\sim 75$% of the nominal particle height which significantly exceeds that obtained from MPyV. This means that the AFM tip climbs almost all the way up the Au NP and that a miscalibration of deflection would not explain the reduced deflection readings on viruses. The most likely explanation is that significant vertical compression occurs during virus manipulation. Two other telling differences between Au NPs and viruses should be noted (Figure 2): i) The lateral force during the Au NP manipulation ($\sim 40$ nN, Figure 2 - top graph) was $\sim 4\times$ higher than the maximum lateral force on MPyV ($\sim 10$ nm, Figure 1); ii) the displaced distance ($\sim 500$ nm as read from where the amplitude drops below 10% of the initial value on Figure 2) was much longer for Au NP, than for MPyV.

To test if these qualitative differences exist when other non-enveloped icosahedral viruses are considered, we have examined the behavior of BMV adsorbed on HOPG, in buffer solution, too. BMV is a single-stranded, positive-sense RNA plant virus that has been studied for nearly 70 years as a model for the broad class of single-stranded RNA icosahedral alphaviruses (Kao and Sivakumaran, 2000). BMV particles are about half the size of MPyV, having a diameter of $\sim$28 nm. Its protein coat is made up of 180 proteins, copies of the same gene (SI, Supplementary Figure S1). Due to a mosaic of charged polar and non-polar aminoacid residues at its surface, BMV readily adsorbs from buffer onto a variety of substrates, and is relatively straightforward to image by AFM at spatial resolutions better than 5 nm (Zeng et al., 2017).

Similarly to MPyV, BMV was displaced along the surface without desorption into the liquid. Figure 3 shows representative lateral force manipulation data for a BMV particle adsorbed in HOPG. After contact with the probe, the lateral force increased to $\sim 8$ nN, plateaued, and gradually decreased back to zero. This plateau represents a stationary state in which resistance to movement is balanced by lateral pushing force. The approximate path length under probe contact was approximately half of the virus perimeter, similar to MPyV.

Figure 3

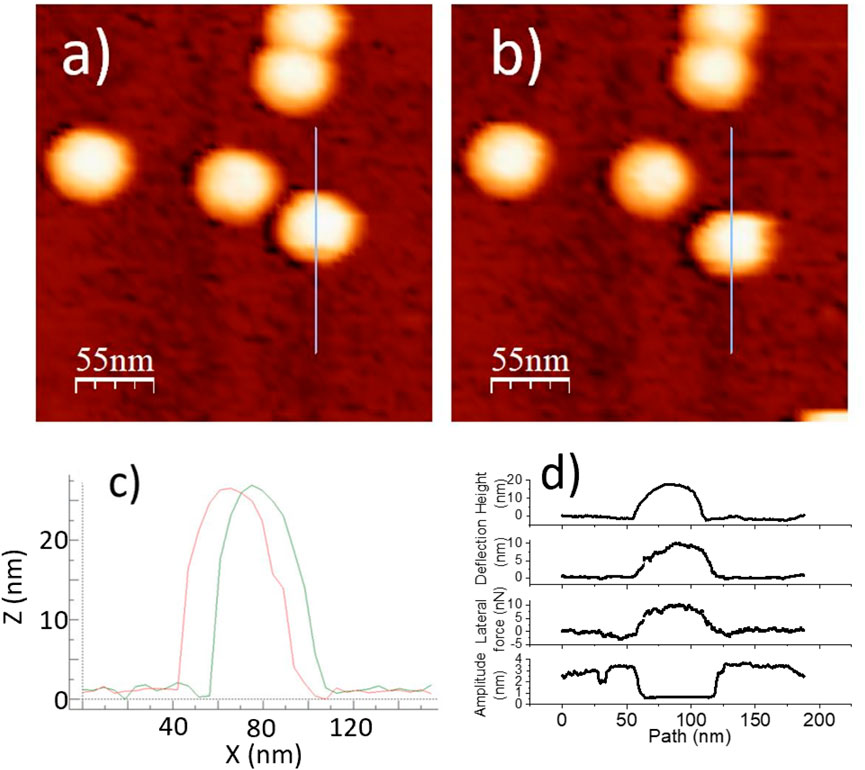
Figure 3. A BMV particle on HOPG to be displaced according to a prescribed probe path during a lateral force manipulation measurement: (a) Before manipulation. (b) After manipulation. (c) Overlay of line profiles, before and after. (d) Topography, deflection, lateral force, and amplitude of manipulation.

As a starting point for further analysis, we refer to previous studies of lateral force manipulation of rigid microparticles for which three types of particle motion have been identified: sliding, spinning, and rolling (Sümer and Sitti, 2008; Ma et al., 2020) (Figure 4). It is reasonable to assume that the same type of motion may occur at nanoscale as well. To those types of motion, we add the possibility that a particle be stuck on the substrate while the tip slides on its top surface, while the cantilever deflects up and the particle compresses down. The latter instance has not been reported on microparticles.

Figure 4

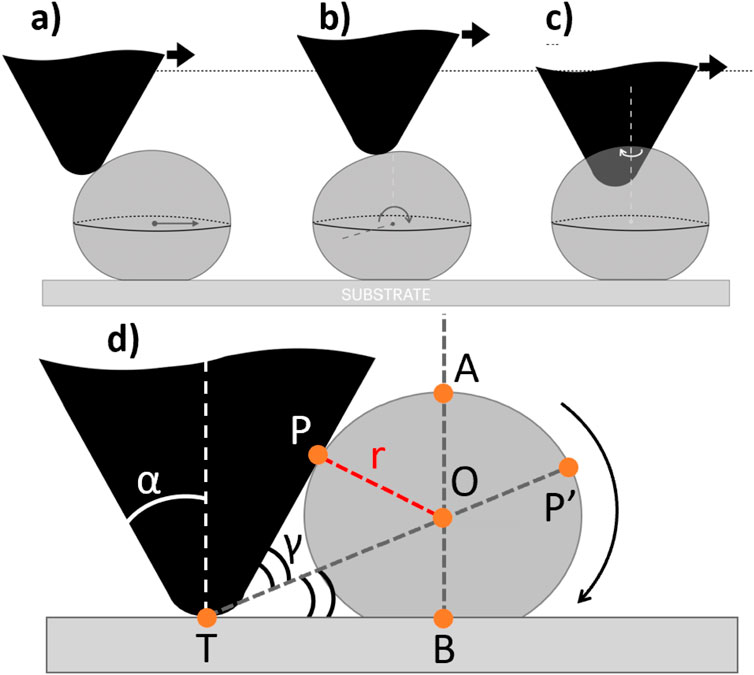
Figure 4. Three motion types for particle undergoing lateral force manipulation: (a) sliding, (b) rolling, and (c) spinning, and diagram of the geometric rolling model (d).

Having access to multi-dimensional data as presented in Figure 1f can help to discriminate between different scenarios of lateral manipulation. This distinction is important to make because each situation informs of different tribological characteristics (e.g., rolling vs. sliding friction, etc.).

We start with particles that spin around the probe, Figure 4c, because these particles were removed from further analysis. These particles were identified as having a brief lateral and deflection signal during manipulation, the final particle location deviating from the intended probe path, Figure 5, (unlike in Figures 3a,b, where the displacement occurred along the probe path). This situation was usually accompanied by an erratic oscillation amplitude trace, Figure 6. Together, these results are consistent with the particle spinning around the probe. We note that such instances were also generally associated with lateral force work values substantially smaller than when probe-particle contact was constant and tight, and the direction of particle motion closely aligned with the direction of pushing–see similar observation on microparticles, in Sümer and Sitti (2008). Thus we have left out of the analysis the particles exhibiting any of the tell-tale signs of spinning around the probe.

Figure 5

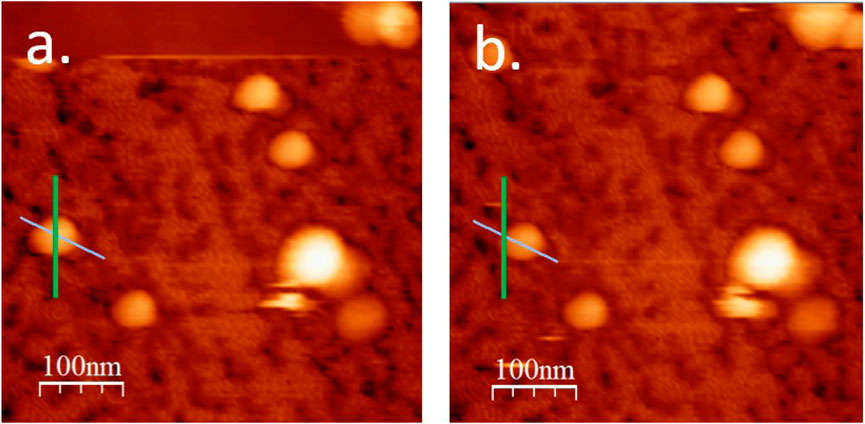
Figure 5. Pre-manipulation (a) and post-manipulation (b) topography of a BMV particle which has undergone spinning during manipulation. Green lines indicate probe path, cyan lines indicate the apparent direction of particle displacement.

Figure 6

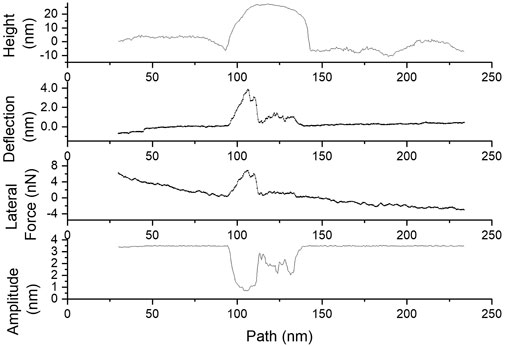
Figure 6. Initial topographic cross-section, deflection, lateral force, and amplitude traces showing characteristics of a particle that exhibits spinning around the probe during manipulation.

Another straightforward scenario to identify is that of a surface-stuck particle. Figure 7 presents data from a BMV particle that has not changed its location on the surface during attempted manipulation. Clearly the particle has not moved on the surface as suggested by neighboring surface features that serve as fiducial markers. In this case, the particle and probe had good contact, but the friction between the tip and particle must have been less than the adhesion between the particle and substrate. As a result, the tip slid across the particle rather than the particle being displaced across the substrate. As we shall see in the following, the number of “stuck” particles can be controlled via the distance of the tip to the surface. Stuck particles could be useful analytically because they can provide independent information on the friction between the probe and the virus.

Figure 7

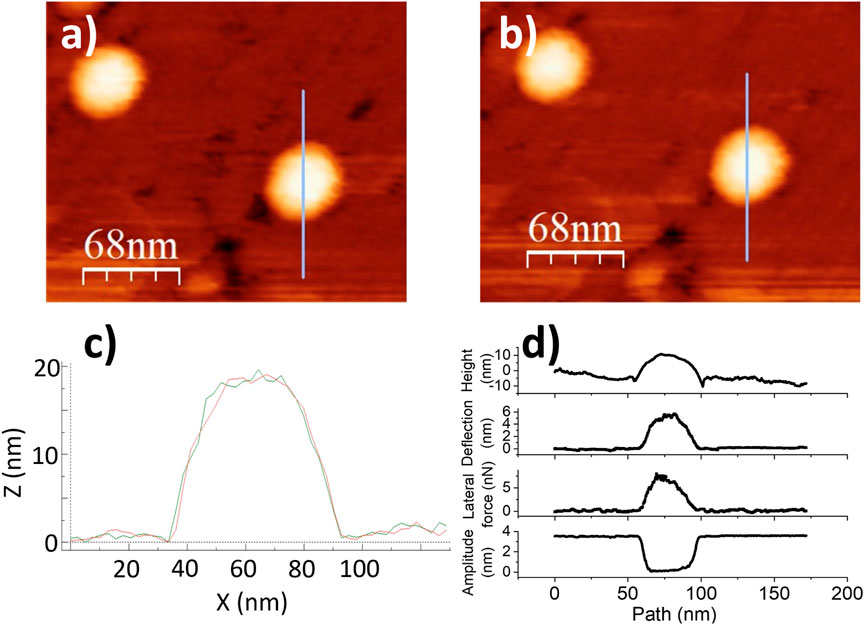
Figure 7. Stuck particle data. (a,b)Topographic images of BMV particles adsorbed on HOPG, before and after lateral force manipulation. The blue line indicates the prescribed probe path. In this case, there was no particle displacement by the tip. (c) Single line scan across the particle showing identical topographic profile before and after. (d) pre-scan topography, deflection, lateral force, and amplitude of oscillation at every point along the manipulation path.

We now turn our attention to the remaining two possible mechanisms of motion: sliding (Figure 4a) and rolling (Figure 4b). In the case of sliding, the path length under probe contact can, in principle, be unlimited. Nevertheless, inhomogeneity of surface interactions can kick the particle out of the probe’s way. However, in the case of rolling, there should be an upper limit for the path length, related to the particle diameter. The geometrical model below provides this limit under the following assumptions (see Figure 4d):

$•$ The particle is rolling onto the substrate while the tip is riding on it it without sliding.

$•$ The particle is spherical.

$•$ The probe interacts with the particle via a flat side. The tip, the contact point, and the center of the particle define a plane that contains the assigned linear trajectory and the normal to the substrate through the center of the particle.

$•$ The initial tip position is very close to the surface.

$•$ Particle deformation is negligible.

$•$ There is no sliding between the tip and the particle and the particle and the surface. In other words, adhesives bonds at these interfaces are tenuous with respect to dynamic friction.

The maximum rolling distance ($m.r.d$.) predicted by this model is:

$m.r.d.=r\left(\pi -2\alpha \right)+2\Vert TB\Vert (2)$

where $\alpha$ is the half-angle of the tip pyramid, taken here to be $\pi /6$ radians.

For $\Vert TB\Vert$ we have:

$\Vert TB\Vert =\frac{r}{\tan \gamma }=\frac{r}{\tan \left(\pi /4-\pi /12\right)}(3)$

where $r$ is the particle radius, and $\gamma$ stands for the $\widehat{PTO}$ angle in Figure 4d). We obtain:

$m.r.d.=r\left(\pi -2\alpha \right)+\frac{2r}{\tan \left(\pi /4-\alpha /2\right)}(4)$

Assuming $r\approx 15$ nm (for BMV) and $\alpha \approx \pi /6$, we obtain: $m.r.d\approx 84$ nm, which is somewhat larger, but close to the experimental value of $\sim 65$ nm (Figure 8). Note that a shortening of the effective particle radius may occur due to deformation during manipulation, which is not included in the model. The top limiting value provided by the rolling model clearly sits on the boundary of traveled distances for both BMV and MPyV, Figure 8. Specifically, one in 53 BMV particles and none of the 52 MPyV particles have been observed to exceed the $m.r.d$. estimate. However, Au particles frequently exceeded their $m.r.d$. estimate. When the actual displacement of the particles exceeds the limit $m.r.d$., which is approximately half of the perimeter of the particles, it is likely that the particles have not moved by simple rolling, as shown in Figure 4a.

Figure 8

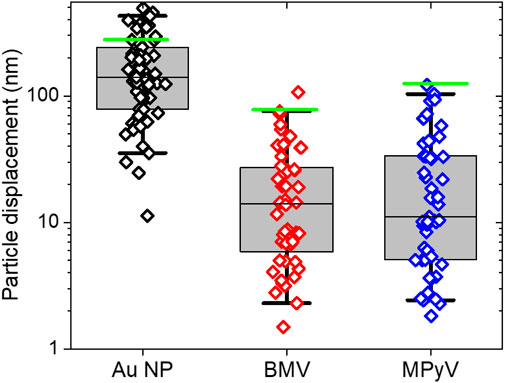
Figure 8. Experimental displacements and calculated maximum rolling distance (green line) for Au nanoparticles (N = 62), BMV (N = 53) and MPyV (N = 52) adhered to HOPG during manipulation in which the probe rides over the rolling particle. Whiskers indicate the middle 95 percent the population, boxes indicate one standard deviation from median of data.

It has already been mentioned that not all adsorbed BMV particles will undergo surface-bound displacement, being “stuck”. It is straightforward to distinguish between displaced particles (Figure 1e) and stuck particles by comparing initial and final locations in the context of surface fiducial markers (Figure 7). The maximum tip deflection for the stuck particle was $\sim 6$ nm, corresponding to a normal force of $\sim 0.6$ nN if we consider a stiffness of the cantilever of 0.07 N/m. Under this normal force, BMV is expected to compress $\sim 5$ nm, (Vaughan et al., 2014), which is significant relative to the radius of the virus (14 nm). The measured initial height of the stuck particle in Figure 7 was about 70% of the nominal diameter of a BMV virion. This low height suggests that the stuck particle might have been structurally altered, most likely at the contact area with the substrate. It is reasonable to expect an increased particle-substrate interaction arising from this alteration, which explains why the particle resisted displacement although the experimental parameters were, in principle, the same as for the displaced BMV particle in Figure 1e.

The presence of stuck particles provides an opportunity to compare friction at the probe/particle interface with the rolling resistance. Control over the fraction of mobile particles can be obtained by following the idea that when the tip radius is comparable to the virus radius, the loading angle will vary considerably as a function of the height of the tip as measured from the substrate ($z_0$ on Figure 1b). Thus, when the tip moves at a distance from the surface that is close to the virus apex height, the tip will merely skim the surface of the virus, exerting reduced forces with respect to the head-on collision case when the tip-substrate distance would be, say, only 5 nm. It follows that there should be a crossover between the tip sliding over the particle vs. the tip causing the particle to roll over the substrate as the tip/surface distance decreases. To test this expectation, we have carried out experiments on BMV/HOPG at 5, 10, 15, and 20 nm trajectory depths, Figure 9, where “depth” is understood here as the difference between the height of the particle and the height of the trajectory over the support surface $\mathit{\text{i.e.}}d-z_0$.

Figure 9

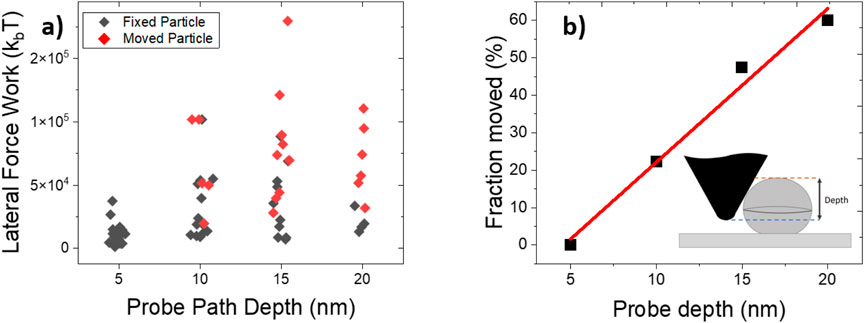
Figure 9. (a) Scatter plots of lateral force work for displaced and fixed particles. (b) Percentage of displaced particles as a function of the tip trajectory depth, defined as particle height minus $z_0$.

For a fixed tip depth, the work of the lateral force is less when the particle is stuck than when it is moving Figure 9a. As expected from a rolling scenario, displacement occurred more frequently at greater tip depths, Figure 9b. Notably, the average lateral force mechanical work for a rolling particle was about $7.3\times 10^4$ kT. This dissipated energy is an order of magnitude higher than the estimated free energy of assembly (Reddy et al., 1998; Perlmutter and Hagan, 2015); presumably, most of it is consumed by breaking surface-particle binding, without measurably perturbing particle structure. This observation indicates a large activation barrier to disassembly by mechanical/adhesive forces. However, this barrier is reachable as suggested by repeated manipulation of a BMV particle, which led to an obvious loss of material (Figure 10).

Figure 10

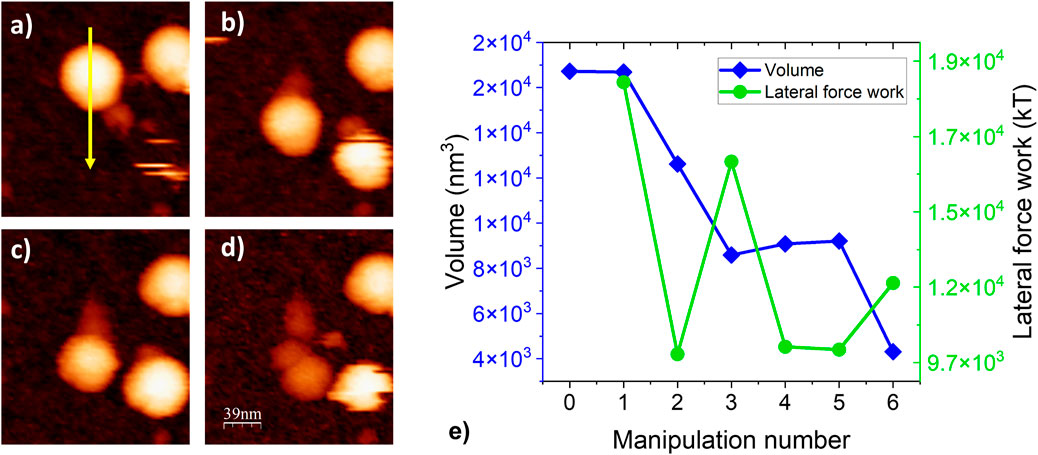
Figure 10. Topographic images of a BMV particle adhered to HOPG throughout a series of manipulations: (a). The particle at left begins fully intact and is pushed by the probe from top to bottom as indicated by the yellow arrow. (b,c) Repeated manipulations lead to a consistent decrease in particle height and (d) cause the formation of a trail of loose proteins until the particle is reduced to a small, loose pile of proteins. (e) Particle volume and lateral work force vs. manipulation number for a series of repeated manipulations performed on one BMV particle.

The trail of debris left by the particle after each manipulation (Figures 10a–d) is a result of strong adhesive forces at the particle/substrate interface inducing capsomer extraction when the particle is moved. The resulting capsid lattice vacancies probably contribute to a weakening of the overall capsid structure, resulting in a cascading effect which eventually results in virion collapse/disassembly as seen in the final image of the series, Figure 10d.

The particle volume and lateral work force throughout the series of manipulations in (Figures 10a–d) are shown in (Figure 10e). From one scan to another, as the particle disassembles and its volume decreases, the lateral work force decreases as well. This indicates that intact particles are generally more resistant to lateral manipulation in comparison to severely structurally disrupted particles.

Changes in environmental conditions can impact the physicochemical properties underlying biological adhesion significantly. For example, the adhesion and hydrophobicity of algal cells are significantly affected by temperature and salinity (Novosel et al., 2022a; Novosel et al., 2022b; Ivošević DeNardis et al., 2024).

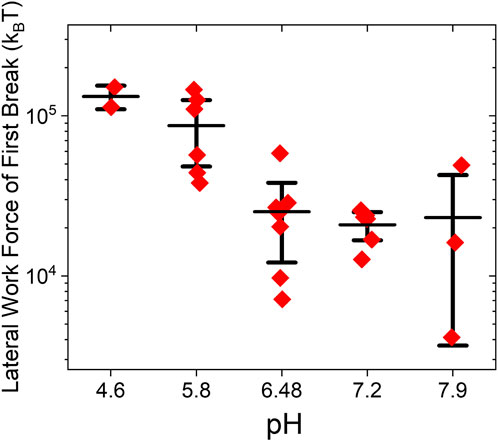
Viruses are sensitive and respond to chemical changes in their environment, too. Specifically, they can prevent or slow down decay when outside a cell host and yet promptly present their genome for replication after entry. Although this work’s primary aim is narrower than that of revealing the entire complexity of parameter landscape affecting static and dynamic virus adhesion, the methods outlined here could benefit investigations seeking to unveil virus response to environmental cues. As an example, we have asked how does the energy required to initiate the mechanical disassembly of BMV by rolling on HOPG vary with the pH of the solution? Figure 11 shows that the magnitude of mechanical work to capsid disruption decreases almost an order of magnitude with increasing solution pH from 4.6 to 7.9. This can be expected because capsid cohesive interactions in cowpea chlorotic mottle virus (CCMV), a close relative of BMV, weaken as pH increases (Wilts et al., 2015; Garmann et al., 2014).

Figure 11

Figure 11. Lateral mechanical work leading to capsid disruption vs. pH in BMV on HOPG.

We now turn our attention to the dynamic response to lateral force manipulation of viruses vs. that of the rigid Au NP. In experiments with 80-nm AuNP in HOPG (Figure 2), the lateral force rapidly reached $\sim 40$ nN, which is 4–5 times higher than the average maximum lateral force measured in BMV, and 2–3 times the force measured on MPyV, Figure 12. Therefore, although the lever arm of the lateral force torque was almost double for the 80 nm Au NP compared to the BMV, the resistance to displacement is greater in Au NPs. We note that the smaller, 24 nm Au NPs coated with CTAB, showed comparable if not slightly larger resistance to lateral force manipulation than the 80 nm Au NPs coated with PDADMAC (see Supplementary Figure S3). If the difference between the two AuNPs sizes was mainly due to contact area, the 80 nm AuNPs would have shown greater resistance to lateral force manipulation than the 24 AuNPs. Thus, we believe that the chemical nature of the ligand played a dominant role here, possibly through stronger hydrophobic interactions of the PDADMAC ligand with the HOPG substrate.

Figure 12

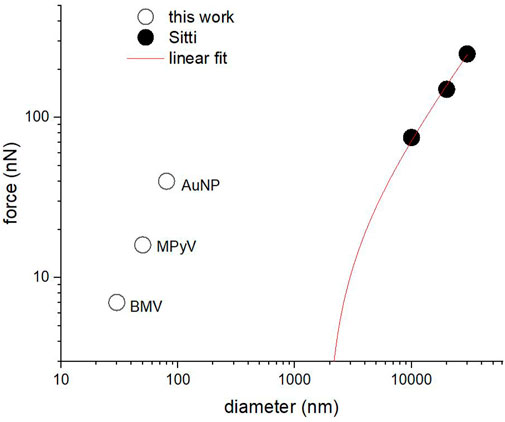
Figure 12. Quasi-static lateral force vs. nominal particle diameter for the three types of particles in this work and for previously published results from ref. (Sümer and Sitti, 2008). The red line represents a linear fit to the Sümer and Sitti data, extrapolated to the diameter range studied in this article.

For the weakly bound 80 nm Au particles, we observe the lateral force maximum occurring in the first half of the manipulation path (Figure 2) while in virus particles, which are mechanically compliant, the maximum is generally observed in the second half of the manipulation path–this might be because virions are able to undergo greater deformation relative to particle size before enough force is applied to induce particle displacement.

It would be interesting to test whether the results obtained here in a liquid might follow a common scaling law with those obtained by Sümer and Sitti from AFM manipulation of polystyrene microparticles in air (Sümer and Sitti, 2008). According to the Derjaguin theory for incompressible spherical particles of radius R in vapor on a flat surface, (Sümer and Sitti, 2008), the adhesion force scales linearly with the radius of the particle (Equation 5).

$F_{\mathit{adh}}\propto R\gamma (5)$

where $\gamma$ stands for the interfacial energy (approx. half the work of adhesion (N Israelachvili, 2011)), typically few tens of mJ/m². Assuming that friction force and adhesion force are also linearly proportional, we fit the force vs. diameter results by Sümer and Sitti from polystyrene microparticles in air (Sümer and Sitti, 2008) with a linear fit and we extrapolate to the nanoscale for comparison with our results for viruses and Au NP in solution. Figure 12 shows the significant differences between, one hand–the lateral forces on viruses vs. nanoparticles of the same scale, and rigid nanoparticles in liquid vs. microparticles in air, on the other hand.

Incompressible Au NPs in water fall well above the extrapolation of data from Sümer and Sitti. Thus, AuNPs adhere more tenuously to the HOPG surface than one might expect, especially since it is well-known that water weakens the adhesion of solids. The opposite appears to happen here, possibly because of the hydrophobic effect which pushes the HOPG and AuNP together (AuNPs are surface functionalized with Au surface adsorbed polymer with polar groups for solubility, but the ligand coating is likely patchy).

Viruses cannot be considered incompressible at adhesion (Zeng et al., 2017). Upon contact, they deform elastically under the influence of attractive surface forces. The Johnson, Kendall, and Roberts (JKR) theory of contact mechanics (Johnson et al., 1971) provides a formal estimate for the radius of the area of contact between an elastic sphere and a flat surface:

$a_0={\left(\frac{9\pi R^2\gamma }{E}\right)}^{1/3}(6)$

with the adhesion force estimated as:

$F_{\mathit{adh}}\approx 3\pi R\gamma (7)$

It is likely that friction is related to adhesion (Guo et al., 2013) If they are proportional, using JKR we can estimate both the ratios between Au NPs and viruses of the interfacial energy $\gamma$ and the area of contact with the surface. To do so, we use (7) to obtain the coefficient between the interfacial energies for Au NPs and MPyV on HOPG like $\frac{{\gamma }_{Au}}{{\gamma }_{\mathit{MPyV}}}=\frac{R_{\mathit{MPyV}}}{R_{Au}}\frac{F_{Au}}{F_{\mathit{MPyV}}}=1.9$, where $F_{Au}$ and $F_{\mathit{MPyV}}$ are the friction forces for Au NPs an MPyV particles, respectively. A similar estimation can be applied to find $\frac{{\gamma }_{Au}}{{\gamma }_{\mathit{BMV}}}=2.0$. Thus, the interfacial energy of Au NPs is twice that of virus particles. Further, we can use the expression (6) to find the ratios of the contact radius with the surface between the compliant viruses and the stiff Au NPs. In the case of MPyV particles we can derive $\frac{a_{\mathit{MPyV}}}{a_{Au}}={\left({\left(\frac{R_{\mathit{MPyV}}}{R_{Au}}\right)}^2\frac{E_{Au}}{E_{\mathit{MpyV}}}\frac{{\gamma }_{\mathit{MPyV}}}{\gamma Au}\right)}^{\frac{1}{3}}=0.34$. In the latter we used the Young Modulus for Au NPs $(E_{Au})$ and MPyV virus $(E_{\mathit{MPyV}})$ as 80 GPa and 0.5 GPa, respectively. For the case of BMV, this coefficient results in $\frac{a_{\mathit{BMV}}}{a_{Au}}=0.46$. This means that the area of contact with the surface is 9 and 4 times larger for MPyV and BMV, respectively, than for the Au NPs. Thus, despite the fact that compliant viruses deform on the surface increasing their area of contact significantly with respect to the Au NPs, they remain less adhered than large and rigid particles. In this case, the higher interfacial energy of Au NPs takes over the geometrical facts of size and area of contact. Now it is pertinent to discuss the forces which are responsible of the interfacial energies of both viruses and Au NPs with the surface. Virus structures are populated with appendages, such as fibers and spikes, which are responsible for the interaction of viruses on the host cell surface. These interactions take place by specific bonds which depend on the biochemistry of the virus appendages and the host receptors (Flint et al., 2004). In our case surfaces are not functionalized with any receptors or antibodies and we only expect nonspecific interactions between the virus capsid and the surface. Consequently, we can assume to deal with non-specific physisorption governed by DLVO interactions as it happens with other biomolecules (Müller et al., 1997). DLVO interaction $F_{\mathit{DLV\; O}}$ include electrostatic $F_{el}$ and van der Waals forces $F_{\mathit{vdW}}$ as $F_{\mathit{DLV\; O}}=F_{el}+F_{\mathit{vdW}}=\frac{4\pi {\sigma }_v{\sigma }_{s}R{\lambda }_D}{{ϵ}_0{ϵ}_e}\exp (-z/{\lambda }_D)+\frac{H_{a}R}{z^2}$. In this expression ${\sigma }_v$ and ${\sigma }_s$ are the charge densities of virus and surface, respectively; ${ϵ}_0$ and ${ϵ}_e$ the electrical permitivities of vacuum and liquid, respectively; $z$ the distance between the virus and the surface and $H_a$ the Hamaker constant. The Debye length ${\lambda }_D$ characterizes the exponential decrease of the electrostatic potential resulting from screening the surface charges with electrolytes, with ${\lambda }_D=0.174/\left[C\right]$ for a concentration $C$ of divalent (1:2 or 2:1) electrolytes. In our case, the divalent concentration of the SAMA buffer is 0.008 M³, therefore ${\lambda }_D=2nm$. This means that the electrostatics is rapidly killed and the particles are attached to the surface through inespecific van der Waals forces. A similar discussion can be elaborated for Au NPs, indicating that van der Waals forces are more intense for Au NPs than for protein capsids. In order to estimate the difference between van der Waals force in viruses and Au NPs, we can use the lateral work used for moving viruses and Au NPs (Figure 13), where Au NPs show $\sim 10$ times larger work values than viruses. This is in agreement with the different values of the Hamaker constant for proteins $(2\times 10^{-20}J)$ and Au NPs $(1.76\times 10^{-19}J)$ (Pinchuk and Jiang, 2015; Roth et al., 1996)

Figure 13

Figure 13. Experimental results for the work exerted by lateral force during manipulations.

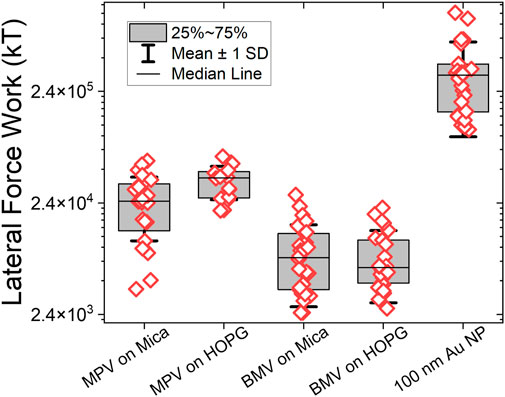
The relative trends shown in Figure 12 remained the same when mica replaced HOPG as a substrate. Specifically, MPyV started moving at 2-3 times the force required for BMV on both substrates. The adhesion of particles to both substrates is believed to be primarily the result of dispersion forces, while the affinity of particles to mica has an added contribution from long-range electrostatic forces (Müller et al., 1997). In any case, the magnitude of the lateral forces measured during displacement is intriguing considering that, typically, forces above 1–5 nN in nanoindentation will lead to virus collapse (Roos, 2011). In this respect, it is important to note that: i) unlike nanoindentation experiments, which measure axial compression, the lateral force measured in our experiments produces shear at the virus/substrate interface. ii) However, there exists a loss of structural integrity due to rolling, when manipulation is prolonged beyond $\sim 100$ nm.

Virus-specific differences on the two substrates were relatively small: MPyV adhered somewhat (25%) stronger to HOPG than to mica, while for BMV there was practically no difference between mica and HOPG (Figure 13).

A molecular interpretation of differences between BMV at MPyV is difficult due to the fact that, in general, the virus surface is a mosaic of polar and non-polar residues as well as flexible and rigid protein domains, which all contribute to non-specific adhesion. We note the presence of large flexible loops on the surface of MPyV, (Stehle and Harrison, 1996), which are normally involved in the entry of MPyV by receptor-mediated endocytosis, while for BMV, which is a plant virus, such surface loops are lacking. BMV is believed to enter plant cells through damage by external perforation to the cell walls.

An intriguing conclusion from these experiments is that, although mechanically compliant and therefore prone to realize a wider contact area, viruses show less resistance to rolling on any of the surfaces tested than rigid, ligand-stabilized Au NPs. The rolling resistance is two or three orders of magnitude less than the sliding friction for a given set of materials (Barber, 2011). This counterintuitive observation highlights the need for an in-depth theoretical treatment. At the same time, it raises the question: Might low resistance to rolling be a built-in capability aimed at increasing the rate of receptor binding and thus accelerating kinetics of cellular binding/entry? Nevertheless, to the best of our knowledge, the mechanism by which viruses diffuse on host cell surfaces, through exopolymeric layers, etc. until they are pinned at the cell entry location are poorly understood. For now, this remains an open question that could be given an answer in the future by experiments similar to those presented here. It would be interesting to see how these data will change when known-specific ligand-receptor interactions are introduced on a model cell surface, such as a supported lipid bilayer. The preliminary work presented here indicates that such explorations should be possible.

Conclusion

Lateral force manipulation by AFM was explored as a possible approach for comparative studies of adhesion interactions in isometric viruses in particular and other mechanically-compliant nanoparticles in general. Virus-probe and virus-support interactions tend to be complex; as such, multi-pronged approaches that address different properties should be utilized. With its set of complementary, simultaneous read-out variables, liquid-cell AFM is a suitable method. It was found that, under physiological buffer conditions, non-enveloped virions of an animal and a plant virus adhere non-specifically in such a way that they can be manipulated on the surface over extended distances relative to their radius without desorption. The finding will be valuable in the design of new experiments that seek to understand the mobility of viruses on biological surfaces.

MPyV and BMV exhibited distinct responses from rigid Au NPs to lateral force manipulation. Although MPyV is several times more resistant to rolling than BMV, the resistance to rolling in both viruses is significantly lower than that of rigid Au NPs, despite the fact that viruses, being mechanically compliant, presumably have a contact area more extended than that of rigid nanoparticles of similar diameter. The mechanical work lateral force measured during the rolling motion of viruses is an order of magnitude greater than the estimated free energy of the assembly of capsids, suggesting a high barrier against disassembly by mechanical forces. Significant virus particle strain was observed during lateral force manipulation for both viruses and should be considered in future modeling seeking to extract information about virus interfacial interactions during the virus life-cycle.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://libraries.indiana.edu/databases/scholarworks.

Author contributions

CA: Formal Analysis, Writing – review & editing, Conceptualization, Writing – original draft, Data curation. CS: Writing – review and editing, Resources, Methodology. IT: Writing – review and editing, Visualization, Formal Analysis, Data curation. PD: Methodology, Project administration, Writing – review and editing, Conceptualization, Validation, Funding acquisition. BD: Funding acquisition, Writing – review and editing, Data curation, Resources, Conceptualization, Investigation, Project administration, Methodology, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The work was partially supported by the U.S. Army Research Office through award #W911NF1310490 and #W911NF-24-1-0225 to BD. BD acknowledges support from project grant # PNRR-I8/C9-CF105 under contract # 760099 from the Romanian Ministry of Research, Innovation, and Digitization. PD acknowledges the Salvador de Madariaga Scholarship PRX21/00317.

Acknowledgments

The authors thank Xingchen Ye for the CTAB-coated Au nanoparticle samples. CA also thanks the Indiana Grad Workers Coalition–United Electric Workers for its support and representation.

Conflict of interest

Author CS was employed by Boehringer Ingelheim Pharma GmbH & Ko. KG.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frbis.2025.1623880/full#supplementary-material

References

Álvarez-Asencio, R. N. (2014). Surface interactions and characterization: an AFM study. Ph.D. thesis. KTH Royal Institute of Technology.

Google Scholar

Baclayon, M., Wuite, G., and Roos, W. (2010). Imaging and manipulation of single viruses by atomic force microscopy. Soft Matter 6, 5273–5285. doi:10.1039/b923992h

CrossRef Full Text | Google Scholar

Barber, J. (2011). Intermediate mechanics of materials. Springer.

Google Scholar

Bhella, D. (2015). The role of cellular adhesion molecules in virus attachment and entry. Phil. Trans. R. Soc. B 370, 20140035. doi:10.1098/rstb.2014.0035

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhushan, B. (1995). Handbook of micro/nano tribology. in Micro/nanotribology and micro/nanomechanics of magnetic storage devices and MEMS (CRC Press), 443–503.

Google Scholar

Bhushan, B. (1998). Micro/Nanotribology using atomic force microscopy/friction force microscopy: state of the art. Proc. Institution Mech. Eng. Part J J. Eng. Tribol. 212, 1–18. doi:10.1243/1350650981541859

CrossRef Full Text | Google Scholar

Bilas, P., Romana, L., Kraus, B., Bercion, Y., and Mansot, J. L. (2004). Quantitative characterization of friction coefficient using lateral force microscope in the wearless regime. Rev. Sci. Instrum. 75, 415–421. doi:10.1063/1.1637436

CrossRef Full Text | Google Scholar

Cantero, M., Cvirkaite-Krupovic, V., Krupovic, M., and de Pablo, P. J. (2023). Mechanical tomography of an archaeal lemon-shaped virus reveals membrane-like fluidity of the capsid and liquid nucleoprotein cargo. Proc. Natl. Acad. Sci. U. S. A. 120, e2307717120. doi:10.1073/pnas.2307717120

PubMed Abstract | CrossRef Full Text | Google Scholar

Carpick, R. W., and Salmeron, M. (1997). Scratching the surface: fundamental investigations of tribology with atomic force microscopy. Chem. Rev. 97, 1163–1194. doi:10.1021/cr960068q

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrillo, J. M. Y., and Dobrynin, A. V. (2012). Dynamics of nanoparticle adhesion. J. Chem. Phys. 137, 214902. doi:10.1063/1.4769389

PubMed Abstract | CrossRef Full Text | Google Scholar

Caspar, D. L. D., and Klug, A. (1962). Physical principles in the construction of regular viruses. Cold Spring Harb. Symposia Quantitative Biol. 27, 1–24. doi:10.1101/sqb.1962.027.001.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Colchero, J. (1993). Reibungskraftmikroskopie; hartung-gorre.

Google Scholar

Cooper, K., Gupta, A., and Beaudoin, S. (2001). Simulation of the adhesion of particles to surfaces. J. Colloid Interface Sci. 234, 284–292. doi:10.1006/jcis.2000.7276

PubMed Abstract | CrossRef Full Text | Google Scholar

De Pablo, P., Colchero, J., Gomez-Herrero, J., Baro, A., Schaefer, D., Howell, S., et al. (1999). Adhesion maps using scanning force microscopy techniques. J. Adhesion 71, 339–356. doi:10.1080/00218469908014547

CrossRef Full Text | Google Scholar

Eppler, A. S., Rupprechter, G., Anderson, E. A., and Somorjai, G. A. (2000). Thermal and chemical stability and adhesion strength of Pt nanoparticle arrays supported on silica studied by transmission electron microscopy and atomic force microscopy. J. Phys. Chem. B 104, 7286–7292. doi:10.1021/jp0006429

CrossRef Full Text | Google Scholar

Falvo, M. R., Washburn, S., Superfine, R., Finch, M., Brooks, F. P., Chi, V., et al. (1997). Manipulation of individual viruses: friction and mechanical properties. Biophysical J. 72, 1396–1403. doi:10.1016/s0006-3495(97)78786-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiévet, F., Ammar-Merah, S., Brayner, R., Chau, F., Giraud, M., Mammeri, F., et al. (2018). The polyol process: a unique method for easy access to metal nanoparticles with tailored sizes, shapes and compositions. Chem. Soc. Rev. 47, 5187–5233. doi:10.1039/c7cs00777a

PubMed Abstract | CrossRef Full Text | Google Scholar

Flint, S. J., Enquist, L. W., Racaniello, V. R., and Skalka, A. M. (2004). Principles of virology. Washington D.C.: ASM Press.

Google Scholar

García-Arribas, A. B., Ibáñez-Freire, P., Carlero, D., Palacios-Alonso, P., Cantero-Reviejo, M., Ares, P., et al. (2024). Broad adaptability of coronavirus adhesion revealed from the complementary surface affinity of membrane and spikes. Adv. Sci. 11, 2404186. doi:10.1002/advs.202404186

PubMed Abstract | CrossRef Full Text | Google Scholar

Garmann, R. F., Comas-Garcia, M., Gopal, A., Knobler, C. M., and Gelbart, W. M. (2014). The assembly pathway of an icosahedral single-stranded RNA virus depends on the strength of inter-subunit attractions. J. Mol. Biol. 426, 1050–1060. doi:10.1016/j.jmb.2013.10.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerba, C. P. (1984). “Applied and theoretical aspects of virus adsorption to surfaces,”Adv. Appl. Microbiol. Editor A. I. Laskin (Academic Press), 30, 133–168. doi:10.1016/s0065-2164(08)70054-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Gopinath, K., Dragnea, B., and Kao, C. (2005). Interaction between brome mosaic virus proteins and RNAs: effects on RNA replication, protein expression, and RNA stability. J. Virology 79, 14222–14234. doi:10.1128/jvi.79.22.14222-14234.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Green, C. P., Lioe, H., Cleveland, J. P., Proksch, R., Mulvaney, P., and Sader, J. E. (2004). Normal and torsional spring constants of atomic force microscope cantilevers. Rev. Sci. Instrum. 75, 1988–1996. doi:10.1063/1.1753100

CrossRef Full Text | Google Scholar

Guo, D., Li, J., Chang, L., and Luo, J. (2013). Measurement of the friction between single polystyrene nanospheres and silicon surface using atomic force microscopy. Langmuir 29, 6920–6925. doi:10.1021/la400984d

PubMed Abstract | CrossRef Full Text | Google Scholar

Guthold, M., Matthews, G., Negishi, A., Taylor, R., Erie, D., Brooks, F. P., et al. (1999). Quantitative manipulation of DNA and viruses with the nanomanipulator scanning force microscope. Surf. Interface Anal. 27, 437–443. doi:10.1002/(sici)1096-9918(199905/06)27:5/6<437::aid-sia505>3.0.co;2-n

CrossRef Full Text | Google Scholar

Heim, L.-O., Blum, J., Preuss, M., and Butt, H.-J. (1999). Adhesion and friction forces between spherical micrometer-sized particles. Phys. Rev. Lett. 83, 3328–3331. doi:10.1103/physrevlett.83.3328

CrossRef Full Text | Google Scholar

Hernando-Pérez, M., Zeng, C., Delalande, L., Tsvetkova, I., Bousquet, A., Tayachi-Pigeonnat, M., et al. (2016). Nanoindentation of isometric viruses on deterministically corrugated substrates. J. Phys. Chem. B 120, 340–347. doi:10.1021/acs.jpcb.5b08362

PubMed Abstract | CrossRef Full Text | Google Scholar

Horcas, I., Fernández, R., Gomez-Rodriguez, J., Colchero, J., Gómez-Herrero, J., and Baro, A. M. (2007). WSXM: a software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 78, 013705. doi:10.1063/1.2432410

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivošević DeNardis, N., Novosel Vlašić, N., Mišić Radić, T., Zemła, J., Lekka, M., Demir-Yilmaz, I., et al. (2024). Behavior and surface properties of microalgae indicate environmental changes. J. Appl. Phycol. 36, 113–128. doi:10.1007/s10811-023-03105-w

CrossRef Full Text | Google Scholar

Jana, N. R., Gearheart, L., and Murphy, C. J. (2001). Seeding growth for size control of 5–40 nm diameter gold nanoparticles. Langmuir 17, 6782–6786. doi:10.1021/la0104323

CrossRef Full Text | Google Scholar

Johnson, K. L., Kendall, K., and Roberts, a. (1971). Surface energy and the contact of elastic solids. Proc. Roy. Soc. Lond. A Mat. 324, 301–313. doi:10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Kao, C. C., and Sivakumaran, K. (2000). Brome mosaic virus, good for an RNA virologist’s basic needs. Mol. Plant Pathol. 1, 91–97. doi:10.1046/j.1364-3703.2000.00017.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kinloch, A. (1980). The science of adhesion: part 1. surface and interfacial aspects. J. Mater. Sci. 15, 2141–2166. doi:10.1007/bf00552302

CrossRef Full Text | Google Scholar

Lee, Y.-J., Schade, N. B., Sun, L., Fan, J. A., Bae, D. R., Mariscal, M. M., et al. (2013). Ultrasmooth, highly spherical monocrystalline gold particles for precision plasmonics. ACS Nano 7, 11064–11070. doi:10.1021/nn404765w

PubMed Abstract | CrossRef Full Text | Google Scholar

Llauró, A., Luque, D., Edwards, E., Trus, B. L., Avera, J., Reguera, D., et al. (2016). Cargo–shell and cargo–cargo couplings govern the mechanics of artificially loaded virus-derived cages. Nanoscale 8, 9328–9336. doi:10.1039/c6nr01007e

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, X., Wang, W., Xie, G., Guo, D., and Wen, S. (2020). Friction measurement and motion state determination of a single polystyrene nanoparticle during manipulation. Micro and Nano Lett. 15, 1140–1145. doi:10.1049/mnl.2020.0383

CrossRef Full Text | Google Scholar

Marshall, S. J., Bayne, S. C., Baier, R., Tomsia, A. P., and Marshall, G. W. (2010). A review of adhesion science. Dent. Mater. 26, e11–e16. doi:10.1016/j.dental.2009.11.157

PubMed Abstract | CrossRef Full Text | Google Scholar

Mateu, M. G. (2012). Mechanical properties of viruses analyzed by atomic force microscopy: a virological perspective. Virus Res. 168, 1–22. doi:10.1016/j.virusres.2012.06.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, Y., Xu, J., Jin, Z., Prakash, B., and Hu, Y. (2020). A review of recent advances in tribology. Friction 8, 221–300. doi:10.1007/s40544-020-0367-2

CrossRef Full Text | Google Scholar

Minor, A. M., and Dehm, G. (2019). Advances in in situ nanomechanical testing. MRS Bull. 44, 438–442. doi:10.1557/mrs.2019.127

CrossRef Full Text | Google Scholar

Morel, N., Tordjeman, P., and Ramonda, M. (2005). Quantitative nanotribology by atomic force microscopy. J. Phys. D. Appl. Phys. 38, 895–899. doi:10.1088/0022-3727/38/6/018

CrossRef Full Text | Google Scholar

Mougin, K., Gnecco, E., Rao, A., Cuberes, M. T., Jayaraman, S., McFarland, E. W., et al. (2008). Manipulation of gold nanoparticles: influence of surface chemistry, temperature, and environment (vacuum versus ambient atmosphere). Langmuir 24, 1577–1581. doi:10.1021/la702921v

PubMed Abstract | CrossRef Full Text | Google Scholar

Moya, A., Alemán, J., Gómez-Herrero, J., Mas-Ballesté, R., and de Pablo, P. J. (2022). Nanotribology and electrical properties of carbon nanotubes hybridized with covalent organic frameworks. Carbon 199, 80–86. doi:10.1016/j.carbon.2022.07.053

CrossRef Full Text | Google Scholar

Müller, D. J., Amrein, M., and Engel, A. (1997). Adsorption of biological molecules to a solid support for scanning probe microscopy. J. Struct. Biol. 119, 172–188. doi:10.1006/jsbi.1997.3875

PubMed Abstract | CrossRef Full Text | Google Scholar

Munz, M. (2010). Force calibration in lateral force microscopy: a review of the experimental methods. J. Phys. D. Appl. Phys. 43, 063001. doi:10.1088/0022-3727/43/6/063001

CrossRef Full Text | Google Scholar

N Israelachvili, J. (2011). Intermolecular and surface forces. 3rd ed. Academic Press, 450.

Google Scholar

Novosel, N., Mišić Radić, T., Levak Zorinc, M., Zemla, J., Lekka, M., Vrana, I., et al. (2022a). Salinity-induced chemical, mechanical, and behavioral changes in marine microalgae. J. Appl. Phycol. 34, 1293–1309. doi:10.1007/s10811-022-02734-x

CrossRef Full Text | Google Scholar

Novosel, N., Mišić Radić, T., Zemla, J., Lekka, M., Čačković, A., Kasum, D., et al. (2022b). Temperature-induced response in algal cell surface properties and behaviour: an experimental approach. J. Appl. Phycol. 34, 243–259. doi:10.1007/s10811-021-02591-0

CrossRef Full Text | Google Scholar

Ogletree, D. F., Carpick, R. W., and Salmeron, M. (1996). Calibration of frictional forces in atomic force microscopy. Rev. Sci. Instrum. 67, 3298–3306. doi:10.1063/1.1147411

CrossRef Full Text | Google Scholar

Oras, S., Vlassov, S., Berholts, M., Lõhmus, R., and Mougin, K. (2018). Tuning adhesion forces between functionalized gold colloidal nanoparticles and silicon AFM tips: role of ligands and capillary forces. Beilstein J. Nanotechnol. 9, 660–670. doi:10.3762/bjnano.9.61

PubMed Abstract | CrossRef Full Text | Google Scholar

Ortega-Esteban, Á., Mata, C. P., Rodríguez-Espinosa, M. J., Luque, D., Irigoyen, N., Rodríguez, J. M., et al. (2020). Cryo-electron microscopy structure, assembly, and mechanics show morphogenesis and evolution of human picobirnavirus. J. VIROLOGY 94, e01542-20. doi:10.1128/jvi.01542-20

PubMed Abstract | CrossRef Full Text | Google Scholar

Perlmutter, J. D., and Hagan, M. F. (2015). Mechanisms of virus assembly. Annu. Rev. Phys. Chem. 66, 217–239. doi:10.1146/annurev-physchem-040214-121637

PubMed Abstract | CrossRef Full Text | Google Scholar

Piersanti, P., White, K., Dragnea, B., and Temam, R. (2022). Modelling virus contact mechanics under atomic force imaging conditions. Appl. Anal. 101, 3947–3957. doi:10.1080/00036811.2022.2044027

CrossRef Full Text | Google Scholar

Pinchuk, P., and Jiang, K. (2015). Size-dependent hamaker constants for silver and gold nanoparticles. Phys. Chem. Interfaces Nanomater. XIV, 168–174. doi:10.1117/12.2187282

CrossRef Full Text | Google Scholar

Rao, A., Schoenenberger, M., Gnecco, E., Glatzel, T., Meyer, E., Brändlin, D., et al. (2007). Characterization of nanoparticles using atomic force microscopy. J. Phys. Conf. Ser. 61, 971–976. doi:10.1088/1742-6596/61/1/192

CrossRef Full Text | Google Scholar

Reddy, V. S., Giesing, H. A., Morton, R. T., Kumar, A., Post, C. B., Brooks, C. L., et al. (1998). Energetics of quasiequivalence: computational analysis of protein-protein interactions in icosahedral viruses. Biophysical J. 74, 546–558. doi:10.1016/s0006-3495(98)77813-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Rimai, D. S., Bowen, L. D., and Mechanics, R. (1994). Of particle adhesion. J. Adhes. Sci. Tech. 8, 1333–1355. doi:10.1163/156856194X00645

CrossRef Full Text | Google Scholar

Roos, W. H. (2011). How to perform a nanoindentation experiment on a virus. Methods Mol. Biol. 783, 251–264. doi:10.1007/978-1-61779-282-3_14

PubMed Abstract | CrossRef Full Text | Google Scholar

Roos, W. H., Gibbons, M. M., Arkhipov, A., Uetrecht, C., Watts, N. R., Wingfield, P. T., et al. (2010). Squeezing protein shells: how continuum elastic models, molecular dynamics simulations, and experiments coalesce at the nanoscale. Biophysical J. 99, 1175–1181. doi:10.1016/j.bpj.2010.05.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Roth, C. M., Neal, B. L., and Lenhoff, A. M. (1996). Van der Waals interactions involving proteins. Biophysical J. 70, 977–987. doi:10.1016/s0006-3495(96)79641-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Sader, J. E., Chon, J. W., and Mulvaney, P. (1999). Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instrum. 70, 3967–3969. doi:10.1063/1.1150021

CrossRef Full Text | Google Scholar

Schwarz, U. D., Köster, P., and Wiesendanger, R. (1996). Quantitative analysis of lateral force microscopy experiments. Rev. Sci. Instrum. 67, 2560–2567. doi:10.1063/1.1147214

CrossRef Full Text | Google Scholar

Sharma, S., LeClaire, M., and Gimzewski, J. (2018). Ascent of atomic force microscopy as a nanoanalytical tool for exosomes and other extracellular vesicles. Nanotechnology 29, 132001. doi:10.1088/1361-6528/aaab06

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon, C., Klose, T., Herbst, S., Han, B. G., Sinz, A., Glaeser, R. M., et al. (2014). Disulfide linkage and structure of highly stable yeast-derived virus-like particles of murine polyomavirus. J. Biol. Chem. 289, 10411–10418. doi:10.1074/jbc.m113.484162

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle, T., and Harrison, S. C. (1996). Crystal structures of murine polyomavirus in complex with straight-chain and branched-chain sialyloligosaccharide receptor fragments. Structure 4, 183–194. doi:10.1016/s0969-2126(96)00021-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Sümer, B., and Sitti, M. (2008). Rolling and spinning friction characterization of fine particles using lateral force microscopy based contact pushing. J. Adhesion Sci. Technol. 22, 481–506. doi:10.1163/156856108x295527

CrossRef Full Text | Google Scholar

Sun, J., Zhang, L., Wang, J., Feng, Q., Liu, D., Yin, Q., et al. (2015). Tunable rigidity of (polymeric core)-(lipid shell) nanoparticles for regulated cellular uptake. Adv. Mater. 27, 1402–1407. doi:10.1002/adma.201404788

PubMed Abstract | CrossRef Full Text | Google Scholar

Tafazzoli, A., and Sitti, M. (2004). “Dynamic modes of nanoparticle motion during nanoprobe-based manipulation,” in 4th IEEE Conference on Nanotechnology, 35–37. doi:10.1109/nano.2004.1392241

CrossRef Full Text | Google Scholar

Tocha, E., Schönherr, H., and Vancso, G. J. (2006). Quantitative nanotribology by AFM: a novel universal calibration platform. Langmuir 22, 2340–2350. doi:10.1021/la052969c

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaughan, R., Tragesser, B., Ni, P., Ma, X., Dragnea, B., and Kao, C. C. (2014). The tripartite virions of the brome mosaic virus have distinct physical properties that affect the timing of the infection process. J. Virol. 88, 6483–6491. doi:10.1128/jvi.00377-14

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, H. K. (2015). Nanomechanical and nanotribological characterization of sub-micron polymeric spheres. University of South Florida. Ph.D. thesis.

Google Scholar

Wilts, B. D., Schaap, I. A. T., and Schmidt, C. F. (2015). Swelling and softening of the cowpea chlorotic mottle virus in response to pH shifts. Biophysical J. 108, 2541–2549. doi:10.1016/j.bpj.2015.04.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolcott, R., Rhoads, D., Bennett, M., Wolcott, B., Gogokhia, L., Costerton, J., et al. (2010). Chronic wounds and the medical biofilm paradigm. J. Wound Care 19, 45–53. doi:10.12968/jowc.2010.19.2.46966

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Z., Bayón, J. L., Kouznetsova, T. B., Ouchi, T., Barkovich, K. J., Hsu, S. K., et al. (2024). Virus-like particles armored by an endoskeleton. Nano Lett. 24, 2989–2997. doi:10.1021/acs.nanolett.3c03806

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, H., Li, J., Bao, G., and Zhang, S. (2010). Variable nanoparticle-cell adhesion strength regulates cellular uptake. Phys. Rev. Lett. 105, 138101. doi:10.1103/physrevlett.105.138101

PubMed Abstract | CrossRef Full Text | Google Scholar

Zambudio, A., Gnecco, E., Colchero, J., Pérez, R., Gómez-Herrero, J., and Gómez-Navarro, C. (2021). Fine defect engineering of graphene friction. Carbon 182, 735–741. doi:10.1016/j.carbon.2021.06.064

CrossRef Full Text | Google Scholar

Zeng, C., Hernando-Pérez, M., Dragnea, B., Ma, X., van der Schoot, P., and Zandi, R. (2017). Contact mechanics of a small icosahedral virus. Phys. Rev. Lett. 119, 038102. doi:10.1103/physrevlett.119.038102

PubMed Abstract | CrossRef Full Text | Google Scholar