Optimal Topology Formation and Adaptation of Integrated Access and Backhaul Networks

1. Introduction

The exponential increase of mobile data traffic requires disrupting approaches for the realization of future wireless systems. To this end, the third-generation partnership project (3GPP) is defining the standardization of the 3GPP new radio (NR), which introduces novel designs and technologies to comply with the requirements for the fifth-generation (5G) networks (3GPP, 2018a). Besides a flexible frame structure and a significantly revised core network design, 5G NR features carrier frequencies up to 52.6 GHz (3GPP, 2019c). The large available bandwidth at millimeter wave (mmWave) frequencies offers the potential of orders of magnitude higher transmission rates than when operating in the congested bands below 6 GHz. However, operating in the mmWave spectrum comes with its own set of challenges, severe path and penetration losses being one of them (Rangan et al., 2014). One promising approach to overcome such limitations is using high gain antennas to help close the link, thus introducing directionality in the communication with electronic beamforming to support mobile users. Network densification is also used to improve the performance by reducing the inter-site distance to establish stronger access channels. An ultra-dense deployment, however, involves high capital and operational expenditures (capex and opex) for network operators (Lopez-Perez et al., 2015), because high-capacity backhaul connections have to be provided to a larger number of cellular base stations than in networks operating at lower frequencies.

The separation of the layers of the protocol stack into different physical equipment (Makris et al., 2018) and the virtualization (Mijumbi et al., 2016), i.e., the usage of software-based protocol stack implementations, can lower the capex and opex by reducing the complexity of individual base stations. To this end, integrated access and backhaul (IAB), in which only a fraction of next-generation node base stations (gNBs) connect to traditional fiber-like infrastructures, while the others wirelessly relay the backhaul traffic, is considered a promising solution (Dhillon and Caire, 2015).

IAB has been standardized in 3GPP Rel-16 (3GPP, 2018b, 2019b). IAB foresees an advanced and flexible solution for gNBs with wireless backhauling capabilities, which includes the support of multi-hop communications, dynamic multiplexing of the resources, and a plug-and-play design to reduce the deployment complexity. Additionally, directional communication through beamforming reduces cross-link interference between backhaul and access links allowing higher densification. Therefore, IAB networks are expected to be one of the key solutions for backhauling in dense networks. However, despite the consensus about IAB's ability to reduce costs, designing an efficient and high-performance IAB network is still an open research challenge.

While research related to IAB networks has gained attention, majority of the work has focused on resource allocation in such networks. In Islam et al. (2017), the authors focus on the joint cost optimal fiber drop deployment, resource allocation, and routing to minimize the operational expenses of an IAB network that operates at mmWave frequencies. In Saha and Dhillon (2019), various backhaul bandwidth partitioning strategies are discussed. Teyeb et al. (2019) provides an overview of the IAB network that is currently being standardized by 3GPP. In Liu et al. (2020), the authors propose an algorithm for the joint incentive and resource allocation design for user-provided networks (UPNs) in IAB. Here, a UPN is a network that allows a user with high channel quality to share the network access with users having poor channel quality.

Besides the resource allocation, one key problem to be tackled is the formation of an efficient IAB topology, such that too frequent updates are mitigated. Topology updates or adaptations in IAB networks are triggered in case of blockage, link failure, or congestion. To this end, we consider the problem of establishing efficient IAB network topologies, specifically the identification of the links that need to be activated to maximize the lower bound of the network capacity. Such a solution can be achieved by exhaustive search solutions. However, such a search across all possible topologies is computationally infeasible for anything more than very simple networks. We therefore present an alternative approach that does not require searching across possible topologies, and compare the resulting topologies to optimal topologies obtained from a dynamic programming approach as well as to sub-optimal topologies resulting from a standard topology formation approach.

In this article, we first summarize the related work and then highlight our main contributions and outcomes in the remainder of this section. In section 2, the IAB system model is introduced. Section 3 describes the optimization problem formulation, while section 4 comprises IAB topology formation baseline algorithms as well as our ideal sequence-based approach together with a solution for its practical implementation. Section 5 presents the simulations results, whereas section 6 concludes the article.

1.1. Related Work

IAB networks have gained interest within the last years, since their definition in 3GPP Rel. 16. In this section, we briefly review related literature and summarize their contribution.

Teyeb et al. (2019) provides an overview of the multi-hop IAB system that is currently being standardized by 3GPP, reviews the major contributions, e.g., the IAB architecture, higher layer protocols, and the physical layer, and explains the rationale behind the design choices. Another brief overview from a more practical point of view is provided in Dehos et al. (2014). Here, the authors discuss the mmWave access and backhaul infrastructure, the antenna and transceiver choices for both links, and present preliminary performance evaluation results. In Rois et al. (2016), the authors also review the design and architecture of IAB networks. In addition, they discuss how a service-driven dynamic radio resource management system can be realized in such an architecture and propose a multi-layer transmission scheme together with initial results.

Resource allocation-related approaches and results can be found in, e.g., Islam et al. (2017, 2018), Li et al. (2017), Saha et al. (2018), Saha and Dhillon (2019), and Liu et al. (2020). In Saha and Dhillon (2019), the authors first focus on a stochastic geometry-based model for analytically characterizing the performance of IAB networks, such as the downlink rate coverage probability. The authors assume a maximum received power-based association approach and demonstrate that offloading users from the macrocells to small cells may not provide similar rate improvements in an IAB setting as it would in a heterogeneous network with fiber-backhauled small cells. By using the same model, the authors focus on resource partitioning in Saha et al. (2018). Here, it is shown that depending on the choice of the partition strategy, there exists an optimal split of access and backhaul bandwidth for which the rate coverage is maximized. Further, there exists a critical volume of cell load (total number of users) beyond which the gains provided by the IAB network disappear and its performance converges to that of the traditional macro-only network. Hence, it is essential to design an efficient IAB network topology. In Islam et al. (2017), the authors focus on the cost optimal fiber drop deployment, resource allocation, and routing jointly to minimize the operational expenses of an IAB network. A mixed integer linear programming-based optimization problem formulation is provided, which is solved with a well-known branch-and-bound based algorithm. Based on simulation results, it is concluded that IAB can significantly reduce the fiber drop deployment cost of the network compared to fixed access backhaul network. In Islam et al. (2018), a joint resource allocation and relay selection in a multi-hop IAB network is investigated to maximize the geometric mean of UE rates and with the aim of demonstrating the advantages of IAB networks over purely access networks. Without providing any algorithmic details, the proposed method focuses on an optimal mesh solution by maximizing a defined objective function. There is no discussion provided on the practical implementation of such an optimization approach. Another resource allocation-related solution is provided in Liu et al. (2020). Here, a UPN is introduced, in which a user with high channel quality shares the network access with users with poor channel quality. The UPN is formed by considering both the access and backhaul link resources and by sharing these dynamically. To this end, a joint incentive and resource allocation design is explored by considering fairness between users and formulated as a Nash bargaining problem. A game-theoretic solution is provided in a centralized as well as distributed manner to improve both the user experience and network throughput. Finally, in Li et al. (2017) a stronger emphasis is placed on the radio resource management challenges in mmWaves, in particular in the joint backhaul and access operation. Then a joint scheduling and resource allocation problem is considered in terms of transmission duration and power allocation to maximize the network throughput in IAB networks. The authors break down the problem into multiple sub-problems and provide heuristic algorithms for the concurrent transmission scheduling, transmission duration allocation, and transmit power allocation with the underlying assumption of an already existing IAB network topology. Although the focus in the current release of 3GPP is on half-duplex transmission for IAB networks, full-duplex options are under discussion. In Zhang et al. (2019), the authors focus on full-duplex transmission. A closed-form solution of ergodic capacity in forms of the probability density function of the end-to-end signal-to-interference-plus-noise ratio is presented for multi-hop IAB networks. An advantage of full-duplex over half-duplex in terms of ergodic capacity is shown. A unmanned aerial vehicles (UAVs)-based IAB network scenario is considered in Fouda et al. (2018, 2019). Here, the authors focus on an optimization framework to find the optimal precoder design for backhaul links, UAV 3D hovering locations, and power allocation for forward link transmissions in order to maximize the overall network sum rate. Different approaches are proposed in Fouda et al. (2018, 2019) for the same problem formulation to investigate the mutual dependence between the spatial configurations of UAVs in the sky and the spatial dynamics of ground user distribution.

Other publications focus on the IAB network simulation and propose end-to-end simulation environment (Polese et al., 2018). Another publication focuses on field trials for IAB networks (Tian et al., 2019) and present preliminary simulation and measurement results.

1.2. Contributions and Outcomes

We consider the topology formation and adaptation problem in IAB networks, which is an essential step in the performance optimization in these networks. The key contributions in this article can be summarized as follows:

• To perform optimal topology formation, we introduce a novel node score that indicates the sum of the minimum capacities of multiple parents along the paths from its corresponding IAB donor to a node.

• We present an optimal topology formation and adaption algorithm based on dynamic programming as a reference approach, which maximizes the total node score of an IAB network or in other words which maximizes the lower bound of the network capacity for a given number of IAB nodes.

• Given that the dynamic programming approach is computationally complex and cannot be applied to a large number of IAB nodes, we propose a practical topology formation approach where the IAB nodes join the network in a specific sequence (referred to as ideal sequence-based topology formation). This approach is significantly less complex and can therefore be applied to large network sizes.

• The proposed ideal sequence-based topology formation approach does not rely on any prior topology (information) and can, therefore, be applied to both, topology formation and topology adaptation.

• We propose a practical solution for the implementation of the ideal sequence-based topology formation, which is based on broadcast signaling of received power thresholds and, hence, makes the proposed approach implementable in practical systems.

• The proposed approach yields very close performance to the optimal dynamic programming approach while outperforming a baseline approach by 26%.

2. IAB System Model

IAB networks consist of IAB donors and IAB nodes. In 3GPP, an IAB donor is defined as a node with a wired backhaul link, which provides the UE's interface to the core network as well as a wireless backhauling functionality to IAB nodes. The IAB donor is equipped with a centralized unit (CU) as well as a distributed unit (DU). The IAB donor holds a CU for the DUs of all IAB nodes and for its own DU. It is assumed that the DUs on an IAB node are served by only one IAB donor, i.e., they cannot be connected to multiple IAB donors. Here, the CU is a logical node that includes the gNB functions, such as transfer of user data, mobility control, radio access network sharing, positioning, and session management. The DU, on the other side, includes a subset of the gNB functions, depending on the functional split option selected (3GPP, 2017). Its operation is controlled by the CU.

An IAB node is a node that supports wireless access to UEs and wirelessly backhauls the access traffic. Each IAB node is equipped with a DU and a mobile terminal (MT) function. The MT function provides a radio and protocol interface to parent IAB nodes and IAB donors. The DU function of the IAB node provides backhaul connectivity to UEs and child IAB nodes. An IAB node can operate as a parent node, when its DU is connected to other IAB nodes' MTs, and as a child node when its MT is connected to another IAB node's DU (see Figure 1).

FIGURE 1

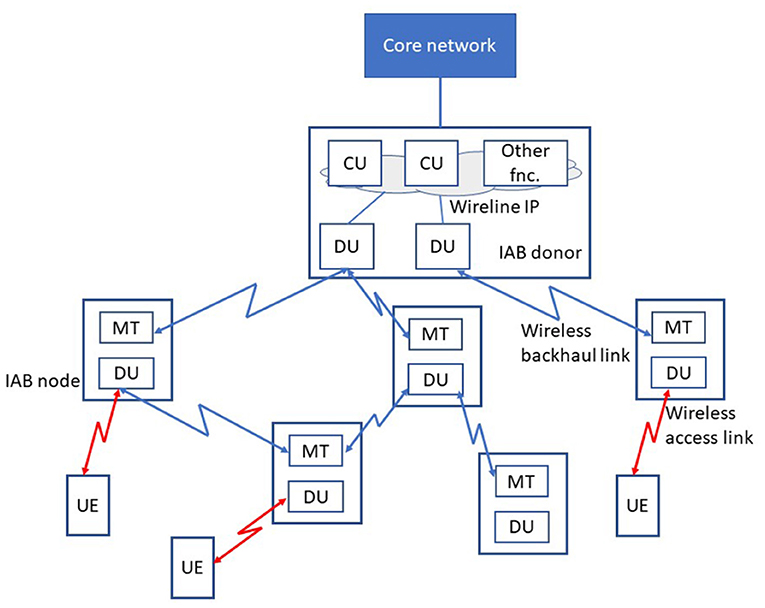
Figure 1. Illustration of an integrated access and backhaul (IAB) network with one IAB donor, five IAB nodes, and three user equipments (UEs).

Inspired from the system level evaluation assumptions for IAB networks defined by 3GPP (2019b), we consider a heterogeneous network scenario with macrocells acting as IAB donors and small cells representing IAB nodes. We define the set of IAB donors as ${D}=\{d_1,d_2,\dots ,d_D\}$ and the set of IAB nodes as ${B}=\{b_1,b_2,\dots ,b_B\}$. Both IAB donors and IAB nodes operate at mmWave bands for backhaul and access transmission and reception (in-band backhauling).

Once an IAB node is activated, it is connected to an already active node, which is either the IAB donor or another IAB node. The resulting IAB network topology can be described as a set of nodes ${N}=\{n_1,n_2,\dots ,n_{|{N}|}\}$ with ${N}={D}\cup {B}$. Each node n_i has a set of parents ${{P}}_{n_i}=\{p_1(n_i),p_2(n_i),\dots ,p_{|{{P}}_{n_i}|}(n_i)\}$ with ${{P}}_{n_i}=\varnothing$ for $n_i\in {D}$, and a set of children ${{C}}_{n_i}=\{c_1(n_i),c_2(n_i),\dots ,c_{|{{C}}_{n_i}|}(n_i)\}$. We define ${T}$ as the set of all possible topologies for the set of all nodes ${N}$. Each possible topology contains the information of an activated link from node n_i to node n_j. The set of all active links (n_i, n_j) in the m'th topology is denoted by ${{T}}_m=\{(n_i,n_j)|{\text{A}}_{n_i,n_j}=1,\forall i,j\}$ for $m=0,....,|{T}|-1$ and A_{ni, nj} is (n_i, n_j)th entry of the adjacency matrix, A, of the IAB topology, i.e., $(n_i,n_j)\in {{T}}_m$ if there is an active link between nodes n_i and n_j. In addition, we define the set of potential parent nodes of topology ${{T}}_m$ as the set of all nodes, which have less than C_max children, i.e., they can accept additional children. We denote this set by ${{P}}_{{{T}}_m}$. Similarly, we define a set of potential children of topology ${{T}}_m$ by ${{C}}_{{{T}}_m}$ as the set of all IAB nodes, which have less than P_max number of parents. Further parameters are listed in Table 1.

TABLE 1

Table 1. List of parameters.

The link spectral efficiency w_{ni, nj} for a link from transmitting node n_i to receiving node n_j with i ≠ j and $n_i,n_j\in {N}$ is defined as follows:

$\begin{array}{ll}{w}_{n_i,n_j}={log}_2\left(1+\frac{p_{n_i,n_j}^{\text{rx}}}{{\sigma }^2}\right),& (1)\end{array}$

with σ² being the additive white Gaussian noise power and assuming interference is negligible due to directionality of links. Here, we disregard the interference from non-assigned nodes since mmWave frequencies used with sufficiently narrow beams are known to be power limited rather than being interference limited.

3. Optimization Problem Formulation for IAB Topology Formation

IAB network topologies may result in multiple hops. Besides the fact that too many hops are not desired due to increased latency, it is also undesirable to have weak links over these hops. Weak links may lead to congestion and should be avoided.

To capture this in our optimization approach, we introduce a score v_ni for each node n_i as follows:

$\begin{array}{ll}{v}_{n_i}={\displaystyle \sum _{n_j\in {{P}}_{n_i}}}min\left\{v_{n_j},w_{n_j,n_i}\right\},& (2)\end{array}$

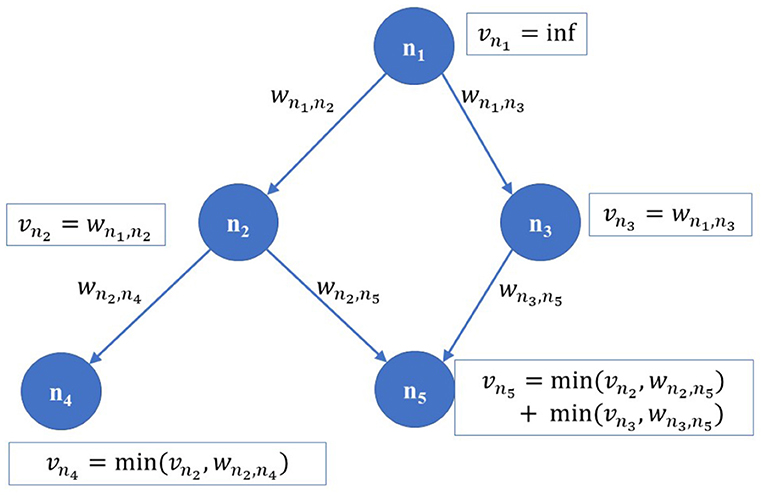
with v_nj being the score of node n_i's parent $n_j\in {{P}}_{n_i}$. The score indicates the sum of the minimum capacities of multiple parents ${{P}}_{n_i}$ along the paths from its corresponding IAB donor to node n_i. Here, the minimum capacity over multiple hops is considered to capture the “bottleneck” link along a path through the min operation. The sum indicates multi-path transmission, in case a node n_i has multiple parents. Figure 2 illustrates the node score calculation for a network with five nodes of a given topology. In case, the node n_i is an IAB donor, its weight is set to infinity since we assume that it has an infinite capacity wired backhaul link. Assuming that each link can use a bandwidth of at least b Hz, the minimum capacity at node n_i is bv_ni.

FIGURE 2

Figure 2. Illustration of node score calculation.

In our optimization problem formulation, we aim to find the optimal topology ${{T}}^{*}\subset {T}$ leading to the best set of parents and children such that the minimum capacity of the network is maximized. We define the following objective function:

$\begin{array}{ll}u({T})={\displaystyle \sum _{n_i\in {N}\backslash {D}}}{v}_{n_i}& (3)\end{array}$

Note that $bu({T})$ is the sum of minimum capacities at each node and is therefore a lower bound on the network capacity. Clearly, maximizing $bu({T})$ is equivalent to maximizing $u({T})$. Furthermore, since the bandwidth b is simply a scaling factor in the minimum network capacity $bu({T})$, we regard $u({T})$ as a measure of the network capacity and name it the total network score.

The optimization problem resulting in the optimal network topology ${{T}}^{*}$ can then be formulated as follows:

$\begin{array}{ll}{{T}}^{*}=arg{\displaystyle \underset{{T}}{max}}u({T}).& (4)\end{array}$

Hence, our optimization problem aims to find for a given set of nodes ${N}$ the optimal topology by considering each node's score and aiming to maximize the total score over all nodes, which is reflecting the lower bound of the network capacity.

4. IAB Network Topology Formation Approaches

IAB nodes follow the same procedures as UEs for attaching to the IAB network (3GPP, 2019a). In the first stage, the IAB MT setup is performed. The MT of an IAB node, in its role as a regular UE, identifies a parent node (another IAB node or an IAB donor). The MT then performs random access and transmits a connection setup request to the CU via the parent node. Following that, the backhaul radio link control channel for carrying control plane traffic to and from the IAB node is established. Then, in the IAB DU setup phase, the DU functionality of the IAB node is configured. Once this is completed, the IAB node can provide service to UEs and can serve as a parent to other IAB nodes. In addition to the initial topology formation, 3GPP discusses the topology adaptation procedure, which is triggered by, e.g., congestion, blockage, or any changes in load conditions. During topology adaptation, the network needs to determine an updated topology and then activate or deactivate links to achieve the updated topology. Based on these procedures, we present three different approaches to determine suitable IAB network topologies¹. The discussed approaches can either be implemented as initial topology formation approaches or as topology adaptation approaches, i.e., they do not rely on any specific pre-conditions of a topology. In all three cases, a fixed number of nodes N is assumed to be assigned.

4.1. Random Topology Formation

The random topology formation approach is a baseline approach and is based on a random sequence of node activation. It represents the topology formation that occurs if IAB nodes arrive (i.e., are activated) in an unplanned manner. The randomly activated node $n_j\in {{C}}_{{{T}}_m}$, with ${{T}}_m$ being the current topology with the already activated set of links, selects its set of parents ${{P}}_{n_j}^{*}=\{p_1^{*}(n_j),\dots ,p_{P_{max}}^{*}(n_j)\}\subset {{P}}_{{{T}}_m}$ from the already activated set of potential parents ${{P}}_{{{T}}_m}$ based on the maximum received power according to:

$\begin{array}{ll}{{P}}_{n_j}^{*}=arg{\displaystyle \underset{{{P}}_{n_j}}{max}}{p}_{p_i(n_j),n_j}^{\text{rx}}& (5)\end{array}$

Once node n_j finds its best parents ${{P}}_{n_j}^{*}$ a link between each parent node n_j and n_i is activated (n_j, n_i). The current topology ${{T}}_m$ is updated according to: ${{T}}_m\leftarrow {{T}}_m\cup (n_j,n_i)$. The newly activated node n_j is removed from the set of potential children: ${{C}}_{{{T}}_m}\leftarrow {{C}}_{{{T}}_m}\backslash n_i$ and added to the set of potential parents: ${{P}}_{{{T}}_m}\leftarrow {{P}}_{{{T}}_m}\cup n_j$. These steps are continued until all potential children are assigned, i.e., ${{C}}_{{{T}}_m}=\varnothing$.

4.2. Dynamic Programming-Based Topology Formation

Dynamic Programming is a powerful design technique for solving optimization problems. It is an algorithmic paradigm that solves a given complex problem by breaking it into sub-problems and stores the results of sub-problems in a cache to avoid computing the same results again. The dynamic programming approach is a centralized approach, in which all information is available at the IAB donor.

The IAB network topology formation problem can be considered as an optimization problem with sub-problems being defined as finding the optimal links. Figure 3 shows an example of one IAB donor and three IAB nodes and the sub-problem of activating the very first link between the IAB donor and IAB node n₂. The spectral efficiencies between each link with w_{ni, nj} ∈ W in this example are given as:

$\text{W}=\left(\begin{array}{llll}0& 18& 19& 20\\ 18& 0& 5& 15\\ 19& 5& 0& 10\\ 20& 15& 10& 0\end{array}\right)$

FIGURE 3

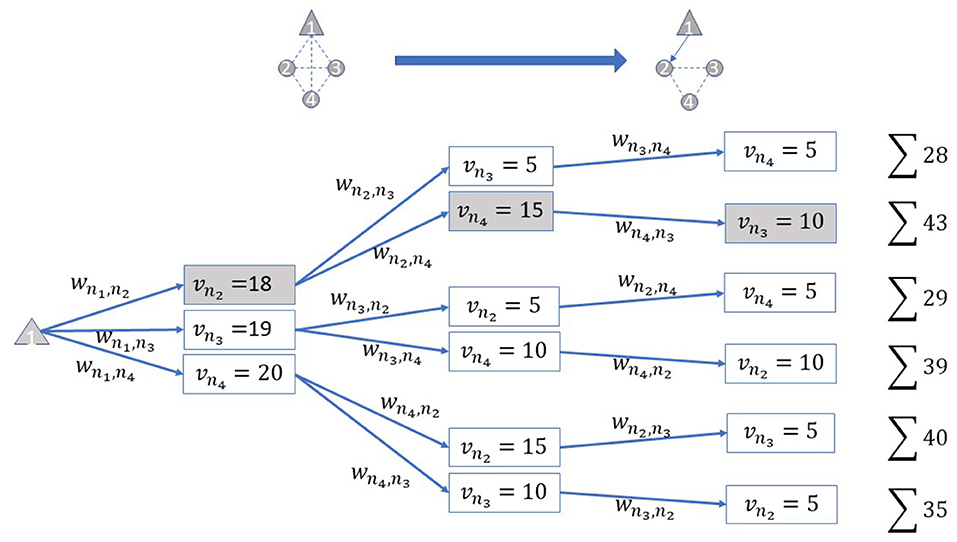
Figure 3. Example of dynamic programming-based topology formation for one integrated access and backhaul (IAB) donor and three IAB nodes. Illustration of all search options for activating the first link between the IAB donor and IAB node n₂. The maximum number of parents and children are P_max = C_max = 1, respectively.

It can be seen that, although the link capacity between the IAB donor and node n₂ is not the largest capacity, it is selected, since the consideration of all descendants in this search step leads to the maximum score. This indicates that selecting the “best” link at each node does not necessarily yield an optimal topology, and therefore a search across possible topologies is needed.

We define the IAB topology formation as a search problem, in which the optimal topology is searched, starting from an unconnected topology by activating one link between two nodes at a time until all the nodes in the network are connected. The newly activated link can be one link between two already activated nodes or one link from one already activated to one newly activated node. Then, by backtracking, we select the connections that yield the optimal topology that maximizes the objective function in Equation (4). To this end, we define a state, an action, and a reward, which are updated after each link activation in the topology until the IAB network topology is completed, i.e., no additional links can be activated under the given requirements of P_max, C_max for the given set of nodes ${N}$, so that the objective function can be maximized. The state, action, and reward are defined as follows:

The state s is defined as the mth topology of network ${{T}}_m\in {T}$. We consider that the start state at m = 0 is a network without links between the nodes, i.e., ${{T}}_0=\varnothing$. We also define an end-state s_end to terminate the search. The end-state s_end is achieved when all the nodes $n_i\in {N}$ are connected to the network such that there is no remaining link activation possible between the nodes to increase the network capacity.

The action a is defined as activating a link between two nodes $n_i\in {{P}}_{{{T}}_m}$ and $n_j\in {{C}}_{{{T}}_m}$ for state $s={{T}}_m$. Once a link is activated between the nodes n_i and n_j, the topology is updated to ${{T}}_n\leftarrow {{T}}_m\cup (n_i,n_j)$, i.e., the next state $s_{\text{next}}={{T}}_n$ is achieved. The set of potential parents and children are then updated to ${{P}}_{{{T}}_n}$ and ${{C}}_{{{T}}_n}$. Note that these sets are defined such that activating a link between n_i and n_j is always feasible under the constraint of maximum number of parents P_max and maximum number of children C_max, respectively. In other words, these two sets only contain node indices that can serve as a parent or that can be a child.

The reward r(s, a) of selecting action a in state s is defined as the spectral efficiency w_{ni, nj} of the newly added link (n_i, n_j).

Given the state, action, and reward, the dynamic programming algorithm can be implemented as a recursion-based approach, such that the resulting topology is the optimal topology ${{T}}^{*}$ and, hence, the optimal objective function $u({{T}}^{*})$. The key steps of the recursive algorithm are summarized in Algorithm 1, where the recursive topology search is given in the function “DPTopology,” which calls itself for every possible next state s_next of the current state s and searches the optimal link addition. The next state is obtained by the function called as “NextState.”

The dynamic programming-based topology formation can be very time consuming and becomes impractical as the size of the network increases. Therefore, we propose an approach in which the parent selection at nodes is sequenced in an ideal manner based on maximum received power.

4.3. Proposed Ideal Sequence-Based Approach

We propose an approach based on ideal sequencing. The ideal sequencing ensures that IAB nodes are activated in the order of links with maximum received power values. This results in each node attaching to a parent with the strongest link, thereby avoiding further topology changes immediately after the nodes are activated. The “ideal”-sequencing approach is described in Algorithm 2.

First, the set of potential parents ${{P}}_{{{T}}_0}$ is defined as the set of IAB donors ${D}$, assuming that all IAB donors are already active. Second, the set of potential children ${{C}}_{{{T}}_0}$ is initialized as the set of IAB nodes ${B}$, assuming that IAB nodes are to be activated. Here, the set of potential parents ${{P}}_{{{T}}_m}$ for the topology ${{T}}_m$ contains the nodes that are already active and can accept new children and the set of potential children ${{C}}_{{{T}}_m}$ for the topology ${{T}}_m$ contains the nodes that can be assigned to a parent node. In each iteration, all nodes $n_j\in {{C}}_{{{T}}_m}$ search for their best P_max parents resulting in node n_j's set of best potential parents ${{P}}_{n_j}^{*}$ (equation 6). Once the set of best potential parents ${{P}}_{n_j}^{*}$ is found for n_j, its best parents' received powers $p_{{{P}}_{n_j}^{*}}^{\text{rx}}$ are compared against the received powers of the best child $n_k^{*}$'s parents so far $p_{{{P}}_{n_k^{*}}^{*}}^{\text{rx}}$. If node n_j's weakest link to its best parents is stronger than the one of the best node $n_k^{*}$ so far, the best node and its set of best parents are updated as $n_k^{*}\leftarrow n_j$ and ${{P}}_{n_k^{*}}^{*}\leftarrow {{P}}_{n_j}^{*}$, respectively. This is repeated for all nodes n_j in ${{C}}_{{{T}}_m}$.

Then, all links between this node $n_k^{*}$ and its parents $p_i^{*}(n_k^{*})$ are activated, and the topology ${{T}}_m$ is updated accordingly. The newly activated node $n_k^{*}$ is removed from the potential set of children ${{C}}_{{{T}}_m}$ and added to the set of potential parents ${{P}}_{{{T}}_m}$. In the last step, ${{P}}_{{{T}}_m}$ is checked for invalid parents, i.e., parents that already serve C_max children are removed from the set. These steps are repeated until all nodes are activated.

The ideal sequence-based topology formation requires knowledge of received powers of all potential links at a centralized controller (e.g., the CU). If an initial topology is already established and all IAB nodes are integrated into the network, then the IAB nodes can perform measurements of received powers and report the measurements to the centralized controller. The centralized controller can then determine the topology according to the Algorithm 2 and direct nodes to attach or reattach to achieve that topology.

ALGORITHM 1

Algorithm 1: Dynamic programming-based topology formation.

ALGORITHM 2

Algorithm 2: Ideal sequencing-based topology formation.

However, if the initial topology is not established, IAB nodes are not able to report measurements to the centralized controller, making the ideal sequence-based topology formation inapplicable to the initial topology establishment scenarios. For such cases, it is possible to approximate the behavior of the ideal sequence-based topology formation by carefully controlling how IAB nodes attach to parents. To this end, we propose a novel signaling approach that makes the ideal-sequencing approach feasible for the initial topology formation in practice. An illustration of the proposed approach is given in Figure 4.

FIGURE 4

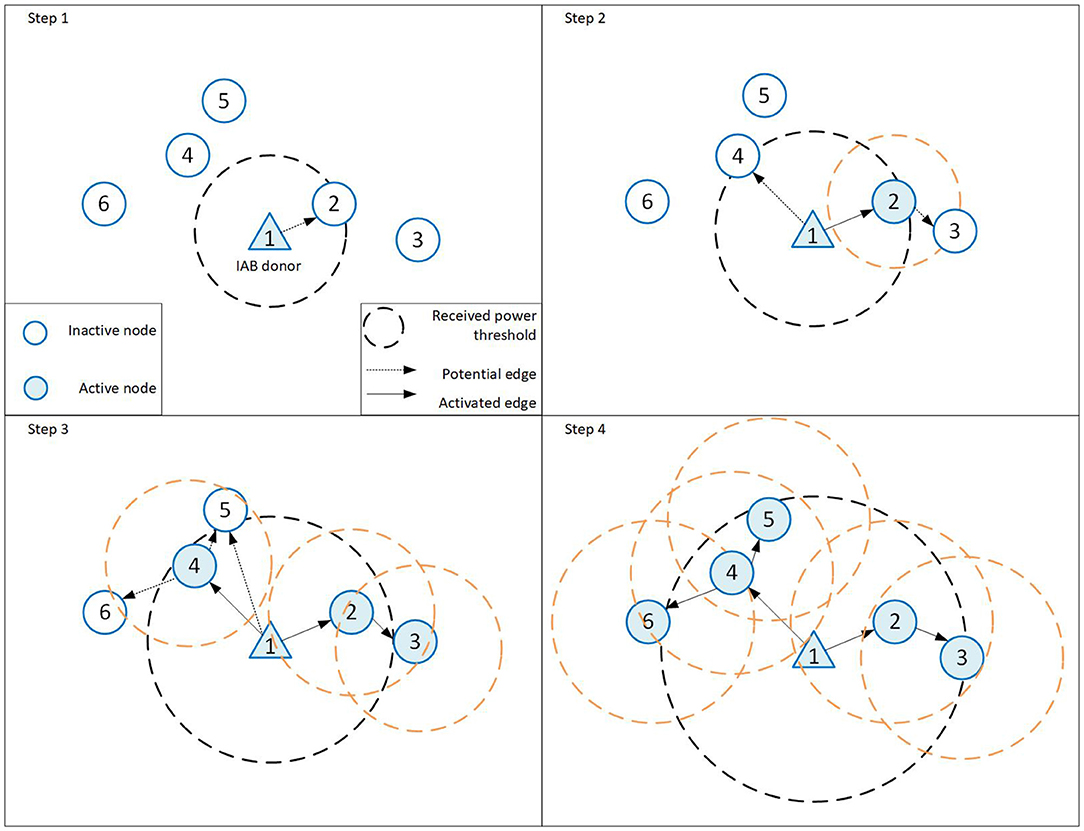
Figure 4. Illustration of the steps for ideal sequence-based edge activation in integrated access and backhaul (IAB) networks through received power threshold broadcasting.

Initially, in step 1, the IAB donor, which is node 1 in the illustration, broadcasts a receive power threshold, which is shown as a circle. This threshold is defined by the CU and shared with all active IAB nodes. It can be included, for example, in the symbol information and broadcasted such that inactive IAB nodes can be listed to it. In step 1, all inactive IAB nodes perform receive power measurements and only node 2 measures node 1 as a potential parent, since its measured receive power is within the broadcasted threshold (inside the circle). Once node 2 is activated, both nodes 1 and 2, broadcast a decreased receive power threshold, in step 2. Note that the range of IAB node 2 is smaller than the range of the IAB donor. This is due to transmit power differences. Since node 4 falls into the receive power threshold of node 1 and node 3 is within the range of node 2, nodes 4 and 3 are activated next. This procedure is continued in steps 3 and 4 until all nodes are activated. In summary, in the proposed procedure, nodes that are already integrated broadcast a receive power threshold. Other nodes seeking to attach only attach to IAB nodes to which they measure a receive power that is above the threshold. This threshold is then gradually decreased, resulting in a sequencing where the links with the largest receive power are activated first. The process is continued with the newly integrated nodes also broadcasting the threshold, until all nodes are integrated. This eliminates the need for centralized control to enable the ideal sequencing in the proposed approach also for the initial topology formation.

5. Simulation Results

In this section, we describe our simulations settings and present the performance results of the three topology formation approaches.

5.1. Simulation Parameters

In our Monte Carlo-based topology formation simulations, we consider the set of IAB donors ${D}$ with D = 1 and the set of IAB nodes ${B}$ with B = [3, 5, 7] nodes. Hence, the total number of nodes is N = D + B = [4, 6, 8]. The IAB donor's transmit power is 40 dBm while the IAB node's transmit power is 33 dBm. We consider a carrier frequency of 30 GHz and the large-scale channel parameters for IAB donor to IAB node are the 5GCM UMa model (with hUE = 10 m) and for IAB node to IAB node the UMi-Street canyon model with (hUE = 10 m), respectively (see 3GPP, 2019b).

The maximum number of children each node can be connected to is C_max = [1, 2, ∞]. Here, C_max = ∞ means that there is no limitation on the number of possible children of each IAB node or IAB donor. For the maximum number of parents, we consider the two cases of P_max = 1 and P_max = 2. While the former one reflects single connectivity and leads to a “tree” topology, the latter reflects dual connectivity and leads to a directed acyclic graph (DAG) topology. Both options are supported by 3GPP.

5.2. Discussion of Results

In this section, we compare the simulation results of the discussed topology formation approaches for both topology types, namely the tree and the DAG topologies. The topology formation approaches are named as “DP” for the dynamic programming approach, as “ideal seq.” for the ideal sequence-based approach, and as “random” for the random sequence-based approach, respectively. Figure 5 shows the cumulative distribution functions (CDFs) of the total score of all three topology formation approaches for the tree topology with C_max = 1 for different numbers of IAB nodes B = [3, 5, 7]. Here, the line type reflects the number of IAB nodes, whereas the color code reflects the different topology formation approaches. It can be observed that the performances of the B = 3 IAB nodes scenarios are very close to each other. This is simply because there is a small number of possible topology options for such a low number of nodes. Hence, the more possible is topologies, the higher is the expected gain in terms of total score. In addition, we can state that for the tree topology with C_max = 1 case, the performance is limited by the backhaul link between the IAB donor and the first(-hop) IAB child. Any node score of the other IAB nodes is limited by the node score of this first IAB child. We have summarized the average total score gain of the proposed ideal sequence approach with the dynamic programming and random sequence approaches for tree and DAG topologies and for C_max = 1 and C_max = 2 for different IAB node numbers in Table 2. It can be observed that in all cases the proposed ideal sequence approach yields very close average total score numbers (up to 0.03%) as compared to dynamic programming. Our proposed approach outperforms the random sequence approach by up to 26% on average.

FIGURE 5

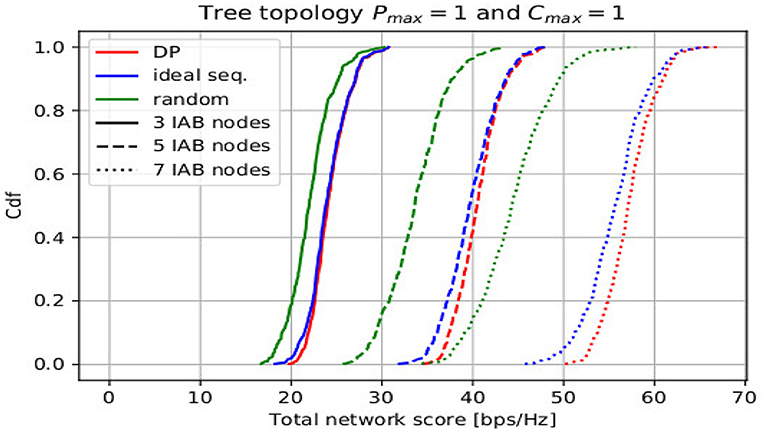
Figure 5. Cumulative distribution function (CDF) of total score for P_max = 1 and C_max = 1 for different number of integrated access and backhaul (IAB) nodes B = [3, 5, 7].

TABLE 2

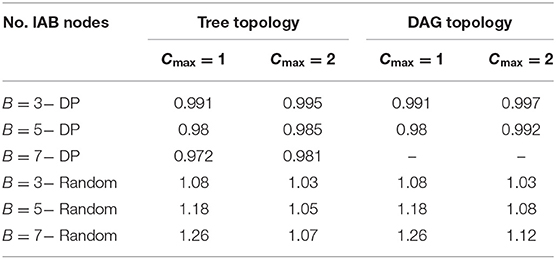
Table 2. Performance gain on average of the proposed ideal sequence-based topology formation as compared to the reference approaches.

Figure 6 depicts the average total score over different number of maximum number of children C_max for different number of IAB nodes B = [3, 5, 7] for the tree topologies. It can be observed that the ideal sequence approach yields very close results to the optimal dynamic programming approach. With the increasing number of maximum number of children C_max, the difference between the three approaches reduces. This is due to the fact that C_max = inf removes the limit on the number of children a node can serve. Given that the donor has a significant transmit power difference to the IAB nodes, the majority of the IAB nodes' maximum receive power will be the one to the IAB donor, so that the majority of the nodes request access from the IAB donor, which, in turn, accepts this request, since it has no limitation on the number of children it can serve. In such a scenario, the resulting topology will be similar for all three approaches, i.e., the majority of the IAB nodes will be connected to the IAB donor. It can further be observed that the increase of the maximum number of children does not necessarily improve the total average score, i.e., there is no significant difference between C_max = 1, C_max = 2, and C_max = inf.

FIGURE 6

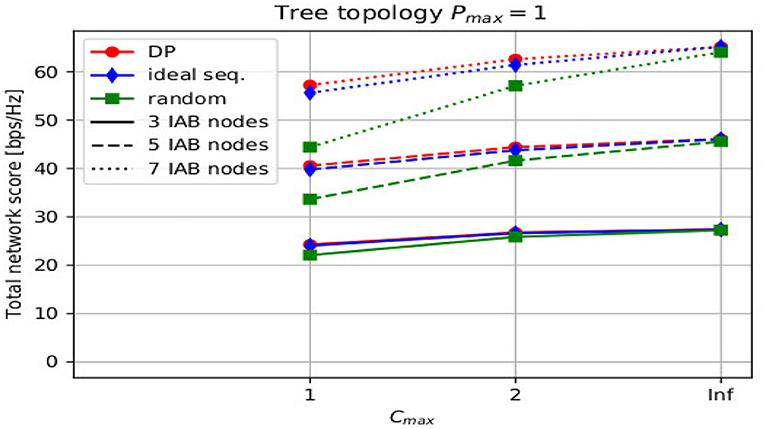
Figure 6. Average total score for different maximum number of children and different number of integrated access and backhaul (IAB) nodes B = [3, 5, 7] for a tree topology, i.e., P_max = 1.

In Figure 7, the average total score over different number of C_max for different number IAB nodes B = [3, 5] for the DAG topologies is depicted. As compared to the tree topology case in Figure 6, the ideal sequence approach performs even closer to the optimal dynamic programming approach. Again, for IAB node number B = 3 all approaches perform very similarly, because of the limited number of options in such a small network. The increase in the maximum number of children shows a larger gain in terms of average total capacity for all three approaches in case of a DAG topology. While this gain is significant when C_max = 1 is increased to C_max = 2, there is limited additional gain to remove the limitation on the maximum number of children with C_max = inf.

FIGURE 7

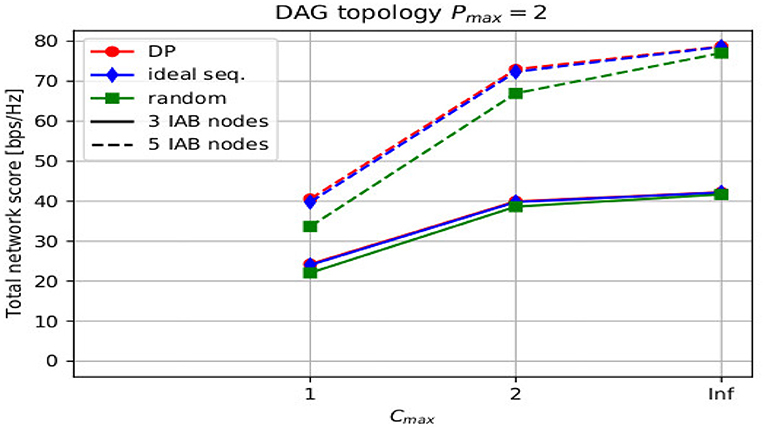
Figure 7. Average total score for different maximum number of children and different number of integrated access and backhaul (IAB) nodes B = [3, 5, 7] for a directed acyclic graph (DAG) topology, i.e., P_max = 2.

5.3. Complexity Comparison

In this section, we discuss the complexity of the proposed ideal sequencing-based topology formation and the dynamic programming-based topology formation approaches. The complexity of the ideal sequencing approach is ${O}(N^3)$, i.e., the complexity increases with the number of nodes in the network and the number of parents a node can be assigned to. The complexity of the dynamic programming approach is given as ${O}\left(2^{\left(\frac{N(N-1)}{2}\right)}\right)$. Dynamic programming searches for all possible topologies are significantly more complex; hence, for large number of nodes, e.g., N = 7, simulations cannot be obtained due to large complexity. In Table 3, we demonstrate some illustrative values for the complexity gain of the ideal sequencing approach and the dynamic programming approach. Here, k₁ ≤ 1 reflects a scaling factor to account for the number of parents and children limitations and k₂ ≤ 1 is a scaling factor to account for caching and the number of parents and children limitations, respectively. In summary, the proposed ideal sequence-based approach yields very close results to the dynamic programming approach while being significantly less complex, especially for increasing number of IAB nodes.

TABLE 3

Table 3. Illustrative values for the complexity gain of the proposed ideal-sequencing approach when compared with the dynamic programming approach.

6. Conclusion

In this paper, we have focused on the topology formation in IAB networks and have proposed an ideal sequence-based topology formation algorithm. We compare the proposed approach with a random sequence-based approach and a dynamic programming-based approach, which reflects an optimal approach. Simulation results demonstrate that our proposed approach significantly outperforms the random sequence-based approach in terms of lower bound of network capacity for various IAB node numbers as well as maximum number of parents and children per node. The proposed approach yields performances extremely close to the optimal dynamic programming while being significantly less complex, and hence, applicable to large IAB networks.

Data Availability Statement

The datasets generated for this article are not readily available because of Intel policy. Requests to access the datasets should be directed to hosein.nikopour@intel.com.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

All authors were employed by Intel Corporation when the article was submitted to Frontiers.

Footnotes

1. ^We focus on the topology formation for IAB nodes only and assume that once the backhaul topology is formed, UEs can get access based on their received power. Without loss of generality, however, the proposed approaches can be extended to topology formation including UEs as well.

References

3GPP (2017). Technical Specification Group Radio Access Network; Study on New Radio Access Technology: Radio Access Architecture and Interfaces. Technical Report (TR) 38.801, 3rd Generation Partnership Project (3GPP).

3GPP (2018a). NR and NG-RAN Overall Description–Rel. 15. Technical Specification (TS) 38.300, 3rd Generation Partnership Project (3GPP). Version 14.2.2.

3GPP (2018b). New WID: Integrated Access and Backhaul for NR. Report 38.300, 3rd Generation Partnership Project (3GPP). Version 14.2.2.

3GPP (2019a). NG-RAN; Architecture Description. Technical Specification (TS) 38.401, 3rd Generation Partnership Project (3GPP).

3GPP (2019b). NR; Study on Integrated Access and Backhaul. Technical Specification (TS) 38.874, 3rd Generation Partnership Project (3GPP).

3GPP (2019c). NR; User Equipement (UE) Radio Transmission and Reception; Part 2: Range 2 Standalone. Technical Specification (TS) 38.101-2, 3rd Generation Partnership Project (3GPP). Version 14.2.2.

Dehos, C., González, J. L., Domenico, A. D., Kténas, D., and Dussopt, L. (2014). Millimeter-wave access and backhauling: the solution to the exponential data traffic increase in 5G mobile communications systems? IEEE Commun. Mag. 52, 88–95. doi: 10.1109/MCOM.2014.6894457

CrossRef Full Text | Google Scholar

Dhillon, H. S., and Caire, G. (2015). Wireless backhaul networks: capacity bound, scalability analysis and design guidelines. IEEE Trans. Wireless Commun. 14, 6043–6056. doi: 10.1109/TWC.2015.2447534

CrossRef Full Text | Google Scholar

Fouda, A., Ibrahim, A. S., Guvenc, I., and Ghosh, M. (2018). “UAV-based in-band integrated access and backhaul for 5G communications,” in IEEE 88th Vehicular Technology Conference (VTC-Fall). (Chicago, IL). doi: 10.1109/VTCFall.2018.8690860

CrossRef Full Text | Google Scholar

Fouda, A., Ibrahim, A. S., Güvenç, Í., and Ghosh, M. (2019). Interference management in uav-assisted integrated access and backhaul cellular networks. IEEE Access 7, 104553–104566. doi: 10.1109/ACCESS.2019.2927176

CrossRef Full Text | Google Scholar

Islam, M. N., Abedini, N., Hampel, G., Subramanian, S., and Li, J. (2018). “Investigation of performance in integrated access and backhaul networks,” in IEEE INFOCOM 2018–IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS). (Honolulu, HI). doi: 10.1109/INFCOMW.2018.8406872

CrossRef Full Text | Google Scholar

Islam, M. N., Subramanian, S., and Sampath, A. (2017). “Integrated access backhaul in millimeter wave networks,” in IEEE Wireless Communications and Networking Conference (WCNC) (San Francisco, CA). doi: 10.1109/WCNC.2017.7925837

CrossRef Full Text | Google Scholar

Li, Y., Pateromichelakis, E., Vucic, N., Luo, J., Xu, W., and Caire, G. (2017). Radio resource management considerations for 5G millimeter waves backhaul and access networks. IEEE Commun. Mag. 55, 86–92. doi: 10.1109/MCOM.2017.1601118

CrossRef Full Text | Google Scholar

Liu, Y., Tang, A., and Wang, X. (2020). Joint incentive and resource allocation design for user provided network under 5G integrated access and backhaul networks. IEEE Trans. Netw. Sci. Eng. 7, 673–685. doi: 10.1109/TNSE.2019.2910867

CrossRef Full Text | Google Scholar

Lopez-Perez, D., Din, M., Claussen, H., and Jafari, A. H. (2015). Towards 1 GBPS/UE in cellular systems: understanding ultra-dense small cell deployments. IEEE Commun. Surv. Tutor. 17, 2078–2101. doi: 10.1109/COMST.2015.2439636

CrossRef Full Text | Google Scholar

Makris, N., Zarafetas, C., Basaras, P., Korakis, T., Nikaein, N., and Tassiulas, L. (2018). “Cloud-based convergence of heterogeneous RANs in 5G disaggregated architectures,” in IEEE International Conference on Communications (ICC). (Kansas City, MO). doi: 10.1109/ICC.2018.8422227

CrossRef Full Text | Google Scholar

Mijumbi, R., Serrat, J., J.-Gorricho, L., Bouten, N., De Turck, F., and Boutaba, R. (2016). Network function virtualization: state-of-the-art and research challenges. IEEE Commun. Surv. Tutor. 18, 236–262. doi: 10.1109/COMST.2015.2477041

CrossRef Full Text | Google Scholar

Polese, M., Giordani, M., Roy, A., Goyal, S., Castor, D., and Zorzi, M. (2018). “End-to-end simulation of integrated access and backhaul at mmWaves,” in IEEE 23rd International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD). (Barcelona). doi: 10.1109/CAMAD.2018.8514996

CrossRef Full Text | Google Scholar

Rangan, S., Rappaport, T. S., and Erkip, E. (2014). Millimiter-wave celluler wireless networks: potentials and challenges. Proc. IEEE 102, 366–385. doi: 10.1109/JPROC.2014.2299397

CrossRef Full Text | Google Scholar

Rois, J. G., Lorenzo, B., González-Castaño, F. J., and Burguillo, J. C. (2016). “Heterogeneous millimeter-wave/micro-wave architecture for 5G wireless access and backhauling,” in European Conference on Networks and Communications (EuCNC). (Athens). doi: 10.1109/EuCNC.2016.7561028

CrossRef Full Text | Google Scholar

Saha, C., Afshang, M., and Dhillon, H. S. (2018). Bandwidth partitioning and downlink analysis in millimeter wave integrated access and backhaul for 5G. IEEE Trans. Wireless Commun. 17, 8195–8210. doi: 10.1109/TWC.2018.2874655

CrossRef Full Text | Google Scholar

Saha, C., and Dhillon, H. S. (2019). Millimeter wave integrated access and backhaul in 5G: performance analysis and design insights. IEEE J. Select. Areas Commun. 37, 2669–2684. doi: 10.1109/JSAC.2019.2947997

CrossRef Full Text | Google Scholar

Teyeb, O., Muhammad, A., Mildh, G., Dahlman, E., Barac, F., and Makki, B. (2019). “Integrated access backhauled networks,” in IEEE 90th Vehicular Technology Conference. (Honolulu, HI). doi: 10.1109/VTCFall.2019.8891507

CrossRef Full Text | Google Scholar

Tian, T., Dou, Y., Ren, G., Gu, L., Chen, J., Cui, Y., et al. (2019). “Field trial on millimeter wave integrated access and backhaul,” in IEEE 89th Vehicular Technology Conference (VTC2019-Spring). (Kuala Lumpur). doi: 10.1109/VTCSpring.2019.8746375

CrossRef Full Text | Google Scholar

Zhang, X., Liu, F., and Xia, H. (2019). “Ergodic capacity analysis for full-duplex integrated access and backhaul system,” in IEEE Global Conference on Signal and Information Processing (GlobalSIP) (Ottawa, ON). doi: 10.1109/GlobalSIP45357.2019.8969094

CrossRef Full Text | Google Scholar