FedPARL: Client Activity and Resource-Oriented Lightweight Federated Learning Model for Resource-Constrained Heterogeneous IoT Environment

1. Introduction

We first discuss the motivations of introducing Federated Proximal, Activity, and Resource-Aware Lightweight model (FedPARL) that can handle system and statistical heterogeneity of the clients and is particularly effective for a resource-constrained Federated Learning (FL)-Internet of Things (IoT) environment. We analyze the existing works in the FL domain and clearly mention how FedPARL can be effective in filling up the gap of prior research considering FL-IoT setting. Further, we describe our research contribution and justify the necessity of conducting this research work. Finally, we briefly highlight the organization of this paper.

1.1. Motivation

Federated Learning has come to the light because of its promising paradigm as a distributed machine learning training over a network of available devices. Prior works focused on distributed optimizations and learning (Chen and Sayed, 2012; Tsianos et al., 2012; Shamir et al., 2014). However, FL has an unique way of generating a cumulative global model by learning from the client's model parameters, and it has two distinctive challenges from conventional distributed optimization: system heterogeneity and statistical heterogeneity (McMahan et al., 2017; Zhao et al., 2018; Yang et al., 2019; Li et al., 2020). The detailed description of the FL challenges (e.g., handling heterogeneity by performing on-device training, considering low participation of network clients, and tackling high communication costs) are discussed in McMahan et al. (2017), Smith et al. (2017), Imteaj et al. (2020), and Li et al. (2020). The earlier invented FL algorithm, Federated Averaging (FedAvg) (McMahan et al., 2017) is an iterative process and optimization approach that generates a global model by learning from the local update of the client. Though the FedAvg algorithm has significant contribution in FL settings, it has missed some underlying challenges that can be observed in a heterogeneous FL-IoT setting. First, the FedAvg assumes all the available clients as uniform capabilities and randomly selects a fraction of local clients for the training phase. However, in a real-world FL setting, we may observe a marginal difference in various clients in terms of their system configurations. Second, FedAvg does not entitle to perform variable or partial amounts of work by the participated clients; rather, it simply drops the participants that fail to perform a given task within a specified time window (Bonawitz et al., 2019). Third, the performance of FedAvg diverges significantly when the client has non-identically distributed data across their devices, i.e., there remains statistical heterogeneity within the FL network (McMahan et al., 2017; Li et al., 2018). Fourth, the FedAvg algorithm does not guarantee convergence in case most of the clients are dropped, or if majority of the clients sends back divergent model update compared to the actual target.

In this paper, we propose a novel FL model, referred to as FedPARL, that can be effective for resource-constrained and highly heterogeneous FL settings. Our developed FL model, FedPARL, is a tri-layer FL model that reduces model size by applying sample-based pruning, supports the effective clients through a trust and resource checking scheme, and allows partial amounts of computational tasks by examining their resource-availabilities. We bridge the gap between systems and statistical heterogeneity by reparameterization of the FedAvg algorithm (McMahan et al., 2017). Instead of dropping the underperformed clients and naively considering the partial amounts of work from the participated clients (that may prolong convergence), we added a proximal term by considering resource-availability of the selected clients. By checking the trust score and resource-availability of the clients, our proposed approach shows more stability than the existing FedProx framework (Li et al., 2018) in a highly resource-constrained FL-IoT environment.

1.2. Background and Related Works

The invention of new distributed optimization and learning techniques has recently been popular due to the extensive growth of data that opens the door to rethink the design of Machine Learning (ML) and data center settings (Boyd et al., 2011; Dekel et al., 2012; Zhang et al., 2013; Shamir et al., 2014; Arjevani and Shamir, 2015; Richtárik and Takáč, 2016a,b; Wang et al., 2018). On one side, the improvements of internet availability, speed, and architecture bring more convenience for IoT services. On the other hand, the ever-growing development of modern edge devices (e.g., smartphones, wearable devices, drones, and sensors) enables performing computation at the edge without passing local sensitive data to the server. The FL technique was invented after being motivated by the same theme (McMahan et al., 2017). Though FL faces many challenges in terms of systems and statistical heterogeneity, privacy, communication overhead, and massively distributed federated network (Yang et al., 2019; Imteaj et al., 2020), the wide popularity of FL approach motivates researchers to develop new optimization techniques suitable for a federated setting. Such novel federated optimization technique outperforms the conventional distributed methods, e.g., mini-batch gradient descent (Dekel et al., 2012), or alternating direction method of multipliers (ADMM) (Boyd et al., 2011). The distributed optimization technique (e.g., Konečnỳ et al., 2016; McMahan et al., 2017; Smith et al., 2017; Zhao et al., 2018; Mohri et al., 2019; Sattler et al., 2019) allows for inexact local model updating that would help to balance between computation and communication in large-scale networks, and permit to active a small subset of devices at any iteration period (McMahan et al., 2017; Smith et al., 2017; Imteaj and Amini, 2019; Li et al., 2020). For instance, a multi-task learning framework is proposed in Smith et al. (2017) to assist FL clients in learning separate but close models through a primal-dual optimization strategy. Although their proposed method guarantees convergence, the approach is not generalizable for non-convex problem. For the non-convex settings, the FedAvg algorithm (McMahan et al., 2017) considers averaging client local SGD update and outperforms existing models. Besides, to avoid the issues regarding active clients and statistical heterogeneity of FedAvg algorithm, couple of works (Stich, 2018; Basu et al., 2019; Haddadpour et al., 2019; Khaled et al., 2019; Malinovsky et al., 2020; Woodworth et al., 2020) have shown efforts to analyze FedAvg algorithm considering non-federated setting, i.e., they assume the data to be identical and uniformly distributed. However, in a heterogeneous setting, it is not proper to assume that each local solver can perform same stochastic process using their local data. Further, the authors in Chen et al. (2020b) proposed a joint learning framework by considering the effect of wireless quality during model training, such as packet errors and limited bandwidth. By considering joint learning, resource factors, and client selection, they formulate objective functions of the optimization problem. Besides, the authors in Yang et al. (2020) investigated the issues regarding effective energy utilization during model computation and transmission for FL over wireless networks. Though wireless quality and optimal energy utilization are two important factors for a resource-constrained IoT environment, these two factors are out-of-scope of this research.

One of the main challenges in federated networks is systems heterogeneity, i.e., the clients within the network may possess variant memory, processing capability, battery life, or bandwidth. Such heterogeneity exacerbates straggler issues and degrades system performance. If the number of stragglers becomes high, then it may take a long time or even fail to reach the target convergence. One solution could be to avoid the resource-constrained clients or not selecting them during the training phase (Bonawitz et al., 2019; Imteaj, 2020; Imteaj et al., 2020). However, dropping the stragglers could limit the number of active clients, and it could bring bias during training or even some dropping clients may have important data with higher volume (Li et al., 2018). Beyond systems heterogeneity of the FL clients, statistical heterogeneity or divergence of client model update is also a concern in federated networks. Some recent FL works (Dinh et al., 2019; Haddadpour and Mahdavi, 2019; Wang et al., 2019; Chen et al., 2020a; Guo et al., 2020; Nguyen et al., 2020) analyze how to guarantee convergence both in theoretically and empirically for an FL setting. The major problem is that they assume all FL clients are resource capable to perform a predefined uniform number of iterations while considering all the devices to participate in the training round. However, such assumptions are not feasible if we consider a realistic FL networks (McMahan et al., 2017; Li et al., 2020). To handle statistical heterogeneity, some works proposed the idea of sharing either the client's local data or the server's proxy data (Huang et al., 2018; Jeong et al., 2018; Zhao et al., 2018). However, the assumption of passing client data to the server or disseminating proxy data to all the clients could violate privacy (Huang et al., 2018; Jeong et al., 2018). The authors in Li et al. (2018) proposed a framework that can handle both systems and statistical heterogeneity. Through generalization of FedAvg algorithm and adding a proximal term, they handle statistical diversity and allow partial amounts of work. However, they randomly select a subset of clients like the FedAvg algorithm (McMahan et al., 2017), which would not be effective in an FL-IoT environment as most of the participants would be inactive or out-of-resources. In the worst case, the random selection of the participants may lead them to choose all the straggler devices that could hardly perform an iteration. Besides, in their simulation, they consider that the straggler or inactive client would take a random local iteration between 1 to E, where E is the local epoch defined by the task publisher for the overall task. In the worst case, it is possible that most of the stragglers need to perform local epochs close to the E. That means, instead of considering the resource-availability or previous history, they randomly assign a local epoch for the straggler or inactive clients. Particularly, in a real-life FL setting, such random assigning of local epoch to the stragglers would result ineffective model update.

In this work, inspired by FedAvg (McMahan et al., 2017) and FedProx (Li et al., 2018), we design a tri-layer FL model, FedPARL that can be effective, specially in an FL-IoT settings. In the initial layer, we perform a sample-based model pruning on the server, so that the server and the client can deal with a smaller model size. In the second layer, we examine the resource-availability (CPU, memory, battery life, and data volume) as well as previous activities and select the proficient and trustworthy clients for the training phase. In the third layer, we perform a generalization of FedAvg algorithm to allow partial works by assigning local epochs according to the client's resource-availability. Our tri-layer FL framework accelerates convergence and improves robustness in a resource-constrained FL-IoT environment.

1.3. Contribution

The main contributions of this paper can be listed as follows:

• We propose a tri-layer FL scheme that helps resource-constrained FL clients consume less resources during training, avoid untrustworthy and out-of-resource clients (e.g., low battery life) during client selection for training and perform variable local epochs based on the client's resource availability.

• We perform model pruning to reduce the size of client model that will be more efficient in an FL-IoT setting.

• We integrate a reward-punishment scheme to incentivize effective clients to participate in future training rounds and to punish the malicious and underperformed clients.

• We allow partial amounts of computational task to be performed by the participating FL clients, and our proposed approach is robust even in an resource-constrained FL-IoT environments.

1.4. Organization

The rest of this paper is organized as follows: section 2 introduces the federated optimization techniques, exposes the existing findings of the existing approaches, and explains the strategy of our proposed FedPARL framework. In section 3, we present the experimental details with simulation results considering model pruning, systems heterogeneity, and statistical heterogeneity, followed by section 4, that concludes the paper.

2. Federated Optimization Techniques

In this section, we highlight the widely popular FedAvg and FedProx algorithm and present the outline of our proposed FedPARL framework. In the FedAvg (McMahan et al., 2017) method, the central server initializes a global model which is updated based on the client local model parameters. The main aim of FedAvg algorithm is to minimize an objective function (loss) which can be expressed as follows:

$\begin{array}{ll}{\displaystyle \underset{w}{\text{min }}}F(w):={\displaystyle \sum _{i=1}^N}{P}_i{F}_i(w),& (1)\end{array}$

where N is the number of devices, P_i ≥ 0 %$\sum _i{P}_i=1$ (P_i ≥ 0) which refers to the impact of each device on the overall FL model, satisfying $\sum _i{P}_i=1$, and F_i denotes the objective function of local device i. Here, we assume that n_i samples are available at each device and $n=\sum _i{n}_i$ is the total data points, hence, $P_i=\frac{n_i}{n}$.

In FedAvg procedure, the central server selects a fraction of clients for the training round, and a local objective function is used as a replacement of the global objective function considering the device's local data. At first, the server initializes a global model that is disseminated to a fraction of local clients which are randomly selected. The clients that are selected for the training phase are called participants. After that, each client trains themselves locally with E number of local epochs by applying stochastic gradient descent (SGD) using their local data as well as the global model information and sends back the model information to the server. Further, the server performs aggregation based on all the received model parameters and update the global model. The iteration process is continued until a specific iteration round or until the global model reaches a convergence. Each iteration process is called a federation (Jiang et al., 2019). However, instead of enforcing all the clients to perform an exact local epoch, we can allow a flexible or inexact local objective function to be solved by each client. The authors in McMahan et al. (2017) discussed that tuning up the number of local epochs plays an important role in reaching convergence. On one side, a higher number of local epochs leads to a more local computation to be performed by the FL clients and reduces the communication overhead with the server that results in faster convergence. On the other side, if the heterogeneous FL clients possess dissimilar local objectives and perform a higher number of local epochs, then model convergence could be negatively affected which may even cause model divergence. Besides, in a heterogeneous FL-IoT environment, setting up higher local epochs may increase the possibility that the FL clients fail to perform assigned computational tasks. Further, if the FL clients perform a lower number of local epochs, it may reduce local computations, but may prolong the communication overhead and convergence time. Therefore, it is vital to set local epochs as sufficiently high while also ensuring robust convergence. As the suitable number of local epochs may change at each training round and depend on device resources, determining the number of local epochs can be considered as a function of on-device data and available system resources. For tuning the local computation and client-server interaction, we adapt an inexact solution that allows flexible local epochs to be performed by each client which is stated below (Li et al., 2018):

Definition 1 (φ-inexact solution). Let us consider a function ${G}(w;w_0)=F(w)+\frac{\beta }{2}\Vert w-w_0|{|}^2,$ and φ ∈ [0, 1], we can say w^* is a φ-inexact solution of ${\text{min}}_{\theta }{G}(w;w_0)$ if $\Vert \nabla {G}(w^{*};w_0)\Vert \le \phi \Vert \nabla {G}(w_0;w_0)\Vert ,$ where ∇${G}$(w; w₀)= ∇F(w) + β(w − w₀).

Here, a smaller φ resembles a higher accuracy. The advantage of φ-inexactness is that it measures the variable local computation to be performed by the selected local client at each training round. As we mentioned earlier, the system's heterogeneity of the clients leads to heterogeneous progress toward solving local problems, and therefore, it is necessary to allow variant of φ considering clients resource-availability and training round.

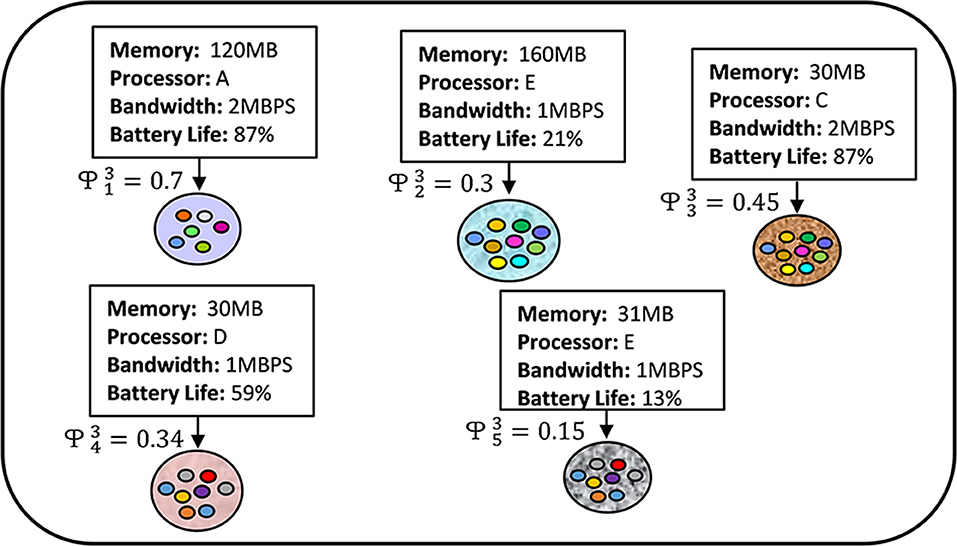
Another federated optimization technique is FedProx (Li et al., 2018), that tolerates partial works of the FL participants. By enabling fractional works of the clients and considering a regularization term, they handle systems and statistical heterogeneity. However, the FedProx framework does not consider any pruning mechanism to reduce model size that could be effective for resource-constrained FL devices and generates higher loss while most of the selected participants have very low resources, i.e., the majority of the selected devices can hardly perform local iterations (see Figure 1). Few other prior works on federated optimization (Konečnỳ et al., 2016; Sahu et al., 2018; Xie et al., 2019; Li and Richtárik, 2020; Pathak and Wainwright, 2020; Reddi et al., 2020) try to leverage federated optimization for heterogeneous network, but none of these works are designed by considering all the features of our proposed FedPARL framework, i.e., pruning, checking model quality and client activity, and accepting partial works from the stragglers.

FIGURE 1

Figure 1. Majority of the clients performing low-partial works that leads to slower convergence.

2.1. Proposed Framework: FedPARL

In this segment, we discuss our FedPARL framework that consists of three layers: (1) sample-based pruning for lightweight model training, (2) activity and resource aware FL client selection strategy, and (3) generalization of the client's local objective function to perform local training epochs according to their available resources.

2.1.1. Sample-Based Pruning

In an FL-IoT environment, as the clients may have constrained resources and limited communication bandwidth, therefore, the typical FL process may face significant challenges to perform training on large-size model. To handle such challenges, we deploy model pruning mechanism for reducing model size that would eventually reduce computation overhead on the client side. The authors in Han et al. (2015) proposed the pruning approach for centralized ML settings, where they initially train a ML model using SGD for a particular number of iterations. After that, a model pruning is performed considering a certain level, i.e., a percentage of model weights are removed that have comparatively the smallest absolute layer-wise values. The model training with the pruning process is repeated until the model reaches the desired model size. As the training and pruning occurred at the same time, we obtain a reduced model size at the end of the training process. However, the centralized pruning techniques (Sen et al., 2009; Han et al., 2015; Zhu and Gupta, 2017; Lee et al., 2018) require all the data samples for training at a central location, which is not applicable for an FL process as the main theme of FL is that the clients would not share their all data samples with an external entity.

To apply the model pruning mechanism on the FL process, we aim to perform model pruning on the server with the concept of sample-based pruning and further carry out local training on the edge clients by sharing that pruned global model. The authors in Jiang et al. (2019) discussed applying FL considering sample-based and sample-less pruning strategy. In this paper, we apply sample-based model pruning due to its high probability of reaching the convergence (Jiang et al., 2019). In sample-based pruning, we consider a small-subset of data samples on the server that are requested from the available clients. The samples may be collected by requesting the clients to share a small portion of their available data that they wish to share, or the server can collect a small sample on its own. Besides, as a device within an FL-IoT environment can act as both server and a client, therefore, that device can use its own data to perform sample-based model pruning. One would expect that the quality of the pruned model would be poor compared to the existing ML-based pruned mechanism (Han et al., 2015). However, while applying pruning mechanism on the FL-IoT environment, we observe that the model quality is marginally reduced with the high deduction of the model size.

After the sample-based initial pruning, the further training and pruning actions can be performed on both server and client side. The process can be done in one or more federations. Particularly, we carry out initial pruning so that only a small size of initial global model is shared with the FL clients, and it does not consume excessive time for the edge device to perform on-device training. When a pruning is performed only on the initial global model to a certain pruning level, we call it a one-shot pruning. We can reduce the model size by performing repeated model pruning in every iterations of the FL process, and we call it a sample-based federated pruning. The benefit of federated pruning over the one-shot pruning is that it reflects the removal of insignificant parameters from the local model, i.e., it incorporates the local data impact available on the client side. The overall pruning process is discussed below:

1. The server collects a small portion of data samples from the environment, or requests the available clients within the FL network to send a small subset of data that they wish to share.

2. If data are requested from the clients, then the available devices share that with the FL server.

3. For the first iteration, a global model is initialized by the server, and in case of further iteration, the global model is updated based on the feedback of the local model of the clients.

4. The server performs a sample-based model pruning until a target pruning level.

5. The pruned model is shared with the FL clients that participated in the training process. Each client updates their model utilizing their updated local data and by learning from the pruned global model.

6. Each participated client is able to share a partial amounts of work in case they have resource-scarcity, and the shared local model is aggregated by the server.

If we apply federated pruning, then the server again performs pruning on the updated global model by removing the parameters having small magnitudes and the iterative process is continued until we obtain a desire pruning level. After reaching the desired pruning level, the usual FL process is executed.

2.1.2. Activity and Resource-Aware Model

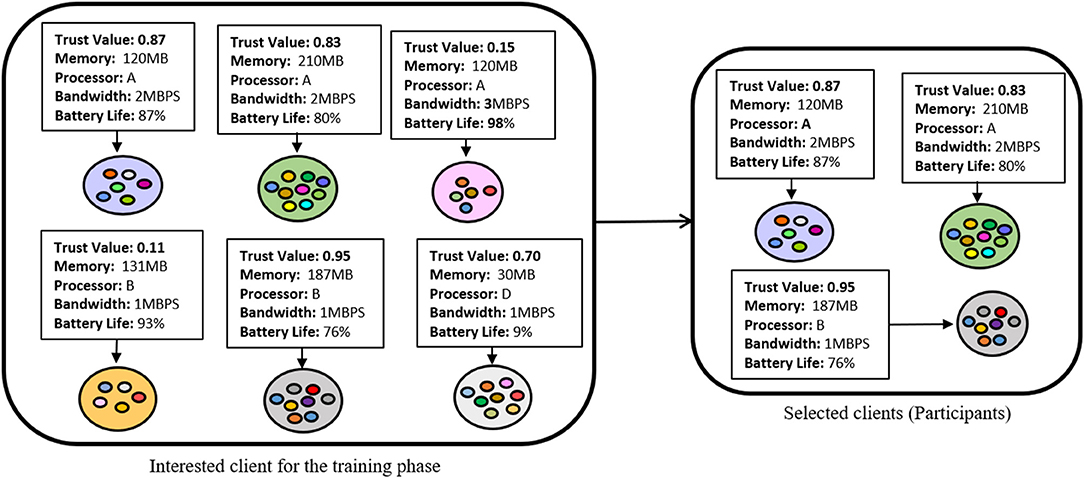
In an FL environment, we may observe clients that have heterogeneous resources and therefore, it is challenging to assign a task that could be performed by all the selected participants. If the majority of selected participants become stragglers, then the target convergence can never be obtained. A client can become a straggler due to underpower in terms of systems requirements for the assigned task completion, or due to network connectivity. The typical FL models assume all the available clients as resource-sufficient and randomly selects clients for the training phase. Besides, in an FL-IoT environment, there is a huge risk of receiving vulnerable local model update by the clients as the IoT devices are comparatively more prone to attack (Imteaj and Amini, 2020). Therefore, it is required to monitor client activities, available resources, and their contributions toward the FL process. By understanding the necessity of examining client activities and observing their resources, we integrate trust and resource-awareness into our proposed FL model. Initially, the FL server publishes a task with minimum system requirements. All the interested clients acknowledge server by sending their resource-availability information, e.g., memory, battery life, bandwidth, and data volume. The server applies the client's information into a function and filters out the ineligible candidates. To handle inappropriate model information, we leverage a trust score mechanism to understand the records of the client activities. In order to assign trust score to the clients, we consider several events, e.g., infusion of improper model, task completion or contributions toward model training, response delay, interested in joining training phase, and inability to participate in the training round due to lack of resources.

Initially, we assign a trust score T_m = 50 to all the network clients. Any client who is interested to be a part of the training phase, met the resource requirement for the model training but is not selected for the training round, we assign a trust score T_Interested = 1 for that client. We assign this score to motivate interested and resource-proficient clients to participate in future tasks. Besides, we provide a reward score T_Reward = 8 to a client if they accomplish the given task within a predefined time period. In case, an FL client becomes a straggler in < 20% of its overall participation, we set a penalty to that client's trust score T_Penalty = −2. If the client becomes a straggler in equal or > 20% but not more than 50% of its participation, then we assign a blame score to that client's trust score, i.e., T_Blame = −8. Further, if any client becomes a straggler in equal or more than 50% of its overall participation, or sends back improper model, we assign a ban score (T_Blame = −16) to that client's trust score. Finally, the trust score is scaled up by dividing by 100 and stored as a trust value (with a range of 0–1). In Figure 2, we illustrated a high-level overview of the client selection process by checking resource-availability and trust score, and in Table 1, we presented the chart of different factors with their associated trust score that we considered for our simulations. The trust score is assigned according to the significance of the events, and we got inspired to design such scoring of event reputation factors for our simulation from Moinet et al. (2017).

FIGURE 2

Figure 2. Client selection based on resource-availability and trust score.

TABLE 1

Table 1. List of trust score corresponding to different factors for an FL-IoT environment.

We present the details of the integration of trust and resource-awareness strategy in the FL model in Algorithm 1. In line 1, function receives parameters of training round i, client id k, global model parameter w_i, maximum time t to finish task, and model diversity threshold γ. The threshold time can be set by the task publisher based on the task difficulty. We also do not fix the model diversity threshold as in the initial training round, the model diversity could be higher compared to the further training rounds. If an FL participant sends back its local model within time t, then we set the unsuccessful record of that client, $U_k^i$ as 0 and add a reward score to that client's existing trust score (lines 2–4). On the other hand, if a client cannot send back its local model within time t, we set the unsuccessful record of that client, $U_k^i$ as 1 (lines 5–6). We examine the previous task record of that client and check whether the $U_k^i$ = 1 event occurs < 20% of that client's overall participation. If so, we add a penalty score to that client's existing trust score (lines 7–8). Particularly, for our simulation setting, we consider that each FL client which shows interest to be a part of FL training may unfortunately fail to accomplish a task at any time and to track their activity, we set this condition of penalty as < 20%. Likewise, if the event $U_k^i$ = 1 event occurs greater or equal to 2% but < 50%, then we add a blame score to that client's existing trust score (lines 9-10). Finally, if the client's unsuccessful event occurs greater or equal to 50%, then we add a ban score to that client's existing trust score (lines 11–12). After assigning the trust value, the updated trust score of the client is appended into a list (line 13). In CheckResource function, we take resources of the clients, e.g., bandwidth (${B}$), memory (${M}$), battery life (${E}$), and data volume (${V}$) and store the resource availability status within a list, ${R}$_k (lines 14–15). After that, we compare the client's resource-availability with the task system requirements, and if it satisfies, then, we add that client's resource availability information into another list, RA (lines 16–18). Finally, the algorithm returns the trust score and resource availability list of the clients (line 19).

ALGORITHM 1

Algorithm 1. Activity and Resource Checking. Training round i^th, global model Gⁱ, local model $L_k^i$, trust score C_k for k^th client, γ indicates deviation, task requirement ${L}$_Req, and t represents timeout.

2.1.3. Allowing Partial Works From FL Participants

In this segment, we explain how the generalization of FedAvg algorithm allows us to accept partial amounts of work from the FL participants. In FedPARL, unlike FedAvg algorithm, we select a subset of clients (called participants) that are comparatively resource-proficient and trustworthy using the concept discussed in section 2.1.2. The server collects some sample data to perform sample-based model pruning to reduce the global model size. After that, the pruned global model is disseminated to all the participants. As we discussed before, the federated clients may have heterogeneous resource limitations in terms of memory, bandwidth, battery levels, processing ability, or network connectivity. It may occur that we select a proficient client that have available system configurations but somehow the device lost the network connection. Besides, it is possible that almost all the interested and available clients have limited resources, and we may have no other choices without considering those devices for the training phase. It is to be noted that each device needs to use its resources to perform each local epoch. Therefore, it is not feasible to force all selected participants (i.e., IoT devices) to perform uniform local iterations. Rather, we consider allowing partial amounts of work from the devices to tackle such challenges (see Figure 3). Based on the resource-availability including the available data volume, we assign local epoch to each participants and perform aggregation on the server on receiving model update from any of the participants. That means, unlike the FedAvg model, we do not drop any stragglers, instead, we let the stragglers to compute a fewer number of iterations according to their available resources. In FedProx, Li et al. (2018) consider a random network clients for the training phase and allow partial work. However, in the worst case, they may end up selecting all the devices with very low resource-availability which may lead their algorithm to perform a very low number of local epochs. Therefore, the global model accuracy would be lower because of the deviate local model updates and it may greatly be impacted when the number of local samples are few. Our resource and trust aware feature of our FedPARL framework tackle the consideration of all straggler client issues by avoiding random selection of participants and further allows partial amounts of work of the clients. Using the idea of Li et al. (2018), we can, allow partial work for our federated clients that are selected through trust and resource-aware strategy and we can define the ${\varphi }_k^c$-inexactness for federated client k at training round c:

FIGURE 3

Figure 3. Partial amounts of work to be performed by the selected clients.

Definition 2 $({\phi }_k^c$-inexact solution ). Let us consider a function ${{G}}_k(w;w_c)={{F}}_k(w)+\frac{\beta }{2}\Vert w-w_c|{|}^2,$ and φ ∈ [0, 1], we call w^* is a ${\phi }_k^c$-inexact solution of $\underset{w}{\text{min}}{{G}}_k(w;w_c)$ if $\Vert \nabla {{G}}_k(w^{*};w_c)\Vert \le {\phi }_k^c\Vert \nabla {{G}}_k(w_c;w_c)\Vert ,$ where ∇${G}$_k(w; w_c)= ∇${F}$_k(w) + β(w − w_c).

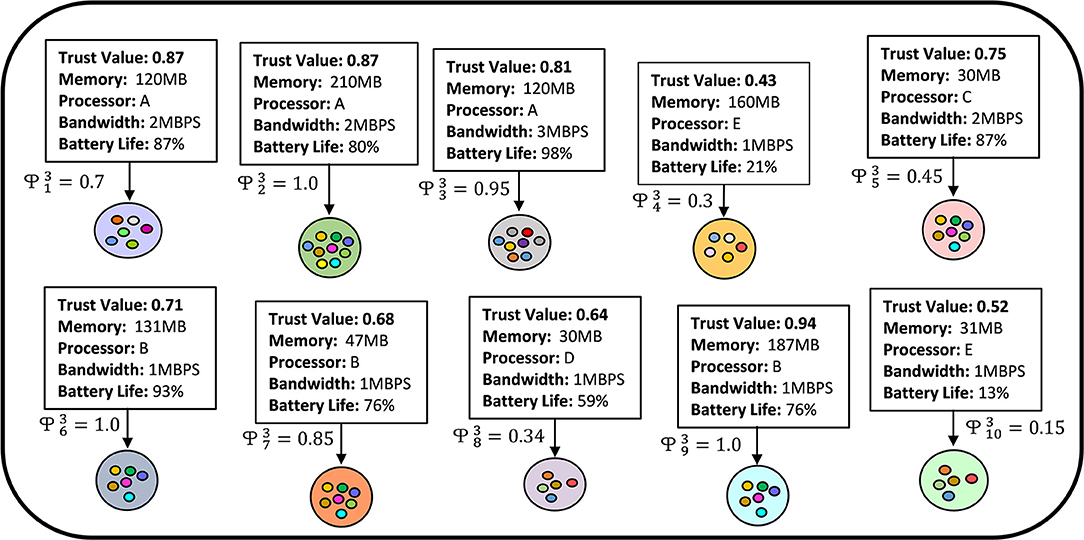
Here, ${\phi }_k^c$ determines how much local computation is needed by the device k to perform in communication round c to solve local problems. That means, ${\phi }_k^c$ is the representation of the variable local iterations of the clients. The systems heterogeneity can be handled by relaxing the ${\phi }_k^c$-inexactness. In Figure 3, we present a conceptual visualization of allowing partial amounts of work to be performed by 10 heterogeneous clients in their third training round. From the figure, we can see that, client 1 and 4 are performing 70 and 30% of the overall tasks due to resource-limitations while the second client is performing the whole task because of their available resources. If we explain it in a more simplified way, then let consider that the task publisher expects 200 local epochs to be performed by all the selected FL clients. However, due to resource-constraint issues, some of the clients may not be able to perform 200 local epochs for generating their local models. For such a case, considering the resource status, the weak clients are allowed to perform a lower number of local epochs, e.g., the first and fourth clients need to perform only 140 and 60 local epochs if the overall computational task is 200 local epochs for the third training round. For the convenience of our simulations, we assign an approximate number of local epochs to different clients considering their heterogeneous resources.

From the above discussion, we understand that variant local works can help us to deal with systems heterogeneity, however, too many local epochs, or local updates through false model injection could generate a diverge local model. The divergence local model update could be handled by adding a proximal term. In FedAvg, each device solves their corresponding local function, while the authors in Li et al. (2018) consider an extra proximal term for each participant while solving local problem which is given below:

$\begin{array}{ll}{\displaystyle \underset{w}{\text{min }}}{{G}}_k\left(w;w^c\right)=F_k(w)+\frac{\beta }{2}\Vert w-w^c{\Vert }^2& (2)\end{array}$

The modified local function helps to restrict the local update closer to the global model which is particularly beneficial while dealing with statistical heterogeneity and also allows partial amounts of work to be performed by heterogeneous clients. The overall process of sample-based pruning mechanism and performing partial amounts of work by the FL participants is presented in Figure 4.

FIGURE 4

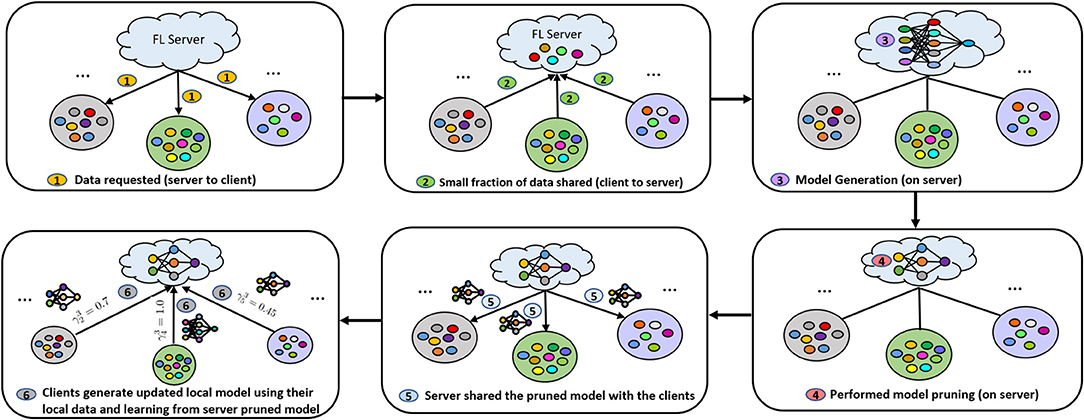
Figure 4. Performing sample-based model pruning on the server and allowing partial amounts of work considering client resource-availability and previous activities.

2.2. Proposed FedPARL Framework

We presented our proposed FedPARL in Algorithm 2. Initially, FL server collects a small samples by sensing environment, or request fractions of samples from the available clients and performs model pruning (line 1). After performing the model pruning, a compressed size of model w₀ is obtained, which is disseminated to all the available clients along with the task requirements (lines 2–3). Each client that is interested to perform the task shares their available resource information with the FL server (line 4). For each training round, the FL server checks available resources of each client by calling CheckResource() function of Algorithm 1 and extracts the trust score and available resource information of each interested clients (lines 5–6). The interested clients are sorted based on their trust ${T}$ and available resources ${R}$, which are stored within a list r (line 7). A fraction of clients from the eligible candidates are chosen, and further, only a few of them are randomly selected for the training phase (lines 8–9). The FL server calls each chosen client to perform local training through ClientLocalUpdate() function and passes the latest global model (lines 10–11). We assume the cumulative number of data samples within the FL network is n, which are partitioned among the available clients having a set of indices ${P}$_k on client k, where n_k = |${P}$_k|. Besides, each client's available local data during a communication round c is indicated by n_c. During training, each chosen client utilizes its local solver to figure out inexact minimizer ${\phi }_k^c$ to solve its local objective function (lines 16–17). After that, each client splits their data into batches, obtains optimal local solution by performing SGD, and sends back model parameters to the FL server (lines 18–22). The FL server performs aggregation upon receiving models from the chosen clients and updates their trust score based on their performance (lines 12–15).

ALGORITHM 2

Algorithm 2. FedPARL Framework. The ${S}$ eligible clients are indexed by u; ${B}$= local minibatch size, ${F}$= client fraction, E= number of local epochs, η= learning rate, and t= timeout.

3. Convergence Analysis

For the convergence analysis of our FedPARL framework, we first discussed a measure of dissimilarity called ${B}$-local dissimilarity that can lead us to prove convergence of our proposed framework. According to Li et al. (2018), the local functions of FL clients are B-locally dissimilar at w if ${𝔼}_k\left[\Vert \nabla F_k(w){\Vert }^2\right]\le$ ||∇f(w)||²${B}$². From here, we can define the value of ${B}$(w), i.e., ${B}$(w) = 1 when ${𝔼}_k\left[\Vert \nabla F_k(w){\Vert }^2\right]=\Vert \nabla f(w){\Vert }^2,$ (w is fixed solution that all the local functions of the clients agree on or all the clients holds the same local functions), and ${B}(w)=\sqrt{\frac{{𝔼}_k\left[\Vert \nabla F_k(w){\Vert }^2\right]}{\Vert \nabla f(w){\Vert }^2}}$ when ||∇f(w)|| ≠ 0. The E_k[·] expresses the expectation over FL clients with masses p_k = n_k/n and $\sum _{k=1}^N{p}_k=1$, where n_k indicates the number of local data samples on each client k and n denotes the total number of data samples over the whole network. In particular, B-dissimilarity definition represents a bounded dissimilarity with a privilege of allowing statistical heterogeneity in an IID scenario. According to bounded dissimilarity, if we have ϵ > 0, there exists a ${B}$_ϵ, i.e., for all the data points $w\in {{S}}_{ϵ}^c=\left\{w\mid \Vert \nabla f(w){\Vert }^2>ϵ\right\},{B}(w)\le {{B}}_{ϵ}$. However, in FL setting, there is a high chance of observing ${B}$(w) > 1 due to the heterogeneous data distributions within the network and larger value of ${B}$(w) indicates larger dissimilarity among the client's local functions.

3.1. Convergence Analysis: Non-convex Case and Variable ϕ's

Let us assume that the local functions F_k are non-convex, and ${L}$-Lipschitz smooth. Besides, we assume that there exists ${L}$₋ > 0, i.e., ${\nabla }^2{F}_k\succcurlyeq -{{L}}_{-}\text{I},$ $\overline{\beta }:=\beta -{{L}}_{-}>0$ and B(w^c) ≤ B. Now, in Algorithm 2, if we choose β, K, and ϕ following the analysis from Li et al. (2018), then we obtain

$\begin{array}{l}{\lambda }^c=(\frac{1}{\beta }-\frac{{\varphi }^c{B}}{\beta }-\frac{{B}\left(1+{\varphi }^c\right)\sqrt{2}}{\overline{\beta }\sqrt{K}}-\frac{{L}{B}\left(1+{\varphi }^c\right)}{\overline{\beta }\beta }-\frac{{L}{\left(1+{\varphi }^c\right)}^2{{B}}^2}{2{\overline{\beta }}^2}\\ -\frac{{L}{{B}}^2{\left(1+{\varphi }^c\right)}^2}{{\overline{\beta }}^{2}K}(2\sqrt{2K}+2))>0& (3)\end{array}$

For iteration c of our algorithm, we can observe an expected decrease of the global objective function that can be expressed as:

$\begin{array}{ll}{𝔼}_{S_c}\left[f(w^{c+1})\right]\le f(w^c)-\lambda \Vert \nabla f(w^c){\Vert }^2,& (4)\end{array}$

where S_c is the set of K devices chosen at iteration c.

In a similar fashion, for variable ϕ's, we have exact similar assumptions, and if we choose β, K, and ϕ of Algorithm 2 following the analysis from Li et al. (2018), then we obtain

$\begin{array}{l}{\lambda }^c=(\frac{1}{\beta }-\frac{{\varphi }^c{B}}{\beta }-\frac{{B}\left(1+{\varphi }^c\right)\sqrt{2}}{\overline{\beta }\sqrt{K}}-\frac{{L}{B}\left(1+{\varphi }^c\right)}{\overline{\beta }\beta }\\ -\frac{{L}{\left(1+{\varphi }^c\right)}^2{{B}}^2}{2{\overline{\beta }}^2}-\frac{{L}{{B}}^2{\left(1+{\varphi }^c\right)}^2}{{\overline{\beta }}^{2}K}(2\sqrt{2K}+2))>0& (5)\end{array}$

Here, also for iteration c, we can observe an expected decrease of the global objective function that can be expressed as:

$\begin{array}{ll}{𝔼}_{S_c}\left[f(w^{c+1})\right]\le f(w^c)-{\lambda }^c\Vert \nabla f(w^c){\Vert }^2,& (6)\end{array}$

where S_c represents the set of K clients chosen at iteration c and ${\varphi }_c={\text{max}}_{k\in S_c}{\varphi }_k^c$

3.2. Convergence Analysis: Convex Case

Let us assume that F_k(·) 's be convex and ${\varphi }_k^c=0$ for any k, c, such that all the clients solve the local problems exactly. Besides, we consider that the assertions that we mentioned in non-convex case (see section 3.1) are satisfied. If $1\ll {B}\le 0.5\sqrt{K},$ then it is viable to choose β ≈ 6${L}$${B}$² which derives that $\lambda \approx \frac{1}{24{L}{{B}}^2}$.

4. Experiments

In this section, we present empirical results of our proposed FedPARL framework. In section 4.1, we provide the experimental details, i.e., our simulation settings with detail description about the dataset we considered. Section 4.2 demonstrates the outperformance of our proposed FedPARL framework compare to the conventional FedAvg (McMahan et al., 2017) and FedProx (Li et al., 2018) algorithms considering system heterogeneity. Further, we present the effectiveness of our FedPARL framework in the presence of statistical heterogeneity within the FL-IoT setting in section 4.3.

4.1. Experimental Details

We perform experimental simulation of our proposed FedPARL framework on different datasets, tasks, and models. We implement sample-based model pruning to generate a lightweight FL model that would be effective for FL-IoT settings. To create an FL-IoT setting, we consider 12 distributed mobile robots that are capable to follow a given set of instructions. Each robot is integrated with variant sizes of memory, battery life, and processor that brings systems heterogeneity. We carry out similar transmission rates to all considered robots for maintaining the simplicity of the FL training process. Among the twelve robots, we assume that eight are unreliable, two have resource-shortage issues, and two generate low-quality models that can be regarded as poisoning attack. We consider the weak clients having low amounts of resources to simulate systems heterogeneity. Besides, we deliberately changed some of the robot client on-device samples to mislead the FL process. The strength of the poisoning attack is dependent on the degree of sample modification. For a better understanding of the effects of statistical heterogeneity, we also evaluate our FedPARL framework by considering synthetic and federated datasets.

To simulate FedPARL framework on synthetic dataset, we follow the synthetic data generation process provided in Shamir et al. (2014) and Li et al. (2018). As discussed in Li et al. (2018), we generated samples (${X}$_k, ${Y}$_k) for each device k, considering model y = argmax(softmax(${W}$x + b)), where, model weights ${W}$ ∈ ℝ^10×60, samples x ∈ ℝ⁶⁰, and bias b ∈ ℝ¹⁰. At first, we generate an IID dataset by keeping the similar value of ${W}$ and b on all the available devices and set ${X}$_k to ensure the same distribution. After that, we define (α, β) = (0, 0), (0.5, 0.5), and (1, 1) to prepare three non-IID datasets (Figures 14–16). Particularly, α helps us to control variance among the local models while β controls bringing variation among the local data located at a device that differs from the other available devices. By controlling α and β, we prepare three other heterogeneous and distributed synthetic datasets. For all the four synthetic datasets, we considered 30 different devices in order to generate a global model with optimized model weights ${W}$ and bias b. For the simulation of FedPARL on federated dataset, we consider two different datasets MNIST (LeCun, 1998) and Sent140 (Go et al., 2009). For MNIST, which is a popular dataset of handwriting digits, we split the overall MNIST dataset among 1,000 clients such that each client has only a sample of two digits. We consider the Sent140 dataset for non-convex setting, which is basically a sentiment analysis of tweets, and we consider 772 clients to distribute the overall datasets.

To better understand the performance and simulate the comparison of FedPARL with existing similar approaches (i.e., FedAvg and FedProx), we implement all the three approaches with the same simulation settings. As FedAvg and FedProx algorithm use SGD as a local solver, hence, to bring fairness, we also apply SGD as a local solver of FedPARL. We maintain the same hyperparameters for all the experiments of a particular dataset that is obtained after proper tuning (e.g., learning rate). For each training phase, we select 10 clients as participants, and we define the number of stragglers, batch size, number of iteration rounds, and learning rate. Our proposed framework is applicable to any sort of heterogeneous FL-IoT environment, and the convergence time of the model training depends on the available FL client's local data and resources.

4.2. Simulation of Trust Score Update

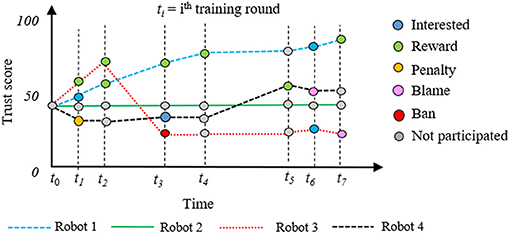
As we discussed in section 2.1.2, the trust score is updated based on the client activities. We consider various events, i.e., interested to perform a task, interested to perform a task, response delay in sending model, incorrect model infusion, or unable to accomplish a task. In Figure 5, we present the trust score update of four distributed mobile robots with respect to time in various training rounds.

FIGURE 5

Figure 5. Activity dependent trust score update of four distributed mobile robots.

4.3. Simulation of Sample-Based Model Pruning

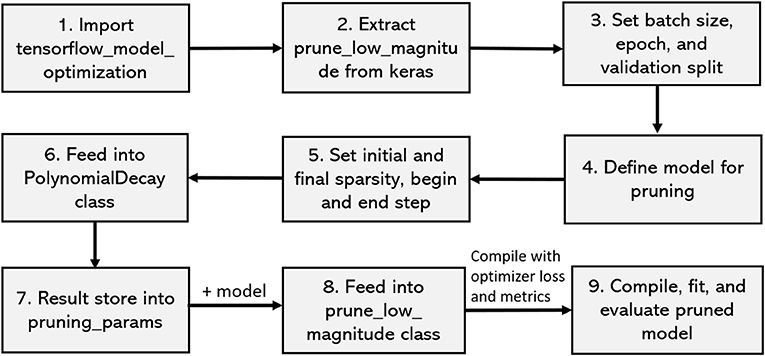
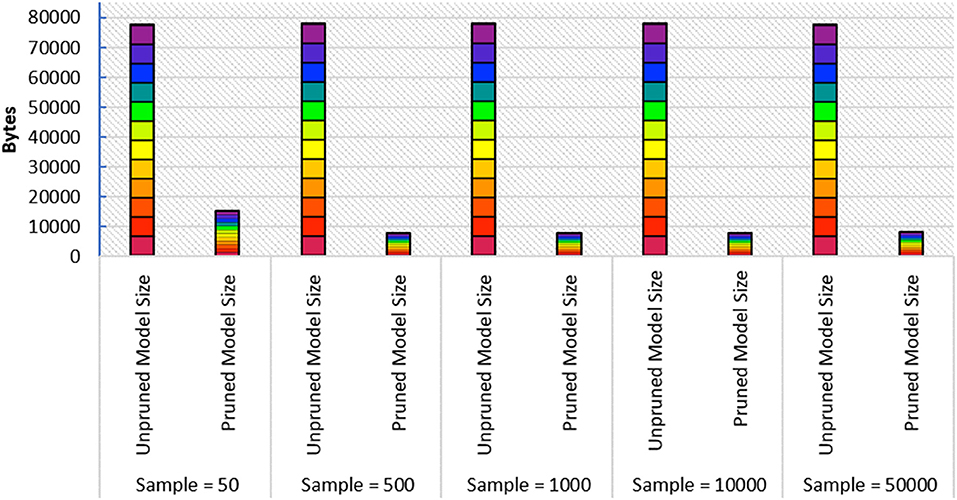
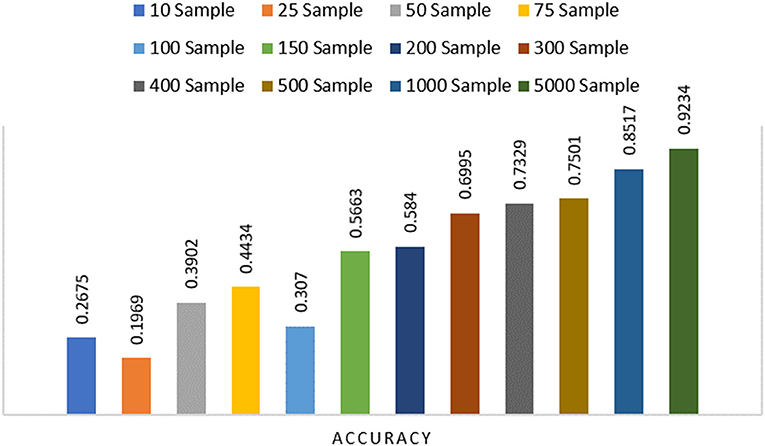
In this paper, we particularly interested to apply our proposed framework on a resource-constraint FL-IoT environment, therefore, producing a lightweight FL model by eliminating the less important features could be effective in accelerating the training period. To perform pruning, we import tensor_model_optimization class from TensorFlow and extract prune_low_magnitude class from Keras. We define a model for pruning by setting up the epoch, batch size, and validation split. We also set up initial and final sparsity, with begin and end step for pruning. After that, we feed the model in PolynomialDecay class, store the parameters, and feed into prune_low_magnitude class. Finally, we compile, fit, and evaluate the pruned model. In Figure 6, we show the steps of our applied pruning process, and in Figure 7, we present the effect of performing model pruning on different sizes of samples considering MNIST (LeCun, 1998) dataset. We can observe that, we obtained significantly lower pruned model size compared to the unpruned model. Besides, in Figure 8, we show how the accuracy varies while performing initial sample-based pruning on different sample sizes. We can see from Figure 8, in some cases, e.g., sample 25 has less accuracy than sample 10. It is because we randomly select small samples for training, therefore, there is a possibility of choosing same type of sample class while missing other ones. When we consider comparatively large samples for training, we do not observe any such cases because there is a high probability of holding all the available classes. Further, we compare our pruned model accuracy with baseline model accuracy for different sample sizes that demonstrates that we lost very small accuracy while performing the model pruning (see Figure 9).

FIGURE 6

Figure 6. Steps of performing model pruning.

FIGURE 7

Figure 7. Performing model pruning and achieving compressed model sizes.

FIGURE 8

Figure 8. Accuracy after performing initial sample-based pruning for different sample sizes.

FIGURE 9

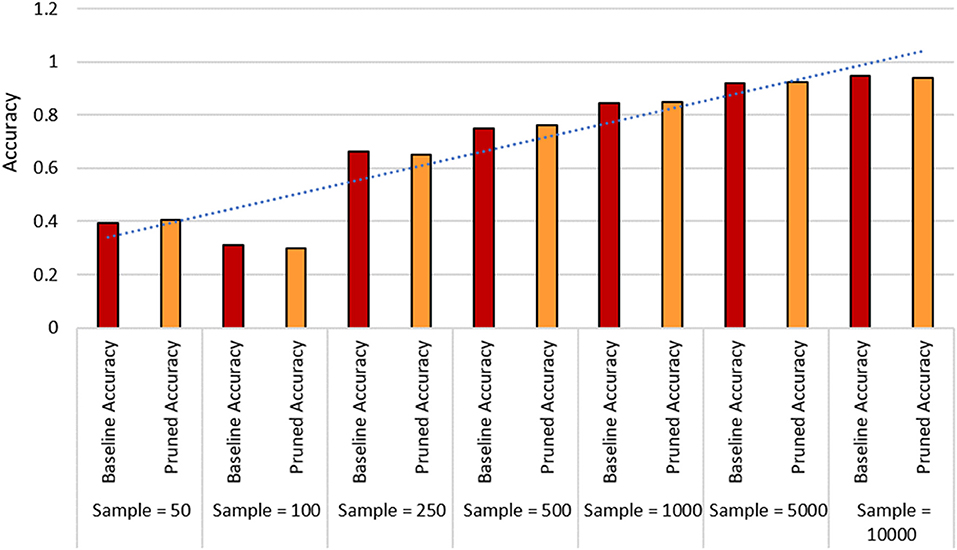
Figure 9. Comparison between baseline accuracy and pruned model accuracy considering different sample sizes.

4.4. Simulation of Handling Systems Heterogeneity

To measure the impact of allowing partial works from the clients, we simulate our federated settings by considering system heterogeneity. We assume that, for each task, there is a global clock cycle and each participated client k measures the amounts of work it needs to perform on iteration c (${\phi }_k^c$) as a function of its available resource constraints and clock cycle. We define a global epochs E to be performed by all the clients and if any client has resource limitations issues to perform E epochs, then that client performs fewer updates considering their resource constraints. For each task, we set the number of clients that could be stragglers, e.g., 0, 10, 25, 50, and 95%, where 0% straggler means all the participated clients can perform the defined number of global epoch E (i.e., there is no system heterogeneity), and 95% straggler means only 5% of the clients could perform the defined number of global epoch E. The conventional FedAvg algorithm simply drops the clients that could not perform the local epoch E, i.e., did not allow any partial solutions. In Figure 10, we simulate the training loss by testing with various number of stragglers (0, 50, and 90%), and we can see that the FedPARL achieves higher training loss compared to the FedAvg and FedProx approaches. We also present the testing accuracy of our proposed FedPARL framework after accepting partial works from the stragglers and can observe that the FedPARL outperforms the FedAvg and FedProx models, particularly when the majority of the clients are stragglers (see Figure 11). From Figures 10, 11, it is evident that system heterogeneity has a negative effect on the convergence of all the datasets, and a higher heterogeneity leads to worse convergence. It is also clear that simply dropping the stragglers from the training rounds degrades the overall performance and allowing partial solutions helps to ensure robustness and improve convergence. We also see that while β > 0, we achieve faster convergence and also in this case, the FedPARL obtains higher accuracy and lower loss than the FedProx. We also investigate two other FL settings with less system heterogeneity. In our first investigation, we limit the local epoch of each device to be exactly 1, i.e., each client can perform only a single local epoch. In such a case, the FedPARL still performs better than the FedAvg model by loosing higher training loss (see Figure 13) and by attaining higher testing accuracy (see Figure 13). In our second investigation, we consider a synthetic IID dataset that does not have any statistical heterogeneity, and for such a setting, FedAvg is more robust than our proposed FedPARL framework. That means, allowing partial works from the clients does not have much effect on the overall performance while considering a synthetic dataset. The simulation results show that though we lose some accuracy while performing pruning, we can still achieve faster convergence with higher accuracy and lower loss if we select the FL client effectively.

FIGURE 10

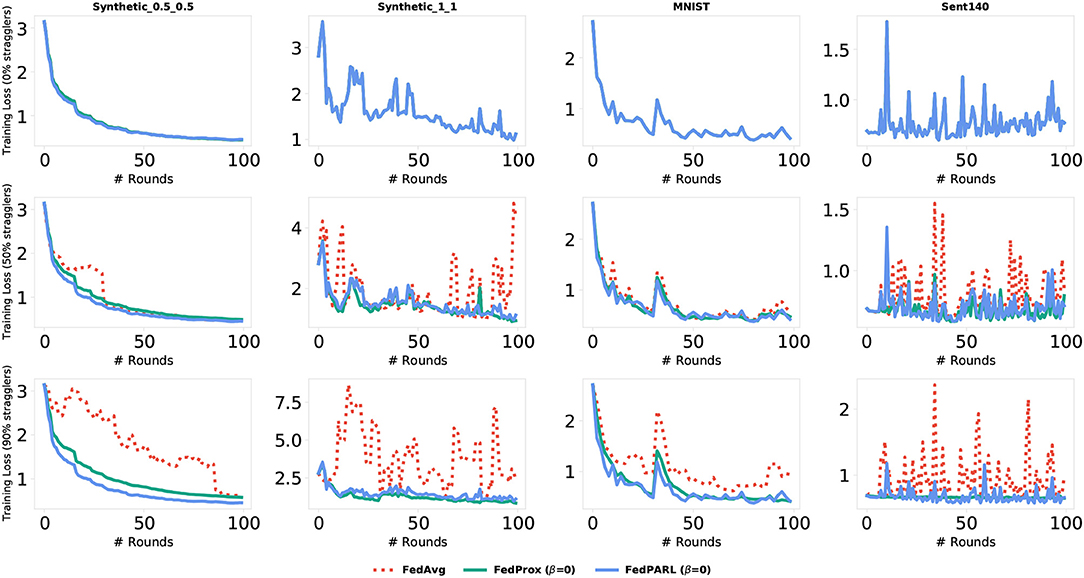
Figure 10. Comparison of training loss of our proposed FedPARL framework (considering no proximal term, i.e., β = 0) with FedAvg and FedProx in the presence of different percentages of stragglers (i.e., 0, 50, and 90%).

FIGURE 11

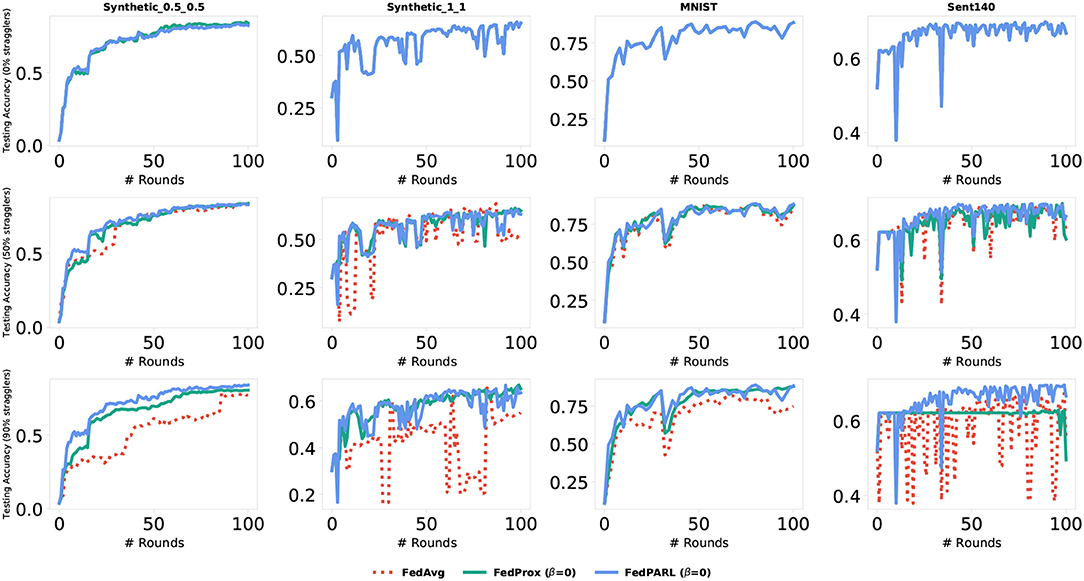
Figure 11. Comparison of testing accuracy of our proposed FedPARL framework (considering no proximal term, i.e., β = 0) with FedAvg and FedProx in the presence of different percentages of stragglers (i.e., 0, 50, and 90%).

FIGURE 12

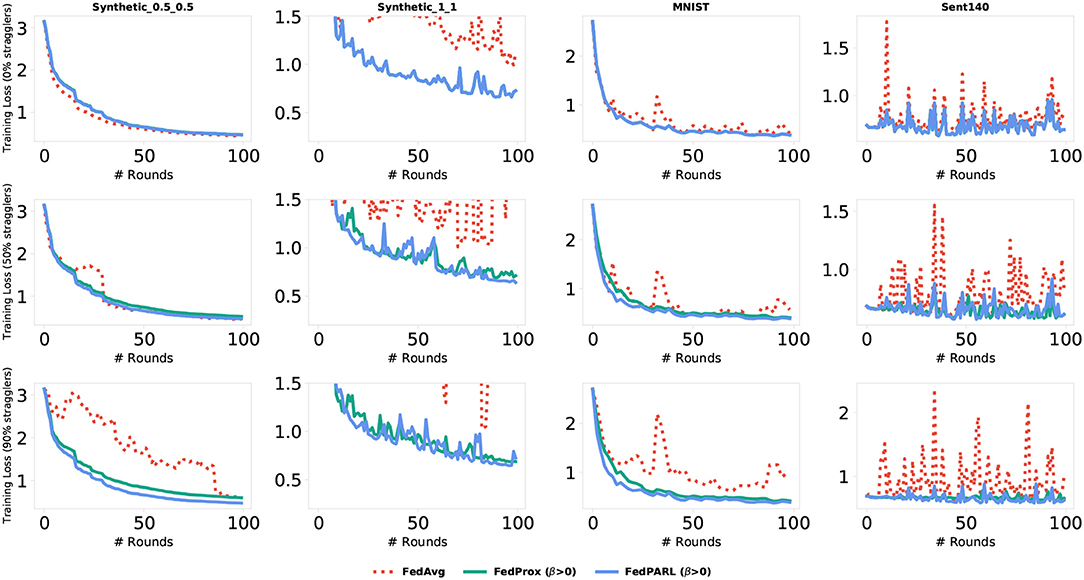
Figure 12. Comparison of training loss of our proposed FedPARL framework (considering β > 1) with FedAvg and FedProx in the presence of stragglers.

FIGURE 13

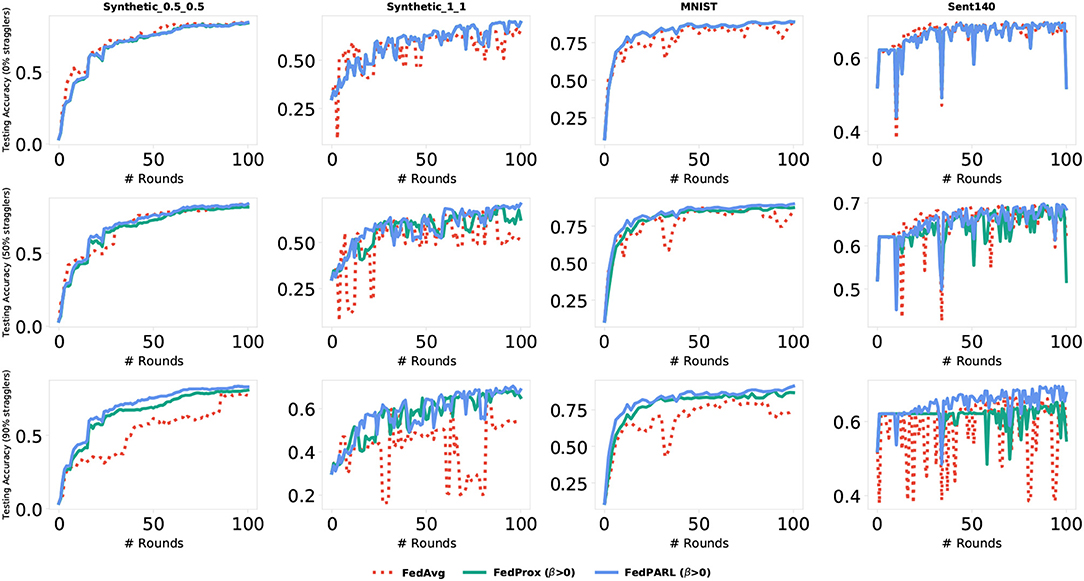
Figure 13. Comparison of testing accuracy of our proposed FedPARL framework (considering β > 1) with FedAvg and FedProx in the presence of stragglers.

4.5. Simulation of Controlling Statistical Heterogeneity

To understand how our proposed FedPARL framework can handle statistical heterogeneity, we simulate the convergence behavior by eliminating proximal term from the client's local objective function. We observe that, when we bring heterogeneity within the dataset, the training performance of the clients starts to degrade. In Figures 14, 15, we show how statistical heterogeneity affects the convergence behavior of four different datasets. For this simulation, we do not consider any system heterogeneity, i.e., we assume each client is resource-proficient and can perform E local epochs. The authors in McMahan et al. (2017) discussed that tuning up the number of local epochs plays an important role in reaching convergence. On one side, a higher number of local epochs leads to more local computation to be performed by the FL clients and reduces the communication overhead with the server that results in faster convergence. On the other side, if the heterogeneous FL clients possess dissimilar local objectives and perform higher number of local epochs, then model convergence could be negatively affected that may even cause model divergence. Besides, in a heterogeneous FL-IoT environment, setting up higher local epochs may increase the possibility that the FL clients fail to perform assigned computational tasks. Further, if the FL clients perform lower number of local epochs, it may reduce local computations, but may prolong the communication overhead and convergence time. Therefore, it is vital to set local epochs sufficiently high while also ensuring robust convergence. As the suitable number of local epochs may change in each training round and depends on device resources, the “best” number of local epochs can be considered as a function of on-device data and available system resources.

FIGURE 14

Figure 14. Simulation of data heterogeneity effects on training loss by considering four synthetic datasets. From left to right, the statistical heterogeneity increases.

FIGURE 15

Figure 15. Simulation of data heterogeneity effects on testing accuracy by considering four synthetic datasets. From left to right, the statistical heterogeneity increases.

We also demonstrate how statistical heterogeneity degrades the performance of FedAvg (β = 0) and how proximal term (β > 0) helps to improve convergence. In synthetic dataset, where statistical heterogeneity does not have nay influence, we can see that FedAvg performs better than FedPARL in terms of training loss (see Figure 14) and testing accuracy (see Figure 15). As statistical heterogeneity increases, we can see that the training loss of FedAvg decreases, and testing accuracy becomes inconsistent or unstable. On the other hand, FedPARL handles the situations effectively and obtains higher training loss with a consistent and higher training accuracy compare to FedAvg and FedProx (see Figures 14, 15). We also simulate the variance of local gradients of FedPARL, FedAvg, and FedProx frameworks (where, lower variance of local gradients indicates better convergence), and FedPARL performs better than FedAvg and FedProx (see Figure 16). We also test our system with the federated dataset and obtained similar results.

FIGURE 16

Figure 16. Simulation of data heterogeneity effects on variance of local gradients by considering four synthetic datasets. From left to right, the statistical heterogeneity increases.

In a heterogeneity FL setting, the activities of the local clients (i.e., amounts of local work) and their model quality directly influence the overall model convergence. Defining a suitable number of local epochs for the clients is essential to utilize the client's resources effectively. Besides, a higher number of local epochs can also cause model overfitting issues. To solve the issue, we perform fine-tuning for local epoch E and after that, allow each resource-constraint device to find out the appropriate number of local epochs to perform locally. Further, if any of the client still sends back a diverge model update to the server, the overall model quality may degrade. To prevent that, applying a proximal term β helps to limit the local model update (Li et al., 2018). Therefore, we allow the clients to perform their device-specific local epochs φ and handle the divergence of model update (if any) by adding a proximal term β. In this way, the model would not be overfitted, and the divergence of model update would not affect the convergence.

One of the challenges of evaluating the best model performance is to properly choose the value of proximal term β. While a large β can slow down the overall convergence time, a small value of β may not have any impact on the overall performance. The authors in Li et al. (2018) figure out the best values of proximal term β for the considered different datasets. For the Synthetic_0_0, Synthetic_1_1, MNIST, Sent140, the best values of β are 1, 1, 1, and 0.01, respectively. From Figures 10–16, we visualize the effects of considering proximal term and show how our proposed FedPARL framework consisting of pruning, activity and resource-awareness with re-parameterization of FedAvg model performs better than the FedAvg and FedProx models. We consider proximal term β = 0 and β > 1 and show how the value of β can increase the stability of a heterogeneous FL-IoT setting. We simulate systems heterogeneity of our FL-IoT environment by forcing 0, 50, and 90% of the participated clients to be stragglers without adding any proximal term and observe the improved convergence in terms of model training loss and testing accuracy while allowing partial amounts of work with model pruning, activity and resource-awareness of FedPARL framework in a heterogeneous network. We also simulate the convergence behavior of our FedPARL framework by considering the proximal term and observe robust and stable performance, particularly, in a heterogeneous setting in the presence of 0, 50, and 90% of stragglers. To that end, we simulate our proposed framework in the presence of data heterogeneity. We obtain higher training loss during model training and achieve improved stable accuracy compared to the FedAvg and FedProx approaches.

5. Conclusion

In this paper, we propose an FL model that can be effectively applied in a resource-constrained IoT environment. The generalization FL objective functions coupling with pruning mechanism and activity and resource-awareness help to generate a lightweight FL model that can handle system and statistical heterogeneity. By selecting trustworthy and proficient clients, performing local training with lightweight model, and allowing variable amounts of work from FL clients, we achieve a robust, stable, and consistent FL model that has remarkable performance within an unreliable heterogeneous network. We have tested our FedPARL framework with various datasets and obtained an improved convergence behavior compared to the existing FL techniques that are implemented with the concept of realistic heterogeneous settings.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

AI and MA: conceptualization, investigation, writing—original draft, and writing–review and editing. MA: resources, funding acquisition, supervision, and project administration.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AI and MA acknowledge the resources and support of Sustainability, Optimization, and Learning for InterDependent networks laboratory (solid lab) members at the Florida International University (www.solidlab.network).

References

Arjevani, Y., and Shamir, O. (2015). “Communication complexity of distributed convex learning and optimization,” in Advances in Neural Information Processing Systems, eds C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett (Cambridge, MA: Curran Associates, Inc.).

Google Scholar

Basu, D., Data, D., Karakus, C., and Diggavi, S. (2019). “Qsparse-local-sgd: distributed sgd with quantization, sparsification and local computations,” in Advances in Neural Information Processing Systems, Vol. 32, eds H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Cambridge, MA: Curran Associates, Inc.).

Google Scholar

Bonawitz, K., Eichner, H., Grieskamp, W., Huba, D., Ingerman, A., Ivanov, V., et al. (2019). Towards federated learning at scale: system design. arXiv 1902.01046.

Google Scholar

Boyd, S., Parikh, N., and Chu, E. (2011). Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Norwell, MA: Now Publishers Inc.

Google Scholar

Chen, J., and Sayed, A. H. (2012). Diffusion adaptation strategies for distributed optimization and learning over networks. IEEE Trans. Signal Process. 60, 4289–4305. doi: 10.1109/TSP.2012.2198470

CrossRef Full Text | Google Scholar

Chen, M., Poor, H. V., Saad, W., and Cui, S. (2020a). Convergence time optimization for federated learning over wireless networks. arXiv 2001.07845.

Google Scholar

Chen, M., Yang, Z., Saad, W., Yin, C., Poor, H. V., and Cui, S. (2020b). A joint learning and communications framework for federated learning over wireless networks. IEEE Trans. Wireless Commun. 20, 269–283. doi: 10.1109/TWC.2020.3024629

CrossRef Full Text | Google Scholar

Dekel, O., Gilad-Bachrach, R., Shamir, O., and Xiao, L. (2012). Optimal distributed online prediction using mini-batches. J. Mach. Learn. Res. 13, 165–202. Available online at: https://jmlr.org/papers/v13/dekel12a.html

Google Scholar

Dinh, C., Tran, N. H., Nguyen, M. N., Hong, C. S., Bao, W., Zomaya, A., et al. (2019). Federated learning over wireless networks: convergence analysis and resource allocation. arXiv 1910.13067.

Google Scholar

Go, A., Bhayani, R., and Huang, L. (2009). Twitter Sentiment Classification Using Distant Supervision. CS224N project report, Stanford 1, 2009.

Google Scholar

Guo, H., Liu, A., and Lau, V. K. (2020). Analog gradient aggregation for federated learning over wireless networks: customized design and convergence analysis. IEEE Internet Things J. 8, 197–210. doi: 10.1109/JIOT.2020.3002925

CrossRef Full Text | Google Scholar

Haddadpour, F., Kamani, M. M., Mahdavi, M., and Cadambe, V. (2019). “Local sgd with periodic averaging:Tighter analysis and adaptive synchronization,” in Advances in Neural Information Processing Systems, Vol. 32, eds H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Cambridge, MA: Curran Associates, Inc.).

Google Scholar

Haddadpour, F., and Mahdavi, M. (2019). On the convergence of local descent methods in federated learning. arXiv 1910.14425.

Google Scholar

Han, S., Pool, J., Tran, J., and Dally, W. (2015). “Learning both weights and connections for efficient neural network,” in Advances in Neural Information Processing Systems, eds C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett (Cambridge, MA: Curran Associates, Inc.).

Google Scholar

Huang, L., Yin, Y., Fu, Z., Zhang, S., Deng, H., and Liu, D. (2018). Loadaboost: loss-based adaboost federated machine learning on medical data. arXiv 1811.12629.

Google Scholar

Imteaj, A. (2020). Distributed Machine Learning for Collaborative Mobile Robots: PhD Forum Abstract. New York, NY: Association for Computing Machinery.

Google Scholar

Imteaj, A., and Amini, M. H. (2019). “Distributed sensing using smart end-user devices: pathway to federated learning for autonomous IoT,” in 2019 International Conference on Computational Science and Computational Intelligence (CSCI) (Las Vegas, NV: IEEE), 1156–1161. doi: 10.1109/CSCI49370.2019.00218

CrossRef Full Text | Google Scholar

Imteaj, A., and Amini, M. H. (2020). “Fedar: activity and resource-aware federated learning model for distributed mobile robots,” in Proceedings of the 19th IEEE International Conference on Machine Learning and Applications (ICMLA) (Miami, FL). doi: 10.1109/ICMLA51294.2020.00185

CrossRef Full Text | Google Scholar

Imteaj, A., Thakker, U., Wang, S., Li, J., and Amini, M. H. (2020). Federated learning for resource-constrained IoT devices: panoramas and state-of-the-art. arXiv 2002.10610.

Google Scholar

Jeong, E., Oh, S., Kim, H., Park, J., Bennis, M., and Kim, S.-L. (2018). Communication-efficient on-device machine learning: federated distillation and augmentation under non-IID private data. arXiv 1811.11479.

Google Scholar

Jiang, Y., Wang, S., Ko, B. J., Lee, W.-H., and Tassiulas, L. (2019). Model pruning enables efficient federated learning on edge devices. arXiv 1909.12326.

Google Scholar

Khaled, A., Mishchenko, K., and Richtárik, P. (2019). Better communication complexity for local sgd. arXiv 1909.04746.

Google Scholar

Konečnỳ, J., McMahan, H. B., Yu, F. X., Richtárik, P., Suresh, A. T., and Bacon, D. (2016). Federated learning: strategies for improving communication efficiency. arXiv 1610.05492.

Google Scholar

LeCun, Y. (1998). The MNIST Database of Handwritten Digits. Available online at: http://yann.lecun.com/exdb/mnist/

Google Scholar

Lee, N., Ajanthan, T., and Torr, P. H. (2018). Snip: Single-shot network pruning based on connection sensitivity. arXiv 1810.02340.

Google Scholar

Li, T., Sahu, A. K., Talwalkar, A., and Smith, V. (2020). Federated learning: challenges, methods, and future directions. IEEE Signal Process. Mag. 37, 50–60. doi: 10.1109/MSP.2020.2975749

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, T., Sahu, A. K., Zaheer, M., Sanjabi, M., Talwalkar, A., and Smith, V. (2018). Federated optimization in heterogeneous networks. arXiv 1812.06127.

Google Scholar

Li, Z., and Richtárik, P. (2020). A unified analysis of stochastic gradient methods for nonconvex federated optimization. arXiv 2006.07013.

Google Scholar

Malinovsky, G., Kovalev, D., Gasanov, E., Condat, L., and Richtarik, P. (2020). From local SGD to local fixed point methods for federated learning. arXiv 2004.01442.

Google Scholar

McMahan, B., Moore, E., Ramage, D., Hampson, S., and Arcas, B. A. (2017). “Communication efficient learning of deep networks from decentralized data,” in Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Vol. 54 of Proceedings of Machine Learning Research, eds A. Singh and J. Zhu (Fort Lauderdale, FL: PMLR), 1273–1282.

Google Scholar

Mohri, M., Sivek, G., and Suresh, A. T. (2019). Agnostic federated learning. arXiv 1902.00146.

Google Scholar

Moinet, A., Darties, B., and Baril, J. L. (2017). Blockchain based trust & authentication for decentralized sensor networks. arXiv 1706.01730.

Google Scholar

Nguyen, H. T., Sehwag, V., Hosseinalipour, S., Brinton, C. G., Chiang, M., and Poor, H. V. (2020). Fast-convergent federated learning. arXiv 2007.13137. doi: 10.1109/JSAC.2020.3036952

CrossRef Full Text | Google Scholar

Pathak, R., and Wainwright, M. J. (2020). Fedsplit: an algorithmic framework for fast federated optimization. arXiv 2005.05238.

Google Scholar

Reddi, S., Charles, Z., Zaheer, M., Garrett, Z., Rush, K., Konečnỳ, J., et al. (2020). Adaptive federated optimization. arXiv 2003.00295.

Google Scholar

Richtárik, P., and Takáč, M. (2016a). Distributed coordinate descent method for learning with big data. J. Mach. Learn. Res. 17, 2657–2681. Available online at: https://jmlr.org/papers/v17/15-001.html

Google Scholar

Richtárik, P., and Takáč, M. (2016b). Parallel coordinate descent methods for big data optimization. Math. Program. 156, 433–484. doi: 10.1007/s10107-015-0901-6

CrossRef Full Text | Google Scholar

Sahu, A. K., Li, T., Sanjabi, M., Zaheer, M., Talwalkar, A., and Smith, V. (2018). On the convergence of federated optimization in heterogeneous networks. arXiv 1812.06127.

Google Scholar

Sattler, F., Wiedemann, S., Müller, K. R., and Samek, W. (2019). Robust and communication-efficient federated learning from non-IID data. IEEE Trans. Neural Netw. Learn. Syst. 31, 3400–3413. doi: 10.1109/TNNLS.2019.2944481

CrossRef Full Text | Google Scholar

Sen, S., Moha, N., Baudry, B., and Jézéquel, J. M. (2009). “Meta-model pruning,” in International Conference on Model Driven Engineering Languages and Systems (Berlin: Springer), 32–46. doi: 10.1007/978-3-642-04425-0_4

CrossRef Full Text | Google Scholar

Shamir, O., Srebro, N., and Zhang, T. (2014). “Communication-efficient distributed optimization using an approximate Newton-type method,” in International Conference on Machine Learning (Beijing), 1000–1008.

Google Scholar

Smith, V., Chiang, C.-K., Sanjabi, M., and Talwalkar, A. S. (2017). “Federated multi-task learning,” in Advances in Neural Information Processing Systems, Vol. 30, eds I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett (Cambridge, MA: Curran Associates, Inc.).

Google Scholar

Stich, S. U. (2018). Local SGD converges fast and communicates little. arXiv 1805.09767.

Google Scholar

Tsianos, K. I., Lawlor, S., and Rabbat, M. G. (2012). “Consensus-based distributed optimization: practical issues and applications in large-scale machine learning,” in 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton) (Monticello, IL: IEEE), 1543–1550. doi: 10.1109/Allerton.2012.6483403

CrossRef Full Text | Google Scholar

Wang, S., Roosta, F., Xu, P., and Mahoney, M. W. (2018). “Giant: globally improved approximate newton method for distributed optimization,” in Advances in Neural Information Processing Systems, Vol. 30, eds S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Cambridge, MA: Curran Associates, Inc.).

Google Scholar

Wang, S., Tuor, T., Salonidis, T., Leung, K. K., Makaya, C., He, T., et al. (2019). Adaptive federated learning in resource constrained edge computing systems. IEEE J. Select. Areas Commun. 37, 1205–1221. doi: 10.1109/JSAC.2019.2904348

CrossRef Full Text | Google Scholar

Woodworth, B., Patel, K. K., Stich, S. U., Dai, Z., Bullins, B., McMahan, H. B., et al. (2020). Is local sgd better than minibatch SGD? arXiv 2002.07839.

Google Scholar

Xie, C., Koyejo, S., and Gupta, I. (2019). Asynchronous federated optimization. arXiv 1903.03934.

Google Scholar

Yang, Q., Liu, Y., Chen, T., and Tong, Y. (2019). Federated machine learning: concept and applications. ACM Trans. Intell. Syst. Technol. 10, 1–19. doi: 10.1145/3298981

CrossRef Full Text | Google Scholar

Yang, Z., Chen, M., Saad, W., Hong, C. S., and Shikh-Bahaei, M. (2020). Energy efficient federated learning over wireless communication networks. IEEE Trans. Wireless Commun. 20, 1935–1949. doi: 10.1109/TWC.2020.3037554

CrossRef Full Text | Google Scholar

Zhang, Y., Duchi, J. C., and Wainwright, M. J. (2013). Communication-efficient algorithms for statistical optimization. J. Mach. Learn. Res. 14, 3321–3363. doi: 10.1109/CDC.2012.6426691

CrossRef Full Text | Google Scholar

Zhao, Y., Li, M., Lai, L., Suda, N., Civin, D., and Chandra, V. (2018). Federated learning with non-IID data. arXiv 1806.00582.

Google Scholar

Zhu, M., and Gupta, S. (2017). To prune, or not to prune: exploring the efficacy of pruning for model compression. arXiv 1710.01878.

Google Scholar