Index Modulation–Aided Mixed Massive Random Access

In this study, a mixed massive random access scheme is considered where part of users transmit both common information and user-specific information, while others transmit only common information. In this scheme, common information is transmitted by index modulation (IM)–aided unsourced random access (URA), while user-specific information is by IM-aided sourced random access (SRA). Practically, IM-aided URA partitions channel blocks of one transmission frame into multiple groups and then employs the IM principle to activate only part of the channel blocks in each group. IM-aided SRA allocates multiple pilot sequences to each user and activates only one pilot sequence whose index carries the data information. At the receiver, the covariance-based maximum likelihood detection (CB-MLD) is employed to recover the active compressed sensing (CS) code words of URA and information of SRA jointly. To stitch the common information at different blocks of URA, a modified tree decoder is proposed to take the IM constraint into account. Furthermore, to relax the strict threshold requirement and improve the performance, an iterative CS detector and tree decoder are employed to decode the common information, where successive signal reconstruction and interference cancellation are utilized. Finally, computer simulations are given to demonstrate the performance of the proposed scheme.

1 Introduction

Massive machine-type communication (mMTC) (Bockelmann et al., 2016) is one of the three main scenarios in the fifth-generation cellular techniques, along with enhanced mobile broadband and ultra-reliable, low-latency communications. The mMTC is motivated by the typical Internet of Things (IoT) applications (Xu et al., 2014), such as smart health care, smart homes, smart manufacturing, and smart transportation. Thus, it is expected to provide wireless connectivity to a massive number of machine-type devices. Unlike human-type communication, in MTC, the packet size of uplink data traffic is short. Therefore, the control signaling overhead becomes very significant compared to the transmit data in the conventional grant-based multiple access. Another feature of mMTC is that the traffic pattern of each device may be sporadic, that is, there are only a small fraction of devices that are active at any time and frequency. Moreover, owing to the massive number of devices, it is impossible to assign orthogonal pilot sequences to all devices (Durisi et al., 2016; Dai et al., 2015; Hasan et al., 2013; Ding et al., 2017).

Unsourced random access (URA) is a promising technique to implement the massive connection in mMTC proposed recently in (Polyanskiy, 2017). In URA, active users transmit signals to base stations (BSs) or access points randomly, and thus avoid the control signaling overhead resulted by the handshake protocol in the grant-based access. Moreover, all users employ the same codebook, and unique pilot allocation for each user required in sourced random access (SRA) can be avoided. This makes URA very suitable for the Internet of Things with a massive number of users. Correspondingly, a receiver at a BS is designed to identify the list of transmit code words, and thus, the per-user probability of error (PUPE) is introduced as a performance metric.

Since the invention of URA, many low-complexity coding schemes have been proposed. In Ordentlich and Polyanskiy (2017), the T-fold slotted ALOHA with the compute-and-forward strategy was proposed. In Vem et al. (2017), this scheme was further studied and an improved scheme was proposed. In this improvement, the user information was first repeated and then transmitted over multiple blocks at the transmitter, and successive interference cancellation (SIC) was utilized at BS.

In Amalladinne (2020), the concatenated URA scheme consisting of inner and outer codes was proposed. In this scheme, the divide-and-conquer strategy was utilized, and the transmit frame is divided into multiple channel blocks. The common compressed sensing (CS) code is employed as an inner code in all blocks and a simple parity-check code as outer tree code across blocks. At BSs, the active code words of inner code are detected through CS-based sparse signal recovery, and the outer tree decoder is utilized to stitch the transmit information sequences in different channel blocks. In Amalladinne et al. (2020a), an enhanced decoder was proposed which performed inner CS detection and outer tree decoding in tandem. This method can reduce the search size of the inner CS detector in later channel blocks and thus reduce the complexity. In Fengler (2019), the concatenated URA scheme was extended to massive MIMO, and covariance-based maximum likelihood detection (CB-MLD) (Haghighatshoar et al., 2018; Fengler et al., 2021) was utilized to perform the inner CS detection. In Xie et al. (2020), the URA for correlated massive MIMO was further studied, and an improved coordinate descent method was proposed to reduce the iteration number. In Fengler et al. (2019), the sparse regression code (SPARC) was utilized in URA, where the approximated messing passing algorithm (AMP) (Donoho et al., 2009; Rangan, 2011) was employed to perform the inner CS detection. In Amalladinne et al. (2020b), motivated by Amalladinne et al. (2020b), an integrating AMP and belief propagation (BP) method was proposed to perform inner CS detection and outer tree decoding in tandem.

In Pradhan et al. (2019), another scheme was proposed for Gaussian channels, where the transmit data are partitioned into two parts. The former is transmitted using a CS code and also acts to determine the corresponding interleaving pattern. The latter is conveyed using low-density parity-check (LDPC)–coded interleave-division multiple access (IDMA) scheme. In Kowshik et al. (2020), this scheme was extended to fading channels, where fading coefficient estimation and LDPC decoding were implemented by the BP algorithm based on the joint factor graph. In Li et al. (2020a), the SPARC-LDPC scheme was proposed for massive MIMO systems, where the CS code in (Pradhan et al., 2019) is replaced by the SPARC. In Marshakov et al. (2019), Pradhan et al. (2020), Zheng et al. (2020), the polar code was taken to replace the LDPC code, in conjunction with the receiver framework of treat interference as noise and SIC (TIN-SIC).

In this article, we extend our earlier works in Liang and Zheng (2020), Liang and Zheng (2021), Liang et al. (2021), and the massive random access scenario where users are divided into two classes is considered. In the first class, users transmit both common and user-specific information. These users need some key devices to transmit user identification (UID)–related information, besides common information uncorrelated to UID. For example, UID-related information can be some urgent event related to its location, and the BS can know the location where urgent event happens and thus make fast response by identifying the active user. In the second class, users transmit only common information. For this scenario, an index modulation (IM) (Basar et al., 2013a; Wen et al., 2017)–aided mixed massive random access is proposed here, where a novel IM-aided URA scheme is presented to transmit common information, and IM-aided SRA (Senel and Larsson, 2018; Ni and Zheng, 2021) is utilized to transmit user-specific information. In IM, only part of resources (time/frequency/space/code sequence) is activated to transmit information by conventional modulations, and the resource activation pattern also carries information. In general, IM has attracted much attention in many aspects due to the potential advantages. For example, better error performance (Basar et al., 2013b; Zheng and Chen, 2017), stronger robustness in the rapidly time-varying channel (Basar et al., 2013c), higher spectral efficiency (Wen et al., 2016), and energy efficiency (Wen et al., 2014). Moreover, in the massive multiple access, IM has been employed in coherent grant-based NOMA (Arslan et al., 2020; Althunibat et al., 2019; Tusha et al., 2020; Li et al., 2020b) and non-coherent grant-free NOMA (Senel and Larsson, 2018; Ni and Zheng, 2021; Ni and Zheng, 2020).

The proposed IM-aided URA is constructed on the general framework of a concatenated URA scheme (Fengler et al., 2019; Amalladinne et al., 2020a) to transmit common information. The motivation is that with the implementation of IM in URA, the signal to be recovered will be sparser, which will facilitate the CB-MLD and result in better decoding performance. On the other hand, the implementation of IM will decrease the number of parity check bits in the outer code, which will increase the complexity of the tree decoder generally. However, the better CB-MLD results will reduce the false alarm probability and thus decrease the number of candidate-active code words. This will instead reduce the complexity of the tree decoder since the CB-MLD results are inputs of the tree decoder. Therefore, with proper design of IM, a better trade-off by IM-aided URA can be expected.

Concretely, in the proposed IM-aided URA, the $N_{tot}$ channel blocks in one transmit frame are partitioned into G groups, each consisting of N consecutive blocks. In each group, only $N_a$ blocks are activated to transmit CS code words. Correspondingly, the transmit information is divided into two parts: the first part is to determine the active channel blocks in each group and the second is to determine the transmitted CS code words in active blocks. In general, the proposed IM-aided URA decreases the average number of active CS code words in each channel block, thus can increase the performance of inner CS detection. In the IM-aided SRA for user-specific information transmission, each user is allocated $D=2^q$ unique pilot sequences, and only one pilot sequence is activated, which is determined by q information bits according to the IM principle.

At the BS, the CB-MLD is first employed block by block to estimate active code words of IM-aided URA and user-specific information of SRA simultaneously. Moreover, to stitch the common information in different blocks, a modified tree decoder is proposed to take the IM signal property into account. Next, to relax the strict threshold requirement and improve the performance, an iterative CS detection and tree decoding are employed to decode the common information, where the covariance of the received signal associated with code words decided in the last iteration is reconstructed and pre-subtracted, and the resulted residual covariance is used for inner CS detection in the current iteration.

The main contributions of this study are summarized as follows:

(1) A mixed massive random access scheme is presented, where part of vital users transmit both common information and user-specific information, while other users transmit only common information. This scheme can model the random access scenario consisting of key devices whose UID is required at the BS and conventional devices whose transmit information is the only interest for the BS.

(2) An IM-aided URA technique is proposed for the common information transmission. Moreover, the corresponding modified tree decoder is presented. The proposed scheme shows better performance than conventional URA when the transmit information is short, for example, 36 bits per frame in our simulations.

(3) An iterative receiver is proposed to decode the common information. The iterative receiver can lift the performance and relax the requirement of thresholds in the inner CS detector, compared with conventional non-iterative receiver.

The rest of this article is organized as follows. In Section 2, the signal model of the proposed mixed massive random access is given. In Section 3, the CB-MLD is presented. In Section 4, a modified tree decoder is described. In Section 4, the proposed iterative receiver is presented. Finally, computer simulation results are given in Section 6, and we conclude this study in Section 7.

Notations: For a set $\mathcal{S}$, $\left|\mathcal{S}\right|$ denotes its size. For a matrix $\mathrm{A}$, $\left|\mathrm{A}\right|$ and $\mathrm{tr}\left(\mathrm{A}\right)$ denote its determinant and trace, respectively. For a vector $\text{v}$, $\mathrm{diag}\left\{\mathrm{v}\right\}$ denotes the diagonal matrix with $\text{v}$ on the main diagonal. The superscripts T and H indicate the transpose and Hermitian transpose of a vector or matrix, respectively. Furthermore, $\mathrm{ℂ}$ denotes the complex field. $\mathcal{CN}\left(0,{\sigma }^2\right)$ denotes that complex Gaussian distribution with zero mean and variance ${\sigma }^2$ is the maximum integer no larger than the argument and $\otimes$ denotes the Kronecker product. The notations $1_n$ and ${\text{e}}_n$ present the all-one vector of length n and the nth column of the identity matrix $\mathrm{I}$ with proper size, respectively. Moreover, the set $\left\{\mathrm{1,2},\dots ,N\right\}$ is abbreviated to $\left[N\right]$. Finally, definitions of some variables in this article are listed in Table 1.

TABLE 1

TABLE 1. Definitions of some variables in the article.

2 Signal Model

2.1 Transmitter

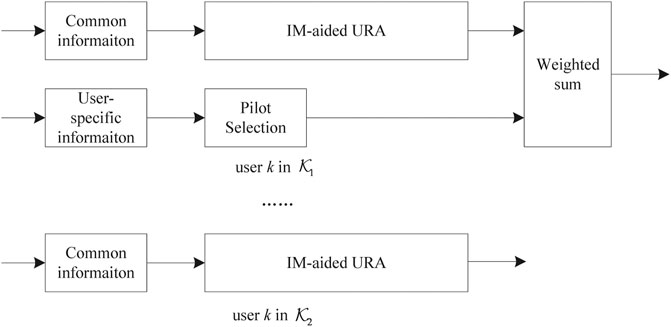
The uplink IM-aided URA considered here consists of K single-antenna users and one M-antennas BS, as shown in Figure 1. In the mMTC-enabled massive MIMO system, K and M are of the order of hundreds or thousands. The K users are divided into two classes. As shown in Figure 2, in the first class with $K_1$ users in set ${\mathcal{K}}_1$, each user transmits both user-specific information and common information to the BS using IM-aided URA and IM-aided SRA, respectively. In the second class with $K_2$ users in set ${\mathcal{K}}_2$, each user transmits only common information via IM-aided URA. Among all the K users, only $K_a$, $K_a\ll K$, users in set ${\mathcal{K}}_a$ are active and transmit information to the BS in one transmit frame. Furthermore, ${\mathcal{K}}_a$ is partitioned into ${\mathcal{K}}_{a,1}$ and ${\mathcal{K}}_{a,2}$, which denote the sets of $K_{a1}$ active users in ${\mathcal{K}}_1$ and $K_{a2}$ active users in ${\mathcal{K}}_2$, respectively. In the proposed mixed massive random access scheme, one transmit frame consists of $N_{tot}$ sub-blocks, each occupying L channel slots. The common information and user-specific information transmissions are described as follows.

FIGURE 1

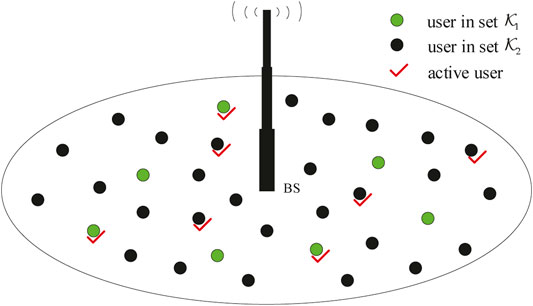
FIGURE 1. Uplink mMTC system. All users are divided into two classes with sets ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$. Users in ${\mathcal{K}}_1$ transmit both user-specific and common information, and users in ${\mathcal{K}}_2$ transmit only common information. Moreover, only part of users in both classes is active due to the sporadic transmission character.

FIGURE 2

FIGURE 2. Block diagram of transmitter in the mixed massive random access.

2.1.1 Common Information Transmission

The common information is transmitted by all active users. For each active user to transmit the common information, the IM-aided URA is employed. In the proposed IM-aided URA, all the $N_{tot}$ sub-blocks in one transmission frame are first divided into G groups, each consisting of consecutive N sub-blocks. Then, each active user transmits common information only by $N_a$ out of N channel blocks in each group. In the activated channel blocks, the concatenated scheme is employed to transmit common information. The inner code of this concatenated scheme uses the CS codebook to facilitate the sparse multiuser detection at the receiver, and the outer code uses simple parity check to ensure the integrity of the transmit information in different sub-blocks (Fengler et al., 2019; Amalladinne et al., 2020a).

The transmitter of the proposed URA-IM scheme is shown in Figure 3. Consider the active user k. The length $B_0$ information sequence ${\mathrm{m}}_k\in {\left\{\mathrm{0,1}\right\}}^{B_0}$ is first encoded by tree code through by random causal parity check bits, and the resulted length $B_1$ coded bit sequence ${\mathrm{c}}_k\in {\left\{\mathrm{0,1}\right\}}^{B_1}$ is further portioned into two parts ${\mathrm{c}}_{k,1}\in {\left\{\mathrm{0,1}\right\}}^{B_2}$ and ${\mathrm{c}}_{k,2}\in {\left\{\mathrm{0,1}\right\}}^{B_3}$, with $B_2+B_3=B_1$. The structure of coded bit sequence ${\mathrm{c}}_k$ is illustrated in Figure 4.

FIGURE 3

FIGURE 3. Transmission of common information by the proposed IM-aided URA.

FIGURE 4

FIGURE 4. Structure of coded bit sequence ${\mathrm{c}}_k$ in the proposed IM-aided URA.

The first part ${\mathrm{c}}_{k,1}={[{\mathrm{c}}_{k,\mathrm{1,1}}^T,\dots ,{\mathrm{c}}_{k,1,G}^T]}^T$ is used as index bits to determine the active channel blocks in G groups. Concretely, in the gth group, ${\mathrm{c}}_{k,1,g}\in {\left\{\mathrm{0,1}\right\}}^{B_4}$ is used to determine the $N_a$ active blocks in this group, and the indices of active blocks are collected as the vector ${\mathrm{i}}_{k,g}={[i\left(k,g,1\right),\dots ,i\left(k,g,N_a\right)]}^T$ with $1\le i\left(k,g,n\right)\le N,n=1,\dots ,N_a$. Define the channel block activity indicator as ${\beta }_{k,g,n}=1$ if the nth block of the gth group is activated by the user k, that is, it exists some m such that $i\left(k,g,m\right)=n$, and ${\beta }_{k,g,n}=0$ otherwise.

The IM principle is utilized to perform the mapping from ${\mathrm{c}}_{k,1,g}$ to ${\mathrm{i}}_{k,g}$. By IM, only $2^{B_4}$ active patterns (APs) are legitimate, and the remaining $\left(\begin{array}{c}N\\ N_a\end{array}\right)-2^{B_4}$ APs are forbidden. Denote the set of $2^{B_4}$ legitimate APs as $\mathcal{AP}=\left\{A{P}_1,\dots ,A{P}_{2^{B_4}}\right\}$ with $A{P}_m,m=1,\dots ,2^{B_4}$ being the $N_a$-dimensional vector including the indices of active blocks in the mth legitimate combination. Obviously, it has $B_4=\mathrm{lo}{\mathrm{g}}_2\left(\begin{array}{c}N\\ N_a\end{array}\right)$, $B_2=B_{4}G$, and ${\mathrm{i}}_{k,g}\in \mathcal{AP}$. The bit sequence ${\mathrm{c}}_{k,1,g}$ is used to determine the AP, for example, $A{P}_m$, and then set ${\mathrm{i}}_{k,g}=A{P}_m$, where m is the decimal representation of ${\mathrm{c}}_{k,1,g}$. An IM mapping example with N = 5, $N_a$ = 2, and $B_4$ = 3 is given in Table 2.

TABLE 2

TABLE 2. IM mapping example with $N=5,N_a=2$, and $B_4=3$.

On the other hand, the second part ${\mathbf{c}}_{k,2}={[{\mathbf{c}}_{k,\mathrm{2,1}}^T,\dots ,{\mathbf{c}}_{k,2,G}^T]}^T$ is used to select the transmit code words from the inner Gaussian CS codebook $\mathbf{A}=\left({\mathbf{a}}_1;\dots ;{\mathbf{a}}_{2^J}\right)\in {\mathrm{ℂ}}^{L\times 2^J}$ with $E\left|\right|{\mathbf{a}}_j|{|}^2=LP,j=1,\dots ,2^J$. Concretely, in the gth group, ${\mathbf{c}}_{k,2,g}={[{\mathbf{c}}_{k,2,g,1}^T,\dots ,{\mathbf{c}}_{k,2,g,N_a}^T]}^T\in {\left\{\mathrm{0,1}\right\}}^{B_5}$ is used to determine the transmit code words ${\mathbf{a}}_{k,g}={[{\mathbf{a}}_{l\left(k,g,1\right)}^T,\dots ,{\mathbf{a}}_{l\left(k,g,N_a\right)}^T]}^T\in {\mathrm{ℂ}}^{L{N}_a}$ in $N_a$ active blocks in this group, with the index $l\left(k,g,n\right)$ being the decimal representation of ${\mathbf{c}}_{k,2,g,n}$ for $n=1,\dots ,N_a$. Obviously, it has $B_5=N_{a}J$ and $B_3=B_{5}G=N_{a}JG$.

Denote ${\mathbf{x}}_{k,g,n}$ as the transmit signal in the nth block of the gth group. It has

${\mathbf{x}}_{k,g,n}={\beta }_{k,g,n}{\mathbf{a}}_{l\left(k,g,m\right)},(1)$

where the index m is such that $i\left(k,g,m\right)=n$ when ${\beta }_{k,g,n}=1$. Then, the transmit signal of the user k in the gth group ${\mathbf{x}}_{k,g}={[{\mathbf{x}}_{k,g,1}^T,\dots ,{\mathbf{x}}_{k,g,N}^T]}^T$ can be presented by

${\mathbf{x}}_{k,g}^T={\displaystyle \sum }_{n=1}^{N_a}{\mathbf{e}}_{i\left(k,g,n\right)}^T\otimes {\mathbf{a}}_{l\left(k,g,n\right)}^T,g=1,\dots ,G,(2)$

where ${\mathbf{e}}_{i\left(k,g,n\right)}$ is the $i\left(k,g,n\right)$-th column of the identity matrix ${\mathbf{I}}_N$.

Finally, the transmit signals of the user k in all groups are collected as ${\mathbf{x}}_k={[{\mathbf{x}}_{k,1}^T,\dots ,{\mathbf{x}}_{k,G}^T]}^T$.

Example 1: Consider the case of $J=4,N=5,\mathbf{a}\mathbf{n}\mathbf{d}{N}_a=2$. Assume the $B_4$ = 3-bit information sequence ${\mathbf{c}}_{k,1,g}$ selects $AP={\left[\mathrm{1,3}\right]}^T$, that is, $i\left(k,g,1\right)=1\text{ and }i\left(k,g,2\right)=3$. The $N_{a}J$ = 8-bit information ${\mathbf{c}}_{k,2,g}$ determines $l\left(k,g,1\right)=3\text{ and }l\left(k,g,2\right)=12$. Then, the transmit signal of the user k in the $N=5$ channel blocks of the gth group is ${\mathbf{x}}_{k,g}=\left({\mathbf{a}}_3,0,{\mathbf{a}}_{12},\mathrm{0,0}\right)$.

Finally, from Figure 2, for the active user k in ${\mathcal{K}}_2$, ${\mathbf{x}}_{k,g,n}$ is sent to BS, and for the active user k in ${\mathcal{K}}_1$, $\sqrt{\rho }{\mathbf{x}}_{k,g,n}$ is sent. Here, ρ is the power factor allocated to common information transmission by the user ${\mathcal{K}}_1$.

Remark 1: By employing the proposed IM-aided URA scheme to transmit common information, the average number of active code words in each block is $N_a{K}_a/N$. Note that the average number of active code words in convention URA (Fengler et al., 2019; Amalladinne et al., 2020a) is $K_a$. The signal to be estimated will be sparser in IM-aided URA, which will result in better CB-MLD performance. This is also the major motivation of this IM-aided URA scheme.

Remark 2: Compared with conventional URA (Fengler et al., 2019; Amalladinne et al., 2020a), the number of parity check bits of the proposed IM-aided URA will be reduced from $GNJ-B_0$ to $\left(B_4+N_a\times J\right)G-B_0$. This will increase the complexity of the outer tree decoder due to the less parity check constraints. On the other hand, due to the sparser signal to be estimated, the number of decided code words of the inner CS detector (also the inputs to outer tree decoder) will be decreased, and thus the complexity of the outer tree decoder can be reduced. In summary, there is a trade-off between negative and positive impacts on complexity due to the introduction of IM in the proposed IM-aided URA. In Section 6, simulation results show that the positive impact outperforms the negative in the case of $B_0=36$-bit information transmission per user.

2.1.2 User-Specific Information Transmission

The user-specific information is also transmitted by active users in ${\mathcal{K}}_1$. To transmit the $q{N}_{tot}$-bit specific information, the IM-aided non-coherent scheme (Senel and Larsson, 2018) is employed here. Concretely, each user in ${\mathcal{K}}_1$ is allocated D length L unique pilot sequences, and this allocation is assumed to be known at the BS which is also used to identify the active user. Denote the $D=2^q$ Gaussian pilot sequences allocated for device k as ${\mathit{\phi }}_{k,1},\dots ,{\mathit{\phi }}_{k,D}$ with ${\mathit{\phi }}_{k,d}={[{\phi }_{k,1},\dots ,{\phi }_{k,L}]}^T$ and $E\left|\right|{\mathit{\phi }}_{k,d}|{|}^2=LP$, $d=1,\dots ,D$. In each block, active user selects only one active pilot sequence as the transmit signal, which is determined by user-specific information according to the IM principle. The transmit user-specific signal of the active user k can be presented as $\sqrt{1-\rho }{\displaystyle \sum }_{d=1}^D{\zeta }_{k,d}^{\left(g,n\right)}{\mathit{\phi }}_{k,d}$, where the pilot activity indicator ${\zeta }_{k,d}^{\left(g,n\right)}=1$ if the dth pilot sequence of the device k is activated in the nth block of the gth group, and ${\zeta }_{k,d}^{\left(g,n\right)}=0$ otherwise.

Remark 3: Here, for simplicity, only one active pilot sequence (Senel and Larsson, 2018) is considered. This can be extended straightforwardly to the case where multiple pilot sequences are activated (Ni and Zheng, 2021).

Finally, the superimposed transmit signal of user k in the nth block of the gth group can be presented by

$\begin{array}{l}{\mathbf{s}}_{k,g,n}={\alpha }_k\left(\sqrt{\rho }{\mathbf{x}}_{k,g,n}+\sqrt{\left(1-\rho \right)}{\displaystyle \sum }_{d=1}^D{\zeta }_{k,d}^{\left(g,n\right)}{\phi }_{k,d}\right),k\in {\mathcal{K}}_1\hfill \\ {\mathbf{s}}_{k,g,n}={\alpha }_k{\mathbf{x}}_{k,g,n},k\in {\mathcal{K}}_2,\hfill \end{array}(3)$

where ${\alpha }_k$ is the user activity indicator and ${\alpha }_k=1$ if user k is active, and ${\alpha }_k=0$ otherwise.

2.2 Received Signal

At the BS, the received signal ${\mathbf{Y}}_{g,n}\in {\mathrm{ℂ}}^{L\times M}$ in the nth block of the gth group can be presented as

$\begin{array}{c}{\mathbf{Y}}_{g,n}={\displaystyle \sum }_{k\in {\mathcal{K}}_1}{\mathbf{s}}_{k,g,n}{\tilde{\mathbf{h}}}_{k,g,n}^T+{\displaystyle \sum }_{k\in {\mathcal{K}}_2}{\mathbf{s}}_{k,g,n}{\tilde{\mathbf{h}}}_{k,g,n}^T+{\mathbf{Z}}_{g,n}\\ ={\displaystyle \sum }_{k\in {\mathcal{K}}_1}{\alpha }_k\left(\sqrt{\rho }{\mathbf{x}}_{k,g,n}{\tilde{\mathbf{h}}}_{k,g,n}^T+\sqrt{\left(1-\rho \right)}\stackrel{D}{{\displaystyle \sum }_{d=1}}{\zeta }_{k,d}^{\left(g,n\right)}{\phi }_{k,d}{\tilde{\mathbf{h}}}_{k,g,n}^T\right)\\ +{\displaystyle \sum }_{k\in {\mathcal{K}}_2}{\alpha }_k{\mathbf{x}}_{k,g,n}{\tilde{\mathbf{h}}}_{k,g,n}^T+{\mathbf{Z}}_{g,n}.\end{array}(4)$

Here, ${\mathbf{Z}}_{g,n}\in {\mathrm{ℂ}}^{L\times M}$ is the Gaussian noise with independent and identically distributed (i.i.d.) entries$\sim \mathcal{CN}\left(0,{\sigma }^2\right)$ and ${\mathbf{c}}_{k,g,n}$ is the channel from device k to the BS in the nth block of the gth group and is assumed to be block-independent and unknown at the BS. Further, it has ${\tilde{\mathbf{h}}}_{k,g,n}=\sqrt{{\omega }_k}{\mathbf{h}}_{k,g,n}$, where ${\omega }_k$ is the large-scale fading coefficient and ${\mathbf{h}}_{k,g,n}$ is the small-scale fading coefficient with i.i.d. entries$\sim \mathcal{CN}\left(\mathrm{0,1}\right)$.

Assuming the first $K_1$ users belong to the first class, after some algebra, Eq. 4 can be rewritten as

${\mathrm{Y}}_{g,n}=\mathrm{A}{\mathrm{B}}_{g,n}{\mathrm{G}}^{1/2}{\mathrm{H}}_{g,n}+\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}^{1/2}\mathrm{H}{\mathrm{\prime }}_{g,n,1}+\mathrm{Z}g,n.(5)$

Here, $\mathrm{G}=\mathrm{diag}\left(\rho {\omega }_1,\dots ,\rho {\omega }_{K_1},{\omega }_{K_1+1},\dots ,{\omega }_K\right)$, ${\mathrm{H}}_{g,n}=[{\mathrm{H}}_{g,n,1},{\mathrm{H}}_{g,n,2}]\in {\mathrm{ℂ}}^{K\times M}$ with ${\mathrm{H}}_{g,n,1}={[{\mathrm{h}}_{1,g,n},\dots ,{\mathrm{h}}_{K_1,g,n}]}^T\in {\mathrm{ℂ}}^{K_1\times M}$ and ${\mathrm{H}}_{g,n,2}={[{\mathrm{h}}_{K_1+1,g,n},\dots ,{\mathrm{h}}_{K,g,n}]}^T\in {\mathrm{ℂ}}^{K_2\times M}$ , ${{\mathrm{H}}^{\mathrm{\prime }}}_{g,n,1}={[1_D^T\otimes {\mathrm{h}}_{1,g,n},\dots ,1_D^T\otimes {\mathrm{h}}_{K_1,g,n}]}^T\in {\mathrm{ℂ}}^{D{K}_1\times M}$. ${\mathrm{B}}_{g,n}\in {\left\{\mathrm{0,1}\right\}}^{2^J\times K}$ is a binary activity matrix. Denote the index of active CS code word as $l\left(k,g,m\right)$ with such m that $i\left(k,g,m\right)=n$ when ${\beta }_{k,g,n}=1$. The kth column ${\mathbf{b}}_k^{\left(g,n\right)}$ of ${\mathbf{B}}_{g,n}$ can be defined as follows: ${\mathbf{b}}_k^{\left(g,n\right)}=0$ if the user k is not active and ${\mathbf{b}}_k^{\left(g,n\right)}$ is the all-zero vector, except a single 1 in position $l\left(k,g,m\right)$ otherwise. Moreover, it has $\mathrm{\Phi }=[{\mathit{\phi }}_{\mathrm{1,1}},\dots ,{\mathit{\phi }}_{1,D},\dots ,{\mathit{\phi }}_{K_1,1},\dots ,{\mathit{\phi }}_{K_1,D}]\in {\mathrm{ℂ}}^{L\times K_{1}D}$ and ${\mathrm{\Lambda }}_{g,n}=\mathrm{diag}\left({\lambda }_{\mathrm{1,1}}^{\left(g,n\right)},\dots ,{\lambda }_{1,D}^{\left(g,n\right)},\dots ,{\lambda }_{K_1,1}^{\left(g,n\right)},\dots ,{\lambda }_{K_1,D}^{\left(g,n\right)}\right)$ with ${\lambda }_{k,d}^{\left(g,n\right)}=\left(1-\rho \right){\alpha }_k{\zeta }_{k,d}^{\left(g,n\right)}{\omega }_k$.

3 Covariance-Based ML Detection

In this section, the CB-MLD is presented. To facilitate the presentation, Eq. 5 is first represented according to the following procedure.

Let ${\gamma }_r^{\left(g,n\right)}={\displaystyle \sum }_{k\in {\mathcal{K}}_{a,1}}\rho {\omega }_k{b}_{r,k}^{\left(g,n\right)}+{\displaystyle \sum }_{k\in {\mathcal{K}}_{a,2}}{\omega }_k{b}_{r,k}^{\left(g,n\right)},r\in \left[2^J\right]$ with $b_{r,k}^{\left(g,n\right)}$ being the rth entry of ${\mathrm{b}}_k^{\left(g,n\right)}$ and ${\mathrm{\Gamma }}_{g,n}=\mathrm{diag}\left({\gamma }_1^{\left(g,n\right)},\dots ,{\gamma }_{2^J}^{\left(g,n\right)}\right)$. Then, Eq. 5 is equivalent to

${\mathrm{Y}}_{g,n}=\mathrm{A}{\mathrm{\Gamma }}_{g,n}^{1/2}\tilde{\mathrm{H}}+\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}^{1/2}\mathrm{H}{\mathrm{\prime }}_{g,n,1}+{\mathrm{Z}}_{g,n},n=1,\dots ,N_a,g=1,\dots ,G,(6)$

where $\tilde{\mathbf{H}}\in {\mathrm{ℂ}}^{2^J\times M}$ has Gaussian i.i.d. entries $\sim \mathcal{CN}\left(\mathrm{0,1}\right)$ and is independent of $\mathrm{H}{\mathrm{\prime }}_{g,n,1}$. Noting that all the data information is conveyed by $\mathbf{\Gamma }$ and $\mathbf{\Lambda }$, the goal of multiuser detection is to recover them.

From Eq. 6, the columns ${\mathbf{y}}_{g,n,m}$, $m=1,\dots ,M$, of ${\mathbf{Y}}_{g,n}$ are i.i.d. vectors with $\sim \mathcal{CN}\left(0,{\displaystyle \sum }_{g,n}\right)$. From Lemma 1 of Ni and Zheng (2021), for the case of only one active pilot sequence considered in Section 2.1.2, it has

$\begin{array}{c}\frac{1}{M}\mathrm{E}\left[\left(\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}^{1/2}\mathrm{H}{\mathrm{\prime }}_{g,n,1}\right){\left(\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}^{1/2}\mathrm{H}{\mathrm{\prime }}_{g,n,1}\right)}^H\right]\\ =\frac{1}{M}\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}{\mathrm{\Phi }}^H={\displaystyle \sum }_{k=1}^{K_1}{\displaystyle \sum }_{d=1}^D{\lambda }_{k,d}^{\left(g,n\right)}{\mathit{\phi }}_{k,d}{\mathit{\phi }}_{k,d}^H.\end{array}(7)$

Then, the covariance matrix ${\mathbf{\Sigma }}_{g,n}$ can be computed by the following equation:

$\begin{array}{c}{\mathrm{\Sigma }}_{g,n}=\frac{1}{M}\mathrm{E}\left[{\mathrm{Y}}_{g,n}{\mathrm{Y}}_{g,n}^H\right]\\ =\mathrm{A}{\mathrm{\Gamma }}_{g,n}{\mathrm{A}}^H+\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}{\mathrm{\Phi }}^H+{\sigma }^2\mathrm{I}\\ =\left(\mathrm{A},\mathrm{\Phi }\right)\left(\begin{array}{cc}{\mathrm{\Gamma }}_{g,n}^{1/2}& \\ & {\mathrm{\Lambda }}_{g,n}^{1/2}\end{array}\right){\left(\mathrm{A},\mathrm{\Phi }\right)}^H+{\sigma }^2\mathrm{I}\\ =\stackrel{2^J}{{\displaystyle \sum }_{r=1}}{\gamma }_r^{\left(g,n\right)}{\mathrm{a}}_r{\mathrm{a}}_r^H+\stackrel{K_1}{{\displaystyle \sum }_{k=1}}\stackrel{D}{{\displaystyle \sum }_{d=1}}{\lambda }_{k,d}^{\left(g,n\right)}{\mathrm{\phi }}_{k,d}{\mathrm{\phi }}_{k,d}^H+{\sigma }^2\mathrm{I}\mathrm{.}\end{array}(8)$

On the other hand, the empirical covariance matrix can be acquired by the following equation:

${\widehat{\Sigma }}_l=\frac{1}{M}{\mathbf{Y}}_{g,n}{\mathbf{Y}}_{g,n}^H=\frac{1}{M}{\displaystyle \sum }_{m=1}^M{\mathbf{y}}_{g,n,m}{\mathbf{y}}_{g,n,m}^H.(9)$

Define the log-likelihood function by the following equation:

$\begin{array}{c}f\left({\mathrm{\gamma }}^{\left(g,n\right)},{\mathrm{\lambda }}^{\left(g,n\right)}\right)=-\frac{1}{M}\log p\left({\mathrm{Y}}_{g,n}|{\mathrm{\gamma }}^{\left(g,n\right)},{\mathit{\lambda }}^{\left(g,n\right)}\right)\\ =-\frac{1}{M}\stackrel{M}{{\displaystyle \sum }_{m=1}}\log p\left({\mathbf{y}}_{g,n,m}|{\gamma }^{\left(g,n\right)},{\lambda }^{\left(g,n\right)}\right)\\ =\log |\mathrm{A}{\mathrm{\Gamma }}_{g,n}{\mathrm{A}}^H+\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}{\mathrm{\Phi }}^H+{\sigma }^2\mathrm{I}|\\ +\mathrm{tr}\left({\left(\mathrm{A}{\mathrm{\Gamma }}_{g,n}{\mathrm{A}}^H+\mathrm{\Phi }{\mathrm{\Lambda }}_{g,n}{\mathrm{\Phi }}^H+{\sigma }^2\mathrm{I}\right)}^{-1}{\widehat{\mathrm{\Sigma }}}_{g,n}\right).\end{array}(10)$

Then, the ML estimate can be acquired by the following equation:

$\left({\widehat{\mathit{\gamma }}}^{\left(g,n\right)},{\widehat{\mathrm{\lambda }}}^{\left(g,n\right)}\right)=\underset{{\mathit{\gamma }}^{\left(g,n\right)}\in {\mathrm{ℝ}}_{+}^{2^J},{\mathit{\lambda }}^{\left(g,n\right)}\in {\mathrm{ℝ}}_{+}^{K_{1}N}}{\mathrm{argma}\mathrm{x}}f\left({\mathrm{\gamma }}^{\left(g,n\right)},{\mathrm{\lambda }}^{\left(g,n\right)}\right).(11)$

This problem is non-convex and can be solved efficiently by decent method (Haghighatshoar et al., 2018; Fengler et al., 2021). For autonomy, this algorithm is summarized in Algorithm 1, whose complexity is linear in $2^J+K_{1}D$.

ALGORITHM 1

Algorithm 1. CB-MLD

After obtaining ${\widehat{\mathit{\lambda }}}^{\left(g,n\right)}$ from Eq. 11, the user-specific information is first determined by threshold-aided detection. Concretely, first compute the metric as follows:

${\varsigma }_k={\displaystyle \sum }_{g=1}^G{\displaystyle \sum }_{n=1}^N\underset{d=1,\dots ,D}{\max }{\widehat{\lambda }}_{k,d}^{\left(g,n\right)},k=1,\dots ,K_1,(14)$

where the max operation is from the fact that only one ${\lambda }_{k,d}^{\left(g,n\right)}$ is non-zero since only one pilot sequence is activated. Then, the user activity is decided by the threshold-aided method. Concretely, the metric ${\varsigma }_k$ is compared with a predetermined threshold ${\gamma }_{th,1}$, and ${\widehat{\alpha }}_k=1$ if ${\varsigma }_k\ge v_{th,1}$ and ${\widehat{\alpha }}_k=0$ otherwise. If ${\widehat{\alpha }}_k=1$, the pilot activity indicator is further estimated as ${\widehat{\zeta }}_{k,d}^{\left(g,n\right)}=1$ if $d=d^{\text{*}}$, and ${\widehat{\zeta }}_{k,d}^{\left(g,n\right)}=0$, otherwise, where

$d^{\text{*}}=\underset{d=1,\dots ,D}{\mathrm{argma}\mathrm{x}}{\widehat{\lambda }}_{k,d}^{\left(g,n\right)}.(15)$

Transmit user-specific information can then be recovered by inverse IM mapping from ${\widehat{\zeta }}_{k,d}^{\left(g,n\right)},d\in \left[D\right]$ to information bits.On the other hand, after obtaining ${\widehat{\gamma }}_r^{\left(g,n\right)},r\in \left[2^J\right],n=1,\dots ,N,g=1,\dots ,G$ from Eq. 11, the set of indices of active code words in the nth block of the gth group is decided by the following equation:

${\mathcal{S}}_{g,n}=\{r\in \left[2^J\right]|{\widehat{\gamma }}_r^{\left(g,n\right)}\ge {\gamma }_{th,2}\},(16)$

where ${\gamma }_{th,2}$ is the predetermined threshold for common information.Note that not all code words in ${\mathcal{S}}_{\mathrm{1,1}}\times {\mathcal{S}}_{\mathrm{1,2}}\times \cdots \times {\mathcal{S}}_{1,N}\times \cdots \times {\mathcal{S}}_{G,1}\times {\mathcal{S}}_{G,2}\times \cdots \times {\mathcal{S}}_{G,N}$ are legal. The outer tree decoder is used to identify the legal code words and then recover the corresponding information sequences. To guarantee the performance, the IM constraint should be integrated into the outer tree decoder, which will be described in the next section.

4 Modified Tree Decoder for Common Information

To take IM constraint into account, the modified outer tree decoder is processed group by group. Here, only the processing of the gth, $g=1,\dots ,G$, group is considered. It is assumed that $N_{path}$ survived paths have been obtained from the processing of the $\left(g-1\right)$-st group, and the corresponding bit streams are denoted as $\mathrm{TC}(l,1:(g-1)(N_{a}J+B_4)),l=1,\dots ,N_{path}$, that is, each path up to the $\left(g-1\right)$-st group has a length $\left(g-1\right)\left(N_{a}J+B_4\right)$ bit stream. The nodes in the decoding tree are partitioned into two classes, index bit node and channel block node, which are associated with the index bit stream ${\mathbf{c}}_{k,1,g}$ and CS bit stream ${\mathbf{c}}_{k,2,g}$, respectively. In the following, the processing procedure of the gth group is presented in detail.

4.1 Index Bit Node Processing

In the index bit node, for each survived path l obtained from the last node processing, the $2^{B_4}$ possible APs are tested. Denote the binary representation of the AP index $ap$ as ${\mathbf{b}}_{ap}$ for $ap=1,\dots ,2^{B_4}$. If the concatenation of $\mathrm{TC}(l,1:(g-1)(N_{a}J+B_4))$ with ${\mathbf{b}}_{ap}$ satisfies the parity check, that is, $A{P}_{ap}$ passes the check, the lth path survives in this node, and the bit stream is updated as $\mathrm{TC}(l,1:(g-1)(N_{a}J+B_4)+B_4)=(\mathrm{TC}(l,1:(g-1)(N_{a}J+B_4)),{\mathrm{b}}_{\mathrm{ap}})$. Moreover, the legitimate APs $A{P}_{ap}$ are saved in $\mathrm{T}{\mathrm{C}}_1$ for the upcoming channel block node processing. The detailed implementations are given in Lines 4–14 in Algorithm 2.

4.2 Channel Block Node Processing

The whole process is done for each survived path l of $\mathrm{TC}$ obtained from the last node processing. For each survived index bit node $A{P}_{ap}$, the channel block nodes positioned by $A{P}_{ap}\left(1\right),\dots ,A{P}_{ap}\left(N_a\right)$ are processed recursively. In the first block node $A{P}_{ap}\left(1\right)$, first, for each code word in ${\mathcal{S}}_{g,A{P}_{ap}\left(1\right)}$, compute the binary representation of the code word index and then test whether it satisfies the parity check. If it passes this check, a new path is found and survives. The same operations in subsequent block nodes are done until all the $N_a$ active block nodes are tested. The detailed implementations are given in Lines 16–31 in Algorithm 2. An illustration of the tree-decoder procedure with $N_a=2$ in the gth group is given in Figure 5.

FIGURE 5

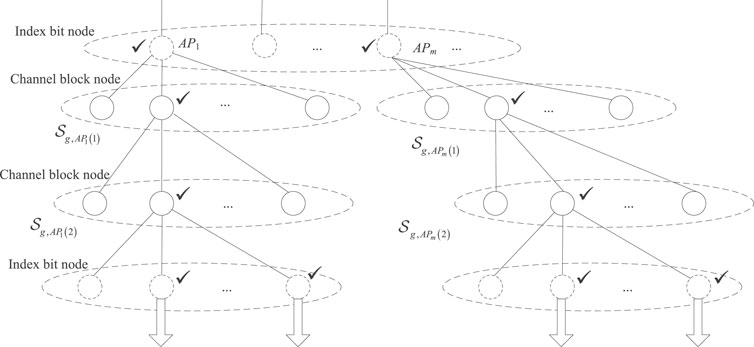
FIGURE 5. Illustration of the modified outer tree decoder in the gth group with $N_a$ = 2. The notation “✓” denotes this node passes the parity-check.

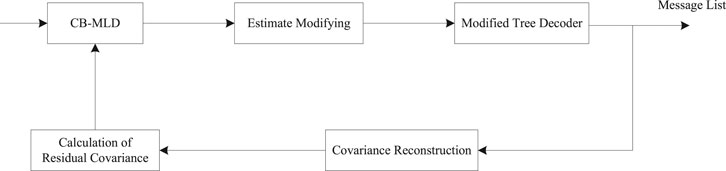
5 Iterative Receiver for Common Informaiton

5.1 Motivations and Ideas

By the CB-MLD described in Section 3, we observe a good decoding performance of user-specific information from extensive simulations. On the other hand, the decoding performance of common information is highly dependent on the threshold ${\gamma }_{th,2}$. However, the optimal ${\gamma }_{th,2}$ is involved with multiple system parameters, and its optimization is very difficult. In general, a larger ${\gamma }_{th,2}$ will result in higher probability of misdetection, while lower probability of false alarm and lower computational complexity of the outer decoder. In Fengler et al. (2019), it is selected carefully through simulations and varies from different system parameters.

Here, the iterative receiver for common information is studied. The basic ideas are two-fold. First, the SIC strategy is employed where the covariance of active code words obtained in former iteration is reconstructed and pre-subtracted from the empirical covariance matrix. This means that the signal to be estimated will be sparser in the subsequent iterations and thus can improve the performance of CB-MLD. Second, the strict threshold requirement can be relaxed since multiple iterations exist, and the threshold should decrease with iteration number. Then, in former iterations, low probability of false alarm can be guaranteed by larger threshold which also alleviates the error propagation. In subsequent iterations, the smaller threshold can reduce the probability of misdetection. In the following text, the iterative receiver is described in detail.

5.2 Covariance Reconstruction and Cancellation of User-Specific Information

Noting that a good decoding performance of user-specific information is observed using CB-MLD, the covariance associated with user-specific information can be reconstructed and canceled first.

ALGORITHM 2

Algorithm 2. Modified Outer Tree Decoder

Denote the set of decided active users associated with user-specific information as follows:

${\widehat{\mathcal{K}}}_{a,1}=\{k\in \left[K_1\right]|{\widehat{\alpha }}_k=1\}.(17)$

Then, the ${\mathbf{\Lambda }}_{g,n}$ can be reconstructed as follows:

${\overline{\mathrm{\Lambda }}}_{g,n}=\mathrm{diag}\left({\overline{\mathit{\lambda }}}^{\left(g,n\right)}\right),(18)$

where

${\overline{\lambda }}_{k,d}^{\left(g,n\right)}=\{\begin{array}{ll}{\lambda }_{k,d}^{\left(g,n\right)}\hfill & k\in {\widehat{\mathcal{K}}}_{a,1}\mathrm{and}d=d^{\text{*}}\hfill \\ 0\hfill & k\in {\widehat{\mathcal{K}}}_{a,1}\mathrm{and}d\ne d^{\text{*}}\hfill \\ 0\hfill & k\notin {\widehat{\mathcal{K}}}_{a,1}\hfill \end{array}.(19)$

Therefore, the covariance is reconstructed and subtracted from the empirical covariance by the following equation:

${\tilde{\widehat{\Sigma }}}_{y,g,n}={\widehat{\Sigma }}_{y,g,n}-\mathbf{\Phi }{\overline{\Lambda }}_{g,n}{\mathbf{\Phi }}^H\approx \mathbf{A}{\mathbf{\Gamma }}_{g,n}{\mathbf{A}}^H+{\sigma }^2\mathbf{I},(20)$

where the approximation ${\overline{\Lambda }}_{g,n}\approx {\mathbf{\Lambda }}_{g,n}$ is utilized and from the good decoding performance of user-specific information by CB-MLD.

5.3 Iterative Receiver for Common Information

The block diagram of the proposed iterative receiver for common information is shown in Figure 6. By using the SIC strategy, the processing in the tth iteration is described as below.

FIGURE 6

FIGURE 6. Block diagram of the proposed iterative receiver for common information.

Denote the modified output list of inner CB-MLD in the tth iteration as follows:

${\mathcal{S}}_{g,n}^t=\{r\in \left[2^J\right]|{\widehat{\gamma }}_{g,n}^r>{\gamma }_{th,2}^t\},(21)$

where ${\gamma }_{th,2}^t$ is the threshold in this iteration. Here, this threshold is set as follows:

${\gamma }_{th,2}^1={\gamma }_0,{\gamma }_{th,2}^t=\max \left({\gamma }_{th,2}^1-{\alpha }^{t-1}\mathrm{\Delta },\epsilon \right),t=\mathrm{2,3},\dots ,(22)$

where ${\gamma }_0>0$ is the initial threshold which is usually set to be a large value to reduce the probability of false alarm, $\mathrm{\Delta }$ is the step size with small positive value, and $\alpha >1$ is the reducing factor with iteration number. Moreover, ε is introduced to avoid the resulted very small threshold by the exponential decreasing rule.

Denote the message list after outer modified tree decoder as follows:

${\mathrm{ℳ}}^t=\left\{\mathrm{r}{=}^{\text{Δ}}{[r_{\mathrm{1,1}},\dots ,r_{1,N},\dots ,r_{G,1},\dots ,r_{G,N}]}^T\right|r_{g,n}\in {\mathcal{S}}_{g,n}^t\mathrm{and}\mathrm{r}\mathrm{passes}\mathrm{the}\mathrm{outer}\mathrm{parity}\mathrm{check}\}(23)$

and the corresponding list in the nth block of group g as follows:

${\mathrm{ℳ}}_{g,n}^t=\left\{r_{g,n}\right|\mathbf{r}\in {\mathrm{ℳ}}^t\}.(24)$

Note that one code word in some sub-frame can appear multiple times in the message list of the tree decoder output. Define the times of index r appears in ${\mathrm{ℳ}}_{g,n}^t$ by the following equation:

$n_r^{g,n,t}=\left|\{r\in \left[2^J\right]|r\in {\mathrm{ℳ}}_{g,n}^t\}\right|(25)$

and the set of indices which appear m times, $m\ge 0$, as follows:

${\mathrm{ℛ}}_{g,n,m}=\{r\in \left[2^J\right]|n_r^{g,n,t}=m\}(26)$

Then, the ${\mathbf{\Gamma }}_{g,n}$ is reconstructed by the equation as follows:

${\overline{\mathrm{\Gamma }}}_{g,n}^t=\mathrm{diag}\left({\overline{\widehat{\mathit{\gamma }}}}^{\left(g,n,t\right)}\right),(27)$

with ${\overline{\widehat{\mathit{\gamma }}}}^{\left(g,n,t\right)}={[{\overline{\widehat{\gamma }}}_1^{\left(g,n,t\right)},{\overline{\widehat{\gamma }}}_2^{\left(g,n,t\right)},\dots ,{\overline{\widehat{\gamma }}}_{2^J}^{\left(g,n,t\right)}]}^T$ and

${\overline{\widehat{\gamma }}}_r^{\left(g,n,t\right)}=\{\begin{array}{c}0,r\notin {\mathrm{ℳ}}_{g,n}^t\hfill \\ \xi \left(n_r^{g,n,t}\right),r\in {\mathrm{ℳ}}_{g,n}^t\end{array}.(28)$

Here, $\xi \left(n_r^{g,n,t}\right)$ is the empirical average of ${\gamma }_r$ associated with the code word ${\mathit{a}}_r$ appearing $n_r^{g,n,t}$ times in the tth iteration and defined as follows:

$\xi \left(n_r^{g,n,t}\right)=\frac{1}{\left|{\mathrm{ℛ}}_{g,n,n_r^{g,n,t}}\right|}{\displaystyle \sum }_{l\in {\mathrm{ℛ}}_{g,n,n_r^{g,n,t}}}{\widehat{\gamma }}_l^{\left(g,n,t\right)},l=1,\dots ,2^J.(29)$

Example 2: Assume ${\mathrm{ℳ}}_{g,n}^t=\left\{\mathrm{2,2,3,3,1}\right\}$ from 5 legal message sequences in ${\mathrm{ℳ}}^t$ and $J=2$. Then, it has ${\mathrm{ℛ}}_{g,n,1}=\left\{1\right\}\text{ and }{\mathrm{ℛ}}_{g,n,2}=\left\{\mathrm{2,3}\right\}$. Furthermore, assume ${\widehat{\gamma }}_1^{\left(g,n,t\right)}=0.2,{\widehat{\gamma }}_2^{\left(g,n,t\right)}=0.4,\text{ and }{\widehat{\gamma }}_3^{\left(g,n,t\right)}=0.5$. Then, it has $\xi \left(1\right)={\widehat{\gamma }}_1^{\left(g,n,t\right)}=0.2$ and $\xi \left(2\right)=0.5\left({\widehat{\gamma }}_2^{\left(g,n,t\right)}+{\widehat{\gamma }}_3^{\left(g,n,t\right)}\right)=0.45$. Finally, ${\overline{\widehat{\gamma }}}_1^{\left(g,n,t\right)}=\xi \left(1\right)=0.2,{\overline{\widehat{\gamma }}}_2^{\left(g,n,t\right)}={\overline{\widehat{\gamma }}}_3^{\left(g,n,t\right)}=\xi \left(2\right)=0.45,\text{ and }{\overline{\widehat{\gamma }}}_4^{\left(g,n,t\right)}=0$.

Next, the reconstructed covariance is subtracted from the residual empirical covariance matrix by the following equation:

${\widehat{\Sigma }}_{y,g,n}^{t+1}={\widehat{\Sigma }}_{y,g,n}^t-\mathbf{A}{\overline{\Gamma }}_{g,n}^t{\mathbf{A}}^H(30)$

with initialization ${\widehat{\Sigma }}_{y,g,n}^1={\tilde{\widehat{\Sigma }}}_{y,g,n}$. The corresponding theoretical residual covariance matrix is

$\begin{array}{c}{\widehat{\Sigma }}_{y,g,n}^{t+1}={\widehat{\Sigma }}_{y,g,n}^t-\mathbf{A}{\overline{\Gamma }}_{g,n}^t{\mathbf{A}}^H\\ =\mathbf{A}\left({\mathbf{\Gamma }}_{g,n}-\stackrel{t}{{\displaystyle \sum }_{t^{\prime }=1}}{\overline{\Gamma }}_{g,n}^{t^{\prime }}\right){\mathbf{A}}^H+{\sigma }^2\mathbf{I}\\ =\mathbf{A}{\tilde{\Gamma }}_{g,n}^t{\mathbf{A}}^H+{\sigma }^2\mathbf{I},\end{array}(31)$

where ${\tilde{\mathrm{\Gamma }}}_{g,n}^t={\mathrm{\Gamma }}_{g,n}-{{{\displaystyle \sum }}^{\text{}}}_{t^{\prime }=1}^t{\overline{\mathrm{\Gamma }}}_{g,n}^{t^{\prime }}$ is the residual after the tth iteration. Then, given ${\widehat{\Sigma }}_{y,g,n}^{t+1}$, the inner CB-MLD is employed again to obtain the estimate ${\widehat{\gamma }}_r^{\left(g,n,t+1\right)}$ of ${\tilde{\Gamma }}_{g,n}^t$. Noting that ${\tilde{\Gamma }}_{g,n}^t$ becomes sparser with the increase in the iteration number, an improved detection performance can be achieved.

Before sending to outer tree decoder, ${\widehat{\gamma }}_r^{\left(g,n,t+1\right)}$ is further modified as

${\widehat{\gamma }}_r^{\left(g,n,t+1\right)}=\max \left({\widehat{\gamma }}_r^{\left(g,n,t+1\right)},{\widehat{\gamma }}_r^{\left(g,n,t\right)}-\xi \left(n_r^{g,n,t}\right)\right).(32)$

This modification is to take the following case into account when ${\widehat{\gamma }}_r^{\left(g,n,t+1\right)}$ is smaller than ${\gamma }_{th,2}^{t+1}$. This case is that some code words appear multiple times, but only less times (including zero time) were accepted by the outer tree decoder in the tth iteration, that is, ${\widehat{\gamma }}_r^{\left(g,n,t\right)}$ is larger than the average $\xi \left(n_r^{g,n,t}\right)$.

ALGORITHM 3

Algorithm 3. Iterative Receiver for Common Information

In summary, the iterative receiver is summarized in Algorithm 3.

Remark 4: In the threshold Eq. 22, four parameters $\epsilon ,{\gamma }_0,\alpha$, and $\mathrm{\Delta }$ are required to be selected properly. From our simulations in Section 6, an experimental setting of these parameters will show good performance for various system settings. However, in the conventional non-iterative receiver, the threshold ${\gamma }_{th,2}$ in Eq. 16 should be different for various system settings to ensure good performance. Therefore, in conjunction with multiple iterations, the threshold setting by Eq. 22 can relax the requirement of threshold selection for various system settings.

6 Simulation Results

In this section, simulation results are given to validate the performance of the proposed IM-aided mixed massive random access. For common information, the per-user probabilities of misdetection and false alarm are defined as follows:

$P_{c,md}=\frac{1}{K_a}{\displaystyle \sum }_{k\in {\mathcal{K}}_a}P({\mathit{m}}_k\in \widehat{\mathrm{ℳ}})(33)$

$P_{c,fa}=\frac{|\widehat{\mathrm{ℳ}}\backslash \{{\mathit{m}}_k,k\in {\mathcal{K}}_a\}|}{\left|\widehat{\mathrm{ℳ}}\right|},(34)$

where $\widehat{\mathrm{ℳ}}$ is the output message list at the receiver and ${\mathit{m}}_k$ is the message sent by the user k. The per-user error probability of common information is defined as $P_{c,e}=P_{c,md}+P_{c,fa}$. For user-specific information, the probabilities of misdetection and false alarm are defined as follows:

$P_{us,md}=1-\frac{\mathrm{E}\left[\right|{\mathcal{K}}_{a,1}{{\displaystyle \cap }}^{\text{}}{\widehat{\mathcal{K}}}_{a,1}\left|\right]}{K_{a,1}}(35)$

$P_{us,fa}=\frac{\mathrm{E}\left[\right|{\widehat{\mathcal{K}}}_{a,1}\backslash {\mathcal{K}}_{a,1}\left|\right]}{K_1-K_{a,1}},(36)$

where ${\widehat{\mathcal{K}}}_{a,1}$ is the decided active user set defined in Eq. 17. Further, the bit error rate (BER) is defined as follows:

$P_{us,e}=P_{us,md}+\left(1-P_{us,md}\right)P_{e,b},(37)$

where $P_{e,b}$ is the BER of the correct decision user in ${\mathcal{K}}_{a,1}{{\displaystyle \cap }}^{\text{}}{\widehat{\mathcal{K}}}_{a,1}$.

The system parameters for common information of the IM-aided URA scheme are $N=2,N_a=1,G=16,N_{tot}=32,J=11,B_0=36,B_1=192,B_2=16,\text{ and }{B}_3=176$. Therefore, there are $B_1-B_0=156$ parity check bits in the outer tree code word, and the total code rate is $36/\left(32\times 100\right)=0.01125$. For comparison, the performance of conventional URA (Fengler et al., 2019) is also given. In conventional URA, the parameters are $N_{tot}=32,J=11,B_0=36,\text{ and }{B}_1=32\times 11=352$, and the number of parity check bits is $B_1-B_0=316$. The total code rate of URA is also 0.01125. The check profile of IM-aided URA is [2,10,. . . ,10,12,12] for the $G{N}_a=16$ active blocks and that of URA is [0,10,. . . ,10,11,11,11,11,11,11] for the $N_{tot}=32$ blocks. All the large-scale fading coefficients are set as $g_k=1,k=1,\dots ,K$, which corresponds to the perfect power control at users. The signal-to-noise ratio (SNR) of common information $\frac{E_b}{N_0}=\frac{P}{R_c{\sigma }^2}$ is fixed as 0dB in all simulations, where $R_c=\frac{B_0}{GNL}$ is the total code rate. Furthermore, in the iterative receiver for common information, the parameters in Eq. 22 are set as $\epsilon =0.08,{\gamma }_0=0.3,\alpha =1.646,\text{ and Δ}=0.06824$. The parameters for user-specific information transmission are $q=2$ and $D=4$.

Moreover, the power allocation coefficient is set as $\rho =0.5$. In general, we set $K_1=0.05K,K_2=0.95K$, $K_a=1/15K=4/3K_1,K_{a1}=0.05K_a,\text{ and }{K}_{a2}=0.95K_a$ in all simulations. This means that a small fraction of users belong to the first class, and all users have the same activity probability. Moreover, 80 transmission frames are tested to obtain all the simulation results.

In Figure 7, the error probability vs. the number of active user $K_a$ is given. Here, no iterative receiver is utilized in URA-IM. The number of BS antennas is $M=200$, and the channel block length is $L=100$. The thresholds ${\gamma }_{th,1}$ and ${\gamma }_{th,2}$ are set to 2 and 0.2 in IM-aided URA and are set to 4 and 0 in conventional URA. These settings of thresholds show good performance from extensive computer simulations. From this figure, for user-specific information, IM-aided URA has better $P_{us,e}$ performance than conventional URA, which can be interpreted by that IM-aided URA, resulting in the signal to be estimated sparser. For common information, IM-aided URA shows better performance than conventional URA when $K_a$ is larger than about 190.

FIGURE 7

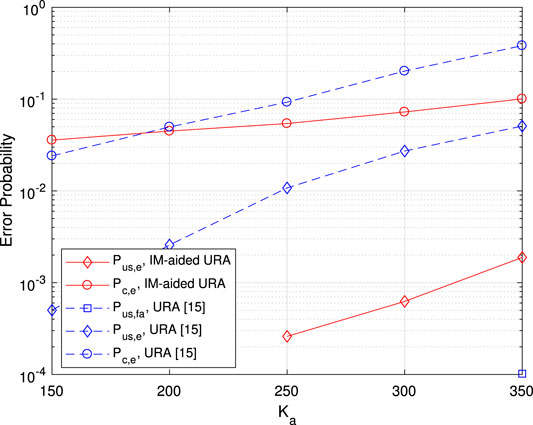
FIGURE 7. Error probability vs. the number of active users $K_a$. Here, the number of BS antennas is M = 200. The channel block length is fixed at L = 100. For user-specific information, misdetection is not observed in both schemes, and false alarm is observed only at $K_a=350$ in conventional URA (Fengler et al., 2019).

In Figure 8, the performance with $M=300$ is given. The other settings are the same as those in Figure 7. From the figure, for user-specific information, $P_{us,e}$, of IM-aided URA is observed only at $K_a=350$, which outperforms that of conventional URA enormously. For common information, IM-aided URA shows better performance than conventional URA when $K_a$ is larger than about 250. Finally, compared with the result in Figure 7 with $M=200$, better performance is achieved with increased M.

FIGURE 8

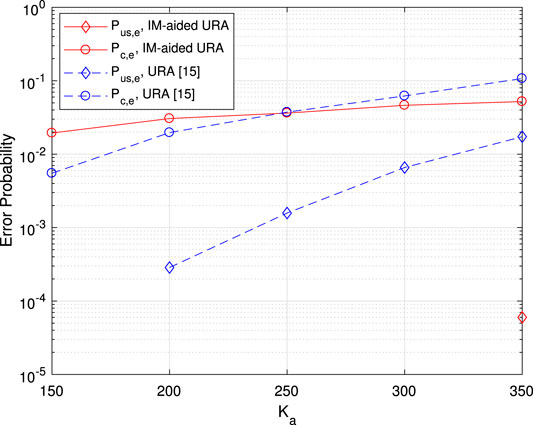
FIGURE 8. Error probability vs. the number of active users $K_a$. Here, the number of BS antennas is $M=300$. The channel block length is fixed at L = 100. For user-specific information, misdetection and false alarm are not observed in both schemes.

Figure 9 gives the error probability vs. channel block length L with fixed $K_a=200\text{ and }M=100$. The other settings are same as those in Figure 7. For user-specific information, the performance of $P_{us,e}$ in the IM-aided URA scheme is much better than that of conventional URA in all L considered here. For common information, the $P_{c,e}$ performance of IM-aided URA is also much better than that of conventional URA.

FIGURE 9

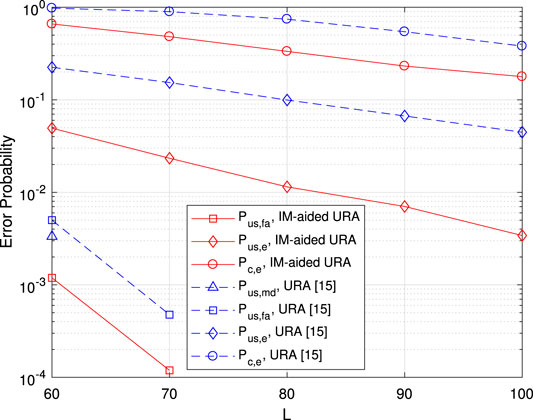
FIGURE 9. Error probability vs. channel blocks length L. Here, the numbers of BS antennas and active users are $M=100$ and $K_a=200$, respectively. For user-specific information, misdetection is observed only at $L=60$ in conventional URA (Fengler et al., 2019) and false alarm is observed only at $L=60$ and $L=70$ in both schemes.

Figure 10 gives the error probability vs. channel block length L with fixed $K_a=M=200$. The other settings are the same as those in Figure 7. For user-specific information, the performance of $P_{us,e}$ in IM-aided URA is much better than that of conventional URA in all L considered here. For common information, from this figure, to achieve $P_{c,e}$ = 0.1 at M = 200, $L\approx 65$ is sufficient for the IM-aided URA scheme, while $L\approx 85$ is required for conventional URA. Noting that the channel is assumed to be unchanged during one block, the channel coherent interval is required to be no shorter than the channel block length. Therefore, the proposed IM-aided URA scheme can work in the scenario with a shorter channel coherent interval.

FIGURE 10

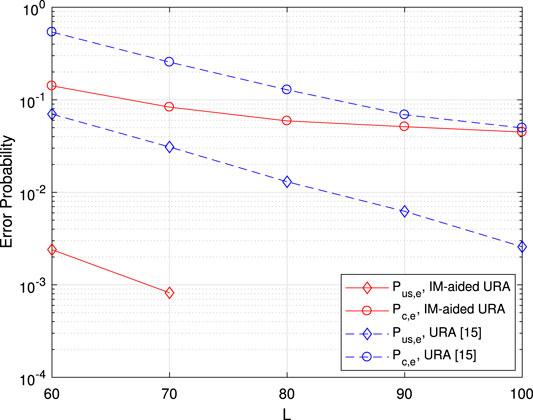
FIGURE 10. Error probability vs. channel blocks length L. Here, the numbers of BS antennas and active users are $M=200$ and $K_a=200$, respectively. For user-specific information, misdetection and false alarm are not observed in both schemes.

Table 3 lists the runtime of the receiver signal processing in both IM-aided URA and URA (Fengler et al., 2019). Here, $L=100,M=200,\text{ and }{K}_a=300$ and the other parameters are same as those in Figure 7. From this table, as analyzed in Remark 1 and Remark 2 of Section 2, the smaller number of average active code words in each channel block results in the complexity reduction of CB-MLD and the decrease of the number of decided code words, and further the complexity reduction of the outer tree decoder.

TABLE 3

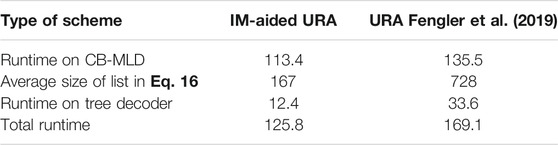
TABLE 3. Runtime of receiver of IM-aided URA and URA (Fengler et al., 2019), $L=100,M=200,K_a=300$ (unit: second).

The case with more common information bit transmission, that is, larger $B_0$, for example, $B_0=64$, is also tested in our simulations. However, in this scenario, the complexity of the outer tree decoder is prohibitively high due to the fact there are only 192–64 = 128 parity check bits. This less parity check constraints make more paths to be survived at each tree node and thus the whole outer decoding tree is very large.

Next, the performance of the iterative receiver is studied. In Figure 11, $P_{c,md}$ of common information in the proposed iterative scheme vs. the iteration number given. All combinations with the number of receive antennas M = 200, 300 and the number of active users $K_a$ = 150 : 50 : 350 are considered. From this figure, the performance improves with the iterative number in all cases. Moreover, the iterative receiver converges very fast. For example, for the case M = $K_a$= 200, only four iterations are required. In Figure 12, the convergence of $P_{c,fa}$ is illustrated. From this figure, $P_{c,fa}$ is small with all iterations. Figure 13 depicts the performance comparison of the proposed iterative receiver and conventional non-iterative receiver at M = 200 and 300, respectively. From this figure, the proposed iterative receiver achieves better $P_{c,e}$ performance.

FIGURE 11

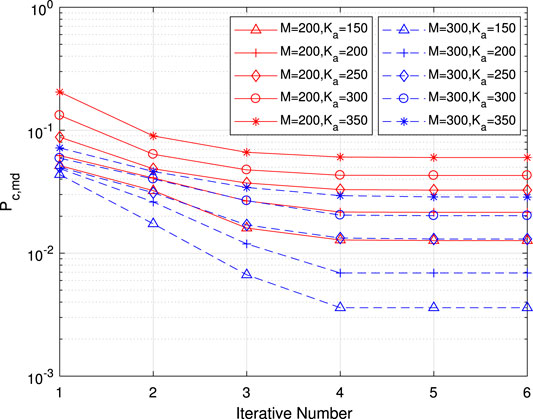
FIGURE 11. Per-user error probability of misdetection for common information as a function of the iterative number for various numbers of antennas and active users.

FIGURE 12

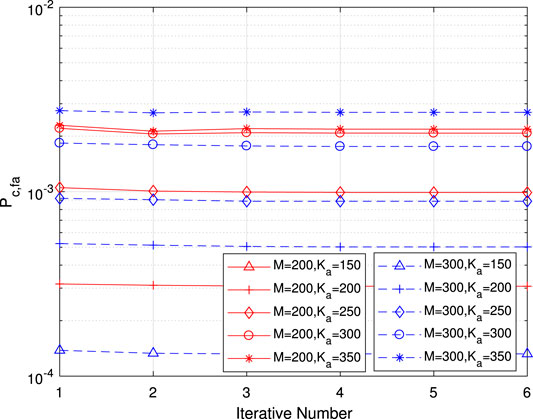
FIGURE 12. Per-user error probability of false alarm for common information as a function of the iterative number for various numbers of antennas and active users.

FIGURE 13

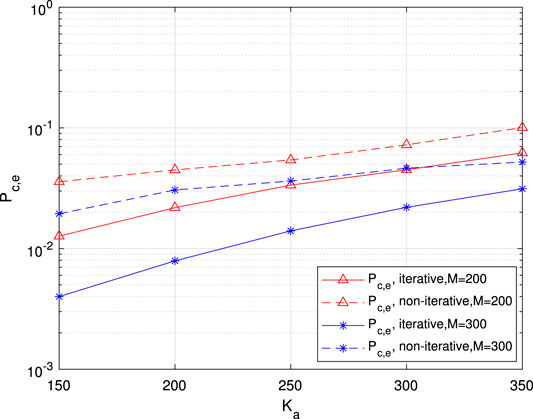
FIGURE 13. Per-user error probability for common information as a function of the number of active users.

Table 4 gives the runtime of the proposed iterative receiver in the case of $M=200$ and $K_a=300$. The runtime of inner CB-MLD, average size of list, and runtime time of outer decoder, are listed in this table. Here, $L=100$ and the other parameters are same as those in Figure 13. It is easy to see that the runtimes of inner CB-MUD and outer decoder decrease in later iterations. This can be interpreted by that in inner CB-MLD, the sparsity of the signal ${\mathbf{\Gamma }}_{g,n}$ to be estimated increases. In the outer decoder, the list size is still large due to the low threshold in later iterations, while most of them cannot pass the parity check.

TABLE 4

TABLE 4. Runtime of the proposed receiver in different iterations, $M=200,K_a=300$ (unit: second).

In non-iterative IM-aided URA receiver, the runtime, as shown in Table 3, is 113.4s for the inner CB-MLD detector, 12.4s for the outer tree decoder, and the whole runtime is 125.8s. From Table 4, in the proposed iterative IM-aided receiver, the total runtime is 396.8s, about 3 times longer than that of the non-iterative IM-aided receiver, although there are five iterations in the iterative receiver. Recalling the superiority of the proposed iterative receiver in terms of the relaxed requirement of thresholds and better PUPE performance, this mild increased complexity is tolerable.

7 Conclusion

In this article, a mixed massive random access was proposed where the considered uplink massive access system consists of users transmitting both common and user-specific information and users transmitting only common information. An IM-aided URA was proposed to transmit common information, and IM-aided non-coherent SRA was utilized to transmit user-specific information. The CB-MLD was employed to recover the user-specific information directly and the active code words associated with common information. Furthermore, the modified outer tree decoder was proposed to stitch the common information in different blocks, and an iterative receiver consisting of inner CS-based detection and outer tree decoding was employed to improve the performance. Finally, simulation results validated the superiority of the proposed mixed random access scheme.

Compared to conventional URA (Fengler et al., 2019), when there are more common information bits, that is, larger $B_0$, and thus less parity check bits due to the IM principle, the modified outer tree decoder of IM-aided URA presented in Section 4 has a prohibitively high complexity. Therefore, more efficient outer tree decoder or smarter application of IM principle deserves further research to make the IM-aided URA suitable for more common information bit transmission.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

ZL and JZ conceived the work and wrote the article and ZL and JN carried out investigations.

Funding

This work was supported in part by the National Natural Science Foundation of China (grant 61671340).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Althunibat, S., Mesleh, R., and Rahman, T. F. (2019). A Novel Uplink Multiple Access Technique Based on index-modulation Concept. IEEE Trans. Commun. 67 (7), 4848–4855. doi:10.1109/TCOMM.2019.2909211

CrossRef Full Text | Google Scholar

Amalladinne, V. K., Pradhan, A. K., Rush, C., Chamberland, J.-F., Narayanan, K. R., et al. (2020). Unsourced Random Access with Coded Compressed Sensing: Integrating AMP and Belief Propagation. arXiv: 2010.04364v1, [cs.IT].

Amalladinne, V. K., Chamberland, J.-F., and Narayanan, K. R. (2020a). A Coded Compressed Sensing Scheme for Unsourced Multiple Access. IEEE Trans. Inform. Theor. 66 (10), 6509–6533. doi:10.1109/TIT.2020.3012948

CrossRef Full Text | Google Scholar

Amalladinne, V. K., Chamberland, J.-F., and Narayanan, K. R. (2020b). An Enhanced Decoding Algorithm for Coded Compressed sensingICASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Barcelona, Spain, 5270–5274. doi:10.1109/ICASSP40776.2020.9054142

CrossRef Full Text

Arslan, E., Dogukan, A. T., and Basar, E. (2020). Index Modulation-Based Flexible Non-orthogonal Multiple Access. IEEE Wireless Commun. Lett. 9 (11), 1942–1946. doi:10.1109/LWC.2020.3009100

CrossRef Full Text | Google Scholar

Basar, E., Aygolu, U., Panayirci, E., and Poor, H. V. (2013a). Orthogonal Frequency Division Multiplexing with index Modulation. IEEE Trans. Signal. Process. 61 (22), 5536–5549. doi:10.1109/TSP.2013.2279771

CrossRef Full Text | Google Scholar

Basar, E., Aygölü, U., and Panaylrcl, E. (2013b). Orthogonal Frequency Division Multiplexing with index Modulation in the Presence of High Mobility. (BlackSeaCom). Georgia: Batumi, 5536–5549. doi:10.1109/BlackSeaCom.2013.6623399

CrossRef Full Text

Basar, E. (2016). Index Modulation Techniques for 5G Wireless Networks. IEEE Commun. Mag. 54 (7), 168–175. doi:10.1109/MCOM.2016.7509396

CrossRef Full Text | Google Scholar

Bockelmann, C., Pratas, N., Nikopour, H., Au, K., Svensson, T., Stefanovic, C., et al. (2016). Massive Machine-type Communications in 5G: Physical and MAC-Layer Solutions. IEEE Commun. Mag. 54 (9), 59–65. doi:10.1109/MCOM.2016.7565189

CrossRef Full Text | Google Scholar

Dai, L., Wang, B., Yuan, Y., Han, S., Chih-lin, I., and Wang, Z. (2015). Non-orthogonal Multiple Access for 5G: Solutions, Challenges, Opportunities, and Future Research Trends. IEEE Commun. Mag. 53 (9), 74–81. doi:10.1109/MCOM.2015.7263349

CrossRef Full Text | Google Scholar

Ding, Z., Lei, X., Karagiannidis, G. K., Schober, R., Yuan, J., and Bhargava, V. K. (2017). A Survey on Non-orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends. IEEE J. Select. Areas Commun. 35 (10), 2181–2195. doi:10.1109/JSAC.2017.2725519

CrossRef Full Text | Google Scholar

Donoho, D. L., Maleki, A., and Montanari, A. (2009). Message-passing Algorithms for Compressed Sensing. Pnas. 106 (45), 18914–18919. doi:10.1073/pnas.0909892106

PubMed Abstract | CrossRef Full Text | Google Scholar

Durisi, G., Koch, T., and Popovski, P. (2016). Toward Massive, Ultrareliable, and Low-Latency Wireless Communication with Short Packets. Proc. IEEE. 104 (9), 1711–1726. doi:10.1109/JPROC.2016.2537298

CrossRef Full Text | Google Scholar

Fengler, A., Caire, G., Jung, P., and Haghighatshoar, S. (2019). Massive MIMO Unsourced Random Access. arXiv: 1901.00828v1, [cs.IT].

Fengler, A., Jung, P., and Caire, G. (2019). SPARCs for Unsourced Random Access. arXiv:1901.06234v1, [cs.IT].

Fengler, A., Haghighatshoar, S., Jung, P., and Caire, G. (2021). Non-Bayesian Activity Detection, Large-Scale Fading Coefficient Estimation, and Unsourced Random Access with a Massive MIMO Receiver. IEEE Trans. Inform. Theor. 67, 2925–2951. doi:10.1109/TIT.2021.3065291

CrossRef Full Text | Google Scholar

Haghighatshoar, S., Jung, P., and Caire, G. (2018). Improved Scaling Law for Activity Detection in Massive MIMO Systems. Proc IEEE ISITVail, 381–385. doi:10.1109/ISIT.2018.8437359

CrossRef Full Text | Google Scholar

Hasan, M., Hossain, E., and Niyato, D. (2013). Random Access for Machine-To-Machine Communication in LTE-Advanced Networks: Issues and Approaches. IEEE Commun. Mag. 51 (6), 86–93. doi:10.1109/MCOM.2013.6525600

CrossRef Full Text | Google Scholar

Kowshik, S. S., Andreev, K., Frolov, A., and Polyanskiy, Y. (2020). Energy Efficient Coded Random Access for the Wireless Uplink. IEEE Trans. Commun. 68 (8), 4694–4708. doi:10.1109/TCOMM.2020.3000635

CrossRef Full Text | Google Scholar

Li, T., Wu, Y., Zheng, M., Wang, D., and Zhang, W. (2020a). SPARC-LDPC Coding for MIMO Massive Unsourced Random Access. arXiv: 2009.10912v2, [cs.IT]. doi:10.1109/GCWkshps50303.2020.9367450

CrossRef Full Text

Li, J., Li, Q., Dang, S., Wen, M., Jiang, X.-Q., and Peng, Y. (2020b). Low-Complexity Detection for Index Modulation Multiple Access. IEEE Wireless Commun. Lett. 9 (7), 1. doi:10.1109/LWC.2020.2974730

CrossRef Full Text | Google Scholar

Liang, Z., and Zheng, J. (2021). Iterative Receiver of Uplink Massive MIMO Unsourced Random Access. Harbin, China: IEEE IWCMCIn press.

Liang, Z., and Zheng, J. (2020). Mixed Massive Random Access. IEEE ICCT, 311–316. doi:10.1109/ICCT50939.2020.9295776

CrossRef Full Text | Google Scholar

Liang, Z., Zheng, J., and Ni, J. (2021). Index Modulation Aided Massive MIMO Un-sourced Random Access. Melbourne, Victoria, Austria: IEEE ISITIn press

Marshakov, E., Balitskiy, G., Andreev, K., and Frolov, A. (2019). A Polar Code Based Unsourced Random Access for the Gaussian MAC. Honolulu, HI, USA: IEEE VTC-fall. doi:10.1109/VTCFall.2019.8891583

CrossRef Full Text

Ni, J., and Zheng, J. (2021). Index Modulation-Based Non-coherent Transmission in grant-free Massive Access. IEEE Trans. Veh. Technol. 70 (1), 1025–1029. doi:10.1109/TVT.2020.3045448

CrossRef Full Text | Google Scholar

Ni, J., and Zheng, J. (2020). Non-Coherent Grant-Free NOMA through Pilot-And Channel Block-Index Modulation. IEEE Wireless Commun. Lett. 10 (4), 1. doi:10.1109/LWC.2020.3040363

CrossRef Full Text | Google Scholar

Ordentlich, O., and Polyanskiy, Y. (2017). Low Complexity Schemes for the Random Access Gaussian Channel. Proc. IEEE ISIT, 2528–2532. doi:10.1109/ISIT.2017.8006985

CrossRef Full Text | Google Scholar

Polyanskiy, Y. (2017). A Perspective on Massive Random-Access. Proc. IEEE ISIT, 2523–2527. doi:10.1109/ISIT.2017.8006984

CrossRef Full Text | Google Scholar

Pradhan, A., Amalladinne, V., Vem, A., Narayanan, K. R., and Chamberland, J.-F. (2019). A Joint Graph Based Coding Scheme for the Unsourced Random Access Gaussian Channel. Proc. IEEE GLOBECOM, 1–6. doi:10.1109/GLOBECOM38437.2019.9013278

CrossRef Full Text | Google Scholar

Pradhan, A. K., Amalladinne, V. K., Narayanan, K. R., and Chamberland, J.-F. (2020). Polar Coding and Random Spreading for Unsourced Multiple Access. arXiv: 1911.01009v1, [cs.IT]. doi:10.1109/ICC40277.2020.9148687

CrossRef Full Text

Rangan, S. (2011). Generalized Approximate Message Passing for Estimation with Random Linear Mixing. Proc IEEE ISIT, 2168–2172. doi:10.1109/ISIT.2011.6033942

CrossRef Full Text | Google Scholar

Senel, K., and Larsson, E. G. (2018). Grant-free Massive MTC-Enabled Massive MIMO: A Compressive Sensing Approach. IEEE Trans. Commun. 66 (12), 6164–6175. doi:10.1109/TCOMM.2018.2866559

CrossRef Full Text | Google Scholar

Tusha, A., Dogan, S., and Arslan, H. (2020). A Hybrid Downlink NOMA with OFDM and OFDM-IM for beyond 5G Wireless Networks. IEEE Signal. Process. Lett. 27 (3), 491–495. doi:10.1109/LSP.2020.2979059

CrossRef Full Text | Google Scholar

Vem, A., Narayanan, K. R., Cheng, J., and Chamberland, J.-F. (2017). A User-independent Serial Interference Cancellation Based Coding Scheme for the Unsourced Random Access Gaussian Channel. Proc. IEEE ITW, 121–125. doi:10.1109/ITW.2017.8278023

CrossRef Full Text | Google Scholar

Wen, M., Cheng, X., Ma, M., Jiao, B., and Poor, H. V. (2016). On the Achievable Rate of OFDM with Index Modulation. IEEE Trans. Signal. Process. 64 (8), 1919–1932. doi:10.1109/TSP.2015.2500880

CrossRef Full Text | Google Scholar

Wen, M., Cheng, X., and Yang, L. (2014). Optimizing the Energy Efficiency of OFDM with index Modulation. IEEE Int. Conf. Commun. Syst., 31–35. doi:10.1109/ICCS.2014.7024760

CrossRef Full Text | Google Scholar

Wen, M., Cheng, X., and Yang, L. (2017). Index Modulation for 5G Wireless Communications (Wireless Networks). Berlin, Germany: Springer.

Xie, X., Wu, Y., Gao, J., and Zhang, W. (2020). Massive Unsourced Random Access for Massive MIMO Correlated Channels. arXiv: 2008.08742v2 [cs.IT]. doi:10.1109/GLOBECOM42002.2020.9347959

CrossRef Full Text

Xu, L. D., He, W., and Li, S. (2014). Internet of Things in Industries: A Survey. IEEE Trans. Ind. Inf. 10 (4), 2233–2243. doi:10.1109/TII.2014.2300753

CrossRef Full Text | Google Scholar

Zheng, J., and Chen, R. (2017). Achieving Transmit Diversity in OFDM-IM by Utilizing Multiple Signal Constellations. IEEE Access 5, 8978–8988. doi:10.1109/ACCESS.2017.2708718

CrossRef Full Text | Google Scholar

Zheng, M., Wu, Y., and Zhang, W. (2020). Polar Coding and Sparse Spreading for Massive Unsourcess Random Access. arXiv: 2007.05739v1, [cs.IT]. doi:10.1109/VTC2020-Fall49728.2020.9348654

CrossRef Full Text