- Department of Electronic Systems, Aalborg University, Aalborg, Denmark
In this paper we envision a federated learning (FL) scenario in service of amending the performance of autonomous road vehicles, through a drone traffic monitor (DTM), that also acts as an orchestrator. Expecting non-IID data distribution, we focus on the issue of accelerating the learning of a particular class of critical object (CO), that may harm the nominal operation of an autonomous vehicle. This can be done through proper allocation of the wireless resources for addressing learner and data heterogeneity. Thus, we propose a reactive method for the allocation of wireless resources, that happens dynamically each FL round, and is based on each learner’s contribution to the general model. In addition to this, we explore the use of static methods that remain constant across all rounds. Since we expect partial work from each learner, we use the FedProx FL algorithm, in the task of computer vision. For testing, we construct a non-IID data distribution of the MNIST and FMNIST datasets among four types of learners, in scenarios that represent the quickly changing environment. The results show that proactive measures are effective and versatile at improving system accuracy, and quickly learning the CO class when underrepresented in the network. Furthermore, the experiments show a tradeoff between FedProx intensity and resource allocation efforts. Nonetheless, a well adjusted FedProx local optimizer allows for an even better overall accuracy, particularly when using deeper neural network (NN) implementations.
1 Introduction
The adoption of ubiquitous Level-5 fully independent system autonomy in road vehicles (as per the SAE ranking system (SAE, 2016)) is barred from progress due to the omnipresence of chaotic traffic in legacy traffic situations. Moreover, a 38% share of prospective users are skeptical of the performance of the autonomous driving systems (Nielsen and Haustein, 2018). As such, lowering the number of negative outcome outliers in autonomous vehicle operation, particularly ones that lead to fatal incidents, can be addressed with an overabundance of statistically relevant data (Yaqoob et al., 2019). Thus, given the privacy requirements and the abundance of the data that is produced by road vehicles and/or unmanned erial vehicles (UAVs) in the role of traffic monitors, the machine learning (ML) problem can be addressed by treating the participatory vehicles as learners in a federated learning (FL) network.
In more detail, FL is an ML technique that distributes the learning across many learners. In this way, many separate models are aggregated in order to acquire one general model at server side (Konečnỳ et al., 2016). In FL, each learner does not have to send heaps of data to a common server for processing, but maintains the data privately. As such, the concept of FL is an extension of distributed ML with four important distinctions: 1) the training data distributions across devices can be non-IID; 2) not all devices have similar computational hardware; 3) FL scales for networks of just few devices to vast networks of millions; 4) FL can be engineered in a way in which privacy is conserved. Given the vast complexity of implementing FL in autonomous vehicular traffic, particularly related to the quickly changing environment, in this paper we focus on solving the issues of non-IID data learnt across several devices with unequal processing power. A list of relevant symbols, and their descriptions are contained in Table 1, and a review on relevant FL literature follows below.
1.1 State of the Art
FL is an emergent field that has gained immense popularity in the last five years. From the relevant literature we highlight several works. (Li et al., 2020) covers the state of the art regarding computational models (Yang et al., 2019), contains a clear understanding of the FL potential and its most prominent applications (Lim et al., 2020). and (Aledhari et al., 2020) provide comprehensive coverage on the communications challenges for the novel edge computation (Niknam et al., 2020), analyzes scenarios of FL where learners use wireless connectivity. Challenges and future directions of FL systems in the context of the future 6G systems is given in (Yang et al., 2021), while (Savazzi et al., 2021) elaborates upon the applications of FL on connected automated vehicles and collaborative robotics (Khan et al., 2020). covers resource allocation and incentive mechanisms in FL implementations. Most of the works on FL concerning UAVs treat the devices as learners (Wang et al., 2020; Zeng et al., 2020; Zhang and Hanzo, 2020). This requires mounting heavy computational equipment on-board, and therefore it is an energy inefficient way of exploiting drones. In contrast, in our prior work (Donevski et al., 2021a) we have investigated techniques for reducing staleness when a UAV acts as an orchestrator by optimizing its flying trajectory.
There is also an interest in wireless resource allocation optimization for FL networks, as covered in the topics that follow. The work of (Chen et al., 2020a) proposes a detailed communications framework for resource allocation given complex wireless conditions and an FL implementation on IID data. This work has a strong contribution to the topic of convergence analysis of wireless implementations of FL with very detailed channel model. The work of (Amiri and Gündüz, 2020) does a detailed convex analysis for distributed stochastic gradient decent (SGD) and optimizes the power allocation for minimizing FL convergence times. The work of (Tran et al., 2019) formulates FL over wireless network as an optimization problem and conducts numerical analysis given the subdivided optimization criteria. However, the aforementioned works perform their analysis on SGD which has been shown to suffer in the presence of non-IID data and unequal work times (Li et al., 2018). The novel local subproblem that includes a proximal optimizer in (Li et al., 2018) achieves 22% improvements in the presence of unequal work at each node.
The learning of both single task and multi task objectives in the presence of unequal learner contributions is a difficult challenge and has received a lot of attention, e.g. in the works of (Smith et al., 2017; Li et al., 2019; Mohri et al., 2019). This also leads to the question of analyzing contributions among many learners with vastly different hardware that is considered in works covering FL incentive mechanisms, by (Kang et al., 2019a; Chen et al., 2020b; Khan et al., 2020; Nishio et al., 2020; Pandey et al., 2020). The incentive based FL implementations rely on estimating each learner’s contribution and rewarding them for doing the work. Hence calculating appropriate rewards becomes a difficult challenge that also comes at the price of computation and communications as shown by (Kang et al., 2019b). Such mechanisms are useful when orchestrating an FL where learners would collect strongly non-IID data and learn with vastly different processing capabilities.
1.2 Drone Traffic Monitors as Federated Learning Orchestrators
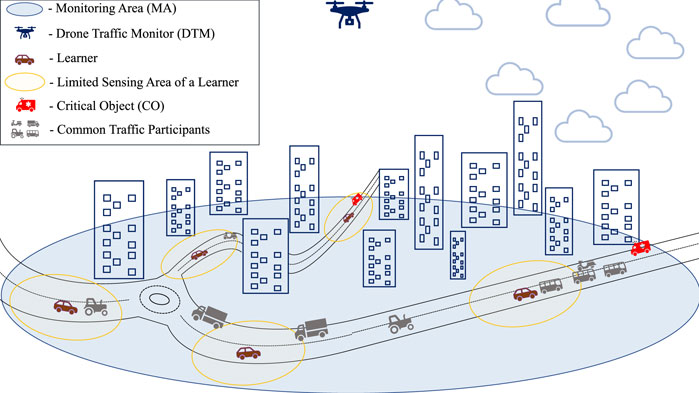
Unmanned erial vehicles (UAVs) or drones could provide an essential aid to the vehicular communication networks by carrying wireless base stations (BSs). In combination with the 5G standardization and the emerging 6G connectivity, drone-aided vehicular networks (DAVNs) (Shi et al., 2018) are capable of providing ultra reliable and low latency communications (URLLC) (Popovski et al., 2018; She et al., 2019) when issuing prioritized and timely alarms. In accord, most benefits of DAVNs come as consequence of the UAV’s capability to establish line of sight (LOS) with very high probability (Mozaffari et al., 2019). The good LOS perspective also benefits visual surveillance, hence enabling UAVs to offer just-in-time warnings for critical objects (COs) that can endanger the nominal work of autonomous vehicles. Though DAVNs expect many roles from the drone, we draw inspiration from UAVs in the role of drone traffic monitors (DTMs) that continuously improve and learn to perform timely and reliable detections of COs. To avoid requiring a plethora of drone-perspective camera footage of the traffic, we propose DTMs that take the role of a federated learning (FL) orchestrator, and autonomous vehicles participate as learners.
This FL architecture with a drone orchestrator, illustrated in Figure 1, exploits the processing and sensing enabled vehicles contained in the monitoring area (MA) to participate both as learners and supervisors. The vehicle-learners receive the drone provided footage, and do the heavy computational work of ML training for the task of computer vision. This is possible since the vehicle-learners have robust sensing capabilities, and when they have the CO in view, can contribute to the learning process due to their secondary perspective (Chavdarova et al., 2018) on the object, and their deeper knowledge of traffic classes. However, even when assuming perfect supervision by the learners, FL is not an easy feat since some knowledge can be obfuscated among omnipresent information and/or contained at computationally inferior straggler learners. In accord, we use a combination of state of the art FL implementation with a novel resource aware solution for balancing work times and learner contributions, which are described in the overview that follows.
1.3 Main Contributions
In this paper, we provide a novel perspective on continuous DTM improvements through an FL implementation onto vehicle-learners. Moreover, we aim to provide a robust and adaptable resource allocation method for improved FL performance in the presence of chaotic, quickly changing, and most importantly imbalanced and non-IID data. Since both computational and data bias cannot be analytically extracted before sampling the ML model received from each learner, we assume heuristic measures such as maximizing the epochs computed, or equalizing the epochs computed across the learners. Moreover, the core contribution of this work is a dynamic resource allocation method based on each learner’s past contributions. To provide full compatibility with heterogeneous learners and non-IID data, we employ these methods in combination with the FedProx algorithm. Finally, we developed an experimental analysis in which the performance is evaluated through its capability to learn an underrepresented class of the dataset, while also balancing overall system accuracy.
The paper organization goes as follows. Section 2 introduces the learning setup and the communications resource allocation setup. Section 3 defines the optimization problem and lists several static and reactive heuristic measures for improving the learning performance, and introduces the learner contribution calculations. This is followed by Section 4 where the experimental setup and the results from the setup are presented. The final, Section 5 summarizes the outcomes and discusses future directions.
2 System Model
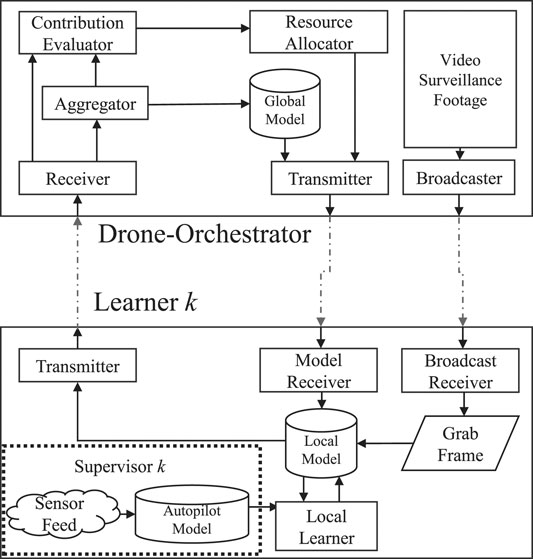
The setup is depicted in Figure 2, where we show the orchestrator block that sends and receives the models through wireless connections, while simultaneously broadcasts the unsupervized video surveillance footage at a constant data rate for all vehicles inside the MA. We assume that each vehicle acts as an ideal supervisor for the objects which are represented both in the broadcasted video and their sensor feed. Given some deadline of completion T, the learner needs to return its locally learnt model to the drone-orchestrator. After receiving the model, the orchestrator aggregates the K models, after which it can also evaluate the contribution of each learner separately. Each learner k has a contribution, that the contribution estimator estimates to be
2.1 Federated Learning
The FL process starts when the orchestrator sends its weights to all K learners, where each learner
where ω are the instantaneous value of the local model weights,
Using stochastic gradient descent (SGD) as a local solver
Due to the expected heterogeneity in the network of learners in the proposed FL implementation, we use the FedProx algorithm. The benefit of FedProx is that it can converge and provide good general models even under partial work and very dissimilar amounts of
where ω is the instantaneous value of the local model weights at the local optimizer,
2.2 Allocation of Wireless Resources
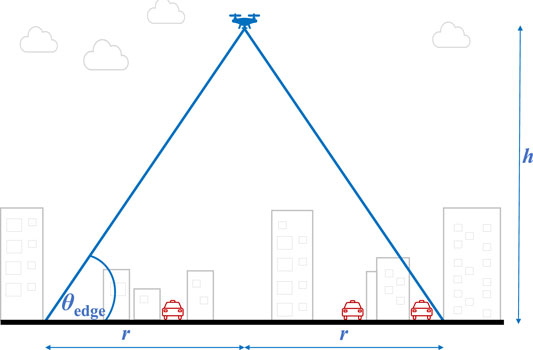
Though the work of (Chen et al., 2020a) covers a detailed cellular model for FL connectivity, drone provided connectivity is generally uniform and can be designed to be predominantly line of sight (Babu et al., 2020). As we illustrate in Figure 3 the drone height h and the projected coverage on the ground with radius r impact the elevation angle at the edge of the MA,
Since our goal of a DMT implementation is to improve the worst case performance of autonomous traffic, we also model the communications system through
where a and b are constants defined by the propagation topology of the environment, as given by (Al-Hourani et al., 2014). Through
where
where
As the size of the processing batch is fixed to B, each device k is tasked with an equal number of floating point operations (FLO) for each epoch, and computes
Given an equal bandwidth allocation to all devices, the total number of epochs is a linear function of
where, D is the total amount of data that needs to be sent in both directions within the deadline of T. We convert the problem to a step-wize nomenclature that gives the relationship between each learner, independent of the length of T but as a relative inter-learner metric:
where
where α is the nominal time reserved for learning, and it is directly influenced by the amount of FLOPs required to compute one epoch. This simplifies to:
where
where β is the portion of time spent transmitting within one round. As per β, it is obvious that it is much more important to investigate the ratio of data load on the channel instead of solely focusing on the achieved rate
Given a no-drop policy (each learner must complete at least one epoch
and the extreme upper bound of
The behavior of the resource function for a single
The entire communications setup is reducible to the analysis of combinations of α and β, as both parameters directly determine the impact that resource allocation has on the system. Moreover, the parameter β modifies the impact of resource allocation for each learner, where systems with high β values stand to benefit the most, while low β values indicate near instantaneous model transfers which cannot be influenced by modifying the bandwidth. On the other hand, α is a system design hyperparameter that indicates the amount of epochs computed within a single round, by an average learner, and it is fully customizable before or even during operation.
3 Analysis
Our goal is to improve the learning of a particular class among the network of FL devices, that may represent a CO, without harming the overall accuracy of the system. Thus, each round i we exploit our control over the wireless resources and optimize the bandwidth allocated to each device
Extracting the direct impact of
3.1 Static Resource Allocation Measures
The naive way of improving the convergence in a heterogeneous setting is maximizing the total amount of work done by all learners as in:
This optimization criteria maximizes the epochs computed across the whole network given the limited radio resources. Since Eq. 16 implies asyncronous amount of work performed among the learners, it may not be considered as a potential maximization metric when using classical FedAvg implementations. However, since we use FedProx as a local optimizer, this is a sufficient naive solution that represents an exploitative behavior from the orchestrator.
Furthermore, given the work on asynchronous FL and the issues of diverse computational hardware in the network (Xie et al., 2019; Mohammad et al., 2020) we identify maximum staleness (Donevski et al., 2021a) as an important criterion toward the precision of the model. We define this as the maximal difference between the fastest and slowest learner:
Nonetheless, minimizing staleness does not extract the full potential of our setup. Therefore, as in (Donevski et al., 2021b) we convene s and the average of the anticipated epochs to a more balanced heuristic metric, named Average Anchored Staleness (AAS) as an optimization metric:
AAS gives a good general overview that is data-agnostic, without the need to assume the impact of data at some particular learner and solely on spatial and computational performance. Like this, AAS provides a resource allocation objective function that serves an equally balanced amount of learning and staleness.
3.2 Contribution Estimation for Reactive Resource Allocation
In the case of DTMs, the considered vehicle supervisors/learners can find themselves in the presence of vastly different objects, and the data they sense changes constantly while they operate. Given the aforementioned, the contribution of each learner is hard to estimate especially in the presence of noisy samples. Hence, we assume that separating the important CO information ahead of time is impossible and only consider reactive approaches such as incentive mechanisms. To use incentive mechanisms we must assume that the validation dataset that is present at the orchestrator has equal representation of all classes. Hence, based on such validation data we can pass the weights ω through an evaluation function
where
We note that the
Following the first round, each device k provides its model to the DTM-orchestrator. After which, the aggregator provides the first aggregate model weights
where
In the case of constantly equal contributions from all learners, the heuristic maximization criteria is reduced to the epoch maximization problem defined in (16). With
4 Results
4.1 Experimental Setup
For a set of learners that are scattered along the MA, our goal is to as closely as possible generate an experimental setup that simulates a realistic learner given the system model in Section 2. Since each learner has a very short amount of time to do the learning for the DTM, we approach the data as fleeting (stored very briefly) and concealed (cannot be known beforehand). Due to the complexity and the issues of reliably simulating the FL performance for full scale traffic footage, we test the performance of the proposed methods through simple and easily accessible computer vision datasets. Each testing scenario was built using either the MNIST dataset (LeCun et al., 1995) of handwritten digits, or the FMNIST (Xiao et al., 2017) dataset consisting of 10 different grayscale icons of fashion accessories.
As we expect that each vehicle contains strongly non-IID data we create a custom data distribution among
In the described setting, the class-number 5 (sixth class counting from zero) assumes the role of a CO. In addition to the CO, class-number three is another non-CO class that is not too common and appears at only three learners. This is an over-exaggerated situation of having the CO data hidden at one node that is also a straggler. We expect this to be a realistic reflection of data in drone orchestrated FLs as nodes carry only a small amount of supervisory data for each class due to the fact that they stumble upon important objects randomly.
For detection, we implement a small convolutional neural network (CNN), common for the global and local models implemented in python tensorflow (Abadi et al., 2015). In more detail, the CNN has only one 3 × 3 layer of 64 channels using the rectifier linear unit (ReLU), that goes to a 2 × 2 polling layer. A dense, fully connected neural network (NN) layer of 64 ReLU activated neurons receives the polled outputs of the convolutional layer, which is then fully connected to a NN layer of 10 soft-max activated neurons, one for each of the 10 categories of the NIST dataset. The local optimizer at each learner is given by the FedProx calculation in Eq. 2, where the cost function
4.2 MNIST Testing
We proceed with the testing of all three approaches for five different values of the proximal importance hyperparameter
In Figure 4 we can notice a limited impact of changing the μ parameter of FedProx, most likely due to the small amount of learners and not as significant straggler impact. This is expected given that (Li et al., 2018) claim strong superiority over FedAvg in the cases of very large portions of stragglers. Interestingly, μ does not have a strong positive impact on the learning performance even in the case of MAX, and therefore, a system designer would most likely introduce a weak proximal term of
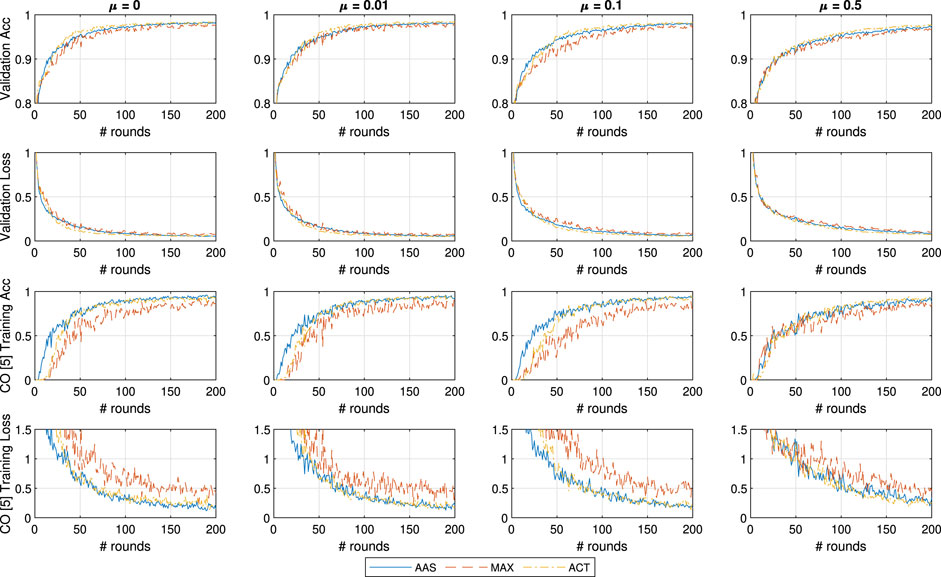
FIGURE 4. General and CO-specific accuracy and loss results obtained when testing all three methods in combination with FedProx using the MNIST dataset.
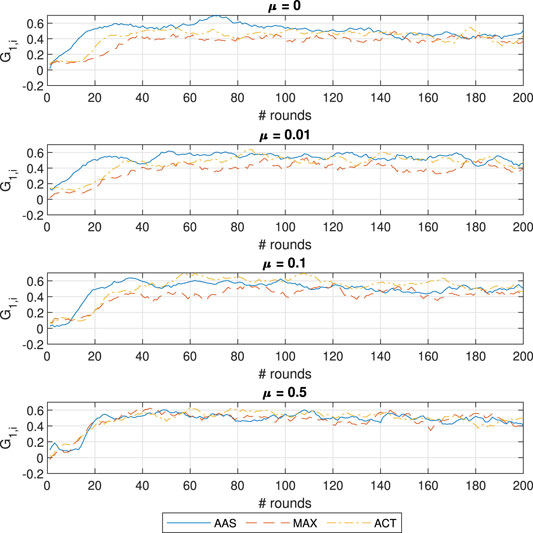
To better investigate the behavior of the ACT approach we illustrate the evolution of the estimated contributions for learner
Most notably, the accuracy of AAS suffers significantly when
4.3 FMNIST Testing
Since modeling common tasks of computer vision on MNIST is a very easy task we repeat the test on the FMNIST dataset. This dataset consists of 10 classes of fashion accessories in equal distribution as the MNIST dataset (a training set of 60,000 examples and a test set of 10,000 examples) and as in the case of MNIST consists of 28 × 28 grayscale images. The dataset classes are: (0) T-shirt/top, 1) Trouser, 2) Pullover, 3) Dress, 4) Coat, 5) Sandal, 6) Shirt, 7) Sneaker, 8) Bag, and 9) Ankle boot; where each item is taken from a fashion article posted on Zalando. Compared to the number MNIST, in FMNIST the intensity of each voxel plays a much bigger role and is scattered across larger parts of the image. We consider the FMNIST dataset as a computer vision task that sufficiently replicates the problem of detecting 10 different types of vehicles, in a much more simplistic context that is furthermore easily replicable.
In Figure 6, we show the learning performance in the same setting and
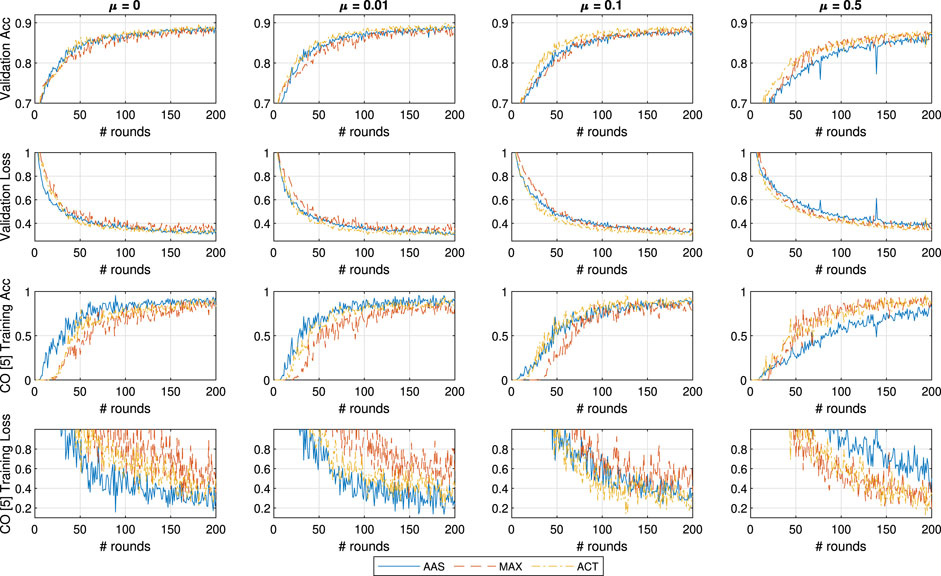
FIGURE 6. General and CO-specific accuracy and loss results obtained when testing all three methods in combination with FedProx using the FMNIST dataset.
Finally, we conclude that even though
4.4 Deeper FMNIST Testing
In this testing scenario we expand the small convolutional neural network by adding another 3 × 3 layer of 64 channels using ReLU activators as a first layer. In Figure 7 we show the outcomes of the testing, where the overall accuracy of the system has been improved to 90%. However, the larger model acted as an equalizer across all three approaches and in the case of
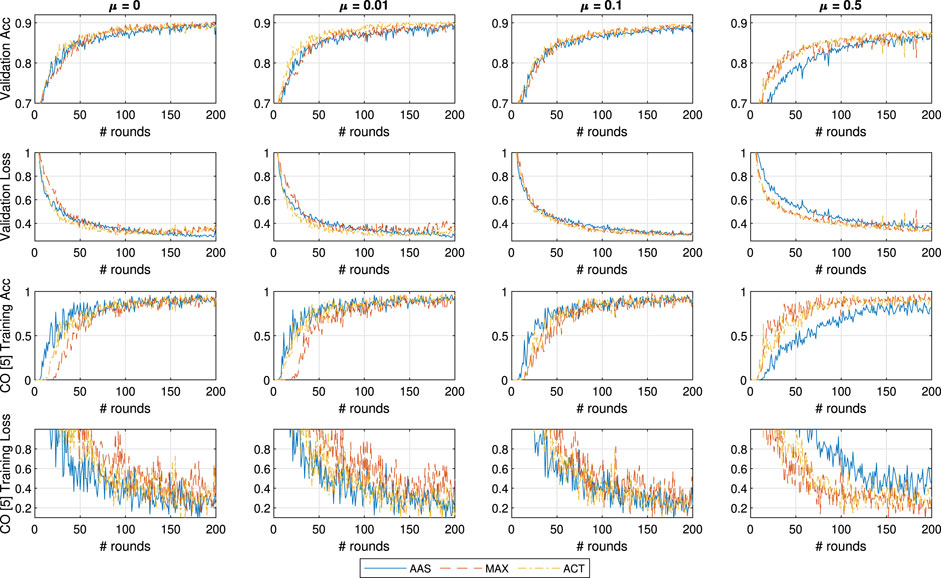
FIGURE 7. General and CO-specific accuracy and loss results obtained when testing, with an extra CNN layer, all three methods in combination with FedProx using the FMNIST dataset.
With the deep model, this effect is diminished for the case of ACT with
It is also interesting to notice that the MAX approach does well with overall accuracy, particularly when compared to the inferior performance in the previous testing sets. Nonetheless, MAX is still inferior to both other approaches when it comes to detecting the CO class. Finally, we focus on the results on
We seek to discover the culprit for the inferiority of AAS in CO discovery when
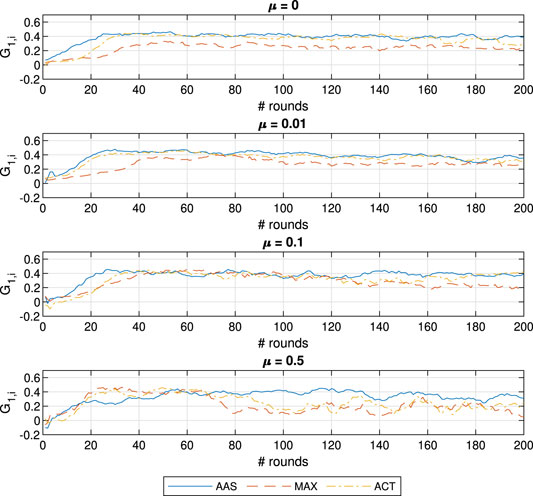
FIGURE 8. Contribution evolution for learner
4.5 Testing Fleeting FMNIST
The final test with the experimental setup is constructed such that we introduce stress in the learning process by introducing temporary losses in the supervision process. This is done by introducing a likelihood that a learner k loses access to a detection class. This would be representative of a learner losing LOS of the object was able to supervise, and is therefore modeled as a two state markov model (such as the Gilbert Elliot (Boban et al., 2016)) that has a good and a bad state. Hence each supervisor has
Hence, to compensate for the smaller dataset, we let the simulations run for 250 rounds, and focus only on
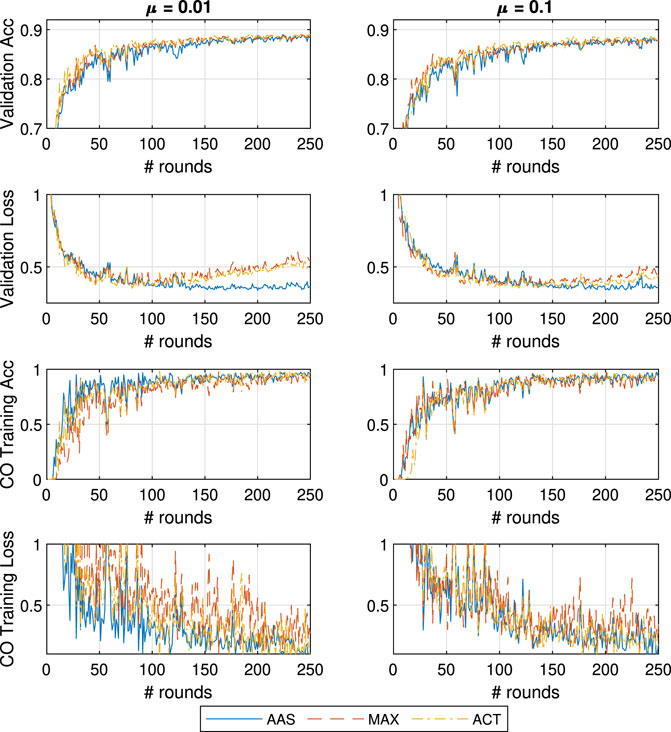
FIGURE 9. General and CO-specific accuracy and loss results obtained when testing, with an extra CNN layer, all three methods in combination with FedProx using the FMNIST in the case of fleeting data.
Focusing on
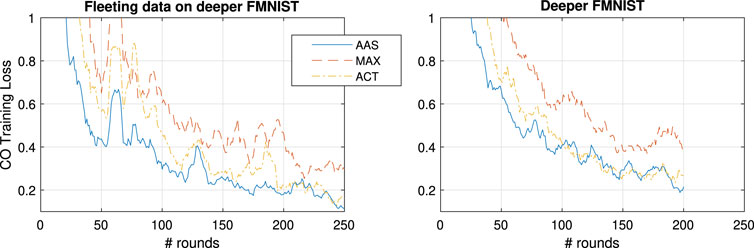
FIGURE 10. 10-point moving average of CO training loss for
4.6 Key Takeaways
We condense several takeaways that were derived from all four experimental runs. The initial and most important conclusion is that the concepts of resource allocation and FedProx are at odds in the case of FL implementations. In more detail, the goal of FedProx is to reduce the impact of each learner individually while resource allocation methods strive to improve the overall performance by exploiting or compensating the heterogeneity of the system. Hence the impact of resource allocation methods is diminished when strengthening the role of the proximal term. Nonetheless, in the many tests a safe balance between both μ and resource allocation ensure good learning behavior. As such, we recommend that all future works consider perturbed gradient descent implementations, such as FedProx, when dealing with non-IID data in heterogeneous FL.
Additionally, in the initial testing of our setup we noticed that testing on MNIST is not sufficient to provide reasonable results for the implementations, due to how trivial the task of recognizing digits is. Moreover, FL implementations, such as the proposed drone implementation, are based in the distributed learning of complex tasks and require deeper NN models. In such cases, it was evident that increasing the total amount of computed epochs benefits the convergence time of the system with potentially harmful effects in CO detection accuracy. Moreover, deeper model implementations did not behave well under strong proximal terms.
As a consequence to this, learning hidden data can be addressed by equalizing the contributions by using AAS or by introducing strong proximal terms. However, the strong proximal terms have potential to slow down the convergence time for all nodes. Hence, the safest implementation to achieving the best combination of convergence time, overall accuracy and CO learning rate is using the ACT approach with a weak proximal term.
Finally, in a case where the data is fleeting, using a
Finally, we extrapolate that defining a proper μ is cardinal. However, the hyperparameter needs to be defined ahead of the deployment of the system. As such, since we would not have access to the training data, the feasibility of implementing AAS is uncertain especially for situations where the presence of data changes quickly. This gives another strong motivation for using reactive measures based on contributions and incentive calculations, such as ACT.
5 Conclusion
In this paper we investigated the learning process in a novel Federated Learning (FL) architecture, where a DTM acts as an orchestrator and traffic participants act as supervisors on its model. Such an implementation expects impairments on the learning process due to unbalanced and non-IID data scattered across heterogeneous learners that have variable computational equipment. We therefore test the ability of two static methods (AAS and MAX), and one incentive based reactive (ACT) resource allocation method to improve the speed of learning CO classes and maintaining good overall model accuracy. The validity of the methods was tested with an experimental FL implementation that uses the novel FedProx algorithm to learn from the MNIST and FMNIST datasets. The testing was conduced across combinations of different FedProx strength, CNN model depth, and fleeting data. From the testing we conclude that both reactive (ACT) resource allocation and FedProx are essential to securing model accuracy. In more detail, due to the inability to anticipate the distribution of the data across the learners, the use of ACT ensures proper operation of the FL implementation. In accord, the combination of properly set FedProx with an ACT implementation provided faster convergence times, better accuracy, but most importantly it matched the AAS method in learning to recognize the CO. Such behavior was consistent across most runs given the varying task complexity, model size, and data presence. The goal of future works would be to look into more advanced proactive approaches, especially for the presence of imperfect data supervision.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
ID: investigation, writing; JN and PP: writing, review, editing, resources, funding acquisition, supervision, and project administration.
Funding
The work was supported by the European Union’s research and innovation program under the Marie Sklodowska-Curie grant agreement No. 812991 “PAINLESS” within the Horizon 2020 Program.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Software available from tensorflow.org.
Al-Hourani, A., Kandeepan, S., and Jamalipour, A. (2014). “Modeling Air-To-Ground Path Loss for Low Altitude Platforms in Urban Environments,” in Proc. of IEEE Global Communications Conference, Austin, TX, USA, October, 2898–2904.
Aledhari, M., Razzak, R., Parizi, R. M., and Saeed, F. (2020). Federated Learning: A Survey on Enabling Technologies, Protocols, and Applications. IEEE Access 8, 140699–140725. doi:10.1109/ACCESS.2020.3013541
Amiri, M. M., and Gündüz, D. (2020). Federated Learning over Wireless Fading Channels. IEEE Trans. Wireless Commun. 19, 3546–3557. doi:10.1109/TWC.2020.2974748
Babu, N., Ntougias, K., Papadias, C. B., and Popovski, P. (2020). “Energy Efficient Altitude Optimization of an Aerial Access Point,” in Proc. of IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, September, 1–7. doi:10.1109/PIMRC48278.2020.9217265
Boban, M., Gong, X., and Xu, W. (2016). “Modeling the Evolution of Line-Of-Sight Blockage for V2v Channels,” in Proc. 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, September, 1–7. doi:10.1109/VTCFall.2016.7881090
Chavdarova, T., Baqué, P., Bouquet, S., Maksai, A., Jose, C., Bagautdinov, T., et al. (2018). “Wildtrack: A Multi-Camera Hd Dataset for Dense Unscripted Pedestrian Detection,” in Proc. of the IEEE Conference on Computer Vision and Pattern Recognition-Fall), Salt Lake City, UT, USA, June, 5030–5039.
[Dataset] Chen, M., Liu, Y., Shen, W., Shen, Y., Tang, P., and Yang, Q. (2020a). Mechanism Design for Multi-Party Machine Learning.
Chen, M., Yang, Z., Saad, W., Yin, C., Poor, H. V., and Cui, S. (2020b). A Joint Learning and Communications Framework for Federated Learning over Wireless Networks. IEEE Trans. Wireless Commun. 20 (1), 269-283. doi:10.1109/TWC.2020.3024629
Donevski, I., Babu, N., Nielsen, J. J., Popovski, P., and Saad, W. (2021a). Federated Learning with a Drone Orchestrator: Path Planning for Minimized Staleness. IEEE Open J. Commun. Soc. 2, 1000-1014. doi:10.1109/OJCOMS.2021.3072003
Donevski, I., and Nielsen, J. J. (2020). “Dynamic Standalone Drone-Mounted Small Cells,” in Proc. of European Conference on Networks and Communications, Dubrovnik, Croatia, June (Dubrovnik, Croatia: EuCNC), 342–347. doi:10.1109/EuCNC48522.2020.9200918
Donevski, I., Nielsen, J. J., and Popovski, P. (2021b). “Standalone Deployment of a Dynamic Drone Cell for Wireless Connectivity of Two Services,” in Proc. of IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, April (Nanjing, China: TBP).
Kang, J., Xiong, Z., Niyato, D., Xie, S., and Zhang, J. (2019a). Incentive Mechanism for Reliable Federated Learning: A Joint Optimization Approach to Combining Reputation and Contract Theory. IEEE Internet Things J. 6, 10700–10714. doi:10.1109/jiot.2019.2940820
Kang, J., Xiong, Z., Niyato, D., Yu, H., Liang, Y.-C., and Kim, D. I. (2019b). “Incentive Design for Efficient Federated Learning in mobile Networks: A Contract Theory Approach,” in Proc. of 2019 IEEE VTS Asia Pacific Wireless Communications Symposium, Singapore, August (Singapore: APWCS), 1–5. doi:10.1109/VTS-APWCS.2019.8851649
Khan, L. U., Pandey, S. R., Tran, N. H., Saad, W., Han, Z., Nguyen, M. N. H., et al. (2020). Federated Learning for Edge Networks: Resource Optimization and Incentive Mechanism. IEEE Commun. Mag. 58, 88–93. doi:10.1109/MCOM.001.1900649
Konečnỳ, J., McMahan, H. B., Yu, F. X., Richtárik, P., Suresh, A. T., and Bacon, D. (2016). Federated Learning: Strategies for Improving Communication Efficiency. arXiv preprint arXiv:1610.05492.
LeCun, Y., Jackel, L. D., Bottou, L., Cortes, C., Denker, J. S., Drucker, H., et al. (1995). Learning Algorithms for Classification: A Comparison on Handwritten Digit Recognition. Neural networks: Stat. Mech. perspective 261, 2.
Li, T., Sahu, A. K., Talwalkar, A., and Smith, V. (2020). Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal. Process. Mag. 37, 50–60. doi:10.1109/MSP.2020.2975749
Li, T., Sahu, A. K., Zaheer, M., Sanjabi, M., Talwalkar, A., and Smith, V. (2018). Federated Optimization in Heterogeneous Networks. arXiv preprint arXiv:1812.06127.
Li, T., Sanjabi, M., Beirami, A., and Smith, V. (2019). Fair Resource Allocation in Federated Learning. In Proc. of International Conference on Learning Representations, Addis Ababa, Ethiopia, April, 2020.
Lim, W. Y. B., Luong, N. C., Hoang, D. T., Jiao, Y., Liang, Y.-C., Yang, Q., et al. (2020). Federated Learning in mobile Edge Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutorials 22, 2031–2063. doi:10.1109/COMST.2020.2986024
Mohammad, U., Sorour, S., and Hefeida, M. (2020). Task Allocation for Asynchronous mobile Edge Learning with Delay and Energy Constraints. arXiv preprint arXiv:2012.00143.
Mohri, M., Sivek, G., and Suresh, A. T. (2019). Agnostic Federated Learning. arXiv preprint arXiv:1902.00146.
Mozaffari, M., Saad, W., Bennis, M., Nam, Y.-H., and Debbah, M. (2019). A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutorials 21, 2334–2360. doi:10.1109/COMST.2019.2902862
Nielsen, T. A. S., and Haustein, S. (2018). On Sceptics and Enthusiasts: What Are the Expectations towards Self-Driving Cars?. Transport policy 66, 49–55. doi:10.1016/j.tranpol.2018.03.004
Niknam, S., Dhillon, H. S., and Reed, J. H. (2020). Federated Learning for Wireless Communications: Motivation, Opportunities and Challenges.
Nishio, T., Shinkuma, R., and Mandayam, N. B. (2020). Estimation of Individual Device Contributions for Incentivizing Federated Learning. arXiv preprint arXiv:2009.09371.
Pandey, S. R., Tran, N. H., Bennis, M., Tun, Y. K., Manzoor, A., and Hong, C. S. (2020). A Crowdsourcing Framework for On-Device Federated Learning. IEEE Trans. Wireless Commun. 19, 3241–3256. doi:10.1109/TWC.2020.2971981
Popovski, P., Nielsen, J. J., Stefanovic, C., Carvalho, E. d., Strom, E., Trillingsgaard, K. F., et al. (2018). Wireless Access for Ultra-reliable Low-Latency Communication: Principles and Building Blocks. Ieee Netw. 32, 16–23. doi:10.1109/mnet.2018.1700258
SAE(2016). Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles. SAE Int., J3016. doi:10.4271/j3016_201609
Savazzi, S., Nicoli, M., Bennis, M., Kianoush, S., and Barbieri, L. (2021). Opportunities of Federated Learning in Connected, Cooperative and Automated Industrial Systems. arXiv preprint arXiv:2101.03367.
She, C., Liu, C., Quek, T. Q. S., Yang, C., and Li, Y. (2019). Ultra-reliable and Low-Latency Communications in Unmanned Aerial Vehicle Communication Systems. IEEE Trans. Commun. 67, 3768–3781. doi:10.1109/tcomm.2019.2896184
Shi, W., Zhou, H., Li, J., Xu, W., Zhang, N., and Shen, X. (2018). Drone Assisted Vehicular Networks: Architecture, Challenges and Opportunities. IEEE Netw. 32, 130–137. doi:10.1109/mnet.2017.1700206
Smith, V., Chiang, C.-K., Sanjabi, M., and Talwalkar, A. S. (2017). “Federated Multi-Task Learning,” in Proc. of Advances in neural information processing systems, 4424–4434.
Tran, N. H., Bao, W., Zomaya, A., Nguyen, M. N. H., and Hong, C. S. (2019). “Federated Learning over Wireless Networks: Optimization Model Design and Analysis,” in IEEE INFOCOM 2019 - IEEE Conference on Computer Communications, Paris, France, April, 1387–1395. doi:10.1109/INFOCOM.2019.8737464
Wang, Y., Su, Z., Zhang, N., and Benslimane, A. (2021). Learning in the Air: Secure Federated Learning for Uav-Assisted Crowdsensing. IEEE Trans. Netw. Sci. Eng., 1. doi:10.1109/TNSE.2020.3014385
Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-mnist: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv preprint arXiv:1708.07747.
Xie, C., Koyejo, S., and Gupta, I. (2019). Asynchronous Federated Optimization. arXiv preprint arXiv:1903.03934.
Yang, Q., Liu, Y., Chen, T., and Tong, Y. (2019). Federated Machine Learning. ACM Trans. Intell. Syst. Technol. 10, 1–19. doi:10.1145/3298981
Yang, Z., Chen, M., Wong, K.-K., Poor, H. V., and Cui, S. (2021). Federated Learning for 6g: Applications, Challenges, and Opportunities. arXiv preprint arXiv:2101.01338.
Yaqoob, I., Khan, L. U., Kazmi, S. A., Imran, M., Guizani, N., and Hong, C. S. (2019). Autonomous Driving Cars in Smart Cities: Recent Advances, Requirements, and Challenges. IEEE Netw. 34, 174–181.
Zeng, T., Semiari, O., Mozaffari, M., Chen, M., Saad, W., and Bennis, M. (2020). “Federated Learning in the Sky: Joint Power Allocation and Scheduling with UAV Swarms,” in Proc. of the IEEE International Conference on Communications (ICC), Next-Generation Networking and Internet Symposium, Dublin, Ireland, June, 1–6.
Keywords: federated learning, contribution, incentive, staleness, convergence, UAV, heterogeneous network, fedprox
Citation: Donevski I, Nielsen JJ and Popovski P (2021) On Addressing Heterogeneity in Federated Learning for Autonomous Vehicles Connected to a Drone Orchestrator. Front. Comms. Net. 2:709946. doi: 10.3389/frcmn.2021.709946
Received: 14 May 2021; Accepted: 22 June 2021;
Published: 12 July 2021.
Edited by:
Mingzhe Chen, Princeton University, United StatesReviewed by:
Jiawen Kang, Nanyang Technological University, SingaporeZhaohui Yang, King’s College London, United Kingdom
Copyright © 2021 Donevski, Nielsen and Popovski. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Igor Donevski, aWdvcmRvbmV2c2tpQGVzLmFhdS5kaw==
 Igor Donevski
Igor Donevski Jimmy Jessen Nielsen
Jimmy Jessen Nielsen Petar Popovski
Petar Popovski